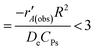Effect of synergy on selective low-temperature dehydrogenation of propane to propylene over a defect-induced copper titanium catalyst

Abstract

The TiO₂-supported Cu catalyst exhibits high activity in the dehydrogenation of propane at low temperatures, enabling the selective production of propylene over a prolonged period. The defect-induced Cu–TiO₂ catalyst provided a propylene yield of 10.4% with high selectivity (∼91.9%) even at 375 °C. Surface analysis shows that the defects on the TiO₂ surface are extrinsic and arise from doping with Cu entities. This enhanced metal–support synergy between Cu and TiO₂ passivates C–C bond breaking, which indirectly reduces methane formation. To understand the effect of different Cu planes on the adsorption of propane molecules for their activation and conversion, the DFT-optimized geometry and reaction coordinates were investigated. The DFT study revealed that the Cu–TiO₂ surface enhances C–H activation at lower temperatures while maintaining an encouraging propylene yield. Furthermore, the kinetic study suggests that adsorption is the rate-limiting step besides the surface reaction, and the activation energy for the propane dehydrogenation reaction is 50.04 kJ mol⁻¹.

---

Introduction

In the past decade, disruptive technology development and deployment have globally dominated the petrochemical industry. Driven by the extreme pricing dynamics of the energy industry, these technologies aim to utilize low-cost and locally abundant feedstocks.¹ Propylene is an important industrial chemical used as a feedstock in producing polypropylene, propylene oxide, glycerine, acrolein, isopropanol, and other critical industrial chemicals. Due to the increasing production of propane from shale and natural gas, propylene production through propane dehydrogenation is an essential industrial process because propylene is economically more important than propane. The current commercial technologies licensed for propane dehydrogenation (C₃H₈ ⇌ C₃H₆ + H₂) are thermodynamically limited and highly endothermic, which means high temperatures are typically required (>550 °C).^1–3 Unfortunately, these high reaction temperatures also favor C–C bond breaking, lowering propylene selectivity and favoring coke formation over the catalyst surface.⁴ The commercial catalyst comprises CrO_x (Catofin®), or Pt–Sn (Oleflex) supported on acidic Al₂O₃, both of which are known for high propylene selectivity and long lifetimes.⁵ However, the environmental toxicity of Cr⁶⁺ species and the high cost of noble Pt have driven the development of alternative catalysts to replace them shortly. Given the fast kinetics of non-oxidative dehydrogenation of propane, achieving conversion with a single-metal catalyst is difficult. However, it is often observed that the product mixture does not follow the predicted equilibrium composition. Therefore, various combinations of metals have been used by researchers to improve product yield, achieving good conversion of propane. Despite all the efforts to find a next-gen PDH catalyst, platinum remains the best choice as a primary catalyst in combination with promoter metals like Sn, Ga, Co, Al, Zr, Mo, etc.^2,5 Considering the rarity and cost of platinum group metals (PGMs), we always aimed to find a suitable non-Pt catalyst for the PDH reaction, achieving a yield and conversion comparable to those of Pt-based catalysts. On the other hand, supports play an important role in product distribution for an identical active metal.⁶ Al₂O₃ is the most commonly used support for heterogeneous catalysts, although the role of alumina as a support is not free of drawbacks. For instance, due to its excess surface acidity, Al₂O₃ can catalyze cracking and coking, resulting in a drop in both activity and selectivity.⁷ Meanwhile, such metal–O-support sites are expected to provide an appropriate barrier for C–H activation and facilitate propylene desorption to prevent coke formation.⁸ Alternatively, lowering the reaction temperature (generally, a commercial PDH unit runs at a temperature between 550 and 640 °C) could result in a considerable propylene yield that automatically reduces coke formation.¹ Inspired by the above and, in retrospect, catalysts like Pt–Sn and CrO_x over Al₂O₃, we prepared Sn-, Pt-, and Cu-promoted Al₂O₃, MnO₂, ZrO₂, and TiO₂ catalysts for the low-temperature dehydrogenation of propane. So far, Cu-doped catalysts have garnered interest because of their appealing ability to activate alkane molecules.⁹ Besides alkane activation, Cu-doped catalysts have also shown a wide range of reactions, including the removal of NO_x from automobile exhaust, hydrogenation of CO/CO₂, photo/electro-catalysis, and the oxygen reduction reaction.¹⁰ Despite their diversified application, Cu-doped catalysts are rarely reported for propane dehydrogenation. In contrast, metal oxides with identical chemical composition and different crystal phases are known to influence catalytic performance.^11,12 Likewise, diverse TiO₂ crystal phase compositions significantly impact both the activity and product selectivity.^13,14 In this work, we have adopted an exciting synthesis strategy to prepare a Cu doped catalyst on different crystal phases of mesoporous titania. This mesoporous Cu/TiO₂ catalyst was found to activate propane's C–H bond at a low temperature and shows excellent thermal stability. To illuminate the origins of such exciting outcomes, a DFT study has been undertaken to analyze the activation barrier of the absorbed propane molecule in different phases of TiO₂ with a fair comparison to the Pt–TiO₂ catalyst.

Experimental

Chemicals required

Titanium(IV) butoxide (TBOT), ethanol, copper chloride, etc., were procured from Merck KGaA, Darmstadt, Germany. Deionized water was prepared in Borosil glass using a double distillation unit and used for the synthesis. All chemicals were used as received, without further purification.

Catalyst preparation

We used titanium oxide as a support and copper as a reducing agent. In a typical process, 20 ml of TBOT in 50 ml of ethanol was taken, and 100 ml of a colloidal solution containing 0.13 g copper chloride was slowly added to it at 40 °C under vigorous stirring. This solution was stirred continuously for 24 h at 60 °C. Then, the temperature was raised to 80 °C to form a slurry-type mixture which eventually dried. The obtained powder was dried at 100 °C for 12 h and calcined at 450 °C for 4 h.

Characterisation techniques

The structures and crystalline phases of the samples were confirmed by powder X-ray diffraction (XRD) patterns using a Rigaku SmartLab X-ray powder diffractometer using a monochromatic Cu Kα radiation source (λ = 0.1542 nm). Diffraction patterns were recorded at room temperature over a 2θ angular range of 10 to 80° and an angle step rate of 0.02°. The surface morphology and microstructures of the samples were characterized by FESEM (FEI Quanta 200 FEG). Furthermore, a JEOL (JEM 2100) high-resolution transmission electron microscope with 200 kV accelerating voltage was used to investigate the particles' nanoscale morphology and internal structures. All the powder samples were ultrasonically dispersed in ethanol for 20 min to make a suspension solution. One droplet of the suspension was then deposited onto a lacey carbon Formvar-coated Cu grid for the TEM study. Morphologies of the samples and EDS mapping were collected using a JEOL/MP instrument (JSM-IT300). In addition, the bonding interactions and chemical states of elements in the synthesized samples were examined by X-ray photoelectron spectroscopy (XPS). XPS analyses were recorded using a Thermo Scientific Corp, K-alpha instrument equipped with a monochromatized X-ray Mg Kα radiation source. The binding energies of all spectra were determined utilising a reference against the C 1s peak at 284.8 eV. N₂ adsorption–desorption isotherms of the samples were measured at −196 °C employing an ASAP 2020 plus, USA chemisorption instrument. The specific surface area was determined using the Brunauer–Emmett–Teller (BET) method, and the pore volume was determined from the N₂ adsorption isotherm at a relative pressure of 0.99. The pore size distribution of the samples was calculated from the desorption branch of the isotherm according to the Barrett–Joyner–Halenda (BJH) method. All the samples were degassed at 120 °C under vacuum for 6 h before the measurement to remove adsorbed water. To estimate the functional groups in the synthesized samples, Fourier transform infrared (FTIR) spectroscopy was performed using a Nicolet spectrometer 8700 (USA) at room temperature in the wavenumber range from 400 to 4000 cm⁻¹ using the KBr pellet technique. A H₂-temperature programmed reduction (H₂-TPR) experiment was performed to measure the reducibility of the prepared samples using a Micromeritics, AutoChem HP 2950 chemisorption analyser connected to a thermal conductivity detector (TCD). Before the H₂-TPR experiment, the sample was pretreated under flowing helium and heated at 650 °C for 2 h. After the pretreatment, it was cooled to room temperature and then placed in 10% H₂ in Ar gas mixture with a total flow rate of 40 ml min⁻¹ in the temperature range from room temperature to 550 °C via a ramp of 10 °C min⁻¹. A TCD was used for analysing the amount of hydrogen consumption. Thermogravimetric (TG) analysis of dry powder samples was carried out on an EXSTAR TG/DTA 6300 instrument. The experiment was conducted under a nitrogen atmosphere at a flow rate of 200 mL min⁻¹, and the temperature was started from room temperature to 1000 °C at a heating rate of 10 °C min⁻¹.

Catalyst performance test

The propane dehydrogenation reaction was carried out in a downflow, continuous, fixed-bed reactor (ID: 8 mm). The reaction temperature was maintained between 325 and 400 °C under atmospheric pressure with a GHSV (gas hourly-space velocity) of 4000–8000 h⁻¹. Nitrogen and propane (feed) were supplied through mass flow controllers (MFCs) into a pre-mixture unit, and the ratio of N₂/C₃H₈ was also varied from 2 to 6 during the study. Before the reaction, 0.25 g of catalyst was heated to 100 °C to remove moisture. After placing the catalyst in the quartz reactor, the reaction temperature was ramped at 3.75 °C min⁻¹ till 325–400 °C in N₂ flow of 20 ml min⁻¹ and kept at this temperature for 1 h to stabilise. Finally, after the reaction, the reactor was cooled to room temperature, and the spent catalysts were recovered for further analysis.

The reaction was carried out at two different times-on-steam; one was 5 h, assuming reaction equilibrium had been established. The catalytic stability was assessed by conducting a prolonged reaction for up to 24 h. The catalysts were regenerated using O₂-balance N₂ to remove the deposited coke from the catalyst surface. The product was analyzed using an RGA (Agilent Technologies 7890B) equipped with a TCD and FID. The conversion, selectivity, and yield were calculated using the formulae given below.

DFT method

The periodic plane-wave-based density functional theory (DFT) method as implemented in the Vienna ab initio simulation package (VASP)¹⁵ was used to study the activity and stability trends of the Cu/TiO₂ catalyst. The Cu/TiO₂ catalyst was modeled using the Cu(111) surface, with a 4 × 4 unit cell and a four-layer surface slab. The Cu(111) surface is the most stable for DFT calculation, and considering the limitation of the server, we took the Cu(111) surface for calculation. The PBE¹⁶ exchange correlation was used along with the PAW pseudopotentials.^17,18 For geometry optimization calculations, energy and force convergence criteria of 10⁻⁶ eV and 0.05 eV Å⁻¹ were used, respectively. The energy and geometry of the transition states (TS) were obtained using the climbing nudged elastic band (CI-NEB) method,¹⁹ where 15 images were used between the initial and final states. For TS calculations, energy and force converge criteria of 10⁻⁶ eV and 0.1 eV Å⁻¹ were used, respectively. For all the DFT calculations, k-point sampling of 3 × 3 × 1 was used.

The activation barriers (E_a) were calculated as the energy difference between the transition state and initial state following the equation,

E_a = E_TS − E_IS

The reaction energies (E_r) were calculated as the energy difference between the final state and initial state, following the equation,

E_r = E_FS − E_IS

Characterization results for fresh and spent catalysts

Fig. 1 shows the diffractograms of both samples confirming the anatase phase of TiO₂ according to JCPDS card no. 21-1272. No additional peaks for Cu-species were detected in the XRD pattern except for anatase TiO₂ in Cu–TiO₂ samples. This observation may suggest that doped Cu is highly dispersed on TiO₂ because it has a low concentration. Alternatively, Cu species have a negligible effect on the crystalline phases of TiO₂. The spent Cu–TiO₂ catalyst was also found to have an identical XRD pattern, implicating no change in crystal structure even after 5 h of time-on-steam. This observation might be due to lower reaction temperature (ΔT = 100–290 °C), causing a significant reduction of coking and phase sintering.²⁰

Fig. 1 (a) XRD and (b) Raman spectra for fresh and spent Cu–TiO₂ catalysts.

The SEM images of fresh and spent Cu–TiO₂ catalysts show a lump-like morphology (Fig. S1 and S2†). Upon closer examination, these lumps appear to have an almost spherical shape (some irregularity exists). No noticeable difference was observed in the surface morphology of the spent catalyst. The purity of the catalyst was also confirmed by SEM-EDS analysis, and the spectrum indicated that the catalysts consist of Cu, Ti, O and C. The distribution of the elements was homogeneous, as further confirmed by SEM–EDX imaging and mapping, as shown in Fig. S1 and S2.† Further, the distribution and size of Cu nanoparticles over the TiO₂ layer were confirmed using HR-TEM. Fig. 2a and b are the TEM and HR-TEM images with the SAED pattern of bare TiO₂, and as seen from the TEM images (Fig. 2c and e), very small and well-dispersed Cu species were anchored tightly onto the surface of TiO₂. The estimated particle sizes are in the range of 11 ± 1.5 nm (Fig. S3†). In the spent catalyst recovered after 5 h of time on steam, the particle sizes were found to remain almost unaffected (Fig. S3†). The HR-TEM images of fresh and spent catalysts (Fig. 2d and f) show lattice fringes with an interplanar distance similar to that of the lattice plane of anatase TiO₂. This data is consistent with the results of XRD. Furthermore, the SAED pattern confirms the crystalline nature of the materials, where the polycrystallinity increases in the case of the spent catalyst. This increase may be due to shape-tailored agglomeration or interconversion among the three crystal phases (rutile, anatase and brookite) of TiO₂, which leads to a change in the catalyst composition.²¹ Further, the HR-TEM images of the prepared TiO₂ exhibit several cracks (Fig. S4†) in the nanostructure, resulting in active sites due to defect additions. In contrast, the Cu–TiO₂ catalysts show voids in the respective fringes at multiple locations. These voids, observable as gaps (Fig. S4†) in the crystal lattice structure through TEM, manifest as discontinuities or interruptions in the periodic lattice fringes and represent defect sites within the Cu–TiO₂ nanostructures. The TEM-EDS imaging and elemental mapping further confirmed the composition and homogeneous distribution of Cu on the TiO₂ surface in the fresh and spent catalysts (Fig. S5–S7†).

Fig. 2 TEM and HRTEM with the SAED patterns of (a and b) TiO₂, (c and d) fresh and (e and f) spent Cu–TiO₂ catalysts.

The N₂ adsorption–desorption isotherms were obtained and shown in Fig. S8(a and c).† The plot of both samples exhibits a type IV isotherm with a classical hysteresis loop between the adsorption and desorption curves, indicating a mesoporous structure, as demonstrated by their pore-size distribution patterns in Fig. S8(b and d).† The pore-size distribution pattern suggests the presence of ≤10 nm pores in the fresh catalyst, which remains almost the same (Fig. S8(b and d)†) for the spent catalyst. Table 1 shows the BET surface area, pore size, and pore volume of the fresh and spent Cu–TiO₂ catalysts. Accordingly, the specific surface area (S_BET) of fresh Cu doped TiO₂ is 79.97 m² g⁻¹, while for the spent catalyst, it was slightly lower, 70.11 m² g⁻¹.

Table 1 The textural properties of Cu promoted TiO₂ catalysts

Catalyst	SBET (m^2 g^−1)	Pore size (nm)	Pore volume (cm^3 g^−1)	H2 uptake (cm^3 g^−1, STP)
a Spent catalyst recovered after 5 h of time-on-steam.
Cu–TiO2	79.97	11.02	0.25	0.612
Cu–TiO2^a	70.11	12.28	0.26	—

---

The broad FTIR band (Fig. S9†) centered at 500–600 cm⁻¹ is assigned to the bending vibration (Ti–O–Ti) bonds in the TiO₂ lattice. The vibration band at 1747 cm⁻¹ can be associated with the asymmetric stretching mode of titanium carboxylate. The peaks between 2924 cm⁻¹ and 2843 cm⁻¹ are assigned to C–H stretching vibrations of alkane groups. The alkane and carboxylate groups come from titanium tetra isopropoxide and 2-propanol, which were used in the synthesis process.²² The broad peak in the 3000–3500 cm⁻¹ range corresponds to the OH groups of adsorbed water molecules on the TiO₂ surface, indicating strong hydrophilicity of the material. Further, the FTIR spectra of both fresh and spent catalysts are almost similar, confirming the catalyst's stability.

The Raman spectrum (Fig. 1b) shows sharp bands at 144, 194, 397, 517, 513, and 639 cm⁻¹ representing anatase TiO₂. The peak located at 639 cm⁻¹ (E_g) is assigned to the Ti–O stretching mode, the peak at 517 cm⁻¹ (A_1g + B_1g) refers to the Ti–O stretching mode, and the peak appearing at 397 cm⁻¹ (E_g) is assigned to the O–Ti–O bending mode.²³ No traces of the Raman band for the rutile or brookite phase confirm the purity of TiO₂. In the spent catalyst, two additional peaks refer to the carbon D and G bands, which are spotted at 1355 and 1623 cm⁻¹, respectively. The G band confirms the in-plane stretching between sp² carbons, whereas the D band represents the disordered sp² carbons originating from structural defects, edge effects, and dangling bonds that break the symmetry.²⁴ This confirms the deposition of coke during the dehydrogenation reaction, the rate of which has been calculated using TGA and found to be 6.6 × 10⁻³ mg h⁻¹. Furthermore, the fresh catalyst (Fig. S10a†) experiences a weight loss (ca. 1.3%) till 800 °C, corresponding to the formation and reorganization of the rutile phase crystalline structure. The spent catalyst, after the 5 h TOS, undergoes a weight loss of ∼2.6% (in N₂) and ∼3.6% (in air); therefore, the difference, i.e., 1%, may be attributed to the amount of carbon deposited during the PDH reaction. Further, a comparison between Cu–TiO₂ and Pt–TiO₂ catalysts for coke deposition (Fig. S10b†) after 24 h TOS shows that Cu–TiO₂ and Pt–TiO₂ catalysts experience a weight loss of ∼5% and ∼9%, respectively, up to 700 °C in a nitrogen atmosphere. From TGA and Raman, it can be concluded that most of the coke is graphitic, with an I_G/I_D ratio of 1.02.

The XP spectrum of Ti 2p in Fig. S11a† shows two main peaks for Ti 2p_3/2 and Ti 2p_1/2, centered at 458.3 and 464.4 eV, respectively, which are attributed to the typical Ti⁴⁺ oxidation state in titania.²⁵ The slight shift toward lower binding energies, compared to the standard data for the pure TiO₂, indicates the presence of lattice defects in the material. These defects arise after the doping of Cu into the mesoporous TiO₂ lattice. It is known that intrinsic defects strongly depend on the synthesis method and the subsequent treatments of the material, while extrinsic defects can arise with appropriate doping.²⁶ This means that the defects on the TiO₂ surface are extrinsic and arise due to the doping of Cu entities. The Cu 2p spectrum (Fig. S11b†) shows the co-existence of Cu²⁺ and Cu⁺ as indicated by two major peaks at 932.8 eV and 953.3 eV, attributed to Cu 2p_3/2 and Cu 2p_1/2, respectively.^27,28 The additional satellite peaks confirm the presence of CuO and therefore, Cu²⁺ species. The splitting energy of 20.5 eV indicated the formation of Cu²⁺. Furthermore, the deconvoluted peak at 932.5 eV in the orbital Cu 2p_3/2 position could be assigned to Cu⁰ or Cu⁺ because the range of the BE for Cu⁰ and Cu⁺ overlaps. For C 1s, the main peak at BE 284.7 eV corresponds to –C–C_sp3 carbon on the catalyst surface. The small shoulder peaks at BE 286.3 and 289.0 eV suggest the formation of C–O and –C=O bonds, respectively. The spent catalyst shows an increment of peak intensity, suggesting the deposition of coke during the reaction. The O 1s spectrum (Fig. S11d†) exhibits two peaks, one at 529.5 and the shoulder peak is attributed to 531.4 eV. The peak at 529.5 eV confirms the formation of the metal–oxygen bond, and the shoulder peak was attributed to the hydroxyl groups or water adsorbed on TiO₂ surfaces. Fig. S9b† shows the reduction pattern Cu–TiO₂ exhibiting two reduction peaks at 169 °C and 257 °C, where the reduction process was completed before 550 °C. Such complete reduction at lower temperatures suggests a very narrow particle size distribution of the Cu-oxide and Ti-oxide crystallites between 60 and 220 nm (as shown in the histogram in Fig. S3†).

Further, the first reduction peak at T_max-171 °C could be assigned to the reduction of CuO to Cu₂O to metallic copper, respectively.²⁷ The existence of these peaks in catalysts is due to CuO present with the support in two different chemical compositions. The first is due to small CuO particles, which were highly dispersed on the TiO₂ support and reduced at comparatively lower temperatures, and the second was described by large size Cu particles, which were reduced at higher temperatures. The higher reduction temperature indicates the presence of slightly larger CuO crystallites.

Results and discussion

First, a steady-state (3 h) was reached with a gas hourly space velocity (GHSV) of 6000 h⁻¹ at 350 °C with 20% propane, balanced with N₂. The study was then expanded to include Pt and Cu as active metals over alumina, MnO₂, ZrO₂, and TiO₂ as supports. The results from Table S1† show that the propane conversion and the formation rate of propylene were the highest for Pt-TiO₂ and the lowest for Cu–MnO₂. It has been found that catalysts using ZrO₂ and MnO₂ as supports are susceptible to methane formation via thermo-catalytic cracking. Consequently, Pt on MnO₂ exhibited 10.3% methane formation, the highest among the various catalyst combinations studied, while Cu–TiO₂ exhibited the lowest methane content (0.8%) in the product stream. In addition, an enhanced metal–support synergy between Cu and TiO₂, which induces defects in TiO₂, passivates C–C bond breaking. This results in relatively less formation of C₁–C₂ hydrocarbons than the other supported metal combinations used in Table S1.† Furthermore, Cu, in combination with TiO₂, showed significant activity by showing an intriguing C₃ yield compared to Pt–TiO₂ and other Cu-based catalysts. From this, it can be concluded that the synergistic combination of Cu and TiO₂ is the best catalyst for the selective conversion of propane at low temperatures. The DFT study (discussed later) revealed that the Cu–TiO₂ surface enhanced –C–H activation at lower temperatures while maintaining an encouraging propylene yield. Overall, it is evident that while Pt-based catalysts efficiently stimulate the C–H bond of propane, Cu-based catalysts are equally effective and selective for propylene, resulting in higher cost efficiencies.

It was observed that varying the gas hourly space velocity from 4000 h⁻¹ to 8000 h⁻¹ the propylene selectivity remained fairly the same, whereas the propane conversion significantly decreased (Fig. 3a). This is due to the increase in GHSV, which means more reactant molecules are passing through the catalyst per unit time. This leads to lower conversion because the residence time of reactants on the catalyst surface decreases. In other words, reactants spend less time interacting with the catalyst, resulting in reduced conversion. Interestingly, at 4000 h⁻¹ GHSV, 7.31% propane conversion with 94.96% propylene selectivity was achieved over the Cu–TiO₂ catalyst. The propane conversion increases with the N₂/propane ratio (Fig. 3b), and at a N₂/propane ratio of 6, the conversion was 8.39%. At the same time, a higher selectivity for propylene was favored at the higher N₂/propane ratio, although the selectivity was not affected significantly by the change in N₂/propane ratio. When the sum of stoichiometric coefficients for all reactants is positive (i.e., more moles of products are formed), adding an inert gas increases the conversion at a fixed total pressure. But in this case, the presence of inert gas helps shift the equilibrium toward product formation. Therefore, if the reaction produces more moles of products than reactants, adding nitrogen (the inert gas) will enhance the conversion of propane to propene and hydrogen. Furthermore, the effect of reaction temperature was studied at 4000 h⁻¹ with a 6 : 1 ratio of N₂/propane. The dehydrogenation of propane is strongly endothermic (∼111 kJ mol⁻¹), equilibrium-limited, and undergoes fast kinetics.²⁹ The theoretical equilibrium conversion calculated at 600 °C under 1 atm is 54.6%.³⁰ However, at such a high reaction temperature, side reactions, particularly cracking of propane or propylene, occur along with the dehydrogenation reaction. Cracking forms lower hydrocarbons, like methane, ethane, and ethylene, along with coke formation. Therefore, to limit the side reaction, lower reaction conditions are always preferred but not compromising the yield of propylene. In line with this, we checked the Cu–TiO₂ catalyst at a reaction temperature between 325 and 400 °C and closely studied the selectivity and yield of propylene. Fig. 3c shows that the activity is proportional to temperature, whereas the selectivity/yield was optimum at temperatures around 350–400 °C. The selectivity for propylene reaches a maximum of 96.6% at 350 °C, while the yield of propylene reaches the highest of 11.2% at 400 °C. Subsequently, higher temperature leads to thermal cracking of propane with heavy coke deposition, causing the deactivation of the working catalyst. This led us to conclude that 375 °C is the optimum temperature for the catalytic dehydrogenation of propane (Fig. 3c).

Fig. 3 Effect of GHSV (a), effect of N₂/C₃H₈ (b) and effect of temperature on the conversion of C₃H₈ and selectivity for C₃H₆ during propane dehydrogenation (c). Reaction conditions: Wt of catalyst–0.25 g (pelletised); reaction temperature, 350 °C (for a and b); GHSV–4000 h^{− 1} (for b and c).

The Cu–TiO₂ catalyst was tested in the reaction for an extended period to check for the loss of its activity and compare it with the Pt–TiO₂ catalyst. Cu–TiO₂ exhibits a decline in both conversion and selectivity over time, as shown in Fig. 4a. From 3 hours to 24 hours, the conversion decreases from 11.89% to 7.57%, while the selectivity declines from 92.62% to 79.12%. Similarly, for the Pt–TiO₂ catalyst, the conversion drops from 14.12% to 10.05%, and the selectivity decreases from 81.79% to 67.15% over the same period (Fig. S12†). Although the Cu–TiO₂ catalyst showed high activity and selectivity for propylene during 24 h of time-on-steam, a slight decrease in conversion and selectivity was noticed every three hours.

Fig. 4 (a) TOS and (b) regeneration cycles over the Cu–TiO₂ catalyst in terms of propane conversion, propylene selectivity, and propylene yield. Reaction conditions: Wt of catalyst–0.25 g (pelletized); reaction temperature, 375 °C; GHSV–4000 h^{− 1}.

The reaction reached a steady state after around 3 h and mass transport calculations (see the ESI†) were performed for the highest rates in the packed bed reactor (PBR). The Weisz–Prater criterion,

gave 6.418 × 10⁻¹⁴, indicating that there is no internal diffusion limitation across the working catalyst. Meanwhile, the Mears criterion
resulted in 2.17 × 10⁻¹⁷ < 3, indicating that there are no constraints on heat transfer or mass transport between inter-phases and intra-particles.^1,31 The reaction kinetics for C₃H₈ dehydrogenation were determined without mass-transport and heat-transfer constraints, and the reaction rate for different concentrations was analyzed using linear regression (detailed below and in the ESI†).

The decrease in selectivity can be explained by an increase in methane concentration with time. It seems that the rate of cracking increases with time, which could be due to the blockage of active sites by coke deposition (as indicated by TGA and Raman spectroscopy). However the catalyst has exceptional stability (activity and selectivity loss is <1%) up to 6 h, compared to commercial processes like CATOFIN, where the cycle time is only 15–30 minutes. On the other hand, C₃ Oleflex comprises a CCR unit. Based on the data, a reaction–regeneration cycle was conducted every 6 h. Likewise, the Cu/TiO₂ catalyst was regenerated after each cycle using 20% O₂ balanced N₂ at 550 °C for 2 h. The results in Fig. 4b show a significant influence of the reaction–regeneration cycles on the stability of the catalyst without any considerable impact on the composition of the gaseous product. It was observed that the propane conversion remained steady at around 10%. However, the selectivity and yield showed a slightly decreasing trend (∼1–2.5%) with subsequent cycles. The propylene yield displayed an increment in the initial cycle but depreciated in the following cycles.

Kinetics study

The reaction kinetics over the Cu–TiO₂ catalyst was determined as a function of temperature and propane partial pressure. The mass (catalyst)-based reaction rates in the kinetic measurements −r_C3H8 were calculated from the conversion versus residence time data as follows:

The rate of propane consumption can be expressed as:

where the negative sign shows that propane is consumed.

−r_C3H8 = rate of propane consumption in μmol g⁻¹.

X_C3H8 = fractional conversion of propane.

F_C3H8 = flow rate of propane in ml h⁻¹ changed to μmol s⁻¹.

W_cat = weight of catalyst in g.

The consumption rates of C₃H₈ were obtained from intrinsic kinetic data in the initial rate region using the differential method of data analysis, which can obtain a wide range by varying the ratio of . In the kinetic tests, a series of experiments were carried out at different initial reactant concentrations, and the initial rates were calculated by differentiating the data and extrapolating them to zero time. Further, the effect of temperature on the reaction rates and product formation over Cu–TiO₂ was investigated at relatively low temperatures of 350–400 °C using appropriate W : F ratios to obtain low conversions (<20%). Experimental data was collected after 5 h to ensure that a steady state was reached and stable performance was achieved.

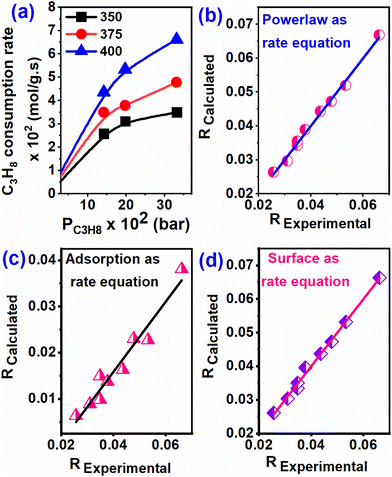
The rates of C₃H₈ consumption are shown in Fig. 5a as functions of C₃H₈ partial pressure and temperature. At all three temperatures (350, 375, and 400 °C), the rates of C₃H₈ dehydrogenation increase monotonically with the C₃H₈ partial pressure but tend to become independent of C₃H₈ partial pressure at lower temperatures. Different rate equations (see the ESI†) e.g. adsorption, surface reaction, and desorption, were considered as elementary reaction steps, neglecting diffusion processes. The rate of propane consumption, calculated (R_calculated) from all elementary steps, was evaluated in terms of the observed rate (R_observed) and presented in Fig. 5(b–d). From the graph (from the regression value), it is evident that the adsorption reaction is the rate-limiting step and is the best-fit mechanism for the dehydrogenation of propane. Furthermore, since it is a heterogeneous reaction, the adsorption reaction limiting model is superior to the surface reaction step and is also considered a rate-determining step. The activation energy was calculated for propane dehydrogenation over the Cu–TiO₂ catalyst between 350 and 400 °C. The Arrhenius equation was plotted against the dataset calculated for the preliminary reaction steps, which were considered to be the rate-determining steps described in the ESI.† Table S3† shows the E_a value for the elementary reactions. From these three equations, the adsorption rate-limiting step emerges from the diagram fitted to the experimental data. Therefore, using the Arrhenius equation of the surface reaction as the rate-limiting step, the activation energy for the propane dehydrogenation reaction was found to be 50.04 kJ mol⁻¹.

Fig. 5 (a) Dependence of the rates of C₃H₈ consumption over Cu–TiO₂ measured at 350, 375, and 400 °C on the C₃H₈ partial pressure. (b–d) Plot of Rcalculated vs. Robserved of the data taken between 350 and 400 °C.

DFT study of propane dehydrogenation

In accordance with the fundamental reaction steps and surface mechanism (in the ESI†) taken into consideration for DFT, Fig. S13(a)† shows that the propane molecule adsorbs physically at the Cu(111) surface of defect-induced TiO₂. In the first dehydrogenation step, the C–H bond was dissociated from CH₃CH₂CH₂, and H adsorbed at the surface as shown in Fig. S13(c).† During the C–H bond dissociation at the TS (Fig. S13(b)†), the C–H bond increases from 1.1 Å to 2.1 Å, whereas in the final state, the C–H bond dissociates (C–H bond distance 3.3 Å, Fig. S13(c)†).

The activation barrier for the first C–H bond dissociation was calculated to be 2.08 eV, as shown in Fig. 6(a and b). Additionally, the dissociation of the first C–H bond was calculated to be endothermic, with an energy change of 0.82 eV (Fig. 6(a–c)). In the second dehydrogenation step, the CH₃CH₂CH₂ intermediate was dehydrogenated to form the desired product, propylene, as has been shown in Fig. 6(d–f). In the TS of the second dehydrogenation step, the C–H bond was elongated from 1.1 Å in the CH₃CH₂CH₂ intermediate (Fig. S13(d)† to 1.8 Å in the TS (Fig. S13(e)†). The activation barrier for the second dehydrogenation step was calculated to be 1.19 eV, as has been shown in Fig. 6(c and d). In the final state, the product propylene (CH₃CHCH₂) was formed as shown in Fig. S13 (f). The second C–H bond dissociation was calculated to be slightly endothermic by 0.06 eV (Fig. 6(c–e)).

Fig. 6 Energy diagram from propane dehydrogenation to propylene (black colour), propylene dehydrogenation (red colour) and C–C bond cleavage of the CH₃CH₂CH₂ intermediate (blue colour).

The undesired products in this reaction are coke and light hydrocarbons e.g., CH₄ and CHCH. Further dehydrogenation of propylene produces CH₃CHCH, which can act as a coke precursor. The dehydrogenation of propylene has been shown in Fig. 7(a–c). In the TS of propylene dehydrogenation, the C–H bond elongates from an initial 1.1 Å (Fig. 7(a)) to 1.8 Å (Fig. 7(b)). In the final state, the C–H bond was completely dissociated to give the coke precursor CH₃CHCH, as can be seen in Fig. 7(c). The activation barrier for the propylene dehydrogenation step was calculated to be 1.53 eV, as has been shown in Fig. 6(e and f). The dehydrogenation of propylene was also calculated to be endothermic by 0.62 eV (Fig. 6(e–g)). The C–C bond cleavage during the propane dehydrogenation can produce light hydrocarbons such as CH₄ and CH₂CH₂. To study the propensity of light alkane formation, the C–C bond cleavage of the CH₃CH₂CH₂ intermediate was studied, as shown in Fig. 7(d–f). During C–C bond cleavage, the C–C bond in CH₃CH₂CH₂ (1.5 Å, Fig. 7(d)) elongates to 2.1 Å in the TS (Fig. 7(e)). The C–C bond is finally dissociated to form CH₃CH₂, and CH₂ is adsorbed onto the Cu(111) surface, as shown in Fig. 7(f). The activation barrier for the C–C bond dissociation was calculated to be high at 2.36 eV, and the reaction was found to be endothermic by 1.42 eV, indicating a lower probability of light alkane formation over Cu catalysts.

Fig. 7 DFT optimized geometry for adsorbates and TS during (a–c) propylene dehydrogenation and (d–f) C–C bond cleavage of the adsorbed CH₃CH₂CH₂ intermediate.

Conclusions

The current findings have shown a better product yield of propylene reported till date, even at a low temperature over a Cu–TiO₂ catalyst. The XP spectra revealed lattice defects in the support TiO₂, which were induced after the doping of Cu into the mesoporous TiO₂ lattice. A successive enhancement in metal–support synergy between Cu and TiO₂ was also evidenced, which results in dissociative adsorption over the Cu (111) plane. Both factors contribute to the low-temperature activation of propane, and an astounding propane conversion of 11.4% with a propylene selectivity of 91.9% was observed at 375 °C. Further, the nano-size particles provide large exposed active centres to activate the –C–H bond. This helps to overcome the activation barrier, which is calculated to be 2.08 eV for the 1st C–H bond dissociation, as calculated using the VASP. From the kinetic study, the adsorption model was found to be superior to the surface reaction step, and both are considered rate-determining steps. The activation energy for the propane dehydrogenation reaction is found to be 50.04 kJ mol⁻¹ as per the surface reaction as a rate-limiting step.

In particular, the use of Cu–TiO₂ catalysts to convert propane to propylene, especially at low temperatures, is among the best reports in the literature. Given the rarity and cost of platinum group metals (PGM), we hope that this finding will help develop a low-cost alkane dehydrogenation catalyst for polymer-grade propylene production in the future petrochemical complex worldwide.

Data availability

The authors verify the data supporting the manuscript's conclusions, which can be found in the article and its ESI.† The corresponding author will provide the raw data supporting the study's conclusions upon a reasonable request. Further, the following database has been used to analyse the physical & chemical characterisation data obtained from XPS, XRD and DFT.

(1) JCPDS card (2002, database)

(2) Handbook of X-ray Photoelectron Spectroscopy (published by Perkin-Elmer Corporation, Physical Electronics Division, 6509 Flying Cloud Drive, Eden Prairie, Minnesota 55 344, USA)

(3) Vienna ab initio simulation package (VASP)

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work was supported by the Science and Engineering Research Board (SERB), New Delhi, under the Core Research Grant (CRG), Award No. CRG/2022/008036 (GAP-0141). H. R. thanks the University Grants Commission (UGC), India, for financial support in the form of an SRF. AcSIR and CSIR-IIP are particularly acknowledged for providing all facilities and registration of postgraduate students. The authors thank Dr. Rajaram Bal for his support. The Analytical Sciences Division of CSIR-Indian Institute of Petroleum is particularly known for its analytical services.

References

1. R. Goyal, O. Singh, A. Agrawal, C. Samanta and B. Sarkar, Advantages and limitations of catalytic oxidation with hydrogen peroxide: from bulk chemicals to lab scale process, Catal. Rev.:Sci. Eng., 2022, 64, 229–285.
2. A. Agrawal, O. Singh, A. Kumar Yadav, S. Tripathi, A. Ray, V. Pawar and B. Sarkar, Low-Temperature Nonoxidative Dehydrogenation of Propane over Sn-promoted Mo-Y Zeolite: Catalytic performance and nature of the active sites, Fuel, 2022, 323, 124350.
3. M.-L. Sun, Z.-P. Hu, H.-Y. Wang, Y.-J. Suo and Z.-Y. Yuan, Design Strategies of Stable Catalysts for Propane Dehydrogenation to Propylene, ACS Catal., 2023, 13, 4719–4741.
4. J. J. H. B. Sattler, J. Ruiz-Martinez, E. Santillan-Jimenez and B. M. Weckhuysen, Catalytic Dehydrogenation of Light Alkanes on Metals and Metal Oxides, Chem. Rev., 2014, 114, 10613–10653.
5. C. Li and G. Wang, Dehydrogenation of light alkanes to mono-olefins, Chem. Soc. Rev., 2021, 50(7), 4359–4381.
6. V. Sharma, A. Agrawal, O. Singh, R. Goyal, B. Sarkar, N. Gopinathan and S. P. Gumfekar, A comprehensive review on the synthesis techniques of porous materials for gas separation and catalysis, The, Can. J. Chem. Eng., 2022, 100, 2653–2681.
7. E. Yang, E. J. Jang, J. G. Lee, S. Yoon, J. Lee, N. Musselwhite, G. A. Somorjai, J. H. Kwak and K. An, Acidic effect of porous alumina as supports for Pt nanoparticle catalysts in n-hexane reforming, Catal. Sci. Technol., 2018, 8, 3295–3303.
8. S. Chen, X. Chang, G. Sun, T. Zhang, Y. Xu, Y. Wang, C. Pei and J. Gong, Propane dehydrogenation: catalyst development, new chemistry, and emerging technologies, Chem. Soc. Rev., 2021, 50(5), 3315–3354.
9. A. Agrawal, R. Goyal, B. M. Abraham, O. Singh, S. Tripathi, M. K. Poddar, R. Bal and B. Sarkar, Synthesis of sub-nanometric Cu2O catalysts for Pd-free C–C coupling reactions, React. Chem. Eng., 2021, 6, 929–936.
10. J. Yu, X. Sun, X. Tong, J. Zhang, J. Li, S. Li, Y. Liu, N. Tsubaki, T. Abe and J. Sun, Ultra-high thermal stability of sputtering reconstructed Cu-based catalysts, Nat. Commun., 2021, 12, 7209.
11. Y. Xie, Y. Yu, X. Gong, Y. Guo, Y. Guo, Y. Wang and G. Lu, Effect of the crystal plane figure on the catalytic performance of MnO2 for the total oxidation of propane, CrystEngComm, 2015, 17, 3005–3014.
12. B. Cui, H. Wang, J. Han, Q. Ge and X. Zhu, Crystal-phase-depended strong metal-support interactions enhancing hydrodeoxygenation of m-cresol on Ni/TiO2 catalysts, J. Catal., 2022, 413, 880–890.
13. C. Autthanit, W. Chatkaew, P. Praserthdam and B. Jongsomjit, Effect of different phase composition in titania on catalytic behaviors of AgLi/TiO2 catalysts via ethanol dehydrogenation, J. Environ. Chem. Eng., 2020, 8, 103547.
14. B. Sarkar, N. Singhal, R. Goyal, A. Bordoloi, L. N. Sivakumar Konathala, U. Kumar and R. Bal, Morphology-controlled synthesis of TiO2 nanostructures for environmental application, Catal. Commun., 2016, 74, 43–48.
15. G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50.
16. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865.
17. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B, 1994, 50(24), 17953.
18. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B, 1999, 59(3), 1758.
19. G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113(22), 9901–9904.
20. X. Gao, Z. Ge, G. Zhu, Z. Wang, J. Ashok and S. Kawi, Anti-Coking and Anti-Sintering Ni/Al2O3 Catalysts in the Dry Reforming of Methane: Recent Progress and Prospects, Catalysts, 2021, 11, 1003.
21. K. Vajda, K. Saszet, E. Z. Kedves, Z. Kása, V. Danciu, L. Baia, K. Magyari, K. Hernádi, G. Kovács and Z. Pap, Shape-controlled agglomeration of TiO2 nanoparticles. New insights on polycrystallinity vs. single crystals in photocatalysis, Ceram. Int., 2016, 42, 3077–3087.
22. B. Rajamannan, S. Mugundan, G. Viruthagiri, P. Praveen and N. Shanmugam, Linear and nonlinear optical studies of bare and copper doped TiO2 nanoparticles via sol gel technique, Spectrochim. Acta, Part A, 2014, 118, 651–656.
23. O. Eroglu and H. Kizil, Pseudocapacitive sodium-ion storage in one-dimensionally structured anatase TiO2 nanofiber anode for high performance sodium-ion batteries, J. Phys. Chem. Solids, 2023, 178, 111352.
24. H. Raghav, L. N. S. K. Konathala, N. Mishra, B. Joshi, R. Goyal, A. Agrawal and B. Sarkar, Fe-decorated hierarchical molybdenum carbide for direct conversion of CO2 into ethylene: Tailoring activity and stability, J. CO2 Util., 2021, 50, 101607.
25. B. Sarkar, R. Goyal, L. N. Sivakumar Konathala, C. Pendem, T. Sasaki and R. Bal, MoO3 Nanoclusters Decorated on TiO2 Nanorods for Oxidative dehydrogenation of ethane to ethylene, Appl. Catal., B, 2017, 217, 637–649.
26. C. Imparato, M. Fantauzzi, C. Passiu, I. Rea, C. Ricca, U. Aschauer, F. Sannino, G. D'Errico, L. De Stefano, A. Rossi and A. Aronne, Unraveling the Charge State of Oxygen Vacancies in ZrO2–x on the Basis of Synergistic Computational and Experimental Evidence, J. Phys. Chem. C, 2019, 123, 11581–11590.
27. B. Sarkar, C. Pendem, L. N. Sivakumar Konathala, R. Tiwari, T. Sasaki and R. Bal, Cu nanoclusters supported on nanocrystalline SiO2–MnO2: a bifunctional catalyst for the one-step conversion of glycerol to acrylic acid, Chem. Commun., 2014, 50, 9707–9710.
28. B. Sarkar, P. Prajapati, R. Tiwari, R. Tiwari, S. Ghosh, S. Shubhra Acharyya, C. Pendem, R. Kumar Singha, L. N. Sivakumar Konathala, J. Kumar, T. Sasaki and R. Bal, Room temperature selective oxidation of cyclohexane over Cu-nanoclusters supported on nanocrystalline Cr2O3, Green Chem., 2012, 14, 2600–2606.
29. L. Ni, R. Khare, R. Bermejo-Deval, R. Zhao, L. Tao, Y. Liu and J. A. Lercher, Highly Active and Selective Sites for Propane Dehydrogenation in Zeolite Ga-BEA, J. Am. Chem. Soc., 2022, 144, 12347–12356.
30. E. H. Stitt, S. D. Jackson and F. King, Kinetic Based Deactivation Modelling of an Isothermal Propane Dehydrogenation Reactor, in Studies in Surface Science and Catalysis, ed. G. F. Froment and K. C. Waugh, Elsevier, 1999, pp. 291–298.
31. S. T. Oyama, X. Zhang, J. Lu, Y. Gu and T. Fujitani, Epoxidation of propylene with H2 and O2 in the explosive regime in a packed-bed catalytic membrane reactor, J. Catal., 2008, 257, 1–4.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5lf00031a

---