Open Access Article
Open Access ArticleCoarse-grained molecular dynamics simulations of mixtures of polysulfamides†
Jay
Shah
 a and
Arthi
Jayaraman
a and
Arthi
Jayaraman
 *abc
*abc
aDepartment of Chemical and Biomolecular Engineering, University of Delaware, Colburn Lab, 150 Academy Street, Newark, DE 19716, USA. E-mail: arthij@udel.edu
bDepartment of Materials Science and Engineering, University of Delaware, 201 DuPont Hall, Newark, Delaware 19716, USA
cData Science Institute, University of Delaware, Ammon Pinizzotto Biopharmaceutical Innovation Center, Suite 147, 590 Avenue 1743, Newark, DE 19713, USA
First published on 20th February 2025
Abstract
Polysulfamides are a new class of polymers that exhibit favorable chemical and physical properties, making them a sustainable alternative to commodity polymers like polyurea. To advance the fundamental understanding of this new class of polymers, Wu et al. [Z. Wu, J. W. Wu, Q. Michaudel and A. Jayaraman, Macromolecules, 2023, 56, 5033–5049]conducted experiments and coarse-grained (CG) molecular dynamics (MD) simulations to connect the polysulfamide backbone design to the assembled structure of polysulfamides due to hydrogen bonding between sulfamides. Their CG MD simulations qualitatively reproduced experimentally observed trends in crystallinity for analogous variations in polysulfamide backbone designs. To bring chemical specificity to this generic CG model of Wu et al. and to facilitate quantitative agreement with experiments in the future, in this work, we modify this older CG model of Wu et al. using structural information from atomistic simulations. Atomistic angle and dihedral distributions involving the sulfamide functional groups are used to modify the donor and acceptor bead positions in the new CG model. Using MD simulations with this new atomistically informed CG model, we confirm that we obtained the structural trends with varying polysulfamide backbone length, bulkiness, and non-uniformity of the segments in repeat units as seen in the previous work by Wu et al. These key structural trends are as follows: (a) shorter contour lengths of segments between sulfamide groups enhance H-bonding between sulfamides, (b) increased bulkiness in the segment hinders sulfamide–sulfamide H-bonding and reduces orientational order among chains in the assembled structure, and (c) non-uniformity in the segments along the backbone does not affect orientational order in the assembled structure. While the trends qualitatively matched between the two models, we observe quantitatively higher positional order and lower orientational order among the assembled chains in the new CG model as compared to the older CG model. This difference in local chain packing arises from a change in the donor–acceptor H-bonding pattern between the two models. In this work, we also use the new CG model to study mixing and demixing in two types of mixtures of polysulfamides: one mixture has chains with varying segment lengths between sulfamide groups and another mixture has chains with different degrees of bulkiness in the backbone. We find that increasing dissimilarity (bulkiness or length) between the two types of chains promotes demixing despite the presence of sulfamide–sulfamide H-bonding interactions.
1 Introduction
Polysulfamides are a new class of polymers synthesized by Michaudel and coworkers using sulfur(VI)-fluoride exchange (SuFEx) click chemistry.1 Polysulfamides demonstrate high thermal stability, adjustable glass transition temperatures (with changing polymer backbone structure), and degradability under environmentally friendly aqueous conditions.1,2 These attractive properties and the similarity between sulfamide3 and urea (Fig. 1) make polysulfamides a potential sustainable alternative to the widely used commodity plastic, polyurea. To demonstrate the suitability of polysulfamides in various applications where polyurea is used,4–13 we will first need to improve our fundamental understanding of these polymers, in particular how the chains organize into multi-scale (Å to hundreds of nm) structures that give rise to the favorable macroscale properties desired for different applications. Specifically, we need a better understanding of how the hydrogen bonding (H-bonding) interactions between the sulfamide groups, along with other interactions due to the various chemical species along the polymer backbone, will affect the local packing of chains and their hierarchical structures.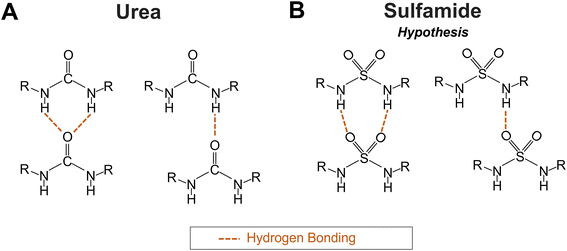 | ||
| Fig. 1 Schematics of the (A) two potential H-bonding patterns in polyurea according to Mattia et al.32 and (B) two hypothesized H-bonding patterns in polysulfamide. | ||
Structural arrangements within polysulfamide chains are characterized via Fourier-transform infrared (FTIR) spectroscopy and powder X-ray diffraction (PXRD).2,14 For example, Wu et al. used FTIR to estimate qualitatively the extent of crystallinity, complementing it with PXRD analysis.14 Just as FTIR has been used to study H-bonding in polyurea,6,7,11,15–19 Wu et al. used FTIR to characterize the H-bonding interactions between N–H (donor) and –SO2– (acceptor) groups in polysulfamides. Their FTIR and PXRD data together showed that the choice of polysulfamide backbone chemistry affects the crystallinity14 which in turn can affect the thermomechanical and other macroscopic properties of polymer materials.20–31 However, the lack of purely crystalline and purely amorphous samples of polysulfamides that are required to quantify the extent of semi-crystallinity in various samples makes it difficult to use these experimental techniques alone to quantify the extent of semi-crystallinity for various designs of polysulfamides. Therefore, to supplement experimental observations, we use molecular simulations to predict how the choice of polysulfamide design impacts the simulated positional and orientational order among the chains.
In previous work, Wu et al. developed a generic coarse-grained (CG) model to study polysulfamides.14 This generic CG model of polysulfamide was developed using ideas from prior CG models from Jayaraman and coworkers which captured the directional interactions, like H-bonding, in other polymers. The generic CG model captures the directional nature of H-bonding interaction33 using a combination of small and large size CG beads, with the smaller “sticky” bead being partially embedded in the larger CG beads; by tuning bonded potentials and the non-bonded isotropic attraction between the sticky beads, the directional H-bonding interaction driving polysulfamide assembly is captured.14 These types of “sticky” site CG models capture directional interactions while maintaining the computational efficiency needed to simulate the larger time and length scales of macromolecular assembly and disassembly. Jayaraman and co-workers have widely used the “sticky” bead model to simulate H-bonding in polymer melts/solutions/mixtures.14,34–42 Such “sticky” bead models have also been demonstrated to be successful in simulating DNA dendrimers,43,44 DNA-linked nanoparticle crystals,45 water-soluble supramolecular polymers,46,47 and nanocomposite tectons.48–50
Wu et al.'s generic CG model for polysulfamides was purely intuitively parameterized to mimic the sulfamide chemical structure as well as the groups (alkyl, aromatic) on either side of the sulfamide CG bead. Using this generic CG model and molecular dynamics (MD) simulations, they studied the effects of polysulfamide backbone design parameters like bulkiness of groups (e.g., aromatic rings versus aliphatic linear chains), length (e.g., number of alkyl carbons), and uniformity of segment lengths on either side of the sulfamide group on the H-bonding-induced self-assembly of polysulfamide chains.14 The computational results were validated through comparisons with experimental data, specifically the FTIR and PXRD data from analogous synthesized polysulfamide structures. The orientational and positional order of the chains in the simulated structures served as a proxy for crystallinity in the synthesized polysulfamides. Both simulations and experiments found that one can increase orientational and positional order by using less bulky segments between sulfamide groups. They also found that non-uniform segments on either side of the sulfamide do not impact the orientational alignment of the chains but increase the short-range positional order among chains.14
While the simulations using the generic CG model effectively capture the relevant length and timescales for polysulfamide assembly and the experimentally observed trends in increasing/decreasing orientational order for varying design choices, the agreement with experiments is at best qualitative. To enable quantitative comparison with experiments in the future, we need a CG model that is not generic but rather mapped to specifically represent the sulfamide chemical structure; e.g., the CG model should have the correct relative locations of the acceptor and donor “sticky” sites and the appropriate stiffness or flexibility of the bonds between the sulfamide groups and the neighboring aliphatic or aromatic segments. Such mapping can be done using information from atomistically detailed configurations sampled with atomistic MD simulations. Atomistic configurations can then be used to refine the placement of beads and bonded and non-bonded potentials in the CG model.51,52 In this paper, we accomplish this refinement of the CG model for polysulfamides and use that new atomistically informed CG model in MD simulations to connect polysulfamide designs and mixtures of designs to the resulting H-bonding-driven spatial arrangements of the segments and chains in the assembled structure. The rationale for exploring polysulfamide mixtures is based on previous observations that polysulfamide backbone design influences the degree of crystallinity and established knowledge that mixing polymers with different native degrees of crystallinity can result in a semi-crystalline structure. The mixing or demixing of the two types of polymers in the mixture (termed miscibility) will also play a role in semi-crystallinity which is crucial for designing materials tailored for specific uses.53
Blend/mixture miscibility is the result of the energetic and entropic driving forces which depend on several factors such as polymer chemistry, sequence, architecture, and mixture composition. The Flory–Huggins54 equation below quantifies the change in free energy upon mixing using a mean-field lattice approach:
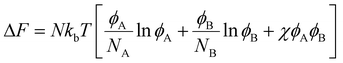 | (1) |
This article is organized as follows: In Section 2, we describe the polysulfamide atomistic model, simulation protocol and conformation analysis. In Section 3, we describe the previous generic CG model briefly before presenting the details of our new CG model informed by atomistic simulations. In Section 4, we discuss the morphologies observed in MD simulations using the generic CG model versus our new atomistically informed CG model. We also present results describing the morphology of mixtures with different polysulfamide designs. In Section 5, we conclude with a discussion on design rules based on the key results from this work.
2 Atomistic simulations
2.1 Systems studied
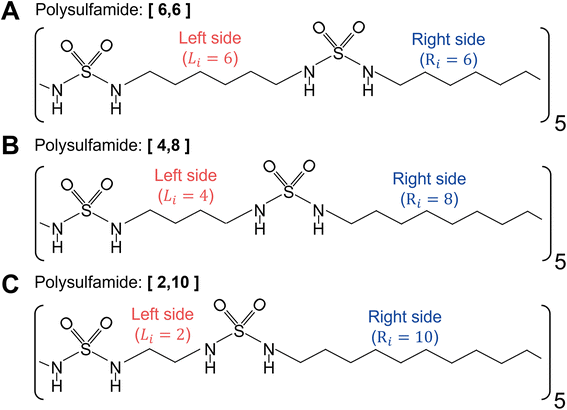
For atomistic simulations, we consider a single polysulfamide chain consisting of five repeat units with each repeat unit comprised of 12 CH2 groups and 2 sulfamide groups. We consider three different backbone designs (Fig. 2) with segments made of varying numbers of CH2 groups between the sulfamide functional groups. We adopt a naming convention [Li,Ri], where Li and Ri represent the number of CH2 beads on the left and right sides of the sulfamide group in the repeat unit, respectively. We have 12 CH2 groups in every repeat unit so Li + Ri = 12. The three polymers we study include the following:i. [6,6] Polysulfamide where sulfamide groups are separated by 6 CH2 on either side, indicating uniform spacing between the sulfamide groups (Fig. 2A).
ii. [4,8] Polysulfamide where sulfamide groups are separated by 4 CH2 on the left side and 8 CH2 on the right side (Fig. 2B).
iii. [2,10] Polysulfamide where sulfamide groups are separated by 2 CH2 on the left side and 10 CH2 on the right side (Fig. 2C).
While the [6,6] chain has uniform segment lengths on either side of the sulfamide group, the [4,8] and [2,10] designs capture increasing non-uniformity in segment lengths on either side of the sulfamide groups.
2.2 Atomistic model and simulation
We perform atomistic simulations of a single polysulfamide chain in an explicit water environment using GROMACS.83 We choose the OPLS-AA force field parameters to model both intra- and inter-chain interactions within the polysulfamide chain.84 We choose OPLS-AA because it is a widely used force field for atomistic polymer simulations85–91 and has been previously applied to simulate polyurea,9,92 which is chemically analogous to polysulfamide. Water molecules are represented using the Simple Point Charge (SPC) model. Short-range electrostatics and van der Waals interactions are cut off at 1.0 nm, and long-range electrostatics are included using the particle mesh Ewald method.93 Additional details including any modifications made to the force field, such as components of the polymer (Fig. S1–S3†), angle, and dihedral specifications (Fig. S4†), are provided in ESI Section 1.†The initial configuration of the single polysulfamide chain in explicit water molecules is relaxed using the steepest descent minimization algorithm to remove overlaps. After the energy minimization step, we equilibrate the system in the NVT (constant number of particles, volume, and temperature) ensemble for 2 ns with a timestep (τ) of 2 fs at a temperature of 350 K. This temperature is chosen as it is above the glass transition temperature of [6,6] polysulfamide (Tg = 345 K).1,14 We use the velocity-rescaling thermostat for this step because it produces the correct NVT ensemble while still having the advantages of first-order decay of temperature deviations.94 After the system achieves the desired temperature in the NVT ensemble, an isothermal–isobaric (NPT) ensemble is run for 4 ns. We maintain a constant pressure of 1.0 bar using the Parrinello–Rahman95 barostat. The production simulation is then conducted in the NPT ensemble for 40 ns (τ = 2 fs), at T = 350 K, P = 1 bar, using the same thermostat and barostat as above. The higher-frequency bonds containing hydrogen atoms are constrained using the LINCS96 method.
2.3 Analysis of atomistic configurations
For data analysis, we use configurations obtained from the 40 ns production trajectory, with coordinates saved every 200 ps.To use the angles and dihedrals sampled in atomistic configurations to inform the relative positions of the donor and acceptor beads in the CG model, we first identify the “Center of Mass (COM)” location for each sulfamide group by calculating the weighted average position of the oxygen, nitrogen, and sulfur atoms; this COM corresponds to the center of the sulfamide CG bead. We then identify the “D1” and “D2” locations as the centers of mass of the –NH groups, respectively; these correspond to the two donor “sticky” beads in the CG model. The centers of the oxygen atoms that correspond to the centers of the “A1” and “A2” acceptor “sticky” beads in the CG model. We then use MDTraj97 to analyze the dihedral distributions of the two –NH groups in the sulfamide functional group and the angle distribution between the donor group – COM – acceptor group to quantify the positions of the acceptor and donor “sticky” beads in the CG model.
3 Coarse-grained (CG) model
3.1 Previously published generic CG model by Wu et al.
Wu et al. developed a generic CG model (Fig. 3) to understand how the polysulfamide design affects H-bonding between sulfamides and the resulting positional and orientational order in assembled polysulfamides.14 We describe the salient features of this model here and direct the reader to the original manuscript for the remaining details of the CG model.14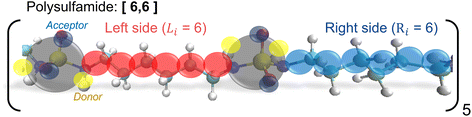 | ||
| Fig. 3 CG representation of the repeat unit in the [6,6] polysulfamide chain with six –CH2 on the left and right sides of the sulfamide group in the repeat unit. | ||
The sulfamide group is represented by 1 CG bead of diameter 1d (∼0.3 nm) and two H-bonding donors and two H-bonding acceptor “sticky” beads of diameter 0.2d, which are partially embedded in the sulfamide CG bead. In this generic CG model, the placement of the donor and acceptor beads on the sulfamide bead is fixed but their relative locations are not mapped to the atomistically observed spatial arrangement; in the new CG model described in the next section, we alter these locations to map to atomistic arrangements.
To capture varying aliphatic and aromatic groups on either side of the sulfamide group, Wu et al. defined other CG beads to represent aliphatic groups (–CH2– with a CG bead of size 0.6d) and aromatic groups (with a CG bead of size 1.5d).
Except for the donor and acceptor beads, every pair of bonded CG beads along the chain is connected by a harmonic bond potential as
| Ubond(r) = kr(r − r0)2 | (2) |
| Uangle(θ) = kθ(θ − θ0)2 | (3) |
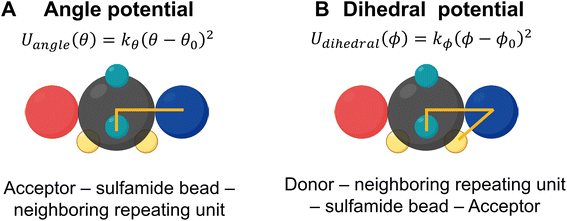
To ensure that the relative locations of the donor and acceptor beads are fixed on the sulfamide bead, Wu et al. incorporated two constraints – an angle constraint between the acceptor, the sulfamide, and the bead adjacent to the sulfamide and another dihedral constraint between the acceptor, the sulfamide, the bead adjacent to the sulfamide, and the donor. These angles are shown in Fig. 4.
To capture an effectively directional H-bonding interaction between the donor and acceptor groups on the sulfamide bead, an isotropic 12–6 Lennard–Jones (LJ) potential98 (eqn (4)) is used between the partially embedded donor and acceptor beads on different sulfamide beads. The partial embedding of the “sticky” beads in the sulfamide bead ensures that the interaction between the donor and acceptor is not isotropic despite using an isotropic LJ potential.
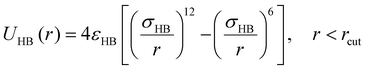 | (4) |
All other non-bonded interactions are represented by a purely repulsive Weeks–Chandler–Andersen (WCA) potential:99
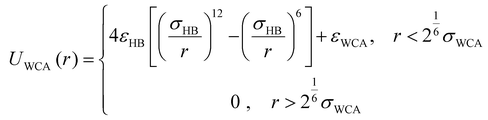 | (5) |
3.2 New atomistically informed CG model
As in the generic CG model, the mapping of the donor and acceptor beads in the new CG model is defined as follows: (1) the donor beads (D1 and D2) are modeled using the center of mass of the N–H group and (2) the acceptor beads (A1 and A2) are positioned at the oxygen (O) atoms. To modify the relative locations of the donor and acceptor beads in the new CG model, we plot the probability distribution of the NH1–N1–N2–NH2 dihedral angle (Fig. 5A). The distribution shows two distinct peaks, corresponding to the two most favorable configurations of the NH (i.e., H-bonding donor) in the sulfamide functional group; in contrast, the generic CG model assumed a dihedral angle of 90° (denoted by the red arrow in Fig. 5A). For all three polysulfamides – [6,6], [4,8], and [2,10] – we observe two peaks at the same angles, highlighting similar structural preferences across the polysulfamide backbone designs. In Fig. 5B, we show the chemical structure of the gauche-like configuration that corresponds to the first peak at a smaller angle (Fig. 5A), and the trans-like configuration corresponding to the second peak at a larger angle (Fig. 5A). Fig. 5C presents the distributions of D1–COM–A1, D1–COM–A2, D2–COM–A1, and D2–COM–A2 angles for all sulfamide groups in the chain observed from two hundred configurations across three independent trials of atomistic simulations of the [6,6] polysulfamide chain (Fig. S5 in the ESI presents the corresponding distributions for the [4,8] and [2,10] polysulfamides†). These distributions exhibit two peaks corresponding to the two configurations that the donors and acceptors adopt in the sulfamide group. Fig. 5D illustrates these two configurations: Configuration-1 (gauche-like) and Configuration-2 (trans-like). We update the bead positions of the H-donor and H-acceptor in the new CG model (Fig. 5E) based on these atomistically observed angle distributions between the donor and acceptor beads. Fig. 5F specifies the exact positions of the donor and acceptor beads within the sulfamide bead.Now that we have defined the new atomistically informed CG model, moving forward, we will refer to the generic CG model as the “older CG model”. The new CG model that incorporates the H-donor and H-acceptor positions from Configuration-1 will be referred to as “Config-1”, and the new CG model using the positions from Configuration-2 will be termed “Config-2”. These distinctions will help clarify how each configuration influences the structural behavior of the polysulfamide chains in the subsequent analyses. In this work, we examine these two configurations to address the role of donor–acceptor positions and understand the H-bonding preferences in each case. Changes in the donor–acceptor positions result in changes in the equilibrium angle (θ0) between adjacent repeating units (Fig. 4). Table 1 highlights the key differences between the older CG model and the updated “Config-1” and “Config-2” CG models.
| Equilibrium value | Older CG model | Updated model (“Config-1”) | Updated model (“Config-2”) |
|---|---|---|---|
| θ 0 | 90° | 81° | 81° |
| ϕ 0 | 45° | 131° | 89.3° |
The other bonded and non-bonded potentials remain unchanged from the older CG model.
3.3 CG molecular dynamics (MD) simulation protocol
We follow the same simulation protocol as reported by Wu et al.14 Briefly, we perform CG MD simulations in an NVT ensemble using the LAMMPS package.100 Each polymer chain is initially in an extended conformation. The total number of chains in the simulation box is 100 in all cases. The chains are relaxed from their initial extended state by compressing the cubic simulation box to a size of 80d; this box size is chosen to avoid self-interaction of chains across the periodic boundaries of the simulation box. We relax the polymer chains using the NVT ensemble with T* = 1 using the Nosé–Hoover thermostat. We set all pairwise non-bonded interactions to the WCA potential. We run the simulation for 12.5 million timesteps, slowly compressing the box to the desired size. This allows the chains to mix properly and relax away from their initial extended form. Additionally, a completely random well-mixed initial configuration state gives us confidence that we do not have an initial configuration bias when we see segregation as the simulation progresses.After this initial relaxation of the polymer chains, we set the non-bonded pairwise interaction between the donor and acceptor beads to the model-stipulated attractive LJ potential. We conduct a simulated annealing procedure where εHB, the LJ interaction strength between donor and acceptor beads (D–A attraction), is increased from 6.0 kT to 12.0 kT in increments of 0.2 kT every 10 million timesteps in the NVT ensemble with T* = 1. This gradual increase in εHB prevents the formation of kinetically trapped assembled polymer structures at high H-bonding strengths. By doing this equilibration and the production stage for the system at each value of εHB before increasing it to the next value of εHB, we avoid kinetic trapping while simultaneously obtaining structural information at different H-bonding strengths that can be replicated in experiments by tuning the solvent quality and/or temperature. For example, increasing the temperature is effectively the same as decreasing the value of εHB. Lastly, for each case, we run three independent trials to account for statistical variability from trial to trial and to confirm that we have avoided kinetically trapped morphologies.
In terms of analyses, similar to Wu et al., we quantify H-bonding propensity, orientational, and positional order among chains in the assembled structures at different εHB as a proxy to relate with experimentally observed semi-crystallinity. Hydrogen-bonding propensity (fHB) is calculated as
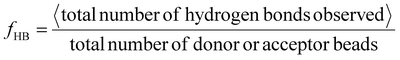 | (6) |
We consider an H-bond to be formed when the distance between the donor and acceptor of different sulfamide beads is less than 0.35d. We quantify orientational order (i.e., alignment) among neighboring chains by plotting the probability of the intersegment angle between H-bonded segments (αHB). Lower values of αHB indicate higher orientational alignment of chain segments within the polysulfamide assembly. This angle is calculated for each pair of sulfamide beads that have at least one hydrogen bond formed between them. For a given sulfamide bead, we define its corresponding sulfamide “segment” as the vector connecting the center of that sulfamide bead to its adjacent bonded bead on the right. We also quantify positional order among chains using the radial distribution function (RDF) between sulfamide beads of different chains, to understand local structural ordering within the assembled polysulfamide structure.
We calculate fHB, αHB and RDF for 10 configurations for each simulation step at each εHB in each trial, starting at t = 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 timesteps and spaced out every 500
000 timesteps and spaced out every 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 timesteps at each εHB. We find that the variation between trials is greater than the variation between the timesteps of an individual trial, so we compute the mean across 10 configurations for each trial and report the average and standard deviation of the three trials’ means.
000 timesteps at each εHB. We find that the variation between trials is greater than the variation between the timesteps of an individual trial, so we compute the mean across 10 configurations for each trial and report the average and standard deviation of the three trials’ means.
4 Results
4.1. Comparing structural trends observed using the new CG model against those observed by Wu et al.
Before we present previously unreported results with the new and improved polysulfamide CG model, we want to compare the trends previously observed for different groups of polysulfamides studied by Wu et al.14 using both their older CG model and our new atomistically informed “Config-1” and “Config-2” CG models. Below is a brief summary of the groups of polysulfamide designs that were studied by Wu et al. (Fig. S6 in the ESI presents the corresponding groups†):• Group 1: This group examines polysulfamides with varying lengths of the aliphatic repeating unit in the backbone.
• Group 2: This group explores variations in non-uniformity of alkyl segments on either side of the sulfamide within the repeat unit.
• Group 3: This group explores variations in bulkiness along the backbone, featuring polymers with aromatic groups of varied sizes separated by a small methylene group.
As done in the work of Wu et al., we also calculate the H-bonding propensity (fHB) and the distribution of the intersegment angle between H-bonded segments (αHB) for systems of polysulfamides in the three groups. In Section 3 in the ESI,† we present a detailed comparison of these results from Wu et al.'s older CG model and our new atomistically informed CG model. To keep this discussion brief, we present the key differences between the two models across all three groups.
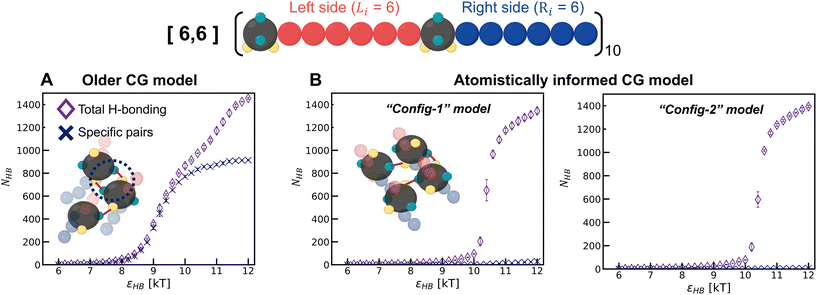
1. The εHB value at which the chains assemble is higher for the two atomistically informed models as compared to the older model. This means that for the atomistically informed model of polysulfamide, the system of polysulfamide chains needs a larger enthalpic gain (from favorable H-bonding contacts) to overcome the entropic loss the chains undergo going from a disordered unassembled state to assembled chains.
2. At the highest H-bonding strength (εHB = 12 kT), the observed value of fHB remains the same for all three models. The distribution of intersegment angles between H-bonded segments (αHB) for the atomistically informed model shifts to higher values and exhibits a broader distribution compared to the older model. This suggests that the chains are less orientationally ordered in the morphologies observed in the MD simulations using the atomistically informed CG model than they were in the older CG model.
To understand the model-induced differences in fHB and orientational order, and to explore the factors contributing to variations in the morphology, we analyze the manner of H-bonding between sulfamides in the configurations sampled with the older CG model and the two atomistically informed CG models (“Config-1” and “Config-2”) at various εHB. In the older CG model, we observe that a pair of sulfamide beads could make two H-bonds with each other – D1 of the first bead with A1 of the second bead and D2 of the first bead with A2 of the second bead; for brevity we call this a “specific” H-bonding pair. Such “specific” H-bonding configurations are not possible with the atomistically informed model of sulfamide. In Fig. 6, we can see that in the older model, “specific” H-bonding is prominent; in contrast, the atomistically informed models show an insignificant number of “specific” pairs, indicating a more extensive network of non-“specific” H-bonding. This lack of “specific” H-bonding between a pair of sulfamide groups broadens the range of intersegmental angles and reduces the orientational order. We think that the loss of entropy that chains undergo upon the formation of such a network of H-bonds is likely more than the loss of entropy that chains undergo when their sulfamide beads are “specifically” H-bonded with each other. As a result, the value of the H-bonding strength (εHB) at which the chains start to assemble is higher for the two atomistically informed models as compared to the older CG model; in other words, with atomistically informed CG models, the energetic gain upon chain assembly has to be higher to compensate for the larger entropic loss than in the case of the older CG model. Lastly, the number of H-bonds vs. H-bonding donor–acceptor strength has a sharper transition for “Config-1” and “Config-2” than for the older CG model, suggesting that the form of the transition also changes from 2nd-order-like in the case of the older model to 1st-order-like in the atomistically informed model.
As both Config-1 and Config-2 exhibit the same structural organization (Fig. S7 in the ESI†) and H-bonding transition behavior (Fig. 6), with neither showing a “specific” H-bonding pattern, for brevity, we use only Config-1 as the representative atomistically informed model for the remainder of the paper.
The qualitative trends in the effect of polysulfamide design on the structure of assembled chains remain consistent between the atomistically informed CG model and the older CG model (Section 3 in the ESI†). We see the same trends observed by Wu et al. wherein increasing bulkiness (aliphatic to aromatic) in the segments between the sulfamide group reduces crystallinity in experiments and orientational and positional order in simulations. Secondly, for alkyl groups between sulfamide beads, the shorter the length of alkyl segment the larger the extent of positional and orientational order. Thirdly, increasing non-uniformity between the segments on either side of the sulfamide increases the local positional order but does not impact the orientational alignment of the self-assembled polysulfamide.14 Having compared the systems of polysulfamides with one type of design, we now shift our focus towards mixtures of different polysulfamide designs.
4.2. Mixture of polysulfamides
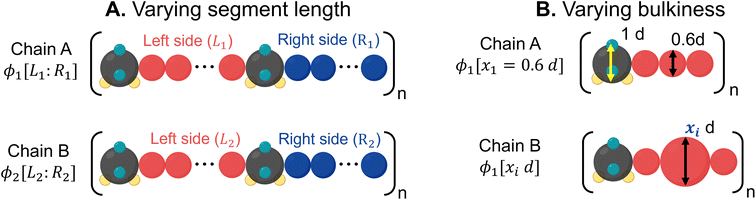
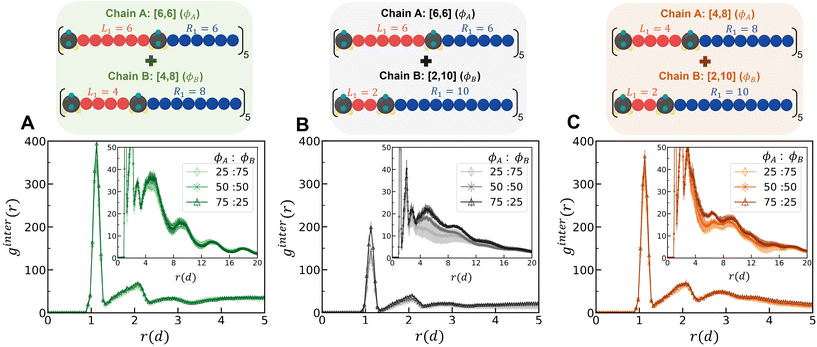
1. Binary mixtures of polysulfamides where the two types of chains differ in the choice of segment length (Fig. 7A) between the sulfamide beads in the repeating unit. In all chains, the repeat unit contains 12 CH2 groups and 2 sulfamide groups; the chains differ in how these groups are distributed in the backbone. Fig. 2 presents the schematics of [6,6], [4,8], and [2,10] repeat units in polysulfamides. We consider three cases: (i) a mixture of [6,6] and [4,8] chains; (ii) a mixture of [6,6] and [2,10] chains; and (iii) a mixture of [4,8] and [2,10] chains.
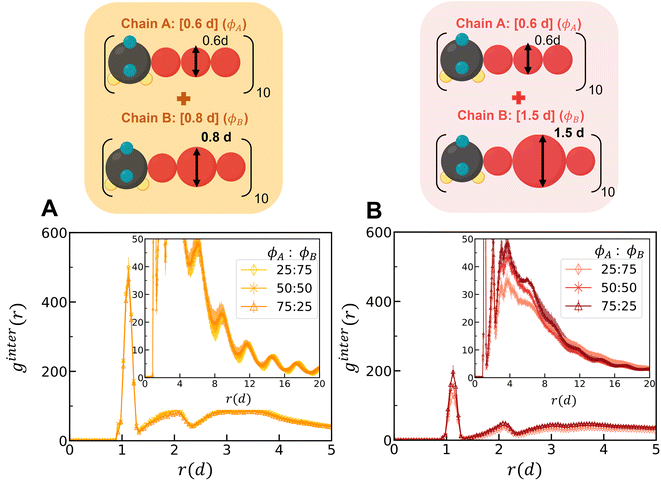
2. Binary mixtures of polysulfamides where the two types of chains differ in the bulkiness of the segments next to the sulfamide (Fig. 7B); in experiments, the bulkiness can be increased through branching in the aliphatic segments or by using aromatic groups along the backbone. Here, the bulkiness in the polysulfamides is denoted by [xid], where xi indicates the size of the bulky bead; for example, in the case of [0.6d], the size of the bulky group bead is 0.6d. We study two cases: (i) a mixture of [0.6d] and [0.8d] polysulfamides and (ii) a mixture of [0.6d] and [1.5d] polysulfamides.
In both cases described above, the mixture composition is denoted by the volume percent of the two chains ϕ1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ2 = 25
ϕ2 = 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75, 50
75, 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 and 75
50 and 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25. In all mixtures, the total number of chains is 100; this keeps the same number density of sulfamides which is defined as the ratio of the total number of sulfamide beads to the volume of the simulation box.
25. In all mixtures, the total number of chains is 100; this keeps the same number density of sulfamides which is defined as the ratio of the total number of sulfamide beads to the volume of the simulation box.
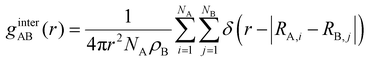 | (7) |
In eqn (7), A and B are sulfamide beads from two different chain types. Nx is the number of sulfamide beads in chain type x (x can be A or B). ρB is the number density of sulfamide in chain type B. Rx,i is the coordinate of the ith sulfamide bead in chain type x. A higher first peak in ginterAB(r) indicates higher mixing between the two types of chains in the mixture.
At all mixture compositions, the first peak for the [6,6] and [2,10] mixture (Fig. 8B) is lower than that for the other mixtures (Fig. 8A and C), indicating a higher degree of demixing for this mixture than for the others. In the RDFs of the sulfamide beads within the same polymer type chains (not shown here), i.e., gA–A(r) and gB–B(r), a higher peak suggests that the sulfamide groups of the same chain type are more clustered together, indicating less mixing of the two types of chains. For all compositions, we find that the extent of chain mixing follows the following order at the highest H-bonding strength (εHB = 12 kT) (Fig. S16†): mixtures of [6,6] and [4,8] > mixtures of [4,8] and [2,10] > mixtures of [6,6] and [2,10].
Despite distinct differences in mixture miscibility, as shown in Fig. S17,† the propensity for H-bonding (fHB) and the probability of the intersegment angle between hydrogen-bonded segments (αHB) for all three mixtures are the same regardless of the specific polysulfamide combinations or mixture compositions. Perhaps, this is expected based on our observation in the homopolymer systems, where there was little to no variation in the propensity for H-bonding (fHB) and the probability of the intersegment angle between hydrogen-bonded segments (αHB) for the [6,6], [4,8], and [2,10] chains despite having different self-assembled morphologies (Fig. S11†).
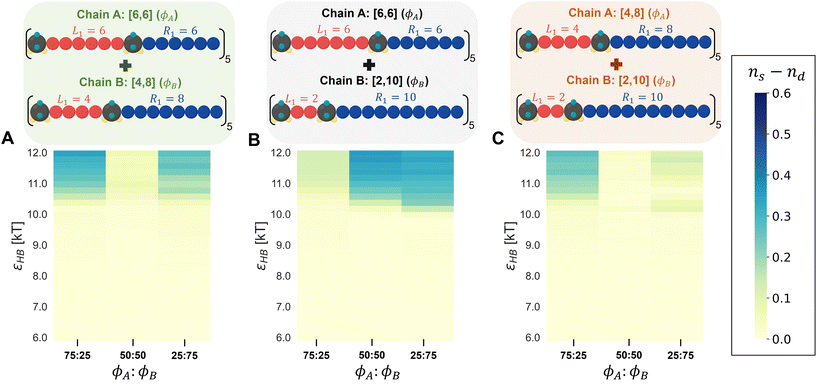
To tease out any difference in H-bonding between different chain types and between the same chain types, we calculate ns, the fraction of H-bonding within the same chains, and nd, the fraction of H-bonding between different chains, i.e., a donor/acceptor from a chain of type A hydrogen bonded with an acceptor/donor from a chain of type B. Eqn (8) and (9) define these fractions:
 | (8) |
 | (9) |
In eqn (8), the denominator for ns is the sum of total number of donors present in the system; in eqn (9), the denominator for nd is the maximum number of cross H-bonding interactions possible which is equal to the number of donors in the chains that is the minority composition in the mixture. If ns ≈ nd, the mixture is considered well-mixed, indicating that the chains in the mixture do not distinguish between different polymer designs when forming hydrogen bonds. If ns ≫ nd, then the mixture is demixed, meaning that the polymers exhibit a strong preference for forming hydrogen bonds with chains of the same design (Fig. S14†).
In Fig. 9, we present a heat map showing the difference in H-bonding between the same chain types (ns) and between the different chain types (nd) at each εHB. The heat map for the [6,6] and [2,10] mixture (Fig. 9B) indicates that demixing (blue) becomes more pronounced with increasing hydrogen-bonding strength (εHB). As the content of [2,10] in the mixture increases, there is a stronger tendency for preferential H-bonding between the same chain types, leading to increased demixing. The mixtures of [6,6] and [4,8], as well as [4,8] and [2,10], consistently show a low difference between ns and nd, indicating that the chains do not distinguish the different polymer designs and remain mixed across all mixture compositions. However, we observe some favorable H-bonding between same-type chains for the 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75 and 75
75 and 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 compositions for the [6,6] and [4,8] mixture. Similarly, for the [4,8] and [2,10] mixture, more favorable H-bonding occurs between same-type chains at a 75
25 compositions for the [6,6] and [4,8] mixture. Similarly, for the [4,8] and [2,10] mixture, more favorable H-bonding occurs between same-type chains at a 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 mixture composition. These heat maps serve as a visual aid into how different combinations of polysulfamides, and their proportions affect the mixture's overall miscibility under various H-bonding conditions.
25 mixture composition. These heat maps serve as a visual aid into how different combinations of polysulfamides, and their proportions affect the mixture's overall miscibility under various H-bonding conditions.
Simply out of curiosity, we also compared these mixture results using the older model from Wu et al. and present those results in Fig. S18–S21.† For the intermolecular RDF (ginter(r)) for the [6,6] and [2,10] mixture, at the same H-bonding strength and mixture composition, we observe a larger peak height with the “Config-1” model, indicating a more mixed mixture than with the older CG model. As stated before, the chains modeled with the older CG model have more specific H-bonds (where the same pair of sulfamide beads form two H-bonds) which are maximized within same type of chains, leading to more demixing than with the “Config-1” model. Even though the RDFs differ, the general trend in miscibility across different blend types and compositions is consistent between the older and the newer models.
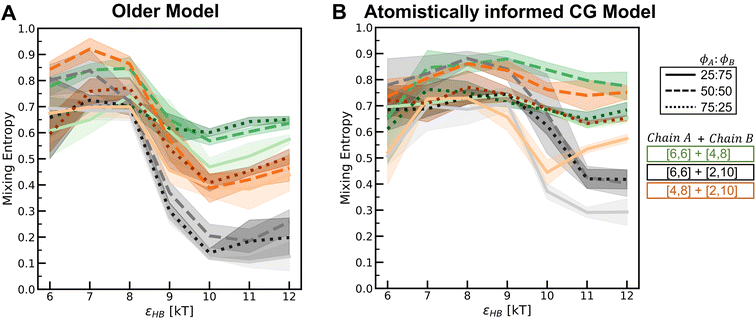
To understand how the relative placement of H-bond donors and acceptors influences the entropy loss upon assembly, we calculate a parameter that can serve as a proxy for the entropy of mixing, defined as
Smix = −p1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p1 − p2 p1 − p2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p2 p2 | (10) |
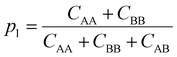 | (11) |
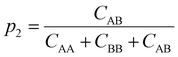 | (12) |
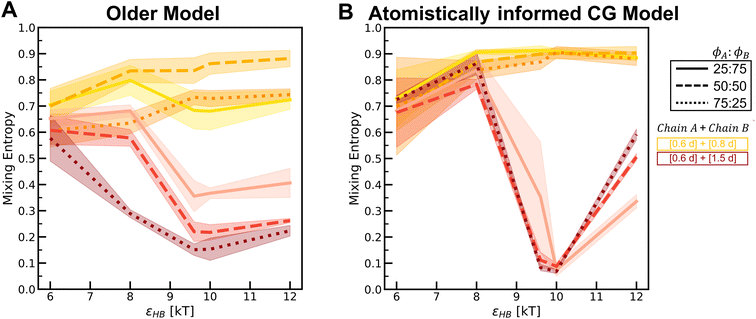
In Fig. 10, we compare the values of this term Smix for the two models across various H-bonding strengths and mixture compositions. In each plot, we can see that as the H-bonding strength (x-axis) increases, the Smix value decreases. At low values of the H-bonding strength, the chains do not assemble and remain dispersed in the solution with a high Smix value. As the H-bonding strength increases, the chains form H-bonds and assemble, and the value of Smix drops. In the assembled state, the more demixed the chains are, the lower the value of Smix. For the mixture [6,6] + [2,10] where we observe a demixed state at high H-bonding strengths, the change in Smix values from low to high H-bonding strengths is smaller for the atomistically informed CG model configurations than for the older CG model.
Simulations of mixtures containing two types of chains with differing bulkiness (simulation snapshots in Fig. S22†) show how mixing two types of chains of varying bulkiness can affect positional and orientational order. In Fig. 11, we quantify the ginter(r) for mixtures at the highest H-bonding strength (εHB = 12 kT) using configurations sampled from the “Config-1” model. The first peak for the mixture of [0.6d] + [0.8d] is higher than that for the mixture of [0.6d] + [1.5d], indicating a greater degree of mixing among chains with similar bulkiness.
In Fig. S23,† we present a heat map showing the difference in H-bonding between the same chain types (ns) and between different chain types (nd) at each εHB. The heat map for the [0.6d] + [1.5d] mixture shows demixing with increasing hydrogen-bonding strength (εHB). As the volume percent of [0.6d] chains in the mixture increases, there is a stronger tendency for preferential H-bonding between the same chain types, indicating that the mixture is evolving towards more demixed domains. In the mixtures of [0.6d] + [0.8d], the [0.8d] chains prefer to form H-bonds with [0.6d]; H-bonding between same-type chains increases with increasing volume percent of the [0.6d] chains in the mixture. In Fig. S24,† we observe a higher peak of gA–A (r) for the mixture of [0.6d] and [1.5d] and a lower first peak of gB–B (r) because the bulkier [1.5d] chains do not aggregate. As a result, the mixtures of [0.6d] + [1.5d] have decreasing propensity of H-bonding with increasing volume percent of the [1.5d] chains (Fig. S25†).
In Fig. S26–S29,† we compare the above results for the “Config-1” model with those we obtained with the older CG model. In Fig. 12, we compare the Smix values between the two models for varying mixture compositions and H-bonding strengths. For both models, the mixture with chains of similar bulkiness, i.e., the [0.6d] + [0.8d] mixture, exhibits more mixed states and a smaller change in Smix values with increasing H-bonding strength. For both models, the mixture with differing bulkiness demonstrates a non-monotonic trend in Smix with increasing H-bonding strength; this effect is more pronounced in the atomistically informed “Config-1” CG model than in the older CG model.
5 Conclusions
In this work, we modified an older generic polysulfamide CG model by incorporating atomistically observed angle and dihedral distributions to refine the donor and acceptor bead positions. This modification provides an atomistically informed representation of the sulfamide functional group, enabling more accurate simulations of polysulfamide chains compared to the older generic CG model of Wu et al. In the first part of this paper, using the new atomistically informed CG model, we captured structural trends in polysulfamide chains that align with those reported by Wu et al. in prior work using the generic CG model. Specifically, we observed that shorter contour lengths between sulfamide groups enhance H-bonding, increased segment bulkiness hinders both H-bonding and orientational order within assembled chains, and chain non-uniformity does not affect orientational order within the assembled chains. While the qualitative trends align with those of the older CG model, the atomistically informed CG model exhibits a quantitatively higher positional order and lower orientational order in the assembled chain structures. This difference in morphology arises from changes in the H-bonding pattern between the two models. In the atomistically informed CG model, H-bonding between donors and acceptors within the same pair of sulfamides is not possible, which reduces the positional and orientational order among the assembled chains as compared to the older CG model.In the second part of this paper, we simulated mixtures of polysulfamides using the atomistically informed CG model with the goal of understanding the factors that influence the mixing or demixing behavior. We establish design principles involving variations in segment length and chain bulkiness for controlling semi-crystallinity (i.e., positional and orientational order) within polysulfamide materials. Our findings suggest that:
(i) In polysulfamide mixtures with varying segment lengths, a larger difference in segment lengths between the two types of polysulfamides in the mixture leads to the formation of demixed domains, despite favorable inter-chain H-bonding. We find the miscibility in mixtures of [6,6] and [4,8] > mixtures of [4,8] and [2,10] > mixtures of [6,6] and [2,10].
(ii) In polysulfamide mixtures with varying bulkiness, less bulky chains tend to aggregate due to H-bonding more readily than bulkier chains. Simulation results show that greater differences between the backbone groups lead to the formation of separate domains by the less bulky chains, resulting in demixing within the mixture. Less bulky groups form aggregates, while bulkier groups intermingle with these aggregates, promoting enhanced mixing. We find that chain mixing follows the order: mixtures of [0.6d] and [0.8d] > mixtures of [0.6d] and [1.5d].
These CG MD simulation results clarify how structural differences influence phase behavior in polysulfamide mixtures, contributing to a deeper fundamental understanding of this new class of polymers – polysulfamides – that have the potential to serve as a sustainable alternative to the commodity plastic, polyurea. Our findings may be specific to one class of polymers but they highlight the role of H-bonding site placement, interaction strength, and side group bulkiness in determining the morphology of polymer mixtures. For other classes of polymers, we direct the reader to the review articles by He et al.101 and Kuo et al.102 that summarize experimental and simulation studies on polymer blends and mixtures and the role of donor acidity, acceptor basicity, side group bulkiness, spacer length, chain rigidity, solvent effects, steric hindrance, and temperature in H-bonding-driven self-assembly.
Author contributions
Jay Shah: conceptualization, methodology, data curation, validation, visualization, writing – original draft, review, and editing. Arthi Jayaraman: funding acquisition, supervision, conceptualization, writing – review and editing.Data availability
On Github we share our Python code and simulation files for running polysulfamide atomistic simulations and performing analysis on coarse-grained configurations (https://github.com/arthijayaraman-lab/Polysulfamide-MD_Simulation).Conflicts of interest
The authors declare no competing interests.Acknowledgements
The authors thank DOE Grant DE-SC0023264 for their financial support. The simulations in this paper were conducted on Bridges-2 at the Pittsburgh Supercomputing Center through the allocation NSF-funded ACCESS #MCB100140. The authors thank Dr. Quentin Michaudel, Dr. Ryan Hayward, Dr. Nitish Nair, Dr. Zijie Wu and Mr. Stephen Kronenberger for valuable input during this work.References
- R. W. Kulow, J. W. Wu, C. Kim and Q. Michaudel, Chem. Sci., 2020, 11, 7807–7812 RSC.
- J. W. Wu, R. W. Kulow, M. J. Redding, A. J. Fine, S. M. Grayson and Q. Michaudel, ACS Polym. Au, 2023, 3, 259–266 CrossRef CAS PubMed.
- B. Gong, C. Zheng, E. Skrzypczak-Jankun and J. Zhu, Org. Lett., 2000, 2, 3273–3275 CrossRef CAS PubMed.
- C. M. Roland, J. N. Twigg, Y. Vu and P. H. Mott, Polymer, 2007, 48, 574–578 CrossRef CAS.
- J. A. Pathak, J. N. Twigg, K. E. Nugent, D. L. Ho, E. K. Lin, P. H. Mott, C. G. Robertson, M. K. Vukmir, T. H. Epps and C. M. Roland, Macromolecules, 2008, 41, 7543–7548 CrossRef CAS.
- Y. P. Ni, F. Becquart, J. D. Chen and M. Taha, Macromolecules, 2013, 46, 1066–1074 CrossRef CAS.
- T. Li, C. Zhang, Z. N. Xie, J. Xu and B. H. Guo, Polymer, 2018, 145, 261–271 CrossRef CAS.
- Y. Chonan, G. Matsuba, K. Nishida and W. B. Hu, Polymer, 2021, 213, 123201 CrossRef CAS.
- M. Manav and M. Ortiz, Polymer, 2021, 212, 123109 CrossRef CAS.
- B. Shojaei, M. Najafi, A. Yazdanbakhsh, M. Abtahi and C. Zhang, Polym. Adv. Technol., 2021, 32, 2797–2812 CrossRef CAS.
- R. Zhang, W. Huang, P. Lyu, S. Yan, X. Wang and J. Ju, Polymers, 2022, 14(13), 2670 CrossRef CAS PubMed.
- M. Madelatparvar, M. S. Hosseini and C. Zhang, Nanotechnol. Rev., 2023, 12, 20220516 CrossRef CAS.
- Z. P. Zhang, L. Qian, J. F. Cheng, Q. Y. Xie, C. F. Ma and G. Z. Zhang, Chem. Mater., 2023, 35, 1806–1817 CrossRef CAS.
- Z. Wu, J. W. Wu, Q. Michaudel and A. Jayaraman, Macromolecules, 2023, 56, 5033–5049 CrossRef CAS PubMed.
- L. S. Teo, C. Y. Chen and J. F. Kuo, Macromolecules, 1997, 30, 1793–1799 CrossRef CAS.
- S.-K. Wang and C. S. P. Sung, Macromolecules, 2002, 35, 883–888 CrossRef CAS.
- I. Yilgor, B. D. Mather, S. Unal, E. Yilgor and T. E. Long, Polymer, 2004, 45, 5829–5836 CrossRef CAS.
- Y. He, D. L. Xie and X. Y. Zhang, J. Mater. Sci., 2014, 49, 7339–7352 CrossRef CAS.
- H. El Hatka, Y. Hafidi and N. Ittobane, Polym. Polym. Compos., 2023, 31 DOI:10.1177/09673911231196380.
- P. J. Flory and D. Y. Yoon, Nature, 1978, 272, 226–229 CrossRef CAS.
- S. Balijepalli and G. C. Rutledge, Comput. Theor. Polym. Sci., 2000, 10, 103–113 CrossRef CAS.
- A. Galeski, Prog. Polym. Sci., 2003, 28, 1643–1699 CrossRef CAS.
- D. M. Bigg, Polym. Eng. Sci., 2004, 28, 830–841 CrossRef.
- S. Doroudiani, C. B. Park and M. T. Kortschot, Polym. Eng. Sci., 2004, 36, 2645–2662 CrossRef.
- R. Seguela, J. Polym. Sci., Part B: Polym. Phys., 2005, 43, 1729–1748 CrossRef CAS.
- C. Regrain, L. Laiarinandrasana, S. Toillon and K. Saï, Int. J. Plast., 2009, 25, 1253–1279 CrossRef CAS.
- J. M. Kim, R. Locker and G. C. Rutledge, Macromolecules, 2014, 47, 2515–2528 CrossRef CAS.
- N. Lempesis, P. J. in‘t Veld and G. C. Rutledge, Macromolecules, 2016, 49, 5714–5726 CrossRef CAS.
- R. Ranganathan, V. Kumar, A. L. Brayton, M. Kröger and G. C. Rutledge, Macromolecules, 2020, 53, 4605–4617 CrossRef CAS.
- D. Barba, A. Arias and D. Garcia-Gonzalez, Int. J. Solids Struct., 2020, 182–183, 205–217 CrossRef CAS.
- C. Y. Li, Polymer, 2020, 211, 123150 CrossRef CAS.
- J. Mattia and P. Painter, Macromolecules, 2007, 40, 1546–1554 CrossRef CAS.
- T. E. Gartner and A. Jayaraman, Macromolecules, 2019, 52, 755–786 CrossRef CAS.
- A. F. Ghobadi and A. Jayaraman, J. Phys. Chem. B, 2016, 120, 9788–9799 CrossRef CAS PubMed.
- J. E. Condon, T. B. Martin and A. Jayaraman, Soft Matter, 2017, 13, 2907–2918 RSC.
- A. Kulshreshtha, K. J. Modica and A. Jayaraman, Macromolecules, 2019, 52, 2725–2735 CrossRef CAS.
- U. Kapoor, A. Kulshreshtha and A. Jayaraman, Polymers, 2020, 12, 2764 CrossRef CAS PubMed.
- Z. Wu, D. J. Beltran-Villegas and A. Jayaraman, J. Chem. Theory Comput., 2020, 16, 4599–4614 CrossRef CAS PubMed.
- A. Kulshreshtha, R. C. Hayward and A. Jayaraman, Macromolecules, 2022, 55, 2675–2690 CrossRef CAS.
- A. Kulshreshtha and A. Jayaraman, Macromolecules, 2022, 55, 9297–9311 CrossRef CAS.
- P. A. Taylor, S. Kronenberger, A. M. Kloxin and A. Jayaraman, Soft Matter, 2023, 19, 4939–4953 RSC.
- Z. J. Wu, A. M. Collins and A. Jayaraman, Biomacromolecules, 2024, 25, 1682–1695 CrossRef CAS PubMed.
- F. W. Starr and F. Sciortino, J. Phys.: Condens. Matter, 2006, 18, L347 CrossRef CAS PubMed.
- J. Largo, F. W. Starr and F. Sciortino, Langmuir, 2007, 23, 5896–5905 CrossRef CAS PubMed.
- F. Vargas Lara and F. W. Starr, Soft Matter, 2011, 7, 2085–2093 RSC.
- D. Bochicchio and G. M. Pavan, ACS Nano, 2017, 11, 1000–1011 CrossRef CAS PubMed.
- D. Bochicchio and G. M. Pavan, J. Phys. Chem. Lett., 2017, 8, 3813–3819 CrossRef CAS PubMed.
- N. Horst, S. Nayak, W. Wang, S. Mallapragada, D. Vaknin and A. Travesset, Soft Matter, 2019, 15, 9690–9699 RSC.
- C. Knorowski and A. Travesset, Curr. Opin. Solid State Mater. Sci., 2011, 15, 262–270 CrossRef CAS.
- J. Xia, M. Lee, P. J. Santos, N. Horst, R. J. Macfarlane, H. Guo and A. Travesset, Soft Matter, 2022, 18, 2176–2192 RSC.
- G. Milano and F. Müller-Plathe, J. Phys. Chem. B, 2005, 109, 18609–18619 CrossRef CAS PubMed.
- V. A. Harmandaris, N. P. Adhikari, N. F. A. van der Vegt and K. Kremer, Macromolecules, 2006, 39, 6708–6719 CrossRef CAS.
- E. Yilgor, E. Burgaz, E. Yurtsever and I. Yilgor, Polymer, 2000, 41, 849–857 CrossRef CAS.
- P. J. Flory, Principles of Polymer Chemistrsy, Cornell University Press, 1953 Search PubMed.
- M. Tambasco, J. E. G. Lipson and J. S. Higgins, Macromolecules, 2006, 39, 4860–4868 CrossRef CAS.
- D. J. Kozuch, W. Zhang and S. T. Milner, Polymers, 2016, 8, 241 CrossRef PubMed.
- S. Antoine, Z. Geng, E. S. Zofchak, M. Chwatko, G. H. Fredrickson, V. Ganesan, C. J. Hawker, N. A. Lynd and R. A. Segalman, Macromolecules, 2021, 54, 6670–6677 CrossRef CAS.
- P. Sotta and P. A. Albouy, Macromolecules, 2020, 53, 3097–3109 CrossRef CAS.
- T. Spyriouni and C. Vergelati, Macromolecules, 2001, 34, 5306–5316 CrossRef CAS.
- S. S. Jawalkar, S. G. Adoor, M. Sairam, M. N. Nadagouda and T. M. Aminabhavi, J. Phys. Chem. B, 2005, 109, 15611–15620 CrossRef CAS PubMed.
- C. Sandoval, C. Castro, L. Gargallo, D. Radic and J. Freire, Polymer, 2005, 46, 10437–10442 CrossRef CAS.
- J. Dudowicz, K. F. Freed and J. F. Douglas, J. Chem. Phys., 2012, 136, 064903 CrossRef PubMed.
- A. Dehghan and A.-C. Shi, Macromolecules, 2013, 46, 5796–5805 CrossRef CAS.
- M. Müller and J. J. de Pablo, Annu. Rev. Mater. Res., 2013, 43, 1–34 CrossRef.
- C. Wu, J. Polym. Sci., Part B: Polym. Phys., 2014, 53, 203–212 CrossRef.
- Q. P. Chen, J. D. Chu, R. F. DeJaco, T. P. Lodge and J. I. Siepmann, Macromolecules, 2016, 49, 3975–3985 CrossRef CAS.
- P. Knychała, K. Timachova, M. Banaszak and N. P. Balsara, Macromolecules, 2017, 50, 3051–3065 CrossRef.
- E. J. García, D. Bhandary, M. T. Horsch and H. Hasse, J. Mol. Liq., 2018, 268, 294–302 CrossRef.
- C. Li and A. Strachan, Polymer, 2018, 135, 162–170 CrossRef CAS.
- A. Ravichandran, C. C. Chen and R. Khare, J. Phys. Chem. B, 2018, 122, 9022–9031 CrossRef CAS PubMed.
- Y. Xu, H. Wu, J. Yang, R. Liu, Z. Zhou, T. Hao and Y. Nie, Comput. Mater. Sci., 2020, 172, 109297 CrossRef CAS.
- J. Ju, A. Jayaraman and R. C. Hayward, Macromolecules, 2023, 56, 4991–5000 CrossRef CAS.
- Z. Peng, N. Stingelin, H. Ade and J. J. Michels, Nat. Rev. Mater., 2023, 8, 439–455 CrossRef.
- S. Xie, K. M. Karnaukh, K.-C. Yang, D. Sun, K. T. Delaney, J. Read de Alaniz, G. H. Fredrickson and R. A. Segalman, Macromolecules, 2023, 56, 3617–3630 CrossRef CAS.
- F. Xiao, S. Deyan, X. Zhang, S. Hu and M. Xu, Polymer, 1987, 28, 2335–2345 CrossRef CAS.
- Y. D. Yoo and S. C. Kim, Polym. J., 1988, 20, 1117–1124 CrossRef CAS.
- E. Dormidontova and G. ten Brinke, Macromolecules, 1998, 31, 2649–2660 CrossRef CAS.
- E. Vargas and M. C. Barbosa, Phys. A, 1998, 257, 312–318 CrossRef CAS.
- W. Nierzwicki and B. Walczynski, J. Appl. Polym. Sci., 1990, 41, 907–915 CrossRef CAS.
- A. Aneja, G. L. Wilkes and E. G. Rightor, J. Polym. Sci., Part B: Polym. Phys., 2003, 41, 258–268 CrossRef CAS.
- Z. Luo and J. Jiang, Polymer, 2010, 51, 291–299 CrossRef CAS.
- K. Doktor, J. C. Vantourout and Q. Michaudel, Org. Lett., 2024, 26, 7501–7506 CrossRef CAS PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- P. K. Jha and R. G. Larson, Mol. Pharm., 2014, 11, 1676–1686 CrossRef CAS PubMed.
- J. Krajniak, S. Pandiyan, E. Nies and G. Samaey, J. Chem. Theory Comput., 2016, 12, 5549–5562 CrossRef CAS PubMed.
- S. H. Jamali, T. V. Westen, O. A. Moultos and T. J. H. Vlugt, J. Chem. Theory Comput., 2018, 14, 6690–6700 CrossRef CAS PubMed.
- A. Iscen, N. C. Forero-Martinez, O. Valsson and K. Kremer, J. Phys. Chem. B, 2021, 125, 10854–10865 CrossRef CAS PubMed.
- S. Li, R. Cui, C. Yu and Y. Zhou, J. Phys. Chem. B, 2022, 126, 1830–1841 CrossRef CAS PubMed.
- B. P. Prajwal, J. M. Blackwell, P. Theofanis and F. A. Escobedo, Chem. Mater., 2023, 35, 9050–9063 CrossRef CAS.
- A. A. Galata and M. Kröger, Macromolecules, 2024, 57, 5313–5329 CrossRef CAS.
- N. Lempesis, P. J. in‘t Veld and G. C. Rutledge, Macromolecules, 2017, 50, 7399–7409 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- B. Hess, H. Bekker, H. Berendsen and J. Fraaije, J. Comput. Chem., 1998, 18, 1463–1472 CrossRef.
- R. T. McGibbon, K. A. Beauchamp, M. P. Harrigan, C. Klein, J. M. Swails, C. X. Hernández, C. R. Schwantes, L.-P. Wang, T. J. Lane and V. S. Pande, Biophys. J., 2015, 109, 1528–1532 CrossRef CAS PubMed.
- J. E. Jones, Proc. R. Soc. London, 1924, 106, 463–477 CAS.
- H. C. Andersen, J. D. Weeks and D. Chandler, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in‘t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- Y. He, B. Zhu and Y. Inoue, Prog. Polym. Sci., 2004, 29, 1021–1051 CrossRef CAS.
- S.-W. Kuo, J. Polym. Res., 2008, 15, 459–486 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4lp00362d |
| This journal is © The Royal Society of Chemistry 2025 |