Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Fabrication of all-organic nanodielectrics reinforced with electrospun polymer fibres for capacitive energy storage
Stavros X.
Drakopoulos†
 *a,
Konstantinos
Loukelis†
b,
Marios
Triantafyllou-Rundell
b,
Constantinos C.
Stoumpos
*a,
Konstantinos
Loukelis†
b,
Marios
Triantafyllou-Rundell
b,
Constantinos C.
Stoumpos
 b,
Maria
Chatzinikolaidou
b,
Maria
Chatzinikolaidou
 bc and
Georgios C.
Psarras
bc and
Georgios C.
Psarras
 d
d
aPrinceton Materials Institute, Princeton University, Princeton, New Jersey 08544, USA. E-mail: sd5541@princeton.edu
bDepartment of Materials Science and Engineering, University of Crete, Heraklion, 70013, Greece
cInstitute of Electronic Structure and Laser (IESL), Foundation for Research and Technology Hellas (FORTH), Heraklion, 70013, Greece
dSmart Materials & Nanodielectrics Laboratory, Department of Materials Science, University of Patras, Patras, 26504, Greece
First published on 4th June 2025
Abstract
Advancements in all-organic dielectrics are crucial for electrical energy storage devices and flexible electronics due to their low cost and easier processability compared to inorganic materials for similar applications. In the present work, epoxy-based all-organic nanodielectric materials were developed for capacitive energy storage applications. To be employed as fillers, nanofibres were developed by means of electrospinning, utilizing two polymers, polyvinyl alcohol (PVA) and chitosan (CS). Three cases were examined with nanofibers consisting of pure PVA (5% w/w in epoxy) and PVA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CS in weight ratios of 5
CS in weight ratios of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 5
1 and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (both 4% w/w in epoxy). The morphological, structural, thermal and dielectric properties of the developed polymer nanodielectric materials were extensively investigated, with a clear focus on their ability to store and recover energy in a capacitor configuration. The presence of CS appeared to significantly increase the dielectric permittivity and restrict charge transport, which is beneficial for energy recovery efficiency, attributed to its strongly insulating nature.
2 (both 4% w/w in epoxy). The morphological, structural, thermal and dielectric properties of the developed polymer nanodielectric materials were extensively investigated, with a clear focus on their ability to store and recover energy in a capacitor configuration. The presence of CS appeared to significantly increase the dielectric permittivity and restrict charge transport, which is beneficial for energy recovery efficiency, attributed to its strongly insulating nature.
1. Introduction
Polymers and polymer composites are important industrial materials that find utility in various products, from everyday items to high-end biomedical and aerospace applications.1–4 Most polymers are characterized by significant electrical resistivity; thus, various polymers and their nanocomposites (polyolefins, vinyl-based polymers, epoxies, etc.) are used in applications involving electrical insulation.5,6 Another, less commonly known, application of polymer nanocomposites involves exploiting their dielectric properties towards the design of electrostatic capacitors in the microelectronics industry.7–11 The dielectric/electrical response of polymer nanocomposites (or nanodielectrics) is governed by interfacial properties, due to the immense interfacial area of nanofillers.12–15 The dielectric interfacial properties depend on the electrical behaviour of the individual constituents and give rise to an additional dipolar effect, namely Maxwell–Wagner–Sillars or interfacial polarization (MWS-IP).15–17 To investigate the complicated electrical response of polymer nanodielectrics, a technique called broadband dielectric spectroscopy (BDS) is often used that provides information on polarization and charge transport phenomena over broad frequency and temperature ranges.18,19The development of all-organic nanodielectrics for capacitive energy storage applications remains an active research area, focusing on key parameters like dielectric permittivity, dielectric breakdown, dielectric loss, cycle life and efficiency.20,21 Compared with typical polymer nanocomposites, all-organic nanodielectrics have been proven to be advantageous towards continuous industrial production.22,23 Additionally, the absence of inorganic fillers does not compromise the dielectric breakdown strength of the nanodielectric material, a common issue in polymer/ceramic nanocomposites.24 As with regular polymer nanocomposites, the interface between the various constituents in an all-organic nanodielectric system plays a significant role in the resulting dielectric performance.16,22 An efficient method to control the interfacial interactions in energy materials is by fabricating fibres via electrospinning,25–27 a method that can be extended towards the development of all-organic nanodielectrics.
The technique of electrospinning is a popular manufacturing method, increasingly employed over the last 15 years to produce polymer fibres of various sizes, porosities and orientations.27,28 In order to tune the properties and the morphology of the resulting electrospun fibres, factors like the dc voltage between the spinneret and the conductive collector and the viscosity of the polymer solution or melt are taken into account.29 Electrospinning is particularly important in the development of new materials in the biomedical sector, including tissue engineering,29,30 drug delivery,31–34 and wound dressings.35–38 In sustainability applications, electrospun materials have been used as filter membranes for microplastic filtration.39 Finally, in the field of energy storage, electrospinning has found applications in nanogenerators, actuators and sensors, for example, in the case of PVDF fibres or PVDF derivatives due to their piezoelectric properties,40–46 and as separators in batteries.47
In this study, fully organic nanodielectrics were engineered using an epoxy resin matrix reinforced with electrospun nanofibres. The nanofibres consist of PVA or PVA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CS blends in 5
CS blends in 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 5
1 and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratios, resulting in ultrathin electrospun nanofibres as determined via scanning electron microscopy (SEM). After the implementation of the nanofibres in the epoxy matrix, their presence was observed to improve the thermal, dielectric, and capacitive properties as opposed to the plain epoxy resin.Their presence introduced interfaces that restricted charge transport while promoting interfacial polarization. Notably, the inclusion of chitosan within the electrospun fibres further improved the dielectric response, contributing to superior material performance.
2 ratios, resulting in ultrathin electrospun nanofibres as determined via scanning electron microscopy (SEM). After the implementation of the nanofibres in the epoxy matrix, their presence was observed to improve the thermal, dielectric, and capacitive properties as opposed to the plain epoxy resin.Their presence introduced interfaces that restricted charge transport while promoting interfacial polarization. Notably, the inclusion of chitosan within the electrospun fibres further improved the dielectric response, contributing to superior material performance.
2. Experimental
2.1. Materials and sample preparation
A commercially available two-part epoxy resin was employed as the matrix material in the developed nanocomposites, namely, ER2223 (Electrolube Ltd, Leicestershire, UK), specifically designed for electronics applications. The epoxy resin consists of an uncured pre-polymer and a curing agent, i.e., the hardener. The pre-polymer is based on 4,4′-(propane-2,2-diyl)diphenol-(epichlorohydrin) (CAS No.: 25068-38-6) and the hardener is 4,4′-methylenedi(cyclohexan-1-amine) (CAS No.: 1761-71-3). The manufacturer also includes 2-[6-(oxiran-2-ylmethoxy)hexoxymethyl]oxirane (CAS No.: 16096-31-4) in the mixture as a reactive diluent. The epoxide rings in 4,4′-(propane-2,2-diyl)diphenol-(epichlorohydrin) react with the primary amine groups in 4,4′-methylenedi(cyclohexan-1-amine) through nucleophilic attack, leading to ring opening and the formation of hydroxyl groups. This process allows crosslinking between multiple epoxide and amine sites, creating a rigid, thermosetting epoxy resin with high mechanical and thermal stability that consists of ether linkages. As fillers, polyvinyl alcohol (PVA) (CAS No.: 9002-89-5) and chitosan (CS) (CAS No.: 9012-76-4) nanofibre blends were developed based on commercially available raw materials. 99% hydrolysed (or higher) PVA powder was purchased from Sigma Aldrich with an average molecular weight ranging from 89![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 98
000 to 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 and a density of 1.19–1.31 g cm−3. 75% deacetylated (or higher) CS powder with a bulk density ranging between 0.15 and 0.3 g cm−3 was also obtained from Sigma Aldrich. To facilitate electrospinning, a non-ionic surfactant, namely, 1,4-Anhydro-D-glucitol 6-[(9Z)-octadec-9-enoate], i.e., Span® 80 (CAS No.: 1338-43-8), was used as purchased from the same company.
000 g mol−1 and a density of 1.19–1.31 g cm−3. 75% deacetylated (or higher) CS powder with a bulk density ranging between 0.15 and 0.3 g cm−3 was also obtained from Sigma Aldrich. To facilitate electrospinning, a non-ionic surfactant, namely, 1,4-Anhydro-D-glucitol 6-[(9Z)-octadec-9-enoate], i.e., Span® 80 (CAS No.: 1338-43-8), was used as purchased from the same company.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1weight ratio in water with an additional 1% v/v acetic acid and (iii) 7% w/w PVA/CS blend in a 5
1weight ratio in water with an additional 1% v/v acetic acid and (iii) 7% w/w PVA/CS blend in a 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
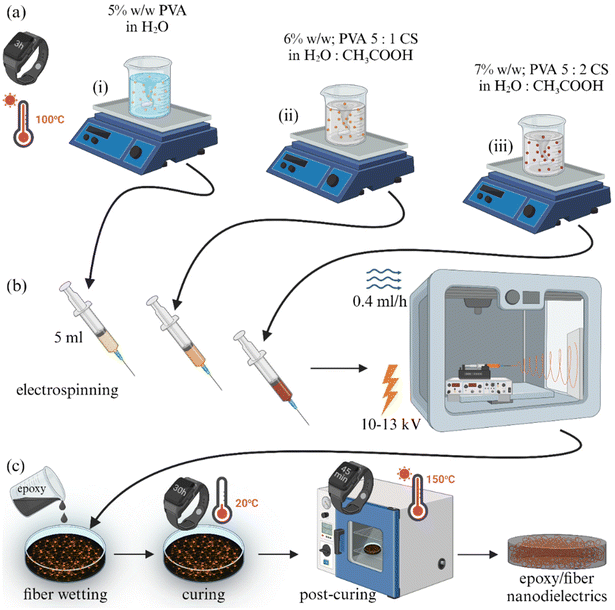
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 weight ratio in water with an additional 1% v/v acetic acid. The acetic acid is expected to evaporate during the electrospinning process due to its volatility.48 In that way, the presence of PVA in the solution was kept constant at 5% w/w in all cases. In order to facilitate the electrospinning process, the non-ionic surfactant Span® 80 was added to each polymer solution at a concentration of 0.2% v/v at the initial mixing stages, due to its surface tension reduction capability, as established by some of us in a previous study.49 Considering that Span® 80 was used at very low concentrations in the preparation of the nanofibrous mat and then implemented in the epoxy resin, we do not expect any effects on the dielectric response.50 Then, 5 ml of each composition were aspirated using a plastic syringe and mounted onto a custom-designed electrospinning device (CommonsLab SCE, Heraklion, Greece). The plunger component of the syringe was driven by an electronic extrusion control platform, while at the end part of the syringe, an 18-gauge metallic spinneret needle was attached and later connected to a syringe pump. For the electrospinning process, a positive electrode clip was fixed to the needle, and a negative electrode clip was connected to a metallic plate (collector) covered with aluminium foil. The distance between the needle tip and the cathode collector plate was kept constant at 12 cm. Electrospinning was conducted at a set speed of 0.4 ml h−1, while the voltage values ranged between 10 and 13 kV. Finally, the electrospun PVA-based scaffolds were subsequently extracted from the aluminium foil that covered the cathode collector. The procedure is shown schematically in Fig. 1.
2 weight ratio in water with an additional 1% v/v acetic acid. The acetic acid is expected to evaporate during the electrospinning process due to its volatility.48 In that way, the presence of PVA in the solution was kept constant at 5% w/w in all cases. In order to facilitate the electrospinning process, the non-ionic surfactant Span® 80 was added to each polymer solution at a concentration of 0.2% v/v at the initial mixing stages, due to its surface tension reduction capability, as established by some of us in a previous study.49 Considering that Span® 80 was used at very low concentrations in the preparation of the nanofibrous mat and then implemented in the epoxy resin, we do not expect any effects on the dielectric response.50 Then, 5 ml of each composition were aspirated using a plastic syringe and mounted onto a custom-designed electrospinning device (CommonsLab SCE, Heraklion, Greece). The plunger component of the syringe was driven by an electronic extrusion control platform, while at the end part of the syringe, an 18-gauge metallic spinneret needle was attached and later connected to a syringe pump. For the electrospinning process, a positive electrode clip was fixed to the needle, and a negative electrode clip was connected to a metallic plate (collector) covered with aluminium foil. The distance between the needle tip and the cathode collector plate was kept constant at 12 cm. Electrospinning was conducted at a set speed of 0.4 ml h−1, while the voltage values ranged between 10 and 13 kV. Finally, the electrospun PVA-based scaffolds were subsequently extracted from the aluminium foil that covered the cathode collector. The procedure is shown schematically in Fig. 1.
| Sample | Epoxy (% w/w) | PVA (% w/w) | Chitosan (% w/w) |
|---|---|---|---|
| Epoxy | 100 | — | — |
| e95(PVA)f5 | 95.0 | 5.00 | — |
e96(PVA5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1CS)f4 1CS)f4 |
96.0 | 3.33 | 0.67 |
e96(PVA5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2CS)f4 2CS)f4 |
96.0 | 2.86 | 1.14 |
2.2. Materials characterization
3. Results and discussion
3.1. Morphology and structure of the electrospun nanofibrous membranes
The surface morphology of the nanofibrous membranes prepared by means of electrospinning was evaluated via SEM images shown in Fig. 2. SEM imaging revealed the formation of elongated fibres, with diameters in the range of a few hundred nanometres. In the case of the (PVA)f sample, more than 50% of the fibre width measurements were found to be in the range of 100–150 nm, whereas the implementation of CS tended to increase the proportion of fibres in the 150–200 nm range. The small-scale differences captured between the three variants can be ascribed to the relatively low amounts of CS mass integration, imposed by electrospinnability processing limitations.51 Minimal bead-like formulations were also evident in all nanofibrous membranes, with no apparent frequency discrepancies among the different compositions. Based on the obtained average fibre thickness and thickness distribution, there are no significant differences expected toward the resulting interfacial area between the epoxy matrix and the nanofibres.Chemical and structural information is provided in Fig. 3, by means of FTIR and XRD, respectively. The chemical composition and integrity of the electrospun membranes and their resulting composites were assessed via FTIR spectroscopy (Fig. 3a). The spectra of CS and PVA were obtained in powder and crystalline forms, respectively. CS exhibited characteristic peaks at 1153 cm−1, 1030 cm−1, 1654 cm−1, and 1587 cm−1, which can be ascribed to C–O–C stretching, C–O stretching, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching (residual N-acetyl groups) and N–H bending, respectively.52 An additional peak at 1320 cm−1 corresponds to C–N stretching. A broad band was evident in the regime of 3600–3200 cm−1, indicative of the C–H, N–H and O–H stretching modes. Pure PVA exhibited a similar but wider band in the same regime, peaking at 3250 cm−1, also due to O–H stretching, with the emersion of two more peaks at 2940 cm−1 and 1420 cm−1, corresponding to C–H bond stretching and bending, respectively, and two additional ones at 1320 cm−1 and 1080 cm−1, which can be attributed to the presence of C–O bonds. The electrospun scaffolds showed similar characteristic peaks to those of their base ingredients, with a stronger inclination towards the pure PVA spectrum, due to its higher mass content compared to CS.53 Pure epoxy and epoxy composite scaffolds exhibited the characteristic vibrational bands of epoxy resin,54 including peaks at 820 cm−1 and 910 cm−1 representative of the C–O–C and C–O stretching respectively and a peak at 1240 cm−1, which is typical of C–O asymmetrical stretch present in the epoxy resin aromatic groups. Moreover, two additional peaks at 1510 cm−1 and 1610 cm−1 were assigned to the contribution of the epoxy resin, due to the C–C and C
O stretching (residual N-acetyl groups) and N–H bending, respectively.52 An additional peak at 1320 cm−1 corresponds to C–N stretching. A broad band was evident in the regime of 3600–3200 cm−1, indicative of the C–H, N–H and O–H stretching modes. Pure PVA exhibited a similar but wider band in the same regime, peaking at 3250 cm−1, also due to O–H stretching, with the emersion of two more peaks at 2940 cm−1 and 1420 cm−1, corresponding to C–H bond stretching and bending, respectively, and two additional ones at 1320 cm−1 and 1080 cm−1, which can be attributed to the presence of C–O bonds. The electrospun scaffolds showed similar characteristic peaks to those of their base ingredients, with a stronger inclination towards the pure PVA spectrum, due to its higher mass content compared to CS.53 Pure epoxy and epoxy composite scaffolds exhibited the characteristic vibrational bands of epoxy resin,54 including peaks at 820 cm−1 and 910 cm−1 representative of the C–O–C and C–O stretching respectively and a peak at 1240 cm−1, which is typical of C–O asymmetrical stretch present in the epoxy resin aromatic groups. Moreover, two additional peaks at 1510 cm−1 and 1610 cm−1 were assigned to the contribution of the epoxy resin, due to the C–C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds in aromatic rings and asymmetrical C–H stretch groups, respectively, as well as multiple smaller peaks centred around the 2950 cm−1 regime, due to C–H bond stretching.
C bonds in aromatic rings and asymmetrical C–H stretch groups, respectively, as well as multiple smaller peaks centred around the 2950 cm−1 regime, due to C–H bond stretching.
 | ||
| Fig. 3 Structural information for all samples under study at room temperature obtained by means of (a) FTIR and (b) XRD. | ||
The amorphous nature of all the composites presented here was determined through X-ray diffraction (XRD) (Fig. 3b). In order to discern the contribution of the electrospun fibres to the epoxy resin, we first investigated them individually. All electrospun membranes showed that there is no periodicity in the structure, as opposed to their base components, a tendency that has been described in the literature for polymeric solutions.55,56 It is interesting to note, however, that the electrospun fibres that contain more chitosan, namely (PVA5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2)f, showed some signs of short-range periodic order exhibiting a higher intensity peak at 2θ = 20°, showcasing the impact of chitosan concentration on crystallinity status. As expected, the epoxy matrix is purely amorphous14 and given the low crystallinity levels of the fibres and low fibrous concentration, all the nanocomposite samples show no signs of crystallinity. Therefore, all epoxy-based scaffolds exhibited a broad band centred around 20°, attributed to the amorphous halo.
2)f, showed some signs of short-range periodic order exhibiting a higher intensity peak at 2θ = 20°, showcasing the impact of chitosan concentration on crystallinity status. As expected, the epoxy matrix is purely amorphous14 and given the low crystallinity levels of the fibres and low fibrous concentration, all the nanocomposite samples show no signs of crystallinity. Therefore, all epoxy-based scaffolds exhibited a broad band centred around 20°, attributed to the amorphous halo.
3.2. Thermal properties
In Fig. 4, the thermoanalytical curves of the developed all-organic nanodielectric materials are displayed, as examined via DSC (Fig. 4a) and TGA (Fig. 4b). To account also for the individual thermal behaviour of the fibres, we included them as dotted lines. The PVA-based fibres clearly show two major thermal events. According to DSC, at approximately 80–85 °C, the calorimetric Tg of PVA is visible, and at around 220 °C the melting of the crystalline phase takes place.57 Pure epoxy exhibits its calorimetric Tg at approximately 100 °C but the step is very broad. With the addition of the PVA-based nanofibres to the epoxy resin, the epoxy's calorimetric Tg becomes better defined. According to the epoxy resin manufacturer, this polymer has a thermal decomposition temperature of 180 °C; hence, we measured the samples up to 160 °C. It is interesting to note that the epoxy Tg values observed here are lower than the values we reported in the past for this specific epoxy resin.14,58 We attribute this variation to differences in the manufacturing process, since in the present case, we performed the initial curing process at room temperature for over 24 h, to ensure good wetting of the nanofibres.The thermal stability of the different nanofibrous membranes and the equivalent epoxy composites was also investigated via TGA (Fig. 4b.) PVA decomposition primarily takes place in the range of 300–500 °C, degrading completely above 650 °C. Electrospun membranes depicted similar temperature-dependent behaviour to those of their base constituents, having already been described thoroughly in a previous study.53 The composite scaffolds showed a comparable thermal disintegration profile to that of the epoxy control, typical of other epoxy-based structures.59 On that note, samples appeared to retain their initial mass at pristine levels up to 400 °C. However, in the regime of 400–470 °C, all scaffolds lost more than 90% of their mass, and by 700 °C, appeared to have fully disintegrated, independently of the encapsulated membrane's chemical composition.
3.3. Dielectric response
The frequency-dependent dielectric properties are most often presented via the complex dielectric permittivity, ε*, which is defined according to eqn (1) shown below:| ε* (ω) = ε′ (ω) − iε′′ (ω) | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 61–63 which is significantly lower than the increase we observe around 100 °C (the calorimetric Tg according to DSC presented in Fig. 4a). As shown by the ε′′ values (Fig. 5b), the segmental relaxation of the epoxy resin is visible in the vicinity of 100 °C for the nanodielectric samples, but not for the plain epoxy sample. Consequently, we attribute the enhancement of the dielectric permittivity values to the co-existence of more complex phenomena. In heterogeneous dielectric materials, a polarization effect is observed, namely, the Maxwell–Wagner–Sillars interfacial polarization (MWS-IP) processes. The interfacial polarization is caused by the mismatch in electrical properties (i.e. in dielectric permittivity and electrical conductivity) between the sample's individual materials, which results in the entrapment of charge carriers and the formation of dipoles at the interfaces.16 MWS-IP is expected to contribute to all samples under study, including the plain epoxy due to impurities and/or residual hardener traces.58 It should be noted that since the calorimetric Tg values of the epoxy resin and the PVA-based nanofibres are very close as discussed earlier in Fig. 4a, the broad peak we observe in Fig. 5b could also be due to the superposition of the 2 segmental relaxation processes (epoxy and PVA-based nanofibres).
61–63 which is significantly lower than the increase we observe around 100 °C (the calorimetric Tg according to DSC presented in Fig. 4a). As shown by the ε′′ values (Fig. 5b), the segmental relaxation of the epoxy resin is visible in the vicinity of 100 °C for the nanodielectric samples, but not for the plain epoxy sample. Consequently, we attribute the enhancement of the dielectric permittivity values to the co-existence of more complex phenomena. In heterogeneous dielectric materials, a polarization effect is observed, namely, the Maxwell–Wagner–Sillars interfacial polarization (MWS-IP) processes. The interfacial polarization is caused by the mismatch in electrical properties (i.e. in dielectric permittivity and electrical conductivity) between the sample's individual materials, which results in the entrapment of charge carriers and the formation of dipoles at the interfaces.16 MWS-IP is expected to contribute to all samples under study, including the plain epoxy due to impurities and/or residual hardener traces.58 It should be noted that since the calorimetric Tg values of the epoxy resin and the PVA-based nanofibres are very close as discussed earlier in Fig. 4a, the broad peak we observe in Fig. 5b could also be due to the superposition of the 2 segmental relaxation processes (epoxy and PVA-based nanofibres).
 | ||
| Fig. 5 The (a) real and (b) imaginary parts of dielectric permittivity as a function of temperature at 0.1 Hz, for all samples under study. (a) Inset magnifies the ε′ values in the temperature range of 30–100 °C. (b) Inset (I) shows the calculation of dc conductivity based on eqn (2), and inset (II) presents the corresponding calculated values for the various samples (the x-axis is for the eyes only). | ||
Enhanced dielectric losses are indicative of the strong contribution of dc conductivity solely to ε′′. Given the thermally activated nature of dc conductivity, the dielectric losses, especially at high temperatures and low frequencies are high and often mask the dipolar response. To determine the dc conductivity value at 160 °C for all samples under study, we employ eqn (3) that allows the accurate estimation of σdc from the frequency-dependent dielectric response:17,64
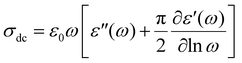 | (2) |
The term (−π/2)(∂ε′/∂ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω) corresponds to derivative permittivity
ω) corresponds to derivative permittivity  , which approximately corresponds to the dipolar part of the imaginary part of dielectric permittivity (omitting the Ohmic conduction part).65 The fittings of eqn (2) are presented in Fig. 5b inset I and the obtained dc conductivity values are shown in inset II. Eqn (2) was applied only in the frequency range of 10−1 to 100 Hz, where the dc conductivity contribution to the imaginary part of dielectric permittivity is prominent; thus, the calculation is not affected by mathematical artifacts.66 Particularly in the case of e95(PVA)f5, the enhanced dc conductivity values might facilitate the parasitic effect of electrode polarization (EP), compared to the plain epoxy and the chitosan-containing sample, leading to ε′ > 100. EP is caused by the immobilization of charge carriers at the interface between the capacitor's electrodes and the dielectric sample that produce very large dipoles that significantly enhance ε′ and ε′′.67,68 As shown in Inset II of Fig. 5b, e95(PVA)f5 is the most conductive sample, which explains the stronger presence of the EP effect as opposed to the rest of the samples.
, which approximately corresponds to the dipolar part of the imaginary part of dielectric permittivity (omitting the Ohmic conduction part).65 The fittings of eqn (2) are presented in Fig. 5b inset I and the obtained dc conductivity values are shown in inset II. Eqn (2) was applied only in the frequency range of 10−1 to 100 Hz, where the dc conductivity contribution to the imaginary part of dielectric permittivity is prominent; thus, the calculation is not affected by mathematical artifacts.66 Particularly in the case of e95(PVA)f5, the enhanced dc conductivity values might facilitate the parasitic effect of electrode polarization (EP), compared to the plain epoxy and the chitosan-containing sample, leading to ε′ > 100. EP is caused by the immobilization of charge carriers at the interface between the capacitor's electrodes and the dielectric sample that produce very large dipoles that significantly enhance ε′ and ε′′.67,68 As shown in Inset II of Fig. 5b, e95(PVA)f5 is the most conductive sample, which explains the stronger presence of the EP effect as opposed to the rest of the samples.
It is evident from inset II of Fig. 5b that the addition of the PVA nanofibres facilitates electrical conduction, thus increasing the σdc values by 4 times. This is no surprise since PVA is significantly less resistive than the plain epoxy employed here, with the PVA conductivity value at 100 °C being 6.15 × 10−9 S cm−1 (ref. 69) as opposed to 1.81 × 10−13 S cm−1 for epoxy, as measured here. The PVA nanofibres create a cohesive network inside the epoxy resin, which is the least resistive path and thus is preferred by the mobile charge carriers. However, the addition of chitosan was observed to significantly restrict conduction and thus decrease σdc values by an order of magnitude or more. Under the assumption that there are short but distinctive PVA and chitosan areas that constitute every nanofibre, the least resistive PVA paths are interrupted by the presence of chitosan. This inevitably leads to charge trapping at the interfaces between PVA and chitosan that results in a significant reduction of the overall σdc of the samples.27 In addition, compared to charge transport observed in the plain epoxy resin, the fact that the chitosan containing samples, e96(PVA5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1CS)f4 and e96(PVA5
1CS)f4 and e96(PVA5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2CS)f4, exhibit lower dc conductivity values than epoxy (by approximately 50 and 25 times, respectively) leads us to the conclusion that charge trapping occurs at the matrix/fibre interface as well.
2CS)f4, exhibit lower dc conductivity values than epoxy (by approximately 50 and 25 times, respectively) leads us to the conclusion that charge trapping occurs at the matrix/fibre interface as well.
As a result of the suppression of charge transport in the presence of chitosan, even at the lowest measured frequency and highest temperature where conductivity losses are expected to contribute to their maximum, the ε′′/ε′ values do not exceed unity. This is indicative of the reinforcing effect that chitosan has on the dielectric properties for capacitor applications, a point that later is going to be discussed further. At 150 °C a rise in the ε′′ values is observed for the chitosan-containing samples, which corresponds to contributions from both σdc and σ-relaxation.70 The presence of σ-relaxation is very typical in carbohydrate polymers and corresponds to the migration of the hydrogen ions as a result of the sufficient residue of hydroxyl groups.71 In our systems, PVA provides additional hydroxyl groups, thus assisting the migration of hydrogen ions.
3.4. Capacitive energy storage and recovery
In a previous study, we observed that the presence of electrospun nanofibres can significantly improve the ability of polymer-based materials to effectively store capacitive energy.27 To test the ability of the developed all-organic epoxy-based nanodielectrics here, we applied 100, 300, and 500 V, each for 60 s (charging step) and then reduced the applied voltage to zero to completely discharge the capacitor for at least 300 s. Below, the stored and recovered energy densities, Us and Ur, were obtained using eqn (3) and (4):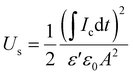 | (3) |
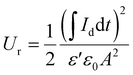 | (4) |
 | (5) |
Fig. 6a shows the experimentally measured direct current over time at 30 °C for the e96(PVA5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1CS)f4 sample, represented as lines. The dc charge current is shown for all three measured voltages (100, 300, and 500 V), along with their corresponding discharge current data obtained after the removal of the voltages. After the application of the dc voltage during the capacitor's charging step, the current progressively decreases over time until it reaches a constant value that corresponds to leakage current due to the charge carriers flowing through the sample/electrode interface. As soon as the dc voltage is removed, the discharge current takes negative values that gradually reach zero indicating that the capacitor is discharged under these temperature/time/voltage conditions. The stored and recovered energy density values, calculated based on eqn (3) and (4), are shown as open symbols. As observed in Fig. 6, both stored/recovered energy density values strongly depend on charging/discharging time with values increasing by almost three orders of magnitude within 60 s.
1CS)f4 sample, represented as lines. The dc charge current is shown for all three measured voltages (100, 300, and 500 V), along with their corresponding discharge current data obtained after the removal of the voltages. After the application of the dc voltage during the capacitor's charging step, the current progressively decreases over time until it reaches a constant value that corresponds to leakage current due to the charge carriers flowing through the sample/electrode interface. As soon as the dc voltage is removed, the discharge current takes negative values that gradually reach zero indicating that the capacitor is discharged under these temperature/time/voltage conditions. The stored and recovered energy density values, calculated based on eqn (3) and (4), are shown as open symbols. As observed in Fig. 6, both stored/recovered energy density values strongly depend on charging/discharging time with values increasing by almost three orders of magnitude within 60 s.
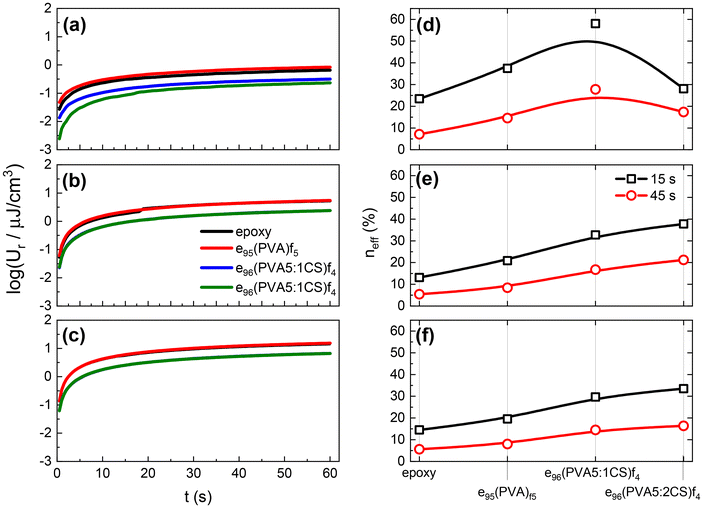
Fig. 7 shows the recovered energy density Ur values as a function of time for all the samples under study after the removal of the dc voltages, namely 100, 300, and 500 V, presented in Fig. 7a, b, and c, respectively. As discussed in Fig. 6, in all cases the Ur values increase over time, reaching a constant value that corresponds to the maximum value that can be recovered under these temperature/time/voltage conditions. With increasing dc voltage, the stored energy density values increase resulting in enhanced recovered energy density values, as shown in Fig. 7a and b. It is evident that the presence of chitosan significantly affects the obtained Ur values. The four samples appear to fall into two categories based on their response, with the plain epoxy and the e95(PVA)f5 samples showing higher Ur values by 2–3 times than the chitosan-containing samples. We attribute the observed differences to the resistive effect that chitosan introduces, thus reducing both the stored and recovered capability of the developed systems. However, reducing the overall conductivity of the nanodielectrics by introducing a resistive phase that disrupts the “less resistive” paths (as discussed earlier in Fig. 5) is beneficial as it is expected to diminish the leakage currents and thus increase the efficiency of the capacitors. Indeed, our findings support exactly this notion, as presented in Fig. 7d–f.
The efficiency, neff, of the examined nanodielectrics calculated at 15 and 45 s is presented in Fig. 7d–f at increasing voltages. It is evident that the presence of electrospun nanofibres is beneficial for the efficiency performance of the systems with all nanodielectrics achieving higher values than the plain epoxy. This effect is attributed to charge trapping at the matrix/fibre interface that restricts the leakage current during charging, which leads to lost charge carriers and thus capacitive energy. Based on the discussion at an earlier point in the manuscript, an enhancement of neff values with the addition of chitosan is expected, which indeed is the case. Especially at the highest applied dc voltage (i.e. 500 V) presented in Fig. 7f, the chitosan-containing samples exhibit neff values that are double those of the plain epoxy and the e95(PVA)f5 systems under the same conditions.
4. Conclusions
In the present work, epoxy-based all-organic nanodielectric materials reinforced with electrospun nanofibres were developed for capacitive energy storage applications. The nanofibres are based on PVA or PVA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CS blends in 5
CS blends in 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 5
1 and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratios. The developed nanodielectrics were extensively studied using various techniques like SEM, FTIR, XRD, DSC, TGA, BDS and dc charge/discharge methods to understand their morphological, structural, thermal and dielectric properties, respectively. Within this study, a particular focus was placed on their dielectric properties and their ability to store and recover energy in a capacitor configuration. The addition of electrospun nanofibres in the epoxy matrix introduces interfaces that hinder charge transport and promote interfacial polarization, particularly in the case of CS. From room temperature up to 100 °C, small additions of CS (on the order of 0.67 to 1.14% w/w) as part of the nanofibrous membranes were observed to double the dielectric permittivity. Moreover, CS significantly restricted electrical conductivity at high temperatures by 25 to 50 times that of the pure epoxy resin, resulting in a significant improvement in the capacitor energy recovery efficiency. Research towards the development of all-organic dielectrics is important for advanced energy storage devices and flexible electronics due to their low cost and easier processability compared to inorganic materials. Finally, the nanofibrous membranes are based on two biocompatible components, namely, the synthetic polymer PVA and the naturally derived polysaccharide chitosan; hence, our work shows that such electrospun fibres could be part of a flexible nanocomposite for bioelectronic applications.
2 ratios. The developed nanodielectrics were extensively studied using various techniques like SEM, FTIR, XRD, DSC, TGA, BDS and dc charge/discharge methods to understand their morphological, structural, thermal and dielectric properties, respectively. Within this study, a particular focus was placed on their dielectric properties and their ability to store and recover energy in a capacitor configuration. The addition of electrospun nanofibres in the epoxy matrix introduces interfaces that hinder charge transport and promote interfacial polarization, particularly in the case of CS. From room temperature up to 100 °C, small additions of CS (on the order of 0.67 to 1.14% w/w) as part of the nanofibrous membranes were observed to double the dielectric permittivity. Moreover, CS significantly restricted electrical conductivity at high temperatures by 25 to 50 times that of the pure epoxy resin, resulting in a significant improvement in the capacitor energy recovery efficiency. Research towards the development of all-organic dielectrics is important for advanced energy storage devices and flexible electronics due to their low cost and easier processability compared to inorganic materials. Finally, the nanofibrous membranes are based on two biocompatible components, namely, the synthetic polymer PVA and the naturally derived polysaccharide chitosan; hence, our work shows that such electrospun fibres could be part of a flexible nanocomposite for bioelectronic applications.
Author contributions
Stavros X. Drakopoulos: conceptualization, methodology, validation, formal analysis, investigation, data curation, writing – original draft, writing – review & editing, visualization, supervision, project administration, and funding acquisition. Konstantinos Loukelis: conceptualization, methodology, validation, formal analysis, investigation, data curation, writing – original draft, writing – review & editing, and project administration. Marios Triantafyllou-Rundell: investigation. Constantinos C. Stoumpos: writing – review & editing, resources, and supervision. Maria Chatzinikolaidou: writing – review & editing, resources, supervision, and funding acquisition. Georgios C. Psarras: methodology, resources, writing – review & editing, supervision, and funding acquisition.Data availability
Data for this article, including BDS, TGA, DSC, FTIR, XRD, SEM, and dc charge/discharge measurements, are available from Dropbox at https://www.dropbox.com/scl/fo/v73xzh69qhlbkhen8t9ub/APQNujnPMPEPwE_iTJsdg4M?rlkey=trvrylqbcdab272quyzvx1ca4&st=dqdxgb0e&dl=0.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The authors would like to thank Electrolube Ltd (https://electrolube.com/) for supporting the current project by providing the ER2223 epoxy resin. K. L. and M. C. acknowledge financial support from the Hellenic Foundation for Research and Innovation (H.F.R.I.) project number HFRI-FM17-1999.References
- A. M. Youssef, Polym.-Plast. Technol. Eng., 2013, 52, 635–660 CrossRef CAS.
- K. S. Ngai, S. Ramesh, K. Ramesh and J. C. Juan, Ionics, 2016, 22, 1259–1279 CrossRef CAS.
- S. Ramakrishna, J. Mayer, E. Wintermantel and K. W. Leong, Compos. Sci. Technol., 2001, 61, 1189–1224 CrossRef CAS.
- J. Njuguna and K. Pielichowski, Adv. Eng. Mater., 2003, 5, 769–778 Search PubMed.
- T. Tanaka, G. C. Montanari and R. Mulhaupt, IEEE Trans. Dielectr. Electr. Insul., 2004, 11, 763–784 CrossRef CAS.
- B. Zhong, Y. Zhang, W. You and Y. Wang, RSC Appl. Polym., 2025, 3, 97–110 RSC.
- R. M. Wallace and G. D. Wilk, Crit. Rev. Solid State Mater. Sci., 2003, 28, 231–285 Search PubMed.
- Z.-M. Dang, J.-K. Yuan, J.-W. Zha, T. Zhou, S.-T. Li and G.-H. Hu, Prog. Mater. Sci., 2012, 57, 660–723 Search PubMed.
- X. Hao, J. Adv. Dielectr., 2013, 03, 1330001 Search PubMed.
- Z.-M. Dang, J.-K. Yuan, S.-H. Yao and R.-J. Liao, Adv. Mater., 2013, 25, 6334–6365 Search PubMed.
- S. Bera, R. M. Thantirige, J. Wu, E. C. Davidson, S. A. Kadam, A. V. Sumant, B. T. Shook, R. Rao, R. Selhorst, M. Singh, A. Karim, D. Raghavan and N. R. Pradhan, ACS Appl. Electron. Mater., 2024, 6, 6582–6590 CrossRef CAS.
- Z.-M. Dang, J.-K. Yuan, S.-H. Yao and R.-J. Liao, Adv. Mater., 2013, 25, 6334–6365 CrossRef CAS PubMed.
- M. Roy, J. K. Nelson, R. K. MacCrone, L. S. Schadler, C. W. Reed, R. Keefe and W. Zenger, IEEE Trans. Dielectr. Electr. Insul., 2005, 12, 629–643 CrossRef CAS.
- S. X. Drakopoulos, K. Loukelis, M. E. Triantafyllou-Rundell, C. C. Stoumpos, M. Chatzinikolaidou and G. C. Psarras, Adv. Compos. Hybrid Mater., 2024, 7, 118 CrossRef CAS.
- S. X. Drakopoulos, J. Wu, S. M. Maguire, S. Srinivasan, K. Randazzo, E. C. Davidson and R. D. Priestley, Prog. Polym. Sci., 2024, 156, 101870 CrossRef CAS.
- G. M. Tsangaris, G. C. Psarras and N. Kouloumbi, J. Mater. Sci., 1998, 33, 2027–2037 CrossRef CAS.
- S. X. Drakopoulos, J. Cui, M. Asandulesa, P. W. M. Blom, A. Nogales and K. Asadi, Macromolecules, 2024, 57, 2661–2668 CrossRef CAS.
- Broadband Dielectric Spectroscopy, ed. F. Kremer and A. Schönhals, Springer Berlin Heidelberg, Berlin, Heidelberg, 2003 Search PubMed.
- G. C. Psarras, Composites, Part A, 2006, 37, 1545–1553 CrossRef.
- V. Sharma, C. Wang, R. G. Lorenzini, R. Ma, Q. Zhu, D. W. Sinkovits, G. Pilania, A. R. Oganov, S. Kumar, G. A. Sotzing, S. A. Boggs and R. Ramprasad, Nat. Commun., 2014, 5, 4845 CrossRef CAS PubMed.
- J. Luo, J. Mao, W. Sun, S. Wang, L. Zhang, L. Tian, Y. Chen and Y. Cheng, Macromol. Chem. Phys., 2021, 222, 2100049 CrossRef CAS.
- Q.-K. Feng, S.-L. Zhong, J.-Y. Pei, Y. Zhao, D.-L. Zhang, D.-F. Liu, Y.-X. Zhang and Z.-M. Dang, Chem. Rev., 2022, 122, 3820–3878 CrossRef CAS PubMed.
- W. Ren, M. Yang, L. Zhou, Y. Fan, S. He, J. Pan, T. Tang, Y. Xiao, C. Nan and Y. Shen, Adv. Mater., 2022, 34, 2207421 CrossRef CAS PubMed.
- Z. Yang, D. Yue, Y. Yao, J. Li, Q. Chi, Q. Chen, D. Min and Y. Feng, Polymers, 2022, 14, 1160 CrossRef CAS PubMed.
- G. Liu, T. Zhang, Y. Feng, Y. Zhang, C. Zhang, Y. Zhang, X. Wang, Q. Chi, Q. Chen and Q. Lei, Chem. Eng. J., 2020, 389, 124443 CrossRef CAS.
- S. Bhattacharya, I. Roy, A. Tice, C. Chapman, R. Udangawa, V. Chakrapani, J. L. Plawsky and R. J. Linhardt, ACS Appl. Mater. Interfaces, 2020, 12, 19369–19376 CrossRef CAS PubMed.
- S. X. Drakopoulos, J. Yang, O. Vryonis, L. Williams, G. C. Psarras and E. Mele, ACS Appl. Polym. Mater., 2022, 4, 8203–8215 CrossRef CAS.
- I. K. Kouparitsas, E. Mele and S. Ronca, Polymers, 2019, 11, 677 CrossRef CAS PubMed.
- J. A. Smith and E. Mele, Front. Bioeng. Biotechnol., 2021, 9, 674738 CrossRef PubMed.
- K. Loukelis, D. Papadogianni, J. E. Kruse and M. Chatzinikolaidou, Carbohydr. Polym. Technol. Appl., 2024, 7, 100454 CAS.
- L. Williams, F. L. Hatton, H. Willcock and E. Mele, Biotechnol. Bioeng., 2022, 119, 1177–1188 CrossRef CAS PubMed.
- J. Wu, Z. Zhang, J. Gu, W. Zhou, X. Liang, G. Zhou, C. C. Han, S. Xu and Y. Liu, J. Controlled Release, 2020, 320, 337–346 CrossRef CAS PubMed.
- J. Wu, S. Xu, C. C. Han and G. Yuan, J. Controlled Release, 2021, 331, 472–479 CrossRef CAS PubMed.
- H. Chen, J. Wu, M. S. U. Rahman, S. Li, J. Wang, S. Li, Y. Wu, Y. Liu and S. Xu, Biomater. Adv., 2023, 148, 213358 CrossRef CAS PubMed.
- E. Mele, J. Mater. Chem. B, 2016, 4, 4801–4812 RSC.
- W. Zhang, S. Ronca and E. Mele, Nanomaterials, 2017, 7, 42 CrossRef PubMed.
- E. Mele, Polymers, 2020, 12, 908 CrossRef CAS PubMed.
- L. Williams, F. L. Hatton, M. C. Righetti and E. Mele, Polymers, 2024, 16, 1005 CrossRef CAS PubMed.
- M. Rist and A. Greiner, RSC Appl. Polym., 2024, 2, 642–655 RSC.
- I. Katsouras, K. Asadi, M. Li, T. B. van Driel, K. S. Kjær, D. Zhao, T. Lenz, Y. Gu, P. W. M. Blom, D. Damjanovic, M. M. Nielsen and D. M. de Leeuw, Nat. Mater., 2016, 15, 78–84 CrossRef CAS PubMed.
- C. Lee, D. Wood, D. Edmondson, D. Yao, A. E. Erickson, C. T. Tsao, R. A. Revia, H. Kim and M. Zhang, Ceram. Int., 2016, 42, 2734–2740 CrossRef CAS.
- Y. Zhao, L. Yin, S. Zhong, J. Zha and Z. Dang, IET Nanodielectr., 2020, 3, 99–106 CrossRef.
- M. M. Abolhasani, M. Naebe, K. Shirvanimoghaddam, H. Fashandi, H. Khayyam, M. Joordens, A. Pipertzis, S. Anwar, R. Berger, G. Floudas, J. Michels and K. Asadi, Nano Energy, 2019, 62, 594–600 CrossRef CAS.
- M. M. Abolhasani, S. Azimi, M. Mousavi, S. Anwar, M. Hassanpour Amiri, K. Shirvanimoghaddam, M. Naebe, J. Michels and K. Asadi, J. Appl. Polym. Sci., 2022, 139, 51907 CrossRef CAS.
- S. Deswal, S. Arab, N. He, W. Gao, B. Lee and V. Misra, RSC Appl. Polym., 2024, 2, 634–641 RSC.
- G. S. Ekbote, M. Khalifa, B. Venkatesa Perumal and S. Anandhan, RSC Appl. Polym., 2023, 1, 266–280 RSC.
- R. A. Green-Warren, A. L. Fassler, A. Juhl, N. M. McAllister, A. Huth, M. Arkhipov, M. J. Grzenda, S. R. Pejman, M. F. Durstock and J. P. Singer, RSC Appl. Polym., 2024, 2, 1074–1081 RSC.
- J. Avossa, G. Herwig, C. Toncelli, F. Itel and R. M. Rossi, Green Chem., 2022, 24, 2347–2375 RSC.
- K. Loukelis, V. Tsampallas, M. Kaliva, M. Vamvakaki and M. Chatzinikolaidou, Carbohydr. Polym., 2025, 348, 122775 CrossRef CAS PubMed.
- H.-J. Lee, B. Doo Chin, S.-M. Yang and O. Ok Park, J. Colloid Interface Sci., 1998, 206, 424–438 CrossRef CAS PubMed.
- K. Y. Lee, L. Jeong, Y. O. Kang, S. J. Lee and W. H. Park, Adv. Drug Delivery Rev., 2009, 61, 1020–1032 CrossRef CAS PubMed.
- X. Xu, B. Bai, H. Wang and Y. Suo, RSC Adv., 2017, 7, 6636–6647 RSC.
- K. Loukelis, V. Tsampallas, M. Kaliva, M. Vamvakaki and M. Chatzinikolaidou, Carbohydr. Polym., 2025, 348, 122775 CrossRef CAS PubMed.
- S. Khanjar, S. Barui, K. Kate and K. P. K. Ajjarapu, Materials, 2024, 17, 4426 CrossRef CAS PubMed.
- E. Kuzelova Kostakova, L. Meszaros, G. Maskova, L. Blazkova, T. Turcsan and D. Lukas, J. Nanomater., 2017, 2017, 1–9 CrossRef.
- M. Koosha, H. Mirzadeh, M. A. Shokrgozar and M. Farokhi, RSC Adv., 2015, 5, 10479–10487 RSC.
- K. Lewandowska, Thermochim. Acta, 2009, 493, 42–48 CrossRef CAS.
- S. X. Drakopoulos, A. C. Patsidis and G. C. Psarras, Mater. Res. Bull., 2022, 145, 111537 CrossRef CAS.
- M. Z. Khan, M. H. Younes, A. Zaib, U. Farooq, A. Khan, M. D. Zahid and U. Hussan, J. Mater. Sci.: Mater. Electron., 2021, 32, 19646–19654 CrossRef CAS.
- S. Bonardd, E. Robles, I. Barandiaran, C. Saldías, Á. Leiva and G. Kortaberria, Carbohydr. Polym., 2018, 199, 20–30 CrossRef CAS PubMed.
- O. Vryonis, S. Riarh, T. Andritsch and A. S. Vaughan, Polymer, 2021, 213, 123312 CrossRef CAS.
- S. Chaudhary, O. Vryonis, A. Vaughan and T. Andritsch, J. Mater. Sci., 2022, 57, 21020–21038 CrossRef CAS.
- O. Vryonis, A. S. Vaughan, T. Andritsch, P. H. F. Morshuis and A. Claverie, Materials, 2022, 15, 6413 CrossRef CAS PubMed.
- S. X. Drakopoulos, J. Karger-Kocsis and G. C. Psarras, J. Appl. Polym. Sci., 2020, 137, 49573 CrossRef CAS.
- M. Wübbenhorst and J. van Turnhout, J. Non-Cryst. Solids, 2002, 305, 40–49 CrossRef.
- S. X. Drakopoulos, G. C. Psarras and S. Ronca, eXPRESS Polym. Lett., 2021, 15, 492–502 CrossRef CAS.
- A. Serghei, M. Tress, J. R. Sangoro and F. Kremer, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 184301 CrossRef.
- R. J. Klein, S. Zhang, S. Dou, B. H. Jones, R. H. Colby and J. Runt, J. Chem. Phys., 2006, 124, 144903 CrossRef PubMed.
- A. Alakanandana, A. R. Subrahmanyam and J. Siva Kumar, Mater. Today: Proc., 2016, 3, 3680–3688 Search PubMed.
- M. Hassan, A. Abukmail, A. Hassiba, K. Mauritz and A. Elzatahry, Nanomaterials, 2018, 8, 888 CrossRef PubMed.
- J. Einfeldt, D. Meißner and A. Kwasniewski, J. Non-Cryst. Solids, 2003, 320, 40–55 CrossRef CAS.
- G. C. Manika and G. C. Psarras, High Voltage, 2016, 1, 151–157 CrossRef.
Footnote |
| † These authors contributed equally to the work. |
| This journal is © The Royal Society of Chemistry 2025 |