Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Eco-friendly solid polymer electrolytes doped with NaClO4 for next-generation energy storage devices: structural and electrochemical insights†
Vipin
Cyriac
 a,
Ismayil
a,
Ismayil
 *a,
Kuldeep
Mishra
*a,
Kuldeep
Mishra
 b,
Ankitha
Rao
c,
Riyadh Abdekadir
Khellouf
d,
Saraswati P.
Masti
e and
I. M.
Noor
fg
b,
Ankitha
Rao
c,
Riyadh Abdekadir
Khellouf
d,
Saraswati P.
Masti
e and
I. M.
Noor
fg
aDepartment of Physics, Manipal Institute of Technology, Manipal Academy of Higher Education, Manipal 576104, Karnataka, India. E-mail: ismayil.mit@manipal.edu; ismayil.486@gmail.com; Tel: +91 98454 97546
bSymbiosis Institute of Technology (SIT), Symbiosis International (Deemed university) (SIU), Pune 412115, Maharashtra, India
cDepartment of Electronics and Communication, Manipal Institute of Technology, Manipal Academy of Higher Education, Manipal 576104, Karnataka, India
dCentre of Polymer Systems, University Institute, Tomas Bata University in Zlin, Tr. T. Bati 5678, 760 01 Zlin, Czech Republic
eDepartment of Chemistry, Karnataka University's Karnataka Science College, Dharwad, Karnataka 580001, India
fIonic Materials and Energy Devices Laboratory, Physics Department, Faculty of Science, Universiti Putra Malaysia, 43400 UPM Serdang, Selangor Darul Ehsan, Malaysia
gPhysics Division, Centre for Foundation Studies in Science of Universiti Putra Malaysia, Universiti Putra Malaysia, 43400 Serdang, Selangor Darul Ehsan, Malaysia
First published on 10th April 2025
Abstract
One of the environmental challenges of energy storage devices is ensuring sustainable manufacturing and disposal practices to minimize hazardous waste. In this study, a blend of green polymers, chitosan (CS) and polyvinyl alcohol (PVA) is used as a host matrix to create flexible ion-conducting films, with ion donating NaClO4 added to enable ion transport. A significant polymer–salt interaction is evident from the FTIR investigations. Impedance spectra reveal a decrease in the bulk resistance with increasing salt content, highlighting the potential of the system for energy storage applications. The optimized bulk conductivity is improved from (1.43 ± 0.26) × 10−8 S cm−1 for the pure blend to (5.23 ± 0.27) × 10−4 S cm−1 for the composition with 35 wt% NaClO4. The ion transport properties, investigated using the Schutt and Gerdes (S–G) model, reveal a strong dependency of conductivity on the carrier concentration over ion mobility. Linear sweep voltammetry (LSV) showed the high electrochemical stability of PCP35 up to 2.6 V. The ionic transference number close to unity confirms the purely ionic nature of the optimized composition. The electric-double layer capacitor (EDLC) comprising the optimized electrolyte composition delivers a specific capacitance of 20.58 F g−1 at 0.05 mA g−1, with energy and power densities of 2.69 W h kg−1 and 97 W kg−1, respectively.
1. Introduction
The global demand for efficient energy storage systems is driven by the increasing implementation of renewable energy sources, particularly wind and solar power, to address climate change concerns and promote environmental sustainability.1 Intermittent energy sources require storage systems to handle their variable outputs and effectively integrate them into power grids. Energy storage technologies enhance the network efficiency, reliability, and energy density. These technologies balance generation and consumption, store surplus energy for later use, and aid in the shift from fossil fuels to renewables. Various storage technologies are being developed and implemented globally to address these challenges and facilitate the transformation of electrical systems into more adaptable platforms.2 Electric double-layer capacitors (EDLCs) are a crucial class of energy storage devices, offering high power density, long cycle life, and fast charge/discharge rates.3 EDLCs outperform batteries in terms of specific power, fast charge–discharge rates, and cycling stability but have lower energy density.4EDLCs store energy via an electric double layer at the electrode–electrolyte interface. An electrolyte is vital for charge storage, with ionic liquids and organic electrolytes providing wider potential windows than aqueous electrolytes.5 Traditional liquid electrolytes pose challenges such as leakage, volatility, and safety risks. Solid-state electrolytes (SSEs) offer a promising alternative with improved safety, higher energy density, and better thermal stability.6 Solid-state electrolytes (SSEs) are classified into inorganic, polymer, and composite types, each with unique properties. Despite their benefits, SSEs face issues such as a lower ionic conductivity than liquid electrolytes, interfacial resistance, and mechanical instability.7
PVA has multiple characteristics that render it suitable for solid electrolyte applications. Its film-forming capability, flexibility, and high tensile strength facilitate the production of durable membranes.8 When combined with salts, PVA-based electrolytes exhibit favourable chemical stability and ionic conductivity, with values ranging from 10−7 to 10−4 S cm−1 at room temperature.9,10 PVA-based gel polymer electrolytes have demonstrated potential in flexible solid-state supercapacitors, exhibiting ionic conductivities of up to 82 mS cm−1.11 These properties make PVA an attractive candidate for various energy-storage applications, including fuel cells and supercapacitors.
Chitosan, a biopolymer derived from chitin, is known for its biodegradability, non-toxicity, and antimicrobial properties. This natural polysaccharide consists mainly of glucosamine and N-acetyl glucosamine residues.12 Its distinctive characteristics are attributed to the presence of free protonable amino groups along its backbone, which also contribute to its solubility under acidic conditions.13 Chitosan's biocompatibility and biodegradability make it ideal for biomedical applications, such as tissue engineering and drug delivery. Its antimicrobial properties are affected by intrinsic, environmental, and microorganism-related factors.14 Also, its application in polymer electrolytes, exhibiting ionic conductivity and film-forming properties, shows promise in energy storage, providing thermal stability for batteries, capacitors, and fuel cells.15
The combination of PVA and CS has been demonstrated to substantially enhance the properties of solid electrolytes. The blending of these polymers results in improved mechanical strength, flexibility, and film-forming capacity in both dry and wet states.16 PVA–CS blends show improved hydrophilicity and water uptake, which can be adjusted through polymer ratios and cross-linking agents. They also exhibit superior biocompatibility and promote cell attachment and proliferation.17 The addition of salts and plasticizers results in a more amorphous structure, enhancing the ionic conductivity and electrochemical performance. These properties make PVA–CS blend electrolytes promising for applications such as supercapacitors and other energy storage devices.18 A brief literature review is provided in Fig. 1 to summarize the optimum conductivity of the PVA–CS system incorporating various proton, magnesium and sodium conducting electrolytes.19–26
 | ||
| Fig. 1 Bar chart summarising the optimum conductivity of the PVA/CS solid polymer electrolytes (SPEs) incorporating proton/magnesium and sodium dopants. | ||
Sodium perchlorate (NaClO4) is a highly effective ionic dopant for solid-state electrolytes due to its superior solubility in hybrid matrices compared to other salts like NaBF4.27 NaClO4 is widely used in polymer electrolytes because of its ability to enhance the ionic conductivity and reduce the crystallinity. The addition of NaClO4 to polymer blends improves ion–polymer interactions and increases the number of mobile carriers.28 The optimal NaClO4 concentrations can yield conductivities of up to 10−4 S cm−1 at room temperature. Computational studies suggest that NaClO4 addition reduces the energy gap in polymer electrolytes, potentially enhancing ionic conductivity.29
The primary objective of this study was to synthesize PVA and CS solid electrolytes using sodium perchlorate monohydrate (NaClO4·H2O) as a dopant and to comprehensively evaluate their structural, morphological, mechanical, and electrochemical properties. These properties were characterized by employing various analytical formalisms, including Nyquist and dielectric formalisms. Furthermore, this study aimed to assess the efficacy of the synthesized electrolytes by incorporating them as both electrolytes and separators in EDLCs to evaluate their performance and potential for practical applications in energy storage devices.
2. Experimental
2.1 Chemicals used
Chitosan (CS, exhibiting a minimum deacetylation of 75% and a viscosity of 200 cP s in a 1% solution) was obtained from Loba Chemie, polyvinyl alcohol (PVA, Mw = 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, degree of hydrolysis = 86%) was sourced from SD Fine Chemicals Pvt Limited, and sodium perchlorate monohydrate (NaClO4·H2O, Mw = 140.46 g mol−1) was purchased from Merck Life Science, Mumbai, to prepare the PVA/CS-NaClO4·H2O host matrix. Glacial acetic acid (Mw = 60.05 g mol−1) was procured from Merck Life Science, Bangalore and deionized water was utilized to make 1% (v/v) acetic acid. The materials employed in fabricating the EDLC electrodes included activated carbon (AC) from Kuraray-Japan, carbon black and polyvinylidene fluoride (PVdF) from Alfa Aesar, and 1-methyl-2-pyrrolidone (NMP) also from Alfa Aesar.
000 g mol−1, degree of hydrolysis = 86%) was sourced from SD Fine Chemicals Pvt Limited, and sodium perchlorate monohydrate (NaClO4·H2O, Mw = 140.46 g mol−1) was purchased from Merck Life Science, Mumbai, to prepare the PVA/CS-NaClO4·H2O host matrix. Glacial acetic acid (Mw = 60.05 g mol−1) was procured from Merck Life Science, Bangalore and deionized water was utilized to make 1% (v/v) acetic acid. The materials employed in fabricating the EDLC electrodes included activated carbon (AC) from Kuraray-Japan, carbon black and polyvinylidene fluoride (PVdF) from Alfa Aesar, and 1-methyl-2-pyrrolidone (NMP) also from Alfa Aesar.
2.2 Polymer blend electrolyte preparation
Electrolyte preparation was performed using a solution casting technique with 1% acetic acid (v/v) as the common solvent. PVA and CS polymer blends with a weight ratio of 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 respectively, were placed in a beaker with different concentrations of the dopant NaClO4·H2O (sample compositions are listed in Table 1). The rationale behind the selection of the polymer blend ratio was based on research conducted by Arof et al.,30 which identified this ratio as the most amorphous blend composition. A higher degree of amorphousness is beneficial for enhanced ion transport in solid polymer electrolytes, which is crucial for improving the performance of the supercapacitor. 100 ml of 1% acetic acid was added to this beaker and the solution was stirred using a magnetic stirrer at 60 °C for 4 h for the PVA to be completely dissolved. This solution was stirred at room temperature for 24 h after it had cooled. The homogenous solution was filtered to remove undissolved CS particles, cast into a polyethylene Petri dish, and kept in an oven at 40 °C for 3 days until the film was completely dry. The peeled films were placed in a silica-filled vacuum desiccator until further characterization. The sample thickness was measured using a Mitutoyo digital micrometer with a least count of 0.001 mm. Multiple measurements were taken, and the average values were reported in Table 1.
40 respectively, were placed in a beaker with different concentrations of the dopant NaClO4·H2O (sample compositions are listed in Table 1). The rationale behind the selection of the polymer blend ratio was based on research conducted by Arof et al.,30 which identified this ratio as the most amorphous blend composition. A higher degree of amorphousness is beneficial for enhanced ion transport in solid polymer electrolytes, which is crucial for improving the performance of the supercapacitor. 100 ml of 1% acetic acid was added to this beaker and the solution was stirred using a magnetic stirrer at 60 °C for 4 h for the PVA to be completely dissolved. This solution was stirred at room temperature for 24 h after it had cooled. The homogenous solution was filtered to remove undissolved CS particles, cast into a polyethylene Petri dish, and kept in an oven at 40 °C for 3 days until the film was completely dry. The peeled films were placed in a silica-filled vacuum desiccator until further characterization. The sample thickness was measured using a Mitutoyo digital micrometer with a least count of 0.001 mm. Multiple measurements were taken, and the average values were reported in Table 1.
| Designation | PVA/CS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NaClO4·H2O (wt% NaClO4·H2O (wt%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) wt%) wt%) |
PVA/CS (g) | NaClO4·H2O (g) | Thickness (mm) |
|---|---|---|---|---|
| PCP0 | 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
2.0 | 0 | 0.168 |
| PCP5 | 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 5 |
1.9 | 0.1 | 0.153 |
| PCP10 | 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
1.8 | 0.2 | 0.096 |
| PCP15 | 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 15 |
1.7 | 0.3 | 0.174 |
| PCP20 | 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 20 |
1.6 | 0.4 | 0.139 |
| PCP25 | 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 25 |
1.5 | 0.5 | 0.139 |
| PCP30 | 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 30 |
1.4 | 0.6 | 0.144 |
| PCP35 | 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 35 |
1.3 | 0.7 | 0.154 |
| PCP40 | 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 40 |
1.2 | 0.8 | 0.107 |
2.3 EDLC fabrication
An EDLC device was constructed using an 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 weight ratio of activated carbon (AC) (1600 m2 g−1 surface area, BET analysis) and carbon black (CB). The AC–CB electrode materials were mixed with a PVDF-NMP binder to form a slurry, which was applied to a stainless-steel electrode and dried at 60 °C, resulting in a 1 mg active material coating. The polymer electrolyte with the highest conductivity (PCP35) was placed between the AC and CB electrodes and the device was characterized using CV, GCD, and EIS techniques.
15 weight ratio of activated carbon (AC) (1600 m2 g−1 surface area, BET analysis) and carbon black (CB). The AC–CB electrode materials were mixed with a PVDF-NMP binder to form a slurry, which was applied to a stainless-steel electrode and dried at 60 °C, resulting in a 1 mg active material coating. The polymer electrolyte with the highest conductivity (PCP35) was placed between the AC and CB electrodes and the device was characterized using CV, GCD, and EIS techniques.
2.4 Electrolyte characterisation
 | (1) |
The complex conductivity, σ*(f), was calculated as:
| σ* = σ′(f) − jσ′′(f) = j2πfε0(ε′ − jε′′) | (2) |
The loss tangent, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, which is the ratio of the imaginary to the real part of the permittivity, was calculated as:
δ, which is the ratio of the imaginary to the real part of the permittivity, was calculated as:
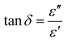 | (3) |
For thermogravimetric analysis (TGA), 5–8 mg of samples were sealed in 40 μL aluminium pans with perforated lids and heated from 30 °C to 500 °C at 10 °C min−1 using a Hitachi STA7200 TGA-DTA instrument. The experiments were performed under an argon atmosphere to prevent oxidation and ensure a controlled environment.
Transference number measurements (TNM) for all the prepared doped SPE films were conducted at room temperature using a Keithley 2636 B source meter. SS blocking electrodes were used in the SS|SPE|SS setup. The TNM experiments lasted 600 s with a data acquisition step size of 0.01 seconds. A constant potential of 100 mV was applied, allowing current monitoring over time and providing insights into the electrochemical characteristics of SPE films.
The total ionic transference number (tion) was calculated using the following formula:
 | (4) |
The ionic conductivity σion was determined from the bulk conductivity and respective transference numbers using the following equation:
| σion = σbulk × tion | (5) |
The specific capacitance of EDLC was obtained from CV using,
 | (6) |
The series capacitance was determined by using a two-electrode system with a factor of 2.
The specific capacitance (Cs) is obtained from the GCD curve using
| Cs = 4C | (7) |
 | (8) |
In this expression, C denotes the EDLC's capacitance, I is the discharge current (mA), ΔV is the effective discharge voltage and m refers to the combined mass of the active material in both electrodes. The factor of 4 accounts for the translation of cell capacitance to a single electrode's mass and capacitance, as an EDLC comprises two capacitors (one on each electrode).31–35
Furthermore, the energy and power densities36 were calculated using,
 | (9) |
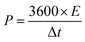 | (10) |
3. Results and discussion
3.1 FTIR spectroscopy
Interactions among the various components of SPEs have been extensively investigated through FTIR spectroscopy. By examining shifts in the wavenumbers corresponding to the stretching and bending vibrations of specific bonds, valuable information on intermolecular interactions can be deduced. The choice of an appropriate polymer host often hinges on the presence of heteroatoms with lone-pair electrons (e.g., oxygen and nitrogen). It is well established that chain polymers can dissolve certain salts owing to favorable interactions between the polymer backbone and cations. Such polymers typically incorporate electronegative atoms such as oxygen or nitrogen within their repeating units.39 Previous literature has already addressed the interaction between PVA and CS.40,41 The miscibility between CS and PVA was likely due to the formation of intermolecular hydrogen bonds between the amino and hydroxyl groups of CS and the hydroxyl groups of PVA.The FTIR spectra of the electrolytes, along with that of the dopant salt, covering wavenumbers from 500 to 4000 cm−1, are displayed in Fig. 2(a), and the corresponding 13 major band assignments of the PVA/CS blend are presented in Table 2. Sodium perchlorate (NaClO4) exhibits characteristic infrared (IR) bands, with the most prominent feature being the strong absorption band at 1050–1110 cm−1 due to the perchlorate ion.42 Additional IR bands for NaClO4 include peaks at 930 cm−1, 760–825 cm−1, 630 cm−1, and 460–495 cm−1.43,44 Owing to the overlap of the ClO4− peak at approximately 1070 cm−1 with the C–O peaks of the polymer blend, a noticeable change in the peak shape of the C–O bending at approximately 1050 cm−1 and C–O stretching at 1025 cm−1 is observed.
 | ||
| Fig. 2 (a) FTIR spectra of PVA/CS-NaClO4·H2O SPEs and NaClO4·H2O salt and (b) interaction scheme of the dopant with PVA and CS. | ||
| Bands | Wavenumbers of functional groups (cm−1) | Ref. | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| PCP0 | PCP5 | PCP10 | PCP15 | PCP20 | PCP25 | PCP30 | PCP35 | PCP40 | ||
| –OH/NH2 stretch | 3256 | 3267 | 3271 | 3337 | 3337 | 3354 | 3368 | 3370 | 3362 | 45 and 46 |
| –CH asymmetric stretch | 2945 | 2946 | 2942 | 2942 | 2949 | 2942 | 2946 | 2950 | 2952 | 47 |
| –CH symmetric stretch | 2918 | 2918 | 2919 | 2918 | 2918 | 2919 | 2919 | 2921 | 2920 | 48 |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch of PVA O stretch of PVA |
1712 | 1711 | 1711 | 1711 | 1711 | 1710 | 1710 | 1710 | 1711 | 49 |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–NHR carboxamide C–NHR carboxamide |
1641 | 1641 | 1642 | 1632 | 1631 | 1632 | 1632 | 1632 | 1631 | 50 and 51 |
| –NH2 bending | 1548 | 1553 | 1553 | 1551 | 1552 | 1552 | 1555 | 1553 | 1552 | 52 |
| –CH stretch | 1410 | 1411 | 1412 | 1412 | 1412 | 1413 | 1413 | 1413 | 1413 | 50 |
| –OH bending | 1378 | 1377 | 1377 | 1378 | 1378 | 1378 | 1378 | 1378 | 1378 | 53 |
| C–H stretch of PVA | 1257 | 1258 | 1262 | 1264 | 1268 | 1268 | 1270 | 1270 | 1271 | 54 |
| C–O bending | 1068 | 1071 | 1073 | 1069 | 1069 | 1071 | 1074 | 1073 | 1070 | 55 |
| C–O stretch of CS | 1024 | 1025 | 1027 | 1028 | 1027 | 1032 | 1034 | 1025 | 1022 | 56 |
| Skeletal vibrations of PVA | 946 | 946 | 948 | 946 | 949 | 949 | 934 | 934 | 934 | 57 |
| CH rocking | 829 | 829 | 834 | 815 | 822 | 826 | 817 | 829 | 837 | 58 |
PVA and CS possess different functional groups such as O–H, C–O, and NH2 attached to the side chains of their polymer backbones. Determining the presence of complexation between salt and polymer hosts relies heavily on the movement of various stretching bands, including C–O, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, OH, O
O, OH, O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–NHR, and NH2. In systems with two polymer hosts, the amine band's location remains relatively stable, showing no notable shifts.59 Nevertheless, significant shifts were observed in the positions of the amine, carbonyl, and hydroxyl bands in this study, suggesting that complexation took place at both oxygen and nitrogen atoms within the blends.
C–NHR, and NH2. In systems with two polymer hosts, the amine band's location remains relatively stable, showing no notable shifts.59 Nevertheless, significant shifts were observed in the positions of the amine, carbonyl, and hydroxyl bands in this study, suggesting that complexation took place at both oxygen and nitrogen atoms within the blends.
The wide spectral band spanning from 3200 cm−1 to 3550 cm−1 can be associated with the combined stretching vibrations of N–H and O–H groups. These vibrations arise from hydrogen bonding interactions, both intermolecular and intramolecular, within the PVA/CS structure.60 This band varies from 3256 cm−1 to 3362 cm−1, indicating the interaction of Na+ ions with the –OH group and/or the NH2 group of PVA/CS. According to previous studies, the amino groups (–NH2) and hydroxyl groups (–OH) in chitosan are the main sites for coordination with metal ions. These groups can form stable complexes with metal ions through coordination bonds.
Sodium ions form preferential bonds with both the amino and hydroxyl groups of chitosan simultaneously. This interaction disrupts some of the inherent hydrogen bonding between the amino and hydroxyl groups within the chitosan molecule.61,62 The interactions between the Na+ ions and PVA functional groups involve the rupture of multiple H-bonds between the –OH groups of the polymer chains.63 This bond breaking and new bond formation lead to the suppression of crystallinity by preventing the reorganization of the polymer. In addition, the wavenumber corresponding to the carboxamide group varied from 1641 cm−1 to 1631 cm−1, indicating an interaction between the Na+ and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups of carboxamide.
O groups of carboxamide.
Several CH bands showed significant variations with the addition of salt. The CH rocking wavenumber varied from 829 cm−1 to 837 cm−1, the CH stretch of PVA varied from 1257 cm−1 to 1271 cm−1, and the CH asymmetric stretch varied from 2945 cm−1 to 2952 cm−1. All these variations indicate the interaction of the ClO4− anion with the CH group of PVA/CS through hydrogen bonding. The CH–O hydrogen bond, though weak, plays a crucial role in stabilizing the crystalline structure of polymers, thereby influencing their physical properties.64 Thus, FTIR studies confirmed the interactions between the salt and polymer matrix. All the possible interactions are shown in Fig. 2(b).
3.2 X-ray diffraction
X-ray diffraction was used to assess the crystallinity of the blended membranes. The impact of dopant concentration on the crystallinity of the SPEs is depicted in Fig. 3(a). Generally, a polymer with crystalline regions will exhibit sharp X-ray diffraction peaks with high intensities, while the X-ray diffraction peaks for an amorphous polymer will be broader.65 The biopolymers PVA and CS were semi-crystalline in nature, each displaying characteristic peaks. PVA has a broad halo centered at 2θ = 19°,49,57 while CS shows peaks at 10°, 19°, and 22°.66 Multiple prior investigations revealed that combining PVA with CS resulted in the merging of characteristic peaks, which centered at 2θ = 19.6°. The observed shift and consolidation of the blend's peak position, when compared to the reported locations of the individual polymers, can be attributed to hydrogen bond formation between reactive functional groups in the blended chains. This positional change suggests complete compatibility between the two polymers.60,67 | ||
| Fig. 3 (a) XRD spectra of PVA/CS-NaClO4·H2O SPEs and (b) deconvoluted XRD patterns of PVA/CS-NaClO4·H2O SPEs. | ||
With the addition of the salt, the intensity of the characteristic peak at 2θ = 19.6° decreased, along with a reduction in the halo portion of the peak corresponding to the PVA/CS membrane. Additionally, the intensity of the diffraction peak at 2θ = 11.52° also diminishes as the salt concentration increases indicating reduction in the crystalline phase of the SPEs.68 The addition of salt to polymer electrolytes initially suppresses crystallinity by disrupting polymer chain organization and promoting amorphous regions.69 Salt ions complex with polymer chains, altering their conformation and hindering crystallization.70 The reduction in the crystalline phase in this system primarily results from the coordination/hydrogen bonding interactions between PVA–CS polymer matrix and the Na salt, as indicated by FTIR studies. This process alters the microstructural nature of the blend composites, shifting from crystalline to amorphous characteristics as the salt concentration increases from 5 wt% to 35 wt%. The suppression of crystallinity generally improves ionic conductivity by enhancing polymer chain mobility.71 However, at higher salt concentrations (40 wt%), crystallinity increased due to ion clustering and reduced polymer mobility.72
The Hermans–Weidinger method is a widely used method for determining the degree of crystallinity in polymers using X-ray diffraction.73 The method involves separating crystalline and amorphous scattering contributions.74 Accordingly, from the deconvoluted XRD spectrum (Fig. 3(b)), the crystallinity (χ) is calculated using eqn (11)
 | (11) |
The process involved in the XRD deconvolution is already reported in our previous works.75,76 The crystallinity of pure blend PVA/CS is 14.94%, which is close to the reported value.77 The value of χ decreases, reaching a minimum of 3.59%, as the NaClO4 content increases up to 35 wt%, due to the enhanced amorphousness of the SPEs. The ions can easily move through the polymer matrix because the amorphous phase has a low energy barrier, which in turn enhances ionic conductivity.78 Hence, PCP35 was found to be the optimum conducting sample. However, the χ value is found to increase for PCP40, possibly due to the onset of salt aggregation caused by ion overcrowding at higher salt concentrations. The polymer host's inability to accommodate the excess salt leads to ion recombination,79 which in turn reduces the ionic conductivity.
3.3 Electrochemical impedance spectroscopy
Fig. 4 shows Nyquist impedance plots of the prepared SPEs. The Nyquist plot illustrates the relationship between the real and imaginary components of impedance, utilizing data obtained across multiple frequencies. For the pure PVA/CS blend (PCP0), this plot manifests as a suppressed semicircle. In contrast, the Nyquist plots of samples ranging from PCP5 to PCP30 exhibit two distinct features: a compressed semicircular region at higher frequencies and an angled linear portion at lower frequencies, consistent across all samples examined. The Nyquist plot of PCP35–PCP40 reveals an inclined spike. The pure PVA/CS blend (PCP0) displayed only a semicircle owing to the absence of ions. However, in PCP5–PCP30, a spike emerges alongside the semicircle, which is attributed to ion movement at the electrode–electrolyte interfaces and within the bulk. The lack of a high-frequency semicircular region in PCP35 and PCP40 suggests that ions primarily contribute to conductivity. In contrast, the observed peak in the low-frequency range is associated with the electric double-layer capacitance occurring at the blocking electrodes.80 As the salt concentration increased, the Nyquist plot evolved from a semicircular pattern (PCP0) to a semicircle with a spike (PCP5–PCP30), and eventually to an inclined spike (PCP35–PCP40). This progression indicates an enhancement in the ion transport properties of the SPEs. | ||
| Fig. 4 Nyquist plot of PVA/CS-NaClO4·H2O SPEs (inset: equivalent circuit obtained through EEC analysis used to fit the Nyquist plot). | ||
The ionic conductivity of the SPE was calculated using the following equation:
 | (12) |
As illustrated in Fig. 4, the Nyquist plots of actual electrolyte systems frequently diverge from the ideal Debye response. These plots often exhibit distorted or flattened semicircles, along with slanted or curved spikes. Such deviations can be attributed to several factors, including variations in the thickness and structure of the polymeric film, as well as the uneven nature of the electrode surface.81 The deviations in the Nyquist plot can be corrected by replacing the capacitor in the equivalent circuit with a constant phase element (CPE). A CPE is a leaky capacitor with an impedance defined by 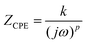 , where 0 ≤ p ≤ 1. When p = 0, the impedance ZCPE is frequency independent and k = R and the CPE acts as a pure resistor. When p = 1,
, where 0 ≤ p ≤ 1. When p = 0, the impedance ZCPE is frequency independent and k = R and the CPE acts as a pure resistor. When p = 1,  , which implies that with k−1 = C, the CPE acts as a pure capacitor with impedance
, which implies that with k−1 = C, the CPE acts as a pure capacitor with impedance  . When 0 ≤ p ≤ 1, the CPE acts as an intermediate between a resistor and a capacitor.82 The EECs used to fit the Nyquist plot are shown in the inset of Fig. 4.83
. When 0 ≤ p ≤ 1, the CPE acts as an intermediate between a resistor and a capacitor.82 The EECs used to fit the Nyquist plot are shown in the inset of Fig. 4.83
The impedance of the equivalent circuit for PCP0 is given by eqn (13)
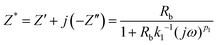 | (13) |
Simplifying eqn (13) and equating the real and imaginary parts yield eqn (14) and (15), respectively.
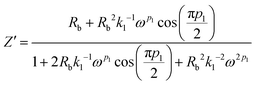 | (14) |
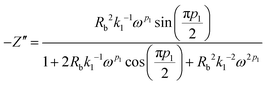 | (15) |
The impedance of the equivalent circuit for PCP5–PCP30 is given by eqn (16).
 | (16) |
Simplifying eqn (16) and equating the real and imaginary parts yield eqn (17) and (18), respectively.
 | (17) |
 | (18) |
The impedance of the equivalent circuit for PCP35–PCP40 is given by eqn (19).
 | (19) |
Simplifying eqn (19) and equating the real and imaginary parts yield eqn (20) and (21), respectively:
 | (20) |
 | (21) |
The above equations were used to fit the Nyquist plots to find out Rb and σ of the SPEs and are listed in Table 3.
| Sample | R b (Ω) | σ (S cm−1) at 25 °C | σ dc (S cm−1) | s | τ (s) | R 2 |
|---|---|---|---|---|---|---|
| PCP0 | 480![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 7500 000 ± 7500 |
(1.43 ± 0.26) × 10−8 | (4.71 ± 1.11) × 10−8 | 0.90 ± 0.01 | — | 0.99 |
| PCP5 | 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 ± 540 900 ± 540 |
(9.80 ± 0.09) × 10−8 | (1.57 ± 0.14) × 10−7 | 0.85 ± 0.01 | — | 0.99 |
| PCP10 | 8160 ± 200 | (4.13 ± 0.10) × 10−7 | (4.26 ± 0.16) × 10−7 | 0.79 ± 0.01 | 3.56 × 10−4 | 0.99 |
| PCP15 | 3430 ± 22 | (1.79 ± 0.01) × 10−6 | (1.61 ± 0.03) × 10−6 | 0.72 ± 0.01 | 1.13 × 10−4 | 0.99 |
| PCP20 | 449.2 ± 7.5 | (1.09 ± 0.01) × 10−5 | (9.49 ± 0.10) × 10−6 | 0.76 ± 0.01 | 1.00 × 10−5 | 0.99 |
| PCP25 | 133.7 ± 1.3 | (3.67 ± 0.03) × 10−5 | (3.50 ± 0.02) × 10−5 | 0.86 ± 0.02 | 2.52 × 10−6 | 0.99 |
| PCP30 | 100.5 ± 1.2 | (5.05 ± 0.05) × 10−5 | (4.69 ± 0.03) × 10−5 | 0.90 ± 0.03 | 2.56 × 10−6 | 0.98 |
| PCP35 | 10.43 ± 0.51 | (5.23 ± 0.27) × 10−4 | (1.27 ± 0.59) × 10−4 | 0.17 ± 0.05 | — | 0.95 |
| PCP40 | 11.8 ± 1.4 | (3.23 ± 0.37) × 10−4 | (1.97 ± 0.03) × 10−4 | 0.53 ± 0.05 | — | 0.98 |
Table 3 displays the DC conductivity values of the prepared electrolytes, which are essential for electrochemical energy storage systems, such as supercapacitors and batteries. According to the literature, the ideal conductivity at room temperature for these systems is around 10−5 to 10−3 S cm−1. Table 3 demonstrates that the addition of salt enhanced the conductivity of the SPEs. The introduction of NaClO4 into the biopolymer matrix substantially improves its ionic conductivity by elevating the quantity of mobile ions, as the doping salt serves as the primary origin of charge carriers. A remarkable increase in conductivity by approximately four orders of magnitude ((5.23 ± 0.27) × 10−4 S cm−1) upon the addition of 35 wt% NaClO4 is observed, making it suitable for energy device applications. However, higher salt concentrations (40 wt% NaClO4) can lead to ion re-association, while lower concentrations limit the number of dissociated ionic carriers, restricting conductivity in both scenarios.
The direct current (DC) conductivity of the electrolyte system can be expressed by the following equation:
| σ = neμ | (22) |
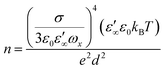 | (23) |
In eqn (23), σ represents the DC conductivity, kB is the Boltzmann constant, ε0 is the vacuum permittivity, and d is the sample thickness. Here, ε∞ denotes the real part of permittivity in the high-frequency region and ωx stands for the angular frequency, where ε′(ωx) = 10ε∞.
The variation in the transport parameters as per the S–G model is illustrated in Fig. 5. The initial increase in conductivity from 5 wt% to 20 wt% salt concentration is primarily attributed to a sharp rise in carrier concentration, resulting in a significant conductivity enhancement. However, for 25 wt% and 30 wt%, the conductivity shows only a minor increment, which aligns with a relatively small increase in carrier concentration. This also coincides with a reduction in crystallinity, improving ion mobility. At higher concentrations (35 wt% and 40 wt%), the carrier concentration continues to increase, but mobility and diffusion coefficients begin to decrease due to ion–ion interactions and collisions caused by the overcrowding of free ions, leading to saturation or slight reduction in overall conductivity. Additionally, the trend of real permittivity (ε′) follows a similar pattern to that of carrier concentration, supporting the relationship n ∝ ε′. Based on these findings, it can be inferred that the carrier concentration (n) has the most dominant influence on dc conductivity, compared to the mobility or diffusion coefficient.
 | ||
| Fig. 5 Variation of transport properties such as n, μ and D as per the S–G model for PVA/CS-NaClO4 SPEs. | ||
3.4 AC conductivity and tangent loss
Fig. 6(a) shows the AC conductivity spectra of the PVA/CS-NaClO4 SPEs at room temperature. The red solid line indicates the Jonscher fit, which is a common model used to describe the AC conductivity of disordered solids and amorphous materials. According to the Jonscher fit, the AC conductivity of the material increases with a higher frequency. The increase in AC conductivity with frequency is a typical behavior of disordered materials, where the conductivity increases owing to hopping conduction mechanisms at higher frequencies. For all salt concentrations, AC conductivity increased with increasing frequency. However, the increase in the conductivity was gradual and less pronounced at low frequencies (f < 105 Hz). At higher frequencies (f > 105 Hz), the conductivity increased more steeply, indicating enhanced charge carrier dynamics and hopping conduction mechanisms. As the salt concentration increased from 0 wt% to 35 wt%, the AC conductivity also increased. Higher salt concentrations provide more charge carriers (ions), which enhances the overall conductivity of the material.Jonscher's law is given by,
| σdc(ω) = σdc + Bωs | (24) |
Fig. 6(c) illustrates the loss tangent (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) as a function of frequency, indicating that each sample exhibits a single relaxation peak. This asymmetrical peak is attributed to the conductivity relaxation in the prepared SPEs. Additionally, modifying the concentration of NaClO4 caused the relaxation peak to move toward higher frequency ranges. The corresponding relaxation time (τ) was obtained using the following relationship:
δ) as a function of frequency, indicating that each sample exhibits a single relaxation peak. This asymmetrical peak is attributed to the conductivity relaxation in the prepared SPEs. Additionally, modifying the concentration of NaClO4 caused the relaxation peak to move toward higher frequency ranges. The corresponding relaxation time (τ) was obtained using the following relationship:
 | (25) |
The results obtained for τ are presented in Table 3. The data show a reduction in τ, which indicates faster ionic dynamics within the SPE system.
3.5 Dielectric analysis
Fig. 7(a) and (b) depict the variations in the real (ε′) and imaginary (ε′′) parts of the dielectric permittivity at ambient temperature for the prepared samples. Log–log scaling is favoured for analysing dielectric spectra because it facilitates the identification, separation, and quantification of distinct contributions to the complex dielectric function. These contributions include the rotational and translational diffusion of ions/electrons as well as charge separation at the interfaces, each exhibiting unique spectral characteristics. Relaxation processes are characterized by a peak in the ε′′ plot and a pronounced step-like decrease in the ε′ plot with increasing frequency. In contrast, conduction phenomena are characterized by an increase in ε′′ as frequency decreases. When conduction is purely ohmic, ε′ remains steady across all frequencies. However, in polymeric materials, non-ohmic conduction or polarization effects lead to a rise in ε′ at lower frequencies.87 Hence at ambient temperatures, the real and imaginary parts of permittivity show two regions – the electrode polarization (EP) region and the dc conductivity region. ε′′ for prepared SPEs at ambient temperature does not show any secondary relaxations. At extremely high frequencies, the ions cannot keep pace with the rapidly changing applied electric field, leading to a sharp decrease in both the real (ε′) and imaginary (ε′′) components of the dielectric permittivity. The high dielectric permittivity observed at low frequencies can be explained by the creation of an electrical double layer at the electrode–electrolyte interface, suggesting the existence of freely moving ions within the system. This correlation is further substantiated by the following equation | (26) |
 | ||
| Fig. 7 Variation in (a) ε′ and (b) ε′′ for PVA/CS-NaClO4 SPEs and (c) ε′ and (d) ε′′ at elevated temperature for the optimum conductivity sample PCP35. | ||
The temperature-dependent plots of ε′ and ε′′ for the PCP35 sample are presented in Fig. 7(c) and (d). Both ε′ and ε′′ exhibit an increase with rising temperature due to the generation of additional free ions. Specifically, as sufficient energy becomes available, the salt dissociates into free Na+ and ClO4− ions, thereby enhancing the number of free ions within the system.
Dielectric spectroscopy is a robust technique for investigating relaxation phenomena arising from the rotational motion of molecular dipoles. Such motion, which can involve entire molecules or specific molecular segments, is examined by analyzing the dielectric response. When the frequency (f) of the applied electric field matches the dipoles’ reorientation time (τ), the complex dielectric function exhibits a characteristic trend: the real part (ε′) decreases in a step-like manner, while the imaginary part (ε′′) shows a pronounced peak. Our research revealed a comparable peak in the ε′′(f) of PCP35, indicating secondary relaxation occurring at elevated temperatures.
3.6 Scanning electron microscopy
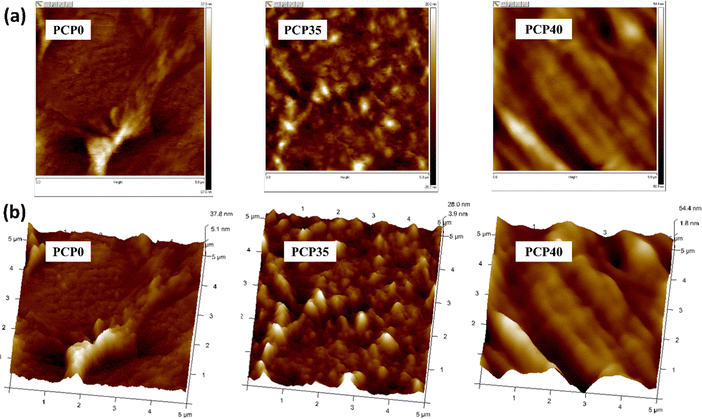
SEM analysis was employed to detect phase separation and interfaces, aiming to evaluate the compatibility among various components in the blend polymer electrolytes. SEM micrographs at 5k× magnification of the present system are shown in Fig. 8. The SEM images reveal that the surface of the samples is smooth and homogeneous, with no evidence of phase separation.88 However, the samples showed an improvement in surface smoothness (see AFM section) up to 35 wt% of dopant. The improvement in surface morphology with increasing salt content is attributed to the high dispersion of salt within the polymer matrix, leading to improvement in amorphous nature.89,90 The evolution of a smoother morphology with increasing salt content is accompanied by a corresponding increase in ionic conductivity.91 At a high salt content (40 wt%), there is a decrease in conductivity and increase in surface roughness (see the AFM section). At higher salt concentrations, ion reassociation was more favorable and led to an increase in the surface roughness. A. K. Arof and coworkers30 prepared PVA/CS-NH4NO3 SPEs and observed a drop in DC conductivity at higher salt concentrations (40 wt%, 50 wt% and 60 wt%). They noted that the ion aggregates protruded from the surface. However, in the current study, no significant salt aggregation was observed on the membrane surface, even at high salt concentrations. This is because of the lower lattice energy of the NaClO4 salt used in this work compared to that of NH4NO3. A lower lattice energy tends to result in less salt aggregation in the polymer matrix at higher concentrations. This was due to the better dissociation and solvation of the ions. On the other hand, higher-lattice-energy salts tend to aggregate more because of stronger ionic interactions and insufficient dissociation in the polymer environment. A similar observation has been reported elsewhere.92 Therefore, the cause of the increased surface roughness might be the “onset of salt aggregation”, and in turn, higher doping levels (over 40 wt%) could result in the salt protruding from the surface of the film.3.7 Atomic force microscopy
AFM primarily utilizes two operational modes: contact and tapping. In the contact mode, the probe remains near the sample, functioning within the repulsive force region. The tapping mode involves the cantilever oscillating near its resonance frequency above the sample surface, briefly touching it during each oscillation. The latter mode is preferable for examining sensitive samples due to reduced lateral forces and has been extensively employed in various polymer studies. The tapping technique's gentler approach makes it particularly well-suited for analyzing delicate materials.93 The morphologies of PCP0, PC35, and PCP40 were examined using AFM. Fig. 9 shows 2D and 3D AFM images of the selected samples in a scanning area of 5 μm × 5 μm. Based on topographic analysis, the RMS roughness values were calculated as 7.06 nm for PCP0, 6.49 nm for PCP35, and 23.6 nm for PCP40 SPEs. The addition of salt transformed the semicrystalline structure of PCP0 into an amorphous one. This transformation is demonstrated by the reduction in the peak height of mountain-valley formation from 37.8 nm to 28.0 nm for PCP35. This improvement in the surface homogeneity might result in better contact between the electrode and electrolyte, leading to enhanced performance of the electrochemical device.94 The increased surface roughness and maximum height (54.4 nm) of PCP40 imply the onset of ion-pairing, depicted as bright mountain regions in the AFM.953.8 Thermal analysis
The DSC thermograms of the current polymer system depicted in Fig. 10 show two regions in the temperature range of RT–250 °C. A broad endotherm from RT to 100 °C indicates the glass transition region and an exothermic region beyond 200 °C indicates the decomposition region of the electrolytes. Tg is found out using the midpoint of the step transition (Fig. S1, ESI†).A single Tg is found across all compositions, indicating the miscible nature of electrolytes. The non-linear variation in the Tg coupled with the absence of melting endotherm indicates the increased amorphous nature of the samples with doping. This non-linear variation can be attributed to the “ion–dipole interactions” resulting from the interaction of the ions of the salt with functional groups in the host blend matrix.96 The decreased Tg of the optimum conducting sample PCP35 with regard to the pristine blend PCP0 indicates the plasticizing effect of the salt.97
The thermal properties of the pure and doped polymer films were studied using TGA to examine the mass loss percentage, phase transitions, and decomposition temperature. Fig. 11 shows the TGA and DTG curves of the prepared electrolytes, and the weight percentages are listed in Table 4.
| Sample | Major decomposition temperature Td (°C) | % weight loss |
|---|---|---|
| PCP0 | 248 | 62.54 |
| PCP5 | 214 | 64.09 |
| PCP10 | 213 | 69.81 |
| PCP15 | 212 | 70.68 |
| PCP20 | 213 | 59.24 |
| PCP25 | 222 | 86.87 |
| PCP30 | 223 | 91.23 |
| PCP35 | 221 | 93.43 |
| PCP40 | 221 | 93.66 |
Analysis of the TGA and initial DTG curves reveals that the SPE film undergoes multiple stages of decomposition, regardless of salt content. Within the temperature span of 30 °C to 120 °C, a mass reduction of about 5–9% is observed. This decrease can be attributed to either the vaporization of acetic acid solvent or the release of water molecules that were either bound to or adsorbed by the samples.98 Here, the water molecules are primarily bonded to the amine or hydroxyl groups present in the polymer blend, which can easily detach in this temperature range.99 The second degradation stage occurs between 180 °C and 237 °C because of the chain scission of the polymer backbone and the breaking of bonds between the dopant and the polymer backbone. The final degradation stage occurs between 350 °C and 500 °C, with a mass loss of approximately 20% due to the loss of the remaining char. The major decomposition temperature Td is found to decrease with increasing dopant. The complex formation between the polymeric system and dopants is reflected in the observed displacement of the decomposition peak.100 For the salt-doped samples, a three-stage decomposition was seen for PCP5–PCP20, whereas for the higher salt concentration sample (PCP25–PCP40), the decomposition stage was reduced to two stages. The degradation of the perchlorate anion in polymers leads to by-products such as chlorine, oxygen, etc, which can further degrade the polymer stability.101 At higher salt concentrations, perchlorate decomposition was dominant, leading to vigorous decomposition of the polymer, reducing the three-stage process to a two-stage process. However, the Td is higher than 150 °C, which is sufficient for the safe operation of these electrolytes in energy devices.
3.9 LSV and TNM studies
The quantitative assessment of the voltage stability range or electrochemical stability window (ESW) for SPEs can be achieved through linear voltammetry. The LSV plot of the sample with optimal conductivity is illustrated in Fig. 12. The voltammograms display linear characteristics with minimal current, indicating the ESW of the SPEs. A sudden increase in current within a specific voltage range signifies an unsafe operational region for the cell. The PCP35 SPE demonstrates an ESW of 2.6 V, which is sufficient for implementing a prototype EDLC cell.The ionic conductivity in an electrolyte medium is facilitated by charge carriers, including cations, anions, and electrons. This conductivity is crucial for the effective operation of electrochemical devices that utilize the electrolyte. The suitability of prepared electrolytes for applications is determined by the ratio of specific charge carriers. This study conducts a measurement of the total ion transport number (tion) to assess the overall ionic contribution to conductivity. Fig. S2 (ESI†) shows a plot of the polarization current against time for the electrolyte membranes using Wagner's DC polarization technique, as described in the literature. The abrupt decrease in the polarization current over time suggests that the fabricated electrolytes were ionically conducting. The quantitative estimation of the total ions (tion) within the fabricated electrolyte membranes can be performed by measuring the initial current (io) and saturation current (is) values from the polarization current versus time plots.
The ion transport numbers and ionic conductivity are tabulated in Table S1 (ESI†). The tion values of these SPE films were found to be close to unity (>0.97), indicating that the optimized electrolyte specimen is predominantly ionic in nature, contributing almost entirely to the ionic conductivity and ion-transport behavior. The results obtained in this study align with other investigations that assess the overall ion transport number in electrolyte systems based on sodium.102,103
3.10 Mechanical studies
The mechanical strength of solid electrolytes is a critical characteristic that must be ensured to prevent puncturing by sodium metal dendrites. The mechanical properties of the solid polymer electrolyte membranes, as determined by using a tensile testing machine, are shown in Fig. 13 and Table S2 (ESI†). | ||
| Fig. 13 (a) Stress–strain graph and (b)–(d) variation of the mechanical parameters for PVA/CS-NaClO4 SPEs. | ||
The mechanical properties of polymer electrolytes are significantly influenced by the salt concentration. An increase in the salt content generally leads to a decrease in the elastic modulus and tensile strength.104 The same was true for the current study. The decrease in mechanical strength can be attributed to the coordination between polymer chains and salt ions at the intramolecular level. This interaction confirms that the addition of salt enhances the amorphous phase of the material.105 Moreover, the values for elongation at break rise as salt concentration increases, indicating stronger molecular interactions within the polymer film.106
4. EDLC characterization
4.1 Cyclic voltammetry
Cyclic voltammetry (CV) is a common technique for assessing capacitive behavior and distinguishing between non-faradaic and faradaic reactions. Initially, CV measurements were conducted at a scan rate of 5 mV s−1 across several voltage windows, as shown in Fig. 14(a). The cell exhibited a stable behavior up to 1 V. Beyond this range, distortions appear, leading to the selection of 0–1 V as the optimal voltage window. Subsequently, CV scans were performed at various scan rates (5–100 mV s−1) within a 0–1 V window, as shown in Fig. 14(b). CV graphs show a nearly symmetrical shape, which reflects a mirror-like current response around the zero line. This symmetry is indicative of electric double-layer capacitance formation at the interface, confirming non-faradaic behavior.107 The absence of redox peaks in the CV profiles indicates a lack of faradaic (charge transfer) processes in the EDLC. As the charging process occurs, positively charged ions move towards the negative electrode, while negatively charged ions travel to the positive electrode. A powerful electric field maintains the ions within the electrolyte and electrons at the electrode. This results in the creation of a double-layer charge on the surface of the carbon electrode, where energy is stored in the form of potential energy.107Furthermore, as shown in Fig. 14(b), deviations from the ideal box-like shape are caused by the internal resistance and porosity of the carbon electrodes, leading to current-dependent potentials. The CV shapes observed in this study closely resemble those reported by Lavall et al.,108 suggesting that charge and discharge processes in these EDLCs are nearly reversible at the electrode/polymer electrolyte interface. Notably, the CV curve's shape transformed from leaf-like to more rectangular as the scan rate was reduced, primarily due to electrode characteristics. The CV's inability to achieve a perfect rectangular form can be attributed to variations in internal resistance and porosity.109
The specific capacitance (Cs) values at each scan rate were calculated from the CV curves using eqn (6) and are presented in Table 5, with the highest value recorded at a low scan rate, which gradually decreased as the scan rate increased. At a low scan rate, a stable double-layer charge forms owing to ion adsorption at the interfacial region, which explains the nearly perfect plateau observed. This occurs because a thick diffuse layer builds up, leading to reduced ohmic resistance. Conversely, at a high scan rate, a thinner diffuse layer formed, resulting in a lower capacitance.110
| Scan rate (mV s−1) | Specific capacitance Cs (F g−1) (before cycling) | Specific capacitance Cs (F g−1) (after cycling) |
|---|---|---|
| 5 | 38.45 | 42.66 |
| 10 | 30.90 | 32.91 |
| 20 | 24.10 | 24.77 |
| 50 | 15.93 | 16.14 |
| 100 | 10.78 | 10.97 |
CV can also be used to assess the stability and performance of an electrochemical cell over time, including the evaluation of the long-term stability of an EDLC after 5000 cycles, as shown in Fig. 14(c). CV analysis was performed after the device completed 5000 cycles, with the results indicating a minimal change in the specific capacitance, as shown in Table 5. This suggests that the EDLC maintains good stability even after extensive cycling.
4.2 Charge–discharge of the EDLC
The GCD technique was employed to evaluate the charge–discharge process of the EDLC. Fig. 14(d) shows the charge–discharge profile of the EDLC with a carbon electrode and electrolyte system. The linear discharge slope confirms the capacitive behavior of the EDLC. The specific capacitance (Cs) and energy and power densities of the EDLC were calculated from the charge–discharge curves using eqn (7), (9) and (10) respectively and the values are shown in Table 6.| Current density (mA g−1) | Specific capacitance (F g−1) | Energy density (W h kg−1) | Power density (W kg−1) |
|---|---|---|---|
| 0.05 | 20.58 | 2.69 | 97.0 |
| 0.06 | 19.03 | 2.49 | 116.4 |
| 0.07 | 17.49 | 2.24 | 134.4 |
| 0.08 | 16.41 | 2.12 | 154.4 |
| 0.09 | 15.55 | 2.00 | 173.2 |
| 0.1 | 14.77 | 1.88 | 191.6 |
| 0.2 | 8.98 | 1.05 | 366.4 |
4.3 EIS analysis of EDLC devices
Fig. 14(e) presents the Nyquist plots of PCP35 with AC–CB electrodes, where a semicircle and a spike are observed in the high- and low-frequency regions, respectively. The total impedance in the Nyquist plots can be divided into three components: bulk electrolyte resistance (represented by the x-intercept at the highest frequency), interfacial impedance between the electrode and bulk solution (shown as a semicircle in the mid-frequency region), and impedance associated with intraparticle pores (indicated by the spike at the low frequency), as shown in Fig. 14(e). The first two components are primarily influenced by the electrolyte solution, whereas the low-frequency tails are governed by both electrode materials and electrolytes.8 The equivalent circuit of the impedance spectra is shown in the inset of Fig. 14(e). The electrical circuit is composed of an ohmic series resistance (Rs) connected in series to a parallel combination of the charge transfer resistance (RCT) and a constant phase element (CPE1). This arrangement is then connected in series with another constant-phase element (CPE2). The initial intersection of the Nyquist plot with the real axis at low frequencies represents the equivalent series resistance (Rs), which stems from internal resistance, wire resistance, and their connections. The second point where the Nyquist plot crosses the real axis corresponds to the charge transfer resistance (RCT) occurring between the electrode and electrolyte interface.111EIS analysis was performed before and after the cycling stability tests to investigate the potential degradation of the EDLC. The Rs and RCT values increased slightly after 5000 cycles. The results presented in Table 7 suggest that no significant potential degradation occurred during long-term cycling and the material almost retained its original properties.
| Element | Cycling | Values |
|---|---|---|
| R s (Ω) | Before | 133 |
| After | 81.25 | |
| R CT (Ω) | Before | 208 |
| After | 120.2 | |
| CPE1 (F cm−2 s(n1−1)) | Before | 0.963 × 10−3 |
| After | 0.188 × 10−3 | |
| CPE2 (F cm−2 s(n2−1)) | Before | 1.264 × 10−3 |
| After | 1.299 × 10−3 |
4.4 Cycling performance and efficiency
Cycling performance serves as a key indicator of EDLC device effectiveness. To assess its cycling stability, the device underwent 5000 cycles at a current density of 0.2 mA g−1. As shown in Fig. 14(f), the cycling test results demonstrate the exceptional stability and efficiency of the device using PCP35 electrolyte. The observed increase in capacitance is attributed to gradual electrolyte penetration into the electrode during charge–discharge cycles. This process leads to progressive activation of electrode surfaces, enhancing electrolyte ion accessibility to micropores. As cycling progresses, electrolyte ions increasingly permeate the inner regions of the electrodes. This deeper penetration expands the effective electrode surface area for ion interactions, boosting capacitance. Extended operation allows for more thorough utilization of the electrode material, contributing to the increase in capacitance. A comparable phenomenon has been documented in other scientific literature reports.112,113 This phenomenon has led to improved performance, enhancing ESR, energy density, and power density of the device, even after 5000 continuous cycles as discussed in the next section.Another important metric for assessing the cycle stability of an EDLC is its coulombic efficiency (η), which can be calculated using the following formula:
 | (27) |
4.5 ESR of the EDLC cell
A key desirable feature of an EDLC assembly is low equivalent series resistance (ESR).110 ESR refers to the internal resistance within a supercapacitor that causes energy loss in the form of heat during charge and discharge cycles. Four primary factors affect ESR: the inherent resistance of the active electrode material, the overall resistance within the electrolyte, the current collector, and the resistance at the interface between the active material and electrolyte.107 The ESR was calculated using the equation below, | (28) |
Insight into the EDLC assembly can be obtained from the ESR response over multiple cycles, as illustrated in Fig. 15(a). The ESR value was recorded at 210 Ω in the first cycle and remained relatively stable until the 5000th cycle. A minimal ESR signifies superior electrode–electrolyte contact, promoting efficient ion transfer into the electrode's surface pores.115 In this study, ESR changes over 5000 cycles were minimal, indicating strong electrode–electrolyte contact. This stability also contributed to an increase in specific capacitance over continuous cycling, as observed in the previous section. Moreover, the ESR values reported here are significantly lower than those reported for other EDLC devices employing other SPEs.116–118
 | ||
| Fig. 15 (a) Specific capacitance and efficiency, (b) ESR, and (c) energy and power density values of a PCP35-based EDLC over 5000 charge–discharge cycles. | ||
Fig. 15(b) illustrates the variation of energy and power densities over 5000 charge–discharge cycles at 0.2 mA g−1 current density. The stored energy in the first cycle was calculated to be 1.08 W h kg−1. With increasing cycle count, the energy density reached a steady state at approximately 1.25 W h kg−1, which was sustained for 5000 cycles. This consistent energy density suggests minimal ionic clustering, implying that ion movement likely encounters a similar energy barrier throughout the process.119 The power density in the first cycle was measured at 360 W kg−1 and fluctuated only slightly, with an average value of 375 W kg−1 throughout 5000 cycles. A comparison of the EDLC parameters from this study with previously reported systems is presented in Table 8.
| Electrolyte system | Specific capacitance | Energy density (W h kg−1) | Power density (W kg−1) | Ref. |
|---|---|---|---|---|
| PVA-gum arabic-NH4NO3 | 2.9 F g−1@5 mV s−1 | 0.43 | 610 | 120 |
| PVA-dextran-NH4I | 4.2 F g−1@50 mV s−1 | 0.55 | 64 | 121 |
| Dextran-NH4Br | 2.46 F g−1@50 mV s−1 | — | — | 122 |
| Chitosan-PEO-LiClO4 | 6.88 F g−1@0.5 mA cm−2 | 1.07 | 321 | 123 |
| PVA–CS–MgCl2 | 5.80 F g−1@5 mV s−1 | — | — | 22 |
| PVA–CS–NaClO4·H2O | 38.45 F g−1@5 mV s−1 | 2.69 | 97 | Present work |
5. Conclusions
In this study, SPEs were successfully prepared by blending CS and PVA using the solution casting method, with NaClO4 added to enable ion transport. Impedance measurements demonstrated that a 35 wt% salt concentration provided the highest DC conductivity, measured at (5.23 ± 0.27) × 10−4 S cm−1. Meanwhile, the AC conductivity spectra distinctly highlight both the electrode polarization and ion-hopping mechanisms. TNM revealed a dominant ionic contribution to the overall conductivity, and electrochemical stability testing confirmed the stability up to 2.6 V, indicating no observable breakdown. Furthermore, cyclic voltammetry (CV) performed on the optimum electrolyte-based EDLC showed the absence of redox peaks, signifying capacitive behaviour. The different scan rates yielded characteristic current–voltage profiles representative of the ion accumulation dynamics. Galvanostatic charge–discharge (GCD) measurements produced nearly ideal triangular voltage profiles with approximately 100% coulombic efficiencies. This corresponds to a specific capacitance of approximately 20.58 F g−1, a power density of 97 W kg−1, and an energy density of 2.69 W h kg−1 at a relatively low current density of 0.05 mA g−1. Overall, these results highlight the potential of this green SPE as an environmentally friendly and high-performance energy-storage material. Incorporating plasticizers or ionic liquids into the optimised polymer matrix can boost ionic mobility, resulting in better electrode–electrolyte contact, lower internal resistance, and improved charge–discharge efficiency. These modifications will be further explored in our upcoming studies to optimize supercapacitor materials, potentially leading to devices with higher energy and power densities.Author contributions
Vipin Cyriac: conceptualization, methodology, data curation, formal analysis, investigation, writing – original draft; Ismayil: methodology, validation, supervision, writing – reviewing and editing; Kuldeep Mishra: visualization, resources, data curation, investigation; Ankitha Rao: formal analysis, investigation; Riyadh Abdekadir Khellouf: visualization, resources; Saraswati P. Masti: resources, data curation; and I. M. Noor: resources, data curation, writing – reviewing and editing.Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
One of the co-authors, Vipin Cyriac, extends his gratitude to the Directorate of Minorities in Bengaluru, India for their support. VC is particularly thankful for the financial assistance provided in the form of a fellowship for minority students, as per the sanction order DOM/Fellowship/CR-10/2019-20 dated June 29, 2020, which made this study possible.References
- F. C. Lucchese, L. N. Canha, W. S. Brignol, B. K. Hammerschmitt, L. N. F. Da Silva and C. C. Martins, 2019 54th International Universities Power Engineering Conference, UPEC 2019 – Proceedings DOI:10.1109/UPEC.2019.8893470.
- R. B. Schainker, 2004 IEEE Power Engineering Society General Meeting, 2004, 2, pp. 2309–2314.
- N. S. Choi, Z. Chen, S. A. Freunberger, X. Ji, Y. K. Sun, K. Amine, G. Yushin, L. F. Nazar, J. Cho and P. G. Bruce, Angew. Chem., Int. Ed., 2012, 51, 9994–10024 CrossRef PubMed.
- F. Béguin, V. Presser, A. Balducci and E. Frackowiak, Adv. Mater., 2014, 26, 2219–2251 CrossRef PubMed.
- D. E. Jiang and J. Wu, J. Phys. Chem. Lett., 2013, 4, 1260–1267 CrossRef PubMed.
- Q. Abbas, M. Mirzaeian, A. G. Olabi and D. Gibson, Encycl. Smart Mater., 2022, 382–392 CrossRef.
- K. Kerman, A. Luntz, V. Viswanathan, Y.-M. Chiang and Z. Chen, J. Electrochem. Soc., 2017, 164, A1731–A1744 CrossRef.
- L. Gautam, S. G. Warkar, S. I. Ahmad, R. Kant and M. Jain, Polym. Eng. Sci., 2022, 62, 225–246 CrossRef.
- N. M. Sadiq, S. B. Aziz and M. F. Z. Kadir, Gels, 2022, 8, 153 CrossRef PubMed.
- T. Yamamoto, M. Inami and T. Kanbara, Chem. Mater., 1994, 6, 44–50 CrossRef.
- S. Alipoori, S. Mazinani, S. H. Aboutalebi and F. Sharif, J. Energy Storage, 2020, 27, 101072 CrossRef.
- T. Jiang, R. James, S. G. Kumbar and C. T. Laurencin, Nat. Synth. Biomed. Polym., 2014, 91–113 Search PubMed.
- R. d S. Victor, A. M. d C. Santos, B. V. de Sousa, G. d A. Neves, L. N. d L. Santana and R. R. Menezes, Materials, 2020, 13, 4995 CrossRef.
- R. C. F. Cheung, T. B. Ng, J. H. Wong and W. Y. Chan, Mar. Drugs, 2015, 13, 5156–5186 CrossRef CAS.
- T. Winie, S. R. Majid, A. S. A. Khiar and A. K. Arof, Polym. Adv. Technol., 2006, 17, 523–527 CrossRef CAS.
- S. Alipoori, S. Mazinani, S. H. Aboutalebi and F. Sharif, J. Energy Storage, 2020, 27, 101072 CrossRef.
- Y. Liu, N. E. Vrana, P. A. Cahill and G. B. McGuinness, J. Biomed. Mater. Res., Part B, 2009, 90B, 492–502 CrossRef CAS PubMed.
- M. M. Nofal, S. B. Aziz, J. M. Hadi, R. T. Abdulwahid, E. M. A. Dannoun, A. S. Marif, S. Al-Zangana, Q. Zafar, M. A. Brza and M. F. Z. Kadir, Materials, 2020, 13, 4890 CrossRef CAS PubMed.
- M. F. Z. Kadir, S. R. Majid and A. K. Arof, Electrochim. Acta, 2010, 55, 1475–1482 CrossRef CAS.
- S. B. Aziz, J. M. Hadi, E. M. A. Dannoun, R. T. Abdulwahid, S. R. Saeed, A. Shahab Marf, W. O. Karim and M. F. Z. Kadir, Polymers, 2020, 12, 1938 CrossRef CAS PubMed.
- M. H. Buraidah and A. K. Arof, J. Non-Cryst. Solids, 2011, 357, 3261–3266 CrossRef CAS.
- P. Nayak, Ismayil and Y. N. Sudhakar, Int. J. Biol. Macromol., 2025, 297, 139797 CrossRef CAS.
- S. B. Aziz, M. J. Ahmed, O. G. Abdullah, A. R. Murad, S. M. Hamad and J. M. Hadi, Electrochim. Acta, 2023, 461, 142659 CrossRef CAS.
- R. N. Sagar, R. Vasachar and S. Hegde, eXPRESS Polym. Lett., 2023, 17, 883–899 CrossRef CAS.
- M. Benítez, J.-E. Diosa and R. A. Vargas, Ionics, 2018, 24, 2029–2034 CrossRef.
- D. C. Bharati, P. Rawat and A. L. Saroj, J. Solid State Electrochem., 2021, 25, 1727–1741 CrossRef CAS.
- J. A. Chaker, C. V. Santilli, S. H. Pulcinelli, K. Dahmouche, V. Briois and P. Judeinstein, J. Mater. Chem., 2007, 17, 744–757 RSC.
- K. K. Ganta, V. R. Jeedi, K. V. Kumar and E. L. Narsaiah, Int. J. Polym. Anal. Charact., 2021, 26, 130–144 CrossRef CAS.
- S. Gupta, V. Shukla, S. K. Gupta, B. K. Pandey and A. K. Gupta, AIP Conf. Proc., 2020, 2269, 030062 CrossRef.
- M. F. Z. Kadir, S. R. Majid and A. K. Arof, Electrochim. Acta, 2010, 55, 1475–1482 CrossRef CAS.
- S. T. Senthilkumar, R. K. Selvan, Y. S. Lee and J. S. Melo, J. Mater. Chem. A, 2012, 1, 1086–1095 RSC.
- D. Sun, X. Yan, J. Lang and Q. Xue, J. Power Sources, 2013, 222, 52–58 CrossRef CAS.
- M. D. Stoller and R. S. Ruoff, Energy Environ. Sci., 2010, 3, 1294–1301 RSC.
- A. Iakunkov, V. Skrypnychuk, A. Nordenström, E. A. Shilayeva, M. Korobov, M. Prodana, M. Enachescu, S. H. Larsson and A. Vtalyzin, Phys. Chem. Chem. Phys., 2019, 21, 17901–17912 RSC.
- B. Andres, A. C. Engström, N. Blomquist, S. Forsberg, C. Dahlström and H. Olin, PLoS One, 2016, 11, e0163146 CrossRef.
- M. F. Shukur, R. Ithnin and M. F. Z. Kadir, Electrochim. Acta, 2014, 136, 204–216 CrossRef CAS.
- T. Qin, S. Peng, J. Hao, Y. Wen, Z. Wang, X. Wang, D. He, J. Zhang, J. Hou and G. Cao, Adv. Energy Mater., 2017, 7, 1700409 CrossRef.
- T. Qin, S. Peng, J. Hao, Y. Wen, Z. Wang, X. Wang, D. He, J. Zhang, J. Hou and G. Cao, Adv. Energy Mater., 2017, 7, 1700409 CrossRef.
- A. M. Stephan, Eur. Polym. J., 2006, 42, 21–42 CrossRef.
- P. Sharma, G. Mathur, N. Goswami, S. K. Sharma, S. R. Dhakate, S. Chand and A. Mathur, e-Polym., 2015, 15, 237–243 Search PubMed.
- J. M. Yang, C. S. Fan, N. C. Wang and Y. H. Chang, Electrochim. Acta, 2018, 266, 332–340 CrossRef.
- K. Kargosha, S. H. Davarani and R. Moosavi, Analyst, 1995, 120, 1945–1948 RSC.
- Y. Chen, Y. H. Zhang and L. J. Zhao, Phys. Chem. Chem. Phys., 2004, 6, 537–542 RSC.
- J. L. Bishop, R. Quinn and M. D. Dyar, Am. Mineral., 2014, 99, 1580–1592 CrossRef PubMed.
- C. Branca, G. D’Angelo, C. Crupi, K. Khouzami, S. Rifici, G. Ruello and U. Wanderlingh, Polymer, 2016, 99, 614–622 CrossRef.
- P. M. B. Chagas, A. A. Caetano, M. A. Rossi, M. A. Gonçalves, T. de Castro Ramalho, A. D. Corrêa and I. do Rosário Guimarães, Environ. Sci. Pollut. Res., 2019, 26, 15973–15988 CrossRef.
- M. L. Duarte, M. C. Ferreira, M. R. Marvão and J. Rocha, Int. J. Biol. Macromol., 2002, 31, 1–8 CrossRef.
- M. Rinaudo, Prog. Polym. Sci., 2006, 31, 603–632 CrossRef.
- V. Cyriac, S. Molakalu Padre, Ismayil, G. Sangam Chandrashekar, C. Chavan, R. Fakeerappa Bhajantri and M. S. Murari, J. Appl. Polym. Sci., 2022, 139, e52525 CrossRef.
- R. K. Prajapati, H. Kumar and A. L. Saroj, Phys. B, 2023, 662, 414962 CrossRef.
- D. C. Bharati, P. Rawat and A. L. Saroj, J. Solid State Electrochem., 2021, 25, 1727–1741 CrossRef.
- S. S. Gaur, P. Dhar, A. Sonowal, A. Sharma, A. Kumar and V. Katiyar, J. Membr. Sci., 2017, 526, 348–354 CrossRef.
- V. Cyriac, Ismayil, K. Mishra, Y. N. Sudhakar, Z. E. Rojudi, S. P. Masti and I. M. Noor, Solid State Ionics, 2024, 411, 116578 CrossRef.
- M. P. Shilpa, V. Cyriac, S. C. Gurumurthy, Ismayil, S. Shet, K. V. Subbaiah and M. S. Murari, Radiat. Phys. Chem., 2024, 218, 111590 CrossRef.
- M. H. Buraidah and A. K. Arof, J. Non-Cryst. Solids, 2011, 357, 3261–3266 CrossRef.
- I. R. Rodrigues, M. M. de Camargo Forte, D. S. Azambuja and K. R. L. Castagno, React. Funct. Polym., 2007, 67, 708–715 CrossRef.
- C. Chavan, R. F. Bhajantri, S. Bulla, H. B. Ravikumar, M. Raghavendra, K. Sakthipandi, K. Yogesh Kumar and B. P. Prasanna, Ceram. Int., 2022, 48, 17864–17884 CrossRef.
- S. S. Gaur, P. Dhar, A. Sonowal, A. Sharma, A. Kumar and V. Katiyar, J. Membr. Sci., 2017, 526, 348–354 CrossRef CAS.
- R. K. Prajapati, H. Kumar and A. L. Saroj, Phys. B, 2023, 662, 414962 CrossRef CAS.
- X. Li, X. Zhu, J. Liang, H. Shi, B. Lan, C. Zhang, T. I. Alanazi and A. M. El Sayed, Phys. Scr., 2023, 98, 085946 CrossRef.
- J. R. B. Gomes, M. Jorge and P. Gomes, J. Chem. Thermodyn., 2014, 73, 121–129 CrossRef CAS.
- J. A. Zhao and F. de Ren, J. Mol. Model., 2020, 26, 1–16 CrossRef PubMed.
- A. Bhattacharya and P. Ray, J. Appl. Polym. Sci., 2004, 93, 122–130 CrossRef CAS.
- H. Sato, Spectrosc. Tech. Polym. Charact., 2021, 435–452 Search PubMed.
- J. H. Kim and Y. M. Lee, J. Membr. Sci., 2001, 193, 209–225 CrossRef CAS.
- P. Nayak, Ismayil, V. Cyriac, S. Hegde, G. Sanjeev, M. S. Murari and Y. N. Sudhakar, J. Non-Cryst. Solids, 2022, 592, 121741 CrossRef CAS.
- D. C. Bharati, P. Rawat and A. L. Saroj, J. Solid State Electrochem., 2021, 25, 1727–1741 CrossRef CAS.
- R. Muchakayala, S. Song, S. Gao, X. Wang and Y. Fan, Polym. Test., 2017, 58, 116–125 CrossRef CAS.
- A. Bartolotta, G. Di Marco, M. Lanza and G. Carini, J. Non-Cryst. Solids, 1994, 172–174, 1195–1201 CrossRef CAS.
- E. Metwalli, M. Rasool, S. Brunner and P. Müller-Buschbaum, ChemPhysChem, 2015, 16, 2882–2889 CrossRef CAS.
- S. Bi, C. N. Sun, T. A. Zawodzinski, F. Ren, J. K. Keum, S. K. Ahn, D. Li and J. Chen, J. Polym. Sci., Part B:Polym. Phys., 2015, 53, 1450–1457 CrossRef.
- N. Molinari, J. P. Mailoa and B. Kozinsky, Chem. Mater., 2018, 30, 6298–6306 CrossRef.
- P. H. Hermans and A. Weidinger, J. Polym. Sci., 1949, 4, 709–723 CrossRef.
- P. H. Hermans and A. Weidinger, Die Makromol. Chem., 1961, 44, 24–36 CrossRef.
- V. Cyriac, Ismayil, I. M. Noor, K. Mishra, C. Chavan, R. F. Bhajantri and S. P. Masti, Cellulose, 2022, 29, 3271–3291 CrossRef.
- V. Cyriac, Ismayil, I. S. B. M. Noor, Z. E. Rojudi, Y. N. Sudhakar, C. Chavan, R. F. Bhajantri and M. S. Murari, Int. J. Energy Res., 2022, 46, 22845–22866 CrossRef.
- S. B. Aziz, M. A. Brza, E. M. A. Dannoun, M. H. Hamsan, J. M. Hadi, M. F. Z. Kadir and R. T. Abdulwahid, Molecules, 2020, 25, 4503 CrossRef CAS PubMed.
- D. Golodnitsky, E. Strauss, E. Peled and S. Greenbaum, J. Electrochem. Soc., 2015, 162, A2551–A2566 CrossRef CAS.
- M. F. Z. Kadir, S. R. Majid and A. K. Arof, Electrochim. Acta, 2010, 55, 1475–1482 CrossRef CAS.
- S. B. Aziz, M. H. Hamsan, M. A. Brza, M. F. Z. Kadir, S. K. Muzakir and R. T. Abdulwahid, J. Mater. Res. Technol., 2020, 9, 8355–8366 CrossRef CAS.
- G. J. Brug, A. L. G. van den Eeden, M. Sluyters-Rehbach and J. H. Sluyters, J. Electroanal. Chem. Interfacial Electrochem., 1984, 176, 275–295 CrossRef CAS.
- T. Winie and A. K. Arof, Phys. Chem. Macromol., 2014, 333–364 CAS.
- S. B. Aziz, R. T. Abdulwahid, H. B. Tahir, A. F. Abdulrahman, A. R. Murad, N. M. Sadiq, M. H. Hamsan, S. I. Al-Saeedi, M. F. Z. Kadir and S. M. Hamad, Solid State Ionics, 2024, 413, 116606 CrossRef CAS.
- H. J. Schütt and E. Gerdes, J. Non-Cryst. Solids, 1992, 144, 14–20 CrossRef.
- B. Natesan, N. K. Karan and R. S. Katiyar, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2006, 74, 042801 CrossRef CAS PubMed.
- J. Pan, K. Li, J. Li, T. Hsu and Q. Wang, Appl. Phys. Lett., 2009, 95, 022902 CrossRef.
- A. Schönhals and F. Kremer, Broadband Dielectric Spectroscopy, Springer Berlin Heidelberg, Berlin, Heidelberg, 2003, pp. 59–98 Search PubMed.
- S. B. Aziz, M. H. Hamsan, R. M. Abdullah and M. F. Z. Kadir, Molecules, 2019, 24, 2503 CrossRef CAS PubMed.
- S. A. M. Noor, A. Ahmad, I. A. Talib and M. Y. A. Rahman, Ionics, 2010, 16, 161–170 CrossRef CAS.
- M. Vahini and M. Muthuvinayagam, J. Mater. Sci.: Mater. Electron., 2019, 30, 5609–5619 CrossRef CAS.
- B. Chatterjee, N. Kulshrestha and P. N. Gupta, Phys. Scr., 2015, 90, 025805 CrossRef.
- S. B. Aziz, S. Al-Zangana, H. J. Woo, M. F. Z. Kadir and O. G. Abdullah, Results Phys., 2018, 11, 826–836 CrossRef.
- D. F. Vieira, C. O. Avellaneda and A. Pawlicka, Electrochim. Acta, 2007, 53, 1404–1408 CrossRef CAS.
- P. K. Singh, B. Bhattacharya, R. M. Mehra and H. W. Rhee, Curr. Appl. Phys., 2011, 11, 616–619 CrossRef.
- Y. D. Kim, Y. K. Jo and N. J. Jo, J. Nanosci. Nanotechnol., 2012, 12, 3529–3533 CrossRef.
- R. He and T. Kyu, Macromolecules, 2016, 49, 5637–5648 CrossRef.
- N. Vijaya, S. Selvasekarapandian, G. Hirankumar, S. Karthikeyan, H. Nithya, C. S. Ramya and M. Prabu, Ionics, 2012, 18, 91–99 CrossRef.
- Y. M. Yusof, H. A. Illias and M. F. Z. Kadir, Ionics, 2014, 20, 1235–1245 CrossRef.
- R. N. Sagar, R. Vasachar and S. Hegde, eXPRESS Polym. Lett., 2023, 17, 883–899 CrossRef CAS.
- D. Bharati and A. Saroj, Polym.-Plast. Technol. Mater., 2023, 62, 989–1007 CAS.
- K. G. Neoh, E. T. Kang and K. L. Tan, J. Appl. Polym. Sci., 1991, 43, 573–579 CrossRef CAS.
- A. Rao, S. Bhat, S. De and V. Cyriac, J. Energy Storage, 2024, 102, 113965 CrossRef.
- R. A. Khellouf, C. Bubulinca, V. Cyriac, J. Cisar, S. Durpekova and V. Sedlarik, J. Energy Storage, 2024, 101, 113769 CrossRef.
- M. M. E. Jacob and A. K. Arof, Polym. Eng. Sci., 2000, 40, 972–978 CrossRef CAS.
- A. Arya and A. L. Sharma, Ionics, 2017, 23(3), 497–540 CrossRef CAS.
- G. Rajesha Shetty and B. Lakshmeesha Rao, Mater. Today: Proc., 2022, 55, 194–200 CAS.
- S. B. Aziz, M. H. Hamsan, M. M. Nofal, W. O. Karim, I. Brevik, M. A. Brza, R. T. Abdulwahid, S. Al-Zangana and M. F. Z. Kadir, Polymers, 2020, 12, 1411 CrossRef CAS PubMed.
- R. L. Lavall, R. S. Borges, H. D. R. Calado, C. Welter, J. P. C. Trigueiro, J. Rieumont, B. R. A. Neves and G. G. Silva, J. Power Sources, 2008, 177, 652–659 CrossRef CAS.
- A. S. F. M. Asnawi, S. B. Aziz, M. M. Nofal, M. H. Hamsan, M. A. Brza, Y. M. Yusof, R. T. Abdilwahid, S. K. Muzakir and M. F. Z. Kadir, Polymers, 2020, 12, 1433 CrossRef CAS.
- H. D. Yoo, J. H. Jang, J. H. Ryu, Y. Park and S. M. Oh, J. Power Sources, 2014, 267, 411–420 CrossRef CAS.
- V. Cyriac, Ismayil, K. Mishra, A. Rao, S. P. Masti and I. M. Noor, Electrochim. Acta, 2024, 507, 145139 CrossRef CAS.
- S. Cho, J. Han, J. Kim, Y. Jo, H. Woo, S. Lee, A. T. Aqueel Ahmed, H. C. Chavan, S. M. Pawar, J. L. Gunjakar, J. Kwak, Y. Park, A. I. Inamdar, H. Kim, H. Kim and H. Im, Curr. Appl. Phys., 2017, 17, 1189–1193 CrossRef.
- C. Zequine, C. K. Ranaweera, Z. Wang, S. Singh, P. Tripathi, O. N. Srivastava, B. K. Gupta, K. Ramasamy, P. K. Kahol, P. R. Dvornic and R. K. Gupta, Sci. Rep., 2016, 6(1), 1–10 CrossRef.
- S. Aziz, E. Dannoun, R. Abdulwahid, M. Kadir, M. Nofal, S. Al-Saeedi and A. Murad, Membranes, 2022, 12, 139 CrossRef CAS PubMed.
- S. N. Asmara, M. Z. Kufian, S. R. Majid and A. K. Arof, Electrochim. Acta, 2011, 57, 91–97 CrossRef CAS.
- M. Selva Kumar and D. K. Bhat, Phys. B, 2009, 404, 1143–1147 CrossRef CAS.
- M. A. Brza, S. B. Aziz, H. Anuar, F. Ali, M. H. Hamsan, M. F. Z. Kadir and R. T. Abdulwahid, Arabian J. Chem., 2020, 13, 7247–7263 CrossRef CAS.
- S. B. Aziz, M. A. Brza, M. H. Hamsan, M. F. Z. Kadir, S. K. Muzakir and R. T. Abdulwahid, J. Mater. Res. Technol., 2020, 9, 3734–3745 CrossRef CAS.
- M. F. Shukur, Characterization of Ion Conducting Solid Biopolymer Electrolytes Based on Starchchitosan Blend and Application in Electrochemical Devices, PhD thesis, University of Malaya (Malaysia), 2015.
- M. Hema, G. Gopinath, A. Sakunthala, S. Krishnasamy, D. Aravind, J. Parameswaranpillai, N. Venkateshan and V. Natarajan, Int. J. Biol. Macromol., 2025, 307, 141956 CrossRef CAS.
- S. B. Aziz, M. A. Brza, M. H. Hamsan, M. F. Z. Kadir, S. K. Muzakir and R. T. Abdulwahid, J. Mater. Res. Technol., 2020, 9, 3734–3745 CrossRef CAS.
- M. H. Hamsan, M. F. Shukur, S. B. Aziz, Y. M. Yusof and M. F. Z. Kadir, Bull. Mater. Sci., 2020, 43, 30 CrossRef CAS.
- S. B. Aziz, M. H. Hamsan, M. A. Brza, M. F. Z. Kadir, R. T. Abdulwahid, H. O. Ghareeb and H. J. Woo, Results Phys., 2019, 15, 102584 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ma00107b |
| This journal is © The Royal Society of Chemistry 2025 |