Open Access Article
Open Access ArticleGenerative design and molecular mechanics characterization of silk proteins based on unfolding behavior†
Wei Lu ab and
Markus J. Buehler
ab and
Markus J. Buehler *abc
*abc
aLaboratory for Atomistic and Molecular Mechanics (LAMM), Massachusetts Institute of Technology, 77 Massachusetts Ave., Cambridge, MA 02139, USA. E-mail: mbuehler@mit.edu
bDepartment of Civil and Environmental Engineering, Massachusetts Institute of Technology, 77 Massachusetts Ave., Cambridge, MA 02139, USA
cCenter for Computational Science and Engineering, Schwarzman College of Computing, Massachusetts Institute of Technology, 77 Massachusetts Ave., Cambridge, MA 02139, USA
First published on 5th May 2025
Abstract
Spider silk exhibits exceptional mechanical properties, biocompatibility, and biodegradability, making it a promising material for bioengineered applications. However, the complexity and diversity of silk proteins, coupled with limited experimental data, have hindered the rational design of silk-based biomaterials. Furthermore, the mechanobiology of these proteins and their impact on silk fiber properties remain underexplored. In this study, we introduce a series of novel silk protein sequences and characterize their nonlinear unfolding behavior and mechanical properties through molecular dynamics (MD) simulations. Focusing on major ampullate spidroin (MaSp) silk proteins, we curate a dataset that integrates experimentally acquired sequences with synthetic sequences generated by SilkomeGPT, a generative model for silk-inspired proteins. Structural predictions are performed using OmegaFold, from which high-fidelity regions are extracted and analyzed. Their unfolding responses are assessed via implicit all-atom MD simulations, enabling characterization of their mechanical behavior. This computationally efficient framework facilitates the rational design of spider silk proteins by linking atomistic and sequence features to larger-scale properties. The developed dataset systematically captures structural uncertainties, while simulations provide atomic-level insights into how protein mechanics contribute to fiber properties, advancing the mechanobiological understanding of spider silk and supporting diverse applications in biomaterials design.
1. Introduction
Spider silk represents one of the nature's most advanced fibrous materials, offering an exceptional balance of strength, toughness, elasticity, and functional diversity. As interest grows in developing bioinspired synthetic alternatives, understanding the molecular basis of silk's mechanical behavior and hierarchical structure has become increasingly important. This study focuses on advancing computational frameworks that integrate generative modeling, protein structure prediction, and atomistic simulations to explore the sequence–structure–property relationships that underpin the performance of silk proteins. In this section, we provide an overview of the biological, structural, and functional complexity of spider silks and highlight key challenges and motivations that shape this work.1.1 Background
Spider silk, a protein-based hierarchical material that has evolved over 300 million years,1,2 is abundantly found in nature, exhibiting unique combinations of material properties, offering inspiration for material design.3–5 Scientists are interested in learning material properties and exploring hierarchical structural relationships for material optimization to achieve targeted features such as enhanced mechanical properties,2,6 thermal stabilities,7,8 controlled electrical conductivity,9,10 and tunable optical properties.11,12 Research on spider silk synthesis, material design, and optimization holds great potential for spider silk applications in industries such as smart materials and bioinspired technologies. However, several gaps persist for in-depth investigation on spider silk, including the high structural complexity, diversity, and limited data on spider silk protein sequences and their associated molecular- and fiber-level mechanical properties. Deepening our knowledge of the relationships across multiple scales and related mechanisms is crucial for spider silk-inspired material synthesis and design. Implementing simulations is therefore an essential method for collecting mechanical data, and incorporating advanced modeling techniques is critical for spider silk data augmentation, structure–property relationship identification, and vast design space exploration for synthetic materials.The strong silk filament and complex hierarchical architectures of spider silks (Fig. 1(a)) provide them with an exceptional combination of mechanical properties, including toughness, strength, and extensibility, while remaining lightweight. The hierarchical structure spans multiple scales, from nanoscale hydrogen-bonded chains to semi-amorphous phases embedded with beta-sheet nanocrystals, progressing to silk fibrils as nanocomposite networks, to silk fibers with fibrils as their building blocks, and finally forming a macroscale spider web structure. Silk material's stiffness and tensile strength stem from the presence of crystalline beta-sheets within the nanocomposites, while its extensibility and flexibility are enhanced by the disordered extensible semi-amorphous matrix and hydrogen bonds.1,3 Additionally, spider silk is biocompatible and biodegradable,13 making it an attractive material for biomedical and environmentally sustainable designs. Spider silk also exhibits supercontraction when exposed to high humidity14–16 due to the transition from the ordered to a disorganized morphology,17 making spider silk a promising material for application in adaptive material design with tunable mechanical properties. Moreover, spider silks are highly diverse and multifunctional, with seven main types that serve various purposes:2 (1) dragline silk: forms and supports the web structure; (2) flagelliform silk: forms the spiral fibers; (3) auxiliary spiral silk: stabilizes the web; (4) aggregate silk: serves as a sticky aqueous coating for capture spiral; (5) pyriform silk: functions in attachments and joints; (6) aciniform silk: used for prey wrapping and forms inner silk of egg sacs; and (7) cylindriform (or tubuliform) silk: forms the outer coating of egg sacs.18–20
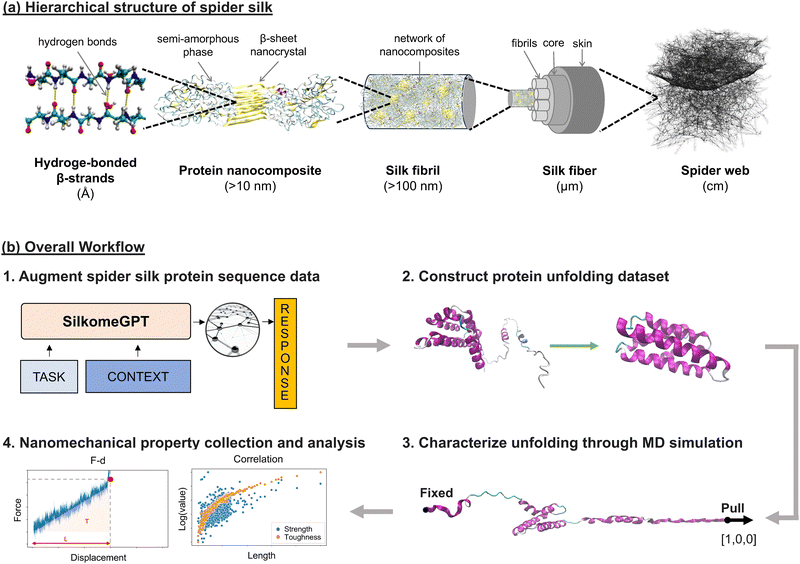 | ||
| Fig. 1 The hierarchical structure of spider silk and the schematic of the overall workflow. Panel (a): illustration of the hierarchical structure of spider silk, spanning from nanoscale hydrogen-bonded chains to semi-amorphous phases embedded with beta-sheet nanocrystals, progressing to silk fibrils as nanocomposite networks, to silk fibers with fibrils as their building blocks, and finally to the macroscale spider web structure (adapted with permission from ref. 2). Panel (b): the workflow consists of four main stages: (1) silk protein sequence generation, (2) dataset construction for simulation, (3) unfolding performance characterization via steered molecular dynamics (SMD), and (4) nanomechanical property collection and analysis. The specific procedure and methods are discussed in the Materials and methods section (Section 4). In step (1), around 2000 silk protein sequences were compiled, comprising ∼1000 real sequences curated from the silkome dataset,2,19 as well as ∼1000 novel sequences generated using the SilkkomeGPT model.2 In step (2), the collected sequences were folded into 3D structures using OmegaFold,21 with high-fidelity subsections extracted for simulation. The subsections with shorter lengths and containing the primary secondary components enhance the simulation efficiency while retaining mechanical significance. In step (3), automated simulations were performed on all 2177 folded structures, including equilibrations to stabilize the proteins and SMD simulates their unfolding performances. The unfolding behavior was characterized through a force–displacement plot during simulations, and the secondary structural changes were discussed. The nanomechanical properties were collected from simulations, with underlying mechanical behavior explored relating to different structural scales of spider silk proteins, as shown in step (4). | ||
Furthermore, each type of silk is primarily composed of different spidroins, the main protein building blocks of silk structures.2,19 Studies on spidroins have explored various aspects,2 including evolution,19 terminal domains22 and repetitive motifs,23 and the presence of different modifications.24 Spidroin proteins consist of repetitive regions flanked by the N-terminal and C-terminal,22,25 with each domain playing distinct roles that collectively contribute to proteins’ overall properties. The repetitive regions form the core secondary structures, governing the silk's mechanical properties, and the terminal domains influence spidroin solubility and silk fiber assembly.22,25 Within spidroin sequences, key amino acid residues26,27 important for mechanical properties include glycine for forming an amorphous matrix, alanine for creating beta-sheet conformations, and proline inducing turns in the protein structure. At larger scales, as silk fibers are composed of various types of spidroins, each spidroin provides specific functions: MaSp1 contributes to silk strength, MaSp2 relates elasticity and supercontraction, and MaSp3 demonstrates exceptional toughness.2,19 Additionally, spidroins undergo structural transitions during the silk spinning process.28 In their native form, spidroins are stored in the liquid form within the glandular sac, predominantly composed of alpha-helices. As the silk is spun into solid fibers, the secondary structure shifts to beta-sheets, driven not only by mechanical stress but also by changes in environmental factors such as pH, ion composition, and temperature. These transformations occur within the distal parts of the duct and are essential for the silk's final mechanical properties and hierarchical structure formation.
Several deep learning techniques29 have been applied to the prediction and generation of spider silk materials at different scales.30 Compared to traditional models based on predefined rules or mathematical equations, deep learning models that automatically learn underlying patterns from data, are more generalizable and flexible for handling complex and large-scale datasets. However, they are often computationally more expensive and less interpretable than traditional models.31 Commonly used machine learning models include neural networks (NNs) and graph neural networks (GNNs).32 The GNN is a type of neural network designed for non-Euclidean data, and aggregates information from neighboring nodes and edges through a message-passing process to capture complex relationships within graph structures. Examples of applications include the use of NNs for predicting the mechanical properties of spider web structures,13,33 and modeling the impact of amino acid sequences on spider silk properties.34 Another commonly introduced models are diffusion models, which iteratively reconstruct new designs through a denoising process by reversing the diffusion model35,36 process that adds Gaussian noise to the input data.
Additionally, transformers,37 with their attention mechanisms for capturing intricate relationships within data, are widely used. There have been works involving the use of both diffusion and transformer models for synthetic spider web design, enabling these models to learn complex web structure relationships.38 Moreover, the generative pre-trained transformer (GPT),39 developed based on the transformer architecture, undergoes pre-training on a large general corpus and fine-tuning on the task-specific dataset, making it highly effective for natural language processing (NLP) tasks. In recent work, SilkomeGPT2 was developed to link spider silk protein sequences to silk fiber properties, enabling both the prediction and design of spider silk proteins relating silk fiber properties.2 This model was trained using a curated dataset reported in ref. 19. Furthermore, vision-language models (VLMs),40–42 which combine transformer and convolutional neural networks, can process both image and text data to perform multimodal tasks. These models have been utilized to generate innovative design ideas by incorporating structural features and design principles from biomaterials. A recent study employed VLMs for structure design and urban planning, drawing inspiration from spider webs and leaves.43 Moreover, several applications of deep learning models for spider web- or silk-inspired designs have emerged, including sensor manufacturing,44 nanoresonators,45 carbon fiber composites46 with improved thermal and mechanical performance, and protein-based adhesives.47 In addition, recent developments in physically based data modeling, such as genetic algorithms, have shown promise for capturing hierarchical material behavior and enabling analytical insights into silk phenomena like supercontraction,48,49 offering a complementary direction to neural network-based approaches.
Apart from deep learning techniques, molecular dynamics (MD) simulation50–52 represents a crucial computational method for studying the behavior of atoms and molecules under varying boundary conditions, based on principles of interatomic interactions. The core idea involves calculating forces between atoms, applying Newton's laws of motion, and updating atomic positions and velocities iteratively through time steps.50 This approach provides detailed three-dimensional insights into atomic-level configurations, which are often difficult to obtain experimentally, especially under specific conditions. In our study on spider silks, we primarily use the simulation tool nanoscale molecular dynamics (NAMD),53 which is well-suited for large-scale biomolecular systems, particularly for nanoscale protein structures like spidroin proteins. The appropriate choice of tools enables us to explore the complex molecular dynamics of fibrous structures with precision and efficiency across multiple scales. Previous studies utilizing MD simulations on spider silks have investigated the effects of electric fields54 on mechanical properties, the influence of hydration conditions,55 and comparisons of atomic behaviors between spider and silkworm silks.56 Coarse-grained (CG) models have also been employed for more efficient exploration of the mechanical properties of spider silks.8
Moreover, combining MD simulations with machine learning (ML) techniques offers a powerful approach for efficiently exploring material properties and behaviors. This integration facilitates the design of hierarchical materials like spider silk by generating and linking data across different scales (e.g., molecular-level proteins and macro-level fibers). Relevant works that combine MD simulations with ML include the prediction of ultimate tensile strength of silk fibers through simulations coupled with deep neural networks (DNNs),6 and ForceGen57 model development for de novo protein design based on unfolding responses. This integration of MD and ML opens up new avenues for the design and analysis of complex materials, allowing for more comprehensive and scalable investigations.
1.2 Motivation and overview of this work
Understanding the mechanobiology of spider silk proteins and their influence on fiber properties, alongside their hierarchical structure, is essential for developing cost-effective synthetic design methods for large-scale data collection and design space exploration. Generating novel sequences using the generative model, SilkomeGPT,2 expands the dataset by covering structural uncertainties and providing fiber-level mechanical properties, supporting exploration across multiple scales. The sequence-dependent folding and unfolding behaviors of spider silk proteins significantly impact the mechanical response of the fiber. Investigating this relationship provides deeper insights into how specific protein sequences and structural motifs contribute to material performance under stress.28 Large-scale data collection and design space exploration, through advanced simulations, protein folding studies, and deep learning, can accelerate the discovery and optimization of novel silk-like materials. Integrating these tools creates a pathway to explore and understand the spider silk protein and silk fibers at different scales, without the high costs of experimental trial and error.2However, gaps exist in terms of existing spider silk studies and available data. First, the availability of spider silk protein data is limited, which hinders thorough analysis. Although the Silkome19 dataset has been developed experimentally, after curation, only about 1000 data points related to MaSp fiber-level mechanisms are usable. Additionally, characterizing the nanomechanical properties of spider silk proteins covering structural uncertainties remains a challenge due to the limited data and computational costs. The complexity, diversity, and hierarchical nature of spider silk further complicate the collective understanding of how its mechanical properties are influenced by structural components (e.g., spidroins) and the multiscale assembly process. Thus, in this work, we aim to investigate the non-linear unfolding behavior and characterize the nanomechanical properties of native aqueous spider silk proteins (the soluble, pre-spinning form of spidroins stored in the spider's glandular lumen). Our approach includes augmenting the dataset using SilkomeGPT2 and filtering high-performing sequences through an iterative recursive approach, collecting high-fidelity protein sections via OmegaFold,21 and conducting MD simulations to explore unfolding behavior and nanomechanical properties on spider silk proteins to enrich the dataset with physical properties obtained from fundamental molecular principles.
2. Results and discussion
This section covers the dataset analysis, discussion of simulation performance, changes in secondary structures during the unfolding process, and the analysis of the characterized nanomechanical properties.2.1 Dataset analysis
Before subsection extraction, a total of 2240 full protein sequences were collected. This dataset includes 1033 actual sequences from the silkome dataset2,19 and 1207 novel sequences generated using SilkomeGPT.2 Detailed methods for dataset development are described in Section 4.1. For data augmentation, property sets were drawn from the distribution of the fiber-level mechanical properties of the 1033 existing sequences (Fig. 2(a1)) and used as inputs to SilkomGPT for generating novel sequences that are then further characterized to extract molecular-level properties and behaviors. A filtering process was applied, resulting in 1207 novel sequences with a selection rate of 1.67% after an iterative recursive filtering process. As shown in Fig. 2(a2), the property distribution of the developed dataset closely resembled that of the native sequences, and the correlation plots show similar structural patterns between the existing and generated sequences, collectively validating our augmentation method. To evaluate the effectiveness of our augmentation strategy, we compared the histogram distributions of eight fiber-level mechanical properties, including toughness, elastic modulus (E), strength, strain at break, and their corresponding standard deviations, between the existing and generated datasets (Fig. 2(a1) and (a2)). The average Pearson correlation coefficient across the binned distributions was r = 0.906, with individual values for each property as follows: [0.8865, 0.9839, 0.7996, 0.9374, 0.7658, 0.9838, 0.9884, and 0.9029]. These values indicate strong alignment between the two distributions, confirming that the generated sequences successfully preserve the statistical characteristics of the original dataset and validating the reliability of the augmentation process.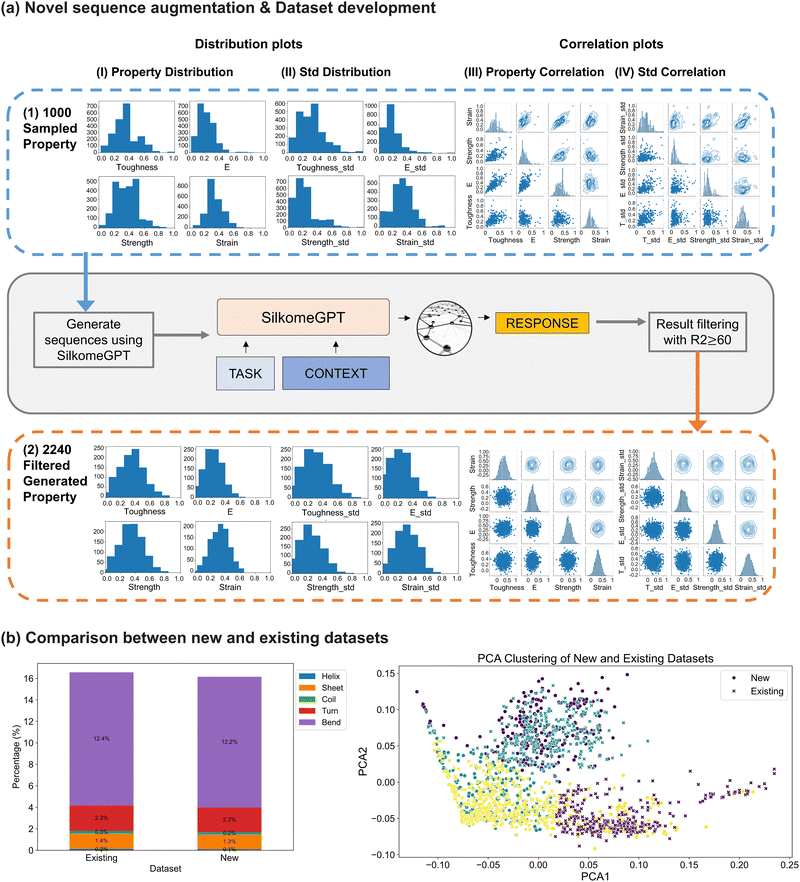 | ||
Fig. 2 Spider silk sequence augmentation through SilkomeGPT,2 and comparison of new and existing datasets. A total of 2240 protein sequences were collected for subsequent protein folding and simulation, comprising 1033 sequences collected from the silkome dataset2,19 and 1207 novel sequences generated using SilkomeGPT.2 In panel (a1), the distribution of available fiber-level mechanical properties of the 1033 existing MaSp sequences is analyzed. These properties include toughness, elastic modulus, tensile strength, strain at break, and four corresponding standard deviation measurements, with details discussed in ref. 2. To augment the dataset with synthetic yet reliable protein sequences, we employed a cyclic-consistent generation model, SilkomeGPT.2 We sampled 1000 random 8-dimensional property sets from the distribution of the existing dataset (panel (a1)). Using these as inputs, we output 206![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 838 novel sequences. After filtering, we retained 1207 designs with a generation R2 value of 60% or higher, yielding a collection rate of 1.67%. As shown in panel (a2), the property distribution of all 2240 collected sequences closely resembles that of the original set. In panel (b), the similarity between the new and existing datasets is evaluated through secondary structure composition and data clustering. The secondary structure composition of the new dataset is observed to closely resemble that of the existing dataset. Using principal component analysis (PCA) following k-mer frequency encoding to transform sequences into vectors, the scatter plot visualizes the distribution of the two datasets in a reduced-dimensional space. Clusters are highlighted in different colors based on K-means clustering. The plot indicates that the new and existing datasets share similar clustering features, with a significant degree of overlap, while also preserving some level of diversity and novelty. Further analysis and comparisons of the datasets are discussed in Section 2.1, while the details of the dataset development process are provided in Section 4.1. 838 novel sequences. After filtering, we retained 1207 designs with a generation R2 value of 60% or higher, yielding a collection rate of 1.67%. As shown in panel (a2), the property distribution of all 2240 collected sequences closely resembles that of the original set. In panel (b), the similarity between the new and existing datasets is evaluated through secondary structure composition and data clustering. The secondary structure composition of the new dataset is observed to closely resemble that of the existing dataset. Using principal component analysis (PCA) following k-mer frequency encoding to transform sequences into vectors, the scatter plot visualizes the distribution of the two datasets in a reduced-dimensional space. Clusters are highlighted in different colors based on K-means clustering. The plot indicates that the new and existing datasets share similar clustering features, with a significant degree of overlap, while also preserving some level of diversity and novelty. Further analysis and comparisons of the datasets are discussed in Section 2.1, while the details of the dataset development process are provided in Section 4.1. | ||
Moreover, the similarity between the new and existing datasets was further evaluated through secondary structure composition analysis and data clustering, as shown in Fig. 2(b). In the first plot of Fig. 2(b), the occurrences of secondary structures were counted and summed across all 2177 protein sequences in each dataset. The analysis reveals similar secondary structure compositions between the new and existing datasets, with comparable distributions of helices, sheets, coils, turns and bends. In the second plot of Fig. 2(b), the dimensionality of the sequence data was reduced using principal component analysis (PCA), following k-mer frequency encoding to transform sequences into vectors. The scatter plot visualizes the distribution of the two datasets in the reduced-dimensional space, with clusters highlighted in different colors based on K-means clustering. Both the new and existing datasets exhibit distinct clusters with a significant degree of overlap, suggesting overall similar clustering features in the reduced space. However, variations are observed, indicating diversity both within and between the datasets. Certain clusters are more strongly represented by one dataset, reflecting regions of unique sequence or motif composition specific to either natural or generated proteins. These dataset-specific clusters may correspond to variations in amino acid motifs, domain architectures, or repeat patterns, which have been shown in prior studies to influence mechanical outcomes such as extensibility, β-sheet formation, or supercontraction behavior19,20,22,48 (e.g., high glycine content promoting flexibility, and alanine promoting β-sheet crystallinity27,48). The generated clusters may capture alternative sequence solutions that remain unexplored in nature but are structurally viable and confirming the novelty and diversity of the new dataset. Conversely, overlap in clusters suggests that SilkomeGPT2 successfully replicates key sequence patterns seen in natural MaSp proteins. To provide a more quantitative comparison of the clustering similarities between the two datasets, additional metrics were computed using the K-means clustering results. The silhouette score difference of 0.0357 indicates minor disparities in clustering cohesion and separation between the datasets. The earth Mover's distance (EMD) difference of 0.00317 reflects small differences in the centroids or feature distributions of the clusters, while the pairwise distance difference of 0.00196 captures slight variations in overall clustering spread or compactness. Note the differences within 0.1 are considered indicative of high clustering similarity.58 These insights suggest that while the new and existing datasets are globally similar, local clustering differences may reflect distinct sequence motifs or structural features that could influence the nanomechanical properties. This highlights the need for future investigation of these differences through sequence–structure–property mapping and experimental validation.
Additionally, novelty and protein type checks were conducted. For the novel sequences generated using SilkomeGPT, the proteins were classified as MaSp, and their novelty was confirmed, as discussed in ref. 2. We further assessed novelty and protein type by selecting four random sequences and evaluating them using the basic local alignment search tool (BLAST).59 Two main criteria were considered: query cover (QC) for sequence alignment, and identity percentage (id%) for composition similarity. Sequences with the values below 50–60% were considered novel.60,61 For each sequence, the ten highest values and the common value ranges for both QC and id% are summarized in Table 1, along with a discussion demonstrating the novelty of these sequences. Additionally, the novel proteins were classified into MaSp types based on similarities to existing protein sequences.
| # | Protein sequence | Length | Highest value of [QC, id%] | Common range of [QC, id%] | Novelty analysis |
|---|---|---|---|---|---|
| 1 | GYPGQPGYSSSSSAIAISLGFASAAGAAVSGAGGNVGYGQDSAGAFGQGAFGGYGQGAGFGGAGGQGGLGGYGQGGSGASSAAAAASDGSGGRGGYGQGGQYLEAAAAAAAAAASAGSDTSAYAKVLAGGGGGGGGAGGLYGPQGGYVGISYGPGAGGSGAGNAVSSASGGYGGSFGTGPGISSPGAAGSRETSGSATSAGSGTGGQGMIGQNIVSYGPFGPGASSYGQYGQSGPVVARSGPTGVSGPGIGGYGQGADASATYLARGQGGYGGVGSLGAGQGGFGAGGAGQGSITIVSLGRYSGVSASVSSAASRLSSPAASARVSSAVSNLVAYGVSNPKFVSNLASALSSSASNPGLSGCEMLVQVLLELIAALVHILNSSSISSMGATDKDSSSADYNVYG | 404 | [24%, 78%] | [22%–19%, 65%–55%] | The low QC values (<20%) indicate novel alignments, despite the moderate composition similarities seen in id% |
| 2 | GAGGPGGYGPGYQGPSGPGSIAAAAGGAEGPGGYGPGYQGPSGPGGAAAAAVGAGGPGGYGPGYQGPSGPGGAAAAAAAAGGSGGPGVYGPVSQGPSGPGAAAAAAAAVGPGGQGGYQGPSGSGGAAATAPSGYGSSVAGPSAYGPVSQAPSGPVSQGPGVYGPSSQGPGVYGPSSQGPGAAAATVSAAASRLSSPASSSRVSSAVSNLVSSGPTSPAALSNVISSMASQVTASNPGLSGCDRLVQVLMELLTSVVVILSSSSIGQVNYGSAGQSAQIVGDSVYQAFA | 288 | [98%, 74%] | [50%–44%, 72%–69%] | Two existing sequences show high QC values but exhibit low composition similarity (id%), suggesting alignment with significant sequence differences |
| 3 | GQGSGEAGQGGYGSGLGGLGGAAAAAALGQGTGGAAQFGSVSGQTGGVEGRIQAASAARGAGQSGLGGAGAGGAGLYGPGGAGGLYGPGSVGPSAAGVGGQGGYGSGLGNGAGIFLEAASRLSSPSSSSRISSAVSTLINSGGADNVLSSTLSNLVSQVSANQPGLSGCDVIVQALLELVSALVHILGSSSIGQVDYNGASYSAQSIGQAVAQALA | 216 | [60%, 92%] | [44%–43%, 82%–76%] | There is a high similarity in composition, but the alignment coverage is minimal, with QC values consistently below 60%, indicating novelty |
| 4 | YGPGSQGPSGPGGAAAAAAAAAAGGPGGQGPGSQGPSGPGGYGPSSAAAAAAAAAGGQGGQGPYGPGQQGPGAYGPSGPGGAAAAAAAAAAGGPGGQGPYGPGQQGPGAYGPSGPGGAAAAAAAAAAGGPGGQGPSGPGQQGPGAYGPSGPGGAAAAAAAAAAGGPGGQGPYGPSQQGPGSYGPSGPGSSVSASVSSAASRLSSPAASSRVSSAVSTLASNGPSNAGVVSSALSSLVSQVSAGQPGLSGCDVLVQALLELVSALVSILGSASIGQVDYSSAGYSAQSLSQAVASILG | 297 | [79%, 86%] | [58%–52%, 79%–75%] | Although reasonable composition similarities are present, the overall alignment coverage is distinct, with QC values below 60%, supporting the novelty of these sequences |
Using the augmented dataset, we folded the full sequences with OmegaFold21 and extracted high-fidelity sections, as the folding performance is unstable for spider silk protein sequences (detailed methods in Section 4.2). The extracted sequences were further refolded to maintain a stable configuration. Fig. 3 illustrates the subsection extraction process and compares pLDDT plots and molecular structures in panels (a) and (b) for three extraction stages: full sequences, extracted subsequences, and refolded subsequences. For the three protein examples with varying lengths and molecular structures, the extracted subsections show high pLDDT values along their amino acids (highlighted in panel (a)). The refolded subsections have similar prediction performance to the original extracted sections, though on average the refolded sections show slightly higher pLDDT values than the extracted ones (76.39 vs. 73.41). As shown in panel (b), the extracted sections predominantly consist of the main secondary structures of original proteins, mostly alpha-helices, which contribute more to the mechanical properties of spider silk, rather than random coils which are less relevant to fiber strength. The refolded subsections generally retain the same molecular structure as the extracted sections, including the key structural shapes (helices and turns) and secondary structure composition, though some variations in alignment and orientation are present. As a result of this extraction process, a dataset of 2177 subsections was created for simulations. The average pLDDT value of the dataset significantly improved from 40.48 (full sequence dataset) to 76.39 (folded subsequence dataset), while the average sequence length decreased from 445 to 125, enhancing the reliability of the protein structures for simulation and significantly improving computational efficiency.
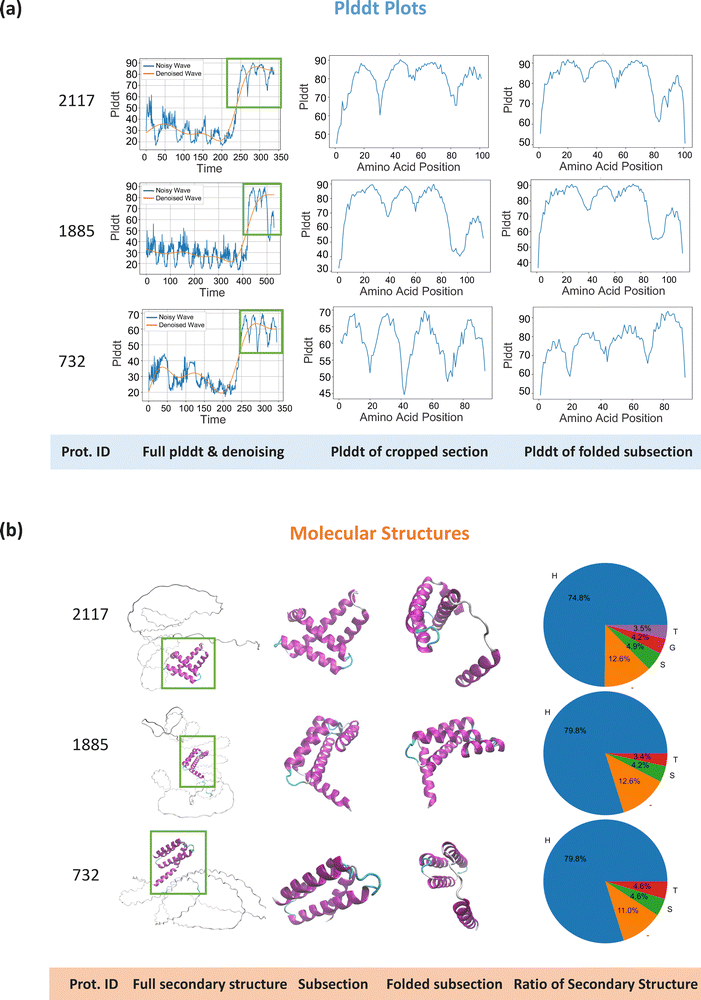 | ||
| Fig. 3 Examples of protein folding and subsection extraction. This figure showcases three protein samples with varying sequence lengths and molecular structures. The pLDDT plots and the visualized secondary structures for the full sequences, extracted subsections, and re-folded subsections are displayed in panels (a) and (b), respectively. In the last column of the panel (b), pie charts visualize the secondary structures composition of proteins, where H represents alpha helix structure, G represents beta-sheet, T represents turns, S represents bend, and – denotes other structures.62 The protein folding was performed using OmegaFold,21 and to extract high-fidelity subsections, the following steps were followed: first, we generated a pLDDT plot for each protein, along with a corresponding denoising plot for continuous section extraction. Next, subsections were extracted based on the denoising curve using two criteria: (1) sections with a denoised value of 50 or higher, as determined by dataset characteristics, and (2) a minimum section length of 10 amino acids to ensure protein fidelity and structural integrity. Once the subsection ranges (start and end amino acid indices) were defined, the corresponding sequences were extracted, and the PDB files were modified accordingly. Finally, folding was reperformed on all extracted subsections to adjust the protein structure. It is important to note that more than one subsection, or none, could be extracted from a single sequence, resulting in a total of 2177 high-fidelity subsections for protein simulation (detailed subsection extraction methods are discussed in Section 4.2). As shown in panel (a), the three subsections examples with varying protein lengths and molecular structures demonstrate reasonable folding performance. The refolded subsections exhibit similar prediction accuracy compared to the extracted sections, with slightly higher average pLDDT values (76.39 vs. 73.41). As shown in panel (b), the extracted sections consist of the main secondary structures found in the original full proteins, which govern the mechanical performance of the protein. The refolded subsections generally retain the same molecular structures, including key structural features and overall secondary structure composition, though variations in orientation and alignment are present. After subsection extraction, the average pLDDT score significantly increased from 40.48 to 76.39, while the average sequence length decreased from 445 to 125, improving both the reliability of the protein structures for simulation and computational efficiency. A detailed analysis of the developed protein dataset is provided in Section 2.1. | ||
Furthermore, the detailed secondary structure composition of the dataset was discussed. As shown in the pie charts in Fig. 3, the three subsection examples contain a higher proportion of alpha-helices and fewer beta-sheets. The analysis of secondary structures was conducted using the dictionary of secondary structure of proteins (DSSP)62 with the following symbols: H represents the alpha helix structure, G represents the beta-sheet, T represents the turns, S represents the bend, and – denotes other structures62 (detailed methods in Section 4.3.3). Additional subsequence examples with beta-sheets are visualized in Fig. 5. However, an analysis of all 2177 sequences revealed that only 66 sequences (∼3%) contained beta-sheet strands. Although MaSp proteins from spider dragline silks are expected to contain more beta-sheets rather than being dominated by alpha-helices, we hypothesize that the protein sequence data collected and augmented are mostly native liquid pre-spinning forms of spidroins before being assembled into solid silk. These liquid forms are primarily composed of alpha-helices and random coils, which undergo a transition to beta-sheets during protein assembly in the spinning process.28 Two main reasons explain this observation: (1) the protein sequence data from the silkome dataset are obtained from RNA extraction from spider glands, where proteins are mostly in their liquid state. (2) The assembled form is influenced by external factors during spinning, such as shear forces, pH, and ion concentration,28 while current folding tools predict structures under more typical conditions found in aqueous environments. While we presume the nanomechanical properties of aqueous proteins are still relevant to the mechanical properties of silk fibers, though the relationship is less direct compared to assembled proteins. Further factors, including the hierarchical structure of spider silk and the assembly process, need to be considered for a more accurate understanding of the relationship between native spider silk proteins and the final silk fibers. This could be an interesting direction for future research, especially in designing synthetic proteins and silk fibers.
2.2 Implicit all-atom modeling for protein unfolding
The analysis of the spider silk protein simulations includes evaluating unfolding behavior, tracking changes in the secondary structure, and assessing the characterized nanomechanical properties.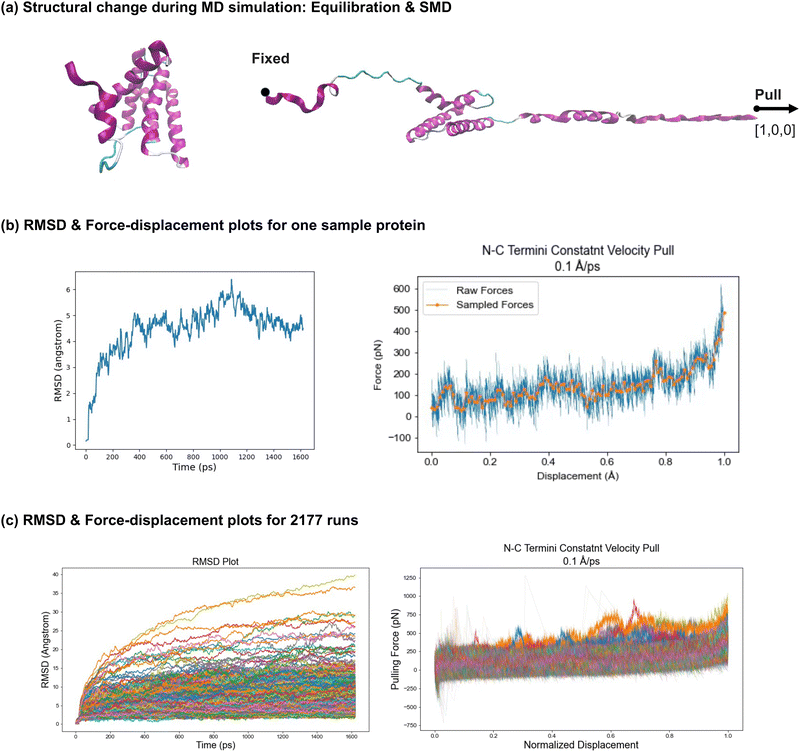 | ||
| Fig. 4 Molecular dynamics simulations of 2177 silk protein structures. Implicit atomistic MD simulations were performed using NAMD53 for all 2177 spider silk proteins to study their unfolding behavior, which included both equilibration and SMD, as visualized in panel (a). During equilibration, the protein configurations were adjusted to stable states, as indicated by the RMSD plots. The RMSD plot of the sample protein in panel (b) (left) shows the protein reaching a stable configuration as the RMSD value converges. Panel (c) (left) displays the RMSD curves converging for all 2177 proteins though with varying RMSD values, showing that all proteins are stabilized before SMD. Following equilibration, SMD simulations were conducted. Force–displacement plots were generated to visualize the unfolding behavior. The force–displacement plot for a sample protein is shown in panel (b) (right), with a smoothed curve provided for easier comparison and force vector characterization. The combined force–displacement curves for all 2177 simulations are displayed in panel (c) (right). For easier comparison, the displacement is normalized across all proteins. Overall, larger pulling forces are required as displacement increases, with steeper slopes near the point where the proteins are nearly fully unfolded, particularly when the monomer backbone is being stretched. Specific regimes are observed during the unfolding process, including (1) rupture of intermolecular bonds, (2) uncoiling of secondary structures, and (3) unfolding of the monomer backbone. Further simulation details are provided in Section 4.3, with detailed discussion in Section 2.2.1, and VMD63 was used for visualization. | ||
The simulation results for a sample protein are shown in Fig. 4(b). The root mean square deviation (RMSD) plot on the left indicates the stability of the protein configuration during the equilibration phase. The RMSD values converge, demonstrating the stability of this sample, and confirming that it is suitable for the subsequent SMD. On the right, the force–displacement plot visualizes the unfolding behavior of the protein under constant velocity. An overall increasing trend is observed as the pulling force increases with increased displacement. Notably, a steeper slope is observed near the end of the stretching phase when the protein is nearly fully unfolded, suggesting that higher forces are required to stretch the protein backbone compared to the forces needed to break hydrogen bonds and uncoil alpha-helices. Several force peaks in the plot indicate disturbances or variations in force during the unfolding process, likely corresponding to the uncoiling of secondary structures, sliding of aligned components, or bond rupture. A smoothed curve is generated in the force–displacement plot, where the force vector corresponds to the number of amino acids in the protein, simplifying trend analysis and enabling comparison with other protein data. Additionally, tensile-related nanomechanical properties, such as strength and toughness, are characterized through the force–displacement plot.
In Fig. 4(c), the plots on the left and right show the RMSD and force–displacement curves, respectively, for all 2177 proteins. The displacements are normalized across all proteins to account for variations in contour lengths and pulling distances, making comparison easier. In the RMSD plot, although values vary across different proteins, all proteins reach stable states before the SMD phase under the same equilibration setup, with curves converging within the defined time frame (1600 ps). In the force–displacement plot, a similar overall trend is observed across all proteins, despite differences in length and configuration. Greater pulling forces are required as the displacement increases, with steeper slopes near the point where the proteins are almost fully unfolded which indicates larger forces are required for stretching the backbone of monomers compared to other unfolding regimes. These regimes include (1) rupture of intermolecular bonds (e.g., hydrogen bonds), (2) uncoiling of secondary structures (e.g., alpha-helices and beta-sheets), and (3) unfolding of the monomer backbone. The force variations among proteins are attributed to differences in configuration, length, secondary structure composition, and folding topology. The force vectors and characterized nanomechanical properties for all 2177 proteins are summarized in a CSV file provided in the ESI,† with further analysis detailed in Section 2.2.3.
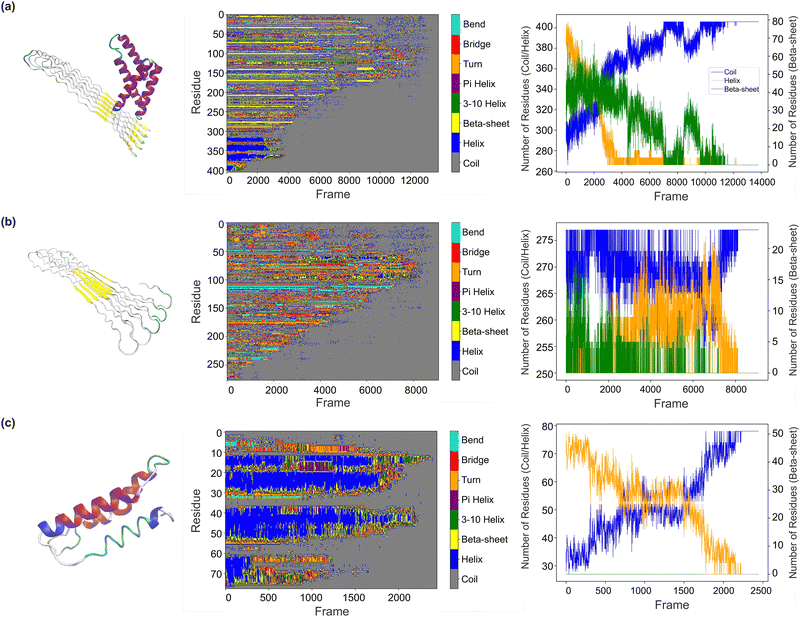 | ||
| Fig. 5 Analysis of secondary structure during the unfolding simulation. Using DSSP62 combined with MDAnalysis64,65 (detailed methods in Section 4.3.2), we explored changes in the secondary structures during protein unfolding. Three different protein examples, with various sequence lengths (407, 278, and 79) and molecular structures, are selected for analysis, as shown in three rows (a)–(c) from top to bottom. In each panel, the first column displays the molecular structure of the protein. The second column is the secondary structure profile which shows the evolution of secondary structure of each residue over time, while the third column presents the changes in the three main secondary structure components (random coil, alpha-helix, and beta-sheet), with secondary structures present in different colors (cyan for bends, red for bridges, orange for turns, purple for pi helices, green for 3–10 helices, yellow for beta-sheets, dark blue for alpha-helices, and grey for coils). In the third column, a line plot indicates the changes in three main structural components (random coil in blue, alpha-helix in yellow, and beta-sheet in green). A corresponding video visualization of these changes is provided in the ESI.† We observed various transitions in secondary structures during the simulation of different proteins, reflecting their dynamic behavior under mechanical stress. These transitions between secondary structure elements may be influenced by factors such as protein stability and structural uncertainty. Although alpha-helix to beta-sheet transitions28 were not prominent in these monomer unfolding simulations—likely due to the absence of additional factors like protein–protein interactions and external conditions—this work establishes a framework for future studies to explore more complex phenomena. Detailed analysis is provided in Section 2.2.2. | ||
Besides, the structural changes during the unfolding process vary among the proteins. The first protein (Fig. 5(a)) has alpha-helices and beta-sheets progressively replaced by coils during the pulling process, with the alpha-helices disappearing earlier than the beta-sheets, likely due to the differing structural integrity of these components. Near the end of unfolding, some coil regions transition back into beta-sheet structures, potentially due to the realignment of amino acids, protein–solvent interactions, or the re-establishment of hydrogen bonds. The second protein (Fig. 5(b)) shows a well-aligned beta-sheet transition into disordered coil structures during unfolding. Interestingly, there is an intermediate phase where random coils transition into alpha-helices, possibly due to the alignment of the protein backbone under force or the intrinsic sequence propensity of certain amino acids. The molecular structure of the third protein (Fig. 5(c)) becomes increasingly disordered as alpha-helices transition into coil regions during unfolding, with minimal beta-sheet formation. A plateau is observed during the helix-to-coil transition, which could indicate structural stabilization or the concurrent unfolding of other components.
In summary, we observed various structural transitions during the simulation, reflecting the dynamic behavior of different proteins under mechanical stress. These transitions between secondary structure elements, such as the conversion of helices to coils, may be influenced by protein stability and structural uncertainties. Although alpha-helix to beta-sheet transitions28 were not prominent in these monomer unfolding simulations (as such transitions typically require chain interactions and external factors like tensile stress, pH, or ion changes), this work provides a framework for future studies to investigate more sophisticated phenomena.
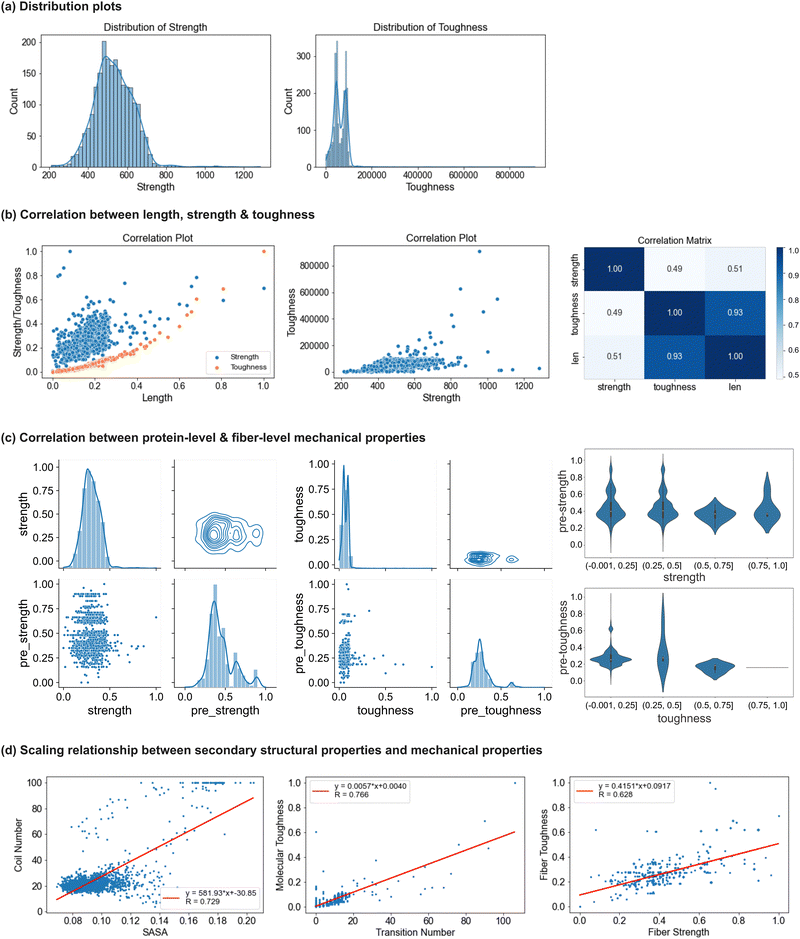
To explore the relationship between the molecular-level protein properties and the mechanical behavior of silk fibers, we analyze the correlation between the molecular-level properties derived from MD simulations and the predicted fiber-level properties using SilkomeGPT (methods discussed in Section 4.3.3). Fig. 6(c) visualizes the analysis of strength and toughness, scaling from the nanomechanical to fiber-level properties. The two plots depict the distributions, correlations, and clustering for strength and toughness, respectively. From the scatter plots, little correlation is observed between the protein-level and predicted fiber-level properties for both strength and toughness. The data points are widely dispersed, and for a given protein property, especially toughness, there is a broad range of predicted fiber values. The contour plots show clustering around mid-range values for both protein and fiber strength and toughness, though the toughness data display a broader spread. This suggests a weak direct correlation across scales, indicating that the hierarchical structure, fiber assembly, and structural factors may play a more significant role in determining final fiber toughness than nanomechanical toughness. Moreover, the histograms reveal moderately right-skewed distributions, with normalized fiber strength showing a broader distribution than protein strength, indicating greater variability in the fiber-level properties. This greater variability in the fiber properties suggests that factors beyond nanomechanical toughness, such as fiber structure, alignment, and molecular interactions, may significantly influence fiber strength and toughness. In the third column of Fig. 6(c), violin plots show the distribution of fiber properties across quartiles of nanomechanical strength and toughness values. For strength, the fiber properties become more consistent and predictable as nanomechanical strength increases. This suggests that stronger proteins are more likely to produce fibers with high and uniform strength. In the lower strength quartiles, the variability is greater, indicating that fiber strength is more influenced by external factors such as fiber alignment and assembly processes. Despite the variability, the similar bell-shaped patterns across the strength quartiles suggest a consistent and predictable relationship between the nanomechanical strength and fiber-level strength. Fibers made from stronger proteins are generally more uniform and reliable in their mechanical performance. In contrast, toughness shows higher variability, especially in the lower quartiles, which suggests greater difficulty in predicting fiber toughness based solely on protein toughness. The sparse data in the fourth toughness quartile further highlight the complexity of toughness as a mechanical property.
The scaling relationships between the secondary structural properties and mechanical properties of spider silk proteins and fibers are analyzed in detail and illustrated in Fig. 6(d). In addition to the nanomechanical and fiber-level mechanical properties previously discussed, several secondary structure-related properties were calculated for all 2177 protein sequences. These properties include solvent-accessible surface area (SASA), the number of main secondary structures such as coils, helices, and sheets in their original protein forms before simulation, and the number of secondary structure transitions across the protein sequences. The analysis reveals positive linear correlations between the key structural and mechanical properties, as quantitatively expressed in the functions labeled in Fig. 6(d). From the three figures shown in Fig. 6(d), respectively, first, a strong positive correlation is observed between SASA and the number of coils, with a correlation coefficient of 0.729. This relationship arises because coil regions, being more flexible and unstructured, lack compact packing, which increases the surface area exposed to solvents. Second, a correlation coefficient of 0.766 highlights the strong relationship between the number of secondary structure transitions and molecular-level toughness. Proteins with a greater number of transitions exhibit higher structural adaptability, enabling more effective stress distribution, energy dissipation, and resistance to breaking, which collectively result in increased toughness. Finally, a positive correlation between the fiber strength and toughness, with a correlation coefficient of 0.628, underscores the hierarchical nature of spider silk fibers. This relationship is attributed to the molecular features of the fibers that enhance energy absorption and stress resistance. Unlike mechanical performance at the molecular level, the applied load on the fiber is distributed across multiple protein chains, and the collective behavior of these different molecular structures further contributes to their exceptional strength and energy absorption. These findings demonstrate the intricate interplay between the secondary structural properties and mechanical performance, highlighting the complex mechanisms that enable spider silk's remarkable material properties.
In summary, strength follows a normal distribution, while toughness shows greater uncertainty. Toughness has a strong positive correlation with protein length, whereas the correlation between the strength and length is less apparent. Strength and toughness exhibit little correlation. Regarding the relationship between the molecular-level and fiber-level properties, both strength and toughness show weak correlation and high variability across scales, with toughness displaying more uncertainty, underscoring the complexity of scaling the nanomechanical properties to fiber-level mechanical behavior, especially for toughness.
3. Conclusions
We developed a cost-effective framework to explore and optimize the design of spider silk proteins for the nanomechanical properties related to their unfolding behavior. We first created a dataset that accounts for protein uncertainties, consisting of 2177 high-fidelity spider silk protein subsections from both natural and augmented novel sequences. Using this dataset, we systematically simulated protein unfolding through consistent MD simulations. We then characterized, collected, and analyzed the nanomechanical properties of these proteins.Key results and findings based on the dataset analysis, simulation performance, and the nanomechanical properties characterized from MD simulations covering structural uncertainties are summarized below:
• Dataset development: the SilkomeGPT model was employed to generate an expanded dataset of spider silk protein sequences, aiming to capture a broader range of structural variabilities for in-depth analysis. The generated sequences were rigorously validated through novelty assessment, molecular structure composition comparisons, and clustering comparison with existing data. After subsection extraction, the average pLDDT value of the dataset improved significantly, from 40.48 to 76.39, which enhanced the reliability of the protein structure for simulation, and the average sequence length decreased from 445 to 125 which improved computational efficiency.
• Simulation observations: as shown in Fig. 4, all 2177 proteins reached stable configurations through equilibration before being subjected to SMD. The force–displacement plots visualize the unfolding behavior of the proteins under constant velocity, showing that the pulling force generally increases with displacement. This behavior follows specific or mixed regimes: (1) rupture of intermolecular bonds (e.g., hydrogen bonds), (2) uncoiling of secondary structures (e.g., alpha-helices and beta-sheets), and (3) unfolding of the monomer backbone. A steeper slope is typically observed near the completion of unfolding, as the protein's backbone is stretched. Force variations likely correspond to secondary structure uncoiling, sliding of aligned components, or bond ruptures.
• Secondary structure transitions: various secondary structure transitions were observed during the simulations, reflecting the dynamic behavior of proteins under mechanical stress. These transitions may be influenced by protein variability and structural uncertainties. While alpha-helix to beta-sheet transitions were not prominent in these monomer unfolding simulations, which indicates the importance of the assembly process, the framework established here provides a basis to further investigate more realistic phenomena.
• Nanomechanical property uncertainties: uncertainties were observed in the nanomechanical properties, particularly for strength and toughness. Toughness shows a positive correlation with protein length, while little correlation was observed between strength and toughness, and strength and length. When correlating the molecular-level properties with fiber-level mechanical properties, both strength and toughness exhibited limited correlation and high variability across scales. This highlights the complexity of scaling the nanomechanical properties to the fiber level and underscores the significant influence of protein uncertainty and the macroscopic assembly process on the fiber-level mechanical properties.
We acknowledge several assumptions and constraints in this work. First, the proteins in the dataset are considered primarily in their native aqueous (soluble) form rather than in assembled solid form, referring to the pre-spinning state in which spidroins are stored in the glandular lumen of spiders. In this phase, the proteins remain dissolved in water and predominantly exhibit alpha-helical and coiled-coil structures, as opposed to the β-sheet-rich conformations found in assembled solid silk fibers. Additionally, only the unfolding performance of monomers, rather than the hierarchical composite structure, was considered when analyzing the relationship between the molecular-level and fiber-level mechanical properties. Furthermore, during the dataset development, it was assumed that the extracted sections with high folding fidelity govern the mechanical and structural behavior of protein structures, which might not fully capture the complexity of the entire protein assembly. To gain a more accurate understanding of the contribution of spider silk proteins to silk fibers, the hierarchical structure of spider silk and the assembly process must be considered. This is an important direction for future research, particularly when designing synthetic proteins and silk fibers.
Still, this work has several potential impacts and implementations. We developed a fundamental framework that connects native/aqueous spidroin protein structures to silk fibers through folding, MD simulations, and deep learning techniques. This approach provides a foundation for future insights into the mechanobiology and nanomechanical behavior of unassembled protein structures, facilitating the design of more realistic synthetic silk fibers. Moreover, our approach contributes to understanding how native protein structures can be translated into solid fibers through the spinning process. The developed approach supports the design of synthetic liquid-form proteins based on their mechanical behavior through cost-effective methods and is also useful for applications such as drug delivery, bioadhesives, and other biotechnological innovations. Additionally, the framework can be applied to analyze other protein-based materials, such as collagen, enzymes, and keratin, thus addressing various design needs across multiple fields. We believe similar generative methods enriched with MD modeling can serve as a general strategy in this field.
In future work, further exploration is needed to investigate the contribution of assembled spider silk proteins to the mechanical properties of silk fibers, particularly by incorporating the factors involved in the spinning process. Research should also focus on how hierarchical features influence the relationship between the nanomechanical properties and the fiber-level mechanical properties, as well as understanding the fundamental building blocks of spider silk and their contribution to overall fiber behavior using simulation techniques. Additionally, with collected nanomechanical data, generative models could be developed or fine-tuned to link spider silk protein sequences with molecular-level properties, supporting data augmentation and expanded design space exploration.
4. Materials and methods
In this section, we discuss the datasets and methodologies used in this work, including the collection and augmentation of the silk protein sequences, protein folding and subsection extraction, molecular dynamics simulations which comprise both equilibration and steered molecular dynamics (SMD), and nanomechanical property characterization and analysis procedures.4.1 Dataset development
A total of 2240 protein sequences were collected, comprising 1033 sequences curated from the silkome dataset1 as discussed in ref. 2 and 1207 novel sequences generated using SilkomeGPT.2 These sequences were subsequently used for protein folding to obtain 3D structures for simulations. The 1033 existing sequences are all from major ampullate spidroin (MaSp), the key protein component of spider dragline silk, which exhibits exceptional mechanical performance and provides the main structural support for the web.19 Due to the limited availability of silk protein data, we employed a cyclic-consistent generation model to augment the dataset with synthetic yet reliable protein sequences.Before generating synthetic sequences using SilkomeGPT, we analyzed the distribution of the related fiber-level mechanical properties of the 1033 existing sequences. These properties include toughness, elastic modulus, tensile strength, strain at break, and four corresponding standard deviation measurements (as shown in Fig. 2(a1)). From this analysis, we drew 1000 random samples of 8-dimensional property sets from the property distribution of the existing dataset. Using these 1000 property sets as input to the SilkomeGPT model and through automated job submissions for systematic silk design, we produced 206![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 838 sequences before filtering.
838 sequences before filtering.
To enhance the reliability of the augmented dataset, we applied an iterative recursive filtering process inspired by the approach in ref. 66, designed as an agentic model that identifies self-consistent sequences, those for which predicted mechanical properties closely match the input target values used during generative design. These predictions were derived from trained regression models, and consistency was quantified using the generation R2 value. At each iteration, the model adapted filtering thresholds based on high-performing sequences to better align with biologically plausible outcomes. Sequences with an R2 value of 60% or higher were retained, a threshold selected through empirical refinement to balance fidelity and novelty. This process yielded 1207 novel sequences from 206![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 838 initial candidates (1.67% yield rate), each meeting the R2 criterion. The full filtering pipeline included: (1) conditioning sequence generation on 8-dimensional mechanical property sets; (2) evaluating predicted-to-target property agreement; (3) excluding low-R2 sequences; and (4) consideration of structure similarity and simulation feasibility. As a result, the filtered dataset, as shown in Fig. 2(a2), closely matches the distribution of the 1033 original protein sequences. This led to a final dataset of 2240 MaSp sequences, comprising 1033 original and 1207 novel sequences, optimized for subsequent protein folding and simulation tasks. The similarity between the new and existing datasets was further evaluated using secondary structure composition analysis and clustering comparisons with PCA, a dimensionality reduction technique (details in Section 2.1 and Fig. 2(b)).
838 initial candidates (1.67% yield rate), each meeting the R2 criterion. The full filtering pipeline included: (1) conditioning sequence generation on 8-dimensional mechanical property sets; (2) evaluating predicted-to-target property agreement; (3) excluding low-R2 sequences; and (4) consideration of structure similarity and simulation feasibility. As a result, the filtered dataset, as shown in Fig. 2(a2), closely matches the distribution of the 1033 original protein sequences. This led to a final dataset of 2240 MaSp sequences, comprising 1033 original and 1207 novel sequences, optimized for subsequent protein folding and simulation tasks. The similarity between the new and existing datasets was further evaluated using secondary structure composition analysis and clustering comparisons with PCA, a dimensionality reduction technique (details in Section 2.1 and Fig. 2(b)).
The novelty and reliability of the generated designs are checked through the basic local alignment search tool (BLAST). Two main assessed criteria include (1) query cover, which indicates the alignment coverage of the sequences, and (2) identity percentage, which measures the similarity in composition. Sequences with either QC and id% values below 50–60% are considered novel.60,61 A summary of the novelty check, along with sample sequence discussions and protein types classified under the MaSp category, is provided in Table 1.
4.2 Protein folding and subsection extraction
To obtain 3D molecular structures for simulation based on protein sequences, we utilized OmegaFold21 for rapid sequence-to-structure prediction. OmegaFold21 was chosen because it delivers comparable prediction performance to AlphaFold267,68 and RoseTTAFold69 for high-resolution protein structures while requiring significantly less computational cost. Unlike other advanced prediction models for protein folding, OmegaFold does not reply on multiple sequence alignments (MSAs) and evolutionary information, making it suitable for large-scale systematic folding tasks. Furthermore, an automated process was developed for high-throughput input script generation and job submission, significantly improving computational efficiency. In addition to the predicted protein structures in the Protein Data Bank (PDB) format, predicted local distance difference test (pLDDT) scores were generated to assess folding performance.We then extracted subsections with high fidelity from the full sequences, to enhance the reliability of the protein structure input for simulations, as well as reduce the simulation cost with shorter protein length, since the current folding prediction for spider silk proteins is unstable and there are performance fluctuations along the sequence, and processing ∼2000 full-length sequences could be computationally intensive. Furthermore, the extraction of high-fidelity subsections not only improves the accuracy of folded structures but also retains the nanomechanical and structural significance, as these subsections contain the main secondary structure components that govern the mechanical behavior of dragline silks (as shown in Fig. 3(b), and discussed in Section 2.1). To extract subsections, we first generated pLDDT plots for each folded protein and drew a corresponding denoising plot using the scipy.signal package in Python.
We find that the denoising step is essential to reduce noise in the original plot, providing a clearer visualization of the overall pattern, facilitating the selection of continuous sequence sections with high pLDDT values, and minimizing interruptions caused by random fluctuations. The extraction of subsections was based on two criteria: (1) a denoised pLDDT value of 50 or higher, with the value determined based on dataset characteristics, and (2) a section length of at least 10 amino acids to ensure the fidelity and integrity of the subsections. Note that more than one subsection, or none at all, could be extracted from a single sequence. Once the subsection ranges (start and end indices of amino acids) were defined, we extracted the sequences and modified the corresponding PDB files. In total, 2177 high-fidelity subsections were collected for protein simulation. Detailed analysis and novelty checks are discussed in Section 2.1. Finally, after subsection extraction, additional folding simulations were performed on the extracted sequences to adjust for any structural changes.
As a result of the extraction process, the average pLDDT value improved significantly from 40.48 to 76.39, while the average sequence length decreased from 445 to 125. The refined dataset includes both FASTA files containing the sequences and PDB files representing the 3D protein structures. The PDB structures of all 2177 subsections were used for MD simulations in this study. Examples of protein folding and subsection extraction for three sequences with varying lengths and structural diversity are shown in Fig. 3. Fig. 3(a) and (b) illustrate the pLDDT plots and the corresponding visualized folded structures for full sequences, extracted subsections, and re-folded subsections.
4.3 Molecular dynamics simulations
Equilibration was performed to adjust the protein configurations to a stable state, verified by convergence of the RMSD values. For the dataset, each protein underwent equilibration for 8 × 105 steps at 2 fs per step under controlled temperature and pressure conditions, following an initial minimization phase of 1 × 104 steps for temperature initialization and relaxation. Uniform equilibration steps were chosen for ease of manipulation, and all proteins were confirmed to reach stable states (see Fig. 4(b) for an example RMSD plot, and Fig. 4(c) for RMSD curves of all 2177 proteins).
SMD simulations were conducted following equilibration, to pull the protein structure at a constant velocity at one end while keeping the other end fixed (visualized on the left in Fig. 4(a)). A force constant of 1.0 kcal mol−1 Å−2 was used, appropriate for biological systems, and a pulling velocity of 0.1 Å ps−1 was selected for a balance between the simulation stability and computational cost. While the pulling velocity of 0.1 Å ps−1 is significantly higher than physiological rates (typically 1 nm s−1 to 1 μm s−1), this choice reflects a practical balance between observing unfolding events and maintaining simulation feasibility. Such higher pulling velocities are widely adopted in SMD studies and allow for qualitative comparison of mechanical responses across sequences.70,71 Forces were recorded every 0.2 ps until the full contour length of each protein was reached, assuming an average amino acid length of 3.6 Å.72 The contour length for each protein was calculated as 3.6 Å multiplied by the number of amino acids. Force–displacement plots were generated to visualize unfolding behavior and to quantitatively assess the nanomechanical properties (an example is shown in Fig. 4(b), with plots for all proteins in Fig. 4(c)). To facilitate comparison, the displacements were normalized across all proteins, and a smoothed force–displacement curve was plotted, with averaged force values calculated over sections corresponding to the number of amino acids in each protein.
Further analysis of secondary structure changes during unfolding is discussed in Section 4.3.2, while detailed methodologies for nanomechanical property characterization and force vector collection are provided in Section 4.3.3.
In Fig. 5, three protein examples shown in three rows with different sequence lengths and molecular structures, display varying secondary structure changes during the unfolding process. In each row, the first column displays the molecular structure of the protein, the second column provides the profile of secondary structure evolution over time, and the third column shows the changes in three main secondary structure components (coil, alpha-helix, and beta-sheet). Video visualizations of the simulation process are available in the ESI.†
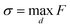 | (1) |
 | (2) |
Additionally, we explored the correlation between the nanomechanical properties of the silk proteins and the mechanical properties of spider silk fibers by analyzing the relationship between the molecular-level properties collected from MD simulations and the predicted fiber-level properties using SilkomeGPT. The overall steps include:
Step (1): inputting all 2177 subsection sequences into SilkomeGPT to estimate fiber-level properties, and collecting the property outputs, through the following two functions, respectively:
Step (2): unnormalizing the outputs using the appropriate scaling parameters from ref. 2,
Step (3): extracting the fiber-level strength and toughness values, saved in CSV files (provided in the ESI†).
The force vector and nanomechanical properties are summarized in CSV files, along with detailed sequence information, provided in the ESI.† A comprehensive analysis of the nanomechanical properties, their correlation with fiber-level mechanical properties, and the scaling relationships with secondary structural properties of spider silk proteins are discussed in Section 2.2.3 and visualized in Fig. 6.
Author contributions
M. J. B. and W. L. developed the overall concept and the algorithm and oversaw the work. W. L. curated the dataset, ran the AI models, conducted MD simulations, analyzed the results, and drafted the paper. W. L. and M. J. B. analyzed the data and edited and wrote the manuscript.Data availability
Data for this article, including codes and datasets, are available at https://github.com/lamm-mit/SilkomeMD Additional data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
We acknowledge support from MIT's Generative AI Initiative.References
- I. Su and M. J. Buehler, Mesomechanics of a three-dimensional spider web, J. Mech. Phys. Solids, 2020, 144, 104096 CrossRef.
- W. Lu, D. L. Kaplan and M. J. Buehler, Generative Modeling, Design, and Analysis of Spider Silk Protein Sequences for Enhanced Mechanical Properties, Adv. Funct. Mater., 2023, 2311324 Search PubMed.
- I. Su and M. J. Buehler, Nanomechanics of silk: The fundamentals of a strong, tough and versatile material, Nanotechnology, 2016, 27(30), 302001 CrossRef PubMed.
- M. A. Meyers, P.-Y. Chen, M. I. Lopez, Y. Seki and A. Y. M. Lin, Biological materials: A materials science approach, J. Mech. Behav. Biomed. Mater., 2011, 4, 626–657 CrossRef PubMed.
- M. A. Meyers, P.-Y. Chen, A. Y.-M. Lin and Y. Seki, Biological materials: Structure and mechanical properties, Prog. Mater. Sci., 2008, 53, 176–196 CrossRef.
- H. Shin, T. Yoon, J. You and S. Na, A study of forecasting the Nephila clavipes silk fiber's ultimate tensile strength using machine learning strategies, J. Mech. Behav. Biomed. Mater., 2024, 157, 106643 CrossRef PubMed.
- K. Spiess, et al., Impact of initial solvent on thermal stability and mechanical properties of recombinant spider silk films, J. Mater. Chem., 2011, 21, 13594–13604 RSC.
- S. Momeni Bashusqeh and N. M. Pugno, Development of mechanically-consistent coarse-grained molecular dynamics model: case study of mechanics of spider silk, Sci. Rep., 2023, 13, 19316 CrossRef CAS PubMed.
- E. Steven, et al., Carbon nanotubes on a spider silk scaffold, Nat. Commun., 2013, 4, 2435 CrossRef PubMed.
- A. T. N. Dao, K. Nakayama, J. Shimokata and T. Taniike, Multilateral characterization of recombinant spider silk in thermal degradation, Polym. Chem., 2017, 8, 1049–1060 RSC.
- N. Huby, et al., Native spider silk as a biological optical fiber, Appl. Phys. Lett., 2013, 102, 123702 CrossRef.
- K. H. Tow, et al., Exploring the use of native spider silk as an optical fiber for chemical sensing, J. Light Technol., 2017, 36, 1138–1144 Search PubMed.
- E. L. Buehler, I. Su and M. J. Buehler, WebNet: A biomateriomic three-dimensional spider web neural net, Extreme Mech. Lett., 2021, 42, 101034 CrossRef.
- L. Batty, Molecular Dynamics Analysis of Supercontraction in Spider Dragline Silk, Massachusetts Institute of Technology, Cambridge, 2013 Search PubMed.
- Y. Liu, Z. Shao and F. Vollrath, Relationships between supercontraction and mechanical properties of spider silk, Nat. Mater., 2005, 4, 901–905 CrossRef CAS PubMed.
- G. V. Guinea, M. Elices, J. Pérez-Rigueiro and G. R. Plaza, Stretching of supercontracted fibers: a link between spinning and the variability of spider silk, J. Exp. Biol., 2005, 208, 25–30 Search PubMed.
- N. Cohen, M. Levin and C. D. Eisenbach, On the origin of supercontraction in spider silk, Biomacromolecules, 2021, 22, 993–1000 Search PubMed.
- L. Eisoldt, A. Smith and T. Scheibel, Decoding the secrets of spider silk, Mater. Today, 2011, 14, 80–86 Search PubMed.
- K. Arakawa, et al., 1000 spider silkomes: Linking sequences to silk physical properties, Sci. Adv., 2022, 8(41), eabo6043 CrossRef CAS PubMed.
- A. D. Malay, H. C. Craig, J. Chen, N. A. Oktaviani and K. Numata, Complexity of Spider Dragline Silk, Biomacromolecules, 2022, 23, 1827–1840 CrossRef CAS PubMed.
- R. Wu, et al., High-resolution de novo structure prediction from primary sequence, bioRxiv, 2022, preprint DOI:10.1101/2022.07.21.500999.
- J. E. Garb, N. A. Ayoub and C. Y. Hayashi, Untangling spider silk evolution with spidroin terminal domains, BMC Evol. Biol., 2010, 10, 1–16 CrossRef PubMed.
- S. Wang, W. Huang and D. Yang, NMR structure note: repetitive domain of aciniform spidroin 1 from Nephila antipodiana, J. Biomol. NMR, 2012, 54, 415–420 CrossRef CAS PubMed.
- N. A. Ayoub, J. E. Garb, A. Kuelbs and C. Y. Hayashi, Ancient Properties of Spider Silks Revealed by the Complete Gene Sequence of the Prey-Wrapping Silk Protein (AcSp1), Mol. Biol. Evol., 2013, 30, 589–601 CrossRef CAS PubMed.
- J. Bauer and T. Scheibel, Dimerization of the Conserved N-Terminal Domain of a Spider Silk Protein Controls the Self-Assembly of the Repetitive Core Domain, Biomacromolecules, 2017, 18, 2521–2528 CrossRef CAS PubMed.
- Y. Liu, A. Sponner, D. Porter and F. Vollrath, Proline and Processing of Spider Silks, Biomacromolecules, 2008, 9, 116–121 CrossRef CAS PubMed.
- J. D. van Beek, S. Hess, F. Vollrath and B. H. Meier, The molecular structure of spider dragline silk: Folding and orientation of the protein backbone, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 10266–10271 CrossRef CAS PubMed.
- A. Rising, M. Widhe, J. Johansson and M. Hedhammar, Spider silk proteins: recent advances in recombinant production, structure–function relationships and biomedical applications, Cell. Mol. Life Sci., 2011, 68, 169–184 CrossRef CAS PubMed.
- A. K. Pandey and S. S. Roy, Natural Language Generation Using Sequential Models: A Survey, Neural Process. Lett., 2023, 55, 7709–7742 CrossRef.
- R. K. Luu, et al., Learning from Nature to Achieve Material Sustainability: Generative AI for Rigorous Bio-inspired Materials Design, 2024 Search PubMed.
- M. I. Jordan and T. M. Mitchell, Machine learning: Trends, perspectives, and prospects, Science, 2015, 349, 255–260 CrossRef CAS PubMed.
- T. N. Kipf and M. Welling, Semi-supervised classification with graph convolutional networks, arXiv, 2016, preprint, arXiv:1609.02907 DOI:10.48550/arXiv.1609.02907.
- W. Lu, Z. Yang and M. J. Buehler, Rapid mechanical property prediction and de novo design of three-dimensional spider webs through graph and GraphPerceiver neural networks, J. Appl. Phys., 2022, 132, 074703 CrossRef CAS.
- Y. Kim, T. Yoon, W. B. Park and S. Na, Predicting mechanical properties of silk from its amino acid sequences via machine learning, J. Mech. Behav. Biomed. Mater., 2023, 140, 105739 CrossRef CAS PubMed.
- L. Yang, et al., Diffusion models: A comprehensive survey of methods and applications, arXiv, 2022, preprint, arXiv:2209.00796 DOI:10.1145/3626235.
- R. K. Luu, M. Wysokowski and M. J. Buehler, Generative discovery of de novo chemical designs using diffusion modeling and transformer deep neural networks with application to deep eutectic solvents, Appl. Phys. Lett., 2023, 122, 234103 CrossRef CAS.
- A. Vaswani, et al., Attention is All you Need, in Advances in Neural Information Processing Systems, ed. I. Guyon, et al., Curran Associates, Inc., 2017, vol. 30, pp. 1–11 Search PubMed.
- W. Lu, N. A. Lee and M. J. Buehler, Modeling and design of heterogeneous hierarchical bioinspired spider web structures using deep learning and additive manufacturing, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2305273120 CrossRef CAS PubMed.
- A. Radford, Improving language understanding by generative pre-training, 2018 Search PubMed.
- T. B. Brown, Language models are few-shot learners, arXiv, 2020, preprint, arXiv:2005.14165 DOI:10.48550/arXiv.2005.14165.
- A. Ramesh, et al., Zero-shot text-to-image generation, International conference on machine learning, Pmlr, 2021, pp. 8821–8831 Search PubMed.
- A. Radford, et al., Learning transferable visual models from natural language supervision, International conference on machine learning, PMLR, 2021, pp. 8748–8763 Search PubMed.
- W. Lu, R. K. Luu and M. J. Buehler, Fine-tuning large language models for domain adaptation: Exploration of training strategies, scaling, model merging and synergistic capabilities, arXiv, 2024, preprint, arXiv:2409.03444 Search PubMed.
- J. Zou, X. Chen, B. Song and Y. Cui, Bionic Spider Web Flexible Strain Sensor Based on CF-L and Machine Learning, ACS Appl. Mater. Interfaces, 2024, 16, 23761–23770 CAS.
- D. Shin, et al., Spiderweb Nanomechanical Resonators via Bayesian Optimization: Inspired by Nature and Guided by Machine Learning, Adv. Mater., 2022, 34, 2106248 CrossRef CAS PubMed.
- S. Ma, H. Li, Q. Huang and J. Fei, Trans-scale interface engineering: Constructing nature-inspired spider-web networks for regulating thermal transport and mechanical performance of carbon fiber/phenolic composites, J. Colloid Interface Sci., 2024, 653, 777–794 Search PubMed.
- X. Zhang, et al., Preparation of Strong and Thermally Conductive, Spider Silk-Inspired, Soybean Protein-Based Adhesive for Thermally Conductive Wood-Based Composites, ACS Nano, 2023, 17, 18850–18863 CrossRef CAS PubMed.
- V. Fazio, A. D. Malay, K. Numata, N. M. Pugno and G. Puglisi, A Physically-Based Machine Learning Approach Inspires an Analytical Model for Spider Silk Supercontraction, Adv. Funct. Mater., 2024, 2420095 Search PubMed.
- V. Fazio, N. M. Pugno, O. Giustolisi and G. Puglisi, Physically based machine learning for hierarchical materials, Cell Rep. Phys. Sci., 2024, 5(2), 101790 CrossRef.
- S. A. Hollingsworth and R. O. Dror, Molecular dynamics simulation for all, Neuron, 2018, 99, 1129–1143 CrossRef CAS PubMed.
- M. Karplus and G. A. Petsko, Molecular dynamics simulations in biology, Nature, 1990, 347, 631–639 CrossRef CAS PubMed.
- A. Hospital, J. R. Goñi, M. Orozco and J. L. Gelpí, Molecular dynamics simulations: advances and applications, Adv. Appl. Bioinf. Chem., 2015, 37–47 Search PubMed.
- J. C. Phillips, et al., Scalable molecular dynamics with NAMD, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- H. Shin, T. Yoon, W. Park, J. You and S. Na, Unraveling the Mechanical Property Decrease of Electrospun Spider Silk: A Molecular Dynamics Simulation Study, ACS Appl. Bio Mater., 2024, 7, 1968–1975 CrossRef CAS PubMed.
- Y. Kim, M. Lee, I. Baek, T. Yoon and S. Na, Mechanically inferior constituents in spider silk result in mechanically superior fibres by adaptation to harsh hydration conditions: a molecular dynamics study, J. R.Soc., Interface, 2018, 15, 20180305 CrossRef PubMed.
- M. Lee, J. Kwon and S. Na, Mechanical behavior comparison of spider and silkworm silks using molecular dynamics at atomic scale, Phys. Chem. Chem. Phys., 2016, 18, 4814–4821 RSC.
- B. Ni, D. L. Kaplan and M. J. Buehler, ForceGen: End-to-end de novo protein generation based on nonlinear mechanical unfolding responses using a language diffusion model, Sci. Adv., 2024, 10, eadl4000 Search PubMed.
- J. Malczewski, 1.15 – Multicriteria Analysis, in Comprehensive Geographic Information Systems, ed. B. Huang, Elsevier, Oxford, 2018, pp. 197–217 DOI:10.1016/B978-0-12-409548-9.09698-6.
- S. F. Altschul, W. Gish, W. Miller, E. W. Myers and D. J. Lipman, Basic local alignment search tool, J. Mol. Biol., 1990, 215, 403–410 CrossRef CAS PubMed.
- B. Ni, D. L. Kaplan and M. J. Buehler, Generative design of de novo proteins based on secondary-structure constraints using an attention-based diffusion model, Chem, 2023, 9, 1828–1849 CAS.
- L. Quan, T. Wu and Q. Lyu, Computational de novo protein design: From secondary to primary, then toward tertiary structures, Chem, 2023, 9, 1625–1627 CAS.
- P. J. A. Cock, et al., Biopython: freely available Python tools for computational molecular biology and bioinformatics, Bioinformatics, 2009, 25, 1422–1423 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, MDAnalysis: A toolkit for the analysis of molecular dynamics simulations, J. Comput. Chem., 2011, 32, 2319–2327 Search PubMed.
- R. J. Gowers, et al., MDAnalysis: A Python Package for the Rapid Analysis of Molecular Dynamics Simulations, 2019 Search PubMed.
- M. J. Buehler, PRefLexOR: Preference-based Recursive Language Modeling for Exploratory Optimization of Reasoning and Agentic Thinking, arXiv, 2024, preprint, arXiv:2410.12375 DOI:10.48550/arXiv.2410.12375.
- J. Jumper, et al., Highly accurate protein structure prediction with AlphaFold, Nature, 2021, 596, 583–589 CrossRef CAS PubMed.
- H.-B. Guo, et al., AlphaFold2 models indicate that protein sequence determines both structure and dynamics, Sci. Rep., 2022, 12, 10696 CrossRef CAS PubMed.
- M. Baek, et al., Accurate prediction of protein structures and interactions using a three-track neural network, Science, 2021, 373, 871–876 CrossRef CAS PubMed.
- M. Gao, D. Craig, V. Vogel and K. Schulten, Identifying unfolding intermediates of FN-III10 by steered molecular dynamics, J. Mol. Biol., 2002, 323, 939–950 CrossRef CAS PubMed.
- B. Isralewitz, M. Gao and K. Schulten, Steered molecular dynamics and mechanical functions of proteins, Curr. Opin. Struct. Biol., 2001, 11, 224–230 CrossRef CAS PubMed.
- S. R. K. Ainavarapu, et al., Contour Length and Refolding Rate of a Small Protein Controlled by Engineered Disulfide Bonds, Biophys. J., 2007, 92, 225–233 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: 1_SI_dataset_md_result.csv: CSV file for details of 2177 spider silk sequence data used for MD simulations, with nanomechanical properties characterized from the simulation. 2_SI_fiber_property_prediction.csv: CSV file containing the predicted fiber-level mechanical properties through SilkomeGPT for 2177 sequences, along with corresponding molecule-level characterized nanomechanical properties. 3_SI_MD_sample_videos_simulation_files.zip: animation of equilibration and SMD for three sample silk protein subsections (as indicated in Fig. 5). See DOI: https://doi.org/10.1039/d5ma00154d |
| This journal is © The Royal Society of Chemistry 2025 |