Is DFT enough? Towards accurate high-throughput computational screening of azobenzenes for molecular solar thermal applications

Abstract

An efficient screening of azobenzene (AB) derivatives for Molecular Solar Thermal (MOST) applications based on ground state properties (energy stored per molecule and Z isomer stability) could be performed with quasi-CASPT2 accuracy. In this work, we show how wavefunction and electron density based methods can be efficiently combined in a computational protocol that yields accurate potential energy profiles with a significant reduction in computational cost compared to that of a fully-CASPT2 characterization. Our results on prototypical electron donor/withdrawing AB derivatives clearly identify pull–pull substitution as the most promising, allowing to draw guidelines for the chemical design of promising azo-MOST candidates.

---

Design, System, Application

In this work we show how DFT and multiconfigurational methods (CASPT2/CASSCF) can be effectively combined in a computational protocol for the characterization of azobenzene derivatives for molecular solar thermal (MOST) applications. MOST materials have attracted increasingly large attention in recent years due to their ability to convert and store solar energy into chemical energy, that could be later released in the form of heat. Our proposed strategy focuses on MOST candidates derived from the azobenzene molecule, whose photochemical E/Z isomerization allows for solar energy conversion. We outline a computational protocol that combines the advantageous computational cost of DFT with the accuracy of multiconfigurational CASPT2/CASSCF methods to obtain key properties for the design of MOST candidates, such as the amount of energy stored per molecule and the metastability of the “charged species” (Z isomer). Despite being a preliminary work, our protocol yields promising results for some prototypical azobenzene derivatives, opening the way for a large-scale computational screening of azobenzene MOST candidates, to be applied in the early stages of molecular design for such materials.

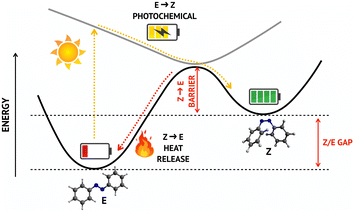
The continuous increase in the global energy demand and the concurrent need to reduce the use of fossil fuels are two of the greatest challenges that the scientific community has been facing over the last decades. In this context, much effort has been put in the search of innovative solutions to capture and store energy from solar radiation, in order to address the problem of day/night discontinuity of this renewable source. Molecular solar thermal (MOST) fuels represent an innovative class of energy storage materials that exploits photoinduced reactions to capture and store solar energy in molecular bonds. Among various MOST systems, azobenzene (AB) based MOST fuels have attracted significant attention^1–6 owing to their low molecular weight, their direct absorption in the UV-vis spectral window (without the need to attach further chromophores) and the excellent reversibility and cyclability.^2,7 AB can switch between E and Z isomers upon exposure to sunlight, thus storing solar energy in the metastable Z configuration, which can later undergo thermal back-isomerization to the E form, releasing heat (Fig. 1). However, the spectral and photochemical properties of AB must be tuned by chemical substitution to match the MOST technology requirements, which are, among others:² (a) efficient light absorption in the most intense region of the solar spectrum; (b) maximum amount of energy stored per molecule; (c) high (meta)stability of the “charged” species to allow for long-term storage.

Fig. 1 Schematic representation of the working principle of AB MOSTs: the photochemical E → Z conversion stores sunlight energy into chemical bonds; later, the energy stored in the “charged” Z isomer can be released as heat via thermal back-isomerization. The energy stored per molecule and the metastability of the Z isomer are quantified by the Z/E gap and by the isomerization barrier, respectively (highlighted in red).

Considered the wide chemical space of possible substituents at the two AB phenyl rings, a high-throughput computational screening of AB MOST candidates represents a powerful strategy to identify the most promising molecules and avoid the actual chemical synthesis of ill–fated derivatives. To allow for a large scale screening campaign, the accuracy of the predictions must necessarily be balanced with an affordable computational cost, an association that almost inevitably drives towards the use of density functional theory (DFT) calculations. However, the determination of the preferred mechanism for the thermal Z → E back-isomerization of AB-based candidates, and the accurate estimation of the associated energy barrier (which directly influences the thermal half-life of the Z isomer, see Fig. 1) has proven to be a challenging task for single reference methods like DFT. Indeed, two main chemical paths are known for the E ⇄ Z conversion of AB and its derivatives: rotation around the central NN bond (hereinafter referred to as torsion) or inversion of one of the two CNN bending angles. In real systems, the two mechanisms coexist and mix, in an interplay that can be strongly affected by chemical substitution and the environment.^8–16 The greatest challenge for predictive calculations is represented by the strong multi-configurational character acquired by the ground state of AB in the region near the transition state (TS), especially along the torsional path, which requires the application of expensive multi-reference methods such as CASSCF/CASPT2.^16–20 Specifically, the strong static correlation on the ground state is not captured by DFT methods, leading to quantitatively and qualitatively wrong potential energy profiles, that challenge the TS optimization along the torsion coordinate (see for example ref. 20 and the discussion in the ESI material of ref. 17).

It is also worth mentioning that some studies on the thermal isomerization of AB proposed a third mechanism, that involves the non adiabatic transfer of population to T₁.^18,19,21 Indeed, the triplet state shows a double crossing with S₀ along the torsion path (see Fig. 2 and S12†), and it could be populated in the presence of a sufficiently large spin-orbit coupling (SOC). However, even if the triplet-mediated mechanism cannot be totally neglected, strong evidence of its predominancy over adiabatic S₀ paths is still missing (see ESI† for a detailed discussion on this topic).

Fig. 2 Potential energy profiles for Z → E isomerization along the torsional (left column) and inversion (right column) for AB (a and b), F₂-AB-F₂ (c and d), NH₂-AB-NH₂ (e and f), NO₂-AB-NO₂ (g and h) and NO₂-AB-NH₂ (i and j) at CASPT2/CASSCF(10,8)/ANO-R1 level (black: S₀; gray: T₁), DFT and BS-DFT (BP86/def2-SVP, orange) and with the combined CASTP2@DFT approach (red). The asymmetric NO₂-AB-NH₂ derivative shows two non-equivalent inversion pathways, which are both reported in (j) with circles (inversion of –NH₂ moiety) and crosses (inversion of –NO₂ moiety).

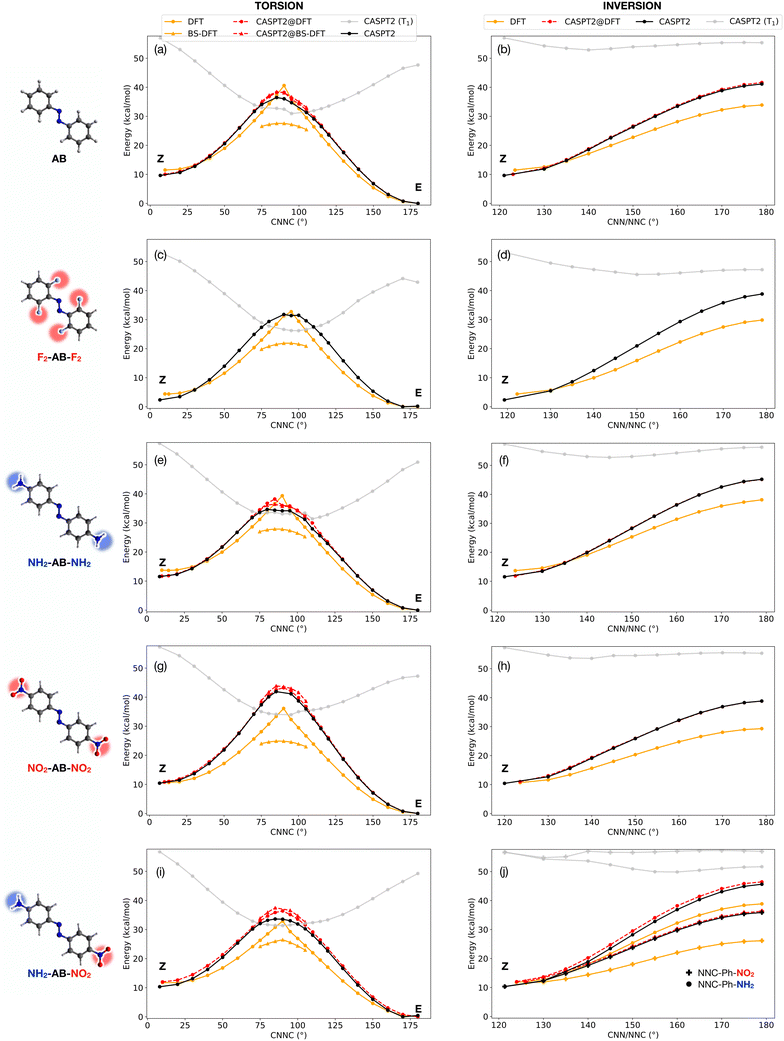
In this work, we systematically compare DFT and CASPT2 methods to obtain potential energy profiles along the thermal isomerization pathway of AB and four of its derivatives. We show how the two methods can be efficiently combined in a computational protocol that reaches quasi-CASPT2 accuracy with a computational cost two orders of magnitude smaller than full CASPT2 characterization (Table S2†), opening the way for high-throughput screening of AB photoswitches. To test the methodology, we considered AB as well as four derivatives (see chemical structures in Fig. 2): 2,2′,6,6′-tetrafluoroazobenzene (F₂-AB-F₂), 4,4′-diaminoazobenzene (NH₂-AB-NH₂), 4,4′-dinitroazobenzene (NO₂-AB-NO₂) and 4,4′-nitroaminoazobenzene (NO₂-AB-NH₂, also known as disperse orange 3). The fluorinated compound was chosen for its known stability of Z isomer,²² while the other derivatives were selected to investigate the effect of “push” amino (electron-donating) and “pull” nitro (electron-withdrawing) substituents. Despite being only few examples, the studied molecules were chosen as prototypes of larger classes of AB derivatives to which our protocol could be potentially applied.

To begin with, the accuracy of several DFT functionals was assessed against CASPT2 in reproducing the torsional profile of pristine AB (Fig. S1†) and its derivatives (Fig. S2†). All the considered DFT functionals performed equally well at minima, delivering similar predictions for the E/Z gap. In contrast, they all diverged from CASPT2 reference calculations when approaching the TS region. In particular, more refined functionals perform better along the inversion pathway, but an inverse trend is observed along torsion, with BP86 (a pure functional based on the generalized gradient approximation) being the closest (although still far) to CASPT2 results. Taking into account its advantageous computational cost, BP86 was chosen for this computational study. The origin of the failure of DFT methods arises from two main reasons. On one side, the lack of multiconfigurational character (static correlation) leads to a poor description of the wavefunction for torsional angles close to 90°, i.e. the region where CASSCF/CASPT2 shows a strong mixing with the S₁ excited state (nπ* open-shell). Concurrently, the inversion barrier is underestimated by DFT due to a lack of dynamic correlation (recovered by perturbative methods like CASPT2 but also MP2, see Fig. S1†). The combination of these effects drives the geometries and energies obtained with TS search at DFT level towards the linear (inversion) TS, with one CNN angle of 180° and an undefined torsion angle (see e.g. ref. 23 and 24 and Fig. S3†). A direct consequence of these artifacts is the impossibility to obtain a fully relaxed DFT geometry for the torsional TS. For this reason, here we rely on relaxed surface scans rather than TS optimizations, adding constraints on CNN/NNC values (see ESI†). This strategy was adopted in the calculations referred to in the following as DFT and CASPT2@DFT. The structures obtained through relaxed surface scans show excellent agreement with fully-relaxed TS structures at CASPT2 level (see Table S1†), validating our strategy. For all the investigated compounds, we have obtained CASPT2/CASSCF(10,8)/ANO-R1 and DFT (BP86/def2-SVP) potential energy profiles along both torsion and inversion pathways, as described in the computational details section (ESI†). The results are shown in Fig. 2, while the adiabatic (S₀) torsion and inversion Z → E energy barriers are reported in Table 1, together with some available experimental values for comparison. Notably, the lowest energy (torsional) barriers predicted by CASPT2 and the hybrid CASPT2@DFT method proposed here are in very good agreement with the experimental values reported for pristine AB and a push–pull derivative similar to NO₂-AB-NH₂ (see Table 1). This further endorses the need for multiconfigurational methods for an accurate description of the electronic energy. Broken-symmetry (BS) DFT was also assessed in the region close to the torsional TS (without any CNN/NNC constraint) where the CASPT2 wavefunction showed a strong multiconfigurational character. Indeed, here we observed a large mixing between the closed-shell and the open-shell singlet configuration of nπ* character, and BS-DFT had already been proposed as a valid alternative in this case.^18,20 For all compounds, DFT and CASPT2 show a qualitatively similar profile along the inversion pathway, but DFT is systematically underestimating the TS energy along this path (average error = −9.9 kcal mol⁻¹). On the other hand, DFT and CASPT2 show qualitative disagreement along torsion: the lack of multiconfigurational character in the DFT solution yields a cusp-like profile, whose gradient and curvature diverge from the CASPT2 profile when moving away from E, Z minima. BS-DFT recovers the correct smooth profile close to the torsional TS, but it strongly underestimates the torsional barrier, with an average error above 10 kcal mol⁻¹ (and a maximum error of 17 kcal mol⁻¹ for NO₂-AB-NO₂). Due to the high computational cost of CASPT2 gradients, which hinders the applicability of the method for a large-scale screening, we propose here the use of DFT for geometry optimizations and potential energy scans (with constrained CNN/NNC angles along the torsional scan), followed by the re-calculation of the energy at CASPT2 level, in a strategy that we will label CASPT2@DFT. In fact, and quite surprisingly, (constrained) DFT and CASPT2 geometries are more similar than what could be expected from the inspection of the energy profiles of Fig. 2. Indeed, CASPT2@DFT (red curves in Fig. 2) shows an excellent agreement with pure CASPT2 calculations along the inversion profile (average error on TS = 1.4 kcal mol⁻¹). Along torsion, the smooth profile is fully recovered, with only a small overestimation of the points of the scan around the TS. However, the overall error on the Z → E TS barrier is lowered by the slight overestimation also of the Z energy by CASPT2@DFT (final average errors on torsional barrier: CASPT2@DFT = 1.6 kcal mol⁻¹, CASPT2@BS-DFT = 2.0 kcal mol⁻¹). In Table 1 we also compare our inversion/torsion potential energy barriers with those obtained using the machine learning (ML) model reported in ref. 17 for azobenzene derivatives and trained on spin-flip DFT data. While the two methods yield similar inversion barriers, our CASPT2@DFT method performs significantly better along torsion, further highlighting the need for multiconfigurational methods along this coordinate. Our results demonstrate that DFT and CASPT2 can be effectively combined for the broad screening of azo-MOSTs: in a first step, the former (cheaper) method can be used to obtain E, Z minima and perform relaxed scans along torsion/inversion (putting constraints on CNN/NNC values along torsion profile). In a second step, the energy of the DFT geometries can be re-computed at CASPT2 level, avoiding the need for expensive gradient calculations. The protocol could be easily extended to include also T₁ and estimate the relevance of the triplet-mediated torsion based on (i) the barrier to reach the S₀/T₁ minimum-energy crossing point (MECP) and (ii) the SOC value at this geometry. The CASPT2 energy profile of T₁ can be tracked along the torsion scan (gray line in Fig. 2) to estimate the energy of the singlet/triplet crossings (see ESI† for a comparison with fully relaxed S₀/T₁ MECPs), and the S₀/T₁ SOC can be evaluated (with only a small increase in computational cost) using the two CASPT2 wavefunctions.

Table 1 Potential energy barriers (kcal mol⁻¹) along Z → E torsion and inversion pathways for the investigated compounds. The data from this work is compared with the potential energy barriers obtained with the ML model available from ref. 17 and with experimental thermal isomerization barriers in gas phase (when available). The mean absolute error (MAE) with respect to reference CASPT2 barriers is reported in the last line for other levels of theory

	Inversion				Torsion						Experiment
	DFT	CASPT2	CASPT2@DFT	ML model^17	DFT^b	BS-DFT	CASPT2	CASPT2@DFT^b	CASPT2@BS-DFT	ML model^17
a For NO2-AB-NH2, the barriers for both inversion paths are reported. The lowest energy barrier is marked with an asterisk and refers to inversion of –NO2 moiety. b DFT geometries were obtained putting constraints on CNN/NNC angles close to torsion TS, see computational details. c For 4-dimethylamino-4′-nitroazobenzene. d In methanol. e In DMSO.
AB	22.4	31.5	32.0	35.8	29.1	16.1	26.8	28.6	28.8	33.1	25 ± 2 (ref. 25)
											28.2 (ref. 26)
											27 ± 4 (ref. 27)
F2-AB-F2	25.5	36.5	34.7	37.2	28.4	17.5	29.4	30.4	29.4	34.8	28.0^e (ref. 28)
NH2-AB-NH2	24.4	34.5	32.5	36.7	25.7	14.2	23.1	26.4	24.6	27.4	21.2^d (ref. 29)
NO2-AB-NO2	18.6	28.4	27.2	30.4	25.4	14.2	31.5	32.2	32.8	32.8
NO2-AB-NH2^a	27.1	35.3	33.9	36.3	21.2	14.7	23.3	24.4	28.5	29.6	24.4 ± 0.7^c (ref. 30)
	14.4*	25.6*	23.8*	27.3
MAE	9.9	—	1.4	2.0	2.8	11.5	—	1.6	2.0	4.7

---

An additional challenge still stands, for the proposed characterization protocol to be broadly applicable: the active space selection in CASSCF/CASPT2 calculations has to be automatized. This is likely the major challenge (besides the computational cost) that has hindered the application of such methods to broad screening procedures. To this end, we have designed a simple and black-box algorithm for active state selection, which is described in detail in the ESI.† Though the validation of such algorithm would require its assessment over a much wider range of AB derivatives, its application to the molecules studied here always yielded correct active spaces, including all the most relevant frontier orbitals of n, π and π* nature (see Fig. S4–S8†).

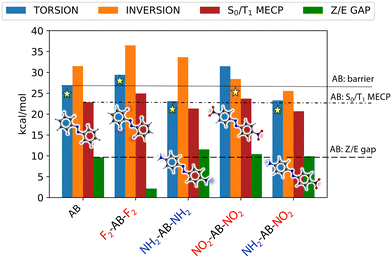
Finally, in order to compare the four derivatives to the parent AB molecule in the light of MOST applications, Fig. 3 collects the reference CASPT2 results (torsion and inversion barriers, barrier to the S₀/T₁ MECP and Z/E gap) for all the investigated compounds. Here, the lowest energy Z → E barrier between torsion and inversion determines the preferred thermal isomerization mechanism on S₀, and its value correlates with the thermal half-life of the “charged” species (i.e., the Z isomer). On the other hand, the Z/E energy gap directly measures the amount of solar energy that can be stored per molecule in gas phase, reflecting the energy density of the final material. Two compounds show a larger Z stability compared to AB: F₂-AB-F₂ and NO₂-AB-NO₂. However, the larger isomerization barrier of the former is mainly due to an increase in Z stability at the expense of the energy stored. This is mainly due to the electrostatic interaction between the F atoms in ortho position and the C atoms of the opposite ring, which can stabilize bent geometries³¹ (i.e., Z isomer and torsional TS, see electrostatic potential maps in Fig. S9†). In contrast, NO₂-AB-NO₂ shows both a larger barrier and a larger Z/E gap with respect to AB, making it the most promising candidate among the ones examined. This finding is in agreement with experimental evidence that electron-withdrawing groups slow down the thermal isomerization of azobenzenes.^29,32 NH₂-AB-NH₂ and NO₂-AB-NH₂ show Z/E gaps similar to (or even greater than) AB, but their relatively low thermal isomerization barrier will probably make them too unstable to store energy for a sufficiently long time. Interestingly, NO₂-AB-NO₂ is the only compound for which the inversion barrier Z → E is lower than the torsional one. This is due to the combined effect of TS destabilization along torsion and TS stabilization along inversion by the pull–pull substitution. Indeed, the –NO₂ group in para position can stabilize the linear (inversion) TS by mesomeric effect²³ (see Fig. S10†) and concurrently disfavour the torsion around the central NN bond (see Fig. S11†). The stabilization of the linear TS is even more relevant in the push–pull derivative NO₂-AB-NH₂ (thanks to the greater delocalization of the positive charge, see Fig. S10–S11(a)† and Table 1). However, in NO₂-AB-NH₂ both torsion and inversion TS are stabilized, making the Z isomer highly unstable. Eventually, we note that the above considerations apply also to the triplet-mediated mechanism: because the SOC value is similar in all the compounds (see Fig. S14†), the barrier to the S₀/T₁ MECP will determine the Z stability. Compared to AB, F₂-AB-F₂ and NO₂-AB-NO₂ show larger gaps to reach the singlet/triplet crossing (Fig. 3), while NH₂-AB-NH₂ and NO₂-AB-NH₂ show lower barriers, in agreement with our findings for the adiabatic torsion/inversion mechanisms.

Fig. 3 CASPT2/CASSCF(10,8)/ANO-R1 potential energy barriers associated with Z → E torsion (blue) and inversion (orange) paths, barrier to reach the S₀/T₁ MECP (red) and Z/E potential energy gap (green) for the considered compounds. For each molecule, the preferred mechanism on S₀ (lowest energy barrier) is labeled with a star. The values associated with the parent AB molecule are highlighted with black horizontal lines for a better comparison.

To summarize, we have put forward a computational scheme for obtaining the ground state potential energy surface of azobenzene photoswitches with quasi-CASPT2 accuracy with a significant reduction of computational cost. This is made possible by combining DFT for the most expensive steps (geometry optimizations, relaxed scans) followed by a more accurate CASPT2 calculation of the energy on the final structures. The procedure has the merit of overcoming the failure of DFT functionals to describe the geometry and electronic structure of the torsional transition state, while retaining an affordable computational cost. We foresee the application of the proposed methodology for large-scale screening of AB photoswitches, and in particular we target their application as molecular solar thermal fuels, for which the evaluation of the energy stored per molecule and of the Z isomer stability is essential. To this end, our results on prototypical AB derivatives (push–push, pull–pull and push–pull) already provide some chemical design guidelines for azo-MOSTs, identifying in NO₂-AB-NO₂ and in the pull–pull substitution as a promising strategy.

Data availability

The following sections are available in the ESI:† assessment of DFT functionals, computational details, computational costs, automatic selection of active space, electrostatic potential maps, stabilization of linear TS by mesomeric effect, stabilization/destabilization of torsion TS, orbital energies, involvement of T₁ in the thermal Z → E isomerization. Data for this article, including cartesian structures, molecular orbitals and raw data for Fig. 2 and 3 are available at https://doi.org/10.6092/unibo/amsacta/7894.

Author contributions

Conceptualization: F. A., I. C., M. G., L. M. - data curation: F. A., L. F. R.-A. - formal analysis: F. A., L. M., I. C., L. S., L. F. R.-A., F. L., F. C. - funding acquisition: L. M., I. C., M. G., I. R., S. O. - investigation: F. A., L. S., L. F. R.-A. - methodology: F. A., I. C., M. G., L. M. - project administration: L. M. - software: F. A., F. C., L. F. R.-A. - supervision: L. M., I. C., M. G., I. R., S. O., E. C. - visualization: F. A. - writing of original draft: F. A., L. M., I. C. - writing the initial draft: F. A. - writing, review & editing: All authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We would like to thank Jérôme Cornil and Ari Serez (University of Mons, Belgium) for useful discussions and data exchange. This work was supported by funding awarded by the International Foundation Big Data and Artificial Intelligence for Human Development (IFAB), Call for Projects 2022–2023, to the project “Getting the MOST out of Sun” (GEM).

References

1. J. Olmsted III, J. Lawrence and G. G. Yee, J. Sol. Energy, 1983, 30, 271–274.
2. L. Dong, Y. Feng, L. Wang and W. Feng, Chem. Soc. Rev., 2018, 47, 7339–7368.
3. Z. Wang, P. Erhart, T. Li, Z.-Y. Zhang, D. Sampedro, Z. Hu, H. A. Wegner, O. Brummel, J. Libuda and M. B. Nielsen, et al. , Joule, 2021, 5, 3116–3136.
4. B. Zhang, Y. Feng and W. Feng, Nano-Micro Lett., 2022, 14, 138.
5. G. F. Martins, B. D. P. Cardoso, N. Galamba and B. J. Cabral, Energy Fuels, 2023, 37, 1731–1756.
6. R. J. Salthouse and K. Moth-Poulsen, J. Mater. Chem. A, 2024, 12, 3180–3208.
7. S. Li, H. Wang, J. Fang, Q. Liu, J. Wang and S. Guo, J. Therm. Sci., 2020, 29, 280–297.
8. C. Ciminelli, G. Granucci and M. Persico, Chem. – Eur. J., 2004, 10, 2327–2341.
9. I. Conti, M. Garavelli and G. Orlandi, J. Am. Chem. Soc., 2008, 130, 5216–5230.
10. G. Tiberio, L. Muccioli, R. Berardi and C. Zannoni, ChemPhysChem, 2010, 11, 1018–1028.
11. J. Casellas, M. J. Bearpark and M. Reguero, ChemPhysChem, 2016, 17, 3068–3079.
12. A. Nenov, R. Borrego-Varillas, A. Oriana, L. Ganzer, F. Segatta, I. Conti, J. Segarra-Marti, J. Omachi, M. Dapor and S. Taioli, et al. , J. Phys. Chem. Lett., 2018, 9, 1534–1541.
13. F. Aleotti, L. Soprani, A. Nenov, R. Berardi, A. Arcioni, C. Zannoni and M. Garavelli, J. Chem. Theory Comput., 2019, 15, 6813–6823.
14. F. Aleotti, A. Nenov, L. Salvigni, M. Bonfanti, M. M. El-Tahawy, A. Giunchi, M. Gentile, C. Spallacci, A. Ventimiglia and G. Cirillo, et al. , J. Phys. Chem. A, 2020, 124, 9513–9523.
15. F. Aleotti, V. Petropoulos, H. Van Overeem, M. Pettini, M. Mancinelli, D. Pecorari, M. Maiuri, R. Medri, A. Mazzanti and F. Preda, et al. , J. Phys. Chem. A, 2023, 127, 10435–10449.
16. L. Hegedüsová, R. KuteI', M. Medved', L. F. Pašteka, M. Cigáň and Š. Budzák, Int. J. Quantum Chem., 2023, 123, e27120.
17. S. Axelrod, E. Shakhnovich and R. Gomez-Bombarelli, ACS Cent. Sci., 2023, 9, 166–176.
18. M. Reimann, E. Teichmann, S. Hecht and M. Kaupp, J. Phys. Chem. Lett., 2022, 13, 10882–10888.
19. A. Cembran, F. Bernardi, M. Garavelli, L. Gagliardi and G. Orlandi, J. Am. Chem. Soc., 2004, 126, 3234–3243.
20. Y. Shao, M. Head-Gordon and A. I. Krylov, J. Chem. Phys., 2003, 118, 4807–4818.
21. N. K. Singer, K. Schlögl, J. P. Zobel, M. D. Mihovilovic and L. González, J. Phys. Chem. Lett., 2023, 14, 8956–8961.
22. C. Knie, M. Utecht, F. Zhao, H. Kulla, S. Kovalenko, A. M. Brouwer, P. Saalfrank, S. Hecht and D. Bléger, Chem. – Eur. J., 2014, 20, 16492–16501.
23. J. Dokić, M. Gothe, J. Wirth, M. V. Peters, J. Schwarz, S. Hecht and P. Saalfrank, J. Phys. Chem. A, 2009, 113, 6763–6773.
24. M. Nucci, A. Núñez, L. M. Frutos and M. Marazzi, Adv. Sustainable Syst., 2022, 6, 2200097.
25. X. Yu, Z. Wang, M. Buchholz, N. Füllgrabe, S. Grosjean, F. Bebensee, S. Bräse, C. Wöll and L. Heinke, Phys. Chem. Chem. Phys., 2015, 17, 22721–22725.
26. J.-Å. Andersson, R. Petterson and L. Tegnér, J. Photochem., 1982, 20, 17–32.
27. W. Zhou, S. Grosjean, S. Bräse and L. Heinke, Z. Phys. Chem., 2018, 233, 15–22.
28. D. Bléger, J. Schwarz, A. M. Brouwer and S. Hecht, J. Am. Chem. Soc., 2012, 134, 20597–20600.
29. A. A. Blevins and G. Blanchard, J. Phys. Chem. B, 2004, 108, 4962–4968.
30. J.-Å. Andersson, J. Photochem., 1983, 22, 245–254.
31. M. Saccone, A. Siiskonen, F. Fernandez-Palacio, A. Priimagi, G. Terraneo, G. Resnati and P. Metrangolo, Acta Crystallogr., Sect. B:Struct. Sci., Cryst. Eng. Mater., 2017, 73, 227–233.
32. A. H. Heindl and H. A. Wegner, Chem. – Eur. J., 2020, 26, 13730–13737.

---

Footnote

† Electronic supplementary information (ESI) available: Assessment of DFT functionals, computational details, computational costs, automatic selection of active space, electrostatic potential maps, stabilization of linear TS by mesomeric effect, stabilization/destabilization of torsion TS, orbital energies, Involvement of T₁ in the thermal Z → E isomerization. See DOI: https://doi.org/10.1039/d4me00183d

---