Real-time autonomous control of a continuous macroscopic process as demonstrated by plastic forming

Abstract

To meet the need for more adaptable and expedient approaches in research and manufacturing, we present a continuous autonomous system that leverages real-time, in situ characterization and an active-learning-based decision-making processor. This system was applied to a plastic film forming process to demonstrate its capability in autonomously determining process conditions for specified film dimensions without human intervention. Application of the system to nine film dimensions (width and thickness) highlighted its ability to explore the search space and identify appropriate and stable process conditions, with an average of 11 characterization-adjustment iterations and a processing time of 19 minutes per width, thickness combination. The system successfully avoided common pitfalls, such as repetitive over-correction, and demonstrated high accuracy, with R² values of 0.87 and 0.90 for film width and thickness, respectively. Moreover, the active learning algorithm enabled the system to begin exploration with zero training data, effectively addressing the complex and interdependent relationships between control factors (material supply rate, applied force, material viscosity) in the continuous plastic forming process. Given that the core concept of this autonomous process can, in principle, be transferred to other continuous material processing systems, these results have implications for accelerating progress in both research and industry.

---

New concepts

In this study, we introduce an autonomous system with real-time characterization and a decision-making processor combining active learning and Bayesian optimization for adaptable process operation. The operation of this closed-loop system is demonstrated on a plastic film forming process. The key innovation lies in the active learning decision-making process, enabling autonomous operation without the need for training data, which is an advantage for complex processes where such data is unavailable. Applied to plastic film processing, the system autonomously determined process conditions for user-selected film dimensions with an average convergence of 11 characterization-adjustment iterations (∼19 minutes). In addition, the process demonstrated resilience, avoiding optimization traps, setting it apart from conventional approaches. The importance of this work lies in integrating AI with automation to create an autonomous system, which combines the strengths of AI-based decision making with automated experimentation. This combination represents a powerful tool for advancing research in exploring complex systems (continuous plastic film forming). The application of this system to a real, macroscopic process further showcases its versatility and potential in fields requiring interdisciplinary approaches. Overall, this system advances autonomous materials processing for continuous systems, making it applicable to new and unexplored materials.

1. Introduction

The formation of macroscopic structures is essential across a wide range of industry sectors, including plastics, rubber, food, and pharmaceuticals. These processes are fundamental for the mass production of everyday products, such as tapes, rods, and sheets (Fig. 1a). As industrial demands evolve and new materials emerge, there is a growing need for more adaptable and efficient fabrication methods. Traditional approaches, which rely on manual adjustments and tuning of manufacturing processes, are often labor- and time-intensive, prompting a shift toward autonomous process control systems.

Fig. 1 Autonomous continuous macroscopic process. (a) Schematic of the continuous macroscopic forming process. (b) Proposed system of autonomous control of the continuous macroscopic process with a closed-loop optimization of experiments with in situ evaluation and calculations of decision making based on active learning. (c) Complexity of material, force, and heat balances in the continuous macroscopic forming process. (d) Trajectory of autonomous control of film dimensions (width and thickness). The inset figure represents changes in sum of squared relative errors of targeted film dimensions.

Autonomous process control extends beyond conventional automation by incorporating independent decision-making capabilities that significantly reduce or even eliminate the need for human intervention. This advancement allows operators to redirect their focus toward more complex scientific and industrial challenges that are not suitable for automation. Moreover, autonomy in process control promotes more objective and unbiased operational decisions, leading to improved productivity and innovation. However, the development of such autonomous systems is particularly challenging in scenarios where prior data for training is lacking. The absence of comprehensive data hampers the development of reliable models for process control, especially when dealing with new materials or uncharted process conditions. While the benefits of autonomous systems are evident, the integration of human insight, whether within the paradigms of “human in the loop” or “human overseeing the loop”, can further enhance the interpretability and effectiveness of these systems. This synergy between human expertise and autonomous technologies is identified as a crucial element in addressing complex manufacturing challenges.^1,2

Autonomous systems generally operate within two paradigms: “maintenance” and “exploration.” Maintenance involves stabilizing a system in response to disturbances, often through well-established methods such as proportional-integral-differential (PID) controllers or, more recently, deep reinforcement learning. For example, a study by Degrave et al. successfully employed a deep reinforcement learning model to maintain plasma stability in a nuclear fusion reactor by controlling magnetic fields.³ In contrast, autonomous exploration focuses on the independent optimization of uncharted parameter spaces without reliance on preset rules, allowing for the discovery of novel process conditions.

Recent advancements in autonomous exploration have been applied across various fields of material science, including organics, inorganics, and nanomaterials. These applications range from optimizing chemical synthesis for both batch⁴ and flow^5–7 reactors to studying organic solar cells and semiconductors, to photocatalysts,^8–11 investigating the structural properties of thin films,^12,13 and combustion synthesis,¹⁴ along with the investigation of magnetic materials¹⁵ and phase-change memory materials.¹ For nanomaterials, autonomous exploration has been applied to the investigation of optimizing growth rates and examining structural changes in the chemical vapor deposition synthesis of vertically aligned carbon nanotubes.^16,17 Additionally, autonomous exploration has been leveraged to refine process protocols, such as developing charging protocols to enhance battery longevity¹⁸ or optimizing drying processes for fuel cell slurries.¹⁹ These advancements have been driven by significant progress in both hardware, such as robotics and automation, and software, including Bayesian optimization and large language models. For instance, Chen et al. demonstrated a powerful application of autonomous exploration in materials research by integrating a pipetting robot with an active learning algorithm based on a neural network model.²⁰ This system enabled the robot to conduct experiments autonomously, rapidly identifying optimal conditions with minimal human input. Similarly, Boiko et al. showcased the potential of large language models when paired with robotics, achieving autonomous cross-coupling reactions. By leveraging the vast knowledge embedded in the language model, the system was able to predict and execute complex chemical reactions autonomously.²¹ These examples highlight the growing influence of autonomous systems in accelerating “exploration” research across various fields, demonstrating how the integration of advanced hardware and sophisticated algorithms can lead to significant breakthroughs in materials science.

Despite these advances, autonomous exploration in continuous macroscopic forming processes has been relatively underexplored, and research in this area remains surprisingly underdeveloped considering its critical role in manufacturing. The integration of precision automation, autonomous control, real-time data processing, and the challenge posed by the lack of prior data for training models presents significant obstacles, particularly in continuous processes that require uninterrupted operation and closed-loop systems for real-time adjustments. While some research has focused on autonomous batch forming processes using 3D printers,^22,23 no research has been conducted on the autonomization of continuous macroscopic forming, despite its direct applicability to numerous continuous synthesis processes as well as its paramount importance for industrial mass production. Unlike batch processes, where results are clearly defined and data can be consolidated after completion, continuous processes demand ongoing autonomous exploration without halting the system. Achieving autonomous control in continuous forming processes remains a formidable challenge due to the complexities of real-time data processing, decision-making, and the absence of pre-existing data.

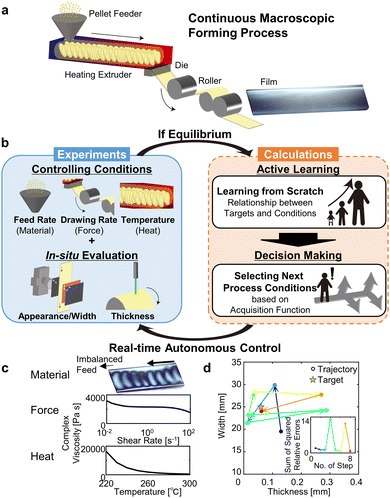
Here, we report an autonomous system for a continuous macroscopic process using real-time in situ characterization feedback (Fig. 1b). As a demonstration, we applied this system to a continuous plastic film forming process to highlight its efficiency and accuracy in achieving diverse target dimensions without human intervention for a system without prior training. In this study, our system controlled the entire plastic forming process, where plastic pellets were fed, melted, transported, and extruded through a slit-shaped “sheet” die, cooled and collected onto a roll.^24,25 Real-time in situ thickness and width monitoring enabled the system to balance various process parameters (material feed rate, draw rate, and applied heat), as illustrated in Fig. 1c. Because of the complex relationships between these factors, the balancing of these factors was critical for not only determining conditions for targeted film dimensions but also to ensure film uniformity.²⁶ Moreover, the optimal balance of these factors was influenced by the chemical structures of the materials, including primary structure, molecular weight distribution, side chains, and substituent modification. In addition, our system showed “instability avoidance” (i.e., the ability to avoid being trapped within a parameter space of unstable states). The accuracy and efficiency of this system were validated by the rapid convergence for nine diverse target values spanning different combinations of widths and thicknesses. Importantly, the decision-making section of our system was based on an active learning algorithm, which required no prior training, and target values could be achieved in an average of 11 iterations (∼19 minutes). Because the basic concept of our autonomous process is transferrable and expandable, thus we believe that our findings will promote the autonomization of continuous forming processes, paving the way for broader applications and implementations in the numerous research and industrial fields.

2. Results and discussion

2.1. Demonstration of an autonomous film forming process

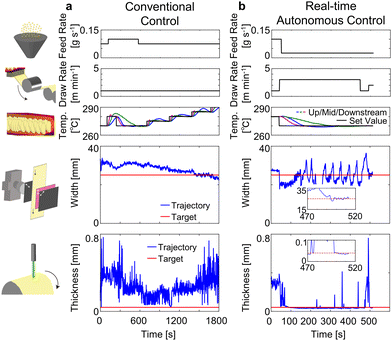
To begin, we demonstrate the ability of our system to efficiently and independently determine the process conditions needed to fabricate a plastic film with user-defined dimensions (width/thickness) by employing an active learning processer to guide the autonomous operation. For this proof-of-concept, polycarbonate was selected as a model system because it represents one of the basic amorphous transparent plastics and showed the widest diversity in achievable dimensions from manual preliminary screening. In short, the autonomous decision-making processor utilized an active learning algorithm based on a Gaussian process regressor with a single objective function, combined with Bayesian optimization using an expected improvement acquisition function. The detailed algorithm and calculation workflow are provided in the ESI† and Fig. S4. The sequence of states (i.e. “trajectory”) following the progress is shown in Fig. 1d. The progression of process adjustments is depicted as a transition from blue to red, with red indicating the endpoint. Star-shaped markers indicate the target positions for width and thickness, while circular markers represent the states during the convergence process. In viewing this trajectory, we can make three observations. First, the conditions to fabricate the film with the target width and thickness were achieved in eight characterization-adjustment iterations, which required only 24 minutes to complete. This highlights one of the features of this system, process efficiency, which would be challenging to achieve through manual operation. This result is particularly significant because the system was not provided with prior training or preset responses, as typically used in PID systems (e.g. air-conditioning). Second, while the trajectory appears random in nature, the sum of squared relative errors at each iteration shows clear reduction indicating the gradual convergence to target values. This process is twice interrupted with abrupt increases in error (Fig. 1d, inset), a behaviour inherent to the active learning process. Third, this demonstration shows an important feature of our system: “instability avoidance,” which we describe as the ability to avoid falling within a parameter domain of unstable conditions from which it becomes trapped due to the decision-making algorithm (Fig. 2). This is analogous to repeated overcorrection in numerical analysis, which is well known by oscillations about the convergence point in the Newton method. To further validate this point, we applied our system to optimize the process conditions for a target film width and thickness using two different approaches: conventional control and real-time active learning.

Fig. 2 Effects of autonomous control. Comparison of time-series profiles of feed rate, draw rate, temperature, and film properties (width, thickness) under (a) conventional and (b) autonomous control.

To compare the exploration of process conditions, we applied a method that mimics human control (Fig. 2a) where only a single condition is selected and adjusted at each iteration. Specifically, this algorithm determines process adjustments by sampling individual parameters and calculating gradients, with this process repeated for each parameter. While conventional systems can be used in some situations, our results showed that the optimal control conditions for the target values of width and thickness could not be identified. Instead, the system became trapped, as discussed earlier, and failed to converge to the target values. We note that autonomous systems designed for “maintaining” desired targets in environments with known process responses often use methods like PID controllers or more advanced approaches, such as deep reinforcement learning. These methods serve as benchmarks for comparison. However, in this study, we focused on “exploring” conditions in a system with unknown process responses, such as in the case of new materials or when expert knowledge is lacking. Although brute-force, systematic searches can theoretically explore all combinations, they are impractical due to the extensive time required. Thus, we selected this approach because it simulates the systematic adjustments characteristic of a human operator.

Using real-time active learning, the model determined process conditions while balancing exploration of unexplored regions within the process space and minimizing error in the projected range (Fig. 2b). This algorithm demonstrated “instability avoidance” and efficiently determined the parameters to achieve the target values. We interpret the two abrupt increases in error in the error plot of Fig. 1d, inset, as resulting from this behaviour. To quantitatively compare the differences between the two approaches, we calculated and plotted the sum of squared relative errors for each process adjustment (Fig. S5, ESI†). As shown in Fig. S5 (ESI†), the conventional process control failed to reach the target values even after 30 minutes, with the error remaining at a finite value. In contrast, our autonomous control achieved the target values in about 8 minutes, with the error approaching zero. Taken together, these results demonstrate that autonomous optimization improves process efficiency and robustness while eliminating the need for human intervention.

2.2. Configuration of the autonomous forming system

Here, we describe the three key components of our plastic film forming system: (1) the plastic forming component; (2) the in situ evaluation component; and (3) the autonomous decision-making processor. The plastic forming component is responsible for the mechanical fabrication and manufacturing in our system. This section controls the feeding of plastic pellets (master batch) into a hopper, applies heat to melt and coalesce the beads into a cohesive molten unit, and extrudes the material through a sheet die to form the basic sheet-like shape, which is then cooled and collected (Fig. 1a). The control parameters of this process (feed rate, temperature, and draw rate) are interconnected, which must be mutually adjusted to avoid instability, such as “draw resonance phenomena”, which are structural distortions or fluctuations as the process attempts to find a stable condition (Fig. 1c). The in situ evaluation component provides in-line and real-time diagnostics of the film dimensions (width and thickness), which then streams into the autonomous processor as a basis for the next decision on process adjustment (Fig. 1b). We refer to this cycle as a “characterization-adjustment” iteration. By leveraging the birefringence of plastics to capture the appearance of the film, real-time detection of the formed plastic shape was made possible using an arrangement of commercially available polarizers and a digital camera. Thickness measurements were conducted using a laser displacement meter, providing continuous, real-time monitoring. Together, these two evaluations afforded real-time evaluation of two key physical film dimensions, width and thickness. We note that while the dimensions could be continuously monitored throughout our process, the frequency of the adjustments was limited by the time required for the plastic forming component to reach its target set-points and for the newly formed plastic to reach the in situ evaluation component.

The autonomous processor represents the core of our system, as it accepts and interprets the forming and evaluation data, decides the appropriate process adjustment, and sends these instructions to the plastic forming component (Fig. 1b). As previously mentioned, due to the complex relationship between the process parameters, such as material grade and temperature-dependent rheological properties, pre-accumulated data for training can often be lacking, particularly for new materials. Even when partial data is available, its usefulness in decision-making is strongly dependent on its diversity. Therefore, our autonomous processor was designed using an active learning algorithm (python3 modAL module²⁷) based on a Gaussian process regressor with a single objective function, which enables autonomous control of the macroscopic forming process, even in the case where no pre-existing data is available. In active learning, in contrast to learning from a fixed training dataset, an untrained model gradually learns from sequential queries and results. As this process continues, the predictive accuracy of the model improves. This method of development is analogous to child development, where initial knowledge is absent, and through gradually learning from various sensory inputs, the child acquires numerous causal relationships, thereby gaining knowledge. In principle, provided with sufficient characterization and control, the evolved model is expected to achieve an expert level of performance.

In our system, the model sequentially learns the relationship between process conditions and the target dimensions. A critical aspect of this learning process is the development of strategies to determine subsequent process conditions. Two key considerations are: (1) multi-objective optimization, specifically the simultaneous optimization of both width (∼10 s mm) and thickness (∼sub-mm), and (2) establishing criteria to efficiently identify the next set of conditions amid uncertain predictions with a limited dataset. To simplify the optimization, we used the sum of squared relative errors as the objective function. This approach is useful when handling targets of different orders of magnitude (width ∼10 s mm and thickness ∼sub-mm), allowing us to consolidate the problem into a single objective function. We further employed Bayesian optimization with an acquisition function, “expected improvement,” to efficiently explore optimal process conditions. This method evaluates both the proximity to the desired target on the current data and the uncertainty in the unexplored regions of the process space. By integrating these techniques into the active learning process, we developed a closed-loop system capable of autonomous process control. This not only eliminated the need for human intervention but also ensured that multiple objectives were effectively managed.

2.3. Demonstration of an autonomous forming process to diverse target values

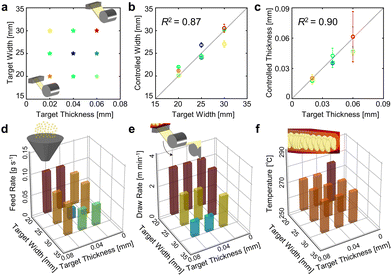
To demonstrate the ability of this system to accurately and efficiently determine process conditions for diverse target dimensions, nine different targets were selected, spanning various combinations of width and thickness. The system was directed to autonomously achieve these values, following the procedure described in Section 2.1 (Fig. 3a). Overall, the target values were reached with exceptional efficiency as evidenced by an average of 11 characterization-adjustment iterations, corresponding to an average processing time of ∼19 minutes. The fastest target required only 3 iterations (1.4 minutes), while the most time-consuming required 32 iterations (50 minutes). It is important to note that, although 32 iterations over 50-minutes might seem lengthy, this equates to one iteration every 1.56 minutes, exemplifying the advantages of autonomous control over manual operation. To highlight the accuracy of the autonomous operation, we compared the target widths and thicknesses to the achieved values (Fig. 3b and c, respectively), which show excellent agreement. The coefficient of determination (R²) between the target and experimentally fabricated plastic dimensions was R² = 0.87 for width and 0.90 for thickness. These results quantify the accuracy and reliability of our autonomous plastic forming system.

Fig. 3 Application of autonomous control to different target conditions. (a) A set of target widths and thicknesses for autonomous control. Comparison of the accuracy of autonomous control of (b) width and (c) thickness. Selected conditions of (d) feed rate, (e) draw rate, and (f) temperature for autonomous control of nine different target conditions.

2.4. Interpretation of the results

These results demonstrate that our plastic forming system can autonomously adjust the process to manufacture films with user-defined dimensions. The complexity observed in the solutions generated by the autonomous processor for the nine target values highlights the sophisticated nature of the optimization process (Fig. 3d–f). Although the optimization results for a three-parameter process are not fully explainable, we believe that this stems from the dependence of the trajectory on the initial conditions and the non-uniqueness of the solutions. Despite this, the results offer valuable material-specific insights. We observed that the trends in the determined process conditions for the feed rate differ significantly from those of the draw rate and temperature. Specifically, as the target width and thickness decrease, both the draw rate and temperature increase. This behavior can be explained by the strong sensitivity of plastic viscosity to small (∼10 °C) changes in temperature. For example, under the same shear rate, plastic viscosity decreases by 30% from 1315 Pa s at 270 °C to 931 Pa s at 280 °C (Fig. S1, ESI†). Consequently, within our range of selected target values, temperature adjustment appeared relatively minor, except in cases of significant dimensional reduction, where temperature was increased to enhance plastic fluidity. In contrast, the draw rate exhibited a clear trend, where higher draw rates were required for reduced dimensions, reflecting the need for greater shear to achieve the desired dimensional reduction. This demonstrates that our system can autonomously determine unbiased process conditions appropriate for a wide range of target values.

2.5. Implications, challenges, and future prospects of our autonomous forming process

While our system has demonstrated effective autonomous optimization for the plastic forming process, there are areas that could be further improved. First, achieving higher accuracy requires more measurement-adjustment iterations, which increases optimization time. Currently, target accuracy is predetermined by the user. In the future, we anticipate that the system will autonomously determine the stopping criterion, dynamically balancing optimization time and accuracy based on the specific requirements of the task.²⁸ Second, our current system relies on a user-defined process range to ensure human and machine safety. For example, insufficient heating combined with a high feed rate could cause excessive torque and potential machine damage, so we set limits based on material rheology. Incorporating real-time diagnostics could enable the system to autonomously adjust these boundaries. Additionally, integrating domain knowledge through large-scale language models could further improve the system's ability to set process control ranges autonomously by leveraging extensive pre-existing data and expertise. Third, introducing additional process controls, such as roller temperature, ambient humidity, and equipment geometry, would enhance the system's versatility and accuracy. To autonomously control more complex structures and properties in plastics, the system must include advanced in situ measurements. For example, near-infrared spectroscopy could monitor and indirectly control crystallinity,^29,30 while novel techniques could infer mechanical properties typically assessed through destructive testing. Integrating advanced measurements is expected to enhance the system's ability to explore and optimize advanced mechanical properties, thereby improving its overall usefulness. Such advancements would further solidify the role of autonomous systems in advanced manufacturing, pushing the boundaries of what is possible in material science and engineering.

3. Conclusions

We have demonstrated an autonomous and continuous macroscopic forming process based on an active learning decision-making algorithm. This system was successfully applied to the manufacture of plastic films, serving as a model system for the approach. With real-time in situ evaluation, the system accurately captured film properties and used them as inputs to the autonomous processor, enabling the necessary measurement-adjustment iterations to autonomously control process conditions, including material input, draw force, and heating, without human intervention. The system also showed high precision in adjusting to optimal process conditions, even when the target film dimensions were altered. Notably, the active learning-based processor required no prior training, achieving film dimension targets in an average of 11 iterations (∼19 minutes). These results highlight the high system efficiency in autonomously determining process conditions without human intervention. Looking ahead, the implementation of such autonomous systems is expected to foster a more innovative and efficient manufacturing environment, where human-machine collaboration enhances productivity. Our findings have the potential to contribute meaningfully to the autonomization of continuous processes, from synthesis to slurries, pastes, and melts, and may open the door to broader applications across various fields. Integrating these systems into industrial practices could play a role in enhancing manufacturing processes, fostering innovation, and improving the quality and consistency of products in diverse sectors.

4. Experimental

All the information about materials and methods is provided in the ESI.†

Author contributions

Conceptualization: S. M., K. H., methodology: S. M., software: S. M., T. H., formal analysis: S. M., investigation: S. M., Y. M., H. N., D. N. F. visualization: S. M., D. N. F., supervision: K. H., writing – original draft: S. M, writing – review & editing: D. N. F. Specifically, S. M. designed all experimental setup, developed the software of the autonomous control, conducted experiments and calculations, and prepared this paper. T. H. developed the software for the real-time connection of multiple instruments. Y. M. contributed to the twin-screw extruder. H. N. contributed to the laser displacement meter. D. N. F. contributed to the investigation of the results, visualization, and writing the manuscript. K. H. supervised and managed the project.

Data availability

The data supporting this article have been included as part of the ESI.† Additional supporting data generated during the present study are available from the corresponding author upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We appreciate Mr Tomohisa Hayashida, and Mrs Megumi Terauchi for their technical support of the experiments. The authors are grateful to Dr Toshiya Okazaki, Dr Hiroshi Morita, and Dr Ken Kokubo for their support. This work was supported by a project (JPNP16010) commissioned by the New Energy and Industrial Technology Development Organization (NEDO).

References

1. A. G. Kusne, H. Yu, C. Wu, H. Zhang, J. Hattrick-Simpers, B. DeCost, S. Sarker, C. Oses, C. Toher, S. Curtarolo, A. V. Davydov, R. Agarwal, L. A. Bendersky, M. Li, A. Mehta and I. Takeuchi, Nat. Commun., 2020, 11, 5966.
2. E. Stach, B. DeCost, A. G. Kusne, J. Hattrick-Simpers, K. A. Brown, K. G. Reyes, J. Schrier, S. Billinge, T. Buonassisi, I. Foster, C. P. Gomes, J. M. Gregoire, A. Mehta, J. Montoya, E. Olivetti, C. Park, E. Rotenberg, S. K. Saikin, S. Smullin, V. Stanev and B. Maruyama, Matter, 2021, 4, 2702.
3. J. Degrave, F. Felici, J. Buchli, M. Neunert, B. Tracey, F. Carpanese, T. Ewalds, R. Hafner, A. Abdolmaleki, D. de las Casas, C. Donner, L. Fritz, C. Galperti, A. Huber, J. Keeling, M. Tsimpoukelli, J. Kay, A. Merle, J.-M. Moret, S. Noury, F. Pesamosca, D. Pfau, O. Sauter, C. Sommariva, S. Coda, B. Duval, A. Fasoli, P. Kohli, K. Kavukcuoglu, D. Hassabis and M. Riedmiller, Nature, 2022, 602, 414.
4. M. Christensen, L. P. E. Yunker, F. Adedeji, F. Häse, L. M. Roch, T. Gensch, G. dos Passos Gomes, T. Zepel, M. S. Sigman, A. Aspuru-Guzik and J. E. Hein, Commun. Chem., 2021, 4, 112.
5. A. M. Schweidtmann, A. D. Clayton, N. Holmes, E. Bradford, R. A. Bourne and A. A. Lapkin, Chem. Eng. J., 2018, 352, 277.
6. M. Rubens, J. H. Vrijsen, J. Laun and T. Junkers, Angew. Chem., Int. Ed., 2019, 58, 3183.
7. S. T. Knox, S. J. Parkinson, C. Y. P. Wilding, R. A. Bourne and N. J. Warren, Polym. Chem., 2022, 13, 1576.
8. S. Langner, F. Häse, J. D. Perea, T. Stubhan, J. Hauch, L. M. Roch, T. Heumueller, A. Aspuru-Guzik and C. J. Brabec, Adv. Mater., 2020, 32, 1907801.
9. C. Kunkel, J. T. Margraf, K. Chen, H. Oberhofer and K. Reuter, Nat. Commun., 2021, 12, 2422.
10. B. Burger, P. M. Maffettone, V. V. Gusev, C. M. Aitchison, Y. Bai, X. Wang, X. Li, B. M. Alston, B. Li, R. Clowes, N. Rankin, B. Harris, R. S. Sprick and A. I. Cooper, Nature, 2020, 583, 237.
11. T. Erps, M. Foshey, M. K. Luković, W. Shou, H. H. Goetzke, H. Dietsch, K. Stoll, B. von Vacano and W. Matusik, Sci. Adv., 2021, 7, eabf7435.
12. B. P. MacLeod, F. G. L. Parlane, T. D. Morrissey, F. Häse, L. M. Roch, K. E. Dettelbach, R. Moreira, L. P. E. Yunker, M. B. Rooney, J. R. Deeth, V. Lai, G. J. Ng, H. Situ, R. H. Zhang, M. S. Elliott, T. H. Haley, D. J. Dvorak, A. Aspuru-Guzik, J. E. Hein and C. P. Berlinguette, Sci. Adv., 2020, 6, eaaz8867.
13. R. Shimizu, S. Kobayashi, Y. Watanabe, Y. Ando and T. Hitosugi, APL Mater., 2020, 8, 111110.
14. B. P. MacLeod, F. G. L. Parlane, C. C. Rupnow, K. E. Dettelbach, M. S. Elliott, T. D. Morrissey, T. H. Haley, O. Proskurin, M. B. Rooney, N. Taherimakhsousi, D. J. Dvorak, H. N. Chiu, C. E. B. Waizenegger, K. Ocean, M. Mokhtari and C. P. Berlinguette, Nat. Commun., 2022, 13, 995.
15. Y. Iwasaki, R. Sawada, E. Saitoh and M. Ishida, Commun. Mater., 2021, 2, 31.
16. P. Nikolaev, D. Hooper, F. Webber, R. Rao, K. Decker, M. Krein, J. Poleski, R. Barto and B. Maruyama, npj Comput. Mater., 2016, 2, 16031.
17. J. Chang, P. Nikolaev, J. Carpena-Núñez, R. Rao, K. Decker, A. E. Islam, J. Kim, M. A. Pitt, J. I. Myung and B. Maruyama, Sci. Rep., 2020, 10, 9040.
18. P. M. Attia, A. Grover, N. Jin, K. A. Severson, T. M. Markov, Y.-H. Liao, M. H. Chen, B. Cheong, N. Perkins, Z. Yang, P. K. Herring, M. Aykol, S. J. Harris, R. D. Braatz, S. Ermon and W. C. Chueh, Nature, 2020, 578, 397.
19. K. Nagai, T. Osa, G. Inoue, T. Tsujiguchi, T. Araki, Y. Kuroda, M. Tomizawa and K. Nagato, Sci. Rep., 2022, 12, 1615.
20. T. Chen, Z. Pang, S. He, Y. Li, S. Shrestha, J. M. Little, H. Yang, T. C. Chung, J. Sun, H. C. Whitley, I.-C. Lee, T. J. Woehl, T. Li, L. Hu and P.-Y. Chen, Nat. Nanotechnol., 2024, 19, 782.
21. D. A. Boiko, R. MacKnight, B. Kline and G. Gomes, Nature, 2023, 624, 570.
22. A. E. Gongora, B. Xu, W. Perry, C. Okoye, P. Riley, K. G. Reyes, E. F. Morgan and K. A. Brown, Sci. Adv., 2020, 6, eaaz1708.
23. J. R. Deneault, J. Chang, J. Myung, D. Hooper, A. Armstrong, M. Pitt and B. Maruyama, MRS Bull., 2021, 46, 566.
24. J. Vlachopoulos and D. Strutt, Mater. Sci. Technol., 2003, 19, 1161.
25. M. Vincent, B. Vergnes, Y. Demay, T. Coupez, N. Billon and J.-F. Agassant, Can. J. Chem. Eng., 2002, 80, 1143.
26. J. S. Lee, H. W. Jung, H.-S. Song, K.-Y. Lee and J. C. Hyun, J. Non-Newtonian Fluid Mech., 2001, 101, 43.
27. T. Danka and P. Horvath, arXiv, 2018, Preprint, arXiv:1805.00979 DOI:10.48550/arXiv.1805.00979.
28. H. Ishibashi, M. Karasuyama, I. Takeuchi and H. Hino, Proceedings of The International Conference on AI and Statistics, 2023, 206, 6463.
29. S. Muroga, Y. Hikima and M. Ohshima, Appl. Spectrosc., 2017, 71, 1300.
30. S. Muroga, Y. Hikima and M. Ohshima, J. Appl. Polym. Sci., 2018, 135, 45898.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mh00051j

---