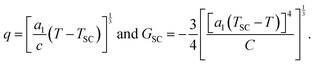Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Stabilizing low symmetry-based functions of materials at room temperature through isosymmetric electronic bistability†
Francisco Javier
Valverde-Muñoz
 a,
Ricardo Guillermo
Torres Ramírez
a,
Ricardo Guillermo
Torres Ramírez
 a,
Elzbieta
Trzop
a,
Elzbieta
Trzop
 ab,
Thierry
Bataille
ab,
Thierry
Bataille
 c,
Nathalie
Daro
d,
Dominique
Denux
d,
Philippe
Guionneau
c,
Nathalie
Daro
d,
Dominique
Denux
d,
Philippe
Guionneau
 d,
Hervé
Cailleau
a,
Guillaume
Chastanet
d,
Boris
Le Guennic
d,
Hervé
Cailleau
a,
Guillaume
Chastanet
d,
Boris
Le Guennic
 c and
Eric
Collet
c and
Eric
Collet
 *abe
*abe
aUniv Rennes, CNRS, IPR (Institut de Physique de Rennes) – UMR 6251, 35000 Rennes, France. E-mail: eric.collet@univ-rennes.fr
bCNRS, Univ Rennes, DYNACOM (Dynamical Control of Materials Laboratory) – IRL 2015, The University of Tokyo, 7-3-1 Hongo, Tokyo 113-0033, Japan
cUniv Rennes, Ecole Nationale Supérieure de Chimie de Rennes, CNRS, ISCR (Institut des Sciences Chimiques de Rennes) – UMR 6226, F-35000 Rennes, France
dUniv. Bordeaux, CNRS, Bordeaux INP, ICMCB, UMR 5026, F-33600 Pessac, France
eInstitut Universitaire de France (IUF), France
First published on 6th February 2025
Abstract
Symmetry-breaking is pivotal for controlling ferroelectric, ferroelastic and/or ferromagnetic functions of materials, which enables applications in sensors, memory devices, transducers or actuators. Commonly, ferroic phases emerge from descending symmetry-breaking, as the laws of thermodynamics dictate that the ordered low entropy phases form at low temperature, which limits practical applications of many materials at room temperature. Rare examples of ascending symmetry-breakings have been observed, but the driving force remains often unclear. Here, we report on a ferroelastic symmetry-breaking occurring at high temperature in a spin-crossover material, studied by magnetic, DSC and X-ray diffraction measurements. Our DFT calculations and our model, based on the Landau theory of phase transitions, explain how the cooperative thermal switching of the molecular spin state drives a ferroelastic symmetry breaking at high temperature, through a coupled Jahn–Teller distortion. Ferroelastic materials have rich properties, with important applications in memory, multifunctional and novel controllable devices. The electronic bistability in soft functional materials represents an important source of entropy gain, capable of overcoming the cost of symmetry-breaking entropy, which opens up new perspectives for stabilizing high-temperature and low-symmetry ferroic functions of advanced materials.
New conceptsIn this manuscript, we present the concept of generating symmetry-breaking based functions of materials at high temperature, which is made possible by coupled electronic instability. Symmetry breaking is responsible for the emergence of functions associated with different types of ferroic orders, enabling applications in sensors, memory devices, transducers or actuators. However, symmetry breaking usually occurs during cooling, as phases with low symmetry are often those with low entropy. This fact severely limits the practical applications of many materials at room temperature. This study highlights the effectiveness of using an electronic bistability, corresponding here to spin-crossover, as a large source of entropy gain upon warming to overcome the entropy cost of a coupled symmetry breaking, corresponding here to a ferroelastic distortion. The importance of the coupling between both types of instabilities has been proven through a combination of magnetic, calorimetric and structural experiments and theoretical models. This communication thus demonstrates a proof-of-concept of ascending symmetry-breaking driven through an isosymmetric electronic instability, which opens up the way to applications for functionalized materials operating at high temperature and more particularly at room temperature. |
1. Introduction
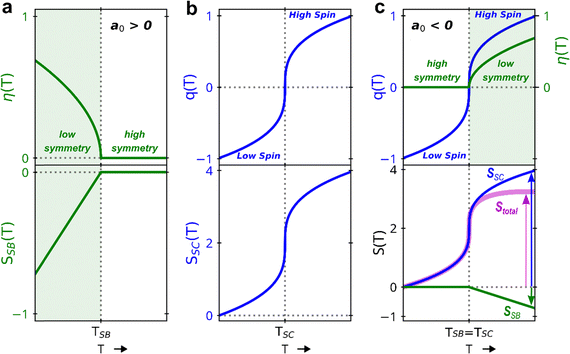
The study of solid-state phase transitions lies at the very heart of materials science.1 The associated changes in physical properties and functions, which can be driven by many external control parameters such as temperature, pressure, magnetic or electric field, and even light, give rise to various types of applications for materials. In a large class of phase transitions, materials exhibit a symmetry-breaking,2,3 where the associated ordering of structural and/or electronic degrees of freedom is responsible for the emergence of various functions related to ferromagnetism, ferroelectricity, ferroelasticity, multiferroicity, or conductivity.4–12 According to thermodynamics, in the general situation of symmetry-breaking (SB), the high temperature (HT) phase always has higher entropy and higher symmetry than the low-symmetry and low temperature (LT) phase. These types of SB processes have been rationalized in the framework of the Landau theory of phase transitions,2,3 where the LT phase results from the loss of some symmetry operators of the HT phase.The degree of SB below a critical temperature TSB is characterized by the order parameter η. In the simplest case, when η is scalar and continuous symmetry breaking occurs, the SB Gibbs energy is expanded in a series of even powers of η:
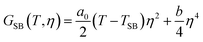 | (1) |
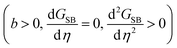 are balanced by the η2 coefficient. For a0 > 0, the high-symmetry phase (η = 0) is stable above TSB. Below TSB, the low-symmetry phase is characterized by two symmetry-equivalent solutions
are balanced by the η2 coefficient. For a0 > 0, the high-symmetry phase (η = 0) is stable above TSB. Below TSB, the low-symmetry phase is characterized by two symmetry-equivalent solutions 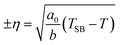 , with
, with 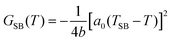 and the SB entropy
and the SB entropy 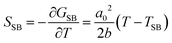 . Fig. 1a illustrates this usual descending symmetry-breaking, stabilizing the low-symmetry phase below TSB, as rationalized through the η(T) and SSB(T) curves. In this way, the symmetry of a material and its entropy commonly increase upon warming, as η decreases and the high-symmetry phase is the high entropy one.
. Fig. 1a illustrates this usual descending symmetry-breaking, stabilizing the low-symmetry phase below TSB, as rationalized through the η(T) and SSB(T) curves. In this way, the symmetry of a material and its entropy commonly increase upon warming, as η decreases and the high-symmetry phase is the high entropy one.
Recently, a counter idea emerged:13,14 can the symmetry of a material decrease with increasing temperature? This situation corresponds to a0 < 0 (Fig. 1c), which means that the SB entropy decreases above TSB. Another source of entropy gain is then required to comply with thermodynamics. Thus, few systems exhibit such unusual and counter-intuitive ascending symmetry-breakings. A famous example is 3He, which exhibits a liquid-to-solid phase transition upon warming.15 It is due to the larger entropy in the solid state, originating from disordered nuclear spins, compared to the quantum Fermi nature of the liquid state. Other ascending symmetry-breakings have attracted sustained interest in superconducting,16 ferroelectrics17 or magnetic18 materials. These are often associated with re-entrant phase transitions, where the low-symmetry phase is intermediate between two high-symmetry LT and HT phases and forms over a narrow temperature range due to competing interactions or frustrations.16,18–20 However, the origin of the increasing entropy, required to stabilize the low-symmetry phase at high temperature, is often difficult to identify. Here, we report on an ascending ferroelastic symmetry-breaking in a molecular spin crossover (SC) material, which cannot be understood by considering only the associated change of symmetry. Our study sheds a new light on the entropy stabilization process.
SC materials21–24 exhibit more or less cooperative thermal conversions of their molecular electronic state from low-spin (LS) to high-spin (HS). This is monitored at the macroscopic scale through the totally symmetric SC parameter 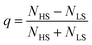 , where NLS and NHS refer to the number of molecules in each state. The spin crossover phenomenon is isosymmetric, i.e. it occurs without change of symmetry, like gas–liquid transitions. SC occurring around TSC is described in the simplest way25,26 through the spin crossover Gibbs energy:
, where NLS and NHS refer to the number of molecules in each state. The spin crossover phenomenon is isosymmetric, i.e. it occurs without change of symmetry, like gas–liquid transitions. SC occurring around TSC is described in the simplest way25,26 through the spin crossover Gibbs energy:
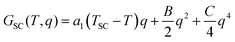 | (2) |
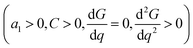 give obvious analytical solutions:
give obvious analytical solutions:The q(T) plot in Fig. 1b shows the SC phenomenon around TSC, which is also an entropy-driven process.21,22 Indeed, the SC entropy increases from LS to HS states, with
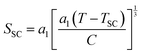 .
.
In several SC materials, spin crossover and symmetry-breaking phenomena compete.25–27 In these SC materials, the coupling of the isosymmetric SC electronic bistability to the SB allows for controlling symmetry-related functions, such as conductivity, magnetic order, multiferroicity or giant magnetoelectric response, through spin state conversion upon thermal, optical or magnetic stimuli.27–33
In particular, ferroelastic materials have rich properties, with important applications in memory, multifunctional and novel controllable devices.4,8–10 However, the ferroelastic phases usually form at low temperature, which limits further applications. Here we present and discuss the unusual emergence of an ascending symmetry-breaking in the high temperature phase of the SC material [FeII(PM-PEA)2(NCS)2]. It exhibits a low-spin high-symmetry phase (LShs) at low temperature and a ferroelastic high-spin low-symmetry phase (HSls), stable above 235 K. Our crystallographic and magnetic measurements highlight the coupling between SC and SB phenomena. DFT calculations reveal a Jahn–Teller instability in the high-spin state, breaking molecular symmetry. Our Landau model, describing the effect of the coupling between the two clearly identified SC and SB instabilities, rationalizes the emergence of a low-symmetry high temperature phase. Fig. 1c schematically shows the concept, where the entropy cost due to symmetry-breaking at high temperature is largely compensated by the entropy gain due to spin crossover.
2. Materials and methods
2.1. Synthetic procedures
Our measurements were performed on black needle-shaped single crystals, obtained in methanol after a few days by slow diffusion of the iron solution through a methanol layer into the ligand solution, in a straight tube under an inert atmosphere. More details can be found in previous work.342.2. Magnetic measurements
We collected data at 5 K min−1 from one single crystal glued with cryogenic GE7031 varnish to a 3 mm wide 15 cm long 0.725 mm thick strip cut out of a 200 mm high purity CZ type Si wafer whose diamagnetic contribution has been previously recorded.2.3. X-ray diffraction
X-ray diffraction measurements of the [FeII(PM-PEA)2(NCS)2] molecular material were performed as a function of temperature on a single crystal from 80 to 300 K and powder from 300 to 520 K. Complete experimental details can be found in the Sections S1–S4 in the ESI.†2.4. DSC measurements
Differential scanning calorimetry measurements were performed in the 115–295 K temperature range under argon on a PerkinElmer calorimeter DSC8000 coupled with a CLN2 regulator setting a scan rate of 5 K min−1 on 8.034 mg of crystals (Section S7 in the ESI†).2.5. Computational details
DFT geometry optimizations were carried out by using the Gaussian 16 (revision A.03) package35 with the PBE0 hybrid functional36,37 and tightening both self-consistent field (10−10 a.u.) and geometry optimization (10−5 a.u.) convergence thresholds (Section S5 in the ESI†).3. Results and discussion
3.1. Spin crossover
The [FeII(PM-PEA)2(NCS)2] compound exhibits a spin-transition with a thermal hysteresis loop.34Fig. 2a shows the temperature dependence of its χMT product, where χM is the molar magnetic susceptibility and T is the temperature. χMT directly relates to the SC parameter q (right axis), through the weighted contribution of the number NHS of paramagnetic HS sites (χHSM with S = 2) and NLS of diamagnetic LS sites (χLSM with S = 0). In the HT phase, χHSMT ≃ 3.5 cm3 K mol−1, which corresponds to a fully HS state (q = 1). As temperature is lowered, q drops around T↓ ≃ 219 K in the LT diamagnetic phase and gradually reaches a fully LS macroscopic state below 150 K. The characteristic χMT value close to 0 corresponds to q = −1. In contrast to polycrystalline powder samples,34,38 single-crystals exhibit a 16 K wide thermal hysteresis, with a clear single-step conversion upon cooling and two different conversion regimes upon heating: the gradual one from 150 K to T↑ ≃ 235 K, followed by a discontinuous jump towards the HS state. It was shown recently that contrary to isosymmetric SC, with symmetric conversion curves around TSC (Fig. 1b), such unsymmetric hysteresis loops are characteristic of the coupling between symmetry-breaking and spin crossover.25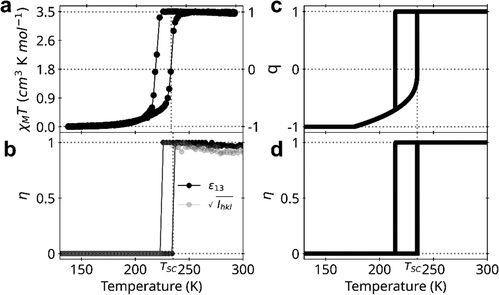 | ||
Fig. 2 Coupled spin transition and ferroelastic distortion. (a) Thermal dependence of the spin transition order parameter q(T), monitored through 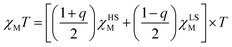 . (b) Thermal dependence of the symmetry-breaking parameter η(T) measured through the ferroelastic distortion |ε13| and the intensity of symmetry-breaking Bragg peaks . (b) Thermal dependence of the symmetry-breaking parameter η(T) measured through the ferroelastic distortion |ε13| and the intensity of symmetry-breaking Bragg peaks 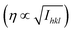 , both normalized to unity for clarity. All measurements are performed on a single crystal. (c) and (d) Corresponding thermal dependence of SB and SC parameters obtained from our Landau model based on eqn (4). , both normalized to unity for clarity. All measurements are performed on a single crystal. (c) and (d) Corresponding thermal dependence of SB and SC parameters obtained from our Landau model based on eqn (4). | ||
3.2. Ferroelastic symmetry-breaking at high temperature
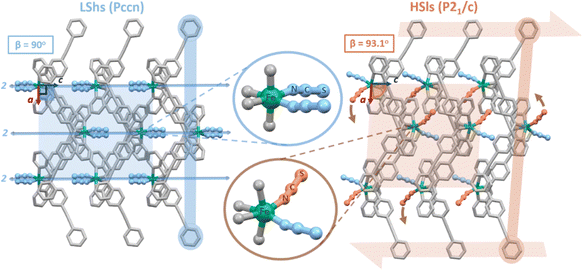
From previous reports on [FeII(PM-PEA)2(NCS)2],34 it was unclear whether the change between orthorhombic LS and monoclinic HS space groups corresponded to a reconstructive process39 or to a group–subgroup symmetry-breaking.3 However, this is a key point for its analysis in the framework of Landau theory, which only accounts for the latter case.2 To learn more about the structural reorganization, we collected X-ray diffraction data on a single crystal upon cooling and heating, to monitor the changes in lattice parameters and Bragg peak intensities (Section S3, ESI†). The ferroelastic phase transition, characterized by the deviation of the lattice β angle from 90° to 93.1°, corresponds to a symmetry-breaking with a group–sub-group relationship between the Pccn space group of the parent-paraelastic LShs and the P21/c space group of the daughter-ferroelastic HSls phase (Fig. 3).40–42 This long-range ferroelastic distortion is monitored through the amplitude of the symmetry-breaking spontaneous strain:4,40,42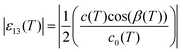 . In principle, a continuous Pccn ↔ P21/c phase transition line can exist. However, Fig. 2 shows that |ε13(T)| ∝ η(T), referred to as the symmetry-breaking order parameter hereafter, changes discontinuously at T↓ ≃ 221 K and T↑ ≃ 235 K (Fig. 2b). η(T) = 0 in the LShs phase and η(T) is almost constant in the HSls phase from 221 to 300 K. The analysis of powder diffraction patterns indicates that the daughter and high temperature ferroelastic HSls phase, characterized by the splitting of (hkl) and (
. In principle, a continuous Pccn ↔ P21/c phase transition line can exist. However, Fig. 2 shows that |ε13(T)| ∝ η(T), referred to as the symmetry-breaking order parameter hereafter, changes discontinuously at T↓ ≃ 221 K and T↑ ≃ 235 K (Fig. 2b). η(T) = 0 in the LShs phase and η(T) is almost constant in the HSls phase from 221 to 300 K. The analysis of powder diffraction patterns indicates that the daughter and high temperature ferroelastic HSls phase, characterized by the splitting of (hkl) and (![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) kl) Bragg peaks, remains stable up to ≃500 K, beyond which the sample melts (Fig. S5, ESI†). This ascending SB from LT to HT phases is also characterized by the change of Bragg peak extinction rules (Section S4, ESI†). The intensities Ihkl of the (0kl) Bragg peaks with l = 2n + 1 and (hk0) Bragg peaks with h + k = 2n + 1 are zero in the Pccn LShs phase and non-zero in the P21/c HSls phase. Fig. 2b shows the thermal dependence of
kl) Bragg peaks, remains stable up to ≃500 K, beyond which the sample melts (Fig. S5, ESI†). This ascending SB from LT to HT phases is also characterized by the change of Bragg peak extinction rules (Section S4, ESI†). The intensities Ihkl of the (0kl) Bragg peaks with l = 2n + 1 and (hk0) Bragg peaks with h + k = 2n + 1 are zero in the Pccn LShs phase and non-zero in the P21/c HSls phase. Fig. 2b shows the thermal dependence of 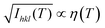 for these symmetry-breaking Bragg peaks, confirming the discontinuous symmetry change between the LT LShs and the HT HSls phases. The lattice parameters (Fig. S3, ESI†) also exhibit discontinuous changes upon heating and cooling during the phase transition, resulting in a large volume strain vs ≃ 0.05 in the HSls phase. These data evidence the concomitant evolutions of the spin transition parameter q through the volume strain vs, the lattice parameters, the intensity of symmetry-breaking Bragg peaks, and the ferroelastic distortion ε13 from the Pccn LS LT phase to the P21/c HS HT phase. These results characterize the coupling between SC and SB phenomena, which exhibit the same thermal hysteresis between LShs and HSls phases. This coupling between both phenomena is known to be driven by long-range elastic interactions.25 The slight broadening of thermal hysteresis in magnetic data (measured at 5 K min−1) compared to quasi-static XRD data is known to be due to kinetic effects.
for these symmetry-breaking Bragg peaks, confirming the discontinuous symmetry change between the LT LShs and the HT HSls phases. The lattice parameters (Fig. S3, ESI†) also exhibit discontinuous changes upon heating and cooling during the phase transition, resulting in a large volume strain vs ≃ 0.05 in the HSls phase. These data evidence the concomitant evolutions of the spin transition parameter q through the volume strain vs, the lattice parameters, the intensity of symmetry-breaking Bragg peaks, and the ferroelastic distortion ε13 from the Pccn LS LT phase to the P21/c HS HT phase. These results characterize the coupling between SC and SB phenomena, which exhibit the same thermal hysteresis between LShs and HSls phases. This coupling between both phenomena is known to be driven by long-range elastic interactions.25 The slight broadening of thermal hysteresis in magnetic data (measured at 5 K min−1) compared to quasi-static XRD data is known to be due to kinetic effects.
Fig. 3 shows the crystalline structure of [FeII(PM-PEA)2(NCS)2] along the b axis of the lattice in the fully LS (90 K) and HS (300 K) states. The crystal packing exhibits a ferroelastic distortion, corresponding to a shear of the molecular layers in the HSls phase. The resulting deviation of the lattice angle β from 90° to 93.1° is related to the loss of the C2 symmetry. In the Pccn LShs space group, the molecules are located on Wyckoff positions with C2 symmetry along the c molecular axis, while in the P21/c HSls phase, the C2 symmetry is lost, with distorted molecules in general positions. This is characterized by an important torsion of the thiocyanate groups and a moderate rearrangement of the PM-PEA ligands in the HSls state, initially equivalent in the LShs state. The intra-molecular structural parameters,43 such as the 〈Fe–N〉 bond lengths and N–Fe–N torsion angles, are characteristic of LS and HS states (Section S2, ESI†). Fig. S6 (ESI†) shows that the monoclinic HSls state can also be quenched by flash cooling at 30 K, while the evolution of vs and ε13 indicates that the relaxation towards the orthorhombic LShs ground phase occurs around 65 K upon heating. These results underline the strong coupling between the molecular spin state (q) and the crystalline and molecular symmetries (η).
Then comes the chicken-egg question: is the spin crossover responsible for symmetry-breaking, or vice versa?
3.3. DFT analysis of the Jahn–Teller distortion in the high spin state
For understanding the coupled molecular changes of spin state and symmetry, we performed DFT calculations on the isolated molecule (Section S5, ESI†). In the LS state, we optimized the molecular structure with C2 point symmetry of the Wyckoff position of the molecular sites in the LShs lattice.The results provide positive frequencies for all the 231 intramolecular vibrational modes with A or B symmetry. This indicates that the molecular structure in the LShs state is stable with respect to the C2 symmetry, with symmetry-equivalent thiocyanate groups and PM-PEA ligands (Fig. 4). The energy diagram of the molecular orbitals in the LShs and HShs states with C2 symmetry shows the degeneracy of some orbitals with symmetric thiocyanate groups. In contrast, the structure of the HShs state with C2 symmetry is unstable, as characterized by the negative frequency of one torsion mode QT (B symmetry, Fig. S9 and Video S1, ESI†).
 | ||
| Fig. 4 Comprehensive summary of DFT calculations. (a) Optimized molecular structure for C2 LShs, C2 HShs and C1 HSls states. The loss of the 2-fold molecular axis in the HSls state with the molecular torsion results in asymmetric orbitals, especially around the NCS groups. (b) Zoomed in image of the FeN4(NCS)2 core, with energy diagram of t2g-like and eg-like orbitals showing the splitting of orbital degeneracy from C2 (LShs and HShs) to C1 (HSls), where only α spins are shown for clarity. The C2 HShs state is unstable along one torsion mode QT (B symmetry), which has a negative frequency. The main atomic motions for QT (see ESI,† Video S1) are schematically represented by arrows for the atoms surrounding the Fe. This Jahn–Teller distortion breaks C2 symmetry and brings the molecule towards the stable HSls state with C1 symmetry. | ||
The molecular torsion along QT stabilises the HS state, as schematically shown in Fig. 4, which lowers molecular symmetry towards C1. The optimized molecular structure in the HSls state with C1 symmetry is stable (all modes have positive frequencies), and the structural distortion of the thiocyanate groups correlates with their asymmetric spin density in the HSls state. The overall molecular distortion in the HSls state provided by DFT calculations is in good agreement with crystallographic data. These calculations reveal the microscopic origin of the symmetry-breaking, due to the Jahn–Teller distortion along QT in the HSls state, characterized by an asymmetric bending of the Fe2+–(NCS−)2 dipoles as the 2-fold molecular axis is lost.
Our DFT results underline again the strong coupling between the spin state and symmetry, as the Jahn–Teller distortion stabilizes the high-spin state.
3.4. Coupled symmetry-breaking and spin crossover
Describing the LShs to HSls phase transition requires considering the contributions of both the SB (eqn (1)) and SC (eqn (2)) phenomena to the Landau thermodynamical potential as well as their coupling terms. This approach was used for other materials25,44 to describe their phase diagrams and explain why SC and SB phenomena can occur sequentially or simultaneously. Hereafter we use the symmetry-relevant potential: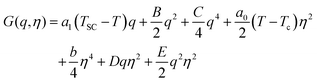 | (3) |
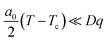 . Then the potential reduces to:
. Then the potential reduces to: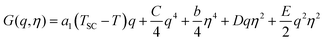 | (4) |
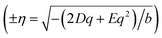 , correspond to the two possible ferroelastic domains in the HSls phase upon the Pccn → P21/c symmetry breaking.40–42Fig. 5 shows how the equilibrium (q, η) values change with temperature, considering the spin transition parameter as explicitly restricted to −1 ≤ q ≤ 1. Fig. 2c and d show the q(T) and η(T) curves calculated from eqn (4). These are in very good agreement with the experimental data, as they reproduce the main experimental features of the phase transition. (i) On heating from the fully LShs state (q = −1, η = 0) a SC starts as q gradually increases (Fig. 2a and c). (ii) Above the critical temperature T↑, the LShs phase is no more stable and a discontinuous transition occurs towards the HSls phase, where q > 0 is stabilized by the SB (η ≠ 0). (iii) The couplings maximize q to 1, which corresponds to the fully HS state. The amplitude of the SB parameter is then constant (
, correspond to the two possible ferroelastic domains in the HSls phase upon the Pccn → P21/c symmetry breaking.40–42Fig. 5 shows how the equilibrium (q, η) values change with temperature, considering the spin transition parameter as explicitly restricted to −1 ≤ q ≤ 1. Fig. 2c and d show the q(T) and η(T) curves calculated from eqn (4). These are in very good agreement with the experimental data, as they reproduce the main experimental features of the phase transition. (i) On heating from the fully LShs state (q = −1, η = 0) a SC starts as q gradually increases (Fig. 2a and c). (ii) Above the critical temperature T↑, the LShs phase is no more stable and a discontinuous transition occurs towards the HSls phase, where q > 0 is stabilized by the SB (η ≠ 0). (iii) The couplings maximize q to 1, which corresponds to the fully HS state. The amplitude of the SB parameter is then constant (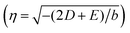 ) in the HSls phase (Fig. 2b and d). (vi) The coupling terms generate an energy barrier in the potential, which stabilizes the HSls (GHL, Fig. 5) and precludes gradual conversion towards LS on cooling. The HSls state is then stable down to T↓, where the LShs phase is reached. The potential in eqn (4) differs therefore in the low-symmetry (η ≠ 0) and high-symmetry (η = 0) phases and the coupling opens a thermal hysteresis for both q and η.
) in the HSls phase (Fig. 2b and d). (vi) The coupling terms generate an energy barrier in the potential, which stabilizes the HSls (GHL, Fig. 5) and precludes gradual conversion towards LS on cooling. The HSls state is then stable down to T↓, where the LShs phase is reached. The potential in eqn (4) differs therefore in the low-symmetry (η ≠ 0) and high-symmetry (η = 0) phases and the coupling opens a thermal hysteresis for both q and η.
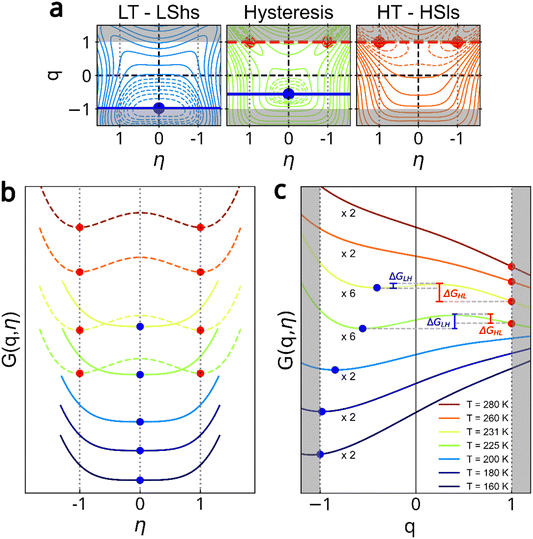 | ||
Fig. 5 Coupled spin crossover and symmetry-breaking. (a) Thermal dependence of the Gibbs energy G(q, η) in the LT LShs phase (q = −1, η = 0 left), HT HSls phase (q = −1, η ≠ 0 right) and inside hysteresis (middle) q is restricted to −1 ≤ q ≤ 1 (clear areas). (b) Cut of G(q, η) along the SB order parameter (η) and SC order parameter (q) axes. q saturates to −1 at LT and gradually increases on approaching T↑, where it discontinuously jumps and saturates to 1 at HT. In the LShs phase η = 0, while in the HSls phase 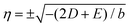 , with |η| normalized to 1 for clarity. The coupling stabilizes q = 1 on cooling down to T↓ as an energy barrier appears from LS to HS (GLH) and HS to LS (GHL) inside thermal hysteresis (curves are rescaled by 2 or 6 for a better visualization). The results are obtained from eqn (4) with a1 = 0.6, C = 35, b = 10, TSC = 235 K, D = −6.5, and E = −12.2. , with |η| normalized to 1 for clarity. The coupling stabilizes q = 1 on cooling down to T↓ as an energy barrier appears from LS to HS (GLH) and HS to LS (GHL) inside thermal hysteresis (curves are rescaled by 2 or 6 for a better visualization). The results are obtained from eqn (4) with a1 = 0.6, C = 35, b = 10, TSC = 235 K, D = −6.5, and E = −12.2. | ||
This cooperative and hysteretic phase transition is mediated by the elastic interactions within the lattice. The emergence of a ferroelastic ordering in the high temperature phase of a SC material, from 235 K to 500 K beyond which the material melts, offers new perspectives for ascending symmetry-breaking. Heat capacity measurements (Section S7 in ESI†) reveal large entropy changes between the HSls and LShs phases upon heating (ΔS = 62.8 J mol−1 K−1) and cooling (ΔS = 67.6 J mol−1 K−1). These values are within the usual 40–80 J mol−1 K−1 range for SC materials.21 The entropy increase from LShs to HSls phases includes contributions from both SB and SC phenomena, which can be estimated based on theoretical calculations:
| ΔStheo = ΔSSB + ΔSSC. |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(1) − R
ln(1) − R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(2) = −5.76 J K−1 mol−1. On the other hand, the SC phenomenon is a large source of entropy gain, responsible for the giant barocaloric effect,21,47 with two main contributions: ΔSSC =ΔSspin + ΔSvib. ΔSspin is due to different spin multiplicities (Ω = 2S + 1) in HS (S = 2) and LS (S = 0) states: ΔSspin = R(ln(5) − ln(1)) = 13.42 J K−1 mol−1. The vibrational entropy difference ΔSvib is mainly due to the lower frequencies of the FeN6 core vibrations in the less bonding HS state compared to LS.21,22
ln(2) = −5.76 J K−1 mol−1. On the other hand, the SC phenomenon is a large source of entropy gain, responsible for the giant barocaloric effect,21,47 with two main contributions: ΔSSC =ΔSspin + ΔSvib. ΔSspin is due to different spin multiplicities (Ω = 2S + 1) in HS (S = 2) and LS (S = 0) states: ΔSspin = R(ln(5) − ln(1)) = 13.42 J K−1 mol−1. The vibrational entropy difference ΔSvib is mainly due to the lower frequencies of the FeN6 core vibrations in the less bonding HS state compared to LS.21,22
We estimated ΔSvib for [FeII(PM-PEA)2(NCS)2] based on our DFT calculations of the frequencies of the vibrational modes in both spin states (Section S5, ESI†), which gives ΔSvib = 58.9 J K−1 mol−1. In this way, we calculate the theoretical entropy increase from LShs to HSls phases, which is clearly dominated by the vibrational entropy: ΔStheo = ΔSSB + ΔSspin + ΔSvib = 66.5 J K−1 mol−1.
This calculated value is in nice agreement with our experimental value ΔS = 62.8 − 67.6 J mol−1 K−1 obtained from calorimetric measurements (Fig. S12, ESI†). Thus, the molecular scale plays a central role in such materials, both for entropy stabilization, through numerous intra-molecular degrees of freedom, and for the Jahn–Teller distortion associated with the ferroelastic symmetry breaking.
Fig. 1c represents schematically this concept of ascending symmetry-breaking, where the SB entropy cost (ΔSSB) can be largely compensated by the isosymmetric entropy gain (ΔSSC) due to electronic bistability. However, a rigorous description of the concerted SC and SB phenomena requires considering the important role of their coupling, as explicitly discussed through our Landau model (Fig. 2 and 5). This coupling, which strongly stabilizes the HSls state, also plays a key role for the stabilization of HSls states trapped by flash cooling (Fig. S6, ESI†) or photoinduced.48 Overall, the LShs → HSls ascending symmetry-breaking reported here corresponds to an entropy-driven process, where the thermal SC starting upon warming drives the cooperative ferroelastic distortion above a critical conversion. This ascending symmetry breaking is the consequence of the collective distortions of the molecules in the lattice, due to cooperative elastic interactions. We can notice that a hypothetical parent para-elastic phase of high spin and high-symmetry (Pccn) could form around 800 K, as suggested by experimental data (see Fig. S5, ESI†), and our Landau model when the strong coupling limit vanishes (Fig. S11, ESI†). However, this HShs phase is not observed as the sample melts around 500 K.
4. Conclusions
Ascending symmetry-breaking is also observed in some spin crossover materials, as re-entrant phase transitions occur during stepwise spin transitions. In this case, a long-range HS–LS order appears on the step, due to competing elastic interactions. The intermediate half-conversion phase (q = 0), in between the high-symmetry LS and HS phases, exhibits symmetry-breaking (η ≠ 0). It is stabilized by a bi-quadratic q2η2 coupling, but it forms only over a narrow temperature range26,27,32,44,49 Instead, our study rationalizes how a symmetry-broken phase can be stabilized, through a coupled isosymmetric electronic bistability, over a broader and higher temperature range, here from 235 K and well above room temperature. Compared with hard-condensed matter, soft SC molecular materials exhibiting electronic bistability hold a large source of vibrational entropy gain. This substantial advantage opens up fascinating prospects for stabilizing robust low-symmetry phases in materials, enabling so the development of future generations of room-temperature ferroic devices, such as switches, force sensors and non-volatile memories.4,50,51Regarding the ferroelastic domains forming after thermal cycling, it is well-established now that domain walls form 2D functional objects in their own right, which can be engineered to give rise to an electric polarization in an otherwise centrosymmetric system or to pyroelectric and electrocaloric effects in ferroelectric.10,32,52 Regarding bulk properties, it was shown that an electric field can be used to substitute non-polar ferroelastic phases53 exhibiting an antiferroelectric array of dipoles (such as the Fe2+–(NCS−)2 bonds in Fig. 3), by a polar phase. The interesting thing about the single domain nature of the ferroelastic crystals [FeII(PM-PEA)2(NCS)2], synthesized at room temperature, is that they can give rise to a single polar domain under the effect of an electric field.
The description of symmetry-breaking in the framework of the Landau theory of phase transitions is universal. Our model, considering a coupled electronic bistability successfully reproduced phase diagrams and the occurrence of simultaneous or sequential electronic bistability and SB phenomena in a broad variety of systems.25,44 The present concept of ascending symmetry-breaking, where molecular positions get frozen during heating, coupled to an electronic instability can also apply to ascending ferroelectricity or ferromagnetism, provided that the associated electrical or magnetic orders couple with an isosymmetric electronic bistability, acting as a source of significant entropy gain. These different types of ferroic orders result from different types of intermolecular interactions, which can be controlled through crystal engineering. This concept opens up the way to a rational design and applications for materials functionalized by their low symmetry and operating at high temperature.
Author contributions
F. J. V. M.: methodology, data curation, formal analysis, and writing – original draft; R. G. T. R.: conceptualization and data curation; E. T.: supervision, methodology, data curation, and formal analysis; T. B.: data curation; H. C.: conceptualization and review; N. D.: sample synthesis; D. D.: data curation; P. G.: data curation; G. C.: data curation; B. L. G.: DFT calculations; and E. C.: funding acquisition, data curation, investigation, conceptualization, supervision, and writing – original draft. All authors critically reviewed and revised the manuscript draft and approved the final version for submission.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported in part by Agence Nationale de la Recherche for financial support under the grant ANR-19-CE30-0004 ELECTROPHONE, ANR-19-CE07-0027 SMAC. E. C. thanks the University Rennes and the Fondation Rennes 1 for funding. F. J. V.-M. acknowledges the support of the European Social Fund (ESF) and Generalitat Valenciana for his postdoctoral fellowship (APOSTD/2021/359) and Région Bretagne (BIENVENÜE). This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 899546. The authors thank Région Bretagne, Ille-Et-Vilaine Department, French Ministry of Research, Rennes Métropole, CNRS, European Union for financial support (CPER Project Mat&Trans 2021–2027). The French GENCI/IDRIS-CINES centers for high-performance computing resources are also acknowledged.References
-
B. Fultz, Phase Transitions in Materials, Cambridge University Press, Cambridge, 2nd edn, 2020 Search PubMed
.
- L. Landau, Ukr. J. Phys., 2008, 53, 25–35 CAS
.
-
J. C. Tolédano and P. Tolédano, The Landau Theory of Phase Transitions, 1987 Search PubMed
.
- E. K. H. Salje, Annu. Rev. Mater. Res., 2012, 42, 265–283 CrossRef CAS
.
- G. Rogez, N. Viart and M. Drillon, Angew. Chem., Int. Ed., 2010, 49, 1921–1923 CrossRef CAS PubMed
.
- T. Ishikawa, S. A. Hayes, S. Keskin, G. Corthey, M. Hada, K. Pichugin, A. Marx, J. Hirscht, K. Shionuma, K. Onda, Y. Okimoto, S. Y. Koshihara, T. Yamamoto, H. Cui, M. Nomura, Y. Oshima, M. A. Jawad, R. Kato and R. J. D. Miller, Science, 2015, 350, 1501–1505 CrossRef CAS PubMed
.
- S. Ohkoshi, K. Nakagawa, M. Yoshikiyo, A. Namai, K. Imoto, Y. Nagane, F. Jia, O. Stefanczyk, H. Tokoro, J. Wang, T. Sugahara, K. Chiba, K. Motodohi, K. Isogai, K. Nishioka, T. Momiki and R. Hatano, Nat. Commun., 2023, 14, 8466 CrossRef CAS PubMed
.
- B. Zhang, S. Sun, Y. Jia, J. Dai, D. T. N. Rathnayake, X. Huang, J. Casasent, G. Adhikari, T. A. Billy, Y. Lu, X. C. Zeng and Y. Guo, Adv. Mater., 2023, 35, 2208336 CrossRef CAS PubMed
.
- X. Xu, F.-T. Huang, K. Du and S.-W. Cheong, Adv. Mater., 2022, 34, 2206022 CrossRef CAS PubMed
.
- S. Pandya, G. A. Velarde, R. Gao, A. S. Everhardt, J. D. Wilbur, R. Xu, J. T. Maher, J. C. Agar, C. Dames and L. W. Martin, Adv. Mater., 2019, 31, 1803312 CrossRef PubMed
.
- D. Yang, L. Luo, Y. Gao, S. Chen and X. C. Zeng, Mater. Horiz., 2019, 6, 1463–1473 RSC
.
- J. Cattermull, M. Pasta and A. L. Goodwin, Mater. Horiz., 2021, 8, 3178–3186 RSC
.
- D. Gonzalez-Cuadra, A. Bermudez, P. R. Grzybowski, M. Lewenstein and A. Dauphin, Nat. Commun., 2019, 10, 2694 CrossRef PubMed
.
- S. Wu, M. L. Klemm, J. Shah, E. T. Ritz, C. Duan, X. Teng, B. Gao, F. Ye, M. Matsuda, F. Li, X. Xu, M. Yi, T. Birol, P. Dai and G. Blumberg, Phys. Rev. X, 2024, 14, 011043 CAS
.
- D. M. Lee, Rev. Mod. Phys., 1997, 69, 645–666 CrossRef CAS
.
- P. Schlottmann, J. Low Temp. Phys., 1975, 20, 123–154 CrossRef CAS
.
- S. S. Sharaya, B. A. Zakharov and E. V. Boldyreva, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2024, 80, 94–104 CrossRef CAS PubMed
.
- H. Kitatani, S. Miyashita and M. Suzuki, J. Phys. Soc. Jpn., 1986, 55, 865–876 CrossRef
.
- A. C. Anderson, W. Reese and J. C. Wheatley, Phys. Rev., 1963, 130, 1644–1653 CrossRef CAS
.
- P. S. Pershan and J. Prost, J. Phys., Lett., 1979, 40, 27–30 CrossRef
.
- W. Nicolazzi and A. Bousseksou, Cron. Chim., 2018, 21, 1060–1074 CrossRef CAS
.
-
M. A. Halcrow, Spin-crossover materials: properties and applications, John Wiley & Sons, Ltd, Chichester, 2013 Search PubMed
.
- J.-F. Dayen, N. Konstantinov, M. Palluel, N. Daro, B. Kundys, M. Soliman, G. Chastanet and B. Doudin, Mater. Horiz., 2021, 8, 2310–2315 RSC
.
- M. Piedrahita-Bello, J. E. Angulo-Cervera, A. Enriquez-Cabrera, G. Molnár, B. Tondu, L. Salmon and A. Bousseksou, Mater. Horiz., 2021, 8, 3055–3062 Search PubMed
.
- E. Collet, G. Azzolina, J. Jeftić and M.-H. Lemée-Cailleau, Adv. Phys.: X, 2023, 8, 2161936 Search PubMed
.
- D. Chernyshov, H.-B. Bürgi, M. Hostettler and K. W. Törnroos, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 094116 CrossRef
.
- M. Shatruk, H. Phan, B. A. Chrisostomo and A. Suleimenova, Coord. Chem. Rev., 2015, 289–290, 62–73 Search PubMed
.
- N. Ortega-Villar, C. M. Muñoz and A. J. Real, Magnetochemistry, 2016, 2, 16 CrossRef
.
- S. Ohkoshi, K. Imoto, Y. Tsunobuchi, S. Takano and H. Tokoro, Nat. Chem., 2011, 3, 564–569 CrossRef CAS PubMed
.
- E. Pardo, C. Train, H. Liu, L.-M. Chamoreau, B. Dkhil, K. Boubekeur, F. Lloret, K. Nakatani, H. Tokoro, S. Ohkoshi and M. Verdaguer, Angew. Chem., 2012, 124, 8481–8485 CrossRef
.
- M. Hervé, G. Privault, E. Trzop, S. Akagi, Y. Watier, S. Zerdane, I. Chaban, R. G. Torres Ramírez, C. Mariette, A. Volte, M. Cammarata, M. Levantino, H. Tokoro, S. Ohkoshi and E. Collet, Nat. Commun., 2024, 15, 267 CrossRef PubMed
.
- V. B. Jakobsen, E. Trzop, E. Dobbelaar, L. C. Gavin, S. Chikara, X. Ding, M. Lee, K. Esien, H. Müller-Bunz, S. Felton, E. Collet, M. A. Carpenter, V. S. Zapf and G. G. Morgan, J. Am. Chem. Soc., 2022, 144, 195–211 CrossRef CAS PubMed
.
- D. Paliwoda, L. Vendier, W. Nicolazzi, G. Molnár and A. Bousseksou, Inorg. Chem., 2022, 61, 15991–16002 CrossRef CAS PubMed
.
- J.-F. Létard, P. Guionneau, E. Codjovi, O. Lavastre, G. Bravic, D. Chasseau and O. Kahn, J. Am. Chem. Soc., 1997, 119, 10861–10862 CrossRef
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford CT, 2016 Search PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS
.
- E. Tailleur, M. Marchivie, P. Negrier, D. Denux, S. Massip, D. Mondieig, G. Chastanet and P. Guionneau, CrystEngComm, 2019, 21, 6246–6251 RSC
.
-
D. Vladimir and P. Toledano, Reconstructive Phase Transitions, In Crystals and Quasicrystals, World Scientific, 1996 Search PubMed
.
- M. A. Carpenter, E. K. H. Salje and A. Graeme-Barber, Eur. J. Mineral., 1998, 10, 621–691 CrossRef CAS
.
-
E. K. Salje, Phase Transitions in Ferroelastic and Co-elastic Crystals, Cambridge University Press, Cambridge, 1991 Search PubMed
.
- V. Janovec, V. Dvořák and J. Petzelt, Czech. J. Phys. B, 1975, 25, 1362–1396 CrossRef
.
- E. Collet and P. Guionneau, Cron. Chim., 2018, 21, 1133–1151 CrossRef CAS
.
- G. Azzolina, R. Bertoni and E. Collet, J. Appl. Phys., 2021, 129, 085106 CrossRef CAS
.
- Y. M. Gufan, Phys. Solid State, 1980, 22, 951 Search PubMed
.
- S. Iwagaki, H. Kakuta, Y. Yamamura, H. Saitoh, M. Hishida, K. Fukada and K. Saito, Crystals, 2020, 10, 361 CrossRef CAS
.
- S. P. Vallone, A. N. Tantillo, A. M. dos Santos, J. J. Molaison, R. Kulmaczewski, A. Chapoy, P. Ahmadi, M. A. Halcrow and K. G. Sandeman, Adv. Mater., 2019, 31, 1807334 CrossRef PubMed
.
- N. Brefuel, H. Watanabe, L. Toupet, J. Come, N. Matsumoto, E. Collet, K. Tanaka and J. P. Tuchagues, Angew. Chem., Int. Ed., 2009, 48, 9304–9307 CrossRef CAS PubMed
.
- H. Watanabe, K. Tanaka, N. Bréfuel, H. Cailleau, J.-F. Létard, S. Ravy, P. Fertey, M. Nishino, S. Miyashita and E. Collet, Phys. Rev. B, 2016, 93, 014419 CrossRef
.
- B. Kundys, M. Viret, D. Colson and D. O. Kundys, Nat. Mater., 2010, 9, 803–805 CrossRef CAS PubMed
.
- N. A. Spaldin and R. Ramesh, Nat. Mater., 2019, 18, 203–212 CrossRef CAS PubMed
.
- G. F. Nataf, M. Guennou, J. M. Gregg, D. Meier, J. Hlinka, E. K. H. Salje and J. Kreisel, Nat. Rev. Phys., 2020, 2, 634–648 CrossRef CAS
.
- P. Tolédano and G. Li, Phys. Rev. B, 2021, 103 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available: Intra-molecular structural reorganization, thermal dependence of lattice parameters and calculations of the volume strain and ferroelastic distortion, symmetry-breaking Bragg peaks, X-ray diffraction experimental details, DFT calculations, the Landau model of coupled symmetry-breaking and spin crossover, and differential scanning calorimetry measurements. Supplementary video 1: unstable torsion mode QT in the HShs state. CCDC 2309697 and 2309698. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4mh01318b |
| This journal is © The Royal Society of Chemistry 2025 |