Tuning of anomalous magnetotransport properties in half-Heusler topological semimetal GdPtBi

Abstract

Half-Heusler compounds from the REPtBi family exemplify Weyl semimetals in which an external magnetic field induces Weyl nodes. These materials exceptionally host topologically non-trivial states near the Fermi level and their manifestation can be clearly seen in the magnetotransport properties. In this study, we tune the Fermi level of the archetypal half-Heusler Weyl semimetal GdPtBi through high-energy electron irradiation, moving it away from the Weyl nodes to investigate the resilience of the contribution of topologically non-trivial states to magnetotransport properties. Remarkably, we observe that the negative longitudinal magnetoresistance, which is a definitive indicator of the chiral magnetic anomaly occurring in topological semimetals, persists even when the Fermi level is shifted by 100 meV from its original position in the pristine sample. Additionally, the anomalous Hall effect shows complex variations as the Fermi level is altered, attributed to the energy-dependent nature of the Berry curvature, which arises from avoided band crossing. Our findings show the robust influence of Weyl nodes on the magneto-transport properties of GdPtBi, irrespective of the Fermi level position, a behaviour likely applicable to many half-Heusler Weyl semimetals.

---

New concepts

Topological materials display unique physical properties due to their non-trivial electronic structure. Although theoretical predictions suggest that over 20% of known inorganic materials could be topologically non-trivial, only a few have been experimentally confirmed through magnetotransport studies. The detection of topologically non-trivial states by magnetotransport is challenging because they are often located far from the Fermi level. Here, we demonstrate that magnetotransport properties of archetypal topological semimetal GdPtBi can be tuned by shifting the Fermi level through high-energy electron irradiation, and more importantly, we found that these properties remain resilient to a moderate shift of the Fermi level. We discovered that (i) negative longitudinal magnetoresistance, a fingerprint of topological semimetals, remains observable even when the Fermi level is shifted by 100 meV from its initial position; (ii) the anomalous Hall effect is highly sensitive to the changes in the Fermi level position. These experimental observations were supported by theoretical calculations, providing a deeper understanding of the interplay between topologically non-trivial states and magnetotransport properties. Our work highlights the potential for tuning and exploring the exceptional properties of topological materials. Similar behaviours are likely to be observed in other topological semimetals with small Fermi surfaces, broadening the scope of their study and application.

1 Introduction

The exceptional physical properties of topological materials make them very promising from the perspective of their possible applications in quantum computing and spintronics.^1–3 According to theoretical predictions, thousands of materials from the Inorganic Crystal Structure Database⁴ have a non-trivial topology of the electronic structure.^5–7 However, there is a much smaller number of experimentally confirmed topological materials. Furthermore, there are only a few dozen materials demonstrating some features of these states in electronic transport properties. This huge difference in numbers seems to be caused by the fact that (i) topologically non-trivial states are located far below or above the Fermi level and do not contribute to electron transport; (ii) topologically non-trivial states coexist with trivial ones in the vicinity of the Fermi level and the latter dominates electron transport. Several half-Heusler phases with the REPtBi (RE-rare earth element) composition form a group of materials that overcome the above limitations and exhibit extraordinary transport properties that stem from topologically non-trivial states.⁸ One such compound is GdPtBi, an archetypal topological Weyl semimetal in which Weyl nodes are induced by a magnetic field.^9,10 Half-Heusler antiferromagnet GdPtBi (Néel temperature, T_N ≈ 9 K) has been reported to demonstrate negative longitudinal magnetoresistance (NLMR),^9,10 the planar Hall effect (PHE)¹¹ and the anomalous Hall effect (AHE),^10,12 all stemming from topologically non-trivial states. The mechanism for the formation of magnetic field induced Weyl nodes in half-Heusler compounds is still debated in the literature, and its source could be Zeeman splitting⁹ or magnetic exchange interactions.¹⁰ Alongside GdPtBi, several other rare earth-based half-Heusler materials have been reported to demonstrate features associated with a chiral magnetic anomaly,^13–17 which is the fingerprint of any topological semimetal.¹⁸ As has been reported, the magnitude of NLMR^9,15 and the AHE¹⁹ varies in the REPtBi series with the change of RE and even changes strongly from sample to sample for the same material. However, there are no systematic studies on how the magnitude of NLMR and the AHE depends on the Fermi level position with respect to topologically non-trivial states. This motivated us to perform our own investigations in order to determine whether the impact of Weyl states on the magnetotransport properties of topological semimetal GdPtBi remains robust against Fermi level shift. In their recent work, Sun et al.²⁰ explored how the AHE, MR and electronic structure depend on external pressure. They found that the AHE disappears at sufficiently high pressure, while the NLMR is almost unaffected by external pressure. Apart from the application of external pressure, the Fermi level can be tuned with other techniques like chemical doping or electrical gating. On the other side, in our recent work, we have successfully used electron irradiation to tune the Fermi level of another half-Heusler material LuPdBi, which is a mixed-parity superconductor.²¹ Moreover, this technique has also been utilized in the study of magneto-transport in magnetic topological insulators.²²

Here, we describe a thorough study of the magneto-transport properties (the Hall effect, and transverse and longitudinal MR) of pristine and electron-irradiated samples of half-Heusler Weyl semimetal GdPtBi. The experimental results are accompanied by the results of theoretical calculations of the electronic structure and the anomalous Hall effect. Our findings indicate that with the Fermi level tuned away from the Weyl nodes, NLMR becomes smaller, and the magnitude of the AHE and the magnetic field at which the AHE occurs change in a complex way, which is in accordance with the results of our theoretical calculations.

2 Results and discussion

2.1 Electrical resistivity

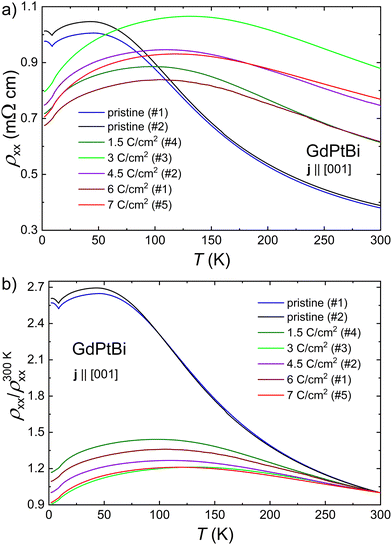
The temperature (T) dependence of the electrical resistivity (ρ) of both pristine samples is almost identical (blue and black curves in Fig. 1a) and resembles the results reported in the literature.^9,10,12 This fact, in conjunction with the observed similarities in other magnetotransport properties (see below) for pristine samples #1 and #2, allows us to assume that all pristine samples, #1 to #5, have the same electron transport properties as they were all cut from the same single crystal. At higher temperatures, ρ(T) demonstrates a semiconducting-like behaviour, which changes to metallic-like at lower T. There is also a pronounced valley in ρ(T) of pristine samples in the vicinity of T_N, and an increase in ρ at T < T_N is associated with the formation of a magnetic superzone gap.²³ Interestingly, the electron-irradiated samples do not exhibit this valley in ρ(T) and their ρ does not increase as T decreases; instead, ρ continues decreasing. A similar impact on the shape of ρ(T) close to T_N has the external pressure, as reported in ref. 20 and has been attributed to the increase in hole concentration. In addition, at higher T, electron irradiation also leads to changes in ρ(T), but these do not show a monotonic behaviour with a gradual increase in the irradiation dose, ϕ. For all irradiated samples, the maxima in ρ(T) (associated with the border between semiconducting- and metallic-like behaviour) shift to higher T (samples become more metallic). In order to eliminate measurement error in the sample size that might affect ρ values, we normalised ρ(T) dependencies to the ρ value at T = 300 K (ρ(T)/ρ(300 K)), as shown in Fig. 1b. The effect of electron irradiation on ρ(T) of GdPtBi differs significantly from that described for metallic materials, in which ρ(T) shifts upward with increasing irradiation dose.²⁴ The observed behaviour of ρ(T) for GdPtBi samples also confirmed the fact that irradiation not only provides the additional carriers, but also enhances the impurity scattering, as evidenced by the larger values of ρ of irradiated samples in the high-temperature region compared to pristine samples, which is in line with the previous report on LuPdBi.²¹

Fig. 1 Temperature dependence of the electrical resistivity (a) and normalised electrical resistivity to the value of ρ recorded at T = 300 K (b) of pristine and irradiated GdPtBi samples, measured with an electrical current (j) applied along the [001] crystallographic direction and in zero magnetic field.

2.2 Hall effect

To quantify the change in carrier concentration and mobility induced by electron irradiation, we have studied the Hall effect (see Fig. 2). Fig. 2a and b show the magnetic field (B) dependence of Hall resistivity (ρ_xy) for all samples studied at T = 10 K and 50 K, respectively. At both values of T, the magnitudes of ρ_xy are almost the same for a given sample, meaning that the concentration and mobility of carriers barely change with a variation of T. The most striking difference is that at T = 10 K the contribution of the anomalous Hall effect (AHE) is pronounced, while at T = 50 K it is absent (see the discussion below). In order to omit uncertainty in the determination of n_H and μ_H caused by the presence of the AHE, we calculated both parameters using the data recorded at T = 50 K. It should be noted that for all studied samples, hole-type carriers dominate electron transport, as previously reported in the literature. Most of the REPtBi have the same type of conductivity.^{9,10,12–14,25,26} Both pristine samples demonstrate almost identical behaviour of ρ_xy(B), indicating that their electron transport parameters are the same, and the slight difference may be due to the different orientation of the samples with respect to the applied current and/or magnetic field or to an error in the estimation of the sample thickness. Electron irradiation also leads to a decrease in ρ_xy values, similar to LuPdBi.²¹ However, in contrast to LuPdBi, ρ_xy of GdPtBi saturates at ϕ ≥ 4.5 C cm⁻². For all studied samples, ρ_xy(B) dependences are almost rectilinear, except for the B regions where the AHE was observed (see below). This implies that the electron transport is dominated by carriers of one type. Therefore, we used the single-band approximation to determine the carrier concentration (n_H), the same model has been used in several works related to GdPtBi^9,10,20 and other REPtBi,²³ which allows us to better compare our data with literature data. We calculated n_H using the formula: n_H = B/(eρ_xy). The obtained n_H(ϕ) dependence for the Hall effect data collected at T = 50 K and under B = 14 T is shown in Fig. 2c, at lower ϕ, n_H increases upon increasing the irradiation dose up to 4.5 C cm⁻², and at higher doses n_H is almost constant. This behaviour is different from that observed for LuPdBi,²¹ where n_H(ϕ) does not saturate but increases over the entire range of studied ϕ values. However, a similar kind of saturation has been reported for electron-irradiated Mn-doped BiSeTe₃ in ref. 22. The saturation can be understood as follows: the rate of electron removal from the band is equal to the defect creation rate multiplied by the number of free electrons captured by one defect. In our case, if the Fermi energy is higher than the electronic level formed on the defect, we continue to deplete the valence band and the hole concentration increases. At some point, the Fermi energy reaches the electronic state, and newly created defects will no longer capture additional electrons. The variation of hole concentration with dose will saturate at the level of Fermi energy, coinciding with the electronic defect.

Fig. 2 Magnetic field dependence of Hall electrical resistivity at T = 10 K (a) and T = 50 K (b). Carrier concentration (c) and carrier mobility (d) as a function of irradiation dose at T = 50 K.

In the case of GdPtBi, the irradiation leads to an increase of n_H by one order of magnitude from a value of 2.6 × 10¹⁸ cm⁻³ for the pristine sample to 2.2 × 10¹⁹ cm⁻³ for the sample irradiated with 4.5 C cm⁻². This increase in n_H is considerably greater than that caused by external pressure (n_H has been found to increase from 1.05 × 10¹⁸ cm⁻³ to 1.28 × 10¹⁸ cm⁻³ when a pressure of 2.1 GPa was applied).²⁰ The n_H values of pristine GdPtBi samples are of the same order of magnitude as those reported in the literature.^9,12,20 Another parameter of electronic transport that can be derived from the Hall effect data is the carrier mobility (μ_H), which was calculated using the formula μ_H = ρ_xy/(ρ_xxB). The dependence of μ_H on the irradiation dose is shown in Fig. 2d. In the pristine samples, the mobility is close to ∼2600 cm² V⁻¹ s⁻¹, and as the irradiation dose increases μ_H decreases. At ϕ ≥ 3 C cm⁻², μ_H is hardly affected by higher doses and only undergoes a slight change, reaching a value of ∼350 cm² (V⁻¹ s⁻¹) for ϕ ≥ 7 C cm⁻². This behaviour is reminiscent of that reported for LuPdBi in ref. 21, but the saturation of mobility occurs at lower irradiation doses. The decreasing behaviour of μ_H(ϕ) and the increasing behaviour of n_H(ϕ) can be understood as a synergy of two effects: (i) a shift of the Fermi level (Fermi pockets become larger, like their effective masses) and (ii) an increase in impurity scattering.

2.3 Magnetoresistance

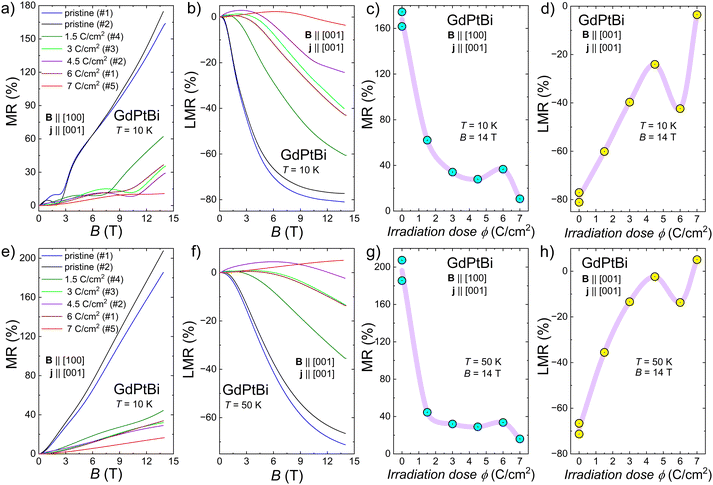
The results of electrical resistivity and Hall effect measurements confirmed that electron irradiation induces a shift in the Fermi level in GdPtBi. Therefore, in the subsequent stage of our research, we investigated the impact of this shift on the magnetotransport properties, with a particular focus on its influence on the chiral magnetic anomaly, which has been previously reported for GdPtBi.^9,10 The magnetoresistance (MR = 100 × [ρ_xx(B)/ρ_xx(B = 0) − 1]) isotherms (measured in both the transverse (j⊥B) and longitudinal (j‖B) geometries) recorded at several different Ts for pristine samples #1 and #2 are shown in the ESI† (see Fig. S1). The results obtained for both pristine samples are very similar to those reported in the literature.^9,10,20 For both samples, the traverse MR does not saturate even in the strongest magnetic field. The nonmonotonous behaviour at low B occurs in the same B range, in which the AHE was observed (see the discussion below). In turn, for both pristine samples LMR is negative up to at least T = 100 K and becomes positive at a higher T value. Negative LMR can be the fingerprint of chiral magnetic anomaly (CMA) or may originate from a parasitic current jetting effect.²⁷ According to several studies, the latter effect can be excluded in GdPtBi.^9,27 We then studied the magnetotransport properties of the irradiated samples, the results obtained at T = 10 K and 50 K are summarized in Fig. 3(a)–(d) and (e)–(h), respectively. Both temperatures are above T_N, but at T = 10 K MR is affected by the AHE, which is negligibly small at T = 50 K. At both T values, magnitudes of TMR and negative LMR for the irradiated samples are smaller than for the pristine samples. The analysis of the behaviour of TMR(B) for different ϕ, at T = 10 K is complicated by the fact that the maximum of the AHE changes its magnitude and position with changing ϕ (see below). However, in a strong magnetic field at T = 10 K, it is evident that, as ϕ increases, the TMR decreases (see Fig. 3(a) and (c)), only with the exception of sample #1 irradiated with 6 C cm⁻², its TMR deviates from the overall trend. Interestingly, this particular sample exhibits a deviation from the general trends in all the transport properties studied here and in all extracted electron transport parameters. At T = 50 K and in the entire range of magnetic fields, TMR gradually decreases with increasing ϕ, with the exception of aforementioned sample #1 irradiated with 6 C cm⁻² (see Fig. 3e and g).

Fig. 3 Transverse magnetoresistance of pristine and electron irradiated samples at T = 10 K (a) and T = 50 K (e). Longitudinal magnetoresistance of pristine and electron irradiated samples at T = 10 K (b) and T = 50 K (f). Transverse (c) and (g) and longitudinal (d) and (h) magnetoresistance as a function of the irradiation dose recorded under B = 14 T and at T = 10 K (c) and (d) and at T = 50 K (g) and (h). Violet lines in (c), (d), (g) and (h) are a guide to the eye.

It should be noted that the position of the anomaly in the transverse magnetoresistance, which in pristine samples takes place at B_p ≈ 2.5 T at T = 10 K, gradually changes in irradiated samples with increasing irradiation dose, B_p becomes larger. For sample #5, the anomaly is not fully developed as the investigated magnetic field range is too small. Assuming that the origin of this anomaly is due to changes in the electronic structure with the magnetic field⁹ (B_p corresponds to the value of the magnetic field at which Weyl states are fully developed), the changes in the anomaly with increasing irradiation dose can be understood as follows: in order to obtain fully formed Weyl states in irradiated samples a higher magnetic field is required. This finding is consistent with the observation that B_p values observed for different samples of GdPtBi vary significantly, but are correlated with the carrier concentration.^9,10,12,20

From the perspective of how the contribution of Weyl states to electron transport changes with Fermi level tuning, measurements of LMR are the most informative. We investigated LMR(B) of all pristine and irradiated samples at T = 10 K and T = 50 K (see Fig. 3b and f). In half-Heuslers materials as well as in several other topological semimetals, the total LMR is a sum of two contributions, positive and negative.^14,16,28 The positive contribution may originate from a weak antilocalization effect²⁹ and/or Fermi surface anisotropy.³⁰ The negative contribution is associated with the chiral magnetic anomaly.¹⁸ Our findings indicate that the contribution of the latter to the overall LMR of GdPtBi is more pronounced at lower temperatures. However, as the irradiation dose increases, this contribution becomes smaller. For both pristine samples under B = 14 T, LMR values are ∼−80% and ∼−70% at T = 10 K and 50 K, respectively. Upon irradiation, LMR gradually decreases (with the exception of sample #1 irradiated with 6 C cm⁻²). At T = 10 K in the entire range of ϕ, LMR is negative in the strongest magnetic fields, whereas in weak magnetic fields, LMR is positive. However, the region in which LMR is positive increases with ϕ. At T = 50 K, the situation is quite similar with the only difference being that LMR is smaller, and for the sample irradiated with 7 C cm⁻², LMR is positive throughout the entire range of B studied. It has been reported in many topological semimetals^{14,16,28,31,32} that with increasing T, CMA becomes less pronounced due to the increasing phonon scattering with temperature.³³

A comparison of the magnetoresistance and Hall effect data revealed two interesting trends. First, transverse MR increases with increasing carrier mobility, and second, LMR increases with increasing carrier concentration (see Fig. 4). Transverse MR dependence is quadratic (Fig. 4a), which corresponds to the semi-classical model according to which MR ∼ μ_H² for low-carrier systems.^21,34 In turn, LMR is found to depend on n_H almost linearly (Fig. 4b), which may indicate that the contribution of topologically non-trivial states to LMR becomes smaller when the Fermi level is shifted from those states (for details see Section 2.5). Previously, a similar behaviour of LMR(n_H) was reported in ref. 9; however, in our investigations, we extended the range of n_H considerably and did this in a more controllable way by gradually changing the irradiation dose.

Fig. 4 Transverse (a) and longitudinal (b) magnetoresistance of pristine and electron irradiated samples as a function of carrier mobility (a) and carrier concentration (b) at T = 50 K and under B = 14 T. Pink lines are a guide to the eye.

2.4 Anomalous Hall effect

As mentioned in previous sections, an anomalous Hall effect was observed in our pristine samples. Consequently, we also studied the impact of electron irradiation on the AHE. GdPtBi was the first half-Heusler phase among the REPtBi compounds where the observation of the AHE has been reported.¹² Following this, numerous studies on the observation of the AHE in REPtBi compounds were conducted.^10,14,26,35 More recently, this study was extended to REPdBi systems.¹⁹ The detailed procedure of the extraction of AHE contribution (Δσ^A_xy) is described in the ESI,† and is the same as that previously reported.³⁵ Δσ^A_xy is the difference between σ_xy(B) dependences measured at T = 10 K and at T = 50 K. For both pristine samples, the difference in Δσ^A_xy(B) curves is minimal across the entire range of magnetic fields covered. A minor discrepancy may be attributed to the misorientation of samples, as it has been shown recently that the AHE in HoPtBi is strongly anisotropic.³⁶ Δσ^A_xy achieves the maximum values of 77.1 Ω⁻¹ cm⁻¹ and 69.4 Ω⁻¹ cm⁻¹ at B_max = 2.6 T and B_max = 2.4 T for pristine samples #1 and #2, respectively (see Fig. 5). These values are comparable to those reported for GdPtBi in ref. 10.

Fig. 5 (a) Anomalous Hall conductivity as a function of magnetic field at T = 10 K for pristine and irradiated samples. (b) Maximum values of anomalous Hall conductivity (right axis) and magnetic field values (left axis) at which these maxima were recorded as a function of irradiation dose at T = 10 K.

It was observed that electron irradiation resulted in a pronounced change in the Δσ^A_xy(B). Irradiation with the smallest dose of ϕ = 1.5 C cm⁻² leads to a shift in the maximum of Δσ^A_xy to the stronger magnetic field, B_max = 6.9 T, and also the magnitude of Δσ^A_xy increases to the value of 174.2 Ω⁻¹ cm⁻¹, the largest observed value of Δσ^A_xy for any of the studied samples. As the irradiation dose is increased further, B_max increases and saturates at a value of ∼10 T within the range of irradiation dose 3–6 C cm⁻². It appears that for the sample irradiated with ϕ = 7 C cm⁻² the maximum in the Δσ^A_xy(B) was not attained in the magnetic field up to 14 T. The irradiation dose dependence of both Δσ^A_xy and B_max is shown in Fig. 5b.

There exist alternative approaches for extracting the AHE contribution. One of them is based on the performing Drude model fitting, which can be used to describe the contribution of the ordinary Hall effect to the total Hall effect. Previously, we used this approach in order to determine the AHE in HoPtBi.¹⁴ However, its applicability is limited in the present study due to the significant dependence of the AHE on the magnetic field among the studied samples (see the ESI,† for more details). The employment of other approaches of AHE extraction,^37–39 which also consider the contributions from extrinsic origins proportional to magnetization, is not applicable in this case. According to the literature, saturation of magnetization in GdPtBi occurs only under B = 25 T at T = 1.4 K,¹⁰ which is much higher than the magnetic field available in our experiments. To eliminate the possibility that extrinsic mechanisms dominate the AHE in GdPtBi, we plotted Δσ^A_xy as a function of magnetization for the pristine sample #1 of GdPtBi (see Fig. S8, ESI†). The absence of a linear relationship between Δσ^A_xy and magnetization indicates that the AHE in our samples is not governed by extrinsic mechanisms. Moreover, the anomalous Hall angle (AHA = Δσ^A_xy/σ_xx) in our samples (10.6% in the pristine #1 sample and 14.6% in sample #1, which was irradiated with ϕ = 6 C cm⁻²) was found to be much larger than 0.1–1%,⁴⁰ which is the typical range for materials where extrinsic mechanisms dominate the AHE.

In order to gain insight into the complex behaviour of Δσ^A_xy(ϕ) and B_max(ϕ) (see Fig. 5), we performed calculations of the electronic structure and anomalous Hall effect for several different values of the magnetic field from the range 0–10 T.

2.5 Electronic band structure calculations

The electronic band structure of GdPtBi is presented in Fig. 6 without and with the inclusion of the magnetic field. In the absence of the magnetic field, the band structure is very similar to those previously reported for GdPtBi^10,12 and other half-Heusler compounds.⁴¹ At Γ point, band touching occurs, with the states around the Fermi level originating from Pt and Bi atoms (see Fig. 6a). Additionally, inversion of Γ₈ (p-type) and Γ₆ (s-type) bands is realized.⁴² The introduction of the magnetic field leads to the lifting of band degeneracy and the emergence of avoided crossing features along high-symmetry directions. Moreover, the appearance of the Fermi surface around the Γ point is observed. The observed effect is similar to that reported for CePtBi,⁴³ GdPtBi¹² and TbPtBi.³⁵

Fig. 6 The electronic band structure in the absence (a) and presence of magnetic field of 5 T (b) and 10 T (c). The inset to panel (a) shows the bulk Brillouin zone with high symmetry points marked.

Time-reversal symmetry breaking introduced by the magnetic field may lead to the appearance of Weyl points.⁴⁴ GdPtBi is an example of a material in which this mechanism occurs.⁹ Our results of the electronic structure calculations corroborate this scenario, six pairs of Weyl nodes exist in the vicinity of Γ point, in accordance with the findings of ref. 10. Furthermore, we also found that an increase in magnetic field strength leads to the gaping of Weyl nodes (see Fig. 6b and c). In general, the results of our electronic structure calculations are consistent with those previously reported for GdPtBi.^10,12 While the Weyl points occur in proximity to the Fermi level, the electronic structure is only minimally impacted by the magnetic field below the Fermi level. The density of states as a function of energy is shown in Fig. S10a (see the ESI†) for various values of the magnetic field. We therefore neglected this change when estimating the position of the Fermi level in the irradiated samples. By comparing the results of electronic structure calculations and carrier concentration obtained from Hall effect measurements, we estimated the position of Fermi level in pristine and electron irradiated samples (see the ESI,† for more details). In general, electron irradiation of GdPtBi caused quite a small change in the Fermi level position. For pristine samples, the Fermi level is situated at −30 meV, while for samples irradiated with a maximal dose of 7 C cm⁻² Fermi level is located at −130 meV, resulting in a relative shift of 100 meV, which is smaller than that we observed in LuPdBi.²¹ The downward shift of the Fermi level indicates that the Weyl nodes contribute less to the total magneto-transport properties. Consequently, we observed a smaller negative LMR with an increasing irradiation dose.

Additionally, anomalous Hall conductivity (AHC) was calculated for several different values of magnetic field (Fig. 7). The AHC exhibits pronounced non-monotonic behaviour as a function of energy, and the magnetic field exerts a significant influence on the AHC(E − E_F) curves. There is a pronounced peak with a maximum close to 50 meV below the Fermi level for 2.5 and 5 T, but as the magnetic field increases further the peak blurs and AHC becomes smaller. In general, the values of AHC obtained from theoretical calculations are of the same order of magnitude as obtained from Hall effect analysis. Moreover, both the theoretical and experimental data show complex variations of the anomalous Hall effect with respect to the magnetic field and the position of the Fermi level. A discrepancy between the two data sets may be attributed to the fact that in the calculations, the assumption of full polarization of magnetic moments was made. This is in turn inconsistent with the values of the magnetic field at which experiments were carried out, whereby GdPtBi is in the canted antiferromagnetic state. For GtPtBi, the magnetic moments are fully saturated above ∼25 T.¹⁰ The realization of large AHC around the Fermi level can be related to (i) the magnetic-filed-induced Weyl points,⁴⁵ and/or (ii) the avoided crossing of the electronic bands.⁴⁶ In the case of GdPtBi, both effects can give rise to a significant Berry phase contribution to the AHE.¹² However, our findings indicate that electron irradiation of GdPtBi results in a downward shift of the Fermi level, causing the Weyl nodes to move further away from it. Hence, the AHE may be mainly dominated by avoided band crossing in GdPtBi, particularly in the case of irradiated samples.

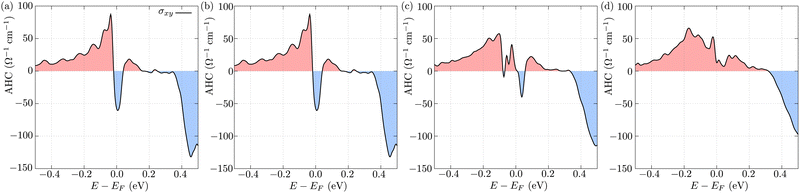Fig. 7 Theoretically obtained anomalous Hall conductivity as a function of energy in the presence of magnetic fields of 2.5 T (a), 5 T (b), 7.5 T (c) and 10 T (d).

3 Conclusions

In summary, we conducted a comprehensive investigation of the magnetotransport properties of pristine and high-energy-electron-irradiated samples of the half-Heusler Weyl semimetal GdPtBi. Comparing the results of Hall effect measurements with theoretical calculations of the electronic structure, we concluded that irradiation shifts the Fermi level far from the magnetic field-induced Weyl nodes. This shift reduces the contribution of Weyl states to observed magnetotransport, evidenced by a decrease in negative longitudinal magnetoresistance as the irradiation dose increases. We observed that negative LMR is proportional to the carrier concentration in GdPtBi, while transverse MR is proportional to the squared carrier mobility. Furthermore, we observed the anomalous Hall effect, which is strongly influenced by electron irradiation. The magnitude of the AHE and the magnetic field values at which AHE peaks vary in a complex manner with the irradiation dose change, consistent with theoretically calculated anomalous Hall conductivity. Our investigation shows that in GdPtBi the impact of Weyl states on the magnetotransport properties is robust against the moderate Fermi level tuning. This finding is applicable to other half-Heusler Weyl semimetals, thereby opening new avenues for their study, as there are not many materials in which Weyl nodes lie sufficiently close to the Fermi level to still observe their contribution to magnetotransport properties.

4 Methods

4.1 Growth and characterization of single crystals

GdPtBi single crystals were grown from Bi-flux as described in ref. 47. X-ray powder diffraction experiments were performed using an Xpert Pro (PANalytical) diffractometer with CuK_α radiation. Refinement of the crystal structure was performed by the Rietveld method using FullProf software,⁴⁸ its results confirmed the MgAgAs-type crystal structure of the studied material, and the obtained lattice parameter is a = 6.684 Å, identical to that reported earlier.¹² The high quality of synthesized single crystals was confirmed and their orientation was assessed by the Laue backscattering technique using a Proto Laue-COS system.

4.2 Electronic transport measurements

Electrical resistivity, magnetoresistance and the Hall effect were investigated using a Quantum Design PPMS platform. A standard four-probe ac-current technique was used and electrical contacts were prepared with a 50 μm-diameter silver wire attached to the samples with silver epoxy paste. ρ_xy(B) and ρ_xx(B) data were measured in the magnetic field range from −14 to 14 T and were then antisymmetrized and symmetrized, respectively, in order to remove the contribution due to the electrical contact misalignment (Fig. S4 in the ESI†).

4.3 Electron irradiation

Irradiations by 2.5 MeV electrons were performed at the SIRIUS platform operated at Laboratoire des Solides Irradiés at École Polytechnique (Palaiseau, France). An electron beam was generated using an NEC Pelltron accelerator coupled with a low temperature irradiation chamber. During irradiation, the sample was immersed in liquid hydrogen at 22 K, delivered with a close cycle re-condenser. Irradiation dose was monitored by integration of the current collected using a Faraday cup placed behind the sample. Irradiation area was limited by a 5 mm diameter diaphragm and the uniformity of damage was granted by sweeping the beam vertically and horizontally at two non-commensurate frequencies. Beam current density was limited to 10 μA cm⁻² to prevent heating of the sample. At the electron energy used in our experiment, 2.5 MeV electrons are relativistic and Rutherford collision is the main channel of energy transfer achieved from impinging electrons to the atoms of the target. This process was examined by N. F. Mott⁴⁹ and the results, probabilities of ejection of the ions from its site and creation of vacancy – interstitial (Frenkel pair), were tabulated by Oen.⁵⁰ Using those tables, we estimated effective cross-sections for defect creation on each sublattice (see Fig. S4 in the ESI†). Removal of samples from the irradiation chamber and transfer at room temperature to another instrument lead to partial annealing of defects, mainly interstitials characterized by lower migration energy. We assume that the remaining damage is of vacancy type. The penetration range of 2.5 MeV electrons is over 1 mm, which is another argument supporting the uniform distribution of defects. In total, we irradiated and then studied 5 samples (named #1–#5), which were cut from the same single crystal. Samples #1 and #2 were also investigated before the irradiation.

4.4 Ab initio calculation

The first-principles density functional theory (DFT) calculations were performed using the projector augmented-wave (PAW) potentials⁵¹ implemented in the Vienna Ab initio Simulation Package (VASP).^52–54 The calculations comprising spin–orbit coupling (SOC) were performed with the generalized gradient approximation (GGA) under the modified Becke–Johnson (mBJ) exchange potential.^55–57 The energy cutoff for the plane-wave expansion was set to 350 eV. The electronic properties were calculated using a 10 × 10 × 10 Γ-centered k-point grid within the Monkhorst–Pack scheme.⁵⁸ As a convergence criterion we took the energy change below 10⁻¹⁰ eV for electronic degrees of freedom. We assumed the experiential lattice constant, while the Gd f-orbitals were treated as core states. The band structure from the exact DFT calculations was used to construct a tight binding model (TBM) using Wannier90 software.⁵⁹ We started the calculations from the s, p, and d orbitals of all atoms, which gave a TBM with 54 orbitals and 108 bands. The band structure in the presence of a magnetic field was calculated from the TBM with an additional Zeeman term.

Author contributions

Orest Pavlosiuk: conceptualization, data curation, formal analysis, investigation, methodology, visualization, writing – original draft, and writing – review & editing. Piotr Wiśniewski: conceptualization, formal analysis, methodology, and writing – review & editing. Romain Grasset: investigation, methodology, visualization, and writing – review & editing. Marcin Konczykowski: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, and writing – review & editing. Andrzej Ptok: data curation, formal analysis, investigation, visualization, writing – original draft, and writing – review & editing. Dariusz Kaczorowski: conceptualization, funding acquisition, methodology, project administration, and writing – review & editing.

Data availability

The data supporting this article have been included as part of the ESI.† Any further relevant data are available from the authors upon reasonable request.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

This research was financially supported by the National Science Centre of Poland, grant no. 2021/40/Q/ST5/00066 and the Agence Nationale de la Recherche project “DYNTOP” ANR-22-CE30-0026-01. The authors acknowledge support from the EMIR&A French network (FR CNRS 3618) on the platform SIRIUS.

Notes and references

1. M. Z. Hasan and C. L. Kane, Rev. Mod. Phys., 2010, 82, 3045.
2. N. P. Armitage, E. J. Mele and A. Vishwanath, Rev. Mod. Phys., 2018, 90, 015001.
3. M. Z. Hasan, S.-Y. Xu, I. Belopolski and S.-M. Huang, Annu. Rev. Condens. Matter Phys., 2017, 8, 289.
4. M. Hellenbrandt, Crystallogr. Rev., 2004, 10, 17.
5. T. Zhang, Y. Jiang, Z. Song, H. Huang, Y. He, Z. Fang, H. Weng and C. Fang, Nature, 2019, 566, 475.
6. M. G. Vergniory, L. Elcoro, C. Felser, N. Regnault, B. A. Bernevig and Z. Wang, Nature, 2019, 566, 480.
7. F. Tang, H. C. Po, A. Vishwanath and X. Wan, Nature, 2019, 566, 486.
8. E. Mun and S. L. Bud'ko, MRS Bull., 2022, 47, 609.
9. M. Hirschberger, S. Kushwaha, Z. Wang, Q. Gibson, S. Liang, C. A. Belvin, B. A. Bernevig, R. J. Cava and N. P. Ong, Nat. Mater., 2016, 15, 1161.
10. C. Shekhar, N. Kumar, V. Grinenko, S. Singh, R. Sarkar, H. Luetkens, S.-C. Wu, Y. Zhang, A. C. Komarek, E. Kampert, Y. Skourski, J. Wosnitza, W. Schnelle, A. McCollam, U. Zeitler, J. Kübler, B. Yan, H.-H. Klauss, S. S. P. Parkin and C. Felser, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 9140.
11. N. Kumar, S. N. Guin, C. Felser and C. Shekhar, Phys. Rev. B, 2018, 98, 041103.
12. T. Suzuki, R. Chisnell, A. Devarakonda, Y.-T. Liu, W. Feng, D. Xiao, J. W. Lynn and J. G. Checkelsky, Nat. Phys., 2016, 12, 1119.
13. O. Pavlosiuk, D. Kaczorowski and P. Wiśniewski, Phys. Rev. B, 2019, 99, 125142.
14. O. Pavlosiuk, P. Fałat, D. Kaczorowski and P. Wiśniewski, APL Mater., 2020, 8, 111107.
15. J. Chen, H. Li, B. Ding, E. Liu, Y. Yao, G. Wu and W. Wang, Appl. Phys. Lett., 2020, 116, 222403.
16. C. Y. Guo, F. Wu, Z. Z. Wu, M. Smidman, C. Cao, A. Bostwick, C. Jozwiak, E. Rotenberg, Y. Liu, F. Steglich and H. Q. Yuan, Nat. Commun., 2018, 9, 4622.
17. J. Chen, H. Li, B. Ding, P. Chen, T. Guo, X. Xu, D. Zheng, H. Zhang, X. Xi and W. Wang, Adv. Funct. Mater., 2021, 2107526.
18. D. T. Son and B. Z. Spivak, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 104412.
19. Y. Zhu, C.-Y. Huang, Y. Wang, D. Graf, H. Lin, S. H. Lee, J. Singleton, L. Min, J. C. Palmstrom, A. Bansil, B. Singh and Z. Mao, Commun. Phys., 2023, 6, 346.
20. Z. L. Sun, K. L. Peng, J. H. Cui, C. S. Zhu, W. Z. Zhuo, Z. Y. Wang and X. H. Chen, Phys. Rev. B, 2021, 103, 085116.
21. K. Ishihara, T. Takenaka, Y. Miao, Y. Mizukami, K. Hashimoto, M. Yamashita, M. Konczykowski, R. Masuki, M. Hirayama, T. Nomoto, R. Arita, O. Pavlosiuk, P. Wiśniewski, D. Kaczorowski and T. Shibauchi, Phys. Rev. X, 2021, 11, 041048.
22. J. Sitnicka, M. Konczykowski, K. Sobczak, P. Skupiński, K. Grasza, Z. Adamus, A. Reszka and A. Wołoś, Phys. Rev. B, 2023, 107, 214424.
23. E. Mun, S. L. Bud'ko and P. C. Canfield, Phys. Rev. B, 2016, 93, 115134.
24. Y. Mizukami, M. Konczykowski, Y. Kawamoto, S. Kurata, S. Kasahara, K. Hashimoto, V. Mishra, A. Kreisel, Y. Wang, P. J. Hirschfeld, Y. Matsuda and T. Shibauchi, Nat. Commun., 2014, 5, 5657.
25. O. Pavlosiuk, D. Kaczorowski and P. Wiśniewski, Phys. Rev. B, 2016, 94, 035130.
26. H. Zhang, Y. L. Zhu, Y. Qiu, W. Tian, H. B. Cao, Z. Q. Mao and X. Ke, Phys. Rev. B, 2020, 102, 094424.
27. S. Liang, J. Lin, S. Kushwaha, J. Xing, N. Ni, R. J. Cava and N. P. Ong, Phys. Rev. X, 2018, 8, 031002.
28. X. Huang, L. Zhao, Y. Long, P. Wang, D. Chen, Z. Yang, H. Liang, M. Xue, H. Weng, Z. Fang, X. Dai and G. Chen, Phys. Rev. X, 2015, 5, 031023.
29. S. Hikami, A. Larkin and Y. Nagaoka, Prog. Theor. Phys., 1980, 63, 707.
30. H. K. Pal and D. L. Maslov, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 214438.
31. O. Pavlosiuk, A. Jezierski, D. Kaczorowski and P. Wiśniewski, Phys. Rev. B, 2021, 103, 205127.
32. Y.-Y. Lv, X. Li, B.-B. Zhang, W. Deng, S.-H. Yao, Y. Chen, J. Zhou, S.-T. Zhang, M.-H. Lu, L. Zhang, M. Tian, L. Sheng and Y.-F. Chen, Phys. Rev. Lett., 2017, 118, 096603.
33. C.-L. Zhang, S.-Y. Xu, I. Belopolski, Z. Yuan, Z. Lin, B. Tong, G. Bian, N. Alidoust, C.-C. Lee, S.-M. Huang, T.-R. Chang, G. Chang, C.-H. Hsu, H.-T. Jeng, M. Neupane, D. S. Sanchez, H. Zheng, J. Wang, H. Lin, C. Zhang, H.-Z. Lu, S.-Q. Shen, T. Neupert, M. Zahid Hasan and S. Jia, Nat. Commun., 2016, 7, 10735.
34. M. N. Ali, L. Schoop, J. Xiong, S. Flynn, Q. Gibson, M. Hirschberger, N. P. Ong and R. J. Cava, EPL, 2015, 110, 67002.
35. Y. Zhu, B. Singh, Y. Wang, C.-Y. Huang, W.-C. Chiu, B. Wang, D. Graf, Y. Zhang, H. Lin, J. Sun, A. Bansil and Z. Mao, Phys. Rev. B, 2020, 101, 161105.
36. J. Chen, X. Xu, H. Li, T. Guo, B. Ding, P. Chen, H. Zhang, X. Xi and W. Wang, Phys. Rev. B, 2021, 103, 144425.
37. N. Nagaosa, J. Sinova, S. Onoda, A. H. MacDonald and N. P. Ong, Rev. Mod. Phys., 2010, 82, 1539.
38. Y. Xu, L. Das, J. Z. Ma, C. J. Yi, S. M. Nie, Y. G. Shi, A. Tiwari, S. S. Tsirkin, T. Neupert, M. Medarde, M. Shi, J. Chang, T. Shang, U. Zürich and C. Zürich, Phys. Rev. Lett., 2021, 126, 076602.
39. Y. Li, N. Kanazawa, X. Z. Yu, A. Tsukazaki, M. Kawasaki, M. Ichikawa, X. F. Jin, F. Kagawa and Y. Tokura, Phys. Rev. Lett., 2013, 110, 117202.
40. K. Wang, Y. Zhang, S. Zhou and G. Xiao, Nanomaterials, 2021, 11, 854.
41. J. C. Souza, M. V. Ale Crivillero, H. Dawczak-Dębicki, A. Ptok, P. G. Pagliuso and S. Wirth, Phys. Rev. B, 2023, 108, 165154.
42. W. Feng, D. Xiao, Y. Zhang and Y. Yao, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 235121.
43. N. Kozlova, J. Hagel, M. Doerr, J. Wosnitza, D. Eckert, K.-H. Müller, L. Schultz, I. Opahle, S. Elgazzar, M. Richter, G. Goll, H. V. Löhneysen, G. Zwicknagl, T. Yoshino and T. Takabatake, Phys. Rev. Lett., 2005, 95, 086403.
44. J. Cano, B. Bradlyn, Z. Wang, M. Hirschberger, N. P. Ong and B. A. Bernevig, Phys. Rev. B, 2017, 95, 161306.
45. A. A. Burkov, Phys. Rev. Lett., 2014, 113, 187202.
46. Y. Yao, L. Kleinman, A. H. MacDonald, J. Sinova, T. Jungwirth, D.-S. Wang, E. Wang and Q. Niu, Phys. Rev. Lett., 2004, 92, 037204.
47. O. Pavlosiuk, D. Kaczorowski and P. Wiśniewski, Acta Phys. Pol., A, 2016, 130, 573.
48. J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55.
49. N. F. Mott, Proc. R. Soc. A, 1929, 124, 425.
50. O. S. Oen, Nucl. Instrum. Methods Phys. Res. B., 1988, 33, 744.
51. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
52. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251.
53. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
54. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
55. A. D. Becke and E. R. Johnson, J. Chem. Phys., 2006, 124, 221101.
56. F. Tran and P. Blaha, Phys. Rev. Lett., 2009, 102, 226401.
57. J. A. Camargo-Martínez and R. Baquero, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 195106.
58. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188.
59. G. Pizzi, V. Vitale, R. Arita, S. Blügel, F. Freimuth, G. Géranton, M. Gibertini, D. Gresch, C. Johnson, T. Koretsune, J. Ibañez-Azpiroz, H. Lee, J.-M. Lihm, D. Marchand, A. Marrazzo, Y. Mokrousov, J. I. Mustafa, Y. Nohara, Y. Nomura, L. Paulatto, S. Poncé, T. Ponweiser, J. Qiao, F. Thöle, S. S. Tsirkin, M. Wierzbowska, N. Marzari, D. Vanderbilt, I. Souza, A. A. Mostofi and J. R. Yates, J. Phys.: Condens. Matter, 2020, 32, 165902.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mh01875c

---