Open Access Article
Open Access ArticleUnveiling selectivity trends for CO2 reduction reaction over Ti3C2Tx MXene: the key role of less-stable intermediate states and coadsorbates†
Pablo
Lozano-Reis
 a and
Kai S.
Exner
a and
Kai S.
Exner
 *abc
*abc
aFaculty of Chemistry, Theoretical Catalysis and Electrochemistry, University of Duisburg-Essen, Universitätsstraße 5, 45141 Essen, Germany. E-mail: kai.exner@uni-due.de
bCluster of Excellence RESOLV, 44801 Bochum, Germany
cCenter for Nanointegration (CENIDE) Duisburg-Essen, 47057 Duisburg, Germany
First published on 21st May 2025
Abstract
The electrochemical conversion of carbon dioxide via the CO2 reduction reaction (CO2RR) is an attractive strategy for the production of value-added chemicals. However, the CO2RR suffers from a selectivity problem due to the large number of carbon-based products that can be obtained and the competing hydrogen evolution reaction (HER). It has been experimentally shown that the ratio and chemical nature of terminal groups, Tx, present on the Ti3C2Tx (Tx = O, OH or F) surface under electrochemical conditions affect selectivity and activity trends of the MXene electrocatalyst. In the present manuscript, we use electronic structure theory calculations to comprehend the selectivity trends in the CO2RR over Ti3C2Tx with different terminal groups, including *OH and *F adsorbates. We show that the traditional modeling approach used in calculations to derive activity and selectivity trends, which only includes the most stable intermediate state in the analysis, is not consistent with experimental observations. Rather, it is necessary to include energetically less favorable intermediate states and coadsorbates in the analysis of mechanistic pathways. Remarkably, the inclusion of less-stable intermediates, although stable on the electrode surface, and coadsorbates opens up new reaction channels that are energetically more favorable, and only by considering these extensions are we able to map our results to the experimental data. We believe that the reported finding is not only limited to the CO2RR or MXene systems, but likely also plays an important role in other catalytic transformations under applied bias.
New conceptsThe present manuscript focuses on resolving selectivity trends for the CO2RR over Ti3C2Tx MXene with different terminal groups, Tx, including *OH and *F adsorbates, using electronic structure theory calculations. The traditional approach in the community to understand selectivity in the CO2RR involves constructing thermodynamic free-energy diagrams for the different reaction channels, where only the most stable intermediate states are considered in the mechanistic analysis. In the case of the CO2RR over Ti3C2Tx MXene, this framework does not reproduce the experimentally observed selectivity trends. We demonstrate that less-stable intermediates and coadsorbates, which also lead to less-stable configurations, must be included in the analysis to determine selectivity trends that are consistent with experimental data. The inclusion of these new configurations, even if they are energetically less favorable, opens new reaction channels that are energetically more favorable and thus can change the activity and selectivity trends compared to the traditional approach. The presented concept of factoring less-stable intermediate states and coadsorbates into the mechanistic analysis based on adsorption free energies is not limited to the CO2RR or MXene systems, and we believe that the proposed framework will guide the design of improved materials for energy conversion and storage processes using computational methods. |
1 Introduction
The sustained combustion of fossil fuels required to fulfill the energy requests of our societies has led to a drastic increase in the anthropogenic CO2 levels, causing devastating effects on the environment and life of many ecosystems. Although a transition to green energies would be desirable, it is still not feasible to cover all energy demands exclusively with green energies.1 CO2 valorization emerges as an appealing strategy to counteract the current situation and represents a carbon neutral route for the generation of value-added energy carriers, while simultaneously reducing the anthropogenic CO2 levels.2 Currently, different strategies are used for CO2 conversion, which include thermo-,3–10 photo-11–14 and electrocatalysis,15–23 among others. Interestingly, CO2 conversion via the electrocatalytic CO2 reduction reaction (CO2RR) is a very interesting process as it is carried out under mild operating conditions, usually at room temperature and moderate pressures. In addition, renewable energy resources can provide the required electricity for electrolysis, making the electrochemical pathway also environmentally attractive.The electrochemical CO2RR is mainly limited by its selectivity challenge. On the one hand, the formation of H2(g) from the hydrogen evolution reaction (HER) (i.e., eqn (1)) is observed for cathodic polarization, which is a competing side reaction under CO2RR conditions.24 On the other hand, there is the possibility of forming multiple C1 products (i.e., eqn (2)–(5)) or multicarbon products (i.e., C2+).25
| 2H+ + 2e− → H2(g), U0 = 0 V vs. RHE (reversible hydrogen electrode) | (1) |
| CO2(g) + 2H+ + 2e− → CO(g) + H2O(l) U0 = −0.10 V vs. RHE | (2) |
| CO2(g) + 2H+ + 2e− → HCOOH(aq) U0 = −0.12 V vs. RHE at pH = 0 | (3) |
| CO2(g) + 6H+ + 6e− → CH3OH(aq) + H2O(l) U0 = 0.03 V vs. RHE | (4) |
| CO2(g) + 8H+ + 8e− → CH4(g) + 2H2O(l) U0 = 0.17 V vs. RHE | (5) |
While the formation of C2+ products in the CO2RR is of greater importance than the formation of C1 products, the former products are normally obtained only from Cu-based catalysts, while CO, HCOOH and H2 are typically observed for other transition metals.25 Interestingly, the emergence of a new class of two-dimensional transition-metal carbides and nitrides, so-called MXenes, with excellent properties for energy conversion and storage, opens new avenues for the development of next-generation catalysts with improved catalytic activity and/or selectivity.26 In this regard, it has been recently shown that the Cu-doped Ti3C2Tx (Tx = O, OH or F) MXene or even its basal planes can produce different C1 products and even C2+ species for the CO reduction reaction (CORR) and CO2RR.27,28 These findings suggest that terminal groups can modulate the CO2RR selectivity and pave the way for the development of MXenes-based catalysts for selective CO2RR.
An atomistic understanding of the mechanism that governs the reaction is essential for the rational design of active and selective catalysts. Interestingly, such understanding can be achieved from electronic structure calculations, usually in the density functional theory (DFT) framework, by materials screening. Such approach offers the opportunity to investigate and identify potential candidate materials that can later be experimentally validated,29,30 which may help overcoming the CO2RR selectivity problem. The traditional approach used in DFT to study electrocatalytic transformations focus on the thermodynamic picture. This is justified by the consideration of Brønsted–Evans–Polanyi relation,31–33 which connects the kinetics and thermodynamics. More precisely, the traditional approach comprises to calculate different configurations of the reaction intermediates in the CO2RR or other electrocatalytic processes to identify the thermodynamically most stable structures.34–38 Thereafter, free-energy diagrams are constructed for these stable reaction intermediates, which allow predicting activity and selectivity trends of materials using descriptor-based analyses.39,40
In this contribution, we aim to introduce a new framework for constructing and analyzing free-energy diagrams to enable a thorough discussion of activity and selectivity trends. In our approach, we factor not only the thermodynamically most stable reaction intermediates but also the less-stable reaction intermediates into the analysis of the elementary reaction steps. We illustrate our methodology using the CO2RR over the Ti3C2Tx MXene with different *OH/*F adsorbates as terminal groups and discuss the role of less-stable intermediates states and coadsorbates, which also give rise to less-stable configurations, on the activity and selectivity. We demonstrate that less-stable intermediate states give rise to energetically favored reaction channels compared to the common assumption of considering the thermodynamically most stable structures only. Interestingly, our predicted activity and selectivity trends are only in good agreement with experimental data if less-stable intermediate states and coadsorbates are considered in the analysis, whereas the traditional approach, focusing on the thermodynamically most stable reaction intermediates only, fails to reproduce the experimentally reported trends.
2 Computational methods
In this study, we apply periodic DFT calculations as implemented in the Vienna Ab initio Simulation Package (VASP) code41–43 to model the CO2RR and HER on different (3 × 3) Ti3C2Tx (Tx = *OH and/or *F) surface models. All calculations have been done using the Perdew–Burke–Ernzerhof (PBE) exchange correlation functional44 alongside Grimme's D3 term to account for dispersion effects.45 We use the computational hydrogen electrode (CHE) approach46 to describe the energetics of proton–electron transfer steps occurring during CO2RR and HER. Transition states (TS) have been located using the Catlearn Bayesian transition state search module (ML-NEB).47 All computational details are provided in Section S1 of the ESI.†3 Surface models and reaction network
Recently Krishnan et al.,28 studied the CO2RR using linear sweep voltammetry (LSV) and chronoamperometry (CA) techniques on the basal plane of the Ti3C2Tx (Tx = *O, *OH, or *F) MXene, which contain a considerable amount of *F adsorbates. Interestingly, they observed suppression of the HER and high selectivity towards CO and CH3OH, while also finding considerable amounts of C2+ species (i.e., ethanol and acetone). Bao et al.27 studied the CORR on Cu-based Ti3C2Tx systems by combining experimental and theoretical approaches. In their LSV experiments, they observed the formation of considerable amounts of ethanol and ethylene for the Cu-based Ti3C2Tx system. However, they found high HER selectivity when the CORR was studied on the basal plane of Ti3C2Tx, with a large fraction of *O and *OH terminal groups. Note that Pourbaix diagrams for the Ti3C2 MXene under cathodic conditions predict that the surface is largely covered by *OH/*O adsorbates, and *F-covered surfaces are found to be stable at low pH.48,49Nevertheless, a larger *F coverage can also be found at different working conditions due to the synthetic conditions used during the MXene preparation.28 The above findings suggest that the *F content can play a significant role in CO2RR selectivity. Notably, in line with the above results, the important role of surface terminations for Ti3C2 MXene on the catalytic HER activity was reported.49 To analyze this effect, we study the CO2RR on different Ti3C2Tx MXene surface models with different ratios of *OH/*F adsorbates (see Fig. 1).
To study the CO2RR and HER on the different surface models, we have considered two different reaction networks. The first reaction network considers the reaction intermediates in their thermodynamically most stable configuration (Fig. 2a) and comprises a total of 18 adsorbates, 7 gas-phase molecules, and 30 elementary steps. For the second reaction network, we have also included other less-stable intermediate states that better connect two intermediate states and provide a more realistic mechanistic description (Fig. 2b). This gives rise to a total of 23 intermediate states, 7 gas-phase molecules, and 41 elementary steps considered in the analysis. Let us emphasize that a proper representation of the ‘natural pathway’ of product formation (without assuming any free internal rotation) can only be achieved if less-stable intermediate states are factored into the mechanistic description. All elementary steps of the CO2RR and HER can be found in Section S2 of the ESI† (i.e., eqn (S5)–(S34)).
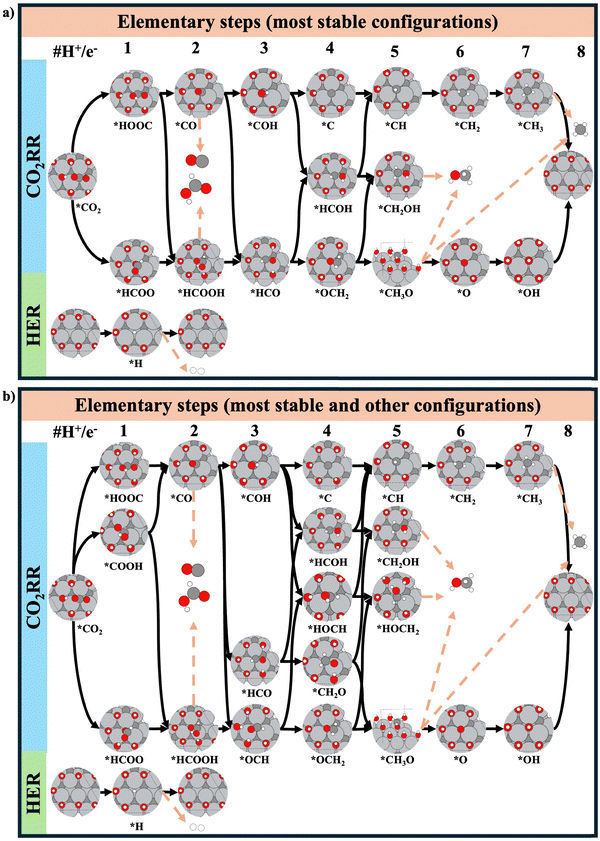 | ||
| Fig. 2 Schematic representation of the elementary steps considered for the CO2RR and HER on the example of the Ti3C2–*7OH surface: (a) only the most stable configuration of a reaction intermediate is considered, (b) besides the most stable configuration of an adsorbate, also less-stable intermediate states are taken into account. Note that we have considered similar adsorbate configurations for the other surface models studied. For the CO2RR, four different C1 products have been factored into the analysis, namely: CO, HCOOH, CH3OH, and CH4. Black arrows represent connections between two adsorbed intermediates, while brown arrows represent product formation. Light grey, dark grey, red and white spheres denote Ti, C, O and H atoms, respectively. All elementary steps are listed in eqn (S5)–(S34) of the ESI† (Section 2). | ||
To derive activity and selectivity trends for the CO2RR and HER over Ti3C2Tx, we have used the following procedure. First, we calculated the adsorption energy of the different intermediate species for the different surface sites shown in the inset of Fig. 1 and determined the energetically preferred surface site corresponding to the fccin site. Note that for adsorbates that can adopt multiple configurations, we performed different geometrical optimizations and used the geometry of the most stable state (Fig. 2a), but also some geometries of the less-stable states (Fig. 2b). Second, we have also located the transition state (TS) for rotations between the less and most stable states and calculated the corresponding rotational barriers. Third, frequency calculations were performed to confirm that all configurations correspond to real minima or TS. In addition, frequency calculations are required to account for the zero-point energy and entropic contributions, which are needed to derive the Gibbs free energy of the different adsorbates. We refer the reader to Section S1.1 (ESI†) for a detailed description of how Gibbs free energies are derived. Fourth, we use the CHE approach46 to describe the energetics of proton–electron transfer steps occurring during the CO2RR and HER and construct free-energy diagrams for the different intermediate states. Fifth, the free-energy diagrams are analyzed using a descriptor-based approach50–52 to derive activity and selectivity trends. Finally, the predicted trends are compared to the experimental data of Krishnan et al.28
4 Results
Let us start by analyzing how the different adsorbates interact with the different Ti3C2Tx surfaces (cf.Fig. 1), as shown in Fig. 3. The interaction is calculated from the formation Gibbs free energy, which is derived using H2(g), CO2(g), H2O(g), and the bare Ti3C2Tx surfaces as references. For a detailed description of how formation Gibbs free energies are calculated, the reader is referred to Section S3 in the ESI.† Note that the more/less negative the formation Gibbs free energy, the stronger/weaker the interaction between the adsorbate and the surface.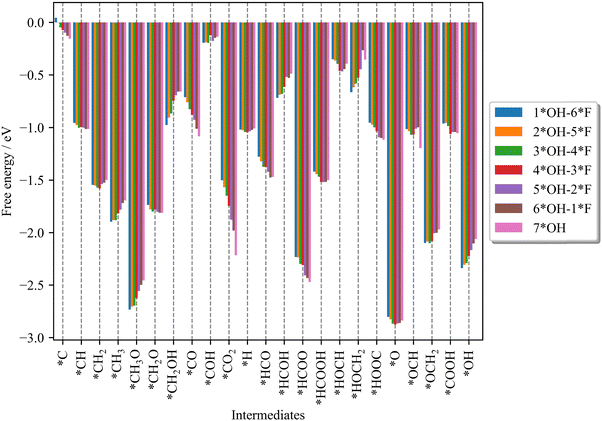 | ||
| Fig. 3 Formation Gibbs free energy for the different reaction intermediates in the CO2RR and HER on the different surfaces (cf.Fig. 1). A description of the calculation of the formation Gibbs free energies can be found in Section S3 of the ESI.† | ||
From Fig. 3, it appears that *H interacts similarly with all the surfaces, which implies that the HER is not largely dependent on the coverage of *F adsorbates. On the other hand, the larger the *F content, the weaker the *CO2 interaction with the surface. As *CO2 can limit the reaction at low cathodic potentials (vide infra), a more exergonic CO2 adsorption is likely to limit the CO2RR activity. Therefore, surfaces with large *F content are likely to increase the CO2RR activity. Regarding CO and HCOOH (i.e., two possible products), the higher the *F coverage, the weaker the CO interaction with the surface, while the interaction of HCOOH remains almost the same. This suggests a positive effect of *F composition on the CO selectivity compared to HCOOH. Until now, we have shown that some trends can be derived for reactants (CO2) and some products (CO and HCOOH) as a function of *F/*OH coverages. However, no clear trends are observed for the intermediate states (Fig. 2). Therefore, free-energy diagrams for the CO2RR and HER for the different surface models are constructed to gain insights into activity and selectivity.
5 Discussion
Let us start this section by defining some important aspects: (i) for the discussion of our results, we have selected the Ti3C2–4*OH–3*F surface model unless otherwise stated. The choice for this surface is because it has a similar *F/*OH composition. (ii) The potential used in our computational setup to construct the free-energy diagrams is U = −0.4 vs. RHE, which is chosen to mimic the potential of −1.1 V vs. Ag/AgCl at pH ≈ 7–8 used in the experiments.28 (iii) Gas-phase error corrections have been incorporated to correctly describe the overall thermodynamics on the free-energy diagrams.53,54 Further details on gas-phase error corrections can be found in Section S4 of the ESI.† (iv) For aqueous (i.e., HCOOH and CH3OH) and ionic species (i.e., HCOO−), solvation and ion corrections have been applied, respectively.55 Note that no changes are observed when using either HCOOH or HCOO− to assess the selectivity for formic acid/formate formation. Therefore, for simplicity, we have considered HCOOH instead of HCOO− in our analysis. For a detailed discussion, the reader is referred to Section S5 of the ESI.† Let us finally point out that, while pH effects can play an important role in modulating catalytic activity,56,57 in this study we are interested in activity and selectivity trends as a function of terminal groups at the experimental working conditions.28To assess the activity and selectivity for the CO2RR and HER, we make use of the descriptor Gmax(U).50,51 This activity descriptor quantifies the largest free-energy span between reaction intermediates of a given mechanism at a given potential (U). The free-energy spans are calculated based on the potential-dependent Gibbs free energy of the different intermediates (Gi(U)), which are derived following eqn (S4) in Section S1.1 of the ESI.† For a detailed description of Gmax(U) in the CO2RR, the reader is referred to Section S6 of the ESI.† When evaluating multiple pathways, the mechanism with the lowest Gmax(U) value is considered the most plausible mechanism. Interestingly, Gmax(U) can incorporate several elementary steps in the analysis, making it a particularly useful descriptor for reactions with a high number of proton–electron transfer steps such as CO2RR. Note that the lower the Gmax(U), the higher the catalytic activity. In our analysis, we extract the lowest Gmax(U) among the different possible mechanism that connect reactants to products (Fig. 2). This evaluation is performed for all products (i.e., H2, CO, HCOOH, CH3OH and CH4) across all different surface models (Fig. 1). Then, based on the Gmax(U) values of the different reaction channels, we derive selectivity trends.
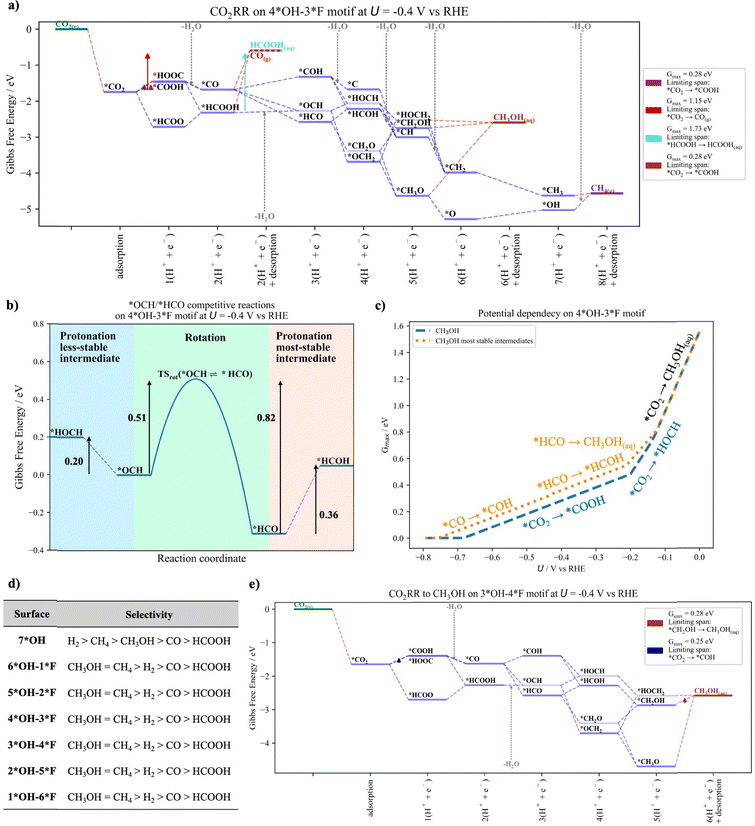
The free-energy diagram for CO2RR, HER and the potential dependency of both reactions for the Ti3C2–*4OH–3*F surface model at U = −0.4 V vs. RHE is shown in Fig. 4. Similar diagrams for the other surfaces can be found in Section S7 of the ESI† (Fig. S5–S10).
Among the different C1 products that can be produced during CO2RR, CH4 and CH3OH are the most selectively produced products as evidenced by their lowest Gmax(U) value (Fig. 4a). Regarding CO and HCOOH, the stronger interaction of *HCOOH with the surface compared to that of *CO and *CO2 hinders its formation, making HCOOH the least selectively produced product. Interestingly, at U = −0.4 V vs. RHE, the HER (Fig. 4b) is suppressed in favor of CO2RR because its Gmax(U) value is larger than that for the formation of CH3OH and CH4. Importantly, the formation of CH3OH and CH4 comprise many proton–electron transfer steps, and their limiting span in the approximation of Gmax(U) consists of several elementary reaction steps. On the other hand, the Gmax for HER consists of a single step (i.e., *H → H2(g)). This implies that Gmax(U) for CO2RR is reduced more efficiently than for HER when switching to more cathodic potentials (Fig. 4c). Nevertheless, HER is still favored at low cathodic potentials (Fig. 4c). This feature for HER is maintained for the MXene surfaces with a *F composition equal to or less than 3*F (see Fig. S5–S10, ESI†). This is because the larger the *F coverage, the weaker the *CO2 interaction with the surface, while the *H interaction is almost the same for all surfaces (Fig. 3). Since *CO2 is encountered in the limiting span at low cathodic potentials, the lower the CO2 adsorption, the lower the Gmax(U) and the higher the selectivity toward the CO2RR.
Let us now analyze the selectivity toward CO2RR and HER at U = −0.4 vs. RHE for all surfaces. From Fig. 4d three interesting patterns can be observed: (i) the highest *OH content favors HER, while increasing the *F content favors CO2RR, in agreement with experiments.27,28 This is because the reaction intermediates of CO2RR interact differently depending on the surface composition, while the *H interaction is similar for all surfaces. (ii) The highest selectivity is observed for CH3OH and CH4 at low to medium *F coverage and switches to CH4 at larger *F composition. The latter is in contrast to experiments in which CO and CH3OH are produced, but no CH4.28 (iii) The lowest selectivity is towards CO and HCOOH. While the latter product is not observed in experiments, the former is the most selectively produced product for MXene surfaces at large *F coverages.28 From these results, it is clear that the traditional model based on the analysis of the thermodynamically most stable intermediate states can only partially predict the experimental observations. In the following sections, we discuss the relevance of including less-stable intermediates states and coadsorbates for a refined mechanistic description to derive selectivity trends that are consistent with the experimental results.
5.1 Effect of including less-stable intermediate states
In this section, we discuss the importance of considering less-stable intermediate states in the activity analysis. There are two main reasons why this is important: (i) the configuration of the two most stable states of two consecutive intermediates may not be well connected. For instance, in Fig. 2a, *HCOOH and *HCO reveal a different orientation on the MXene surface: to connect these intermediate states, not only a proton–electron transfer but also an internal rotation is needed. The tacit assumption that adsorbed species can rotate freely with a small energy penalty may not hold true, especially for systems with high coverage. This situation is particularly evident in MXenes, where multiple terminal groups cover the surface and thus rotations from one intermediate state to another can be difficult (vide infra). Therefore, for a better mechanistic description, it appears important to consider configurations that truly connect two intermediate states, even if these new configurations correspond to energetically less-stable intermediates. This allows a more accurate and better representation of the ‘natural pathway’ (without free internal rotation) of a given mechanism. Note that this can also change the predicted activity to lower activities. (ii) By including less-stable intermediate states in the analysis, the number of possible pathways from the reactants to products increases. This enhances the possibilities of finding new pathways with a lower energy and thus higher catalytic activity. Note that we do not consider different sites, but rather the same site with different configurations for the adsorbate.Fig. 5a depicts the free-energy diagram for CO2RR including also less-stable intermediates states (marked in light blue). Similar figures for the other surfaces can be found in Section S8 of the ESI† (Fig. S11–S16). Interestingly, there is a decrease in the Gmax(U) and a change of the limiting span for CH3OH and CH4 compared to the situation where only the most stable intermediate states are considered (Fig. 4a). Let us focus on the example of CH3OH and discuss the differences. The limiting span when the most stable states are considered is *HCO → *HCOH, which changes to *CO2 → *COOH if also less-stable intermediate states are considered. The inclusion of less-stable intermediate states (i.e., *OCH, *HOCH and *HOCH2) opens up new, energetically favorable pathways through these intermediate states. Interestingly, the formation of *OCH from *CO is still exergonic, and the free energy required to form *HOCH from *OCH is lower than the free energy required for the transition of *HCO to *HCOH. Finally, both the formation of *HOCH2 and CH3OH(aq) are downhill in free energy. This situation changes the limiting span to *CO2 → *COOH and reduces the Gmax(U) while increasing the catalytic activity. Note that, while including less-stable intermediate states can lead to new pathways with improved catalytic activity, also situations with lower catalytic activity can be encountered. In particular, we found this situation for the formation of CH3OH on the Ti3C2–7*OH surface model (see Fig. S11b, ESI†) in the potential range of (−0.55 < U < −0.45 V vs. RHE), which is a result of the rigorous connection of two consecutive intermediates, namely *HCOOH and *OCH (or *HCO). A detailed description can be found in Section S9 of the ESI.†
While we have shown above that including less-stable intermediate states can lead to new reaction channels with improved catalytic activity, it is still not clear whether the less-stable intermediate sates are truly accessible during catalytic operation. To gain deeper insights into their stability and feasibility as new reaction channels, we have calculated the rotational free-energy barrier between the less and most stable intermediate states, as summarized in Table S3 of Section S10 of the ESI.† The rotational energy barrier is then compared with the energy required for the competing protonation reactions, as shown in Fig. 5b for the *OCH and *HCO intermediates as a representative example. Before analyzing Fig. 5b, let us first discuss the accessibility of the *OCH and *HCO intermediates. On the hand, *OCH and *HCO can be formed after *CO protonation, both being exergonic processes (Fig. 5a). On the other hand, if no free internal rotations are assumed, only *OCH—the less-stable intermediate state—can be formed after *HCOOH protonation, with a small free-energy penalty of 0.14 eV. This suggests that the formation of *OCH is more probable and therefore more accessible than *HCO. Nevertheless, the stability of the less-stable intermediate state is still unclear and questions whether *OCH will transition to *HCO or protonate instead.
As shown in Fig. 5b, the rotation of *OCH to *HCO and the reverse process (green region) have a free-energy barrier of 0.51 and 0.82 eV, respectively, while their protonation to *HOCH (blue region) and *HCOH (salmon region) are endergonic processes with a reaction energy of 0.20 and 0.36 eV, respectively. From Fig. 5b it is evident that the rotation from one state to another requires a higher energy barrier (kinetics) compared to the thermodynamic barrier for their protonation, which points to a high stability of the intermediate and suggests that the intermediate will protonate rather than rotate to the other state. Note that for a better comparison, the knowledge of the free-energy barrier for the protonation step is required. While we have not explicitly calculated the protonation energy barriers, they are known to be small (0.15 eV to 0.25 eV).58,59 Particularly, the *HCO protonation to *HCOH is a process with a small free-energy barrier of 0.16 eV for the Cu(100) surface.60 Therefore, if these values are considered (and added to the reaction energy if necessary), the protonation step is also kinetically more favorable (lower free-energy barrier) than the rotation, which suggests that the intermediate will prefer to protonate rather than rotate. Finally, it is important to consider that protonation steps are potential dependent while rotations are not. Therefore, at large cathodic overpotentials, the protonation step is clearly preferred over rotation to the more stable intermediate. Similarly, a high stability of the less-stable intermediate states is also observed for the other surfaces and less-stable intermediates states (i.e., *HOCH and *HOCH2), with the only exception of *OCH and *HOCH2 on the 7*OH and 6*OH–1*F surfaces, as summarized in Section S10 of the ESI.† Overall, these results point to a high stability of the less-stable intermediate states and their feasibility as new reaction channels.
The tacit assumption used in previous works34–38 that the most thermodynamically stable configurations of two consecutive reaction intermediates are well connected may not be true. For an improved mechanistic description, reaction intermediates must be well connected to each other and must not exhibit internal rotations, especially for those systems with high coverage. This implies that energetically less-stable intermediate states have to be considered in the analysis, which can lead to increased or reduced catalytic activity for a particular reaction channel.
Fig. 5c illustrates the potential dependency of CO2RR to CH3OH when the most stable (and also less-stable) intermediate states are considered in the analysis. The effect of incorporating less-stable intermediate states in the analysis is rapidly observed (i.e., at U < −0.15 V vs. RHE) and is maintained under larger cathodic potentials. Initially, the limiting span (i.e., *CO2 → CH3OH(aq)) is limited by the strong *CO2 adsorption and thus no effects are observed. At medium cathodic potentials (i.e., −0.45 < U < −0.15 V vs. RHE), the limiting span for the most stable intermediates is either governed by the presence of the intermediate states *HCO or *HCOH. In contrast, the consideration of the less-stable intermediate states switches the mechanism to an energetically favorable path, which contains neither *HCO nor *HCOH. Finally, at large cathodic potentials (i.e., U < −0.45 V vs. RHE), the limiting span for the most stable intermediate states is *CO → *COH. While in this case no other less-stable configurations are considered for *CO and *COH, the *CO intermediate can form *OCH, which then evolves to CH3OH via a less energy-intensive pathway, and the limiting span switches to *CO2 → *COOH.
Let us now evaluate the effect of including less-stable intermediate states on the CO2RR selectivity for the different surface models at working conditions (i.e., U = −0.4 V vs. RHE). As visible in Fig. 5d, H2 is still the most selectively produced product for the Ti3C2–7*OH surface as observed in experiments with large *OH coverage.27 With increasing *F coverage, CH3OH and CH4 become the more selectively produced products, which is in better agreement with the experiments at high *F content,28 where the most selectively produced products are CO and CH3OH. Interestingly, only when including also less-stable intermediate states in our analysis, we can predict a high selectivity toward CH3OH compared to the traditional approach (Fig. 4d). We suggest that this change of selectivity is a result of the different *CH2OH and *HOCH2 interactions with the surfaces, as exemplified in Fig. 5e for the CO2RR to CH3OH on the Ti3C2–*3OH–4*F surface model. If only the most stable intermediate states are considered (dark blue lines) the limiting span is *CH2OH → CH3OH(aq). However, when the less-stable *HOCH2 intermediate state is incorporated into the analysis, the step *HOCH2 → CH3OH(aq) is not energetically demanding and the limiting span switches to *CO2 → *COH with a decrease in the Gmax(U). A change in the limiting span *CH2OH → CH3OH(aq) is also observed for the other surfaces with high *F coverage as shown in Fig. S14–S16 in Section S8 in the ESI.†
So far, we have addressed the underestimation of the selectivity toward CH3OH for surfaces with high *F content. From our results, we conclude that for large *F composition, the selectivity trend is in the order of CH3OH > CH4 > H2 > CO > HCOOH, which is still not entirely consistent with the experiments where CO is the major product followed by CH3OH.28 In the following section, we discuss the importance of coadsorbates in the search for less-stable configurations that direct the selectivity toward CO. However, before we move on to the next section, there is still one thing that deserves further explanation. The reader may wonder why we just claimed that the selectivity toward CH3OH is larger than toward CH4 when the Gmax(U) of CH3OH and CH4 are the same (cf.Fig. 5d). We come to this conclusion because electrocatalytic processes with a smaller number of proton–electron transfer steps result in a larger exchange current density, which translates into higher electrocatalytic activity.61 While CH3OH formation requires 6 proton–electron transfer steps, the formation of CH4 requires 8, and therefore we argue that CH3OH formation is kinetically preferred over CH4 formation, in line with experimental observations.28
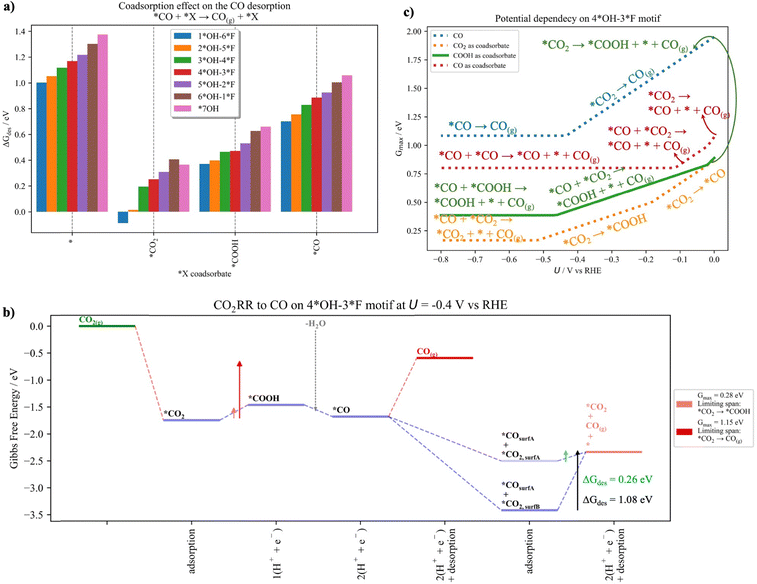
5.2 Effect of including coadsorbates
In this section we evaluate the CO formation in the presence of coadsorbates and discuss how this situation can modify the catalytic activity. We have shown in the previous section that our predicted selectivity toward CO disagrees with experiments.28 The main limitation for CO formation is the strong interaction of *CO2 and *CO with the surface, which limits CO production at low and large cathodic potentials, respectively (Fig. 4c). Therefore, we have evaluated how the presence of coadsorbates may affect the CO formation. To do so, we have studied the CO2RR to CO on the neighboring available site (see Fig. S18 in Section S11 in the ESI†) and evaluated how *CO2, *COOH and *CO coadsorbates affect the CO production.Fig. 6a depicts the CO desorption energy without coadsorbates and when *CO2, *COOH and *CO are present as coadsorbates, respectively. From Fig. 6a, it is evident that the presence of neighboring species reduces the CO desorption energy for all the surface models. Larger changes are observed for *CO2 and *COOH compared to *CO, which we attribute to increased steric effects for the former intermediates. Interestingly, as shown in Fig. 6b, the presence of a *CO2 coadsorbate leads to a decrease of the descriptor Gmax(U), which we trace to a less-stable configuration compared to the situation where the two intermediates are not direct neighbors. Note that the terminology “surfA” and “surfB” is used to distinguish between directly adjacent sites and non-adjacent sites, respectively. It turns out that the new less-stable configuration (*CO2,surfA) reduces the *CO desorption energy compared to the situation without the coadsorbate or without direct proximity to CO (*CO2,surfB). Detailed free-energy diagrams including also *COOH and *CO as coadsorbates for all the surfaces can be found in Section S12 of the ESI.†
Finally, we evaluate how the presence of coadsorbates changes the activity descriptor Gmax(U) as a function of the applied potential (Fig. 6c). For the potential dependency of the other surfaces, we direct the reader to Section S12 of the ESI.† Note that in Fig. 6c, we have considered four different scenarios for the *CO desorption, namely: (i) no coadsorbate is present or (ii) *CO2, (iii) *COOH, or (iv) *CO is present as a coadsorbate. As explained above, when no coadsorbate is present, *CO2 adsorption and *CO desorption are limiting the span at low and large cathodic potentials (i.e., *CO2 → CO(g) and *CO → CO(g)), respectively (blue line). As evident from Fig. 6b, the presence of coadsorbates modifies the energetics in such a way that Gmax(U) is reduced with the concomitant increase of the catalytic activity. Particularly the presence of a neighboring *CO2 substantially reduces the Gmax(U) and thus promotes CO formation. Interestingly, at working conditions (i.e., U = −0.4 V vs. RHE), it is no longer the *CO desorption that is limiting the span but rather formation of the *COOH intermediate (*CO2 → *COOH). As shown by the horizontal lines in Fig. 6c, there is a threshold electrode potential where *CO desorption is the limiting step and switching to higher cathodic potentials does not lead to an increase in catalytic activity. Therefore, weakening the *CO interaction with the surface by producing less-stable configurations due to the presence of coadsorbates is an efficient way to control CO formation. To conclude, we suggest that after CO2 adsorbs on the neighboring site, *CO will efficiently desorb and the remaining *CO2 can be converted into another C1 species (Fig. 6b).
5.3 Selectivity trends
Finally, let us evaluate the selectivity on the different surfaces if less-stable intermediate states and coadsorbates effects are considered in our analysis. Table 1 summarizes the calculated Gmax(U) at working conditions (U = −0.4 V vs. RHE) for the different products and the predicted selectivity based on such values. We refer the interested reader to Section S13 of the ESI† for the potential dependency of all surface models when less-stable intermediate states and coadsorbates are included in the analysis.| Surface | G max (U = −0.4 V vs. RHE) | Selectivity | ||||
|---|---|---|---|---|---|---|
| H2(g) | CO(g) | HCOOH(aq) | CH3OH(aq) | CH4(g) | ||
| 7*OH | 0.61 | 0.70 | 1.71 | 0.70 | 0.68 | H2 > CH4 > CO > CH3OH > CO > HCOOH |
| 6*OH–1*F | 0.62 | 0.48 | 1.73 | 0.48 | 0.48 | CO ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH3OH CH3OH ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH4 > H2 > HCOOH CH4 > H2 > HCOOH |
| 5*OH–2*F | 0.64 | 0.39 | 1.73 | 0.39 | 0.39 | CO ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH3OH CH3OH ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH4 > H2 > HCOOH CH4 > H2 > HCOOH |
| 4*OH–3*F | 0.64 | 0.28 | 1.73 | 0.28 | 0.28 | CO ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH3OH CH3OH ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH4 > H2 > HCOOH CH4 > H2 > HCOOH |
| 3*OH–4*F | 0.64 | 0.25 | 1.68 | 0.25 | 0.25 | CO ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH3OH CH3OH ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH4 > H2 > HCOOH CH4 > H2 > HCOOH |
| 2*OH–5*F | 0.63 | 0.20 | 1.66 | 0.20 | 0.20 | CO ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH3OH CH3OH ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH4 > H2 > HCOOH CH4 > H2 > HCOOH |
| 1*OH–6*F | 0.62 | 0.14 | 1.63 | 0.14 | 0.14 | CO ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH3OH CH3OH ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH4 > H2 > HCOOH CH4 > H2 > HCOOH |
From Table 1, different three clear trends can be observed: (i) while HER is favored for the fully hydroxylated surface, the selectivity shifts toward CO2RR with increasing *F content, which is in line with experiments.27,28 (ii) The larger the *F coverage, the more active (i.e., lower Gmax(U)) is the Ti3C2Tx surface for CO2RR. (iii) HCOOH formation is not feasible for the selected systems. Focusing on the most selectively generated CO2RR products, the predicted selectivity using the descriptor Gmax(U) is the same for CO, CH3OH, and CH4. Nevertheless, reactions with a smaller number of proton–electron transfer steps are generally faster (higher exchange current density) than reactions that require more proton–electron transfer steps. As the CO2RR to CO, CH3OH, and CH4 consists of 2, 6, and 8 proton–electron transfer steps, respectively, we suggest that the selectivity for the *F-covered surfaces is in the order: CO > CH3OH > CH4 > H2 > HCOOH, which is consistent with the experiments.28 This qualitative agreement with the experimental data could only be achieved if less-stable intermediate states and coadsorbates are included in our computational analysis.
6 Conclusions
In the present manuscript, we introduce a new way of thinking for the investigation of proton-coupled electron transfer steps with applications in energy conversion and storage from a computational perspective. While the traditional approach used in electronic structure theory to derive activity and selectivity trends is based on the construction of free-energy diagrams using the thermodynamically most stable intermediate structures only, we ponder on the importance of incorporating also less-stable intermediate states and coadsorbates in the analysis of adsorption free energies. We benchmark our new concept using the CO2RR over Ti3C2Tx (Tx = *OH and/or *F) surfaces with different *OH/*F coverage as a model system. We demonstrate that less-stable intermediate states lead to energetically favored reaction channels, and only by including these new pathways, we find good agreement with experimental data. Notably, we also show based on rotational barriers that the less-stable intermediates are stable on the electrode surface, which corroborates their feasibility as new reaction channels. In addition, we demonstrate the key aspect of including coadsorbate species in the analysis, which also give rise to less-stable configurations and are particularly relevant for CO formation. We believe that the introduced concept of considering less-stable intermediate states and coadsorbates when analyzing free-energy diagrams to predict activity and selectivity trends is not a unique feature of the CO2RR over Ti3C2Tx, but rather a universal feature to be considered in future computational research to develop improved materials for energy conversion applications.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
PLR and KSE thank the Ministry of Culture and Science of the Federal State of North Rhine-Westphalia (NRW Return Grant) for financial support to carry out this study. KSE further acknowledges funding by RESOLV Cluster of Excellence, funded by the Deutsche Forschungsgemeinschaft under Germany's Excellence Strategy – EXC 2033 – 390677874 – RESOLV.References
- F. Barbir, Transition to Renewable Energy Systems with Hydrogen as an Energy Carrier, Energy, 2009, 34, 308–312 CrossRef CAS
.
- Q. Lu and F. Jiao, Electrochemical CO2 Reduction: Electrocatalyst, Reaction Mechanism, and Process Engineering, Nano Energy, 2016, 29, 439–456 CrossRef CAS
.
- M. Götz, J. Lefebvre, F. Mörs, A. M. Koch, F. Graf, S. Bajohr, R. Reimert and T. Kolb, Renewable Power-to-Gas: A Technological and Economic Review, Renewable Energy, 2016, 85, 1371–1390 CrossRef
.
- A. Mazza, E. Bompard and G. Chicco, Application of Power to Gas Technologies in Emerging Electrical Systems, Renewable Sustainable Energy Rev., 2018, 92, 794–806 CrossRef CAS
.
- P. Lozano-Reis, H. Prats, P. Gamallo, F. Illas and R. Sayós, Multiscale Study of the Mechanism of Catalytic CO2 Hydrogenation: Role of the Ni(111) Facets, ACS Catal., 2020, 10, 8077–8089 CrossRef CAS
.
- P. Lozano-Reis, H. Prats, R. Sayós and F. Illas, Limitations of Free Energy Diagrams to Predict the Catalytic Activity: The Reverse Water Gas Shift Reaction Catalyzed by Ni/TiC, J. Catal., 2023, 425, 203–211 CrossRef CAS
.
- P. Lozano-Reis, P. Gamallo, R. Sayós and F. Illas, Comprehensive Density Functional and Kinetic Monte Carlo Study of CO2 Hydrogenation on a Well-Defined Ni/CeO2 Model Catalyst: Role of Eley-Rideal Reactions, ACS Catal., 2024, 14, 2284–2299 CrossRef CAS PubMed
.
- M. A. A. Aziz, A. A. Jalil, S. Triwahyono and A. Ahmad, CO2 Methanation over Heterogeneous Catalysts: Recent Progress and Future Prospects, Green Chem., 2015, 17, 2647–2663 RSC
.
- R. P. Ye, J. Ding, W. Gong, D. M. Argyle, Q. Zhong, Y. Wang, K. C. Rusell, Z. Xu, G. A. Russel, Q. Li, M. Fan and Y. G. Yao, CO2 hydrogenation to high-value products via heterogeneous catalysis, Nat. Commun., 2019, 10, 5698 CrossRef CAS PubMed
.
- D. Dolz, R. De Armas, P. Lozano-Reis, A. Morales-García, F. Viñes, R. Sayós and F. Illas, Understanding the Reverse Water Gas Shift Reaction over Mo2C MXene Catalyst: A Holistic Computational Analysis, ChemCatChem, 2024, 16, e202400122 CrossRef CAS
.
- P. Li, Z. Qi and D. Yan, Rare Earth Er-Nd Dual Single-AtomicCatalysts for Efficient Visible-light Induced CO2 Reduction to CnH2n+1OH (N = 1, 2), Angew. Chem., Int. Ed., 2024, 63, e202411000 CrossRef CAS PubMed
.
- P. Chen, B. Lei, X. Dong, H. Wang, J. Sheng, W. Cui, J. Li, Y. Sun, Z. Wang and F. Dong, Rare-Earth Single-Atom La-N Charge-Transfer Bridge on Carbon Nitride for Highly Efficient and Selective Photocatalytic CO2 Reduction, ACS Nano, 2020, 14, 15841–15852 CrossRef CAS PubMed
.
- S. Ji, Y. Qu, T. Wang, Y. Chen, G. Wang, X. Li, J. Dong, Q. Y. Chen, W. Zhang, Z. Zhang, S. Liang, R. Yu, Y. Wang, D. Wang and Y. Li, Rare-Earth Single Erbium Atoms for Enhanced Photocatalytic CO2 Reduction, Angew. Chem., Int. Ed., 2020, 59, 10651–10657 CrossRef CAS PubMed
.
- X. Li, L. Li, G. Chen, X. Chu, X. Liu, C. Naisa, D. Pohl, M. Löffler and X. Feng, Accessing parity-forbidden d-d transitions for photocatalytic CO2 reduction driven by infrared light, Nat. Commun., 2023, 14, 4034 CrossRef CAS PubMed
.
- S. Nitopi, E. Bertheussen, B. S. Scott, X. Liu, K. A. Engstfeld, S. Horch, B. Seger, E. L. I. Stephens, K. Chan, C. Hahn, J. K. Norskov, T. F. Jaramillo and I. Chorkendorff, Progress and Perspectives of Electrochemical CO2 Reduction on Copper in Aqueous Electrolyte, Chem. Rev., 2019, 119, 7610–7672 CrossRef CAS PubMed
.
- L. E. Clark, C. Hahn, T. F. Jaramillo and A. T. Bell, Electrochemical CO2 Reduction over Compressively Strained CuAg Surface Alloys with Enhanced Multi-Carbon Oxygenate Selectivy, J. Am. Chem. Soc., 2017, 139(44), 15848–15857 CrossRef PubMed
.
- W. Fan, Y. Liu, C. Zhang, X. Chen, D. He, M. Li, Q. Hu, X. Jiao, Q. Chen and Y. Xie, Confined CO in a Sandwich Structure Promotes C-C Coupling in Electrocatalytic CO2 Reduction, Mater. Horiz., 2024, 11, 4183–4189 RSC
.
- L. R. L. Ting, O. Piqué, S. Y. Lim, M. Tanhaei, F. Calle-Vallejo and B. S. Yeo, Enhancing CO2 Electroreduction to Ethanol on Copper-Silver Composites by Opening an Alternative Catalytic Pathway, ACS Catal., 2020, 10, 4059–4069 CrossRef CAS
.
- A. D. Handoko, F. Wei, Jenndy, B. S. Yeo and Z. W. Seh, Understanding Heterogeneous Electrocatalytic Carbon Dioxide Reduction Through Operando Techniques, Nat. Catal., 2018, 1, 922 CrossRef CAS
.
- Q. Kong, X. An, Q. Liu, L. Xie, J. Zhang, Q. Li, W. Yao, A. Yu, Y. Jiao and C. Sun, Copper-based Catalysts for the Electrochemical Reduction of Carbon Dioxide: Progress and Future Prospects, Mater. Horiz., 2023, 10, 698–721 RSC
.
- J. Peng, Z. Shi, J. Jiang, P. Zhang, J. P. Hsu and N. Li, Charge-orbital Synergistic Engineering of TM@Ti3C2O1−xBx for Highly Selective CO2 Electrochemical Reduction, Mater. Horiz., 2023, 10, 4278–4292 RSC
.
- Y. Y. Birdja, E. Pérez-Gallent, M. C. Figueiredo, A. J. Göttle, F. Calle-Vallejo and M. T. M. Koper, Advances and Challenges in Understanding the Electrocatalytic Conversion of Carbon Dioxide to Fuels, Nat. Energy, 2019, 4, 732–745 CrossRef CAS
.
- X. Zhang, S. X. Guo, K. A. Gandionco, A. M. Bond and J. Zhang, Electrocatalytic Carbon Dioxide Reduction: from Fundamental Principles to Catlayst Design, Mater. Today Adv., 2020, 7, 100074 CrossRef
.
- P. Saha, S. Amanullah and A. Dey, Selectivity in Electrochemical CO2 Reduction, Acc. Chem. Res., 2022, 55, 134–144 CrossRef CAS PubMed
.
- O. Christensen, A. Bagger and J. Rossmeisl, The Missing Link for Electrochemical CO2 Reduction: Classification of CO vs. HCOOH Selectivity via PCA, Reaction Pathways and Coverage Analysis, ACS Catal., 2024, 14, 2151–2161 CrossRef CAS
.
- B. Anasori, M. R. Lukatskaya and Y. Gogotsi, 2D metal carbides and nitrides (MXenes) for energy storage, Nat. Rev. Mater., 2017, 2, 16098 CrossRef CAS
.
- H. Bao, Y. Qui, X. Peng, J. Wang, Y. Mi, S. Zhao, X. Liu, Y. Liu, R. Cao, L. Zhuo, J. Ren, J. Sun, J. Luo and X. Sun, Isolated Copper Single Sites for High-performance Electroreduction of Carbon Monoxide to Multicarbon products, Nat. Commun., 2021, 12, 283 CrossRef PubMed
.
- S. Krishnan, S. Marimuthu, M. K. Singh and D. K. Rai, Two-dimensional Ti3C2Tx MXene Nanosheets for CO2 Electroreduction in Aqueous Electrolytes, Energy Adv., 2023, 2, 1166 RSC
.
- J. Greely, T. F. Jaramillo, J. Bonde, I. Chorkendorff and J. K. Norskov, Computational High-throughput Screening of Electrocatalytic Materials for Hydrogen Evolution, Nat. Mater., 2006, 5, 909 CrossRef PubMed
.
- B. C. Yeo, H. Nam, H. Nam, M. C. Kim, H. W. Lee, S. C. Kim, S. O. Won, D. Kim, K. Y. Lee, S. Y. Lee and S. S. Han, High-throughput Computational-Experimental Screening protocol for the Discovery of Bimetallic Catalysts, npj Comput. Mater., 2021, 7, 137 CrossRef CAS
.
- S. Wang, V. Petzold, V. Tripkovic, J. Kleis, J. G. Howalt, E. Skúlason, E. M. Fernández, G. Jones, A. Toftelund, H. Falsig, M. Björketun, F. Studt, F. Abild-Pedersen, J. Rossmeisl, J. K. Norskov and T. Bligaard, Universal Transition State Scaling Relations for (De)Hydrogenation over Transition Metals, Phys. Chem. Chem. Phys., 2011, 13, 20760–20765 RSC
.
- S. Wang, B. Temel, J. Shen, G. Jones, L. C. Grabow, F. Studt, T. Bligaard, F. Abild-Pedersen, C. H. Christensen and J. K. Norskov, Universal Brønsted-Evans-Polanyi Relations for C–C, C–O, C–N, N–O, N–N and O–O Dissociation Reactions, Catal. Lett., 2011, 141, 370–373 CrossRef CAS
.
- H. Ooka, J. Huang and K. S. Exner, The Sabatier Principle in Electrocatalysis: Basics, Limitations, and Extensions, Front. Energy Res., 2021, 9, 654460 CrossRef
.
- Z. Chen, M. R. Gao, N. Duan, J. Zhang, Y. Q. Zhang, T. Fan, J. Zhang, Y. Dong, J. Li, Q. Liu, X. Yi and J. L. Luo, Tuning Adsorption Strenght of CO2 and its Intermediates on Tin Oxide-based Electrocatalyst for Efficient CO2 Reduction towards Carbonaceous Products, Appl. Catal., B, 2020, 277, 119252 CrossRef CAS
.
- O. Piqué, F. Viñes, F. Illas and F. Calle-Vallejo, Elucidating the Structure of Ethanol-Producing Active Sites at Oxide-Derived Cu Electrocatalysts, ACS Catal., 2020, 10, 10488–10494 CrossRef
.
- Y. Xie, P. Ou, X. Wang, Z. Xu, Y. C. Li, Z. Wang, J. E. Huang, J. Wicks, C. McCallum, N. Wang, Y. Wang, T. Chen, B. T. W. Lo, D. Sinton, J. C. Yu, Y. Wang and E. H. Sargent, High Carbon Utilization in CO2 Reduction to Multicarbon Products in Acidic Media, Nat. Catal., 2022, 5, 564–570 CrossRef CAS
.
- D. Bao, Q. Zhang, F. L. Meng, H. X. Zhong, M. M. Shi, Y. Zhang, J. M. Yan, Q. Jiang and X. B. Zhang, Electrochemical Reduction of N2 under Ambient Conditions for Aritificial N2 Fixation and Renewable Energy Storage Using N2/NH3 Cycle, Adv. Mater., 2017, 29, 1604799 CrossRef PubMed
.
- X. Yu, Y. Xu, L. Li, M. Zhang, W. Qin, F. Che and M. Zhong, Coverage Enhancement Accelerates Acidic CO2 Electrolysis at Ampere-level Current with High Energy and Carbon Efficiencie, Nat. Commun., 2024, 15, 1711 CrossRef CAS PubMed
.
- K. S. Exner, Controlling Stability and Selectivity in the Competing Chlorine and Oxygen Evolution Reaction over Transition Metal Oxide Electrodes, ChemElectroChem, 2019, 6, 3401–3409 CrossRef CAS
.
- K. S. Exner, Desing Criteria for the Competing Chlorine and Oxygen Evolution Reactions: Avoid the OCl Adsorbate to Enhance Chlorine Selectivity, Phys. Chem. Chem. Phys., 2020, 22, 22451 RSC
.
- G. Kresse and J. Hafner, Ab Initio Molecular Dynamics for Liquid Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed
.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-energy Calculations Using a Plane-wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed
.
- G. Kresse and J. Furthmüller, Efficiency
of Ab-initio Total Energy Calculations for Metals and Semiconductors Using a Plane-wave Basis Set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, Origin of the Overpotential for Oxygen Reduction at a Fuel-Cell Cathode, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef PubMed
.
- J. A. Garrido Torres, P. C. Jennings, M. H. Hansen, J. R. Boes and T. Bligaard, Low-Scaling Algorithm for Nudged Elastic Band Calculations Using Surrogate Machine Learning Model, Phys. Rev. Lett., 2019, 122, 156001–156005 CrossRef CAS PubMed
.
- M. López, K. S. Exner, F. Viñes and F. Illas, Computational Pourbaix Diagrams for MXenes: A Key Ingredient toward Proper Theoretical Electrocatalytic Studies, Adv. Theory Simul., 2023, 6, 2200217 CrossRef
.
- L. Meng, L.-K. Yan, F. Viñes and F. Illas, Effect of Terminations on the Hydrogen Evolution Reaction Mechanism on Ti3C2 MXene, J. Mater. Chem. A, 2023, 11, 6886–6900 RSC
.
- K. S. Exner, A universal Descriptor for the Screening of Electrode Materials for Multiple-Electron Processes: Beyond the Thermodynamic Overpotential, ACS Catal., 2020, 10, 12607–12617 CrossRef CAS
.
- S. Razzaq and K. S. Exner, Materials Screening by the Descriptor Gmax(η): The Free-Energy Span Model in Electrocatalysis, ACS Catal., 2023, 13, 1740–1758 CrossRef CAS PubMed
.
- K. S. Exner, On the Mechanistic Complexity of Oxygen Evolution: Potential-dependent Switching of the Mechanism at the Volcano Apex, Mater. Horiz., 2023, 10, 2086–2095 RSC
.
- L. Granda-Marulanda, A. Rendón-Calle, S. Builes, F. Illas, M. T. M. Koper and F. Calle-Vallejo, A Semiempirical Method to Detect and Correct DFT-Based Gas-Phase Errors and Its Application in Electrocatalysis, ACS Catal., 2020, 10, 6900–6907 CrossRef CAS
.
- R. Urrego-Ortiz, S. Builes, F. Illas and F. Calle-Vallejo, Gas-phase Errors in Computational Electrocatalysis: a Review, EES Catal., 2024, 2, 157–179 RSC
.
- E. Tayyebi and K. S. Exner, Refining Free-Energy Calculations for Electrochemical Reactions: Unveiling Corrections beyond Gas-Phase Errors for Solvated Species and Ions, J. Phys. Chem. C, 2024, 128, 13732–13742 CrossRef CAS
.
- D. Zhang, Z. Wang, F. Liu, P. Yi, L. Peng, Y. Chen, L. Wei and H. Li, Unraveling the pH-Dependent Oxygen Reduction Performance on Single-Atom Catalysts: From Single-to-Duela-Sabatier Optima, J. Am. Chem. Soc., 2024, 146, 3210–3219 CrossRef CAS PubMed
.
- D. Zhang, F. She, J. Chen, L. Wei and H. Li, Why Do Weak-Binding M-N-C Single-Atom Catalysts Posses Anomalously High Oxygen Reduction Activity?, J. Am. Chem. Soc., 2025, 157, 6076–6086 CrossRef PubMed
.
- M. J. Janik, C. D. Taylor and M. Neurock, First-Principles Analysis of the Initial Electroreduction Steps of Oxygen over Pt(111), J. Electrochem. Soc., 2009, 156, B126–B135 CrossRef CAS
.
- V. Tripkovic, E. Skúlason, S. Siahrostmai, J. K. Nørskov and J. Rossmeisl, The Oxygen Reduction Reaction Mechanism on Pt(111) from Density Functional Theory Calculations, Electrochim. Acta, 2010, 55, 7975–7981 CrossRef CAS
.
- T. Cheng, H. Xiao and W. A. Goddard, Free-Energy Barriers and Reaction Mechanisms for the Electrochemical Reduction of CO on the Cu(100) Surface, Including Multiple Layers of Explicit Solvent at pH 0, J. Phys. Chem. Lett., 2015, 23, 4767–4773 CrossRef PubMed
.
- K. S. Exner, I. Sohrabnejad-Eskan and H. Over, A Universal Approach to Determine the Free Energy Diagram of an Electrocatalytic Reaction, ACS Catal., 2018, 8, 1864–1879 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Computational details, elementary steps for CO2RR and HER, calculation of formation Gibbs free energies, gas-phase error corrections, CO2RR to HCOOH under different pH conditions, activity descriptor Gmax(U), free energy diagrams and potential dependency for CO2RR and HER for the different Ti3C2Tx surface models for different assumptions, negative effect of including less-stable intermediate states, rotational energy barriers, and schematic representation of CO2RR to CO on the neighboring site of a preadsorbed CO. Relevant inputs and outputs for the different calculations have been also made available a public GitHub repository: https://github.com/plozanore/CO2RR_selectivity_key_role_of_less-stable_intermediate_states. See DOI: https://doi.org/10.1039/d5mh00168d |
| This journal is © The Royal Society of Chemistry 2025 |