Bioinspired wood-based wedge-shaped surface with gradient wettability for enhanced directional liquid transport and fog harvesting

Abstract

Inspired by cactus spine and desert beetle back structures, we developed a wood-based wedge-shaped surface with gradient wettability for efficient and controlled spontaneous directional liquid transport. Utilizing the natural anisotropic and porous structure of wood, the wedge-shaped surface exhibited a continuous gradient wettability after chemical treatments combined with UV-induced modifications. The resulting surface enabled highly efficient directional liquid transport with transport rates reaching up to 8.9 mm s⁻¹ on horizontal placement and 0.64 mm s⁻¹ on vertical surfaces against gravity. By integrating geometric curvature and surface energy gradients, the innovative design achieved synergistic Laplace pressure-driven and wettability-driven liquid motions. To further demonstrate its potential for practical application, a fog-driven power device constructed using the gradient wettability wood with cactus spines not only enhanced water harvesting and energy conversion capabilities but also offered an environmentally friendly system. This study expanded the design toolbox for bioinspired liquid management surfaces, offering promising applications in water resource management, energy harvesting, and microfluidic devices.

---

New concepts

This study introduces a new concept that synergistically utilizes the natural anisotropic structure of wood with biomimetic features derived from cactus spines and desert beetle backs. Unlike traditional synthetic materials or micro-nanofabricated surfaces, we leveraged the inherent properties of wood to create a wedge-shaped surface with a continuous gradient wettability. This innovative design integrates the geometric curvature and surface energy gradients, enabling spontaneous and highly efficient directional liquid transport both horizontally and vertically against gravity. This concept fundamentally differs from existing approaches by offering a scalable, environmentally friendly solution that eliminates the reliance on complex fabrication techniques. It bridges the gap between natural inspiration and practical application, expanding the toolbox for sustainable material design. Our findings not only advanced the understanding of liquid transport mechanisms but also opened new avenues for applications in water harvesting, microfluidics, and energy conversion technologies, demonstrating the transformative potential of bioinspired materials in addressing global resource challenges.

1. Introduction

Directional liquid transport technology has significant promise in engineering applications, including microfluidics,^1–3 energy harvesting,^4,5 water resource management,^6–9 and medical devices.^10,11 Efficient liquid transport systems are essential for addressing global challenges, including water scarcity, sustainable energy development, and advanced healthcare technologies. Recent advancements in directional liquid transport have significantly enhanced liquid manipulation efficiency, enabling precise control and high-performance applications. However, despite these advancements, current technologies face considerable challenges, particularly in achieving high transport efficiency, environmental sustainability, and adaptability to diverse operational environments.

Traditional directional liquid transport materials include metals^12,13 (e.g., copper, aluminum), polymers^14–16 (e.g., PDMS, PTFE), and silicon-based materials.^17,18 Metals are widely used for their excellent mechanical strength and thermal conductivity, such as in the construction of gradient surfaces with copper nanopillar arrays for fog collection and liquid guidance.¹⁹ Polymers are favored for their ease of fabrication and customizable surface chemistry, as demonstrated by PDMS surfaces with microstructures that enable wettability gradient-driven droplet manipulation.²⁰ Silicon-based materials, while popular due to their compatibility with micro–nanofabrication techniques, face limitations in broader application due to the high cost of processing equipment and chemical reagents.²¹ In terms of structural design, various geometries significantly influence the efficiency of liquid directional transport. Conical and wedge-shaped structures are among the most used, generating Laplace pressure gradients through curvature differences to drive droplets from high- to low-curvature regions.^22–24 For example, Yu et al.²⁵ reported a titanium dioxide-coated conical spine utilized for water collection and transport. This design demonstrated high efficiency in liquid guidance and revealed the mechanism of directional self-transport of water droplets beneath oil on its surface. Similarly, microgrooves or channels guide droplets along predefined paths, minimizing dispersion and enhancing control, which is particularly useful in microfluidic devices.^26,27 Furthermore, hierarchical structures, combining microscale and nanoscale features, amplify wettability contrasts and enhance driving forces, resulting in markedly improved liquid transport performance.^28,29 Despite these advancements, these designs often rely on precise and sophisticated micro–nanofabrication techniques, such as laser etching and chemical vapor deposition. Such processes are not only costly but also less environmentally friendly, posing significant challenges for large-scale implementation and sustainable applications.

Wood, with its unique microstructure and sustainability, exhibits immense potential and advantages in directional liquid transport. As a natural material, its porous network and anisotropic structure provide an ideal foundation for constructing liquid transport channels.^30–34 The internal vessels and tracheids create vertically aligned pathways, enabling rapid liquid flow with minimal resistance.^35–39 Moreover, the distinct characteristics of earlywood and latewood, such as differences in density and porosity, enhance the diversity and controllability of liquid transport. Earlywood, with its thin cell walls, facilitates efficient fluid conduction, while latewood, with thicker cell walls and a denser structure, effectively regulates flow.^40–42 This natural hierarchical arrangement requires no complex processing, making wood inherently suited for designing surfaces for directional liquid transport. For example, Wang et al.⁴³ leveraged the structural differences between earlywood and latewood, combined with selective chemical modifications, to create wood surfaces with specific gradient wettability for liquid directional transport. Overall, wood's inherent structural features, ease of processing, and functionalization position it as a versatile and sustainable material for advanced liquid transport systems. Recent studies have explored wood's potential for directional liquid transport, but few have utilized bioinspired principles to enhance its performance.

Nature offers an abundance of efficient designs for directional liquid transport. For instance, a cactus spine exhibits a conical curvature that generates Laplace pressure gradients, driving liquid motion, while the backs of desert beetles demonstrate gradient wettability that facilitate directional droplet movement. These systems combine the geometric structure and surface energy to achieve exceptional liquid transport efficiency under challenging conditions. Inspired by these mechanisms, bioinspired materials have increasingly been used to mimic nature's designs for advanced applications. However, these efforts often rely on synthetic materials or micro–nanofabrication techniques, which are costly, environmentally unfriendly, and difficult to scale up.

This study bridges the gap between natural materials and bioinspired principles by integrating the anisotropic structure of wood with the bioinspired mechanisms of cacti and desert beetles. By leveraging wood's hierarchical architecture and natural transport channels, combined with surface modifications that mimic gradient wettability and curvature-driven pressure differentials, this work introduces a sustainable and scalable solution for directional liquid transport. The conical geometry of cacti spines and a wedge-shaped wood surface was combined to obtain a controlled gradient wettability, enabling synergistic liquid motion driven by both Laplace pressure and surface energy gradients. Compared with previously reported wood-based liquid transport systems that mainly focus on either structural anisotropy or chemical modification alone, our design integrated geometric shape, inherent anisotropic structure, and a precisely tunable gradient wettability. This unique combination significantly improved directional liquid transport efficiency, avoided the complexity and high cost associated with traditional micro–nanofabrication methods, and enhanced scalability and environmental friendliness. Experimental results revealed that the gradient wettability wedge-shaped wood enabled unidirectional liquid transport under both horizontal and inclined conditions. In horizontal placement, the liquid transport rate reached up to 8.9 mm s⁻¹, while under inclined placement (e.g., at a 90° angle), the liquid (4 μL) still achieved upward transport against gravity at a rate of 0.64 mm s⁻¹. These findings systematically elucidated the mechanism of the synergistic interaction between geometric driving forces and gradient wettability. Furthermore, utilizing this gradient wettability wedge-shaped wood, a highly efficient fog-driven energy device was developed, demonstrating performance significantly superior to traditional fog collection systems. This innovative design not only expanded the methodology for creating bioinspired liquid management surfaces but also provided critical insights for advancing developments in the field of water collection and energy conversion.

2. Materials and methods

2.1 Materials

Scots pine (Pinus sylvestris L.) wood was sourced from Fulinmen Wood Co., Ltd (Sichuan, China). Before use, the wood was processed into samples with dimensions of 20 mm × 2 mm × 2 mm (L × R × T, wedge angle: 5°), 20 mm × 3 mm × 2 mm (L × R × T, wedge angle: 9°), and 20 mm × 5 mm × 2 mm (L × R × T, wedge angle: 15°). Silane coupling agent KH-550, poly(vinylidene fluoride-co-hexafluoropropylene) (PVDF–HFP), dimethylformamide (DMF), and anatase titanium dioxide (TiO₂) nanoparticles (30–60 nm) were purchased from Macklin Biochemical Co., Ltd. Sodium chlorite (NaClO₂, ∼80%) and hydrogen peroxide (H₂O₂, 30%) were obtained from Shanghai Aladdin Biochemical Technology Co., Ltd., while acetic acid (CH₃COOH, ∼99%) and ethanol were supplied by Nanjing Chemical Reagent Co., Ltd. All chemicals were used as received without further purification.

2.2 Preparation of wedge-shaped wood with a grooved structure

First, the natural wedge-shaped wood (NWW) was pretreated in a 1 wt% NaOH aqueous solution at 80 °C for 1 hour. Subsequently, the pretreated wood was immersed in a 1 wt% NaClO₂ aqueous solution at 80 °C for 2 hours, with the solution pH adjusted to 4.6 using CH₃COOH, resulting in the delignified wedge-shaped wood (DWW). The DWW was thoroughly washed with anhydrous ethanol to remove residual chemicals and then dried by freeze-drying.

A plasticizing solution was prepared by dissolving 2 g of PVDF–HFP in 100 mL of DMF at 60 °C in a water bath for 1 hour until fully dissolved. The DWW was immersed in the plasticizing solution under a vacuum pressure of 0.095 MPa for 12 hours, resulting in PVDF–HFP-impregnated wedge-shaped wood (PWW). The PWW was washed several times with deionized water and stored in anhydrous ethanol for further use (Fig. 1). The wedge angles (5°, 9°, and 15°) were specifically selected to systematically evaluate the influence of geometric gradients on directional liquid transport performance. A smaller wedge angle (5°) generates higher Laplace pressure, facilitating rapid liquid transport ideal for microfluidics or precision liquid handling, while a larger angle (15°) provides greater structural stability, which is more suitable for scaling up to practical applications such as large-area fog harvesting. The 9° wedge angle was deliberately chosen as a representative middle ground, offering a balance between transport efficiency (as seen in 5°) and structural robustness (as in 15°), making it ideal for evaluating scalability under practical conditions.

Fig. 1 The preparation process of gradient wettability wedge-shaped wood (GWW).

2.3 Preparation of gradient-wettability wedge-shaped wood

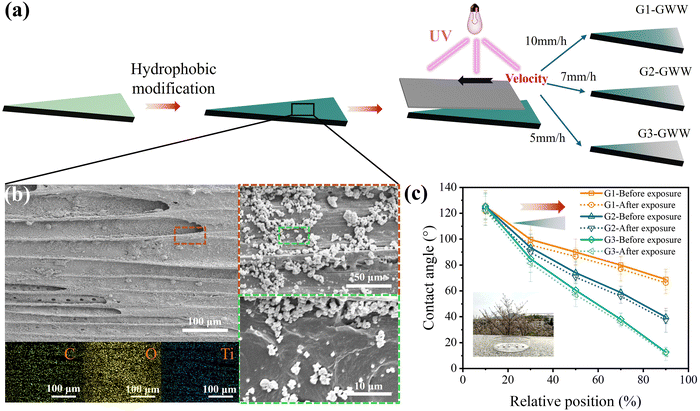
First, 3 g of titanium dioxide (TiO₂) was added to 60 mL of anhydrous ethanol and stirred vigorously for 30 minutes, followed by ultrasonication for 30 minutes to achieve a uniform dispersion. Then, 0.15 g of silane coupling agent KH-550 was slowly added dropwise into the TiO₂ ethanol solution, stirred for 30 minutes, and sonicated again for 30 minutes to ensure homogeneity. The PWW was immersed in the prepared solution, stirred gently for 5 minutes, and then sonicated for another 5 minutes. The sample was removed, rinsed thoroughly with ethanol, and dried in an oven for 6 hours, resulting in hydrophobic wedge-shaped wood (HWW).

The HWW was then exposed to UV light with a wavelength of 365 nm, positioned 5 cm away from the lamp. A light-blocking film was used to cover the entire surface of the HWW and was gradually moved along the wedge's length from the base to the tip (Fig. 1). The film's movement rates were set to 10 mm h⁻¹, 7 mm h⁻¹, and 5 mm h⁻¹, respectively, to produce three gradient wettability wedge-shaped woods (GWW): G1-GWW, G2-GWW, and G3-GWW.

2.4 Design and application testing of the fog-driven power device

The fog-driven power device integrated the unique features of gradient wettability wedge-shaped wood (G3-GWW, wedge angle: 9°) and cactus spines (Echinopsis tubeiflora) for efficient fog collection and droplet transport. The cactus spine, connected to the tip of the gradient wettability wedge, utilized its biomimetic micro-nano structure and wettability gradient to capture fog from the air and guide microdroplets toward the wedge's tip. A pivot is positioned beneath the wedge, with a 0.5 g counterweight suspended below the tip, allowing the wedge to tilt under the weight of the collected water droplet, facilitating its detachment. The wedge then automatically resets, making the device reusable and modular in design.

In the manual water-dropping experiment, a micropipette was used to add 5 μL of water at the tip of the device. A high-resolution camera recorded the device's response, including the rotation of the wedge and the detachment of the droplet. In the simulated fog environment, a commercial ultrasonic humidifier (Model: JSQ107, Guangdong Zhigao Air Conditioner Co., China) was used in a sealed chamber to simulate fog conditions with a fogging rate of 200 mL h⁻¹ and a fog density of 10 g m⁻³. The device was positioned 50 mm directly below the nozzle of the humidifier, with real-time monitoring of droplet capture, transport, and detachment processes.

To evaluate the stability and repeatability of a single fog-harvesting unit, an additional test was conducted. In this setup, the fog stream was aligned horizontally with the cactus spine of the individual fog-harvesting unit. The fog flow rate was controlled using a wind tunnel setup with an adjustable speed range of 0.5–2 m s⁻¹, monitored using an anemometer. The humidifier generated fog with a consistent density of 10 g m⁻³, and the device was tested at a distance of 30 mm from the nozzle. The detachment frequency and weight fluctuation of droplets collected by the single unit were recorded over 10 continuous cycles, with each droplet's weight monitored using a precision balance (accuracy: 0.1 mg). This setup ensured consistent fog exposure to the cactus spine, allowing detailed assessment of the stability and repeatability of the device under controlled conditions.

2.5 Characterization

The morphology and elemental distribution of the samples were analyzed using an environmental scanning electron microscope (ESEM) equipped with energy dispersive X-ray spectroscopy (ESEM-EDS, XL30ESEM-FEG, USA) under an accelerating voltage of 20 kV and a working distance of 10 mm. The three-dimensional surface profile of the samples was measured using a high-resolution 3D scanning system (Keyence, VHX-7000, Japan). Fourier-transform infrared spectroscopy (FTIR, Nexus 670, USA) was employed to detect compositional changes, with spectra recorded at a resolution of 2 cm⁻¹ over a range of 4000 to 400 cm⁻¹ and 32 scans. Elemental composition was determined via X-ray photoelectron spectroscopy (XPS, AXIS Ultra DLD, USA). The wettability of the samples was measured using a contact angle tester (FCA2000A, Shanghai Aifid Precision Instruments Co., Ltd), and droplet movement on the sample surfaces was recorded. Mechanical properties were evaluated using a universal testing machine (100 MTS system, Zwick, Germany).

3. Results and discussion

3.1 Preparation and characterization of grooved wedge-shaped wood

In Fig. 2a, the optical image of NWW reveals alternating light and dark bands on the wood surface, corresponding to earlywood and latewood, respectively. Earlywood, formed during the rapid growth phase of wood, is characterized by thin fiber cell walls and large lumen areas, whereas latewood, formed during the slower growth phase, has thicker cell walls and smaller lumens.^44,45 A 3D profilometry analysis confirmed the relatively smooth surface of NWW. SEM cross-sectional images further illustrate the intact structure of NWW, with tightly connected tracheids, while longitudinal sections reveal well-aligned tracheid arrangements, forming natural grooves that facilitate directional liquid transport. After delignification, DWW exhibited a light white surface, and its 3D profilometry revealed slight surface roughness. This change was attributed to the partial removal of lignin and hemicellulose, which exacerbated the structural differences between the earlywood and the latewood. SEM cross-sections show significant separation between tracheids in DWW, resulting from the effective removal of lignin-rich cell corners. However, longitudinal sections maintained the orderly arrangement of tracheids, with no significant structural alterations. Notably, the 3D profilometry of PWW highlighted pronounced groove structures. This was due to the excellent flexibility and hydrophilicity of PVDF–HFP, which uniformly infiltrated the cell lumens and walls during impregnation. Given the porous nature of earlywood, PVDF–HFP preferentially accumulated in these regions. During drying or subsequent processing, the greater volume shrinkage in earlywood created distinct groove structures. SEM images corroborated this observation, showing PVDF–HFP filling the intercellular spaces in cross-sections, while longitudinal sections retained the orderly arrangement of cell lumens. These structural features established a robust foundation for directional liquid transport.

Fig. 2 Morphology and structure of the samples. (a) Digital photographs and 3D profiles of the sample surfaces; (b) SEM images of the microstructures in cross-section and longitudinal section.

3.2 Preparation and characterization of gradient wettability wedge-shaped wood

To fabricate gradient wettability wedge-shaped wood (GWW), a method combining directional movement of a light-blocking mask and continuous ultraviolet (UV) irradiation was employed. As shown in Fig. 3a, PWW was immersed in a hydrophobic TiO₂-modified solution to obtain hydrophobic wedge-shaped wood (HWW). Scanning electron microscopy (SEM) images and elemental mapping confirmed the uniform distribution of TiO₂ nanoparticles within the wood cell cavities (Fig. 3b). This uniform distribution ensured consistent hydrophobicity across the wood surface, providing a solid foundation for subsequent wettability modulation. The photosensitivity of TiO₂ played a pivotal role in transforming hydrophobic wedge-shaped wood into gradient wettability wedge-shaped wood. Under UV irradiation, TiO₂ generates photoexcited electron-hole pairs, inducing surface photocatalytic reactions. These reactions form hydroxyl groups (–OH) and other hydrophilic moieties, increasing surface free energy and gradually converting the hydrophobic surface into a hydrophilic one.^46–48 By controlling UV exposure, the wettability of TiO₂-modified wood surfaces can be precisely regulated. To create a wettability gradient on the wedge surface, a movable light-blocking mask was employed. Under continuous UV irradiation, the mask moved at a constant speed from the bottom to the top of the wedge-shaped wood. This controlled movement resulted in varying UV exposure durations across the surface, causing differences in the extent of photocatalytic reactions and thus forming a gradient wettability. Regions with longer UV exposure developed higher hydroxyl content with a larger hydrophilicity, whereas regions with shorter exposure retained higher hydrophobicity. By adjusting the movement speed of the light-blocking mask, the wettability gradient could be precisely tailored. Three movement speeds were tested: 10 mm h⁻¹, 7 mm h⁻¹, and 5 mm h⁻¹, corresponding to three types of gradient wettability wedge-shaped wood: G1, G2, and G3. The contact angle for G1 decreased from 125° to 70°, for G2 from 125° to 40°, and for G3 from 125° to 10° (Fig. 3c). This controllable wettability gradient provided the driving force for directional liquid transport. This method offered significant advantages by preserving the natural microstructure of the wood while enabling precise modulation of surface wettability. The gradient wettability wedge-shaped wood utilized the photocatalytic properties of TiO₂ and the controlled motion of the light-blocking mask to achieve a seamless transition from hydrophobic to hydrophilic. By fine-tuning the mask's movement speed, the gradient wettability can be customized to suit various applications, including directional liquid transport, microfluidic devices, and biomimetic materials.

Fig. 3 (a) The preparation process for the three gradient wettability wedge-shaped wood samples. (b) The microstructure and compositional distribution of HWW. (c) Comparison of contact angle distributions before and after 7-day natural sunlight exposure for G1-GWW, G2-GWW, and G3-GWW.

To evaluate the environmental stability of the gradient wettability on wedge-shaped wood surfaces, particularly under prolonged sunlight exposure, a 7-day outdoor test under natural solar radiation (average intensity ∼50 mW cm⁻²) was conducted. Three representative samples (G1-GWW, G2-GWW, and G3-GWW) were selected, and their gradient wettability were measured before and after exposure. As shown in Fig. 3c, all samples retained their characteristic gradient wettability, with less than 8% reduction in contact angle across the measured positions. Among them, G1-GWW exhibited the highest stability, with only minor changes in contact angles, while G3-GWW showed slightly larger variations due to its steeper initial gradient. This stability was attributed to the chemical structure of PVDF–HFP, whose strong C–F and C–H bonds provided inherent resistance to photodegradation and environmental oxidation.^49,50 These results indicated that the PVDF–HFP-based gradient surfaces possessed reliable short-term UV resistance and maintained functional surface performance under realistic outdoor conditions. Future work will focus on integrating UV-resistant coatings to further enhance long-term durability for extended applications.

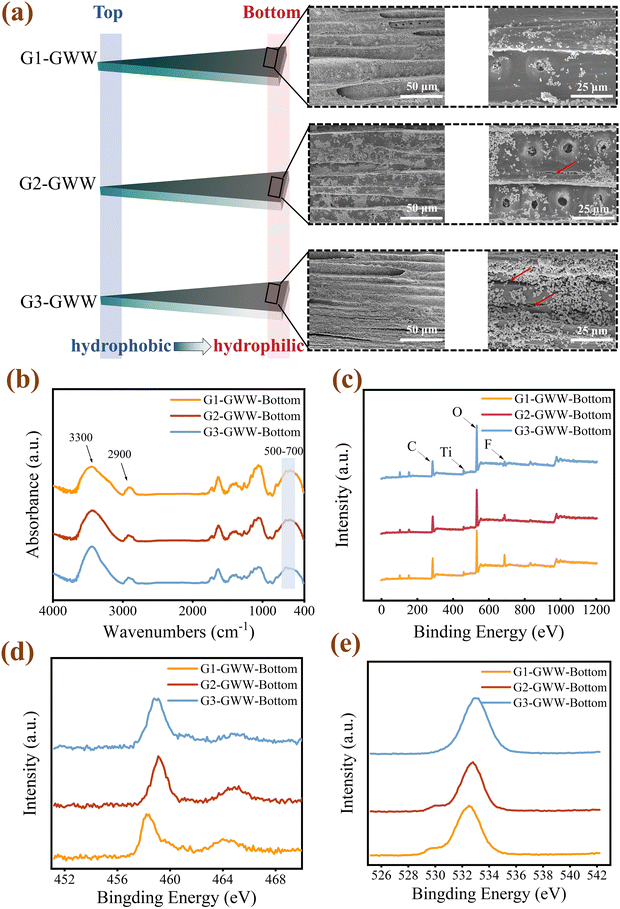
Further analysis was conducted on the bottom regions of the gradient wettability wedge-shaped wood samples (G1-GWW, G2-GWW, and G3-GWW) to investigate their microstructure and compositional changes. This choice was made because the formation of gradient wettability was closely tied to UV exposure time. The bottom, as the initial position of the movable light-shielding mask, underwent the longest UV irradiation, providing a clearer representation of the photocatalytic reaction's effects on the microstructure and chemical composition. Systematic characterization of the bottom region was therefore critical for uncovering the intrinsic mechanisms underlying the formation of gradient wettability. SEM analysis revealed that TiO₂ nanoparticles were uniformly distributed across the microstructure of the sample surfaces, ensuring consistency in the photocatalytic modification process (Fig. 4a). Notably, in G3-GWW-bottom, prolonged UV exposure caused visible surface cracking, likely due to changes in surface tension induced by the abundant hydroxyl groups generated during the photocatalytic reaction, which led to the formation of microcracks. FTIR analysis highlighted significant chemical changes on the sample surfaces. Key features include the O–H stretching vibration peak at 3300 cm⁻¹ (hydroxyl groups), the C–H stretching vibration peak around 2900 cm⁻¹, and the Ti–O vibration peak within 500–700 cm^−1 51 (Fig. 4b). With increasing UV radiation exposure, the O–H peak intensity in G3-GWW-bottom showed a marked increase, indicating a substantial rise in hydroxyl content and supporting the transformation of the surface from hydrophobic to hydrophilic. Changes in the C–H stretching vibration peak further confirmed the impact of UV photocatalysis. Additionally, the relative weakening of the Ti–O peak intensity suggested that the photocatalytic reaction generates more active sites on the TiO₂ surface, thereby enhancing the gradient-driven wettability effect. The XPS full spectrum analysis revealed that the bottom surfaces of all three samples contain C, O, Ti, and F elements, with the F peak intensity following the trend G1-GWW-bottom > G2-GWW-bottom > G3-GWW-bottom (Fig. 4c). This decrease in F element content with increased UV exposure time likely resulted from PVDF–HFP decomposition and F element desorption under high UV energy. The Ti characteristic peak (458.5 eV) shifted to higher binding energies and became sharper, indicating changes in the chemical environment of Ti, such as Ti–O bond rearrangement or enhanced binding with hydroxyl groups⁴⁶ (Fig. 4d). Moreover, the O–Ti peak at 530.0 eV gradually weakened, suggesting intensified redox reactions on the TiO₂ surface during the prolonged UV exposure, which might have consumed surface O–Ti bonds (Fig. 4e). These findings demonstrated that UV radiation significantly influenced the surface element distribution and chemical bonding, thereby enabling continuous surface transition from the hydrophobic to hydrophilic state. This understanding provided critical insights into the construction mechanisms of wood surface with a gradient wettability and laid a theoretical foundation for its application in directional liquid transport and functional surface design.

Fig. 4 Characterization of the microstructure and chemical composition of the bottom surface of gradient wettability wedge woods. (a) SEM analysis of bottom surfaces of GWW samples. (b) FTIR spectra of GWW bottom surfaces. (c) XPS survey spectra of GWW samples. (d) High-resolution XPS spectra of the Ti 2p region for GWW samples. (e) High-resolution XPS spectra of the O 1s region for GWW samples.

3.3 The water directional transport performance and mechanism of gradient wettability wedge-shaped wood

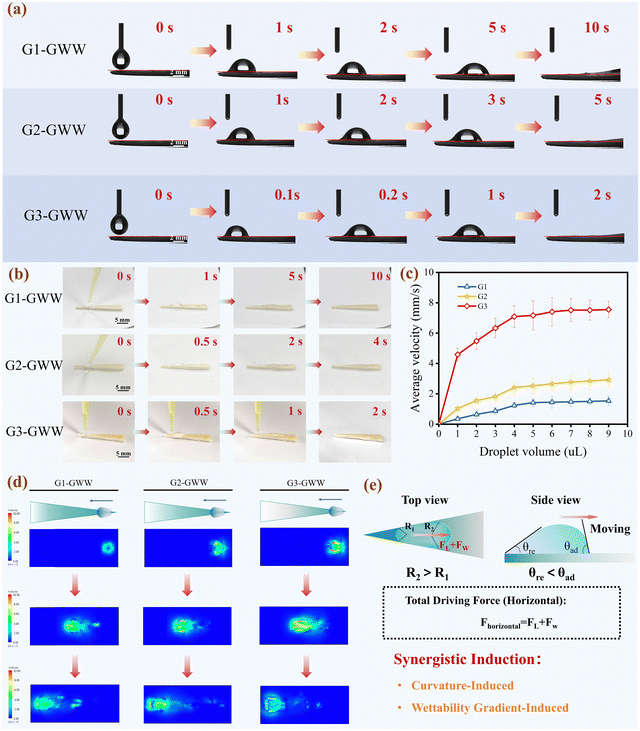
The Fig. 5 series comprehensively present an experimental and numerical analysis of directional droplet transport behaviors and underlying mechanisms on wedge-shaped wood surfaces featuring varying gradient wettability (G1-GWW, G2-GWW, and G3-GWW, all with a wedge angle of 9°). As clearly illustrated in Fig. 5a and Video S1 (ESI†), significant differences were observed among the three GWW surfaces regarding the efficiency of directional droplet transport. Specifically, a droplet of 4 μL volume traveled from the tip to the base in 10 s on G1-GWW, 5 s on G2-GWW, and merely 2 s on G3-GWW. These observations explicitly indicated that a steeper wettability gradient significantly amplified the driving forces, thereby enhancing the overall transport efficiency, with G3-GWW demonstrating the highest directional transport performance due to its steepest gradient wettability. The sequential optical images captured at a 45° tilted view by a high-resolution camera (Fig. 5b and Video S2, ESI†) provided a more comprehensive visualization of the droplet spreading process. This angled perspective clearly revealed the real-time evolution of droplet morphology and contact line dynamics on the GWW surfaces. Notably, droplets on the G3-GWW surface exhibited the fastest forward movement of the contact line, accompanied by the most significant deformation in droplet shape, followed by G2-GWW and G1-GWW, respectively. These qualitative observations were in good agreement with the quantitative time-resolved measurements shown in Fig. 5a, together elucidating the enhanced directional transport capability associated with steeper gradient wettability. In contrast, Fig. S8 (ESI†) revealed that the superhydrophilic wedge-shaped wood surfaces exhibited immediate absorption of water droplets upon contact. This rapid infiltration highlighted a key limitation of superhydrophilic surfaces: while they exhibited strong water affinity, they lacked the wettability gradient necessary to induce and sustain directional droplet motion. Therefore, despite facilitating water uptake, superhydrophilic treatments hindered surface-driven transport. In contrast, the gradient-wettability wood (GWW) surfaces with the engineered wettability gradient enabled efficient and directional droplet movement. Additionally, Fig. S9 (ESI†) illustrated the accumulation of water droplets at the bottom after multiple transport cycles on G3-GWW, further supporting the effectiveness of directional transport. Despite multiple droplet transfers, the droplets consistently accumulated at the base of the G3-GWW surface, which not only confirmed the repeatability and reliability of the transport but also highlighted the sustained efficiency of the transport process. Fig. 5c further revealed the average transport rates of the three GWW samples under varying droplet volumes. For droplets ranging from 1 to 4 μL, all samples showed a significant increase in transport rate with increasing droplet volume. This was attributed to the larger contact area and stronger gradient wettability-driven forces associated with the bigger droplets.⁵² Larger droplets also more effectively overcame surface tension and interfacial adhesion, resulting in higher transport rates. However, when the droplet volume exceeded 4 μL, the transport rate plateaued, indicating that the combined effects of gradient wettability and geometric driving forces had reached an equilibrium, rendering further volume increases less influential. Among the samples, G3-GWW consistently demonstrated the highest transport rates across all droplet volumes. At a droplet volume of 9 μL, G3-GWW achieved an average rate of 7.55 mm s⁻¹, significantly outperforming G2-GWW and G1-GWW. These results underscored the major role of the wettability gradient in enhancing liquid transport efficiency. Numerical simulations were performed to investigate the directional transport of droplets on horizontally oriented wedge-shaped surfaces with varying gradient wettability (G1, G2, and G3; wedge angle: 9°), as shown in Fig. 5d. The results revealed that both the spreading velocity and droplet deformation increased with the steepness of the gradient wettability. Specifically, G3-GWW, with the largest gradient, exhibited the fastest transport and most pronounced deformation, driven by stronger capillary forces. In contrast, G1 and G2 surfaces showed slower motion and weaker deformation due to reduced surface energy gradients. Curvature analysis further indicated that as the droplet advanced toward more hydrophilic regions, the decreasing front curvature radius led to elevated Laplace pressure, thereby enhancing the directional motion. These findings were consistent with the theoretical model (Tables S1 and S2, ESI†), confirming that wettability gradients and curvature effects jointly governed droplet dynamics and directional transport performance. Fig. 5e schematically summarizes the driving mechanism on a horizontally oriented GWW surface. The mechanism of water directional transport in GWW can be attributed to the synergistic effects of geometric and gradient wettability-driven forces. The driving force for droplet movement on the surface can be described by the following equation:

F_horizontal = F_L + F_W (1)

The geometric driving force (F_L) originates from the Laplace pressure difference caused by the curvature variation on the wedge-shaped surface. The formula for F_L is expressed as:where, σ represents the surface tension of the liquid, while R₁ and R₂ are the radii of curvature at the tip and base of the wedge, respectively. Since R₁ < R₂, the Laplace pressure is greater in the tip region and lower at the base, creating a driving force that pushes the droplet from the tip toward the base.

Fig. 5 (a) Contact-angle goniometer snapshots showing directional motion of water droplets on three gradient-wettability wedge-wood surfaces (GWWs) with an identical wedge angle of 9°. (b) Optical camera images of droplet transport on the same three GWWs. (c) Average transport velocity of droplets with different initial volumes on the three GWWs. (d) Numerical simulation of water migration on the three GWWs (wedge angle = 9°). (e) Schematic illustrating the droplet-migration mechanism on a horizontally oriented GWW surface.

Additionally, the gradient wettability driving force (F_W) arises from differences in surface free energy, expressed as:

F_W = γ(cos θ_rec − cos θ_adv) (3)

where, γ represents the surface free energy of the liquid, while θ_rec and θ_adv are the receding and advancing contact angles, respectively. On a gradient wettability surface, θ_rec < θ_adv, which drives the droplet to move from the hydrophobic region to the hydrophilic region.

In summary, when the surface is placed horizontally, the combined effect of the geometric driving force (F_L) and the gradient wettability driving force (F_W) propels the droplet along the surface in a directional manner.

3.4 The influence of wedge angle on droplet transport performance

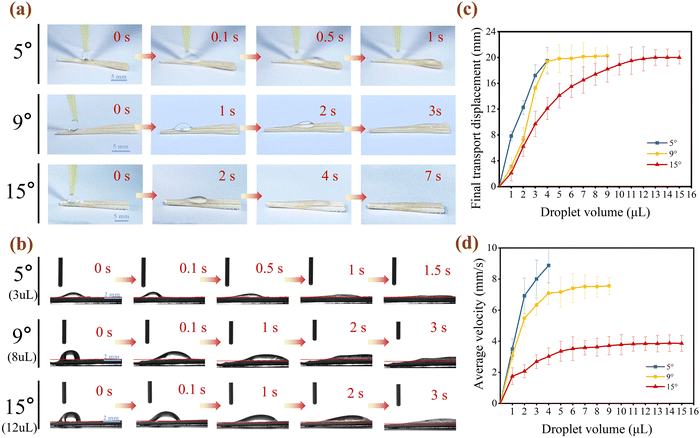
Based on the systematic study of water transport performance in three gradient wettability wedge woods (G1-GWW, G2-GWW, and G3-GWW), G3-GWW exhibited the highest transport efficiency and fastest droplet mobility. Consequently, this study focused on G3-GWW, further preparing samples with wedge angles of 5°, 9°, and 15° to explore the effect of wedge angle on droplet transport performance, including transport rate and distance. This analysis provided insights for optimizing the design of gradient wettability wedge wood. Fig. 6a, b and Videos S3 and S4 (ESI†) present sequential video snapshots captured at a 45° tilted view and a side view, clearly demonstrating the directional transport behavior of droplets on G3-GWW surfaces with different wedge angles. For a 3 μL droplet, the shortest transport time to the wedge base was observed on the 5° GWW, reaching the base in just 1.5 seconds, indicating superior transport efficiency. In contrast, the same droplet required approximately 3.0 seconds on both the 9° and 15° GWWs. These results suggested that smaller wedge angles can significantly accelerate droplet transport, with the 5° configuration excelling in time-based efficiency, while the 9° and 15° samples yielded comparable but slower responses.

Fig. 6 Video snapshots showing the directional droplet transport on G3-GWW samples with three different wedge angles, captured from (a) a 45° tilted view and (b) a side view. (c) Final transport distances of droplets with varying volumes on G3-GWW samples with different wedge angles. (d) Average transport velocities of droplets with varying volumes on G3-GWW samples with different wedge angles.

Further analysis of the influence of wedge angle on droplet transport distance and velocity is shown in Fig. 6c and d. The results revealed that the wedge angle not only significantly impacted droplet transport velocity but also played a critical role in determining the maximum transport distance and load-carrying capacity. Specifically, the 5° wedge angle exhibited a steep increase in both transport distance and velocity as the droplet volume increased from 1 to 4 μL, with the transport distance rising from 7.8 mm to 19.5 mm and velocity from 3.47 mm s⁻¹ to 8.9 mm s⁻¹. However, droplets larger than 4 μL could not be stably transported, likely due to the combination of high capillary force and insufficient lateral confinement, resulting in detachment from the surface. This indicated that while the 5° wedge angle provided a strong geometric driving force (resulting from a pronounced curvature difference, R₁ < R₂), its structural limitations reduced the droplet stability and load-carrying capacity, making it suitable for efficient transport of small droplets. In contrast, the 9° wedge angle demonstrated superior transport performance across a broader range of droplet volumes. Both transport distance and velocity increased steadily with volume from 1 to 7 μL, with transport distance saturating at 20 mm from 7 μL onward, and velocity stabilizing at approximately 7.5 mm s⁻¹ for droplets between 7 and 9 μL. These results suggested that the 9° wedge angle achieved an optimal balance between geometric and gradient wettability driving forces, making it ideal for medium-sized droplet transport with high stability and load-carrying capacity. For the 15° wedge angle, both transport velocity and distance exhibited slower, more linear growth. The droplet transport distance increased gradually from 2.01 mm (1 μL) to 20 mm (15 μL), while velocity rose from 1.68 mm s⁻¹ to a peak of 3.85 mm s⁻¹ at 14 μL before slightly declining. This behavior was attributed to the relatively weaker geometric gradient inherent to the wider wedge angle, with transport relying primarily on the wettability gradient. However, the larger wedge angle ensured superior droplet stability and load-carrying capacity, making it suitable for the steady transport of large droplets, despite the reduced transport efficiency compared to narrower wedge geometries. As shown in Table S3 (ESI†), GWW demonstrated superior performance in terms of droplet transport velocity and directional liquid spreading compared to other materials with gradient wettability. This enhancement is primarily attributed to the synergistic effect of the optimized wedge-shape structures and the precisely engineered gradient wettability, which facilitated rapid and sustained droplet motion.

In summary, the wedge angle had a dual effect on droplet transport performance.⁵³ Smaller wedge angles (e.g., 5°) provided stronger geometric driving forces, enabling efficient transport of small droplets but had a limited load-carrying capacity. Medium wedge angles (e.g., 9°) achieved an optimal balance among the transport velocity, distance, and stability, making them versatile for a wide range of droplet sizes. Larger wedge angles (e.g., 15°) were better suited for stable transport of large droplets but at the cost of reduced velocity and efficiency. These findings provided clear guidance for the design and optimization of gradient wettability wedge wood, enabling the selection of appropriate wedge angles based on specific application requirements.

3.5 The influence of inclination angle on droplet transport performance

To comprehensively reveal the motion characteristics of droplets on a gradient-wetting wedge-shaped wood surface, a contact angle goniometer and a digital camera were combined to video-record the droplet transport process from both side-view and 45° inclined perspectives (Fig. 7a, Fig. S10, Video S5, ESI†). The side-view perspective aids in observing the contact angle changes and the advancing rate of the front edge, allowing quantification of the driving force imparted by the gradient wettability. In contrast, the 45° view offers a more intuitive visualization of the droplet contour deformation and its three-dimensional movement path along the wedge-shaped structure. The results showed that with increasing tilt angle, droplets exhibited asymmetric deformation, characterized by decelerated forward motion and enhanced rearward stretching, revealing the competitive relationship between gravitational force and the surface-induced gradient wettability.

Fig. 7 (a) Video snapshots of directional droplet transport on G3-GWW (wedge angle: 9°) at different inclination angles. (b) Average transport velocities of droplets with varying volumes on G3-GWW (wedge angle: 9°) at different inclination angles. (c) Mechanism of droplet transport on inclined G3-GWW.

To further investigate the impact of tilt angle on the droplet transport behavior on the gradient wettability wedge-shaped wood (G3-GWW), the migration distance and transport speed of droplets with different volumes were systematically examined under different tilt angles (0°, 30°, 45°, 60°, 90°) (Fig. 7b and Fig. S11, ESI†). At the horizontal state (0°), the droplets exhibited the best transport performance, with the migration distance significantly increasing with the droplet volume. For example, a 3 μL droplet could travel up to 15.2 mm, and droplets ≥6 μL achieved a maximum distance of 20 mm. Corresponding transport speeds increased from 2.56 mm s⁻¹ to 5.56 mm s⁻¹, demonstrating a clear volume responsiveness. As the tilt angle increased, both the migration distance and speed showed a decreasing trend. At 30°, although the 6 μL droplet maintained a 20 mm travel distance, the speed of larger droplets decreased markedly. For instance, the speed of an 8 μL droplet dropped to 1.51 mm s⁻¹, indicating that gravity was gradually becoming a limiting factor. At 45° and 60°, the droplet transport performance further decreased, and the transport speed of larger droplets significantly slowed. At 60°, for example, the speed of a 5 μL droplet was only 0.54 mm s⁻¹, reflecting a strong counteracting effect of the larger gravitational component on the driving mechanism. Under vertical conditions (90°), the droplet motion was the most constrained, with the maximum migration distance of 20 mm and speed of only 0.39 mm s⁻¹ (for a 4 μL droplet), indicating strong suppression of directional motion by gravitational forces at steep inclinations. To better understand the impact of inclination on droplet transport in gradient wettability wedge wood, it was essential to analyze the underlying mechanism under the combined effects of gravity and surface driving forces (Fig. 7c). The directional transport of droplets on inclined gradient wettability wedge wood was governed by the geometric driving force (F_L), gradient wettability driving force (F_W), and the gravitational component (F_g sin α). The total driving force can be expressed as:

F_inclined = F_L + F_W − F_g sin α (4)

where α represents the inclination angle of the wedge wood. Under inclined conditions, due to the unique characteristics of the gradient wettability, θ_rec > θ_adv, the gradient wettability driving force (F_W) was negative, meaning its direction was opposite to the droplet's transport direction and could no longer directly drive the droplet's movement. However, despite F_W < 0, it still played a supporting role in adjusting droplet deformation and maintaining hydrodynamic stability. Under these conditions, the droplet's transport capability primarily depended on the balance between the geometric driving force (F_L) and the combined effects of the gravitational component and the negative gradient wettability driving force.⁵⁴ Transport occurred when the geometric driving force (F_L) overcame the sum of these opposing forces, expressed as:

F_L > F_g sin α − F_W (5)

Directional droplet transport remained achievable under inclined conditions. The geometric driving force, derived from the surface curvature difference (R₁ < R₂), served as the primary driving force for droplet movement. A larger curvature difference generated a stronger driving force, effectively counteracting the opposing effects of the gravitational component and the negative gradient wettability driving force. Thus, to ensure smooth transport of droplets from the tip to the base under inclined conditions, it was crucial to optimize surface geometry by increasing the curvature difference and strategically controlling the distribution of the gradient wettability. This approach helped to maintain droplet stability and facilitate deformation adjustments during transport.

The study of inclined gradient wettability wedge wood highlighted the synergy between geometric design and surface functionalization to achieve controllable directional droplet transport, overcoming the challenges posed by gravity and other external factors. This research not only validated the cooperative mechanism of gradient wettability and geometric driving forces but also provided theoretical insights and technical guidance for designing liquid management and transport systems in complex environments. Furthermore, it demonstrated broad application prospects in fields such as energy harvesting, microfluidics, and sensing technologies.

3.6 Design and application of a fog-driven power device

The fog-driven power device leveraged the unique functionalities of GWW and cactus spines, presenting an innovative design for liquid management and energy conversion. As shown in Fig. 8a, a cactus spine was connected to the top end of the GWW, forming a coupled unit to efficiently collect atmospheric fog. The cactus spine, with its natural micro/nanostructures and wettability gradient, captured tiny fog droplets and directed them toward the top of the GWW surface. Once the droplets accumulated, the combined effects of the geometric and wettability gradient driving force on the GWW surface rapidly transported the water droplets to the base. Upon reaching the bottom, the weight of the droplets caused the wedge to tilt, releasing water and resetting the device under the influence of a counterweight. This repetitive cycle enabled continuous, self-sustained operation, as illustrated in Fig. 8b, c and Video S6 (ESI†).

Fig. 8 (a) Components and potential applications of the fog-driven power device. (b) Schematic representation of the working process of the fog-driven power device. (c) Operation of the fog-driven power device under manually introduced water droplets. (d) Operation of the fog-driven power device in a simulated fog environment.

To evaluate the stability and sustainability of the device during the fog collection process, we monitored the detachment frequency and weight fluctuation of individual fog-harvesting units (Fig. S12, ESI†). Experimental results revealed that during 10 collection cycles, the weight of each collected droplet remained consistently around 6.2 mg, with droplets detaching approximately every 100 seconds. This consistent performance underscores the device's excellent stability in dynamic fog-harvesting conditions. During manual droplet experiments (Fig. 8c), the device responded sensitively to the weight of water droplets, demonstrating excellent mechanical flexibility and stability. In a simulated fog environment (Fig. 8d and Video S6, ESI†), the device efficiently captured and transported water droplets, showcasing its practicality and high efficiency. By integrating the kinetic energy of droplets with the mechanical response of the wedge structure, this fog-driven device not only efficiently collected water but also revealed significant potential for converting ambient environmental energy into useful mechanical motion. To further improve the fog harvesting efficiency and validate scalability for practical applications, a multi-spine array integrated with GWW to create an array-type fog harvesting collector was fabricated (Fig. S13, ESI†). The array-type collector effectively expanded the fog-capturing area and increased droplet collection density, achieving an impressive fog harvesting rate of approximately 7.2 kg m⁻² h⁻¹. The array structure facilitated uniform droplet distribution across multiple wedge-shaped wood surfaces, which accelerated water transport and improved the mechanical responsiveness of the fog-driven power device. These results clearly indicated that the array-type cactus spine–GWW collector not only significantly enhanced fog harvesting efficiency but also scaled easily for real-world implementations. Moreover, the comparative analysis summarized in Table S4 (ESI†) highlights that the integration of cactus spine-inspired structures with gradient wettability wedge wood in a modular design achieved superior fog-collection efficiency compared to previously reported bioinspired fog-harvesting surfaces. This remarkable enhancement originates primarily from the combination of droplet nucleation, directional transport, and rapid removal facilitated by the combined structure and wettability features. Such comparative evaluations validated the effectiveness of our structural design and demonstrated its advantages over existing droplet transport and fog collection systems.

This device offered multiple critical advantages. Firstly, its bioinspired architecture synergistically integrated the fog collection capability of cactus spines with the liquid transport efficiency of GWW, achieving a unique cooperative effect. The implementation of the multi-spine array structure further improved the collection yield and operational stability, providing a scalable and modular strategy for practical deployment. Secondly, the successful implementation of a scalable multi-unit array structure enhances both collection yield and operational stability, providing a practical modular strategy suitable for real-world applications. Additionally, the device design is structurally simple, inherently self-powered, reusable, and highly cost-effective, further highlighting its practical utility. Moreover, this innovative device has substantial potential for addressing critical applications such as water harvesting in arid environments, industrial condensate management, and small-scale energy harvesting. Further optimization can enhance its adaptability to complex environments. For example, improving the gradient wettability and geometric structure of the GWW can enable more efficient liquid transport and energy conversion. Incorporating additional bioinspired materials and multifunctional coatings can further boost its collection efficiency and durability. This fog-driven power device provided a novel approach to liquid management and energy utilization technologies, offering critical scientific and technological support for achieving sustainable development goals.

4. Conclusion

This study introduced a bioinspired wedge-shaped wood surface with gradient wettability, thereby enabling efficient and controlled spontaneous directional liquid transport. By carefully leveraging the natural anisotropic structure of wood and incorporating gradient wettability through precise chemical and photochemical modifications, the resulting wood surface demonstrated synergistic effects of Laplace pressure and surface energy gradients. In particular, these features facilitated outstanding liquid transport performance under both horizontal and inclined conditions, exhibiting a transport rate of up to 8.9 mm s⁻¹ on horizontal surfaces and 0.64 mm s⁻¹ upward against gravity on vertical surfaces. Moreover, the application of this system in a fog-driven power device underscored its significant potential in water resource management and energy conversion. Over 10 continuous cycles, the device consistently detached droplets weighing approximately 100 mg every 30 seconds, verifying its reliability and stability.

Notably, this work not only offered a scalable approach for developing bioinspired liquid management surfaces but also provided a sustainable alternative to synthetic materials by capitalizing on wood. As a renewable and biodegradable natural resource, wood confers considerable environmental benefits, such as reduced reliance on petroleum-based synthetic materials, diminished environmental footprint, and enhanced sustainability. Additionally, the simplicity and cost-effectiveness of the processing methods render this wood-based design readily scalable for real-world applications, including outdoor fog harvesting facilities and sustainable liquid management systems. Furthermore, the integration of geometric design and surface functionality unlocks new opportunities for tailored applications in microfluidics, environmental engineering, and biomedical devices. In this context, future research could focus on further optimizing gradient control for diverse liquids and environmental conditions, as well as enhancing the durability, responsiveness, and multifunctionality of the wood-based surfaces.

Author contributions

Kaiwen Chen: conceptualization, formal analysis, data curation, software, investigation, writing – original draft, visualization. Luyao Chen: investigation, writing – review & editing. Xianfu Xiao: writing – review and editing. Cheng Hao: writing – review and editing. Haonan Zhang: investigation, writing – review & editing. Tongtong Fu: investigation, writing – review & editing. Wei Shang: investigation, writing – review & editing. Hui Peng: supervision, writing – review & editing. Tianyi Zhan: supervision, writing – review & editing. Ning Yan: supervision, funding acquisition, writing – review & editing. Jianxiong Lyu: supervision, funding acquisition, writing – review & editing.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This work was financially supported by the National Key Research and Development Program of China (2023YFD2200501), the National Natural Science Foundation of China (No. 32171705), the Natural Science and Engineering Research Council of Canada (RGPIN-2017-06737) and the Postgraduate Research & Practice Innovation Program of Jiangsu Province (KYCX23_1176). The authors would like to acknowledge the sponsorship from the China Scholarship Council (CSC No. 202308320323).

Notes and references

1. M. Xie, Z. Zhan, C. Zhang, W. Xu, C. Zhang, Y. Chen, Z. Dong and Z. Wang, Small, 2023, 19, 2300047.
2. J. Xiang, J. Liao, Z. Zhu, P. Li, Z. Chen, J. Huang and X. Chen, Phys. Fluids, 2023, 35, 062005.
3. D. F. Yan, Y. Lu, J. Y. Lin, W. H. Li and J. L. Song, Appl. Phys. Lett., 2024, 125, 071601.
4. L. Zhong, H. Chen, L. Zhu, M. Zhou, L. Zhang, D. Yu, S. Wang, X. Han, Y. Hou and Y. Zheng, ACS Nano, 2024, 18, 10279–10287.
5. W. He, C. Shan, S. Fu, H. Wu, J. Wang, Q. Mu, G. Li and C. Hu, Adv. Mater., 2023, 35, 2209657.
6. S. Meng, C. Yao, G. Liu, H. Chen, T. Hu, Z. Zhang, J. Yang and W. Yang, ACS Appl. Mater. Interfaces, 2024, 16, 62892–62901.
7. Z. Qiu, F. Yu, D. Xu, Z. Wang, J. Huang, S. Wang, Y. Yang, Y. Wang, J. Li, Z. Xiao, Y. Xie and K. Zhang, Chem. Eng. J., 2023, 455, 140563.
8. D. Yan, J. Lin, Y. Chen, X. Yang, Y. Lu and J. Song, Adv. Sci., 2025, 2417024.
9. T. Xiang, S. Xie, G. Chen, C. Zhang and Z. Guo, Mater. Horiz., 2025, 12, 1084–1105.
10. Y. Lin, C. Wang, D. Miao, N. Cheng, N. Meng, A. A. Babar, X. Wang, B. Ding and J. Yu, ACS Appl. Mater. Interfaces, 2022, 14, 18944–18953.
11. L. Zhou, F. Liu, J. You, B. Zhou, W. Guo, W. Qu, X. Ren and G. Gao, Adv. Healthcare Mater., 2024, 13, 2303460.
12. D. Yan, Y. Chen, J. Liu and J. Song, Small, 2023, 19, 2301745.
13. Y. Liu, X. Peng, L. Zhu, R. Jiang, J. Liu and C. Chen, ACS Appl. Mater. Interfaces, 2023, 15, 59920–59930.
14. C. Chen, L.-A. Shi, Z. Huang, Y. Hu, S. Wu, J. Li, D. Wu and J. Chu, Adv. Mater. Interfaces, 2019, 6, 1900297.
15. W.-Y. Xiao, X. Liu, W. Wang, X. Zhang, Y. Wang, J. Lan, B. Fan, L. Shi, X. Wan and S. Wang, Macromol. Rapid Commun., 2023, 44, 2200814.
16. Y. Zao, M. You, J. Ma, X. Du, Y. Jin, D. Li, Z. Xu and C. Chen, Green Chem., 2025, 27, 2319–2330.
17. K. Funayama, A. Miura and H. Tanaka, Sci. Rep., 2023, 13, 6440.
18. Y. Liu, J. Chen, H. Zhang, H. Gou and G. Dong, Tribol. Int., 2024, 194, 109552.
19. M. Aliabadi, A. Zarkesh, H. Siampour, S. Abbasian, M. Mahdavinejad and A. Moshaii, ACS Appl. Nano Mater., 2021, 4, 8733–8743.
20. S. H. Lee, B. S. Kang and M. K. Kwak, ACS Appl. Mater. Interfaces, 2022, 14, 14721–14728.
21. P. Xue, J. Nan, T. Wang, S. Wang, S. Ye, J. Zhang, Z. Cui and B. Yang, Small, 2017, 13, 1601807.
22. H. Dai, Z. Dong and L. Jiang, Sci. Adv., 2020, 6, eabb5528.
23. Y. Wu, J. Feng, H. Gao, X. Feng and L. Jiang, Adv. Mater., 2019, 31, 1800718.
24. Y. Chen, K. Li, S. Zhang, L. Qin, S. Deng, L. Ge, L.-P. Xu, L. Ma, S. Wang and X. Zhang, ACS Nano, 2020, 14, 4654–4661.
25. X. Yu, H. Lai, H. Kang, Y. Liu, Y. Wang and Z. Cheng, ACS Appl. Mater. Interfaces, 2022, 14, 6274–6282.
26. Y. Li, Z. Cui, G. Li, H. Bai, R. Dai, Y. Zhou, Y. Jiao, Y. Song, Y. Yang, S. Liu and M. Cao, Adv. Funct. Mater., 2022, 32, 2201035.
27. J. Wang, S. Yi, Z. Yang, Y. Chen, L. Jiang and C.-P. Wong, ACS Appl. Mater. Interfaces, 2020, 12, 21080–21087.
28. X. Xiao, C. Zhang, H. Ma, Y. Zhang, G. Liu, M. Cao, C. Yu and L. Jiang, ACS Nano, 2019, 13, 4083–4090.
29. X. Su, D. Hao, P. Li, M. Yang, X. Guo, X. Ai, T. Zhao and L. Jiang, J. Mater. Chem. A, 2023, 11, 7702–7710.
30. K. Chen, J. Zhu, Y. Tan, F. Sun, J. Gan, H. Peng, T. Zhan and J. Lyu, Chem. Eng. J., 2023, 470, 144356.
31. X. Chen, S. M. He, M. M. Falinski, Y. X. Wang, T. Li, S. X. Zheng, D. Y. Sun, J. Q. Dai, Y. H. Bian, X. B. Zhu, J. Y. Jiang, L. B. Hu and Z. J. Ren, Energy Environ. Sci., 2021, 14, 5347–5357.
32. L. A. Berglund and I. Burgert, Adv. Mater., 2018, 30, 1704285.
33. X. Wang, W. Tian, Y. Ye, Y. Chen, W. Wu, S. Jiang, Y. Wang and X. Han, Adv. Colloid Interface Sci., 2024, 326, 103142.
34. L. Wang, J. Wei, M. You, Y. Jin, D. Li, Z. Xu, A. Yu, J. Li and C. Chen, Carbohydr. Polym., 2025, 354, 123345.
35. Q. L. Fu, F. Ansari, Q. Zhou and L. A. Berglund, ACS Nano, 2018, 12, 2222–2230.
36. Y. Q. Luo, F. Song, C. Xu, X. L. Wang and Y. Z. Wang, Chem. Eng. J., 2020, 383, 123168.
37. Y. H. Cai, Y. Yu, J. F. Wu, K. L. Wang, Y. M. Dong, J. F. Qu, J. D. Hu, L. W. Zhang, Q. L. Fu, J. Z. Li, Q. C. Zhang and D. Tian, EcoMat, 2022, 4.
38. K. Chen, X. Xiao, C. Hao, F. Sun, H. Zhang, Y. Tan, J. Zhu, H. Peng, T. Zhan, J. Lyu and N. Yan, Chem. Eng. J., 2025, 506, 160185.
39. K. Chen, J. Zhu, C. Hao, H. Zhang, Y. Tan, X. Xiao, F. Sun, X. Han, H. Peng, T. Zhan, J. Lyu and N. Yan, npj Clean Water, 2025, 8, 27.
40. F. Sun, R. Li, J. Zhu, H. Peng, Z. Li, J. Jiang, T. Zhan, L. Cai and J. Lyu, Ind. Crops Prod., 2024, 220, 119185.
41. T. Zhan, H. Liu, J. Zhu, F. Sun, H. Peng and J. Lyu, Wood Sci. Technol., 2023, 57, 1369–1383.
42. J. Fan, A. Guyot, K. T. Ostergaard and D. A. Lockington, Agric. For. Meteorol., 2018, 249, 264–274.
43. Y. Wang, T. Tian and E. Cabane, ACS Sustainable Chem. Eng., 2017, 5, 11686–11694.
44. C. Lu, J. Wu, Q. Jiang, Y. Liu, L. Zhou, Y. You, Y. Cheng and S. Liu, J. Wood Sci., 2021, 67, 72.
45. R. A. Garcia, J. Rosero-Alvarado and R. E. Hernández, Wood Mater. Sci. Eng., 2023, 18, 570–579.
46. Z. Yanqing, S. jifu, H. Qizhang, W. Leilei and X. Gang, Chem. Commun., 2017, 53, 2363–2366.
47. X. Zhou, S. Yu, J. Zang, Z. Lv, E. Liu and Y. Zhao, J. Alloys Compd., 2019, 798, 257–266.
48. K. Nakata, H. Kimura, M. Sakai, T. Ochiai, H. Sakai, T. Murakami, M. Abe and A. Fujishima, ACS Appl. Mater. Interfaces, 2010, 2, 2485–2488.
49. T. M. W. J. Bandara, A. M. J. S. Weerasinghe, M. A. K. L. Dissanayake, G. K. R. Senadeera, M. Furlani, I. Albinsson and B. E. Mellander, Electrochim. Acta, 2018, 266, 276–283.
50. C. M. Costa and S. Lanceros-Mendez, Curr. Opin. Electrochem., 2021, 29, 100752.
51. S. Peng, W. Meng, J. Guo, B. Wang, Z. Wang, N. Xu, X. Li, J. Wang and J. Xu, Langmuir, 2019, 35, 2760–2771.
52. X. Zhu, H. Wang, Q. Liao, Y. D. Ding and Y. B. Gu, Exp. Therm. Fluid Sci., 2009, 33, 947–954.
53. S. Wang, C. Wang, Z. Peng and S. Chen, J. Phys. Chem. C, 2019, 123, 1798–1805.
54. M. He, P. Wang, B. Xu, L. Jiang and H. Liu, Adv. Funct. Mater., 2018, 28, 1800187.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5mh00440c

---