Spontaneous helix formation in a polar smectic phase

Abstract

In soft ferroelectric crystals, the depolarization field can be reduced by a periodic distortion of the polarization direction. In the polar nematic and tilted smectic phases, this process is energetically favored, as it only requires changes in the director orientation. We demonstrate the spontaneous formation of a helical structure in the proper ferroelectric tilted smectic (SmC^H_P) phase, formed below the heliconical polar nematic (N_TBF) phase. The helical pitch in the smectic phase is approximately 600 nm and remains nearly constant across the entire temperature range of the phase. Under weak electric field, the helix reorients while its structure remains largely intact; however, in stronger field the helix is destroyed as the electric polarization aligns along the electric field.

---

New concepts

We present a novel form of molecular organization—the spontaneous formation of a heliconical lamellar structure composed of achiral molecules, which exhibit proper ferroelectric properties. This helical structure, with a pitch in the submicron range, creates a photonic band gap for circularly polarized visible light. This phenomenon exemplifies spontaneous mirror symmetry breaking. Samples with this periodic structure act as diffraction gratings, and their characteristics can be precisely manipulated by external stimuli. For instance, the axis of the heliconical structure can be easily reoriented using a weak electric field.

Introduction

As suggested by the prefix ‘ferro’, ferroelectrics are analogous to ferromagnets. They belong to a broad class of materials characterized by a long-range order of electric dipoles, which results in spontaneous electric polarization and they are distinguished by reversible switching of polarization with the application of an external electric field. Dipole order leads to uncompensated bound charges at the surfaces of ferroelectric films that generate an internal electric field, known as the depolarization field, which opposes the polarization. For a given electric polarization of 1 μC cm⁻², the internal electric fields within the crystal can reach magnitudes of up to 10⁹ V m⁻¹. In order to reduce the depolarization field, a ferroelectric crystal splits into domains, i.e. regions with different directions of polarization. In crystals, these domains are formed along specific crystallographic directions. The process of domain formation is driven by a balance of free energy: while the formation of domains reduces electrostatic energy, there is an energy penalty for the creation of domain walls.¹ In the recently discovered ferroelectric phase of soft matter-ferroelectric nematic phase, N_F, the depolarization energy can be reduced through different mechanisms. These include the formation of domains with splay deformation^2,3 or the formation of a helical structure.⁴ Such mechanisms would be quite unusual for solid crystals, because it would require a periodic distortion of the crystal lattice.^5,6 However, in soft matter systems, like liquid crystals, in particular in polar nematics^7–10 that do not have periodic positional structure, this process is much easier as it requires only changes in director orientation. In liquid crystals, where the polarization is aligned along the director, the formation of a helix could fully cancel the polarization provided that the helical axis is perpendicular to the director as in the cholesteric phase. This structure has been proposed theoretically as a ground state for the N_F phase.^11,12 However, the experimental evidence supporting this hypothesis is currently limited.¹³ Alternatively, the polarization can only be partially compensated in the case of a heliconical structure, in which the director makes an oblique angle with respect to the helix axis. The heliconical structure has been confirmed for a variant of ferroelectric nematic phase (the phase was given the acronym N_TBF to show that the structure is similar to the twist bend nematic phase; however, experiments show a much longer helix), and a distinct phase transition has been observed between the uniform N_F and the helical N_TBF phases.⁴ Heliconical nematic phase has been observed so far for a limited number of mesogens.^14,15 The heliconical structure was also suggested for the axially polar tilted smectic phase, SmC^H_P.¹⁶ In this communication, we demonstrate convincing evidence for the sequence of ferroelectric nematic and ferroelectric smectic phases, both of which exhibit spontaneous helix formation.

Results and discussion

The studied material (see Fig. 1a for its molecular structure and the ESI,† for details of its synthesis) exhibits a sequence of five liquid crystalline phases upon cooling from the isotropic liquid phase: Iso → N → N_x → N_F → N_TBF → SmC^H_P. Upon rapid cooling, recrystallization of the material could be easily prevented, and the smectic phase was observed at room temperature. This phase sequence was confirmed by differential scanning calorimetry (DSC) measurements (Fig. S1 and Table S1, ESI†).

Fig. 1 (a) Molecular structure of the studied compound. (b) Layer spacing, d, (in SmC^H_P phase) and average longitudinal distance of molecules in N_F and N_TBF phases deduced form X-ray diffraction studies (black circles) and the width (FWHM) of the related diffraction signal (blue squares) measured vs. temperature; note that the signal width becomes instrumental-resolution-limited in the smectic phase. (c) 2D X-ray diffraction pattern recorded in the SmC^H_P phase (at T = 30 °C) with superimposed intensity vs. diffraction angle obtained by integration of the pattern over the azimuthal angle. The high angle signal is diffused, proving liquid-like order of molecules inside the smectic layers.

It was observed that each phase transition was accompanied by a distinct thermal effect, with the exception of the N_F–N_TBF phase transition where enthalpy changes were below the detection limit (<0.001 J g⁻¹). The subsequent LC phases are as follows: paraelectric N, antiferroelectric N_x (sometimes named also SmZ_A^17,18) with a periodic structure of domains with antiparallel direction of polarization, ferroelectric N_F, the N_TBF phase – a ferroelectric phase with a heliconical structure and the heliconical tilted smectic SmC^H_P. The X-ray diffraction studies (Fig. 1) further validated the sequence of nematic and smectic phases: all four nematic phases display only diffuse diffraction signals, characteristic of short-range positional order. However, the low-angle signal, related to the longitudinal distance between molecules, gradually narrows as the temperature decreases, indicating increasing positional correlations in the material. In the smectic phase, this signal width becomes limited by the machine's resolution, proving true long-range order of molecular positions. Furthermore, the signal moves to smaller angles, which indicates a reduction in layer spacing, as the tilt increases with decreasing temperature. Conversely, the high-angle diffraction signal, associated with the transverse distance between molecules, remains diffuse across all the LC phases, which is characteristic of a liquid-like order. The orientational order of molecules was assessed by optical birefringence (Δn) measurements (Fig. 2), performed in cells having planar aligning polymer layers rubbed parallel to secure the same anchoring conditions at both surfaces (this allows the formation of twisted domains along the cell thickness to be avoided). In the N and N_x phases the birefringence monotonically increases on cooling, however with slightly different slope, following growth of orientational order of molecules. A small jump at the transition to the N_F phase indicates that the appearance of polar order is accompanied by a weak, step-like increase in orientational order. In the N_TBF phase, Δn decreases as the tilting of molecules and formation of a helical structure reduces the refractive index along the helix axis and increases the refractive index perpendicular to the helix.¹⁹ The continuous changes of birefringence indicate that at the N_F–N_TBF phase transition, tilt increases continuously from zero and reaches ∼25 deg. before the transition to the SmC^H_P phase. The decrease of birefringence related to the increase of molecular tilt continues in the smectic phase; however, the values of Δn in the SmC^H_P phase are not fully reliable, because the sample alignment becomes worse in this phase.

Fig. 2 Optical birefringence vs. temperature measured in a thin (1.8-μm-thick) planar cell with parallel rubbing at both surfaces.

The polar properties of the nematic and smectic phases were confirmed by dielectric spectroscopy and polarization reversal current measurements. Although interpretation of dielectric spectroscopy results for strongly polar materials can be challenging,^20,21 the data clearly indicate that upon entering the N_F phase the dipole order becomes long-range and a strong dielectric response emerges (Fig. S2, ESI†). Above this temperature in the paraelectric N and antiferroelectric N_x phases, the dielectric response is weak and no distinct dielectric modes are observed in the studied frequency range. In the N_F and N_TBF phases, a strong dielectric response is observed at frequencies below 10 kHz, and the mode weakens and shifts to lower frequencies in the smectic phase. A polarization switching current peak was detected under the application of a triangular voltage in the N_F, N_TBF, and SmC^H_P phases (Fig. S3, ESI†). Far from the phase transition to the polar phase, the spontaneous electric polarization is ∼4.5 μC cm⁻², which is close to the maximum value (4.6 μC cm⁻², estimated as 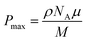, taking μ = 12D, ρ = 1.3 g cm⁻³ and M = 670 g) and points to nearly perfect order of all molecular dipoles.²² The dipole moment was estimated based on the assumptions that lateral substitution with a single F atom changes the molecular dipole by 0.5D.¹⁵ In the smectic phase, the threshold voltage at which the polarization reversal takes place starts to increase on cooling.

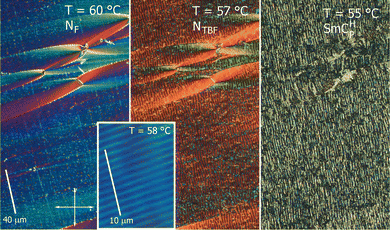
When observed under a polarized light microscope in a cell with a polymer anchoring layer with parallel rubbing on both surfaces, the texture of the N phase is uniform, with the extinction directions along the polarizers. In the N_F phase the texture is essentially unchanged with few defects developing around the glass spacers (Fig. 3), in which the director departs in a parabolic way from the rubbing direction.²³

Fig. 3 The textures of the N_F, N_TBF and SmC^H_P phases in a 3-μm-thick planar cell with parallel rubbing direction, the periodicity of the stripes visible in the images of N_TBF and SmC^H_P is dependent on the cell thickness. In the inset: the stripes are directly related to the helix pitch, which can be observed only in the vicinity of the N_TBF–N_F phase transition where the helix unwinds.

In the N_TBF phase, the texture becomes more complex, with stripes parallel to the rubbing direction, and the period of these stripes is dependent on the cell thickness, being roughly two times larger (e.g. in a 3-μm-thick cell the strip periodicity was 5.5 μm). In the SmC^H_P phase the texture is similar; however, the stripes are less regular. The light diffraction experiment revealed that in addition to the aforementioned stripes, which are easily detectable in microscopic observations, the sample also has additional, sub-micron periodicity in both the N_TBF and SmC^H_P phases, due to the helical pitch. It was observed that in the N_TBF phase, the helix unwinds on heating as the N_F phase is approached (Fig. 4), and this allowed the direct observation of the related periodicity by microscopy, as a regular array of strips with ∼1 μm spacing, running perpendicular to the cell rubbing direction (Fig. 3).

Fig. 4 (a) Helical pitch vs. temperature and, in the inset, light diffraction patterns in the N_TBF and SmC^H_P phases, where the intensive spots are from diffraction on the helical structure. (b) Models of the heliconical arrangement of molecules in the N_TBF and SmC^H_P phases, the color gradient of the rods reflects dipolar character of the molecules. (c) AFM image of the SmC^H_P phase supercooled to room temperature, the stripe periodicity is ∼600–700 nm.

Near the transition to the SmC^H_P phase, the helical pitch of the N_TBF phase reaches around 600 nm and remains almost constant in the SmC^H_P phase. The material can be easily supercooled to room temperature, allowing the confirmation of the periodic structure by atomic force microscopy (AFM) (at higher temperatures, adhesion is too strong and viscosity is too low for such measurements). A clear pattern with a periodicity of 600–700 nm was observed, consistent with light diffraction measurements (Fig. 4c and Fig. S4, ESI†). The piezoresponse force microscopy (PFM) measurements confirmed that in the area exposed to a strong electric field, electric polarization becomes re-oriented along the field direction and the orientation of polarization remains after the field is removed (Fig. S5, ESI†).

The SmC^H_P phase was also studied under an applied electric field, and two different sample geometries were used: (i) planar cells with parallel rubbing at both surfaces and an electric field applied across the cell thickness, and (ii) planar cells with parallel rubbing at both surfaces and an in-plane electric field perpendicular to the rubbing direction. In the first case, the weak electric field caused re-arrangement of the smectic layers from planar (bookshelf) to homeotropic alignment (with the helix axis along the electric field). The field-treated sample exhibited significantly lower birefringence compared to the untreated texture and displayed several tens of micrometer-size domains with optical activity (Fig. 5). These domains had a randomly distributed sign of optical activity, demonstrating that both left- and right-handed helices are formed with equal probability. Applying a stronger electric field disrupted the helices by aligning the dipole moments within the layers along the direction of the field, which lead to the disappearance of optical activity of the texture.

Fig. 5 (a) Texture of the SmC^H_P phase obtained upon cooling the sample from the N_TBF phase in a 3-μm-thick cell with parallel rubbing on both surfaces. Scale bar corresponds to 20 μm. (b) Application of a weak electric field across the cell thickness (<1 V μm⁻¹) realigned the helix from planar to homeotropic position. This orientation of the helix remains after removing the electric field. By uncrossing the polarizers (±10 degree) optically active domains are detected showing that the left- and right-handed helices coexist. (c) Under increasing electric field applied across the cell thickness, optical activity diminishes; in a sufficiently strong electric field (>2 V μm⁻¹) the helix is destroyed and the uniform state with electric polarization aligned along the electric field is obtained (homeotropic texture).

Reorientation of the helix axis direction in the cells with an in-plane electric field was monitored by observing laser diffraction patterns. As expected, prior to the application of an electric field, the diffraction spots, related to the helical structure, were positioned along the rubbing direction. Above a certain threshold (∼15 V mm⁻¹, at T = 56 °C), the electric field caused a rotation of the helix axis, as evidenced by the appearance of the diffraction spots positioned along the electric field (perpendicular to the rubbing direction). However, reducing the field to zero did not fully restore the original helix orientation; instead, two sets of diffraction spots were visible, originating from distinct areas in the sample with the helix oriented in perpendicular directions (Fig. 6a). Apparently, the field treated sample is divided along its thickness; in the bulk of the sample, the helix remains aligned along the direction in which the electric field had been applied, while in the surface regions the helix is oriented along the rubbing direction. The application of an a.c. electric field results in sequential changes of the diffraction spot intensities, as the relative size of the bulk and surface regions changes (Movie S1, ESI†). Although in both the bulk and surface regions, the helix axis is still oriented perpendicular to the sample surface, after switching-off the field, the sample exhibited texture with optically active domains (Fig. 6b). This suggest that those regions are interconnected by screw dislocations, and such a boundary facilitates easy growth of one region at the expense of the other under an electric field. The process of the reorientation of the helical axis direction and the distortion of the helix has also been followed by monitoring the changes of the azimuthal direction of the optical axis and birefringence (Fig. S6, ESI†). Two clear regimes were detected, under a weak electric field, mainly changes of the optical axis direction were found, while above a certain threshold a strong increase in the birefringence was observed due to a decrease of the tilt angle of the heliconical structure.

Fig. 6 (a) Laser light diffraction patterns in the SmC^H_P phase from a 2.5-μm-thick planar cell with in-plane electrodes. Under applied voltage only the diffraction spots along the field direction are visible. When the electric field is switched off, two sets of diffraction spots are visible, along and perpendicular to the rubbing direction (yellow dashed lines). (b) Optical texture in the same cell observed after application of an a.c. electric field, where domains with the opposite sign of optical activity are clearly visible by slight de-crossing of polarizers (arrows). Scale bar corresponds to 20 μm. (c) The same sample area under an applied in-plane electric field, E = 50 V mm⁻¹. The optical axis (layer normal) is along the electric field.

Conclusions

Recently, unambiguous evidence was given that apart from the polar, orthogonal SmA_F phase with uniform electric polarization along the director, also its tilted version – the polar smectic C_F phase exists.^24,25 In these phases, similarly as in the polar nematic N_F phase, a strong internal electric field (depolarization field) might be reduced by the formation of random structures of polar domains. Here we show the alternative pathway, wherein a strong depolarization field is reduced by a spontaneously formed helical structure. This structure is a smectic analogue of the recently discovered N_TBF phase. In the tilted smectic phase, the helical pitch is in the sub-micron range and the transition from N_TBF to SmC^H_P phase occurs without significant changes in helical pitch. The axis of the heliconical structure can be reoriented by a small electric field while its structure remains intact.

The SmC^H_P phase is yet another example of spontaneous mirror symmetry breaking in nature. Such structures are common among crystals, their symmetry elements are various 2-, 3-, 4-, and 6-fold screw axes and typically they feature nm-scale helices. In the field of liquid crystals, similar phenomena, driven primarily by steric interactions, usually also occur at the nanoscale. Well-known examples include the N_TB phase²⁶ and helical columnar phases.²⁷ However, it is rather rare for spontaneously formed helices to exhibit significantly larger periodicities.²⁸ The results reported here seem to support the conclusion that, when spontaneous symmetry breaking is induced by dipolar interactions, the resulting helical structures in the nematic or smectic phases can develop a much longer pitch. However, coupling between structural helicity and polar order is only just beginning to be explored and many questions become open, for example if there is a relation between helix handedness and the polar axis, how the helix responds to electric fields, etc.

Author contributions

Conceptualization: EG, PK, and DP; investigation: EG, MM, LF, JK, JŻ, JH, PK, and DP; writing – original draft: EG and DP; writing – review & editing: EG, MM, LF, JK, JŻ, JH, PK, and DP; funding acquisition: MM.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the project FerroFluid, EIG Concert Japan 9th Joint call (EIG CONCERT-JAPAN/9/89/FerroFluid/2023).

Notes and references

1. A. Pramanick, A. D. Prewitt, J. S. Forrester and J. L. Jones, Crit. Rev. Solid State Mater. Sci., 2012, 37, 243–275.
2. P. Medle Rupnik, E. Hanžel, M. Lovšin, N. Osterman, C. J. Gibb, R. J. Mandle, N. Sebastián and A. Mertelj, Adv. Sci., 2025, 2414818.
3. Z. Ma, M. Jiang, A. Sun, S. Yi, J. Yang, M. Huang, S. Aya and Q.-H. Wei, arXiv, 2024, preprint, arXiv.2411.12336 DOI:10.48550/arXiv.2411.12336.
4. J. Karcz, J. Herman, N. Rychłowicz, P. Kula, E. Górecka, J. Szydlowska, P. W. Majewski and D. Pociecha, Science, 2024, 384, 1096–1099.
5. H. J. Zhao, P. Chen, S. Prosandeev, S. Artyukhin and L. Bellaiche, Nat. Mater., 2021, 20, 341–345.
6. D. D. Khalyavin, R. D. Johnson, F. Orlandi, P. G. Radaelli and A. Belik, Science, 2020, 369, 680–684.
7. H. Nishikawa, K. Shiroshita, H. Higuchi, Y. Okumura, Y. Haseba, S. Yamamoto, K. Sago and H. Kikuchi, Adv. Mater., 2017, 29, 1702354.
8. R. J. Mandle, S. J. Cowling and J. W. Goodby, Phys. Chem. Chem. Phys., 2017, 19, 11429–11435.
9. A. Mertelj, L. Cmok, N. Sebastián, R. J. Mandle, R. R. Parker, A. C. Whitwood, J. W. Goodby and M. Čopič, Phys. Rev. X, 2018, 8, 041025.
10. X. Chen, E. Korblova, D. Dong, X. Wei, R. Shao, L. Radzihovsky, M. A. Glaser, J. E. Maclennan, D. Bedrov, D. M. Walba and N. A. Clark, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 14021–14031.
11. A. G. Khachaturyan, J. Phys. Chem. Solids, 1975, 36, 1055–1061.
12. L. Paik and J. V. Selinger, arXiv, 2024, preprint, arXiv.2408.10347 DOI:10.48550/arXiv.2408.10347.
13. P. Kumari, B. Basnet, M. O. Lavrentovich and O. D. Lavrentovich, Science, 2024, 383, 1364.
14. H. Nishikawa, D. Okada, D. Kwaria, A. Nihonyanagi, M. Kuwayama, M. Hoshino and F. Araoka, Adv. Sci., 2024, 11, 2405718.
15. G. J. Strachan, E. Górecka, J. Hobbs and D. Pociecha, J. Am. Chem. Soc., 2025, 147, 6058–6066.
16. C. J. Gibb, J. Hobbs, D. I. Nikolova, T. Raistrick, S. R. Berrow, A. Mertelj, N. Osterman, N. Sebastián, H. F. Gleeson and R. J. Mandle, Nat. Commun., 2024, 15, 5845.
17. X. Chen, V. Martinez, E. Korblova, G. Freychet, M. Zhernenkov, M. A. Glaser, C. Wang, C. Zhu, L. Radzihovsky, J. E. Maclennan, D. M. Walba and N. A. Clark, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2217150120.
18. E. Cruickshank, P. Rybak, M. M. Majewska, S. Ramsay, C. Wang, C. Zhu, R. Walker, J. M. D. Storey, C. T. Imrie, E. Gorecka and D. Pociecha, ACS Omega, 2023, 8, 36562–36568.
19. C. Meyer, G. R. Luckhurst and I. Dozov, J. Mater. Chem. C, 2015, 3, 318–328.
20. N. A. Clark, X. Chen, J. E. MacLennan and M. A. Glaser, Phys. Rev. Res., 2024, 6, 013195.
21. V. Matko, E. Gorecka, D. Pociecha, J. Matraszek and N. Vaupotic, Phys. Rev. Res., 2024, 6, L042017.
22. C. Parton-Barr, H. F. Gleeson and R. J. Mandle, Soft Matter, 2024, 20, 672–680.
23. P. Kumari, O. Kurochkin, V. G. Nazarenko, O. D. Lavrentovich, D. Golovaty and P. Sternberg, Phys. Rev. Res., 2024, 6, 043207.
24. G. J. Strachan, E. Górecka, J. Szydłowska, A. Makal and D. Pociecha, Adv. Sci., 2025, 12, 2409754.
25. J. Hobbs, C. J. Gibb, D. Pociecha, J. Szydłowska, E. Górecka and R. J. Mandle, Angew. Chem., Int. Ed., 2025, 64, e202416545.
26. R. Mandle, Molecules, 2022, 27, 2689.
27. F. Vera, J. L. Serrano and T. Sierra, Chem. Soc. Rev., 2009, 38, 781–796.
28. D. Pociecha, N. Vaupotič, M. Majewska, E. Cruickshank, R. Walker, J. M. D. Storey, C. T. Imrie, C. Wang and E. Gorecka, Adv. Mater., 2021, 33, 2103288.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental methods, synthesis details and analytical data, and supplementary results. See DOI: https://doi.org/10.1039/d5mh00469a

---