Dirac-cone induced metallic conductivity in Cu₃(HHTP)₂: high-quality MOF thin films fabricated via ML-driven robotic synthesis

Abstract

Metal–organic frameworks have garnered interest for over 25 years in energy and electronics, yet their adoption in devices has been hindered by low electrical conductivity, largely attributed to activated transport. Our study demonstrates a significant shift, revealing metallic conductivity in Cu₃(HHTP)₂ thin films—240 S m⁻¹ at room temperature and 300 S m⁻¹ at 100 K, a departure from its presumed semiconductive nature. Achieved through robotic, AI-based layer-by-layer assembly in a self-driving laboratory, this method produces SURMOFs with minimal defects, optimized via rapid surrogate characterization techniques. Our research, supported by both electronic structure calculations and experimental verification, identifies a persistent Dirac cone in the hexagonal D_6h symmetry of 2D sheets as crucial for the observed metallic behavior. Notably, even with ABAB stacking in the bulk, this Dirac cone feature maintains metallic conductivity, enhancing at lower temperatures. This breakthrough not only clarifies the conduction mechanism in Cu₃(HHTP)₂ but also highlights the SDL's potential in developing high-quality MOF thin films for future applications. Our findings indicate that tailoring the Dirac cone's energy could lead to a new class of highly conductive, metallic MOFs.

---

New concepts

We report the first metal–organic framework (MOF) thin film exhibiting true metallic conductivity, overcoming a long-standing limitation in the field. Using a self-driving laboratory and robotic synthesis, we optimized the growth of Cu₃(HHTP)₂ thin films, achieving conductivities >200 S m⁻¹ at room temperature and enhanced values at low (100 K) temperatures—a hallmark of metallic behavior. This represents a conceptual and experimental breakthrough: while metallic conductivity in MOFs has been theoretically predicted, it has remained elusive in practice, particularly in thin-film form required for device integration. We demonstrate that previous failures stemmed from microstructural defects such as domain boundaries. Our approach enables precise control over crystallinity and domain size, unlocking intrinsic conductivity characteristics. Our theoretical analysis reveals that of Cu₃(HHTP)₂ exhibits symmetry-protected Dirac cones in both 2D and 3D, analogous to graphene, and offer a new experimental platform to explore exotic transport phenomena, from spin liquids to Klein tunneling. Our work not only introduces a novel route to functional, conductive MOF films, but also redefines the design criteria for electronic MOFs. By integrating automated synthesis, predictive characterization, and theoretical insights, this study opens transformative avenues for MOFs in next-generation electronics, quantum materials, and designer systems with tunable electronic properties.

Metal–organic frameworks (MOFs), known for their exceptional structural and functional versatility, present significant potential for the development of sophisticated materials suited for a wide range of applications under temperatures below 200 °C.¹ Originally, the exploration of MOFs was propelled by their capabilities in gas storage and separation,² while applications to field-effect transistors,³ organic light-emitting diodes,⁴ supercapacitors,⁵ highly sensitive sensors,⁶ and data storage technologies⁷ have been hampered by the low electrical conductivity of most MOF materials.

It is remarkable that, despite the synthesis of over 120 000 metal–organic framework materials, only a select few demonstrate significant electrical conductivity, and only a handful displays metallic characteristics.⁸ This rarity is primarily attributed to inadequate interaction between the electronic states of the metal ions in the MOF Secondary Building Units (SBUs) and the organic linkers, which leads to the formation of wide band-gap materials with predominantly flat bands. While for a small number of bulk MOFs metallic conductivity has been observed (the first one was a CoTHT (triphenylenehexathiolate) MOF reported in 2017^8a) in small single crystals (several 100 μm in size), efforts to fabricate thin films with high (above 100 S m⁻¹) or even metallic conductivity – vital for applications in sensors and energy⁹ have been unsuccessful (see also Table S1 in the ESI†).

Cu₃(HHTP)₂, among other triphenylene-based cMOFs (conductive MOFs),¹⁰ consist of conjugated, two-dimensional honeycomb monolayers formed by connecting aromatic HHTP (hexahydroxytriphenylene) units by Cu²⁺ ions that stack in an alternating ABAB fashion, creating 2.3 nm wide channels running along the crystallographic [001] direction³ (see Fig. 1). The highest reported electrical conductivity for Cu₃(HHTP)₂ amounts to around 150 S m⁻¹ at room temperature, observed in needle-shaped single crystals roughly 350 μm in size.¹¹ Such conductivity places Cu₃(HHTP)₂ among lightly doped semiconductors, like silicon, and conductive polymers such as poly(3,4-ethylenedioxythiophene)polystyrenesulfonate (PEDOT:PSS). The conduction mechanism of Cu₃(HHTP)₂ remains debated in recent studies due to the lack of low-temperature measurements.¹¹

Fig. 1 Left: Structure of the Cu₃HHTP₂ cMOF. Note the AB stacking for the Bilayer and the ABAB stacking for the bulk. Right: Theoretical results for UV-vis obtained using TD-DFT (see text). Blue: absorption of bare linker before coupling. Orange: absorption of linker coupled to three Cu⁺⁺ SBUs. The insets show the electron density difference upon the excitation: electron donating (blue) and accepting (red) regions.

While the conductivity of bulk Cu₃(HHTP)₂ at 150 S m⁻¹ highlights its potential for energy storage and sensor applications, it is imperative to create oriented Cu₃(HHTP)₂ thin films with high electrical conductivity. Solving this challenge is crucial for enhancing sensor functionality and conducting advanced characterizations, e.g., via ultraviolet photoelectron spectroscopy (UPS) and for studies of spin liquids at low temperatures.¹²

The growing interest in Cu₃(HHTP)₂ thin films has spurred extensive efforts to synthesize them on diverse substrates. Although many studies have achieved oriented and crystalline coatings for this and other cMOFs, their electrical conductivity remained below a few S m⁻¹, significantly lower – by two orders of magnitude – compared to that of Cu₃(HHTP)₂ single crystals (see Table S2 in the ESI†). Moreover, the thin film structural integrity of this and other cMOF thin films often does not match the corresponding single crystals. Metallic MOF thin films have not yet been reported.

Achieving high structural quality and minimizing structural flaws in Cu₃(HHTP)₂ coatings are challenging due to difficulties in identifying optimal synthesis conditions. While high temperatures (around 150 °C) are effective for the solvothermal synthesis of MOF powders, they are unsuitable for the low-temperature layer-by-layer (LBL) process,¹³ which has yielded the best results reported so far for thin Cu₃(HHTP)₂ layers.¹⁴ The LBL method, requiring room temperature deposition to yield MOF thin films referred to as SURMOFs, shifts the focus from thermodynamic to kinetic control.

As a result, previously reported conditions for the solvothermal synthesis of bulk Cu₃(HHTP)₂ materials provide limited assistance. Instead, it is essential to optimize various experimental parameters for growth on appropriately functionalized substrates, the number of which is substantially larger than in solvothermal synthesis. The traditional trial-and-error method for determining experimental conditions for LBL growth is extremely tedious.^4,15

To meet this challenge, we employed a semi-autonomous robotic lab, where a machine learning (ML) approach is used to optimize the structure, orientation, and electrical conductivity of Cu₃(HHTP)₂ SURMOFs (surface anchored MOFs) grown on SiO₂ substrates. These substrates were functionalized applying plasma treatment, as the use of SAMs (self-assembled monolayer) is considerably more challenging and less reliable on SiO₂ surfaces than on noble metals. Moreover, Au substrates were avoided due to the risk of short circuits during electrical conductivity measurements. In line with previous studies on HKUST-1 thin films,¹⁶ ultrasonic treatment was integrated into the robotic set-up and applied twice in each LBL cycle. Analogous to previous work, where ultrasonication was found to reduce defect densities,¹⁷ ultrasonication was found to enhance film quality, without compromising film integrity. One of the key challenges in this approach is the rapid and reproducible determination of SURMOF electrical conductivity. Initially this crucial value was examined by 4-probe-conduction measurements, contacting the samples from above using a linear line of 4 spring-loaded “Pogo Pins”. However, this approach was too slow to be directly integrated into the ML-based optimization process.

Analysis of MOF thin films indicated that changes in optical absorption were linked to changes in electrical conductivity, with substantial conductivity correlating with significant shifts in the UV-vis spectrum (Fig. 1). We hypothesized that the appearance of UV-vis bands at around 600 nm is correlated with a conjugation of adjacent HHTP monomers, which was corroborated by density functional theory (TD-DFT) calculations of the UV-vis absorption spectra of Cu₃(HHTP)₂ (see Fig. 1 & ESI†). Due to the size of the system and the computational setup required for such calculations, molecular fragments comprising Cu₃(HHTP)₂ were considered (see ESI†). While the HHTP chromophores exhibit minimal absorption in the 575 to 625 nm regime before assembly into the Cu₃(HHTP)₂ MOF structure (Fig. 1), there is a high correlation between the degree of structure in the theoretical models and a marked increase in optical absorption in the range of 575–625 nm, The red-shift in the UV-vis spectra arises because the electronic wavefunctions spread across several HHTP linkers in the presence of the SBU, as well from the stacking of the layered material (see ESI†).

For the ML-based synthesis optimization process, we therefore used the integrated optical absorption in the 575 to 625 nm region in combination with the crystallinity and the lateral size of the Cu₃(HHTP)₂ domains as determined from the width of the in-plane XRD peaks (see Fig. 2) to compute the fitness function governing the ML approach. For the optimization process, we selected a particular ML tool called “SyCoFinder”,^15d which can simultaneously optimize multiple parameters while targeting diverse objectives.

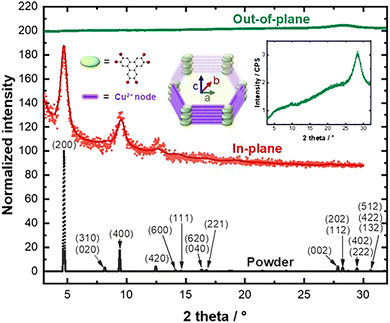Fig. 2 Simulated diffractograms of Cu₃(HHTP)₂ (black); in-plane (red) and out-of-plane (green) XRD measurements.

A total of five synthesis parameters were optimized in the ML process, i.e., the concentrations of all reactants and the amount of growth modulator (H₂O), as well as the length of the sonication cycles in the synthesis process and the postsynthetic defect healing time (see ESI†). To ensure precise control and reproducibility of SURMOF synthesis, experiments were performed by an autonomous robotic lab setup in a glove box with a controlled atmosphere.

After two rounds of machine learning-based optimization we achieved almost entirely black samples and the fitness function reached a plateau. Analysis of the structural parameters, notably the intensity and width of the diffraction peaks, revealed exceptional structural quality of the resulting samples that exceeds most previously documented outcomes for Cu₃(HHTP)₂ thin films. Analysis of synthesis parameters (see Table S1, and Fig. S1, ESI†) revealed that no single parameter alone enhances the synthesis; instead, optimization must involve four of the five parameters simultaneously. In a next step, the electrical conductivity of several samples prepared under the set of optimum parameters was rigorously tested. We began by depositing 100 × 100 μm² sized gold (Au) contact pads with a contact separation of 100 μm in a solvent-free process by vacuum-based thermal evaporation, onto the top surface of the Cu₃(HHTP)₂ films (see Fig. S4, ESI†). Confirming ohmic behavior of the individual contacts through current (I)/voltage (V) curves, we then utilized a 4-point method to measure electrical conductivity. The measurements yielded conductivity values reaching up to 110 S m⁻¹ at room temperature, with an average value of 107.8 ± 3.9 S m⁻¹, slightly lower than those reported for bulk Cu₃(HHTP)₂ single crystals (150 S m⁻¹ (ref. 11)).

The nature of cMOF electrical conductivity remains controversial, as most experimental observations point to semiconducting behavior with activated transport with activation energies between 0.48 eV to 1.14 eV.¹⁸ For example, clear activated transport was measured for Cu₃(HHTN)₂¹⁹ or Ga₉(HOTP)₄,²⁰ the latter supported by electronic structure calculations. Generally speaking, electronic structure calculations remained inconclusive, with metallic²¹ and semiconducting behavior observed for the same material Cu₃(HHB)₂.²² Several studies have pointed out the relevance of structural distortions,²³ the presence of water,²⁴ and/or magnetic ordering.²³ Only analyses of the mono- and bilayer electronic structures for Cu₃(HHTP)₂ have been documented;²⁵ however, investigations into the bulk electronic structure are lacking.

From an experimental standpoint, the key to distinguishing between metallic and semiconducting behavior lies in analyzing temperature-dependent changes in electrical conductivity. The corresponding measurements for the 100 μm spaced electrodes revealed a significant decrease of conductivity with reduced temperatures within our SURMOFs (see Fig. S5, ESI†), measurements for a reduced electrode distance (15 μm) revealed similar results. This observation strongly points towards an activated conduction process with a small activation energy of 82 meV, suggestive of an intrinsic semiconductor with a small band gap. This behavior aligns with prior reports on the electrical conductivity of Cu₃(HHTP)₂ thin films (see table S2 in ESI†), yet is inconsistent with reported²⁶ and our own UPS data (see Fig. S8, ESI†), where no indications of a band gap of ∼100 meV were seen.

It has gone largely unnoticed that, from a theoretical point of view, the hexagonal D_6h symmetry of the single Cu₃(HHTP)₂ planes comprising this cMOF implies that the band-structure must exhibit a Dirac cone, as in graphene²⁷ (Fig. 2 top). To explore this issue, we have carried out comprehensive electronic structure calculations (for details see the ESI†) to determine the electronic band structure of Cu₃(HHTP)₂. In Fig. 3 (top), we show the density of states and the band structure of Cu₃(HHTP)₂ monolayers exhibiting a unit cell with D_6h symmetry. In addition to the expected flat bands originating from the molecular HHTP orbitals, a Dirac cone is clearly visible at the K point. While the precise position of the Dirac cone in terms of the k-vectors is dictated by symmetry, the energy, i.e. the points where the linear dispersion curves intersect, depends on the electronic structure of the metal ions. In the present case, for the Cu₃(HHTP)₂ monolayers the Dirac cone is shifted upward by about 0.1 eV above the Fermi energy (E_F), leading to a finite density of states at E_F, thus predicting 2D metallic behavior.

Fig. 3 Density of states as obtained from DFT calculations for a Cu₃(HHTP)₂ monolayer (with D_6h symmetry, top) and the Cu₃(HHTP)₂ bulk (bottom). Left panel: Band energies relative to the Fermi energy, obtained from a high-spin calculation. The bands of the two spin channels are indicated in different colors. The Dirac cones (top) and their remnants in the 3D structure are illustrated by green circles. Right panel: Total (black) and projected density of states as a function of energy. Green, blue and black lines indicate the partial DOS corresponding to oxygen, carbon, and copper, respectively in the two spin channels.

The ABAB stacking in the 3D bulk structure of Cu₃(HHTP)₂ distorts the monolayer band structure (Fig. 2 bottom), but remnants of the Dirac cone and the corresponding low effective mass of the carriers remain. In addition to a hybridization of the bands a vertical shift of the Dirac cone is visible, yielding a further increase of density of states at the Fermi edge.

These findings imply that, despite the temperature-dependent electrical conductivity in the initial experiments suggesting otherwise, a band gap should not exist. Our calculations indicate metallic behavior in perfect Cu₃(HHTP)₂. Similar to graphite, charge carriers move within individual planes, while transport across the 2D sheets is limited by a small band gap.

The most straightforward explanation for the discrepancy between the semiconducting behavior concluded from the experimental temperature dependence of I/V measurements and the metallic behavior suggested from the DFT calculations results from the presence of domain boundaries, which have to be crossed by the electrons on their fairly long path (100 μm) from the negative to the positive electrode.

Determining the intrinsic conductivity of the material requires measurements with electrode distances below the size of the Cu₃(HHTP)₂ SURMOF domains, which are around 100 nm, as determined from the FWHM values of the in-plane XRD peaks. However, such small spacings cannot be achieved with the mask-based technique used for contact fabrication in the experiments reported above but require lithographic methods. This is challenging since the SURMOF must withstand the lithographic process, including immersion in different solvents.²⁸ After optimizing the synthesis process (see the ESI†), we successfully positioned 4-terminal electrodes 100 nm apart on the SURMOFs, as shown in Fig. 4a and b (for details, see the ESI†). Interestingly, measurements recorded using a 4-point method, where ohmic transport has been confirmed for the individual contacts (see Fig. S6, ESI†), revealed a completely different scenario for such closely spaced electrodes. Room temperature conductivity increased to 240 S m⁻¹ setting, a new record for this cMOF and surpassing previous bulk values of 150 S m⁻¹.

Fig. 4 (a) Scanning electron microscopy image of a contacted for Cu₃(HHTP₂) SURMOF. (b) Schematic of experimental setup used for charge transport measurements (c) experimental electrical conductivities (σ) measured using a 4-point method for Cu₃HHTP₂ SURMOFs with a thickness of 650 nm. The distance between the contacts amounts to 100 nm.

More importantly, lowering the temperature to 100 K now leads to a substantial 15% increase in conductivity to 295.8 ± 5.9 S m⁻¹, instead of the strong decrease observed for the larger electrode distances, see Fig. 4c a second, independent substrate showed a conductivity of 300.6 ± 5.9 S m⁻¹ at 100 K. This observation unambiguously excludes hopping or any other form of activated transport and provides clear evidence of intrinsic metallic behavior within individual domains of our Cu₃(HHTP)₂ SURMOFs. Furthermore, the structural integrity of the film is demonstrated by the fact that the conductivity follows a similar trend upon subsequent cooling and heating cycles (see Fig. S7, ESI†). In this study, the ML algorithm optimized parameters for SURMOF thicknesses around 600 nm. For potential device applications requiring thinner layers, future work will extend ML optimization to these thinner SURMOFs.

It is interesting to note that the DFT calculations also predict strong spin polarization. As discussed in previous work,¹² the single d electron of the Cu⁺⁺ species gives rise to the formation of different spin-up and spin-down bands. In the case of a coupling between adjacent Cu₃(HHTP)₂ planes, in principle, magnetic effects as observed for the Cu⁺⁺-containing SURMOF-2 might be expected.²⁹ The availability of planar substrate will, in the future, allow us to study the intrinsic electronic properties of this highly interesting material. In addition to spin liquid also the investigation of other, even more exotic effects will become possible, e.g. Klein tunneling³⁰ predicted to occur in the presence of linear dispersion bands.

Conclusion

In conclusion, we have provided compelling experimental evidence that near-perfect MOF thin films grown using an ML-based process to drive a robot-based autonomous experimental synthesis and characterization station exhibit metallic behavior, with an electrical conductivity of 240 S m⁻¹ at 300 K increasing to 300 S m⁻¹ at 100 K. To our knowledge, this is the first MOF thin film exhibiting metallic electrical transport. Experimental UPS data reveal a low density of states at the Fermi edge consistent with DFT-based electronic structure calculations exhibiting a Dirac cone, which is responsible for a low density of states at the Fermi edge, in full accord with the experimental data. These findings suggest that the inherent limitations of electronic conductivity stemming from low mixing of the electronic states on the SBU and the organic linkers can be overcome by the exploitation of the 2D hexagonal symmetry that results in the presence of the Dirac cone. We note that the Dirac cone is a ubiquitous feature of the entire class of materials²⁵ (see ESI†). In metallic systems, the electronic conductivity is inversely proportional to the effective mass of the charge carriers, which in turn results from the curvature of the bands. Low electronic coupling between the lattice sites in conventional MOFs results in flat bands with low conductivity, as is observed in essentially all crystalline MOF materials. However, these considerations do not pertain to the linear band-structure near the Dirac cone, resulting in zero-mass Dirac fermions, which are responsible for the high conductivity of perfect hexagonal materials. Cu₃(HHTP)₂ is an ideally self-doped material, because the Dirac cone does not coincide with the Fermi energy, resulting in a finite density of states at the Fermi surface.

Our results suggest, following prior observations,^8c that exploitation of a 2D hexagonal symmetry in MOF materials induces a metallic symmetry induced conductivity not present in other non-hexagonal MOFs while avoiding, through the presence of the charge transfer between metals and linkers, the coincidence of the Dirac cone and the Fermi surface. This finding paves the way to exploit MOF materials with 2D hexagonal symmetry in challenging electronic applications. These findings notwithstanding, it is essential to synthesize the materials to ensure sufficient quality. Here, we have demonstrated the development of surrogate characterization techniques that enable the synthesis of highly conductive, metallic MOF thin films without the need to characterize the conductivity of the samples during the optimization cycles.

The availability of high-quality 2D MOF thin films opens up the possibility to investigate further properties of such 2D systems, e.g. the formation of spin liquids or other, more exotic effects occurring at lower temperatures. We anticipate that machine learning-driven robotic synthesis labs will significantly enhance the optimization of synthesis parameters for MOF thin films, including other layered MOFs and cMOFs. Improvements are also anticipated with respect to the size of the SURMOF domains, which would enable the use of larger electrode separations—particularly when combined with specially functionalized Si(111) substrates.³¹

Data availability

All data relevant for our paper are either provided in the ESI† or are available from the authors on request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

JFP, RTW, WW, and CW acknowledge partial funding from the German Research Foundation (DFG) Priority Program 1928 “Coordination Networks: Building Blocks for Functional Systems” (COORNETs). CS, LP, WW, and CW acknowledge funding by the German Research Foundation (DFG) through the Germany's Excellence Strategy in the context of 3DMM2O. CS, LP, WW and CW thank the Carl Zeiss Foundation for the financial support. CCBB acknowledges funding by the São Paulo Research Foundation (2023/09820-2). CCBB is a Productivity Research Fellow from the Brazilian National Council for Scientific and Technological Development (CNPq 309011/2023-0). The authors acknowledge access to the high-performance computer HoreKa at the NHR Center NHR@KIT. We thank Yohanes Pramudya and Saibal Jana for helpful discussions regarding the band-structure calculations and Alexei Nefedov for measuring the UPS data.

References

1. G. Férey, Chem. Soc. Rev., 2008, 37, 191–214.
2. (a) H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 974; (b) S. Kitagawa, R. Kitaura and S.-I. Noro, Angew. Chem., Int. Ed., 2004, 43, 2334–2375.
3. A.-Q. Wu, W.-Q. Wang, H.-B. Zhan, L.-A. Cao, X.-L. Ye, J.-J. Zheng, P. N. Kumar, K. Chiranjeevulu, W.-H. Deng, G.-E. Wang, M.-S. Yao and G. Xu, Nano Res., 2021, 14, 438–443.
4. H. Tsai, S. Shrestha, R. A. Vilá, W. Huang, C. Liu, C.-H. Hou, H.-H. Huang, X. Wen, M. Li, G. Wiederrecht, Y. Cui, M. Cotlet, X. Zhang, X. Ma and W. Nie, Nat. Photonics, 2021, 15, 843–849.
5. D. Sheberla, J. C. Bachman, J. S. Elias, C. J. Sun, Y. Shao-Horn and M. Dinca, Nat. Mater., 2017, 16, 220–224.
6. X. Chen, Y. Lu, J. Dong, L. Ma, Z. Yi, Y. Wang, L. Wang, S. Wang, Y. Zhao, J. Huang and Y. Liu, ACS Appl. Mater. Interfaces, 2020, 12, 57235–57244.
7. L. Pan, Z. Ji, X. Yi, X. Zhu, X. Chen, J. Shang, G. Liu and R.-W. Li, Adv. Funct. Mater., 2015, 25, 2677–2685.
8. (a) A. J. Clough, J. M. Skelton, C. A. Downes, A. A. de la Rosa, J. W. Yoo, A. Walsh, B. C. Melot and S. C. Marinescu, J. Am. Chem. Soc., 2017, 139, 10863–10867; (b) A. J. Clough, N. M. Orchanian, J. M. Skelton, A. J. Neer, S. A. Howard, C. A. Downes, L. F. J. Piper, A. Walsh, B. C. Melot and S. C. Marinescu, J. Am. Chem. Soc., 2019, 141, 16323–16330; (c) G. Skorupskii, K. N. Le, D. L. M. Cordova, L. M. Yang, T. Y. Chen, C. H. Hendon, M. Q. Arguilla and M. Dinca, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2205127119.
9. Y. Peng, J. Xu, J. Xu, J. Ma, Y. Bai, S. Cao, S. Zhang and H. Pang, Adv. Colloid Interface Sci., 2022, 307, 102732.
10. N. Contreras-Pereda, S. Pané, J. Puigmartí-Luis and D. Ruiz-Molina, Coord. Chem. Rev., 2022, 460, 214459.
11. R. W. Day, D. K. Bediako, M. Rezaee, L. R. Parent, G. Skorupskii, M. Q. Arguilla, C. H. Hendon, I. Stassen, N. C. Gianneschi, P. Kim and M. Dincă, ACS Cent. Sci., 2019, 5, 1959–1964.
12. P. Ninawe, A. Jain, M. Sangole, M. Anas, A. Ugale, V. K. Malik, S. M. Yusuf, K. Singh and N. Ballav, Chem. – Eur. J., 2024, 30, e202303718.
13. O. Shekhah, H. Wang, S. Kowarik, F. Schreiber, M. Paulus, M. Tolan, C. Sternemann, F. Evers, D. Zacher, R. A. Fischer and C. Wöll, J. Am. Chem. Soc., 2007, 129, 15118–15119.
14. G.-D. Wu, H.-L. Zhou, Z.-H. Fu, W.-H. Li, J.-W. Xiu, M.-S. Yao, Q.-H. Li and G. Xu, Angew. Chem., Int. Ed., 2021, 60, 9931–9935.
15. (a) B. D. Dhanapala, D. L. Maglich and M. E. Anderson, Langmuir, 2023, 39, 12196–12205; (b) O. Lugier, U. Pokharel and S. Castellanos, Cryst. Growth Des., 2020, 20, 5302–5309; (c) L. Pilz, M. Koenig, M. Schwotzer, H. Gliemann, C. Wöll and M. Tsotsalas, Adv. Funct. Mater., 2024, 34, 2404631; (d) S. M. Moosavi, A. Chidambaram, L. Talirz, M. Haranczyk, K. C. Stylianou and B. Smit, Nat. Commun., 2019, 10, 539.
16. (a) L. Pilz, C. Natzeck, J. Wohlgemuth, N. Scheuermann, P. G. Weidler, I. Wagner, C. Wöll and M. Tsotsalas, Adv. Mater. Interfaces, 2023, 10, 2201771; (b) Z. G. Gu, A. Pfriem, S. Hamsch, H. Breitwieser, J. Wohlgemuth, L. Heinke, H. Gliemann and C. Wöll, Microporous Mesoporous Mater., 2015, 211, 82–87.
17. W. J. Wang, D. I. Sharapa, A. Chandresh, A. Nefedov, S. Heissler, L. Heinke, F. Studt, Y. M. Wang and C. Wöll, Angew. Chem., Int. Ed., 2020, 59, 10514–10518.
18. (a) V. Rubio-Giménez, M. Galbiati, J. Castells-Gil, N. Almora-Barrios, J. Navarro-Sánchez, G. Escorcia-Ariza, M. Mattera, T. Arnold, J. Rawle, S. Tatay, E. Coronado and C. Martí-Gastaldo, Adv. Mater., 2018, 30, 1704291; (b) X. Zhang, X. Tian, N. Wu, S. Zhao, Y. Qin, F. Pan, S. Yue, X. Ma, J. Qiao, W. Xu, W. Liu, J. Liu, M. Zhao, K. Ostrikov and Z. Zeng, Sci. Adv., 2024, 10, eadl6498.
19. Z. Meng and K. A. Mirica, Nano Res., 2021, 14, 369–375.
20. G. Skorupskii, G. Chanteux, K. N. Le, I. Stassen, C. H. Hendon and M. Dinca, Ann. N. Y. Acad. Sci., 2022, 1518, 226–230.
21. M. Choe, J. Y. Koo, I. Park, H. Ohtsu, J. H. Shim, H. C. Choi and S. S. Park, J. Am. Chem. Soc., 2022, 144, 16726–16731.
22. Z. Meng, C. G. Jones, S. Farid, I. U. Khan, H. M. Nelson and K. A. Mirica, Angew. Chem., Int. Ed., 2022, 61, e202113569.
23. R. Wang, C. Z. He and W. X. Chen, Nanoscale, 2023, 15, 11083–11089.
24. M. R. Momeni, Z. Zhang, D. Dell'Angelo and F. A. Shakib, Phys. Chem. Chem. Phys., 2021, 23, 3135–3143.
25. P. H. Souza and W. Orellana, J. Phys. Chem. C, 2025, 129, 3285–3291.
26. Y. M. Jo, K. Lim, J. W. Yoon, Y. K. Jo, Y. K. Moon, H. W. Jang and J. H. Lee, ACS Cent. Sci., 2021, 7, 1176–1182.
27. (a) A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Modern Phys., 2009, 81, 109–162; (b) P. Miró, M. Audiffred and T. Heine, Chem. Soc. Rev., 2014, 43, 6537–6554.
28. L. G. S. Albano, T. P. Vello, D. H. S. de Camargo, R. M. L. da Silva, A. C. M. Padilha, A. Fazzio and C. C. B. Bufon, Nano Lett., 2020, 20, 1080–1088.
29. S. Friedländer, J. X. Liu, M. Addicoat, P. Petkov, N. Vankova, R. Rüger, A. Kuc, W. Guo, W. C. Zhou, B. Lukose, Z. B. Wang, P. G. Weidler, A. Pöppl, M. Ziese, T. Heine and C. Wöll, Angew. Chem., Int. Ed., 2016, 55, 12683–12687.
30. P. E. Allain and J. N. Fuchs, Eur. Phys. J., 2011, 83, 301–317.
31. P. Thissen, J. Wohlgemuth, P. Weidler, D. Smilgies, L. Heinke, N. Schewe, M. Koenig, P. Krolla and C. Wöll, Adv. Funct. Mater., 2024, 34, 2301535.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5mh00813a

‡ Equal contribution.

---