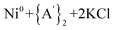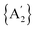Open Access Article
Open Access ArticleSolvent influence on the mechanism of a mechanochemical metal-halide metathesis reaction†
Sourabh Kumar a,
Dillon Button-Jennings
a,
Dillon Button-Jennings b,
Timothy P. Hanusa
b,
Timothy P. Hanusa b and
Ashlie Martini
b and
Ashlie Martini *a
*a
aDepartment of Mechanical Engineering, University of California Merced, Merced, California 95343, USA. E-mail: amartini@ucmerced.edu; sourabhkumar@ucmerced.edu
bDepartment of Chemistry, Vanderbilt University, Nashville, Tennessee 37235, USA. E-mail: dillon.a.button-jennings@vanderbilt.edu; t.hanusa@vanderbilt.edu
First published on 9th April 2025
Abstract
Solvents have long been integral to the success of synthetic chemistry, influencing reaction rates, mechanisms, and product selectivity. However, mechanochemistry—typically involving the grinding and mixing of solid reagents—offers an alternative environment that is solvent-free or at least greatly minimizes solvent use, and that drives reactions through mechanical force. In a recent study, the reaction between the salt of a bulky allyl anion, K[A′] (A′ = 1,3-(SiMe3)2C3H3), and a nickel halide gave very different outcomes depending on whether the reaction was conducted without solvent using a solid material, with a starting solvated complex, [Ni(py)4Cl2], modified by a small amount of pyridine, or in pyridine solution. Under certain conditions, halide metathesis occurred, forming the allyl complex  in near quantitative yield. Under others, a redox reaction dominated, generating allyl radicals that coupled and left {A′}2 (1,3,4,6-tetrakis(trimethylsilyl)hexa-1,5-diene) as the major product. To understand these differing outcomes, the formation mechanisms of
in near quantitative yield. Under others, a redox reaction dominated, generating allyl radicals that coupled and left {A′}2 (1,3,4,6-tetrakis(trimethylsilyl)hexa-1,5-diene) as the major product. To understand these differing outcomes, the formation mechanisms of  under varying solvent conditions were investigated here using Density Functional Theory (DFT). The effects of the reaction conditions on factors such as Gibbs free energy change, bond energy behavior, and transition states collectively suggest that electrostatic stabilization dominates in the solvent phase. In the case of solvate-assisted conditions, a complete energy profile diagram of the reaction between [Ni(py)4Cl2] and 2K[A′], leading to
under varying solvent conditions were investigated here using Density Functional Theory (DFT). The effects of the reaction conditions on factors such as Gibbs free energy change, bond energy behavior, and transition states collectively suggest that electrostatic stabilization dominates in the solvent phase. In the case of solvate-assisted conditions, a complete energy profile diagram of the reaction between [Ni(py)4Cl2] and 2K[A′], leading to  and KCl, was calculated, with evidence for one of the intermediates ([A′Ni(py)Cl]) being provided by experiments. Calculations confirm that coordination of pyridine to the nickel, whether from the free liquid or (preferentially) from the pyridine solvate, weakens the Ni–Cl bond so that metathesis can proceed easily. If pyridine is absent (i.e., under solvent-free conditions), the redox route will have a kinetic advantage in the reaction. This study provides molecular-level insights for understanding and optimizing solvent-assisted grinding processes.
and KCl, was calculated, with evidence for one of the intermediates ([A′Ni(py)Cl]) being provided by experiments. Calculations confirm that coordination of pyridine to the nickel, whether from the free liquid or (preferentially) from the pyridine solvate, weakens the Ni–Cl bond so that metathesis can proceed easily. If pyridine is absent (i.e., under solvent-free conditions), the redox route will have a kinetic advantage in the reaction. This study provides molecular-level insights for understanding and optimizing solvent-assisted grinding processes.
1. Introduction
Reactions induced by mechanical force1–3 have emerged as green alternatives for synthesizing organic molecules, metal complexes, and advanced materials.4,5 The mechanical energy required to form such products can often be supplied by well-established milling and grinding techniques.6 The use of solid-state mechanochemical methods is not a guarantee of synthetic success, however, as some reactions under grinding and milling conditions can be less efficient than solvent-based approaches, resulting in decreased reactivity, lower yields, and possibly different products.7,8 Interestingly, studies have shown that adding a small amount of solvent during grinding (“liquid-assisted grinding”, LAG) can substantially influence the mechanochemical reactivity and the yield of the resulting products.9 The solvent contribution in grinding or milling conditions, often defined by a volume/mass ratio (η = μL of solvent added/mg of reagents), has been categorized into four distinct regimes: dry (neat) grinding (η = 0); LAG (0 < η ≲ 2); slurries/pastes (η = 2 − 12); and pure solution-based reactions (η > 12). The LAG technique has shown promise in speeding up reactions and providing high yields with controlled reactivity, underscoring the importance of solvent optimization in mechanochemical synthesis.A variation on the LAG technique, in which LAG quantities of solvents are initially present as metal solvates or hydrates, rather than the free liquid, has been termed “solvate-assisted grinding” (SAG).10 As a result, LAG and SAG are critical adjuncts to mechanochemical synthesis, offering more efficient and sustainable alternatives for synthesizing compounds ranging from pharmaceuticals11 and organometallic compounds10 to metal–organic frameworks12 and covalent organic frameworks.13
To study the contribution of solvents in chemical reactions, it is common to compare different solvents' effects on the reaction outcomes.14 The solvent choice depends on the reaction's aim, but solvents can be usefully classified based on the magnitude of their dielectric constant (ε).14 The dielectric constant (relative permittivity) of a solvent describes the material's response to an external electric field, and studies have shown that global parameters such as chemical potential and hardness decrease from the gas phase (i.e., solvent-free) to the solvent phase due to the increase in the dielectric constant.15 The effect of changes in the dielectric constant on mechanochemical synthesis can take various forms, but changes in reaction selectivity are possible outcomes.16 For example, combining a solvent's dielectric constant (under LAG conditions) with appropriate counter-ion pairing enhanced the selectivity of a Wittig reaction.17 In another case, the relative polarity (and hence the dielectric constant) of a LAG additive was a key factor in switching the kinetics and chemoselectivity of the reaction between a difluorinated diketone and (PhS)2.18 A detailed understanding of solvent contributions to mechanochemical reactions will involve evaluating dielectric constants' effects, an area that has been poorly explored in organometallic contexts.
Computational tools are well-suited for exploring the reaction consequences of changes in dielectric constants,19 and among these, density functional theory20,21 (DFT) has often been used to explore solution-based methods for synthesizing materials. For example, DFT was used to show that suppression of the collective response of solvent molecules resulted in a decrease in the dielectric permittivity.22 In another investigation, a combination of DFT and molecular dynamics (MD) simulations was employed to demonstrate that the dielectric constant was influenced by varying temperatures and electrolyte compositions.23 A recent computational study highlighted the disparities between reactions performed under dry and LAG conditions.24 In this case, DFT coupled with microkinetic modeling was used to investigate the influence of solvent concentration and the dielectric environment on Diels–Alder reactions and the synthesis of N-sulfonylguanidines.
Experimental work can complement computational efforts to analyze solvent effects in mechanochemistry. A recent experimental study systematically compared solvent effects on the synthesis of organometallic complexes under various milling conditions.10 The synthesis of sterically bulky bis(allyl) complexes  from the binary metal chlorides, MCl2 (M = Cr, Fe, Co, Ni) and solvated metal chloride complexes, MLnCl2 (L = tetrahydrofuran (THF), pyridine) in various conditions, including solvent-free, LAG, SAG (using a pyridine-solvated complex), and pure solution (THF and pyridine) was examined.10 Two distinct pathways were identified during the reactions, each accompanied by characteristic products. One involved halide metathesis, leading to the formation of
from the binary metal chlorides, MCl2 (M = Cr, Fe, Co, Ni) and solvated metal chloride complexes, MLnCl2 (L = tetrahydrofuran (THF), pyridine) in various conditions, including solvent-free, LAG, SAG (using a pyridine-solvated complex), and pure solution (THF and pyridine) was examined.10 Two distinct pathways were identified during the reactions, each accompanied by characteristic products. One involved halide metathesis, leading to the formation of  complexes; the other involved a redox process, generating neutral radicals from the starting allyl anions that then coupled to form 1,3,4,6-tetrakis(trimethylsilyl)hexa-1,5-diene
complexes; the other involved a redox process, generating neutral radicals from the starting allyl anions that then coupled to form 1,3,4,6-tetrakis(trimethylsilyl)hexa-1,5-diene 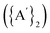 .
.
The presence of solvent was found to influence the reaction outcome significantly. It should be noted that in the case of nickel, [Ni(py)4Cl2] was the metal solvate used; it provided an amount of pyridine equivalent to η = 0.55, which is both well within the standard LAG region and is not greatly different from the amount used with separately added liquid pyridine (η = 0.70). Hence, the LAG/SAG reactions differed primarily in whether the pyridine was initially present as a free liquid or was metal-bound, not in its amount relative to nickel. The results of this study10 are summarized in Fig. 1, which shows that the NiCl2 reaction with two equivalents of K[A′] led to different proportions of the bis(allyl)metal complex  . The underlying reasons for the solvent effect on the reaction outcome remained uncertain, and further investigation is required to explore the mechanisms responsible for this phenomenon. It was unclear, for example, why a pyridine-coordinated nickel complex provided the
. The underlying reasons for the solvent effect on the reaction outcome remained uncertain, and further investigation is required to explore the mechanisms responsible for this phenomenon. It was unclear, for example, why a pyridine-coordinated nickel complex provided the  complex with a much greater yield than the equivalent amount of NiCl2 + free pyridine.
complex with a much greater yield than the equivalent amount of NiCl2 + free pyridine.
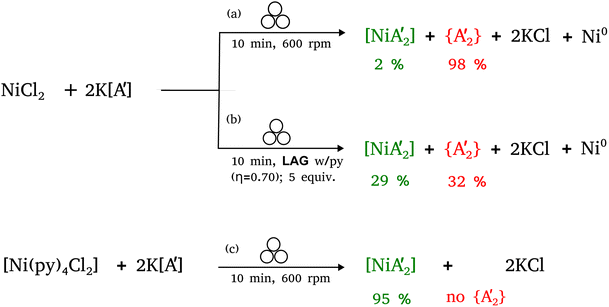 | ||
Fig. 1 Reaction schemes for  synthesis using (a) neat grinding, (b) liquid-assisted grinding (LAG), and (c) solvate-assisted grinding (SAG).10 The green and red text represent the experimentally observed yields for synthesis using (a) neat grinding, (b) liquid-assisted grinding (LAG), and (c) solvate-assisted grinding (SAG).10 The green and red text represent the experimentally observed yields for 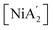 and and  , respectively. , respectively. | ||
In the family of transition metal allyl complexes, those containing nickel were among the first to be synthesized,25 and nickel derivatives continue to be important in developing high-performance catalysts for olefin polymerization.26–29 Thus, of the possible systems to study, we focused on the molecular-level reaction mechanism of 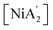 formation under different conditions (solvent-free, in solvents, and using a solvated starting material) using DFT calculations complemented with experimental evidence. This molecular-level approach is a critical first step in understanding larger-scale LAG and SAG processes.
formation under different conditions (solvent-free, in solvents, and using a solvated starting material) using DFT calculations complemented with experimental evidence. This molecular-level approach is a critical first step in understanding larger-scale LAG and SAG processes.
2. Computational details
The model systems described the synthesis of sterically bulky bis(allyl) complex from the binary metal chloride (NiCl2), and from solvated metal chloride complexes, MLnCl2 (L = tetrahydrofuran (THF), pyridine). The computational calculations were performed using the Gaussian 16 quantum chemistry program package.30 DFT methods were employed at the B3PW91
from the binary metal chloride (NiCl2), and from solvated metal chloride complexes, MLnCl2 (L = tetrahydrofuran (THF), pyridine). The computational calculations were performed using the Gaussian 16 quantum chemistry program package.30 DFT methods were employed at the B3PW91![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31 (hybrid GGA density functional)/def2-TZVPP32,33 level of theory. Dispersion correction via Grimme's D3 correction34 with additional Becke-Johnson damping35 (i.e., D3(BJ)) method was applied uniformly across all calculations using the “EmpiricalDispersion = GD3BJ” keyword. Tight convergence criteria (“opt = tight” keyword i.e., RMS force criterion to 1 × 10−5) and an SG1 integration grid (“int(grid = sg1)”), a pruned version of (50 radial shells, 194 angular points per shell) were used to ensure accuracy. The optimized geometries of ground and transition states were subjected to vibrational analysis at the same level of theory, yielding zero and one imaginary frequency, respectively. For Ni(II)-based complexes and structures involved in
31 (hybrid GGA density functional)/def2-TZVPP32,33 level of theory. Dispersion correction via Grimme's D3 correction34 with additional Becke-Johnson damping35 (i.e., D3(BJ)) method was applied uniformly across all calculations using the “EmpiricalDispersion = GD3BJ” keyword. Tight convergence criteria (“opt = tight” keyword i.e., RMS force criterion to 1 × 10−5) and an SG1 integration grid (“int(grid = sg1)”), a pruned version of (50 radial shells, 194 angular points per shell) were used to ensure accuracy. The optimized geometries of ground and transition states were subjected to vibrational analysis at the same level of theory, yielding zero and one imaginary frequency, respectively. For Ni(II)-based complexes and structures involved in 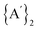 molecule synthesis, both singlet (S0) and triplet (T1) spin states were tested for reactants and products. The lowest-energy spin state was adopted for each structure, and the effect of spin state on reaction energetics was systematically analyzed. An implicit solvent model using the Polarizable Continuum Model (PCM) was employed to account for solvation effects, with pyridine and THF as the solvents. The electron localization function (ELF) and electron densities at the bond critical points (BCP) were evaluated using the Quantum Theory of Atoms in Molecules (QTAIM) framework,36 employing the Multiwfn 3.7 software package.37
molecule synthesis, both singlet (S0) and triplet (T1) spin states were tested for reactants and products. The lowest-energy spin state was adopted for each structure, and the effect of spin state on reaction energetics was systematically analyzed. An implicit solvent model using the Polarizable Continuum Model (PCM) was employed to account for solvation effects, with pyridine and THF as the solvents. The electron localization function (ELF) and electron densities at the bond critical points (BCP) were evaluated using the Quantum Theory of Atoms in Molecules (QTAIM) framework,36 employing the Multiwfn 3.7 software package.37
3. Experimental details
3.1 General considerations
Unless noted otherwise, syntheses were conducted under the exclusion of air and moisture using Schlenk line and glovebox techniques. Proton (1H) and carbon (13C) NMR spectra (Fig. S1–S4†) were obtained at ambient temperature on a Bruker AV-400 MHz spectrometer at 400 and 100 MHz, respectively, and were referenced to the residual resonances of C6D6.3.2 Materials
HCl in dioxane (4 M) was purchased from Sigma Aldrich. was prepared according to the literature procedure.38 [A′NiCl] was prepared from
was prepared according to the literature procedure.38 [A′NiCl] was prepared from  and HCl in dioxane as described in the ESI.† Inhibitor-free tetrahydrofuran (THF) and hexanes were degassed and dried by passage through activated alumina columns on an MBRAUN SPS system and then stored over 4A molecular sieves before use. Pyridine was degassed and dried by storage over 50% w/v KOH before use. Deuterated benzene was purchased from Cambridge Isotopes, degassed, and stored over 4A molecular sieves before use.
and HCl in dioxane as described in the ESI.† Inhibitor-free tetrahydrofuran (THF) and hexanes were degassed and dried by passage through activated alumina columns on an MBRAUN SPS system and then stored over 4A molecular sieves before use. Pyridine was degassed and dried by storage over 50% w/v KOH before use. Deuterated benzene was purchased from Cambridge Isotopes, degassed, and stored over 4A molecular sieves before use.
3.3 Mechanochemical protocol
Planetary milling was performed with a Retsch PM100 mill, a 50 mL zirconia grinding jar, and a safety clamp for air-sensitive grinding. Mechanochemical reactions were run by adding the solid reagents into a grinding jar with approximately 25 g of 5 mm zirconia ball bearings (0.34 g each).3.4 Synthesis of [A′Ni(py)Cl]
In a typical reaction, [A′NiCl] (0.0107 g, 0.038 mmol) is dissolved in ca. 2.5 mL of hexanes in an oven-dried 20 mL glass scintillation vial and sealed under an N2 atmosphere. To this red solution, 10 μL of pyridine is added dropwise and stirred overnight. The orange solution is slowly evaporated to deposit orange needles of [A′Ni(py)Cl] (0.0117 g, 85%). Anal. calcd for C14H26ClNNiSi2: C, 46.88; H, 7.31; N, 3.91. Found: C, 46.34; H, 7.45; N, 3.45. Proton NMR spectra were unusually broad and difficult to assign, a condition that existed across multiple preparations and solution concentrations. Representative spectra can be found in the ESI (Fig. SI3 and SI4).†4. Results and discussion
4.1 Steric crowding and electronic effects in [Ni(py)4Cl2]
The metal halide solvate used in this study is [Ni(py)4Cl2], a monomeric complex originally made by the dropwise addition of a heated ethanolic solution of pyridine to an ethanolic solution of NiCl2(H2O)6,39 although it can be generated mechanochemically as well.10 Its single crystal X-ray structure reveals long Ni–Cl and Ni–N bonds (2.44 Å and 2.13 Å, respectively), which represent 8% and 9% elongations over the sum of the single-bond covalent radii (2.26 Å and 1.95 Å, respectively),40 and hint at some degree of steric crowding in the molecule.The level of steric congestion in [Ni(py)4Cl2] can be visualized in the encapsulation of the metal coordination sphere. As estimated with the program Solid-G,41 and in particular by the value of Gcomplex (the net percentage of the coordination sphere covered by the ligands), the value for [Ni(py)4Cl2] is high (92.8%) (Fig. 2(A and B)). The observed bond lengthening and inferred steric crowding suggest that the complex may be primed for ligand dissociation. Moreover, the ELF and electron densities at the BCP were studied for NiCl2 and [Ni(py)4Cl2] molecules. As shown in Fig. 2(C), in NiCl2, the ELF plots reveal significant overlap of the outer electron clouds between Ni and Cl atoms, indicating a strong interaction in Ni–Cl bonds. This overlap is absent in [Ni(py)4Cl2], where pyridine ligands around Ni reduce electron cloud overlap with Cl (Fig. 2(D)). Additionally, the electron density at the Ni–Cl bond critical point (shown by white points between Ni and Cl atoms) is higher in NiCl2 (0.1243 a.u.) than in [Ni(py)4Cl2] (0.0493 a.u.), confirming a stronger Ni–Cl interaction in NiCl2 due to the absence of competing pyridine ligands.
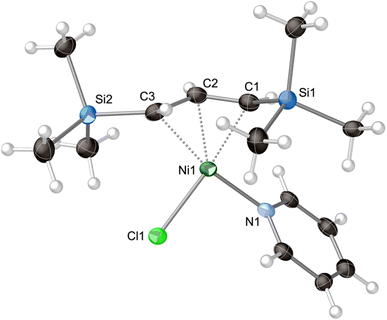
4.2 Formation and structure of [A′Ni(py)Cl]
One of the species identified through computational modeling as a potential intermediate in the formation of from K[A′] and [Ni(py)4Cl2] is the mono(allyl) complex [A′Ni(py)Cl] (also denoted IM 4, see Section 4.3). Although previously unknown, [A′Ni(py)Cl] can be formed from [{A′Ni(μ-Cl)}2] (Fig. S5†), itself a new compound generated through the reaction of
from K[A′] and [Ni(py)4Cl2] is the mono(allyl) complex [A′Ni(py)Cl] (also denoted IM 4, see Section 4.3). Although previously unknown, [A′Ni(py)Cl] can be formed from [{A′Ni(μ-Cl)}2] (Fig. S5†), itself a new compound generated through the reaction of 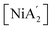 with HCl in dioxane. Slow evaporation of a hexane solution of the compound yields red needles, which allowed its crystal structure to be determined (synthetic and crystallographic details are in the ESI†).
with HCl in dioxane. Slow evaporation of a hexane solution of the compound yields red needles, which allowed its crystal structure to be determined (synthetic and crystallographic details are in the ESI†).
The stoichiometric addition of pyridine into a hexanes solution of [{A′Ni(μ-Cl)}2] produces [A′Ni(py)Cl]. Attempts to coordinate additional pyridine molecules by using excess pyridine were not successful. Orange crystals of [A′Ni(py)Cl] were obtained from the slow evaporation of a hexanes solution, and a single crystal X-ray study established its monomeric nature (Fig. 3). The complex displays an η3-bonded allyl ligand and terminal chloride and pyridine ligands, arranged so that the Cl, N, and C1/C3 carbons of the allyl ligand form a roughly square planar arrangement around the nickel (sum-of-squares error for the least-squares plane through the four atoms = 0.051 Å2). The TMS groups on the A′ ligand are in a syn, anti-relationship. As is typical for transition metal-bound A′ ligands,42 the silicon atom of the syn substituent (Si2) is deflected somewhat from the C3 allyl plane toward the nickel atom (0.36 Å). Conversely, the silicon atom of the anti-substituent (Si1) is strongly displaced from the C3 plane (0.83 Å), away from the metal center.
4.3 Computational modeling of  formation
formation
Under ball milling conditions, mechanical activation can enhance the reactivity of solid reactants by breaking bonds and facilitating ion and radical formation.43 The ΔG° values for the formation of  from NiCl2 and K[A′] were calculated at 298.15 K under solvent-free conditions (ε = 1.0) and in pyridine (ε = 12.4) and THF (ε = 7.4) solvents. As demonstrated in Table 1, the NiCl2 + 2K[A′] reaction can exhibit two different product formation outcomes
from NiCl2 and K[A′] were calculated at 298.15 K under solvent-free conditions (ε = 1.0) and in pyridine (ε = 12.4) and THF (ε = 7.4) solvents. As demonstrated in Table 1, the NiCl2 + 2K[A′] reaction can exhibit two different product formation outcomes  for each environment (with solvents and solvent-free).
for each environment (with solvents and solvent-free).
Under all conditions examined, the formation of  products has negative ΔG° values, indicating the spontaneity of the halide metathesis reaction in the forward direction. Conversely, the positive ΔG° values associated with the
products has negative ΔG° values, indicating the spontaneity of the halide metathesis reaction in the forward direction. Conversely, the positive ΔG° values associated with the  products formed via a redox process imply a non-spontaneous reaction in the forward direction. The solvents' polar nature and their ability to coordinate with metal ions stabilize transition states involved in both reaction types, and the ΔG° values are more positive under solvent-free conditions (by 10% and 26% for the halide metathesis and redox routes, respectively), although the changes are much larger in absolute terms for the halide metathesis path (roughly 42 and 6 kJ mol−1, respectively).
products formed via a redox process imply a non-spontaneous reaction in the forward direction. The solvents' polar nature and their ability to coordinate with metal ions stabilize transition states involved in both reaction types, and the ΔG° values are more positive under solvent-free conditions (by 10% and 26% for the halide metathesis and redox routes, respectively), although the changes are much larger in absolute terms for the halide metathesis path (roughly 42 and 6 kJ mol−1, respectively).
The dielectric constant under solvent-free conditions and with solvents can affect the Ni–Cl and K–C bond energies and the product formation. We thus examined the bond energies in the different environments. As shown in Fig. 4(A), as the Ni–Cl bond length increases, the energy under solvent-free conditions rises rapidly, reaching a constant value at approximately 400 kJ mol−1. In contrast, the energy increases only up to ∼240 kJ mol−1 in either solvent. Similarly, in the case of the K–C bond, in Fig. 4(B), the energy remains low in the solvents when compared to the solvent-free phase. This energy disparity indicates that electrostatic stabilization dominates the solvent phase and causes ionic forms to be much more stable in high dielectric constant environments than in the solvent-free phase. This result implies that electrostatic stabilization in the solvent phase could improve milling efficiency compared to solvent-free conditions.
The rupture of the Ni–Cl and K–C bonds will result in the formation of Ni2+, Cl−, K+, and [A′]– species, and depending on the experimental milling conditions, reduction of Ni2+ to elemental nickel (Ni0) may also happen. If the latter is the case, concomitant oxidation of the [A′]– anion to the neutral [A′]˙ radical will occur, and subsequently, two of the {A′}˙ neutral radicals can combine and form the  (hexadiene) molecule. Based on transition state search calculations for forming the
(hexadiene) molecule. Based on transition state search calculations for forming the  molecule, we explored the reaction's energy profile, which proceeds through a diradical transition state pathway. In our calculations, the dimer
molecule, we explored the reaction's energy profile, which proceeds through a diradical transition state pathway. In our calculations, the dimer  molecule is assigned a singlet spin state, while A* (radical species) was treated as a doublet. During the transition state, the diradical species (A*–A*) was modeled as a triplet. Fig. 5(A) and (B) show the energy profile diagram of
molecule is assigned a singlet spin state, while A* (radical species) was treated as a doublet. During the transition state, the diradical species (A*–A*) was modeled as a triplet. Fig. 5(A) and (B) show the energy profile diagram of  formation by the reaction between identical radical molecules for rac and meso forms. The resulting transition states in the solvent-free phase for the rac and meso forms of
formation by the reaction between identical radical molecules for rac and meso forms. The resulting transition states in the solvent-free phase for the rac and meso forms of  are found at the 153.3 and 172.6 kJ mol−1 energy barriers, respectively. However, these energy barriers do not change appreciably when solvent is present (ca. 2–3% decrease). Hence, there is no significant solvent assistance required for the neutral radicals to combine.
are found at the 153.3 and 172.6 kJ mol−1 energy barriers, respectively. However, these energy barriers do not change appreciably when solvent is present (ca. 2–3% decrease). Hence, there is no significant solvent assistance required for the neutral radicals to combine.
In the previous experimental work, SAG conditions were created by employing the insoluble pyridine solvate complex ([Ni(py)4Cl2]) during grinding.10 Computationally, we used the same solvated complex in the triplet (T1) spin state at the molecular level to study this effect (cf. Fig. S6†). The coordinated pyridine moieties donate electron density to the nickel center, weakening the Ni–Cl interaction and adding steric pressure to boost chloride loss. In describing the behavior of the Ni–Cl bond energy for the solvated complex, as shown in Fig. 4(A), it should be remembered that the bonds were already elongated to 2.443 Å compared to the distance in the NiCl2 molecule (2.023 Å).44 As the bond length increases, the energy rises but remains below that of the NiCl2 molecule in the solvents until ca. 4.2 Å. Some caution should be advised in interpreting this finding, given the difference in how the pyridine is modeled with the solvate (explicit pyridine molecules) and the solution (implicit pyridine via the dialectic content). Nevertheless, it is clear that the coordination of pyridines in [Ni(py)4Cl2] leads to substantial Ni–Cl bond weakening, considerably greater than that in the solvent-free environment.
Fig. 6 shows the computed schematic energy profile diagram illustrating the synthesis of  from the reaction of the pyridine-solvated complex [Ni(py)4Cl2] with 2K[A′]. To facilitate understanding of the reaction mechanism, the process was divided into two steps, introducing a single K[A′] species at each step.
from the reaction of the pyridine-solvated complex [Ni(py)4Cl2] with 2K[A′]. To facilitate understanding of the reaction mechanism, the process was divided into two steps, introducing a single K[A′] species at each step.
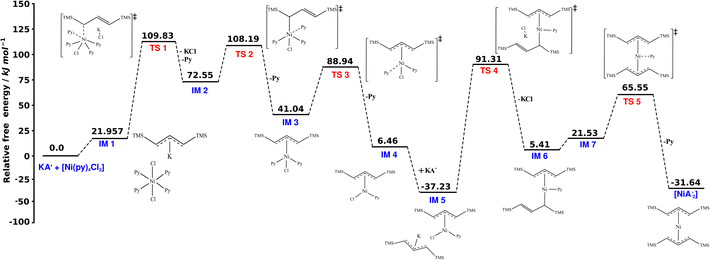 | ||
Fig. 6 Schematic representation of the synthesis of the allyl complex 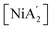 using the pyridine-solvated complex (i.e., [Ni(py)4Cl2]) reaction with 2K[A′]. The TS 3, TS 4 and TS 5 structures are optimized at the B3LYP level as optimization with B3PW91 was not possible. The final energies reported here are at the B3PW91/def2-TZVPP level of theory. The molecular coordinates are attached in ESI.† using the pyridine-solvated complex (i.e., [Ni(py)4Cl2]) reaction with 2K[A′]. The TS 3, TS 4 and TS 5 structures are optimized at the B3LYP level as optimization with B3PW91 was not possible. The final energies reported here are at the B3PW91/def2-TZVPP level of theory. The molecular coordinates are attached in ESI.† | ||
Initially, the reaction begins by forming an intermediate (IM 1), accompanied by a modest energy increase (∼22 kJ mol−1), attributable to interactions between both molecules (i.e., K[A′] and [Ni(py)4Cl2]). Subsequently, the formation of an Ni–C bond, and rupture of Ni–Cl and Ni–N bonds causes a substantial energy rise, bringing the system to the first transition state (TS 1). The release of the first pyridine ligand and KCl from TS 1 likely leads to the formation of intermediate IM 2. Loss of another pyridine ligand, likely aided by the steric bulk of the η1–[A′] ligand, leads to the second transition state (TS 2). Electron redistribution resulting in the conversion of the initially η1-bound [A′] ligand to the delocalized η3-bound conformation culminates in the formation of the intermediate IM 3. Further relaxation and pyridine loss occur through transition state TS 3 followed by intermediate IM 4 ([A′Ni(py)Cl]).
Subsequently, introducing the second K[A′] species prompts the formation of a fifth intermediate (IM 5), accompanied by an energy decrease of approximately 44 kJ mol−1 due to interactions between both molecules. Unlike the previous decreasing energy trend, the system shows an increase in the energy and progresses through the formation of the fourth transition state (TS 4), attributed to the Ni–C bond formation and Ni–Cl bond rupture. The release of the KCl from TS 4, associated with the decrease in energy, leads to the generation of the sixth intermediate (IM 6). The transition from IM 6 to the fifth transition state (TS 5) involves an energy rise, associated with converting the second [A′] ligand, originally η1-bound, to the more sterically demanding η3-bound conformation. Ultimately, the system again releases energy, losing the last pyridine, and yields  , exhibiting an overall energy release consistent with the exothermic nature of the reaction mechanism. There is no
, exhibiting an overall energy release consistent with the exothermic nature of the reaction mechanism. There is no  species in this reaction profile diagram, in agreement with the lack of
species in this reaction profile diagram, in agreement with the lack of  in the SAG experimental results.
in the SAG experimental results.
Given these results, it might initially appear inconsistent that under solvent-free conditions, the formation of  is calculated to be spontaneous (ΔG° = −370 kJ mol−1), and the generation of
is calculated to be spontaneous (ΔG° = −370 kJ mol−1), and the generation of  is non-spontaneous (ΔG° = +31 kJ mol−1), even though the experimental production of
is non-spontaneous (ΔG° = +31 kJ mol−1), even though the experimental production of  is almost quantitative and the formation of
is almost quantitative and the formation of  is only a trace (Fig. 1). Several factors must be considered to put these results into context. One is that the energy involved in K–C bond cleavage, which makes the allyl anion free for subsequent reaction, is considerably less than that for Ni–Cl scission (Fig. 4). Even in the unsolvated case, the energy of disrupting the K–C interaction is roughly half that of Ni–Cl cleavage, and the difference is greater in the presence of solvents (e.g., in pyridine, the K–C/Ni–Cl energy ratio is roughly one-fourth). This is partially a result of separating the anions from either mono-positive (K+) or dipositive (Ni2+) centers, so simple charge considerations (Z+Z–/r) would suggest that the former requires less energy. Hence, the availability of the [A′]– anion is not a critical issue in the reaction scheme, and the differences in reaction outcome must lie in the ease of Ni–Cl bond separation.
is only a trace (Fig. 1). Several factors must be considered to put these results into context. One is that the energy involved in K–C bond cleavage, which makes the allyl anion free for subsequent reaction, is considerably less than that for Ni–Cl scission (Fig. 4). Even in the unsolvated case, the energy of disrupting the K–C interaction is roughly half that of Ni–Cl cleavage, and the difference is greater in the presence of solvents (e.g., in pyridine, the K–C/Ni–Cl energy ratio is roughly one-fourth). This is partially a result of separating the anions from either mono-positive (K+) or dipositive (Ni2+) centers, so simple charge considerations (Z+Z–/r) would suggest that the former requires less energy. Hence, the availability of the [A′]– anion is not a critical issue in the reaction scheme, and the differences in reaction outcome must lie in the ease of Ni–Cl bond separation.
A second critical point is that although the coordination of pyridine to NiCl2 weakens the Ni–Cl bond, the coordination process is not immediate under mechanochemical conditions. It has been found that a 10 min grind of NiCl2 with 5 equiv. of pyridine generates a mixture of compounds, primarily [Ni(py)4Cl2] and [Ni(py)2Cl2], the latter being a polymeric sub-solvate of NiCl2.10 Depending on the reagents available, that length of time is sufficient to produce the hexadiene  in 98% yield or the
in 98% yield or the  complex in 95% yield (Fig. 1). In solvent-free conditions, and without Ni–Cl bond weakening, the facile separation of the allyl anion from K+ allows the redox process to start immediately, converting the allyl ligand to its radical form and making it unavailable for reaction with a Ni2+ center.
complex in 95% yield (Fig. 1). In solvent-free conditions, and without Ni–Cl bond weakening, the facile separation of the allyl anion from K+ allows the redox process to start immediately, converting the allyl ligand to its radical form and making it unavailable for reaction with a Ni2+ center.
Conversely, when that pyridine is pre-coordinated in the [Ni(py)4Cl2] solvate, Ni–Cl bond cleavage and subsequent metathesis can begin without delay, taking advantage of the generally more favorable free energy condition associated with the metathesis compared to the redox process (Table 1). If pyridine is added as a LAG solvent, however, it takes time for it to coordinate and weaken the Ni–Cl bonds so that metathesis can begin, during which time the redox process can proceed. The result is that provided in Fig. 1B, i.e., both  form in comparable amounts.
form in comparable amounts.
While our study provides valuable insights, certain aspects warrant further consideration to fully capture the complexities of mechanochemical reactions. First, in this study, a continuum solvent model was employed to estimate the influence of solvent on the mechanochemical reaction. This model assumes a homogeneous and infinite solvent environment, which differs from the highly localized and dynamic solvent distributions in ball milling reactions. In ball milling, the solvent often exists as a thin layer on particle surfaces or confined in small cavities, and its distribution is disrupted by mechanical forces. Although the continuum approximation cannot capture these localized effects, it serves as a useful first approximation for evaluating solvent polarity and dielectric effects on reaction energetics.24 Second, the gas-phase calculations do not fully account for solid-state effects such as lattice stabilization and extended intermolecular interactions. This is a limitation because there are elements of kinetic influence in these reactions that are not fully described with thermodynamic values. Regardless, the calculations reported here offer valuable insights into the intrinsic thermodynamics of the mechanochemical reactions. These calculations also lay the groundwork for future studies. Such studies may incorporate periodic DFT calculations45,46 or hybrid quantum-mechanical/molecular-mechanical (QM/MM) approaches that more accurately capture the structural and energetic influences of the solid environment. They may also employ MD simulations with explicit solvent models or coarse-grained approaches that could better capture the localized nature of solvent in ball milling, including its role under LAG conditions and its impact on reaction pathways. Such refinements will bridge computational predictions with experimental outcomes, yielding a comprehensive picture of mechanochemical reactivity.
5. Conclusions
Using DFT methods, we evaluated the potential reasons for the differing reaction outcomes in formation from NiCl2 and K[A′] under three distinct environments: solvent-free, in solvents (pyridine and THF), and with a solvated complex. By employing bond energy scans to examine the bond energy behavior and the free energy changes among various products, we determined the reactivity of NiCl2 in both solvent-free conditions and solvents. Furthermore, based on the free energy profile diagram of
formation from NiCl2 and K[A′] under three distinct environments: solvent-free, in solvents (pyridine and THF), and with a solvated complex. By employing bond energy scans to examine the bond energy behavior and the free energy changes among various products, we determined the reactivity of NiCl2 in both solvent-free conditions and solvents. Furthermore, based on the free energy profile diagram of  , we found that in the pyridine-solvated Ni-complex [Ni(py)4Cl2], the reaction is driven by the weakening of Ni–Cl bonds due to electron donation from the pyridine groups; the subsequent rupture of Ni–N bonds is likely facilitated by the bulk of the pyridines and the allyl ligands [A′]. The weakening of Ni–Cl interactions due to pyridine ligands is also evidenced by ELF clouds and electron densities at bond critical points between the Ni and Cl atoms. Ultimately, the reaction's outcome depends on a competition between halide metathesis and a redox reaction, with Ni–Cl bond weakening being crucial to the speed of metathesis and
, we found that in the pyridine-solvated Ni-complex [Ni(py)4Cl2], the reaction is driven by the weakening of Ni–Cl bonds due to electron donation from the pyridine groups; the subsequent rupture of Ni–N bonds is likely facilitated by the bulk of the pyridines and the allyl ligands [A′]. The weakening of Ni–Cl interactions due to pyridine ligands is also evidenced by ELF clouds and electron densities at bond critical points between the Ni and Cl atoms. Ultimately, the reaction's outcome depends on a competition between halide metathesis and a redox reaction, with Ni–Cl bond weakening being crucial to the speed of metathesis and  formation. A significant advantage of using the [Ni(py)4Cl2] complex over simple NiCl2/pyridine LAG is that the solvate provides ‘pre-activated’ bonds at the reaction's onset, granting the metathesis reaction a kinetic advantage over the competing redox route. When pyridine is introduced as a free liquid (as in LAG), the slower formation of Ni-pyridine bonds permits the redox process to proceed concurrently, generating
formation. A significant advantage of using the [Ni(py)4Cl2] complex over simple NiCl2/pyridine LAG is that the solvate provides ‘pre-activated’ bonds at the reaction's onset, granting the metathesis reaction a kinetic advantage over the competing redox route. When pyridine is introduced as a free liquid (as in LAG), the slower formation of Ni-pyridine bonds permits the redox process to proceed concurrently, generating  alongside
alongside  . Although not specifically examined here, it is highly likely that this analysis is relevant to the related iron system as well.10 By comparing solvent-free, solvent-based, and solvated complex conditions, this study highlights the role of solvents on the reactivity and stability of intermediates, which is essential for optimizing reaction conditions in synthetic chemistry. The findings provide valuable insights into designing more efficient and selective mechanochemical reactions, particularly in complex organometallic systems.
. Although not specifically examined here, it is highly likely that this analysis is relevant to the related iron system as well.10 By comparing solvent-free, solvent-based, and solvated complex conditions, this study highlights the role of solvents on the reactivity and stability of intermediates, which is essential for optimizing reaction conditions in synthetic chemistry. The findings provide valuable insights into designing more efficient and selective mechanochemical reactions, particularly in complex organometallic systems.
Data availability
Crystallographic data for the structures have been deposited with the Cambridge Crystallographic Data Centre as CCDC 2392374 ([{A′NiCl}2]) and 2392373 ([A′Ni(py)Cl]). Copies of the data can be obtained free of charge on application to CCDC, 12 Union Road, Cambridge CB2 1EZ, UK (fax: (+44)1223-336-033; e-mail: E-mail: deposit@ccdc.cam.ac.uk).Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the NSF Center for the Mechanical Control of Chemistry (CMCC), CHE-2303044. The CMCC is part of the Centers for Chemical Innovation Program. The authors thank Prof. Nathan D. Schley (Vanderbilt Univ.) for collecting and solving the crystallographic data for .
.
References
- E. M. Gutman, Mechanochemistry of Solid Surfaces, World Scientific, 1994 Search PubMed.
- R. Rana, R. Bavisotto, K. Hou, N. Hopper and W. T. Tysoe, Chem. Methods, 2021, 1, 340–349 CrossRef CAS.
- J. Yeon, X. He, A. Martini and S. H. Kim, ACS Appl. Mater. Interfaces, 2017, 9, 3142–3148 CrossRef CAS PubMed.
- K. J. Ardila-Fierro and J. G. Hernández, ChemSusChem, 2021, 14, 2145–2162 CrossRef CAS PubMed.
- X. Liu, Y. Li, L. Zeng, X. Li, N. Chen, S. Bai, H. He, Q. Wang and C. Zhang, Adv. Mater., 2022, 34, 2108327 Search PubMed.
- V. Martinez, T. Stolar, B. Karadeniz, I. Brekalo and K. Užarević, Nat. Rev. Chem., 2023, 7, 51–65 CrossRef CAS PubMed.
- H. Shin, S. Lee, H. S. Jung and J.-B. Kim, Ceram. Int., 2013, 39, 8963–8968 CrossRef CAS.
- R. R. Ferreira, A. G. Souza, L. L. Nunes, N. Shahi, V. K. Rangari and D. dos Santos Rosa, Mater. Today Commun., 2020, 22, 100755 CrossRef CAS.
- L. E. Wenger and T. P. Hanusa, Chem. Commun., 2023, 59, 14210–14222 RSC.
- H. P. DeGroot and T. P. Hanusa, Organometallics, 2021, 40, 3516–3525 CrossRef CAS , (the initially reported isolated yield for [NiÁ2] in reaction (c) was 69%. That reaction was conducted in stainless steel jars; a reinvestigation in ZrO2 equipment found that the yield is now 95%, possibly due to the greater hardness and chemical inertness of ZrO2 relative to stainless steel. In either stainless steel or ZrO2, no {Á}2 formation was observed (D. Button-Jennings, unpublished results))..
- P. Ying, J. Yu and W. Su, Adv. Synth. Catal., 2021, 363, 1246–1271 CrossRef CAS.
- F. C. Strobridge, N. Judaš and T. Friščić, CrystEngComm, 2010, 12, 2409–2418 RSC.
- G. Das, D. B. Shinde, S. Kandambeth, B. P. Biswal and R. Banerjee, Chem. Commun., 2014, 50, 12615–12618 RSC.
- W. Morris, E. D. Lorance and I. R. Gould, J. Phys. Chem. A, 2019, 123, 10490–10499 CrossRef CAS PubMed.
- R. Kar and S. Pal, Int. J. Quantum Chem., 2010, 110, 1642–1647 CrossRef CAS.
- J. G. Hernández and C. Bolm, J. Org. Chem., 2017, 82, 4007–4019 CrossRef PubMed.
- K. L. Denlinger, L. Ortiz-Trankina, P. Carr, K. Benson, D. C. Waddell and J. Mack, Beil. J. Org. Chem., 2018, 14, 688–696 CrossRef CAS.
- J. L. Howard, M. C. Brand and D. L. Browne, Angew. Chem. Int. Ed., 2018, 57, 16104–16108 CrossRef CAS PubMed.
- J. J. Varghese and S. H. Mushrif, React. Chem. Eng., 2019, 4, 165–206 RSC.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- P. Hohenberg and W. Kohn, Phys. Rev, 1964, 136, B864 CrossRef.
- C. Zhang, S. Yue, A. Z. Panagiotopoulos, M. L. Klein and X. Wu, Phys. Rev. Lett., 2023, 131, 076801 CrossRef CAS PubMed.
- N. Yao, X. Chen, X. Shen, R. Zhang, Z.-H. Fu, X.-X. Ma, X.-Q. Zhang, B.-Q. Li and Q. Zhang, Angew. Chem. Int. Ed., 2021, 60, 21473–21478 CrossRef CAS PubMed.
- B. S. Pladevall, A. de Aguirre and F. Maseras, ChemSusChem, 2021, 14, 2763–2768 CrossRef CAS PubMed.
- G. Wilke and B. Bogdanović, Angew. Chem., 1961, 73, 756 CrossRef CAS.
- M. Chen and C. Chen, Angew. Chem. Int. Ed., 2018, 57, 3094–3098 CrossRef CAS PubMed.
- M. Xu, F. Yu, P. Li, G. Xu, S. Zhang and F. Wang, Inorg. Chem., 2020, 59, 4475–4482 CrossRef CAS PubMed.
- T. Liang, S. B. Goudari and C. Chen, Nature Commun., 2020, 11, 372 CrossRef CAS PubMed.
- R. Zhang, R. Gao, Q. Gou, J. Lai and X. Li, Polymers, 2022, 14, 3809 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson and H. Nakatsuji, et al., Gaussian 16 Rev. C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1992, 96, 2155–2160 CrossRef CAS.
- F. Weigend and R. Ahlrichs, PhysChemChemPhys, 2005, 7, 3297–3305 RSC.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132 Search PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comp. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9–15 CrossRef CAS.
- T. Lu and F. Chen, J. Comp. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- H. P. DeGroot, I. R. Speight, W. W. Brennessel and T. P. Hanusa, ACS Org. Inorg. Au, 2024, 4, 658–672 CrossRef CAS PubMed.
- G. J. Long and P. J. Clarke, Inorg. Chem., 1978, 17, 1394–1401 CrossRef CAS.
- B. Cordero, V. Gómez, A. E. Platero-Prats, M. Revés, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Dalton Trans., 2008, 2832–2838 RSC.
- I. A. Guzei and M. Wendt, Dalton Trans., 2006, 3991–3999 RSC.
- K. T. Quisenberry, J. D. Smith, M. Voehler, D. F. Stec, T. P. Hanusa and W. W. Brennessel, J. Am. Chem. Soc., 2005, 127, 4376–4387 Search PubMed.
- D. Jędrzkiewicz, J. Mai, J. Langer, Z. Mathe, N. Patel, S. DeBeer and S. Harder, Angew. Chem. Int. Ed., 2022, 61, e202200511 CrossRef PubMed.
- R. E. Bachman, K. H. Whitmire, S. Mandal and P. K. Bharadwaj, Cryst. Struct. Commun., 1992, 48, 1836–1837 CrossRef.
- A. M. Belenguer, T. Friščić, G. M. Day and J. K. M. Sanders, Chem. Sci., 2011, 2, 696–700 RSC.
- S. Lukin, T. Stolar, I. Lončarić, I. Milanović, N. Biliškov, M. d. Michiel, T. Friščić and I. Halasz, Inorg. Chem., 2020, 59, 12200–12208 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2392374 ([{A′NiCl}2]) and 2392373 ([A′Ni(py)Cl]). For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4mr00136b |
| This journal is © The Royal Society of Chemistry 2025 |