Open Access Article
Open Access ArticleSmart drug delivery: a DFT study of C24 fullerene and doped analogs for pyrazinamide†
Azam
Moumivand
a,
Fereshteh
Naderi
 *a,
Omid
Moradi
*a,
Omid
Moradi
 a and
Batoul
Makiabadi
b
a and
Batoul
Makiabadi
b
aDepartment of Chemistry, Shahr-e-Qods Branch, Islamic Azad University, Tehran, Iran. E-mail: fnaderi1@gmail.com; Neginmmm64@gmail.com; moradi.omid@gmail.com; Web: https://scholar.google.com/citations?user=pdCrLOYAAAAJ&hl=en
bDepartment of Chemical Engineering, Sirjan University of Technology, Sirjan, Iran. E-mail: bmakiabadi@yahoo.com; Web: https://scholar.google.com/citations?user=N6z-rHsAAAAJ&hl=en
First published on 17th December 2024
Abstract
The potential applicability of the C24 nanocage and its boron nitride-doped analogs (C18B3N3 and C12B6N6) as pyrazinamide (PA) carriers was investigated using density functional theory. Geometry optimization and energy calculations were performed using the B3LYP functional and 6-31G(d) basis set. Besides, dispersion-corrected interaction energies were calculated at CAM (Coulomb attenuated method)-B3LYP/6-31G(d,p) and M06-2X/6-31G(d,p) levels of theory. The adsorption energy (Eads), enthalpy (ΔH), and Gibbs free energy (ΔG) values for C24-PA, C18B3N3-PA, and C12B6N6-PA structures were calculated. The molecular descriptors such as electrophilicity (ω), chemical potential (μ), chemical hardness (η) and chemical softness (S) of compounds were investigated. Natural bond orbital (NBO) analysis confirms the charge transfer from the drug molecule to nanocarriers upon adsorption. Based on the quantum theory of atoms in molecules (QTAIM), the nature of interactions in the complexes was determined. These findings suggest that C24 and its doped analogs are promising candidates for smart drug delivery systems and PA sensing applications, offering significant potential for advancements in targeted tuberculosis treatment.
Introduction
Tuberculosis (TB) is a prevalent and often fatal infectious disease caused by various species of mycobacteria, particularly Mycobacterium tuberculosis.1 TB remains one of the most significant infectious diseases of our time, capable of affecting all organs of the body, especially the lungs. Despite widespread optimism in the 1980s that TB would be controlled by the turn of the century, the World Health Organization (WHO) declared it a global emergency in 1993.2,3 According to WHO reports, approximately 10 million people were diagnosed with TB in 2017, with the number increasing to about 6.4 million in 2019. Annually, around 1.3 million patients succumb to TB.4 The treatment of TB has become increasingly challenging due to the emergence of drug-resistant strains of Mycobacterium tuberculosis. In 2012, there were about 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cases of multidrug-resistant TB (MDR-TB), resulting in an estimated 170
000 cases of multidrug-resistant TB (MDR-TB), resulting in an estimated 170![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 deaths. The situation is exacerbated when these strains develop resistance to multiple drugs, undermining the significant advances made in TB control over the past century.5 Currently, more than 8 million people worldwide contract TB each year, and approximately one-third of the global population harbors the bacterium asymptomatically. Despite significant efforts to control TB, the emergence of drug resistance remains a critical concern, underscoring the need for rapid and accurate diagnosis to facilitate timely and effective treatment.
000 deaths. The situation is exacerbated when these strains develop resistance to multiple drugs, undermining the significant advances made in TB control over the past century.5 Currently, more than 8 million people worldwide contract TB each year, and approximately one-third of the global population harbors the bacterium asymptomatically. Despite significant efforts to control TB, the emergence of drug resistance remains a critical concern, underscoring the need for rapid and accurate diagnosis to facilitate timely and effective treatment.
One of the four first-line anti-tuberculosis drugs is pyrazinamide (PA), which, in addition to shortening the treatment period from nine to six months, eradicates the organism by destroying the active and inactive forms of bacillus tuberculosis in the acidic environment inside the macrophages.6 Like other drugs, PA has important side effects, such as fever, anorexia, liver enlargement, jaundice, and liver failure. Targeted drug delivery is a new way to reduce problems caused by direct drug use and drug resistance.7–9 Considering the common challenges of using drugs such as PA, the controlled release of the drug has attracted the attention of researchers. Targeted drug delivery and controlled release has advantages such as the possibility of drug delivery in nanometer dimensions, the ability to maintain the drug concentration in a relatively constant amount for a certain time, the ability to adjust the drug release rate depending on the place of drug delivery, and the ability to transfer several drug substances to a specific tissue or organ.10,11 Nowadays, drug delivery based on nanocarriers is at the center of attention of many companies acting in the pharmaceutical industry since nanomaterials have special properties and potential applications that make them superior to the traditional drug delivery vectors. The use of nanocarriers in medical science helps to increase the availability of the drug at the site of disease, and reduces the dose frequency and adverse side effects.12–15 As new drugs are developed, significant efforts have been directed toward exploring innovative delivery routes. Targeted delivery systems represent a promising solution to overcome the limitations of conventional methods. To realize this potential, a wide range of nanoparticles have been proposed and extensively studied.16–20 These nanoparticles must interact well with biological environments and pass through the cell membrane to deliver therapeutic molecules. Fullerenes (C60) are one of the pioneering classes of carbon-based nanoparticles, which have been widely studied for targeted drug delivery applications.21 Fullerenes have a unique structure and have suitable properties for interaction with drugs. Although fullerene toxicity is somewhat of a concern, several water-soluble fullerene derivatives have shown acceptable cytotoxicity for drug delivery applications.22 Recently, new fullerene-like compounds and hexagonal boron nitrides have been developed, and their potential applications as advanced delivery systems have been investigated.23–27 Studies provide a detailed drug interaction mechanism with boron nitride fullerenes (BNF) and reveal that the BNF can be a smart drug delivery vehicle for the drugs.23,28–30 In this study, the interaction of the pyrazinamide drug with C24, C18B3N3, and C12B6N6 nanocages was investigated using density functional theory (DFT) calculations. To achieve this, we employed a range of analytical tools, including adsorption energy (Eads), thermochemical parameters (ΔH and ΔG), frontier molecular orbitals, ionization energy, electrophilicity, chemical hardness, softness, electronegativity, natural bond orbitals (NBO), and atoms in molecules (AIM), as well as NMR, IR, and UV-Vis spectroscopy. These comprehensive analyses provide a detailed understanding of the interaction mechanisms and potential applications of these nanocages in drug delivery and sensing systems.
Computational details
All of the calculations were performed using the Gaussian 09 package.31 In the first stage, geometry optimization and energy calculations were carried out using the B3LYP32,33 functional and 6-31G(d)34 basis set. Besides, dispersion-corrected adsorption energies employing CAM-B3LYP35 and M06-2X36 functionals with the 6-31G(d,p)34 basis set were calculated. The counterpoise procedure (CP)37 was used to correct for basis set superposition error (BSSE) in the calculation of the adsorption energies. To obtain the thermal and Gibbs free energies and ensure that the optimized structures are true local minima on the potential energy surface (not saddle points or transition states), the vibrational frequency calculations were performed at all computational levels. All reported structures were identified as true minima on the PES. The adsorption energy (Eads) of the obtained structures of the interaction between pristine and doped C24 with PA at T = 298 K and P = 1 atm is given by the following equation:| Eads = Ecomplex − (Enanocage + EPA) | (1) |
Natural bond orbital analysis provides a chemical viewpoint of van der Waals interactions using a donor–acceptor type interpretation of molecular orbitals.38 Therefore, we used NBO analyses to calculate the charge distribution over the atoms of interacting species and to estimate the stabilization energies (E(2)) of bond–antibond interactions. The energy difference between the highest occupied (HOMO) and the lowest unoccupied molecular orbital (LUMO), known as Eg, for a system is given as:
| Eg = ELUMO − EHOMO | (2) |
The electronic sensitivity of the pristine and doped C24 nanocage toward PA is calculated as follows:
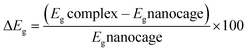 | (3) |
Quantum molecular descriptors (also known as the conceptual density functional theory (CDFT) parameters), including the electronegativity (χ), global hardness (η), electrophilicity index (ω), ionization potential (I), electron affinity (A), and electronic chemical potential (μ), were calculated with the help of HOMO and LUMO values. The electrophilicity index (ω) measures the stability of a compound in the presence of an additional electronic charge from the environment. In a charge transfer process, higher values of ω indicate the higher electrophilic power of the structure.39,40
| μ = −χ = −(EHOMO + ELUMO)/2 | (4) |
| η = (ELUMO − EHOMO)/2 | (5) |
| ω = μ2/2η | (6) |
The ionization energy (I) and electron affinity (A) can be expressed as −EHOMO and −ELUMO, respectively. Chemical shielding (CS) calculations were performed using the gauge-including atomic orbital (GIAO) method.41 The chemical shift isotropy (σiso) and anisotropy (Δσ) parameters were calculated applying principal components (σ11 ≤ σ22 ≤ σ33) of the chemical shift tensor, as follows:
| σiso (ppm) = (σ11 + σ22 + σ33)/3 | (7) |
| Δσ (ppm) = σ33 − (σ11 + σ22)/2 | (8) |
The NBO and AIM analysis was carried out at the M06-2X/6-31G(d) level of theory.38,42
Results and discussion
Optimized geometry of the adsorbents
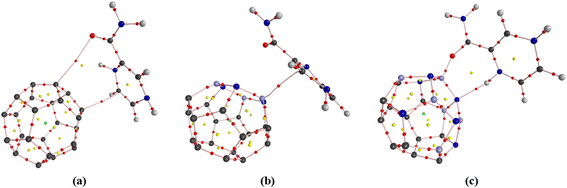
The fully optimized geometry, highest occupied molecular orbital (HOMO), lowest unoccupied molecular orbital (LUMO), and molecular electrostatic potential (MEP) maps of the adsorbent nanocages (C24, C18B3N3, and C12B6N6) are shown in Fig. 1. The optimized structures of these nanocages are characterized by two hexagons joined by twelve pentagons with D6, C3, and C3 point groups for C24, C18B3N3, and C12B6N6, respectively. The C–C bond length within the hexagons of C24 is about 1.42 Å; however, the value of the C–C bond length is in the range of 1.36 Å to 1.53 Å in pentagons. The average value of the C–C bond length is calculated to be about 1.44 Å, which is in agreement with the reported values in the literature.43,44 The C18B3N3 is derived by substituting the carbon atoms of a hexagon of C24 with boron and nitrogen atoms as one in between. Thus, C18B3N3 includes a B3N3 ring, six pentagons with C3BN formula, six pentagons with C5 formula, and a C6 ring. The average length of C–C, B–C, N–C, and B–N bonds is about 1.47, 1.57, 1.46, and 1.48 Å, respectively. In the structure of C12B6N6, five distinct types of rings are present: a B3N3 ring, six pentagons with B2N2C formula, three C4N pentagons, three C4B pentagons, and a C6 ring. Here, the C–C, B–C, N–C, and B–N average bond lengths are about 1.47 Å, 1.54 Å, 1.41 Å, and 1.50 Å, respectively.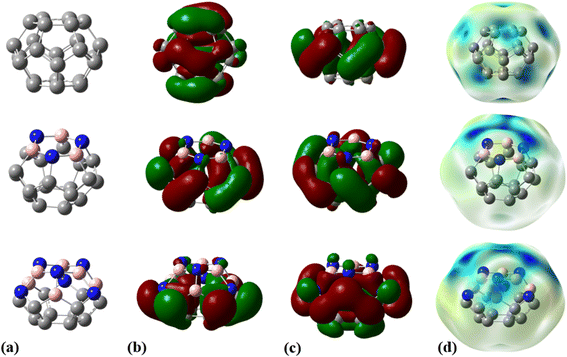 | ||
| Fig. 1 (a) Optimized geometries, (b) HOMOs, (c) LUMOs, and (d) MEP plots for C24, C18B3N3, and C12B6N6 nanocages at the M06-2X/6-31G(d,p) level of theory. | ||
The molecular electrostatic potential (MEP) plot is a valuable tool for determining the electron density distribution over the atoms of a molecule and predicting its most reactive sites. It is widely known that the chemical and physical properties of a molecule are associated with its electrostatic potential. Therefore, the MEP plot can be utilized to characterize electrophilic and nucleophilic sites within an electrostatic interaction.45 In a MEP contour, the surfaces are defined based on electron density and represented by an RGB color model, in which red regions are more negative than −0.010 a.u., yellow shows the regions with electron density between 0 and −0.010 a.u., green regions are between 0.010 and 0.0 a.u., and blue color represents regions more positive than 0.010 a.u. Fig. 2 reveals that O13, N8, and N10 atoms are the most negatively charged centers of the PA molecule. Additionally, the oxygen atom is more prone to contribute to the nucleophilic attack. The most positive atoms are C12 (0.68 |e|), H9 (0.45 |e|), H16 (0.43 |e|), H11 (0.41 |e|), and H15 (0.42 |e|), respectively, as shown by NBO analysis, which is in agreement with the MEP plot of the PA molecule.
 | ||
| Fig. 2 (a) Optimized geometry, (b) MEP, (c) HOMO, and (d) LUMO profiles of PA at the M06-2X/6-31G(d,p) level of theory. | ||
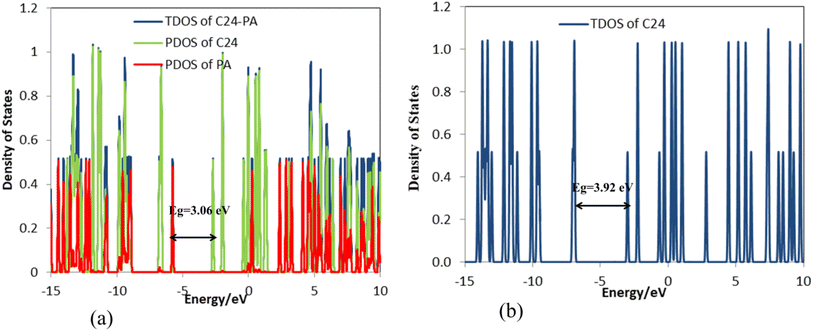
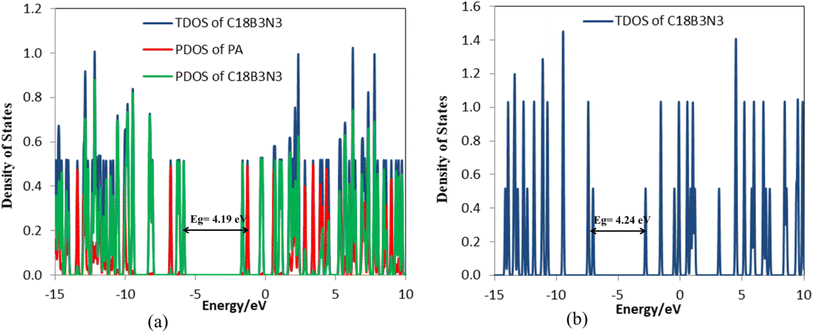
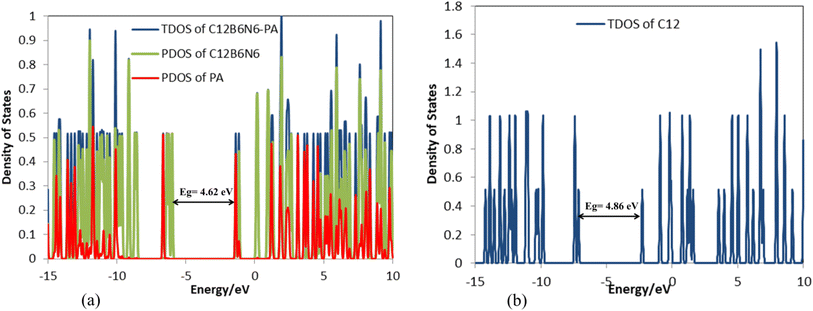
The frequency calculations were performed at the M06-2X/6-31G(d,p) level of theory. The vibrational frequency modes of C24, C18B3N3, and C12B6N6 appear in a positive range of 343–1630 cm−1, 345–1603 cm−1, and 282–1473 cm−1, respectively, indicating that the optimized geometries are true local minima on the potential energy surface. Frontier molecular orbitals (HOMO and LUMO) of a molecule play a vital role in determining its reactivity. HOMO and LUMO energy levels are usually considered as the electron-donating and electron-accepting abilities of an organic molecule. A higher EHOMO value indicates that the molecule can donate electrons, while a lower ELUMO implies the molecule's willingness to accept electrons. Considering eqn (2), it can be concluded that molecules with a low HOMO–LUMO energy gap are more polarizable and have high chemical reactivity and low kinetic stability.46 The HOMO levels of C24 are distributed over the C–C bonds throughout the nanocage except some C–C bonds in pentagons, whereas the LUMO levels are located on the C–C bonds of 5-membered rings. In the case of C18B3N3 and C12B6N6, the HOMO levels are mainly located on the N atoms and C–C bonds of pentagons, while the LUMO levels are situated on the B atoms and C–C bonds. The HOMO–LUMO energy gaps of C24, C18B3N3, and C12B6N6 are about 3.92, 4.24, and 4.86 eV, respectively, indicating that these nanocages are semiconductors. In the following sections, we will discuss the role of frontier molecular orbitals in the electronic properties of molecules.
Adsorption of PA on the C24 nanocage
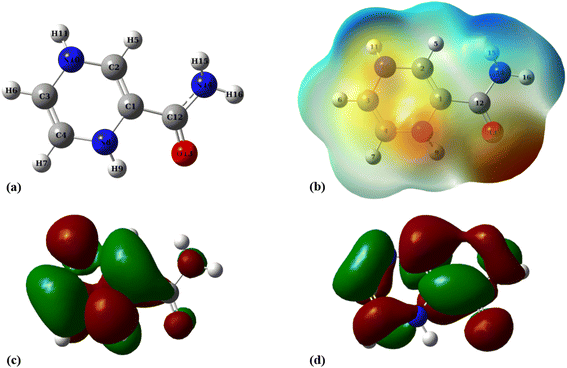
Aimed at identifying the most stable C24-PA configuration, we considered all probable orientations of the PA molecule on the surface of C24 using the MEP plots of adsorbent and adsorbate molecules. All initial configurations were optimized employing the B3LYP/6-31G(d), CAM-B3LYP/6-31G(d,p) and M06-2X/6-31G(d,p) levels of theory. The adsorption energies (Eads) for different configurations have been summarized in Table 1. More precisely it should be said that in the initial structures of C24-PA, the drug molecule approached the 5- and 6-membered rings of C24 through (a) N8–H9, (b) N10–H11, (c) C12–O13, and (d) NH2 group. The last configuration was the structure where PA is adsorbed in parallel on top of C24. After careful optimization and performing vibrational frequency calculations, it was found that the drug molecule adopts a parallel orientation towards C24. From Table 1, adsorption energies depend on both the method and basis set. Also, the energy difference between the configurations is significant in different methods. The amount of adsorption energy at the B3LYP/6-31G(d), CAM-B3LYP/6-31G(d,p), and M06-2X/6-31G(d,p) levels is −13.88 kJ mol−1, −25.72 kJ mol−1, and −125.58 kJ mol−1, respectively. The minimum interaction distance between PA and C24 in the mentioned theoretical levels is 2.85 Å, 2.81 Å, and 2.82 Å, respectively (Fig. 3).| Method | E ads (kJ mol−1) | E bsseads (kJ mol−1) | ΔH (kJ mol−1) | ΔG (kJ mol−1) |
|---|---|---|---|---|
| B3LYP/6-31G(d) | ||||
| C24-PA | −13.88 | −1.34 | −9.86 | 27.48 |
| C18B3N3-PA | −25.72 | −5.75 | −22.16 | 21.98 |
| C12B6N6-PA | −125.58 | −98.05 | −120.99 | −70.88 |
| CAM-B3LYP/6-31G(d,p) | ||||
| C24-PA | −14.81 | −8.34 | −9.57 | −35.40 |
| C18B3N3-PA | −124.73 | −97.78 | −119.43 | −68.50 |
| C12B6N6-PA | −138.55 | −124.21 | −309.76 | −83.07 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| M06-2X/6-31G(d,p) | ||||
| C24-PA | −45.95 | −29.98 | −40.08 | −3.62 |
| C18B3N3-PA | −163.63 | −56.62 | −155.81 | −95.25 |
| C12B6N6-PA | −156.48 | −137.69 | −150.71 | −99.17 |
 | ||
| Fig. 3 (a) Optimized geometry, (b) MEP, (c) HOMO, and (d) LUMO profiles of C24-PA at the M06-2X/6-31G(d,p) level of theory. | ||
The values of enthalpy (ΔH) and Gibbs free energy changes (ΔG) of the C24-PA complex are negative (with the exception of the B3LYP/6-31G(d) level), indicating that an exothermic and spontaneous reaction has occurred.
The changes in bond length and bond angles of the drug molecule, upon interaction with C24 at the M06-2X/6-31G(d,p) level of theory are illustrated in Tables 2 and S1,† respectively. The length of the C1–C2, C4–N8, C1–N8, N8–H9, and C12–O13 bonds increases while the length of other bonds decreases upon complexation. The results show that the interaction between the drug molecule and C12B6N6 has no significant effect on the bond lengths of the PA molecule. The most obvious change in the bond angles of the PA molecule is related to the C12–N14–H16 angle, which ranges from 114.5° to 119.1°. Table 3 summarizes the quantum chemistry reactivity parameters of the nonionic surfactants, including EHOMO, ELUMO, and their associated energy gap (Eg), ionization potential (I), electron affinity (A), electronegativity (χ), electronic chemical potential (μ), chemical hardness (η), electrophilicity index (ω), and dipole moments (in Debye). Frontier molecular orbital (FMO) analysis implies that the EHOMO and ELUMO of C24 become more stable by about 1.15 and 0.29 eV, respectively, upon complex formation (Fig. 4). Therefore, the Eg value decreases by 21.9%; thus, the electronic properties of C24 change considerably in the presence of PA molecules. The reduction of parameters ω, χ, A, and I is in agreement with the reduction of Eg. It is also observed that with the decrease of the Eg value, the softness and chemical hardness have increased and decreased, respectively, which indicates the tendency of the nanocarrier to interact with PA. The decrease in electrophilicity by 0.42 eV after interaction with the PA molecule confirms the charge transfer from the drug to the nanocarrier. The dipole moment of the C24-PA complex is significantly higher than that of its components. Therefore, the solubility of the C24-PA complex is expected to be higher than the solubility of C24 and PA.
| Bond | Bond length (Å) | Δr | |
|---|---|---|---|
| After interaction | Before interaction | ||
| C1–C2 | 1.343 | 1.341 | 0.002 |
| C3–C4 | 1.331 | 1.333 | −0.002 |
| C2–H5 | 1.083 | 1.085 | −0.002 |
| C3–H6 | 1.081 | 1.082 | −0.001 |
| C4–H7 | 1.082 | 1.083 | −0.001 |
| C4–N8 | 1.418 | 1.403 | 0.015 |
| N8–H9 | 1.017 | 1.011 | 0.006 |
| C1–N8 | 1.425 | 1.407 | 0.018 |
| C2–N10 | 1.400 | 1.413 | −0.013 |
| C3–N10 | 1.423 | 1.434 | −0.011 |
| N10–H11 | 1.011 | 1.016 | −0.005 |
| C1–C12 | 1.481 | 1.486 | −0.005 |
| C12–O13 | 1.223 | 1.221 | 0.002 |
| C12–N14 | 1.367 | 1.369 | −0.002 |
| N14–H15 | 1.009 | 1.009 | 0.000 |
| N14–H16 | 1.007 | 1.007 | 0.000 |
| Structure | E HOMO (eV) | E LUMO (eV) | E g (eV) | E F (eV) | I (eV) | A (eV) | χ (eV) | η (eV) | μ (eV) | S (1/eV) | ω (eV) | μ (Debye) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PA | −5.68 | 0.31 | 5.99 | 0.15 | 5.68 | −0.31 | 2.69 | 3.00 | −2.69 | 0.17 | 1.20 | 2.73 |
| C24 | −6.92 | −3.00 | 3.92 | −1.50 | 6.92 | 3.00 | 4.96 | 1.96 | −4.96 | 0.25 | 6.27 | 0.00 |
| C24-PA | −5.77 | −2.70 | 3.06 | −1.35 | 5.77 | 2.70 | 4.24 | 1.53 | −4.24 | 0.33 | 5.86 | 3.79 |
| C18B3N3 | −7.04 | −2.80 | 4.24 | −1.40 | 7.04 | 2.80 | 4.92 | 2.12 | −4.92 | 0.24 | 5.70 | 1.10 |
| C18B3N3-PA | −5.84 | −1.65 | 4.19 | −0.83 | 5.84 | 1.65 | 3.75 | 2.10 | −3.75 | 0.24 | 3.35 | 11.46 |
| C12B6N6 | −7.14 | −2.27 | 4.87 | −1.14 | 7.14 | 2.27 | 4.70 | 2.43 | −4.70 | 0.21 | 4.55 | 2.10 |
| C12B6N6-PA | −6.00 | −1.38 | 4.62 | −0.69 | 6.00 | 1.38 | 3.69 | 2.31 | −3.69 | 0.22 | 2.95 | 14.48 |
The mechanism of action of a chemical sensor is directly related to the change in its resistance due to charge exchange with the chemical agent. It is known that the Eg is a dependable indicator to determine the sensitivity of a sensor towards a molecule. The electrical conductivity of a molecule decreases with increasing Eg.47,48 The population of conduction electrons of a nanostructure increases significantly upon the decrease of Eg and vice versa. Changing the population of conducting electrons after the adsorption process causes the generation of an electrical signal.49 The work function (Φ) is another electronic parameter that is affected by the adsorption process and is defined as the minimum amount of energy (i.e., thermodynamic work) required to remove an electron from a solid to a point in the vacuum immediately outside the solid surface (i.e., the Fermi level) and is defined as follows:
| Φ = Vel(+∞) − EF | (9) |
| EF = EHOMO + (ELUMO − EHOMO)/2 | (10) |
The Φ-type sensors apply a Kelvin oscillator instrument to calculate the values of Φ before and after adsorption.32,50 In these sensors, the adsorption of a molecule changes the gate voltage and produces an electrical signal that leads to chemical agent detection.51 The value of Φ is changed by about −0.147 eV going from C24 to C24-PA; therefore, C24 can be used as a Φ-type sensor for PA detection.
To understand the donor–acceptor (bond–antibond) interactions between the drug molecule and the nanocages, NBO analysis has been performed at the M06-2X/6-31G(d,p) level of theory. In this analysis, all possible interactions between filled (donors) Lewis-type NBOs and empty (acceptors) non-Lewis NBOs are examined. Then, their energetic relevance is evaluated by second order perturbation theory. These interactions are called delocalization corrections to the zeroth-order natural Lewis structure because they result in a donation of electrons from the localized NBOs of the idealized Lewis structure into the empty non-Lewis orbitals. The stabilization energy (E(2)) associated with delocalization i → j is defined as:
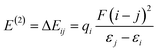 | (11) |
Adsorption of PA on the C18B3N3 nanocage
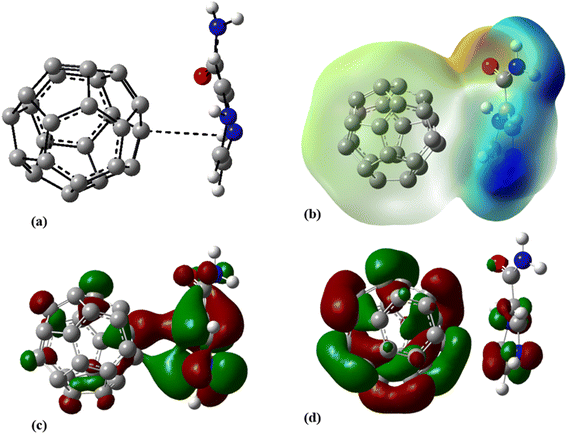
To improve the interaction between the C24 and PA drug molecule, we adopted the doping technique so that six carbon atoms were replaced by three boron and three nitrogen atoms to form the C18B3N3 nanocage. The most stable complex between C18B3N3 and the PA drug molecule was obtained by adopting a method similar to that used for C24-PA. The drug molecule approached the 5- and 6-membered rings of C18B3N3, B, and N heteroatoms through (a) N8–H9, (b) N10–H11, (c) C12–O13, and (d) NH2 group. Adsorption of PA on the surface of the C18B3N3 nanocage is an exothermic process. The adsorption energies of PA on the C18B3N3 at the mentioned levels of theory are reported in Table 1. The nearest interaction distance between PA and C18B3N3 is 1.5 Å, in which the drug molecule has adopted a parallel orientation towards C18B3N3 (Fig. 5). It seems that the weak π–π interactions are also effective in stabilizing the C18B3N3 complex. The values of ΔH and ΔG of the C18B3N3-PA complex at T = 298 K and P = 1 atm are shown in Table 1, which are more negative than the corresponding values of C24-PA.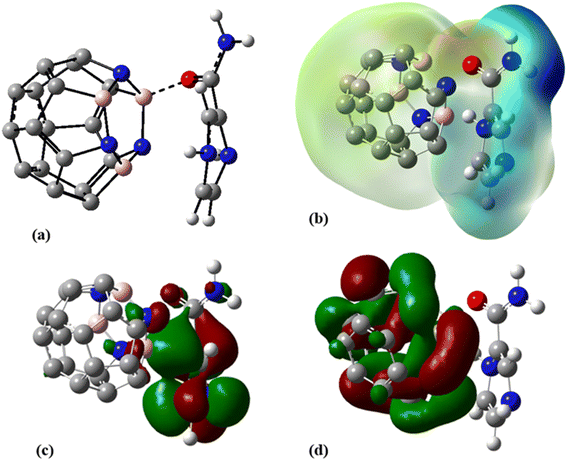 | ||
| Fig. 5 (a) Optimized geometry, (b) MEP, (c) HOMO, and (d) LUMO profiles of C18B3N3-PA at the M06-2X/6-31G(d,p) level of theory. | ||
Tables 4 and S3† show the structural parameters (bond lengths and bond angles) of the drug molecule before and after interaction with the C18B3N3 nanostructure. The interaction between the drug molecule and C18B3N3 does not have a significant effect on the length of bond of the PA molecule and is similar to the structure of C24PA. In any case, these changes are very small and can be ignored. The greatest decrease in the bond angle due to PA adsorption on the C18B3N3 surface is related to the C4–N8–H9 angle, which decreased by 8.8°, while C12–N14–H15 and C1–C12–N14 bond angles show increases of 3.8° and 2.6°, respectively. Frontier molecular orbital (FMO) analysis reveals that EHOMO of C18B3N3 changes from −7.04 eV to −5.84 eV after adsorption of PA; also, ELUMO stabilizes by approximately 1.14 eV (Fig. 5). Therefore, the Eg value decreases by 1.2%; thus, the electronic properties of C18B3N3 are sensitive to the presence of PA molecules. Here again the reductions in parameters ω, χ, A, and I are in agreement with the reduction in Eg (Fig. 6).
| Bond | Bond length (Å) | Δr | |
|---|---|---|---|
| After interaction | Before interaction | ||
| C1–C2 | 1.352 | 1.341 | 0.012 |
| C3–C4 | 1.331 | 1.333 | −0.002 |
| C2–H5 | 1.084 | 1.085 | −0.001 |
| C3–H6 | 1.080 | 1.082 | −0.002 |
| C4–H7 | 1.082 | 1.083 | −0.001 |
| C4–N8 | 1.423 | 1.403 | 0.02 |
| N8–H9 | 1.019 | 1.011 | 0.008 |
| C1–N8 | 1.427 | 1.407 | 0.020 |
| C2–N10 | 1.375 | 1.413 | −0.038 |
| C3–N10 | 1.427 | 1.434 | −0.0.007 |
| N10–H11 | 1.011 | 1.016 | −0.005 |
| C1–C12 | 1.450 | 1.486 | −0.036 |
| C12–O13 | 1.284 | 1.221 | 0.063 |
| C12–N14 | 1.324 | 1.369 | −0.045 |
| N14–H15 | 1.008 | 1.007 | 0.001 |
| N14–H16 | 1.011 | 1.009 | 0.002 |
The decrease in electrophilicity upon adsorption of PA is calculated to be approximately 0.159 eV, showing that charge transfers from the drug molecule to C18B3N3. Table S4† represents the partial atomic charges of the PA molecule before and after interaction with C18B3N3. The charge of C1, C4, N8, and O13 atoms increased by approximately 0.048, 0.012, 0.001, and 0.022 |e|, respectively. The comparison of the total atomic charges of PA and C18B3N3 shows that due to the formation of a complex between PA and C18B3N3, 0.398 |e| of charge is transferred from the drug to the nanocarrier.
The NBO analysis results showed that the highest values of stabilization energies E(2) of the C18B3N3 nanocarrier are BD*(2) C33–C34 → BD*(2) C23–C24; E(2) = 49.82 kcal mol−1, BD*(2) C29–C30 → BD*(2) C31–C32; E(2) = 50.27 kcal mol−1, BD*(2) C27–C28 → BD*(2) C25–C26; E(2) = 49.69 kcal mol−1, BD(2) C33–C34 → LP*(1) B21; E(2) = 45.12 kcal mol−1, and BD(2) C25–C26 → LP*(1) B21; E(2) = 44.91 kcal mol−1. The antibonding orbitals of boron atoms are the most important non-Lewis acceptors. The greatest values of stabilization energy in the C18B3N3-PA complex are related to transitions within the C18B3N3 molecule: BD*(2) C33–C34 → BD*(2) C23–C24; E(2) = 34.89 kcal mol−1, BD*(2) C29–C30 → BD*(2) C31–C32; E(2) = 42.29 kcal mol−1, BD*(2) C27–C28 → BD*(2) C25–C26; E(2) = 37.10 kcal mol−1, and BD*(2) C37–C36 → BD*(2) C23–C24; E(2) = 57.13 kcal mol−1. The most important stabilization energies related to the interaction between C18B3N3 and PA are BD(2) C25–C26 → LP*(1) B21; E(2) = 46.33 kcal mol−1 and BD(1) C25–C26 → LP*(1) B21; E(2) = 3.43 kcal mol−1, which indicates charge transfer from the drug molecule to C18B3N3.
Adsorption of PA on the C12B6N6 nanocage
In the next step, 12 carbon atoms of C24 were replaced by six boron atoms and six nitrogen atoms to obtain the C12B6N6 structure. In the most stable C12B6N6-PA complex, the oxygen atom of the drug molecule has established a bond with one of the boron atoms of the nanostructure with a length of 1.523 Å, which leads to an adsorption energy of −125.58 kJ mol−1, −138.55 kJ mol−1, and −156.48 kJ mol−1 at the B3LYP/6-31G(d), CAM-B3LYP/6-31G(d,p), and M06-2X/6-31G(d,p) levels of theory, respectively (Fig. 7 and Table 1). | ||
| Fig. 7 (a) Optimized geometry, (b) MEP, (c) HOMO, and (d) LUMO profiles of C12B6N6-PA at the M06-2X/6-31G(d,p) level pf theory. | ||
Table 5 shows that despite the relatively strong interaction between the drug molecule and C12B6N6, the geometrical parameters of PA did not change significantly. However, the bond length changes are more evident in the areas involved in the interaction with the nanostructure. For example, after forming the C12B6N6-PA complex, the C–O bond length of PA has increased by approximately 0.057 Å. The process of bond length changes in C12B6N6-PA is similar to that in the C18B3N3-PA and C24-PA complexes. Additionally, the lengths of C1–C12 and C1–N8 bonds increased, which can be attributed to resonance effects. The highest bond angle increase due to PA adsorption on the C12B6N6 surface is related to C1–C12–N14, C2–N10–H11, and C12–N14–H16 angles, which increased by 4.7°, 2.5° and 2.4°, respectively. The C1–C12–O13 bond angle decreased from 120.1° to 115.4° (Table S5†).
| Bond | Bond length (Å) | Δr | |
|---|---|---|---|
| After interaction | Before interaction | ||
| C1–C2 | 1.350 | 1.341 | 0.009 |
| C3–C4 | 1.329 | 1.333 | −0.004 |
| C2–H5 | 1.084 | 1.085 | −0.001 |
| C3–H6 | 1.080 | 1.082 | −0.002 |
| C4–H7 | 1.081 | 1.083 | −0.002 |
| C4–N8 | 1.416 | 1.403 | 0.013 |
| N8–H9 | 1.014 | 1.011 | 0.003 |
| C1–N8 | 1.425 | 1.407 | 0.018 |
| C2–N10 | 1.375 | 1.413 | −0.038 |
| C3–N10 | 1.433 | 1.434 | −0.001 |
| N10–H11 | 1.009 | 1.016 | −0.007 |
| C1–C12 | 1.450 | 1.486 | −0.036 |
| C12–O13 | 1.278 | 1.221 | 0.057 |
| C12–N14 | 1.326 | 1.369 | −0.043 |
| N14–H15 | 1.006 | 1.007 | −0.001 |
| N14–H16 | 1.024 | 1.009 | 0.015 |
According to Table 3, the Eg of C12B6N6 has decreased by 0.24 eV after interaction with the drug molecule, which indicates the high reactivity of the nanocarrier (Fig. 8). The significant decrease of Eg shows that the electronic properties of C12B6N6 are very sensitive to the presence of drug molecules in the environment, and therefore, C12B6N6 can be used as a PA sensor. The reduction in parameters ω, χ, A, and I is in agreement with the reduction in Eg. It is also observed that with the decrease in the Eg value, the softness and chemical hardness have increased and decreased, respectively, which indicates the tendency of the nanocarrier to interact with the PA molecule. A considerable decrease in the electrophilicity parameter by 1.60 eV confirms the charge transfer from the drug to the nanocarrier.
Table S6† shows that the partial charge of PA atoms is affected by the presence of the C12B6N6 nanocarrier in the environment. Therefore, the charges of the C1, C3, N8, and O13 atoms increased by 0.029, 0.001, 0.009, and 0.020 |e|. On the other hand, the charges of the C2, N14 and N10 atoms have become more positive by 0.078, 0.067, and 0.053 |e| respectively. Additionally, NBO calculations show that due to the formation of a complex between PA and C12B6N6, a charge amount of 0.324 |e| is transferred from the drug to the nanocarrier. The dipole moment is an important parameter for understanding the symmetry of the complex; the higher the dipole moment, the higher the interaction between the adsorbate and adsorbent molecules.52 The significant increase in the dipole moment of C12B6N6 indicates that the solubility of C12B6N6-PA increases upon the adsorption process.
Examining the stabilization energies E(2) shows that the most important electron transfers of the drug molecule are: LP(1) N14 → BD*(2) C12–O13; E(2) = 56.14 kcal mol−1, LP(1) N10 → BD*(2) C1–C2; E(2) = 34.28 kcal mol−1, LP(1) N8 → BD*(2) C1–C2; E(2) = 33.13 kcal mol−1, LP(2) O13 → BD*(1) C12–N14; E(2) = 29.41 kcal mol−1, and BD(2) C1–C2 → BD*(2) C12–O13; E(2) = 19.41 kcal mol−1. The most important donors are free electron pairs of nitrogen and oxygen that fill the C1–C2 and C12–O13 antibonding orbitals. Additionally, the greatest stabilization energy E(2) values of the nanocarrier are: LP(1) N25 → LP*(1) B17; E(2) = 24.73 kcal mol−1, LP(1) N29 → LP*(1) B19; E(2) = 24.75 kcal mol−1, BD(2) N17–B19 → LP*(1) B19; E(2) = 62.33 kcal mol−1, BD(2) N17–B19 → LP*(1) B121; E(2) = 63.09 kcal mol−1, and BD(2) N33–B21 → LP*(1) B19; E(2) = 62.86 kcal mol−1. As seen, non-Lewis acceptors are antibonding orbitals of boron atoms. Regarding the donor–acceptor transitions in the C12B6N6-PA complex, it should be said that the largest amounts of stabilization energy are related to transitions within the C12B6N6 molecule which are: BD*(2) C24–N25 → LP*(1) B23; E(2) = 99.29 kcal mol−1, LP(1) C2 → LP*(1) C4; E(2) = 90.21 kcal mol−1, LP(1) C26 → BD*(2) C24–N25; E(2) = 74.59 kcal mol−1, BD(2) N27–B18 → LP*(1) B17; E(2) = 70.14 kcal mol−1, and BD*(2) C12–N14 → BD*(2) C1–C2; E(2) = 69.22 kcal mol−1. The most important stabilization energies related to the interaction between C12B6N6 and PA are: BD(2) B17–N18 → BD*(1) B17–O13; E(2) = 13.34 kcal mol−1, LP(2) O13 → BD*(1) B17–N25; E(2) = 6.22 kcal mol−1, and BD(2) C12–N14 → BD*(1) B17–O; E(2) = 1.35 kcal mol−1, which is in agreement with the increase of the C12–O13 bond and also bond formation between the PA oxygen and the boron atom of C12B6N6. As can be seen, the replacement of carbon atoms with boron and nitrogen atoms increased the stabilization energies.
Atoms in molecule analysis
Bader's quantum theory of atoms in molecules (QTAIM)53 was utilized to explore electron density and bonding characteristics of the investigated systems. This theory states that upon chemical bond formation between two atoms a bond critical point (BCP) appears between them. The characteristics of BCPs are of great relevance in determining the electron density (ρC) and its corresponding Laplacian (∇2ρC), and therefore, designating the nature of interactions at a molecular level. ∇2ρC is the second derivative of a scalar function and provides information about the tendency of electron density to concentrate or deplete. The total electronic energy density at the BCP (HC) elucidates the energetic properties of BCPs and it is the sum of the local kinetic energy density (GC) and local potential energy density (VC) at the BCP.| HC = GC + VC | (12) |
On the other hand, the virial theorem states a relation between the Laplacian of the electron density at BCP and its other characteristics.
| (1/4)∇2ρC = 2GC + VC | (13) |
A negative value of the Laplacian indicates the concentration of the electron density among the nuclei of interacting atoms, and one may assume a shared interaction such as covalent bonds and lone pairs. A positive Laplacian electron density value at corresponding BCP shows the depletion of electron density as in ionic, van der Waals, and hydrogen bond interactions. Fig. 9 illustrates the molecular graph of C24-PA, C18B3N3-PA, and C12B6N6-PA complexes obtained from AIM calculations. The graphs were obtained at the M06-2X/6-31G(d,p) level of theory. Large circles correspond to attractors and small red and yellow circles are bond and ring critical points, respectively. However, sometimes ∇2ρC > 0 but the total electronic energy density, HC, is negative and such a situation is attributed to the partially covalent interaction. Fig. 9 shows that the adsorption of the PA molecule on the surface of the C24 nanocage led to the appearance of two critical points between the drug and the nanostructure. The electron density properties calculated for the C24-PA complex reveal that for the O13PA⋯C19 interaction ∇2ρC > 0 and HC > 0; hence, this interaction belongs to the category of electrostatic interactions. The C4PA⋯C20 interaction has more electron density (0.006 a.u.), and the values of ∇2ρC (0.019 a.u.) and HC (0.001 a.u.) are positive. Therefore, this bond is also the result of an electrostatic interaction (Table 6).
| Complex | Interaction site | ρ C | ∇2ρC | G C | V C | H C | Type of interaction |
|---|---|---|---|---|---|---|---|
| C24-PA | O13(PA)⋯C19 | 0.010 | 0.031 | 0.007 | −0.006 | 0.001 | Electrostatic |
| C4(PA)⋯C20 | 0.006 | 0.019 | 0.004 | −0.003 | 0.001 | ||
| C18B3N3-PA | O(PA)⋯B17 | 0.117 | 0.512 | 0.194 | −0.259 | −0.065 | Partly covalent |
| C12B6N6-PA | O13(PA)⋯B17 | 0.126 | −0.138 | 0.209 | −0.280 | −0.071 | Covalent |
| H(PA)⋯N18 | 0.033 | 0.089 | 0.023 | −0.024 | −0.001 | Partly covalent |
AIM calculations showed that only one critical point has appeared between O13 of the PA molecule and B17 of the C18B3N3 nanostructure, for which the values of ρC, ∇2ρC and HC are 0.117, 0.512, and −0.065 a.u. respectively. Therefore, the OPA⋯B17 interaction is partially covalent. The electron density properties calculated for the C12B6N6-PA complex show that the O13PA⋯B17 bond possesses a significant charge density (0.126 a.u.). Moreover, the values of ∇2ρC (−0.138 a.u.) and HC (−0.071 a.u.) are negative. Therefore, as we mentioned before, the O13PA⋯B17 bond is a covalent interaction. AIM calculations show that the HPA⋯N18 interaction has lower values of ρC and ∇2ρC > 0; however, this interaction is categorized as a partly covalent interaction because ∇2ρC > 0 and HC < 0.
NMR and IR spectra
The changes in charge density around the nuclei involved in the adsorption process can be very efficient in verifying the nature of host–guest interactions because the magnitude of these variations reveals the contribution of each nucleus to the interaction.54 Therefore, we performed NMR chemical shift calculations using the GIAO method to investigate the nature of interactions involved in the adsorption of PA on the surface of C24, C18B3N3, and C12B6N6. The chemical shift (CS) principal components (σii), CS isotropy (σiso), and CS anisotropy values of 13C, 15N, 17O, and 1H for the surfactant molecules calculated at the M06-2X/6-31G(d,p) level of theory are shown in Tables S7 to S13.† The isotropy (σiso) parameter shows the average value of the CS tensor, while the anisotropy (Δσ) parameter specifies the orientations of the CS tensor at the atomic site. The calculated chemical shift tensors for 13C, 15N, 17O, and 1H nuclei are sensitive to complex formation at the active site. The values of σiso and Δσ parameters of the C12, O13, and N14 atoms of the drug molecule increase significantly due to the adsorption on C12B6N6. After complex formation, the values of σiso and Δσ of the N8 and N10 atoms in the PA molecule decrease and increase, respectively. The value of σiso for C1 to C4 atoms in the drug molecule increases, while the Δσ value for these atoms decreases. The changes in the σiso and Δσ values of the PA atoms in C18B3N3-PA and C24-PA complexes also follow the same trend. The values of σiso and Δσ parameters of the C10, C11, C12, B13, B14, and B15 atoms of the C12B6N6 nanocage increase due to complex formation, while the values of σiso and Δσ of the C1, C5, C8, N18, B19, B20, N22, N23, and N24 atoms have decreased. In general, the results obtained from NMR spectra are in agreement with the previous results. Fig. S2 to S7† show the IR spectra of the compounds investigated in this study. Fig. S6† shows that a new peak appears in the region of 3300 cm−1 after C12B6N6-PA complex formation, which indicates the interaction between the functional groups of the host and guest molecules. Although the interaction of the drug molecule with C18B3N3 and C24 nanocarriers also leads to changes in the IR spectrum of the nanocages, due to the orientation of the interacting molecules, the intensity and the location of the peaks are different.UV-Vis spectra
The interaction between light and matter has always been of interest and is used to investigate the electronic properties of molecules precisely. The UV-Vis spectrum of the PA molecule (Fig. S9†) shows that the highest peak corresponds to the wavelength of 228 nm with f = 0.099. The higher the value of f, the higher the transition peak. The highest peak for the C12B6N6 molecule appears at 327 nm with f = 0.002 and for C12B6N6-PA at 496 nm with f = 0.069. In general, as shown in Tables S15–S20 and Fig. S9–S14,† adsorption of PA on the surface of nanocarriers, the wavelengths of the C24, C18B3N3, and C12B6N6, and thus, the highest peaks are shifted to higher values. Therefore, a redshift occurs after the adsorption process.Conclusions
In this study, we investigated the potential of the pristine C24 nanocage and its doped boron nitride analogs (C18B3N3 and C12B6N6) as carriers for the pyrazinamide (PA) drug using density functional theory (DFT). All calculations including geometry optimization, vibrational frequencies, QTAIM, NBO, NMR, and IR were carried out using the B3LYP/6-31G(d), CAM-B3LYP/6-31G(d,p) and M06-2X/6-31G(d,p) levels of theory. To calculation of the dispersion energy, the modified CAM-B3LYP and M06-2X methods were used. The results show that the adsorption energies calculated by B3LYP, CAM-B3LYP, and M06-2X methods are different. The M06-2X values are greater than those calculated by B3LYP and CAM-B3LYP methods. The adsorption energy (Eads), enthalpy (ΔH), and Gibbs free energy (ΔG) of C24-PA, C18B3N3-PA, and C12B6N6-PA complexes were calculated using the B3LYP/6-31G(d), CAM-B3LYP/6-31G(d,p) and M06-2X/6-31G(d,p) levels of theory. The results show that the interaction of the drug with the nanocages is exothermic and a spontaneous reaction has occurred at all theoretical levels (with the exception of the B3LYP/6-31G(d) level for C24-PA and C18B3N3). The results show that doping has increased the conductivity of nanocages. On the other hand, the interaction of PA with nanocages leads to a reduction in the energy gap of complexes. The Eg values of C24, C18B3N3, and C12B6N6 at the M06-2X/6-31G(d,p) level decrease by approximately 21%, 1.2%, and 5%, respectively, upon complexation. Furthermore, the decrease of Eg in complexes suggests that nanocages can be utilized for sensing PA molecules. Despite the relatively strong interactions between the drug molecule and nanocages, the geometrical parameters of PA did not change significantly. The changes in the atomic charges of the PA molecule due to the interaction with C24, C18B3N3, and C12B6N6 confirm a charge transfer of 0.07, 0.327, and 0.398 |e| from the drug to the nanocage, respectively. Based on the NBO results, the replacement of carbon atoms with boron and nitrogen atoms increased the stabilization energies (E(2)). AIM calculations revealed that the observed interactions between the nanocage and PA drug in C12B6N6-PA and C18B3N3-PA nanocages are stronger than those with the C24-PA nanocage. The results show that all three types of nanocages can be used as drug delivery systems for PA molecules.Ethics approval and consent to participate
This study did not involve human subjects, animal experimentation, or other activities necessitating ethical review.Consent for publication
The authors of this manuscript confirm that all authors have reviewed and approved the final version of the manuscript for submission to the journal of Nanoscale Advances.Data availability
The datasets generated during the current study are available upon request from the corresponding author. Additionally, some of the data and materials supporting this article have been included in the main text and ESI.†Author contributions
F. Naderi: conceived and designed the study, reviewing, editing of the manuscript, conceptualization, supervision; A. Moumivand: writing, software; O. Moradi: validation, visualization, methodology; B. Makiabadi: editing of the manuscript.Conflicts of interest
All authors declare that they have no competing interests.Acknowledgements
No funding was received to assist with the preparation of this manuscript.References
- V. Kumar, A. K. Abbas, N. Fausto and R. N. Mitchell, Cervical cancer, in Robbins Basic Pathology, Saunders Elsevier, Philadelphia, 8th edn, 2007 Search PubMed.
- C. A. Whittle and C. G. Extavour, Genome Biol. Evol., 2016, 8, 2722–2736 CrossRef CAS PubMed.
- S. K. Sharma and A. Mohan, Chest, 2006, 130, 261–272 CrossRef CAS PubMed.
- M. J. Reid, N. Arinaminpathy, A. Bloom, B. R. Bloom, C. Boehme, R. Chaisson, D. P. Chin, G. Churchyard, H. Cox and L. Ditiu, The Lancet, 2019, 393, 1331–1384 CrossRef PubMed.
- J. L. Khawbung, D. Nath and S. Chakraborty, Comp. Immunol., Microbiol. Infect. Dis., 2021, 74, 101574 CrossRef CAS PubMed.
- M. Najafimosleh, K. Ghazi-Saiedi, P. Farnia, F. Mohammadi and A. Velayati, J. Clin. Microbiol., 2008, 11, 14–21 Search PubMed.
- R. Esfandiarpour, F. Badalkhani-Khamseh and N. L. Hadipour, Colloids Surf., B, 2022, 215, 112513 CrossRef CAS PubMed.
- S. Bazyari-Delavar, F. Badalkhani-Khamseh, A. Ebrahim-Habibi and N. L. Hadipour, J. Nanopart. Res., 2021, 23, 1–12 CrossRef PubMed.
- F. Badalkhani-Khamseh, A. Ebrahim-Habibi, N. L. Hadipour and M. Behmanesh, Chem. Eng. Sci., 2023, 267, 118283 CrossRef CAS.
- M. Yahyavi, F. Badalkhani-Khamseh and N. L. Hadipour, J. Mol. Liq., 2023, 377, 121393 CrossRef CAS.
- U. Sahebi, H. Gholami, B. Ghalandari, F. Badalkhani-khamseh, A. Nikzamir and A. Divsalar, J. Mol. Liq., 2021, 344, 117758 CrossRef CAS.
- M. N Kumar, J. Pharm. Pharm. Sci., 2000, 3, 234–258 Search PubMed.
- W. Gao, G. Ye, X. Duan, X. Yang and V. C. Yang, Int. J. Nanomed., 2017, 12, 1047–1064 CrossRef CAS PubMed.
- M. A. A. Ibrahim, A.-s. S. M. Rady, A. M. A. Mandarawe, L. A. Mohamed, A. M. Shawky, T. H. A. Hasanin, P. A. Sidhom, M. E. S. Soliman and N. A. M. Moussa, Pharmaceuticals, 2022, 15, 1181 CrossRef CAS PubMed.
- M. Zarghami Dehaghani, B. Bagheri, F. Yousefi, A. A Nasiriasayesh, A. H. Mashhadzadeh, P. Zarrintaj, N. Rabiee, M. Bagherzadeh, V. Fierro, A. Celzard, M. R. Saeb and E. Mostafavi, Int. J. Nanomed., 2021, 16, 1837–1847 CrossRef PubMed.
- F. Naderi, Russ. J. Phys. Chem. A, 2016, 90, 1385–1390 CrossRef CAS.
- M. Ashiq, M. N. Zahid, Y. Malik, A. A. Alghamdi, S. A. M. Abdelmohsen and J. Iqbal, BioNanoSci, 2024, 1–22 Search PubMed.
- F. B. Balıbey, F. Bahadori, G. E. Kizilcay, A. Tekin, E. Kanimdan and A. Kocyigit, Pharm. Dev. Technol., 2023, 28, 843–855 CrossRef PubMed.
- M. Anafcheh, F. Naderi, Z. Khodadadi, F. Ektefa and R. Ghafouri, Silicon, 2019, 11, 323 CrossRef CAS.
- F. Naderi and V. Veryazov, J. Chem. Chem. Eng., 2017, 11, 30–36 CAS.
- J. Singh, P. Nayak, G. Singh, M. Khandai, R. R. Sarangi and M. K. Kar, C-J. Carbon Res., 2023, 9, 1–28 Search PubMed.
- J. M. Ashcroft, D. A. Tsyboulski, K. B. Hartman, T. Y. Zakharian, J. W. Marks, R. B. Weisman, M. G. Rosenblum and L. J. Wilson, Chem. Commun., 2006, 28, 3004–3006 RSC.
- R. P. Singh and P. Ramarao, Toxicol. Sci., 2013, 136, 131–143 CrossRef CAS PubMed.
- M. Anafcheh, R. Ghafouri and F. Naderi, Phys. E, 2012, 44, 1992–1998 CrossRef CAS.
- G. I. Giannopoulos, Nanomater., 2022, 12, 2711 CrossRef CAS PubMed.
- S. M. Sharker, Int. J. Nanomed., 2019, 14, 9983–9993 CrossRef PubMed.
- Z. Edis, J. Wang, M. K. Waqas, M. Ijaz and M. Ijaz, Int. J. Nanomed., 2021, 16, 1313–1330, DOI:10.2147/IJN.S289443.
- H. Xu, X. Tu, G. Fan, Q. Wang, X. Wang and X. Chu, J. Mol. Liq., 2020, 318, 114315 CrossRef CAS.
- S. Bibi, S. Ur-rehman, L. Khalid, I. A. Bhatti, H. N. Bhatti, J. Iqbal, F. Q. Bai and H. X. Zhang, RSC Adv., 2022, 12, 2873–2887 RSC.
- T. M. Joseph, D. K. Mahapatra, A. Esmaeili, L. Piszczyk, M. S. Hasanin, M. Kattali, J. Haponiuk and S. Thomas, Nanomater., 2023, 13, 574 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- S. Bazyari-Delavar, F. Badalkhani-Khamseh, A. Ebrahim-Habibi and N. L. Hadipour, Comput. Theor. Chem., 2020, 1189, 112983 CrossRef CAS.
- K. Gholivand, L. Sarmadi-Babaee, M. Faraghi, F. Badalkhani-Khamseh and N. Fallah, Chem. Phys. Impact, 2022, 5, 100099 CrossRef.
- M. M. Francl, W. J. Pietro, W. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2006, 120, 215–241 Search PubMed.
- J. S. Wright, C. Rowley and L. Chepelev, Mol. Phys., 2005, 103, 815–823 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- E. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO, Version 3.1, Gaussian Inc., Pittsburgh, PA, 1992 Search PubMed.
- N. M. O'boyle, A. L. Tenderholt and K. M. Langner, J. Comput. Chem., 2008, 29, 839–845 CrossRef PubMed.
- K. Gholivand, M. Faraghi, M. Mirzaei-Saatlo, F. Badalkhani-Khamseh, G. Salimi and A. Barzegari, J. Mol. Struct., 2023, 1274, 134505 CrossRef CAS.
- K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260 CrossRef CAS.
- F. Biegler-König and J. Schönbohm, J. Comput. Chem., 2002, 23, 1489–1494 CrossRef PubMed.
- Y. Chang, J. Zhang, H. Sun, B. Hong, Z. An and R. Wang, Int. J. Quantum Chem., 2005, 105, 142–147 CrossRef CAS.
- M. R. Hossain, M. M. Hasan, S. U. D. Shamim, T. Ferdous, M. A. Hossain and F. Ahmed, Comput. Theor. Chem., 2021, 1197, 113156 CrossRef.
- R. Esfandiarpour, M. R. Hosseini, N. L. Hadipour and A. Bahrami, J. Mol. Model., 2019, 25, 163 CrossRef PubMed.
- M. Salehpour, Z. Saadati and L. Asadi, Comput. Theor. Chem., 2022, 1209, 113573 CrossRef CAS.
- J. Beheshtian, M. Noei, H. Soleymanabadi and A. A. Peyghan, Thin Solid Films, 2013, 534, 650–654 CrossRef CAS.
- E. Cagatay, P. Köhler, P. Lugli and A. Abdellah, IEEE Sens. J., 2015, 15, 3225–3233 Search PubMed.
- J. Blakemore, Solid State Physics, ed. 2nd ed., WB Saunders Company, 1974 Search PubMed.
- I. Baikie, S. Mackenzie, P. Estrup and J. Meyer, Rev. Sci. Instrum., 1991, 62, 1326–1332 CrossRef CAS.
- G. Korotcenkov, Sensing Layers in Work-function-type Gas Sensors, Handbook of Gas Sensor Materials, Springer, 2013 Search PubMed.
- A. S. Rad, P. Valipour, A. Gholizade and S. E. Mousavinezhad, Chem. Phys. Lett., 2015, 639, 29–35 CrossRef CAS.
- R. F. Bader, Acc. Chem. Res., 1985, 18, 9–15 CrossRef CAS.
- F. Badalkhani-Khamseh, A. Bahrami, A. Ebrahim-Habibi and N. L. Hadipour, Chem. Phys. Lett., 2017, 684, 103–112 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4na00560k |
| This journal is © The Royal Society of Chemistry 2025 |