 Open Access Article
Open Access ArticleHigh-throughput approach to measure number of nanoparticles associated with cells: size dependence and kinetic parameters†
Ceri J.
Richards
 ab,
Paula
Melero Martinez
ab,
Paula
Melero Martinez
 a,
Wouter H.
Roos
b and
Christoffer
Åberg
a,
Wouter H.
Roos
b and
Christoffer
Åberg
 *a
*a
aPharmaceutical Analysis, Groningen Research Institute of Pharmacy, University of Groningen, 9713 AV Groningen, Netherlands. E-mail: christoffer.aberg@rug.nl
bMolecular Biophysics, Zernike Institute for Advanced Materials, University of Groningen, 9747 AG Groningen, Netherlands
First published on 4th November 2024
Abstract
Understanding how nanoparticle properties influence uptake by cells is highly important for developing nanomedicine design principles. For this, quantitative studies where actual numbers of cell-associated particles are determined are highly relevant. However, many techniques able to measure particle numbers suffer from low-throughput or place requirements on the types of nanoparticles that can be measured. Here we show the usage of flow cytometry to measure numbers of cell-associated nanoparticles for particles ranging in size from 100–500 nm, and extend this range to 40–500 nm by separate calibration. For the 100 nm particles, we corroborate the numbers by direct, low-throughput, counting using fluorescence microscopy. Applying flow cytometry we subsequently investigated the effect of particle size on the number of cell-associated particles for various timespans up to 5 h and found only a minor effect of size between 40, 100, and 200 nm particles. Next, we measured the kinetic rate constants describing the adsorption, desorption, and internalization for the 100 nm particles specifically. In general, we found values in accordance with previous literature. We foresee the future usage of the methodology applied here to investigate the kinetics of nanoparticle cellular uptake for a variety of particle types.
Introduction
Nanoparticles have been extensively researched over the past few decades for drug delivery purposes.1–3 Such nanomedicines offer several advantages over conventional drug delivery methods, including targeting to particular sites of interest,1,4,5 triggered drug release,6,7 and co-delivery.8,9 There have been several successful translations of nanocarriers onto the market including Onpattro10 and more recently the vaccines against SARS-CoV-2.11–15 Building on these successes, the development of nanomedicines will be further aided through an increasing use of quantitative approaches to study particle uptake.In particular, for multiple reasons it is desirable to quantify nanoparticle uptake into cells in terms of actual particle numbers. Firstly, in addition to knowing the applied particle dose, it is important to know the number of particles that successfully enter cells and thereby the amount of drug delivered.16 Moreover, determining the number of internalized particles allows for direct comparison of the uptake efficiency of different types of particles, e.g., in terms of size,17–22 material,21 or shape.17,23 Thereby, promising particle designs can be identified and developed. Finally, by quantifying particle numbers, parameters such as the particle adsorption, desorption and internalization rate constants become accessible.16,20,21,24–27 Characterization of these parameters allows for the validation and development of a theoretical basis for the kinetics of nanoparticle uptake into cells.16,24,26,27
Several techniques are available to quantify particle numbers within cells. One approach is to use techniques such as electron microscopy,28,29 fluorescence microscopy,21,30 or darkfield imaging22 and count the number of particles visualized within sectioned cells. However, these approaches are typically labour-intensive and low throughput. In contrast, techniques such as inductively coupled plasma atomic emission spectroscopy are high-throughput, but only applicable to metallic particles such as gold,17 and destroy the sample. Likewise, other approaches such as magnetophoresis or electron spin resonance are limited to the study of specific particle types.24
In contrast, flow cytometry is a high-throughput technique which can measure thousands of individual cells per minute, does not destroy the sample, and can be used to detect any type of fluorescently labelled particle or particle that scatters sufficiently strongly. Previous literature has shown that flow cytometry can be used to resolve the fluorescence signal of single particles in cells, though the particles were micron-sized31 or just below.32 While Garcia Romeu et al. could detect single particles in the nano-range using flow cytometry, the particles were inside cell-extracted organelles,33 so their approach does not allow assessing properties on a per-cell basis. Detecting single particles in cells, specifically in the size regime of interest for nanomedicines, is thus challenging.
An alternative is to use a different method to quantify uptake in terms of particle numbers, and then use such measurements to calibrate results measured using flow cytometry. Shim et al. adopted this approach by using the scattering signal from flow cytometry to measure cell uptake of silver nanoparticles ranging from 40 nm to 200 nm, and then converting these measurements to particle numbers using separate measurements by inductively coupled plasma mass spectrometry.18 While their approach is thus limited to metallic particles, a complementary approach would be to perform the particle number measurement using fluorescence, thereby substantially extending the range of particles that can be measured.
This is the approach we took here. Using low concentrations we were able to resolve single spherical carboxylated polystyrene nanoparticles of diameter 500, 200, and 100 nm when associated with cells. A fluorescence intensity calibration curve was determined from the measured signals of the 500–100 nm particles and used to estimate the signal of a single 40 nm particle associated with a cell. We then performed classical particle uptake kinetics experiments and converted the cellular fluorescence intensities to numbers of particles. In doing so, we were able to quantitatively compare the number of cell-associated particles for nanoparticles ranging in size from 40 nm to 200 nm. In contrast to previous studies,17–20,22,31 we did not find an uptake maximum for ∼50 nm particles. Lastly, by performing concentration-dependent experiments and experiments on energy depleted cells,20,24,25 we were able to quantify the cellular adsorption, desorption and internalization rate constants for the 100 nm particles.
Results and discussion
Fluorescent spherical carboxylated polystyrene nanoparticles of (nominal) diameters ranging from 40 nm to 500 nm were used as a model particle system as they exhibit a bright fluorescence signal and their interactions with cells and even tissue have been extensively studied.19,34–40 Particle dispersions were characterized using dynamic light scattering and Doppler velocimetry (ESI Table S1 and Fig. S1†) which showed that all particle sizes displayed colloidal stability in cell medium supplemented with 10% foetal bovine serum (complete medium), as previously reported.19,34,40–42 Human Embryonic Kidney (HEK) cells were exposed to the spherical fluorescent polystyrene nanoparticles dispersed in complete medium for various timespans and measured using flow cytometry. Flow cytometry measures the total fluorescence intensity of all cell-associated particles, i.e., both internalized particles and particles adsorbed to the (outer) cell membrane, on an individual cell basis. Note, however, that the signal measured using flow cytometry, while quantitative, does not give the actual number of nanoparticles, but rather just their fluorescence. Consequently, our first goal was to determine the conversion required to translate the flow cytometry data from measurements of cell fluorescence intensities to numbers of associated particles per cell. Thus, the intensity of a single nanoparticle associated with a cell needed to be determined for each particle size. To achieve this, we used low particle concentrations and short exposure times to obtain samples with zero to only a few particles associated with each cell.First, we assessed the background intensity of control cells not exposed to particles (Fig. 1a–c). We present the data both in terms of a histogram (right panels) of the distribution of cell intensities in the nanoparticle (FITC) channel, together with the same data displayed as a density plot (left panels) of the fluorescence signal in the nanoparticle (FITC) channel and a second channel (Pacific Blue). The reason for using a second channel is that this allows an easier visualization and separation of the various subpopulations; this is the case even when using an “empty” channel (i.e., a channel where there is no fluorescence, only background). In all cases, control cells show a single population with a background fluorescence intensity of approximately 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 a.u (Fig. 1a–c; note the different scales of the different panels).
000 a.u (Fig. 1a–c; note the different scales of the different panels).
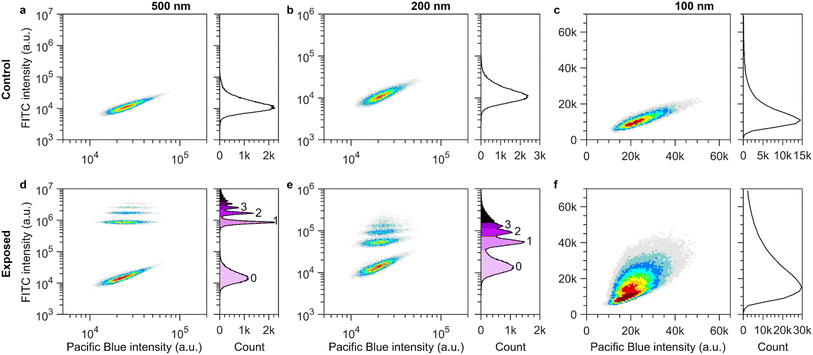 | ||
Fig. 1 Subpopulations of cells containing 0, 1, 2 etc. nanoparticles resolved using flow cytometry. Left panels show density plots of the particle signal (FITC) against an empty channel signal (Pacific Blue). The heat map indicates density, where red corresponds to high cell counts and grey to low cell counts. Right panels show histograms of the particle (FITC) signal per cell. (a–c) Control cells. The FITC distributions show a singular peak corresponding to the cell background intensity of approximately ∼15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 a.u. Cells with larger FITC signal show higher signal in the empty (Pacific Blue) channel, i.e., control cells which show higher autofluorescence do so in both channels. (d–f) Cells exposed to nanoparticles of different sizes. (d) Cells exposed to 500 nm nanoparticles at a nominal concentration of 0.58 × 109 particles per mL (40 μg mL−1) for 60 min. The lowest cluster in the density plot is in the same region as the control cells shown in panel a. Therefore, the lowest cluster corresponds to cells with no nanoparticles. Additional clusters of cells are observed at higher FITC intensities. The clusters are well separated and the histogram (right) shows easily distinguishable peaks. Each group corresponds to cells containing an additional nanoparticle, i.e., 1, 2, 3 etc. particles. (e) Cells exposed to 200 nm particles at a nominal concentration of 1.71 × 109 particles per mL (7.5 μg mL−1) for 60 min. As in panel d, the lowest cluster corresponds to cells with no associated nanoparticles. Successive groups can be distinguished in both the density plot (left) and histogram (right) where each group corresponds to cells with an additional nanoparticle. (f) Cells exposed to 100 nm nanoparticles at a nominal concentration of 1.37 × 1010 particles per mL (7.5 μg mL−1) for 15 min. The histogram (right) is broader than the one measured for control cells (panel c) rather than showing individual peaks as in panels d–e. However, plotting across two variables (density plot, left), a cluster of cells containing 1 nanoparticle can be distinguished from the lower group containing no nanoparticles. Note that different scales were used for the different particle sizes due to their different fluorescence intensities. Note also that results are presented in a logarithmic scale to show the whole range of cell fluorescence; ESI Fig. S2 and S3† show the results equivalent to panels d and e in linear scale. 000 a.u. Cells with larger FITC signal show higher signal in the empty (Pacific Blue) channel, i.e., control cells which show higher autofluorescence do so in both channels. (d–f) Cells exposed to nanoparticles of different sizes. (d) Cells exposed to 500 nm nanoparticles at a nominal concentration of 0.58 × 109 particles per mL (40 μg mL−1) for 60 min. The lowest cluster in the density plot is in the same region as the control cells shown in panel a. Therefore, the lowest cluster corresponds to cells with no nanoparticles. Additional clusters of cells are observed at higher FITC intensities. The clusters are well separated and the histogram (right) shows easily distinguishable peaks. Each group corresponds to cells containing an additional nanoparticle, i.e., 1, 2, 3 etc. particles. (e) Cells exposed to 200 nm particles at a nominal concentration of 1.71 × 109 particles per mL (7.5 μg mL−1) for 60 min. As in panel d, the lowest cluster corresponds to cells with no associated nanoparticles. Successive groups can be distinguished in both the density plot (left) and histogram (right) where each group corresponds to cells with an additional nanoparticle. (f) Cells exposed to 100 nm nanoparticles at a nominal concentration of 1.37 × 1010 particles per mL (7.5 μg mL−1) for 15 min. The histogram (right) is broader than the one measured for control cells (panel c) rather than showing individual peaks as in panels d–e. However, plotting across two variables (density plot, left), a cluster of cells containing 1 nanoparticle can be distinguished from the lower group containing no nanoparticles. Note that different scales were used for the different particle sizes due to their different fluorescence intensities. Note also that results are presented in a logarithmic scale to show the whole range of cell fluorescence; ESI Fig. S2 and S3† show the results equivalent to panels d and e in linear scale. | ||
We then exposed the cells to the 500 nm particles at a nominal concentration (calculated based on the size and mass concentration stated by the manufacturer) of 0.58 × 109 particles per mL (40 μg mL−1). Upon such an exposure, multiple well-separated populations of cells could be distinguished in both the density plot and histogram (Fig. 1d), as also previously shown in other works.31,32 The intensity distribution of the lowest cluster (light purple shading) overlaps with the control group (Fig. 1a) and therefore represents the cells within the sample that had no associated nanoparticles. At a shorter exposure time of 5 min (compared to the 60 min shown in Fig. 1d), the next successive group appeared and as the exposure time increased both the number of groups and the total number of cells within each cluster increased (ESI Fig. S2†). Therefore, we surmise that the successive groups are subpopulations of cells with 1, 2, 3 etc. associated nanoparticles.31,32
Using fluorescence, we could also resolve the 200 nm particles (Fig. 1b and e and ESI Fig. S3†), though the spacing between the groups is greatly diminished compared to the 500 nm particles. This is expected based on the smaller number of fluorophores per particle for smaller particles reported by the manufacturer.43 For cells exposed to 100 nm particles, separate cell populations could not be distinguished in the intensity histogram; instead, the overall distribution broadened compared to the control cells (Fig. 1f). However, if plotted across two variables, as in the density plot, two maxima (red colouration in the heatmap) can be distinguished. The lower maximum corresponds to cells with no associated particles, whilst the second maximum corresponds to cells with a single associated 100 nm particle (Fig. 1f). In contrast to e.g. metal or metal oxide particles,18 these polystyrene particles do not scatter light sufficiently strongly to be differentiated from the background signal (ESI Fig. S4†) so a strong enough fluorescence, as well as the particles having a similar fluorescence, are prerequisites for distinguishing individual particles.
In order to determine the intensity of single 500 nm and 200 nm particles, we performed a global fit to the cell fluorescence intensity distributions across all exposure times (ESI Fig. S2 and S3;† for further details on the fitting see the ‘Materials and Methods’ section). The fitted distributions corresponded well to the measured data. Accordingly, we used the fitted value for the peak-to-peak separation distance as the value for the fluorescence intensity of a single particle associated with a cell. This resulted in a value of 828![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 7000 a.u. and 40
000 ± 7000 a.u. and 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 1000 a.u for the 500 and 200 nm particles, respectively. In the case of the 100 nm particles, manual gating of the density plot was performed to separate the population of cells with 1 particle and no particles. The intensity of a single 100 nm particle was thereby found to be 5800 ± 600 a.u.
000 ± 1000 a.u for the 500 and 200 nm particles, respectively. In the case of the 100 nm particles, manual gating of the density plot was performed to separate the population of cells with 1 particle and no particles. The intensity of a single 100 nm particle was thereby found to be 5800 ± 600 a.u.
We further planned to determine the fluorescence intensity of single 40 nm particles, but the fluorescence signal of a single 40 nm particle would be too weak to distinguish from the cell background with the cytometer used here. Therefore, we determined a scaling relation between the intensities measured using flow cytometry and the number of fluorophores per particle reported by the manufacturer43 for the 500–100 nm particles (ESI Fig. S5;† for details see the ‘Materials and Methods’ section). Using the scaling relation, we calculated the expected particle intensity of a single cell-associated 40 nm particle to be 261 a.u. (231–294 a.u. lower–upper values with standard error).
Finally, we noted a small shift in the cell background fluorescence signal upon exposure to the particles, which we interpret to stem from the cellular internalization of free dye molecules.36,44 When converting measured fluorescence intensities to particle numbers, we consequently applied an additional background correction (see ESI† section ‘Shift of cell fluorescence background’ for details).
Maintaining the cytometer settings used for the results presented above we were able to measure cells containing very high fluorescence intensities in the nanoparticle channel without saturating the detector. For example, for the data presented in Fig. 1d, the object with highest fluorescence intensity measured (6.4 × 1013 a.u.) would equate to a cell containing 7.7 × 107, 1.6 × 109, 1.1 × 1010, and 2.5 × 1011 particles for the 500 nm, 200 nm, 100 nm, and 40 nm nanoparticles, respectively. Thus, our approach can easily be used to measure numbers of associated particles for much higher particle concentrations and exposure times than used here.
To confirm whether our approach to converting nanoparticle cell fluorescence to nanoparticle numbers was accurate, we compared the converted flow cytometry results to results obtained from low-throughput, but spatially resolved, fluorescence microscopy (Fig. 2). We avoided the 40 nm particles, as their lower fluorescence makes particle counting more difficult and, additionally, their smaller size increases the probability of finding two particles within the same diffraction-limited spot, both properties that make them unsuitable for testing the accuracy of the flow cytometry quantification. Instead, we focussed on the 100 nm particles, as those were the most difficult to resolve using flow cytometry (Fig. 1c and f) and hence their counting was more important to corroborate. Thus, cells were exposed to 100 nm nanoparticles for 2 h (note the substantially longer exposure time compared to Fig. 1). For the microscopy, optical z-sectioning was performed to capture the entire cell volume, after which the number of fluorescent objects associated with each cell was counted (Fig. 2a and b). Conventional (diffraction-limited, as opposed to superresolution) optical microscopy cannot resolve several particles too close together (e.g., within the same organelle). A correction for possible multi-particle objects was therefore applied (Fig. 2c; see ESI† discussion section ‘Fluorescence imaging’ for details).45 Ultimately, we thereby obtained an average of 20 ± 2 particles per cell. Conversely, measuring cell fluorescence using flow cytometry and applying the conversion described above results in an average of 21 ± 4 particles per cell, which corresponds very well to the value obtained from fluorescence microscopy (Fig. 2d). Overall, we thus confirm that the flow cytometry approach used herein accurately determines the number of particles per cell for small particle sizes, with the added advantage of measuring large populations of cells in a high-throughput manner.
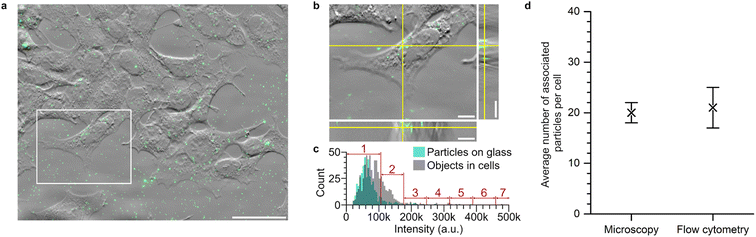 | ||
Fig. 2 Association of 100 nm nanoparticles to cells measured using flow cytometry and fluorescence microscopy. The 100 nm particles were exposed to cells for 2 h at a nominal concentration of 1.14 × 1010 particles per mL (6.26 μg mL−1) and subsequently measured by both fluorescence microscopy and flow cytometry. (a and b) Phase gradient contrast and fluorescence microscopy images of cells (grey) exposed to 100 nm particles (green) for 2 h. (a) Maximum intensity z projection image of the nanoparticles within the cellular volumes overlaid with a phase gradient contrast image of the cells. The white box indicates the single cell that is shown in detail in panel b. Scale bar is 50 μm. (b) Phase gradient contrast and fluorescence image of a single z section of the cell indicated in panel a. Right shows the view in the y–z plane whereas bottom shows the view in the x–z plane along the yellow lines of the main panel. Multiple fluorescent objects can be seen within the cell volume. Scale bars are 10 μm. (c) Histograms of the intensities of particles on glass (cyan bars) and objects identified within cells (grey bars) from images such as those shown in panels a and b. Particles on glass were assumed to be singular, based on the fact that the particles are well-dispersed (ESI Table S1 and Fig. S1†) and thus their average intensity was used as the intensity of a single particle. Fluorescent objects within cells were then classified as containing 1, 2, 3 etc. particles dependent on the total intensity of the object. (d) After this correction, the average number of particles per cell was 20 ± 2. For the flow cytometry, the average fluorescence intensity of ∼15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cells was measured (see ESI Fig. S6† for the corresponding distribution) and converted to the average number of particles associated per cell using the procedure outlined above. Three independent experiments were performed, each with 3 replicates per data point. Symbols (error bars) are the mean (standard deviation) across the averaged values for each independent experiment. The average number of particles associated with a cell after 2 h was 21 ± 4. 000 cells was measured (see ESI Fig. S6† for the corresponding distribution) and converted to the average number of particles associated per cell using the procedure outlined above. Three independent experiments were performed, each with 3 replicates per data point. Symbols (error bars) are the mean (standard deviation) across the averaged values for each independent experiment. The average number of particles associated with a cell after 2 h was 21 ± 4. | ||
Next, we used this approach to directly compare the association kinetics of nanoparticles of various sizes. Several works have reported a maximum in uptake by cells for a particle diameter around 50 nm;17–20,22,31 however, many of these reports did not explicitly assess uptake on a particle number basis,19,20,22,31 making this an interesting question to test with our approach. Thus, particle dispersions containing the same nominal particle concentration (in terms of number of particles) of either 200, 100, or 40 nm particles were used. Up to now we worked with nominal concentrations (estimated based on the mass concentration and size given by the manufacturer) as the exact number was inconsequential; when comparing different particle sizes, it is, however, imperative to have control over the concentration. We consequently assessed the actual particle concentrations with fluorescence microscopy and applied a correction factor to the association kinetics data (see ‘Materials and Methods’ section for details). We note that, in addition to small differences from the nominal concentrations for different sizes or batches of the stock nanoparticles, the stock concentrations also changed over timespans of months, likely due to solvent evaporation upon repeated usage. Thus, it is important to measure the actual particle concentrations at a similar moment as when the exposure experiments are performed, as was done here.
To follow the association kinetics, cells were exposed to particle dispersions for times spanning 0–5 h, as these shorter times allow decoupling association kinetics from other processes, such as the cell division cycle.35 It is important to note that the number of particles was always in excess, so that, to a very good approximation, the extracellular particle concentration remained constant throughout the experiment (ESI discussion section ‘Estimate of extracellular particle numbers’). The experiment was performed in triplicate, while some 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cells were measured for each time. Thus the inter-experiment variability could be assessed whilst also yielding a very good quantification of the mean uptake. To keep these two sources of variability distinct, we present independent experiments separately (Fig. 3 and ESI S7,† respectively).
000 cells were measured for each time. Thus the inter-experiment variability could be assessed whilst also yielding a very good quantification of the mean uptake. To keep these two sources of variability distinct, we present independent experiments separately (Fig. 3 and ESI S7,† respectively).
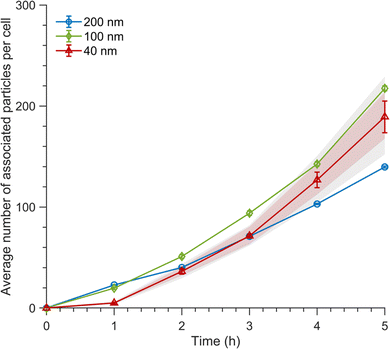 | ||
Fig. 3 Association kinetics of 200, 100 and 40 nm nanoparticles. Association kinetics of particles exposed to cells for various timespans for the 200 nm particles, 100 nm particles and 40 nm particles at a nominal concentration of 1.14 × 1010 particles per mL (50, 6.26, and 0.40 μg mL−1, respectively) for all particle sizes. The average fluorescence intensity of ∼30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cells was measured by flow cytometry and converted to the average number of particles associated with cells using the procedure outlined above. A correction was applied due to the discrepancies between the nominal concentrations and the actual measured particle concentrations (see Materials and Methods for details). Mean values are the average over cells from one independent experiment and the error is given by the standard error of the mean. The pink shading shows the mean values calculated using the lower and upper estimates of the fluorescence intensity of a single 40 nm particle (ESI Fig. S5;† for details see the ‘Materials and Methods’ section). The grey shading shows the standard error of the mean when using the upper and lower estimates. The data from two other independent experiments are shown in ESI Fig. S7.† 000 cells was measured by flow cytometry and converted to the average number of particles associated with cells using the procedure outlined above. A correction was applied due to the discrepancies between the nominal concentrations and the actual measured particle concentrations (see Materials and Methods for details). Mean values are the average over cells from one independent experiment and the error is given by the standard error of the mean. The pink shading shows the mean values calculated using the lower and upper estimates of the fluorescence intensity of a single 40 nm particle (ESI Fig. S5;† for details see the ‘Materials and Methods’ section). The grey shading shows the standard error of the mean when using the upper and lower estimates. The data from two other independent experiments are shown in ESI Fig. S7.† | ||
Fig. 3 shows the association kinetics as a function of time for the different particle sizes. We observe a similar qualitative trend regardless of particle size, where for short times there is limited particle association with cells, which later starts increasing more rapidly at timescales of a few hours. Interestingly, while we do observe quantitative differences between the different particle sizes, the effect is relatively small. Additionally, the large variability between independent experiments and the error in the estimate of the fluorescence intensity of a single 40 nm particle make drawing conclusions on the effect of particle size difficult. Nevertheless, our data clearly does not reflect previous literature which indicates that particle uptake would be maximal for the 40 nm particles, whilst the larger particles would have reduced uptake.17–20,22,31,46 Partly, this discrepancy may stem from differing approaches to matching the concentrations of the applied dispersion, as some previous studies have used the same mass concentrations for each particle size.20,22,31 Nevertheless, other studies have, as done here, matched the particle number concentrations.17,19
Lastly, we investigated the association kinetics of the 100 nm particles in further detail. By using data converted to actual numbers of particles, we are able to directly compare experimental results with proposed kinetic models and, additionally, evaluate kinetic rate constants, something that is often overlooked. Kinetic models based (essentially) on the Langmuir adsorption model have previously been used to describe the uptake of nanoparticles by cells,16,20,21,24,25 as discussed in detail in a recent review.16 In one such model one writes the time, t, derivative of the number of particles adsorbed to the membrane, Nm, and the number of internalized particles, Ni, as
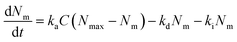 | (1) |
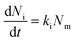 | (2) |
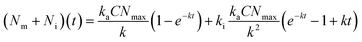 | (3) |
To separately address all three kinetic parameters used in the model, i.e., the adsorption, ka, desorption, kd, and internalization, ki, rate constants, it is necessary to perform experiments in which adsorbed and internalized particles can be discriminated from one another.16 Therefore, we simultaneously performed experiments at 4 °C and 37 °C.20,24,25 At 4 °C, internalization of these particles does not occur and hence only the adsorbed fraction is measured.34,36,40 To describe this we use an adapted form of eqn (3) which only describes adsorption16
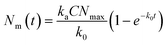 | (4) |
Fig. 4a shows the adsorption data obtained when exposing cells to 100 nm nanoparticles at 4 °C (see ESI Fig. S8a and b† for repeat experiments). For all concentrations, the number of particles bound to the cell membrane rapidly increases in the first 15 min and begins to saturate at around 3 h of exposure. We fitted eqn (4) to the data obtained at 4 °C for the various particle concentrations and found that the model fits the data well (Fig. 4a and ESI S8a and b,† dotted lines). Fitting to each repeat experiment separately gives independent values for k0, which allows us to estimate the associated error. Fig. 4b shows k0 as a function of concentration, from which a subsequent linear fit enables us to find the adsorption rate constant, ka, from the slope and the desorption rate constant, kd, from the intercept (since k0 = kaC + kd). We thus found ka = 1.35 ± 0.04 × 10−21 s−1 m3 (or 8.1 ± 0.3 × 105 M−1 s−1) and kd = 1.19 ± 0.05 × 10−4 s−1 (error given by standard error of the fit). The ka value we find is approximately twice as large as previously reported for 100 nm carboxylated polystyrene particles by Doiron et al.20 However, given expected differences stemming from the usage of different cell lines, we conclude that our ka value is in accordance with the previous report20 as they are within the same order of magnitude. Doiron et al. found a negative kd value for 100 nm particles, which is unphysical, nevertheless they and others have found values of 1.7 × 10−4 s−1 and 0.44 × 10−4 s−1 for other nanoparticle types.20,24 Thus our kd value is likewise in good agreement with previous literature.
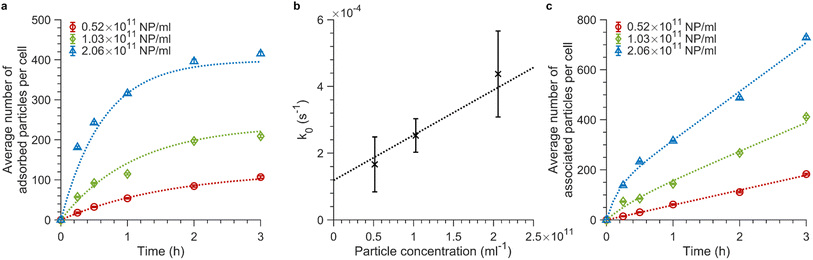 | ||
Fig. 4 Adsorption and association kinetics of 100 nm nanoparticles at different concentrations. (a and c) Association kinetics of 100 nm particles exposed to cells for various timespans. The average fluorescence intensity of ∼15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cells was measured by flow cytometry and converted to average number of particles associated with cells using the procedure outlined above. Three particle concentrations were investigated: 0.52 × 1011, 1.03 × 1011, and 2.06 × 1011 particles per mL (or 28.6, 56.6, and 113.2 μg mL−1). The concentration values are corrected from the nominal concentrations based on the number of particles measured in a known volume using fluorescence microscopy (see ‘Materials and Methods’ for details; the corresponding nominal concentrations are 0.455 × 1011, 0.909 × 1011, and 1.82 × 1011 particles per mL or 25, 50, and 100 μg mL−1). The data shown in panel a and c are the mean values from one independent experiment and the error is given by the standard error of the sample. Data and fits of the other two experiments are shown in ESI Fig. S8.† (a) Adsorption kinetics of particles exposed to cells at 4 °C when only adsorption and desorption processes are present. Eqn (4) was fitted (dotted lines) to the experimental data (symbols) to good agreement. (b) k0 values obtained from separate fits to individual curves such as those shown in panel a, plotted as a function of the particle concentration. The datapoints (error) are the mean (standard deviation) of the fitted k0 values over independent experiments. Since we expect k0 = kaC + kd, a straight line was fitted to the data (dotted line) to yield the ka and kd values. (c) Total association kinetics (adsorbed and internalized particles) of the 100 nm particles exposed to cells at 37 °C, for which adsorption, desorption and internalization all occur. Eqn (3) (in rewritten form) was fitted across the various particle concentrations with ki as a global (shared) parameter (see ‘Materials and Methods’ section for details). The fits (dotted lines) describe the experimental data (symbols) well. 000 cells was measured by flow cytometry and converted to average number of particles associated with cells using the procedure outlined above. Three particle concentrations were investigated: 0.52 × 1011, 1.03 × 1011, and 2.06 × 1011 particles per mL (or 28.6, 56.6, and 113.2 μg mL−1). The concentration values are corrected from the nominal concentrations based on the number of particles measured in a known volume using fluorescence microscopy (see ‘Materials and Methods’ for details; the corresponding nominal concentrations are 0.455 × 1011, 0.909 × 1011, and 1.82 × 1011 particles per mL or 25, 50, and 100 μg mL−1). The data shown in panel a and c are the mean values from one independent experiment and the error is given by the standard error of the sample. Data and fits of the other two experiments are shown in ESI Fig. S8.† (a) Adsorption kinetics of particles exposed to cells at 4 °C when only adsorption and desorption processes are present. Eqn (4) was fitted (dotted lines) to the experimental data (symbols) to good agreement. (b) k0 values obtained from separate fits to individual curves such as those shown in panel a, plotted as a function of the particle concentration. The datapoints (error) are the mean (standard deviation) of the fitted k0 values over independent experiments. Since we expect k0 = kaC + kd, a straight line was fitted to the data (dotted line) to yield the ka and kd values. (c) Total association kinetics (adsorbed and internalized particles) of the 100 nm particles exposed to cells at 37 °C, for which adsorption, desorption and internalization all occur. Eqn (3) (in rewritten form) was fitted across the various particle concentrations with ki as a global (shared) parameter (see ‘Materials and Methods’ section for details). The fits (dotted lines) describe the experimental data (symbols) well. | ||
Next, we exposed cells to the same particle dispersions but at 37 °C (Fig. 4c and ESI S8c and d†). The number of cellular nanoparticles initially increases substantially within the first 15 min of exposure time, as was also the case at 4 °C. This arises from the dominance of the adsorption kinetics over slower internalization processes within the first minutes of particle exposure.34 At longer timescales, adsorption and internalization reach a steady state resulting in the observed slower linear increase in (Nm + Ni)(t).34 We fitted eqn (3) (in rewritten form; see the ‘Materials and Methods’ section for details) across the various particle concentrations, with the demand that ki be the same. Again, we found good agreement between the model and the data (Fig. 4c and ESI S8c and d,† dotted line), yielding ki = 5 ± 2 × 10−4 s−1 (error given by standard deviation across repeats). Previous studies report various ki values.20,24,27 Some are of the same order of magnitude for various types of nanoparticles,24,27 though Doiron et al. found a three orders of magnitude smaller value for 100 nm carboxylated polystyrene particles.20
Aside from assessing the kinetic rate constants, we can also use the data to assess cell-to-cell variability in nanoparticle uptake, now not in terms of fluorescence,35,47 but in terms of numbers (ESI Fig. S9†). We observe that, even after 3 h of uptake, there are still cells that have not taken up any nanoparticles, while the cells that take up the most have taken up some 500–1000 particles (depending upon concentration). This highlights the large cell-to-cell variability in nanoparticle uptake, a topic of some interest35,47,48 that has yet to be fully understood.32,47 It likely also explains why we do not observe more than a handful of peaks in the fluorescence distributions (cf.Fig. 1); the large cell-to-cell variability leads to very few cells in the higher order peaks, making them difficult to identify.
Conclusions
Extending upon previous work,31,32 here we have shown that flow cytometry can be used to measure the actual numbers of particles associated with cells for nanoparticles in the size regime of interest for nanomedicine. While we here used HEK cells, there should not be any major issue in using the same methodology for other cell types (see our previous work on HeLa cells,32 for example). We show that our method is feasible for particles as small as 100 nm, with the possibility to extend to smaller particles, such as the 40 nm nanoparticles used here, by separate calibration. It should be noted that fundamentally it is not particle size itself that matters, but that the nanoparticles have a sufficiently strong fluorescence signal to be distinguished from the background fluorescence of the cell. Furthermore, the homogeneity of the labelling is also important, as a very heterogeneous labelling would cause successive peaks to overlap when measured using flow cytometry. Many different types of particles may be fluorescently labelled, including liposomes and lipid nanoparticles, the particles currently of most interest in nanomedicine. Nevertheless, the fluorescence may be weaker than the particles used here, for example, because the particle is a labelled version of a nanomedicine and extensive labelling may disturb the structure of the particle.Nevertheless, we envisage that this limitation can be substantially mitigated in future work. First, it may be possible to further improve upon the signal-to-noise ratio between cell background and single nanoparticle fluorescence by using a flow cytometer with higher dynamic range or, in general, with improved abilities as flow cytometry continues to develop. Second, and more immediately, the particles we used here and the results we present could be used as ‘calibration’ in the following sense: a particle may have a weaker fluorescence compared to the particles used here, but there are several techniques that could measure its fluorescence relative to (one of) the particles used here. This could, for example, be done by suspending an equal number of particles and measuring bulk fluorescence, or it could be done on a single-particle basis using fluorescence microscopy, in either case paying attention to the excitation and emission wavelengths used so that they match the flow cytometry. Once the fluorescence of a particle of interest is known relative to our particles, then knowing the uptake of one of the particles we used both in terms of numbers and in terms of fluorescence, will allow flow cytometry measurements of the particle of interest to be converted from fluorescence to numbers.
Indeed, the idea of recalibrating flow cytometry measurements to numbers has already been successfully demonstrated in the literature for silver nanoparticles.18 For silver particles, or nanoparticles containing metals in general, inductively coupled plasma mass spectrometry provides a useful means of quantifying particle numbers. Conversely, their side scattering can be used in flow cytometry. By using both sets of measurements, flow cytometry measurements can thereby be converted to numbers. It may even be possible to use flow cytometry alone to measure particle numbers by side scattering, assuming the particle scatters strongly enough that it can be distinguished from the scattering of the cell, in a manner analogous to what we have demonstrated here for fluorescence. In any case, the approach developed here is complementary, extending the range of nanoparticles where cell uptake can be quantified in terms of numbers, from nanoparticles containing metals, to nanoparticles that can be fluorescently labelled.
Utilizing this methodology, we reported the association kinetics of spherical carboxylated polystyrene nanoparticles ranging in size from 40 to 200 nm in terms of actual numbers of associated particles. While previous literature has shown that there is an uptake maximum for ∼50 nm particles with smaller and larger particles being taken up less,17,19,22,46 we could not corroborate this finding. It would be interesting to extend upon the work presented here to particles smaller than 40 nm, for which a lower number of cell-associated particles is anticipated if the idea of an uptake maximum at ∼50 nm is true.17,19,22,46 However, for the current setup, that would require further extrapolation of the fluorescence signal for the next smallest particle supplied by the manufacturer (20 nm) which would have a large degree of error.
Lastly, we applied a kinetic model16,34 to estimate the adsorption, desorption and internalization rate constants for the 100 nm spherical carboxylated polystyrene particles. The model fits the data very well and allowed us to evaluate all three rate constants from the data. In general, we find values that are within the same order of magnitude as reported in previous works for a variety of nanoparticle and cell systems.20,21,24,27 However, the found internalization rate constant was larger than the desorption rate constant, which may appear implausible given that desorption processes are expected to occur frequently whereas internalization is rarer.40,49 It should be noted that the adsorption and desorption kinetics were assessed at 4 °C and that the rate constants may depend upon temperature. To avoid this issue, alternative methods to halt particle internalization could be used in the future, for example cell treatment with sodium azide,36,50 though that is also not without compromises. However, the far larger effect is most likely the fact that there is a finite time between particle exposure and flow cytometry measurement, which allows the shorter-adsorbed particles to desorb. This effect must be taken into account when interpreting the desorption (and possibly the internalization) rate constants.
Overall, quantification of the number of cell-associated particles allowed for facile and direct comparison of various particles and validation of the proposed kinetic model.16,34 We foresee further usage of this high-throughput approach to investigate effects on uptake kinetics taking into account other particle properties, such as particle shape or functionalization strategies. Moreover, quantitative approaches can be used to further explore and validate kinetic models with a goal towards better understanding the mechanisms governing particle–cell interactions.16,24,26,27
Experimental
Cell culture
Human embryonic kidney (HEK) cells (American type culture collection, no. CRL-1573, lot no. 63966486) were used throughout. Cultures were maintained at 37 °C under a 5% CO2 and humidified atmosphere in complete medium, consisting of Dulbecco's minimal essential medium (Gibco) supplemented with 10% foetal bovine serum (Gibco). Cells used in the experiments were from cultures that tested negative for mycoplasma.Nanoparticles
40, 100, 200, and 500 nm fluorescent yellow-green (505/515 nm excitation/emission) carboxylated polystyrene nanoparticles were purchased from Invitrogen. Particle dispersions were prepared by adding nanoparticles to complete medium and incubating at 37 °C for at least 1 h prior to experiments. To identify single particles in cells, a nominal particle concentration of 7.5 μg mL−1 for the 100 and 200 nm particles, and a nominal concentration of 40 μg mL−1 for the 500 nm particles were used. For the size-dependent kinetics experiments, dispersions with the same nominal particle number concentration were prepared for all particle sizes. Firstly, the same volume of particle stock concentration (12.5 μL) was added to complete medium (4.988 mL) to achieve dispersions of 125, 50 and 50 μg mL−1 for the 40, 100, and 200 nm particles, respectively. Each bulk dispersion was then diluted to achieve a final nominal concentration of 1.14 × 1010 particles per mL for all particle sizes. Estimation of the particle concentrations was based on the nominal particle size and mass concentration given by the manufacturer. For measurement of kinetic rate constants, a bulk dispersion of 100 μg mL−1 of the 100 nm particles was prepared, divided into separate tubes and diluted to achieve nominal concentrations of 100, 50, and 25 μg mL−1 (1.82 × 1011, 0.909 × 1011, and 0.455 × 1011 particles per mL, respectively). Dispersions applied to cells for the 4 °C condition were first incubated at 37 °C to allow corona formation, and then cooled to 4 °C 30 min prior to and during cell exposure.Nanoparticle dispersion characterization
Characterization of particle size, state of agglomeration and charge in complete medium was performed using a Malvern ZetaSizer Nano ZS (Malvern Instruments) and ZetaSizer Software version 7.13 (Malvern Instruments). The complete medium dispersions were prepared at a nominal concentration of 100 μg mL−1 as described above and compared to particles dispersed in phosphate buffered saline (PBS, Gibco) at the same concentration. Three repeat measurements were performed with minimally 10 runs each. The values stated are the mean and standard deviation across repeats.(Nominal) particle concentrations can be estimated based on the particle mass concentration supplied by the manufacturer. However, for a more precise estimate, the actual particle concentrations were measured using fluorescence microscopy.19 Particles were dispersed in 100% glycerol (ThermoFisher Scientific) and diluted as per the procedure described above, followed by a final 10× dilution. The nominal final concentrations were then 1.14 × 109 particles per mL for the 40, 100, and 200 nm particles, respectively. Particle dispersions were imaged using a Celldiscoverer 7 microscope (Zeiss) with a 50× plan-apochromatic water immersion objective and a 470 nm LED in wide field modality. Optical z-sectioning was performed and the number of particles in each volume was counted using the ImageJ/Fiji51,52 plugin TrackMate.53 This was compared to lower-throughput but higher precision confocal measurements (Celldiscover 7 with the Airyscan detector, 488 nm laser) which yielded similar outcomes for the particle concentration. Between 4500–13 500 particles were counted from wide field volumes for each particle size. The measured concentrations were 0.56 ± 0.04 × 109, 1.01 ± 0.03 × 109 and 1.37 ± 0.03 × 109 particles per mL for the 40, 100, and 200 nm particles, respectively.
To show that these concentrations correspond to single particles, rather than particle agglomerates that we do not resolve in microscopy, we assessed the state of particle agglomeration in glycerol from widefield fluorescence timelapse. The particles were imaged using a Ti2 microscope (Nikon) with a 60× plan-apochromatic oil immersion objective and a 470 nm LED. Subsequently the fluorescent objects were tracked using the ImageJ/Fiji51,52 plugin TrackMate,53 and their time and ensemble-averaged mean square displacement was evaluated (ESI Fig. S10†). The mean square displacement was fitted with a straight line in the interval from 0.001 to 5 s to obtain the object diffusion coefficients. The object size was subsequently determined from the diffusion coefficients using the Stokes–Einstein equation and the viscosity of 100% glycerol at 25 °C.54
Flow cytometry
Cells were exposed to the nanoparticle dispersions by removal of the cell medium, addition of the particle-containing medium, and subsequently maintaining the cells at 37 °C under a 5% CO2 and humidified atmosphere. All experiments included reference control samples, i.e., cells to which no particle dispersion was added. For experiments performed at 4 °C, cells were maintained at 4 °C for 30 min prior to particle exposure and throughout exposure. Cells were then washed and returned to 37 °C with 5% CO2 and humidified atmosphere for 3 h to allow cellular entry of the adsorbed particles. This procedure has been previously described to obtain more consistent results.34 To prepare cells for flow cytometry measurements, the cells were washed three times, trypsinized, and centrifuged, after which the cell pellet was resuspended in PBS. The samples were kept on ice until the flow cytometry measurement. A NovoCyte Quanteon flow cytometer was used to measure the side and forward scattering signal for each cell, as well as the nanoparticle fluorescence signal (488/530 nm excitation/emission, ‘FITC’) and an empty channel (405/445 nm excitation/emission, ‘Pacific Blue’).Flow cytometry analysis
Debris and doublet cells were gated out of the cell population using the side area, forward area and forward height scattering signals with Kaluza Analysis software (version 2.1). To determine the fluorescence intensity of single 200 nm and 500 nm particles, the distributions of recorded nanoparticle (FITC) signals were fitted in MATLAB version R2018a. The lowest intensity peaks, corresponding to cells with no particles, were fitted using a lognormal distribution whereas successive peaks were each fitted with a Gaussian distribution (ESI Fig. S2 and S3†). Fitting was performed whilst maintaining the same separation between successive peaks, i.e., the fluorescence intensity of a single particle was constant regardless of the number of particles within a cell. Fitting was performed globally across all samples, ranging from 0 to 60 min particle exposure, within one independent experiment. The reported fluorescence signal for single particles and error was calculated as the average and standard deviation of the fitted peak separation distances from three independent experiments.For the 100 nm particles, gating was manually performed on the density plots of the nanoparticle signal (FITC) vs. an empty signal (Pacific Blue) in order to separate the population of cells with no particles and cells with one particle (Fig. 1c and f). The fluorescence intensity of a single 100 nm particle was calculated as the difference in the average nanoparticle (FITC) signal of the two gated populations. Reported values are means and standard deviations of three independent experiments.
The fluorescence intensity of a single 40 nm particle was found by comparison of the number of fluorescein equivalents per particle size determined by the manufacturer43 and the intensity values we obtained from our measurements of the 100, 200, and 500 nm particles. MATLAB was used to perform a linear regression of the logarithm of the company values to the logarithm of our measured values (ESI Fig. S5†). The obtained scaling factor was then used to convert the number of fluorescein equivalents reported by the manufacturer into the expected intensity of a 40 nm particle in our experimental setup. An upper and lower bound for the intensity of a 40 nm particle was calculated from the standard error of the fit.
The background shift observed upon particle exposure was determined by measuring the fluorescence intensity of cells not exposed and exposed to particles at 4 °C for various timespans (15–60 min). The background shift was calculated as the difference between the average fluorescence signal upon particle exposure at 4 °C (across all timespans) and control cells (ESI Table S4†).
To convert fluorescence signals to numbers of associated particles, the difference between the average signal of a sample and its corresponding control was calculated. Then the background shift, determined as described in the previous paragraph, was subtracted and the resultant value was divided by the previously determined intensity of a single particle of that size.
Finally, we corrected the discrepancy between the nominal particle concentrations and the measured particle concentrations for the kinetic experiments shown in Fig. 3, 4 and ESI S7 and S8.† For the size-dependent kinetics experiments (Fig. 3 and ESI S7†), the number of cell-associated particles was multiplied by the ratio of the nominal and measured particle concentrations. That is, the results are reported as if the cells had been exposed to dispersions of the nominal concentration for all particle sizes (assuming uptake is proportional). This allows direct comparison between the various particle sizes. In contrast, for the measurement of kinetic rate constants (Fig. 4 and ESI S8†), the measured concentrations were used instead of the nominal concentration values, i.e., 1.82 × 1011, 0.909 × 1011, and 0.455 × 1011 particles per mL.
Fluorescence microscopy and analysis
Cells were seeded onto 35 mm Petri dishes with a 1.5 glass bottom microwell (MatTek corp.) two days prior to experiments. Cells were then exposed to 100 nm nanoparticle dispersion with a nominal concentration of 1.14 × 1010 particles per mL (6.26 μg mL−1) for 2 h. Subsequently, cells were washed with PBS to remove particles in dispersion and then the cells were fixed with 4% paraformaldehyde (VWR). Cells were imaged using a Celldiscoverer 7 microscope (Zeiss) with a 50× plan-apochromatic water immersion objective. Phase gradient contrast imaging was used to identify the cellular boundaries and the nanoparticles were imaged using the 470 nm LED. Optical z sections were taken 0.5 μm apart throughout the entire cellular volumes. Cells were then manually segmented in ImageJ/Fiji51,52 based on the phase gradient contrast images. The number of fluorescent objects within each cell volume was subsequently manually counted. The total intensity of each fluorescent object was determined and compared to the distribution of intensities of single 100 nm particles on glass (Fig. 2c). A correction for multiparticle objects was applied and the average number of nanoparticles per cell was calculated for 37 cells (see ESI† discussion section ‘Fluorescence imaging’ for details). Reported values are the mean and standard error of the mean.Kinetic model fitting
Model fitting was performed in MATLAB version R2018a. Fits were separately performed on the data from three independent experiments using the inverse of the standard errors as weights. All fits to the data had R2 values higher than 0.95.For the 4 °C experiments, eqn (4) was fitted to the data for each particle concentration, substituting kaCNmax with the parameter A and subsequently using A and k0 as fitting parameters. The reported k0 values in Fig. 4b are the average over the three independent experiments for each particle concentration and the error is given by the standard deviation across independent experiments. A straight line was then fitted to the averaged k0 values as a function of particle concentration using the inverse standard error as weights. The ka and kd values were determined from this fit and the reported errors are given by the standard error of the fit.
For the corresponding 37 °C experiments, the equation
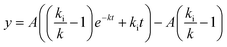 | (5) |
was fitted. Eqn (5) is a rewritten form of eqn (3) where A has been substituted for kaCNmax/k. For the fit, A and k were allowed to be different (local fitting parameters) for each particle concentration, whereas ki was enforced to be the same (global fitting parameter) across the data for different concentrations. Each independent experiment was separately fitted and the reported ki value and error are the mean and standard deviation across the three independent experiments.
Data availability
All relevant data are within the manuscript and its ESI.†Author contributions
CÅ and WHR designed research. CJR performed all experiments and analysis, except for the particle size determination in glycerol performed by PMM. CJR drafted the first version of the manuscript, after which all authors prepared the final version.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
CJR was supported by a scholarship under the Molecular Life and Health Programme of the Faculty of Science and Engineering, University of Groningen and PMM was supported by a Research Grant awarded to CÅ from the same faculty. Flow cytometry experiments were conducted at the Flow Cytometry Unit of the University Medical Center, Groningen. Fluorescence imaging was performed at the University Medical Center Groningen Imaging and Microscopy Center. We thank H. C. van der Mei and H. J. Kaper at the Department of Biomedical Engineering, University Medical Center Groningen for access to the Malvern ZetaSizer Nano. We also thank A. Salvati at the Groningen Research Institute of Pharmacy for the HEK cells. Finally, we thank I. de Boer and E. Niemeijer for their work (reported in ref. 32) which aided this work.References
- J. Shi, P. W. Kantoff, R. Wooster and O. C. Farokhzad, Nat. Rev. Cancer, 2017, 17, 20–37 CrossRef CAS PubMed.
- P. Decuzzi, D. Peer, D. D. Mascolo, A. L. Palange, P. N. Manghnani, S. M. Moghimi, Z. S. Farhangrazi, K. A. Howard, D. Rosenblum, T. Liang, Z. Chen, Z. Wang, J.-J. Zhu, Z. Gu, N. Korin, D. Letourneur, C. Chauvierre, R. van der Meel, F. Kiessling and T. Lammers, Nanotechnology, 2020, 32, 012001 CrossRef.
- D. Bobo, K. J. Robinson, J. Islam, K. J. Thurecht and S. R. Corrie, Pharm. Res., 2016, 33, 2373–2387 CrossRef CAS.
- G. Villaverde and A. Baeza, Beilstein J. Nanotechnol., 2019, 10, 168–181 CrossRef CAS.
- A. Akinc, W. Querbes, S. De, J. Qin, M. Frank-Kamenetsky, K. N. Jayaprakash, M. Jayaraman, K. G. Rajeev, W. L. Cantley, J. R. Dorkin, J. S. Butler, L. Qin, T. Racie, A. Sprague, E. Fava, A. Zeigerer, M. J. Hope, M. Zerial, D. W. Sah, K. Fitzgerald, M. A. Tracy, M. Manoharan, V. Koteliansky, A. de Fougerolles and M. A. Maier, Mol. Ther., 2010, 18, 1357–1364 CrossRef CAS.
- D. B. Pacardo, F. S. Ligler and Z. Gu, Nanoscale, 2015, 7, 3381–3391 RSC.
- H.-J. Li, J.-Z. Du, X.-J. Du, C.-F. Xu, C.-Y. Sun, H.-X. Wang, Z.-T. Cao, X.-Z. Yang, Y.-H. Zhu, S. Nie and J. Wang, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 4164–4169 CrossRef CAS.
- A. Lee, D. Di Mascolo, M. Francardi, F. Piccardi, T. Bandiera and P. Decuzzi, Nanomed. Nanotechnol. Biol. Med., 2016, 12, 2139–2147 CrossRef CAS PubMed.
- O. Taratula, A. Kuzmov, M. Shah, O. B. Garbuzenko and T. Minko, J. Controlled Release, 2013, 171, 349–357 CrossRef CAS.
- A. Akinc, M. A. Maier, M. Manoharan, K. Fitzgerald, M. Jayaraman, S. Barros, S. Ansell, X. Du, M. J. Hope, T. D. Madden, B. L. Mui, S. C. Semple, Y. K. Tam, M. Ciufolini, D. Witzigmann, J. A. Kulkarni, R. van der Meel and P. R. Cullis, Nat. Nanotechnol., 2019, 14, 1084–1087 CrossRef CAS PubMed.
- A. Khurana, P. Allawadhi, I. Khurana, S. Allwadhi, R. Weiskirchen, A. K. Banothu, D. Chhabra, K. Joshi and K. K. Bharani, Nano Today, 2021, 38, 101142 CrossRef CAS.
- Y. H. Chung, V. Beiss, S. N. Fiering and N. F. Steinmetz, ACS Nano, 2020, 14, 12522–12537 CrossRef CAS PubMed.
- S. Friedrichs and D. M. Bowman, Nat. Nanotechnol., 2021, 16, 362–364 CrossRef CAS.
- A. E. Nel and J. F. Miller, ACS Nano, 2021, 15, 5793–5818 CrossRef CAS PubMed.
- T. Kisby, A. Yilmazer and K. Kostarelos, Nat. Nanotechnol., 2021, 16, 843–850 CrossRef CAS PubMed.
- C. Åberg, Nanoscale Adv., 2021, 3, 2196–2212 RSC.
- B. D. Chithrani, A. A. Ghazani and W. C. W. Chan, Nano Lett., 2006, 6, 662–668 CrossRef CAS PubMed.
- Y. J. Shim, M. K. Ha and T. H. Yoon, Nanomaterials, 2021, 11, 3079 CrossRef CAS.
- J. A. Varela, M. G. Bexiga, C. Åberg, J. C. Simpson and K. A. Dawson, J. Nanobiotechnol., 2012, 10, 39 CrossRef CAS PubMed.
- A. L. Doiron, B. Clark and K. D. Rinker, Biotechnol. Bioeng., 2011, 108, 2988–2998 CrossRef CAS PubMed.
- K. Yaehne, A. Tekrony, A. Clancy, Y. Gregoriou, J. Walker, K. Dean, T. Nguyen, A. Doiron, K. Rinker, X. Y. Jiang, S. Childs and D. Cramb, Small, 2013, 9, 3118–3127 CrossRef CAS PubMed.
- L. Q. Chen, L. Fang, J. Ling, C. Z. Ding, B. Kang and C. Z. Huang, Chem. Res. Toxicol., 2015, 28, 501–509 Search PubMed.
- R. Agarwal, V. Singh, P. Jurney, L. Shi, S. V. Sreenivasan and K. Roy, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 17247–17252 CrossRef CAS.
- C. Wilhelm, F. Gazeau, J. Roger, J. N. Pons and J.-C. Bacri, Langmuir, 2002, 18, 8148–8155 CrossRef CAS.
- T. T. Goodman, J. Chen, K. Matveev and S. H. Pun, Biotechnol. Bioeng., 2008, 101, 388–399 CrossRef CAS.
- W. Chen, D. Z. D'Argenio, A. Sipos, K.-J. Kim and E. D. Crandall, Am. J. Physiol.: Regul., Integr. Comp. Physiol., 2021, 320, R36–R43 CrossRef CAS.
- H. Jin, D. A. Heller, R. Sharma and M. S. Strano, ACS Nano, 2009, 3, 149–158 CrossRef CAS.
- A. Elsaesser, C. A. Barnes, G. McKerr, A. Salvati, I. Lynch, K. A. Dawson and C. V. Howard, Nanomedicine, 2011, 6, 1189–1198 CrossRef CAS PubMed.
- C. Brandenberger, C. Mühlfeld, Z. Ali, A.-G. Lenz, O. Schmid, W. J. Parak, P. Gehr and B. Rothen-Rutishauser, Small, 2010, 6, 1669–1678 CrossRef CAS PubMed.
- H. Peuschel, T. Ruckelshausen, C. Cavelius and A. Kraegeloh, BioMed Res. Int., 2015, 2015, e961208 Search PubMed.
- T. dos Santos, J. Varela, I. Lynch, A. Salvati and K. A. Dawson, Small, 2011, 7, 3341–3349 CrossRef CAS PubMed.
- B. Yang, C. J. Richards, T. B. Gandek, I. de Boer, I. Aguirre-Zuazo, E. Niemeijer and C. Åberg, Front. nanotechnol., 2023, 5, 1181362 CrossRef.
- H. Garcia Romeu, S. Deville and A. Salvati, Small, 2021, 17, 2100887 CrossRef CAS.
- A. Lesniak, A. Salvati, M. J. Santos-Martinez, M. W. Radomski, K. A. Dawson and C. Åberg, J. Am. Chem. Soc., 2013, 135, 1438–1444 CrossRef CAS PubMed.
- J. A. Kim, C. Åberg, A. Salvati and K. A. Dawson, Nat. Nanotechnol., 2012, 7, 62–68 CrossRef CAS PubMed.
- A. Salvati, C. Åberg, T. dos Santos, J. Varela, P. Pinto, I. Lynch and K. A. Dawson, Nanomed. Nanotechnol. Biol. Med., 2011, 7, 818–826 CrossRef CAS.
- J. A. Varela, C. Åberg, J. C. Simpson and K. A. Dawson, Small, 2015, 11, 2026–2031 CrossRef CAS PubMed.
- R. Bartucci, C. Åberg, B. N. Melgert, Y. L. Boersma, P. Olinga and A. Salvati, Small, 2020, 16, 1906523 CrossRef CAS PubMed.
- I. de Boer, C. J. Richards and C. Åberg, Pharmaceutics, 2022, 14, 136 CrossRef CAS PubMed.
- C. J. Richards, T. C. Q. Burgers, R. Vlijm, W. H. Roos and C. Åberg, ACS Nano, 2023, 17, 16517–16529 CrossRef CAS PubMed.
- N. Vtyurina, C. Åberg and A. Salvati, Nanoscale, 2021, 13, 10436–10446 RSC.
- C. J. Richards, M. Ahmadi, M. C. A. Stuart, B. J. Kooi, C. Åberg and W. H. Roos, Nanoscale, 2023, 15, 248–258 RSC.
- In Molecular Probes Handbook: A Guide to Fluorescent Probes and Labelling Techniques, ed. I. Johnson and M. Spence, Life Technologies Corporation, California, 11th edn, 2010, ch. 6, pp. 191–235 Search PubMed.
- T. Tenuta, M. P. Monopoli, J. Kim, A. Salvati, K. A. Dawson, P. Sandin and I. Lynch, PLoS One, 2011, 6, e25556 CrossRef CAS.
- C. Åberg, J. A. Varela, L. W. Fitzpatrick and K. A. Dawson, Sci. Rep., 2016, 6, 34457 CrossRef.
- W. Jiang, B. Y. S. Kim, J. T. Rutka and W. C. W. Chan, Nat. Nanotechnol., 2008, 3, 145–150 CrossRef CAS PubMed.
- C. Åberg, V. Piattelli, D. Montizaan and A. Salvati, Nanoscale, 2021, 13, 17530–17546 RSC.
- P. Rees, J. W. Wills, M. R. Brown, C. M. Barnes and H. D. Summers, Nat. Commun., 2019, 10, 2341 CrossRef.
- K. A. Dawson and Y. Yan, Nat. Nanotechnol., 2021, 16, 229–242 CrossRef CAS PubMed.
- A. Lesniak, F. Fenaroli, M. P. Monopoli, C. Åberg, K. A. Dawson and A. Salvati, ACS Nano, 2012, 6, 5845–5857 CrossRef CAS PubMed.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675 CrossRef CAS PubMed.
- J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld, B. Schmid, J.-Y. Tinevez, D. J. White, V. Hartenstein, K. Eliceiri, P. Tomancak and A. Cardona, Nat. Methods, 2012, 9, 676–682 CrossRef CAS PubMed.
- J.-Y. Tinevez, N. Perry, J. Schindelin, G. M. Hoopes, G. D. Reynolds, E. Laplantine, S. Y. Bednarek, S. L. Shorte and K. W. Eliceiri, Methods, 2017, 115, 80–90 CrossRef CAS PubMed.
- J. B. Segur and H. E. Oberstar, Ind. Eng. Chem., 1951, 43, 2117–2120 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: additional experimental results and fits to the data. See DOI: https://doi.org/10.1039/d4na00589a |
| This journal is © The Royal Society of Chemistry 2025 |
