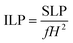DOI:
10.1039/D4NA00685B
(Paper)
Nanoscale Adv., 2025, Advance Article
Gd3+ doped CoCr2O4 nanoparticles: tuning the physical properties and optimizing the hyperthermia efficacy†
Received
20th August 2024
, Accepted 21st January 2025
First published on 21st January 2025
Abstract
Tuning the physical properties of nanomaterials is essential to enhance their capabilities for modern technological applications. Incorporating appropriate dopant ions is expected to modify the physical properties of nanomaterials significantly. In this study, the microstructural, magnetic, electronic and optical properties of cobalt chromite nanoparticles have been tuned by incorporating Gd ions to obtain the optimized conditions for self-heating efficiency. Four chromite samples with varying Gd3+ dopant concentrations [CoGdxCr2−xO4: x = 0, 0.04, 0.08 and 0.12] were prepared using the standard chemical co-precipitation method and their physical properties were explored thoroughly. The Gd3+ dopants in the host CoCr2O4 structure were shown to be capable of regulating the physical properties of the doped nanomaterials. Formation of a pure cubic spinel crystallographic phase together with size, shape and developed microstrain in the synthesized doped chromites were analyzed precisely and it was found that the mean size decreased gradually as the Gd content increased. Higher Gd content chromite nanoparticles showed a distinct blue shift in their absorption spectra and an increase in specific surface area, as evidenced by the BET study confirming the reduction in mean diameter. Substituted Gd ions also tuned the dielectric characteristics of the host chromite nanomaterial. A careful investigation of electrical conductivity in varying electric fields indicated that electron hopping occurs mostly during charge conduction. All the chromite samples exhibited lossy dielectric behavior as the dopant fraction increased. Introducing Gd ions in nanocrystalline cobalt chromite diluted the magnetic properties, which was evident from the reduction of the coercive field, and also provided the superparamagnetic ground state above 95 K. The spin-spiral transition became visible near 26 K as the Gd content in pure CoCr2O4 nanoparticles increased. The induction heating properties of nanosized chromite samples were modified using Gd doping, and the impacts of both the anisotropic energy barrier and magnetic dipole–dipole interactions on hyperthermia efficacy were extensively investigated. All of the prepared chromite samples at low concentration (1 mg mL−1) attained temperatures between 34.7 °C and 35.7 °C from ambient temperature in 900 seconds with an observed drop in the induction heating temperature with increasing Gd content in nanosized cobalt chromites. It was observed that the dispersion level of nanoparticles in solution also determined the heating efficiency. It was observed that Gd doped CoCr2O4 nanoparticles have the potential to be used in magnetic hyperthermia applications.
1. Introduction
Nanomaterial engineering has emerged as a prominent research topic in recent years, with the aim of improving their functioning for use in a variety of modern technologies. Modifying the size, shape, composition and synthesis routes of nanomaterials, as well as introducing dopant ions in appropriate percentages, has been shown to be an effective way of modifying their physical properties. Tuning the physical properties of magnetic nanoparticles to make them suited for various applications, particularly in biomedicine, targeted drug delivery, and hyperthermia, has been an active area of research. In this direction, magnetic nanoparticles from the spinel cubic group have demonstrated higher potential. Being a group member of the spinel cubic family, the multiferroic cobalt chromite (CoCr2O4) nanomaterial with tunable physical properties can be used for hyperthermia applications. When magnetic nanoparticles are subjected to a varying magnetic field, they dispel magnetic energy in heat form, which can be used in hyperthermia and thermally induced drug delivery.1–4 Because of low hysteresis loss, superparamagnetic nanoparticles have emerged as a promising candidate for hyperthermia applications. In this direction, suspensions containing superparamagnetic nanoparticles have recently been examined for targeting cancer cells and forcing them to explode, resulting in tumour reduction.2–5 Researchers have been trying to improve the efficacy of the self-heating process of magnetic nanoparticles by modifying size, shape, doping ions and their percentages. Both the composition and shape of the magnetic nanoparticles, in addition to their size, play an important role in regulating the magnetic properties which have a major impact on the hyperthermia efficacy of the system.4–6 Varying the composition of the magnetic nanoparticles is an effective technique to adjust their response during induction heating. Adequate heat must be supplied throughout the tumor cells while leaving the surrounding normal tissues unharmed to make magnetic nanoparticles clinically viable and cancer elimination possible.4–8 Thus, optimizing the hyperthermia efficacy of magnetic nanomaterials is essential. In this study, we adjusted the composition of pure CoCr2O4 nanoparticles by introducing Gd ions in appropriate amounts to optimize the hyperthermia efficiency of the chromite system.
The multiferroic cobalt chromite (CoCr2O4) crystallizes in space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, where magnetic Co2+ ions occupy tetrahedral (A) sites, while Cr3+ ions reside in octahedral (B) sites, forming a normal spinel cubic crystal structure.9,10 This material behaves like a ferrimagnetic system below Curie temperature (≈97 K) and the superexchange interactions (A–O–B) present between two different types of sublattices (A and B) are responsible for the ferrimagnetic nature. A spiral ferrimagnetic ordering may also be seen in the spinel cobalt chromite system below 26 K.9–12 Significant changes in the magnetic properties of the cobalt chromite system have been observed at low temperatures and in the nanoscale domain. Variations in the fabrication method, size, shape, dopant ions, and doping percentages can drastically modify the physical properties of CoCr2O4 nanoparticles, including their magnetic, optical, structural, and dielectric responses.12
m, where magnetic Co2+ ions occupy tetrahedral (A) sites, while Cr3+ ions reside in octahedral (B) sites, forming a normal spinel cubic crystal structure.9,10 This material behaves like a ferrimagnetic system below Curie temperature (≈97 K) and the superexchange interactions (A–O–B) present between two different types of sublattices (A and B) are responsible for the ferrimagnetic nature. A spiral ferrimagnetic ordering may also be seen in the spinel cobalt chromite system below 26 K.9–12 Significant changes in the magnetic properties of the cobalt chromite system have been observed at low temperatures and in the nanoscale domain. Variations in the fabrication method, size, shape, dopant ions, and doping percentages can drastically modify the physical properties of CoCr2O4 nanoparticles, including their magnetic, optical, structural, and dielectric responses.12
All the physical properties of nanocrystalline CoCr2O4 can be adjusted by introducing 4f rare-earth metal ions in a suitable ratio. Due to the paramagnetic nature of rare-earth ions at room temperature, the incorporation of rare-earth ions obeying the percolation limit in a nanosized chromite system can dilute the magnetic behavior, resulting in the emergence of superparamagnetic phenomena. Among rare-earth metal ions, due to the half-filled 4f shells, the magnetic moment of the Gd3+ (4f7) ion is localized and originates entirely from spin contributions.13–15 All the Gd3+ ions behave magnetically alike to 3d transition metals since there is no orbital contribution to the magnetic moment. Gd ions display ferromagnetic ordering below the Curie temperature (293 K) and they are paramagnetic metal ions above the Curie temperature. As the Gd3+ (0.938 Å) ions are larger than the Cr3+ (0.615 Å) ions, substituting Gd3+ ions in the CoCr2O4 crystal structure within the percolation limit causes lattice deformation and dramatically alters the physical properties of the host chromite system.9,16 There are numerous top-down and bottom-up synthesis strategies available for producing doped chromite nanoparticles. Among all available approaches, the typical chemical co-precipitation process enables researchers to prepare doped chromite nanoparticles with high size and shape homogeneity. It is also a less expensive, simpler, and faster synthesis method for fabricating spinel cubic doped chromite nanoparticles smaller than 20 nm.9,13–16
In this study, we introduced Gd3+ ions into pure CoCr2O4 nanoparticles and comprehensively examined their influence on the physical properties of the host system. Doping of Gd3+ ions below the solubility limit in place of Cr3+ ions significantly altered the microstructural, dielectric, optical, electronic and magnetic properties of the nanocrystalline cobalt chromite.13 We also tuned the magnetic anisotropy energy barrier with Gd ions and tried to optimize the hyperthermia efficacy of the doped chromite nanomaterials. An attempt was made to investigate the effect of magnetic dipolar interactions on the hyperthermia efficiency of the prepared chromite systems. Although the localized magnetic hyperthermia properties of doped cobalt ferrite nanoparticles have been investigated, fewer research materials are accessible for the hyperthermia application of cobalt chromite nanoparticles. Despite the fact that Cr ions are hazardous heavy metals that are detrimental to humans, animals, and plants, the toxicity of Cr in chromites can be reduced by applying a biopolymer coating like chitosan, gelatin, or guar gum, which makes them suitable for several applications involving hyperthermia.17 Including optimization of hyperthermia efficacy via tuning magnetic anisotropy, we have thoroughly investigated the effects of incorporated Gd ions in tuning various physical properties of the host material. Different characterization techniques used in this study helped to understand the alteration of several physical properties of cobalt chromite nanoparticles via varying the percentage of Gd dopants. Although many research works on doped spinel ferrite systems are available, the effects of large-sized rare-earth ion doping on spinel chromite systems have not been fully explored. Varying calcination temperature to achieve nanoparticles with different sizes is the most common method. Here, in our synthesized nanocrystalline Gd-doped cobalt chromites, the observed decrement in mean sizes was due to the effect of gradual doping of large sized rare-earth ions while the calcination temperature was fixed. In addition to that, although Gd3+ ions are in the rare-earth group, they behave like 3d transition metal ions (quenching of orbital momentum) due to the half-filled 3d shells. Tuning several physical properties of a nanomaterial is essential for efficient use in multiple technological applications. By incorporating Gd3+ ions within a certain limit, tunable physical properties of cobalt chromite nanoparticles have been achieved. In addition to the hyperthermia applications, Gd-doped CoCr2O4 nanoparticles with tuned physical properties can be efficiently used in data storage, spintronics, catalysis, sensors, detectors, supercapacitors, solar cells, and various modern devices. This paper is not only focused on hyperthermia efficacy, but it also describes more effectively the modification of physical properties of CoCr2O4 nanoparticles due to the incorporation of Gd dopants.
2. Experimental details
2.1. Synthesis of pure and doped CoCr2O4 nanoparticles
Pristine and Gd incorporating CoCr2O4 nanoparticles containing different Gd contents were fabricated using the conventional co-precipitation technique with the chemical formula CoCr2−xGdxO4 (x = 0.00, 0.04, 0.08 and 0.12).9,13 The prepared chromite samples were named Gd-00 (CCO), Gd-04 (CCO), Gd-08 (CCO) and Gd-12 (CCO) according to the enhancement of Gd ions. The synthesis procedure is described in detail in the ESI† part of this publication.
2.2. Characterization
All the characterization techniques used to investigate the physical properties and self-heating efficiency of Gd doped CoCr2O4 nanoparticles are discussed in detail in the ESI† section of this manuscript.
3. Results and discussion
3.1. Study of X-ray diffraction patterns
Fig. 1(a) depicts room temperature powder X-ray diffractograms of all the prepared samples containing Gd doped cobalt chromite nanoparticles of different percentages. All the samples displayed characteristic peaks of cubic spinel crystal structure in the diffraction profiles with a highly intense (311) diffraction peak. The non-existence of any foreign diffraction peak instead of characteristic peaks of the cubic spinel crystal structure also ensured the phase purity of all chromite samples.9–12 All of the peaks in the diffractograms belong to the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group and correspond exactly to ICDD Card No. 080-1668. The GSAS software with EXPGUI interface was used to perform the Rietveld refinement of all the X-ray diffraction patterns. In the fitting process, the Pseudo–Voigt function was utilized to shape the profile peaks. The fitting parameters i.e. goodness of fit (χ2) were noted to have values within 1.03 to 1.11 and R-factors (RP and RWP) were found to be below 3% confirming the perfect agreement between the obtained data and typical diffraction pattern. It should be emphasized that the observed broadening in the diffracted peaks is due to the prepared chromite samples being in the nanometric domain. With the increment of Gd dopants in cobalt chromite samples, a gradual enhancement in peak broadening was noticed.13–15 Three major factors are responsible for the XRD peak broadening in the nanosize domain, i.e. crystallite size effect, intrinsic microstrain in the nanocrystals and instrumental effects. In order to eliminate the instrumental broadening effects, a reference diffractogram of pure LaB6 powder having a large grain size was used under similar conditions.16 After subtracting instrumental line-width, the overall broadening β (FWHM of peak) is the combination of crystallite size (βsize) and intrinsic microstrain (βstrain) broadening effects as given below18
m space group and correspond exactly to ICDD Card No. 080-1668. The GSAS software with EXPGUI interface was used to perform the Rietveld refinement of all the X-ray diffraction patterns. In the fitting process, the Pseudo–Voigt function was utilized to shape the profile peaks. The fitting parameters i.e. goodness of fit (χ2) were noted to have values within 1.03 to 1.11 and R-factors (RP and RWP) were found to be below 3% confirming the perfect agreement between the obtained data and typical diffraction pattern. It should be emphasized that the observed broadening in the diffracted peaks is due to the prepared chromite samples being in the nanometric domain. With the increment of Gd dopants in cobalt chromite samples, a gradual enhancement in peak broadening was noticed.13–15 Three major factors are responsible for the XRD peak broadening in the nanosize domain, i.e. crystallite size effect, intrinsic microstrain in the nanocrystals and instrumental effects. In order to eliminate the instrumental broadening effects, a reference diffractogram of pure LaB6 powder having a large grain size was used under similar conditions.16 After subtracting instrumental line-width, the overall broadening β (FWHM of peak) is the combination of crystallite size (βsize) and intrinsic microstrain (βstrain) broadening effects as given below18| |
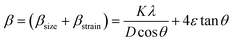 | (1) |
where K is the sphericity parameter (≈0.89 for spherical nanoparticles), λ denotes the wavelength of characteristic copper Kα X-ray radiation (≈1.5406 Å), ε is the intrinsic microstrain in the nanocrystals and θ stands for Bragg's angle. Reconfiguring the terms of eqn (1), we obtain the following equation9,13| |
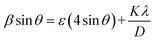 | (2) |
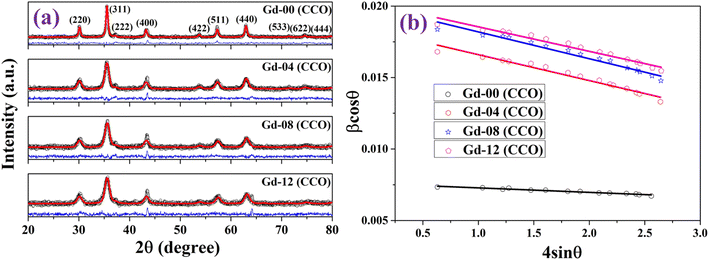 |
| | Fig. 1 (a) Powder X-ray diffraction patterns and (b) Williamson–Hall (W–H) plot of the prepared chromite samples. | |
A graph is plotted (β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ against 4
θ against 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) to separate the contributions of size and microstrain effects in the broadening which is termed as the Williamson–Hall (WH) plot. Fig. 1(b) depicts the WH plots of all of the Gd substituted chromite nanoparticles. The WH curve is a straight line and the slope of the straight line gives the microstrain (ε) in nanocrystals whereas the intercept on the β
θ) to separate the contributions of size and microstrain effects in the broadening which is termed as the Williamson–Hall (WH) plot. Fig. 1(b) depicts the WH plots of all of the Gd substituted chromite nanoparticles. The WH curve is a straight line and the slope of the straight line gives the microstrain (ε) in nanocrystals whereas the intercept on the β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ axis is Kλ/D used to obtain the mean size of nanoparticles.9
θ axis is Kλ/D used to obtain the mean size of nanoparticles.9
The mean crystallite sizes (D) obtained using the WH plot ranged from 6.8 nm to 18.2 nm respectively. The values of D were noticed to reduce for higher Gd content chromite samples. Incorporating comparatively large-sized Gd3+ (0.938 Å) ions in place of Cr3+ (0.615 Å) ions hindered the crystal growth during synthesis, leading to a decrement in mean sizes of doped chromite nanoparticles.13–16 All the obtained values of mean crystallite size (D), density (ρ), lattice parameter (a), microstrain (ε) and refinement parameters are shown in Table S1.† A compressive type of microstrain was noted in all the chromite nanoparticles and it also increased gradually with increasing Gd concentration compared to the undoped sample. The discrepancy in ionic radii between Gd3+ and Cr3+ ions may be responsible for the observed behavior. As noticed from Table S1,† a significant increment in lattice constant (a) was found with increasing Gd dopants in chromite samples. This is attributed to the incorporation of large-sized Gd ions in the host spinel structure. The density of the doped chromite samples also increased due to the heavy Gd ion doping.13,15,18
Generally, pure cobalt chromite exhibits a normal cubic spinel structure and also shows ferrimagnetic ordering below room temperature. In the pure CoCr2O4 material, all the tetrahedral voids are occupied by the Co2+ ions whereas all the octahedral voids are occupied by the Cr3+ ions respectively. K. Manjunatha et al. also theoretically and experimentally verified the normal spinel cubic structure of cobalt chromite.19 We can easily calculate the average ionic radius (rA and rB) of both tetrahedral (A) and octahedral (B) sublattices theoretically by using the mentioned relationships9,13,16
| | |
rA = [C(Co2+)r(Co2+)]
| (3) |
| |
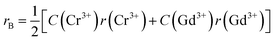 | (4) |
where
C represents the fractional concentration of metal ions occupying tetrahedral (A) and octahedral (B) voids. Both the
r(Cr
3+) and
r(Gd
3+) denote the ionic radius of Cr
3+ (0.615 Å) ions and Gd
3+ (0.938 Å) ions in B-sites whereas
r(Co
2+) is the ionic radius of Co
2+ (0.58 Å) ions in A-sites respectively. Substitution of large-sized Gd
3+ ions within the percolation limit leads to a systematic enhancement of
rB (see Table S2
†).
9,13 We have estimated the theoretical lattice constant (
ath) of the prepared chromite systems by using the stated equation
17| |
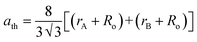 | (5) |
where
Ro (≈1.32 Å) denotes the radius of oxygen anions. The obtained values of theoretical lattice constant (
ath) were also noted to increase with incorporating more Gd ions in cobalt chromites. Table S2
† contains the obtained values of cationic radii, oxygen positional parameter and hopping length of all the synthesized chromite samples. Doping of large-sized cations may produce lattice distortion in the spinel cubic crystal structure. By studying the oxygen positional parameter (
u), we can gain insight into the extent of deformation within the spinel structure caused by doping. Essentially, ‘
u’ stands for the relative movement of O
2− ions in both tetrahedral and octahedral sublattices. Although the value of ‘
u’ is 0.375 for an ideal spinel cubic system if the origin is taken at a tetrahedral site the calculated values of ‘
u’ for spinel chromites are always slightly greater than 0.375.
9,20 This is due to the fact that the average size of tetrahedral voids is lower than that of octahedral voids, and during metal ion adoption in tetrahedral voids, a minor displacement of O
2− ions occurs, resulting in microstrain in the host lattice. All the values of ‘
u’ for the synthesized cobalt chromite systems are estimated
via the following relation
20| |
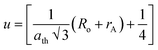 | (6) |
As observed from Table S2,† values of ‘u’ reduced with increasing Gd percentage as the lattice constant increased systematically. The doping of metal ions also alters the hopping length of the host system. Normally, the hopping length provides the basic information of the charge conduction process and magnetic interactions for a spinel cubic chromite system. Hopping lengths, i.e. 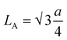 for tetrahedral (A) sublattices and
for tetrahedral (A) sublattices and 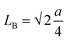 for octahedral (B) sublattices, were noticed to increase for higher Gd content chromite nanoparticles because of the enhancement of the lattice parameter (see Table S2†).16,20 The increasing hopping lengths also reflect the demand for more energy to beat the electrostatic repulsion for a successful hopping of electrons. It is well known that the cationic distribution of tetrahedral voids is reflected by the intensity of diffracted X-rays from the (422) and (220) crystallographic planes in the diffractograms. Similarly, the intensity of diffracted X-rays from the (222) plane also reveals information regarding the cationic distribution of octahedral voids. The ratio of intensities, i.e. I220/I222 and I422/I222, was noted to reduce with increasing Gd dopants in the host chromite system confirming that all the Gd ions have occupied octahedral sites (see Table S3†).13 The superexchange interactions (A–O–B) between tetrahedral (A) and octahedral (B) sublattices, which are responsible for ferrimagnetic ordering in chromites, are substantially influenced by both the bond lengths and angles. A schematic representation of A–O–B superexchange interactions for spinel cubic chromites is shown in Fig. S1.† To understand the strength of the A–O–B interactions, bond angles between magnetic ions are measured using the given relations20
for octahedral (B) sublattices, were noticed to increase for higher Gd content chromite nanoparticles because of the enhancement of the lattice parameter (see Table S2†).16,20 The increasing hopping lengths also reflect the demand for more energy to beat the electrostatic repulsion for a successful hopping of electrons. It is well known that the cationic distribution of tetrahedral voids is reflected by the intensity of diffracted X-rays from the (422) and (220) crystallographic planes in the diffractograms. Similarly, the intensity of diffracted X-rays from the (222) plane also reveals information regarding the cationic distribution of octahedral voids. The ratio of intensities, i.e. I220/I222 and I422/I222, was noted to reduce with increasing Gd dopants in the host chromite system confirming that all the Gd ions have occupied octahedral sites (see Table S3†).13 The superexchange interactions (A–O–B) between tetrahedral (A) and octahedral (B) sublattices, which are responsible for ferrimagnetic ordering in chromites, are substantially influenced by both the bond lengths and angles. A schematic representation of A–O–B superexchange interactions for spinel cubic chromites is shown in Fig. S1.† To understand the strength of the A–O–B interactions, bond angles between magnetic ions are measured using the given relations20
| | |
θ1 = cos−1[(p2 + q2 − c2)/2pq]
| (7) |
| | |
θ2 = cos−1[(p2 + r2 − e2)/2pr]
| (8) |
The insertion of Gd3+ ions in the host chromite systems strengthens the superexchange interactions and favours the ferrimagnetic ordering, as evidenced by an increase in the values of bond angle (see Table S3†).
3.2. Studies on HRTEM micrographs
HRTEM images of the prepared chromite nanoparticles were captured to examine the size, shape and crystallographic structure. Fig. 2(a–d) show the HRTEM micrographs of all the pristine and doped chromite nanoparticles with increasing Gd content respectively. Minimal agglomeration among the chromite nanoparticles was noticed in the micrographs, which might be attributed to the magnetic dipole–dipole interactions and van der Waals attractions.9,16–20 The presence of almost spherical shape nanoparticles with good size and shape regularity was observed in all the micrographs. Using ImageJ software, histograms were drawn and average particle sizes were obtained for all Gd-doped chromite nanoparticles, which are found to be 19.1 ± 0.1 nm [Gd-00(CCO)], 9.1 ± 0.1 nm [Gd-04(CCO)], 8.9 ± 0.1 nm [Gd-08(CCO)] and 7.3 ± 0.1 nm [Gd-12(CCO)] respectively. The obtained sizes followed the identical trend of mean crystallite size as estimated from WH curves. Additionally, the (311) crystal planes of the Gd-04(CCO) sample were identified and d-spacing was measured [see Fig. 2(e)], which was found to be 2.51 Å.21 The Selected Area Electron Diffraction (SAED) pattern of Gd-04(CCO) chromite nanoparticles is depicted in Fig. 2(f). The formation of clearly visible concentric rings in the SAED pattern confirmed the highly nanocrystalline nature of the chromite sample. The observed circular rings formed by electron diffractions in the SAED pattern were spotted with their respective Miller indices. A detailed examination of the SAED pattern disclosed that the first two rings are sufficiently closed; however, the third ring is far from those two rings, implying the presence of an fcc-like crystallographic structure in the synthesized chromite nanomaterial.20 Similar types of morphology and spotty SAED ring patterns were also reported in doped cobalt chromites.22,23
 |
| | Fig. 2 (a–d) HRTEM micrographs of Gd-00 (CCO), Gd-04 (CCO), Gd-08 (CCO) and Gd-12 (CCO) samples. (e) Interplanar spacing of (311) planes for the Gd-04 (CCO) sample and (f) SAED pattern of the Gd-04 (CCO) sample. | |
3.3. Analysis of Raman spectra
The vibrational Raman spectrum is widely utilized to analyze the microstructure of nanoparticles. It is established that the change in polarizability must be non-zero for a material to have Raman active modes. Raman spectra of all the chromite samples recorded at room temperature and fitted with the Lorentzian function are illustrated in Fig. 3. In cobalt chromite, all Co2+ ions occupy tetrahedral voids whereas both the Cr3+ and Gd3+ ions occupy octahedral sites forming the normal cubic spinel structure.9,13 All the synthesized cobalt chromite samples correspond to the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group and contain two different types of interpenetrating sublattices. A complete unit cell of spinel cubic chromite contains 56 atoms and 14 atoms in the smallest Bravais cell. As per group theory, there are five Raman active modes (A1g + Eg + 3T2g) present in the ideal cubic spinel system9,18 and all the tetrahedral (A) sites and octahedral (B) sites correspond to Td and D3d point groups respectively. All the obtained Raman active modes of the prepared chromite systems are listed in Table 1. All the nanosized Gd3+ ion doped cobalt chromite samples exhibited five characteristic Raman active modes [A1g(1), A1g(2), T2g(1), T2g(2), and T2g(3)]. The two observed A1g modes belong to the symmetric stretching of oxygen atoms along the M3+–O2− (M = Cr and Gd) bond in the tetrahedral sites. The Raman active T2g(3) mode reflects the asymmetric bending of the O atom with respect to Cr, the T2g(2) mode is assigned to the asymmetric stretching vibration of the M3+–O2− (M = Cr and Gd) bond and the T2g(1) mode arise due to the translational motion of the entire CrO4 tetrahedron. All Raman active modes with wave numbers more than 600 cm−1 are assigned to tetrahedral sublattices, whereas those below 600 cm−1 are assigned to octahedral sublattices. Substitution of comparatively large size Gd3+ ions along with cation vacancies may minutely distort the spinel cubic crystal structure and lead to a lowering of crystal symmetry.13,18 The observed minute shift in Raman active modes towards low wave number (red shift) is attributed to the modified reduced mass. The doping of comparatively heavier Gd (157.25 g) ions in place of Cr (51.99 g) ions changed the reduced mass of the M–O (M = Cr, Gd) bond. The shift of Raman active modes due to doping can be understood by using the stated formula9,13
m space group and contain two different types of interpenetrating sublattices. A complete unit cell of spinel cubic chromite contains 56 atoms and 14 atoms in the smallest Bravais cell. As per group theory, there are five Raman active modes (A1g + Eg + 3T2g) present in the ideal cubic spinel system9,18 and all the tetrahedral (A) sites and octahedral (B) sites correspond to Td and D3d point groups respectively. All the obtained Raman active modes of the prepared chromite systems are listed in Table 1. All the nanosized Gd3+ ion doped cobalt chromite samples exhibited five characteristic Raman active modes [A1g(1), A1g(2), T2g(1), T2g(2), and T2g(3)]. The two observed A1g modes belong to the symmetric stretching of oxygen atoms along the M3+–O2− (M = Cr and Gd) bond in the tetrahedral sites. The Raman active T2g(3) mode reflects the asymmetric bending of the O atom with respect to Cr, the T2g(2) mode is assigned to the asymmetric stretching vibration of the M3+–O2− (M = Cr and Gd) bond and the T2g(1) mode arise due to the translational motion of the entire CrO4 tetrahedron. All Raman active modes with wave numbers more than 600 cm−1 are assigned to tetrahedral sublattices, whereas those below 600 cm−1 are assigned to octahedral sublattices. Substitution of comparatively large size Gd3+ ions along with cation vacancies may minutely distort the spinel cubic crystal structure and lead to a lowering of crystal symmetry.13,18 The observed minute shift in Raman active modes towards low wave number (red shift) is attributed to the modified reduced mass. The doping of comparatively heavier Gd (157.25 g) ions in place of Cr (51.99 g) ions changed the reduced mass of the M–O (M = Cr, Gd) bond. The shift of Raman active modes due to doping can be understood by using the stated formula9,13| |
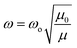 | (9) |
where both the symbols μ0 and μ represent the reduced mass of Cr–O and Gd–O bonds whereas both ωo and ω are the corresponding phonon wave numbers. It is widely known that the A1g and T2g Raman active modes have a significant influence on the microstructural, elastic, thermodynamic, and electrical properties of the spinel cubic system; thus, a small shift in these modes can modify all the physical properties.13,18
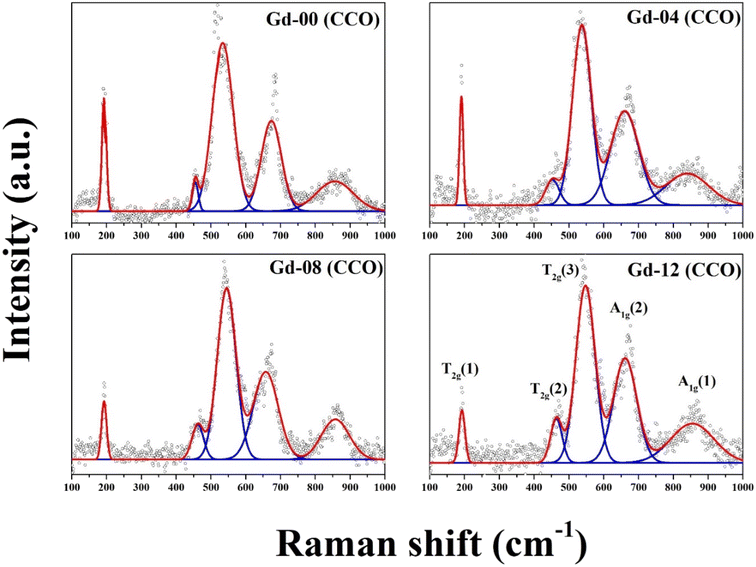 |
| | Fig. 3 Room temperature Raman spectra of the prepared chromite samples. | |
Table 1 Raman active modes at 300 K for all the chromite samples
| Sample-id |
Raman shift (cm−1) |
| A1g(1) |
A1g(2) |
T2g(3) |
T2g(2) |
T2g(1) |
| Gd-00 (CCO) |
856.7 |
675.1 |
534.3 |
455.1 |
192.7 |
| Gd-04 (CCO) |
841.3 |
660.7 |
535.1 |
454.3 |
189.6 |
| Gd-08 (CCO) |
857.8 |
657.4 |
545.3 |
461.6 |
191.2 |
| Gd-12 (CCO) |
854.8 |
659.7 |
547.4 |
464.7 |
191.9 |
Analyzing the vibrational Raman active modes of a specific nanomaterial allows one to investigate its elastic properties such as force constant (k), bulk modulus (B), rigidity modulus (G), Young's modulus (E), Poisson's ratio (σ), Debye temperature (θD), and so on. We have obtained elastic parameters of all the synthesized chromite samples using the Waldron method with the help of two vibrational Raman active modes [A1g(1) and T2g(2)] assigned to tetrahedral and octahedral sublattices.18,24 All the estimated values of elastic parameters are listed in Tables S4 and S5, which can be found in the ESI section.†
As per the Waldron approach, the force constants (kt and ko) of both the tetrahedral (A) and octahedral (B) sublattices depend on the vibrational frequency and molecular weight of the cations which can be derived from the following relations24–26
| | |
kt = 7.62 × MA × ν12 × 10−7 N m−1
| (10) |
| | |
ko = 5.31 × MB x ν22 × 10−7 N m−1
| (11) |
where both
MA and
MB represent the molecular weight of cations occupied in the tetrahedral and octahedral sites respectively. In the Gd doped spinel CoCr
2O
4 system, all Co
2+ ions occupy tetrahedral sites whereas both the Gd
3+ and Cr
3+ ions prefer to occupy octahedral voids; thus, the values of
MA and
MB have been calculated by obeying this proposed cationic distribution. The obtained force constant values for tetrahedral sites are larger than those for octahedral sites due to the inverse relation between force constant and bond length. The incorporation of heavier Gd
3+ dopants in the octahedral sublattices of the host matrix strengthens the metal bonds, as evidenced by an increase in force constant
KO with the increase of Gd
3+ ion concentration. The capacity of a material to resist the deformation under an applied force is known as rigidity which can be quantified by the stiffness constant.
13,18 The stiffness constant (
C11) for the spinel chromite system can be represented in terms of the effective force constant (
k) and the lattice parameter (
a), as stated below
24–26| |
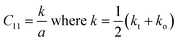 | (12) |
The estimated values of C11 were noticed to increase with the increase of heavier Gd3+ ion content in the host chromite structure. To determine the velocity (Vl and Vs) of longitudinal and shear waves in spinel cubic chromites, both the stiffness constant (C11) and the density (ρ) were used, as given below13,18
| |
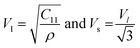 | (13) |
All the calculated values of wave velocities are collected in Table S4 (in the ESI†). The substitution of heavier Gd ions in cobalt chromites increased density, which reduced wave velocities compared to the pristine sample. One can also calculate the mean elastic wave velocity (Vm) in terms of longitudinal wave velocity (Vl) and transverse wave velocity (Vs) as follows24–26
| |
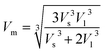 | (14) |
While discussing the elastic properties of a material, the modulus determines the capacity to support loads and maintain the shape. The rigidity modulus (G) of all the chromite samples was calculated based on the shear wave velocity (Vs) and bulk density (ρ) by using the following expression13
One can also obtain the bulk modulus (B) of a solid with the help of stiffness constants (C11 and C12) using the stated relation13,18
| |
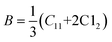 | (16) |
Spinel cubic chromite is an isotropic material with cubic symmetry, and hence the stiffness constant value C11 ≈ C12 can be used as per the Waldron technique. As a result, the bulk modulus (B) for spinel cubic chromite becomes equal to the stiffness constant (C11). As observed in Table S5 (in the ESI†), the calculated values of both B and G followed an overall increasing trend with the enhancement of rare-earth Gd3+ ion concentration in chromite nanoparticles. Poisson's ratio (σ) for an isotropic elastic material with positive values of both bulk modulus (B) and rigidity modulus (G) must be less than 0.5 and can be determined using the given equation24–26
| |
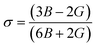 | (17) |
The values of σ were calculated for all the samples and found to be constant (0.35), supporting the isotropic elasticity theory. The obtained values of σ and G were used to determine the Young's modulus (E) of all prepared samples by using the stated relationship13,18,24
Calculated values of Young's modulus (E) for all the samples are presented in Table S5 (in the ESI†) and are also noticed to increase for higher Gd3+ ion-rich samples due to the increase of the average force constant (k) of the system. The incorporation of Gd3+ ions in the nanocrystalline chromite system provided strength to the interatomic bonds between atoms, leading to a gradual rise in the elastic modulus of the system. The Debye temperature provides information regarding lattice vibration and also correlates the elastic properties of a solid with its thermodynamic properties. The Debye temperature (θD) of all the chromite systems was determined using the stated formula13,18
| |
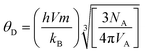 | (19) |
where
VA is the average atomic volume (
M/
qρx);
M indicates the molecular weight of the system,
q represents the number of atoms per formula unit (which is equal to 7), and other symbols have their usual meaning.
A systematic increment in the values of θD was noted in Gd3+ ion-rich nanocrystalline spinel chromites, suggesting that lattice vibrations are hindered (amplitude reduced) due to the increase of heavier Gd3+ ions. It is known that the lattice vibration with maximum amplitude occurs at Debye temperature (θD) and the heat capacity of a solid remains constant above θD whereas heat capacity varies with the cube of temperature (T3) below θD. The mean square lattice displacement (w) of a solid varies inversely with both the rigidity modulus (G) and lattice constant (a) as follows13
| |
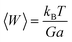 | (20) |
The increase in rigidity modulus (G) as well as lattice constant (a) for higher Gd3+ ion-rich chromite samples also resulted in hindered lattice vibrations.
3.4. Studies on Tauc plots
The UV-visible spectrum is commonly used to analyze the optical characteristics as well as optical bandgap of a nanomaterial having a semiconducting nature. The absorption spectrum at room temperature was collected for all pure and doped chromite samples ranging from 100 nm to 800 nm respectively. As per the literature, pure CoCr2O4 in bulk form is a magnetic semiconductor with an indirect optical band gap around 2.1 eV at room temperature.9 The optical band gap of cubic spinel chromites has been derived using the following relation, as shown below20| | |
α(ν)·hν ≈ C(hν − Eo)n
| (21) |
where C is a constant, Eo signifies the optical band gap of the synthesized chromite samples, α denotes the absorption coefficient and n is an arbitrary index. For specific optical transitions, the index is permitted to attain fixed values of 0.5, 1.5, 2, 3, etc. For a semiconducting material, when direct allowed and direct forbidden optical transitions take place, the index n attains constant values i.e. 0.5 and 1.5 respectively. In the case of indirect allowed and indirect forbidden optical transitions, ‘n’ has values 2 and 3. For determining the absorption coefficient (α) of all the chromite systems, the two following fundamental relationships and absorbance (A) data were used as stated below9,16| |
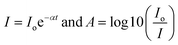 | (22) |
Hence, 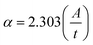 , where t stands for the width of the cuvette. Determination of the indirect optical band gap (Eo) of the as-synthesized chromites was performed by plotting a graph between (αhν)1/2 and photon energy (hν), which is termed a Tauc plot. Tauc plots of all the samples are depicted in Fig. S2.† The estimated values of indirect band gap (Eo) were observed to be 2.03 ± 0.01 eV [Gd-00(CCO)], 2.14 ± 0.01 eV [Gd-04(CCO)], 2.17 ± 0.01 eV [Gd-08(CCO)] and 2.21 ± 0.01 eV [Gd-12(CCO)] respectively. Higher Gd content chromite samples exhibited a blue shift in their EM wave absorption spectrum. The observed systematic enhancement (blue shift) in the indirect optical band gap is attributed to the reduction of mean diameters with increasing Gd percentage in CoCr2O4 nanoparticles, which decreases the overlapping of atomic orbitals.15,20 A careful examination of the absorption spectra of the prepared chromite nanoparticles demonstrates that all samples have an opaque nature in the yellow and red bands of the electromagnetic (EM) spectrum. All the Gd doped chromite nanoparticles have notable absorption properties in the yellow and red domains of the EM spectrum, making them suitable for several optical applications.20
, where t stands for the width of the cuvette. Determination of the indirect optical band gap (Eo) of the as-synthesized chromites was performed by plotting a graph between (αhν)1/2 and photon energy (hν), which is termed a Tauc plot. Tauc plots of all the samples are depicted in Fig. S2.† The estimated values of indirect band gap (Eo) were observed to be 2.03 ± 0.01 eV [Gd-00(CCO)], 2.14 ± 0.01 eV [Gd-04(CCO)], 2.17 ± 0.01 eV [Gd-08(CCO)] and 2.21 ± 0.01 eV [Gd-12(CCO)] respectively. Higher Gd content chromite samples exhibited a blue shift in their EM wave absorption spectrum. The observed systematic enhancement (blue shift) in the indirect optical band gap is attributed to the reduction of mean diameters with increasing Gd percentage in CoCr2O4 nanoparticles, which decreases the overlapping of atomic orbitals.15,20 A careful examination of the absorption spectra of the prepared chromite nanoparticles demonstrates that all samples have an opaque nature in the yellow and red bands of the electromagnetic (EM) spectrum. All the Gd doped chromite nanoparticles have notable absorption properties in the yellow and red domains of the EM spectrum, making them suitable for several optical applications.20
3.5. BET studies
In the BET technique, the absorption of N2 gas molecules in the solid surface forms the basis for analyzing the surface properties including morphology, nature of pores, size of pores and specific surface area. A thorough understanding of these surface properties is required for nanomaterials to investigate their potential uses. This is because the surface of nanomaterials plays an important role in determining their physical properties. In this regard, the physical adsorption–desorption process of N2 gas was performed for each nanocrystalline chromite sample. By modifying the surface of nanomaterials, the modulation of surface-related phenomena can be done.27 To obtain the adsorption–desorption isotherms, all the nanosized chromite samples were kept at 250 °C with an N2 gas flow for 18 hours. Analysis of various surface parameters, including the surface area and porous nature of all the chromite samples, was done by using N2 adsorption–desorption isotherms, as depicted in Fig. S3(a–d).† All the isotherms manifest that the adsorption curve gradually increased in the low-pressure region, followed by a sharp rise when P/PO reached 0.80. All recorded isotherms are consistent with a standard type IV adsorption isotherm, suggesting the presence of a mesoporous structure.27–29 It should be noted that the specific surface area was found to increase with increasing Gd percentage in CoCr2O4 nanoparticles [see Fig. S3(e)†]. We have obtained the specific surface areas of 47.3 m2 g−1 [Gd-00(CCO)], 50.8 m2 g−1 [Gd-04(CCO)], 58.5 m2 g−1 [Gd-08(CCO)] and 69.7 m2 g−1 [Gd-12(CCO)] with the corresponding pore radius in the domain of 8.5 ± 0.3 nm respectively. These obtained results are also consistent with the XRD data as the specific surface area of nanoparticles increases with increasing Gd dopants.27
3.6. Analysis of FTIR spectra
The FTIR spectrum is used mainly for the analysis of the chemical bonds and functional groups of a compound. This specific characterization technique uses infrared light to scan the sample and provides information on chemical properties precisely. Fig. S4 (in the ESI†) illustrates the FTIR spectra of all the nanosized doped chromites, collected at room temperature. According to several studies, the spinel cubic structured materials exhibit two different vibrational bands of metal–oxygen (M–O) bonds between 400 cm−1 and 600 cm−1. The existence of these two vibrational bands further confirms the creation of the spinel cubic crystallographic phase in the material.5,27 For our synthesized chromite samples, the first distinctive absorption peak was obtained around 580 cm−1, indicating the stretching of metal–oxygen (Co–O) bonds at tetrahedral (A) coordinated sites. Another second observed absorption peak near 400 cm−1 for all the samples resulted from stretching M–O (M = Cr, Gd) bonds at octahedral (B) coordinated sites. The physical properties of nanocrystalline doped CoCr2O4 are mostly determined by the cation distribution at tetrahedral and octahedral coordinated sites. A minute shift towards a lower wave number of characteristic peaks was noticed with increasing Gd concentration in chromite nanoparticles. This type of pattern was also observed in vibrational Raman spectra. The observed small vibrational band near 900 cm−1 is attributed to the Co–O bond. An absorption peak was observed near 3500 cm−1 prominently for the pure cobalt chromite sample due to the O–H bond vibrations.5,27,30 The observed weak absorption band near 1630 cm−1 in the samples is due to the C–O vibration of carboxyl groups. The vibrational bands in the FTIR spectra of the doped spinel chromite system can be impacted by several factors including the reduced mass of the system, spring constant and bond length of the metal–oxygen bonds.5
3.7. Analysis of electrical conductivity
Normally, an ideal dielectric material is a poor conductor of electricity and highly resistive but, in reality, especially for lossy dielectrics, charge conduction is still possible through the movement of ions, trapped charges, dopant ions and hopping of electrons under an application of electric field. By measuring the electrical conductivity, the charge conduction process of a lossy dielectric material can be properly described. The electron conduction mechanism under an applied electric field for chromite nanoparticles with an indirect band gap (≈2 eV) is highly complex, as opposed to a perfect conductor.5,30–33 Typically, when nanocrystalline spinel chromites are exposed to an alternating electric field, the hopping of electrons via lattice sites occurs which results in charge conduction. Electrons obtain enough energy from the applied electric field to break the electrostatic barrier of lattice sites, allowing for the hopping process. The electrical conductivity of nanosized doped chromites often increases initially with the increasing frequency of the applied field but then drops further because the hopping frequency fails to follow the field frequency. An identical behaviour of conductivity in Gd doped chromite nanoparticles was also seen. The overall electrical conductivity (σt) of spinel chromite nanomaterials consists of both dc and ac conductivity components, as described below5| | |
σt(T, ω) = σdc (T) + σac (T, ω)
| (23) |
where σdc represents the frequency independent part of electrical conductivity which is a function of temperature only. The band conduction of charge carriers, mainly electrons, is primarily responsible for the dc conductivity in chromite nanomaterials. The ac component of conductivity, denoted as σac in eqn (23), varies with both frequency and temperature, respectively. A power law is frequently followed by the ac part of the conductivity. In the case of spinel chromites, the power law is generally followed by the ac component of the conductivity as given31–34where C(T) gains a fixed value if both the temperature and composition of the dielectric medium remain constant, and n is a unitless exponent with values ranging from 0 to 1. As the exponent approaches zero, the charge conduction in response to an alternating field becomes fully frequency independent.31 The electrical conductivity data of doped spinel chromite systems under varied field frequencies were collected at room temperature. A logarithmic plot of ac conductivity against frequency is depicted in Fig. 4(a). The log–log plot of conductivity vs. frequency formed a linear line and by performing a linear fitting, the slope of the curve was obtained, which supplied the exponent value. All the synthesized doped chromite nanoparticles have exponent values ranging from 0.60 to 0.84 [see Fig. S5†], which is between 0 and 1, demonstrating that electron hopping at 300 K is a possible charge conduction pathway.5,31–35
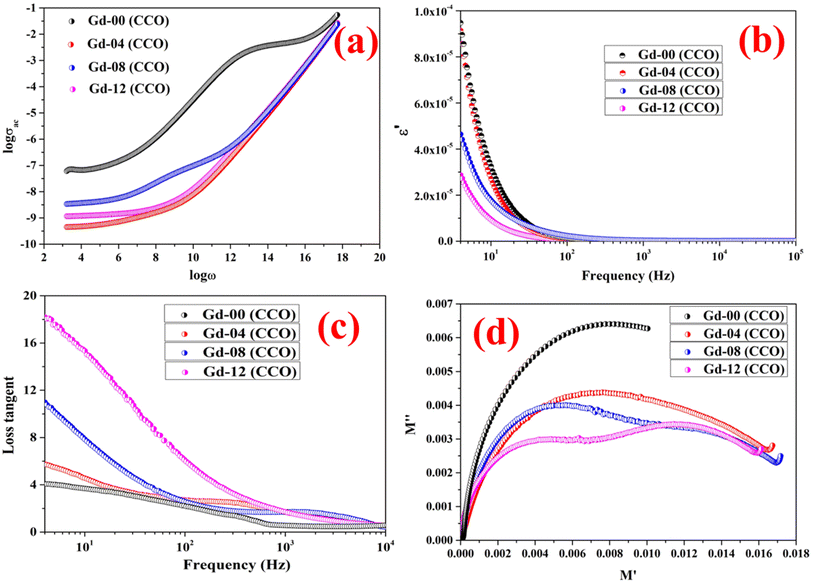 |
| | Fig. 4 (a) Logarithmic graph of ac conductivity vs. frequency, (b) semilogarithmic plot of the real part of dielectric constant vs. frequency, (c) loss-tangent graph, and (d) Cole–Cole plots of all the chromite samples. | |
3.8. Studies on dielectric response
Both the charge holding and polarization capacity of a dielectric material can be determined by analyzing the real component of the dielectric constant against applied field frequency. The polarization formed in a dielectric substance under an applied field is directly related to its ability to store electrical energy and determines the merit of storage applications.5,31 By varying the applied field frequencies, the dielectric behavior of each chromite sample was captured at 300 K. Fig. 4(b) displays the semi-log plot of the real component (ε′) of the dielectric constant against field frequencies determined at 300 K for all doped chromite systems. As described in Koop's theory, a perfect dielectric material is made of resistive grain boundaries and conductive grains. Due to the resistive behavior of grain boundaries when compared with grains, electrons accumulate near the grain boundaries, resulting in the formation of polarization.31 As found in Fig. 4(b), the pure CoCr2O4 nanoparticles have a higher value of ε′ than other doped chromite samples below 80 Hz, indicating negligible polarization loss. At low frequencies, the insertion of Gd ions in nanosized chromites resulted in a steady decrement of ε′, indicating that the doped chromites gradually lose their charge storage capabilities and become a lossy dielectric material. The comparatively high ε′ value of pure CoCr2O4 nanoparticles indicated a minimal polarization loss and effectiveness as an insulating material. All of the doped chromite systems were unable to maintain the polarization charges when the applied field frequency increased because they did not respond to frequency changes.31–35
Polarization loss in a dielectric material can be understood precisely by examining the loss tangent, representing a ratio of the imaginary to real part of the dielectric constant. Several factors including defects, vacancies, impurities, dopant ions and imperfections in lattices contribute effectively to deciding the dielectric loss of a dielectric material. Fig. 4(c) depicts a semi-log plot of loss tangent against alternating field frequencies, obtained at 300 K for all the chromite samples. The resulting polarization loss at room temperature was noted to be significant in all samples below 10 Hz. The electrons jump between lattice sites during charge conduction in all chromites when subjected to an external varying field frequency; therefore, maximum polarization loss occurs when the electron hopping frequency matches the field frequency.5,31,36 With increasing Gd content in nanocrystalline chromites, polarization loss becomes more prominent. An identical pattern of loss tangent was noted for all the pristine and doped chromite samples under an alternating applied field. Beyond 100 Hz frequency, all the synthesized chromites failed to respond to the frequency change, resulting in a considerable fall in loss tangent values. Maximum energy was transferred when both the electron hopping and applied field frequencies became equal. With Gd ion substitution, these chromite nanomaterials acted as a lossy dielectric.32
3.9. Studies on Cole–Cole plots
A dielectric material is considered to be made of grains and grain boundaries. Basically, grains are separated by the grain boundaries, which are seen as defects in a lattice plane. When a dielectric material experiences an alternating electric field, both the grains and grain boundaries actively participate in deciding the overall dielectric behavior of that dielectric material. Following Koop's theory, grains are considered to be conductive whereas grain boundaries are resistive in nature. The separation of active contributions of grains and grain boundaries from the overall dielectric response can be done by drawing a Cole–Cole plot.31,32 The Cole–Cole graph between dielectric modulus for all the chromite samples was formulated by using the values of real and imaginary parts of the dielectric constant as follows36| |
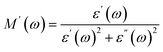 | (25) |
| |
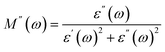 | (26) |
The Cole–Cole plot drawn between the real (M′) and imaginary (M′′) parts of the dielectric modulus for all the chromites was found to be semicircular in shape. Fig. 4(d) demonstrates the Cole–Cole graph (M′′ vs. M′) of synthesized Gd doped CoCr2O4 nanoparticles. A detailed investigation of the Cole–Cole plot (M′′ vs. M′) revealed that each chromite sample contained one semicircular shaped curve, implying that the non-conductive grain boundaries were dominated effectively in determining the dielectric response of all the nanosized doped chromites compared to the conductive grains. With the doping of Gd ions in the nanocrystalline cobalt chromite structure, the radius of the semicircle decreased gradually, indicating an increase in dc conductivity in the doped chromite samples.5,32,36
For analyzing the change in total dc resistance originating from grain and grain boundary contributions with the increase in doping percentage, the Cole–Cole plot (Z′′ vs. Z′) of 4% and 12% Gd doped chromite samples was fitted using ZSIMP WIN (version 3.20) software and equivalent circuits were obtained.37 The fitted Cole–Cole graphs drawn in between Z′′ and Z′ for Gd-04 (CCO) and Gd-12 (CCO) samples together with equivalent circuits are shown in Fig. S6(a–c).† The equivalent circuit used to fit the Cole–Cole plot of doped samples contains mainly three components, i.e., a resistor, inductor, and a constant phase element (CPE). The obtained values of overall dc resistance were found to be 0.57 MΩ and 1.42 MΩ for Gd-04 (CCO) and Gd-12 (CCO) samples, respectively. Hence, an increment in the doping concentration increases the total resistance and modifies the dielectric response of pure CoCr2O4 nanoparticles.37
3.10. Studies on magnetic properties
The magnetic properties of the as-synthesized CoCr2O4 nanoparticles doped with different Gd percentages were investigated by recording both the magnetic hysteresis loops and temperature dependent magnetization curves. M(H) curves were registered at two distinct temperatures (5 K and 150 K) for all the synthesized samples and are illustrated in Fig. 5(a and b), respectively. A careful examination of hysteresis loops revealed that all the chromite samples showed ferrimagnetic behavior with significant coercive field (HC) and saturation magnetization (MS) at low temperatures (say 5 K) and they also behaved as paramagnetic nanomaterials at 150 K with insignificant coercivity.9 All the magnetic parameters evaluated from hysteresis curves are collected in Table S6 (in the ESI†). The applied ±70 kOe magnetic field failed to saturate the magnetization curves of all the chromite samples obtained at 150 K. An attentive observation of the hysteresis loops registered at 150 K revealed a minimal increase in maximum magnetization (M7T) with increasing Gd dopants in chromite nanoparticles.9 Rare-earth Gd3+ (7.9 μB) ions have a higher magnetic moment than Cr3+ (3.8 μB) ions, and hence replacing Cr ions with Gd ions results in an increase in magnetization.13,16 The comparatively large hysteresis loop area observed for pure cobalt chromite nanoparticles was evidence for the hard ferromagnetic nature at 5 K. Spinel cubic cobalt chromite contains two types of sublattices, i.e. tetrahedral (A) and octahedral (B) coordinated sites. The observed ferrimagnetism in normal spinel chromites is due to the magnetic superexchange interactions (A–O–B) involving oxygen atoms.5,20 As the magnetic moments appear from two distinct sublattices that are antiparallel, the overall magnetic moment (μT) of the spinel chromite system is the algebraic subtraction of individual magnetic moments (μB and μA) of octahedral (B) and tetrahedral (A) coordinated sites, i.e., μs = (μB − μA). All the hysteresis curves obtained at 5 K exhibited significant coercivity and were also observed to decrease with the increase of Gd percentage in chromite samples [see Table S6 (in the ESI†)].9,18 It is an established fact that the coercivity (HC) of magnetic nanoparticles varies with their mean particle diameter (D) which can be expressed as38| |
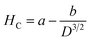 | (27) |
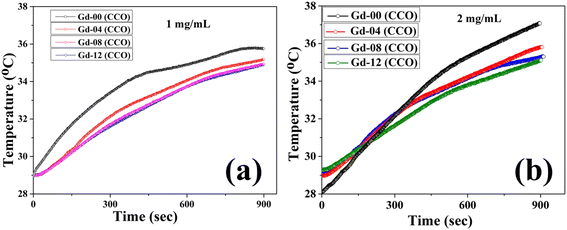
where both a and b are arbitrary constants. Incorporation of large-sized Gd3+ ions in the cobalt chromite system leads to the decrement of mean particle size, and thereby the coercive field of the system decreases at 5 K. As observed from Table S6 (in the ESI†), a notable increment in saturation magnetization (MS) was found at 5 K. Both the increase in magnetic moment due to the doping of Gd3+ ions and the decrement in coercivity are mainly responsible for this increment of MS at 5 K. The decrement in mean diameter for higher Gd dopant content chromites may introduce various surface effects such as spin pinning, randomness in spins and spin canting,13–15 all of which have a substantial impact on the magnetic anisotropy of the chromite samples. The effective anisotropy constant (Keff) of all the prepared chromites was determined at low temperature (5 K) by using the stated relation14,15| |
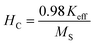 | (28) |
 |
| | Fig. 5 Hysteresis loops of chromite samples recorded at (a) 5 K and (b) 150 K. | |
Estimated values of Keff at 5 K for all the samples are shown in Table S6 (in the ESI†) and were also observed to alter with the increment of Gd3+ ion concentration.
The temperature dependent magnetization (M–T) curves were acquired in zero field-cooled (ZFC) and field-cooled (FC) methods in the presence of 200 Oe dc magnetic field for all the chromite samples and are shown in Fig. S7.† All the M(T) data were collected during the warming cycle, which ranged from 10 K to 120 K. It is clearly seen from the M(T) graphs that the magnetization drops to near zero around 95 K for all chromite samples, which basically indicates the Curie temperature (TC) of the magnetic systems. The long-range magnetic ordering from the paramagnetic state takes place at TC in chromites.9 The Curie temperature (TC) for each Gd-doped chromite sample was measured by drawing a linear line along the magnetization to the temperature axis. The estimated values of TC were observed to be 94.8 K [Gd-00 (CCO)], 95.2 K [Gd-04 (CCO)], 95.7 K [Gd-08 (CCO)] and 96.3 K [Gd-12 (CCO)] respectively as per the increase in Gd ions in pure CoCr2O4 nanoparticles; this is slightly lower than the TC of bulk CoCr2O4 (≈97 K). Substitution of Gd3+ ions, which have a greater magnetic moment than Cr3+ ions, altered the TC of the pure chromite system; hence, increasing Gd ions in the host matrix resulted in a modest rise in TC.39,40 While lowering the temperature from 120 K, both the ZFC and FC curves in the M(T) plot showed a fast increase before reaching a maximum temperature (Tmax).5 There is a precise temperature where both the ZFC and FC curves begin to diverge, which is termed as irreversible temperature (Tirr), and it was found to be between 92 and 94 K for chromite samples. Normally, the spin-spiral transition (TS) for CoCr2O4 nanoparticles is identified around 24 K; however, in our samples, with the doping of Gd ions, TS became noticeable near 26 K. Typically, the nature of the dopant, dopant concentration, size of nanoparticles, and preparation processes all have a significant impact on TS.9
3.11. Analysis of hyperthermia properties
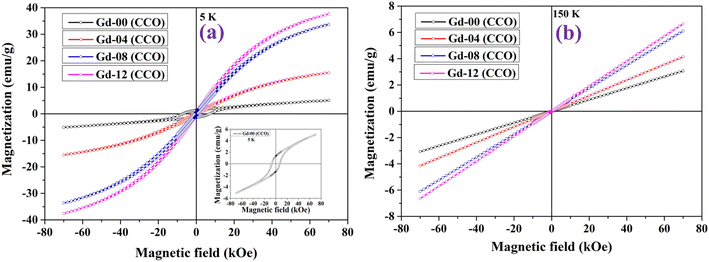
Hyperthermia is a heat generation procedure commonly employed in cancer cell treatment that involves elevating cell temperatures up to 43 °C for a specific period of time in order to burst cancer cells and diminish tumour growth. Magnetic nanoparticles dissipate energy in heat form when they are exposed to an alternating magnetic field. This heat generated in a controlled manner can be used in treating cancer cells. In this direction, both soft magnetic nanomaterials and superparamagnetic nanoparticles have been mainly used in recent times to explore their induction heating efficiency.2–5 We have also explored the hyperthermia efficacy of all CoGdxCr2−xO4 samples prepared in this work. Under subjection to an alternating magnetic field, chromite nanoparticles released thermal energy. The three key components, i.e. eddy current loss, relaxation loss, and hysteresis loss, all play a substantial role in heat generation. Because of the minuscule coercive field, the soft magnetic nanomaterials and superparamagnetic nanoparticles can reduce hysteresis and eddy current losses in the heat-generating mechanism. In this case, only the relaxation losses, specifically Néel relaxation and Brownian relaxation losses, dominate the heat generating process in the presence of an oscillating magnetic field. Magnetic nanoparticles in solid form do not experience Brownian relaxation as per magnetic relaxation dynamics.2,5,41 Furthermore, Néel relaxation is dominant for magnetic nanoparticles with an average size of less than 20 nm. The amplitude (H) and frequency (f) of the applied alternating magnetic field must be limited to a certain value when treating cancer cells in the human body. The acceptable range, i.e. Hf ≤ 4.5 × 108 A m−1 s, is referred to as the Hertz limit and must be followed while selecting values of ‘H’ and ‘f’ for the applied field.2,5 As per the experimental evidence, the product of Hf ≈ 4.85 × 108 A m−1.sec, generated from a coil of 30 cm loop diameter, can be used for magnetic hyperthermia therapy without significant discomfort for the human body, while using a coil having a much smaller loop diameter than 30 cm, the product of Hf may not exceed 5 × 109 A m−1 s.4 Related to testing the self-heating efficacy of the as-prepared nanoparticles, we used a coil with a loop diameter of 6 cm, total number of turns of 8, and a current of 249 A to generate a magnetic field. For hyperthermia treatment involving iron oxide nanoparticles with high SAR, an alternating magnetic field of 500 kHz frequency and an amplitude of 10 kA m−1 are a good combination.42,43 Obeying the Hertz limit, the induction heating response to time for all the chromite samples was obtained at 1 mg mL−1 concentration, dissolved in distilled water over 15 minutes under an ac magnetic field with amplitude H = 14.92 kA m−1 and frequency f = 337 kHz as depicted in Fig. 6(a). It can be seen that all of the prepared chromite samples (1 mg mL−1) attained temperatures between 34.7 °C and 35.7 °C from ambient temperature in 900 seconds. A minute drop was observed in the induction heating temperature with increasing Gd content in pure cobalt chromite samples. This is attributed to the dilution of the magnetic moment as Gd ions are paramagnetic at room temperature and the emergence of the superparamagnetic nature of nanoparticles with increasing Gd dopants.13
 |
| | Fig. 6 (a) Time dependent temperature curve of all the samples at 1 mg mL−1 concentration and (b) time dependent temperature curve of the Gd-12 (CCO) sample at 2 mg mL−1 concentration. | |
The efficacy of heat dissipation by the prepared chromite samples under subjection to an alternating magnetic field can be assessed using a quantity termed the Specific Absorption Rate (SAR). It basically quantifies the dissipated power per unit mass. SAR values for all synthesized chromite samples were determined by measuring the initial slope of the temperature rise graph [Fig. 6(a)] in an adiabatic way using the stated relation2,5
| |
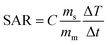 | (29) |
where
C stands for the specific heat (4.186 J g
−1 °C) of the sample solution (distilled water),
ms and
mm are the mass of the solution and mass of the sample respectively and
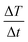
represents the initial slope of the induction heating graph representing the variation of temperature against time. The induction heating efficiency of doped chromite samples can be compared directly using a quantity known as intrinsic loss power (ILP), which provides a normalized value of SAR. The ILP of all the prepared chromites was determined using the following formula
44| |
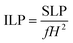 | (30) |
where
f represents the applied field frequency and
H is the applied field amplitude. The obtained SAR and ILP values for all the chromite samples are shown in
Table 2. The inclusion of rare-earth Gd
3+ ions in cobalt chromite nanoparticles lowered both the SAR and ILP. The completely paramagnetic character of Gd dopants at room temperature as well as dilution of the overall magnetic moment of the system are responsible for this observed behavior of SAR and ILP. All the incorporated Gd
3+ ions in the spinel cobalt chromite system supported the lowering of mean size and emergence of superparamagnetic character at room temperature; therefore, the magnetic anisotropy energy barrier was automatically reduced. Our observations suggest a linear relationship between the magnetic anisotropy energy barrier and SAR.
2–5 The reduction in anisotropy energy barrier with increasing Gd content in chromites favors the decrease in SAR value. The heating efficiency of magnetic nanoparticles is directly related to the anisotropy energy barrier. The incorporation of Gd ions in chromites provides room for tuning the heating efficiency by adjusting the anisotropy energy barrier. Tailoring of anisotropy barrier properties is essential and may offer proper control for practical hyperthermia application as desired. The superparamagnetic properties of magnetic nanoparticles can also be tuned by modifying the magnetic anisotropy, which opens the door for several practical uses. Our results support the Stoner–Wohlfarth model, which states that the optimal heating efficiency can be reached for a magnetic system with the highest anisotropic energy barrier.
4 A schematic representation of both the SAR and anisotropy energy barrier (Δ
E) with respect to Gd concentration is shown in
Fig. 7. For the Néel relaxation of spin moments in magnetic nanoparticles, the energy barrier (Δ
E) needs to be crossed. The increase in Δ
E theoretically means longer Néel relaxation; thereby, more heat must be released during induction heating.
4 With increasing Gd dopants in chromites, the value of Δ
E decreases which leads to a reduction in SAR. A comparison of the acquired SAR values of our samples with other nanomaterials available in the literature has been performed and is shown in
Table 3.
Table 2 SAR and ILP values of all the synthesized chromite samples
| Sample id |
SAR (W g−1) |
ILP × 10−4 (nH m2 g−1) |
| Gd-00 (CCO) |
35.31 |
4.71 |
| Gd-04 (CCO) |
33.53 |
4.47 |
| Gd-08 (CCO) |
32.61 |
4.35 |
| Gd-12 (CCO) |
32.22 |
4.30 |
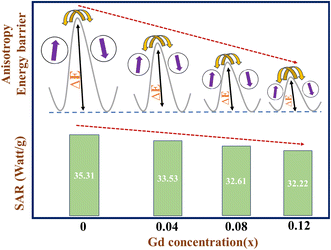 |
| | Fig. 7 Schematic diagram of anisotropy energy barrier (ΔE) and SAR with respect to Gd concentration. | |
Table 3 Size, preparation method, and SAR values of the present work compared with those of other nanomaterials available in the literature
| Compound |
Synthesis method |
Size (nm) |
H (kA m−1) |
f (kHz) |
SAR (W g−1) |
References |
| γ-Fe2O3 |
Sol–gel method |
5–10 |
9.6 |
141 |
20 |
45 |
| γ-Mn0.2Fe1.8O3 |
Thermal decomposition |
5–28 |
12 |
425 |
23 |
46 |
| γ-Fe2O3 |
Co-precipitation method |
10–20 |
70.4 |
108 |
13 |
47 |
| γ-MnxFe2−xO3 |
Thermal decomposition in ethylene glycol |
30 |
6 |
386 |
22–28 |
48 |
| Fe3O4 |
Co-precipitation method |
28 |
6.3 |
400 |
36 |
49 |
| CoFe2O4/Ni0.5Zn0.5Fe2O4 |
Co-precipitation method |
9 |
16.80–30.16 |
265 |
25 |
50 |
| Zn–Co ferrite |
Co-precipitation method |
8.6–13 |
23.04 |
340 |
10 |
51 |
| Ga–Mn ferrite |
Sol–gel method |
13.5–17.4 |
0–1.2 |
50–1200 |
10.6–19.9 |
52 |
| Chitosan–Mn ferrite |
Seed mediated growth method |
12.1 |
52.24 |
266 |
1.20 |
53 |
| MWCNT@MnFe2O4 |
Solvothermal method |
3.3–3.8 |
12.89 |
336 |
21.6–28.9 |
2 |
| Gd doped cobalt chromite nanoparticles |
Co-precipitation method |
6.8–18.2 |
14.92 |
337 |
32.2–35.3 |
This work |
It was previously recognized that the heat dissipation efficacy of magnetic nanomaterials depends on the anisotropy barrier. In this direction, both the strength and frequency of the applied field play a crucial role. The dispersion level of nanoparticles in solution has also influenced the dependency of the SAR on the anisotropy energy. A well-dispersed solution of magnetic nanoparticles may significantly change the correlation between the SAR and magnetic anisotropy energy barrier.54–56
Further, to understand the effect of sample concentration on the self-heating response of doped chromite nanoparticles, we studied the SAR of all the Gd doped chromite samples by raising the concentration to double (2 mg mL−1). The change in temperature due to the self-heating was not too high (between 35 °C and 37 °C) for all the samples when the concentration became double under the same alternating magnetic field in 900 seconds [see Fig. 6(b)].2 We have also calculated the SAR values which were found to be within the range of 46.21 W g−1 to 34.67 W g−1 for all samples after doubling the concentration (2 mg mL−1) and observed that the SAR followed the identical reduction trend with increasing Gd percentage in cobalt chromite nanoparticles. No notable change in heating efficiency was observed in doped chromite samples. Therefore, the concentration of doped chromite nanoparticles doesn't significantly affect the self-heating efficiency. As concentration increases, the dipolar interactions between nanoparticles increase, which may potentially lead to fast agglomeration in the solution. To confirm the rapid agglomeration of chromite nanoparticles caused by dipole–dipole interactions, we evaluated the hydrodynamic diameter of all the samples in the solution at two distinct concentrations (0.5 mg mL−1 and 1 mg mL−1) using the dynamic light scattering (DLS) technique.57 The hydrodynamic sizes were noted to be 100.71 nm [Gd-00 (CCO)], 93.78 nm [Gd-04 (CCO)], 91.28 nm [Gd-08 (CCO)], and 78.82 nm [Gd-12 (CCO)] at 1 mg mL−1 concentration with increasing Gd content in the samples (see Fig. S8†). At a much lower concentration (0.5 mg mL−1), the hydrodynamic sizes were found to decrease and the obtained values were 57.30 nm [Gd-00 (CCO)], 50.74 nm [Gd-04 (CCO)], 37.84 nm [Gd-08 (CCO)], and 32.67 nm [Gd-12 (CCO)] respectively (see Fig. S9†). When the sample concentration doubles, the hydrodynamic size increases significantly, which verifies the occurrence of rapid agglomeration in the solution. It was observed that the comparatively high concentration of magnetic nanoparticles in a solution led to significant agglomeration. Hydrodynamic diameter is frequently used to check the stability and the agglomeration of nanoparticles in a particular solution. Most of the time, it is found to be greater than the actual size (obtained from HRTEM images). Therefore, our results stated that the dipole–dipole interactions must be taken into account with the anisotropy energy barrier when discussing the self-heating efficiency of doped chromite nanoparticles.58 A proper understanding of the correlated effect of the dipole–dipole interactions and magnetic anisotropy barrier is essential to reach the optimized conditions for self-heating efficiency.4
4. Conclusion
In this work, the tuning of physical properties, including microstructural, magnetic, elastic, optical, and dielectric characteristics of pure CoCr2O4 nanoparticles via Gd ion doping, along with their efficacy in heat generation for hyperthermia applications has been investigated thoroughly. In this direction, we have successfully prepared four samples of Gd-incorporating cobalt chromite nanoparticles via a typical wet chemical co-precipitation technique. The cationic distribution and the spinel cubic crystal structure of the prepared samples were examined in detail by analyzing X-ray diffraction patterns, FTIR spectra, and Raman active modes obtained at room temperature. Scrutinization of the Williamson–Hall (WH) plot revealed that the mean crystallite size reduced with increasing Gd ions in CoCr2O4 nanoparticles, and the presence of a compressive microstrain was detected in the samples. Average crystallite sizes dropped consistently with increasing Gd concentration, with values ranging from 6.8 nm to 18.2 nm. The lattice constant was noted to increase for higher Gd-content chromite nanoparticles. An excellent harmony between the mean particle size evaluated from HRTEM micrographs and the mean crystallite size determined from WH plots for all the doped chromite samples was noticed. The increase in specific surface area obtained from the BET experiment for higher Gd content chromite samples confirmed both the XRD and HRTEM results. Higher Gd content chromite samples showed a regular increase in their indirect optical band gap due to the decrement in the mean sizes. All the characteristic Raman active modes existed in the synthesized samples and several elastic parameters were evaluated using the Waldron approach. The investigation of dielectric properties revealed that the Gd ion doping transformed the host chromite sample into a lossy dielectric nanomaterial. During electrical conduction, electrons were transferred through the hopping mechanism, and the grain boundaries contributed efficiently to governing the dielectric properties of the prepared nanomaterials. The magnetization was noticed to reduce to near zero around 95 K for all the as-prepared chromite samples, indicating the long-range ferrimagnetic to paramagnetic transition. The spin-spiral transition was also visible close to 26 K in the doped chromite samples. The diminishing of magnetic nature with increasing Gd ions in CoCr2O4 nanoparticles resulted in a superparamagnetic ground state at room temperature, allowing for the optimization of the self-heating capabilities. Both the reduced mean diameter and modified anisotropy constant due to the Gd doping effectively tuned the magnetic anisotropy energy barrier, which allows us to obtain the optimized conditions of induction heating for the nanocrystalline-doped chromite samples. Furthermore, we observed that the magnetic dipole–dipole interactions considerably impact induction heating efficiency, which prevails when agglomeration among chromite nanoparticles increases due to the concentration changes. Our findings also indicate that when evaluating the self-heating efficiency of doped chromite nanoparticles, the magnetic dipolar interactions must be considered in addition to the anisotropy energy barrier. On the basis of these obtained results, we conclude that a proper understanding of the linked impacts of magnetic anisotropy and dipolar interactions on the heating efficiency of magnetic nanoparticles is required to optimize it for different biological applications.
Data availability
The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.
Author contributions
MPG: conceptualization, methodology, resources, validation, discussion, writing part of the original draft, writing – review and editing. RS: methodology and formal analysis. GP: helped with hyperthermia measurements and formal analysis. JPB: discussion and methodology. DC: conceptualization, methodology, validation, resources, supervision, discussion, and writing – review and editing.
Conflicts of interest
The authors declare no competing financial interest.
Acknowledgements
The authors thank the SAIC-IASST for providing instrumental facilities. MPG thanks DST-SERB for fellowship through the NPDF (PDF/2023/001314) scheme. All the authors are also thankful to IISER Bhopal for providing the magnetic data of samples. RS thanks UGC, New Delhi for fellowship. The authors thank IASST, Guwahati for the in-house project.
References
- S. R. Ansari, N. J. Hempel, S. Asad, P. Svedlindh, C. A. S. Bergström, K. Löbmann and A. Teleki, ACS Appl. Mater. Interfaces, 2022, 14, 21978–21988 CrossRef CAS PubMed.
- P. Seal, N. Paul, P. D. Babu and J. P. Borah, Appl. Phys. A:Mater. Sci. Process., 2019, 125, 290 CrossRef CAS.
- C. Pucci, A. Degl'Innocenti, M. Belenli Gümüş and G. Ciofani, Biomater. Sci., 2022, 10, 2103–2121 RSC.
- G. Phukan, M. Kar and J. P. Borah, ACS Appl. Mater. Interfaces, 2023, 16, 261–271 CrossRef PubMed.
- M. P. Ghosh, N. J. Mondal, R. Sonkar, B. Boro, J. P. Borah and D. Chowdhury, ACS Appl. Nano Mater., 2024, 7, 7028–7042 CrossRef CAS.
- S. K. Paswan, P. Kumar, S. Kumari, S. Datta, M. Kar, J. P. Borah and L. Kumar, J. Alloys Compd., 2024, 973, 172830 CrossRef CAS.
- S. Laurent, S. Dutz, U. O. Häfeli and M. Mahmoudi, Adv. Colloid Interface Sci., 2011, 166, 8–23 CrossRef CAS PubMed.
- X. Liu, Y. Zhang, Y. Wang, W. Zhu, G. Li, X. Ma, Y. Zhang, S. Chen, S. Tiwari, K. Shi, S. Zhang, H. M. Fan, Y. X. Zhao and X. J. Liang, Theranostics, 2020, 10, 3793–3815 CrossRef CAS PubMed.
- M. P. Ghosh, S. Mohanty, R. Roy, S. Chatterjee and S. Mukherjee, J. Magn. Magn. Mater., 2024, 590, 171632 CrossRef.
- G. C. Pandey, D. Gangwar, H. Tripathi, G. Aquilanti and C. Rath, Mater. Chem. Phys., 2021, 271, 124861 CrossRef CAS.
- C. Rath, P. Mohanty and A. Banerjee, J. Magn. Magn. Mater., 2011, 323, 1698–1702 CrossRef CAS.
- P. Choudhary and D. Varshney, Mater. Res. Express, 2017, 4, 076110 CrossRef.
- M. P. Ghosh, S. Mandal and S. Mukherjee, Eur. Phys. J. Plus, 2020, 135, 41 CrossRef CAS.
- K. Tanbir, M. P. Ghosh, R. K. Singh and S. Mukherjee, J. Mater. Sci.: Mater. Electron., 2020, 31, 3529–3538 CrossRef CAS.
- K. Tanbir, M. P. Ghosh, R. K. Singh, M. Kar and S. Mukherjee, J. Mater. Sci.: Mater. Electron., 2019, 31, 435–443 CrossRef.
- M. P. Ghosh and S. Mukherjee, J. Magn. Magn. Mater., 2020, 498, 166185 CrossRef.
- S. Ali, A. Chaudhary, M. Rizwan, H. T. Anwar, M. Adrees, M. Farid, M. K. Irshad, T. Hayat and S. A. Anjum, Environ. Sci. Pollut. Res., 2015, 22, 10669–10678 CrossRef CAS PubMed.
- M. P. Ghosh and S. Mukherjee, J. Am. Ceram. Soc., 2019, 102, 7509–7520 CrossRef CAS.
- K. Manjunatha, V. J. Angadi, R. a. P. Ribeiro, M. C. Oliveira, S. R. De Lázaro, M. R. D. Bomio, S. Matteppanavar, S. Rayaprol, P. D. Babu and U. M. Pasha, New J. Chem., 2020, 44, 14246–14255 RSC.
- M. P. Ghosh and S. Mukherjee, J. Magn. Magn. Mater., 2019, 489, 165320 CrossRef CAS.
- S. Goswami, P. K. Manna, S. Bedanta, S. K. Dey, M. Chakraborty and D. De, J. Phys. D: Appl. Phys., 2020, 53, 305303 CrossRef CAS.
- V. J. Angadi, K. Manjunatha, M. C. Oliveira, E. Longo, S. R. De Lázaro, R. A. P. Ribeiro and S. V. Bhat, Appl. Surf. Sci., 2022, 574, 151555 CrossRef.
- K. Manjunatha, V. J. Angadi, M. C. Oliveira, S. R. De Lazaro, E. Longo, R. a. P. Ribeiro, S. O. Manjunatha and N. H. Ayachit, J. Mater. Chem. C, 2021, 9, 6452–6469 RSC.
- E. E. Ateia, E. Takla and A. T. Mohamed, Appl. Phys. A:Mater. Sci. Process., 2017, 123, 631 CrossRef.
- A. V. Anupama, V. Rathod, V. M. Jali and B. Sahoo, J. Alloys Compd., 2017, 728, 1091–1100 CrossRef CAS.
- K. B. Modi, J. Mater. Sci., 2004, 39, 2887–2890 CrossRef CAS.
- N. J. Mondal, R. Sonkar, B. Boro, M. P. Ghosh and D. Chowdhury, Nanoscale Adv., 2023, 5, 5460–5475 RSC.
- A. Makofane, D. E. Motaung and N. C. Hintsho-Mbita, Ceram. Int., 2021, 47, 22615–22626 CrossRef CAS.
- S. A. Jadhav, S. B. Somvanshi, M. V. Khedkar, S. R. Patade and K. M. Jadhav, J. Mater. Sci.: Mater. Electron., 2020, 31, 11352–11365 CrossRef CAS.
- P. Choudhary, P. Saxena, A. Yadav, A. K. Sinha, V. N. Rai, M. D. Varshney and A. Mishra, J. Supercond. Novel Magn., 2019, 32, 2639–2645 CrossRef CAS.
- A. Aakash, M. P. Ghosh and S. Mukherjee, Appl. Phys. A:Mater. Sci. Process., 2019, 125, 853 CrossRef.
- M. P. Ghosh, P. Kumar, M. Kar and S. Mukherjee, J. Mater. Sci.: Mater. Electron., 2020, 31, 17762–17772 CrossRef.
- D. Varshney and K. Verma, Mater. Chem. Phys., 2013, 140, 412–418 CrossRef CAS.
- Z. Ž. Lazarević, Č. Jovalekić, D. L. Sekulić, A. Milutinović, S. Baloš, M. Slankamenac and N. Ž. Romčević, Mater. Res. Bull., 2013, 48, 4368–4378 CrossRef.
- R. K. Panda, R. Muduli, S. K. Kar and D. Behera, J. Alloys Compd., 2014, 615, 899–905 CrossRef CAS.
- R. Sonkar, N. J. Mondal, B. Boro, M. P. Ghosh and D. Chowdhury, J. Phys. Chem. Solids, 2024, 185, 111715 CrossRef CAS.
- S. Mohanty and S. Mukherjee, J. Alloys Compd., 2022, 892, 162204 CrossRef CAS.
- M. P. Ghosh and S. Mukherjee, Mater. Res. Bull., 2020, 125, 110785 CrossRef CAS.
- D. Kumar, P. Mohanty, V. P. Singh, J. K. Galivarapu, A. Banerjee, V. Ganesan and C. Rath, Mater. Res. Bull., 2014, 54, 78–83 CrossRef CAS.
- D. Kumar, A. Banerjee, A. Mahmoud and C. Rath, Dalton Trans., 2017, 46, 10300–10314 RSC.
- S. Ota and Y. Takemura, J. Phys. Chem. C, 2019, 123, 28859–28866 CrossRef CAS.
- B. Kozissnik, A. C. Bohorquez, J. Dobson and C. Rinaldi, Int. J. Hyperthermia, 2013, 29, 706–714 CrossRef PubMed.
- R. Hergt and S. Dutz, J. Magn. Magn. Mater., 2006, 311, 187–192 CrossRef.
- G. Naresh, J. P. Borah, C. Borgohain and N. Paul, Mater. Res. Express, 2021, 8, 115014 CrossRef CAS.
- P. E. Le Renard, R. Lortz, C. Senatore, J.-P. Rapin, F. Buchegger, A. Petri-Fink, H. Hofmann, E. Doelker and O. Jordan, J. Magn. Magn. Mater., 2011, 323, 1054–1063 CrossRef CAS.
- N. K. Prasad, K. Rathinasamy, D. Panda and D. Bahadur, J. Mater. Chem., 2007, 17, 5042 RSC.
- F. Sonvico, S. Mornet, S. Vasseur, C. Dubernet, D. Jaillard, J. Degrouard, J. Hoebeke, E. Duguet, P. Colombo and P. Couvreur, Bioconjugate Chem., 2005, 16, 1181–1188 CrossRef CAS PubMed.
- T. Sadhukha, L. Niu, T. S. Wiedmann and J. Panyam, Mol. Pharm., 2013, 10, 1432–1441 CrossRef CAS PubMed.
- B. Samanta, H. Yan, N. O. Fischer, J. Shi, D. J. Jerry and V. M. Rotello, J. Mater. Chem., 2008, 18, 1204 RSC.
- M. R. Phadatare, J. V. Meshram, K. V. Gurav, J. H. Kim and S. H. Pawar, J. Phys. D: Appl. Phys., 2016, 49, 095004 Search PubMed.
- C. Gómez-Polo, V. Recarte, L. Cervera, J. J. Beato-López, J. López-García, J. A. Rodríguez-Velamazán, M. D. Ugarte, E. C. Mendonça and J. G. S. Duque, J. Magn. Magn. Mater., 2018, 465, 211–219 CrossRef.
- J. Sánchez, D. A. Cortés-Hernández, J. C. Escobedo-Bocardo, J. M. Almanza-Robles, P. Y. Reyes-Rodríguez, R. A. Jasso-Terán, P. Bartolo-Pérez and L. E. De-León-Prado, Ceram. Int., 2016, 42, 13755–13760 CrossRef.
- D.-H. Kim, D. E. Nikles and C. S. Brazel, Materials, 2010, 3, 4051–4065 CrossRef CAS PubMed.
- J. Carrey, B. Mehdaoui and M. Respaud, J. Appl. Phys., 2011, 109, 8 CrossRef.
- S. Ota, T. Yamada and Y. Takemura, J. Nanomater., 2015, 2015, 1–8 Search PubMed.
- K. Simeonidis, C. Martinez-Boubeta, D. Serantes, S. Ruta, O. Chubykalo-Fesenko, R. Chantrell, J. Oró-Solé, Ll. Balcells, A. S. Kamzin, R. A. Nazipov, A. Makridis and M. Angelakeris, ACS Appl. Nano Mater., 2020, 3, 4465–4476 CrossRef CAS PubMed.
- M. Bellusci, C. Aliotta, D. Fiorani, A. La Barbera, F. Padella, D. Peddis, M. Pilloni and D. Secci, J. Nanopart. Res., 2012, 14, 904 CrossRef.
- C. L. Dennis and R. Ivkov, Int. J. Hyperthermia, 2013, 29, 715–729 CrossRef PubMed.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Rahul Sonkar
*a,
Rahul Sonkar ab,
Gongotree Phukanc,
Jyoti Prasad Borahc and
Devasish Chowdhury
ab,
Gongotree Phukanc,
Jyoti Prasad Borahc and
Devasish Chowdhury *ab
*ab
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, where magnetic Co2+ ions occupy tetrahedral (A) sites, while Cr3+ ions reside in octahedral (B) sites, forming a normal spinel cubic crystal structure.9,10 This material behaves like a ferrimagnetic system below Curie temperature (≈97 K) and the superexchange interactions (A–O–B) present between two different types of sublattices (A and B) are responsible for the ferrimagnetic nature. A spiral ferrimagnetic ordering may also be seen in the spinel cobalt chromite system below 26 K.9–12 Significant changes in the magnetic properties of the cobalt chromite system have been observed at low temperatures and in the nanoscale domain. Variations in the fabrication method, size, shape, dopant ions, and doping percentages can drastically modify the physical properties of CoCr2O4 nanoparticles, including their magnetic, optical, structural, and dielectric responses.12
m, where magnetic Co2+ ions occupy tetrahedral (A) sites, while Cr3+ ions reside in octahedral (B) sites, forming a normal spinel cubic crystal structure.9,10 This material behaves like a ferrimagnetic system below Curie temperature (≈97 K) and the superexchange interactions (A–O–B) present between two different types of sublattices (A and B) are responsible for the ferrimagnetic nature. A spiral ferrimagnetic ordering may also be seen in the spinel cobalt chromite system below 26 K.9–12 Significant changes in the magnetic properties of the cobalt chromite system have been observed at low temperatures and in the nanoscale domain. Variations in the fabrication method, size, shape, dopant ions, and doping percentages can drastically modify the physical properties of CoCr2O4 nanoparticles, including their magnetic, optical, structural, and dielectric responses.12![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group and correspond exactly to ICDD Card No. 080-1668. The GSAS software with EXPGUI interface was used to perform the Rietveld refinement of all the X-ray diffraction patterns. In the fitting process, the Pseudo–Voigt function was utilized to shape the profile peaks. The fitting parameters i.e. goodness of fit (χ2) were noted to have values within 1.03 to 1.11 and R-factors (RP and RWP) were found to be below 3% confirming the perfect agreement between the obtained data and typical diffraction pattern. It should be emphasized that the observed broadening in the diffracted peaks is due to the prepared chromite samples being in the nanometric domain. With the increment of Gd dopants in cobalt chromite samples, a gradual enhancement in peak broadening was noticed.13–15 Three major factors are responsible for the XRD peak broadening in the nanosize domain, i.e. crystallite size effect, intrinsic microstrain in the nanocrystals and instrumental effects. In order to eliminate the instrumental broadening effects, a reference diffractogram of pure LaB6 powder having a large grain size was used under similar conditions.16 After subtracting instrumental line-width, the overall broadening β (FWHM of peak) is the combination of crystallite size (βsize) and intrinsic microstrain (βstrain) broadening effects as given below18
m space group and correspond exactly to ICDD Card No. 080-1668. The GSAS software with EXPGUI interface was used to perform the Rietveld refinement of all the X-ray diffraction patterns. In the fitting process, the Pseudo–Voigt function was utilized to shape the profile peaks. The fitting parameters i.e. goodness of fit (χ2) were noted to have values within 1.03 to 1.11 and R-factors (RP and RWP) were found to be below 3% confirming the perfect agreement between the obtained data and typical diffraction pattern. It should be emphasized that the observed broadening in the diffracted peaks is due to the prepared chromite samples being in the nanometric domain. With the increment of Gd dopants in cobalt chromite samples, a gradual enhancement in peak broadening was noticed.13–15 Three major factors are responsible for the XRD peak broadening in the nanosize domain, i.e. crystallite size effect, intrinsic microstrain in the nanocrystals and instrumental effects. In order to eliminate the instrumental broadening effects, a reference diffractogram of pure LaB6 powder having a large grain size was used under similar conditions.16 After subtracting instrumental line-width, the overall broadening β (FWHM of peak) is the combination of crystallite size (βsize) and intrinsic microstrain (βstrain) broadening effects as given below18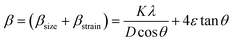
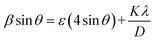

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ against 4
θ against 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) to separate the contributions of size and microstrain effects in the broadening which is termed as the Williamson–Hall (WH) plot. Fig. 1(b) depicts the WH plots of all of the Gd substituted chromite nanoparticles. The WH curve is a straight line and the slope of the straight line gives the microstrain (ε) in nanocrystals whereas the intercept on the β
θ) to separate the contributions of size and microstrain effects in the broadening which is termed as the Williamson–Hall (WH) plot. Fig. 1(b) depicts the WH plots of all of the Gd substituted chromite nanoparticles. The WH curve is a straight line and the slope of the straight line gives the microstrain (ε) in nanocrystals whereas the intercept on the β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ axis is Kλ/D used to obtain the mean size of nanoparticles.9
θ axis is Kλ/D used to obtain the mean size of nanoparticles.9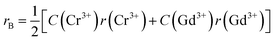
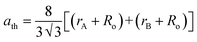
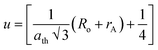
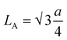 for tetrahedral (A) sublattices and
for tetrahedral (A) sublattices and 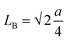 for octahedral (B) sublattices, were noticed to increase for higher Gd content chromite nanoparticles because of the enhancement of the lattice parameter (see Table S2†).16,20 The increasing hopping lengths also reflect the demand for more energy to beat the electrostatic repulsion for a successful hopping of electrons. It is well known that the cationic distribution of tetrahedral voids is reflected by the intensity of diffracted X-rays from the (422) and (220) crystallographic planes in the diffractograms. Similarly, the intensity of diffracted X-rays from the (222) plane also reveals information regarding the cationic distribution of octahedral voids. The ratio of intensities, i.e. I220/I222 and I422/I222, was noted to reduce with increasing Gd dopants in the host chromite system confirming that all the Gd ions have occupied octahedral sites (see Table S3†).13 The superexchange interactions (A–O–B) between tetrahedral (A) and octahedral (B) sublattices, which are responsible for ferrimagnetic ordering in chromites, are substantially influenced by both the bond lengths and angles. A schematic representation of A–O–B superexchange interactions for spinel cubic chromites is shown in Fig. S1.† To understand the strength of the A–O–B interactions, bond angles between magnetic ions are measured using the given relations20
for octahedral (B) sublattices, were noticed to increase for higher Gd content chromite nanoparticles because of the enhancement of the lattice parameter (see Table S2†).16,20 The increasing hopping lengths also reflect the demand for more energy to beat the electrostatic repulsion for a successful hopping of electrons. It is well known that the cationic distribution of tetrahedral voids is reflected by the intensity of diffracted X-rays from the (422) and (220) crystallographic planes in the diffractograms. Similarly, the intensity of diffracted X-rays from the (222) plane also reveals information regarding the cationic distribution of octahedral voids. The ratio of intensities, i.e. I220/I222 and I422/I222, was noted to reduce with increasing Gd dopants in the host chromite system confirming that all the Gd ions have occupied octahedral sites (see Table S3†).13 The superexchange interactions (A–O–B) between tetrahedral (A) and octahedral (B) sublattices, which are responsible for ferrimagnetic ordering in chromites, are substantially influenced by both the bond lengths and angles. A schematic representation of A–O–B superexchange interactions for spinel cubic chromites is shown in Fig. S1.† To understand the strength of the A–O–B interactions, bond angles between magnetic ions are measured using the given relations20![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group and contain two different types of interpenetrating sublattices. A complete unit cell of spinel cubic chromite contains 56 atoms and 14 atoms in the smallest Bravais cell. As per group theory, there are five Raman active modes (A1g + Eg + 3T2g) present in the ideal cubic spinel system9,18 and all the tetrahedral (A) sites and octahedral (B) sites correspond to Td and D3d point groups respectively. All the obtained Raman active modes of the prepared chromite systems are listed in Table 1. All the nanosized Gd3+ ion doped cobalt chromite samples exhibited five characteristic Raman active modes [A1g(1), A1g(2), T2g(1), T2g(2), and T2g(3)]. The two observed A1g modes belong to the symmetric stretching of oxygen atoms along the M3+–O2− (M = Cr and Gd) bond in the tetrahedral sites. The Raman active T2g(3) mode reflects the asymmetric bending of the O atom with respect to Cr, the T2g(2) mode is assigned to the asymmetric stretching vibration of the M3+–O2− (M = Cr and Gd) bond and the T2g(1) mode arise due to the translational motion of the entire CrO4 tetrahedron. All Raman active modes with wave numbers more than 600 cm−1 are assigned to tetrahedral sublattices, whereas those below 600 cm−1 are assigned to octahedral sublattices. Substitution of comparatively large size Gd3+ ions along with cation vacancies may minutely distort the spinel cubic crystal structure and lead to a lowering of crystal symmetry.13,18 The observed minute shift in Raman active modes towards low wave number (red shift) is attributed to the modified reduced mass. The doping of comparatively heavier Gd (157.25 g) ions in place of Cr (51.99 g) ions changed the reduced mass of the M–O (M = Cr, Gd) bond. The shift of Raman active modes due to doping can be understood by using the stated formula9,13
m space group and contain two different types of interpenetrating sublattices. A complete unit cell of spinel cubic chromite contains 56 atoms and 14 atoms in the smallest Bravais cell. As per group theory, there are five Raman active modes (A1g + Eg + 3T2g) present in the ideal cubic spinel system9,18 and all the tetrahedral (A) sites and octahedral (B) sites correspond to Td and D3d point groups respectively. All the obtained Raman active modes of the prepared chromite systems are listed in Table 1. All the nanosized Gd3+ ion doped cobalt chromite samples exhibited five characteristic Raman active modes [A1g(1), A1g(2), T2g(1), T2g(2), and T2g(3)]. The two observed A1g modes belong to the symmetric stretching of oxygen atoms along the M3+–O2− (M = Cr and Gd) bond in the tetrahedral sites. The Raman active T2g(3) mode reflects the asymmetric bending of the O atom with respect to Cr, the T2g(2) mode is assigned to the asymmetric stretching vibration of the M3+–O2− (M = Cr and Gd) bond and the T2g(1) mode arise due to the translational motion of the entire CrO4 tetrahedron. All Raman active modes with wave numbers more than 600 cm−1 are assigned to tetrahedral sublattices, whereas those below 600 cm−1 are assigned to octahedral sublattices. Substitution of comparatively large size Gd3+ ions along with cation vacancies may minutely distort the spinel cubic crystal structure and lead to a lowering of crystal symmetry.13,18 The observed minute shift in Raman active modes towards low wave number (red shift) is attributed to the modified reduced mass. The doping of comparatively heavier Gd (157.25 g) ions in place of Cr (51.99 g) ions changed the reduced mass of the M–O (M = Cr, Gd) bond. The shift of Raman active modes due to doping can be understood by using the stated formula9,13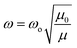
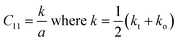
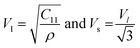
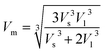
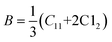
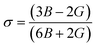
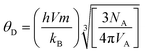
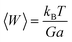
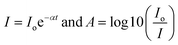
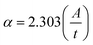 , where t stands for the width of the cuvette. Determination of the indirect optical band gap (Eo) of the as-synthesized chromites was performed by plotting a graph between (αhν)1/2 and photon energy (hν), which is termed a Tauc plot. Tauc plots of all the samples are depicted in Fig. S2.† The estimated values of indirect band gap (Eo) were observed to be 2.03 ± 0.01 eV [Gd-00(CCO)], 2.14 ± 0.01 eV [Gd-04(CCO)], 2.17 ± 0.01 eV [Gd-08(CCO)] and 2.21 ± 0.01 eV [Gd-12(CCO)] respectively. Higher Gd content chromite samples exhibited a blue shift in their EM wave absorption spectrum. The observed systematic enhancement (blue shift) in the indirect optical band gap is attributed to the reduction of mean diameters with increasing Gd percentage in CoCr2O4 nanoparticles, which decreases the overlapping of atomic orbitals.15,20 A careful examination of the absorption spectra of the prepared chromite nanoparticles demonstrates that all samples have an opaque nature in the yellow and red bands of the electromagnetic (EM) spectrum. All the Gd doped chromite nanoparticles have notable absorption properties in the yellow and red domains of the EM spectrum, making them suitable for several optical applications.20
, where t stands for the width of the cuvette. Determination of the indirect optical band gap (Eo) of the as-synthesized chromites was performed by plotting a graph between (αhν)1/2 and photon energy (hν), which is termed a Tauc plot. Tauc plots of all the samples are depicted in Fig. S2.† The estimated values of indirect band gap (Eo) were observed to be 2.03 ± 0.01 eV [Gd-00(CCO)], 2.14 ± 0.01 eV [Gd-04(CCO)], 2.17 ± 0.01 eV [Gd-08(CCO)] and 2.21 ± 0.01 eV [Gd-12(CCO)] respectively. Higher Gd content chromite samples exhibited a blue shift in their EM wave absorption spectrum. The observed systematic enhancement (blue shift) in the indirect optical band gap is attributed to the reduction of mean diameters with increasing Gd percentage in CoCr2O4 nanoparticles, which decreases the overlapping of atomic orbitals.15,20 A careful examination of the absorption spectra of the prepared chromite nanoparticles demonstrates that all samples have an opaque nature in the yellow and red bands of the electromagnetic (EM) spectrum. All the Gd doped chromite nanoparticles have notable absorption properties in the yellow and red domains of the EM spectrum, making them suitable for several optical applications.20
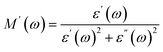
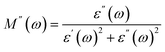
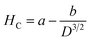
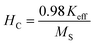

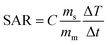
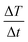 represents the initial slope of the induction heating graph representing the variation of temperature against time. The induction heating efficiency of doped chromite samples can be compared directly using a quantity known as intrinsic loss power (ILP), which provides a normalized value of SAR. The ILP of all the prepared chromites was determined using the following formula44
represents the initial slope of the induction heating graph representing the variation of temperature against time. The induction heating efficiency of doped chromite samples can be compared directly using a quantity known as intrinsic loss power (ILP), which provides a normalized value of SAR. The ILP of all the prepared chromites was determined using the following formula44