Open Access Article
Open Access ArticleInvestigating the structure–property correlations of pyrolyzed phenolic resin as a function of degree of carbonization†
Ivan Gallegos *a,
Vikas Varshney
*a,
Vikas Varshney b,
Josh Kemppainen
b,
Josh Kemppainen a and
Gregory M. Odegard
a and
Gregory M. Odegard a
a
aMichigan Technological University, 1400 Townsend Dr, Houghton, MI 49931, USA. E-mail: igallego@mtu.edu
bAir Force Research Laboratory, Wright-Patterson Air Force Base, 2941 Hobson Way, OH 45433, USA
First published on 9th January 2025
Abstract
Carbon–carbon (C/C) composites are attractive materials for high-speed flights and terrestrial atmospheric reentry applications due to their insulating thermal properties, thermal resistance, and high strength-to-weight ratio. It is important to understand the evolving structure–property correlations in these materials during pyrolysis, but the extreme laboratory conditions required to produce C/C composites make it difficult to quantify the properties in situ. This work presents an atomistic modeling methodology to pyrolyze a crosslinked phenolic resin network and track the evolving thermomechanical properties of the skeletal matrix during simulated pyrolysis. First, the crosslinked resin is pyrolyzed and the resulting char yield and mass density are verified to match experimental values, establishing the model's powerful predictive capabilities. Young's modulus, yield stress, Poisson's ratio, and thermal conductivity are calculated for the polymerized structure, intermediate pyrolyzed structures, and fully pyrolyzed structure to reveal structure–property correlations, and the evolution of properties are linked to observed structural features. It is determined that reduction in fractional free volume and densification of the resin during pyrolysis contribute significantly to the increase in thermomechanical properties of the skeletal phenolic matrix. A complex interplay of the formation of six-membered carbon rings at the expense of five and seven-membered carbon rings is revealed to affect thermal conductivity. Increased anisotropy was observed in the latter stages of pyrolysis due to the development of aligned aromatic structures. Experimentally validated predictive atomistic models are a key first step to multiscale process modeling of C/C composites to optimize next-generation materials.
Introduction
Carbon–carbon (C/C) composites are a class of materials that are often used as ablatives during terrestrial atmospheric reentry. In these composites, the matrix characteristics vary depending on the polymeric precursors used and the processing conditions employed.1,2 At one extreme, the pyrolysis process may result in an isotropic glassy carbon characterized by fullerene-related structures with defects. On the opposite end of the spectrum, the pyrolysis process may result in graphitized structures with preferential alignment producing anisotropic behavior.3C/C composites are fabricated via a cyclic process known as polymer-infiltration pyrolysis (PIP) in which a reinforced pre-impregnated preform (prepeg) in the net shape of the service part is first cured then pyrolyzed at temperatures greater than 800 °C to transform the organic precursor into a carbonaceous material. The resulting porous structure is then re-impregnated with uncured polymer resin and the process is repeated for several cycles to counter the shrinkage and porosity resulting from the curing and pyrolysis processes, respectively.2,4 Phenolic resins are common precursors for C/C matrices which polymerize through a condensation reaction to produce linear phenol chains known as novolacs, which can then be ground into a powder and mixed with a hardener to produce a highly branched network of phenols called Bakelite. This stiff network of branched phenols provides the desired higher char yields (Cy) during the pyrolysis process due to a lack of low molecular weight compounds which would otherwise volatilize with ease.5,6
Molecular dynamics (MD) is a well-established computational modeling method that can provide insight into the pyrolysis process and structure–property correlations at the nano length scale. Several software packages are available for running MD simulations, but perhaps the most well-known is the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS).7 The choice of the MD force field, which dictates interatomic interactions, is critical to accurately capture the chemistry of the high-temperature processes observed in pyrolysis. Two general types of force fields include fixed-bond force fields and reactive force fields.8 With fixed-bond force fields, the bonded topology is explicitly defined and reactivity may occur through topology-based algorithms, such as the REACTER tool integrated in LAMMPS.9 However, the former requires knowledge of reaction chemistry a priori, which can be difficult for high temperature pyrolysis processes whose chemical evolution are difficult to track in situ. Reactive force fields, on the other hand, allow chemical reactions to occur naturally based on the concept of bond order, such as with the reactive ReaxFF force field developed by van Duin et al.10 ReaxFF has been applied to simulate a variety of material systems and processes, including coal combustion,11 protein/DNA interactions in aqueous solutions,12 polymer crosslinking and mechanical properties,13 catalysis,14 and synthesis of 2D materials.15,16
There have been numerous MD studies involving the simulation of polymerization and/or pyrolysis of phenolic resins. Izumi et al.17 were among the first to propose an atomistic model simulating the polymerization of phenolic resins. Monk et al.18 analyzed several approaches to producing crosslinked phenolic structures and found an iterative approach was preferred for predicting thermal properties. Shudo et al.19 developed a large-scale model (∼232![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms) of crosslinked phenolic resin utilizing a pseudo-reaction model and determined the degree of crosslinking was highly dependent on initial configuration, where longer chain molecules of phenols resulted in lower degrees of crosslinking compared to monomeric phenols due to steric hindrance. In a subsequent study, Shudo et al.20 predicted the Young's modulus (E) and mass densities (ρ) based on that pseudo-reaction model. Izumi et al.21 developed a united-atom MD model using the pseudo-reaction-based approach to crosslink phenolic resins while introducing a geometric constraint to avoid highly strained structures. Jiang et al.22 modeled the initial stages of the pyrolysis of a phenolic resin using the ReaxFF force field to determine the first volatilized chemical species. Desai et al.23 also modeled the initial stage of pyrolysis for phenolic resins while investigating interfacial effects and the molecular structures evolved. Qi et al.24 performed a comprehensive comparison between ReaxFF and density-functional theory (DFT) methods for modeling the initial stages of the pyrolysis of phenolic resins. Bauschlicher et al.25 determined that ReaxFF had the highest average absolute error compared to the various DFT methods reported by Qi et al.24 in terms of reaction energies and barrier heights. Zhong et al.26 also modeled the initial stages of the pyrolysis process of phenolic resins using ReaxFF to study the behavior of phenolic hydroxyl groups and determined that phenoxyl radicals reduce the stability of benzene rings, thus damaging the backbone of the structure. Harpale et al.27 used a combination of a fixed-bond force field (Polymer Consistent Force Field, or PCFF) and a reactive force field (ReaxFF) to model the pyrolysis of a highly crosslinked phenolic network and developed a thermal material response model to predict heat transfer within the pyrolyzed structure. Purse et al.28 demonstrated a method for simulating the complete pyrolysis process of a cured phenol-formaldehyde within ∼2 ns of simulation time using reactive MD. Yan et al.29 recently modeled the pyrolysis process of crosslinked and non-crosslinked phenolic structures by switching from a fixed-bond force field (PCFF) to a reactive force field (ReaxFF) and determined that structures observed in the highly-crosslinked phenolic resins remained deep into the pyrolysis process. Gissinger et al.30 developed an algorithm to remove chemical species with a desired mass range during pyrolysis which enabled the accurate prediction of Cy of several polymer precursor systems. However, despite the methods reported for simulating polymerization and pyrolysis of phenolic resins, to date there has not been a study of the evolving thermomechanical properties as a function of these processes.
000 atoms) of crosslinked phenolic resin utilizing a pseudo-reaction model and determined the degree of crosslinking was highly dependent on initial configuration, where longer chain molecules of phenols resulted in lower degrees of crosslinking compared to monomeric phenols due to steric hindrance. In a subsequent study, Shudo et al.20 predicted the Young's modulus (E) and mass densities (ρ) based on that pseudo-reaction model. Izumi et al.21 developed a united-atom MD model using the pseudo-reaction-based approach to crosslink phenolic resins while introducing a geometric constraint to avoid highly strained structures. Jiang et al.22 modeled the initial stages of the pyrolysis of a phenolic resin using the ReaxFF force field to determine the first volatilized chemical species. Desai et al.23 also modeled the initial stage of pyrolysis for phenolic resins while investigating interfacial effects and the molecular structures evolved. Qi et al.24 performed a comprehensive comparison between ReaxFF and density-functional theory (DFT) methods for modeling the initial stages of the pyrolysis of phenolic resins. Bauschlicher et al.25 determined that ReaxFF had the highest average absolute error compared to the various DFT methods reported by Qi et al.24 in terms of reaction energies and barrier heights. Zhong et al.26 also modeled the initial stages of the pyrolysis process of phenolic resins using ReaxFF to study the behavior of phenolic hydroxyl groups and determined that phenoxyl radicals reduce the stability of benzene rings, thus damaging the backbone of the structure. Harpale et al.27 used a combination of a fixed-bond force field (Polymer Consistent Force Field, or PCFF) and a reactive force field (ReaxFF) to model the pyrolysis of a highly crosslinked phenolic network and developed a thermal material response model to predict heat transfer within the pyrolyzed structure. Purse et al.28 demonstrated a method for simulating the complete pyrolysis process of a cured phenol-formaldehyde within ∼2 ns of simulation time using reactive MD. Yan et al.29 recently modeled the pyrolysis process of crosslinked and non-crosslinked phenolic structures by switching from a fixed-bond force field (PCFF) to a reactive force field (ReaxFF) and determined that structures observed in the highly-crosslinked phenolic resins remained deep into the pyrolysis process. Gissinger et al.30 developed an algorithm to remove chemical species with a desired mass range during pyrolysis which enabled the accurate prediction of Cy of several polymer precursor systems. However, despite the methods reported for simulating polymerization and pyrolysis of phenolic resins, to date there has not been a study of the evolving thermomechanical properties as a function of these processes.
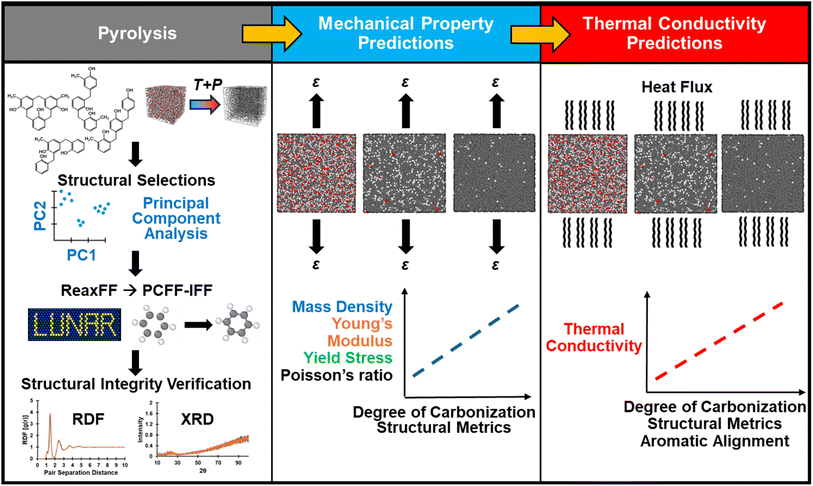
The objective of this work is to investigate the structure–property correlation evolution of crosslinked phenolic networks during the pyrolysis process at the atomic length scale. We previously reported on an experimentally-validated protocol for modeling the full polymerization and pyrolysis processes for phenolic resins using the ReaxFF force field.31 Using the same methodology, simulated pyrolysis was performed on the polymerized structure, while determining intermediate molecular structures to track changes in the properties as the material transformed from an organic precursor to a fully pyrolyzed structure. Following a structural analysis, specific intermediate pyrolyzed structures were converted to a fixed-bond force field and equilibrated to accurately quantify the evolution of mass density (ρ), mechanical properties, and thermal conductivity (κ). The structural integrity between the reactive force field structures and the corresponding fixed-bond force field structures was verified through radial distribution function (RDF) and simulated X-ray diffraction (XRD) methods. The effect of the growth of aligned aromatic structures on κ was also quantified. It is shown that the evolution of ρ and free volume in the system have the most pronounced effects on properties, and models with a high degree of aromatic alignment exhibited anisotropic behavior in κ. The models showed an increased anisotropic response due to the formation of aromatically aligned regions as they approached a fully pyrolyzed state. It is important to understand the effect of nano length scale structural configurations of the resulting pyrolyzed structures to tailor the processes for manufacturing large-scale structural components for improved material performance. Specifically, understanding composite performance is inherently a multiscale problem in which matrix property evolution at the nano length scale, reinforcement architecture at the micro scale, and tow geometry at the meso scale all contribute to macro scale properties and damage initiation. By modeling an otherwise unobservable process in MD, such as the matrix evolution from an uncured stage up to a fully pyrolyzed state, we come a step closer to understanding the mechanisms associated with the evolution of properties of pyrolyzed skeletal phenolic resin networks in an economical and time-efficient manner. Data generated from nanoscale models can serve as valuable inputs for larger length scales via an Integrated Computational Materials Engineering (ICME) approach.32–38
Methods
All simulations were performed using the LAMMPS February 2023 software package. Reactive and fixed-bond force fields were used to simulate pyrolysis and to perform property prediction simulations, respectively. Specifically, the complex chemical and structural changes that occur during pyrolysis inherently require a reactive force field capable of modeling bond formation and dissociation. However, reactive force fields, such as ReaxFF developed by van Duin et al.,10 can be computationally expensive due to the bond order-based formulation which consequently requires reassignment of partial atomic charges at each timestep.39 Therefore, a fixed-bond force field was chosen for property prediction after considering the system sizes involved in this study (ranging from ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to ∼30
000 to ∼30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms). Switching from the bond order based reactive force field ReaxFF to the fixed-bond force field PCFF-IFF40,41 was accomplished using the LAMMPS Utility for Network Analysis and Reactivity (LUNAR) package developed by Kemppainen et al.,42 which was also used for the analysis of ringed structures, atomic hybridization, aromatic alignment, and free volume. For the models using PCFF-IFF the cut-off radius for pairwise interactions was specified at 12 Å and long-range electrostatic interactions were computed with a particle–particle particle-mesh (PPPM) solver. Molecular visualizations were performed using OVITO43 and the TopoTools plugin to the Visual Molecular Dynamics (VMD) software.44,45 The complete modeling procedure can be summarized in three main steps as outlined in the flowchart in Fig. 1: (1) pyrolysis, (2) mechanical property predictions, and (3) κ predictions.
000 atoms). Switching from the bond order based reactive force field ReaxFF to the fixed-bond force field PCFF-IFF40,41 was accomplished using the LAMMPS Utility for Network Analysis and Reactivity (LUNAR) package developed by Kemppainen et al.,42 which was also used for the analysis of ringed structures, atomic hybridization, aromatic alignment, and free volume. For the models using PCFF-IFF the cut-off radius for pairwise interactions was specified at 12 Å and long-range electrostatic interactions were computed with a particle–particle particle-mesh (PPPM) solver. Molecular visualizations were performed using OVITO43 and the TopoTools plugin to the Visual Molecular Dynamics (VMD) software.44,45 The complete modeling procedure can be summarized in three main steps as outlined in the flowchart in Fig. 1: (1) pyrolysis, (2) mechanical property predictions, and (3) κ predictions.
Pyrolysis
The ReaxFF CHON-2019 parameter set46 was used to pyrolyze a polymerized phenolic resin structure (30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 960 atoms) built in a previous study.31 In brief, the initial molecules as depicted in Fig. 1 (top-left of first pane) were developed in Chem3D as pre-branched “triphenols”, and the exported 3D MOL files were converted to LAMMPS-readable data files, densified, and equilibrated at room temperature to simulate an uncured phenolic resin. The models were then heated to high temperature to polymerize and subsequently cooled to room temperature and equilibrated to obtain this study's initializing structure of polymerized phenolic resin characterized by a highly branched phenolic network. For further details on the model development of the polymerized structure, readers can refer to the previous study.31
960 atoms) built in a previous study.31 In brief, the initial molecules as depicted in Fig. 1 (top-left of first pane) were developed in Chem3D as pre-branched “triphenols”, and the exported 3D MOL files were converted to LAMMPS-readable data files, densified, and equilibrated at room temperature to simulate an uncured phenolic resin. The models were then heated to high temperature to polymerize and subsequently cooled to room temperature and equilibrated to obtain this study's initializing structure of polymerized phenolic resin characterized by a highly branched phenolic network. For further details on the model development of the polymerized structure, readers can refer to the previous study.31
Charges were assigned with the “fix qeq/reaxff” command.47 The CHON-2019 parameter set was chosen as it was designed specifically for hydrocarbon pyrolysis processes and has been used in numerous works involving simulated pyrolysis,48–51 as well as investigating radiation effects on flattened carbon nanotubes (flCNTs)52 and interfacial interactions involving amorphous carbon.53 Specifically, the polymerized structure was heated from 300 K to 3200 K at a heating rate of 10 K ps−1 in the constant volume and temperature (NVT) ensemble. The system was then held at 3200 K for 1 ns at 2 GPa hydrostatic pressure in the constant volume and energy (NVE) and the constant pressure and enthalpy (NPH) ensembles while deleting volatilized chemical species using the “delete” option of the “fix reaxff/species” command developed by Gissinger et al.30 Compounds between 2–50 Da in mass were deleted to simulate the volatilization of hydrogen gas and low molecular weight hydrocarbons. Three unique replicates were built by heating and pyrolyzing with different velocity seeds. The reader may refer to Fig. S1 of the ESI† for a detailed flowchart describing the entire pyrolysis simulation process.
The structural and chemical evolution was tracked every 10 ps during a 1 ns pyrolysis simulation by quantifying the Cy, chemical composition (C, H, and O), C hybridization (sp, sp2, and sp3 hybridized), and C-only ringed content (5, 6, and 7-membered C rings, and total number of C rings). Similar to the previous study,31 all structural metrics except for Cy were quantified as a function of instantaneous mass percent. For example, to get the mass percent of 6-membered C rings at a time t during pyrolysis, the mass of all C atoms forming part of 6-membered C-only rings was summed and divided by the total mass of the system at that time t. Cy was calculated as a mass percent relative to the total mass of the polymerized (i.e., non-pyrolyzed) system.
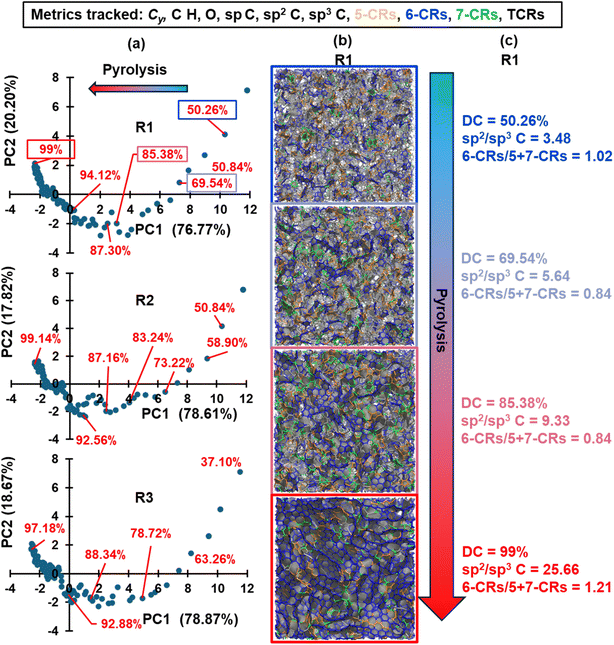
To differentiate the structural variance between pyrolyzed structures during different stages of pyrolysis, a principal component analysis (PCA) was performed on each replicate based on the 11 structural and chemical metrics (Cy, %C, %H, %O, sp C, sp2 C, sp3 C, 5-membered C rings, 6-membered C rings, 7-membered C rings, and total C rings). The PCA method is a linear dimensionality-reduction technique that transforms a large set of variables into a smaller set that still contains most information. This is accomplished by first constructing the data set's covariance matrix, computing the eigenvectors, identifying the principal components (PC) based on the eigenvectors corresponding to the largest eigenvalues, and linearly mapping the data to lower-dimensional space.54 A PCA plot consisting of the first and second principal components (PC1 and PC2) was generated for each replicate to visualize the variance developed and only unique structures that were reasonably distant from each other in reduced dimensions were chosen to proceed with the mechanical property and κ predictions. As will be shown in the pyrolysis results section, 21 unique structures were identified (initial polymerized structure, 7 intermediate pyrolyzed structures for replicates 1 and 2, and 6 intermediate pyrolyzed structures for replicate 3).
The chosen structures were converted from the reactive ReaxFF force field to the fixed-bond class II Interface Force Field41 based on the Polymer-Consistent Force Field40 (PCFF-IFF) using the LUNAR package's atom_typing and all2lmp modules by providing the data files and their respective atomic bond order values computed with the “fix reaxff/bonds” command. Bond order values were output every 0.01 ps and averaged over 0.1 ps to avoid identifying transient bonds as part of the bonded structure. The PCFF-IFF parameter set has been successfully used in a number of studies to accurately predict ρ, thermomechanical properties, and wetting contact angles of a number of polymer systems, including epoxies (DGEBA-DETDA), bismaleimides (BMI), polybenzoxazine (PBZ), polyether ether ketones (PEEK), polyamide composites, carbon nanotubes (CNTs), flCNTs, polymer-boron nitride (BN) composites, and BN nanotubes (BNNTs).55–61 For a full description of the energy terms of the PCFF-IFF force field, we refer the reader to Heinz et al.41
Due to the complex geometries observed during the early stages of pyrolysis, the LUNAR package was unable to provide a fully parameterized force field for some of the structures generated by ReaxFF (for example, a C–O–C triangular ring) because of a lack of parameters in PCFF-IFF for such unrealistic configurations. In these cases, parameters were manually chosen by looking through the PCFF-IFF parameters and finding the next best match. For example, if an oxygen atom in a six-membered ring was unable to be parameterized, the parameters for an oxygen atom in a five-membered ring were used. These manually selected bond, angle and dihedral parameters are included in Tables S1–S3† (respectively) of the ESI.†
Once unique structures were chosen based on the PCA plots, the PCFF-IFF data files were assigned a velocity seed at 0.1 K, heated to 300 K at a heating rate of 0.1 K ps−1, and held at 300 K in the constant pressure and temperature (NPT) ensemble for 1 ns to equilibrate the structures. Variable timesteps ranging from 0.1 to 1 fs were used depending on the degree of carbonization, where structures associated with a lower degree of carbonization (DC) required smaller timesteps to prevent instabilities due to the complex geometries observed in models in the early stages of pyrolysis. The degree of carbonization was calculated by normalizing the percent mass loss at any time t (Mloss(t)) with respect to the maximum (Mloss(max)) and minimum (Mloss(min)) possible mass losses:
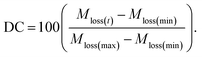 | (1) |
The Cy for phenolic resins has been observed to vary between 50–55%,2 so Mloss(max) is 50%. The polymerized structure developed in the previous study31 was a simplified approach to go from an uncured to fully cured state and the resulting crosslinked structure is representative of a fully polymerized branched phenolic resin. Since the starting point in this study is this fully polymerized structure, Mloss(min) is defined as 0% when no pyrolysis has occurred.
Converting from a reactive to a fixed-bond force has some structural implications considering that the former have no explicit bonding topology while the latter does, which leads to different mathematical expressions for system energy and thus potentially different structural configurations upon equilibration. A brief overview (including energy expressions) of the reactive ReaxFF and fixed-bond PCFF-IFF force fields can be found in the SI. To ensure no significant structural changes had occurred during the conversion process from ReaxFF to PCFF-IFF, the equilibrated PCFF-IFF structures were heated to the pyrolysis temperature of 3200 K (to have a direct comparison to the ReaxFF structures produced at that temperature) and analyzed via RDF and simulated XRD. The resulting RDF and XRD plots of the two force fields were compared by superimposing the ReaxFF and PCFF-IFF curves on top of each other to qualitatively check for any differences. The RDF plot was generated by performing an all-particle coordination analysis in OVITO, while the XRD plot was generated by using the “compute xrd” command in LAMMPS as described by Coleman et al.62 using a Cu-Kα radiation wavelength of 1.54 Å and scanning from 10° to 100° 2θ values. Diffraction data was output every 0.01 ps and averaged over 0.1 ps. Once structural integrity during the conversion process was verified, ρ of the equilibrated PCFF-IFF data files was calculated by averaging the last 100 ps of the 1 ns equilibration step. Refer to Fig. 1 (first pane) for a graphical summary of the steps described in this section.
Mechanical property predictions
The PCFF-IFF structures were processed with the auto_morse_bond_update module in the LUNAR package to convert the harmonic bond potentials to Morse bond potentials. These operations were performed to convert the force field from PCFF-IFF to the Reactive Interface Force Field (IFF-R).63 The Morse bond potential allows for bond dissociation during deformation and has been applied to predict physical properties of amorphous thermoset polymers (DGEBA-DETDA, BMI, polyamides, PBZ), flCNT/polymer interfaces, graphene/polymer composites, amorphous/crystalline thermoplastics (PEEK), and BNNTs/polymer interfaces.32–34,57,58,61,64–67 For a technical description of the implementation of a Morse bond potential in ReaxFF-produced pyrolyzed structures, the readers are referred to the ESI.†The MD models were subjected to uniaxial tension at a strain rate of 2 × 108 s−1 by deforming the simulation cell along each principal axis up to 40% strain or up to failure. E was calculated by performing a linear regression within the linear portion of the stress–strain plots as described by Odegard et al.68 and the reported values of E are the triaxial averages. Poisson's ratio (ν) was calculated through a linear regression of transverse vs. longitudinal strain as specified by Radue et al.,69 and the reported values of ν are the triaxial averages. Yield stress (σy) was identified via the end of linearity in the stress–strain plots. It should be emphasized that mechanical properties predicted in MD represent the response of structures with only molecular length scale defects (such as 5-CRs, 7-CRs, etc.) but absence of larger scale defects (such as porosity, voids, crack initiation, etc.) due to the nanometer length scale limitations. While properties in the linear elastic regime can be compared to experimental literature with greater confidence, it is extremely difficult to extrapolate failure associated properties via an MD model due to a lack of larger length scale defects which ultimately contribute to their macroscopic mechanical response. Hence, the focus of this work should be considered to appreciate the trends for structure–property relationships during pyrolysis rather than direct experimental validation.
All properties were predicted as a function of six metrics: the degree of carbonization (DC, %), ρ (g cm−3), percent mass of sp2 hybridized C (sp2 C, mass%), percent mass of 6-membered C rings (6-CRs, mass%), percent mass of total C-only rings (TCRs, mass%), and fractional free volume (FFV, %). These metrics were chosen as the independent variables for the production simulations as they quantify the chemistry, morphology, and property spectrum of glassy carbon. The DC quantifies the degree of pyrolysis and ρ is generally known to control the stiffness of polymer networks. The formation of 6-CRs rings and total TCRs is expected to increase the mechanical properties and κ by increasing the sizes of aromatic backbones which transfer load and heat. During pyrolysis, decreasing levels of FFV are expected to lead to increases in the mechanical properties.
The FFV was calculated with the free_volume module of the LUNAR package using a voxelization approach in which the simulation box is divided into cubic voxels and voxels are determined to either form part of atomic volume or free volume depending on whether there is atomic overlap with the voxel. Voxels with a linear dimension of 0.25 Å and a 1.06 Å probe diameter were used to simulate the ortho-positron particle size used in positron analysis lifetime spectroscopy (PALS) studies.70–72 Atomic sizes were modeled as hard spheres with van der Waals radii from Batsanov et al.73 and the boundary conditions of the free volume analysis were set to be periodic to be consistent with the MD models. For further information on the free volume calculation, refer to Kemppainen et al.42
For each predicted property, the corresponding data points in the depicted plots (Fig. 2, 5 , 7 and 8) represent one or more values (triaxial values in the case of mechanical and thermal properties) to avoid cluttering of visual data. For ρ, values within a 1% difference were averaged, while the other structural metrics were averaged if they were within a 2% difference. For example, if multiple replicate models had DC values within 2%, their resulting properties were averaged, and the corresponding standard deviation was calculated. The ρ and triaxial properties for each of the 21 structures are included in Table S4 of the ESI.†
It is well known that high strain rates affect the observed mechanical response of many organic materials due to their viscoelastic nature. Because MD is restricted to the nanosecond time scale, the strain rates employed (∼108 s−1) are orders of magnitude higher than experimental strain rates. Odegard et al.68 and Radue et al.69 observed a higher simulated mechanical response for a bisphenol-F epoxy system using the ReaxFF force field when compared to experimental values at strain rates of 2 × 108 s−1. Furthermore, Odegard et al.33 and Patil et al.32 also observed an overprediction at respective strain rates of 2 × 108 s−1 and 1 × 108 s−1 for the same epoxy system using the fixed-bond IFF-R force field when compared to experimental values. Patil et al.74 addressed the strain rate effect by proposing a phenomenological approach to correct MD overpredictions. Nonetheless, we have demonstrated in our previous work31 that the predicted mechanical properties of phenolic-based materials modeled with the CHON-2019 ReaxFF parameter set agree well with experimental values for nanoscale glassy carbon thin films.75–77 The lack of an observed strain rate effect is likely due to the lack of viscoelasticity in glassy carbons whose mechanical response is similar to that of ceramics. While some strain-rate dependent behavior has been observed in the mechanical response of ceramics, it has been attributed to microscale events (crack nucleation and propagation) which are not captured in the MD nano length scale.78 Thus, the strain rate correction approach of Patil et al.74 was not used in this study.
Thermal conductivity predictions
There are two common methods for determining κ in MD: (1) nonequilibrium molecular dynamics (NEMD) and equilibrium molecular dynamics (EMD).79 The EMD method utilizes the Green–Kubo formalism via the fluctuation-dissipation theorem80 and determines κ using
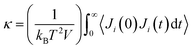 | (2) |
It has recently been shown that the NEMD and EMD approaches for calculating κ, while reliable for systems with only pairwise interactions, provide incorrect values for potentials that contain many-body interactions.82–84 Surblys et al.82 proved that the atomic stress approximation produces incorrect heat flux (and, hence, κ) and suggested modifying the atomic stress to include a “centroid” form. This formulation has been adopted into LAMMPS via the “compute centroid/stress/atom” command but as of the writing of this work does not support pair styles with many-body interactions or models with long range coulombic or dispersion forces. In a follow up study, Surblys et al.84 implemented the centroid atomic stress form to flexible, semi-flexible, and rigid water models to verify its validity. Boone et al.83 also observed the same errors in κ predictions as Surblys et al. and created a software patch to LAMMPS that implements an approach for 3- and 4-body potentials. Thus, while the authors are aware of the issues of using NEMD or EMD for predicting κ, it should be noted that the nature of this study is investigation of trends rather than direct experimental comparisons. While a direct experimental comparison will be made whenever possible, this work is focused on the evolution of properties as a function of the several metrics tracked during simulated pyrolysis. For a direct experimental validation of the pyrolysis methodology employed in this work, refer to our previous work.31
The EMD method was chosen due to it requiring a single cubic model to predict the anisotropic nature of κ, which was expected to be more pronounced in the end stages of pyrolysis as aligned aromatic structures formed in later stages of pyrolysis.31 The HFACF was calculated using the “fix ave/correlate” command in LAMMPS by sampling every 10 ps for a total of 2000 samples, and integration was performed numerically using the trapezoidal rule with the LAMMPS built-in “trap()” function embedded in the “variable” command. The κ values were averaged from the last 50 ps of an 8 ns simulation at 300 K in the NVT ensemble with variable time steps ranging from 0.1 to 0.25 fs (depending on the DC). For κ predictions, the PCFF-IFF force field was used since the simulations were performed at equilibrium (300 K) and no bonds were expected to dissociate.
The resulting data for κ were averaged and plotted as a function of the DC, ρ, sp2 C, 6-CRs, TCRs, and FFV. To quantify the effect of aromaticity on κ, the aromatic alignment was analyzed for each of the 21 structures by fitting a plane to each identified 5, 6, and 7-membered C-only rings, calculating their normal vector (n), taking the average of all normal vectors (N), and calculating the angle between N and the normal vector of each principal plane (nxy, nxz, and nyz), which themselves are equivalent to the principal axes (nxy = (0,0,1), nxz = (0,1,0), and nyz = (1,0,0). The measured angles are denoted as θi (i ∈ {x,y,z}) depending on which principal axis N is measured against, and a larger θi value corresponds to more alignment along the ith direction. This approach quantifies the effect of individual aromatic rings on κ, but not the effect of clusters of fused aromatic rings (continuous cluster consisting of 5, 6, and/or 7-membered C-only rings) which were expected to develop as pyrolysis progressed. Therefore, a second approach to quantifying the effect of aromaticity on κ was implemented where n for each aromatic ring in a fused aromatic ring cluster was averaged (nf), followed by an average of all nf to determine the overall fused aromatic rings normal (Nf). The angle between Nf and any of the principal axes is denoted as θfi and a larger θfi indicates preferential alignment along the ith direction. The reader is referred to Fig. S3 of the ESI† for a visual of the aromatic alignment calculations, and the triaxial κ, θi, and θfi values for each model are tabulated in Table S5 of the ESI.†
Results and discussion
Pyrolysis
The evolution of Cy, chemical composition, C hybridization, and C-ring content is summarized in Fig. 2 for all three replicates. Each plotted curve is the average of the three replicates at the corresponding simulation time in intervals of 10 ps. Just as in our previous study,31 the three models behaved similarly during the pyrolysis process as noted by the small error bars representing standard deviation placed every 50 ps (to avoid visual cluttering in the plots). Most chemical and structural changes occur within the first ∼300 ps of the pyrolysis simulation, with gradual changes occurring after that. The number of atoms at the end of pyrolysis was reduced to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 233, 10
233, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 201, and 10
201, and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 419 for replicates 1, 2, and 3, respectively. The average Cy was 50.78 ± 0.45% and agrees with the known literature values for phenolic resin of 50–55%.2
419 for replicates 1, 2, and 3, respectively. The average Cy was 50.78 ± 0.45% and agrees with the known literature values for phenolic resin of 50–55%.2
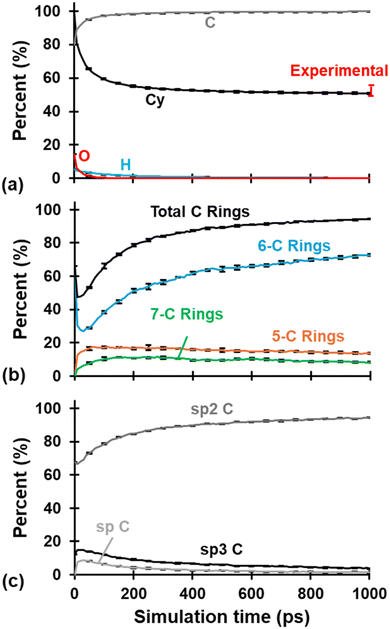 | ||
| Fig. 2 (a) Cy and chemical evolution, (b) C ring content evolution, and (c) C hybridization evolution. Each curve is the average of the three replicates and includes standard deviation error bars every 50 ps. Experimental Cy values from Savage.2 | ||
The resulting PCA plots for each replicate are shown in column (a) in Fig. 3, while columns (b) and (c) show the respective molecular visualization and select metrics of replicate R1 as pyrolysis progresses. The PC1 and PC2 axes represent the first and second principal components and the explained variance of each component is included in parentheses. PC1 and PC2 combined explained over ∼97% of the variance in all three studied replicates, and PC1 has a higher explained variance, indicating that horizontal distances between data emphasize structural uniqueness more than vertical distance. The arrow indicates the direction of pyrolysis, where the blue to red gradient represents the transition of a polymerized structure to pyrolyzed structure (this convention is applied to all the applicable figures below). In agreement with Fig. 2, the models exhibit a higher degree of structural variance in the early stages of pyrolysis as the polymerized phenolic resins volatilize and restructure to form a carbonaceous matrix. Towards the end stages of pyrolysis, the clustering of data in Fig. 3a suggests that changes are more gradual in nature, and it can be expected that, for a given replicate, the structural characteristics of a model at DC = 99% (labeled in red for replicate R1 in Fig. 3a) of simulated pyrolysis are practically the same as those of a model at DC = 98.98%. Based on the trends observed in Fig. 3, specific structures for each replicate were chosen (specified by the red data labels) for further analysis and property predictions.
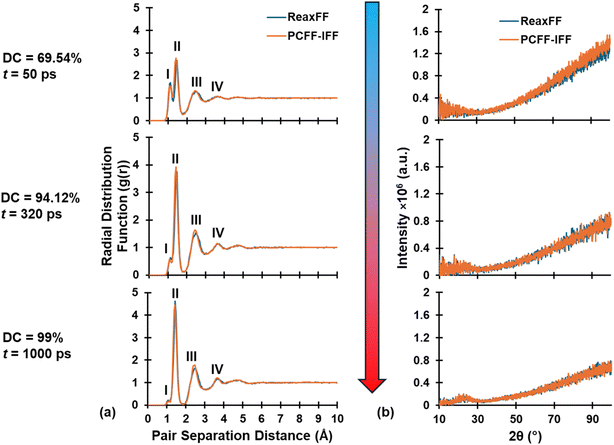
RDF and XRD plots for replicate R1 at various stages (DC = 69.54%, 94.12%, and 99% from top to bottom) during pyrolysis are shown in Fig. 4a and b, respectively, with ReaxFF and PCFF-IFF predictions superimposed. Specifically, the RDF and simulated XRD spectra demonstrate that ReaxFF-produced pyrolyzed structures remained intact after conversion and equilibration in PCFF-IFF. If major structural changes had occurred upon conversion from a reactive force field to a fixed-bond force field, the resulting structures would not be viable for analysis as they would not be representative of ReaxFF-produced pyrolyzed models. Similar trends were observed for the remaining replicates at various points during pyrolysis. As shown in Fig. 4a, the RDF plots are characterized by four distinct peaks respectively labeled I, II, III, and IV. The first peak (I) at ∼1.08 Å represents heteroatomic bonds (C–H, O–H, and H–H) which disappear due to heteroatom volatilization as pyrolysis progresses. The second peak's (II) increase in height is attributed to the increase in sp2 hybridized C–C bonds (bond length of ∼1.43 Å), while the increase in narrowing of the peak can be attributed to greater stability and more order in sp2 C–C bonds as pyrolysis progresses. The third (III) and fourth (IV) peaks are simply the second and third nearest neighbors and thus also increase in height and narrow in width for the same reasons and the second peak.
The evolution of ρ is shown in Fig. 5, which shows an exponential-like increase at higher DC values (Fig. 5a). The evolution of sp2 C (Fig. 5b) followed a linear trend and was consistent among the three replicates. The evolution of 6-CRs (Fig. 5c) and TCRs (Fig. 5d) also followed a linear trend but decreased significantly from the polymerized state upon initial volatilization followed by a steady increase. This explains the initial drop in ρ (DC = 37.1–50.55%) relative to the polymerized state and the exponential-like increase as the pyrolyzed structure densified due to the structural changes (DC > 50.55%). The fully polymerized ρ (pattern-filled data point) was 1.23 g cm−3 and agrees with literature values for crosslinked phenolic resins (1.2–1.25 g cm−3),85 while the ρ at the end of pyrolysis was 2.11 ± 0.01 g cm−3 and agrees with experimental values for the skeletal ρ of glassy carbon.86–88 The skeletal ρ was chosen as the experimental comparison because it excludes open pores, making it a better comparison with MD nano length scale glassy carbon models which lack the microporosity observed in bulk samples (i.e., bulk ρ measurements in experiments will be lower than skeletal ρ). While the polymerized ρ may look like an outlier along the trend, it's worth noting that the organic precursor intrinsically behaves differently from the resulting ceramic-like glassy carbon material. For a full list of the predicted ρ values at key stages of pyrolysis, refer to Table S4 of the ESI.†
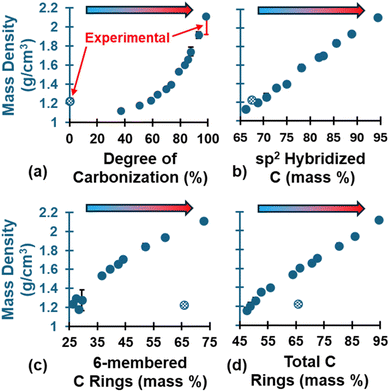 | ||
| Fig. 5 Evolution of ρ as a function of (a) DC, (b) sp2 C, (c) 6-CRs, and (d) TCRs. The patten-filled data point is the polymerized structure. This convention will be applied to all subsequent figures. Polymerized experimental values from Ashby.85 Pyrolyzed experimental values from Chekanova,86 Letellier,87 and Burket.88 Experimental values are indicated in red error bars for DC = 0% and 100%. | ||
The evolution of the FFV is plotted in Fig. 6 as a function of sp2 C, 6-CRs, and TCRs, which shows that FFV first increases upon initial volatilization and corroborates the decrease in ρ observed in Fig. 5. The exponential-like trend highlights the compounding effect all three metrics have on the densification of the pyrolyzed structure. While the chemical evolution converges within the first ∼400 ps of the pyrolysis simulation (Fig. 2), the structural changes occurring, specifically the evolution of hybridization state of C and ring content, continue to have major structural changes in the later stages of pyrolysis. Refer to Fig. S4–S6 of the ESI† for a size distribution analysis of pockets of free volume.
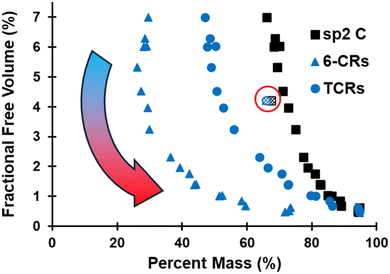 | ||
| Fig. 6 Evolution of FFV as a function of sp2 C, 6-CRs, and TCRs. The pattern-filled data points (circled in red) indicate the polymerized structure. | ||
Mechanical property predictions
The evolution of E, σy, and ν is shown in Fig. 7 as a function of (a) DC, (b) ρ, and (c) FFV. Also included in Fig. 7d are representative stress–strain plots for one model as pyrolysis progresses. A trend is observed where stiffness increases based on the stress values observed in the linear elastic regime. The polymerized model shows a failure strain >30%, while the pyrolyzed model shows a failure strain >20%, which is much higher than experimentally reported values for glassy carbon in tension of ∼1%.89 This discrepancy arises from the presence of only molecular length scale (5-CRs and 7-CRs) defects in MD models which lack access to higher length scale defects (porosity, voids, crack initiation sites) that contribute to the mechanical response. Specifically, MD simulations inherently operate at the nanoscale, focusing on atomic interactions and molecular behavior. Macroscopic properties, such as fracture energy and toughness, are influenced by a multitude of factors, such as porosity, fiber orientation, interphase properties, and presence of defects. Thus, it is important to make an appropriate comparison of mechanical properties within the linear elastic regime (i.e., with respect to nanostructures) and note the limitations of predicting properties past the linear regime.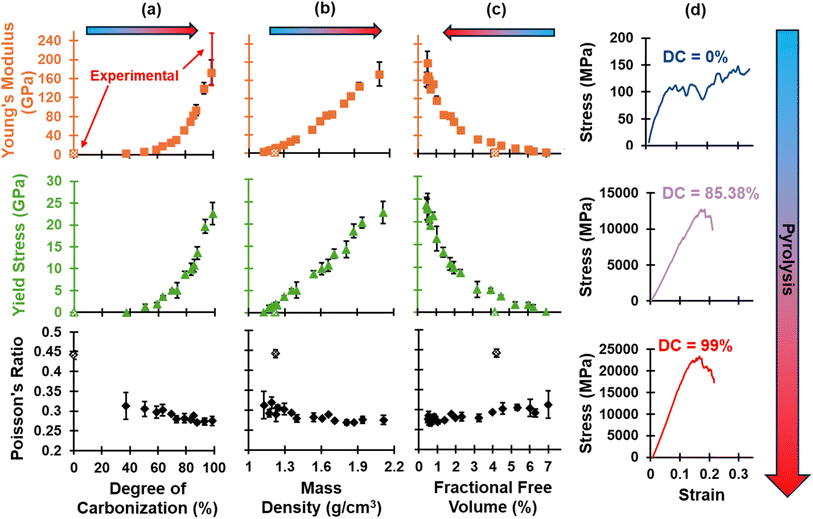 | ||
| Fig. 7 Evolution of E, σy, and ν as a function of (a) DC, (b) ρ, and (c) FFV, and (d) representative stress–strain plots for replicate R1 at three stages of pyrolysis. Experimental E values are indicated in red error bars for DC = 0% and DC = 100% and are from Ashby85 for polymerized phenolic resins and from He,75 Suk,76 and Yoon77 for pyrolyzed nano samples of glassy carbon. | ||
The polymerized E is 1.57 ± 0.14 GPa, which is lower than the reported values of 2.76–4.83 GPa.85 Focusing on the trends, Fig. 7a shows that E increases with an exponential-like trend as a function of the DC similarly to ρ (Fig. 5a), possibly due to the exponential-like reduction in free volume as densification occurs at later stages of simulated pyrolysis. At the end of the 1000 ps pyrolysis simulation, the average E was 164.47 ± 19.64 GPa, which falls within the low range of reported experimental values of 146–256 GPa for a nanoscale thin film of glassy carbon.75–77 The sudden decrease in 6-CRs and TCRs (Fig. 6) from the polymerized state to the early stages of pyrolysis indicate the crosslinked network immediately volatilizes upon the start of the pyrolysis process and gradually restructures into a glassy carbon matrix. It is also observed that as pyrolysis proceeds, the standard deviation of E increases (Fig. 7) due to the anisotropic behavior of pyrolyzed models as partially graphitized regions preferentially align, which was expected based on our previous study.31 The same trends observed in E are observed in σy, namely the exponential-like trend when plotted as a function of DC and FFV and the increase in standard deviation due to induced anisotropy at later stages of pyrolysis. The polymerized state has a notably lower σy of 0.09 ± 0.01 GPa than the fully pyrolyzed state, which is 22.54 ± 2.42 GPa. Lastly, ν decreases in a linear-like trend as the polymer is pyrolyzed. The polymerized model has a ν value of 0.44 ± 0.01, while the fully pyrolyzed state has a value of 0.27 ± 0.01. For a full list of the predicted properties in this section, refer to Table S4 of the ESI.†
Thermal conductivity predictions
The evolution of κ is shown in Fig. 8 as a function of (a) DC, (b) ρ, and (c) FFV, as well as (d) the evolution of sp2 hybridized C and ring content. The polymerized model has a κ value of 0.38 ± 0.01 W mK−1 and agrees with literature values from Pizzi et al.90 while fully pyrolyzed models have a κ value of 3.97 ± 0.86 W mK−1 and agree with literature values from Ferrer-Argemi et al.91 for crosslinked phenolic resins and glassy carbon nanowires, respectively. As seen with mechanical properties (Fig. 7), κ follows an exponential-like trend as pyrolysis progresses. While κ increases significantly (κ = 2.46 ± 0.01 W mK−1 and κ = 2.98 ± 0.58 W mK−1) upon initial volatilization (DC = 37.1% and 50.55%, respectively) relative to the polymerized state (κ = 0.38 ± 0.01 W mK−1) due to transformation from an organic precursor matrix to a carbonaceous matrix, it then decreases as the material continues to pyrolyze (DC = 58.84–73.22%) before increasing with an exponential-like trend (DC > 73.22%). The initial decrease followed by exponential-like increase can be explained in terms of the evolution of aromatic rings (d): between DC = 37.1–73.22%, 5-CRs and 7-CRs increase while 6-CRs decrease as the carbonaceous matrix rearranges due to volatilization, followed by an exponential-like increase of 6-CRs at DC > 73.22% at the expense of 5- and 7-CRs. In the context of pure graphite, non-6 membered C rings can lead to Stone–Wales defects92 and isolated 5-CRs or 7-CRs which lack resonance and are prone to greater degree of vibrational energy scattering, thus impeding thermal transport to a certain degree93,94 and explaining why κ only increases with an exponential-like trend at DC > 73.22%.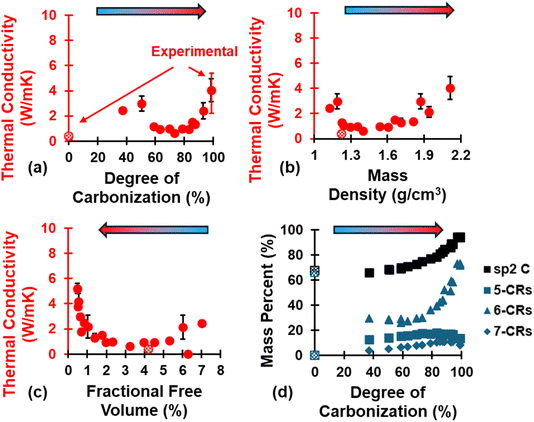 | ||
| Fig. 8 Evolution of κ as a function of (a) DC, (b) ρ, and (c) FFV, and of (d) sp2 C and ring content as a function of DC. Experimental values for polymerized and pyrolyzed phenolic resin from “Handbook of Thermoset Plastics”90 and Ferrer-Argemi et al.91 (respectively) and are indicated in red error bars for DC = 0% and 100%. | ||
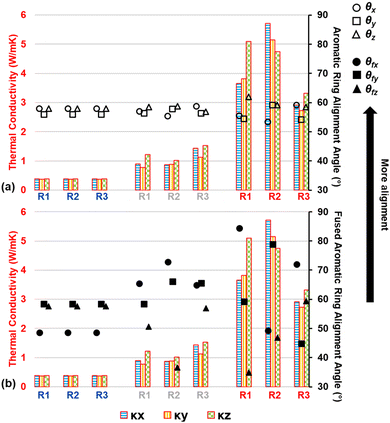
It was observed that as pyrolysis proceeded, the standard deviation gradually increased in magnitude, likely due to the anisotropic heat flow as aromatic structures aligned along specific orientations. Fig. 9 shows the triaxial components of κ (κx, κy, and κz), the aromatic ring alignment angles (θi, Fig. 9a), and the fused aromatic ring alignment angles (θfj, Fig. 9b) for each replicate (labeled R1, R2, and R3) at polymerized (blue replicate labels), semi-pyrolyzed (grey replicate labels), and pyrolyzed (red replicate labels) states. Each bar represents a component of κ and the corresponding vertically aligned scatter point represents the alignment relative to that axis. For example, the first bar (from left to right) represents κx = 0.39 W mK−1 for R1, and the scatter point on top of it is θx = 57.95° in Fig. 9a and θfx = 48.61° in Fig. 9b for the polymerized state. A complex interplay of effect of aromatic rings and fused aromatic rings on κ is revealed by analyzing θi and θfi for each replicate at various stages during pyrolysis. Since all replicates have the same polymerized structure as a starting point (DC = 0%), they share the same κ values which are isotropic in nature with an average κ = 0.38 ± 0.01 W mK−1. For R1 at a semi-pyrolyzed state (DC = 69.54%) and fully pyrolyzed state (DC = 99%), most aromatic alignment (Fig. 9a) occurs along the xz plane, which seems to corroborate the highest κ occurring along the z direction. In contrast, these same models show the most fused aromatic ring alignment (Fig. 9b) along the xy plane, which does not correlate with the highest κ occurring along the z axis. R2 exhibits most aromatic alignment (Fig. 9a) along the yz plane at semi-pyrolyzed (DC = 83.24%) and fully-pyrolyzed (DC = 99.14%) states and has a higher κ along the z direction for the half-pyrolyzed state and along the x direction for the fully-pyrolyzed state. In terms of fused aromatic ring clusters (Fig. 9b), R2 shows more alignment along the xy plane, which does not correlate with the highest κ occurring along the z direction for the semi-pyrolyzed state but does correlate with the highest κ occurring along the x axis for the pyrolyzed fully-pyrolyzed state. R3 has more aromatic ring alignment (Fig. 9a) along the xz plane for semi-pyrolyzed (DC = 88.34%) and fully-pyrolyzed (DC = 97.18%) states which seems to correlate with the higher κ occurring along the z direction for both states. In terms of fused aromatic ring alignment (Fig. 9b), however, the semi-pyrolyzed state has more alignment along the xy plane, contradicting the higher κ along the z direction, while the pyrolyzed state shows more alignment along the xz plane and corroborates the higher κz value. For a full list of the predicted properties in this section and aromatic alignment angles, refer to Table S5 of the ESI.†
Given the intrinsic high thermal conductivity of graphene along the graphitic direction, the mixed correlation between fused ring alignment (which aligns with graphitic direction) and directional thermal conductivity may appear unexpected. However, we believe that there are two competing factors acting against each other leading to mixed correlation. While a greater alignment of fused rings would ideally allow for more efficient transport of thermal energy spatially, even a single defect (non-6-membered ring or a vacancy defect) within the fused rings cluster can negate or worsen the efficiency of that transfer by acting as a thermal energy scattering site. Moreover, a non-6-membered ring also introduces local curvature which changes the overall directionality of the fused ring cluster.
Conclusions
Three MD models of a polymerized phenolic resin structure (∼30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms) were pyrolyzed (∼10
000 atoms) were pyrolyzed (∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms after pyrolysis) and ρ, mechanical properties, and κ were tracked as a function of the DC to determine which structural metrics significantly affected each property. The Cy of the fully pyrolyzed state agreed with experimental values. All predicted properties were plotted as a function of the DC, ρ, and the FFV to investigate the structure–property correlations of glassy carbon as it evolved from the pyrolysis a crosslinked phenolic resin.
000 atoms after pyrolysis) and ρ, mechanical properties, and κ were tracked as a function of the DC to determine which structural metrics significantly affected each property. The Cy of the fully pyrolyzed state agreed with experimental values. All predicted properties were plotted as a function of the DC, ρ, and the FFV to investigate the structure–property correlations of glassy carbon as it evolved from the pyrolysis a crosslinked phenolic resin.
The three replicates evolved similarly during simulated pyrolysis (Fig. 2), and select models were chosen for property predictions based on their structural variance analyzed via a principal component analysis (Fig. 3). It was shown that the FFV and densification had major influence on the increase of E, σy, and κ as shown by an exponential-like trend (Fig. 5, 7 and 8). An in-depth investigation into the evolution of structure–property correlations was conducted by tracking sp2 hybridized C and C ring content during simulated pyrolysis and analyzing their effect on FFV (Fig. 6). It was found that FFV increased upon initial volatilization before reducing as pyrolysis progresses, consequently increasing mechanical properties. κ, however, decreased in the initial stages of pyrolysis (Fig. 8a) due to an increase in Stone–Wales defects (5- and 7-CRs) and decrease in 6-CRs (Fig. 8d), with the former lacking resonance and impeding thermal transport. Once 6-CRs began increasing at the expense of 5- and 7-CRs, however, κ increased with an exponential-like trend.
The standard deviation at higher DC showed an increase for E, σy (Fig. 7a) and κ (Fig. 8a), indicating that the isotropic polymerized structures gained some anisotropy as they partially graphitized into aligned aromatic regions towards later stages of pyrolysis. E, ρ, and κ of the polymerized and pyrolyzed states matched experimental values from literature. Finally, while the highest component of κ of some pyrolyzed models corresponded to the alignment of aromatic rings, it was shown that clusters of fused aromatic rings also influenced thermal transport properties (Fig. 9). All the predicted properties for each replicate are tabulated in Tables S4 (mass densities and mechanical properties) and S5† (thermal conductivities and aromatic alignment angles) for the selected pyrolyzed structures based on the PCA method.
This work highlights one of the key aspects of MD simulations: the ability to capture properties of materials mid-processing in otherwise unobservable experimental processes. While experimental data for fully pyrolyzed materials can be found, experimental data for intermediately pyrolyzed materials is scarce due to the destructive nature and testing conditions (high temperatures, vacuums) required to pyrolyze a physical sample. By experimentally validating nano scale simulation methods at beginning (polymerized) and end (pyrolyzed) points of the pyrolysis process, intermediate matrix properties can be predicted as a function of the degree of pyrolysis and subsequently used as inputs to micro scale modeling techniques to predict process-induced residual stresses, damage, and ultimately failure. This multiscale ICME-based modeling approach provides valuable insight into composite multiscale failure mechanisms and can direct experimentalists in processing parameters optimization to improve composite performance by mitigating process-induced damage mechanisms.32–38
Data availability
The raw data and processed data required to reproduce these findings cannot be shared at this time because it is part of on-going studies but may be available upon request.Author contributions
Ivan Gallegos: conceptualization, methodology, software, validation, formal analysis, investigation, writing – original draft, visualization. Vikas Varshney: conceptualization, methodology, resources, writing – review & editing, supervision, project administration. Josh Kemppainen: software, formal analysis, resources, data curation, writing – review & editing, visualization. Gregory M. Odegard: resources, writing – review & editing, supervision, project administration, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was partially supported by the NASA Space Technology Research Institute (STRI) for Ultra-Strong Composites by Computational Design (US-COMP), grant NNX17AJ32G. Superior, a high-performance computing cluster at Michigan Technological University (MTU), and Department of Defense Supercomputing Resource Center (DSRC) resources were used in obtaining the MD simulation results presented in this publication. The authors would like to thank the Computational Mechanics & Materials Research (CMMR) Lab members at MTU for valuable discussion and insights.References
- G. Gordon, Space exploration: mass ratios for different missions, presented in Part at the AIAA SPACE 2007 Conference & Exposition, 2007 Search PubMed.
- G. Savage, Carbon–Carbon Composites, Springer, 1993 Search PubMed.
- K. Jurkiewicz, S. Duber, H. Fischer and A. Burian, J. Appl. Crystallogr., 2017, 50, 36–48 CrossRef CAS.
- J. E. Sheehan, K. Buesking and B. Sullivan, Annu. Rev. Mater. Sci., 1994, 24, 19–44 CrossRef CAS.
- A. Gardziella, L. A. Pilato and A. Knop, Phenolic Resins: Chemistry, Applications, Standardization, Safety and Ecology, Springer Science & Business Media, 2013 Search PubMed.
- K. Hirano and M. Asami, React. Funct. Polym., 2013, 73, 256–269 CrossRef CAS.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in't Veld, A. Kohlmeyer, S. G. Moore and T. D. Nguyen, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- L. Monticelli and D. P. Tieleman, Biomolecular Simulations: Methods and Protocols, 2013, pp. 197–213, DOI:10.1007/978-1-62703-017-5_8.
- J. R. Gissinger, B. D. Jensen and K. E. Wise, Macromolecules, 2020, 53, 9953–9961 CrossRef CAS.
- A. C. Van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 9396–9409 CrossRef CAS.
- Y. Xiao, J.-F. Zeng, J.-W. Liu, X. Lu and C.-M. Shu, Fuel, 2022, 318, 123583 CrossRef CAS.
- T. P. Senftle, S. Hong, M. M. Islam, S. B. Kylasa, Y. Zheng, Y. K. Shin, C. Junkermeier, R. Engel-Herbert, M. J. Janik and H. M. Aktulga, npj Comput. Mater., 2016, 2, 1–14 CrossRef.
- A. Vashisth, C. Ashraf, W. Zhang, C. E. Bakis and A. C. Van Duin, J. Phys. Chem. A, 2018, 122, 6633–6642 CrossRef CAS.
- Y. K. Shin, H. Kwak, A. V. Vasenkov, D. Sengupta and A. C. Van Duin, ACS Catal., 2015, 5, 7226–7236 CrossRef CAS.
- A. Lele, P. Krstic and A. C. Van Duin, J. Phys. Chem. A, 2022, 126, 568–582 CrossRef CAS PubMed.
- N. Nayir, Y. Wang, S. Shabnam, D. R. Hickey, L. Miao, X. Zhang, S. Bachu, N. Alem, J. Redwing and V. H. Crespi, J. Phys. Chem. C, 2020, 124, 28285–28297 CrossRef CAS.
- A. Izumi, T. Nakao and M. Shibayama, Soft Matter, 2012, 8, 5283–5292 RSC.
- J. D. Monk, J. B. Haskins, C. W. Bauschlicher Jr and J. W. Lawson, Polymer, 2015, 62, 39–49 CrossRef CAS.
- Y. Shudo, A. Izumi, K. Hagita, T. Nakao and M. Shibayama, Polymer, 2016, 103, 261–276 CrossRef CAS.
- Y. Shudo, A. Izumi, K. Hagita, T. Nakao and M. Shibayama, Polymer, 2017, 116, 506–514 CrossRef CAS.
- A. Izumi, Y. Shudo, K. Hagita and M. Shibayama, Macromol. Theory Simul., 2018, 27, 1700103 CrossRef.
- D.-e. Jiang, A. C. Van Duin, W. A. Goddard III and S. Dai, J. Phys. Chem. A, 2009, 113, 6891–6894 CrossRef CAS PubMed.
- T. G. Desai, J. W. Lawson and P. Keblinski, Polymer, 2011, 52, 577–585 CrossRef CAS.
- T. Qi, C. W. Bauschlicher Jr, J. W. Lawson, T. G. Desai and E. J. Reed, J. Phys. Chem. A, 2013, 117, 11115–11125 CrossRef CAS PubMed.
- C. W. Bauschlicher Jr, T. Qi, E. J. Reed, A. Lenfant, J. W. Lawson and T. G. Desai, J. Phys. Chem. A, 2013, 117, 11126–11135 CrossRef PubMed.
- Y. Zhong, X. Jing, S. Wang and Q.-X. Jia, Polym. Degrad. Stab., 2016, 125, 97–104 CrossRef CAS.
- A. Harpale, S. Sawant, R. Kumar, D. Levin and H. B. Chew, Carbon, 2018, 130, 315–324 CrossRef CAS.
- M. Purse, B. Holmes, M. Sacchi and B. Howlin, J. Mater. Sci., 2022, 57, 7600–7620 CrossRef CAS.
- Y. Yan, J. Xu, S. Liu, M. Wang and C. Yang, Chem. Eng. Sci., 2023, 272, 118606 CrossRef CAS.
- J. R. Gissinger, S. R. Zavada, J. G. Smith, J. Kemppainen, I. Gallegos, G. M. Odegard, E. J. Siochi and K. E. Wise, Carbon, 2023, 202, 336–347 CrossRef CAS.
- I. Gallegos, J. Kemppainen, J. R. Gissinger, M. Kowalik, A. Van Duin, K. E. Wise, S. Gowtham and G. M. Odegard, Carbon Trends, 2023, 12, 100290 CrossRef CAS.
- S. U. Patil, S. P. Shah, M. Olaya, P. P. Deshpande, M. Maiaru and G. M. Odegard, ACS Appl. Polym. Mater., 2021, 3, 5788–5797 CrossRef CAS.
- G. M. Odegard, S. U. Patil, P. P. Deshpande, K. Kanhaiya, J. J. Winetrout, H. Heinz, S. P. Shah and M. Maiaru, Macromolecules, 2021, 54, 9815–9824 CrossRef CAS.
- P. S. Gaikwad, A. S. Krieg, P. P. Deshpande, S. U. Patil, J. A. King, M. Maiaru and G. M. Odegard, ACS Appl. Polym. Mater., 2021, 3, 6407–6415 CrossRef CAS.
- M. Maiaru, Effect of uncertainty in matrix fracture properties on the transverse strength of fiber reinforced polymer matrix composites, presented in part at the 2018 AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 2018 Search PubMed.
- R. J. D'Mello, A. M. Waas, M. Maiaru and R. Koon, Integrated Computational Modeling For Efficient Material and Process Design for Composite Aerospace Structures, presented in Part at the AIAA Scitech 2020 Forum, 2020 Search PubMed.
- P. P. Deshpande, S. S. Shah, S. U. Patil, K. Kashmari, M. Olaya, G. M. Odegard and M. Maiaru, Multiscale Modelling of the Cure Process in Thermoset Polymers Using ICME, presented in Part at the American Society for Composites Thirty-Fifth Technical Conference, 2020 Search PubMed.
- S. S. Shah and M. Maiaru, Microscale Analysis of Virutally Cured Polymer Matrix Composites Accounting for Uncertainty in Matrix Properties During Manufacturing, Presented in Part at the American Society for Composites Thirty-Third Technical Conference, 2018 Search PubMed.
- H. M. Aktulga, S. A. Pandit, A. C. Van Duin and A. Y. Grama, SIAM J. Sci. Comput., 2012, 34, C1–C23 CrossRef.
- H. Sun, S. J. Mumby, J. R. Maple and A. T. Hagler, J. Am. Chem. Soc., 1994, 116, 2978–2987 CrossRef CAS.
- H. Heinz, T.-J. Lin, R. Kishore Mishra and F. S. Emami, Langmuir, 2013, 29, 1754–1765 CrossRef CAS PubMed.
- J. Kemppainen, J. R. Gissinger and G. M. Odegard, J. Chem. Inf. Model., 2024, 64, 5108–5126 CrossRef CAS PubMed.
- A. Stukowski, Model. Simulat. Mater. Sci. Eng., 2009, 18, 015012 CrossRef.
- A. Kohlmeyer and J. Vermaas, TopoTools: Release 1.9, 2022, DOI:10.5281/zenodo.598373.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS.
- M. Kowalik, C. Ashraf, B. Damirchi, D. Akbarian, S. Rajabpour and A. C. Van Duin, J. Phys. Chem. B, 2019, 123, 5357–5367 CrossRef CAS.
- H. M. Aktulga, J. C. Fogarty, S. A. Pandit and A. Y. Grama, Parallel Comput., 2012, 38, 245–259 CrossRef.
- J. Kemppainen, I. Gallegos, A. S. Krieg, J. R. Gissinger, K. E. Wise, M. Kowalik, J. A. King, S. Gowtham, A. van Duin and G. M. Odegard, ACS Appl. Eng. Mater., 2023, 1, 2555–2566 CrossRef CAS PubMed.
- C. Ashraf and A. C. Van Duin, J. Phys. Chem. A, 2017, 121, 1051–1068 CrossRef CAS PubMed.
- L. Zhang, M. Kowalik, Z. Gao, C. M. Ashraf, S. Rajabpour, C. Bumgardner, Y. Schwab, B. Damirchi, J. Zhu and D. Akbarian, Carbon, 2020, 159, 432–442 CrossRef CAS.
- A. Vashisth, M. Kowalik, J. C. Gerringer, C. Ashraf, A. C. Van Duin and M. J. Green, ACS Appl. Nano Mater., 2020, 3, 1881–1890 CrossRef CAS.
- P. S. Gaikwad, M. Kowalik, A. van Duin and G. M. Odegard, RSC Adv., 2022, 12, 28945–28953 RSC.
- P. S. Gaikwad, M. Kowalik, B. D. Jensen, A. Van Duin and G. M. Odegard, ACS Appl. Nano Mater., 2022, 5, 5915–5924 CrossRef CAS PubMed.
- R. Bro and A. K. Smilde, Anal. Methods, 2014, 6, 2812–2831 RSC.
- S. U. Patil, M. S. Radue, W. A. Pisani, P. Deshpande, H. Xu, H. Al Mahmud, T. Dumitrică and G. M. Odegard, Comput. Mater. Sci., 2020, 185, 109970 CrossRef CAS.
- P. P. Deshpande, M. S. Radue, P. Gaikwad, S. Bamane, S. U. Patil, W. A. Pisani and G. M. Odegard, Langmuir, 2021, 37, 11526–11534 CrossRef CAS.
- W. A. Pisani, M. S. Radue, S. U. Patil and G. M. Odegard, Composites, Part B, 2021, 211, 108672 CrossRef CAS.
- W. A. Pisani, D. N. Wedgeworth, M. R. Roth, J. K. Newman and M. K. Shukla, J. Phys. Chem. C, 2021, 125, 15569–15578 CrossRef CAS.
- S. S. Bamane, P. S. Gaikwad, M. S. Radue, S. Gowtham and G. M. Odegard, Polymers, 2021, 13, 2162 CrossRef CAS PubMed.
- G. Sachdeva, S. U. Patil, S. S. Bamane, P. P. Deshpande, W. A. Pisani, G. M. Odegard and R. Pandey, J. Mater. Res., 2022, 37, 4533–4543 CrossRef CAS.
- W. A. Pisani, M. R. Roth, M. K. Shukla, D. N. Wedgeworth and J. K. Newman, Engineer Research and Development Technical Report, 2023, DOI:10.21079/11681/46713.
- S. Coleman, D. Spearot and L. Capolungo, Model. Simulat. Mater. Sci. Eng., 2013, 21, 055020 CrossRef CAS.
- J. J. Winetrout, K. Kanhaiya, J. Kemppainen, P. J. in't Veld, G. Sachdeva, R. Pandey, B. Damirchi, A. van Duin, G. M. Odegard and H. Heinz, Nat. Commun., 2024, 15, 7945 CrossRef CAS PubMed.
- W. A. Pisani, J. K. Newman and M. K. Shukla, Ind. Eng. Chem. Res., 2021, 60, 13604–13613 CrossRef CAS.
- G. M. Odegard, S. U. Patil, P. S. Gaikwad, P. Deshpande, A. S. Krieg, S. P. Shah, A. Reyes, T. Dickens, J. A. King and M. Maiaru, Soft Matter, 2022, 18, 7550–7558 RSC.
- K. Kashmari, H. Al Mahmud, S. U. Patil, W. A. Pisani, P. Deshpande, M. Maiaru and G. M. Odegard, ACS Appl. Eng. Mater., 2023, 1, 3167–3177 CrossRef CAS PubMed.
- S. S. Bamane, M. B. Jakubinek, K. Kanhaiya, B. Ashrafi, H. Heinz and G. M. Odegard, ACS Appl. Nano Mater., 2023, 6, 3513–3524 CrossRef CAS.
- G. M. Odegard, B. D. Jensen, S. Gowtham, J. Wu, J. He and Z. Zhang, Chem. Phys. Lett., 2014, 591, 175–178 CrossRef CAS.
- M. S. Radue, B. D. Jensen, S. Gowtham, D. R. Klimek-McDonald, J. A. King and G. M. Odegard, J. Polym. Sci., Part B:Polym. Phys., 2018, 56, 255–264 CrossRef CAS PubMed.
- Y. Yampolskii and V. Shantarovich, in Materials Science of Membranes for Gas and Vapor Separation, 2006, pp. 191–210, DOI:10.1002/047002903X.ch6.
- J. C. Jansen, M. Macchione, E. Tocci, L. De Lorenzo, Y. P. Yampolskii, O. Sanfirova, V. P. Shantarovich, M. Heuchel, D. Hofmann and E. Drioli, Macromolecules, 2009, 42, 7589–7604 CrossRef CAS.
- Y. C. Jean, Microchem. J., 1990, 42, 72–102 CrossRef CAS.
- S. S. Batsanov, Inorg. Mater., 2001, 37, 871–885 CrossRef CAS.
- S. U. Patil, A. S. Krieg, L. K. Odegard, U. Yadav, J. A. King, M. Maiaru and G. M. Odegard, Soft Matter, 2023, 19, 6731–6742 RSC.
- H. He and M. F. Thorpe, Phys. Rev. Lett., 1985, 54, 2107 CrossRef CAS PubMed.
- J. W. Suk, S. Murali, J. An and R. S. Ruoff, Carbon, 2012, 50, 2220–2225 CrossRef CAS.
- J. Yoon, Y. Jang, K. Kim, J. Kim, S. Son and Z. Lee, Carbon, 2022, 196, 236–242 CAS.
- G. Ravichandran and G. Subhash, Int. J. Solids Struct., 1995, 32, 2627–2646 Search PubMed.
- P. K. Schelling, S. R. Phillpot and P. Keblinski, Phys. Rev. B, 2002, 65, 144306 Search PubMed.
- D. J. Evans and G. P. Morriss, Statistical Mechanics of Nonequilibrium Liquids, ANU Press, 2007 Search PubMed.
- S. Chinkanjanarot, J. M. Tomasi, J. A. King and G. M. Odegard, Carbon, 2018, 140, 653–663 CrossRef CAS.
- D. Surblys, H. Matsubara, G. Kikugawa and T. Ohara, Phys. Rev. E, 2019, 99, 051301 CAS.
- P. Boone, H. Babaei and C. E. Wilmer, J. Chem. Theory Comput., 2019, 15, 5579–5587 CAS.
- D. Surblys, H. Matsubara, G. Kikugawa and T. Ohara, J. Appl. Phys., 2021, 130, 215104 CAS.
- M. F. Ashby, Materials and the Environment: Eco-Informed Material Choice, Elsevier, 2012 Search PubMed.
- V. D. Chekanova and A. S. Fialkov, Russ. Chem. Rev., 1971, 40, 413 Search PubMed.
- M. Letellier, A. Szczurek, M. C. Basso, A. Pizzi, V. Fierro, O. Ferry and A. Celzard, Carbon, 2017, 112, 208–218 CAS.
- C. L. Burket, Doctor of Philosophy Dissertation, The Pennsylvania State University, 2007.
- W. V. Kotlensky and D. B. Fischbach, Tensile and Structural Properties of Glassy Carbon, Jet Propulsion Laboratory, California Institute of Technology, 1965 Search PubMed.
- A. Pizzi and C. C. Ibeh, Handbook of Thermoset Plastics, Elsevier Inc, 3rd edn, 2014 Search PubMed.
- L. Ferrer-Argemi, E. S. Aliabadi, A. Cisquella-Serra, A. Salazar, M. Madou and J. Lee, Carbon, 2018, 130, 87–93 CAS.
- S. K. Tiwari, S. K. Pandey, R. Pandey, N. Wang, M. Bystrzejewski, Y. K. Mishra and Y. Zhu, Small, 2023, 19, 2303340 CAS.
- S. Ebrahimi and M. Azizi, Mol. Simul., 2018, 44, 236–242 CAS.
- Y. Zhang, Y. Cheng, Q. Pei, C. Wang and Y. Xiang, Phys. Lett. A, 2012, 376, 3668–3672 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4na00824c |
| This journal is © The Royal Society of Chemistry 2025 |