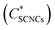Gum Arabic induced assembly of cellulose nanocrystals in aqueous media

Abstract

Entropy-driven assembly of nematic liquid-crystal phases of cellulose nanocrystals (SCNCs) in aqueous suspensions results in the emergence of a cholesteric liquid crystalline phase (N* phase). We report that a solvated, non-adsorbing, highly branched natural polysaccharide, Gum Arabic (GA), strongly affects the assembly of the SCNCs and modifies the phase diagram: GA leads to significant crowding of the SCNC rods and induces a new liquid–liquid phase transition, where SCNC-rich and GA-rich droplets coexist. The solvated GA does not induce coagulation or gelation of the suspended SCNCs (at low concentrations of 1–3 wt% of GA). In the SCNC-rich droplets, finite-sized nematic nano-islands assemble and further evolve into cholesteric tactoids and nucleate the formation of the N* phase at significantly lower concentration (about 1.5 wt%) than in GA-free suspensions. We observe that the inter-particle distance and the chiral pitch of the N* phase are determined by the concentration of GA (for a given SCNC concentration). The resulting mesophases are characterized via transmission electron microscopy at cryogenic temperatures (cryo-TEM), small-angle X-ray scattering (SAXS), and polarized optical microscopy (POM). Our findings indicate that GA can be used to tune the phase diagram and optical properties of SCNC suspensions, and overcome kinetic barriers that lead to gelation or kinetic arrest.

---

1. Introduction

Highly anisotropic colloidal rods are known to self-assemble from suspensions into (lyotropic) liquid crystalline (LC) phases due to the interplay between different entropic contributions.^1–3 In these systems, non-isotropic excluded volume interactions among the rods drive their co-alignment and the formation of nematic LC phases above a threshold concentration.^4–6

An important example of self-assembling colloidal rods, with a typical aspect ratio of 10–15, is that of sulfuric-acid hydrolyzed cellulose nanocrystals (SCNCs).^7,8 SCNCs are highly crystalline cylindrical nanorods obtained via acid hydrolysis of cellulose-rich sources, such as wood or cotton pulp.⁹ SCNCs form electrostatically stabilized aqueous suspensions due to the sulfate half-ester groups at their surface.⁹ In water, above a threshold concentration 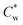, the suspensions undergo a first-order liquid–liquid phase transition to a chiral nematic (cholesteric, N*) mesophase that coexists with an isotropic phase (I).^10–12 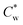, typically between 3–4 wt%, depends on the dimensions of the SCNCs and their surface charge.¹³

The cholesteric phase is nucleated by micron-sized nematic droplets (tactoids) that are formed within the isotropic phase. As was observed experimentally, and rationalized theoretically, tactoids only form above a minimal volume of around V ≈ 8 ± 6 × 10³ μm³.^3,14,15 The shape (spherical, ellipsoidal, or spindle-shaped), degree of anisotropy, range of orientational ordering, structure, onset of chirality, and the assembly of tactoids into the cholesteric (N*) phase have been thoroughly investigated.^14–17 Fewer studies characterized nanometric assemblies of SCNCs in the isotropic regime, and their role in the evolution of the N* phase.^14,15,18

As mentioned above, SCNC self-assembly is driven by repulsive excluded volume (entropic) interactions. Thus, it is expected that (attractive) depletion interactions, such as those induced by non-adsorbing polymers that lead to particle crowding, would modify the chemical potential of the combined system and the balance of the different entropic interactions.¹⁸ SCNC crowding could destabilize the suspensions and induce flocculation, modify the (equilibrium) interparticle distance, reduce the nucleation barrier for the assembly of tactoids,^19,20 and modify their structure.

A few attempts to utilize non-adsorbing linear polymers for inducing depletion interactions in SCNC suspensions were reported.^21,22 Using high molecular weight and relatively high concentrations of linear polymers, required for a significant depletion effect, the studies mainly observed polymer-induced gelation and kinetic arrest (see Section 1 of the ESI† for a summary of the findings).^23–25 Recently, it was suggested that branched polymers should be significantly more effective depletants and would induce colloidal crowding already at relatively low polymer concentrations.²⁶

Gum Arabic (GA) is a highly branched natural polysaccharide used since the days of antiquity to stabilize nanoparticles and colloids in aqueous media.²⁷ It has been used by the ancient Egyptians as a dispersing agent for carbonaceous particles, adhesive and embalming fluids.²⁸ Nowadays, this hydrocolloid is highly used in food, pharmaceuticals, cosmetics, textile, paper, ink, adhesive, paint and printing.²⁹ GA is known to exhibit Newtonian (non-viscoelastic) dynamic behavior up to high concentrations (above 10 wt%) probably due to its hyperbranched structure.³⁰ The polysaccharide comprises a mixture of molar masses ranging from 5 kg mol⁻¹ to 1000 kg mol⁻¹ with a mean molar mass around 500 kg mol⁻¹. The three main fractions comprise a hyperbranched arabinogalactan-rich polysaccharide fraction (88%), a polysaccharide–protein conjugates (AGP, 10%), and a fraction of glycoproteins (GP, 2%).³¹ In the dilute regime investigated here, at pH above its pK_a (about 2.4),³² GA forms (negatively) charged molecular assemblies with typical dimensions of 2–7 nm.³³

In the study presented here, we describe the effect of low concentrations of GA (up to about 3 wt%) on the assembly of SCNCs in dilute suspensions (1–3 wt% SCNCs, 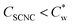).³³ GA does not adsorb onto SCNCs (see paragraph 2.3 of the ESI†) and is expected to exhibit significant depletion interactions already at low concentrations, due to its branched structure. Visual inspection shows that the threshold concentration for the emergence of the I–N* transition is reduced in GA solutions. In addition, the volume fraction of the N* phase, for a given SCNC concentration, is increased as compared to GA-free suspensions.

Using transmission electron microscopy at cryogenic temperatures (Cryo-TEM) and Small Angle X-ray scattering (SAXS), we also observe that GA induces significant crowding of SCNCs, followed by liquid–liquid phase separation into coexisting SCNC-rich and GA-rich droplets. In the SCNC-rich droplets, nematic nano-islands of SCNCs³⁴ are observed to form pre-tactoid assemblies that are not observed in GA-free suspensions. The nematic assemblies grow into micron-sized tactoids and further into a macroscopic cholesteric SCNC phase as the concentration of GA is increased (N* is already observed in 1.5 wt% SCNC suspensions that contain 3 wt% GA). Polarized optical microscopy (POM) is used to characterize the chiral pitch in tactoids and SCNC mesophases. Below we describe the observations in detail and discuss their molecular and colloidal origins.

2. Experimental

2.1. Materials

Cellulose nanocrystal (SCNC) suspension (10 wt%, Na⁺ counterion, pH ∼7) was purchased from Cellulose Lab Canada (CAS# 9004-34-6, https://www.celluloselab.com/). The SCNC typical dimensions, as reported by the manufacturer, are 5–20 nm wide and 140–200 nm long. SCNC suspensions form electrostatically stabilized suspensions in water. The negative charges are attributed to the half-sulphate ester groups on their surface (pK_a ∼1.99).

Gum Arabic (GA) powder was purchased from Sigma-Aldrich, Rehovot, Israel (CAS# 9000-01-5, https://www.sigmaaldrich.com/IL/en/product/sigma/g9752). GA molecules are negatively charged at pH = 7 (pK_a ∼2.2) due to the ionization of the carboxylic groups.³²

2.2. Preparation methods

2.2.1. Preparation of solutions. Concentrated solutions of GA were prepared by dissolving the powder in water at room temperature. The solutions were mixed for 2 hours using a magnetic stirrer and diluted to the final concentration.

2.2.2. Preparation of suspensions. As-received SCNC aqueous slurry (10 wt% suspension in water) was diluted to a desired concentration using Millipore water (18 MΩ cm). Then, the suspension was tip-sonicated (Ultrasonic processor model VCX-130, Sonics & Materials Inc.) at 30% amplitude (130 W, 20 kHz) for 4 minutes. All suspensions were cooled during sonication to prevent the hydrolysis of the sulfate groups at the SCNC surface due to overheating.³⁵

2.2.3. Preparation of GA-SCNC mixtures. GA powder was weighed and dissolved in sonicated SCNC suspensions to get the desired concentration combination.

2.3. Characterization

2.3.1. Small-angle X-ray scattering (SAXS). Measurements were carried out using SAXSLAB GANESHA 300-XL CuKα radiation generated by a Genix 3D Cu-source with an integrated monochromator, 3-pinhole collimation, and a two-dimensional Pilatus 300 K detector. Scattering intensity I(q) was recorded in the range of 0.007 < q < 0.25 Å⁻¹. The scattering vector q = (4π/λ)·sin θ, 2θ is the scattering angle and λ the wavelength. The measurements were performed under vacuum at ambient temperature (22–23 °C). The specimens were sealed in thin-walled quartz capillaries about 1.5 mm in diameter and 0.01 mm wall thickness; the scattering curves were corrected for counting time and background absorption. The 2D SAXS patterns were azimuthally averaged to produce one-dimensional intensity profiles, I vs. q, using the two-dimensional data reduction program SAXSGUI. The scattering spectra of the solvent were subtracted from the corresponding solution data using the Irena package in Igor Pro 9 from WaveMetrics (Portland, Oregon).³⁶

2.3.2. Cryogenic transmission electron microscopy (Cryo-TEM). The samples were prepared by applying a 3 μL drop to a TEM grid (300 mesh Cu Lacey substrate, Ted Pella, Ltd., Redding, CA, USA) following a short pre-treatment of the grid via glow discharge. The excess liquid was blotted, and the specimen was vitrified by rapid plunging into liquid ethane precooled by liquid nitrogen using a vitrification robot system (Vitrobot Mark IV, FEI). The rapid cooling results in a physical fixation of the liquid state, so as to preserve the native assemblies, and prevents the formation of either cubic- or hexagonal ice. The vitrified samples were examined at −179 °C using an FEI Tecnai 12 G2 TWIN TEM operated at 120 kV and equipped with a Gatan model 626 cold stage. The images were recorded by a 4 K × 4 K FEI Eagle CCD camera in low-dose mode. TIA (Tecnai Imaging & Analysis) software was used to record the images.

2.3.3. Polarized optical microscopy (POM). POM images of SCNC suspensions were taken using an Olympus BX53-F2 microscope equipped with a high-resolution Olympus DP74 camera. Images were taken using polarizers in a perpendicular arrangement and analyzed using ImageJ.

3. Results

In the study presented here, we investigated the effect of GA (1–3 wt%) on the organization of SCNCs in dilute suspensions (below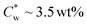 ). SAXS, cryo-TEM imaging, and POM were used to characterize the mesophases formed by SCNCs in GA solutions.

3.1. SCNC suspensions in water

The macroscopic phase diagram of SCNCs in GA-free suspensions is presented in Fig. S2 of the ESI.† In this system, the onset of the isotropic–cholesteric (I–N*) biphasic regime is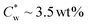 . POM images of the lower (N*) phase present the typical fingerprint pattern with a concentration-dependent helical Pitch (Fig. S2C of the ESI†). As reported before,³⁷ SAXS analysis (Fig. S3 and Table S2 of the ESI†) indicates that the inter-particle distance, d₀, scales with the concentration of the SCNCs, with a power law dependence of d₀ ∼ C^−0.38 at SCNC concentrations < 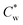, and d₀ ∼ C^−0.48 at .

Typical cryo-TEM images show long-range nematic order in the N* phase and a random orientation of rods in the isotropic phase (Fig. 1A and B, respectively). Low-magnification images of these suspensions are presented in Fig. S4 of the ESI,† indicating that this is characteristic of the whole sample.

Fig. 1 Cryo-TEM images of 4 wt% suspensions of SCNCS in water. (A) The N* (lower) phase, and (B) the isotropic (upper) phase.

3.2. Suspensions of SCNCs in GA solutions

The SAXS curves of GA solutions (Fig. S1†) are consistent with previous measurements,³³ indicating that the solutions comprise negatively charged aggregates with inter-aggregate distance d₀ that decreases with GA concentration (Fig. S1B of the ESI†) as d₀ ∼ c^−0.33, as expected for a dilute solution of a charged hydrocolloid.³³

Isothermal Titration Calorimetry (ITC) and zeta potential measurements (see Section 2.3 and Fig. S5 of the ESI†) indicate that the negatively charged GA does not adsorb onto the SCNCs.

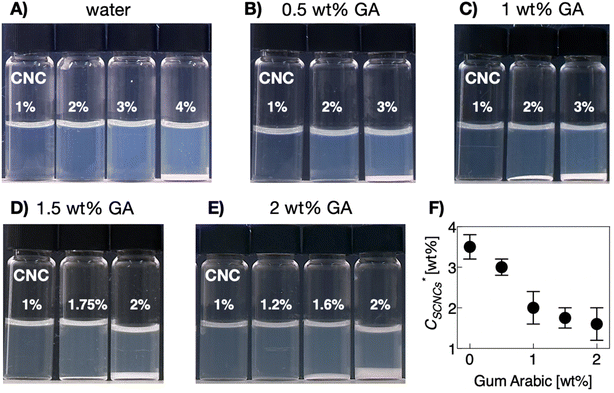
While GA-free suspensions of SCNCs are fully isotropic at these concentrations (Fig. S2 of the ESI†), a birefringent phase of SCNCs emerges in GA solutions at SCNC concentrations <2 wt% (Fig. 2). For example, in solutions of 2 wt% GA, a birefringent phase is observed already at a SCNC concentration of 1.6 wt% (Fig. 2E). Clearly, the presence of GA reduces the threshold concentration for the emergence of the LC phase (Fig. 2F).

Fig. 2 Images of vials containing SCNC suspensions in (A) water, (B) 0.5 wt% GA, (C) 1 wt% GA, (D) 1.5 wt% GA, (E) 2 wt% GA, and (F) the threshold concentration of the cholesteric SCNC phase as a function of GA concentration.

Cryo-TEM images of SCNC suspensions (1–2 wt%) in GA solutions are presented in Fig. 3). In these images, the SCNCs appear as rod-like structures, while GA (with a typical diameter of about 2–4 nm) as dark spots. In the GA-free suspensions (Fig. 3A and C), SCNCs are randomly oriented with a typical interparticle distance, d₀, of about 60 ± 19 nm for 1 wt% SCNCs. The density of the rods is uniform, and neither aggregation nor vacancies are observed. A different organization is observed in GA solutions, for example Fig. 3B and D. Here, crowding of SCNCs into nanometric islands of co-aligned rods with a typical interparticle distance that depends on the concentration of GA is observed (Table S2 of the ESI†). The SCNCs form islands of co-aligned rods and the background (areas between the islands) is full of dark dots, which is the GA (seen more clearly in the higher magnification Fig. 3E, and in stained samples (Fig. S9 of the ESI†).

Fig. 3 Cryo-TEM images of single-phase (isotropic) suspensions of SCNCs: (A) 1 wt% SCNCs in water, (B) 1 wt% SCNCs in aqueous solution of 3 wt% GA, (C) 2 wt% SCNCs in water, (D) 2 wt% SCNCs in aqueous solution of 1.5 wt% GA. (E) Higher, and (F) lower magnification images of D. Scale bar in A–E is 100 nm.

Thus, the presence of GA affects the self-assembly pattern of the SCNCs causing them to co-align close to each other in islands, and leaving vacancies depleted from SCNCs (but rich with GA) in between the islands. The GA-rich and SCNC-rich liquid phases co-exist within the optically isotropic SCNC phases.

The SCNC interparticle distance in the islands is much smaller than that in GA-free suspensions of the same SCNC concentration. For example, interparticle distance of d₀ = 22 ± 6 nm is measured in nematic islands, present in suspensions of 1 wt% SCNCs in 3 wt% GA solution (Fig. 3B and Table S2 of the ESI†) rather than 60 ± 19 nm in the GA-free suspension.

The lower magnification image (Fig. 3F) shows that the clustering of SCNCs into nanometric islands of nematic alignment appears all over the sample.

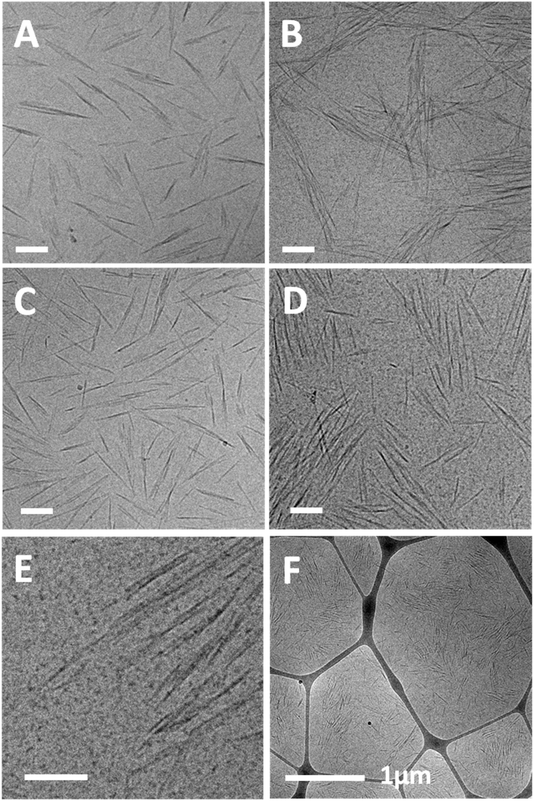
SAXS measurements of similar suspensions are presented in Fig. 4A and B. 1D scattering curves of 1 and 2 wt% SCNC suspensions in GA show a peak at low q values, and suspensions of 2 wt% SCNCs show also a shoulder at mid-q values, q₁, with q₁/q₀ = 2, indicative of lamellar symmetry.³⁸ The structure of the scattering curve and the presence of two peaks is more evident in the Lorentz (log–log) plot presented in Fig. 4C (and Fig. S2 of the ESI†). Typical interparticle distances, d₀, are presented in Fig. 4F (and Table S2 of the ESI†). For a given SCNC concentration, the presence of GA induces crowding of the rods, in consistency with the cryo-TEM results. For example, d₀ = 63 ± 19 nm in GA-free suspensions of 1 wt% SCNCs, while d₀ = 22 ± 13 nm in 1 wt% SCNC suspension that contains 3 wt% GA. These values of d₀ are significantly smaller than those measured in GA-free suspensions of SCNCs (Fig. S3B of the ESI†) and are similar to the inter-aggregate distance measured in native solutions of GA (Table S1 of the ESI†). We also note that in aqueous (GA-free) suspensions of SCNCs, similar values of d₀ are measured at high concentrations of 8 and 10 wt% SCNCs (Fig. S3 of the ESI†).

Fig. 4 (A) 1D SAXS curves of 1 (■), and (B) 2 wt% (●) SCNC suspensions in GA solutions. Color code: water, 0.5 wt% GA, 1 wt% GA, 1.5 wt% GA, 2 wt% GA, 3 wt% GA. The curves are shifted for better visualization. (C) Lorentz (log–log) plots of two curves (2 wt% SCNCs + 2 wt% GA, 3 wt% GA) superposition experiment: 1D SAXS curves obtained from 1 wt% SCNCs in GA solutions: (D) in 1 wt% GA, (E) in 2 wt% GA. (F) The interparticle distance d₀ as a function of GA concentration, 1 wt% SCNCs (), 2 wt% SCNC () from SAXS, and inter-particle distances obtained from cryo-TEM images ().

The scattering patterns of SCNC suspension in GA solutions are composed of contributions from both SCNCs and GA (Fig. 4D and E). To investigate the contributions of the different components, we performed a linear superposition analysis using the scattering patterns of the single components, 1 wt% GA solutions, and 1 wt% SCNCs in water, separately. It can be observed that the measured scattering pattern of 1 wt% SCNCs in a solution of 1 wt% GA could not be reconstructed, as it deviates from the superposed curve. In these curves, the SAXS signal is dominated by the scattering from the SCNCs though. The actual location of q₀ is determined by the GA-induced crowding of the SCNCs.

In Fig. 5, we present isotropic 2D SAXS patterns measured in 2 wt% SCNCs in water and in the upper phase (optically isotropic phase) of solutions with 2 wt% GA (Fig. 5A and B, respectively; see also Fig. S7 of the ESI†). POM analysis of 2 wt% SCNC suspensions that contain GA at C_GA ≥ 1 wt% reveals the presence of birefringent domains with typical dimensions of 30–40 μm. The interference patterns exhibit the typical Maltese cross and fingerprint pattern that characterize cholesteric tactoids under polarized light (Fig. 5F).¹¹ Note that while the typical size of these tactoids is much larger than the nematic assemblies observed in the cryo-TEM images (Fig. 3), they do not form a non-isotropic phase on the mesoscopic scale.

Fig. 5 2D SAXS pattern of 2% SCNCs (A) in water, and (B) in 2 wt% GA solution. POM images of (C) 1 wt% and (D) 2 wt% SCNC suspensions in water. POM images of the (upper) optically isotropic phase of 2 wt% SCNCs in (E) 1 wt% GA solution (F) 2.5 wt% GA solutions.

A similar investigation of 3 wt% SCNC suspensions in 1 wt% GA is presented in Fig. 6. Cryo-TEM images reveal that, unlike the GA-free suspensions, the distribution of SCNCs is not uniform across the samples. Differently, while in the upper phase small nematic islands of SCNCs are observed (Fig. 6A) and the phase is optically isotropic, large areas of co-aligned SCNCs are present in the lower phase (Fig. 6B) forming a birefringent phase. The inter-particle distance, as calculated from cryo-TEM measurements, is similar in the two phases and is determined by the concentration of GA (Table S3†). In these images, the segregation of the mixed SCNC-GA phase into SCNC-rich droplets that co-exist with GA-rich droplets is clearly observed. POM images (Fig. S8C and F†) reveal the presence of cholesteric tactoids in the upper phase and a continuous birefringent (lower) phase.

Fig. 6 Cryo-TEM images obtained from suspensions of 3 wt% SCNCs in 1 wt% GA (A) Optically isotropic, and (B) the birefringent phase. Bar 100 nm. The insets show the 2D SAXS patterns obtained from the suspensions (see also Fig. S8A and D of the ESI†).

We note that while other polymers were observed to be depleted from the LC phase,^21,22 the presence of GA in the LC phase is substantial.

2D SAXS patterns of these suspensions (presented in the inset of Fig. 6) clearly show that the upper phase is isotropic while the lower phase is not. The 1D scattering curves (Fig. S8B and E†) exhibit the typical structure of SCNC phases, with a nematic character but a smaller inter-particle distance (below 20 nm).

4. Discussion

The role of entropy in the formation of nematic liquid-crystal phases of colloids and nanoparticles was rationalized by a few theories.^4,5,39 The Onsager model developed for infinitely long rods,⁴ models describing rods with finite aspect ratios,⁴⁰ polydispersity,^41,42 and charged rods⁴³ suggest that excluded volume interactions drive the assembly of the rods. Thus, the phase diagram is dominated by the high aspect ratio of the hard rods.

The models can be used for rationalization of the I–N transition observed in SCNC suspensions: a first-order liquid–liquid phase transition that proceeds mainly via nucleation and growth of nematic droplets (tactoids).² The orientational order of the nematic phase is attributed to the trade-off between the minimization of the excluded volume interactions and the maximization of the translational entropy of the nanorods. In SCNC suspensions, the nematic phase is chiral (cholesteric), and the nucleating tactoids exhibit a chiral nematic (N*) structure.² The N* phase is characterized by inter-particle (SCNC) distance and chiral pitch that decrease with increasing SCNC concentration.^{2,10,13,44,45} While the origins of tactoids chirality are still debated,^2,46 the evolution of micron-sized tactoids, and their chiral nature already at inter-particle distance of 50–60 nm was reported in many studies.^2,16

A major challenge in SCNC self-assembly (and colloidal assembly in general), is the kinetic accessibility of a target mesophase. Whether the desired structures are thermodynamically stable (here, the equilibrium cholesteric phase) or metastable (quenched thin films, photonic structures) kinetic arrest prevents their realization.⁴⁷ The high aspect ratio of SCNCs (10 to 1000) combined with their polydispersity result in arrested gel-like states that inhibit their equilibration into the chiral nematic phase due to kinetic barriers.⁴⁸ Thus, interactions that reduce the kinetic barrier may facilitate the nucleation of the cholesteric phase. Indeed, the role of depletion agents in triggering the emergence of desired phases or self-assembly, that are difficult to access due to kinetic barriers via crowding of colloidal objects has long been explored.^49,50

In addition, since SCNC self-assembly is driven by reduction of excluded volume (entropic driving force), it is expected that modification of the entropic balance by (attractive) depletion interactions induced by non-adsorbing polymers³⁴ would modify their self-assembly.⁵¹ Indeed, the negatively charged GA (at pH > pK_a of the polymer) that does not adsorb onto the (negatively charged) SCNCs, is observed to induce crowding in the SCNC suspensions and assist in the nucleation of the N* phase. The branched structure of GA intensifies the depletion effect of the polymer and minimizes the formation of entangled networks (at the low concentrations investigated here). Thus, we do not observe any gelation or kinetic arrest in GA-solutions of SCNCs (see the summary in Section 1 ESI†). Therefore, GA can be used to modify and tune the formation of SCNC mesophases and consequentially their optical properties.

Cryo-TEM and SAXS analysis suggest that GA induces significant crowding of the SCNCs to interparticle distances that are smaller than those observed even at high SCNC concentrations (8 and 9 wt%) in GA-free suspensions.^44,45

Two observations indicate that the introduction of depletion-induced entropic attraction between the rods strongly modifies the chemical potential of the combined system.¹⁸ First, the appearance of sub-micron areas that are either enriched or depleted of SCNCs (and correspondingly of GA) in cryo-TEM images, indicating that a new liquid–liquid phase transition takes place within the mesoscopically isotropic phase of the SCNC-GA suspensions (Fig. 3 and 6). Thus, GA-rich droplets coexist with SCNC-rich droplets. Second, the observation that the inter-particle distance of both SCNCs and GA is similar, and follows the typical values measured in GA solutions (of a given concentration) (Fig. 4C). Following theoretical models,^{6,19,20,34,40,51} we suggest that new liquid–liquid phase separation results from the depletion-induced crowding of SCNCs by the solvated GA. Thus, the reduction of the osmotic pressure of the polymer, due to the increase in free volume that drives the crowding of the SCNC system, followed by the entropic gain from the alignment of rod-like particles results in the formation of pre-tactoid bundles, at relatively low SCNC concentrations.

A summary of the quantitative effect of GA concentration on the crowding of SCNCs is presented in Fig. 7. In Fig. 7A, we present the dependence of the SCNC inter-particle distance, d₀(SCNCs), on GA concentration. In Fig. 7B, the inter-colloid distance in GA solutions of different concentrations (d₀(GA)) is shown, and in Fig. 7C the inter-SCNC distance d₀ (SCNCs) in GA-free suspensions. We observe that for a given concentration of SCNCs (Fig. 7A, 1 wt% or 2 wt% SCNCs), d₀(SCNCs) decreases with GA concentration, with a scaling exponent of (−0.35). This dependence on GA concentration is similar to the dependence of the inter-particle distance of GA in aqueous solutions (Fig. 7B) more than the dependence of d₀(SCNCs) on the concentration of SCNCs in GA-free suspensions (Fig. 7C). Furthermore, the values of d₀(SCNCs) in the GA solutions are significantly reduced as compared to the native SCNC suspensions, indicating that the SCNC rods are crowded in GA solutions.

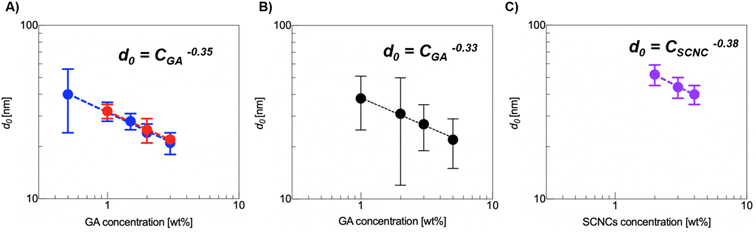Fig. 7 (A) The interparticle distance, d₀, as a function of GA concentration for 1 wt% SCNCs () and 2 wt% SCNCs (). (B) The inter-aggregate distance, d, in GA solutions. (C) d₀ in aqueous (GA-free) suspensions of SCNCs, the isotropic regime. The values were calculated from SAXS measurements (Fig. 4, 6 and Tables S1–S3 of the ESI†).

To summarize, the observations presented here indicate that depletion interactions induced by the presence of non-adsorbing branched polysaccharide (GA) modify the self-assembly and phase behavior of SCNC suspensions. The osmotic pressure exerted by the flexible polymers, and entropic gain from the alignment of the SCNC rods result in the crowding of the suspended SCNCs, leading to a new liquid–liquid phase transition within the optically isotropic SCNC phase. GA reduces the nucleation barrier and enables the assembly of pre-tactoids nematic nano-islands that evolve into cholesteric droplets (tactoids) in very low SCNC concentrations.

5. Conclusions

Crowding of SCNCs induced by an efficient depletion agent, the non-adsorbing highly branched natural polysaccharide, GA, seems to modify the entropy-driven assembly of SCNCs. Thus, GA can be exploited to tune the self-assembly pathway of SCNCs by inducing crowding, trigger the emergence of the desired N* phase, tune the pitch of the cholesteric phase, and bypass gelation and kinetic arrest. This approach does not require chemical modification of the SCNCs, and can be applied to a wide variety of SCNCs that differ in their surface charge, biological origins, polydispersity and shape.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Rachel Yerushalmi-Rozen holds the Stanley D. and Nikki Waxberg professorial chair in Advanced Materials. The support of the Israel Science Foundation (ISF grant 474-24) is acknowledged.

References

1. J. P. F. Lagerwall, C. Schütz, M. Salajkova, J. Noh, J. H. Park, G. Scalia and L. Bergström, Cellulose Nanocrystal-Based Materials: From Liquid Crystal Self-Assembly and Glass Formation to Multifunctional Thin Films, NPG Asia Mater., 2014, e80,  DOI:10.1038/am.2013.69.
2. C. Schütz, J. R. Bruckner, C. Honorato-Rios, Z. Tosheva, M. Anyfantakis and J. P. F. Lagerwall, From Equilibrium Liquid Crystal Formation and Kinetic Arrest to Photonic Bandgap Films Using Suspensions of Cellulose Nanocrystals, Crystals, 2020, 199,  DOI:10.3390/cryst10030199.
3. K. M. Salikhov, M. Kleman and O. D. Lavrentovich, Soft Matter Physics. An Introduction, Appl. Magn. Reson., 2004, 27(3–4), 563,  DOI:10.1007/bf03166751.
4. L. Onsager, The Effects of Shape on the Interaction of Colloidal Particles, Ann. N. Y. Acad. Sci., 1949, 51(4), 627,  DOI:10.1111/j.1749-6632.1949.tb27296.x.
5. P. J. Flory, Phase Equilibria in Solutions of Rod-like Particles, Proc. R. Soc. London, Ser. A, 1956, 234(1196) DOI:10.1098/rspa.1956.0016.
6. P. J. Flory and A. Abe, Statistical Thermodynamics of Mixtures of Rodlike Particles. 1. Theory for Polydisperse Systems, Macromolecules, 1978, 11(6), 1119,  DOI:10.1021/ma60066a011.
7. R. H. Marchessault, F. F. Morehead and N. M. Walter, Liquid Crystal Systems from Fibrillar Polysaccharides, Nature, 1959, 184(4686), 632,  DOI:10.1038/184632a0.
8. J. F. Revol, H. Bradford, J. Giasson, R. H. Marchessault and D. G. Gray, Helicoidal Self-Ordering of Cellulose Microfibrils in Aqueous Suspension, Int. J. Biol. Macromol., 1992, 14(3), 170,  DOI:10.1016/S0141-8130(05)80008-X.
9. M. S. Reid, M. Villalobos and E. D. Cranston, Benchmarking Cellulose Nanocrystals: From the Laboratory to Industrial Production, Langmuir, 2017, 1583,  DOI:10.1021/acs.langmuir.6b03765.
10. Y. Habibi, L. A. Lucia and O. J. Rojas, Cellulose Nanocrystals: Chemistry, Self-Assembly, and Applications, Chem. Rev., 2010, 110(6), 3479,  DOI:10.1021/cr900339w.
11. R. M. Parker, G. Guidetti, C. A. Williams, T. Zhao, A. Narkevicius, S. Vignolini and B. Frka-Petesic, The Self-Assembly of Cellulose Nanocrystals: Hierarchical Design of Visual Appearance, Adv. Mater., 2018, 30(19), 1704477,  DOI:10.1002/adma.201704477.
12. T. G. Parton, R. M. Parker, G. T. van de Kerkhof, A. Narkevicius, J. S. Haataja, B. Frka-Petesic and S. Vignolini, Chiral Self-Assembly of Cellulose Nanocrystals Is Driven by Crystallite Bundles, Nat. Commun., 2022, 13(1), 2657,  DOI:10.1038/s41467-022-30226-6.
13. C. Honorato-Rios, A. Kuhnhold, J. R. Bruckner, R. Dannert, T. Schilling and J. P. F. Lagerwall, Equilibrium Liquid Crystal Phase Diagrams and Detection of Kinetic Arrest in Cellulose Nanocrystal Suspensions, Front. Mater., 2016, 3, 21,  DOI:10.3389/fmats.2016.00021.
14. A. V. Kaznacheev, M. M. Bogdanov and S. A. Taraskin, The Nature of Prolate Shape of Tactoids in Lyotropic Inorganic Liquid Crystals, J. Exp. Theor. Phys., 2002, 95(1), 57–63,  DOI:10.1134/1.1499901/METRICS.
15. M. Bagnani, P. Azzari, C. De Michele, M. Arcari and R. Mezzenga, Elastic Constants of Biological Filamentous Colloids: Estimation and Implications on Nematic and Cholesteric Tactoid Morphologies, Soft Matter, 2021, 17(8), 2158–2169,  10.1039/D0SM01886D.
16. P. X. Wang, W. Y. Hamad and M. J. MacLachlan, Structure and Transformation of Tactoids in Cellulose Nanocrystal Suspensions, Nat. Commun., 2016, 7(1), 11515,  DOI:10.1038/ncomms11515.
17. A. G. Dumanli, G. Kamita, J. Landman, H. van der Kooij, B. J. Glover, J. J. Baumberg, U. Steiner and S. Vignolini, Controlled, Bio-Inspired Self-Assembly of Cellulose-Based Chiral Reflectors, Adv. Opt. Mater., 2014, 2(7), 646–650,  DOI:10.1002/ADOM.201400112.
18. M. Joynul Abedin, P. van der Schoot, G. Garnier and M. Majumder, Nematic to Cholesteric Transformation in the Cellulose Nanocrystal Droplet Phase, Langmuir, 2023, 39(17), 6142–6150,  DOI:10.1021/acs.langmuir.3c00284.
19. S. Asakura and F. Oosawa, On Interaction between Two Bodies Immersed in a Solution of Macromolecules, J. Chem. Phys., 1954, 22(7), 1255–1256,  DOI:10.1063/1.1740347.
20. J. F. Joanny, L. Leibler and P. G. De Gennes, Effects of Polymer Solutions on Colloid Stability, J. Polym. Sci. Polym. Phys. Ed, 1979, 17(6), 1073–1084,  DOI:10.1002/POL.1979.180170615.
21. C. D. Edgar and D. G. Gray, Influence of Dextran on the Phase Behavior of Suspensions of Cellulose Nanocrystals, Macromolecules, 2002, 35(19), 7400–7406,  DOI:10.1021/MA0204195/ASSET/IMAGES/LARGE/MA0204195F00008.JPEG.
22. Q. Sun, V. Lutz-Bueno, J. Zhou, Y. Yuan and P. Fischer, Polymer Induced Liquid Crystal Phase Behavior of Cellulose Nanocrystal Dispersions, Nanoscale Adv., 2022, 4, 4863–4870,  10.1039/d2na00303a.
23. H. Oguzlu, I. Dobyrden, X. Liu, S. Bhaduri, P. M. Claesson and Y. Boluk, Polymer Induced Gelation of Aqueous Suspensions of Cellulose Nanocrystals, Langmuir, 2021, 37(10), 3015–3024,  DOI:10.1021/ACS.LANGMUIR.0C02336/SUPPL_FILE/LA0C02336_SI_001.PDF.
24. H. Oguzlu and Y. Boluk, Interactions between Cellulose Nanocrystals and Anionic and Neutral Polymers in Aqueous Solutions, Cellulose, 2017, 24(1), 131–146,  DOI:10.1007/S10570-016-1096-6/METRICS.
25. R. Bardet, N. Belgacem and J. Bras, Flexibility and Color Monitoring of Cellulose Nanocrystal Iridescent Solid Films Using Anionic or Neutral Polymers, ACS Appl. Mater. Interfaces, 2015, 7(7), 4010–4018,  DOI:10.1021/AM506786T/SUPPL_FILE/AM506786T_SI_001.PDF.
26. E. Moghimi, I. Chubak, M. Kaliva, P. Kiany, T. Chang, J. Ahn, N. Patelis, G. Sakellariou, S. A. Egorov, D. Vlassopoulos and C. N. Likos, Colloidal Gelation Induced by Ring Polymers, Phys. Rev. Res., 2024, 6(1), 013079,  DOI:10.1103/PhysRevResearch.6.013079.
27. R. Bandyopadhyaya, E. Nativ-Roth, O. Regev and R. Yerushalmi-Rozen, Stabilization of Individual Carbon Nanotubes in Aqueous Solutions, Nano Lett., 2001, 2(1), 25–28,  DOI:10.1021/nl010065f.
28. S. H. Newburger, Industrial Gums: Polysaccharides and Their Derivatives, J. Assoc. Off. Agric. Chem., 1961, 44(4), 804,  DOI:10.1093/jaoac/44.4.804a.
29. N. Prasad, N. Thombare, S. C. Sharma and S. Kumar, Gum Arabic – A Versatile Natural Gum: A Review on Production, Processing, Properties and Applications, Ind. Crops Prod., 2022, 187(Part A), 115304,  DOI:10.1016/j.indcrop.2022.115304.
30. X. Li, Y. Fang, H. Zhang, K. Nishinari, S. Al-Assaf and G. O. Phillips, Rheological Properties of Gum Arabic Solution: From Newtonianism to Thixotropy, Food Hydrocolloids, 2011, 25(3), 293–298,  DOI:10.1016/J.FOODHYD.2010.06.006.
31. R. C. Randall, G. O. Phillips and P. A. Williams, The Role of the Proteinaceous Component on the Emulsifying Properties of Gum Arabic, Food Hydrocolloids, 1988, 2(2), 131–140,  DOI:10.1016/S0268-005X(88)80011-0.
32. D. J. Burgess and J. E. Carless, Microelectrophoretic Studies of Gelatin and Acacia for the Prediction of Complex Coacervation, J. Colloid Interface Sci., 1984, 98(1), 1–8,  DOI:10.1016/0021-9797(84)90472-7.
33. Y. Dror, Y. Cohen and R. Yerushalmi-Rozen, Structure of Gum Arabic in Aqueous Solution, J Polym Sci B Polym Phys, 2006, 44(22), 3265–3271,  DOI:10.1002/polb.20970.
34. H. N. W. Lekkerkerker and R. Tuinier, Colloids and the Depletion Interaction; Lecture Notes in Physics, Springer Netherlands, Dordrecht, 2011, vol. 833,  DOI:10.1007/978-94-007-1223-2.
35. D. Klemm, F. Kramer, S. Moritz, T. Lindström, M. Ankerfors, D. Gray and A. Dorris, Nanocelluloses: A New Family of Nature-Based Materials, Angew. Chem. Int. Ed., 2011, 50(24), 5438–5466,  DOI:10.1002/anie.201001273.
36. J. Ilavsky and P. R. Jemian, Irena: Tool Suite for Modeling and Analysis of Small-Angle Scattering, J. Appl. Crystallogr., 2009, 42(2), 347–353,  DOI:10.1107/S0021889809002222.
37. Y. Liu, C. Schütz, G. Salazar-Alvarez and L. Bergström, Assembly, Gelation, and Helicoidal Consolidation of Nanocellulose Dispersions, Langmuir, 2019, 35(10), 3600–3606,  DOI:10.1021/am506786t.
38. P. Alexandridis, U. Olsson and B. Lindman, A Record Nine Different Phases (Four Cubic, Two Hexagonal, and One Lamellar Lyotropic Liquid Crystalline and Two Micellar Solutions) in a Ternary Isothermal System of an Amphiphilic Block Copolymer and Selective Solvents (Water and Oil), Langmuir, 1998, 14(10) DOI:10.1021/la971117c.
39. S. Martellucci and A. N. Chester, Phase Transitions in Liquid Crystals. 1992, 290,  DOI:10.1007/978-1-4684-9151-7.
40. S. D. A. Lee, Numerical Investigation of Nematic Ordering Based on a Simple Hard-rod Model, J. Chem. Phys., 1987, 87(8), 4972–4974,  DOI:10.1063/1.452811.
41. H. H. Wensink and G. J. Vroege, Isotropic–Nematic Phase Behavior of Length-Polydisperse Hard Rods, J. Chem. Phys., 2003, 119(13), 6868–6882,  DOI:10.1063/1.1599277.
42. C. A. De Filippo, S. Del Galdo, P. Corsi, C. De Michele and B. Capone, On the Role of Polydispersity on the Phase Diagram of Colloidal Rods, Soft Matter, 2023, 19(9), 1732–1738,  10.1039/D2SM01355J.
43. A. Stroobants, H. N. W. Lekkerkerker and T. Odijk, Effect of Electrostatic Interaction on the Liquid Crystal Phase Transition in Solutions of Rodlike Polyelectrolytes, Macromolecules, 1986, 19(8) DOI:10.1021/ma00162a020.
44. D. Attia, N. Cohen, G. Ochbaum, Y. Levi-Kalisman, R. Bitton and R. Yerushalmi-Rozen, Nano-to-Meso Structure of Cellulose Nanocrystal Phases in Ethylene-Glycol-Water Mixtures, Soft Matter, 2020, 16(4) 10.1039/d0sm01025a.
45. N. Cohen, D. Attia, Y. Levi-Kalisman, R. Bitton and R. Yerushalmi-Rozen, Emergent Hybrid Mesophases in Ternary Mixtures of Cellulose Nanocrystals - Pluronic Micelles-Water, Polym. Adv. Technol., 2022, 33(11), 3800–3809,  DOI:10.1002/PAT.5647.
46. S. Dussi and M. Dijkstra, Entropy-Driven Formation of Chiral Nematic Phases by Computer Simulations, Nat. Commun., 2016, 7(1), 1–10,  DOI:10.1038/ncomms11175.
47. P. Bertsch, S. Isabettini and P. Fischer, Ion-Induced Hydrogel Formation and Nematic Ordering of Nanocrystalline Cellulose Suspensions, Biomacromolecules, 2017, 18(12) DOI:10.1021/acs.biomac.7b01119.
48. R. Jadrich and K. S. Schweizer, Theory of Kinetic Arrest, Elasticity, and Yielding in Dense Binary Mixtures of Rods and Spheres, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2012, 86(6), 061503,  DOI:10.1103/PhysRevE.86.061503.
49. Y. Hata, T. Sawada and T. Serizawa, Macromolecular Crowding for Materials-Directed Controlled Self-Assembly, J. Mater. Chem. B, 2018 10.1039/C8TB02201A.
50. T. L. Madden and J. Herzfeld, Liquid Crystal Phases of Self-Assembled Amphiphilic Aggregates, Philos. Trans. R. Soc., A, 1993, 344(1672), 357–375,  DOI:10.1098/rsta.1993.0095.
51. T. P. Fraccia and G. Zanchetta, Liquid–Liquid Crystalline Phase Separation in Biomolecular Solutions, Curr. Opin. Colloid Interface Sci., 2021, 56, 101500,  DOI:10.1016/j.cocis.2021.101500.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4na00981a

---