Activation energy of aluminate dissolution in metakaolin: MLFF-accelerated DFT study of vdW and hydration shell effects

Abstract

This research utilizes computational chemistry to investigate the complex mechanisms driving the dissolution of thermally activated metakaolin (MK) clay, a key supplementary cementitious material (SCM) in the manufacturing of concrete and geopolymer-based materials, thereby contributing to a reduced carbon footprint. A thorough exploration of the dissolution process is fundamental for fully understanding its pozzolanic reactivity. Expanding on our recent investigations into SiO₄⁴⁻ dissolution in MK, this work addresses critical data gaps in understanding the dissolution behavior of aluminate species. The findings complement essential input for microscopic forward dissolution rate computations using the atomistic kinetic Monte Carlo (kMC) upscaling approach. To this end, the study calculates the atomistic activation energy (ΔE_a) of aluminate species at the transition state for the hydrolysis reaction using machine learning force fields (MLFF) based on density functional theory (DFT) and the improved dimer method (IDM) under far-from-equilibrium conditions, focusing on three activators: NaOH, KOH, and water. The analysis explores both the presence and absence of van der Waals (vdW) interactions, along with varying geometric configurations of hydration shells surrounding cations (Na⁺, K⁺) and the hydroxide anion (OH⁻). The findings indicate that KOH generally exhibits lower ΔE_a than NaOH, especially when vdW interactions are considered. Moreover, the findings emphasize that reduced hydration shells around KOH and NaOH lead to lower ΔE_a for the dissolution of aluminate species.

---

1. Introduction

MK is the key component of calcined clays due to its pozzolanic reactivity and is widely utilized in various applications within the construction industry.^1–3 MK (calcined) clay is derived from dehydroxylation (DHX) of kaolinite by heating it to temperatures between 400 and 700 °C.⁴ In other words, the primary mineral phase, known as “ideal or ordered kaolinite” (Al₂(OH)₄Si₂O₅), undergoes dehydroxylation to form MK (Al₂Si₂O₇) at temperatures between 500–700 °C. In contrast, “low-crystallinity” or “disordered kaolinites” which have stacking faults, dehydroxylate into metadiskaolinite at lower temperatures ranging from 400–700 °C. Complete dehydroxylation at stationary points leads to an expansion of around 4% for MK supercells and approximately 8% for metadiskaolinite supercells, compared to their ideal and disordered kaolinite counterparts, as demonstrated in the study by Izadifar et al.⁴ Kaolinite calcination produces millions of tons of MK annually, which is utilized as a SCM in the production of concrete and geopolymer-based materials.⁵ Replacing up to 30% of the cement by weight with MK typically results in concrete that is more cohesive with reduced bleeding, enhanced compressive strength,^6,7 lower CO₂ emissions,⁸ and decreased porosity.⁷ Additionally, it offers improved resistance to attacks from sulfates, chlorides, and other aggressive agents,⁹ including minerals and organic acids.^10–12 Meta-clay materials and industrial byproducts, which are rich in reactive silica and alumina, exhibit reactivity that is primarily governed by their dissolution rates. This makes them ideal for improving ecological efficiency by optimizing cement replacement and producing geopolymers,^13,14 leading to a reduced carbon footprint. To fully harness their potential, atomistic simulation techniques will be employed to investigate the dissolution processes of these materials, providing crucial insights into their reactivity and facilitating the development of more effective formulations for sustainable construction applications.

Atomistic simulation techniques have recently been essential in uncovering the microstructure of materials like cement clinker,^15,16 hydrated cement phases,^17,18 and glasses,¹⁹ as well as the connection between atomistic configurations and their reactivity.^20,21 Approaches such as density functional theory (DFT),²² molecular dynamics (MD),²³ and ab initio molecular dynamics^24,25 computational methods are widely employed in chemistry and materials science to study reaction mechanisms, mechanical behavior,^26,27 and other material properties. Coopamootoo and Masoero²⁸ examined the dissolution of tricalcium silicate at screw dislocations within finite grains, considering various facet orientation combinations but excluding crystallographic defects. Their study revealed that dissolution proceeds by consuming kink particles in a sequential, layer-by-layer fashion, initiating at low-coordinated sites located at the intersections of facets, such as edges and corners. These sites were found to have comparable dissolution rates. Furthermore, the dissolution rates of defect-free, finite-sized crystals showed a linear relationship with β, aligning with the principles of traditional transition state theory (TST). N'Guessan et al.²⁹ investigated the leaching of Al and silicon in various alkali hydroxide solutions. They found that the dissolution of kaolinites was influenced by the concentration of hydroxides, with Na⁺ promoting greater dissociation than K⁺ due to its higher charge density. Briki et al.³⁰ observed that the reaction of slag slowed down during both the initial and final stages. In the first 30 minutes of exposure to a slag-NaOH solution, they identified a non-steady state dissolution phase for Al, Si, and sulfur ions, which was followed by a steady state and then a decline in the release rates of Al and silicon due to precipitation. Chen et al.³¹ developed an integrated dissolution model for alite (tricalcium silicate)³² to examine the effects of varying hydrodynamic conditions on dissolution rates, from low to high. The model combined surface topography with ion transport using the kMC approach, effectively addressing both dilute and near-saturated conditions. Their simulation outcomes were largely consistent with existing literature. Valentini³³ also reported modeling dissolution-precipitation kinetics of MK using the cellular automaton reaction-diffusion model HydratiCA. Moreover, Izadifar et al.^16,18 investigated the microscopic forward dissolution rates of β-C₂S cement clinker, and portlandite under far-from-equilibrium conditions through atomistic kMC^16,18,34 upscaling approach, utilizing atomistic ΔE_a derived from MetaD molecular dynamics (MD) simulations methods.^15,17,35 Most recently, Izadifar et al.³⁶ analyzed the nucleation mechanisms of alkaline aluminosilicate gels, including MK, by examining the binding energies (ΔG_reaction) of four distinct monomer species through a coarse-grained Monte Carlo (CGMC) approach. Valencia et al.³⁷ also employed CGMC simulations, utilizing octree cells to investigate the nucleation of geopolymers at various pH levels.

In VASP, the IDM by Heyden et al.,³⁸ is used to optimize the transition states. This approach determines the minimum energy pathway, tracking atomic movements between initial and final states. The ΔE_a is identified by maximizing the potential energy along the unstable mode or decay direction (dimer axis), while energy minimization occurs in all other directions. Although there has been significant research on clays, few atomistic computational studies have been reported that specifically examine the reactivity of protonated silicate tetrahedra in MK (calcined) clay, while considering the effects of neighboring aluminate and silicate units. Izadifar et al.²⁰ applied the IDM and transition-state theory (TST) within the framework of DFT to calculate the atomistic ΔE_a for the dissolution of MK silicate tetrahedra by water molecules, excluding the effects of vdW interactions under far-from-equilibrium conditions. They found that the ΔE_a needed to break the oxo-bridging bond with a neighboring silicate unit was higher than that for an aluminate unit, attributed to ionic interactions. Most recently, Izadifar et al.²¹ used the IDM to explore how reaction enthalpy evolves during the hydrolysis and breakdown of silicate tetrahedra (SiO₄)⁴⁻ including water as an activator in MK under far-from-equilibrium conditions. The computations, based on TST, aimed to determine the ΔE_a for (SiO₄)⁴⁻ dissolution in MK, incorporating two activators of NaOH and KOH with and without contribution of vdW interaction and hydration shell around cations. Cheng et al.³⁹ also utilized the dimer method to locate transition states, which were verified to have a single imaginary vibrational frequency through DFT calculations.

Comprehending the dissolution mechanism of MK at the macro scale is essential for enhancing its application as a supplementary cementitious material and as a cement-free geopolymer binder. Additionally, it is important to note that the ΔE_a for aluminate species dissolution is currently lacking in atomistic simulations. The primary objective of this study is to calculate the atomistic ΔE_a at the transition state for the hydrolysis reaction using MLFF⁴⁰ based on DFT through the IDM to determine the change in reaction enthalpy under far-from-equilibrium conditions. The computations, based on Transition State Theory (TST), focus on determining the atomistic ΔE_a for the dissolution of aluminate species by formation of aluminum hydroxide hydrate Al(OH)₃(H₂O)₃, in MK, considering three activators, NaOH, KOH, and water. The study examines scenarios both with and without the contributions of vdW interactions and various geometry hydration shells around cations (Na⁺ and K⁺) and the hydroxide anion (OH)⁻. Additionally, to enable comparisons of the calculated (ΔE_a) values derived from high-alkaline environments (NaOH and KOH), the study also includes computations of (ΔE_a) for the hydrolysis reaction in the presence of water, considering both the inclusion and exclusion of vdW interactions. In addition to our previous observations on SiO₄⁴⁻ dissolution in MK,^20,21 the findings from this study address the existing data gaps vital for 6-fold coordination (Al^VI) dissolution of aluminate species, preparing all the input data for performing microscopic forward dissolution rate calculations, which are crucial for the atomistic kMC upscaling approach.

2. Materials and computational methods

2.1. Materials

The surface energies (γ) for low Miller index facets were determined for three different surface orientations: 001, 010, and 100, as detailed in recent study.²¹ The calculated values were 0.0057, 0.116, and 0.18 eV Å⁻¹ for the 001, 100, and 010 orientations, respectively. These results reveal that the 001 or 001̄ surface orientation exhibits the highest exposure and reactivity among the surfaces in clay-derived materials like MK. The structure of MK corresponds to the 001 and 001̄ surfaces, and simulations have been conducted to study the dissolution of Al^VI from 001̄ surface that include breaking of the ionic bond from the neighboring oxygen (i) attached to adjacent silicate unit, as shown in Fig. 1. An overview of the model scenarios, including activators, their abbreviations, and the corresponding hydration shell configurations, is presented in Table 1. The dissolution of Al on the MK 001̄ surface depends on the type of activator used and the varying number of water molecules with hydroxide in hydration shells surrounding the activators. The hydration shell configurations and number of water molecules were selected based on well-established coordination chemistry principles and are supported by prior studies.⁴¹ Thus, in order to make a comprehensive investigations, we modeled sixfold and fourfold hydration shells around potassium (K⁺) and sodium (Na⁺), and three to fourfold hydration around hydroxide anions (OH⁻). Fig. 1A–E (corresponding to models 1–5) presents a variety of potential scenarios for aluminate species dissolution, emphasizing the effects of different activators and hydration shells, including KOH, NaOH, and H₂O. In Fig. 1A (K-1) and B (Na-1), the potassium (K⁺) and sodium (Na⁺) cations exhibit octahedral coordination, while the hydroxide anions (OH⁻) are tetrahedrally coordinated. In Fig. 1C (K-2) and D (Na-2), the cations are arranged in a tetrahedral coordination, while the hydroxide anions show a trigonal planar coordination. Fig. 1E (W) also shows the initial structure of reactant, including a water molecule as the absorbent on the MK surface.

Fig. 1 Model scenarios for dissolution of aluminate species through different activators of (A and C) potassium hydroxide (KOH), (B and D) sodium hydroxide (NaOH), and (E) water (H₂O). In scenarios (A) and (B), the cations (K⁺ and Na⁺) exhibit octahedral coordination, while the hydroxide anions (OH⁻) adopt tetrahedral coordination. In scenarios (C) and (D), the cations exhibit tetrahedral coordination, and the hydroxide anions adopt trigonal planar coordination. Silicon ions are shown in blue; aluminum cations, in light blue; oxygen ions, in red; hydrogen protons, in white; sodium cations, in yellow; potassium cations, in purple.

Table 1 Overview of model scenarios with different activators, corresponding hydration shell configurations, and abbreviated name (based on Fig. 1). In the hydration shell configuration, coordination numbers of six, four, and three around cations and hydroxide anions correspond to octahedral, tetrahedral, and trigonal planar geometries, respectively. Note that the first number in each cell refers to the activating cation (K⁺ or Na⁺), and the second number refers to the hydroxide anion (OH⁻)

	(A)	(B)	(C)	(D)	(E)
Scenario (model)	1	2	3	4	5
Activator	KOH	NaOH	KOH	NaOH	Water
Hydration shell configuration	6–4	6–4	4–3	4–3	—
Number of water molecules in the shell	5–3	5–3	3–2	3–2	—
Abbreviated name (Fig. 1)	K-1	Na-1	K-2	Na-2	W

---

2.2. Computational methods

The density functional theory (DFT)⁴² quantum mechanical modeling approach was employed via the Vienna Ab initio Simulation Package (VASP).^43–46 Electron–ion interactions were defined using the projector augmented wave (PAW) approach and pseudopotentials.⁴⁷ For correlation exchange and correlation functionals, the Perdew–Burke–Ernzerhof (PBE) parameterization within the generalized gradient approximation (GGA) was selected.⁴⁸ The Brillouin zone sampling was conducted by a well-converged k-sampling equivalent to a 1 × 1 × 1 Monkhorst–Pack k-points mech-size for the entire system.⁴⁹ Structural relaxations used a plane-wave cutoff energy of 400 eV, with electronic self-consistency cycles converged to 1 × 10⁻⁴ eV and ionic forces relaxed below 1 × 10⁻³ eV Å⁻¹. Interactions of vdW were incorporated via the Grimme DFT-D3 dispersion correction with zero-damping, a widely used method known for its balance between computational efficiency and accuracy across a range of molecular and condensed-phase systems. Structural model analyses were visualized with the three-dimensional VESTA software.⁵⁰ Fig. 2A and B illustrate two distinct approaches of IDM³⁸ and nudged elastic band (NEB)^51,52 for computation of the transition state (TS) along the reaction pathways between M and N, and P and R, respectively. In VASP and for this study, modified version of the original dimer method,⁵³ proposed by Heyden et al.,³⁸ is implemented, resulting in a reduction in the number of gradient calculations per cycle from six to four or three gradients along with one energy calculation, thereby enhancing algorithm performance. As shown in Fig. 2A, the TS at the saddle point has been determined through computation of the most negative vibrational mode of the trail structure, diagonalized Hessian matrix and identify eigenvector with negative eigenvalue indicating the desired transformation (trail dimer axis) and finally potential energy maximization along dimer axis and minimization along all other directions between two minima of M and N the reaction pathway. Conversely, interpolation method like NEB, indicates multiple configurations (images) distributed along the path between P and R and connected via harmonic springs, resulting slow convergence near the minimum-energy pathway as shown in Fig. 2B. The unstable direction is estimated locally for each image (empty circle) as a tangent to the chain connecting the images and the stable states. For each image, a relaxation step using ab initio forces orthogonal to (and harmonic forces parallel with) the local tangent is performed. Although more images provide a better representation of the chain, the calculations become more expensive, still less accurate than IDM, and defining the initial position of the images is not always straightforward, particularly in the case of transformations involving curvilinear atomic motion.^51,52

Fig. 2 Methods for transition state identification along the reaction pathway (A) improved dimer method (IDM)^38,53 representing intrinsic reaction coordinates (IRC) between M and N (B) nudged elastic band (NEB) highlighting minimum energy path between R and P.^51,52

Fig. 3 shows four SCF calculations of force, implemented for relaxation of IDM on the potential energy surface (PES). Fig. 3A indicates the trail structure q and the trail initial direction (dimer axis, u_ε) is taken from the most negative vibrational mode of the trail structure (q, using finite differences method). Fig. 3B shows an additional point on the PES forward along the trial direction is defined q + δu_ε. The first and second points together define the dimer. Fig. 3C and D show the rotation of dimer on the PES about q by angle ϕ₁ to maximize the negative curvature and a new direction is defined by rotating u_ε by ϕ_min to minimize the negative curvature of the PES λ, respectively. The potential energy is maximized along the unstable direction, (i.e., dimer axis) while it is minimized in all other directions. Rotation followed by translation is followed iteratively until convergence, i.e. the saddle point, is reached.³⁸ It is essential to note that the curvature along dimer axis must be negative during dimer method calculation. In other words, long sequence of positive values indicates that the algorithm has failed to converge to the correct transition state. In such cases, it is necessary to start with a new geometry to recompute the curvature.

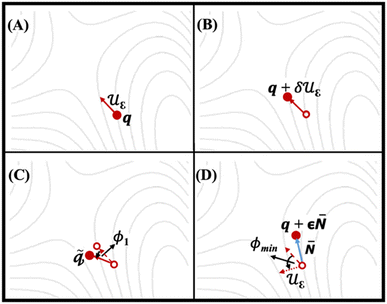Fig. 3 The IDM process relaxes on the potential energy surface (PES) over four ionic steps. Solid arrows represent the dimer axis (u_ε), while solid circles denote the structures where forces are computed at each step. Empty circles and dashed lines indicate the structures and dimer axes from preceding steps, respectively. The dotted arrow illustrates the dimer axis after rotation by ϕ_min.³⁸

A way to greatly reduce computational cost is by machine learning.^54,55 Here, in the prediction of the target property, the method automatically interpolates between known training systems. Nevertheless, there is still the problem of how to choose the proper (minimal) training data. One very efficient and automatic way to solve that is to adapt on-the-fly learning. On-the-fly training base on the ab initio calculations is employed as the training set for MLFF.^40,56 During the early steps of the simulations, specifically the first 20–30 ionic relaxation steps, the forces, energies, and stress tensors from DFT calculations are collected and stored. This data serves as the training set for the MLFF. For each new atomic configuration, VASP will check how well the MLFF predictions match the DFT-calculated forces. If the predictions are accurate (i.e., within a certain threshold defined by ML_CTIFORCE), the MLFF predictions are used for the next ionic step. We set the force deviation threshold (ML_CTIFORCE) to 0.002 eV Å⁻¹, meaning a DFT calculation was triggered whenever the predicted forces deviated beyond this value. If the MLFF's predictions deviate significantly from DFT, VASP triggers another full DFT calculation. The new DFT data is then used to update and improve the MLFF.

3. Results

3.1 Activation energy computation incorporating vdW contributions

Our study aims to determine the activation energy at the saddle point using the IDM, which converges more efficiently than the NEB. While NEB maps the minimum energy path, it often struggles with convergence and requires multiple images, leading to computational inefficiencies. IDM, in contrast, directly locates the saddle point without predefined reaction coordinates, offering a more precise and cost-effective approach. To provide a comprehensive analysis, the dissolution behavior of aluminate species has been computed under 5 different models of K-1, Na-1, K-2, Na-2, and W, as depicted in Fig. 1. These scenarios encompass a range of conditions designed to capture the complexity of aluminate species dissolution processes. Specifically, the energy barrier (activation energy, ΔE_a) for the hydrolysis reaction during the dissolution of AlO(OH)₂(H₂O)₃ in MK has been evaluated. This evaluation considers different hydration shell geometry surrounding three activators NaOH, KOH, and water both with and without the inclusion of vdW interactions, as presented in Fig. 4–13. To enable a meaningful comparison, Fig. 14 and Table 2 juxtaposes our findings on the dissolution of aluminate species in MK with the dissolution mechanism of SiO₄⁴⁻ reported in recent publication,²¹ respectively. This comparison provides the differences in dissolution kinetics, the ΔE_a profiles, and the influence of structural and chemical environments for aluminate and silicon-based species. The first scenario, referred to as model 1 and illustrated in Fig. 4, incorporates KOH as the absorbent, accounting for the contribution of vdW interactions. The initial optimized structure (Fig. 4A), which features KOH as the activator, reveals a potassium cation in an octahedral coordination (6-fold coordination), positioned 6.73 Å away from oxygen (i), while the hydroxide anions (OH⁻) are tetrahedrally coordinated (4-fold coordination).

Fig. 4 Model 1: (A) the optimized geometric structure of K-1 (illustrated in Fig. 1A) showing the breaking of the oxygen atom (i), which is bonded to the neighboring Al cation through an ionic bond with the contribution of vdW interactions. (B) The transition state was identified at the saddle point using the IDM. (C) The optimized geometric structure of the product after fully saturation of the oxygen (i) with a potassium cation (ionic bond). Energy barrier of hydrolysis reaction (ΔE_a), and binding energy (ΔG_reaction) obtained from first-principles calculations.

Fig. 5 Model 2: (A) the optimized geometric structure of Na-1 (illustrated in Fig. 1B) showing the breaking of the oxygen atom (i), which is bonded to the neighboring Al cation through an ionic bond with the contribution of vdW interactions. (B) The transition state was identified at the saddle point using the IDM. (C) The optimized geometric structure of the product after fully saturation of the oxygen (i) with a sodium cation (ionic bond).

Fig. 6 Model 3: (A) the optimized geometric structure of K-2 (illustrated in Fig. 1C) showing the breaking of the oxygen atom (i), which is bonded to the neighboring Al cation through an ionic bond with the contribution of vdW interactions. (B) The transition state was identified at the saddle point using the IDM. (C) The optimized geometric structure of the product after fully saturation of the oxygen (i) with a potassium cation (ionic bond).

Fig. 7 Model 4: (A) the optimized geometric structure of Na-2 (illustrated in Fig. 1D) showing the breaking of the oxygen atom (i), which is bonded to the neighboring Al cation through an ionic bond with the contribution of vdW interactions. (B) The transition state was identified at the saddle point using the IDM. (C) The optimized geometric structure of the product after fully saturation of the oxygen (i) with a sodium cation (ionic bond).

Fig. 8 Model 5: (A) the optimized geometric structure of W (illustrated in Fig. 1E) showing the breaking of the oxygen atom (i), which is bonded to the neighboring Al cation through an ionic bond with the contribution of vdW interactions. (B) The transition state was identified at the saddle point using the IDM. (C) The optimized geometric structure of the product after fully saturation of the oxygen (i) with a proton (covalent bond).

Fig. 9 Model 1: (A) the optimized geometric structure of K-1 (illustrated in Fig. 1A) showing the breaking of the oxygen atom (i), which is bonded to the neighboring Al cation through an ionic bond without the contribution of vdW interactions. (B) The transition state was identified at the saddle point using the IDM. (C) The optimized geometric structure of the product after fully saturation of the oxygen (i) with a potassium cation (ionic bond).

Fig. 10 Model 2: (A) the optimized geometric structure of Na-1 (illustrated in Fig. 1B) showing the breaking of the oxygen atom (i), which is bonded to the neighboring Al cation through an ionic bond without the contribution of vdW interactions. (B) The transition state was identified at the saddle point using the IDM. (C) The optimized geometric structure of the product after fully saturation of the oxygen (i) with a sodium cation (ionic bond).

Fig. 11 Model 3: (A) the optimized geometric structure of K-2 (illustrated in Fig. 1C) showing the breaking of the oxygen atom (i), which is bonded to the neighboring Al cation through an ionic bond without the contribution of vdW interactions. (B) The transition state was identified at the saddle point using the IDM. (C) The optimized geometric structure of the product after fully saturation of the oxygen (i) with a potassium cation (ionic bond).

Fig. 12 Model 4: (A) the optimized geometric structure of Na-2 (illustrated in Fig. 1D) showing the breaking of the oxygen atom (i), which is bonded to the neighboring Al cation through an ionic bond without the contribution of vdW interactions. (B) The transition state was identified at the saddle point using the IDM. (C) The optimized geometric structure of the product after fully saturation of the oxygen (i) with a sodium cation (ionic bond).

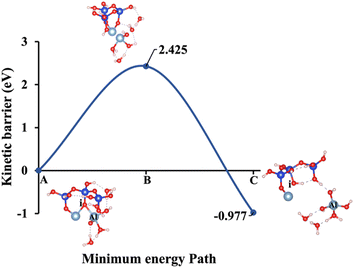Fig. 13 Model 5: (A) the optimized geometric structure of W (illustrated in Fig. 1E) showing the breaking of the oxygen atom (i), which is bonded to the neighboring Al cation through an ionic bond without the contribution of vdW interactions. (B) The transition state was identified at the saddle point using the IDM. (C) The optimized geometric structure of the product after fully saturation of the oxygen (i) with a proton (covalent bond).

Fig. 14 ΔE_a for aluminate species dissolutions. Dissolution of aluminate species in the presence of different activators (KOH, NaOH), as shown (labeled) in Fig. 1. The computations considered through various hydration shell around cations and hydroxide anions, with and without the inclusion of vdW interaction.

Table 2 Reported SiO₄⁴⁻ dissolution for four distinct scenarios (detailed in Table 1 from our recent study) under the influence of KOH and NaOH, with and without vdW interaction²¹

Model	A0S1
Activator	KOH	NaOH	KOH	NaOH
vdW interaction	Yes	Yes	No	No
Hydration shell	Yes	Yes	Yes	Yes
Activation energy (eV)	1.462	1.949	0.788	3.276

---

At the transition state (Fig. 4B), the potassium cation approaches the oxygen (i) more closely within 2.76 Å, and the product's optimized geometric structure through exothermic reaction is achieved as potassium get closer through ionic reaction with oxygen (i) within 2.61 Å, resulting Al^VI formation. The initial optimized structure, referred to as model 2, incorporates NaOH as the activator, is shown in Fig. 5A. In this configuration, the sodium cation exhibits octahedral coordination and is positioned 6.01 Å away from oxygen (i). At the transition state (Fig. 5B), the sodium cation is located at a distance of 2.85 Å. In the optimized geometric structure of the product (Fig. 5C), resulting from the ionic reaction, oxygen (i) is positioned 2.61 Å from the sodium cation. KOH (model 1) requires 66.44% less ΔE_a than NaOH (model 2), considering vdW interactions in a configuration where the cation exhibits octahedral coordination and the hydroxide anions (OH⁻) exhibit tetrahedral coordination. This is due to the larger ionic radius of K⁺ (1.38 Å vs. 1.02 Å for Na⁺) results in a lower charge density and weaker electrostatic interactions with the aluminosilicate framework, facilitating structural disruption and making Al–O bonds easier to break. Additionally, the lower hydration energy of K⁺ allows for more effective ion exchange and interaction with the aluminosilicate network, further reducing the ΔE_a required for aluminate species dissolution in KOH compared to NaOH.

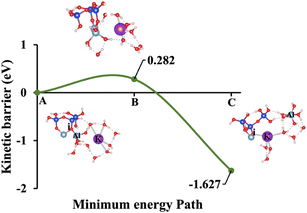
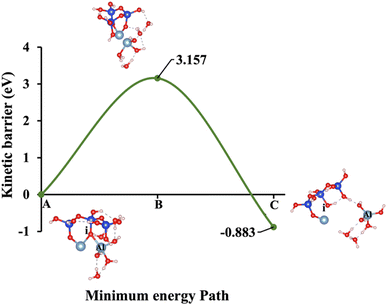
Models 3 and 4 represent KOH and NaOH with contribution of vdW interactions, respectively, where the cations are arranged in tetrahedral coordination, while the hydroxide anions exhibit trigonal planar coordination, as shown in Fig. 6 and 7. Fig. 6A shows that the potassium cation is optimized at a distance of 5.28 Å from oxygen (i), which 1.45 Å closer compared to the octahedral coordination shown in Fig. 4 due to less hydration shell around the cation. In contrast, an identical distance of 2.61 Å is observed for model 3C, when compared to model 1C. Lower ΔE_a for aluminate species dissolution were observed when the hydration shells surrounding KOH or NaOH were reduced, allowing for stronger cation–surface interactions and enhanced bond cleavage in the aluminosilicate network. Thus, the ΔE_a required for the configuration in model 3, using KOH as the activator, is 264.54% lower than that of model 1. Model 4, which employs NaOH activator, demands also 6.02% less ΔE_a than model 2. A similar trend was observed in the ΔE_a for KOH compared to NaOH with identical hydration shells around activators, with KOH requiring 470.21% less ΔE_a. Fig. 8, representing model 5, highlights the contribution of water in Al bond breaking. It illustrates that a high energy of 3.157 eV is needed to reach the transition state.

3.2 Activation energy computation excluding vdW contributions

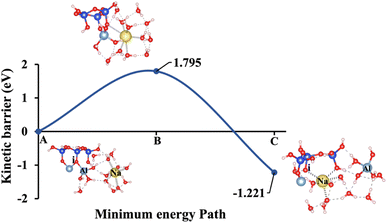
To fully understand the effect of excluding vdW interactions on the ΔE_a of a hydrolysis reaction and ΔG_reaction calculations, we analyze identical geometric structures depicted in Fig. 9–13. The vdW interactions between atoms and molecules are crucial in numerous chemical systems. They maintain the equilibrium condition with electrostatic and exchange–repulsion interactions, collectively shaping the system's behavior.⁵⁷ The lower computed energy barrier required to reach the transition state, resulting in a more favorable ΔE_a. Without vdW interactions, this interaction is absent, and the system requires more energy to overcome the barrier, leading to a higher (less favorable) ΔE_a. For instance, Fig. 9, depicting model 1 without vdW interactions, shows a 29.46% higher ΔE_a for KOH compared to the identical geometric structure that includes vdW interactions, as illustrated in Fig. 4.

Fig. 10, illustrating model 2 without vdW interactions, reveals a 4.91% increase in the ΔE_a for KOH compared to the corresponding geometric structure that includes vdW interactions, as shown in Fig. 5. Likewise, Fig. 11, depicting model 3 without vdW interactions, shows a 6.03% rise in the ΔE_a for KOH relative to its vdW-inclusive counterpart in Fig. 6. Similarly, Fig. 12, representing model 4 without vdW interactions, exhibits a 9.46% higher ΔE_a for KOH compared to the identical structure incorporating vdW interactions, as illustrated in Fig. 7. Although vdW forces affect relative energy differences, such as ΔE_a, they are generally weaker than covalent and electrostatic interactions. As a result, their inclusion primarily shifts energy levels rather than altering the molecular geometry, ultimately lowering the ΔE_a. Thus, no significant changes in geometric structures were observed when vdW interactions were included, compared to the identical geometries obtained without vdW interactions.

4. Discussion

To provide a comprehensive understanding of species dissolution in MK, it is essential to compare aluminate species examined in this study with Si dissolution.²¹ Fig. 14 summarizes the computed ΔE_a for aluminate species dissolution in this study, considering scenarios with and without vdW interactions and different hydration shell geometries around Na⁺, K⁺, and OH⁻. Table 2, adapted from recent study,²¹ provides the activation energies of SiO₄⁴⁻ dissolution, including the effects of KOH and NaOH activators, both with and without vdW contributions for different simulation models. To ensure an accurate comparison between aluminate species and SiO₄⁴⁻ dissolution, the A0S1 simulation model was selected for SiO₄⁴⁻ dissolution. This is because A0S1 represents the dissolution of Si tetrahedral monomer, where the product geometry from the S0S0 model is reused as the reactant geometry in A0S1. The dissolution process involves the protonation of the bridging oxygen, which is ionically bonded to the neighboring aluminum cation, facilitating the dissolution of the silicate tetrahedra. Although the dissolution of aluminate species exhibited a low ΔE_a of less than 2 eV for all models with KOH and NaOH activators (Table 3), the dissolution of SiO₄⁴⁻ in the presence of a NaOH activator without vdW contribution requires a ΔE_a exceeding 3 eV at the transition state. To compare the ΔE_a for SiO₄⁴⁻ dissolution (Table 2), 1.462 eV is required in the presence of a KOH activator, while 1.949 eV is needed with a NaOH activator, both considering the contribution of vdW interactions. Accordingly, the ΔE_a for SiO₄⁴⁻ dissolution is 418.4% and 21.2% higher than that of aluminate species in models 3 (0.282 eV) and 4 (1.608 eV), respectively, which incorporate vdW interactions in the presence of KOH and NaOH activators.

Table 3 Overview of ΔE_a and ΔG_reaction for all five presented model scenarios based on Fig. 1, both with and without vdW interaction contributions

Scenario (model)	1	2	3	4	5
ΔEa/ΔGreaction including vdW (eV)	1.028/−1.325	1.711/−0.997	0.282/−1.627	1.608/−1.529	3.157/−0.883
ΔEa/ΔGreaction excluding vdW (eV)	1.331/−1.257	1.795/−1.221	0.299/−1.667	1.760/−1.430	2.425/−0.977
Activator	KOH	NaOH	KOH	NaOH	Water

---

To summarize, Table 3 shows the detailed comparison of ΔE_a and ΔG_reaction across all five model scenarios based on Fig. 1, highlighting the variations in energy values with and without the inclusion of vdW interaction contributions. To place our findings in context, the study by Morrow et al.⁵⁸ on ΔE_a for aluminate dissolution in aluminosilicate systems is also referenced here to enable a comprehensive comparison. Their work emphasizes the sensitivity of computed values to the choice of density functionals and basis sets, employing B3LYP, PBE1PBE, and M05-2X functionals in combination with the 6311+G(d,p) and MG3S basis sets, but without accounting for hydration shells or KOH and NaOH activators. In contrast, our study addresses this gap by incorporating diverse hydration shells and alkali activators, using the PBE(GGA) functional with plane-wave basis set. Table 4 presents a comparative summary of all ΔE_a values from both their study and this study. As a result, the differences in activation energy can be attributed to the use of different activators, the inclusion of hydration shell effects, and the choice of exchange–correlation functional in our calculations. However, for the KOH activator, our results align well with theirs, showing a lower activation energy that is consistent with their findings. Therefore, the most favorable computed ΔE_a in our study correspond to configurations involving vdW interactions with KOH (0.282 eV) and NaOH (1.608 eV) activators, where cations adopt tetrahedral coordination and hydroxide anions exhibit trigonal planar coordination during aluminate species dissolution, in good agreement with the study reported by Marcus.⁴¹

Table 4 The computed ΔE_a obtained using the B3LYP, PBE1PBE, and M05-2X functionals, as reported by Morrow et al.,⁵⁸ are compared with those calculated using the PBE (GGA) functional in this study

	B3LYP		PBE1PBE		M05-2X		PBE(GGA)
	6311+G(d,p)	MG3S	6311+G(d,p)	MG3S	6311+G(d,p)	MG3S	Plane-wave
ΔEa for Al dissolution(eV)	0.404	0.363	0.539	0.363	0.757	0.560	0.282	1.608

---

5. Conclusion

This paper aims to calculate the atomistic ΔE_a at the transition state for the hydrolysis reaction using MLFF based on DFT, employing IDM to determine the change in reaction enthalpy under far-from-equilibrium conditions. The computations, grounded in TST, aim to determine the atomistic ΔE_a for the dissolution of aluminate species, leading to the formation of aluminum hydroxide hydrate Al(OH)₃(H₂O)₃ in an alkaline medium in MK, considering three activators: NaOH, KOH, and water. For this purpose, the study investigates both the presence and absence of vdW interactions, along with various geometric configurations of hydration shells surrounding cations (Na⁺, K⁺) and the hydroxide anion (OH⁻). The results showed that reduced hydration shells around KOH and NaOH led to lower ΔE_a for aluminate species dissolution by strengthening cation–surface interactions and facilitating bond cleavage within the aluminosilicate network. A higher activation energy (ΔE_a) was observed for NaOH compared to KOH under identical hydration shell conditions, both with and without vdW interactions. In the absence of vdW interactions, the system experiences a higher energy barrier, making the activation process less favorable. Building upon earlier observations on SiO₄⁴⁻ dissolution in MK, this study aims to bridge critical data gaps essential for understanding the dissolution of aluminate species in its 6-fold coordinated state (Al^VI). The findings will complement all input data for microscopic forward dissolution rate calculations, which play a key role in the atomistic kMC upscaling methodology.

Abbreviations

MK	metakaolin
DHX	dehydroxylation
SCM	supplementary cementitious material
ΔEa	activation energy
ΔGreaction	binding energy
kMC	kinetic Monte Carlo
MLFF	machine learning force fields
IDM	improved dimer method
NEB	nudged elastic band
IRC	intrinsic reaction coordinates
CGMC	coarse-grained Monte Carlo
DFT	density functional theory
MD	molecular dynamics
VDW	van der Waals
TST	transition state theory
VASP	Vienna Ab initio Simulation Package
GGA	generalized gradient approximation
PAW	projector augmented wave

Data availability

All relevant data supporting this study are fully included in the Results and Discussion section of this article.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge the financial support of the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) within the Priority Programme “Net-Zero Concrete” (SPP 2436), under project number 541788011, titled “Supplementary Cementitious Materials Reactivity: Chemistry-Structure Relationships for Dissolution Kinetics by Upscaling Atomistic Modeling (SuperUptom).” Computational work was conducted on the Lichtenberg High-Performance Computer at TU Darmstadt.

References

1. S. Hollanders, R. Adriaens, J. Skibsted, Ö. Cizer and J. Elsen, Pozzolanic Reactivity of Pure Calcined Clays, Appl. Clay Sci., 2016, 132–133, 552–560,  DOI:10.1016/j.clay.2016.08.003.
2. R. Fernandez, F. Martirena and K. L. Scrivener, The Origin of the Pozzolanic Activity of Calcined Clay Minerals: A Comparison between Kaolinite, Illite and Montmorillonite, Cem. Concr. Res., 2011, 41(1), 113–122,  DOI:10.1016/j.cemconres.2010.09.013.
3. O. R. Kavitha, V. M. Shanthi, G. P. Arulraj and V. R. Sivakumar, Microstructural Studies on Eco-Friendly and Durable Self-Compacting Concrete Blended with Metakaolin, Appl. Clay Sci., 2016, 124–125, 143–149,  DOI:10.1016/j.clay.2016.02.011.
4. M. Izadifar, P. Thissen, A. Steudel, R. Kleeberg, S. Kaufhold, J. Kaltenbach, R. Schuhmann, F. Dehn and K. Emmerich, Comprehensive examination of dehydroxylation of kaolinite, disordered kaolinite, and dickite: experimental studies and density functional theory, Clays Clay Miner., 2020, 68(4), 319–333,  DOI:10.1007/s42860-020-00082-w.
5. J. Davidovits, Geopolymers: Inorganic Polymeric New Materials, J. Therm. Anal., 1991, 37(8), 1633–1656,  DOI:10.1007/BF01912193.
6. A. A. Ramezanianpour and H. Bahrami Jovein, Influence of Metakaolin as Supplementary Cementing Material on Strength and Durability of Concretes, Constr. Build. Mater., 2012, 30, 470–479,  DOI:10.1016/j.conbuildmat.2011.12.050.
7. Y. Luo, X. Gao, D. Wang, Y. Liu, Q. Zhang, J. Li, Z. Tian and G. Xue, Study on the Efflorescence Behavior of Concrete by Adding Metakaolin, J. Build. Eng., 2024, 83, 108396,  DOI:10.1016/j.jobe.2023.108396.
8. K. N. Kumar, R. Divahar, M. Gupta, P. S. A. Raj, S. P. Sangeetha and P. S. Joanna, Elimination of Global Warming Gas Emissions by Utilizing High Reactive Metakaolin in High Strength Concrete for Eco-Friendly Protection, Mater. Res. Express, 2023, 10(8), 085507,  DOI:10.1088/2053-1591/acead8.
9. O. Vogt, N. Ukrainczyk and E. Koenders, Effect of Silica Fume on Metakaolin Geopolymers' Sulfuric Acid Resistance, Materials, 2021, 14(18), 5396,  DOI:10.3390/ma14185396.
10. T. Dong, S. Xie, J. Wang, Z. Chen and Q. Liu, Properties and Characterization of a Metakaolin Phosphate Acid–Based Geopolymer Synthesized in a Humid Environment, J. Aust. Ceram. Soc., 2020, 56(1), 175–184,  DOI:10.1007/s41779-019-00376-w.
11. M. M. A. Elahi, C. R. Shearer, A. Naser Rashid Reza, A. K. Saha, M. N. N. Khan, M. M. Hossain and P. K. Sarker, Improving the Sulfate Attack Resistance of Concrete by Using Supplementary Cementitious Materials (SCMs): A Review, Constr. Build. Mater., 2021, 281, 122628,  DOI:10.1016/j.conbuildmat.2021.122628.
12. M. Rezaei, A. Delnavaz and M. Delnavaz, Experimental Investigation of Metakaolin Ingredients on Bonding of Steel Fibers to Cement in Paste of Steel Fiber Concrete under Sulfate and Sulfate–Chloride Attack, Appl. Clay Sci., 2024, 260, 107549,  DOI:10.1016/j.clay.2024.107549.
13. A. B. Moradikhou, A. Esparham and M. Jamshidi Avanaki, Physical & Mechanical Properties of Fiber Reinforced Metakaolin-Based Geopolymer Concrete, Constr. Build. Mater., 2020, 251, 118965,  DOI:10.1016/j.conbuildmat.2020.118965.
14. A. Albidah, A. S. Alqarni, H. Abbas, T. Almusallam and Y. Al-Salloum, Behavior of Metakaolin-Based Geopolymer Concrete at Ambient and Elevated Temperatures, Constr. Build. Mater., 2022, 317, 125910,  DOI:10.1016/j.conbuildmat.2021.125910.
15. K. M. Salah Uddin, M. Izadifar, N. Ukrainczyk, E. Koenders and B. Middendorf, Dissolution of β-C2S Cement Clinker: Part 1 Molecular Dynamics (MD) Approach for Different Crystal Facets, Materials, 2022, 15(18), 6388,  DOI:10.3390/ma15186388.
16. M. Izadifar, N. Ukrainczyk, K. M. Salah Uddin, B. Middendorf and E. Koenders, Dissolution of β-C2S Cement Clinker: Part 2 Atomistic Kinetic Monte Carlo (KMC) Upscaling Approach, Materials, 2022, 15(19), 6716,  DOI:10.3390/ma15196716.
17. K. M. Salah Uddin, M. Izadifar, N. Ukrainczyk, E. Koenders and B. Middendorf, Dissolution of Portlandite in Pure Water: Part 1 Molecular Dynamics (MD) Approach, Materials, 2022, 15(4), 1404,  DOI:10.3390/ma15041404.
18. M. Izadifar, N. Ukrainczyk, K. M. Salah Uddin, B. Middendorf and E. Koenders, Dissolution of Portlandite in Pure Water: Part 2 Atomistic Kinetic Monte Carlo (KMC) Approach, Materials, 2022, 15(4), 1442,  DOI:10.3390/ma15041442.
19. K. Gong and C. E. White, Predicting CaO-(MgO)-Al2O3-SiO2 Glass Reactivity in Alkaline Environments from Force Field Molecular Dynamics Simulations, Cem. Concr. Res., 2021, 150, 106588,  DOI:10.1016/j.cemconres.2021.106588.
20. M. Izadifar, N. Ukrainczyk and E. Koenders, Silicate Dissolution Mechanism from Metakaolinite Using Density Functional Theory, Nanomaterials, 2023, 13(7), 1196,  DOI:10.3390/nano13071196.
21. M. Izadifar, N. Ukrainczyk and E. Koenders, Atomistic Insights into Silicate Dissolution of Metakaolinite under Alkaline Conditions: Ab Initio Quantum Mechanical Investigation, Langmuir, 2024, 40(37), 19332–19342,  DOI:10.1021/acs.langmuir.4c00890.
22. M. Izadifar, W. Sekkal, L. Dubyey, N. Ukrainczyk, A. Zaoui and E. Koenders, Theoretical Studies of Adsorption Reactions of Aluminosilicate Aqueous Species on Graphene-Based Nanomaterials: Implications for Geopolymer Binders, ACS Appl. Nano Mater., 2023, 16318–16331,  DOI:10.1021/acsanm.3c02438.
23. W. Sekkal, M. Izadifar, A. Zaoui, N. Ukrainczyk and E. Koenders, Theoretical Investigation of Protective Graphene-Coated Metakaolin Geopolymer Interface under Moisture and Chemical Composition Effects, Powder Technol., 2023, 430, 119007,  DOI:10.1016/j.powtec.2023.119007.
24. C. Dreßler and D. Sebastiani, Effect of Anion Reorientation on Proton Mobility in the Solid Acids Family CsH _y XO ₄ (X = S, P, Se, y = 1, 2) from Ab Initio Molecular Dynamics Simulations, Phys. Chem. Chem. Phys., 2020, 22(19), 10738–10752,  10.1039/C9CP06473G.
25. J. Jia, Y. Liang, T. Tsuji, C. R. Miranda, Y. Masuda and T. Matsuoka, Ab Initio Molecular Dynamics Study of Carbonation and Hydrolysis Reactions on Cleaved Quartz (001) Surface, J. Phys. Chem. C, 2019, 123(8), 4938–4948,  DOI:10.1021/acs.jpcc.8b12089.
26. B. Mortazavi, X. Zhuang, T. Rabczuk and A. V. Shapeev, Atomistic Modeling of the Mechanical Properties: The Rise of Machine Learning Interatomic Potentials, Mater. Horiz., 2023, 10(6), 1956–1968,  10.1039/D3MH00125C.
27. B. Mortazavi, S. Ahzi, V. Toniazzo and Y. Rémond, Nitrogen Doping and Vacancy Effects on the Mechanical Properties of Graphene: A Molecular Dynamics Study, Phys. Lett. A, 2012, 376(12–13), 1146–1153,  DOI:10.1016/j.physleta.2011.11.034.
28. K. Coopamootoo and E. Masoero, Simulations of Tricalcium Silicate Dissolution at Screw Dislocations: Effects of Finite Crystal Size and Mechanical Interaction Potentials, Cem. Concr. Res., 2024, 175, 107384,  DOI:10.1016/j.cemconres.2023.107384.
29. N. E. N'Guessan, E. Joussein, A. Courtin-Nomade, E. Paineau, M. Soubrand, O. Grauby, V. Robin, C. D. Cristina, D. Vantelon, P. Launois, P. Fondanèche, S. Rossignol, N. Texier-Mandoki and X. Bourbon, Role of Cations on the Dissolution Mechanism of Kaolinite in High Alkaline Media, Appl. Clay Sci., 2021, 205, 106037,  DOI:10.1016/j.clay.2021.106037.
30. Y. Briki, M. Zajac, M. B. Haha and K. Scrivener, Factors Affecting the Reactivity of Slag at Early and Late Ages, Cem. Concr. Res., 2021, 150, 106604,  DOI:10.1016/j.cemconres.2021.106604.
31. J. Chen, P. Martin, Z. Xu, H. Manzano, J. S. Dolado and G. Ye, A Dissolution Model of Alite Coupling Surface Topography and Ions Transport under Different Hydrodynamics Conditions at Microscale, Cem. Concr. Res., 2021, 142, 106377,  DOI:10.1016/j.cemconres.2021.106377.
32. H. Manzano, E. Durgun, I. López-Arbeloa and J. C. Grossman, Insight on Tricalcium Silicate Hydration and Dissolution Mechanism from Molecular Simulations, ACS Appl. Mater. Interfaces, 2015, 7(27), 14726–14733,  DOI:10.1021/acsami.5b02505.
33. L. Valentini, Modeling Dissolution–Precipitation Kinetics of Alkali-Activated Metakaolin, ACS Omega, 2018, 3(12), 18100–18108,  DOI:10.1021/acsomega.8b02380.
34. P. Martin, J. J. Gaitero, J. S. Dolado and H. Manzano, New Kinetic Monte Carlo Model to Study the Dissolution of Quartz, ACS Earth Space Chem., 2021, 5(3), 516–524,  DOI:10.1021/acsearthspacechem.0c00303.
35. R. Dupuis, J. S. Dolado, J. Surga and A. Ayuela, Doping as a Way To Protect Silicate Chains in Calcium Silicate Hydrates, ACS Sustain. Chem. Eng., 2018, 6(11), 15015–15021,  DOI:10.1021/acssuschemeng.8b03488.
36. M. Izadifar, N. C. Valencia, P. Xiao, N. Ukrainczyk and E. Koenders, 3D Off-Lattice Coarse-Grained Monte Carlo Simulations for Nucleation of Alkaline Aluminosilicate Gels, Materials, 2023, 16(5), 1863,  DOI:10.3390/ma16051863.
37. N. C. Valencia, M. Izadifar, N. Ukrainczyk and E. Koenders, Coarse-Grained Monte Carlo Simulations with Octree Cells for Geopolymer Nucleation at Different pH Values, Materials, 2023, 17(1), 95,  DOI:10.3390/ma17010095.
38. A. Heyden, A. T. Bell and F. J. Keil, Efficient Methods for Finding Transition States in Chemical Reactions: Comparison of Improved Dimer Method and Partitioned Rational Function Optimization Method, J. Chem. Phys., 2005, 123(22), 224101,  DOI:10.1063/1.2104507.
39. G. Cheng, X.-X. Wang, S.-H. Zhang, K.-K. Zhu, Z.-J. Sui, X.-G. Zhou, D. Chen and Y.-A. Zhu, On the Product and Transition-State Shape Selectivities in 2-Heptene Isomerization, Chem. Phys. Lett., 2023, 812, 140263,  DOI:10.1016/j.cplett.2022.140263.
40. R. Jinnouchi, F. Karsai and G. Kresse, On-the-Fly Machine Learning Force Field Generation: Application to Melting Points, Phys. Rev. B, 2019, 100(1), 014105,  DOI:10.1103/PhysRevB.100.014105.
41. Y. Marcus, Thermodynamics of Solvation of Ions. Part 5.—Gibbs Free Energy of Hydration at 298.15 K, J. Chem. Soc., Faraday Trans., 1991, 87(18), 2995–2999,  10.1039/FT9918702995.
42. W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140(4A), A1133–A1138,  DOI:10.1103/PhysRev.140.A1133.
43. G. Kresse and J. Hafner, Ab Initio Molecular Dynamics for Liquid Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558–561,  DOI:10.1103/PhysRevB.47.558.
44. G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186,  DOI:10.1103/PhysRevB.54.11169.
45. G. Kresse and J. Furthmüller, Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6(1), 15–50,  DOI:10.1016/0927-0256(96)00008-0.
46. B. Mortazavi, Structural, Electronic, Thermal and Mechanical Properties of C60-Based Fullerene Two-Dimensional Networks Explored by First-Principles and Machine Learning, Carbon, 2023, 213, 118293,  DOI:10.1016/j.carbon.2023.118293.
47. G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775,  DOI:10.1103/PhysRevB.59.1758.
48. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868,  DOI:10.1103/PhysRevLett.77.3865.
49. H. J. Monkhorst and J. D. Pack, Special Points for Brillouin-Zone Integrations, Phys. Rev. B, 1976, 13(12), 5188–5192,  DOI:10.1103/PhysRevB.13.5188.
50. K. Momma and F. Izumi, It VESTA: A Three-Dimensional Visualization System for Electronic and Structural Analysis, J. Appl. Crystallogr., 2008, 41(3), 653–658,  DOI:10.1107/S0021889808012016.
51. G. Mills, H. Jónsson and G. K. Schenter, Reversible Work Transition State Theory: Application to Dissociative Adsorption of Hydrogen, Surf. Sci., 1995, 324(2–3), 305–337,  DOI:10.1016/0039-6028(94)00731-4.
52. H. Jónsson, G. Mills and K. W. Jacobsen, Nudged Elastic Band Method for Finding Minimum Energy Paths of Transitions, in Classical and Quantum Dynamics in Condensed Phase Simulations, World Scientific, Lerici, Villa Marigola, 1998, pp. 385–404,  DOI:10.1142/9789812839664_0016.
53. G. Henkelman and H. A. Jónsson, Dimer Method for Finding Saddle Points on High Dimensional Potential Surfaces Using Only First Derivatives, J. Chem. Phys., 1999, 111(15), 7010–7022,  DOI:10.1063/1.480097.
54. B. Mortazavi, M. Shahrokhi, F. Shojaei, T. Rabczuk, X. Zhuang and A. V. Shapeev, A First-Principles and Machine-Learning Investigation on the Electronic, Photocatalytic, Mechanical and Heat Conduction Properties of Nanoporous C₅ N Monolayers, Nanoscale, 2022, 14(11), 4324–4333,  10.1039/D1NR06449E.
55. B. Mortazavi, I. S. Novikov, E. V. Podryabinkin, S. Roche, T. Rabczuk, A. V. Shapeev and X. Zhuang, Exploring Phononic Properties of Two-Dimensional Materials Using Machine Learning Interatomic Potentials, Appl. Mater. Today, 2020, 20, 100685,  DOI:10.1016/j.apmt.2020.100685.
56. Z. Li, J. R. Kermode and A. De Vita, Molecular Dynamics with On-the-Fly Machine Learning of Quantum-Mechanical Forces, Phys. Rev. Lett., 2015, 114(9), 096405,  DOI:10.1103/PhysRevLett.114.096405.
57. S. Grimme, Semiempirical GGA-type Density Functional Constructed with a Long-range Dispersion Correction, J. Comput. Chem., 2006, 27(15), 1787–1799,  DOI:10.1002/jcc.20495.
58. C. P. Morrow, S. Nangia and B. J. Garrison, Ab Initio Investigation of Dissolution Mechanisms in Aluminosilicate Minerals, J. Phys. Chem. A, 2009, 113(7), 1343–1352,  DOI:10.1021/jp8079099.

---