Correlated excitonic signatures of individual van der Waals NiPS₃ antiferromagnet nanoflakes

Abstract

Composite quasi-particles with emergent functionalities in spintronic and quantum information science can be realized in correlated materials due to entangled charge, spin, orbital, and lattice degrees of freedom. Here we show that by reducing the lateral dimension of correlated antiferromagnet NiPS₃ flakes to tens of nanometers and thickness to less than ten nanometers, we can switch-off the bulk spin–orbit entangled exciton in the near-infrared (1.47 eV) and activate visible-range (1.8–2.2 eV) transitions. These ultra-sharp lines (<120 μeV at 4.2 K) share the spin-correlated nature of the bulk exciton by displaying a strong linear polarization below Néel temperature. Furthermore, exciton photoluminescence lineshape analysis indicates a polaronic character VIA coupling with at-least 3 phonon modes and a comb-like Stark effect through discretization of charges in each layer. These findings augment the knowledge on the many-body nature of excitonic quasi-particles in correlated antiferromagnets and also establish the nanoscale correlated antiferromagnets as a promising platform for integrated magneto-optic devices.

---

New concepts

Excitons in 2D antiferromagnetic bulk NiPS₃ help comprehend the complex phenomena in many-body physics by the display of correlated photophysical properties. In this communication, we study such correlated 2D antiferromagnet at nanoscale level. We realize the nanoflakes of NiPS₃ through chemical synthesis route utilizing metathesis reaction. Various optical spectroscopy studies reveal correlated excitonic signatures of coupling with many types of quasi-particles such as spin, phonon, and charge. Compared to other semiconductor nanostructures, here the combination of smaller lateral dimension, correlated antiferromagnetic structure and van der Waals interlayer stacking configuration contribute to those distinct excitonic signatures. This report suggests that the lateral size manipulation can be an additional way of controlling the optical properties of correlated 2D antiferromagnet other than the usual vertical layering of such materials. This result can lead towards an integrated magneto-optic device with further efforts targeting a control over size, edge, thickness, composition and defects.

1. Introduction

Excitons – quasi-particle bound states of electron–hole pairs – are investigated extensively as they serve as the foundation of almost all modern photonic technologies.¹ The efforts of the past decades focused on uncorrelated excitons in conventional semiconductors where quasi-particles weakly interact with one another. Currently, correlated excitons are generating significant interest due to their intrinsic many-body interactions entangling charge, spin, orbital, and lattice degrees of freedoms.^2–4 A wide breadth of emergent quantum phenomena beyond the physics of conventional semiconductors, such as excitonic insulators,⁵ exciton condensates,⁶ and exciton Hall effects,⁷ have been recently reported, while charge fractionalization⁸ and exciton-mediated superconductivity⁹ are still elusive. Among a few classes of materials capable of supporting such exciting phenomena, e.g. transition metal dichalcogenides,¹⁰ topological insulators,¹¹ and twisted bilayer graphene,¹² the correlated van der Waals magnets have risen to the forefront due to the coexistence of long-range magnetic correlations, strong electron–phonon coupling, and a robust excitonic response all under two-dimensional (2D) confinement.^13–15

A member of this material family, NiPS₃, is a charge-transfer antiferromagnetic (AFM) insulator similar to the hole-doped high-T_c cuprates.¹⁶ Owing to strong Ni-d and S-p hybridization in the valence (conduction) bands,¹⁷ a co-existence of d–d and charge-transfer electron–hole pairs is expected.¹⁸ Concomitantly, several optical transitions from UV to NIR are reported in absorption,¹⁹ reflectance,²⁰ and photo-conductivity studies.¹⁶ These studies report a strong absorbing transition at 2.2 eV assigned to a charge-transfer state.¹⁶ Photoluminescence (PL) spectroscopy of bulk samples shows an emission peak at 1.47 eV that has been attributed to a spin-correlated exciton arising below the Néel transition temperature T_N (150 K).²¹ This exciton is assigned to a spin–orbit entangled state (SO-X) displaying an ultra-narrow linewidth,²¹ phonon-bound states,²⁰ spin-correlated behavior,²² thickness-dependent PL,²¹ polariton formation,²³ and can be controlled using light-pumping²⁴ and external magnetic fields.²² However, to date, whether or not reduction of the lateral dimension influences these fascinating phenomena has not been explored. This approach would not only benefit from the scalable top-down and bottom-up fabrication approaches, but could also advance the fundamental understanding of excitons in nanoscale correlated insulators in parallel with excitons in nanoscale semiconductors.²⁵ Aiming to address this question, we have conducted single nanostructure optical spectroscopy studies on individual nanoflakes (NF) of NiPS₃.

2. Results

2.1. Chemical synthesis of NiPS₃ nanoflakes

2.1.1. Materials. Sodium sulfide nonahydrate, Na₂S·9H₂O (99.99+% purity), nickel(II) chloride hexahydrate, NiCl₂·6H₂O (99.99+% purity), and phosphorous(III) trichloride, PCl₃ (99% purity), were purchased from Sigma-Aldrich. Acetone (98+% purity) was purchased from KMG Chemicals and used without further purification.

2.1.2. Preparation. Crystalline NFs of NiPS₃ were prepared via a 2-stage process. First, a solution phase stage utilized the metathesis reaction of highly ionic M₄P₂S₆ (M = Na, Li) with a common nickel salt (NiCl₂ or Ni(NO₃)₂). The Na₄P₂S₆ was synthesized according to the literature procedure.²⁶ In a typical reaction, 6 mL of PCl₃ (∼70 mmol) was added dropwise to an ice-cooled solution of Na₂S·9H₂O (75 g, 312 mmol) in 100 mL of water under static nitrogen atmosphere. During the addition, a white precipitate slowly formed, and the slurry was left to stir for 2 hours. After the stirring, the precipitate was filtered, dissolved in a minimal amount of boiling water, and placed in a refrigerator for 4 hours for crystallization. The collected crystalline powder was then placed in a vacuum oven for drying.

To obtain NiPS₃, a small portion of synthesized Na₄P₂S₆ (32 mg, 0.092 mmol) was dissolved in water (5 mL) followed by the addition of NiCl₂·6H₂O (45 mg, 0.189 mmol). The solution immediately turned red with subsequent gelation. Then, 3 mL of water was added followed by the precipitation with acetone to remove the excess of NaCl. Such post-synthetic treatment resulted in a formation of mostly amorphous matrix with ∼3nm crystalline domains. The product was centrifuged at 5000 cfm, supernatant was decanted, and the dark-red precipitate dried in vacuum at room temperature and annealed at 375 °C for 30 minutes under nitrogen, which led to the crystallization of NiPS₃ nanoflakes. After annealing and cooling down, a colloidal solution of NiPS₃ NFs was prepared via dissolution of annealed NiPS₃ in deionized water. A 100 μL of the suspended nanoflake solution was dropcasted onto Si/SiO₂ substrates for optical spectroscopy on individual nanoflakes and on TEM grids for imaging.

2.2. Crystalline nanoflakes of NiPS₃

The lateral sizes of the NFs are in the range of 20–100 nm with thicknesses ranging from 1–10 nm obtained from scanning probe image (Fig. 1a). The high crystallinity of individual NFs is verified by HR-TEM image and a representative FFT pattern is shown in Fig. 1b. The figure displays a single crystal NiPS₃ NF of 50 nm in size oriented along the [001] direction with 5.0 Å (020) plane spacing consistent with that reported for chemical vapor transport CVT grown bulk NiPS₃ (CVT-bulk). Fig. S1 (ESI†) shows two more HR-TEM images of different NFs; one highly crystalline flake displaying a (111) lattice plane, and the other comprising a large central grain with smaller randomly oriented grains attached mostly on the side of the central one. These findings together with the XRD data (Fig. 1c and Fig. S2, ESI†) and Raman spectroscopy (Fig. 1d and Fig. S3, ESI†) provide clear evidence that the proposed chemical approach is capable of producing NiPS₃ nanoflakes with compositional uniformity and crystallinity comparable to the CVT-bulk sample albeit some NFs may by produced as polycrystalline ensembles with random orientation of individual grains.

Fig. 1 Images of NiPS₃ nanoflakes. (a) Scanning probe image of nanoflakes with 20–100 nm lateral sizes and 1–10 nm thicknesses. (b) A single crystal NiPS₃ nanoflake of 50 nm in size oriented along the [001] direction, as confirmed by the fast Fourier transform (FFT). (c) XRD of NiPS₃ nanoflakes shows the crystalline peaks. (d) Raman spectrum of NiPS₃ nanoflakes at 298 K.

2.3. Ultra-sharp PL emission

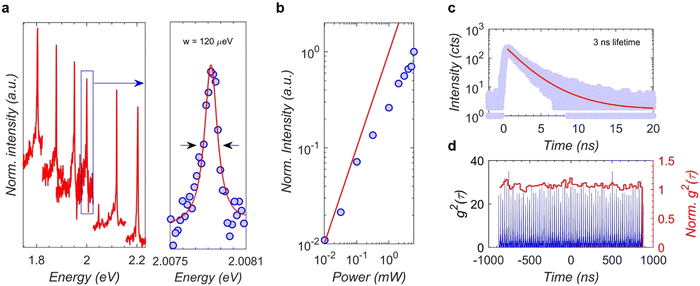
Upon checking the PL of individual NFs at 4.2 K, different individual NFs emit PL peaks between 1.8 eV and 2.2 eV in the visible spectral range (Fig. 2a) which is different from the previously reported many body excitonic transition SO-X at 1.47 eV for CVT-bulk. Interestingly, the main PL peak of the NF is characterized by a spectral resolution-limited linewidth of 120 μeV (Fig. 2a), which is three times narrower than that reported for the SO-X.²² The pump-dependent PL study (Fig. 2b and Fig. S4, ESI†) shows that the intensity of the sharp emission peak has a sub-linear increase with pump power. Further, a time resolved PL study (Fig. 2c) reveals a lifetime of ∼3 ns, which is more than two orders of magnitude longer than ∼10 ps reported for the SO-X peak.^20,22 The key characteristic of this emission: (1) flake-to-flake variation of emission energies, (2) narrow linewidth, (3) sub-linear power dependence, and (4) long PL decay times are similar to those of excitons confined in quantum dots and defects. However, the 20–100 nm size of our NFs is not sufficient to provide a strong quantum confinement to induce 300–700 meV blueshift from 1.47 eV SO-X peak since the CVT-bulk exciton is reported to have a high binding energy of over several hundred meV with a small Bohr radius of ∼0.6 nm.²³ Second-order autocorrelation measurements also yield Poissonian photon-statistics (Fig. 2d) instead of the photon-antibunching typically observed in quantum dots and defects. While this raises the question about the origin of PL from the NFs, which is discussed later in the Discussion section, first we report the preceding interesting studies revealing that the PL emissions from NFs display clear signatures of correlation with spin, phonon and charge degrees of freedom.

Fig. 2 Ultra-sharp PL from nanoflakes. (a) PL from six different nanoflakes showing a peak range from 1.8–2.2 eV, and a resolution limited linewidth of 120 μeV. (b) A sub-linear dependence to excitation power density. (c) PL lifetime of 3 ns. (d) Second-order autocorrelation showing Poissonian photon-statistics.

2.4. Signature of spin-correlated exciton

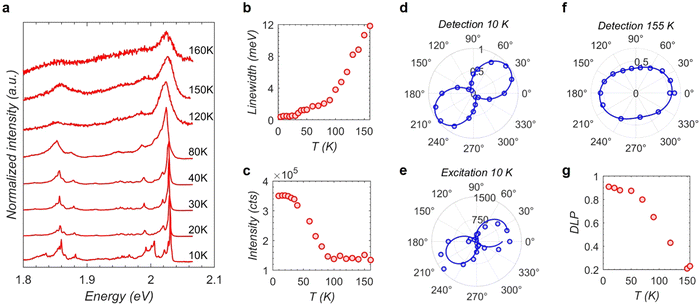
A temperature-dependent PL from a NF is shown in Fig. 3a. The ultra-sharp PL linewidth of NFs at low temperatures increases with rising temperature. An analysis of the linewidth reveals that while the linewidth increases slowly with a slope of 0.025 meV K⁻¹ from 10-to-90 K, the slope drastically increases to 0.14 meV K⁻¹ for 90-to-160 K (Fig. 3b). The integrated intensity (Fig. 3c) shows a similar temperature-dependence with decreased intensities beyond 90 K. Further, the PL of NFs is resolved into vertical (s) and horizontal (p) polarization components (see ESI,† S15) and the analysis shows an anisotropic or unequal intensities along s and p. A polar plot for I_s/(I_s + I_p) collected at 10 K by rotating the polarization analyzer in the detection path is shown in Fig. 3d. The data points are fitted to a sinusoidal function and the maximum anisotropy is obtained at an angle of about 30° for this NF. At this angle, the degree of linear polarization DLP = (I_s − I_p)/(I_s + I_p) is about 90%. Similar experiments on other NFs (Fig. S5, ESI†) also revealed a near-unity linear polarization for all those NFs at low temperatures. The NFs exhibit such anisotropic emission while changing the excitation polarization as well (Fig. 3e).

Fig. 3 Spin-correlated PL in nanoflakes. (a) Temperature-dependent PL from a nanoflake (b) and (c) linewidth and intensity display a sudden change beyond 100 K indicating a temperature-dependent PL from NFs. (d) and (e) Polar plot showing a near unity degree of linear polarization at 10 K under detection and excitation polarization analysis. (f) Polar plot showing a drop in degree of linear polarization to 20% at 155 K. (g) Degree of linear polarization for different temperatures. A residual degree of linear polarization is still present beyond the bulk T_N.

Next, the DLP is analyzed for the increase in the sample temperature. A polar plot for the detection polarization analysis collected at 155 K in Fig. 3f indicates the DLP has reduced to about 20% compared to a near-unity DLP at 10 K. In Fig. 3g, the trend of DLP vs. temperature is shown where a sudden decrease of the value beyond 90 K is observed similar to the PL linewidth and intensities discussed before. The DLP reaches a minimum value of about 20–40% at about 140 K for different NFs (Fig. S5, ESI†) and this residual DLP does not vanish completely at higher temperatures collected up to about 160 K. The polarization resolved PL becomes too weak beyond this temperature to get an accurate DLP. Interestingly, the above discussed temperature-dependent PL behaviors such as linewidth, intensities and DLP perfectly mirror those reported for SO-X of CVT-bulk sample.^20–22,27 To find the influence of AFM order on the PL, magnetization experiment was conducted on NFs (Fig. S6, ESI†) that exhibit an antiferromagnetic behavior with T_N in the range of 170–190 K. It is believed that the magnetic susceptibility comprises antiferromagnetic contribution from the interior of the NFs and the paramagnetic contribution from the uncompensated spins arising across the edge of the NFs. This attribution is further supported by the inflection point at 110 K (Fig. S6, ESI†), which is most likely the consequence of AFM and paramagnetic contributions overlapping with each other. While more size selective studies are needed, the anisotropic polarized PL showing apparent T_N dependence provide evidence that the ultra-sharp PL emission of the NFs is strongly correlated to the spins of NiPS₃'s zig-zag antiferromagnetic order. We, however, note that it would be premature for us to distinguish whether the linearly polarized emission originates from the spin orientation or the zig-zag ferromagnetic chain as such reasonings are inconclusive even for CVT-bulk SO-X emission.^20–22,27

2.5. Low energy tail resulting from exciton phonon coupling

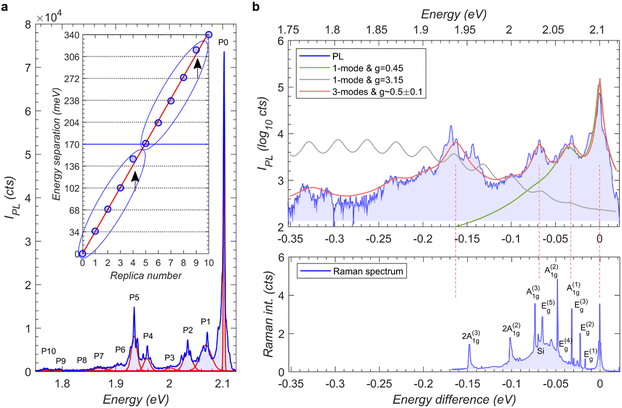
The ultra-sharp PL emission peak (P0) from the NFs at cryogenic temperatures displays a low energy tail that is composed of up to 10 spectral peaks (P1–P10) spread over 340 meV (Fig. 4a collected at 10 K). See Fig. S7 (ESI†) for low energy tail peaks displaying similar polarization orientation as the main peak suggesting a phonon replica feature (also, Section 2.6 discusses the tail peaks following the spectral jump direction of the main PL peak). The positions of these peaks yielded by simple individual Gaussian fits are separated from one another by an average value of ∼34–35 meV (Fig. 4a). Thus this phonon tail appear similar to the exciton-A⁽¹⁾_1g-phonon bound states reported in linear dichroism²⁰ and ultrafast spectroscopy²⁸ studies of the high energy range of 1.5–2 eV in CVT-bulk sample (the earlier work however reported a lower peak to peak energy separation of 28 meV attributed to larger exciton–phonon coupling). A closer inspection of the NF's low energy peak however reveals multiple significantly different features that are reproduced across different NFs (Fig. S8, ESI†). Specifically, while P1–P3 appears successively weaker as they should for higher order phonon replica of a single phonon mode, the intensities of P4 and P5 increase back. This intensity modulation pattern of P0–P5 is repeated in P5 to P10.

Fig. 4 Exciton–phonon bound states in nanoflakes. (a) Low-resolution grating spectrum (blue line) of a nanoflake collected at 10 K showing the main peak P0 and 10 tail peaks labelled from P1 to P10. Red lines are individual Gaussian fits to different peaks. Inset: Tail peak positions from the central emission energy of P0 fitted with a linear function giving a slope of ∼34 meV. Arrows show that P4 and P9 slightly deviate from the linear function. Ellipsoid shows the pattern of P0–P4 repeats at P5–P9. (b) PL lineshape (blue) fitted with the Holstein model accounting for 3 phonon modes with g ∼ 0.5 ± 0.1 (red). For the lowest phonon mode, lineshapes were calculated using g = 0.45 (green), and g = 3.15 (gray). Raman spectrum of CVT-bulk NiPS₃ collected at 4.2 K is also shown.

To understand this complex phonon tail, we construct Holstein exciton–phonon model (see ESI,† S9). First, the case of an exciton coupled to a single A⁽¹⁾_1g phonon at 32.8 meV with a moderate coupling g = 0.45 is considered. The resulting fit (Fig. 4b, green line) can only reproduce the spectral lineshape up to P1 with the intensity monotonically decreasing to zero for the higher order phonon modes. Increasing the coupling strength to 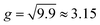, as used in ref. 27 yields a Gaussian envelope of replicas that almost nullifies the zero-phonon line peak P0 in contrast to the experimental spectra (Fig. 4b, gray line). Since these single phonon models at moderate and strong coupling do not reasonably reproduce the peak pattern, and the Raman spectrum of both NF and CVT-bulk NiPS₃ reveals 8 independent Raman active phonon modes (Fig. 4b and Fig. S3, ESI†), we explore the possibility that the replicas are characterized by coupling to multiple phonon modes of NiPS₃. Here, a minimum of 3 phonon modes are required to fit the intensity modulation pattern of the phonon replicas. Specifically, phonon energies of 32.8, 68.5 and 163 meV with moderate coupling strength of g ∼ 0.5 ± 0.1 generate the red line in Fig. 4b that reproduces the PL lineshape reasonably well. While the energies of the first two modes are in good accord with the A⁽¹⁾_1g and E⁽⁵⁾_g or A⁽³⁾_1g modes, respectively, the third mode does not match with any of the fundamental Raman modes reported for NiPS₃. This phonon is tentatively assigned to a Raman inactive mode that becomes bright only after coupling to the exciton, similar to that observed in an another 2D magnet CrI₃.²⁹ This analysis suggests a rich manifold of phonon modes coupled to the exciton in NiPS₃ resulting in the observed multiple phonon replicas, rather than a single strongly coupled phonon mode.

2.6. Discrete spectral jumps and capacitor charging model

The PL spectrum shown in Fig. 4a reveals that each peak is a superposition of sharp lines. This is further investigated by acquiring a series of 400 high-resolution PL spectra at 1s intervals (Fig. 5a). This shows the P0 sharp line undergoing discrete spectral jumps and those near P1 follow the magnitude and direction of the former. A time integrated PL spectrum is shown in Fig. 5b that displays a series of sharp PL peaks covering the entire spectral range of P0 to P5 with a comb-like pattern. The zoom-in view of this pattern (Fig. 5b inset) and histogram of consecutive peak-to-peak energy separation (Fig. 5c) further reveal that two adjacent peaks are separated by a regular energy step of δ₁ ∼ 1.9 ± 0.1 meV with some peaks having a lower intensity shoulder separated by δ₂ ∼ 0.75 ± 0.1 meV. These findings provide clear evidence that the spectral lines jump randomly in time but in regular steps of energy. Spectral jumps in other nanoscale light emitters such as quantum dots or single molecules are attributed to the Stark shift of excitonic emission resulting from the electric field of photo-excited carriers trapped in the surrounding.^30,31 Since the configuration and number of trapped carriers are random in both time and space, so too are the spectral jumps in most nanoscale emitters. The observation of spectral jumps with regular energy intervals across different NFs (Fig. S8, ESI†) suggests that electric field fluctuations responsible for the Stark shift of the emission lines are occurring in regular increments.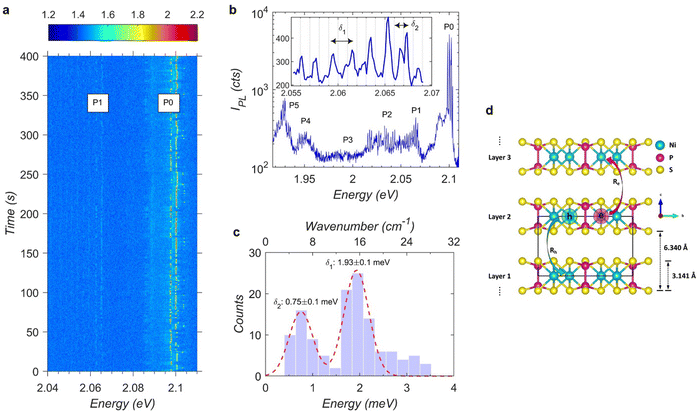

Fig. 5 Spectral lines jump in regular steps of energies in nanoflakes. (a) A time dependent spectral image sequence of PL collected at 10 K from the same nanoflake shown in Fig. 4 with 1s each acquisition under a high-resolution grating spectrometer. P0 sharp line undergoes discrete spectral jumps which are followed in magnitude and direction by the P1 sharp lines. (b) A time integrated spectral plot collected with high-resolution grating spectrometer displayed in log scale. Discrete jumps are visible over the entire span of P0-to-P5 and the inset shows a small window with noticeable equidistant consecutive peak separations marked as δ₁ and δ₂. (c) Histogram of consecutive peak difference gives a value of ∼1.9 meV for δ₁ and ∼0.7 meV for δ₂. (d) A schematic of the proposed parallel-capacitor charging model where inter-layer electron (hole) hopping with the rate R_e (R_h) upon photo-excitation creates a homogeneous electric field in adjacent layers assuming the charges are delocalized in the plane.

To explain this, we propose a charging model (see ESI,† S10) in which the electric field inside the NF fluctuates in magnitude and direction from one layer to the next as a consequence of excess charge carriers that are uniformly delocalized within the layers (Fig. 5d). As such, each individual layer of the NF contributes to a uniform electric field, with one sign in the layers above and with the other sign in the layers below. A charging event is attributed to the interlayer tunneling of energetic electrons or holes after photo-excitation while the carriers are still hot. This transfer of an electron to an adjacent layer while leaving the hole behind (or vice versa) gives the uniform field of a parallel plate capacitor straddling the barrier between layers which is on the order of 10⁵ V m⁻¹ and sufficient enough to induce regular Stark shifts in the order of ∼1 meV. To validate this model, Kinetic Monte Carlo simulations are performed and the results show reasonable agreement with the experimental data (Fig. S11–S13, ESI†). The calculations provide support for our attribution of discrete Stark shifts in energy steps, occurring randomly in time, to interlayer charge hopping dynamics creating a homogeneous electric field. An alternating pattern of major peaks with energy shifts δ₁ ∼ 2 meV separated by minor peaks in intervals of δ₂ ∼ 1 meV emerges as the natural consequence of non-radiative decay preferentially occurring in charged layers (see ESI,† S10 with accompanying Fig. S12 and S13, ESI†) which provides additional validation of the model.

3. Discussion

Optical absorption experiments in CVT-bulk NiPS₃ had reported several transitions ranging from 0.7–2.2 eV suggesting a complex excitonic states in this material.^16,19,21 The ultra-sharp SO-X PL peak reported in CVT-bulk NiPS₃, at a lower emission energy of 1.47 eV than the predicted optical bandgap of ∼1.8 eV,¹⁶ has generated interest due to their spin-correlated optical properties.^16,20–23 Several assignments have been made for SO-X such as: Zhang-Rice singlet²¹ or self-doping induced high density traps²² or defect-bound states²⁶ or even simple band-edge exciton³² suggesting that the topic is still under debate. Our report of new PL emission from NFs of NiPS₃ raises interesting questions about their physical origin. Here we present insights into some of the possibilities.

First, it is known that nanoscale dimension could induce quantum confinement of bulk excitons. Our findings altogether clearly show that reducing the lateral dimension of NiPS₃ flakes to nanometer scale results in the emergence of new high-energy excitonic transitions mirroring all the key characteristics of CVT-bulk SO-X state, such as: ultra-narrow linewidth, spin-induced linear polarization, and low-energy tail reflecting rich and complex exciton–phonon coupling. On the other hand, the preliminary analysis presented earlier suggests that this emission is unlikely to be a consequence of quantum confinement of the bulk SO-X state due to the expected Bohr radius (<1 nm) being much smaller than the lateral dimensions of our NFs in tens of nm.

Second, we conducted first-principles based calculations of exciton states in bulk NiPS₃ (see ESI,† S11). The results (Fig. S14, ESI†) reproduced an exciton state with a high oscillator strength at the 1.445 eV very close to the reported bulk SO-X state in PL studies. More interestingly, the calculation shows that while low energy exciton states display electron and hole wave functions that are quasi uniform in the unit cell, a high density of exciton states observed in the 1.8 to 2.2 eV range display a highly anisotropic charge-transfer-like wave function where electrons and holes localized on different magnetic sublattices.¹⁸ This result is in agreement with experiments^16,19,20 attributing an absorption feature in the same energy range to this charge-transfer exciton. However, PL studies^20–22,32 in CVT-bulk NiPS₃ do not report any emission from this state. The emission energies of NFs falling in the similar energies of charge transfer state could indicate that they are activated here suggesting a complex and different excitonic binding characters in NiPS₃. Further computational heavy simulations would be required to verify if nano-sized flakes have any differences in the exciton states than bulk.

Third, the defects in either on the surface or interstitials of nanomaterials can trap charge carriers and produce PL peaks different than the bandgap excitons. Further, the edge states in nanomaterials, formed by the arbitrary and the abrupt end of the atomic arrangements in the ends, can cause significant differences in optical properties than the bulk. For instance, surface modified nanodiamond has higher energy PL peaks than the bulk diamond³³ and different nanoribbon configuration has varying excitonic states than the bulk graphene.³⁴ The PL peaks in NFs could also be the consequence of the defects and/or edge states.

Among the three possibilities discussed above, defects and/or edge states are most likely the physical origin of the high-energy PL peaks in NFs. The signatures of narrow linewidth and sub-linear power dependence indeed indicate the nature of defects. Additionally, the PL peaks in NFs have signatures of correlated excitons associated with spin, phonon and charge degrees of freedom. While the spin correlation is also observed in CVT-bulk SO-X, there are excitonic signatures as a consequence of the nanoscale size of the NFs. The temperature dependent PL data suggest that there is a non-vanishing degree of linear polarization even above the bulk T_N which could either be the short-range AFM order or the arbitrary edge states could have a different spin orientation than the middle of the flakes inducing a weak degree of polarization. Further, the phonon coupling to the main PL peak is interpreted as exciton coupled to multiple phonon modes in NFs than a single strong coupling reported in bulk. Moreover, the discrete energetic comb nature of spectral jumps, arising from the discretization of charges stored in each layers producing uniform field, in the NFs is not observed in any other defects or nanoscale emitters. The capacitor charging model proposed here predicts such a shift might be the consequence of hopping of a single electron (or hole) between adjacent layers. Corresponding to the lateral size of the NFs, the calculation involves a capacitor plate area of about ∼20 × 20 nm² which gives rise to a large shift in electric field for the charge of a single electron (see eqn (S2.2) in the ESI,† S10). If a similar proposition is applied for a bulk exciton where a minimum confocal microscope spot size is about ∼1 × 1 μm², the capacitor plate area would be comparatively larger than that of a NF leading to a reduced shift in the electric field. While there is a possibility that a spectral jump could happen in the bulk exciton too, the magnitude of spectral shift would be in a fraction of a meV which is supported by the non-observance of any jumps in SO-X (Fig. S15, ESI†). Finally, reports are emerging that evince other members of the transition-metal thiophosphates material family, e.g., FePS₃ and MnPS₃, exhibit similar traits to NiPS₃ including such as strong exciton-magnon and exciton–phonon coupling.^24,35,36 Our results then suggest that defects and/or edge states could play a key role in shaping the optical spectra of other transition-metal thiophosphates, in particular their NFs where similar high-energy PL peaks may appear.

4. Conclusions

An ultra-sharp excitonic photoluminescence in chemically synthesized NiPS₃ nanoflakes has been observed in the visible range which is different from the bulk exciton emission occuring in the near infrared. The PL analysis indicate the possible influence of defects and edge states as a physical origin. The combination of smaller lateral dimension, correlated antiferromagnetic structure and van der Waals interlayer stacking configuration contribute to those distinct excitonic signatures. To further elucidate the connection between defects/edge states and the high-energy PL peaks, further microscopy experiments and large scale theoretical calculations are needed to examine the correlation between edge morphology/defects and optical response of the NFs.

Author contributions

H. H. conceived and led the experiment. V. C. performed the optical experiments, analyzed the data, plotted the graphics, and drafted the manuscript. C. R. D., D. P., and S. A. I. synthesized the nanoflakes. J. W., and M. M. S. obtained the TEM images. M. A. C., V. C., M. T. P., L. M., and E. F. W. performed the Raman spectroscopy. C. T. T., X. L., and H. Z. assisted V. C. in the PL experiments. A. C. J. assisted V. C. in the scanning probe measurements. C. A. L., and J.-X. Z. provided inputs for theoretical models. A. P., and D. H. D. provided theoretical grounds for interpreting the spectroscopic data using the Holstein exciton-polaron model along with the charge fluctuating capacitor model. V. C., and H. H. finalized the manuscript with inputs from C. A. L., S. A. I., A. P., and D. H. D.

Data availability

Data for this article are available at figshare.com at https://doi.org/10.6084/m9.figshare.26157673.v1.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was performed at the Center for Integrated Nanotechnologies, an Office of Science User Facility operated for the U.S. Department of Energy (DOE) Office of Science (OS). Los Alamos National Laboratory (LANL), an affirmative action equal opportunity employer, is managed by Triad National Security, LLC for the U.S. Department of Energy's NNSA, under contract 89233218CNA000001. C. R. D., D. P., C. A. L., J.-X. Z., M. A. C., and A. P. acknowledge support for the works from Laboratory Directed Research and Development (LDRD) program 20200104DR. S. A. I., and C. T. T. are supported by LDRD 20220757ER. H. H., V. C., X. L., and H. Z. acknowledge partial support by Quantum Science Center, a National QIS Research Center supported by DOE, OS. M. T. P. acknowledges support from LDRD awards 20210782ER and 20210640ECR. A. C. J. is supported by DOE BES QIS program LANLE3QR.

References

1. S. W. Koch, M. Kira, G. Khitrova and H. M. Gibbs, Nat. Mater., 2006, 5, 523–531.
2. D. N. Basov, R. D. Averitt and D. Hsieh, Nat. Mater., 2017, 16, 1077–1088.
3. F. Giustino, J. H. Lee, F. Trier, M. Bibes, S. M. Winter, R. Valentí, Y.-W. Son, L. Taillefer, C. Heil, A. I. Figueroa, B. Plaçais, Q. Wu, O. V. Yazyev, E. P. A. M. Bakkers, J. Nygård, P. Forn-Díaz, S. De Franceschi, J. W. McIver, L. E. F. F. Torres, T. Low, A. Kumar, R. Galceran, S. O. Valenzuela, M. V. Costache, A. Manchon, E.-A. Kim, G. R. Schleder, A. Fazzio and S. Roche, J. Phys. Mater., 2020, 3, 042006.
4. E. Dagotto, Science, 2005, 309, 257–262.
5. L. Ma, P. X. Nguyen, Z. Wang, Y. Zeng, K. Watanabe, T. Taniguchi, A. H. MacDonald, K. F. Mak and J. Shan, Nature, 2021, 598, 585–589.
6. Y. Morita, K. Yoshioka and M. Kuwata-Gonokami, Nat. Commun., 2022, 13, 5388.
7. M. Onga, Y. Zhang, T. Ideue and Y. Iwasa, Nat. Mater., 2017, 16, 1193–1197.
8. B. Seradjeh, J. E. Moore and M. Franz, Phys. Rev. Lett., 2009, 103, 066402.
9. A. Kavokin and P. Lagoudakis, Nat. Mater., 2016, 15, 599–600.
10. A. Kogar, M. S. Rak, S. Vig, A. A. Husain, F. Flicker, Y. I. Joe, L. Venema, G. J. MacDougall, T. C. Chiang, E. Fradkin, J. van Wezel and P. Abbamonte, Science, 2017, 358, 1314–1317.
11. R. Mori, S. Ciocys, K. Takasan, P. Ai, K. Currier, T. Morimoto, J. E. Moore and A. Lanzara, Nature, 2023, 614, 249–255.
12. D. Kim, B. Kang, Y. B. Choi, K. Watanabe, T. Taniguchi, G. H. Lee, G. Y. Cho and Y. Kim, Nano Lett., 2023, 23, 163–169.
13. H. Kurebayashi, J. H. Garcia, S. Khan, J. Sinova and S. Roche, Nat. Rev. Phys., 2022, 4, 150–166.
14. Q. H. Wang, A. Bedoya-Pinto, M. Blei, A. H. Dismukes, A. Hamo, S. Jenkins, M. Koperski, Y. Liu, Q. C. Sun, E. J. Telford, H. H. Kim, M. Augustin, U. Vool, J. X. Yin, L. H. Li, A. Falin, C. R. Dean, F. Casanova, R. F. L. Evans, M. Chshiev, A. Mishchenko, C. Petrovic, R. He, L. Zhao, A. W. Tsen, B. D. Gerardot, M. Brotons-Gisbert, Z. Guguchia, X. Roy, S. Tongay, Z. Wang, M. Z. Hasan, J. Wrachtrup, A. Yacoby, A. Fert, S. Parkin, K. S. Novoselov, P. Dai, L. Balicas and E. J. G. Santos, ACS Nano, 2022, 16, 6960–7079.
15. K. S. Burch, D. Mandrus and J. G. Park, Nature, 2018, 563, 47–52.
16. S. Y. Kim, T. Y. Kim, L. J. Sandilands, S. Sinn, M. C. Lee, J. Son, S. Lee, K. Y. Choi, W. Kim, B. G. Park, C. Jeon, H. D. Kim, C. H. Park, J. G. Park, S. J. Moon and T. W. Noh, Phys. Rev. Lett., 2018, 120, 136402.
17. C. Lane and J.-X. Zhu, Phys. Rev. B, 2020, 102, 075124.
18. C. Lane and J.-X. Zhu, arXiv, 2022, preprint DOI:10.48550/arXiv.2209.13051.
19. E. J. K. B. Banda, J. Phys. C: Solid State Phys., 1986, 19, 7329–7335.
20. K. Hwangbo, Q. Zhang, Q. Jiang, Y. Wang, J. Fonseca, C. Wang, G. M. Diederich, D. R. Gamelin, D. Xiao, J. H. Chu, W. Yao and X. Xu, Nat. Nanotechnol., 2021, 16, 655–660.
21. S. Kang, K. Kim, B. H. Kim, J. Kim, K. I. Sim, J. U. Lee, S. Lee, K. Park, S. Yun, T. Kim, A. Nag, A. Walters, M. Garcia-Fernandez, J. Li, L. Chapon, K. J. Zhou, Y. W. Son, J. H. Kim, H. Cheong and J. G. Park, Nature, 2020, 583, 785–789.
22. X. Wang, J. Cao, Z. Lu, A. Cohen, H. Kitadai, T. Li, Q. Tan, M. Wilson, C. H. Lui, D. Smirnov, S. Sharifzadeh and X. Ling, Nat. Mater., 2021, 20, 964–970.
23. F. Dirnberger, R. Bushati, B. Datta, A. Kumar, A. H. MacDonald, E. Baldini and V. M. Menon, Nat. Nanotechnol., 2022, 17, 1060–1064.
24. C. A. Belvin, E. Baldini, I. O. Ozel, D. Mao, H. C. Po, C. J. Allington, S. Son, B. H. Kim, J. Kim, I. Hwang, J. H. Kim, J. G. Park, T. Senthil and N. Gedik, Nat. Commun., 2021, 12, 4837.
25. G. D. Scholes and G. Rumbles, Nat. Mater., 2006, 5, 683–696.
26. T. Fincher, G. LeBret and D. A. Cleary, J. Solid State Chem., 1998, 141, 274–281.
27. D. S. Kim, D. Huang, C. Guo, K. Li, D. Rocca, F. Y. Gao, J. Choe, D. Lujan, T. H. Wu, K. H. Lin, E. Baldini, L. Yang, S. Sharma, R. Kalaivanan, R. Sankar, S. F. Lee, Y. Ping and X. Li, Adv. Mater., 2023, 35, e2206585.
28. E. Ergecen, B. Ilyas, D. Mao, H. C. Po, M. B. Yilmaz, J. Kim, J. G. Park, T. Senthil and N. Gedik, Nat. Commun., 2022, 13, 98.
29. W. Jin, H. H. Kim, Z. Ye, G. Ye, L. Rojas, X. Luo, B. Yang, F. Yin, J. S. A. Horng, S. Tian, Y. Fu, G. Xu, H. Deng, H. Lei, A. W. Tsen, K. Sun, R. He and L. Zhao, Nat. Commun., 2020, 11, 4780.
30. P. Frantsuzov, M. Kuno, B. Jankó and R. A. Marcus, Nat. Phys., 2008, 4, 519–522.
31. S. A. Empedocles and M. G. Bawendi, J. Phys. Chem. B, 1999, 103, 1826–1830.
32. C.-H. Ho, T.-Y. Hsu and L. C. Muhimmah, npj 2D Mater. Appl., 2021, 5, 8.
33. V. N. Mochalin, O. Shenderova, D. Ho and Y. Gogotsi, Nat. Nanotechnol., 2011, 7, 11–23.
34. H. Wang, H. S. Wang, C. Ma, L. Chen, C. Jiang, C. Chen, X. Xie, A.-P. Li and X. Wang, Nat. Rev. Phys., 2021, 3, 791–802.
35. R. Dhakal, S. Griffith and S. M. Winter, npj Quantum Mater., 2024, 9, 64.
36. Z. Wang, X.-X. Zhang, Y. Shiomi, T.-H. Arima, N. Nagaosa, Y. Tokura and N. Ogawa, Phys. Rev. Res., 2023, 5, L042032.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nh00390j

---