Open Access Article
Open Access ArticleUnraveling energetics and states of adsorbing oxygen species with MoS2 for modulated work function†
Hejin
Yan
,
Hongfei
Chen
,
Xiangyue
Cui
,
Qiye
Guan
,
Bowen
Wang
and
Yongqing
Cai
 *
*
Joint Key Laboratory of the Ministry of Education, Institute of Applied Physics and Materials Engineering, University of Macau, Taipa, Macau, China. E-mail: yongqingcai@um.edu.mo
First published on 6th November 2024
Abstract
MoS2 and related transition metal dichalcogenides (TMDs) have recently been reported as having extensive applications in nanoelectronics and catalysis because of their unique physical and chemical properties. However, one practical challenge for MoS2-based applications arises from the easiness of oxygen contamination, which is likely to degrade performance. To this end, understanding the states and related energetics of adsorbed oxygen is critical. Herein, we identify various states of oxygen species adsorbed on the MoS2 surface with first-principles calculations. We reveal a “dissociative” mechanism through which a physisorbed oxygen molecule trapped at a sulfur vacancy can split into two chemisorbed oxygen atoms, namely a top-anchoring oxygen and a substituting oxygen, both of which show no adsorbate induced states in the bandgap. The electron and hole masses show an asymmetric effect in response to oxygen species with the hole mass being more sensitive to oxygen content due to a strong hybridization of oxygen states in the valence band edge of MoS2. Alteration of oxygen content allows modulation of the work function up to 0.5 eV, enabling reduced Schottky barriers in MoS2/metal contact. These results show that oxygen doping on MoS2 is a promising method for sulfur vacancy healing, carrier mass controlling, contact resistance reduction, and anchoring of surface electron dopants. Our study suggests that tuning the chemical composition of oxygen is viable for modulating the electronic properties of MoS2 and likely other chalcogen-incorporated TMDs, which offers promise for new optoelectronic applications.
New conceptsMoS2 has been extensively explored for integration into advanced electronics and is leading the trend of next-generation semiconductor devices. However, the low formation energy of sulfur vacancies leads to intrinsic n-type doping character and degrades the original material performance. Furthermore, the existence of ubiquitous oxygen species, likely to be introduced during manufacturing, processing, or ambient exposure, emphasizes the need for investigation of the atomic-scale mechanism of oxygen doping. Here, we discover a “dissociative” mechanism of molecular oxygen trapped at sulfur vacancies to facilitate single-atomic oxygen doping in MoS2, setting the foundation for forming molybdenum oxy-sulfide. Density-functional theory calculations show that there exist two favorable states of single-atomic oxygen: the top stacking and bottom substituting states. Interestingly, the oxygen doping induces a lattice strain field which competes with the stoichiometry to tune the carrier mass. Furthermore, we demonstrate modulation of the work function and accordingly the Schottky barrier in MoS2/metal contact with varying oxygen concentrations. This sets the foundation of oxygen doping engineering of MoS2 for sulfur vacancy healing, contact resistance reduction, and anchoring of surface electron dopants for a plethora of applications. |
Introduction
Molybdenum disulfide (MoS2), an emerging two-dimensional (2D) material consisting of a Mo monolayer sandwiched between two S monolayers, has recently attracted extensive attention due to its high mechanical flexibility and intriguing electronic properties.1–3 Monolayer and few-layer MoS2 are being intensively explored for field effect transistors,4,5 sensors,6,7 photocatalysis,8 energy harvesting,9–11 and other advanced optoelectronics.12–14 Extraordinary performance was obtained by depositing MoS2 on high-dielectric oxides leading to carrier mobility up to 200 cm2 V−1 s−1 and a high switching ratio of ∼108, making it a substitute for classical silicon semiconductors for miniaturization.15Thus far, extension of Moore's law by continually scaling down silicon-based integrated circuits has encountered a dilemma.16 As a 2D alternative, MoS2 is a promising material for balancing device minimization and performance optimization.17 Its atomic level thickness and moderate carrier mobility are favorable for gate controllability.18,19 Nevertheless, the semiconducting character and weak dielectric screening make monolayer MoS2 extremely sensitive to intrinsic defects, extrinsic adsorbates, and strain. Indeed, as the most common natural defect, sulfur vacancy (VS), at a typical defect density of 1013 cm−2, degrades carrier mobility due to defective bandgap states and lifting of Schottky barriers through Fermi-level pinning.20,21
Owing to their atomically thin character and high surface-to-volume ratio, MoS2 nanostructures are subjected to environmental doping by molecular adsorbates which has a pronounced effect on their electronic and optoelectronic properties.22,23 On the other hand, it has been widely recognized that molecular adsorbate doping is an effective technique for defect passivation in 2D electronics.24,25 Among various possible adsorbates, oxygen species must be the most prevalent impurity source after or during growth of 2D materials. Unintentional uptake of O species in a MoS2 layer may arise from (1) synthesis due to incomplete sulfurization of MoO3 or the presence of oxygen using chemical vapor deposition;26–30 (2) introducing oxide substrates, normally Al2O3 or SiO2, and high-dielectric capping layers like HfO2 or ZrO2 during device integration, where oxygen vacancies in the oxides, generated by gate voltage or temperature gradient, can be formed and the depleted O atoms are susceptible to recapture by the MoS2 layer;31–34 (3) exposing MoS2 layers to atmospheric adsorbates in ambient conditions during application.35 Other processes with a high possibility of introducing O impurities include adopting an ionic-liquid gate, liquid-phase exfoliation, plasma-assisted nano-printing, and synthesizing MoS2-based nanohybrids.36–40 Compared with a perfect surface, the adhesion and effect of O species should be more prominent if the layer is partially reduced by forming VS in the basal plane or dissected for ribbons or nanoflakes due to abundant dangling bonds. In contrast to the well-understood effects of O on graphene (bandgap opening and formation of graphene oxide) and boron nitride (BN), a clear picture of O species evolution in MoS2 is still absent; to be specific, the energetics and kinetics of O species and the impact of adsorbed O species on structural modification and electronic properties of MoS2 are still unclear,41,42 although their pronounced effects on healing of vacancy sites and reducing the MoS2/metal contact barrier have been recognized.43,44
In this work, we present a theoretical investigation of the surface affinity of MoS2 toward O species based on a first-principles study. We identify the possible adsorbing states and types of oxygen atoms on MoS2. A dissociative mechanism of molecular oxygen adsorbing at a VS into two atomic species, a substituting oxygen and a top oxygen, is revealed. We demonstrate substantial atomic displacements and gradient strains surrounding each single oxygen dopant. Through the uptake of more oxygen atoms, lattice strain is developed and scaled with the oxygen content. We show an opposite effect on electron and hole mass with this chemical functionalization, but the electron mass is less sensitive to the oxygen content than the hole mass. Finally, a surface decoration modulated work function is also demonstrated with implication for reducing the Schottky barriers.
Results and discussion
Energetics, dynamics and states of adsorbed oxygen species
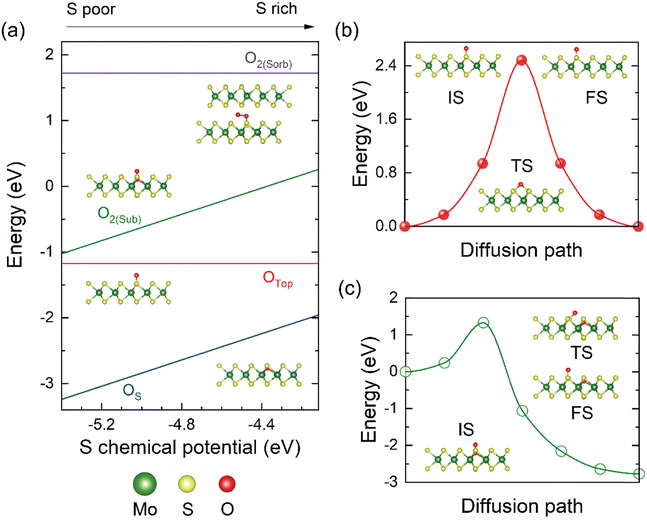
In the graphene case, more than one type of oxygen species is involved in modifying the properties.45 Here, energetics and stability of O species on a MoS2 monolayer are quantitatively evaluated by considering the following potential adsorption configurations (Fig. 1(a)): oxygen adsorption above the anionic plane sitting atop a S atom (OTop), oxygen atom substituting a S atom (OS) which is equivalent to the oxygen atom occupying the S vacancy, and molecular O2 substituting a S atom which is equivalent to formation of peroxide species or oxygen molecule trapped by a S vacancy (O2(Sub)). Other possible adsorptions states, like O occupying above the hollow position defined by the equilateral triangle formed by three S atoms, are unstable (Fig. S1 and Table S1, ESI†). The formation energy (Ef) for the OTop is −1.2 eV with an O–S bond length of 1.483 Å. For the OS case, this state shows the lowest Ef of −3.25 eV under the S-poor condition. This indicates that the substituting O species is very likely to occur in the MoS2 layer, especially for films after reducible gas treatment, e.g., a hydrogen plasma increases the VS on the MoS2 basal plane.46,47 The substituting O atom relaxes about 0.412 Å toward the middle Mo layer with an O–Mo bond length of 2.052 Å. For the O2(Sub) structure, Ef is still negative but higher than that of the OS type. The O–O bond length is elongated to 1.374 Å compared with 1.211 Å of a free O2 molecule, implying a strong activation of the O–O bond by populating the 2π* antibonding orbital of the O2 molecule.Binding of an O2 molecule above the anionic basal plane of perfect MoS2 is unstable and shows very weak physisorption on the monolayer. However, for multi-layer or bulk MoS2, oxygen molecules may be trapped inside the van der Waals (vdWs) gap, denoted as O2(Sorb). As shown in Fig. 1(a), the adsorption is an endothermic process with a positive Ef of 1.7 eV. In this meta-stable configuration, one of the O atoms forms a chemical bond with a S atom in one MoS2 layer, while the other is tilted toward the gap above the center of a triangle formed by S atoms of the same MoS2 layer. The O–O and the O–S bond lengths are 1.465 Å and 1.591 Å, respectively. Additionally, the much longer O–O bond in O2(Sorb) within the vdWs gap than that in O2(Sub) trapped at the vacancy suggests higher amounts of electrons transferring to occupy the 2π* antibonding orbital of the O2 molecule, probably due to a denser electron density in the vdWs gap. Therefore, through thermal activation under finite temperature, we can still expect the entry and adsorption of O2 molecules in bulk or multi-layer MoS2 despite the ultraweak adsorption above the basal plane of the surface. Fig. 1(b) shows activation barriers calculated by the climbing image nudged elastic band (CI-NEB) method for the O species diffusing on the surface. For OTop species, the barrier for O jumping along the neighboring lattice is around 2.4 eV. For O2(Sub), there is likely to be a dissociative process via O2(Sub) → OTop + OS, where the protruding O atom moves to the top of its neighboring S atom simultaneously breaking the O–O bonding and the activation energy is around 1.2 eV, much lower than that of the OTop species. This indicates a viable way of filling VS through molecular oxygen while forming oxygen decoration. Notably, the low-temperature preparation of MoS2 below 100 °C is plagued by the increased adsorption of water, serving as an additional oxygen contamination source, and the related H2O molecule adsorption and dissociation on MoS2 have been reported.48,49 Here, the energy barriers for O2 dissociation in bulk-phase MoS2 are also considered (Fig. S2, ESI†). This barrier height is correlated with the stability of bulk-phase MoS2, as the diffusion and dissociation of O2 molecules change the interlayer vdWs interactions and promote the exfoliation of the MoS2 monolayer.
Atomic displacement and gradient strain surrounding oxygen dopants
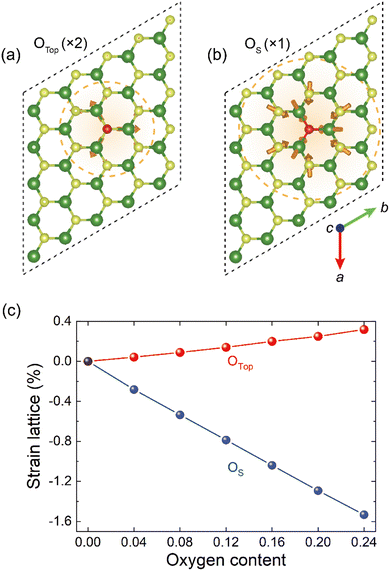
Fig. 2(a) and (b) illustrate the relaxation of periphery S/Mo atoms around the single OTop and OS dopant centers in the supercell, respectively. The introduction of O species in the MoS2 monolayer causes gradient strains, leading to the host lattice expansion (for OTop) and contraction (for OS). For the OTop species, the three nearest Mo atoms relaxed outward by about 0.029 Å. The magnitude of the strain field, indicated by the length of orange arrows, decays rapidly away from the oxygen species; for instance, the second-nearest-neighbor S atoms relax only outwardly by about 0.003 Å. For the OS, there is a strong compressive field around the substituting dopant center with stronger O–Mo binding and a shorter O–Mo bond length, due to a smaller atomic radius and a lower electronegativity of the O atom than that of the S atom. The three neighboring Mo atoms move inward 0.129 Å, and the next-nearest S species relaxed inward 0.065 Å with appreciable strain even extends to about 4 or 5 nearest neighbors. In a word, we identify a sizable strain field associated with a substitutional oxygen dopant in MoS2. This is expected to be true in other 2D materials. With the lack of a continual lattice in 3D crystal, 2D materials are prone to generate a larger area of buffering region with the formation of gradient strain around the dopant.We next examine the effect of varying the content of oxygen dopants. To simulate the ambient condition where oxygen sources largely access one surface of MoS2, the other side would be blocked due to the substrate. In this extreme condition, all O atoms are modeled to adsorb on one facet of the S–Mo–S layer. As for the case of O adsorbing on both facets, all the O species are uniformly distributed with maximized separation, and the more complicated oxygen cluster formation on the surface is not considered (see Fig. S3 and S4 for the optimized structures, ESI†). Notably, the uptake of O atoms does not induce any dangling bonds, which is favorable for keeping planeness and speed of transporting carriers.50
Highly concentrated O-doped MoS2 becomes molybdenum oxy-sulfide (MoSyOx), and here the evolution of the lattice constant of two types of molybdenum oxy-sulfide (MoS2Ox containing OTop and MoS2−xOx containing OS with x being the content of oxygen normalized to normal chemical formula) layer with different stoichiometry is calculated and shown in Fig. 2(c). For the OTop case, the lattice constant increases gradually, and the strain (δ)–O content (x) relation scales as δ = C × x with C fitted to be 1.32, consistent with the previous expansive strain field around the dopant center shown in Fig. 2(a). For the OS case, introducing OS causes significant compressive strain on the lattice. The δ–x relation also follows δ = C × x with C fitted to −6.36, showing a much larger distortion of the MoS2 host lattice than the OTop case. For instance, for the O content with x of 0.24, the induced lattice strain is 0.3% for OTop and −1.5% for OS. While here the results are only calculated for single-layer MoS2, similar scaling behavior of the lattice constant with oxygen dopant would be true for multi-layer MoS2 and for adsorption evenly at both basal planes of MoS2 (Tables S2 and S3, ESI†). For the latter, due to the intercalation of O or O2 species (Fig. 1) in the vdWs gap, the lattice constant normal to the atomic plane would also increase with the O content. From an experimental perspective, Burrns et al. used high-resolution transmission electron microscopy (HR-TEM) to detect local strain fields induced by vacancies in MoS2. They suggest that O atoms adsorbed on a vacant S site, denoted as OS in our work, lead to the lattice contraction at high irradiation fluences.51 This phenomenon aligns with the trend in Fig. 2(b). Recently, Kumar et al. found the combination of tensile strain and the absence of charged oxygen adatoms, denoted as OTop in our work, triggering a drastic photoluminescence (PL) redshift of ∼130 meV for MoS2.52 These findings suggest that surface oxygen dopants and induced lattice strain field have profound effects on modifying the electronic properties.
Modulation of band structure, effective mass and work function
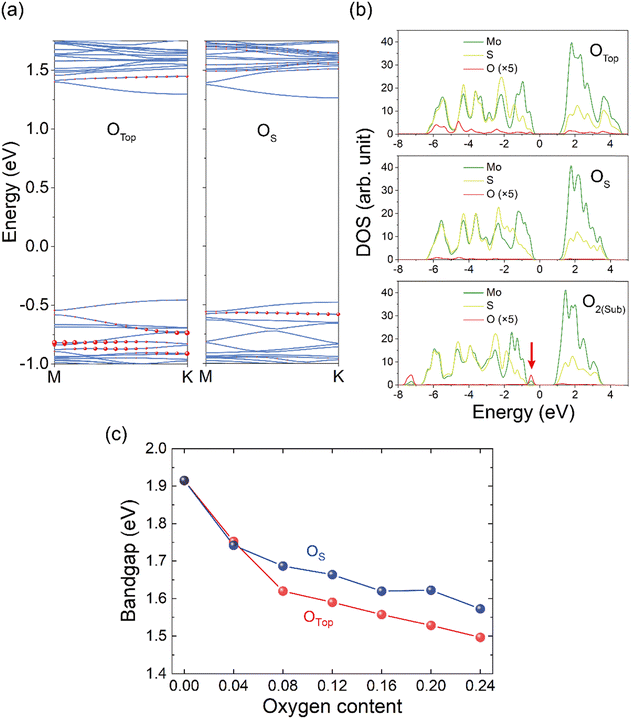
We next show the evolution of the electronic structures of MoS2 after surface oxygen treatment. Fig. 3(a) shows band structures of the OTop and OS cases, where the contribution of O atoms is projected out and their components are scaled by the size of red circle markers at each k point and band. In contrast to the bandgap opening of graphene oxide,53 there is no strong modification of bandgap with mild O decoration. The bandgap of the oxygen-decorated MoS2 monolayer decreases almost linearly with the oxygen content varying from 0.04 to 0.24 for OTop and OS oxygen species (Fig. 3(c)). As an iso-valent dopant, the addition of oxygen, either the substitutional OS or the top OTop, does not induce any defective levels in the bandgap, thus trapping of carriers by these two types of O species is unlikely to be prominent. However, there is evident modification of the valence band edge through orbital hybridization, while modulation of the conduction band edge is tiny as there is negligible O hybridization with Mo atoms.Since band edges are critically important in terms of effective mass of carriers and deformation energy of the frontier orbitals, the adsorption of O species may influence the performance of the MoS2 layer such as mobility of carriers, especially for holes. Fig. 3(b) presents the partial density of states (PDOS) for OTop, OS, and O2(Sub). For OTop and OS, the O states spread over the whole valence band and no defective states occur in the gap. In contrast, for O2(Sub) adsorption, the clamped O2 at the S vacancy site induces new states above the valence top. From the plot of surface charge density of valence band maximum (VBM) and conduction band minimum (CBM) shown in Fig. S5a and c (ESI†), these O states are strongly localized, suggesting relatively weak hybridization of the molecule with the MoS2 substrate. The additional peak located ∼0.3 eV above the VBM corresponds to the π orbital of surface O2. According to these results, the shallow defective level would have a weak effect on carrier mobility, as O2(Sub) is metastable and has a tendency to transfer into the OTop and OS states.
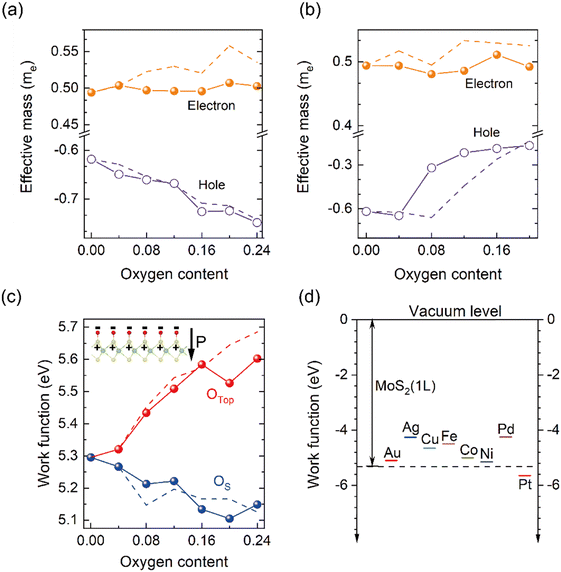
Fig. 4 shows the evolution of electron/hole effective mass with the content of O species. Electron (hole) mass of pristine MoS2 monolayer is 0.46 me (−0.60 me), consistent with a previous report of 0.47 me (−0.60 me).54 Upon uptake of O species, for OTop cases (Fig. 4(a)), the magnitude of hole mass increases steadily from −0.60 me for zero oxygen content to −0.75 me with O content x of 0.24. In contrast, the trend for the OS case (Fig. 4(b)) starts with a plateau occurring at the onset corresponding to the dilute doping limit, the hole mass then decreases with increasing O content and levels off at −0.22 me at x equal to 0.12 me. For both cases, the value of electron mass fluctuates around ∼0.50me, and the adsorption of O species has a weaker effect on electron mass than on hole mass. According to Fig. 3(a) and (b), this is due to a weaker hybridization of O states with Mo orbitals at the CBM while a strongly coupled O component at the VBM (also see Fig. S6 and S7, ESI†). Similar results also hold true for oxygen species distributing on both facets of sulfur in MoS2 (Fig. S8 and S9, ESI†).
In fact, such doping-level-controlled carrier mass is a synergetic effect of chemical variation and strain modification after introduction of O species. For the OTop case, the adsorption only leads to a tiny strain within the range of O content x ≤ 0.24; thus the increasing hole mass is solely attributed to the chemical variation of the top O atoms above the S atoms. However, for OS, as shown in Fig. 2(b), it induces significant strain on the host lattice. To decouple the effect of the chemical modification of O atoms from strain field and identify dominant factors affecting the carrier mass, we performed additional calculations with a frozen lattice where the lattice constant is kept the same for all the O content to exclude the strain effect. The lattice constants of the OTop and OS models with varied oxygen content are fixed to the same lattice values as their 0.04 oxygen content cases, respectively (see Table S2 and S3 for details, ESI†). The x-electron/hole mass relationship for the frozen lattice is represented by the dashed lines in Fig. 4(a) and (b). For OTop, the lines associated with holes for the frozen lattice are nearly overlapped with those for the relaxed lattice. This is reasonable considering the moderate structural relaxation of the host layer with O uptake. For OS, both trends of with/without strain are similar, showing a lighter hole mass with greater oxygen incorporation. However, there is a clear deviation of the hole mass between the relaxed and fixed cases. For x between 0.08 and 0.2, the hole mass of frozen lattice is linearly correlated with x indicating the substituting O decreases the hole mass (violet dashed line in Fig. 4(b)). While for the relaxed lattice, the slope of the line continually decreases, and the hole mass levels off to −0.22me at a doping content of 0.12 (violet solide line in Fig. 4(b)). Therefore, compressive strain induced by dense OS tends to promote the hole mass.
A similar strain effect has also been found in other types of sulfide semiconductor.55 In a word, upon introduction of O, while the chemical modification decreases the hole mass, there is a concomitant increase of hole mass due to the compressive strain, thus decreasing the slope of the x-hole mass profile in the relaxed lattice case. This inherent strain accompanied by the O doping would play an important role in affecting the electronic properties and accordingly carrier transport behavior in field effect transistors (FETs). Our study shows that creating OS species with an appropriate O content may effectively decrease the hole mass thus promoting the hole mobility, whereas the electron mass is less affected. Compared with the VS-induced flat defect states (Fig. S10b, ESI†) for trapping and scattering charge carriers, the adsorbed oxygen atoms somehow heal the vacancies and mitigate the defect effect on carrier mobilities. Indeed, Wei et al. fabricated oxygen-doped MoS2 monolayer at the wafer scale, and the final FET device shows high mobilities with an average of 78 cm2 V−1 s−1, being greater than that of intrinsic MoS2 FETs of 48 cm2 V−1 s−1.56 Tang et al. also suggested that moderate oxygen doping significantly improves the carrier mobilities of MoS2 by removing VS.57
Next, we demonstrate that by controlling the type and content of O species, the work function (W) of the hybrid MoSyOx layer can be tuned, which is highly desired for electronic devices to control band alignment with metal electrodes. Several metals have been proven to form a Schottky contact at the MoS2/metal interface, and an effective strategy for reducing the Schottky barrier height (SBH) is the shifting of W of MoS2.58–60 In Fig. 4(c), W is calculated by subtracting the Fermi energy from the electrostatic potential in the middle of the vacuum layer (eqn (5)).61,62W of the MoSyOx layer increases monotonically from 5.3 to 5.6 eV for OTop species with x increasing from 0 to 0.24. In contrast, W decreases gradually with increasing OS content, implying overall effective surface positive charges with the presence of OS species. The modification from 5.6 eV (for OTop) to 5.15 eV (for OS) at an O content of 0.24 indicates a large modulation space of W (around 0.5 eV) with the addition and control of O species in the film. Due to the larger electronegativity of an oxygen atom than that of a sulfur atom, the oxygen is negatively charged, and the sulfur is positively charged. A dipole is induced associated with the oxygen–sulfur pair with the dipole direction pointing inwardly from the adsorbing oxygen atom to its bonded sulfur atom (see the inset in Fig. 4(c)). On the OTop surface, the exterior negatively charged oxygen inhibits electrons escaping from the surface and promotes W. While for the OS surface, the reversed dipole direction is favorable for surface electron escape, hence reducing W. Fig. 4(d) shows the comparison and alignment of W of pristine MoS2 monolayer and common metal electrodes. By considering the variance of W induced by different types and varying content of oxygen as shown in Fig. 4(c), Au, Co, Ni, and Pt are predicted to be suitable for contact with the MoSyOx layer due to a low SBH. For comparison, Gupta et al. used Kelvin probe force microscopy (KPFM) to measure W of MoS2, for which the existence of MoO3–x phase alters W from 4.98 to 5.56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eV.63 In fact, such dopant-controlled electronic structures were also observed in other TMDs. Oberoi et al. adopted a self-limiting oxidation method to convert a top-layer WSe2 channel to WOxSey alloy, achieving high-performance p-type FETs with a 5-fold improvement in the on-state performance and a 9-fold reduction in the contact resistance.64
eV.63 In fact, such dopant-controlled electronic structures were also observed in other TMDs. Oberoi et al. adopted a self-limiting oxidation method to convert a top-layer WSe2 channel to WOxSey alloy, achieving high-performance p-type FETs with a 5-fold improvement in the on-state performance and a 9-fold reduction in the contact resistance.64
Due to the relatively wide bandgap of MoS2 and thus an enlarged SBH, the contact resistance of the MoS2/metal junction is supposed to be much larger than that of the graphene/metal junction.65 A variable W of the MoS2 layer is highly important for tuning the SBH. The demonstrated tunable range of W of ∼0.5 eV by O doping is large compared to the intrinsic bandgap of the monolayer (1.8 eV). Therefore, surface modification can significantly modulate the barrier of carrier injection at a metal/MoS2 contact and may even allow control of carrier polarity in the film by tuning the content and the type of O species in the monolayer. For silicon or other oxide as the channel material, the energetic alignment at the interface can be controlled by dopants or defects.66 However, unlike graphene, the presence of a finite gap of MoS2 may create in-gap states upon doping which will trap the charges and affect the carrier mobility. Here we prove that the introduction of iso-chemical species like substituting O, being free of in-gap levels, is highly important for tuning the properties of MoS2 for various applications. The strain-chemical–property relationships inherent in the O modification can be tuned by controlling the adsorbing states of O species on the MoS2 monolayer, enabling a synergetic effect of strain and chemical functionalization. Moreover, due to the more electronegative O species, this 2D MoS2–O hybrid layer can act as a host for assembling with positively charged nanoclusters or particles.37
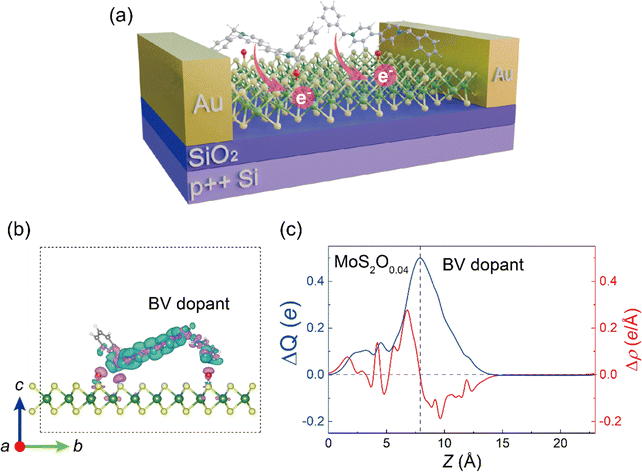
Finally, we demonstrate a proof-of-concept device based on the physicochemical properties of the MoSyOx layer in this work. Fig. 5(a) shows the device structure of benzyl viologen molecule (BV)-doped MoS2Ox FETs with Au layer as contact metal. BV is a common n-type dopant with strong reductant ability for nanomaterials.22,67,68Fig. 5(b) shows the MoS2O0.04/BV interface model, where a BV molecule interacts with MoS2O0.04 through the stretched oxygen site, and it can be seen that the BV molecule loses electrons (cyan surface for electron loss) which transfer to the MoS2O0.04 side (pink surface for electron gain). To quantify the interaction between the surface O species and BV molecules, the planar-averaged differential charge density Δρ and transferred charge ΔQ are considered, defined as:
| Δρ = ρMoS2O0.04/BV − ρMoS2O0.04 − ρBV | (1) |
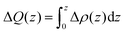 | (2) |
Conclusions
To summarize, the ubiquitous presence of oxygen species in the environment and synthesis processes renders a high possibility of oxygen uptake in MoS2 samples. Here based on DFT calculations, we reveal the energetics, forms, and effects of oxygen adsorbates and dopants in MoS2. We identify the two most stable forms of oxygen, surface atomic adsorbate OTop and substituting oxygen OS, both of which are electronically inert and free of in-gap dopant-induced states despite appreciable local strains around the dopants. These dopant states would occur through a dissociative mechanism of O2 trapped at the VS overcoming an energy barrier of ∼1.2 eV. We predict that the hole mass is more sensitive to the oxygen content than the electron mass, due to less hybridization of oxygen with CBM. Controlling the oxygen stoichiometry allows modulation of the work function up to ∼0.5 eV, which is favorable for reducing the SBH and contact resistance with metal electrodes. Our study elucidates the mechanism for controlling oxygen dopants on the MoS2 monolayer to achieve modulated carrier mass and work function, motivating further study of emerging optoelectronic devices based on 2D materials.Methods
The Vienna ab initio simulation package (VASP) with the projected augmented wave (PAW) potential is adopted for density functional theory (DFT) calculations.69 Exchange and correlation energy of electrons are considered through the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) functional.70 The DFT-D2 method of Grimme is used to describe the vdWs interactions, this correction having been widely adopted for multiple low-dimensional materials.71 The energy cutoff is set to 450 eV and sampling of the Brillouin zone is performed by using a uniform 3 × 3 × 1 dense k-point grid. Energy and forces are converged until 10−5 eV and 0.01 eV Å−1, respectively. A slab model is based on a 5 × 5 × 1 supercell with a vacuum space with a thickness of 15 Å to avoid interactions from periodic replicas. The vacuum layer thickness is tested for the coverage of work function (see Fig. S11, ESI†). Spin polarization is considered in all calculations. The lattice constraint values are calculated by comparing the lattice constants of oxygen-adsorbed systems and those of the pristine MoS2 monolayer. The chemical potential (μ) should be considered for the formation of MoS2 film. Here, the energy values based on DFT results are used for estimating the formation energy of O adsorbates on MoS2 within the allowed crystal growth conditions with the chemical potential of sulfur species (μs) varying from S-poor to S-rich conditions. The stability of these O adsorbates is estimated by judging Ef defined as: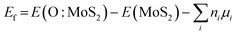 | (3) |
| μMoS2 = 2μs + μO | (4) |
| W = Evac − EF | (5) |
Author contributions
Hejin Yan and Yongqing Cai: conceptualization, methodology, and writing – original draft. Hongfei Chen and Xiangyue Cui: software and validation. Qiye Guan: data curation and validation. Bowen Wang: visualization and investigation. Yongqing Cai: supervision. All authors participated in general discussion and manuscript revision.Data availability
All relevant data are available from the authors on reasonable request and/or are included within the article and the ESI.†Conflicts of interest
The authors declare that they have no conflict of interest.Acknowledgements
This work is supported by Natural Science Foundation of Guangdong Province, China (2024A1515011161) and the Science and Technology Development Fund from Macau SAR (FDCT-0163/2019/A3, 0085/2023/ITP2, 0120/2023/RIA2). This work was performed in part at the High-Performance Computing Cluster (HPCC) which is supported by Information and Communication Technology Office (ICTO) of the University of Macau.References
- A. Daus, S. Vaziri, V. Chen, Ç. Köroğlu, R. W. Grady, C. S. Bailey, H. R. Lee, K. Schauble, K. Brenner and E. Pop, Nat. Electron., 2021, 4, 495–501 CrossRef CAS
.
- J. Tang, Q. Wang, J. Tian, X. Li, N. Li, Y. Peng, X. Li, Y. Zhao, C. He and S. Wu, Nat. Commun., 2023, 14, 3633 CrossRef CAS
.
- A. Liu, X. Zhang, Z. Liu, Y. Li, X. Peng, X. Li, Y. Qin, C. Hu, Y. Qiu and H. Jiang, Nano-Micro Lett., 2024, 16, 119 CrossRef
.
- S. Das, A. Sebastian, E. Pop, C. J. McClellan, A. D. Franklin, T. Grasser, T. Knobloch, Y. Illarionov, A. V. Penumatcha and J. Appenzeller, Nat. Electron., 2021, 4, 786–799 CrossRef CAS
.
- Y. Zou, P. Li, C. Su, J. Yan, H. Zhao, Z. Zhang and Z. You, ACS Nano, 2024, 18, 9627–9635 CrossRef CAS PubMed
.
- S. Aftab, M. Z. Iqbal, S. Hussain, H. H. Hegazy, F. Kabir, S. H. A. Jaffery and G. Koyyada, Chem. Eng. J., 2023, 144039 CrossRef CAS
.
- Y. Kim, I. Sohn, D. Shin, J. Yoo, S. Lee, H. Yoon, J. Park, S.-M. Chung and H. Kim, Adv. Eng. Mater., 2024, 26, 2301063 CrossRef CAS
.
- D. Panchal, A. Sharma and S. Pal, Mater. Today Sustain., 2023, 21, 100264 Search PubMed
.
- T. Wu, Y. Song, Z. Shi, D. Liu, S. Chen, C. Xiong and Q. Yang, Nano Energy, 2021, 80, 105541 CrossRef CAS
.
- D. Guo, X.-x Xue, M. Jiao, J. Liu, T. Wu, X. Ma, D. Lu, R. Zhang, S. Zhang, G. Shao and Z. Zhou, Chem. Sci., 2024, 15, 16281–16290 RSC
.
- G. Shao, J. Xu, S. Gao, Z. Zhang, S. Liu, X. Zhang and Z. Zhou, Carbon Energy, 2024, 6, e417 CrossRef CAS
.
- X. Huang, C. Liu and P. Zhou, npj 2D Mater. Appl., 2022, 6, 51 CrossRef CAS
.
- S. Aftab, H. H. Hegazy and F. Kabir, Adv. Mater. Technol., 2023, 8, 2201897 CrossRef CAS
.
- Y. Jing, X. Tan, Z. Zhou and P. Shen, J. Mater. Chem. A, 2014, 2, 16892–16897 RSC
.
- B. Radisavljevic and A. Kis, Nat. Mater., 2013, 12, 815–820 CrossRef CAS PubMed
.
- Y. Shen, Z. Dong, Y. Sun, H. Guo, F. Wu, X. Li, J. Tang, J. Liu, X. Wu and H. Tian, Adv. Mater., 2022, 34, 2201916 CrossRef CAS PubMed
.
- F. Wu, H. Tian, Y. Shen, Z. Hou, J. Ren, G. Gou, Y. Sun, Y. Yang and T.-L. Ren, Nature, 2022, 603, 259–264 CrossRef CAS PubMed
.
- J. Xu, L. Chen, Y.-W. Dai, Q. Cao, Q.-Q. Sun, S.-J. Ding, H. Zhu and D. W. Zhang, Sci. Adv., 2017, 3, e1602246 CrossRef PubMed
.
- K. Santosh, R. C. Longo, R. Addou, R. M. Wallace and K. Cho, Nanotechnology, 2014, 25, 375703 CrossRef
.
- J. Hong, Z. Hu, M. Probert, K. Li, D. Lv, X. Yang, L. Gu, N. Mao, Q. Feng and L. Xie, Nat. Commun., 2015, 6, 6293 CrossRef CAS
.
- C. Kim, I. Moon, D. Lee, M. S. Choi, F. Ahmed, S. Nam, Y. Cho, H.-J. Shin, S. Park and W. J. Yoo, ACS Nano, 2017, 11, 1588–1596 CrossRef CAS PubMed
.
- J. Jang, J.-K. Kim, J. Shin, J. Kim, K.-Y. Baek, J. Park, S. Park, Y. D. Kim, S. S. Parkin and K. Kang, Sci. Adv., 2022, 8, eabn3181 CrossRef CAS
.
- M. Yarali, Y. Zhong, S. N. Reed, J. Wang, K. A. Ulman, D. J. Charboneau, J. B. Curley, D. J. Hynek, J. V. Pondick and S. Yazdani, Adv. Electron. Mater., 2021, 7, 2000873 CrossRef CAS
.
- E. Mitterreiter, B. Schuler, A. Micevic, D. Hernangómez-Pérez, K. Barthelmi, K. A. Cochrane, J. Kiemle, F. Sigger, J. Klein and E. Wong, Nat. Commun., 2021, 12, 3822 CrossRef CAS PubMed
.
- X. Zhang, Z. Shao, X. Zhang, Y. He and J. Jie, Adv. Mater., 2016, 28, 10409–10442 CrossRef CAS
.
- H. Liu, M. Si, S. Najmaei, A. T. Neal, Y. Du, P. M. Ajayan, J. Lou and P. D. Ye, Nano Lett., 2013, 13, 2640–2646 CrossRef CAS
.
- Y.-H. Lee, X.-Q. Zhang, W. Zhang, M.-T. Chang, C.-T. Lin, K.-D. Chang, Y.-C. Yu, J. T.-W. Wang, C.-S. Chang and L.-J. Li, Adv. Mater., 2012, 24, 2320–2325 CrossRef CAS PubMed
.
- J. V. Pondick, J. M. Woods, J. Xing, Y. Zhou and J. J. Cha, ACS Appl. Nano Mater., 2018, 1, 5655–5661 CrossRef CAS
.
- X. Wang, H. Feng, Y. Wu and L. Jiao, J. Am. Chem. Soc., 2013, 135, 5304–5307 CrossRef CAS
.
- Y.-H. Lee, L. Yu, H. Wang, W. Fang, X. Ling, Y. Shi, C.-T. Lin, J.-K. Huang, M.-T. Chang and C.-S. Chang, Nano Lett., 2013, 13, 1852–1857 CrossRef CAS PubMed
.
- J.-K. Huang, Y. Wan, J. Shi, J. Zhang, Z. Wang, W. Wang, N. Yang, Y. Liu, C.-H. Lin and X. Guan, Nature, 2022, 605, 262–267 CrossRef CAS PubMed
.
- Y. Y. Illarionov, T. Knobloch, M. Jech, M. Lanza, D. Akinwande, M. I. Vexler, T. Mueller, M. C. Lemme, G. Fiori and F. Schwierz, Nat. Commun., 2020, 11, 3385 CrossRef CAS PubMed
.
- C. Zhang, T. Tu, J. Wang, Y. Zhu, C. Tan, L. Chen, M. Wu, R. Zhu, Y. Liu and H. Fu, Nat. Mater., 2023, 22, 832–837 CrossRef CAS
.
- Y. Jin, J. Sun, L. Zhang, J. Yang, Y. Wu, B. You, X. Liu, K. Leng and S. Liu, Adv. Mater., 2023, 35, 2212079 CrossRef CAS
.
- Y. Jiang, Z. Liu, H. Zhou, A. Sharma, J. Deng and C. Ke, Nanotechnology, 2023, 34, 405701 CrossRef CAS PubMed
.
- M. M. Perera, M.-W. Lin, H.-J. Chuang, B. P. Chamlagain, C. Wang, X. Tan, M. M.-C. Cheng, D. Tománek and Z. Zhou, ACS Nano, 2013, 7, 4449–4458 CrossRef CAS
.
- S. Kc, R. C. Longo, R. M. Wallace and K. Cho, J. Appl. Phys., 2015, 117, 135301 CrossRef
.
- S. Wang, X. Zeng, Y. Zhou, J. Lu, Y. Hu, W. Wang, J. Wang, Y. Xiao, X. Wang and D. Chen, ACS Appl. Electron. Mater., 2022, 4, 955–963 CrossRef CAS
.
- H. Nam, S. Wi, H. Rokni, M. Chen, G. Priessnitz, W. Lu and X. Liang, ACS Nano, 2013, 7, 5870–5881 CrossRef CAS PubMed
.
- Y. A. Kabachii, A. S. Golub, S. Y. Kochev, N. D. Lenenko, S. S. Abramchuk, M. Y. Antipin, P. M. Valetsky, B. D. Stein, W. E. Mahmoud and A. A. Al-Ghamdi, Chem. Mater., 2013, 25, 2434–2440 CrossRef CAS
.
- L. Wang, Z. Chen, C. R. Dean, T. Taniguchi, K. Watanabe, L. E. Brus and J. Hone, ACS Nano, 2012, 6, 9314–9319 CrossRef CAS PubMed
.
- Q. He, Z. Zeng, Z. Yin, H. Li, S. Wu, X. Huang and H. Zhang, Small, 2012, 8, 2994–2999 CrossRef CAS PubMed
.
- P.-C. Shen, Y. Lin, C. Su, C. McGahan, A.-Y. Lu, X. Ji, X. Wang, H. Wang, N. Mao and Y. Guo, Nat. Electron., 2022, 5, 28–36 CrossRef CAS
.
- I. Lee, M. Kang, S. Park, C. Park, H. Lee, S. Bae, H. Lim, S. Kim, W. Hong and S. Y. Choi, Small, 2024, 20, 2305143 CrossRef CAS
.
- H. Shin, Y. Luo, A. Benali and Y. Kwon, Phys. Rev. B, 2019, 100, 075430 CrossRef CAS
.
- A. Soman, R. A. Burke, Q. Li, M. D. Valentin, T. Li, D. Mao, M. Dubey and T. Gu, ACS Appl. Mater. Interfaces, 2020, 12, 37305–37312 CrossRef CAS
.
- B. H. Kim, M. Park, M. Lee, S. J. Baek, H. Y. Jeong, M. Choi, S. J. Chang, W. G. Hong, T. K. Kim and H. R. Moon, RSC Adv., 2013, 3, 18424–18429 RSC
.
- T. Jurca, M. J. Moody, A. Henning, J. D. Emery, B. Wang, J. M. Tan, T. L. Lohr, L. J. Lauhon and T. J. Marks, Angew. Chem., Int. Ed., 2017, 56, 4991–4995 CrossRef CAS
.
- C. Ataca and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 195410 CrossRef
.
- F.-X. R. Chen, N. Kawakami, C.-T. Lee, P.-Y. Shih, Z.-C. Wu, Y.-C. Yang, H.-W. Tu, W.-B. Jian, C. Hu and C.-L. Lin, Appl. Phys. Lett., 2022, 121, 151601 CrossRef CAS
.
- K. Burns, A. M. Z. Tan, H. Gordon, T. Wang, A. Gabriel, L. Shao, R. G. Hennig and A. Aitkaliyeva, Phys. Rev. B, 2020, 102, 085421 CrossRef CAS
.
- K. S. Kumar, A. K. Dash, H. Sabreen H, M. Verma, V. Kumar, K. Watanabe, T. Taniguchi, G. S. Gautam and A. Singh, 2D Mater., 2024, 12, 045003 CrossRef
.
- A. Nourbakhsh, M. Cantoro, T. Vosch, G. Pourtois, F. Clemente, M. H. Van Der Veen, J. Hofkens, M. M. Heyns, S. De Gendt and B. F. Sels, Nanotechnology, 2010, 21, 435203 CrossRef
.
- Y. Cai, G. Zhang and Y.-W. Zhang, J. Am. Chem. Soc., 2014, 136, 6269–6275 CrossRef CAS
.
- B. Hou, Y. Zhang, H. Zhang, H. Shao, C. Ma, X. Zhang, Y. Chen, K. Xu, G. Ni and H. Zhu, J. Phys. Chem. Lett., 2020, 11, 3116–3128 CrossRef CAS PubMed
.
- Z. Wei, J. Tang, X. Li, Z. Chi, Y. Wang, Q. Wang, B. Han, N. Li, B. Huang and J. Li, Small Methods, 2021, 5, 2100091 CrossRef CAS PubMed
.
- J. Tang, Z. Wei, Q. Wang, Y. Wang, B. Han, X. Li, B. Huang, M. Liao, J. Liu and N. Li, Small, 2020, 16, 2004276 CrossRef CAS PubMed
.
- X. Zheng, A. Calò, E. Albisetti, X. Liu, A. S. M. Alharbi, G. Arefe, X. Liu, M. Spieser, W. J. Yoo and T. Taniguchi, Nat. Electron., 2019, 2, 17–25 CrossRef CAS
.
- X. Liu, M. S. Choi, E. Hwang, W. J. Yoo and J. Sun, Adv. Mater., 2022, 34, 2108425 CrossRef CAS
.
- X. Tong, E. Ashalley, F. Lin, H. Li and Z. M. Wang, Nano-Micro Lett., 2015, 7, 203–218 CrossRef PubMed
.
- H. Gao, M. Hu, J. Ding, B. Xia, G. Yuan, H. Sun, Q. Xu, S. Zhao, Y. Jiang and H. Wu, Adv. Funct. Mater., 2023, 33, 2213410 CrossRef CAS
.
- Q. Guan, H. Yan and Y. Cai, Adv. Mater. Interfaces, 2022, 9, 2101838 CrossRef CAS
.
- S. Gupta, A. Johnston and S. Khondaker, J. Appl. Phys., 2022, 131, 164303 CrossRef CAS
.
- A. Oberoi, Y. Han, S. P. Stepanoff, A. Pannone, Y. Sun, Y.-C. Lin, C. Chen, J. R. Shallenberger, D. Zhou and M. Terrones, ACS Nano, 2023, 17, 19709–19723 CrossRef CAS PubMed
.
- S. Das, H.-Y. Chen, A. V. Penumatcha and J. Appenzeller, Nano Lett., 2013, 13, 100–105 CrossRef CAS
.
- S. Nagarajan, D. Hiller, I. Ratschinski, D. König, S. C. Smith, T. Mikolajick and J. Trommer, Adv. Mater. Interfaces, 2024, 11, 2300600 CrossRef CAS
.
- D. Kiriya, M. Tosun, P. Zhao, J. S. Kang and A. Javey, J. Am. Chem. Soc., 2014, 136, 7853–7856 CrossRef CAS
.
- X. Tong, E. Ashalley, F. Lin, H. Li and Z. M. Wang, Nano-Micro Lett., 2015, 7, 203–218 CrossRef PubMed
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS
.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed
.
- L. Bengtsson, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 12301 CrossRef CAS
.
-
W. M. Haynes, CRC handbook of chemistry and physics, CRC press, 2016 Search PubMed
.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS
.
- V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033 CrossRef CAS
.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nh00441h |
| This journal is © The Royal Society of Chemistry 2025 |