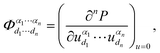Prediction methods for phonon transport properties of inorganic crystals: from traditional approaches to artificial intelligence
Yi
Wei
 a,
Zhixiang
Liu
a,
Zhixiang
Liu
 a and
Guangzhao
Qin
a and
Guangzhao
Qin
 *ab
*ab
aState Key Laboratory of Advanced Design and Manufacturing Technology for Vehicle, College of Mechanical and Vehicle Engineering, Hunan University, Changsha 410082, P. R. China. E-mail: gzqin@hnu.edu.cn
bKey Laboratory of Computational Physical Sciences (Fudan University), Ministry of Education, P. R. China
First published on 29th October 2024
Abstract
In inorganic crystals, phonons are the elementary excitations describing the collective atomic motions. The study of phonons plays an important role in terms of understanding thermal transport behavior and acoustic properties, as well as exploring the interactions between phonons and other energy carriers in materials. Thus, efficient and accurate prediction of phonon transport properties such as thermal conductivity is crucial for revealing, designing, and regulating material properties to meet practical requirements. In this paper, typical strategies used to predict phonon transport properties in modern science and technologies are introduced, and relevant achievements are emphasized. Moreover, insights into the remaining challenges as well as future directions of phonon transport-related exploration are proposed. The viewpoints of this paper are expected to provide a valuable reference to the community and inspire relevant research studies on predicting phonon transport properties in the near future.
1. Introduction
In inorganic crystalline materials, the atoms forming the crystal lattice cannot remain static due to the finite temperature effect and atomic interactions. Consequently, atoms vibrate collectively around their equilibrium positions, remaining in an excited state. From the perspective of quantum physics, the energy of lattice vibrations is supposed to be quantized, leading to the development of the phonon concept. Consequently, such atomic collective vibration is described as a type of elementary excitation or quasi-particle. Phonons not only carry the atomic vibrational energy and propagate throughout the crystals, exhibiting wave-like properties such as frequency and group velocity, but also behave as quasi-particles with quasi-momentum, possessing particle-like properties such as mean free path (MFP) and density of states (DOS). The dispersion relationship1 has been developed to describe the relationship between energy and quasi-momentum of phonons. Over the past decades, there has been growing interest in studying phonon transport properties, highlighting the attractive prospects in terms of thermal management, energy transport, quantum computing, etc.The study of phonons is of great significance to solid-state physics, electronics, optoelectronics, and other emerging applications in modern science and technology, as they play an important role in determining numerous solid physical and chemical properties, including but not limited to thermal and electrical conductivity, interfacial thermal transport, thermal energy storage, etc. As a typical example, the thermal conductivity of non-magnetic crystals (κ = κe + κL) is mainly contributed by phonon and electron transport.2 However, as for semiconductors and insulators, phonons are the dominant contributors to κ. According to the kinetic theory of phonons, the lattice thermal conductivity (κL) is directly proportional to the constant volume specific heat of the system (cv), the average phonon group velocity (vg), and the average phonon mean free path (l), which can be expressed as:3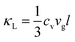 . In addition, electron–phonon interactions (EPIs) are the origin of numerous important physical effects,4 such as superconductivity,5–8 charge density wave9–12 and phonon mediated electron transport.13–15 Furthermore, the interactions between phonons and magnons,16–21 as well as phonon–exciton coupling,22–24 can also have a significant impact on material properties. With the progress of modern science and technology, it is feasible to satisfy future application needs through targeted screening, regulation, and design of materials with advanced phonon transport properties.
. In addition, electron–phonon interactions (EPIs) are the origin of numerous important physical effects,4 such as superconductivity,5–8 charge density wave9–12 and phonon mediated electron transport.13–15 Furthermore, the interactions between phonons and magnons,16–21 as well as phonon–exciton coupling,22–24 can also have a significant impact on material properties. With the progress of modern science and technology, it is feasible to satisfy future application needs through targeted screening, regulation, and design of materials with advanced phonon transport properties.
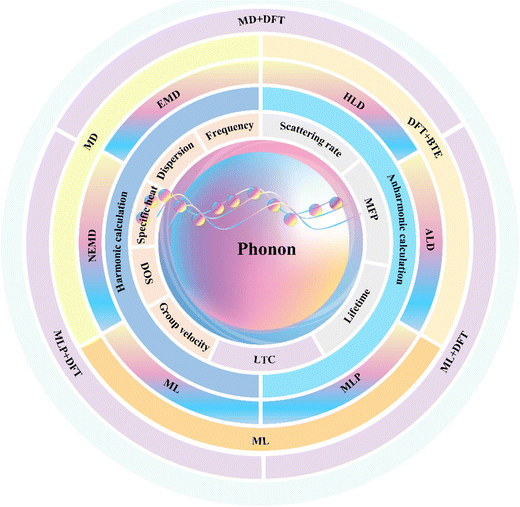
Although phonon transport properties can be measured using experimental techniques like Raman25 spectroscopies, infrared (IR)26 spectroscopies, inelastic neutron scatterings,27 thermoreflectance thermal imaging (TTI),28 X-ray diffraction (XRD),29–33 as well as the popular laser-based technologies,34 expensive resources and equipment are still highly in demand, and these methods are limited to provide complete phonon transport properties with arbitrary bands or modes.35 In contrast, computer simulations can directly yield full and comprehensive information about phonons, such as phonon band structure, group velocity, etc. To predict phonon transport properties, several types of strategies with different levels of computational speed, accuracy, and complexity have been developed, which can be further categorized into empirical models, density functional theory (DFT) based phonon Boltzmann transport equation (BTE) calculations, molecular dynamic (MD) simulations, and data-driven machine learning (ML) methods, including machine learning potentials (MLPs, also known as machine learning force field, MLFF) (Fig. 1). The principles and the application scopes of these methods differ from each other, and their relevant information have already been reviewed and summarized in numerous reports (ref. 36–48). These pervious reports solely focus on the advancements of one prediction method, i.e. machine learning,38–40,45,46 molecular dynamic (MD) simulations,42,43 and limited kinds of materials;44,47 while others fail to provide a systematic introduction for all existing methods.36,37,41,48 Based on the facts, this review is organized to fill the gap and provide an unprecedented comprehensive summary of existing strategies available for various phonon transport properties predictions. Further details will be discussed in the subsequent sections.
This article comprises four main sections. In the first part we briefly highlight the great significance of predicting phonon transport properties. In the second part we delve into fundamental theories associated with the definition of phonons and their corresponding properties. Serving as the focal point, the third section expounds on the principles, characteristics, and applications of various phonon property prediction methods as illustrated in Fig. 1, with a particular emphasis on the latest progress in both the theory and application aspects. In the final section we summarize the article and offer intriguing insights into the future trends of phonon property prediction methods.
2. Basic theory of phonons
The origin of the phonon concept can be traced back to the ancient Greek word “φωvη”, which means “voice”. As a quantum that characterizes the vibration mode of condensed matter, the emergence of phonons is intensely linked to the advancement of quantum physics. In 1930, I. Tamm (1958 Nobel Prize winner in Physics) introduced the concept of “elastic quantum”.49 Later in 1932, Soviet physicist Jacov Frenkel created the term “phonon” for describing the concept of elastic quantum and defined its physical meaning as “sound or heat associated with the elastic (or acoustic) waves, which serve for the description of heat motion in solid body”.50With the evolution of quantum mechanics theory, scientists subsequently referred to the energy quantum of a collective motion state, which is generated by the vibration wave of a certain field or the interactions of multiple bodies, as an elementary excitation in the medium. Under this definition, the motion of individual atoms in a crystal lattice can be regarded as an ensemble of individual fundamental excitation units with both energy and momentum. Phonons were soon endowed with a more accurate definition, now characterized as elementary excitation or quasi-particle components that make up the ensembles of lattice vibrations.
Frequency, dispersion, specific heat, density of states (DOS), group velocity, scattering rate, mean free path (MFP), and lifetime as listed in Fig. 1 are important indicators for characterizing phonon transport properties from two distinct perspectives: harmonicity and anharmonicity. In lattice dynamics, also referred to as phonon dynamics, anharmonic properties in thermodynamics stem from the anharmonicity of phonons, causing strong phonon–phonon scattering. Based on this theory, the atomic interactions can be replaced by the interactions between phonons, as atomic displacement u in crystals is minimal compared to the distance d between atoms. With the relationship η = u/d, an ideal phonon gas model (harmonic approximation) is developed to describe phonon transport and atomic interactions. However, according to the semi-empirical Lindemann criterion,51η is not constant and will increase to 0.1 if the temperature reaches the melting point Tm. While higher-order phonon scatterings (anharmonicity) can be neglected before Tm,52,53 anharmonic effects in some specific phonon modes may still be significant and cause many anomalous phonon behaviors.
Atoms vibrate collectively around their equilibrium positions Rd, leading to a trivial displacement 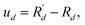 where d symbolizes the atom site index and
where d symbolizes the atom site index and 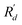 denotes the present positions. The potential energy of periodical crystal lattice
denotes the present positions. The potential energy of periodical crystal lattice 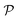 can be expanded to a Taylor polynomial with respect to ud:
can be expanded to a Taylor polynomial with respect to ud:
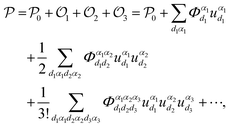 | (1) |
where α represents the Cartesian coordinate,
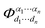 denotes the nth-order interatomic force constant (FC) terms, and
denotes the nth-order interatomic force constant (FC) terms, and 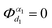 because of the equilibrium positions when being calculated.
because of the equilibrium positions when being calculated.
2.1 Phonon dispersion relationship
Under the hypothesis of harmonic approximation, eqn (1) can be simplified as: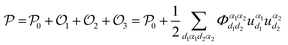 | (2) |
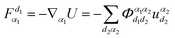 can be obtained. The atoms α1 and α2 distinctively correspond to the (l, k) and (l′, k′), where k and l are the k-th atom in the l-th primitive cell. From Newton's second law of motion,54 it can be inferred that:
can be obtained. The atoms α1 and α2 distinctively correspond to the (l, k) and (l′, k′), where k and l are the k-th atom in the l-th primitive cell. From Newton's second law of motion,54 it can be inferred that: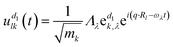 | (3) |
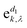 corresponds to the k-th atomic vector of the phonon mode λ, Λλ is the wave amplitude, and Rl denotes the lattice vector of the l-th primitive cell. Then the equation characterizing the phonon dispersion relationship ω(q) can be derived from eqn (3):
corresponds to the k-th atomic vector of the phonon mode λ, Λλ is the wave amplitude, and Rl denotes the lattice vector of the l-th primitive cell. Then the equation characterizing the phonon dispersion relationship ω(q) can be derived from eqn (3):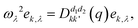 | (4) |
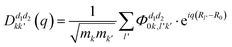 .
.
2.2 Relationship between different phonon transport properties
While only considering the three-phonon scattering process, the potential energy (eqn (1)) can be expressed as: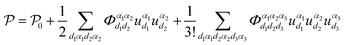 | (5) |
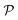 can be written as:
can be written as: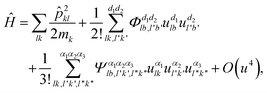 | (6) |
![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) lk is the momentum operator of the k-th atom, and O(u4) is the abbreviated higher-order term. As for the lattice thermal conductivity (LTC) calculation, with the Boltzmann transport equation:
lk is the momentum operator of the k-th atom, and O(u4) is the abbreviated higher-order term. As for the lattice thermal conductivity (LTC) calculation, with the Boltzmann transport equation: 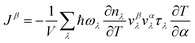 and Fourier's law:
and Fourier's law: 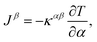 54,55 the final LTC solution can be expressed as:
54,55 the final LTC solution can be expressed as: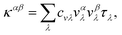 | (7) |
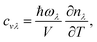 where V is the volume of the unit cell, vαλ and vβλ are the components of group velocity: vλ = ∂nλ/∂q along the α and β directions, and nλ represents the Bose–Einstein distribution function. With Matthiessen's rule, the relationship between total relaxion time τλ and scattering rates considering different scattering mechanisms (phonon–phonon scattering rate
where V is the volume of the unit cell, vαλ and vβλ are the components of group velocity: vλ = ∂nλ/∂q along the α and β directions, and nλ represents the Bose–Einstein distribution function. With Matthiessen's rule, the relationship between total relaxion time τλ and scattering rates considering different scattering mechanisms (phonon–phonon scattering rate 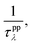 phonon impurity scattering rate
phonon impurity scattering rate 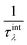 and phonon boundary scattering rate
and phonon boundary scattering rate 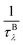 ) can be summarized as:
) can be summarized as: 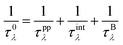 .
.
3. Common strategies to predict phonon transport properties
To date, several types of previously mentioned strategies, which are abbreviated as DFT+BTE, ML, and MD in Fig. 1, have emerged as benchmarks for phonon transport properties prediction. Although differing from each other, these methods are interrelated, and the combination of multiple methods often yields more accurate results. According to different theories used to describe atomic interactions, they can be broadly categorized into the following two groups.56 Among them, the atomic simulation solution that considers underlying electronic structures mainly refers to the DFT+BTE method. Another solution mainly relies on numerical analysis or empirical scheme calculations, which includes empirical models, MD simulation, as well as data-driven ML approaches. In this section, we provide a brief overview of the principles, advantages, disadvantages, as well as application scope of these methods. Emphasis will be placed on our recent research utilizing the above-mentioned strategies to investigate unique phonon transport properties exhibited in various material systems.3.1 Solving phonon Boltzmann transport equation (BTE) calculations based on density functional theory (DFT) calculations.
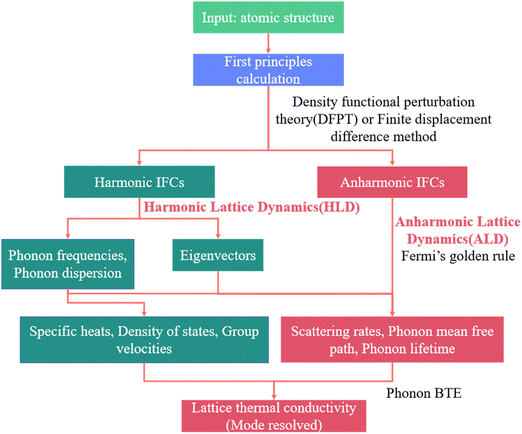
Due to the exponential growth in computational power in recent years,57 computational simulation has emerged as one of the most essential tools for predicting phonon transport properties. Two widely used atomic simulation methods are quantum mechanical simulation implemented based on first principles calculations with density functional theory (DFT) and force field simulation achieved by molecular dynamics (MD). The process of DFT-based calculations is outlined in Fig. 2.58 Phonon transport properties like phonon frequencies, dispersion curves, specific heat, DOS, and group velocities can be predicted through harmonic lattice dynamics (HLD) calculations,59 while phonon lifetime, scatting rates, and MFP of phonons require excessive anharmonic lattice dynamics (ALD) calculations.41,57 By solving the Schrödinger equation60 with DFT calculations,61 the derivatives of crystal potential energy with respect to the atomic displacements, known as the interatomic force constants (IFCs) with experimental accuracy,62 can be obtained, which are then utilized to further calculate phonon transport properties. From a mathematic perspective, atomic forces, i.e., the first order derivative of potential energy with respect to atomic displacements, are essential or central tasks for both harmonic and anharmonic phonon calculations, since higher order derivatives can be reduced to the lower order calculation by the finite difference method. With only the initial atomic structure information as input, full phonon transport properties can be calculated in high precision without any parameter fitting.58 Many packages have been developed for implementing DFT+BTE calculations, including ShengBTE,63 AlmaBTE,64 phono3py,65 d3q,37 and AFLOW-AAPL.66 Once HLD calculations are completed, MD simulation can also be used to replace tedious DFT calculations for ALD calculations, which will be discussed later in the subsequent MD section.As mentioned in the introduction, thermal transport in non-metal crystals is mainly dominated by phonons.67 However, for specific phonon modes, anharmonicity may be significant and lead to many anomalous behaviors. According to perturbation theory, the lowest anharmonic order terms typically involve three phonons: one phonon splitting into two, or two phonons combining into a new phonon. In addition, higher order anharmonicity involving four phonon interactions is shown in Fig. 3(a). It has been assumed for decades that the three-phonon scattering dominates phonon transport in solids, as lots of calculations considering only three-phonon scatterings exhibit astonishing consistency with experimental results.
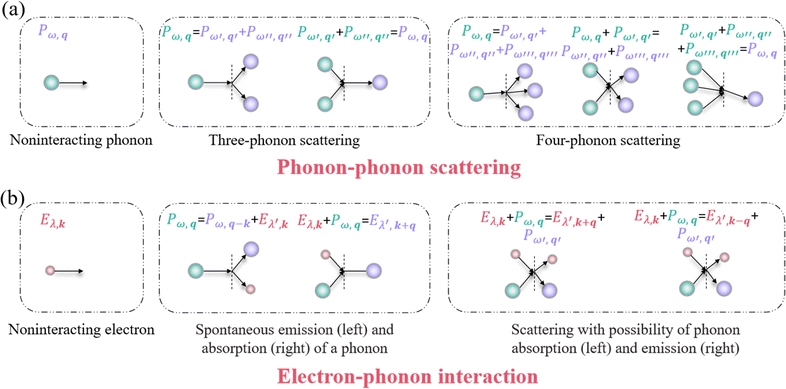 | ||
| Fig. 3 Schematic diagram of two spontaneous scattering processes, classified by the participating particles. (a) Phonon–phonon scattering. (b) Electron–phonon scattering.41,68 | ||
| Ref. | Material system | Underlying mechanism | Thermal conductivity calculation results (W m−1 K−1) | Experimental results (W m−1 K−1) |
|---|---|---|---|---|
| 72 | Two-dimensional (2D) phosphorene | Resonant bonding; van der Waals interactions | 8.77 (zigzag) | — |
| 3.26 (armchair) | ||||
| 73 | Carbon allotropes: lonsdaleite, Bct-C4, and Z-carbon | Chemical bonding | 1686.67 (lonsdaleite) | — |
| 1686.67 (Bct-C4) | ||||
| 1411.02 (Z-carbon) | ||||
| 74 | Carbon allotropes: BCO-C16vs. graphene and T-carbon vs. diamond | Interatomic covalent bonds | 452.47 (BCO-C16![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) ) ) |
2200 (natural diamond) |
777.68 (BCO-C16![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) ) ) |
3409.08 (graphene) | |||
190.18 (BCO-C16![[c with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0063_20d1.gif) ) ) |
||||
| Graphene (3151.53) | ||||
| T-carbon (33.06) | ||||
| Diamond (2388.69) | ||||
452.47 (BCO-C16![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) ) ) |
||||
| 71 | Mg3Sb2−xBix (x = 0, 1, and 2) monolayers | Chemical bonding | 0.51 (Mg3Sb2) 1.86 (Mg3SbBi) 0.25 (Mg3Bi2) | — |
| 75 | Intermetallic clathrates: the binary type-I M8Si46 (M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sr, Ba, Tl, and Pb) clathrates Sr, Ba, Tl, and Pb) clathrates |
Rattling vibrations; | 1.69 | 1.7 |
| n-type doping | ||||
| 76 | Three chalcopyrite structures: TlBiS2, TlBiSe2, and TlBiTe2 | Higher transferred charges; | 0.8826 (TlBiS2) | — |
| Stereo-chemically lone-pair electrons; | 0.9383 (TlBiSe2) | |||
| Metavalent bonding | 0.2841 (TlBiTe2) | |||
| 77 | 2D group III-nitrides (h-BN, h-AlN, h-GaN) | The electronic origin of strain engineering: | 245.45 (h-BN) | 227–625 (h-BN) |
| related to lone-pair electrons | 74.43 (h-AlN) | |||
| 14.93 (h-GaN) | ||||
| 78 | Three-dimensional cubic boron arsenide (c-BAs) and two-dimensional graphene-like BAs (g-BAs) | Lone-pair electrons or making the lone-pair electrons stereochemically active induced low κ | 1400 | — |
| 79 | Monolayer h-AlN | Isolated electron pairs | 74.43 | — |
| 80 | 2D single-crystal carbon nitride (C3N) | The interaction between lone-pair N–s electrons and bonding electrons; | 103.02 | — |
| Temperature and strain effect | ||||
| 81 | Silicon nanowire (SiNW) arrays doped with Co (Cp*)2 | Surface chemical control; | 44 (oxygen plasma) | — |
| Surface chemical control | 40 (vapor HF-treated) | |||
| 21 (Co(Cp)2-doped Si nanowires) | ||||
| 82 | Ferroelectric bilayer boron nitride (BN) | The effect of in-plane electric fields; | 840 | — |
| 69 | CaM (M = O, S, Se, Te) | Bonding nature tuned by external strain | 19.50 (CaO) | — |
| 23.63 (CaS) | ||||
| 11.29 (CaSe) | ||||
| 5.50 (CaTe) | ||||
| 19.50 (CaO) | ||||
| 83 | Van der Waals (vdW) materials Fe3GeTe2 | Strong laser-polarization control; | — | — |
| Asymmetric in-plane and out-of-plane inter-atomic interactions | ||||
| 84 | SiSnSb2 and GeSnSb2 monolayers | Rashba effect modulated by the external electric field | 0.94 eV Å (SiSnSb2) | — |
| 1.27 eV Å (GeSnSb2) | ||||
| 85 | Bilayer graphene, monolayer silicene, and germanene | External electric fields | 0.034 (Ez = 0.4 V Å−1) | — |
| 31 | g-B3X5 (X = N, P, and As) | Non-bonding delocalized electrons | 21.08 (g-B3N5) | 500 (g-BN) |
| 2.50 (g-B3P5) | 1300 (c-BAs) | |||
| 1.85 (g-B3As5) | 1600 (c-BN) |
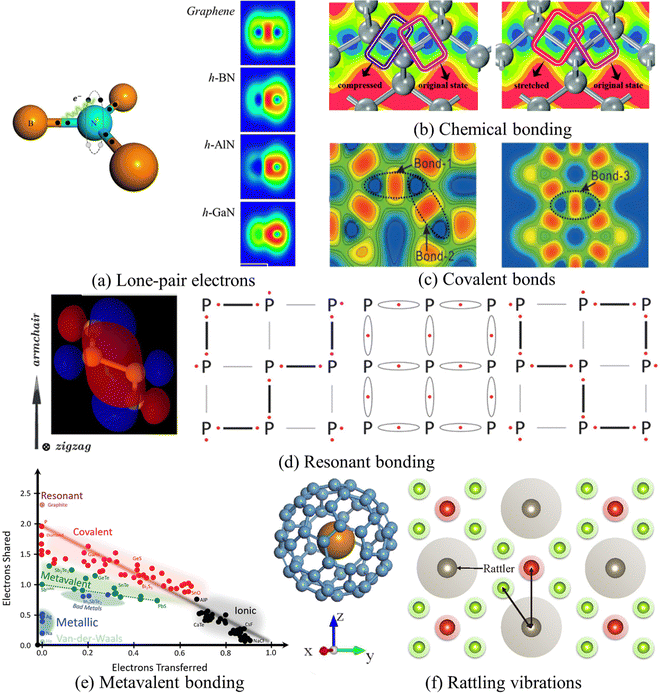 | ||
| Fig. 4 The physical mechanism underlying phonon anharmonicity. The subfigures are from ref. 72–77, 86 and 87. Details about these references can be found in Table 1. (a) Lone-pair electrons mechanism.77 Diagram plot of interactions between the non-bonding lone-pair N–s electrons and the covalently bonding electrons (left), and the side view of the electron localization function (ELF) in h-(B/Al/Ga) N and graphene (right). Copyright 2018 by Elsevier. (b) ELF contour changes of the C–C chemical bond in diamond from original states (pink box), when being stretched or compressed by 0.15 Å along the bond axis, highlighted in red or purple respectively.73 Copyright 2019 by Royal Society of Chemistry (RSC). (c) ELF plot of BCO-C16, showing three different covalent bonds using 2D projection.74 Copyright 2017 by American Physical Society (APS). (d) Schematic plots of resonant bonding behavior in phosphorene. Four subgraphs individually represent: the side-view highest occupied molecular orbital (HOMO) plot of the p-type σ bond, where blue and red colors stand for positive and negative values compared to the isosurface level valence-band maximum (0.03).72 Copyright 2016 by American Physical Society (APS). The generation process of resonant bonding, affected by a hybrid wave function. When the hybrid energy value reaches its minimum, the resonant bonding is subsequently formed (middle one); two limited covalent bonding cases are on the left and right sides respectively.86 Copyright 2018 by Wiley. (e) Pairplot of the electron transfer (ET) and the number of electrons shared (ES) between pairs of adjacent atoms in common materials: from GeTe to GeSe, from Sb2Te3 to Sb2Se3, and from Bi2Se3 to Sb2Se3, represented by the pseudo-binary lines. With all these lines, the transition nature from metavalent (green) to covalent (red) bonding can be spotted.88 Copyright 2021 by Wiley. (f) Schematic diagram of the rattling model (left) including a cage-like structure with a guest atom lying in its center; the key spirit of the rattling model (right), where gray, green, and red solid circles denote different atoms, and the shaded area around atoms represents the vibration range of the corresponding atom.87 Copyright 2022 by American Chemical Society (ACS). | ||
Despite the significant progress made in the research of anharmonic properties of phonons in recent years, quantitatively describing phonon transport remains a challenging task, primarily due to the incomplete consideration of interactions in the simulation process. Specifically, there are still several mechanisms that are often neglected, and we are making efforts to explore these areas.
| Ref. | Material system | Underlaying mechanism | Thermal conductivity calculation results (W m−1 K−1) | Experimental results (W m−1 K−1) |
|---|---|---|---|---|
| 96 | Zintl phase Mg3Sb2 | Four-phonon scattering | 1.94 (in-plane) 2.19 (cross-plane) | 0.398 (single crystal) |
| 97 | Single-crystalline barium titanate (BTO) thin films | Scaling of ferroelectric materials; | 250 MW m−2 K−1 (BTO–STO interface) | 5.7 (for bulk crystals) |
| Four-phonon scattering | 4.8 (for single crystals) | |||
| 95 | Full Heusler CsK2Bi and CsK2Sb | Four-phonon scattering; | 0.14 (CsK2Sb) 0.13 (CsK2Bi) | — |
| Antibonding-induced anharmonic rattling of Cs atoms |
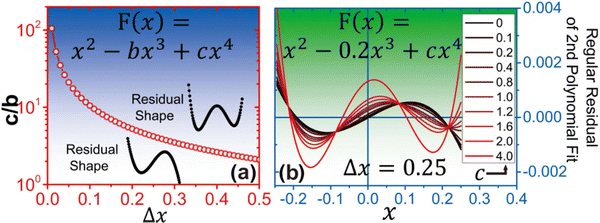 | ||
| Fig. 5 (a) The relationship between the ratio of fourth order to third order terms (denoted c/b) and the minor disturbance Δx, which describes the physical atomic displacement from its equilibrium position. (b) Variation of residual shape with the change of c/b, when Δx is fixed as 0.25. Adapted from ref. 93. Copyright 2017 by American Physical Society (APS). | ||
It has been demonstrated that this analytical method is not limited to measuring phonon anharmonicity in systems with intrinsic strong anharmonicity, but can also be applied to study temperature-induced anharmonicity. However, no conclusive evidence suggests a clear relationship between this method and the four-phonon scattering phase space (another very important property for studying the three-phonon-process four-phonon scattering) and so far. Despite the limitation, this analysis method has already been successfully applied in ref. 95. It can be anticipated that integrating this method with machine learning techniques could potentially be beneficial to high-throughput pre-screening of large-scale materials whose four-phonon scattering are significantly strong, prior to engaging in the highly expensive four-phonon BTE calculations.
| Ref. | Material system | Underlying mechanism | Thermal conductivity calculation results (W m−1 K−1) | Experimental results (W m−1 K−1) |
|---|---|---|---|---|
| 112 | Wurtzite gallium nitride (GaN) | The large electronegativity difference between Ga and N atoms; | 225 | 227 |
| Fröhlich EPI | ||||
| 113 | The layered metal oxide PdCoO2 | EPI | 56.8 (in-plane) | |
| 44.3 (cross-plane) | ||||
| 114 | High-pressure phase of Li (cI16) between 45 GPa and 76 GPa | EPI effect; | — | — |
| Metal-to-semiconductor transition at different pressures | ||||
| 115 | Superconducting hydrogen sulfide (H3S) at high pressures | The influence of the intrinsic EPI competes with the weakened phonon–phonon interactions (PPI) | 91 | — |
| 116 | Ultrahigh temperature ZrB2- and TiB2-based ceramics | PPI, EPI and grain boundary scattering (GBS); temperature-independent κph | 49 (ZrB2) 35.26 (TiB2) | 51 (ZrB2) 35.26 (TiB2) |
| 117 | Janus monolayer MoSSe | The interactions between electrons and phonons | 27 (external electric fields Ez = 0 V Å−1) | — |
| 118 | Silicene | Electron phonon coupling manipulation driven by an external electric field. | 0.091 (Ez = 0.5 V Å−1) | — |
| 19.21 (Ez = 0 V Å−1) |
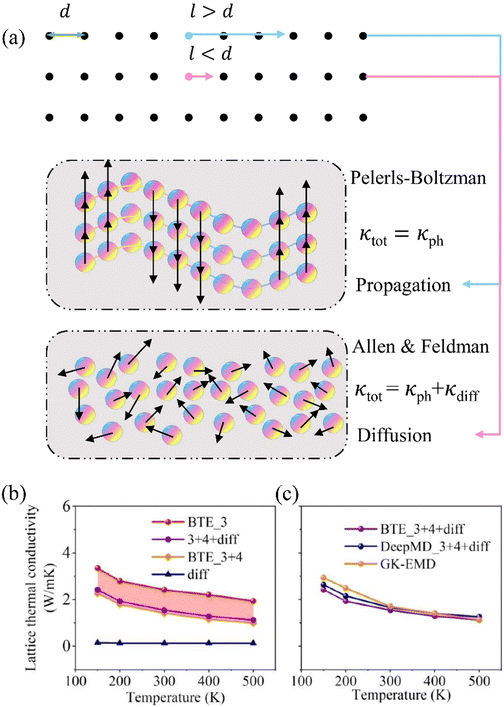 | ||
| Fig. 6 (a) Visualization of the differences between propagation and diffusion transport. When the MFP of phonons (l) is lower than the minimum distance between atoms (d), phonon transport follows the theory of Allen and Feldman and exhibits diffusion transport behavior (κdiff), and the total thermal conductivity κtot = κph + κdiff. Otherwise, only propagation phonons exist and κtot can be described by the Pelerls–Boltzman theory as κph. Comparison of (b) BTE calculated κ as a function of temperature considering different physical mechanisms and (c) using different simulation methods: DFT+BTE method and MLP based GK-EMD method.123 Copyright 2022 by American Chemical Society (ACS). | ||
Recently, a paper123 on two-dimensional (2D) paraelectric SnSe has been published as a study case to provide quantitative analysis of detailed phonon transport mechanisms, including three-phonon scattering, four-phonon scattering, and diffusion transport behavior. Additionally, we investigated the effect of temperature on phase transition anharmonicity. Notably, the existence of anomalous diffusion transport behavior has been observed due to the MFP of 2D SnSe being smaller than the atomic distance (≈3 Å). The calculation results considering different physical mechanisms with DFT+BTE are depicted in Fig. 6(b). It can be seen that the κ decreases with rising temperature. Compared with calculation results only considering the three-phonon scattering mechanism, the κ decreases significantly when taking into account the four-phonon scattering mechanism. Furthermore, κdiff exhibits limited sensitivity to temperature variations, which is consistent with the conclusions drawn from extensive research studies. Notably, the highest κdiff can even account for 15% of the κtot, highlighting the substantial contribution of diffusion transport to κtot in 2D material systems. The comparison of thermal conductivity results achieved by BTE, DeePMD, and GK-EMD methods is shown in Fig. 6(c). It can be seen that the GK-EMD calculation results exhibited an extraordinarily similar trend to the BTE results combined with diffusion transport, but slightly higher than the BTE results. The difference is particularly notable at low temperatures, which can be attributed to the omission of quantum effects in classical MD simulations.
3.2 Classical molecular dynamics (MD) simulation
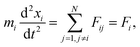 | (8) |
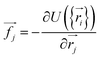 | (9) |
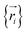 . The total potential energy can be divided into contributions of different parts as:
. The total potential energy can be divided into contributions of different parts as: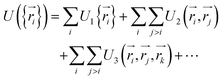 | (10) |
Empirical potentials, guided by physical and chemical insights, are widely used in classical MD simulations. These empirical potentials are typically characterized by an analytical function, which can be derived by fitting experimental results and first-principles calculations. Commonly used empirical potentials include pairwise Lennard-Jones potential for inert gas and colloidal systems, Morse potential for covalent systems, three-body Tersoff125 and Stillinger Weber potential126 for covalent systems, and embedded atom method potential127 for metal systems and alloys. These functions enable accurate modeling of atomic interactions, which is crucial for understanding and predicting material properties.
In MD simulation, the interactions between individual atoms are determined by the interatomic potential, which will directly determine the quality of MD simulation. The entire system also needs to follow certain simulation conditions, such as temperature (T), pressure (P), heat flux, etc. Depending on whether the system is in a steady state with constant temperature, the thermal transport properties prediction of materials by MD simulations can be categorized into two types: equilibrium molecular dynamics simulation (EMD) and non-equilibrium molecular dynamics simulation (NEMD). In EMD simulations, which rely on the Green–Kubo method, the system maintains a constant temperature and volume, i.e. employing the NVE ensemble. This approach enables the balance of space and time, where the thermal conductivity is calculated as the integral of the heat flux autocorrelation function over time:
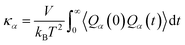 | (11) |
Another method is the NEMD method based on Fourier's law, and the principal diagram is shown in Fig. 7. Initially, it is necessary to satisfy the initial equilibrium conditions of temperature (T) and pressure (P) in the model. Subsequently, thermostats under different temperatures are applied at the two ends of the system to induce heat flux (Q), which can be calculated through energy exchange rates. Finally, with the response to temperature changes of the system along the z-axis, i.e., 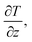 κ can be obtained through Fourier's law:
κ can be obtained through Fourier's law:
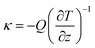 | (12) |
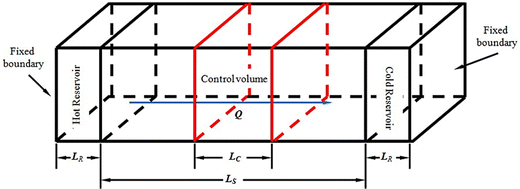 | ||
| Fig. 7 Schematic of the frequency domain direct decomposed method (FDDDM) and time domain direct decomposition method (TDDDM), where LS, LC, and LR are the length of the system, control volume, and thermostats, respectively. The Q stands for the heat current in the system.128,129 Copyright 2015 by American Physical Society (APS). | ||
As demonstrated in Table 6, MD simulations have been widely used for large-scale materials systems with high complexity, especially for bulk, low dimensional,130–137 interfacial,138–141 nanoparticle,140 amorphous142 and inhomogeneous143 material systems, where calculations through DFT+BTE are challenging or even impractical. This situation drives our research towards more efficient, economical, and predictable directions. Additionally, the MD is the closest simulation method to experiments, which can achieve simulation under extreme experimental conditions and reveal the physical mechanism intuitively by offering a microscopic evolution diagram of the system at the atomic level.
Herein, a recent influential MD simulation study is presented. Polycrystalline Si nanowires (NWs) were constructed using the Voronoi algorithm, as well as bulk Si, perfect Si NWs, and amorphous Si NW systems illustrated in Fig. 8(a). Subsequently, thermal conductivity κ was calculated using the GK-EMD and NEMD method, respectively, to verify the accuracy of the results. The calculated κ of bulk silicon was then compared with previously reported experimental, DFT, and MD simulation results. In Fig. 8(d), it is observed that the NEMD calculated κ of perfect and amorphous Si NWs gradually approaches the GK-EMD results at the lengths of approximately 310 and 130 nm, respectively. However, as inferred from Fig. 8(e), polycrystalline Si NWs do not exhibit significant size-effects along the length direction. Consequently, precise results can be efficiently obtained solely through NEMD simulation, benefiting from its unique features outlined in Table 6.
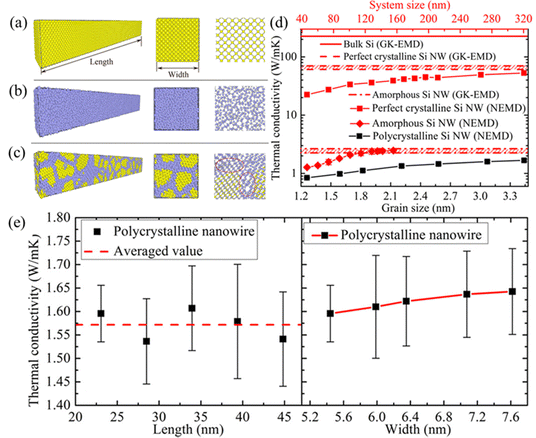 | ||
| Fig. 8 The construction of (a) perfect Si NWs, (b) amorphous Si NWs, and (c) polycrystalline Si NWs. (d) NEMD calculated κ of (a)–(c) and bulk Si as a function of grain size, compared with the GK-EMD results. (e) GK-EMD calculated κ of polycrystalline Si NWs as a function of system length and cross-sectional width.141 Copyright 2016 by American Chemical Society (ACS). | ||
| Calculation method | Ref. | System | Physical mechanism | Thermal conductivity calculation results (W m−1 K−1) | Experimental results (W m−1 K−1) |
|---|---|---|---|---|---|
| EMD | 153 | Lead telluride (PbTe) | Twin boundary | 2.85 | 2.4 |
| 133 | Extremely thin Si NWs | The impact of NW diameter changes | ≈1180 (0.75 nm) | ≈210 (bulk) | |
| ≈50 (2.3 nm) | |||||
| 142 | Amorphous lithium–sulfur (a-LixS) | The varying concentration (x) of Li ions affect competition between propagating and non-propagating phonons | 0.61–0.89 (x ∈ (0.4, 1.2)) | — | |
| (x ∈ (1.2, 1.6)) | |||||
| ≈0.85 (x ∈ (1.6, 2.0)) | |||||
| NEMD | 138 | Single crystal silicon and amorphous polyethylene (PE) interface | Solid stiffness and bonding strength across the interface | 0.121 | 0.135 |
| 139 | Single-crystal silicon and amorphous PE interface | Solid stiffness and bonding strength across the interface | G K = 17.4 ± 1.3 MW m−2 K−1 0.33 (polymer) | G K = 107 W m−2 K−1 (interface) | |
| 0.3 (polymer) | |||||
| 140 | Zinc oxide (ZnO) nanoparticles in liquid tetradecane (C14H30) | Particle size effect on the interface | 0.121 | 0.135 (320 K) | |
| 156 | Self-assembled monolayer (SAM) of alkanethiol molecules covalently bonded to (111) gold SAM-Si interface | Bonding strength at the interface | G K = 10 MW m−2 K−1 (Si-SAM-Au) | G K = 15/60 MW m−2 K−1 (Si-SAM-Au with weak/strong SiSAM interfaces) | |
| 132 | SiC substrate with the square-shape pillar array combined with epitaxial GaN as the nanostructured interface (SiC/GaN) | The characteristic dimensions of the square-shape pillar array effect | 0.670 GW m−2 K−1 | — | |
| 157 | Si/Ge superlattice nanowires | Two competing mechanisms: interface modulation and coherent phonons | 45.3 (Si NW) 6.03 (Si0.5Ge0.5) 4.44 (Si/Ge) 1.35 (SLNW) | ∼40 ± 10 (Si NW by MD) | |
| 134 | Pure Si NWs, five-fold twinned Si NWs (5T-Si NWs) and alloyed Si NWs | Five-fold twin boundary; Ge-doping | 1.41 (alloyed Si NWs) | 2.4 (pure amorphous Si NWs by MD) 1 (Si-based nanomaterials by MD) | |
| 131 | The perfect graphyne nanotube (GNT) | Lattice vibration mismatch | 373.4 ((2,2) CNT for 100 nm length) 80.45 ((2,1) CNT for 100 nm length) 10 (GNT) | ∼3400 (a single-walled CNT) | |
| 135 | Graphyne and graphyne nanoribbons | Surface dominated phonon modes lead to width dependent κ | 8 | — | |
| 143 | Pure iron | Phonon-dislocation scattering; | 59.45 (dislocation) 73.03 (perfect) | — | |
| Both EMD and NEMD | 141 | Polycrystalline Si nanowires (NWs), compared with perfect Si NW and amorphous Si NW | Structural disorder inside the grains suppresses propagons and make diffusons the main heat carriers | 160 | 156 |
| 130 | Two-dimensional silicene | The influence of anisotropy and bonding strength changes caused by buckling structures | 5.5 | 150 | |
| 158 | GaN-BAs heterostructures | The competition between grain size and boundary resistance | 1510 (BAs) a = 217, c = 229 (for GaN along the a and c axis) 260 (MW m−2 K−1 for GaN-BAs) | 1300 (BAs) | |
| a = 217 | |||||
| c = 228 or 195 (for GaN) | |||||
| AIMD | 159 | Wurtzite BAs (w-BAs) | Four-phonon scattering | 1036 | — |
| 160 | Lanthanum Tungsten Nitride (LaWN3) | The coherences' coupling of vibrations involving N atoms | 2.47 | — | |
| 161 | Few-layer black phosphorus (BP) | Four-phonon scattering | 71.75 (κZZ) 71.75 (κAC) | — | |
3.3 Data-driven machine learning (ML) methods
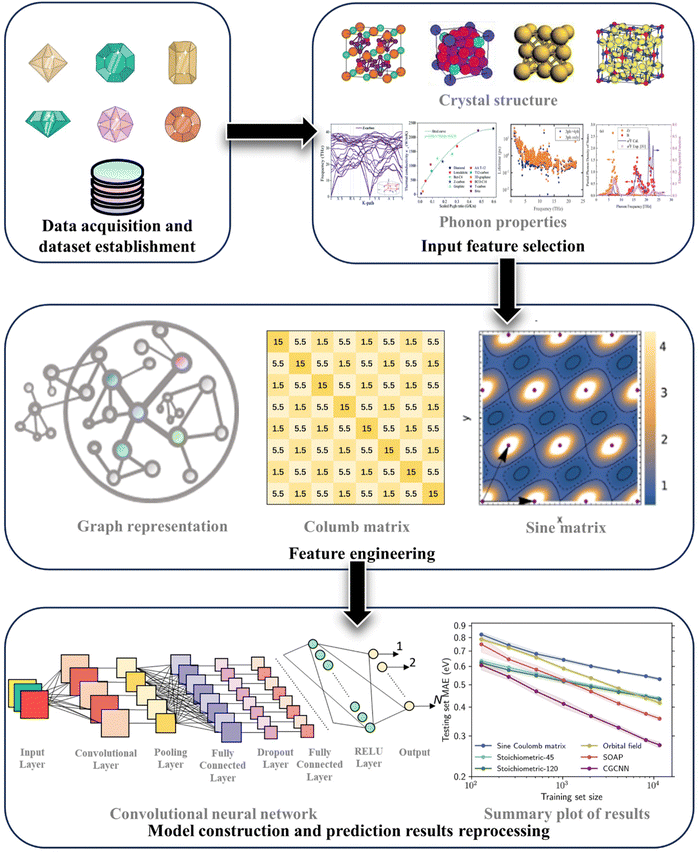 | ||
| Fig. 9 Typical workflow of material properties prediction using machine learning models. Subfigures are adopted from ref. 38, 73, 97, 116, 162 and 163. Copyright 2021 by Wiley, Copyright 2019 by Royal Society of Chemistry (RSC), Copyright 2023 by Wiley, Copyright 2020 by Elsevier, and Copyright 2021 by Wiley and Copyright 2021 by Cell Press. | ||
(1) Data acquisition and dataset establishment. The majority of collected data originates from atomic simulations or experiments. Notably, the implementation of the Materials Genome Project in the past decade has accelerated the vigorous development of materials databases. Many famous databases, such as the Materials Project,164 AFLOW,165 OQMD,166 ICSD,167etc. have significantly facilitated rapid data acquisition.
(2) Input feature selection. The available features for ML inputs include structural details, chemical environments, and other vital material information. These features include both harmonic and anharmonic properties, along with conditional factors like temperature and pressure.
(3) Feature engineering. It is highly advisable to systematically store the most representative materials information. At present, the most frequently used structural descriptors in feature extraction include Smooth Overlap of Atomic Positions (SOAP),168 Coulomb matrix,169 Sine matrix,38,170 graph representation methods,171etc.
(4) Modeling the relationship between material information and target properties. Beyond simple machine learning regression models like linear regression, Gaussian regression, kernel ridge regression, and ensemble learning algorithms such as extreme gradient boosting (XGBoost),172 gradient boosting decision trees (GBDT),173etc., the field of materials science also utilizes deep learning algorithms. Some commonly employed algorithms include feed-forward neural network (FNN),174 convolutional neural network (CNN),175 and the increasingly popular graph neural network (GNN),176,177etc.
The ML models can be utilized to unearth the optimal structure that exhibits target phonon transport properties throughout the entire design space. However, some shortcomings still exist, as shown in Table 6. One of the most pressing challenges faced by ML is the small sample sizes. Thus, current solutions lie in pre-trained models, which involves leveraging easily accessible material information to pre-train the models for predicting challenging-to-calculate target material properties. A typical example is the development of machine learning potentials (MLPs).
| Method | Ref. | Regressor | Algorithm | Implementation |
|---|---|---|---|---|
| Behler–Parrinello neural-network potential (BPNNP) | 187 | (2007) | NN | LAMMPS |
| Gaussian approximation potentials (GAP) | 188 and 189 | (2010) | GPR | GAP code; LAMMPS |
| Spectral neighbor analysis potential (SNAP) | 190 and 191 | (2015) | Linear fit | LAMMPS |
| Adaptive, generalizable, and neighborhood informed (AGNI) force fields | 192–194 | (2015) | KRR | LAMMPS |
| Moment tensor potentials (MTP) | 195 and 196 | (2016) | Linear fit | LAMMPS |
| Artificial neural networks | 197 and 198 | (2007) | NN | RuNNer; LAMMPS |
| aenet-Fortran | 199 | (2016) | NN | aenet |
| Amp | 200 | (2016) | NN | amp |
| Voronoi RF | 201 | (2017) | Fingerprint | Matbench |
| CGCNN | 171 | (2017) | GNN | cgcnn |
| SchNet | 202 and 203 | (2018) | NN | SchNetPack |
| DeePMD | 181 and 182 | (2018) | NN | DeePMD-kit; LAMMPS |
| DimeNet | 204 | (2020) | GNN | Dimenet |
| Neuroevolution potential (NEP) | 205 and 206 | (2021) | NN | GPUMD; LAMMPS |
| DeepMoleNet | 207 | (2021) | Transformer | DeepMoleNet |
| MEGNet | 208 | (2021) | GNN | Megnet; Matbench |
| BOWSR | 209 | (2021) | GNN | maml; lammps; Matbench |
| Wrenformer | 210 | (2021) | Transformer | Matbench |
| ALIGNN | 211 | (2021) | GNN | Alignn; Matbench |
| Neural equivariant interatomic potential (NequIP) | 212 | (2022) | GNN | nequip |
| Graph neural networks with three-body interactions (M3GNet) | 213 | (2022) | GNN | m3gnet; Matbench |
| Tensor embedded atom network (TeaNet) | 214 | (2022) | GNN | — |
| So3krates | 215 | (2022) | MPNN | MLFF |
| MACE | 216 | (2022) | GNN | mace-torch |
| ænet-Pytorch | 180 | (2023) | NN | anet-Pytorch |
| Allegro | 217 | (2023) | GNN | Allegro; LAMMPS |
| Crystal Hamiltonian graph neural network (CHGNet) | 183 | (2023) | GNN | Chgnet; Matbench |
| TorchMD-Net 2.0 | 218 | (2024) | Transformer | Torchmd-net |
| SevenNet | 219 | (2024) | GNN | Seven; Matbench |
| eqV2 DeNS | 220 | (2024) | Transformer | Fairchem; Matbench |
| ORB MPtrj | 221 | (2024) | GNN | Orb-models; Matbench |
The entire MLP development process depicted in Fig. 10164 is similar to that of ML methodologies for material property prediction. The process consists of three key components: database, descriptors, and ML algorithms for training PES. The database forms the foundation of model development, requiring a large collection of material structure data along with corresponding property data such as energy and atomic forces, which are typically gathered via high-throughput DFT calculations or from public databases.
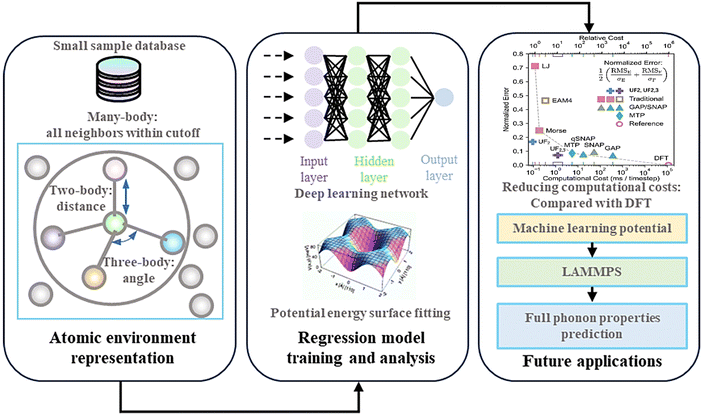 | ||
| Fig. 10 The schematic of machine learning potentials (MLPs) developments and applications. Some subfigures are derived from ref. 184, 222 and 223. Copyright 2019 by Wiley, Copyright 1997 by American Physical Society (APS) and Copyright 2023 by Springer Nature. | ||
The next challenge is to encode the atomic structure in a way that captures the complete atomic environment, ensuring the generated descriptors are comprehensive. After this step, appropriate input for the model can be obtained. The third step involves training the models for PES prediction. Then the trained model will be frozen, saved, and deployed as an MLP package with interfaces of MD software for prediction purposes.
[1] Empirical models improvement with ML techniques. Empirical models, initially formulated to predict phonon transport properties, include several conspicuous and representative examples, namely the Callaway,224 Klemens,225 Holland,226 and Slack227 models, which were developed in the 1950–1970s. As emphasized in Table 6, they offer a fast computational speed. However, the main limitations stem from the unprovable accuracy and lack of extrapolation ability,228 due to interpolation fitting with only a few thermal conductivity values, and the complexity of calculating material properties in a high-throughput manner. Notably, the Slack model, proposed by G. A. Slack in 1973,227 is widely used for analyzing phonon dispersion and transport properties based on low-frequency assumptions, which is written as:227
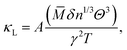 | (13) |
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) is the averaged atomic mass, δ = V/n represents the average volume per atom, n stands for the number of atoms in the primitive cell, Θ is the Debye temperature, T denotes the absolute temperature, and γ is the Grüneisen parameter of the material. The variable coefficient A in eqn (13) can be expressed as:
is the averaged atomic mass, δ = V/n represents the average volume per atom, n stands for the number of atoms in the primitive cell, Θ is the Debye temperature, T denotes the absolute temperature, and γ is the Grüneisen parameter of the material. The variable coefficient A in eqn (13) can be expressed as: 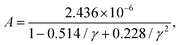 which was refined by Jia et al. in 2017229 exploiting a dataset containing rock salt, zinc blende, and wurtzite materials. The modification considered the contribution of anharmonicity. The corrected factor A takes the following form:
which was refined by Jia et al. in 2017229 exploiting a dataset containing rock salt, zinc blende, and wurtzite materials. The modification considered the contribution of anharmonicity. The corrected factor A takes the following form: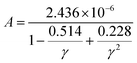 | (14) |
| Methods | Working principle | Applications scope | Advantages | Disadvantages |
|---|---|---|---|---|
| Empirical models | Interpolation fitting of the BTE solutions and the experimental thermal conductivity with low-frequency constraints | High throughput rough prediction | Fast calculation speed; | Mainly relies on interpolation fitting; |
| Fast calculation speed; | Insufficient sample size; | |||
| Lack of accuracy and transferability;228 | ||||
| DFT | Quantum mechanical simulation: implemented by solving the Schrödinger equation60 with DFT | <500 atoms nanoscale systems with a length scale of 10−1–102 nm;58 | Only the initial atomic structure information is required as input, high-precision full phonon transport properties are accessible | Uncertainty lies in the calculation process; not including high-order phonon processes.230 |
| Low-temperature conditions; | ||||
| Lower-order anharmonicity | ||||
| AIMD | Using DFT to calculate the electronic structure and atomic forces, and apply classical MD integration methods to solve Newton's equations of motion | Relatively more microscopic scale simulation than DFT | High computational accuracy | Computational cost scales cubically with respect to the number of electronic degrees of freedom;152 |
| Neither large systems nor a long period of time simulation.35 | ||||
| MD in common | Force field simulation: obtain the energy and momentum of the atomic objects at different times by solving Newton's motion equations | Bulk, low dimensional, interfacial, and inhomogeneous231 material systems; extreme experimental conditions; | Naturally include the complete anharmonic nature of atomic interactions; | Ignore the quantum effects when considering the interatomic forces; unable to clearly provide different physical mechanisms contributions to phonon transport;123 not suitable for metal systems. |
| Closest simulation method to experiments | ||||
| EMD | Green–Kubo method | Suitable for studying defects, polycrystalline, amorphous, and anisotropic materials | Obtain the intrinsic κ without external force; the calculation process is relatively simple; | Numerical integration is difficult to converge in terms of time and system size. The system size should be large enough to eliminate size effects, and the larger the mean free path (MFP) of the system, the longer the simulation time; Sensitive to initial conditions and requires multiple independent simulations to obtain the average value. |
| NEMD | Fourier's law | Mainly used for the calculation of finite-size materials; | The calculation process is simpler than EMD232 | Severe size-dependent; |
| Can only obtain κ in a single direction.43 | ||||
| Empirical potentials | Fitting experimental results and first principles calculations | High throughput rough prediction; | Several orders of magnitude faster than DFT; | Not accurate due to a fixed mathematical function of atomic interactions generated by people's chemical and physical insights; |
| A short simulation time of 10−6–102 ns with a large length scale of 10−2–103 nm;124,231,233 | ||||
| Handle simple systems; | Not transferable. | |||
| Machine learning potentials | Fitting 3N dimensional potential energy surface (PES) functions | Simulation of hundreds of thousands of atoms | DFT-level accuracy with the speed faster than DFT; | Descriptor construction difficulty; |
| Poor transferability, only suitable for one system; “curse of dimensionality”;184 | ||||
| Cannot include long-range interactions. | ||||
| Machine learning | Data driven machine learning model for direct properties prediction | Entire design space | Several orders of magnitude faster than DFT; | Overcomplete or incomplete descriptors;234 |
| Several orders of magnitude faster than DFT; | Difficult to obtain complete phonon transport properties235,236 and predict properties beyond the training scope; | |||
| Small sample size: still require tedious DFT-level calculations as training data | ||||
However, the revised Slack model generally overestimates κ as tested on a larger dataset. We have undertaken the following efforts to improve the performance of the Slack model. In 2021, a genetic programming-based (GP) symbolic regression (SR) model has been developed by Hu et al.237 to optimize the Slack model, and demonstrate the effectiveness of this optimized Slack model by comparing with different algorithms on the same dataset. The results indicate that the performance of the model exceeds that of the original Slack model, exhibiting impressive reliability. The improved Slack model in formulaic form is as follows:
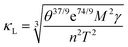 | (15) |
However, materials with high κ > 120 W m−1 K−1 cannot form a reasonable statistical distribution of data due to the small number of such materials and is eliminated as an abnormal value. Consequently, this can impact the accuracy of predictions made by the model for high κL materials. Recognizing this limitation, in 2021, Qin et al. reconstructed an optimized Slack model238 based on a dataset of 353 material samples without outlier handling, focusing merely on the calculated κ values. For this purpose, the study employed the simplest and most interpretable least squares method to refine the variable coefficient A in eqn (13) based on the 353 material samples. The newly generated factor A for the Slack model takes the following form:
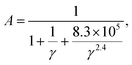 | (16) |
Using the dataset containing 353 materials, a comparison analysis was conducted between the calculated κ values and the predictions of the new Slack model. Compared to ref. 229, the new model exhibited superior performance. While the dataset used in this work has a greater deal of material samples collection and thus enabling a more objectively reflect on the true relationships between material properties, it is important to acknowledge that this model simply relies on the interpolation for fitting parameter A. Furthermore, the study did not employ a rigorous testing set separation, limiting its generalization capabilities.
Drawing from these conclusions, Qin et al. further employed deep learning models in 2022 to enhance the Slack model with a generalization ability test on a dataset of 3716 Slack model rough estimation samples included.239 Eight basic properties of materials were constructed as inputs of machine learning models, and the relationship between different material properties and thermal conductivity has been revealed. By applying deep learning combined with a semi-supervised technique, it can be demonstrated that the newly developed model has achieved superior performance, exceeding previous efforts with a prediction error lower than one order of magnitude, and the limited performance of the original model229 primarily stemmed from its inability to account for anharmonicity. However, the primary limitation lies in the absence of a clear Slack formula.
Although the ML method can be used to explore the formula representation of κ, the descriptors or parameters necessary for formula derivation are challenging to calculate through resource intensive DFT calculations quickly, in particular when dealing with thousands of new materials. Consequently, a more efficient and robust approach that can bypass this tedious formula derivation process is urgently required.
[2] Data-driven machine learning (ML) assisted properties prediction. Contributions in this field can be broadly categorized into two parts: one is the development and application of graph neural networks (GNN), and the other one mainly focuses on the development of novel machine learning potentials (MLPs). With the prosperity of GNNs, more and more MLPs based on this type of framework have been developed, showing excellent performance.
At present, GNN has been widely applied to multi-scale material properties predictions. According to Gong et al.,185 the main types of GNN optimization strategies includes (i) more geometric information coverage,213,240–242 (ii) attention mechanism optimization,243–245 and (iii) readout function optimization.244,246,247 The latter two strategies mainly concentrate on network modification. In this article, we will introduce recent GNN advancements from two perspectives: (i) feature extraction optimization by incorporating domain knowledge of materials, including the basic CGCNN architecture,171 M3GNet,213 and CHGNet,183 and (ii) network optimization, taking GATGNN as an example.
Dating back to the year 2018, a graph neural network architecture SchNet serving as a neural network potential (NNP) was proposed by K. T. Schütt et al..248 Xie et al.171 pioneered the crystal graph convolutional neural networks (CGCNN, shown in Fig. 11(a)) for crystal structure representation. Rosen et al.163 used CGCNN model to predict band gaps of metal–organic frameworks (MOFs) and the model was proved to be of high accuracy when comparing with DFT calculation results.
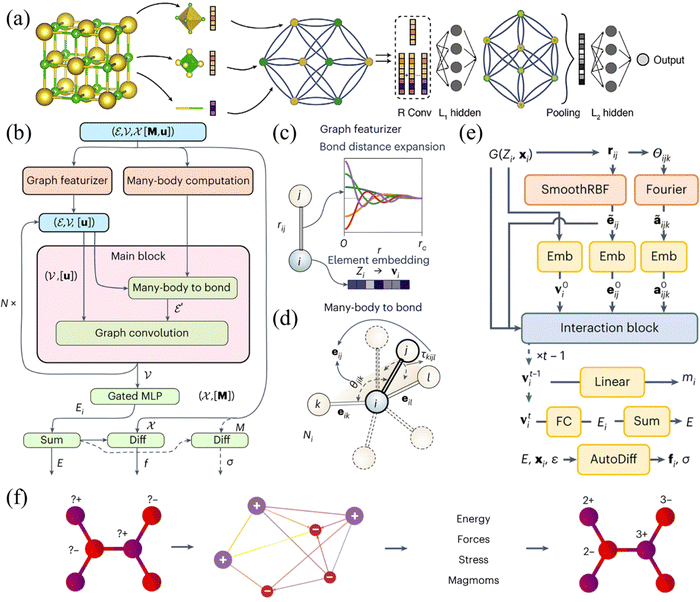 | ||
| Fig. 11 (a) The architecture of the basic CGCNN model.171 Copyright 2018 by American Physical Society (APS). The main steps include: (i) converting the crystal structure into a crystal graph, where nodes in the crystal graph represent the atoms, and the edges represent atomic connections; (ii) with the crystal graph as input, the predictions are output through a convolutional neural network (composed of convolutional, hidden, and pooling layers). (b) Total workflow of M3GNet.213 Copyright 2022 by Springer Nature. G = (ε, ν, χ, [M, u]) represents the initial materials graph, where eij ∈ ε denotes the bonds between atom i and j; νi ∈ V and xi ∈ χ represent atomic information and coordinates of i, respectively; M and u stand for the optional crystal lattice matrix and global state information. G then is passed to the (c) graph featurizer to encode the atomic numbers of elements and to expand atomic distance rij < rc into basis function, and later processed by (d) many-body computing module to transforms the many-body interactions into bond information eij, by using angles θjik and τkijl, and bond lengths rik, rij, and ril, to represent the full bonding environment Ni. (e) The architecture of CHGNet, consisting of basis expansions, embeddings, interaction blocks and output layers. Input graph (G(Zi, xi)) is a combination of atomic numbers Zi and Cartesian coordinates xi. Atomic distances rij and angles θijk can be extracted from G(Zi, xi). The former is expanded by the smooth radial Bessel function (SmoothRBF) into ẽij for both the atom and bond graph, and the latter is expanded by Fourier basis functions to create ãijk with trainable frequency. Zi, ẽij and ãijk are embedded into node features v0i, edge features e0ij and angle features a0ijk, then passed to interaction blocks. After going through (t − 1) convolution layers, magnetic moment mi is derived from node-wise features vt−1i through the linear layer; total energy E is the sum of the nonlinear projections (generate via fully connected (FC) layers) of final atom features vti; forces fi and stress (σ) will be obtained via auto-differentiation (AutoDiff) with three inputs: energy E, atomic Cartesian coordinates xi and lattice strain tensor (ε). (f) Total workflow of CHGNet.182 Copyright 2023 by Springer Nature. A periodic crystal structure with unknown atomic charges is passed to the network as the input, to predict the energy, force, stress and magmoms, with prediction results of the pretrained model, a charge-decorated structure is available. | ||
Many efforts focus on geometric feature descriptors construction. Some outstanding examples among them are ref. 213 and 241, which are dedicated to incorporating the angle/body information into a crystal graph. The integral architecture of the model is shown in Fig. 11(b), mainly consisting of three modules: crystal structure featurizer module, main block, and readout module used for outputting the energy, force and stress prediction results. Compared with traditional GNNs, the graph featurizer (Fig. 11(c)) encodes the atomic number of each element composition of the crystal, and converts the atomic distance rij (within the cutoff radius rc) to the basis function. The many-body computing module (Fig. 11(d)) then calculates the atomic interactions, like dihedrals τ and related perspectives θ for three-body calculation, which will soon be aggregated to bonds. Subsequently, bond, atom, and other optional state information will be iteratively updated through standard graph convolution layers, and the predicted results will be ultimately outputted.
Another typical example that contributes to the feature extraction process, by incorporating the charge information of the crystal structure, is the CHGNet proposed by Deng et al.,183 by means of pretraining the model to predict magnetic moment as intermediate variables. The framework and workflow of CHGNet are shown in Fig. 11(e) and (f) respectively. A periodic crystal structure with unknown atomic charges is provided as input to the network, then converted to a corresponding atom graph where nodes represent atoms and edges represent atomic connections. Three-body interaction can be calculated by an auxiliary bond graph, with edges expressing angle information between bonds, and nodes containing bonding information. Through a uniquely designed network structure (Fig. 11(e)), the pretrained model will make a prediction of energy, force, stress and magmoms, enabling further prediction of essential charge information from these intermediate variables. The interpretation of different variables used in the entire process can be found in the caption of Fig. 11.
In the field of network optimization, Coley et al.249 first introduced the concept of a global attention (GAT) mechanism into the traditional graph convolutional networks (GCN) for chemical reactivity prediction. This approach learns the sum of reaction probability between one atom and its neighboring atoms, with the GAT coefficient weighted by the influence strength. However, in the newly developed GATGNN framework,244 differing from previous work, global features are represented by both the significance of the atomic positions in the entire crystal graph using clustering algorithms, and the elemental fraction of the crystal. Furthermore, as illustrated in Fig. 12(a), the integration of state-of-the-art ResNet-style skip connections and differential group normalization (DGN) to the original GATGNN network243 has addressed the oversmoothing issue, which enables the accurate large-scale prediction by simply adding network layers without the need for tedious hyperparameter tuning.
 | ||
| Fig. 12 (a) The architecture of deep GATGNN and its application in (b) heat capacity prediction and (c) Γ-point phonon frequency prediction. The orange dashed ellipse is a guide for the eyes. (a) was adopted from ref. 243, copyright 2022 by American Chemical Society (ACS), (b) was adopted from ref. 249, copyright 2022 by American Chemical Society (ACS) and (c) was adopted from ref. 250, copyright 2024 by American Institute of Physics (AIP). | ||
Since then, this model has been widely applied in predicting material properties and has achieved extraordinary performance, becoming a powerful tool for high-throughput screening materials with outstanding properties. By training the deeperGATGNN model on a self-constructed database containing 3377 cubic crystal structures from four different space groups,250 the accuracy of the deeperGATGNN model was verified, and 22 materials with high heat capacity were successfully identified from a pool of 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 026 candidate materials from OQMD.166 Notably, one of these materials exhibited an abnormally high heat capacity, even exceeding the Dulong–Petit limit (Fig. 12(b)). Additionally, the deeperGATGNN model was demonstrated to be equally effective in predicting Γ-point lattice vibration frequencies when tested on two datasets comprised of a 15
026 candidate materials from OQMD.166 Notably, one of these materials exhibited an abnormally high heat capacity, even exceeding the Dulong–Petit limit (Fig. 12(b)). Additionally, the deeperGATGNN model was demonstrated to be equally effective in predicting Γ-point lattice vibration frequencies when tested on two datasets comprised of a 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mixed-structure and 35
000 mixed-structure and 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 552 rhombohedra samples (Fig. 12(c)).251
552 rhombohedra samples (Fig. 12(c)).251
Motivated by the drawbacks of the previously developed deeperGATGNN models, which are neither suitable for predicting complete phonon transport properties nor accessible to predict beyond the training set scope, a fundamentally new approach inspired by the MLP method has been applied to address the issue. Quoting spatial density neural network force fields (SDNNFFs) as an example,235 this novel approach aims to learn and predict DFT-level material properties by training on atomic force vectors. The generation process of SDNNFFs is illustrated in Fig. 13. Within this framework, only three hyperparameters are considered: cutoff radius (Rc), grid resolution (k), and the local density cutoff factor (D). With convergence testing, 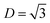 is finally chosen as the optimal value. Subsequently, a comparative analysis of prediction results has been calculated among different combinations of Rc and k. Results indicate that SDNNFF can more accurately approximate DFT-level predictions compared to previously developed methods, and the value of D also shows underlying scalability.
is finally chosen as the optimal value. Subsequently, a comparative analysis of prediction results has been calculated among different combinations of Rc and k. Results indicate that SDNNFF can more accurately approximate DFT-level predictions compared to previously developed methods, and the value of D also shows underlying scalability.
 | ||
| Fig. 13 Overall development process of SDNNFFs, including first principles calculation, descriptor construction, network training, and application in MD. The dark green circle is a guide for the eyes.235 Copyright 2020 by American Physical Society (APS). | ||
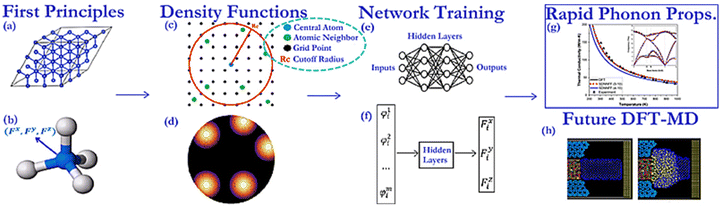
The developed MLPs can not only be applied to predict thermodynamic and transport properties but also be useful for fourth-order anharmonicity analysis.119,136,252 It is revealed in Fig. 14(a) from ref. 252 that the time consumption of MLPs, including a Deep Potential Smooth Edition (DPSE) neural network and the aforementioned potential SDNNFF, is lower than AIMD. Benefiting from its high-precision features, DPSE is employed to predict the phonon transport properties of two molten salts: LiF (50% Li) and FLiBe (66% LiF and 33% BeF2), along with MD simulation. Fig. 14(b) and (c) show that the DPSE predicted κ is very close to the experimental values, showing remarkable accuracy. Additionally, in ref. 136, the moment tensor potential (MTP) was utilized to predict the atomic forces in the layered material crystalline supercell of Bi2O2Se, and use the GPU_PBTE method to further reduce computational costs. Concurrently, the influence of the twist strategy on phonon transport properties has also been studied.
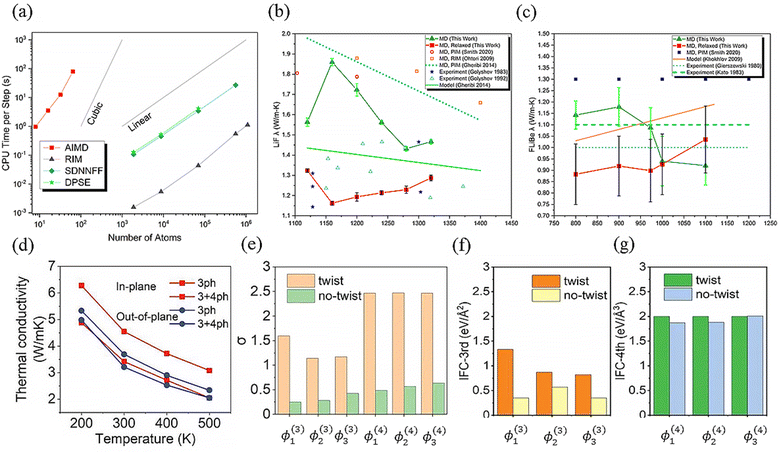 | ||
| Fig. 14 (a) Comparison of CPU time consumption using different methods, namely AIMD and MLP methods: rigid ion model (RIM), SDNNFF, and DPSE. The calculated κ of (b) LiF and (c) FLiBe changed with varying temperatures. (d) Temperature-dependent in-plane and out-of-plane κ of Bi2O2Se, considering third order and fourth order phonon scattering. Mean absolute value of (f) third-order interatomic force constants (IFCs) in the triplets: ϕSe1Se2Bi1ϕ(3)1, ϕSe1Bi1Bi1ϕ(3)2, and ϕSe1Bi2Bi2ϕ(3)3; (f) fourth-order IFCs in the quadruplets: ϕSe1Bi1Bi1ϕ(4)1, ϕSe1Se2Bi1Bi1ϕ(4)2, and ϕSe1Se2ϕ(4)3. (g) Standard deviation σ of the above triplets and quadruplets with and without twisting. (a)–(c) were adopted from ref. 252, copyright 2021 by American Chemical Society (ACS) and (d)–(g) from ref. 136, copyright 2022 by Wiley. | ||
4. Summary and outlook
In conclusion, this review provides a comprehensive overview of current prediction methods for phonon transport properties and emphasized their significance in materials physics and chemistry. This article summarized traditional simulation methods such as DFT+BTE and empirical MD simulations, as well as the novel data-driven ML algorithms. The breakthroughs in ML prediction method were highlighted, and their working principles, advantages, disadvantages, and recent applications were detailed. We also emphasized recent advancements in phonon property prediction, including methodological innovations and their application across different material systems. Finally, we aim to summarize the remaining challenges faced by different prediction methods in practical applications, and identify areas that need further exploration in the future.4.1 DFT+BTE
For DFT+BTE calculations, two primary challenges emerge. Firstly, the calculation accuracy remains a concern. Currently, calculations that predominantly consider the three-phonon scattering mechanism may lack precision, due to the exclusion of other phonon transport mechanisms that may impact anharmonicity. These mechanisms include higher-order phonon scattering, and a two-channel scattering mechanism. For instance, the above-mentioned residual analysis method93 could serve as a useful tool to evaluate the effect of four-phonon scattering on anharmonicity, which could help save excessive computational resources. In addition, for materials with ultra-low κ, it is necessary to consider both the contributions of quasi-particle propagation (non-diffusive transport) of phonons and quasi-wave tunneling (diffusive transport) to κ. Moreover, considering only phonon interactions is insufficient to fully capture the complexities of thermal transport. There may be a need to explore more incoherent physical mechanisms, i.e. quantum effects like the quantum confinement effect,253–255 as well as the interactions between phonons and other particles that have not been fully investigated, such as electron–phonon coupling, spin–phonon coupling,256 phonon–spin–orbit coupling, piezo-phonon coupling257 and phonon–isotope scattering.258 Moreover, spin caloritronics102,103 has also provided a novel perspective for interpreting the underlying thermal transport mechanism99–101 by introducing the previously ignored heat–spin–charge interactions. Establishing a standardized framework for quantifying the contribution of different mechanisms and revealing the phonon anharmonicity origin in different material systems will become major challenges, like the sinusoidal phonon dispersion model proposed by Pei et al.,259,260 although it underestimates the theoretical limit of κL, it still shows a more effective estimation for thermoelectric materials.Secondly, the computational speed remains a bottleneck. The existing DFT+BTE computing frameworks, despite the remarkable accuracy, are hampered by the huge computing resources they demand. Potential solutions lie in two directions. On the one hand, improvements can be made in the existing DFT calculation framework. Prior work261 has put forward a strategy to determine the cutoff radius by analyzing the easily accessible second-order harmonic force constant, thereby eliminating the need for tedious and time-consuming third-order force constant cutoff radius testing. On the other hand, combining DFT+BTE with ML methods has the potential to reduce computational costs while enabling high-throughput screening of materials with desirable phonon transport properties.262,263
4.2 Empirical MD simulations
Despite the natural incorporation of high-order phonon interactions and successful applications in predicting phonon transport properties across various systems, several challenges remain to be addressed. Firstly, expanding the application range is crucial, especially in fully exploiting their ability to simulate real experimental conditions and ensure accurate predictions of phonon transport properties in extreme situations. Secondly, the neglect of multi-carrier interactions and quantum effects in the spectral thermal transport properties43 is a noteworthy issue. Taking the metal–non-metal interface as a typical example, MD methods cannot take into account the influence of electron–phonon coupling on interfacial phonon transport. A potential solution is integrating MD with other methods, such as two-temperature models, to fully capture the complexity of multi-carrier interactions.264 Meanwhile, despite the computational efficiency achieved by the empirical potential, poor accuracy and transferability issues arise subsequently. Therefore, there is an urgent need for more universal and accurate potentials to compensate for this deficiency, with MLPs emerging as promising solutions to address these challenges.4.3 Data-driven machine learning (ML) methods
Although data-driven ML methods have shown great potential in balancing computational efficiency with accurate phonon transport properties prediction, several challenges still limit their further widespread application.[1] Sample size and multi-task learning. As ML models and MLPs require a large amount of DFT-level accuracy data for training and predicting certain phonon transport properties, like thermal conductivity, they still face limitations in sample size. Solutions mainly lie in the establishment of databases and the development of models. One approach is to establish public databases that encompass comprehensive computational properties, which can provide valuable resources for training and validating ML models.
Another approach is model-based solution. Some potentials like DeePMD181,182 and neuroevolution potential (NEP)205,206 can now achieve high-throughput calculations by parallelizing graphics processing units. Meanwhile, pre-trained models with easily accessible properties for transfer learning can be utilized to predict target properties that would otherwise produce high DFT computational costs. The approach involves leveraging a pre-trained model and fine-tuning it with a limited amount of target data that are resource-consuming. Successful cases are M3GNet213 and CHGNet183 that have been elucidated previously. Recently, the transform mechanism has also been introduced in MLP models like TorchMD-Net 2.0218 and DeepMoleNet207 to improve their predicting performances.
Moreover, recent MLP research studies have paid more attention to the development of on-the-fly force field methods, aiming at solving the difficulties in constructing training sets for MLPs, which typically require a vast amount of DFT calculation data, as well as the tedious data selection and parameter optimization processes. For example, ref. 265 and 266 proposed a strategy to judge whether DFT calculation is necessary during the dataset preparation, by utilizing statistical methods such as the Bayesian inference to estimate the uncertainty of easily accessible energy, forces, and/or the stress tensor. If the uncertainty falls below a certain threshold, then the computed tensor will be used to replace the expensive DFT calculations to integrate the equations of motion. Otherwise, DFT calculations are performed. Additionally, ref. 267 also provides an adaptive Bayesian inference method for data augmentation using the Gaussian process (GP) regression model within an active learning framework.
[2] Standardized characterization of atomic structure. Existing characterization schemes are mainly based on domain knowledge, and the introduction of the graph neural network (GNN) has provided a promising plan for solving the general characterization problem of atomic structure. Nevertheless, the construction of node and edge features in GNN still requires careful consideration. In this regard, the Atomistic Line Graph Neural Network (ALIGNN)241 offers an elegant solution by incorporating bond length and bond angle properties, while the GATGNN model243,244 highlights the significance of incorporating the GAT mechanism.
[3] Generalization capabilities and limitations in the application scope. Current machine learning research mainly depends on intrinsic interpolation, making it challenging to extrapolate and predict material properties beyond the training scope, especially for complex systems like interfaces, transition zones, superlattices, and composites. Therefore, the designed model should ideally possess a generative nature, rather than an interpolative one, to better support inverse design.268 This requires the model to grasp hidden laws within the data and to generate ideal structures with specific properties. Additionally, there is a growing interest in discovering “materials outliers” or generating “first materials” with specific properties through data-driven approaches rather than relying solely on prior intuition. This enables the creation of entirely new materials derived from fundamental building blocks. Ongoing efforts have been made to explore and advance these directions. For instance, a newly published study162,269 has successfully designed an efficient crystal structure generation model based on generative adversarial network (GAN). The GNoME270 model developed by the Google DeepMind also propose a GNN framework as a stable structure generation tool. With an active learning method to augment the data, over 380![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures were generated, far beyond the existing knowledge scope, despite the unproved stability of these structures.
000 structures were generated, far beyond the existing knowledge scope, despite the unproved stability of these structures.
Moreover, numerous studies combine multiple methods to achieve the final results. In ref. 72, 95, 123, 130 and 232, ML models were developed based on the datasets generated by various simulation methods. This approach has become a prevalent trend, making it possible to ensure the accuracy of results and complement the deficiencies of each method. With AI as a powerful tool, we anticipate more exciting discoveries in the future.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Key R&D Program of China (2023YFB2408100), the National Natural Science Foundation of China (Grant No. 52006057), the Fundamental Research Funds for the Central Universities (Grant No. 531119200237), the State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body at Hunan University (Grant No. 52175013), the Natural Science Foundation of Chongqing, China (No. CSTB2022NSCQ-MSX0332), and the Outstanding Youth Project (23B0024) of Hunan Provincial Department of Education.References
- M. Und and T. V. K. Born, Uber Schwingungen In Raumgittern – in PHYSIKALISCHE ZEITSCHRIFT 15 APRIL, 1912, See Description, 1912.
- J. M. Ziman, Electrons and Phonons: The Theory of Transport Phenomena in Solids, OUP, Oxford, 2001 Search PubMed.
- C. Kittel, Introduction to Solid State Physics, John Wiley & Sons, Inc, 2005 Search PubMed.
- F. Giustino, Rev. Mod. Phys., 2017, 89, 015003 CrossRef.
- W. L. McMillan, Phys. Rev., 1968, 167, 331–344 CrossRef CAS.
- A. Lanzara, P. V. Bogdanov, X. J. Zhou, S. A. Kellar, D. L. Feng, E. D. Lu, T. Yoshida, H. Eisaki, A. Fujimori, K. Kishio, J.-I. Shimoyama, T. Noda, S. Uchida, Z. Hussain and Z.-X. Shen, Nature, 2001, 412, 510–514 CrossRef CAS PubMed.
- J. R. Schrieffer, Theory of Superconductivity, CRC Press, Boca Raton, 2019 Search PubMed.
- P. B. Allen and R. C. Dynes, Phys. Rev. B: Solid State, 1975, 12, 905–922 CrossRef CAS.
- C.-W. Chen, J. Choe and E. Morosan, Rep. Prog. Phys., 2016, 79, 084505 CrossRef PubMed.
- H. Luo, Q. Gao, H. Liu, Y. Gu, D. Wu, C. Yi, J. Jia, S. Wu, X. Luo, Y. Xu, L. Zhao, Q. Wang, H. Mao, G. Liu, Z. Zhu, Y. Shi, K. Jiang, J. Hu, Z. Xu and X. J. Zhou, Nat. Commun., 2022, 13, 273 CrossRef CAS.
- N. Nhat Quyen, W.-Y. Tzeng, C.-E. Hsu, I.-A. Lin, W.-H. Chen, H.-H. Jia, S.-C. Wang, C.-E. Liu, Y.-S. Chen, W.-L. Chen, T.-L. Chou, I.-T. Wang, C.-N. Kuo, C.-L. Lin, C.-T. Wu, P.-H. Lin, S.-C. Weng, C.-M. Cheng, C.-Y. Kuo, C.-M. Tu, M.-W. Chu, Y.-M. Chang, C. S. Lue, H.-C. Hsueh and C.-W. Luo, Nat. Commun., 2024, 15, 2386 CrossRef CAS PubMed.
- S.-H. Lee, Y. C. Park, J. Chae, G. Kim, H. J. Kim, B. K. Choi, I. H. Lee, Y. J. Chang, S.-H. Chun, M. Jung, J. Seo and S. Lee, J. Mater. Chem. C, 2022, 10, 16657–16665 RSC.
- U. Vool, A. Hamo, G. Varnavides, Y. Wang, T. X. Zhou, N. Kumar, Y. Dovzhenko, Z. Qiu, C. A. C. Garcia, A. T. Pierce, J. Gooth, P. Anikeeva, C. Felser, P. Narang and A. Yacoby, Nat. Phys., 2021, 17, 1216–1220 Search PubMed.
- J. Coulter, R. Sundararaman and P. Narang, Phys. Rev. B, 2018, 98, 115130 CrossRef CAS.
- A. Levchenko and J. Schmalian, Ann. Phys., 2020, 419, 168218 CAS.
- V. Sampath, N. D’Souza, D. Bhattacharya, G. M. Atkinson, S. Bandyopadhyay and J. Atulasimha, Nano Lett., 2016, 16, 5681–5687 CrossRef CAS.
- A. K. Biswas, S. Bandyopadhyay and J. Atulasimha, Appl. Phys. Lett., 2013, 103, 232401 CrossRef.
- P. G. Gowtham, D. Labanowski and S. Salahuddin, Phys. Rev. B, 2016, 94, 014436 CrossRef.
- V. G. Baryakhtar and A. G. Danilevich, Low Temp. Phys., 2017, 43, 351–358 CrossRef CAS.
- C. Berk, M. Jaris, W. Yang, S. Dhuey, S. Cabrini and H. Schmidt, Nat. Commun., 2019, 10, 2652 CrossRef.
- Z. Shen, G.-T. Xu, M. Zhang, Y.-L. Zhang, Y. Wang, C.-Z. Chai, C.-L. Zou, G.-C. Guo and C.-H. Dong, Phys. Rev. Lett., 2022, 129, 243601 CrossRef CAS PubMed.
- Y. Lv, C. Yin, C. Zhang, X. Wang, Z.-G. Yu and M. Xiao, Nat. Commun., 2021, 12, 2192 CrossRef CAS.
- H.-Y. Chen, D. Sangalli and M. Bernardi, Phys. Rev. Lett., 2020, 125, 107401 CrossRef CAS PubMed.
- G. Antonius and S. G. Louie, Phys. Rev. B, 2022, 105, 085111 CrossRef CAS.
- T. R. Hart, R. L. Aggarwal and B. Lax, Phys. Rev. B: Solid State, 1970, 1, 638–642 CrossRef.
- Y. J. Chabal, Surf. Sci. Rep., 1988, 8, 211–357 CrossRef CAS.
- A. A. Maradudin and A. E. Fein, Phys. Rev., 1962, 128, 2589–2608 CrossRef CAS.
- Z.-K. Liu, Y. Shen, H.-L. Li and B.-Y. Cao, Rare Met., 2024, 43, 389–394 CrossRef CAS.
- E. Burkel, Rep. Prog. Phys., 2000, 63, 171 CrossRef CAS.
- H.-T. Niu, Y. Zhang, G. Xiao, X.-H. He and Y.-G. Yao, Rare Met., 2023, 42, 1283–1293 CrossRef CAS.
- L.-F. Yu, J.-Y. Xu, C. Shen, E. Zhou, J. Wu, H.-B. Zhang, X. Zheng, H.-M. Wang and G.-Z. Qin, Rare Met., 2023, 42, 210–221 CrossRef CAS.
- P.-D. Tao, S.-G. Wang, L. Chen, J.-F. Ying, L. Lv, L.-W. Sun, W.-B. Chu, K. Nishimura, L. Fu, Y.-Z. Wang, J.-H. Yu, N. Jiang, W. Dai, Y.-K. Lv, C.-T. Lin and Q.-W. Yan, Rare Met., 2023, 42, 3662–3672 CrossRef CAS.
- T. Sheng, X.-Z. Liu, L.-X. Qian, B. Xu and Y.-Y. Zhang, Rare Met., 2022, 41, 1375–1379 CrossRef CAS.
- Y. K. Koh and D. G. Cahill, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 075207 CrossRef.
- A. J. H. McGaughey and J. M. Larkin, Annu. Rev. Heat Transfer, 2014, 17, 49–87 CrossRef.
- H. Bao, J. Chen, X. Gu and B. Cao, ES Energy Environ., 2018, 1, 16–55 Search PubMed.
- L. Paulatto, F. Mauri and M. Lazzeri, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 214303 CrossRef.
- S. Li, Y. Liu, D. Chen, Y. Jiang, Z. Nie and F. Pan, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1558 CAS.
- N. Fedik, R. Zubatyuk, M. Kulichenko, N. Lubbers, J. S. Smith, B. Nebgen, R. Messerly, Y. W. Li, A. I. Boldyrev, K. Barros, O. Isayev and S. Tretiak, Nat. Rev. Chem., 2022, 6, 653–672 CrossRef CAS PubMed.
- X. Qian and R. Yang, Mater. Sci. Eng., R, 2021, 146, 100642 CrossRef.
- B. Wei, Q. Sun, C. Li and J. Hong, Sci. China: Phys., Mech. Astron., 2021, 64, 117001 Search PubMed.
- A. J. H. McGaughey and J. M. Larkin, Annu. Rev. Heat Transfer, 2014, 17, 49–87 CrossRef.
- Y.-X. Xu, H.-Z. Fan and Y.-G. Zhou, Rare Met., 2023, 42, 3914–3944 CrossRef CAS.
- G. P. Srivastava, Rep. Prog. Phys., 2015, 78, 026501 CrossRef CAS PubMed.
- T. P. Senftle, S. Hong, M. M. Islam, S. B. Kylasa, Y. Zheng, Y. K. Shin, C. Junkermeier, R. Engel-Herbert, M. J. Janik, H. M. Aktulga, T. Verstraelen, A. Grama and A. C. T. van Duin, npj Comput. Mater., 2016, 2, 1–14 CrossRef.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555 Search PubMed.
- J. P. Ewen, D. M. Heyes and D. Dini, Friction, 2018, 6, 349–386 Search PubMed.
- H. Kim, G. Park, S. Park and W. Kim, ACS Nano, 2021, 15, 2182–2196 Search PubMed.
- I. Tamm, Z. Physik, 1930, 62, 545–568 Search PubMed.
- J. Frenkel, Nature, 1933, 131, 860 Search PubMed.
- A. M. Bratkovsky, V. G. Vaks and A. V. Trefilov, Phys. Lett. A, 1984, 103, 75–78 CrossRef.
- M. I. Katsnelson and A. V. Trefilov, AIP Conf. Proc., 2004, 708, 727–730 CrossRef CAS.
- Y. Chen, K. M. Ho and B. N. Harmon, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 283–288 CrossRef CAS.
- G. P. Srivastava, The Physics of Phonons, CRC Press, Boca Raton, 2nd edn, 2022 Search PubMed.
- J. M. Ziman, Electrons and Phonons: The Theory of Transport Phenomena in Solids, Oxford University Press, 2001 Search PubMed.
- L. Pizzagalli, J. Godet, J. Guénolé, S. Brochard, E. Holmstrom, K. Nordlund and T. Albaret, J. Phys.: Condens. Matter, 2013, 25, 055801 CrossRef CAS PubMed.
- A. Togo, J. Phys. Soc. Jpn., 2023, 92, 012001 CrossRef.
- H. Bao, J. Chen, X. Gu and B. Cao, ES Energy Environ., 2018, 1, 16–55 Search PubMed.
- C. G. Sammis, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1973, 29, 582–583 CrossRef.
- R. M. Martin, Electronic Structure: Basic Theory and Practical Methods, Cambridge University Press, Cambridge, 2nd edn, 2020 Search PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- D. A. Broido, M. Malorny, G. Birner, N. Mingo and D. A. Stewart, Appl. Phys. Lett., 2007, 91, 231922 CrossRef.
- W. Li, J. Carrete, N. A. Katcho and N. Mingo, Comput. Phys. Commun., 2014, 185, 1747–1758 CrossRef CAS.
- J. Carrete, B. Vermeersch, A. Katre, A. Van Roekeghem, T. Wang, G. K. H. Madsen and N. Mingo, Comput. Phys. Commun., 2017, 220, 351–362 CrossRef CAS.
- K. Mizokami, A. Togo and I. Tanaka, Phys. Rev. B, 2018, 97, 224306 CrossRef CAS.
- J. J. Plata, P. Nath, D. Usanmaz, J. Carrete, C. Toher, M. de Jong, M. Asta, M. Fornari, M. B. Nardelli and S. Curtarolo, npj Comput. Mater., 2017, 3, 1–10 CrossRef CAS.
- C.-D. Zhou, B. Liang, W.-J. Huang, J.-G. Noudem, X.-J. Tan and J. Jiang, Rare Met., 2023, 42, 2825–2839 CrossRef CAS.
- H. Schober, EPJ Web Conf., 2012, 22, 00012 CrossRef CAS.
- Z. Yang, K. Yuan, J. Meng, X. Zhang, D. Tang and M. Hu, Nanotechnology, 2021, 32, 025709 CrossRef CAS.
- Y. Sun, Y. Zhou, R. Gurunathan, J.-Y. Zhang, M. Hu, W. Liu, B. Xu and G. J. Snyder, J. Mater. Chem. C, 2021, 9, 8506–8514 RSC.
- Z. Chang, J. Ma, K. Yuan, J. Zheng, B. Wei, M. Al-Fahdi, Y. Gao, X. Zhang, H. Shao, M. Hu and D. Tang, Front. Mech. Eng., 2022, 8, 876655 CrossRef.
- G. Qin, X. Zhang, S.-Y. Yue, Z. Qin, H. Wang, Y. Han and M. Hu, Phys. Rev. B, 2016, 94, 165445 CrossRef.
- F. Q. Wang, M. Hu and Q. Wang, J. Mater. Chem. A, 2019, 7, 6259–6266 RSC.
- S.-Y. Yue, G. Qin, X. Zhang, X. Sheng, G. Su and M. Hu, Phys. Rev. B, 2017, 95, 085207 CrossRef.
- J.-Y. Yang, L. Cheng and M. Hu, Appl. Phys. Lett., 2017, 111, 242101 CrossRef.
- M. Al-Fahdi, X. Zhang and M. Hu, J. Mater. Sci., 2021, 56, 18534–18549 CrossRef CAS.
- G. Qin, Z. Qin, H. Wang and M. Hu, Nano Energy, 2018, 50, 425–430 CrossRef CAS.
- G. Qin, J. Xu, H. Wang, Z. Qin and M. Hu, J. Phys. Chem. Lett., 2023, 14, 139–147 CrossRef CAS PubMed.
- H. Wang, L. Yu, J. Xu, D. Wei, G. Qin, Y. Yao and M. Hu, Int. J. Therm. Sci., 2021, 162, 106772 CrossRef CAS.
- G. Qin, J. Lin, H. Wang, J. Hu, Z. Qin and M. Hu, J. Mater. Chem. C, 2022, 10, 12080–12090 RSC.
- Y. Pan, Y. Tao, G. Qin, Y. Fedoryshyn, S. N. Raja, M. Hu, C. L. Degen and D. Poulikakos, Nano Lett., 2016, 16, 6364–6370 CrossRef CAS.
- Z. Yang, K. Yuan, N. Li, X. Zhang and M. Hu, ACS Appl. Energy Mater., 2022, 5, 8781–8790 CrossRef CAS.
- Y. Gong, M. Hu, N. Harris, Z. Yang, T. Xie, A. Teklu, N. Kuthirummal, J. Koenemann, X. Xu, S.-W. Cheong, W. McLoud and C. Gong, npj 2D Mater. Appl., 2022, 6, 1–7 CrossRef.
- Q. Tian, P. Li, J. Wei, Z. Xing, G. Qin and Z. Qin, Phys. Rev. B, 2023, 108, 115130 CrossRef CAS.
- E. Zhou, D. Wei, J. Wu, G. Qin and M. Hu, Phys. Chem. Chem. Phys., 2022, 24, 17479–17484 RSC.
- G. Qin and M. Hu, Small, 2018, 14, 1702465 CrossRef.
- J. Li, W. Hu and J. Yang, J. Am. Chem. Soc., 2022, 144, 4448–4456 CrossRef CAS.
- L. Guarneri, S. Jakobs, A. von Hoegen, S. Maier, M. Xu, M. Zhu, S. Wahl, C. Teichrib, Y. Zhou, O. Cojocaru-Mirédin, M. Raghuwanshi, C.-F. Schön, M. Drögeler, C. Stampfer, R. P. S. M. Lobo, A. Piarristeguy, A. Pradel, J.-Y. Raty and M. Wuttig, Adv. Mater., 2021, 33, 2102356 CrossRef CAS PubMed.
- T. Feng, L. Lindsay and X. Ruan, Phys. Rev. B, 2017, 96, 161201 CrossRef.
- J. S. Kang, M. Li, H. Wu, H. Nguyen and Y. Hu, Science, 2018, 361, 575–578 CrossRef CAS PubMed.
- S. Li, Q. Zheng, Y. Lv, X. Liu, X. Wang, P. Y. Huang, D. G. Cahill and B. Lv, Science, 2018, 361, 579–581 CrossRef CAS.
- F. Tian, B. Song, X. Chen, N. K. Ravichandran, Y. Lv, K. Chen, S. Sullivan, J. Kim, Y. Zhou, T.-H. Liu, M. Goni, Z. Ding, J. Sun, G. A. G. Udalamatta Gamage, H. Sun, H. Ziyaee, S. Huyan, L. Deng, J. Zhou, A. J. Schmidt, S. Chen, C.-W. Chu, P. Y. Huang, D. Broido, L. Shi, G. Chen and Z. Ren, Science, 2018, 361, 582–585 CrossRef CAS.
- S.-Y. Yue, X. Zhang, G. Qin, S. R. Phillpot and M. Hu, Phys. Rev. B, 2017, 95, 195203 CrossRef.
- S. Weisberg, Applied Linear Regression, John Wiley & Sons, Ltd, 2005, pp. 167–193 Search PubMed.
- K. Yuan, X. Zhang, Z. Chang, D. Tang and M. Hu, J. Mater. Chem. C, 2022, 10, 15822–15832 RSC.
- Z. Chang, J. Zheng, Y. Jing, W. Li, K. Yuan, J. Ma, Y. Gao, X. Zhang, M. Hu, J. Yang and D. Tang, Phys. Chem. Chem. Phys., 2022, 24, 20891–20900 RSC.
- A. Negi, A. Rodriguez, X. Zhang, A. H. Comstock, C. Yang, D. Sun, X. Jiang, D. Kumah, M. Hu and J. Liu, Adv. Sci., 2023, 10, 2301273 CrossRef CAS.
- Y. Zhu, Y. Xia, Y. Wang, Y. Sheng, J. Yang, C. Fu, A. Li, T. Zhu, J. Luo, C. Wolverton, G. J. Snyder, J. Liu and W. Zhang, Research, 2020, 2020, 4589786 CAS.
- G. Yang, L. Sang, C. Zhang, N. Ye, A. Hamilton, M. S. Fuhrer and X. Wang, Nat. Rev. Phys., 2023, 5, 466–482 CrossRef CAS.
- H. Adachi, K. Uchida, E. Saitoh and S. Maekawa, Rep. Prog. Phys., 2013, 76, 036501 CrossRef.
- K. Uchida, Proc. Jpn. Acad., Ser. B, 2021, 97, 69–88 CrossRef CAS.
- H. Yu, S. D. Brechet and J.-P. Ansermet, Phys. Lett. A, 2017, 381, 825–837 CrossRef CAS.
- A. Brataas, B. van Wees, O. Klein, G. de Loubens and M. Viret, Phys. Rep., 2020, 885, 1–27 CrossRef CAS.
- Y. Cao, G. Xing, H. Lin, N. Zhang, H. Zheng and K. Wang, iScience, 2020, 23, 101614 CrossRef CAS.
- L. J. Sham and J. M. Ziman, in Solid State Physics, ed. F. Seitz and D. Turnbull, Academic Press, 1963, vol. 15, pp. 221–298 Search PubMed.
- E. Lüscher, Phys. unserer Zeit, 1978, 9, 33 CrossRef.
- H. Y. Fan, Phys. Rev., 1951, 82, 900–905 CrossRef CAS.
- Y. P. Varshni, Physica, 1967, 34, 149–154 CrossRef CAS.
- A. Göbel, T. Ruf, M. Cardona, C. T. Lin, J. Wrzesinski, M. Steube, K. Reimann, J.-C. Merle and M. Joucla, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 15183–15190 CrossRef.
- P. B. Allen and J. P. Nery, Phys. Rev. B, 2017, 95, 035211 CrossRef.
- V. D’Innocenzo, G. Grancini, M. J. P. Alcocer, A. R. S. Kandada, S. D. Stranks, M. M. Lee, G. Lanzani, H. J. Snaith and A. Petrozza, Nat. Commun., 2014, 5, 3586 CrossRef.
- J.-Y. Yang, G. Qin and M. Hu, Appl. Phys. Lett., 2016, 109, 242103 CrossRef.
- L. Cheng, Q.-B. Yan and M. Hu, Phys. Chem. Chem. Phys., 2017, 19, 21714–21721 RSC.
- S.-Y. Yue, L. Cheng, B. Liao and M. Hu, Phys. Chem. Chem. Phys., 2018, 20, 27125–27130 RSC.
- J.-Y. Yang and M. Hu, Phys. Chem. Chem. Phys., 2018, 20, 24222–24226 RSC.
- J.-Y. Yang, W. Zhang, C. Xu, J. Liu, L. Liu and M. Hu, Int. J. Heat Mass Transfer, 2020, 152, 119481 CrossRef CAS.
- D. Wei, E. Zhou, X. Zheng, H. Wang, C. Shen, H. Zhang, Z. Qin and G. Qin, npj Comput. Mater., 2022, 8, 1–7 CrossRef.
- G. Qin, Z. Qin, S.-Y. Yue, Q.-B. Yan and M. Hu, Nanoscale, 2017, 9, 7227–7234 RSC.
- Y. Luo, X. Yang, T. Feng, J. Wang and X. Ruan, Nat. Commun., 2020, 11, 2554 CrossRef CAS PubMed.
- Z. Zeng, C. Zhang, Y. Xia, Z. Fan, C. Wolverton and Y. Chen, Phys. Rev. B, 2021, 103, 224307 CrossRef CAS.
- B. Wu, Y. Zhou and M. Hu, J. Phys. Chem. Lett., 2018, 9, 5704–5709 CrossRef CAS PubMed.
- Y. Xia, V. Ozoliņš and C. Wolverton, Phys. Rev. Lett., 2020, 125, 085901 CrossRef CAS PubMed.
- J. Sun, C. Zhang, Z. Yang, Y. Shen, M. Hu and Q. Wang, ACS Appl. Mater. Interfaces, 2022, 14, 11493–11499 CrossRef CAS.
- D. Frenkel and B. Smit, Understanding molecular simulation: from algorithms to applications, 2nd edn, 1996, vol. 50 Search PubMed.
- J. Tersoff, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 5566–5568 CrossRef PubMed.
- F. H. Stillinger and T. A. Weber, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 5262–5271 CrossRef CAS PubMed.
- M. S. Daw and M. I. Baskes, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 6443–6453 CrossRef CAS.
- Y. Zhou, X. Zhang and M. Hu, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 195204 CrossRef.
- Y. Zhou and M. Hu, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 195205 CrossRef.
- X. Zhang, H. Xie, M. Hu, H. Bao, S. Yue, G. Qin and G. Su, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 054310 CrossRef.
- M. Hu, Y. Jing and X. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 155408 CrossRef.
- E. Lee, T. Zhang, M. Hu and T. Luo, Phys. Chem. Chem. Phys., 2016, 18, 16794–16801 RSC.
- Y. Zhou, X. Zhang and M. Hu, Nano Lett., 2017, 17, 1269–1276 CrossRef CAS PubMed.
- Y. Gao, Y. Zhou and M. Hu, J. Mater. Chem. A, 2018, 6, 18533–18542 RSC.
- Y. Jing, M. Hu, Y. Gao, L. Guo and Y. Sun, Int. J. Heat Mass Transfer, 2015, 85, 880–889 CrossRef CAS.
- J. Sun, M. Hu, C. Zhang, L. Bai, C. Zhang and Q. Wang, Adv. Funct. Mater., 2022, 32, 2209000 CrossRef CAS.
- W.-J. Ren, S. Lu, C.-Q. Yu, J. He and J. Chen, Rare Met., 2023, 42, 2679–2687 CrossRef CAS.
- M. Hu, S. Shenogin and P. Keblinski, Appl. Phys. Lett., 2007, 91, 241910 CrossRef.
- M. Hu, P. Keblinski and P. K. Schelling, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 104305 CrossRef.
- M. Hu, D. Poulikakos, C. P. Grigoropoulos and H. Pan, J. Chem. Phys., 2010, 132, 164504 CrossRef PubMed.
- Y. Zhou and M. Hu, Nano Lett., 2016, 16, 6178–6187 CrossRef CAS.
- Y. Gao, H. Fan, Y. Zhou and M. Hu, Adv. Funct. Mater., 2023, 33, 2214501 CrossRef CAS.
- Y. Sun, Y. Zhou, J. Han, M. Hu, B. Xu and W. Liu, J. Appl. Phys., 2020, 127, 045106 CrossRef CAS.
- L. Verlet, Phys. Rev., 1967, 159, 98–103 CrossRef CAS.
- C. Lorenz and N. L. Doltsinis, in Handbook of Computational Chemistry, ed. J. Leszczynski, Springer Netherlands, Dordrecht, 2012, pp. 195–238 Search PubMed.
- R. Car and M. Parrinello, Phys. Rev. Lett., 1985, 55, 2471–2474 CrossRef CAS PubMed.
- F. Gygi, E. W. Draeger, M. Schulz, B. R. de Supinski, J. A. Gunnels, V. Austel, J. C. Sexton, F. Franchetti, S. Kral, C. W. Ueberhuber and J. Lorenz, Proceedings of the 2006 ACM/IEEE conference on Supercomputing, Association for Computing Machinery, New York, NY, USA, 2006, p. 45-es Search PubMed.
- K. He, N. Kumar, L. Zhao, Z. Wang, K. F. Mak, H. Zhao and J. Shan, Phys. Rev. Lett., 2014, 113, 026803 CrossRef CAS PubMed.
- Y. Hasegawa, J.-I. Iwata, M. Tsuji, D. Takahashi, A. Oshiyama, K. Minami, T. Boku, F. Shoji, A. Uno, M. Kurokawa, H. Inoue, I. Miyoshi and M. Yokokawa, Proceedings of 2011 International Conference for High Performance Computing, Networking, Storage and Analysis, Association for Computing Machinery, New York, NY, USA, 2011, pp. 1–11 Search PubMed.
- S. Das, P. Motamarri, V. Gavini, B. Turcksin, Y. W. Li and B. Leback, Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, Association for Computing Machinery, New York, NY, USA, 2019, pp. 1–11 Search PubMed.
- A. Nakata, J. Baker, S. Mujahed, J. T. L. Poulton, S. Arapan, J. Lin, Z. Raza, S. Yadav, L. Truflandier, T. Miyazaki and D. R. Bowler, J. Chem. Phys., 2020, 152, 164112 CrossRef CAS.
- W. Jia, H. Wang, M. Chen, D. Lu, L. Lin, R. Car, E. Weinan and L. Zhang, SC20: International Conference for High Performance Computing, Networking, Storage and Analysis, 2020, pp. 1–14 Search PubMed.
- Y. Zhou, J.-Y. Yang, L. Cheng and M. Hu, Phys. Rev. B, 2018, 97, 085304 CrossRef CAS.
- S.-Y. Yue, X. Zhang, S. Stackhouse, G. Qin, E. Di Napoli and M. Hu, Phys. Rev. B, 2016, 94, 075149 CrossRef.
- S.-Y. Yue, X. Zhang, G. Qin, J. Yang and M. Hu, Phys. Rev. B, 2016, 94, 115427 CrossRef.
- L. Hu, L. Zhang, M. Hu, J.-S. Wang, B. Li and P. Keblinski, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 235427 CrossRef.
- M. Hu and D. Poulikakos, Nano Lett., 2012, 12, 5487–5494 CrossRef CAS.
- J. Wu, E. Zhou, A. Huang, H. Zhang, M. Hu and G. Qin, Nat. Commun., 2024, 15, 2540 CrossRef CAS.
- Z. Liu, X. Yang, B. Zhang and W. Li, ACS Appl. Mater. Interfaces, 2021, 13, 53409–53415 CrossRef CAS.
- Z. Tong, Y. Zhang, A. Pecchia, C. Yam, L. Zhou, T. Dumitrică and T. Frauenheim, Adv. Sci., 2023, 10, 2205934 CrossRef CAS PubMed.
- D. Tristant, A. Cupo, X. Ling and V. Meunier, ACS Nano, 2019, 13, 10456–10468 CrossRef CAS.
- Y. Zhao, M. Al-Fahdi, M. Hu, E. M. D. Siriwardane, Y. Song, A. Nasiri and J. Hu, Adv. Sci., 2021, 8, 2100566 CrossRef CAS.
- A. S. Rosen, S. M. Iyer, D. Ray, Z. Yao, A. Aspuru-Guzik, L. Gagliardi, J. M. Notestein and R. Q. Snurr, Matter, 2021, 4, 1578–1597 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- S. Curtarolo, W. Setyawan, S. Wang, J. Xue, K. Yang, R. H. Taylor, L. J. Nelson, G. L. W. Hart, S. Sanvito, M. Buongiorno-Nardelli, N. Mingo and O. Levy, Comput. Mater. Sci., 2012, 58, 227–235 CrossRef CAS.
- J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, JOM, 2013, 65, 1501–1509 CrossRef CAS.
- M. Hellenbrandt, Crystallogr. Rev., 2004, 10, 17–22 CrossRef CAS.
- M. A. Caro, Phys. Rev. B, 2019, 100, 024112 CrossRef CAS.
- M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301 CrossRef PubMed.
- F. Faber, A. Lindmaa, O. A. von Lilienfeld and R. Armiento, Int. J. Quantum Chem., 2015, 115, 1094–1101 CrossRef CAS.
- T. Xie and J. C. Grossman, Phys. Rev. Lett., 2018, 120, 145301 CrossRef CAS PubMed.
- T. Chen and C. Guestrin, Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Association for Computing Machinery, New York, NY, USA, 2016, pp. 785–794 Search PubMed.
- J. H. Friedman, Ann. Stat., 2001, 29, 1189–1232 Search PubMed.
- Irie and Miyake, in IEEE 1988 International Conference on Neural Networks, 1988, pp. 641–648 vol. 1.
- Y. LeCun, B. Boser, J. S. Denker, D. Henderson, R. E. Howard, W. Hubbard and L. D. Jackel, Neural Comput., 1989, 1, 541–551 CrossRef.
- A. Sperduti and A. Starita, IEEE Trans. Neural Netw., 1997, 8, 714–735 CAS.
- P. Frasconi, M. Gori and A. Sperduti, IEEE Trans. Neural Netw., 1998, 9, 768–786 CrossRef CAS.
- L. Zhang, H. Wang, R. Car and E. Weinan, Phys. Rev. Lett., 2021, 126, 236001 CrossRef CAS.
- L. Zhang, J. Han, H. Wang, R. Car and E. Weinan, Phys. Rev. Lett., 2018, 120, 143001 CrossRef CAS PubMed.
- J. López-Zorrilla, X. M. Aretxabaleta, I. W. Yeu, I. Etxebarria, H. Manzano and N. Artrith, J. Chem. Phys., 2023, 158, 164105 CrossRef.
- S. Chmiela, A. Tkatchenko, H. E. Sauceda, I. Poltavsky, K. T. Schütt and K.-R. Müller, Sci. Adv., 2017, 3, e1603015 CrossRef PubMed.
- H. Wang, L. Zhang, J. Han and W. E, Comput. Phys. Commun., 2018, 228, 178–184 CrossRef CAS.
- B. Deng, P. Zhong, K. Jun, J. Riebesell, K. Han, C. J. Bartel and G. Ceder, Nat. Mach. Intell., 2023, 5, 1031–1041 CrossRef.
- V. L. Deringer, M. A. Caro and G. Csányi, Adv. Mater., 2019, 31, 1902765 CrossRef CAS.
- S. Gong, K. Yan, T. Xie, Y. Shao-Horn, R. Gomez-Bombarelli, S. Ji and J. C. Grossman, Sci. Adv., 2023, 9, eadi3245 CrossRef PubMed.
- M. Ishimaru, M. Yamaguchi and Y. Hirotsu, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 235207 CrossRef.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 136403 CrossRef PubMed.
- A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115 CrossRef.
- A. P. Thompson, L. P. Swiler, C. R. Trott, S. M. Foiles and G. J. Tucker, J. Comput. Phys., 2015, 285, 316–330 CrossRef CAS.
- M. A. Wood and A. P. Thompson, J. Chem. Phys., 2018, 148, 241721 CrossRef PubMed.
- V. Botu and R. Ramprasad, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 094306 CrossRef.
- T. D. Huan, R. Batra, J. Chapman, S. Krishnan, L. Chen and R. Ramprasad, npj Comput. Mater., 2017, 3, 1–8 CrossRef CAS.
- V. Botu, R. Batra, J. Chapman and R. Ramprasad, J. Phys. Chem. C, 2017, 121, 511–522 CrossRef CAS.
- A. V. Shapeev, Multiscale Model. Simul., 2016, 14, 1153–1173 CrossRef.
- E. V. Podryabinkin and A. V. Shapeev, Comput. Mater. Sci., 2017, 140, 171–180 CrossRef CAS.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- A. Singraber, J. Behler and C. Dellago, J. Chem. Theory Comput., 2019, 15, 1827–1840 CrossRef CAS.
- N. Artrith and A. Urban, Comput. Mater. Sci., 2016, 114, 135–150 CrossRef CAS.
- A. Khorshidi and A. A. Peterson, Comput. Phys. Commun., 2016, 207, 310–324 CrossRef CAS.
- L. Ward, R. Liu, A. Krishna, V. I. Hegde, A. Agrawal, A. Choudhary and C. Wolverton, Phys. Rev. B, 2017, 96, 024104 CrossRef.
- K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, J. Chem. Phys., 2018, 148, 241722 CrossRef.
- K. T. Schütt, P. Kessel, M. Gastegger, K. A. Nicoli, A. Tkatchenko and K.-R. Müller, J. Chem. Theory Comput., 2019, 15, 448–455 CrossRef.
- J. Gasteiger, J. Groß and S. Günnemann, arXiv, 2020, preprint, arXiv:2003.03123 DOI:10.48550/arXiv.2003.03123.
- Z. Fan, Z. Zeng, C. Zhang, Y. Wang, K. Song, H. Dong, Y. Chen and T. Ala-Nissila, Phys. Rev. B, 2021, 104, 104309 CrossRef CAS.
- Z. Fan, Y. Wang, P. Ying, K. Song, J. Wang, Y. Wang, Z. Zeng, K. Xu, E. Lindgren, J. M. Rahm, A. J. Gabourie, J. Liu, H. Dong, J. Wu, Y. Chen, Z. Zhong, J. Sun, P. Erhart, Y. Su and T. Ala-Nissila, J. Chem. Phys., 2022, 157, 114801 CrossRef CAS PubMed.
- Z. Liu, L. Lin, Q. Jia, Z. Cheng, Y. Jiang, Y. Guo and J. Ma, J. Chem. Inf. Model., 2021, 61, 1066–1082 CrossRef CAS.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Chem. Mater., 2019, 31, 3564–3572 CrossRef CAS.
- Y. Zuo, M. Qin, C. Chen, W. Ye, X. Li, J. Luo and S. P. Ong, Mater. Today, 2021, 51, 126–135 CrossRef CAS.
- R. E. A. Goodall, A. S. Parackal, F. A. Faber, R. Armiento and A. A. Lee, Sci. Adv., 2022, 8, eabn4117 CrossRef CAS.
- K. Choudhary and B. DeCost, npj Comput. Mater., 2021, 7, 1–8 CrossRef.
- S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, Nat. Commun., 2022, 13, 2453 CrossRef CAS.
- C. Chen and S. P. Ong, Nat. Comput. Sci., 2022, 2, 718–728 CrossRef.
- S. Takamoto, S. Izumi and J. Li, Comput. Mater. Sci., 2022, 207, 111280 CrossRef CAS.
- T. Frank, O. Unke and K.-R. Müller, Adv. Neural Inf. Proc. Sys., 2022, 35, 29400–29413 Search PubMed.
- I. Batatia, P. Benner, Y. Chiang, A. M. Elena, D. P. Kovács, J. Riebesell and G. Csányi, arXiv, 2023, preprint, arXiv:2401.00096 DOI:10.48550/arXiv.2401.00096.
- A. Musaelian, S. Batzner, A. Johansson, L. Sun, C. J. Owen, M. Kornbluth and B. Kozinsky, Nat. Commun., 2023, 14, 579 CrossRef CAS.
- R. P. Pelaez, G. Simeon, R. Galvelis, A. Mirarchi, P. Eastman, S. Doerr, P. Thölke, T. E. Markland and G. De Fabritiis, J. Chem. Theory Comput., 2024, 20, 4076–4087, DOI:10.1021/acs.jctc.4c00253.
- Y. Park, J. Kim, S. Hwang and S. Han, J. Chem. Theory Comput., 2024, 20, 4857–4868 CrossRef CAS.
- L. Barroso-Luque, M. Shuaibi, X. Fu, B. M. Wood, M. Dzamba, M. Gao, A. Rizvi, C. L. Zitnick and Z. W. Ulissi, arXiv, 2024, preprint, arXiv:2410.12771 DOI:10.48550/arXiv.2410.12771.
- orbital-materials/orb-models, https://github.com/orbital-materials/orb-models, (accessed 22 October 2024).
- A. P. Graham, F. Hofmann, J. P. Toennies, L. Y. Chen and S. C. Ying, Phys. Rev. Lett., 1997, 78, 3900–3903 CrossRef CAS.
- S. R. Xie, M. Rupp and R. G. Hennig, npj Comput. Mater., 2023, 9, 1–9 CrossRef.
- J. Callaway, Phys. Rev., 1959, 113, 1046–1051 CrossRef CAS.
- P. G. Klemens, Proc. Phys. Soc., London, Sect. A, 1955, 68, 1113 CrossRef.
- M. G. Holland, Phys. Rev., 1963, 132, 2461–2471 CrossRef CAS.
- G. A. Slack, J. Phys. Chem. Solids, 1973, 34, 321–335 CrossRef CAS.
- J. D. Chung, A. J. H. McGaughey and M. Kaviany, J. Heat Transfer, 2004, 126, 376–380 CrossRef CAS.
- T. Jia, G. Chen and Y. Zhang, Phys. Rev. B, 2017, 95, 155206 CrossRef.
- J. E. Turney, E. S. Landry, A. J. H. McGaughey and C. H. Amon, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 064301 CrossRef.
- A. Rohskopf, H. R. Seyf, K. Gordiz, T. Tadano and A. Henry, npj Comput. Mater., 2017, 3, 1–7 CrossRef CAS.
- K. Fujiwara, M. Daimo, Y. Ueki, T. Ohara and M. Shibahara, Int. J. Heat Mass Transfer, 2019, 144, 118695 CrossRef CAS.
- B. Liao, Nanoscale Energy Transport: Emerging phenomena, methods and applications, IOP Publishing, 2020 Search PubMed.
- X. Qian and R. Yang, Mater. Sci. Eng., R, 2021, 146, 100642 CrossRef.
- A. Rodriguez, Y. Liu and M. Hu, Phys. Rev. B, 2020, 102, 035203 CrossRef CAS.
- A. Rodriguez, C. Lin, H. Yang, M. Al-Fahdi, C. Shen, K. Choudhary, Y. Zhao, J. Hu, B. Cao, H. Zhang and M. Hu, npj Comput. Mater., 2023, 9, 20 CrossRef CAS.
- C. Loftis, K. Yuan, Y. Zhao, M. Hu and J. Hu, J. Phys. Chem. A, 2021, 125, 435–450 CrossRef CAS.
- G. Qin, A. Huang, Y. Liu, H. Wang, Z. Qin, X. Jiang, J. Zhao, J. Hu and M. Hu, Mater. Adv., 2022, 3, 6826–6830 RSC.
- G. Qin, Y. Wei, L. Yu, J. Xu, J. Ojih, A. D. Rodriguez, H. Wang, Z. Qin and M. Hu, J. Mater. Chem. A, 2023, 11, 5801–5810 RSC.
- T. Hsu, T. A. Pham, N. Keilbart, S. Weitzner, J. Chapman, P. Xiao, S. R. Qiu, X. Chen and B. C. Wood, npj Comput. Mater., 2022, 8, 1–9 CrossRef.
- K. Choudhary and B. DeCost, npj Comput. Mater., 2021, 7, 1–8 CrossRef.
- R. Gurunathan, K. Choudhary and F. Tavazza, Phys. Rev. Mater., 2023, 7, 023803 CrossRef CAS.
- S.-Y. Louis, Y. Zhao, A. Nasiri, X. Wang, Y. Song, F. Liu and J. Hu, Phys. Chem. Chem. Phys., 2020, 22, 18141–18148 RSC.
- S. S. Omee, S.-Y. Louis, N. Fu, L. Wei, S. Dey, R. Dong, Q. Li and J. Hu, Patterns, 2022, 3, 100491 CrossRef PubMed.
- K. Yan, Y. Liu, Y. Lin and S. Ji, Adv. Neural Inf. Pro. Sys., 2022, 35, 15066–15080 Search PubMed.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Chem. Mater., 2019, 31, 3564–3572 CrossRef CAS.
- Z. Wu, P. Jain, M. Wright, A. Mirhoseini, J. E. Gonzalez and I. Stoica, Advances in Neural Information Processing Systems, Curran Associates, Inc., 2021, vol. 34, pp. 13266–13279 Search PubMed.
- K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, J. Chem. Phys., 2018, 148, 241722 CrossRef.
- C. W. Coley, W. Jin, L. Rogers, T. F. Jamison, T. S. Jaakkola, W. H. Green, R. Barzilay and K. F. Jensen, Chem. Sci., 2019, 10, 370–377 RSC.
- J. Ojih, U. Onyekpe, A. Rodriguez, J. Hu, C. Peng and M. Hu, ACS Appl. Mater. Interfaces, 2022, 14, 43277–43289 CrossRef CAS PubMed.
- N. Nguyen, S.-Y. V. Louis, L. Wei, K. Choudhary, M. Hu and J. Hu, ACS Omega, 2022, 7, 26641–26649 CrossRef CAS PubMed.
- A. Rodriguez, S. Lam and M. Hu, ACS Appl. Mater. Interfaces, 2021, 13, 55367–55379 CrossRef CAS PubMed.
- S. Liu, Z. Chang, X.-L. Zhang, K.-P. Yuan, Y.-F. Gao and D.-W. Tang, Rare Met., 2023, 42, 3064–3074 CrossRef CAS.
- J. Mao, Z. Liu and Z. Ren, npj Quantum Mater., 2016, 1, 1–9 Search PubMed.
- S. W. Oxandale, C. Reinke, S. R. Das and I. El-Kady, Commun. Mater., 2023, 4, 1–8 CrossRef.
- G. Qin, H. Wang, L. Zhang, Z. Qin and M. Hu, J. Mater. Chem. C, 2020, 8, 3520–3526 RSC.
- D.-H. Wei, E. Zhou, J.-Y. Xu, H.-M. Wang, C. Shen, H.-B. Zhang, Z.-Z. Qin and G.-Z. Qin, Rare Met., 2024, 43, 770–779 CrossRef CAS.
- A. Wang, S.-H. Li and H. Bao, Rare Met., 2023, 42, 3651–3661 CrossRef CAS.
- Z. Chen, X. Zhang, S. Lin, L. Chen and Y. Pei, Natl. Sci. Rev., 2018, 5, 888–894 CrossRef CAS.
- J. Ma, Small Sci., 2023, 3, 2200052 CrossRef.
- G. Qin and M. Hu, npj Comput. Mater., 2018, 4, 1–6 CrossRef CAS.
- H. Zou, Y.-Y. Tian, L.-G. Zhang, R.-H. Xue, Z.-X. Deng, M.-M. Lu, J.-X. Wang and L.-B. Liu, Rare Met., 2024, 43, 309–323 CrossRef CAS.
- D. Chen, F. Jiang, L. Fang, Y.-B. Zhu, C.-C. Ye and W.-S. Liu, Rare Met., 2022, 41, 1543–1553 CrossRef CAS.
- Z. Liang and M. Hu, J. Appl. Phys., 2018, 123, 191101 CrossRef.
- R. Jinnouchi, F. Karsai and G. Kresse, Phys. Rev. B, 2019, 100, 014105 CrossRef CAS.
- R. Jinnouchi, J. Lahnsteiner, F. Karsai, G. Kresse and M. Bokdam, Phys. Rev. Lett., 2019, 122, 225701 Search PubMed.
- J. Vandermause, S. B. Torrisi, S. Batzner, Y. Xie, L. Sun, A. M. Kolpak and B. Kozinsky, npj Comput. Mater., 2020, 6, 1–11 Search PubMed.
- T.-T. Wu, G.-L. Dai, J.-J. Xu, F. Cao, X.-H. Zhang, Y. Zhao and Y.-M. Qian, Rare Met., 2023, 42, 3269–3303 CrossRef CAS.
- Y. Zhao, E. M. D. Siriwardane, Z. Wu, N. Fu, M. Al-Fahdi, M. Hu and J. Hu, npj Comput. Mater., 2023, 9, 38 Search PubMed.
- A. Merchant, S. Batzner, S. S. Schoenholz, M. Aykol, G. Cheon and E. D. Cubuk, Nature, 2023, 624, 80–85 Search PubMed.
| This journal is © The Royal Society of Chemistry 2025 |