Inverse design of chiral structures for giant helical dichroism†
Chia-Chun
Pan‡
 a,
Munseong
Bae‡
b,
Hongtao
Wang
a,
Munseong
Bae‡
b,
Hongtao
Wang
 c,
Jaesung
Lim
d,
Ranjith Rajasekharan
Unnithan
a,
Joel K. W.
Yang
c,
Haejun
Chung
*b and
Sejeong
Kim
c,
Jaesung
Lim
d,
Ranjith Rajasekharan
Unnithan
a,
Joel K. W.
Yang
c,
Haejun
Chung
*b and
Sejeong
Kim
 *a
*a
aDepartment of Electrical and Electronic Engineering, University of Melbourne, VIC, Australia. E-mail: sejeong.kim@unimelb.edu.au
bDepartment of Electronic Engineering, Hanyang University, Seoul, Korea. E-mail: haejun@hanyang.ac.kr
cEngineering Product Development, Singapore University of Technology and Design, Singapore
dDepartment of Physics, Hanyang University, Seoul, Korea
First published on 12th April 2025
Abstract
Investigating chiral light-matter interactions is essential for advancing applications in sensing, imaging, and pharmaceutical development. However, the chiroptical response in natural chiral molecules and subwavelength chiral structures is inherently weak, with the conventional characterization tools limited to optical methods that utilize circularly polarized light. To overcome this, optical vortex beams, characterized by helical wavefronts, have emerged as a compelling research focus. Helical dichroism (HD) represents the differential absorbance of vortex beams with opposite signs of topological charges. By using inverse design for topology optimization, we design the chiral structure for enhanced HD response under OAM beam incidence, demonstrating a giant HD response of ∼107% with topological charges |±![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) | = 3 at the wavelength of 800 nm. This study reveals distinct helicity-dependent interactions between the chiral structure and OAM beams, highlighting the potential for highly sensitive chiral devices.
| = 3 at the wavelength of 800 nm. This study reveals distinct helicity-dependent interactions between the chiral structure and OAM beams, highlighting the potential for highly sensitive chiral devices.
New conceptsThis work is the first demonstration of using inversely designed chiral structures to enhance helical dichroism (HD). Helical dichroism, which utilizes optical vortex beams with opposite signs of topological charge to distinguish chiral objects, is a relatively new area of interest in chiral sensing. Only a few papers have explored chiral structures designed for HD so far. Currently, there is a lack of design strategies to optimize the chiral geometry for HD enhancement, which is where inverse design can play a crucial role. In this study, we employed an adjoint optimization method to generate chiral structures made of SiN that maximize HD. We report the highest HD contrast achieved to date, which opens potential applications of dielectric material-based chiral structures for sensitive chiral sensing. |
Introduction
Chirality refers to a geometric property of objects where they cannot be superposed onto their mirror images. Identifying chirality is important, particularly for chiral molecules, also known as enantiomers, as their opposite-handedness may have drastically different effects on biological systems.1–3 For instance, left-handed ibuprofen has the desired effect of pain relief, whereas right-handed ibuprofen has no effect. Therefore, the study of the interactions between light and chiral materials has gained momentum as a method to differentiate one enantiomer from another, with the majority of research efforts focusing on light with spin angular momentum (SAM), i.e., circularly polarized light.4–6 Chiral molecules preferentially absorb either left-handed circularly polarized (LCP) light or right-handed circularly polarized (RCP) light, resulting in an intensity contrast in the transmission or reflection spectra. This intensity contrast is known as circular dichroism (CD).4,7,8 However, the CD contrast is often weak when measured from natural chiral molecules due to the small size of the target molecules relative to the wavelength of incident light and the beam spot size.9–11 Chiral metamaterials, which are artificially created, can address this issue and enhance the CD contrast. Many previous studies have reported various chiral nanostructures that exhibit a large CD contrast.12–14 As a result, incorporating chiral nanostructures in CD measurements can improve signal contrast, enabling high-sensitivity chiral sensing at low material density, which can be advantageous for chiral molecule detection and pharmaceutical development.Recent findings suggest that utilizing optical vortex beams—beams carrying orbital angular momentum (OAM)—can offer greater chiral sensitivity compared to beams carrying SAM.15 OAM beams possess unlimited degree of freedom defined by the topological charge denoted as ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) . Here, topological charge
. Here, topological charge ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) represents the number of phase rotations per wavelength, theoretically showing unlimited integer numbers.16–18 OAM beams are characterized by helical wavefronts in the azimuthal phase form exp(−i
represents the number of phase rotations per wavelength, theoretically showing unlimited integer numbers.16–18 OAM beams are characterized by helical wavefronts in the azimuthal phase form exp(−i![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) θ), where θ denotes the azimuthal angle. Similar to CD measurements, chiral molecules exhibit different absorption for OAM beams of opposite handedness, resulting in an intensity contrast in the spectrum, a phenomenon referred to as helical dichroism (HD).19,20 J. Ni et al., measured the HD of a chiral structure as a function of the varying topological charges of OAM beams, achieving an experimental HD of 20%,21 followed by a report by N. Dai et al., observing a further increase in the HD signal to 50%.22 The infinite degree of freedom afforded by OAM beams makes them particularly advantageous for probing complex chiral systems, optimizing light-matter interactions, and designing advanced chiroptical devices, thus opening new avenues for exploring and engineering chiral phenomena.
θ), where θ denotes the azimuthal angle. Similar to CD measurements, chiral molecules exhibit different absorption for OAM beams of opposite handedness, resulting in an intensity contrast in the spectrum, a phenomenon referred to as helical dichroism (HD).19,20 J. Ni et al., measured the HD of a chiral structure as a function of the varying topological charges of OAM beams, achieving an experimental HD of 20%,21 followed by a report by N. Dai et al., observing a further increase in the HD signal to 50%.22 The infinite degree of freedom afforded by OAM beams makes them particularly advantageous for probing complex chiral systems, optimizing light-matter interactions, and designing advanced chiroptical devices, thus opening new avenues for exploring and engineering chiral phenomena.
The design of chiral nano/microstructures to enhance HD has largely followed similar structural designs used for CD, often emphasizing intuitively chiral geometries such as spiral or helical forms.21–23 However, no established design strategy specifically targeting the enhancement of HD currently exists, leaving the process largely dependent on intuition. Meanwhile, inverse design provides a robust framework for photonic design. All previously reported chiral structures used in HD experiments deployed the parameter-sweep method, a forward design approach. In this method, the optical response is initially calculated using an intuitively chosen chiral geometry, and the geometric parameters are then varied to identify the optimal resulting response. In contrast to traditional design methods, which typically depend on intuition, trial-and-error, or prior experience, inverse design enables the exploration of non-intuitive photonic design spaces with enhanced functionality, allowing for the realization of compact and high-performance devices. Specifically, topology optimization with adjoint sensitivity analysis, commonly referred to as adjoint optimization and facilitated by the Born approximation and Lorentz reciprocity,24,25 has been successfully applied to multifunctional photonic devices exhibiting high functionalities.26–28 This approach proves particularly effective for designing structures that enable precise control over subwavelength-scale light-matter interactions tailored to a specific functionality. By leveraging the potential of inverse design, custom-tuned chiroptical responses with high HD can be accurately realized.
In this work, we report the inverse-designed chiral structure that maximizes the reflectance intensity contrast when incident light beams with positive and negative OAM topological charges are applied. The induced HD responses for topological charges |![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) | = ± 3 reached approximately 107%, while simulations from previous work reported a maximum value of less than 50%. It is also worth noting that the optimization was performed using SiN, a dielectric material, which typically has weaker light–matter interaction than metals and requires a thicker layer. Despite this, the inverse-designed SiN structure achieved significant chiral interaction even with subwavelength thickness. This novel approach lays the groundwork for next-generation chiral structures, broadening their applications from chirality-sensitive devices and chiroptical spectroscopy to advancements in drug development.
| = ± 3 reached approximately 107%, while simulations from previous work reported a maximum value of less than 50%. It is also worth noting that the optimization was performed using SiN, a dielectric material, which typically has weaker light–matter interaction than metals and requires a thicker layer. Despite this, the inverse-designed SiN structure achieved significant chiral interaction even with subwavelength thickness. This novel approach lays the groundwork for next-generation chiral structures, broadening their applications from chirality-sensitive devices and chiroptical spectroscopy to advancements in drug development.
Results and discussion
Our proposed inverse design method optimizes the chiral structure to maximize the helical dichroic response. While many chiral structures have been designed using metals due to their ability to provide strong light confinement in a small footprint, dielectric structures can offer advantages as they are not subject to quenching near the surface. In this work, SiN is selected as the material for the chiral structure. It has a relatively high refractive index (n ≈ 2.0) within its transparency window and shows nearly zero absorption across a broad range of wavelengths, including the visible. Additionally, SiN is a dielectric material with mature fabrication technology that is CMOS-compatible. The chiral structure preferentially interacts with one handedness over the other, leading to differences in reflectance intensity. Fig. 1a conceptually illustrates that the inverse-designed structure interacts favorably with the OAM beam carrying a positive topological charge (depicted as orange helical light), leading to a lower reflected light intensity. Conversely, Fig. 1b shows the weaker interaction between a beam with a negative topological charge (represented as green helical light) and the same chiral structure shown in Fig. 1a. This weaker interaction results in less light absorption, which causes a smaller reduction in the intensity of the reflected light beam. HD is calculated from the reflectance difference between the positive (R![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) +) and negative (R
+) and negative (R![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) −) topological charges in relation to their mean values using the equation expressed as:21,22
−) topological charges in relation to their mean values using the equation expressed as:21,22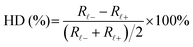 | (1) |
This equation is used in other papers to define HD as well, with a value range of 0 to 200%.
In this work, three-dimensional (3D) numerical simulations are conducted using the finite-difference time-domain (FDTD) method, implemented through MEEP, an open-source simulation tool.29Fig. 2 illustrates the two subsets of adjoint gradient analysis, consisting of forward and adjoint simulations for positive ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) (Fig. 2a) and negative
(Fig. 2a) and negative ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) (Fig. 2b), respectively. The adjoint gradient is computed as the matrix product of two electromagnetic field distributions within the design region: the forward field induced by the input OAM source and the adjoint field generated by the corresponding adjoint source. To simulate the OAM beam propagating along the z-direction in the simulation, Laguerre Gaussian (LG) mode beam is used where the equation is shown below:30
(Fig. 2b), respectively. The adjoint gradient is computed as the matrix product of two electromagnetic field distributions within the design region: the forward field induced by the input OAM source and the adjoint field generated by the corresponding adjoint source. To simulate the OAM beam propagating along the z-direction in the simulation, Laguerre Gaussian (LG) mode beam is used where the equation is shown below:30
 | (2) |
 , Lp|
, Lp|![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) | is the associated Laguerre polynomials, p represents the radial index (≥0), and it is commonly considered as 0.
| is the associated Laguerre polynomials, p represents the radial index (≥0), and it is commonly considered as 0. 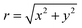 is the radial distance, w(z′) is the beam width at z′, ψ(z′) = (|
is the radial distance, w(z′) is the beam width at z′, ψ(z′) = (|![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) | + 1)arctan
| + 1)arctan 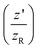 is the Guoy phase. Here, z′ = z0 − z where z0 is the position of the LG beam waist, and z is the axial distance between the LG beam waist (z0) and source position. The functional form of the beam width and z′ is as follows:
is the Guoy phase. Here, z′ = z0 − z where z0 is the position of the LG beam waist, and z is the axial distance between the LG beam waist (z0) and source position. The functional form of the beam width and z′ is as follows:  where w0 is the beam waist at z′ = 0, zR stands for the Rayleigh range, defined as
where w0 is the beam waist at z′ = 0, zR stands for the Rayleigh range, defined as 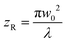 . Unlike circularly polarized light, which is inherently limited to two states, the topological charges of OAM beams, denoted by
. Unlike circularly polarized light, which is inherently limited to two states, the topological charges of OAM beams, denoted by ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) , can theoretically span an infinite range of integer values. The infinite degrees of freedom offered by OAM beams make them particularly advantageous for probing complex chiral systems and designing advanced chiroptical devices. The linearly polarized OAM beam profiles with topological charge range
, can theoretically span an infinite range of integer values. The infinite degrees of freedom offered by OAM beams make them particularly advantageous for probing complex chiral systems and designing advanced chiroptical devices. The linearly polarized OAM beam profiles with topological charge range ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) from −3 to +3 are visually represented in Fig. S1 (ESI†), demonstrating both intensity and phase profiles. The wavelength of the incident OAM beam is set to λ = 800 nm, with the beam waist w(z0) = 800 nm. The height of the SiN layer is set to 800 nm, with a minimum feature size of 200 nm, well above the smallest patterns that electron beam lithography (EBL) can achieve. The SiN layer is sitting on a 600 nm-thick SiO2 substrate with a refractive index of 1.45.
from −3 to +3 are visually represented in Fig. S1 (ESI†), demonstrating both intensity and phase profiles. The wavelength of the incident OAM beam is set to λ = 800 nm, with the beam waist w(z0) = 800 nm. The height of the SiN layer is set to 800 nm, with a minimum feature size of 200 nm, well above the smallest patterns that electron beam lithography (EBL) can achieve. The SiN layer is sitting on a 600 nm-thick SiO2 substrate with a refractive index of 1.45.
The figure of merit (FoM) for each subset is defined as the reflectance of the helical incidence beam with positive and negative topological charges (R![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ±) as follows:
±) as follows:
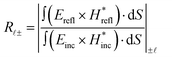 | (3) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) represents the topological charge of the helical incidence beam, Erefl and Hrefl are the reflected electric and magnetic fields at the output monitor, Einc and Hinc are the incident electric and magnetic fields at the output monitor for normalization, and S denotes the size of the output monitor. The amplitude of the adjoint source is determined from the partial derivative of R
represents the topological charge of the helical incidence beam, Erefl and Hrefl are the reflected electric and magnetic fields at the output monitor, Einc and Hinc are the incident electric and magnetic fields at the output monitor for normalization, and S denotes the size of the output monitor. The amplitude of the adjoint source is determined from the partial derivative of R![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ± with respect to the electric field within the output monitor, obtained from the forward simulation. Fig. 2c shows the final gradient for HD maximization: a weighted summation of the two calculated gradients with positive and negative factors. The weight factors for the gradient of R
± with respect to the electric field within the output monitor, obtained from the forward simulation. Fig. 2c shows the final gradient for HD maximization: a weighted summation of the two calculated gradients with positive and negative factors. The weight factors for the gradient of R![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ± in each iteration are determined as follows:
± in each iteration are determined as follows: | (4) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) + minimization, and w2 is the weight factor for R
+ minimization, and w2 is the weight factor for R![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) − maximization. The simulation volume for the inverse design is defined as 5 μm × 5 μm × 2.3 μm, encompassing the SiO2 substrate and the OAM sources with targeted topological charges |
− maximization. The simulation volume for the inverse design is defined as 5 μm × 5 μm × 2.3 μm, encompassing the SiO2 substrate and the OAM sources with targeted topological charges |![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) | = ± 3.
| = ± 3.
Each iterative optimization process begins with the forward simulations of the LG beam propagation with |±![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) | = 3, followed by the corresponding adjoint simulations to collect the material density gradient for HD maximization, as shown in Fig. 2. Then, the external gradient ascent algorithm updates the geometry of the chiral structure until the fabrication constraint factor31 reaches a predefined threshold, and the algorithm no longer satisfies the Armijo sufficient condition.32Fig. 3 illustrates the evolution of the FoM and the reflectance spectra as the number of iterations increases. In our case, after slightly more than 160 iterations, the change in FoM approaches nearly zero, and the geometry becomes fully binarized. The background purple gradation in Fig. 3 intuitively represents the degree of binarization, illustrating how the refractive index profile transitions from a gray, continuous state to a fully binary, discrete state during the optimization process. The top subplots of Fig. 3 visualize the transition from the initial 5 μm × 5 μm grayscale structure to the final binarized design of SiN (purple) and Air (white). Each subplot is connected by dashed lines to its corresponding iteration number. R
| = 3, followed by the corresponding adjoint simulations to collect the material density gradient for HD maximization, as shown in Fig. 2. Then, the external gradient ascent algorithm updates the geometry of the chiral structure until the fabrication constraint factor31 reaches a predefined threshold, and the algorithm no longer satisfies the Armijo sufficient condition.32Fig. 3 illustrates the evolution of the FoM and the reflectance spectra as the number of iterations increases. In our case, after slightly more than 160 iterations, the change in FoM approaches nearly zero, and the geometry becomes fully binarized. The background purple gradation in Fig. 3 intuitively represents the degree of binarization, illustrating how the refractive index profile transitions from a gray, continuous state to a fully binary, discrete state during the optimization process. The top subplots of Fig. 3 visualize the transition from the initial 5 μm × 5 μm grayscale structure to the final binarized design of SiN (purple) and Air (white). Each subplot is connected by dashed lines to its corresponding iteration number. R![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) − (green line) and R
− (green line) and R![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) + (orange line) represent the reflectance spectra for incident OAM beams with −3 and +3 topological charge modes, respectively. As the iteration process approaches the final stage, R
+ (orange line) represent the reflectance spectra for incident OAM beams with −3 and +3 topological charge modes, respectively. As the iteration process approaches the final stage, R![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) − exhibits approximately 20% reflectance, while only 6% reflectance is observed for R
− exhibits approximately 20% reflectance, while only 6% reflectance is observed for R![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) +, clearly indicating that our inverse design method successfully developed the HD freeform structure.
+, clearly indicating that our inverse design method successfully developed the HD freeform structure.
To evaluate the performance of the inverse-designed chiral structure in Fig. 3, we import the structure into a new simulation environment and place it on a glass substrate with substrate thickness H2 = 600 nm as shown in Fig. 4a. The simulation domain incorporates the incident OAM beams with topological charges, |±![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) |, varying from 0 to 10. Fig. 4b and c show the time-averaged electric field distributions for the incident OAM beams with
|, varying from 0 to 10. Fig. 4b and c show the time-averaged electric field distributions for the incident OAM beams with ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = +3 and
= +3 and ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = −3, respectively. The series of images at various cross-sections visualize the light interaction above and within the chiral structure. Both the chiral structure and the field profile show the 2-fold rotational symmetry (C2 symmetry), which we intentionally implemented in the optimization constraint. Fig. 4 shows the electric field intensity profile at various monitor locations, i.e., z = 0, 0.2, 0.4, 0.6, 0.8, and 1.6 μm, for the positive topological charge (Fig. 4b) and the negative topological charge (Fig. 4c). The near-field images differ based on the sign of the topological charge of the input beam, producing a dichroic response, as confirmed by the reflection intensity at z = 1.6 μm. Interestingly, the field intensity profile of topological charge
= −3, respectively. The series of images at various cross-sections visualize the light interaction above and within the chiral structure. Both the chiral structure and the field profile show the 2-fold rotational symmetry (C2 symmetry), which we intentionally implemented in the optimization constraint. Fig. 4 shows the electric field intensity profile at various monitor locations, i.e., z = 0, 0.2, 0.4, 0.6, 0.8, and 1.6 μm, for the positive topological charge (Fig. 4b) and the negative topological charge (Fig. 4c). The near-field images differ based on the sign of the topological charge of the input beam, producing a dichroic response, as confirmed by the reflection intensity at z = 1.6 μm. Interestingly, the field intensity profile of topological charge ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = −3 at the reflection plane denoted with the blue outline in Fig. 4a presents the clear diagonal (y = x) line distribution, possibly due to the C2 symmetric shape of the freeform structure. We conducted additional simulations using Lumerical FDTD Solutions software to ensure that the results are consistent and robust against potential slight variations in simulation settings across different platforms. This helically dichroic behavior is demonstrated in Fig. 4d, which shows the difference between positive and negative topological charges |±
= −3 at the reflection plane denoted with the blue outline in Fig. 4a presents the clear diagonal (y = x) line distribution, possibly due to the C2 symmetric shape of the freeform structure. We conducted additional simulations using Lumerical FDTD Solutions software to ensure that the results are consistent and robust against potential slight variations in simulation settings across different platforms. This helically dichroic behavior is demonstrated in Fig. 4d, which shows the difference between positive and negative topological charges |±![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) | from 0 to 10. MEEP simulation results are represented by orange and green lines with circular data points (subscript A), while Lumerical simulation results are represented by yellow and blue lines with triangular data points (subscript B). Both results show the largest reflectance difference at |±
| from 0 to 10. MEEP simulation results are represented by orange and green lines with circular data points (subscript A), while Lumerical simulation results are represented by yellow and blue lines with triangular data points (subscript B). Both results show the largest reflectance difference at |±![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) | = 3, which is in good agreement with the desired performance when optimizing the structure under the incident OAM mode |±
| = 3, which is in good agreement with the desired performance when optimizing the structure under the incident OAM mode |±![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) | = 3. Fig. 4e results display a peak HD at topological charge 3, where the reflectance difference is maximized, with the numerically highest HD signal of ∼107% at 800 nm wavelength. Note that if topological charges |±
| = 3. Fig. 4e results display a peak HD at topological charge 3, where the reflectance difference is maximized, with the numerically highest HD signal of ∼107% at 800 nm wavelength. Note that if topological charges |±![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) | are not at 3, the HD responses exhibit ∼75% at topological charges |±
| are not at 3, the HD responses exhibit ∼75% at topological charges |±![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) | = 4 and still show ∼30% when topological charges |±
| = 4 and still show ∼30% when topological charges |±![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) | = 7. The performance suggests that the chiral structure exhibits broadband helically dichroic responses across various OAM topological charges. Both simulation tools show the same trend in helical dichroism as the topological charge varies. The consistency between these two independent numerical implementations strengthens the reliability of our computational predictions and supports the robustness of the designed chiral structure's performance.
| = 7. The performance suggests that the chiral structure exhibits broadband helically dichroic responses across various OAM topological charges. Both simulation tools show the same trend in helical dichroism as the topological charge varies. The consistency between these two independent numerical implementations strengthens the reliability of our computational predictions and supports the robustness of the designed chiral structure's performance.
Conclusion
In this report, we present the first-ever inverse-designed chiral structure to enhance the contrast in helical dichroism. The adjoint optimization method, known for its effectiveness in various design problems, was employed in this study. This approach resulted in a threefold increase in helical dichroism compared to conventional chiral structures, such as spiral arms. By leveraging adjoint optimization methods, we designed a chiral structure that exhibits a record-breaking helical dichroism response of ∼107% for topological charges![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = ±3 at 800 nm. The HD value can be further improved by relaxing constraints used in our simulation, such as the minimum feature size, height, and material. Inverse design is especially effective when an intuitive design strategy or governing physics principles are lacking, as in the case of chirality design. The designed chiral structures are feasible for fabrication since the inverse design process incorporated practical constraints, including a minimum feature size and minimum gap size, ensuring compatibility with fabrication techniques such as EBL. In addition, substrate effects were also taken into consideration. The improved HD contrast demonstrated in this research has the potential to significantly enhance the sensitivity for detecting chiral molecules, which could enable the measurement of smaller sample volumes, thus pushing the limits of current detection capabilities. This study expands the promising applications of inverse design to helical dichroism and opens new possibilities for practical applications ranging from sensitive chiral molecular detection and advanced spectroscopic techniques to innovative pharmaceutical development.
= ±3 at 800 nm. The HD value can be further improved by relaxing constraints used in our simulation, such as the minimum feature size, height, and material. Inverse design is especially effective when an intuitive design strategy or governing physics principles are lacking, as in the case of chirality design. The designed chiral structures are feasible for fabrication since the inverse design process incorporated practical constraints, including a minimum feature size and minimum gap size, ensuring compatibility with fabrication techniques such as EBL. In addition, substrate effects were also taken into consideration. The improved HD contrast demonstrated in this research has the potential to significantly enhance the sensitivity for detecting chiral molecules, which could enable the measurement of smaller sample volumes, thus pushing the limits of current detection capabilities. This study expands the promising applications of inverse design to helical dichroism and opens new possibilities for practical applications ranging from sensitive chiral molecular detection and advanced spectroscopic techniques to innovative pharmaceutical development.
Data availability
The data supporting this article can be found in the GitHub repository: https://github.com/munseo/Helical_Dichroism.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) under the following grant numbers: (RS-2024-00405947), (RS-2024-00338048), and (RS-2024-00414119). It was also supported by the Global Research Support Program in the Digital Field (RS-2024-00412644) under the supervision of the Institute of Information and Communications Technology Planning & Evaluation (IITP), and by the Artificial Intelligence Graduate School Program (RS-2020-II201373, Hanyang University), also supervised by the IITP. Additionally, this research was supported by the Artificial Intelligence Semiconductor Support Program (IITP-(2025)-RS-2023-00253914), funded by the IITP, and by the Korea government (MSIT) grant (RS-2023-00261368, RS-2025-02218723, RS-2025-02283217). This work received support from the Culture, Sports, and Tourism R&D Program through a grant from the Korea Creative Content Agency, funded by the Ministry of Culture, Sports and Tourism (RS-2024-00332210). This research is also supported by MTC IRG (Project No. M22K2c0088) from the Agency for Science, Technology and Research (A*STAR), and Grant No. NRF-CRP30-2023-0003 from the National Research Foundation.References
- N. H. Cho, et al., Bioinspired chiral inorganic nanomaterials, Nat. Rev. Bioeng., 2023, 1(2), 88–106 CrossRef CAS.
- A. M. Evans, Comparative pharmacology of S(+)-ibuprofen and (RS)-ibuprofen, Clin. Rheumatol., 2001, 20, 9–14 CrossRef.
- S. Hamidi and A. Jouyban, Pre-concentration approaches combined with capillary electrophoresis in bioanalysis of chiral cardiovascular drugs, Pharm. Sci., 2015, 21(4), 229–243 CrossRef.
- S. S. Oh and O. Hess, Chiral metamaterials: enhancement and control of optical activity and circular dichroism, Nano Convergence, 2015, 2, 1–14 CrossRef.
- A. Y. Zhu, et al., Giant intrinsic chiro-optical activity in planar dielectric nanostructures, Light: Sci. Appl., 2018, 7(2), 17158 CrossRef CAS PubMed.
- C.-L. Yu, et al., High circular polarized nanolaser with chiral gammadion metal cavity, Sci. Rep., 2020, 10(1), 7880 CrossRef CAS PubMed.
- R. W. Woody, [4] Circular dichroism, Methods Enzymol., 1995, 246, 34–71 CAS.
- N. Berova, K. Nakanishi and R. W. Woody, Circular dichroism: principles and applications, John Wiley & Sons, 2000 Search PubMed.
- A. Lininger, et al., Chirality in light–matter interaction, Adv. Mater., 2023, 35(34), 2107325 CrossRef CAS PubMed.
- L. A. Warning, et al., Nanophotonic approaches for chirality sensing, ACS Nano, 2021, 15(10), 15538–15566 CrossRef CAS PubMed.
- X. Duan, S. Yue and N. Liu, Understanding complex chiral plasmonics, Nanoscale, 2015, 7(41), 17237–17243 RSC.
- D.-H. Kwon, P. L. Werner and D. H. Werner, Optical planar chiral metamaterial designs for strong circular dichroism and polarization rotation, Opt. Express, 2008, 16(16), 11802–11807 CrossRef CAS.
- T. Cao, et al., Strongly tunable circular dichroism in gammadion chiral phase-change metamaterials, Opt. Express, 2013, 21(23), 27841–27851 CrossRef.
- W. Bian, et al., Sandwich-type planar chiral metamaterials for exploring circular dichroism, Plasmonics, 2024, 19(1), 389–394 CrossRef.
- Y. Shen, et al., Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities, Light: Sci. Appl., 2019, 8(1), 90 CrossRef.
- M. Babiker, et al., Orbital angular momentum exchange in the interaction of twisted light with molecules, Phys. Rev. Lett., 2002, 89(14), 143601 CrossRef CAS PubMed.
- L. Allen, et al., Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes, Phys. Rev. A, 1992, 45(11), 8185 CrossRef PubMed.
- D. L. Andrews and M. Babiker, The angular momentum of light, Cambridge University Press, 2012 Search PubMed.
- J. Mun, et al., Electromagnetic chirality: from fundamentals to nontraditional chiroptical phenomena, Light: Sci. Appl., 2020, 9(1), 139 CrossRef CAS.
- T. Wu, R. Wang and X. Zhang, Plasmon-induced strong interaction between chiral molecules and orbital angular momentum of light, Sci. Rep., 2015, 5(1), 18003 CrossRef CAS.
- J. Ni, et al., Giant helical dichroism of single chiral nanostructures with photonic orbital angular momentum, ACS Nano, 2021, 15(2), 2893–2900 CrossRef CAS PubMed.
- N. Dai, et al., Robust Helical Dichroism on Microadditively manufactured copper helices via photonic orbital angular momentum, ACS Nano, 2023, 17(2), 1541–1549 CrossRef CAS PubMed.
- Y. C. Lim, et al., Strong Chiral Response of Chiral Plasmonic Nanoparticles to Photonic Orbital Angular Momentum, Adv. Opt. Mater., 2025, 13(5), 2402268 CrossRef CAS.
- C. M. Lalau-Keraly, et al., Adjoint shape optimization applied to electromagnetic design, Opt. Express, 2013, 21(18), 21693–21701 CrossRef PubMed.
- O. D. Miller, Photonic design: From fundamental solar cell physics to computational inverse design, University of California, Berkeley, 2012 Search PubMed.
- A. D. White, et al., Inverse design of optical vortex beam emitters, ACS Photonics, 2022, 10(4), 803–807 Search PubMed.
- S. Molesky, et al., Inverse design in nanophotonics, Nat. Photonics, 2018, 12(11), 659–670 CrossRef CAS.
- M. Bae, et al., Inverse design and optical vortex manipulation for thin-film absorption enhancement, Nanophotonics, 2023, 12(22), 4239–4254 CrossRef CAS.
- A. F. Oskooi, et al., MEEP: A flexible free-software package for electromagnetic simulations by the FDTD method, Comput. Phys. Commun., 2010, 181(3), 687–702 CrossRef CAS.
- A. Longman and R. Fedosejevs, Mode conversion efficiency to Laguerre-Gaussian OAM modes using spiral phase optics, Opt. Express, 2017, 25(15), 17382–17392 CrossRef CAS PubMed.
- A. M. Hammond, et al., High-performance hybrid time/frequency-domain topology optimization for large-scale photonics inverse design, Opt. Express, 2022, 30(3), 4467–4491 CrossRef CAS PubMed.
- A. Asl and M. L. Overton, Analysis of the gradient method with an Armijo–Wolfe line search on a class of non-smooth convex functions, Opt. Methods Software, 2020, 35(2), 223–242 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5nh00058k |
| ‡ These authors are equally contributed. |
| This journal is © The Royal Society of Chemistry 2025 |




