Boosting quantum efficiency and suppressing self-absorption in CdS quantum dots through interface engineering

Abstract

Applications of photoluminescence (PL) from semiconductor quantum dots (QDs) have faced the dichotomy of excitonic emission being susceptible to self-absorption and shallow defects reducing quantum yield (QY) catastrophically, and doped emissions sacrificing the tunability of the emission wavelength via a quantum size effect, making it extremely challenging, if not impossible, to optimize all desirable properties simultaneously. Here we report a strategy that simultaneously optimizes all desirable PL properties in CdS QDs by leveraging interface engineering through the growth of two crystallographic phases, namely wurtzite and zinc blende phases, within individual QDs. These engineered interfaces result in sub-bandgap emissions via ultrafast energy transfer (∼780 fs) from band-edge states to interface states protected from surface defects, enhancing stability and prolonging the PL lifetime. These sub-bandgap emissions involving the interface states show a high Stokes shift, significantly reducing self-absorption while achieving near-ideal quantum efficiencies (> 90%); we also achieved extensive emission tunability by controlling the QD size without sacrificing efficiency. Theoretical calculations confirm that the interface states act as planar antennas for an efficient energy transfer from the bandgap states, while the extended nature of these states imparts tunability via quantum confinement effects, underpinning remarkable optical performance. This interface-engineered approach offers a powerful strategy to overcome limitations in QD-based optoelectronic applications.

---

Introduction

Optical properties of semiconductor QDs have generated a lot of interest due to the discovery of size-dependent quantum confinement of charge carriers and tunability of the optical bandgap of materials.^1,2 This tunability has been made use of in various fields such as optoelectronics, biological applications, photovoltaic and photocatalytic devices, and quantum technologies.^3–6 Although early studies in this area originated from the need to understand the evolution of physical properties from molecules to bulk materials,^7,8 technological interest in creating novel materials with distinct physical properties has dominated the research in colloidal QDs in recent literature.^9–13 This shift in research interest was necessitated by the demand to solve several intrinsic problems in an otherwise novel class of materials.^14–16 For example, the unique set of properties of the QD band edge emission, such as tunability, solution processability, and reasonable stability, is eclipsed by the presence of strong self-absorption, which arises due to a small Stokes shift in emission resulting in quenching of the emission. Several strategies have been employed to address this challenge, including incorporating molecular-like states into the system with a small percentage of dopant atoms,^14,17–19 using type II interfaces to achieve smaller emission energies,^20–23 and altering the shape of QDs to induce symmetry-forbidden excitons at the Highest Occupied Molecular Orbital (HOMO) level.^24,25 Unfortunately, most of these efforts to avoid self-absorption lead to samples whose PL quantum yields are somewhat limited even in the dilute limit; in many cases, they also limit the tunability of the emission wavelength.

The PL quantum yield is also known to be seriously compromised by the presence of various defects, such as impurities, surface states, and vacancies that are universally present.^25,26 For example, it is well-known that localized surface defect traps can dramatically reduce the PL quantum yield.^27,28 Consequently, much effort has been invested in creating special structures, such as core–shell and core-graded shell structures, to remove defects that would otherwise provide states within the bandgap leading to lower energy deexcitation pathways for reducing the quantum yields.^29–33 Besides reducing bandgap photoluminescence efficiency, defect states also often give rise to sub-bandgap emissions of low efficiency, whose energy is not usually controllable with the particle size.^26,34,35 This inability to control the emission energy related to defect states arises from the fact that these involve localized states; therefore, the relevant wave functions are often insensitive to the size of the QD, limiting the scope of their application. This study aims to overcome these challenges by designing a specialized midgap state through the intergrowth of two crystallographic phases within each QD. This design allows for Stokes shifting, tunable emissions with nearly ideal quantum yield and minimal self-absorption, thus effectively addressing the limitations mentioned earlier.

The foundation of our approach lies in the realization that the energy difference between wurtzite (WZ) and zinc blende (ZB) phases is a few meV for CdS in the bulk form;^36,37 consequently, CdS nanocrystals can be stabilized both in ZB and WZ crystallographic phases by subtle tuning of synthesis conditions.³⁰ The cubic ZB structure and hexagonal WZ structure are distinguished by the closely packed layer sequence of ABCABC… and ABAB… types, respectively. In the present work, we fine-tuned the synthesis conditions to give rise to intergrowths of ZB and WZ phases within the QDs that are characterized by a layer of a wrong sequence of ABA embedded in QDs with an otherwise ZB structure (ABCABC… sequence of layer stacking). This sample will henceforth be referred to as CdS with an engineered interface in the rest of the manuscript, while the standard reference sample will be referred to as pristine CdS. The interface of the two phases in the CdS QDs with the engineered intergrowth is extended throughout the spherical QD along the interfacial plane.³⁸ The wave function corresponding to this interfacial state is expected to be essentially two-dimensional, extending all the way up to the QD boundary and, therefore, gives rise to the size-dependent tunable emissions, which is not achievable by a localized defect state present in transition metal doped QDs. In addition, most of this phase-engineered plane lies within the bulk of the nanocrystal and away from the surface; therefore, states associated with these intergrowth planes are more protected from the surface states than the band-edge states, namely, the HOMO and LUMO, of the QDs. This should help these states avoid the usual difficulties contributed by the ever-present surface defects, such as a drastic reduction in the intensity of the bandgap PL or its degradation over time. If these intergrowth planes provide energies within the bandgap of the QD, the Stokes shift associated with the emission arising from these engineered states will also largely avoid self-absorption. We report here the realization of all these attributes, showing near-ideal PL efficiency with tunability but minimal self-absorption from such specially designed CdS QDs with engineered interfaces.

Methods

Materials

Cadmium acetate, dihydrate (Cd(OAc)₂, 2H₂O, 99.9%), myristic acid (99.9%), S powder (99.9%), 1-octadecene (ODE), and oleylamine were purchased from Sigma Aldrich and were used without further purification.

Synthesis of nanocrystals

In a typical synthesis, cadmium acetate, dihydrate (26.7 mg, 1 mmol), myristic acid (76 mg, 1 mmol) and 4 ml ODE were placed in a reaction flask and heated to 220 °C for 10 minutes under an argon atmosphere. An optically clear solution was obtained. On cooling to room temperature, a turbid white suspension of cadmium myristate was obtained. At this stage sulfur powder (1.6 mg, 0.5 mmol) and 2 ml of ODE were added. The mixture was degassed thoroughly in a vacuum for 10 minutes by heating to around 100 °C and subsequently heated to 220 °C under an argon atmosphere. At 220 °C, 1 ml of oleylamine was added dropwise. The colorless solution turned yellow at this point. The reaction mixture was maintained at this temperature for 30 minutes to complete the growth of the QDs and subsequently cooled to room temperature. The presence of intergrowth planes has been established from an X-ray diffraction (XRD) pattern in these samples. The intergrowth planes can also be seen in transmission electron microscopy images with predominant Stokes shifted emission. For the synthesis of pristine QDs the same procedure was followed as described above; but finally at the last stage, the resulting sample was annealed at 250 °C for 5 hours to make all QDs free of intergrowth planes. CdS/ZnS core–shell QDs were synthesized by modifying a method reported earlier.³⁹ Details of this synthesis are discussed in the ESI.† Following the synthesis, all QDs were cleaned thoroughly in double distilled ethanol and re-dispersed in n-hexane to record optical absorption and emission spectra, and transmission electron microscope images.

Characterization

XRD patterns of the samples were recorded in a PANalytical diffractometer using Cu K_α radiation. To construct simulated diffraction patterns of both pristine QDs and interface engineered QDs, DIFFaX v1.812 software was used.⁴⁰ A model consisting of ZB CdS with various combinations of sizes and the number of WZ CdS layers as intergrowth is used to simulate diffraction patterns of interface engineered QDs. Steady state absorption spectra were recorded in a PerkinElmer 2100 DV instrument. PL emission spectra were recorded in an Edinburgh Instruments FLS920 Series fluorescence spectrometer with a 450 W continuous Xe arc lamp as an excitation source. The absolute quantum yield of the samples was measured using an integrating sphere in the fluorescence spectrometer. Time resolved PL decay was recorded by the same instrument using a time-correlated single photon counting (TCSPC) module with a 405 nm picosecond pulsed semiconductor diode laser at 5 MHz repetition rate as the excitation source. Transmission electron microscope (TEM) and high-resolution TEM (HRTEM) images were captured on a UHR FEG-TEM, JEOL JEM-2100F electron microscope using a 200 kV electron source. We recorded the up-conversion photoluminescence (UPL) decay using a dilute solution of QDs in n-hexane in a quartz cuvette with a path length of 1 mm and a 400 nm laser as the excitation source. The pump beam was generated by focusing a 100 fs 1 kHz Ti:Sapphire laser (800 nm) on a BBO crystal. The beam was focused on the sample with a cross-section of 7 × 10⁻⁴ cm²; the sample was stirred throughout the measurement to avoid photo-degradation. The luminescence was collected by parabolic mirrors using a 420 nm long pass filter. Finally, the sample emission was focused on a nonlinear BBO crystal, where it overlapped with the delayed 800 nm gate pulse. The up-converted photons were detected using a CCD detector with the help of an optical fiber.

Semi-empirical tight binding calculation of the electronic structure

An intergrowth of the WZ and ZB phases, which has been characterized experimentally in interface engineered QDs, was theoretically generated by a simple alteration of the stacking sequence of the cation and the anion in the QDs. More specifically, the clusters were generated by growing alternate shells of cation and anion surrounding a central atom keeping underlying crystallographic symmetry of either the ZB or WZ phase. The intergrowth of one structure within the other is achieved by a simple alteration of the stacking sequence since the essential difference between the ZB (ABAB….) and WZ (ABCABC…) structure is in the stacking of alternate layers of the cation (Cd) and anion (S). For example, one can incorporate a layer of ABC stack within the ABAB type as follows: …ABABABCABABAB…, where the inserted intergrowth is shown in italics. Alternately, we may have a sequence such as …ABCABCABABCABC… or multiple layers of intergrowth as well as multiple intergrowths within the same QD. Electronic structure calculations on these clusters were performed using a semi-empirical tight binding (TB) model similar to earlier reported literature.^41–43 For the TB model, a sp³d⁵ basis was used for both cation and anion and interaction up to the 2nd nearest neighbor for each atom of the system was considered. TB parameters are extracted by carrying out a least-squared error minimization fitting of the bulk ab initio band dispersion obtained from the linearized augmented plane wave (FP-LAPW) method, as reported earlier.⁴² The obtained parameters have been used directly for the electronic structure calculation of QDs. The surface states are passivated with a layer of artificial H-like atoms in the outermost shell. The eigenvalue spectrum of each of these QDs thus generated has been calculated by directly diagonalizing the TB Hamiltonian in real space. The band edge positions and the total and atom projected density of states have then been computed. The states arising from the intergrowth planes near the valence band maximum (VBM) and the conduction band minimum (CBM) were determined from the computed electronic density of states of these clusters. Dipole selection rules were used to determine the optically allowed band gap transitions⁴⁴ obtained from the symmetry-selective joint density of states calculations. Finally, to obtain the bandgap as a function of size, the excitonic binding energy due to the electron–hole attraction was subtracted as has been done in earlier literature.^1,42

Ab initio electronic structure calculations

We have also carried out ab initio electronic structure calculations within a plane wave implementation of density functional theory with VASP.^45,46 Projected augmented wave potentials⁴⁷ have been used to represent the ionic potentials. HSE06⁴⁸ have been used for the exchange–correlation functional as they have been found to accurately give the band gap of semiconductors.⁴⁹ A cut-off energy of 274.3 eV was used for the plane wave basis set, and calculations were performed for the bulk as well as a ZB–WZ heterostructure consisting of 15 layers growing in the [001] direction, consisting of 3 layers of WZ CdS sandwiched between 6 layers of ZB CdS on either side. A k-point mesh of 2 × 2 × 1 was used, with a vacuum of 20 Å in the [001] direction for the heterostructures. This has been added to reduce interactions between different units in the [001] direction, present because of the periodic implementation of the density functional theory that we use. Structural optimizations were carried out until the forces on each atom were less than 10⁻³ eV Å⁻¹. The surface atoms were passivated with pseudo-hydrogens.⁵⁰

Results and discussion

Interface engineering of CdS QDs: structural analysis

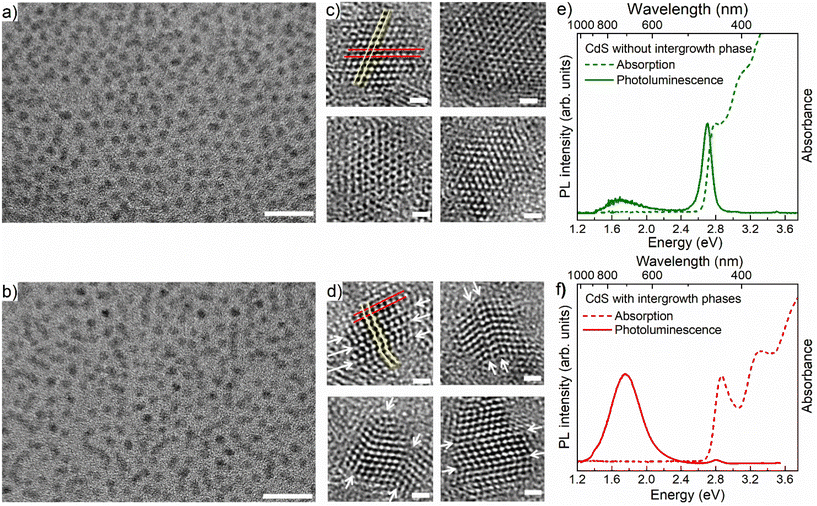
Fig. 1a and b show typical TEM images of large collections of pristine CdS QDs and interface-engineered CdS QDs, respectively, with a relatively lower resolution; corresponding high-resolution images of the same are shown in Fig. 1c and d, respectively. Details of the synthesis methodology of these two types of QDs are discussed in the Methods section. From Fig. 1a and b, it is evident that most of the particles are spherical in shape and approximately 4 nm in size for both types of QD, namely the pristine and interface-engineered QDs. Corresponding size distribution analyses are shown in Fig. S1.† While Fig. 1a and b and S1† suggest nearly identical particle sizes, shapes, and distributions, higher-resolution images in Fig. 1c and d reveal distinct differences. Well-defined lattice fringes in the latter figures indicate variations between the two samples. HRTEM images in Fig. 1c and d show a sequence of {111} planes identified by an interplanar distance of 0.34 nm. We have marked a pair of adjacent {111} planes by red lines in the first HRTEM images in Fig. 1c and d. The QDs shown in Fig. 1c, synthesized at a higher temperature (250 °C) with extended annealing (5 h), were intentionally made free of intergrowth planes. As expected, HRTEMs in Fig. 1c exhibit uniform lattice fringes across particles, confirming the absence of intergrowth planes in the pristine CdS QDs. Conversely, intergrowth planes emerge when synthesizing QDs under kinetically controlled conditions, characterized by a lower temperature (220 °C) and reduced annealing time (1/2 h). The presence of intergrowth planes is evident from the arrangement of the {111} planes in Fig. 1d. In the pristine QDs these planes are arranged in a sequence such that atoms in consecutive planes form a straight line across the entire QD, as shown by the yellow thin line in the first HRTEM image in Fig. 1c. We can also see the atomic arrangements along a line perpendicular to the red lines, showing alternate planes that appear on top positions with one plane in between these two shifted laterally, defining the ABAB… stacking of the zinc blende structure. However, in the interface engineered QDs, one can easily identify the mismatch in the sequence of these planes at multiple places in a single QD, such that the yellow line connecting atoms in consecutive planes, shown in the first HRTEM image in Fig. 1d, no longer defines a straight line. A closer look along a direction perpendicular to the red lines reveals a disruption of ABAB... pattern, giving rise to three consecutive nonrepeating planes suggestive of ABC-type arrangements of the {111} planes. We have identified locations of mismatch in the sequence of {111} planes in each HRTEM image in Fig. 1d and marked those locations by a pair of white arrows across the QDs for easy identification.

Fig. 1 Bright field TEM images of CdS quantum dots: (a) pristine CdS QDs and (b) CdS QDs with engineered interfaces. HRTEM images in (c) and (d) correspond to samples (a) and (b), respectively. A pair of adjacent {111} planes in the first HRTEM images in (c) and (d) are marked by red parallel lines. Positions of intergrowth planes are marked with white arrows in each HRTEM image of (d). Scale bars are 20 nm in length in (a) and (b) and 1 nm in each of the images in (c) and (d). Optical absorption and emission spectra (e) and (f) correspond to samples (a) and (b), respectively. QDs show predominant band edge emission as shown in (e), in the absence of an intergrowth plane, while in the presence of intergrowth planes, almost exclusively Stokes shifted sub-bandgap PL emission is seen in (f).

The exploration of intergrowths involving the ZB and WZ phases in II–VI semiconductor QDs is feasible using X-ray diffraction (XRD) analysis.^51–53 Ref. 51 investigated the effects of incorporating ZB intergrowth layers within a WZ lattice of CdSe on its XRD pattern. In our present investigation, the scenario is reversed, featuring a WZ intergrowth within a ZB structure. To understand the influence of WZ intergrowths on the diffraction patterns of these ZB QDs, we employ simulations for various numbers of intergrowth layers within the ZB cluster. The simulation considers a cluster size ranging from 3.3 to 4.7 nm, accounting for the particle size distribution determined by TEM results (refer to Fig. S1b†). The results for CdS QDs with 0%, 16.6%, 25% and 33.3% wurtzite layers distributed within the ZB structure are shown in Fig. S2a.† We conducted a comparative analysis between the experimental XRD pattern of the sample featuring extensive intergrowth planes and the simulated XRD patterns of CdS QDs in both the pure ZB phase (Fig. S2b†) and with 25% WZ intergrowth layers (Fig. S2c†). The observed mismatch between the experimental and simulated patterns of QDs in the pure ZB phase (Fig. S2b†) is evident. Notably, our analysis reveals that the simulated XRD pattern for CdS QDs with 25% WZ intergrowth layers offers the most accurate representation of the experimental XRD obtained for this particular sample, as illustrated in Fig. S2c.†

Effect of the intergrowth plane on optical properties

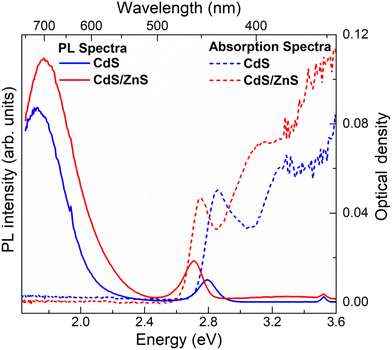
Fig. 1e and f show the absorption and PL spectra of the pristine and interface-engineered QDs, respectively. Both samples have nearly identical excitonic absorption at about 2.8 ± 0.05 eV and band edge emission maxima at about 2.75 ± 0.05 eV. The photoluminescence of these two samples exhibits a notable difference. In the interface-engineered CdS (Fig. 1f), there is a clear and prominent dominance of the greatly Stokes shifted, sub-bandgap PL emission at 1.75 eV. This is in stark contrast to the pristine CdS quantum dots (QDs) depicted in Fig. 1e, where the excitonic emission is dominant, with only a weak sub-bandgap PL emission originating from deep defect states. Evidently, there is nothing surprising about the PL emission (Fig. 1e) from the pristine CdS QDs, with its predominant band edge emission being similar to those earlier reported in the literature.^54,55

It is to be noted that interface-engineered CdS QDs were synthesized at a lower temperature (220 °C) and by annealing for a shorter time (30 minutes), which provides a kinetically controlled synthesis condition compared to the higher temperature (250 °C) and longer annealing time (5 h) used for the synthesis of the thermodynamically stable pristine CdS QDs. With the introduction of the intergrowth planes by the kinetically controlled synthetic strategy, we observe the PL to be almost exclusively dominated by a Stokes shifted PL emission compared to the absorption edge (Fig. 1f), suggesting a successful synthesis strategy. As further proof of the Stokes shifted PL emission peak arising from the presence of the interfaces at the intergrowth planes, we note that the QDs with kinetically stabilized intergrowth planes can always be converted into thermodynamically stable pristine CdS QDs by annealing at a high temperature. The consequences of such thermal annealing on the PL emission are illustrated in Fig. S3,† indicating a progressive decrease of the Stokes shifted emission relative to the bandgap emission with an increasing annealing time. This suggests that the origin of the Stokes shifted emission is the kinetically stabilized intergrowth planes and not the surface defect states. To further validate the nature of midgap states responsible for the Stokes shifted emission, interface-engineered CdS QDs were overcoated with a wide bandgap material, ZnS, which passivates the surface defect states of CdS QDs. Details of synthesis methodology and characterization of CdS/ZnS core–shell QDs are discussed in ESI.† A comparison of size distribution analyses from the TEM images (Fig. S1b and S4b†) shows an increase in size of the QDs upon overcoating with ZnS. Fig. 2 shows the optical absorption and PL emission spectra of interface-engineered CdS QDs before and after overcoating with the ZnS shell. The red shift of the excitonic absorption in the core–shell QDs (red dashed lines) compared to that in the core-only CdS QDs (blue dashed lines) indicates successful growth of the shell without any significant alloying. An alloying of CdS and ZnS would shift the bandgap of the core–shell QDs towards that of ZnS, implying a blue shift of the absorption peak. Excitonic emissions (solid lines) also show a red shift for the core–shell QDs, consistent with the red shift of the absorption spectra. We find that the Stokes shifted emission, attributed to the presence of the intergrowth states in this sample, is not quenched on overcoating the sample with ZnS, with the core–shell sample continuing to show essentially the same Stokes shifted intense PL emissions as the uncoated sample. This clearly establishes that the sub-bandgap PL emission in these QDs cannot be attributed to surface defect states in the CdS QDs, but arises from the interfaces at the intergrowth planes.

Fig. 2 Optical absorption (dashed lines) and PL emission (solid lines) spectra of interface-engineered CdS QDs are shown in blue. Those spectra of the same batch of CdS QDs after overcoating with ZnS shell are shown in red.

Tunability and quantum yield of the Stokes shifted emission

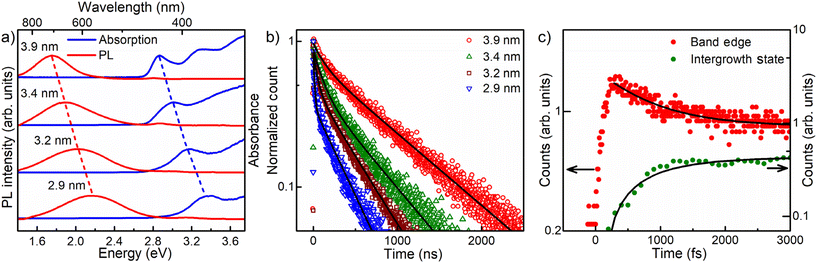
One of the desirable attributes of bandgap PL emissions from QDs is the ability it affords to tune the emission over a large range of the visible spectrum with high quantum efficiencies, thereby holding out immense possibilities of diverse applications in display and lighting technologies, including white light generation by combining different color components. Traditionally, in the literature, achieving significant tunability and high efficiency for Stokes shifted PL emissions has posed considerable challenges, with only a handful of exceptions documented.^11,19 For instance, while non-tunable Mn-doping in II–VI semiconductor quantum dots is recognized for its high quantum yield,^56,57 Mn doping in perovskite halides has demonstrated delayed emission. This delay arises from the gradual transition from Mn levels into the band edge, enhancing the efficiency.⁵⁸ Here in this work, we show that the presence of engineered interfaces in CdS QDs achieves remarkable tunability and high efficiency simultaneously. To demonstrate the tunability, we synthesized interface-engineered CdS QDs of four different sizes with average diameters of 2.9, 3.2, 3.4, and 3.9 nm, using the same synthesis methodology by varying the temperature from 170 °C to 220 °C and optimizing the growth time. TEM images and size distribution analyses of these QDs are shown in Fig. 1b, S1b and S5.† The optical absorption and PL spectra obtained from these QDs are shown in Fig. 3a. Clearly, the absorption energy decreases with increasing QD size due to the systematic deconfinement effects on the bandgap, as expected.^42,43 Most interestingly, a systematic and equally pronounced shift in the sub-bandgap PL emission is evident as a function of the QD size in Fig. 3a, establishing the tunability of this PL emission in sharp contrast to most other cases of defect emissions. We measured the absolute PL QYs of all four samples of four different sizes, using an integrating sphere, and the values obtained are tabulated in Table 1. We found extraordinarily high QY (>90%) for the three out of four samples. One of the samples shows a lower QY value (75.5%). It is to be noted that even 75% QY value has been rarely reported for any group II–VI QD sample and never for CdS QDs.

Fig. 3 (a) Evolution of optical absorption and emission spectra showing the extensive tunability of the Stokes shifted emission from the interface states at the intergrowth by changing the size of the CdS nanoparticles via quantum confinement effects. (b) Time-resolved photoluminescence intensities from the intergrowth states of the CdS QDs for four different QD sizes. The black lines represent a biexponential fit to each decay profile. (c) Up-conversion photoluminescence data of the CdS QDs (3.9 nm) with intergrowth phases for bandgap emission at 2.75 eV (red circle) and for the Stokes shifted interface state emission at 2.07 eV (green circle) with corresponding calculated fits (black solid lines).

Table 1 Results of biexponential fittings of photoluminescence decay, showing the decay time-scales (τ) and the corresponding total contributions (Aτ), and quantum yields of CdS QDs with intergrowth phases of four different sizes

Diameter (nm)	Total QY (%)	E Emission (eV)	A 1 τ 1 (%)	τ 1 (ns)	A 2 τ 2 (%)	τ 2 (ns)
2.9	92.4	2.11	4.8	14.0	95.2	352.9
3.2	92.5	2.04	7.2	50.0	92.8	450.3
3.4	75.5	1.98	12.7	111.4	87.3	631.6
3.9	99.2	1.92	4.6	129.3	95.4	880.6

---

Charge carrier dynamics in interface engineered CdS QDs

To understand the underlying carrier dynamics responsible for these remarkable optical properties arising from interface-engineered CdS QDs, we recorded the time-resolved PL decay of both band-edge and intergrowth-related red-shifted emissions of the four sizes of CdS QDs, as mentioned earlier in the text. The time-resolved band-edge emission intensities are shown in Fig. S6.† The results of fitting these intensity decay profiles are shown in Table S1.† We found the time-dependence of the PL intensity requiring two decay time scales in all four cases, with the faster one at ∼1 ns and a slower one (∼10–20 ns). The contribution from the slower decay process was found to increase systematically with the QD size, becoming ∼78% for the larger QDs. Therefore, we associate this slower decay channel to the intrinsic excitonic emission process while attributing the faster decay channel from contributions arising from the presence of shallow trap states, such as surface states.^59,60

The emission arising from the interface-engineered states shows an interesting dependency of the emission lifetime on the QD size, as shown in Fig. 3b. It was found that these emission decays could be described for all four QDs with a minimum of two decay constants, employing the bi-exponential function A₁exp(−t/τ₁) + A₂exp(−t/τ₂). The results of exponential fitting of the decay profile of these samples are listed in Table 1, establishing systematic trends with the QD size. To begin with, we note that the second decay component, with a lifetime of τ₂, dominates PL intensity with a contribution (A₂τ₂) ≥ 90% in most cases. Since the emissions from the interface-engineered QDs have QY ≥ 90%, it is clear that τ₂ is the lifetime of the recombination responsible for the intense sub-bandgap emission. We attribute the shorter timescale, τ₁, arising from decay channels involving defect states with minor contributions, mostly less than 10% as evidenced by the values of A₁τ₁ shown in Table 1. Such decay channels are provided by deep defect levels of the system, as can also be seen from the broad weak sub-bandgap emission from the pristine sample without any intergrowth states, as shown in Fig. 1e.

Despite a very short τ₁ compared to τ₂, the net contribution (A₁τ₁) from this nonradiative decay channel is uniformly small across all four samples. This is, of course, the root of the extraordinarily high QYs of these samples, and its origin possibly lies in the fact that the intergrowth planes are mostly protected from surfaces, meeting the surface only along a line, unlike the bandgap states that span essentially the entire surface of the QDs. This ensures relatively small magnitudes of matrix elements to transfer charges or energy from the interface-engineered states to localized surface defect states. This leads to low probabilities of such processes that adversely affect the quantum yields. Both τ₁ and τ₂ increase monotonically with the increase in the size of the QDs, as seen from the data in Table 1. Such a systematic increase of time constants reflects the increase in the spatial extent of the states arising from the intergrowth planes with the increase in the QD size.

We note that the very short time-scale dynamics of population and decay of states responsible for the Stokes shifted emission cannot be probed via TCSPC measurements, appearing as the sharp, almost vertical, rise near the zero of the time-axis in Fig. 3b, due to the inherent resolution limitation of this technique. To probe this important short time domain, we study the charge dynamics of CdS QD ensembles in the femtosecond timescale using up-conversion photoluminescence (UPL) measurements. The PL emission kinetics for band-edge and intergrowth states are shown for 3.9 nm CdS QDs with intergrowth planes in Fig. 3c. The result of the band edge emission shown with the red filled circle shows a sharp rise within the first ∼270 fs followed by a multi-exponential decay. The results of exponential fits are shown in Table S2.† This initial rapid increase of the band edge emission intensity reflects the timescale of exclusively populating the band-edge states following the photoexcitation. The multi-exponential decay indicates the presence of more than one process contributing to the PL, one of which is much larger than the timescale of the instrument (∼3000 fs), as apparent from the approximate flatness of the decay plot in the longer time regime; this is consistent with the recombination timescale of tens of nanoseconds obtained from the TCSPC measurements. However, there is clearly a faster process leading to the decay of the UPL signal for the bandgap emission in Fig. 3c, and our fitting, shown by the black line through the data points, estimates the timescale of this decay of the PL intensity to be ∼780 fs. We have also shown the UPL data for the sub-bandgap emission at 2.07 eV from the interface states of the intergrowth of phases with the green filled circle in Fig. 3c; this plot makes it obvious that the kinetics of populating the intergrowth state is slower compared to that for the band-edge emission, as evidenced by the slower rise of the intergrowth state emission signal. The increase in the upconverted photoluminescence (UPL) of the sub-bandgap emission is also given by a rise time of ∼780 fs, as shown by the fitted line through the data points, which is in agreement with the decay time of the bandgap emission. This suggests that the interface states are not directly populated in the excitation step but are populated via a fast, sub-ps time-scale, sensitization from the bandgap states.

Consequences of intergrowth planes on the electronic structure

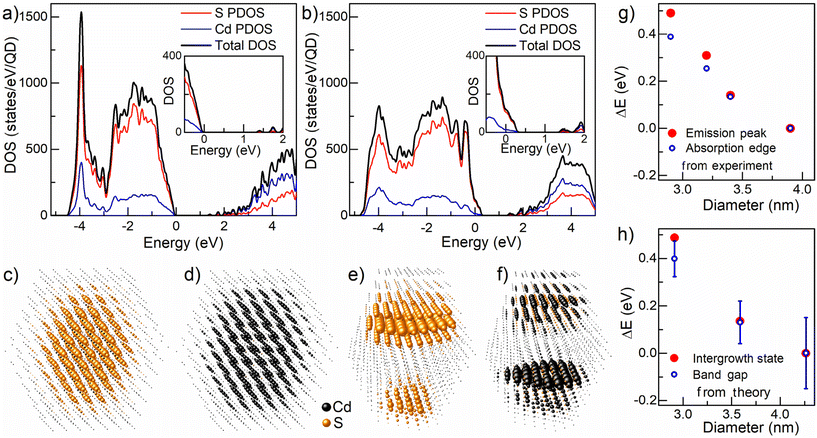
To understand the microscopic origin of this sub-picosecond energy transfer, we turn our attention to detailed electronic structure calculations. We discuss our results in terms of the energy distribution of the electronic states and the nature of the corresponding wave functions associated with such ZB and WZ intergrowth planes vis-à-vis those of the pristine CdS QDs. We have performed the electronic structure calculation using the semi-empirical tight binding method and details of the calculation are discussed in the Methods section. The overall electronic density of states (DOS) of pristine CdS QDs and interface-engineered CdS QDs are shown in Fig. 4a and b, respectively. The top of the valence band of the pristine CdS QDs is marked as zero on the energy scale. While overall features remain similar between the two cases (Fig. 4a and b), these results clearly show the introduction of new electron states in the presence of the intergrowth planes just above the zero on the energy scale with an expanded view shown in the inset to Fig. 4b for clarity. The bottom of the conduction band shows modifications for the sample with intergrowth planes compared to the pristine QDs in terms of the DOS but not in terms of any energy shift. The low densities of states involved in extending the top of the valence band do not impact the absorption spectrum significantly, as illustrated by the dipole-selection rule imposed, symmetry-selective joint densities of states shown for the pristine CdS QDs present in the ZB phase and QDs with intergrowth planes in Fig. S7.† While we show results for only one size of the QDs in Fig. S7,† we found very similar results for different sizes as well. This indicates that the bandgaps estimated from the absorption edges, as done experimentally, will not be very different between the QDs of the same size present in the pristine sample and QDs with intergrowth planes, in agreement with experimental results. However, photoluminescence always involves the lowest accessible energy states; this implies that the hole will transfer itself to the top of the occupied state and the electron to the bottom of the unoccupied states in every case. This ensures that the PL, in the case of the QDs present in the intergrowth planes, will make use of the low density of states extension above the valence band and below the conduction band, thereby reducing its energy (red-shifted) with respect to the measured bandgap. The PL of the QDs present in the ZB phase, of course, appears at the bandgap, not considering the small corrections due to the excitonic binding energy.

Fig. 4 Total and atom-resolved electronic density of states of (a) pristine ZB CdS QDs and (b) CdS QDs with the engineered interface of ∼4 nm diameter. Insets in figures (a) and (b) show enlarged views of the band edge region. Weights of the wave functions of (c) the top of the occupied states (TOS) and (d) the bottom of the unoccupied states (BUS) of the same ZB CdS QD. Corresponding wave-function weights for (e) TOS and (f) BUS of the CdS QDs with an engineered interface of similar size. In (c)–(f), the size of the sphere at any atomic site is proportional to the total weight of the wave function at that site. Variation of intergrowth state energy and band gap with size (g) from experimental absorption and emission spectra and (h) from theoretically calculated electronic structure. These variations are shown with respect to the largest-sized QD considered in each case (experiment and theory).

Since PL is controlled by the top of the occupied states (TOS) and the bottom of the unoccupied states (BUS), the site-projected weights of the corresponding wave functions are shown in Fig. 4c–f, representing the spatial extension of the relevant wave functions responsible for the PL in each case. Fig. 4c and d represent site-projected weights of the TOS and BUS of the pristine QDs, respectively, while Fig. 4e and f represent corresponding weights for the QDs with intergrowth planes. While the overall DOS in Fig. 4a and b are quite similar, visual representations of only those wave functions that are relevant for the PL in Fig. 4c–f underscores the drastic differences between the pristine CdS QDs present in the ZB phase (Fig. 4c and d) and interface engineered CdS QDs (Fig. 4e and f). We note from Fig. 4a and b that the position of TOS of the interface engineered QDs shifts towards higher energy while the position of BUS remains unchanged compared to those of the pristine QDs, establishing a red-shifted PL for the interface engineered CdS QDs. We shall now consider how these spatial distributions of the pertinent wave functions aid in comprehending the origin of the experimental observations presented in this study. A distinct perspective on the site-projected weights of the TOS and BUS is presented in Fig. S8,† clearly illustrating the localization of wave functions at the interface region of the interface-engineered quantum dot compared to the pristine quantum dots. The wave functions for TOS and BUS in the pristine QDs (Fig. 4c and d) are expectedly found to be distributed throughout the QDs, with higher weights near the center but gradually extending towards the surface and the near-surface regions of the nanocrystal; this makes them susceptible to transfer energy to defect states localized near the surface. In contrast, the interface states in the interface-engineered quantum dots avoid substantial portions of the surface and near-surface regions, remaining confined to the interface layers within the bulk of the quantum dots. This protected nature of the intergrowth states is responsible for the high quantum yields achieved here from the Stokes shifted emissions; the large Stokes shifts (Fig. 1f) also help achieve high quantum yields by forbidding energy transfers to shallow defect levels that lie at higher energies.

Clearly, the extraordinarily high QYs are not only ensured by the protected nature and the energetics of the TOS and BUS in the interface-engineered QD; these spectacular QYs are also crucially dependent on the extremely fast (∼780 fs) transfer of the excitation from the higher energy bandgap states reached by the photoexcitation process as evidenced in Fig. 3c. This is much faster than the lifetime (∼10–20 ns) of the bandgap PL emission, ensuring almost complete transfer of the excitation to the intergrowth states. This extremely fast process is achieved by the antenna-like effect of the intergrowth states, as can be easily visualized by comparing each layer with the calculated band edge positions shown in Fig. 4c and e, as well as in Fig. 4d and f. Evidently, the intergrowth states (Fig. 4e and f) extend across the QDs along a plane where the bandgap states (Fig. 4c and d) also exhibit the most significant contributions. The extended wave function along the interface of the intergrowth structures acts as planar antennas, facilitating the rapid transfer of bandgap excitations to the planes at the interface region. These calculated results also explain the prolonged lifetime (∼350–900 ns) associated with the photoluminescence from these intergrowth states in terms of the spatial localization of the TOS and BUS on opposite interfaces across the intergrowth structures within the nanocrystal.

Going beyond the above qualitative explanations for the experimental observations, these theoretical considerations also provide quantitative estimates of shifts in the absorption spectra and shifts in the PL emission from both types of samples as a function of the QD size. As already discussed, shifts in the absorption spectra can be calculated from the dipole-symmetry selected joint densities of states for each system, while the shifts in the emission position can be estimated from the smallest gap existing in each system including the mid-gap states formed due to presence of intergrowth planes in interface engineered QDs. The shift in emission peaks for pristine QDs is trivial, expectedly tracking the shift in the absorption edges as a function of the QD size and therefore, not discussed further here. Experimental shifts for quantum dots with intergrowth planes (see Fig. 1f), measured with the largest-sized (∼3.9 nm) quantum dots as the reference, are depicted in Fig. 4g. The open blue circles illustrate the shift in the absorption edge, while the red filled circles indicate the shifts in the emission peak. It is clear from this figure that the emission peak, although substantially shifted from the absorption peak, shows a similar extent of tuning with the QD size, illustrating the wide tunability achieved here for a Stokes shifted sub-bandgap PL emission for the first time. The corresponding calculated values are depicted in Fig. 4h, showcasing the remarkable ability of the calculated results to provide a quantitative explanation for the experimental data in Fig. 4g. This establishes a clear interpretation of the emission peaks as originating from the intergrowth states on a quantitative basis.

To complement the tight-binding calculations, we have also performed ab initio density functional theoretical calculations using hybrid HSE06 functionals for both bulk ZB CdS and a specific finite-sized heterostructure with a total thickness of 4.6 nm consisting of a 3-layer CdS with the WZ structure sandwiched between two 6-layer ZB CdS. The effectiveness of the HSE06 level of calculations is first confirmed by the calculated bandgap (2.5 eV) of the pure ZB CdS bulk system in agreement with experimental results. This approach is applied to calculate the electronic structure of the interface-engineered heterostructure of ZB(6)–WZ(3)–ZB(6). We have analyzed the results in terms of the orbital momentum- and layer-resolved charge densities for all electron states, including the valence band maxima and conduction band minima, and found the band alignments of the three layers, which are shown in Fig. S9 of the ESI,† defining the QD heterostructure as one with Type II interfaces. As the wurtzite layer has an intrinsic dipole moment associated with it, an electric field is set up that points from the bottom layer to the top layer. This leads to a shift of the band edges of each layer with the calculated band edge positions shown in green in Fig. S9.† We found a calculated difference between the TOS and BUS of ∼1.6 eV in quantitative agreement with our experimental PL results. These results provide a quantitative explanation for the significantly Stokes shifted emissions from these samples with the intergrowth structure.

Reduced self-absorption and white light emission from interface engineered QDs

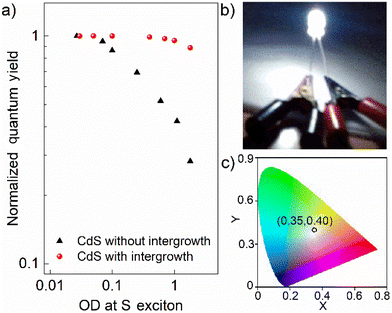
Finally, even though one obtains a high QY in dilute QDs, very often, these exceptional optical characteristics lose their utility for practical applications, such as in LEDs, due to self-absorption. Self-absorption swiftly diminishes the effective quantum efficiency of a macroscopic ensemble of these QDs. Hence, measuring QY as a function of increasing optical density (OD) is critical for practical applications. Fig. 5a shows the normalized quantum yields as a function of the OD at the S exciton of the pristine and interface-engineered CdS QDs. All samples were excited at 3.54 eV to measure these quantum yields. For the pristine CdS QDs, the PL quantum yield is mainly from the contribution of the band edge emission, which has a significant overlap with the optical absorption spectrum, as shown in Fig. 1e. Consequently, we find a significant decrease in the emission quantum yield at high optical densities for the pristine CdS, indicating a pronounced self-absorption. On the other hand, for interface-engineered CdS QDs, we see that the quantum yield remains essentially invariant with the optical density. This invariance of the intergrowth plane related PL emission with the number density of QDs in the medium directly verifies the reduced self-absorption. This pronounced suppression of self-absorption is, of course, a consequence of large Stokes shifts of the PL arising from these intergrowth planes (see Fig. 1f). Fortuitously, it turns out that the PL spectrum of 3.0 nm CdS with the intergrowth planes essentially gives rise to a nearly pure white emission due to its appropriate coverage of the visible region of the electromagnetic spectra. Coupled with the strong suppression of the self-absorption process, this makes it an ideal source for white light generation for lighting applications. We demonstrate this by dispersing this sample in a PMMA matrix to coat a UV diode for the generation of white light. This UV diode acts as a colorless excitation source. Upon passing current, the diode emits UV radiation that is absorbed by the overcoated QD film with a high optical density to maximize the absorption; the UV photoexcited electrons and holes recombine almost exclusively via the intergrowth states to emit white light that pass through the film without self-absorption, giving rise to the white light as shown in Fig. 5b with the corresponding CIE coordinates shown in Fig. 5c, thereby establishing itself as a promising single-component white light emitter. Additionally, we also found that these interface-engineered CdS QDs show significant photostability when irradiated with a UV source. Fig. S10† shows the OD normalized PL emission spectra for as prepared sample and the same sample after being illuminated by a 4 W UV lamp for 6 hours. We find that the emission spectra are almost identical, exhibiting a remarkable photostability over a long period of time.

Fig. 5 (a) The normalized quantum yield of CdS QDs without and with intergrowth phases as a function of optical density (OD) at S exciton. (b) Prototype device, emitting white light after coating a UV LED with 3.0 nm diameter CdS quantum dots with designed intergrowth phases embedded in PMMA. (c) Coordinate in CIE diagram shows that emission from this CdS-coated LED is in the white region.

Conclusions

We have shown that controlled intergrowth planes generated inside the bulk of CdS QDs give rise to a sizeable red-shifted PL spectrum with all the desirable properties and avoid all known disadvantages of QD bandgap and dopant emissions. A series of samples establish near-ideal quantum efficiency, the absence of self-absorption, and a wide tunability of the emission. The emission characteristics allow us to establish a proof of concept for a white light LED based on a single component. We have used a semi-empirical tight binding theory and ab initio density functional theory to provide a microscopic understanding of these remarkable properties. The use of carefully introduced intergrowth planes in QDs to modify their properties via the interface states opens the door to a fundamentally new way to tune the optical properties of such semiconductor QDs.

Author contributions

S. D.: methodology, data curation, software, formal analysis, and writing the original draft. B. B.: methodology, data curation, and review/editing of the final draft. A. M.: data curation, and review/editing of the final draft. P. M.: data curation and review/editing of the final draft. A. M.: data curation and review/editing of the final draft. A. D.: data curation and review/editing of the final draft. A. P.: methodology, validation, and review/editing of the final draft. P. M. software and review/editing of the final draft. R. V. resources, supervision, and writing of the final draft. D. D. S. conceptualization, resources, supervision, project administration, funding acquisition, and writing of the final draft.

Data availability

The data supporting this article have been included in the main manuscript or as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Rohit Rohj for his help in X-ray diffraction measurements. The authors also thank IISc, JNCASR, Science and Engineering Research Board (SERB), and the Department of Science and Technology, Government of India, for financial support. SD thanks CSIR for a research fellowship. AD acknowledges SERB, India, for the National Post-Doctoral Fellowship (PDF/2016/002531). DDS thanks the Jamsetji Tata Trust and the CSIR Bhatnagar Fellowship for their support.

References

1. L. E. Brus, J. Chem. Phys., 1984, 80, 4403–4409.
2. E. Jang and H. Jang, Chem. Rev., 2023, 123, 4663–4692.
3. R. Gill, M. Zayats and I. Willner, Angew. Chem., Int. Ed., 2008, 47, 7602–7625.
4. M. V. Kovalenko, L. Manna, A. Cabot, Z. Hens, D. V. Talapin, C. R. Kagan, V. I. Klimov, A. L. Rogach, P. Reiss, D. J. Milliron, P. Guyot-Sionnnest, G. Konstantatos, W. J. Parak, T. Hyeon, B. A. Korgel, C. B. Murray and W. Heiss, ACS Nano, 2015, 9, 1012–1057.
5. J. M. Pietryga, Y.-S. Park, J. Lim, A. F. Fidler, W. K. Bae, S. Brovelli and V. I. Klimov, Chem. Rev., 2016, 116, 10513–10622.
6. C. R. Kagan, L. C. Bassett, C. B. Murray and S. M. Thompson, Chem. Rev., 2021, 121, 3186–3233.
7. L. E. Brus, P. F. Szajowski, W. L. Wilson, T. D. Harris, S. Schuppler and P. H. Citrin, J. Am. Chem. Soc., 1995, 117, 2915–2922.
8. M. Nirmal and L. Brus, Acc. Chem. Res., 1998, 32, 407–414.
9. A. Saha, K. V. Chellappan, K. S. Narayan, J. Ghatak, R. Datta and R. Viswanatha, J. Phys. Chem. Lett., 2013, 4, 3544–3549.
10. D. D. Sarma, P. K. Santra, S. Mukherjee and A. Nag, Chem. Mater., 2013, 25, 1222–1232.
11. A. Hazarika, A. Pandey and D. D. Sarma, J. Phys. Chem. Lett., 2014, 5, 2208–2213.
12. A. Saha, A. Figueroba and G. Konstantatos, Chem. Mater., 2020, 32, 2148–2155.
13. Y. Liu, Y. Gao, Q. Yang, G. Xu, X. Zhou, G. Shi, X. Lyu, H. Wu, J. Liu, S. Fang, M. I. Ullah, L. Song, K. Lu, M. Cao, Q. Zhang, T. Li, J. Xu, S. Wang, Z. Liu and W. Ma, Angew. Chem., Int. Ed., 2023, 62, e202300396.
14. N. Pradhan and X. Peng, J. Am. Chem. Soc., 2007, 129, 3339–3347.
15. F. S. Riehle and K. Yu, Chem. Mater., 2020, 32, 1430–1438.
16. H. Zhang, C. Sun, L. Sun, W. Xu, W. Wu, J. Chen, B. Wang, J. Yu, P. Cui, F. Zhang and Y. Tang, Angew. Chem., Int. Ed., 2022, 61, e202203851.
17. N. Pradhan and D. D. Sarma, J. Phys. Chem. Lett., 2011, 2, 2818–2826.
18. G. K. Grandhi and R. Viswanatha, J. Phys. Chem. Lett., 2013, 4, 409–415.
19. A. Hazarika, A. Layek, S. De, A. Nag, S. Debnath, P. Mahadevan, A. Chowdhury and D. D. Sarma, Phys. Rev. Lett., 2013, 110, 267401.
20. R. Xie, X. Zhong and T. Basché, Adv. Mater., 2005, 17, 2741–2745.
21. S. Sengupta, N. Ganguli, I. Dasgupta, D. D. Sarma and S. Acharya, Adv. Mater., 2011, 23, 1998–2003.
22. A. Saha, S. Chattopadhyay, T. Shibata and R. Viswanatha, J. Mater. Chem. C, 2014, 2, 3868–3872.
23. A. Dalui, A. Chakraborty, U. Thupakula, A. H. Khan, S. Sengupta, B. Satpati, D. D. Sarma, I. Dasgupta and S. Acharya, J. Phys. Chem. C, 2016, 120, 10118–10128.
24. Z. Yu, J. Li, D. B. O’Connor, L. W. Wang and P. F. Barbara, J. Phys. Chem. B, 2003, 107, 5670–5674.
25. P. Geiregat, A. J. Houtepen, L. K. Sagar, I. Infante, F. Zapata, V. Grigel, G. Allan, C. Delerue, D. Van Thourhout and Z. Hens, Nat. Mater., 2017, 17, 35.
26. L. R. Powell, Y. Piao, A. L. Ng and Y. Wang, J. Phys. Chem. Lett., 2018, 9, 2803–2807.
27. N. Chestnoy, T. D. Harris, R. Hull and L. E. Brus, J. Phys. Chem., 1986, 90, 3393–3399.
28. A. J. Houtepen, Z. Hens, J. S. Owen and I. Infante, Chem. Mater., 2017, 29, 752–761.
29. P. K. Santra, R. Viswanatha, S. M. Daniels, N. L. Pickett, J. M. Smith, P. O'Brien and D. D. Sarma, J. Am. Chem. Soc., 2009, 131, 470–477.
30. A. Nag, A. Hazarika, K. V. Shanavas, S. M. Sharma, I. Dasgupta and D. D. Sarma, J. Phys. Chem. Lett., 2011, 2, 706–712.
31. G. K. Grandhi, R. Tomar and R. Viswanatha, ACS Nano, 2012, 6, 9751–9763.
32. E. Marino, T. E. Kodger, R. W. Crisp, D. Timmerman, K. E. MacArthur, M. Heggen and P. Schall, Angew. Chem., Int. Ed., 2017, 56, 13795–13799.
33. N. Kirkwood, J. O. V. Monchen, R. W. Crisp, G. Grimaldi, H. A. C. Bergstein, I. du Fossé, W. van der Stam, I. Infante and A. J. Houtepen, J. Am. Chem. Soc., 2018, 140, 15712–15723.
34. S. Ithurria, P. Guyot-Sionnest, B. Mahler and B. Dubertret, Phys. Rev. Lett., 2007, 99, 265501.
35. R. Zeng, T. Zhang, G. Dai and B. Zou, J. Phys. Chem. C, 2011, 115, 3005–3010.
36. S. Datta, T. Saha-Dasgupta and D. D. Sarma, J. Phys.: Condens. Matter, 2008, 20, 445217.
37. S. Datta, M. Kabir, T. Saha-Dasgupta and D. D. Sarma, J. Phys. Chem. C, 2008, 112, 8206–8214.
38. Y. Gao and X. Peng, J. Am. Chem. Soc., 2014, 136, 6724–6732.
39. D. Chen, F. Zhao, H. Qi, M. Rutherford and X. Peng, Chem. Mater., 2010, 22, 1437–1444.
40. M. M. J. Treacy, J. M. Newsam and M. W. Deem, Proc. R. Soc. London, Ser. A, 1991, 433, 499–520.
41. S. Sapra, N. Shanthi and D. D. Sarma, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 205202.
42. S. Sapra and D. D. Sarma, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 125304.
43. R. Viswanatha, S. Sapra, T. Saha-Dasgupta and D. D. Sarma, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 045333.
44. S. Gokhale, S. R. Barman and D. D. Sarma, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 14526–14530.
45. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
46. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
47. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
48. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106.
49. A. J. Garza and G. E. Scuseria, J. Phys. Chem. Lett., 2016, 7, 4165–4170.
50. X. Huang, E. Lindgren and J. R. Chelikowsky, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 165328.
51. C. B. Murray, D. J. Norris and M. G. Bawendi, J. Am. Chem. Soc., 1993, 115, 8706–8715.
52. J. N. Wickham, A. B. Herhold and A. P. Alivisatos, Phys. Rev. Lett., 2000, 84, 923–926.
53. A. G. Butterfield, L. T. Alameda and R. E. Schaak, J. Am. Chem. Soc., 2021, 143, 1779–1783.
54. W. W. Yu, L. Qu, W. Guo and X. Peng, Chem. Mater., 2003, 15, 2854–2860.
55. Y. C. Cao and J. Wang, J. Am. Chem. Soc., 2004, 126, 14336–14337.
56. B. B. Srivastava, S. Jana, N. S. Karan, S. Paria, N. R. Jana, D. D. Sarma and N. Pradhan, J. Phys. Chem. Lett., 2010, 1, 1454–1458.
57. S. Acharya, D. D. Sarma, N. R. Jana and N. Pradhan, J. Phys. Chem. Lett., 2010, 1, 485–488.
58. K. R. Pradeep, P. Jain, K. Gahlot, A. Yadav, A. Camellini, M. Zavelani-Rossi, G. Cerullo, C. Narayana, S. Narasimhan and R. Viswanatha, ACS Energy Lett., 2020, 5, 353–359.
59. G. Schlegel, J. Bohnenberger, I. Potapova and A. Mews, Phys. Rev. Lett., 2002, 88, 137401.
60. X. Wang, L. Qu, J. Zhang, X. Peng and M. Xiao, Nano Lett., 2003, 3, 1103–1106.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr02990a

---