Electronic and geometric effects in an Au@NiO core–shell nanocatalyst on the oxidative esterification of aldehydes

Abstract

Strong metal–support interactions (SMSIs) are important in heterogeneous catalysis to control stability, activity, and selectivity. Core–shell nanostructures as a unique SMSI system not only stabilize the metal nanoparticles in the core, but also offer tunable structural and electronic properties via their interaction with the support shell. The Au@NiO_x core–shell system, for example, is the first commercial nanogold catalyst to produce bulk chemicals via the oxidative esterification of aldehydes. However, how the SMSI effect in Au@NiO_x manifests on its oxidative esterification activity is unclear. Here we use a model of an Au₁₃@(NiO)₄₈ core–shell nanocatalyst to examine the Au–NiO interaction and the associated electronic and geometric factors in enabling the oxidation of a hemiacetal (an intermediate from a ready reaction between an aldehyde and an alcohol) to an ester. We found 1.27 (e⁻) electrons flowing from the NiO shell to the Au core, leading to a higher oxide state of Ni atoms and the stabilization of key intermediates on the NiO shell. More importantly, lower activation energy was found on the Au₁₃@(NiO)₄₈ catalyst than on the Au(111) and NiO(100) surfaces for the rate-limiting step. Microkinetic modeling confirmed the high activity of the Au₁₃@(NiO)₄₈ catalyst in ester production in the experimental temperature range. Our work demonstrates the unique geometric and electronic effects of the Au@NiO_x core–shell nanostructure on the catalytic oxidative esterification of aldehydes.

---

Introduction

Oxide supports can not only increase the thermal stability of metal nanoparticles (NPs) and maintain dispersion, but also influence catalytic properties arising from strong metal–support interactions (SMSIs).¹ These interactions alter catalytic properties via charge transfer between the metal and support, creating new catalytically active sites at the interfaces by taking advantage of the synergy between the metal and the support materials.^2,3 Tauster et al. reported the first SMSI of Group 8–10 noble metals supported on TiO₂ and found that the SMSI reduces the chemisorption capacity of H₂ and CO on metals to nearly zero.⁴ Since then, the SMSI effect has been explored in other metal oxides (for instance, V₂O₃,⁵ Nb₂O₅,⁶ Ta₂O₅,⁷ and CeO₂ ⁸) and metal NPs (such as Au,⁹ Cu,¹⁰ and Ni¹¹). Meanwhile, supported Au nanocatalysts have attracted extensive interest since the pioneering discoveries by Haruta,¹² Hutchings,¹³ and Goodman,¹⁴ owing to their effectiveness in catalyzing many important reactions.^15–17 However, the commercialization of Au nanocatalysts has been hampered by the fact that Au NPs are liable to sinter during reactions or even under storage.¹⁸

As a special SMSI system, the core–shell design of a metal NP inside an oxide shell not only stabilizes metal core NPs, but also introduces tunable structural and electronic properties arising from the core–shell interaction.¹⁹ For instance, Dai and coworkers tuned the Au₁₄₄@Fe₂O₃ core–shell catalyst to increase the catalytic activity for CO oxidation.²⁰ Zhang et al. manipulated the TiO_x overlayer on Ru nanocatalysts to regulate their catalytic reactivity for the Fischer–Tropsch synthesis,²¹ while Polo-Garzon et al. found alcohol-induced formation of TiO_x on Au NPs that can be controlled to fully or partially cover surface Au sites to modulate CO oxidation activity.²²

The first commercial Au nanocatalyst for the production of bulk chemicals was based on a core–shell design: Suzuki et al. invented the Au@NiO_x core–shell catalyst that was found to have high activity, selectivity, and long lifetime for the aerobic oxidative esterification of aldehydes, compared with conventional supported Au NP catalysts.²³ Esterification is one of the most fundamental transformations in organic synthesis and the product ester is widely used in industries and cosmetics. Aerobic oxidative esterification of aldehydes with alcohols is an attractive method for the synthesis of esters because of its environmentally benign and neutral conditions. To understand the high activity of the Au@NiO_x core–shell catalyst for oxidative esterification of aldehydes, Hayashi et al. employed a NiO/Au slab model to represent the Au@NiO_x core–shell NP and simulated the reaction pathways of direct oxidative esterification using density functional theory (DFT).^24,25 Their findings attributed the high activity to the strong basic site on the NiO surface due to Ni vacancies in the subsurface. However, it remains unclear whether these findings based on the slab model can be directly translated to the real catalyst, which comprises 2–3 nm Au NPs with a thin NiO_x shell.

Given the rich sites on a NP surface such as corners and edges, the study of oxidative esterification using a true Au@NiO_x core–shell model instead of the NiO/Au slab model could offer new and more insights into the geometric effect of the core–shell structure on the reaction. Herein, we employ a core–shell model of the Au@NiO_x NP catalyst in our DFT computation to examine the geometric structure and electronic interaction between the metal core and the oxide shell and their impacts on oxidative esterification. For comparison, we also examine the Au(111) and NiO(100) surfaces. Microkinetic modeling (MKM) will be further used, based on DFT energetics, to simulate the catalytic activity. Below, we first explain in detail the DFT method, our catalyst models, and the MKM approach.

Computational details

All the DFT calculations were performed with the Vienna ab initio simulation package (VASP).^26,27 The electron–core interactions were described by the projected augmented wave (PAW) method²⁸ and electron exchange–correlation was expressed at the generalized gradient-approximation (GGA) level using the Perdew–Burke–Ernzerhof (PBE) functional.²⁹ A cutoff energy of 500 eV was adopted for the plane-wave basis set. All calculations were performed with spin polarization. For structural optimization, a convergence threshold of 0.02 eV Å⁻¹ was set in force and the total energy was converged to within 10⁻⁵ eV. van der Waals interaction was included via Grimme's method (DFT-D3).³⁰ DFT+U was used for the chemistry on NiO (100),³¹ with U − J = 6.3 eV.³²

The Au₁₃@(NiO)₄₈ core–shell NP was constructed from the icosahedral Au₅₅ NP³³ by replacing its outer layer with NiO. This was followed by placing the core–shell NP inside a 25 × 25 × 25 ų cubic box and fixing the center Au atom. Only the Γ-point was used for sampling the Brillouin zone for the core–shell model. For the NiO(100) and Au(111) slabs, a five-layered 4 × 4 supercell of 40 Ni and 40 O atoms and a four-layered 4 × 4 supercell of 64 Au atoms were constructed, respectively. A vacuum layer of 15 Å was added in the z direction and the Brillouin zone was sampled using a 3 × 3 × 1 k-point mesh for the two slab models.

Simulated annealing via ab initio molecular dynamics (AIMD) was performed at 500 K for 500 steps (1 fs per step), followed by cooling to 300 K to relax the core–shell model before the DFT geometry optimization. The quasi-Newton algorithm^34–36 was used to obtain stable and transition-state structures. To locate the transition state (TS), the climbing-image nudged elastic band (NEB)^37,38 method was used with a convergence criterion of 0.05 eV A⁻¹. The adsorption energy of key species on the surface was calculated according to E_ads = E_sur–mol − E_sur − E_mol, where E_sur–mol, E_sur, and E_mol represent the energies of the adsorbed configuration, the surface, and the isolated adsorbate, respectively. Bader charge analysis was used to obtain the partial atomic charges.³⁹ VESTA was used to draw the structures.⁴⁰

The MKMCXX code was used for microkinetic modeling.⁴¹ A simple plug flow reactor mode was assumed under the reaction conditions of 300–700 K and 1.0 bar for a mixture of 40% aldehydes, 40% methanol, and 20% O₂ balance in mole fractions. More details can be found in the ESI.†

Results and discussion

Pathways of the oxidative esterification of acetaldehyde with methanol

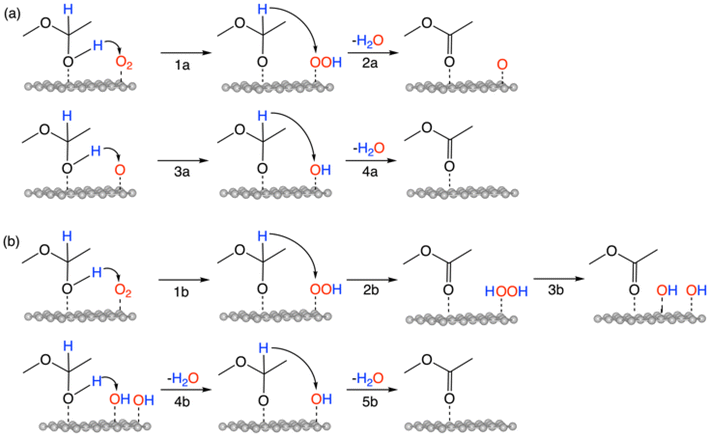
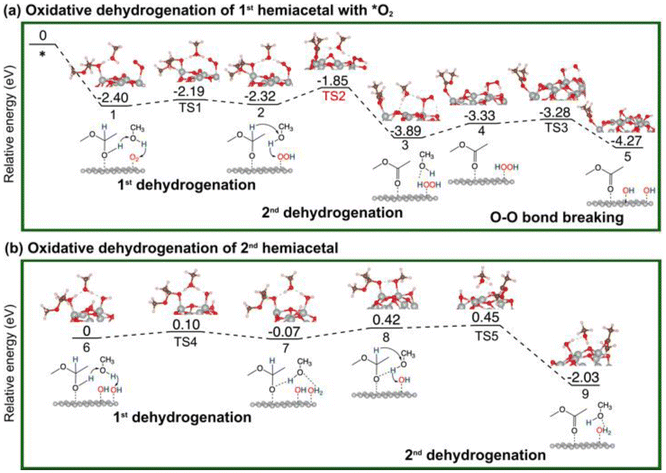
The overall reaction of oxidative esterification involves two molecules of aldehyde reacting with two molecules of alcohol and one molecule of O₂ to produce two molecules of ester and two molecules of water. The commercial process converts methacrolein and methanol to methyl methacrylate (MMA), a monomer used in the production of acrylic plastics. Here for simplicity, we use acetaldehyde as a reactant (Scheme 1). The first step, hemiacetalization between acetaldehyde and methanol, readily occurs,²⁵ so we focus on the subsequent oxidative dehydrogenation of the hemiacetal to the ester, which is the key reaction to be catalyzed. We propose two pathways for this process (Scheme 2): (a) the oxo pathway (_oxo) and (b) the hydrogen peroxide pathway (_H₂O₂). The two pathways share the same first step: the 1^st dehydrogenation of the hemiacetal (steps 1a and 1b in Scheme 2) by O₂ to form *OOH. The _oxo pathway (Scheme 2a) continues with 2^nd dehydrogenation, O–OH₂ cleavage, and H₂O formation/desorption, leading to the 1^st ester product and an *O (step 2a); this is followed by the 2^nd hemiacetal adsorption and dehydrogenation by the *O, leading to the formation of the 2^nd ester product and the 2^nd water molecule (steps 3a and 4a). In the _H₂O₂ pathway (Scheme 2b), the 2^nd dehydrogenation of the first hemiacetal leads to the formation of the 1^st ester product and *HOOH on the surface (step 2b), which then dissociates into two *OH groups (step 3b). The second hemiacetal then reacts with the two *OH groups via two sequential dehydrogenation steps, forming the 2^nd ester product and two water molecules (steps 4b and 5b). Of note, only the _H₂O₂ pathway was explored previously for the NiO/Au slab model.²⁵ Before proceeding to explore both the _oxo and _H₂O₂ pathways, we examine the geometric and electronic properties of the Au₁₃@(NiO)₄₈ model catalyst.

Scheme 1 The overall reaction of the oxidative esterification of acetaldehyde with methanol via a hemiacetal intermediate.

Scheme 2 Oxidative dehydrogenation of a hemiacetal: (a) the _oxo pathway; (b) the _H₂O₂ pathway.

Structure and charge transfer in the Au₁₃@(NiO)₄₈ core–shell catalyst and adsorption of reactants and products

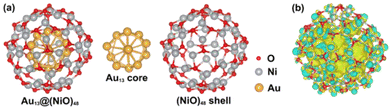
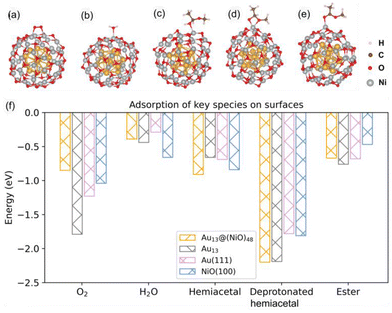
In the optimized Au₁₃@(NiO)₄₈ core–shell model (Fig. 1a), 48 Ni atoms and 48 O atoms are bonded mainly via a hexagonal structure to form a shell surrounding a centered-icosahedral Au₁₃ core with an Au–O distance of ∼3.1 Å and an Au–Ni distance of ∼2.7 Å. In the (NiO)₄₈ shell, the average coordination numbers of Ni and O atoms are around 3. The diameter of the core–shell model is ∼1.1 nm, about half the measured sizes of the Au@NiO particles (2–3 nm).²³ The interaction energy between the Au₁₃ core and the (NiO)₄₈ shell was estimated to be −0.7 eV per NiO, computed from the difference in energy between the core–shell structure and the frozen, isolated Au₁₃ core and the (NiO)₄₈ shell. This highly favorable energetics suggests a strong electronic/chemical interaction between the Au₁₃ core and the (NiO)₄₈ shell. The calculated Bader charges show that 1.27 electrons (e⁻) transfer from the (NiO)₄₈ shell to the Au₁₃ core. The charge density difference plot clearly shows electron accumulation in the Au₁₃ core and depletion of the shell (Fig. 1b). Although the charge transfer direction is usually from a metal to an oxide, the Au metal is special in that it has the highest electronegativity among all metals. Au also has high work functions of 5.30–5.45 eV for thin films,⁴² while the NiO films tend to have lower work functions of 4.4–4.8 eV.^43,44 Because electrons will transfer from a lower work function material to a higher one when the two materials establish electronic contact and their vacuum levels align, our computed charge transfer direction from the NiO shell to the Au core is fully consistent with the experimentally measured work functions. The slightly oxidized NiO shell will greatly influence the adsorption of reactants and the subsequent surface reactions, which are explored as follows.

Fig. 1 (a) Structures of the Au₁₃@(NiO)₄₈ core–shell model, the Au₁₃ core, and the (NiO)₄₈ shell. (b) Charge density difference plot (isosurface values = ±6.6 × 10⁻⁴ e Å⁻³): yellow, electron accumulation; cyan, electron depletion. Note that the Au₁₃ core geometry in (a) slightly deforms from the perfect icosahedral shape due to the interaction with the shell.

Although the optimized Au₁₃@(NiO)₄₈ structure is not perfectly symmetric (Fig. 1a), the local coordination environments of Ni and O show some uniformity in the (NiO)₄₈ shell: most of the Ni sites have three O atoms in the first coordination shell. So we just chose the most representative Ni site for our study to reduce the computational cost of exploring all different sites and pathways. Fig. 2a–e show the adsorption geometries of five key species of oxidative esterification (namely, O₂, H₂O, hemiacetal, deprotonated hemiacetal, and ester) on Au₁₃@(NiO)₄₈, while the adsorption energies are shown in Fig. 2f. Adsorption energies on Au₁₃, Au (111), and NiO (100) are included for comparison (see Fig. S1 and Table S1† for details). One can see that the adsorption of the O₂ molecule becomes weaker, while the adsorption of the hemiacetal becomes stronger on the Au₁₃@(NiO)₄₈ core–shell structure than on Au₁₃, Au (111), and NiO (100). The adsorption energies of H₂O and ester molecules on the Au₁₃@(NiO)₄₈ core–shell structure are in the middle of the values among the four different systems. Comparing the four neutral adsorbates (O₂, H₂O, hemiacetal, and ester) on the four different surfaces (Fig. 2f), one notices an interesting balanced-out effect: the four molecules adsorb moderately strongly with a similar strength on the Au₁₃@(NiO)₄₈ core–shell structure. This aligns well with Sabatier's principle for the “just right” adsorption strength. The adsorption of deprotonated hemiacetal, which will be examined in detail below, is strong on all four surfaces and slightly stronger on the core-shell structure and the Au₁₃ cluster.

Fig. 2 Optimized adsorption structures on the Au₁₃@(NiO)₄₈ core–shell nanocatalyst: (a) O₂; (b) H₂O; (c) hemiacetal; (d) deprotonated hemiacetal; (e) ester; and (f) adsorption energies on Au₁₃@(NiO)₄₈, Au₁₃, Au(111), and NiO(100).

Oxidative dehydrogenation of a hemiacetal on Au₁₃@(NiO)₄₈

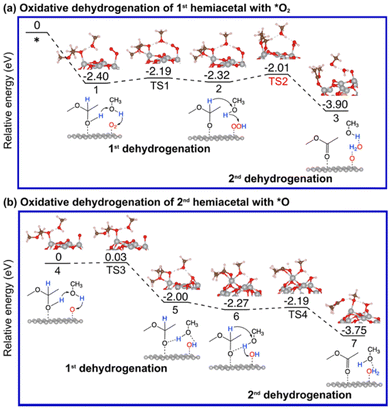
As mentioned earlier, the reaction between an aldehyde and an alcohol to form a hemiacetal is facile, and we found that this is indeed the case between acetaldehyde and methanol on Au₁₃@(NiO)₄₈, Au(111), and NiO(100) (Fig. S2†). We note that unlike the conventional homogeneous process where an acidic proton is needed to catalyze the reaction, the mechanism of the hemiacetal reaction is different on the Au₁₃@(NiO)₄₈ catalyst where the nucleophilic attack and the proton transfer take place simultaneously via a four-membered-ring transition state with a very low activation energy of 0.24 eV (Fig. S2a†). This facileness of the hemiacetal reaction has also been found by Hayashi et al. in their slab model of the NiO/Au catalyst.²⁵ Therefore, we focus on the subsequent steps of oxidative dehydrogenation of the hemiacetal to produce ester and water molecules. Both the hemiacetal and O₂ adsorb on a Ni site of Au₁₃@(NiO)₄₈ in a monodentate mode (state 1 in Fig. 3a). We found that the 1^st dehydrogenation step is facilitated by hydrogen transfer from the adsorbed hemiacetal to *O₂ via a methanol reactant (the corresponding transition state is denoted as TS1 in Fig. 3a; E_a = 0.21 eV). The deprotonated hemiacetal adsorbs on the Ni site in a bidentate mode (state 2 in Fig. 3a), where the two Ni–O bonds are 1.86 and 2.01 Å. The 2^nd dehydrogenation step is a bifurcation point into two different pathways: (a) the _oxo pathway and (b) the _H₂O₂ pathway.

Fig. 3 Energy profiles and key structures of the oxidative dehydrogenation of a hemiacetal to produce ester and water molecules via the _oxo pathway on Au₁₃@(NiO)₄₈: (a) formation of the 1^st ester; (b) formation of the 2^nd ester.

The _oxo pathway. In this pathway, the 2^nd dehydrogenation leads to the formation of a water molecule, an ester product (methyl acetate), and *O (from O–OH₂ cleavage). We found this step to be facile and very downhill (the corresponding transition state is denoted as TS2 in Fig. 3a; E_a = 0.31 eV). After desorption of the water and ester products, the oxidative dehydrogenation of the second hemiacetal by *O proceeds (Fig. 3b) in a similar fashion with very low activation energies (TS3 and TS4). The deprotonated hemiacetal is similarly stabilized in a bidentate mode on a Ni site (state 5 in Fig. 3b).

The _H₂O₂ pathway. In this pathway, the 2^nd dehydrogenation step (the corresponding transition state is denoted as TS2 in Fig. 4a; E_a = 0.47 eV) leads to the formation of the first ester production and *HOOH (state 3 in Fig. 4a). Next, the HOOH readily splits into two *OH (TS3 in Fig. 4a; E_a = 0.05 eV), which are adsorbed on two neighboring Ni atoms (state 5). After desorption of the first ester product, dehydrogenation of the second hemiacetal proceeds via sequential hydrogen transfers to the two *OH to form water (Fig. 4b). The 1^st dehydrogenation is slightly downhill with an energy barrier of 0.10 eV (TS4) and the reaction is slightly exothermic to form 7. The 2^nd dehydrogenation step is much more downhill with an even smaller energy barrier of 0.06 eV (TS5). Comparing the two pathways in Fig. 3 and 4, we found that both have relatively low activation energies, with the highest activation energy occurring in the _H₂O₂ pathway (E_a = 0.47 eV).

Fig. 4 Energy profiles and key structures of the oxidative dehydrogenation of a hemiacetal to produce ester and water molecules via the _H₂O₂ pathway on Au₁₃@(NiO)₄₈: (a) formation of the 1^st ester; (b) formation of the 2^nd ester.

Oxidative dehydrogenation of hemiacetals on Au(111) and NiO(100)

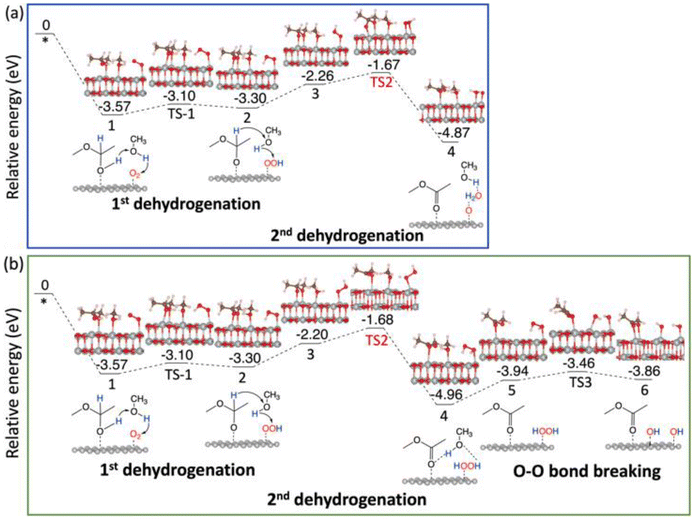
For comparison, we have also explored the reaction pathways on Au(111) (Fig. 5 and Fig. S3†) and NiO(100) (Fig. 6 and Fig. S4†) in the oxidative dehydrogenation of hemiacetals. On Au(111), the 1^st dehydrogenation step has an activation energy of 0.23 eV (the corresponding transition state is denoted as TS1 in Fig. 5a). In the subsequent _oxo pathway, the 2^nd dehydrogenation step has an activation energy of 0.68 eV (the corresponding transition state is denoted as TS2). After desorbing the first ester product, dehydrogenations of the second hemiacetal proceed with activation energies of 0.13 eV and 0.36 eV (Fig. S3a†). In the _H₂O₂ pathway, the 2^nd dehydrogenation of the 1^st hemiacetal has a relatively high activation barrier of 0.81 eV (the corresponding transition state is denoted as TS2 in Fig. 5b). The O–O bond breaking of HOOH is slightly unfavorable with an energy barrier of 0.37 eV (TS3). The subsequent oxidative dehydrogenation of the 2^nd hemiacetal (Fig. S3b†) has activation energies of 0.02 and 0.31 eV for the 1^st and 2^nd dehydrogenation steps, respectively. The formation of the second water molecule is also very energetically favorable with a reaction energy of −2.24 eV.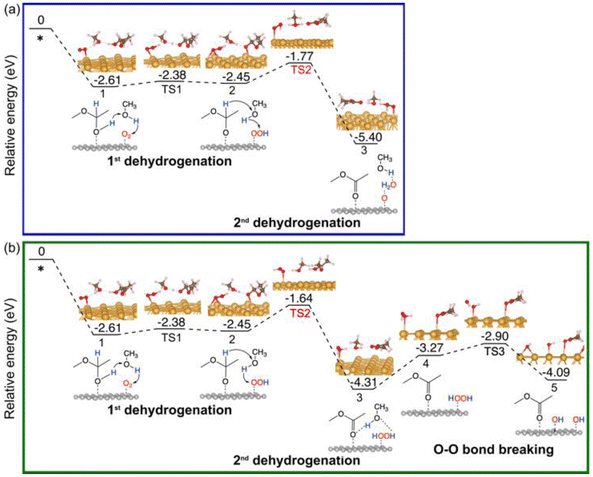

Fig. 5 Energy profiles of the oxidative dehydrogenation of the 1^st hemiacetal on Au (111): (a) via the _oxo pathway; (b) via the _H₂O₂ pathway.

Fig. 6 Energy profiles of the oxidative dehydrogenation of the 1^st hemiacetal on NiO(100): (a) via the _oxo pathway; (b) via the _H₂O₂ pathway.

On NiO(100), the 1^st dehydrogenation step of the oxidative dehydrogenation of the hemiacetal has an activation energy of 0.47 eV (the corresponding transition state is denoted as TS1 in Fig. 6a). In the subsequent step, both pathways experience an unfavorable configuration for the 2^nd dehydrogenation. In the _oxo pathway, there is an uphill energy of 1.04 eV for the configuration change, followed by an activation energy of 0.57 eV (the corresponding transition state is denoted as TS2) for the 2^nd dehydrogenation step. After desorbing the first ester product, the 1^st dehydrogenation of the second hemiacetal proceeds spontaneously with no activation energy, and the 2^nd dehydrogenation of the second hemiacetal occurs with an activation energy of 0.24 eV (Fig. S4a†). In the _H₂O₂ pathway, the uphill energy climbs for 1.10 eV, followed by an activation barrier of 0.52 eV (the corresponding transition state is denoted as TS2 in Fig. 6b) in the 2^nd dehydrogenation. The O–O bond breaking of HOOH is unfavorable with an energy barrier of 0.48 eV (TS3). Similar to the _oxo pathway, the 1^st dehydrogenation of the second hemiacetal proceeds spontaneously, and the subsequent oxidative dehydrogenation of the 2^nd hemiacetal (Fig. S4b†) has an activation energy of 0.24 eV. Hence the _H₂O₂ pathway is slightly more favorable compared to the _oxo pathway.

Comparing Au₁₃@(NiO)₄₈, Au(111), and NiO(100) for the oxidative dehydrogenation of hemiacetals, we found that the rate-limiting steps (the second dehydrogenation of the first hemiacetal) have activation energies of 0.3–0.5 eV on Au₁₃@(NiO)₄₈, but 0.7–0.8 eV on Au(111), and 0.5–0.6 eV on NiO(100). To understand this difference, we next analyze the difference in adsorption of key intermediates.

Comparison of key intermediates on Au₁₃@(NiO)₄₈, Au(111), and NiO(100)

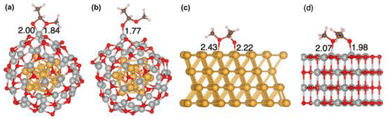
Because the rate-limiting step is the dehydrogenation of the deprotonated hemiacetal, here we focus on the adsorption of the deprotonated hemiacetal in the three systems. We found that the bidentate model can be better stabilized on Au₁₃@(NiO)₄₈ (Fig. 7a) than monodentate adsorption on Au₁₃@(NiO)₄₈ (Fig. 7b) and the bridging mode on Au(111) and NiO(100) surfaces (Fig. 7c and d), as also reflected in adsorption energies (Fig. 2f; Table S2†). The bidentate mode was also observed in the transition state structures on Au₁₃@(NiO)₄₈ (Fig. S5†). The particular bidentate mode on Au₁₃@(NiO)₄₈ arises from the low coordination of Ni²⁺, the more favorable steric environment of the spherical core–shell structure than a flat structure (Fig. S6†), and the slightly higher oxide state than Ni²⁺, which stabilize the deprotonated hemiacetal. In contrast, we found that the dehydrogenation of the hemiacetal in the monodentate mode on Au₁₃@(NiO)₄₈ would have a higher activation energy (Fig. S7†).

Fig. 7 Adsorption structures and modes of a deprotonated hemiacetal: (a) bidentate on Au₁₃@(NiO)₄₈; (c) monodentate on Au₁₃@(NiO)₄₈; (c) bridging on Au(111); and (d) bridging on NiO(100). Ni–O and Au–O distances are given in Å.

Microkinetic modeling of the oxidative dehydrogenation of hemiacetal pathways on Au₁₃@(NiO)₄₈, Au(111), and NiO(100)

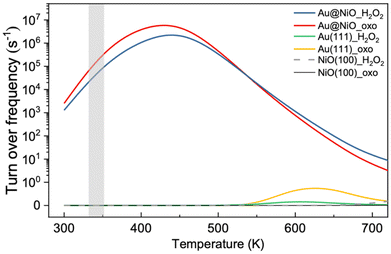
Based on the DFT energy profiles, we carried out microkinetic modeling of the oxidative dehydrogenation of hemiacetal pathways on Au₁₃@(NiO)₄₈ in comparison with Au(111) and NiO(100). We simulated the ester production rates as a function of temperature for both the _oxo and _H₂O₂ pathways. From Fig. 8, one can see that from 300 K up to 500 K, the Au₁₃@(NiO)₄₈ nanocatalyst is highly active for the oxidative dehydrogenation of a hemiacetal to an ester, in agreement with the experiment which was run at 358 K.²³ Only after 600 K does Au(111) begin to show activity. In addition, there is a switchover of the preferred pathway from _oxo to _H₂O₂ for the Au₁₃@(NiO)₄₈ system at 510 K. At the experimental temperatures (358 K), our simulations indicate that the reaction proceeds mainly via the _oxo pathway. Although both the previous slab model and the present core–shell model confirmed the experimental hypothesis of the oxidized NiO being the key to oxidative esterification catalysis,²³ the present work offers a new perspective of the electronic effect due to the charge transfer between the Au core and the NiO shell as well as a geometric factor of enhanced adsorption of hemiacetals.

Fig. 8 Microkinetic modeling of the oxidative dehydrogenation of a hemiacetal to produce esters on Au₁₃@(NiO)₄₈, Au(111), and NiO(100) and water molecules via the _oxo and _H₂O₂ pathways. The gray area indicates the experimental temperature range for this reaction.

Comparison of the Au₁₃@(NiO)₄₈ model with the NiO/Au slab model

It is informative to compare the present mechanistic study using the Au₁₃@(NiO)₄₈ core–shell model with the previous work by Hayashi et al. employing a NiO/Au slab model.^24,25 Both studies found that the oxidized form of NiO is crucial in enabling the oxidative dehydrogenation of hemiacetals, but the difference is how the oxidized NiO appears; in the present work, the oxidation of NiO stems from the charge transfer from the NiO shell to the Au shell while maintaining the 1 : 1 stoichiometry of Ni : O, whereas in the slab model of Hayashi et al., the Ni atom was manually removed to create a Ni vacancy and a NiO_x (x > 1) layer. We think that in the real Au@NiO catalyst, both scenarios could be present, even though our work here shows that oxidation of the NiO shell could evolve naturally from the NiO/Au interface.

The other difference is that in our Au₁₃@(NiO)₄₈ core–shell model, we found that the _oxo pathway is preferred over the _H₂O₂ pathway for the moderate temperatures at which the reaction was conducted experimentally, while Hayashi et al. examined only the _H₂O₂ pathway in their slab model. Moreover, the strong bidentate adsorption state of the deprotonated hemiacetal was found to be an important intermediate in our Au₁₃@(NiO)₄₈ core–shell model, which was not found in the slab model. In addition, the activation energies for the key steps in our Au₁₃@(NiO)₄₈ core–shell model are generally lower than those in the slab model with Ni vacancies. However, we note that the aldehyde reactant is different between the two studies: we used acetaldehyde as a model reactant, while Hayashi et al. used a real reactant, namely methacrolein, as in the commercial process. In summary, we think that the two models are complementary and provide a more complete picture of the Au@NiO catalyst.

Conclusions

We have simulated the superior performance of the Au@NiO nanocatalyst in the oxidative esterification of aldehydes using a more realistic Au₁₃@(NiO)₄₈ core–shell model. We found that 1.27 (e⁻) electrons transfer from the (NiO)₄₈ shell to the Au₁₃ core, leading to a slightly oxidized NiO shell. This core–shell construction has an important consequence in balancing the adsorption energies of reactants and key intermediates: weakening O₂ adsorption and strengthening hemiacetal adsorption. Facile formation of a hemiacetal between acetaldehyde and methanol was found on the Au₁₃@(NiO)₄₈ surface. DFT energetics and MKM modeling of subsequent dehydrogenation of the hemiacetal by molecular oxygen confirmed the superior activity of Au₁₃@(NiO)₄₈ over Au(111) and NiO(100) in producing the ester and water at moderate temperatures (300 K–450 K). The low coordination, spherical structure, and high oxide state of Ni atoms in Au₁₃@(NiO)₄₈ stabilized the key intermediates via a bidentate adsorption mode, a geometry not observed in slab models. Our work has demonstrated the unique electronic and geometric effects of the Au@NiO core–shell nanostructure in enabling the oxidative esterification of aldehydes.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was sponsored by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Chemical Sciences, Geosciences, and Biosciences Division, Catalysis Science Program. This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under contract no. DE-AC02-05CH11231. SZ thanks the National Academic Infrastructure for Supercomputing in Sweden (NAISS) (allocation no. NAISS 2024/5-22 and NAISS 2024/6-130) in Linköping, Sweden.

References

1. T. Pu, W. Zhang and M. Zhu, Angew. Chem., Int. Ed., 2023, 62, e202212278.
2. C. Gao, F. Lyu and Y. Yin, Chem. Rev., 2021, 121, 834–881.
3. T. W. Deelen, C. H. Mejía and K. P. de Jong, Nat. Catal., 2019, 2, 955–970.
4. S. J. Tauster, S. C. Fung and R. L. Garten, J. Am. Chem. Soc., 1978, 100, 170–175.
5. S.-I. Ito, C. Chibana, K. Nagashima, S. Kameoka, K. Tomishige and K. Kunimori, Appl. Catal., A, 2002, 236, 113–120.
6. K. Kunimori, K. Ito, K. Iwai and T. Uchijima, Chem. Lett., 1986, 15, 573–576.
7. S. J. Tauster and S. C. Fung, J. Catal., 1978, 55, 29–35.
8. M. Mao, H. Lv, Y. Li, Y. Yang, M. Zeng, N. Li and X. Zhao, ACS Catal., 2016, 6, 418–427.
9. H. Tang, J. Wei, B. Qiao, X. Pan, L. Li, J. Liu, J. Wang and T. Zhang, J. Am. Chem. Soc., 2016, 138, 56–59.
10. R. Belgamwar, R. Verma, T. Das, S. Chakraborty, P. Sarawade and V. Polshettiwar, J. Am. Chem. Soc., 2023, 145, 8634–8646.
11. R. Ye, L. Ma, X. Hong, T. R. Reina, W. Luo, L. Kang, G. Feng, R. Zhang, M. Fan, R. Zhang and J. Liu, Angew. Chem., Int. Ed., 2023, e202317669.
12. M. Haruta, T. Kobayashi, H. Sano and N. Yamada, Chem. Lett., 1987, 16, 405–408.
13. G. J. Hutchings, J. Catal., 1985, 96, 292–295.
14. M. Valden, X. Lai and D. W. Goodman, Science, 1998, 281, 1647–1650.
15. M. Sankar, Q. He, R. V. Engel, M. A. Sainna, A. J. Logsdail, A. Roldan, D. J. Willock, N. Agarwal, C. J. Kiely and G. J. Hutchings, Chem. Rev., 2020, 120, 3890–3938.
16. T. Ishida, T. Murayama, A. Taketoshi and M. Haruta, Chem. Rev., 2020, 120, 464–525.
17. Y. Zhang, J. Zhang, B. Zhang, R. Si, B. Han, F. Hong, Y. Niu, L. Sun, L. Li, B. Qiao, K. Sun, J. Huang and M. Haruta, Nat. Commun., 2020, 11, 558.
18. R. Zanella and C. Louis, Catal. Today, 2005, 107–108, 768–777.
19. P. Wu, S. Tan, J. Moon, Z. Yan, V. Fung, N. Li, S. Z. Yang, Y. Cheng, C. W. Abney, Z. Wu, A. Savara, A. M. Momen, D. Jiang, D. Su, H. Li, S. Zhu, H. Zhu and S. Dai, Nat. Commun., 2020, 11, 3042.
20. M. Lukosi, C. Tian, X. Li, S. M. Mahurin, H. M. Meyer, G. S. Foo and S. Dai, Catal. Lett., 2018, 148, 2315–2324.
21. Y. Zhang, X. Yang, X. Yang, H. Duan, H. Qi, Y. Su, B. Liang, H. Tao, B. Liu, D. Chen, X. Su, Y. Huang and T. Zhang, Nat. Commun., 2020, 11, 3185.
22. F. Polo-Garzon, T. F. Blum, V. Fung, Z. Bao, H. Chen, Z. Huang, S. M. Mahurin, S. Dai, M. Chi and Z. Wu, ACS Catal., 2020, 10, 8515–8523.
23. K. Suzuki, T. Yamaguchi, K. Matsushita, C. Iitsuka, J. Miura, T. Akaogi and H. Ishida, ACS Catal., 2013, 3, 1845–1849.
24. A. Hayashi, Y. Ato, K. Tada, H. Koga, T. Kawakami, S. Yamanaka and M. Okumura, e-J. Surf. Sci. Nanotechnol., 2018, 16, 242–246.
25. A. Hayashi, Y. Ato, K. Tada, H. Koga, T. Kawakami, S. Yamanaka and M. Okumura, J. Phys. Chem. C, 2020, 124, 17039–17047.
26. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
27. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
28. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
29. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
30. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
31. S. Dudarev, G. Botton, S. Savrasov, C. Humphreys and A. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
32. A. M. Ferrari and C. Pisani, J. Chem. Phys., 2007, 127, 174711.
33. F. Hidalgo, C. Noguez and M. Olvera de la Cruz, Nanoscale, 2014, 6, 3325–3334.
34. W. H. Press, B. P. Flannery, S. A. Teukolsky and W. T. Vetterling, Numerical Recipes, 2nd ed, Cambridge University Press, New York, 1986.
35. J. Nocedal, Math. Comput., 1980, 35, 773–782.
36. D. Shanno, Math. Comput., 1970, 24, 647.
37. G. Henkelman and H. Jonsson, J. Chem. Phys., 2000, 113, 9978–9985.
38. D. Sheppard and G. Henkelman, J. Comput. Chem., 2011, 32, 1769–1771.
39. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
40. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
41. I. A. W. Filot, B. Zijlstra and E. J. M. Hensen, MKMCXX, a C++ program for constructing microkinetic models, 2018, https://www.mkmcxx.nl.
42. W. M. H. Sachtler, G. J. H. Dorgelo and A. A. Holscher, Surf. Sci., 1966, 5, 221–229.
43. E. L. Ratcliff, J. Meyer, K. X. Steirer, A. Garcia, J. J. Berry, D. S. Ginley, D. C. Olson, A. Kahn and N. R. Armstrong, Chem. Mater., 2011, 23, 4988–5000.
44. S. Hietzschold, S. Hillebrandt, F. Ullrich, J. Bombsch, V. Rohnacher, S. Ma, W. Liu, A. Köhn, W. Jaegermann, A. Pucci, W. Kowalsky, E. Mankel, S. Beck and R. Lovrincic, ACS Appl. Mater. Interfaces, 2017, 9, 39821–39829.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr03302g

---