Open Access Article
Open Access ArticleBlue CdSe/CdS core/crown nanoplatelet light-emitting diodes obtained via a design-of-experiments approach†
Matilde
Cirignano‡
ab,
Hossein
Roshan‡
 b,
Emanuele
Farinini
c,
Alessio
Di Giacomo
d,
Sergio
Fiorito
b,
Emanuele
Farinini
c,
Alessio
Di Giacomo
d,
Sergio
Fiorito
 b,
Davide
Piccinotti
b,
Sirous
Khabbazabkenar
b,
Francesco
Di Stasio
b,
Davide
Piccinotti
b,
Sirous
Khabbazabkenar
b,
Francesco
Di Stasio
 *b and
Iwan
Moreels
*b and
Iwan
Moreels
 *d
*d
aDipartimento di Chimica e Chimica Industriale, Università Degli Studi di Genova, Via Dodecaneso 31, 16146 Genoa, Italy
bPhotonic Nanomaterials, Istituto Italiano di Tecnologia, Via Morego 30, 16163 Genoa, Italy. E-mail: francesco.distasio@iit.it
cDepartment of Pharmacy, University of Genova, Viale Cembrano 4, 16148 Genoa, Italy
dDepartment of Chemistry, Ghent University, Krijgslaan 281-S3, 9000 Gent, Belgium. E-mail: iwan.moreels@ugent.be
First published on 13th November 2024
Abstract
Obtaining efficient blue emission from CdSe nanoplatelets (NPLs) remains challenging due to charge trapping and sub-bandgap emission. Thanks to a design-of-experiments (DoE) approach, we significantly improved the NPL synthesis, obtaining precise control over the lateral aspect ratio (length/width). We raised the photoluminescence quantum efficiency up to 66% after growth of a CdS crown, with complete elimination of trap-state emission. Using these 3.5 monolayer, blue-emitting CdSe/CdS core/crown NPLs (λ = 460 nm), we fabricated light-emitting diodes (LEDs) with narrowband (16 nm) blue electroluminescence, an external quantum efficiency of 1.3% and low turn-on voltage of 2.9 V after DoE optimization. Our findings show that NPLs are a promising system to obtain LEDs that emit a saturated blue color.
Introduction
In 19931 Murray et al. synthesized nearly monodisperse CdE (E = S, Se, Te) semiconductor nanocrystallites, initiating a sharp rise in research on colloidal quantum dots (QDs). The unique QD photophysical properties originate from the quantum confinement effect, where charges are confined in three dimensions.2 Modifying their diameter serves as an effective approach to manipulate their opto-electronic properties, which can also be tuned through composition and overall shape. Regarding the latter, colloidal two-dimensional (2D) nanoplatelets (NPLs), which exhibit strong quantum confinement along one direction only, have emerged as a fascinating class of nanomaterials, with exceptional structural and optical properties.3 These thin nanosheets possess a high aspect ratio and large surface area, and showcase a narrow emission line width, large exciton binding energy, giant oscillator strength at cryogenic temperatures, large absorption cross section, fast fluorescence lifetime, and large optical gain coefficient.4,5Among the various types of colloidal 2D nanoplatelets, those based on cadmium selenide (CdSe) have garnered the most attention due to mature synthesis strategies.6,7 Through precise control of the synthetic parameters, such as reaction time and temperature, and precursor concentration, it is possible to synthesize CdSe NPLs with well-defined thickness and lateral dimensions.8 This tunability, as well as the expansion to other material compositions, enables to tailor the NPL absorption and emission properties across a broad spectral range, spanning ultra-violet,9 visible10–12 and near-infrared regions,13–16 making this class of materials attractive for various optoelectronic devices, such as light-emitting diodes (LEDs),17 photodetectors,18 and solar cells.19
Nakamura's pioneering work in 1991 on lattice matching and growth of GaN on a sapphire substrate20 led to the development of the first blue LED, with 0.18% efficiency.21 Colloidal QDs offered the potential for a different type of device, not constrained by the need for lattice matching between stacked layers, an advantage exploited by demonstrating a colloidal QD LED in 1994.22 Three decades later, both device efficiency and operational stability progressed considerably, thanks to significant efforts in producing highly luminescent and stable QDs, comprehending the underlying QD and device physics, and designing appropriate device structures, which includes efficient electron and hole transport layers.23–25
Achieving the desired QD properties to translate this into efficient devices requires careful control of synthesis parameters. Traditional one-variable-at-a-time (OVAT) approaches to synthesis optimization are time-consuming, inefficient and often overlooks complex interactions between factors. Design of Experiments (DoE) is a powerful tool to address these challenges.26 By systematically varying multiple parameters simultaneously and analyzing their collective influence, DoE enables efficient exploration of the experimental parameter space, reveals possible interactions between variables, and eventually allows for the identification of optimal reaction conditions. Moreover, a DoE approach reduces experimental efforts by decreasing the number of experiments required compared to traditional OVAT approaches.
Here, we demonstrate a significant improvement in the synthesis of blue-emitting 3.5 monolayer (ML) CdSe NPLs through a multi-step DoE. This is followed by CdS crown growth to obtain NPLs reaching a photoluminescence quantum efficiency (PL QE) of 66%. Differently from core/shell structures that involve complete encapsulation of the core with one or more layers of CdS,22 CdSe/CdS core/crown NPLs are extended only laterally.27,28 The core/shell heterostructures exhibit quasi-type II behavior, with a red shifted emission and reduced emission rate, similar to their QD counterparts.29–31 On the other hand, CdSe/CdS core/crown heterostructures maintain a type-I behavior due to the weak lateral confinement of charge carriers, resulting in a minimal red shift of the emission and a similar emission rate as the core-only NPLs.32–37 As a result, the lateral size of the crown can be tuned without significantly affecting the core exciton transition.38
The core/crown heterostructure introduces additional benefits, such as increased stability and improved PL QE.35,36,39,40 Yet, the majority of studies concerning core/crown NPLs concentrate on the green35,37,41,42 and red13,27,35 regions of the spectrum, neglecting the potential of UV-to-blue-emitting CdSe NPLs. Recently, a report on triangle-shaped alloyed CdSe/CdSe1−xSx core/crown NPLs demonstrated a narrow PL linewidth and a PL QE approaching unity.43 This is due to the more homogeneous crown growth around a symmetrical core. Nevertheless, LEDs fabricated with this material presented an external quantum efficiency (EQE) of only 1.16%, a modest brightness (46 cd m−2) and a turn-on voltage of 3.6 V.43 Rectangular NPLs in the same work reached 90% PL QE but no LEDs were fabricated with this material.
Our aim is to initiate from a recently published synthesis for 3.5 ML NPLs12,34 with a rectangular shape, and to increase their PL QE in order to fabricate blue-emitting LEDs with improved characteristics. Different experimental designs enabled us to increase the PL QE from 5%, as previously reported,12 to 15%. Next, using core/crown 3.5 ML CdSe/CdS NPLs with a final PL QE of 66%, low trap density and negligible QD byproducts, we fabricated LEDs reaching an EQE of 1.3%, a turn-on voltage of 2.9 V and a maximum luminance of 150 cd m−2.
Results and discussion
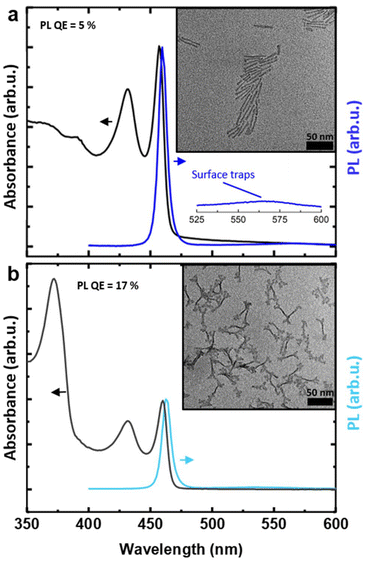
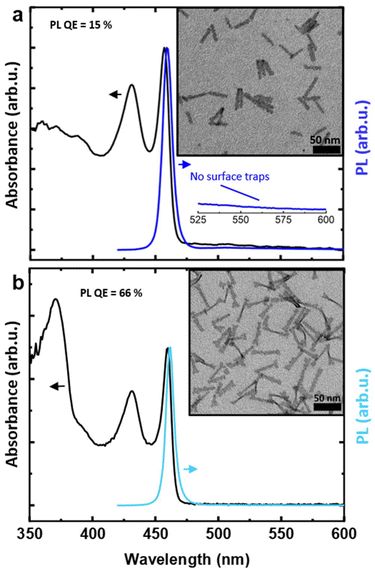
We started from the hot-injection synthesis of 3.5 ML CdSe NPLs reported by Di Giacomo et al.,12 using cadmium stearate as precursor. Fig. 1a shows the normalized absorbance and PL spectrum of this initial sample (IS). The first excitonic peak is centered at 457 nm, while the PL lies at 460 nm, in the blue color range. A second, broad PL signal can be discerned between 525 and 600 nm, which can be ascribed to in-gap trap states, arising from incomplete passivation of dangling bonds at the side facets.36,44 The modest band-edge PL QE (5%) can also be attributed to the presence of such trap states.45 A TEM image (Fig. 1a, inset) shows NPLs with length of 36.6 nm ± 3.8 nm (std. dev.), and width of 4.4 nm ± 0.7 nm (std. dev.), yielding an aspect ratio of 8.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
As a first step, via a Definitive Screening Design (DSD) we proceeded with identification of the significant factors affecting this result. DSD is a statistical experimental design technique, used to efficiently explore multiple variables, or input factors, that may influence the selected responses. It enables the estimation of both linear and quadratic effects of the variables on the responses. To execute the DSD, six synthesis input factors were chosen, as listed in Table 1. These variables yielded an impact on the syntheses conducted in previous works.42,46,47 More specifically, Di Giacomo et al. observed a dependence of the reaction yield on the length of the cadmium carboxylate precursor,12 with shorter ligands having higher yields due to a suppression of QD byproduct formation. Different chain lengths, presumably due to a different packing order, also control the NPL width and aspect ratio.12 The reaction time and temperature can also influence length and width of NPLs,42 and for completeness, we also investigated the influence of the cadmium precursor and propionic acid concentration, and of the injection temperature of propionic acid, which induces the 2D growth. We chose three input levels, labelled as −1, 0, 1 (except for X1, for which we used a carbon chain length of 16 instead of 15 for the intermediate level, therefore the coded level of the experimental matrix equals 0.33 instead of 0). Our DSD required the execution of 13 experiments (ESI, Table S1†). The measured responses (output variables) are listed in Table 2. The PL QE should be maximized. The fraction of quantum dot byproducts fQD should be minimized. It is evaluated by dividing the maximal absorption value in the 475–525 nm spectral region, likely arising from QD absorption, by the absorption value of the first NPL absorption peak at 457 nm. The trap band intensity Itr should also be minimized. It is evaluated by dividing the maximal value of the emission in the 525–600 nm spectral region by the NPL emission peak value at 460 nm.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of carboxylic acid to cadmium, see methods
1 ratio of carboxylic acid to cadmium, see methods
| Variable no. | Variable name | Level values | ||
|---|---|---|---|---|
| Low (−1) | Medium (0) | High (+1) | ||
| X 1 | Carboxylic acid chain length [no. carbon atoms] | 12 | 15 | 18 |
| X 2 | Cadmium carboxylate amount [mmol] | 0.8 | 1.0 | 1.2 |
| X 3 | Propionic acid amount [mmol] | 0.2 | 0.99 | 1.78 |
| X 4 | Reaction time [min] | 8 | 14 | 20 |
| X 5 | Injection temperature [°C] | 185 | 195 | 205 |
| X 6 | Growth temperature [°C] | 210 | 217.5 | 225 |
| Response | Goal | |
|---|---|---|
| Y 1 | PL QE [%] | Maximize |
| Y 2 | QD fraction fQD [%] | Minimize |
| Y 3 | Trap band intensity Itr [%] | Minimize |
Upon conducting an initial analysis of the responses, a correlation between Itr and PL QE becomes evident, as illustrated in Fig. S1.† This reveals that all experiments yielding PL QE values higher than 1% are consistently associated with a low Itr. This indicates that nonradiative recombination pathways are minimized, allowing for a higher proportion of radiative recombination and a higher PL QE. It also implies that we only have to optimize the synthesis toward high PL QE (response Y1), as Itr (response Y3) will be minimized accordingly.
The responses can be quantified via a multilinear regression model, which includes both linear and quadratic terms, resulting in a total of 13 coefficients. The general model equation (eqn (1)) reads:
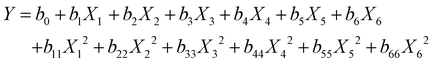 | (1) |
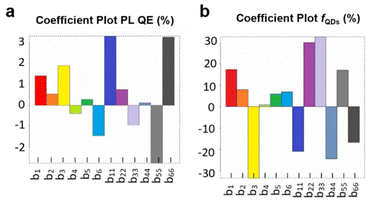
It consists of a constant term (b0), six linear terms (biXi), and six quadratic terms (biiXi2). Data analysis was performed with the software Chemometric Agile Tool.48 The model coefficients for each response are summarized in Table S2.† Note that, as each Xi represents the normalized level value, ranging from −1 to +1, a large model coefficient bi or bii directly implies that the input factor has a large influence on the response. X1 (chain length of long ligands), X2 (amount of long ligands) and X3 (amount of propionic acid) present large coefficients for the responses (Fig. 2a and b), which means that they strongly influence both PL QE and fQD. On the other hand, X4 (reaction time) shows small linear and quadratic coefficients, meaning that it does not strongly impact the outcome of the synthesis. X5 and X6 (injection and growth temperature, resp.) also show a sizeable influence on the outcome of the reaction.
We further explored these dependencies in a second set of syntheses, where we shifted the range of parameters (Table S3†) to the region of higher PL QE. First, we chose to fix the carboxylic acid chain length (X1) to 18 carbons in this run, as stearic acid gave the best results, and we did not want to increase the length further for practical reasons. Second, the amount of stearic acid (X2) was slightly increased, to 1–1.4 mmol, as well as the amount of propionic acid, to 0.94–2.67 mmol (X3), as run one showed that a higher concentration ligands improves the PL QE. Similarly, the injection temperature (X5) was raised to 185–215 °C, and the growth temperature (X6) to 200–250 °C. In these temperature ranges, we observed that the PL QE keeps improving with increasing X5, while no clear dependency on X6 was observed (Fig. S2†).
Based on these results, a final DoE was executed, with now only the cadmium stearate (X2) and propionic acid (X3) amounts as variables. Parameter ranges used were slightly higher for X2 compared to the previous run, and intermediate for X3 (Table 3). The other input factors were kept fixed according to the results of the initial sets of experiments. In particular, we selected stearic acid (X1) as long-chained carbonate ligand, a reaction time (X4) of 16 minutes, an injection temperature (X5) of 215 °C, limited for practical reasons to avoid growth of 4.5 ML NPLs, and a growth temperature (X6) of 220 °C, slightly above the injection temperature. To determine the optimal synthesis conditions, we now chose a Central Composite Face-centered design (CCF). This design is employed to investigate linear (biXi), quadratic (biiXi2) and interaction (bijXi·Xj) terms, and contains more input data than the DSD, which should allow us to zoom in on the optimal synthesis. It is derived from two-level Factorial Designs (2k) and is complemented by incorporating “star points” located on the surfaces of a k-dimensional cube. The measured responses are the same as in the first experimental run (Table 2).
| Variable no. | Variable name | Level values | |
|---|---|---|---|
| Low (−1) | High (+1) | ||
| X 2 | Cadmium stearate amount [mmol] | 1.4 | 1.5 |
| X 3 | Propionic acid [mmol] | 1.47 | 1.87 |
With 3 degrees of freedom available to estimate 6 coefficients, the multi-linear regression models are computed as follows:
| Y = c0 + c1X2 + c2X3 + c12X2X3 + c11X22 + c22X32 | (2) |
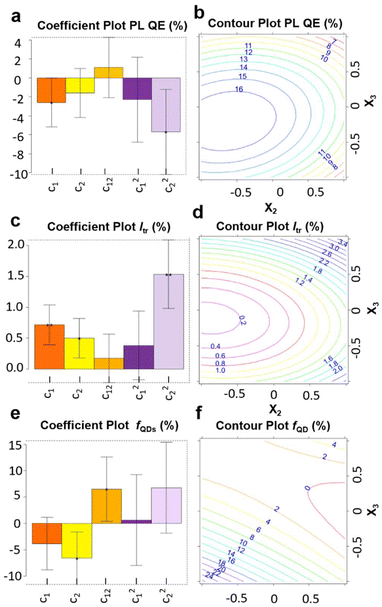
The coefficients are listed in Table S4.† Coefficient plots and contour plots of the three responses (PL QE, Itr and fQD) are shown in Fig. 3. Upon analyzing the PL QE contour plot (Fig. 3b), we can conclude that a cadmium stearate amount of about 1.4–1.45 mmol, and a propionic acid amount of about 1.56–1.68 mmol are advised to maximize the PL QE. The response Itr (Fig. 3c and d), which should be minimized, exhibits a similar 2D contour plot as for the PL QE, confirming the correlation between PL QE and Itr observed earlier (Fig. S1†). Turning to the response fQD (Fig. 3d and e), which also needs to be minimized, an interaction between the propionic acid and cadmium stearate is observed, as evidenced by the coefficient c12 (light orange bar in Fig. 3e). The contour plot (Fig. 3f) shows that, when working with low amounts of cadmium stearate, a high level of propionic acid reduces fQD, while the effect of propionic acid is almost negligible at high amounts of cadmium stearate. More importantly, we noticed that the optimal synthesis conditions for a high PL QE and a low fQD are not located in the same region.
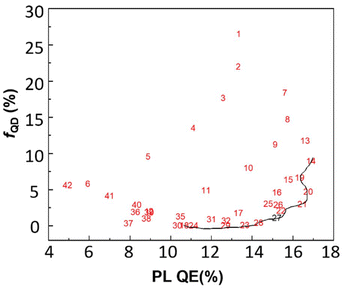
To find a compromise between these conflicting demands of high PL QE and low fQD, Pareto optimality49 was employed. Within this approach, a Pareto front is constructed, which represents a collection of optimal solutions, also called nondominated points. They have the distinctive quality that no improvement in one objective is possible without sacrificing another. A Pareto front algorithm was applied to the PL QE (to be maximized), fQD (to be minimized) and Itr (to be minimized). A grid of experimental conditions, within the region of interest of Fig. 3, was established using the CCF regression models, using a step of 0.02 mmol for the cadmium stearate amount and a step of 0.067 mmol for the propionic acid amount. Plotting the correlation with PL QE and fQD (Fig. 4) resulted in the identification of 12 nondominated points, traced by the black line. Interestingly, we observe that we can increase the PL QE up to about 16%, without substantially increasing fQD, however, at this point, fQD rises sharply.
One then typically manually selects the best compromise lying on the Pareto front. We chose a cadmium stearate amount of 1.44 mmol and propionic acid amount of 1.74 mmol (equal to 130 μL), associated with point number 27 in Fig. 4. These settings predict a high PL QE, while keeping fQD at acceptably low levels (Table 4). They were experimentally tested three times to evaluate the predictability of the model. As listed, the experimental results align well with predicted values for each response.
| PL QE | f QD | I tr | |
|---|---|---|---|
| Prediction | 15.2 | 1.1 | 0.7 |
| Experiment 1 | 12.5 | 1.3 | 0.8 |
| Experiment 2 | 15.5 | 1.1 | 0.7 |
| Experiment 3 | 14.3 | 1.2 | 0.6 |
| Experiment (avg.) | 14.1 | 1.2 | 0.7 |
The absorbance and PL spectra, and TEM image of the final sample (Table 4, Experiment 2) are shown in Fig. 5a. The NPLs have a length of 33.1 nm ± 3.5 nm and a width of 5.1 nm ± 0.7 nm, yielding an 6.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 aspect ratio, lower than the initial sample (Fig. 1a). More importantly, the PL QE increased significantly, to 15%. In other words, through DoE optimization, here in combination with the Pareto front algorithm, we obtained a sample with a substantially improved PL QE and suppressed Itr.
1 aspect ratio, lower than the initial sample (Fig. 1a). More importantly, the PL QE increased significantly, to 15%. In other words, through DoE optimization, here in combination with the Pareto front algorithm, we obtained a sample with a substantially improved PL QE and suppressed Itr.
Next, we employed an established crowning procedure34 with slight modifications to grow a crown of CdS on these 3.5 ML CdSe NPLs. This resulted in a core/crown NPL length of 43.3 nm ± 5.3 nm and width of 7.0 nm ± 1.1 nm, and 66% PL QE (Fig. 5b). This is a marked improvement compared to the 17% obtained after crown growth of the initial sample (Fig. 1b), despite the observation that the crown is somewhat smaller compared to the initial core/crown sample, as evidenced by the smaller amplitude of the CdS band-edge absorption around 370 nm. While the PL QE of 66% still falls below the values of 90–100%,43 achieved by synthesizing CdSe/CdSexS1−x core/alloyed crown NPLs in a single-step procedure (i.e. without intermediate CdSe core purification), we did substantially improve on our earlier results,34 where we obtained a PL QE of 55% on CdSe/CdS core/crown NPLs prepared via a two-step, seeded growth procedure.
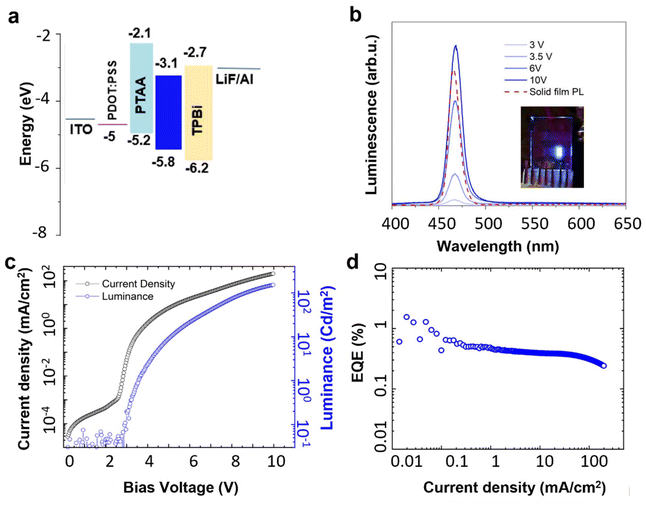
As a first step toward fabricating light-emitting diodes (LEDs) using these materials, X-ray photoelectron spectroscopy (XPS) and ultraviolet photoelectron spectroscopy (UPS) were performed on the optimized 3.5 ML CdSe/CdS core/crown NPLs. These measurements served to establish the energetic position of the valence band maximum (VBM) with respect to the vacuum level, and subsequently the valence and conduction band offsets. Fig. S3† shows a low-resolution XPS spectrum, where peaks for Cd, Se, C, O are observed. Fig. S4a and S4b† show high-resolution XPS spectra of carbon and of the valence band, respectively. Carbon was used to calibrate the energy scale. The position of the VBM was extracted from Fig. S4b† (1.8 eV) and it was used to calibrate the energy scale of the UPS spectrum. A UPS spectrum is shown in Fig. S4c and S4d† in the two regions of low kinetic energy and low binding energy. The onset at low kinetic energy gives the work function of the system (4.0 eV) whereas the onset at low binding energy is the position of the VBM (1.8 eV) with respect to the work function. This results in a VBM to vacuum energy level of (4.0 + 1.8) = 5.8 eV (Fig. 6a).
Following the XPS/UPS analysis, we proceeded with LED fabrication. First, we determined a device structure enabling electroluminescence (EL) from the NPL active layer, exploiting our knowledge on green-emitting LEDs.50,51 We identified a device architecture different from other structures used for II–VI core-crown NPL LEDs,43,52 employing aluminum/lithium fluoride as cathode and indium tin oxide (ITO) as anode. The LED includes 1,3,5-tris(1-phenyl-1H-benzimidazol-2-yl)benzene (TPBi) as the electron transport layer, and poly[bis(4-phenyl)(2,4,6-trimethylphenyl)amine] (PTAA) and poly(3,4-ethylenedioxythiophene)-poly(styrene sulfonate) (PEDOT:PSS) as the hole transport layer. The layer thicknesses are controlled through evaporation rate (for TPBi) and concentration/speed of the spin coating process (for PEDOT:PSS and PTAA). Fig. 6a shows the energy diagram of the LED structure under zero bias. As discussed, the values of the emissive layer were obtained via XPS/UPS analysis, while values for the other layers were taken from literature.50
We optimized our LED structure via a CCF design using the TPBi thickness and PTAA concentration as input factors (ranging from 30 to 40 nm, and from 10 to 18 mg mL−1, respectively). The EQE and luminance responses of all samples are shown in Fig. S5.† The luminance appeared to vary randomly between 50 and 150 cd m−2, and we could not model these results. The EQE, however, showed clearer trends. The model equation and coefficients are listed in Table S5† and represented graphically in Fig. S6a.† A contour plot of the modeled EQE (Fig. S6b†) shows that optimal values are obtained for thicknesses of 35–40 nm for TPBi, and concentrations of 14–18 mg mL−1 for PTAA, respectively, i.e. in the upper right corner of the contour plot, where we obtain an average EQE of 0.95–1%.
The typical EL spectrum produced from an optimized LED was measured under different applied biases and is shown in Fig. 6b (input factors: 40 nm TPBi, 18 mg mL−1 PTAA). In the inset, we present a picture of the same LED under operation. Importantly, the EL closely resembles the PL spectrum measured on a solid NPL film, before integrating them into the device. The PL spectrum shows a peak at 465 nm and FWHM of 14 nm, while the EL spectrum shows a peak at 467 nm and FWHM of 16 nm. These values compare favorably to blue QD or quantum rod LEDs, where typically larger PL and EL FWHM values are reported,53,54 and are comparable to other reports on NPL LEDs (Table S6†).43,55,56 The low-energy side of the EL spectrum does not display any significant broad features across various current densities, indicating the suppression of emission from trap states in our devices.
A CIE diagram of the electroluminescence, collected at a 6 V, is shown in Fig. S7a.† It shows that our blue LED has CIE coordinates (x = 0.16, y = 0.11), close to the NTSC standard for blue (x = 0.14, y = 0.08). Note that these coordinates can still be improved. Inspecting the EL spectrum on a logarithmic scale (Fig. S7b†), we can notice a weak trap band centered at 550 nm. Filtering this out with a (simulated) 525 nm short-pass filter should not strongly impact the luminance, while at the same time it significantly improves the color purity, as we would obtain CIE coordinates (x = 0.127, y = 0.073). This shows that narrow-band blue-emitting NPLs have a significant potential to produce saturated blue emission. In Fig. 6c, the current density and EL intensity of the same LED are plotted versus applied bias. The turn-on voltage of 2.9 V (3 V averaged over all devices with the same TPBi and PTAA thickness) is remarkably close to the band gap of the emissive layer (2.7 eV). We obtained a maximum luminance of 150 cd m−2 (average value of 105 cd m−2). The EQE (Fig. 6d), which peaks at 1.3% (average value of 1%) at a current density of 48 mA cm−2 and luminance of 0.2 cd m−2, remains almost flat over the current density range measured. The reduced roll-off at high luminance, typically associated with Auger recombination and thermal degradation of the active region,57 is therefore largely avoided.
Conclusions
The core synthesis of 3.5 ML CdSe/CdS NPLs was optimized through design of experiments and Pareto optimality, achieving a 66% PL QE in combination with a suppressed trap band emission after growth of a CdS crown. LEDs were fabricated with a novel structure, comprising TPBi and PTAA charge transport layers. By employing a design of experiments on the device level, an high EQE for blue-emitting NPL LEDs was obtained, in combination with a high luminance and low turn-on voltage approaching the NPL band gap. Overall, our results demonstrate an effective method for PL QE and LED EQE optimization, respectively, which can easily be extended to other NPL and QD materials and LED architectures.Materials and methods
Chemicals
Sulfur (≥99%), cadmium oxide (CdO, ≥99.99%), 1-octadecene (ODE, technical grade, 90%), oleic acid (OA, 90%), stearic acid (C18, ≥97.0%), palmitic acid (C16, ≥99%) and lauric acid (C12, 98.0%) were purchased from Sigma-Aldrich. Propionic acid (>99.5%), hexane (>99%), disolol® (ethanol, EtOH, 98%), 2-propanol (IPA, > 99%), and acetonitrile (ACN, 99.9%) were purchased from Chem Lab. Selenium powder (≥99.99%) was purchased from Acros Organics. All chemicals were used without further purification.Cadmium carboxylate (Cd(OOCR)2) preparation
All cadmium carboxylates were prepared starting from CdO. In a three-neck flask, 2 g (15.7 mmol) of CdO was added to 40 mmol of the respective carboxylic acid. Under stirring, the system was heated under N2 atmosphere to 210 °C, until a colorless solution was obtained. The reaction was kept at 210 °C for 20 minutes and then cooled. During cooling, between 110 and 80 °C, the mixture was connected to a vacuum line to remove water produced in the condensation reaction. The colorless solution was rapidly transferred to centrifugation tubes, acetone was added, and a white solid precipitated after centrifugation. The solid fraction was centrifuged with acetone three additional times to purify the Cd(OOCR)2 reaction product, and then dried overnight under vacuum.Synthesis of 3.5 ML CdSe NPLs
In a 50 mL three-neck round-bottom flask, a variable amount of Cd(OOCR)2 (Table S1†) and 0.63 mmol of Se powder were mixed with 24 mL of ODE. The suspension was degassed for 1 h at 90 °C, followed by heating the mixture, under N2, to 160 °C for 10 min. A variable amount of propionic acid (Table S1†), dispersed in 1 mL of ODE, was swiftly injected into the flask at a variable temperature (Table S1†). Temperature was then raised to a variable higher value (Table S1†) and kept for variable time (Table S1†). The reaction proceeded for a given growth time (Table S1†), then heating was removed to cool the system.Purification of 3.5 ML CdSe NPLs
The reaction mixture was transferred into vials and placed on a hot plate at 60 °C. In the vial, 8 mL of CHCl3 and 8 mL of ACN were added. CHCl3 is used to disperse the NPLs, while ACN is used to precipitate them. The mixture was centrifuged at 5000 rpm for 5 minutes. The liquid containing byproducts (quantum dots and unreacted carboxylic acid) was discarded and the solid was dispersed in 8 mL of CHCl3, the temperature was set to 60 °C and 8 mL of ACN were added. The mixture was centrifuged again at 5000 rpm for 5 minutes. This procedure was repeated four additional times. The final solid, containing 3.5 ML CdSe NPLs and QD byproducts, was dispersed in 8 mL n-hexane and a mixture of 1.5 mL of IPA and 1.1 mL of ACN was added. The mixture was centrifuged at 4800 rpm for 14 minutes. Under these conditions NPLs precipitate while quantum dots remain in suspension. The solid was dispersed in 6 mL n-hexane and stored in the fridge prior to use.Preparation of the sulfur stock solution
Sulfur (0.56 mol), propionic acid (2.93 mmol) and 50 μL of OA were added to ODE (15 mL). The mixture was sonicated at 35 °C for 20 min to achieve complete dissolution. The precipitation of solids could occur after time and the mixture should then be sonicated before use.Preparation of the cadmium oleate (Cd(OA)2) solution
CdO (1.926 g, 15 mmol) was mixed with OA (15 mL, 45 mmol) in ODE (15 mL). The mixture was degassed under vacuum at 80 °C for 1 hour. Afterward, the solution was heated to 240 °C under inert atmosphere. Upon achieving transparency (after approximately 15 minutes), the mixture was cooled to 110 °C and placed under vacuum for 20 min, to remove water, produced in the condensation reaction. The mixture was finally poured into vials for storage until use. The mixture solidifies at room temperature so the wax was melted prior to use.CdS crown growth around 3.5 ML CdSe NPLs
To determine the concentration of core NPLs, we used the absorption coefficient reported by Achtstein et al.58 and rescaled the amounts of solvent and sulfur stock solution accordingly. In a three-neck round-bottom flask, 12 nmol of 3.5 ML NPLs dispersed in n-hexane, OA (30 μL) and cadmium octanoate (0.18 mmol) were added to 15 mL ODE. The mixture was degassed under vacuum at 60 °C for 1 hour, and then the temperature was set to 185 °C under N2 atmosphere. While heating, 5 mL of the sulfur stock solution was added dropwise to the flask with a syringe pump (rate: 8 mL h−1). When the injection finished, the mixture was left to react for an additional 10 minutes. After this, the heating mantle was removed and 0.8 g of a molten Cd(OA)2/ODE solution was added to the flask to quench the reaction. At 80 °C, the crude product was transferred into centrifugation tubes to proceed with purification.Purification protocol for CdSe/CdS core/crown NPLs
The crude synthesis product was mixed with 15 mL of toluene and 10 mL of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) solution of IPA
1 (v/v) solution of IPA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ACN. The suspension was centrifuged for 10 min at 4500 rpm. The NPLs precipitated under these conditions. The supernatant was discarded, the solid was redispersed in n-hexane. The same procedure was repeated two times. The final n-hexane dispersion was centrifuged at 4200 rpm to remove the unreacted carboxylates. The solid was discarded and the supernatant, containing CdSe/CdS core/crown NPLs, was stored.
ACN. The suspension was centrifuged for 10 min at 4500 rpm. The NPLs precipitated under these conditions. The supernatant was discarded, the solid was redispersed in n-hexane. The same procedure was repeated two times. The final n-hexane dispersion was centrifuged at 4200 rpm to remove the unreacted carboxylates. The solid was discarded and the supernatant, containing CdSe/CdS core/crown NPLs, was stored.
Transmission electron microscopy TEM
Bright field TEM images were acquired on a JEOL JEM-1010 or a JEOL JEM-1011 microscope equipped with a thermionic gun at 100 kV accelerating voltage. The samples were prepared by drop-casting diluted colloidal suspensions onto 200-mesh carbon-coated copper grids.Optical characterization
UV–visible absorption spectra were recorded with a Varian Cary 300 UV–vis absorption spectrophotometer (liquid sample) and Cary 5000. PL and PL QE measurements were carried out on NPL solutions and thin films with an Edinburgh Instruments fluorescence spectrometer (FLS920), which included a Xenon lamp with a monochromator for steady-state PL. The PL spectra recorded from films were obtained with an excitation wavelength of 400 nm. A calibrated integrating sphere was used to record the PL QE on films that were deposited onto ITO/glass substrates.X-Ray fluorescence spectroscopy
Specimens for XPS were prepared from concentrated NPL solutions, dropped on freshly cleaved highly oriented pyrolytic graphite substrates in a glovebox. XPS measurements were carried out on a Kratos Axis Ultra DLD spectrometer using a monochromatic Al Kα source, operated at 20 mA and 15 kV. High resolution analyses were carried out at a pass energy of 10 eV. A Kratos charge neutralizer system was used on all specimens. Spectra were charge-corrected to the main line of the carbon 1 s spectrum (adventitious carbon) set to 284.8 eV. Spectra were analyzed using CasaXPS software (version 2.3.24).Ultraviolet photoelectron spectroscopy
UPS measurements were performed using a He I (21.22 eV) discharge lamp, on an area of 55 μm in diameter, at pass energy of 10 eV and with a dwell time of 100 ms. The instrument used was the same as for XPS measurements. A Kratos charge neutralizer system was used on all specimens. The work function was measured from the threshold energy for the emission of secondary electrons during He I excitation. A −9.0 V bias was applied to the sample to precisely determine the low kinetic energy cut-off, as discussed by Helander et al.59 Then, the position of the VBM against the vacuum level was estimated by measuring its energetic distance from the work function.LED fabrication
Patterned ITO glass substrates were cleaned sequentially in cleaning solution, acetone, and isopropanol using ultrasonic methods, followed by drying with a nitrogen gun. Subsequently, the treated ITO glass underwent a 3 minute pretreatment under O2 plasma. PEDOT:PSS was spin coating at 4000 rpm for 40 seconds onto the treated ITO glass and then annealed at 120 °C for 10 minutes in ambient conditions. The ITO/PEDOT:PSS substrates were transferred to a glovebox, where a PTAA hole transport layer was spin coated at 2000 rpm for 45 seconds and annealed at 80 °C for 10 minutes. The CdSe/CdS NPL solution (in octane) was spin coated onto the substrates at 1500 rpm for 45 seconds to form the emitting layer. Finally, in a thermal evaporation chamber, a TPBi electron transport layer and a LiF/Al electrode (0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 nm) were sequentially deposited at high vacuum (∼10−6 mbar).
100 nm) were sequentially deposited at high vacuum (∼10−6 mbar).
Czerny-Turner HRS-500 spectrometer
The LED electroluminescence measurements were carried out with a Czerny-Turner HRS-500 spectrometer (Princeton Instruments) coupled with PIXIS CCD camera. The software used was “Lightfield” (Princeton Instruments).Author contributions
The manuscript was written through contributions of all authors.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the UGent BOF GOA (Grant GOA01G02124 SATOMA) and from the European Research Council via the ERC-StG “NANOLED” (Grant 851794). D. P. and F. D. S. acknowledge support from the European Union's Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement no. 101062372 (ELDOPP). S. F. and F. D. S. acknowledge support from the Italian Ministry of University and Research (PNRR MUR project PE0000023-NQSTI). A part of the TEM measurements were performed at the UGent TEM Core Facility. The authors acknowledge Dorwal Marchelli and Mirko Prato for support in the optical analyses and in the XPS/UPS measurements, respectively.References
- C. B. Murray, D. J. Noms and M. G. Bawendi, J. Am. Chem. Soc., 1993, 115, 8706–8715 CrossRef CAS.
- A. L. Efros and L. E. Brus, ACS Nano, 2021, 15, 6192–6210 CrossRef CAS.
- M. Nasilowski, B. Mahler, E. Lhuillier, S. Ithurria and B. Dubertret, Chem. Rev., 2016, 116, 10934–10982 CrossRef CAS PubMed.
- S. Ithurria and D. V. Talapin, J. Am. Chem. Soc., 2012, 134, 18585–18590 CrossRef CAS.
- C. Bouet, M. D. Tessier, S. Ithurria, B. Mahler, B. Nadal and B. Dubertret, Chem. Mater., 2013, 25, 1262–1271 CrossRef CAS.
- J. Joo, J. S. Son, S. G. Kwon, J. H. Yu and T. Hyeon, J. Am. Chem. Soc., 2006, 128, 5632–5633 CrossRef CAS PubMed.
- J. Yu and R. Chen, InfoMat, 2020, 2, 905–927 CrossRef CAS.
- Z. Zhang and H. Sun, Adv. Photonics Res., 2021, 2, 2100045 CrossRef CAS.
- P. D. Cunningham, I. Coropceanu, K. Mulloy, W. Cho and D. V. Talapin, ACS Nano, 2020, 14, 3847–3857 CrossRef CAS.
- F. Fan, P. Kanjanaboos, M. Saravanapavanantham, E. Beauregard, G. Ingram, E. Yassitepe, M. M. Adachi, O. Voznyy, A. K. Johnston, G. Walters, G. H. Kim, Z. H. Lu and E. H. Sargent, Nano Lett., 2015, 15, 4611–4615 CrossRef CAS.
- M. D. Tessier, C. Javaux, I. Maksimovic, V. Loriette and B. Dubertret, ACS Nano, 2012, 6, 6751–6758 CrossRef CAS.
- A. Di Giacomo, C. Rodà, A. H. Khan and I. Moreels, Chem. Mater., 2020, 32, 9260–9267 CrossRef CAS.
- A. H. Khan, V. Pinchetti, I. Tanghe, Z. Dang, B. Martín-García, Z. Hens, D. Van Thourhout, P. Geiregat, S. Brovelli and I. Moreels, Chem. Mater., 2019, 31, 1450–1459 CrossRef CAS.
- L. Biesterfeld, M. T. Vochezer, M. Kögel, I. A. Zaluzhnyy, M. Rosebrock, L. F. Klepzig, W. Leis, M. Seitz, J. C. Meyer and J. Lauth, Chem. Mater., 2024, 36, 7197–7206 CrossRef CAS.
- E. Izquierdo, A. Robin, S. Keuleyan, N. Lequeux, E. Lhuillier and S. Ithurria, J. Am. Chem. Soc., 2016, 138, 10496–10501 CrossRef CAS PubMed.
- E. Bossavit, H. Zhang, N. Ledos, M. Cavallo, D. Mastrippolito, L. Curti, A. Khalili, A. Colle, P. Lample, M. Weis, F. Margaillan, X. Lafosse, Y. Prado, E. Péronne, D. Pierucci, S. Ithurria, D. Boschetto, B. T. Diroll, A. Degiron and E. Lhuillier, Adv. Funct. Mater., 2024, 2403532 CrossRef CAS.
- Y. Guo, F. Gao, P. Huang, R. Wu, W. Gu, J. Wei, F. Liu and H. Li, Energy Mater. Adv., 2022, 9857943 CAS.
- D. C. Oertel, M. G. Bawendi, A. C. Arango and V. Bulović, Appl. Phys. Lett., 2005, 87, 1–3 CrossRef.
- J. H. Bang and P. V. Kamat, ACS Nano, 2009, 3, 1467–1476 CrossRef CAS PubMed.
- S. Nakamura, T. Mukai and M. Senoh, Jpn. J. Appl. Phys., 1991, 30, 1998–2001 CrossRef.
- S. Nakamura, Y. Harada and M. Seno, Appl. Phys. Lett., 1991, 58, 2021–2023 CrossRef CAS.
- S. Colvin, M. Schlamp and A. P. Alivisatos, Nature, 1994, 370, 354–357 CrossRef.
- K.-H. Lee, J.-H. Lee, W.-S. Song, H. Ko, C. Lee, J.-H. Lee and H. Yang, ACS Nano, 2013, 7, 7295–7302 CAS.
- H. Shen, W. Cao, N. T. Shewmon, C. Yang, L. Song Li and J. Xue, Nano Lett., 2015, 15, 1211–1216 Search PubMed.
- S. Cho, Y. Kim, S. Lee and J. Y. Woo, Korean J. Chem. Eng., 2024, 53, 4674–4706 Search PubMed.
- R. Leardi, Anal. Chim. Acta, 2009, 652, 161–172 CAS.
- S. Pedetti, S. Ithurria, H. Heuclin, G. Patriarche and B. Dubertret, J. Am. Chem. Soc., 2014, 136, 16430–16438 CAS.
- V. Dzhagan, A. G. Milekhin, M. Y. Valakh, S. Pedetti, M. Tessier, B. Dubertret and D. R. T. Zahn, Nanoscale, 2016, 8, 17204–17212 Search PubMed.
- B. Mahler, B. Nadal, C. Bouet, G. Patriarche and B. Dubertret, J. Am. Chem. Soc., 2012, 134, 18591–18598 CAS.
- P. Reiss, M. Protière and L. Li, Small, 2009, 5, 154–168 CAS.
- D. V. Talapin, J. H. Nelson, E. V. Shevchenko, S. Aloni, B. Sadtler and A. P. Alivisatos, Nano Lett., 2007, 7, 2951–2959 CrossRef CAS.
- Y. Yao, X. Bao, Y. Zhu, X. Sui, A. Hu, P. Bai, S. Wang, H. Yang, X. Liu and Y. Gao, Nano Res., 2023, 16, 10420–10428 CrossRef CAS.
- H. Yang, W. Xiang, X. Zhao, X. Ge, B. Zhu, Y. Cui and J. Zhang, Opt. Laser Technol., 2022, 156, 108615 CrossRef CAS.
- C. Rodà, A. Di Giacomo, L. C. Tasende Rodríguez, M. Chandra Sekhar, J. Leemans, Z. Hens, P. Geiregat and I. Moreels, Nano Lett., 2023, 23, 3224–3230 Search PubMed.
- C. Dabard, V. Guilloux, C. Gréboval, H. Po, L. Makke, N. Fu, X. Z. Xu, M. G. Silly, G. Patriarche, E. Lhuillier, T. Barisien, J. I. Climente, B. T. Diroll and S. Ithurria, Nat. Commun., 2022, 13, 1–10 Search PubMed.
- J. Leemans, S. Singh, C. Li, S. Ten Brinck, S. Bals, I. Infante, I. Moreels and Z. Hens, J. Phys. Chem. Lett., 2020, 11, 3339–3344 Search PubMed.
- Q. Li, K. Wu, J. Chen, Z. Chen, J. R. McBride and T. Lian, ACS Nano, 2016, 10, 3843–3851 CrossRef CAS.
- A. Schlosser, R. T. Graf and N. C. Bigall, Nanoscale Adv., 2020, 2, 4604–4614 RSC.
- S. Delikanli, B. Canimkurbey, P. Ludwig Hernández-Martínez, F. Shabani, A. Tarik Isik, I. Ozkan, I. Bozkaya, T. Bozkaya, F. Isik, E. Goksu Durmusoglu, M. Izmir, H. Akgun and H. Volkan Demir, J. Am. Chem. Soc., 2023, 145, 12033–12043 CrossRef CAS PubMed.
- S. Delikanli, B. Guzelturk, P. L. Hernández-Martínez, T. Erdem, Y. Kelestemur, M. Olutas, M. Z. Akgul and H. V. Demir, Adv. Funct. Mater., 2015, 25, 4282–4289 CrossRef CAS.
- F. Fan, P. Kanjanaboos, M. Saravanapavanantham, E. Beauregard, G. Ingram, E. Yassitepe, M. M. Adachi, O. Voznyy, A. K. Johnston, G. Walters, G. H. Kim, Z. H. Lu and E. H. Sargent, Nano Lett., 2015, 15, 4611–4615 CrossRef CAS PubMed.
- G. H. V. Bertrand, A. Polovitsyn, S. Christodoulou, A. H. Khan and I. Moreels, Chem. Commun., 2016, 52, 11975–11978 RSC.
- A. Hu, P. Bai, Y. Zhu, Z. Tang, L. Xiao and Y. Gao, Small, 2022, 18, 2204120 CrossRef CAS PubMed.
- S. Singh, R. Tomar, S. Ten Brinck, J. De Roo, P. Geiregat, J. C. Martins, I. Infante and Z. Hens, J. Am. Chem. Soc., 2018, 140, 13292–13300 CrossRef CAS PubMed.
- I. Du Fossé, S. Ten Brinck, I. Infante and A. J. Houtepen, Chem. Mater., 2019, 31, 4575–4583 CrossRef.
- T. Sugimoto, Interface, 1987, 28, 65–108 CAS.
- Z. Hens and R. K. Čapek, Coord. Chem. Rev., 2014, 263–264, 217–228 CrossRef CAS.
- R. Leardi, C. Melzi and G. Polotti, CAT (Chemometric Agile Tool), freely downloadable from https://gruppochemiometria.it/index.php/software.
- N. Gunantara, Cogent Eng., 2018, 5, 1502242 CrossRef.
- J. Dai, H. Roshan, M. De Franco, L. Goldoni, F. De Boni, J. Xi, F. Yuan, H. Dong, Z. Wu, F. Di Stasio and L. Manna, ACS Appl. Mater. Interfaces, 2024, 16, 11627–11636 CrossRef CAS PubMed.
- J. Dai, C. Zhao, J. Xu, H. Roshan, H. Dong, F. Di Stasio, F. Yuan, B. Jiao and Z. Wu, Org. Electron., 2024, 124, 106941 CrossRef CAS.
- M. İzmir, A. Sharma, S. Shendre, E. G. Durmusoglu, V. K. Sharma, F. Shabani, H. D. Baruj, S. Delikanli, M. Sharma and H. V. Demir, ACS Appl. Nano Mater., 2022, 5, 1367–1376 CrossRef.
- K. Mallem, M. F. Prodanov, C. Dezhang, M. Marus, C. Kang, S. B. Shivarudraiah, V. V. Vashchenko, J. E. Halpert and A. K. Srivastava, ACS Appl. Mater. Interfaces, 2022, 14, 18723–18735 CrossRef CAS.
- H. Shen, Q. Lin, W. Cao, C. Yang, N. T. Shewmon, H. Wang, J. Niu, L. S. Li and J. Xue, Nanoscale, 2017, 9, 13583–13591 RSC.
- F. Zhang, S. Wang, L. Wang, Q. Lin, H. Shen, W. Cao, C. Yang, H. Wang, L. Yu, Z. Du, J. Xue and L. S. Li, Nanoscale, 2017, 9, 13583–13591 RSC.
- Y. Yang, C. Zhang, X. Qu, W. Zhang, M. Marus and B. Xu, IEEE Trans. Nanotechnol., 2019, 18, 220–225 CAS.
- H. Roshan, D. Zhu, D. Piccinotti, J. Dai, M. De Franco, M. Barelli, M. Prato, L. De Trizio, L. Manna and F. Di Stasio, Adv. Sci., 2024, 11, 2400734 CrossRef CAS.
- A. W. Achtstein, A. Antanovich, A. Prudnikau, R. Scott, U. Woggon and M. Artemyev, J. Phys. Chem. C, 2015, 119, 20156–20161 CrossRef CAS.
- M. G. Helander, M. T. Greiner, Z. B. Wang and Z. H. Lu, Appl. Surf. Sci., 2010, 256, 2602–2605 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Synthesis parameters and model coefficients. XPS spectra. LED fabrication parameters and model coefficients. EQE and luminance of LED devices. See DOI: https://doi.org/10.1039/d4nr03461a |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2025 |