Photoabsorption of silver cluster cations in an ion trap: nonlinear action spectra via multi-photon dissociation vs. directly measured linear absorption spectra

Abstract

We report photodissociation processes and spectral measurements upon photoabsorption of size-selected cationic silver clusters, Ag_N⁺, stored in an ion trap. The experiment shows that small clusters (N ≲ 15) dissociate upon one-photon absorption, whereas larger ones require multiple photons up to five in the present study. The emergence of multi-photon processes is attributed to collisional cooling in the presence of a buffer helium gas in the trap, which competes with size-dependent dissociation rates. These observations are explained by simulations that consider the two competing effects, where the statistical Rice–Ramsperger–Kassel (RRK) theory is employed to evaluate dissociation rates. Action spectra of photodissociation are compared with linear absorption spectra directly measured by cavity-ring-down-type high-sensitivity spectroscopy, revealing that the profiles of the action spectra are sharpened by the nonlinear effects in the multi-photon regime. This observation demonstrates the importance of the linear absorption measurement to obtain both spectral profiles and cross sections for large clusters that exhibit multi-photon dissociation.

---

1. Introduction

Metal nanoparticles are known to exhibit characteristic optical properties different from the corresponding bulk. Out of them, plasmonic excitation or collective excitation of electrons, which is prominent in silver nanoparticles, attracts much attention¹ because of its various potential applications such as optical sensing,² energy harvesting,³etc., while fundamental aspects are also studied recently, such as the origin of size effects on the plasmonic behaviors of supported nanoparticles.⁴ These features of nanoparticles have motivated studies of further smaller particles, i.e., metal clusters that are composed of several to several hundred atoms. For example, Tiggesbäumker et al. examined the photoabsorption of size-selected silver cluster cations, Ag_N⁺, in an ion beam by photodissociation action spectroscopy.^5–7 A relatively broad single absorption band observed for Ag₉⁺ was interpreted as evidence of collective excitation of electrons, accompanied by a large oscillator strength. On the other hand, Rayner et al. reported a structure-rich photodissociation spectrum of Ag₉Kr⁺ (ref. 8) in contrast to the above-mentioned Ag₉⁺; the difference was attributed to the temperature of the sample clusters, which was estimated to be 100 K for Ag₉Kr⁺,⁸ whereas ∼2000 K for Ag₉⁺.^6,9 A similar temperature effect has been reported for the spectral profiles of sodium clusters.^10,11 These results emphasize the importance of the temperature of the clusters prepared for measurement. Photoabsorption and relevant optical responses have been investigated as well for silver clusters embedded in matrices^12–17 or supported on substrates,^18–21 including surface second-harmonic-generation spectroscopy^18,19 and two-photon photoemission spectroscopy.^20,21 Among these studies, Yu et al. reported the photoabsorption spectra of Ag_N in solid neon at 6 K for several sizes from N = 5 up to 120,¹⁷ where the size-dependent evolution of absorption maxima was discussed. Although absorption maxima and spectral profiles have been obtained by these advanced experimental studies, it is not common to perform the quantitative evaluation of absorption cross sections or oscillator strengths that are important in characterizing the collectiveness of excitation, because it is difficult to precisely control the number of sample clusters that interact with incident photons.

In this context, an ion trap provides us with a unique opportunity to control and characterize the temperature and the number of sample ions.²² The temperature is well-defined by a buffer gas thermalizing the cluster ions. The number of clusters stored in the trap is accurately measured as ion current. Furthermore, the spatial distribution of ions can be characterized by tomographic measurement.²³ It is thus possible to obtain the numbers of irradiated clusters and incident photons, and hence quantitative cross sections. Taking advantage of these features of an ion trap, we are tackling the measurement of UV–Vis spectra of Ag_N⁺ by photodissociation action spectroscopy in an extensive size range from several to a hundred atoms. During these experiments, we encountered multi-photon dissociation processes in relatively large clusters (N ≳ 15), which is in contrast to one-photon processes in small ones. Multi-photon dissociation may not yield action spectra that are equivalent to linear absorption spectra in spectral profiles as well as in cross sections.

Multi-photon dissociation has been reported previously. For example, Walther et al. performed photofragmentation experiments using discrete wavelengths of the harmonics of a pulsed Nd:YAG laser on gold cluster cations, Au_N⁺ (N = 4–23), where they found two-photon dissociation processes for N = 7, 9, 11, and 13 and above at the second harmonic (2.33 eV) excitation in the visible range; they further examined the dissociation processes by employing the statistical Rice–Ramsperger–Kassel (RRK) theory.²⁴ As for the infrared (IR) range, Oomens et al. reported the action spectra of cationic polyaromatic hydrocarbons,^25–27 where the ions stored in a Paul-type quadrupole ion trap are irradiated with multiple micropulses from the free electron laser for infrared experiments (FELIX). Because of the low photon energy in the IR region, the process involves as many as 50 photons. The multi-photon dissociation technique has been applied to even larger systems such as peptide molecules²⁸ using visible pulses and megadalton-size DNA²⁹ using an IR cw CO₂ laser.

The present paper reports the photoabsorption of size-selected Ag_N⁺ stored in an ion trap in the UV–Vis range both by photodissociation action spectroscopy, which allows an indirect probe of absorption, and by cavity-ring-down (CRD) spectroscopy that directly measures extinction of light with high sensitivity. As for action spectroscopy, we explore one- and multi-photon dissociation mechanisms in addition to spectral measurements, which are found to be governed by two competing processes: dissociative relaxation and collisional cooling by the buffer helium gas introduced into the trap. The origin of multiple photons involved in the processes, i.e., intra- or inter-pulse, is also discussed for the present experimental conditions. We then demonstrate CRD spectroscopy that enables us to measure intrinsic photoabsorption spectra quantitatively without relying on photodissociation. It is thus possible to obtain linear absorption spectra even for large clusters, which otherwise exhibit nonlinear profiles in photodissociation spectra due to multi-photon processes. The CRD technique has such an advantage but only in a limited spectral range. These features are discussed for the two complementary techniques.

2. Experimental procedures

The experimental setup has been described in our previous reports.^30–33 Briefly, silver cluster cations were generated by a magnetron-sputtering-type cluster ion source.^34,35 The cluster size of interest was selected using a quadrupole mass filter (MAX-16000, Extrel CMS). The clusters were then loaded in a homemade 40 cm linear ion trap, where a buffer helium gas was introduced to decelerate and thermalize the clusters at a gas pressure regulated using a needle valve (see the ESI† for details). After 500 ms of thermalization, the cluster ions were irradiated with a controlled number of laser pulses from a tunable 5 ns optical parametric oscillator (50 Hz, NT230–50, EKSPLA). After waiting for another 500 ms to allow clusters to be dissociated, the reduced intensity of the parent clusters was recorded through a second quadrupole mass filter (MAX-16000, Extrel CMS) by employing an ammeter. The same procedure was also performed to measure the intensity of cluster ions without laser irradiation. A photodissociation yield, D, was thus obtained from this series of measurements. At the same time, the number of incident photons, N_photon, was monitored using a photodiode (S1337-1010BQ, Hamamatsu Photonics K.K.) calibrated using a power meter (3A-P, Ophir) beforehand. In this study, we measured the photodissociation yield as a function of the number of incident photons for various sizes of cluster ions. The number of photons was carefully controlled to keep photodissociation yields as low as 2%–10%. The photon energy, hν, was fixed at the absorption maximum, which was determined in advance by measuring the photodissociation cross section:as a function of photon energy, where r is the laser radius, γ is the fraction of the trapped clusters irradiated (see the ESI†), N_dis is the decrease in the number of parent clusters upon photoabsorption and N_parent is the number of parent clusters measured without laser irradiation.

There are three parameters in our apparatus: the pressure and the temperature of the buffer helium gas, p_buffer and T_buffer, and the number of laser pulses, N_pulse. We also investigated the influence of these parameters on the dissociation process of the cluster. As for temperature control, the buffer helium gas was introduced into the trap without any temperature regulation for room-temperature experiments, whereas it was cooled down by liquid nitrogen before flowing into the trap so that T_buffer reaches as low as 120 K for low-temperature experiments.

In addition to the above photodissociation action spectroscopy, photoabsorption spectroscopy was performed to observe the transmission of light through the stored cluster ions, which allows the direct measurement of photoabsorption without relying on photodissociation. In this technique, clusters stored in the ion trap are probed by photons travelling back and forth in a high-finesse optical cavity consisting of two high-reflectivity mirrors (the CRD technique³⁶), which provides us with extremely high sensitivity for obtaining a linear absorption spectrum of size-selected cluster ions.^30–32 See the ESI† for more details.

3. Results and discussion

3.1. Emergence of multi-photon dissociation

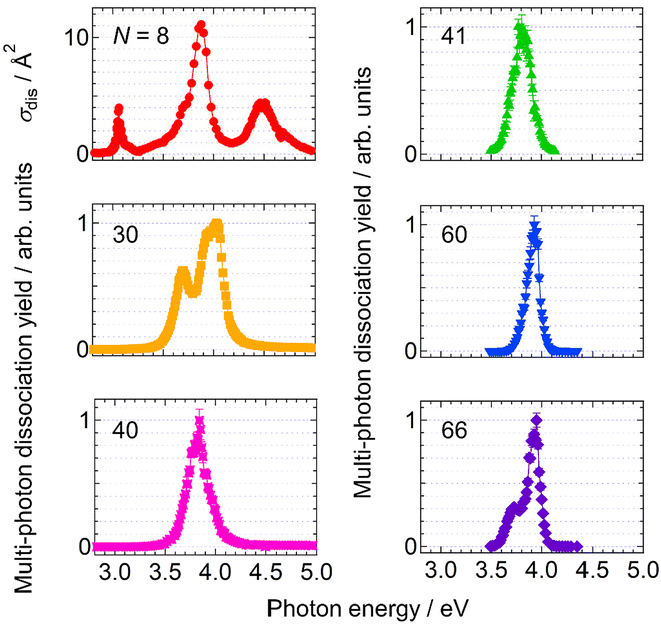
Firstly, the photodissociation cross section or yield of Ag_N⁺ was measured as a function of photon energy. The results of N = 8, 30, 40, 41, 60 and 66 are shown in Fig. 1. The spectrum of Ag₈⁺ exhibits several absorption maxima in the spectral range between 3.0 and 5.0 eV, whereas those of N = 30, 40, 41, 60 and 66 show one or two peaks in the relatively narrow range between 3.5 and 4.0 eV. Although these spectra provide important information on electron excitation in silver clusters, here we focus on the dissociation processes rather than the spectral features.

Fig. 1 Photodissociation spectra of Ag_N⁺. Measurements for N ≥ 41 were performed only in the vicinity of 4 eV, where their absorption bands were observed. See the text for the definition of the multi-photon dissociation yield in the ordinate.

Fig. 2 shows photodissociation yields measured as a function of the number of incident photons. The measurements were performed at photon energies of spectral maxima in Fig. 1. Generally, larger clusters require more photons (i.e., plots are located on the right-hand side) than smaller ones. In addition, it should be noted that the increasing rate of the dissociation yield shows significant size dependence. The values of the slopes, M, of the best linear fits in Fig. 2 are summarized in Table 1. For N = 8, the dissociation yields were almost proportional to the number of incident photons as we naively expect. On the other hand, the larger clusters exhibited dramatic increases in the photodissociation yields; the yield increases quadratically at N = 30. The value of the slope even reaches M ∼ 5 at N = 66. This size dependence clearly shows the emergence of multi-photon processes at larger sizes: the value of the slope, M, reflects the number of photons necessary for dissociation. In these cases, D/N^M_photon would be a good measure for photoabsorption, instead of the photodissociation cross section defined by eqn (1) because the dissociation yields are proportional to the M-th power of N_photon. We call this value, D/N^M_photon, a multi-photon dissociation yield. These results indicate that the photodissociation action spectra of large clusters do not always reflect linear photoabsorption spectra due to multi-photon processes.

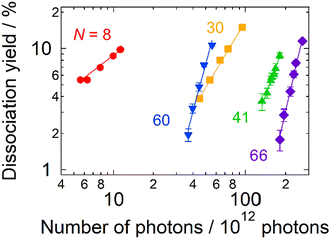Fig. 2 The photodissociation yield of Ag_N⁺ as a function of the number of incident photons in 10 pulses as adjusted by the pulse energy. The symbols denote experimental data. The solid lines are the best linear fits to the logarithmic plots (see Table 1 for details). The data were obtained at photon energies at photoabsorption maxima. The pressure and the temperature of the buffer gas were ∼1 Pa and 300 K, respectively.

Table 1 The values of the slopes of the best fits presented in Fig. 2

N	Slope, M	Photon energy/eV
8	0.83 ± 0.06	3.87
30	1.82 ± 0.08	4.03
41	2.8 ± 0.2	3.86
60	3.7 ± 0.2	3.87
66	4.7 ± 0.2	3.92

---

Out of a series of sizes examined, N = 15, 17 and 18 exhibited complex features; one-photon dissociation was major at higher photon energies, whereas two-photon processes became dominant at lower photon energies (see the ESI† for more details).

3.2. Origin of multi-photon processes: dissociation vs. collisional cooling

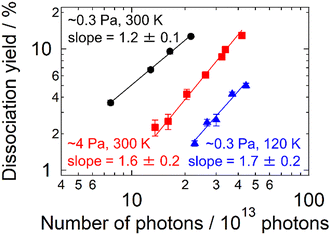
The present experimental results revealed the contribution of multi-photon processes to the photodissociation of Ag_N⁺ in an ion trap, particularly in the large cluster-size regime. What governs the dissociation process of the present clusters? The buffer helium gas introduced into the trap is one of the candidate factors. To confirm the influence of the buffer gas, measurements similar to those in Fig. 2 were carried out by varying the pressure, p_buffer, and the temperature, T_buffer. As for the pressure, two conditions were examined: p_buffer = 0.3 and 4 Pa. Fig. 3 displays the result of Ag₁₅⁺ measured at 4.03 eV. The plots were shifted to a higher N_photon side at a higher pressure (i.e., from black plots to red ones). M = 1.2 ± 0.1 at the lower pressure, suggesting dominant one-photon dissociation, whereas the M value increased to 1.6 ± 0.2 at the higher pressure, reflecting a contribution of two-photon processes. The effect of the buffer-gas temperature was also investigated. The blue plots in Fig. 3 indicate the dissociation yields measured at T_buffer = 120 K for p_buffer = 0.3 Pa. Comparison between T_buffer = 120 (blue plots) and 300 K (black plots) at the same p_buffer suggests that cold clusters prefer multi-photon processes rather than one-photon processes. These results indicate that the buffer gas is one of the essential factors determining the dissociation process that clusters undergo.

Fig. 3 The photodissociation yield of Ag₁₅⁺ as a function of the number of incident photons in 10 pulses. The measurement was performed under three different conditions of the buffer-gas pressure and temperature as indicated. The solid lines are the best linear fits to the logarithmic plots; the values of the slopes are indicated. The photon energy for excitation was 4.03 eV.

In this context, we discuss the origin of the size-dependent multi-photon contribution. Here we assume that clusters experience internal conversion and intramolecular vibrational energy redistribution (IVR) after photoabsorption in the same manner as proposed by Bouakil et al.²⁸ In addition, we focus on two competing processes that determine the pathway of clusters following photoabsorption: dissociative relaxation and collisional cooling by the buffer gas, both of which occur in vibrationally hot Ag_N⁺ clusters created upon photoabsorption. The balance between these two effects determines whether dissociation is induced by a single photon or by multiple photons. Here the statistical RRK theory^37–39 is employed to estimate the dissociation rate upon photoabsorption. The RRK theory has been employed for the analysis of dissociation energies of clusters upon one- and two-photon dissociation.²⁴ We extended this approach to the simulation of multi-photon processes including those with more than two photons by incorporating the cooling effect. The formulations, results and detailed discussion of the simulation are described in the ESI.† The result of N = 8 shows rapid dissociation, which is consistent with the present experiment showing that Ag₈⁺ dissociates upon one-photon absorption (Fig. S4†). On the other hand, Ag₁₉⁺ exhibits two-photon dissociation due to the cooling rate being higher than the dissociation rate by one photon (Fig. S5†). The model also explains the emergence of the three-photon process for Ag₄₁⁺ (Fig. S6†). The photon-energy dependence of photodissociation processes observed for N = 15, 17 and 18 was also reproduced by the present simulation (Fig. S7† for N = 18). In summary, the two competing processes of dissociative relaxation and collisional cooling by the buffer gas were found to be responsible for size- and energy-dependent photodissociation dynamics.

3.3. Multi-photon dissociation: does it take place inter- or intra-pulse?

In the present model, two types of multi-photon processes are possible: inter-pulse and intra-pulse. If the dissociation lifetime of the clusters photoexcited by a single photon is longer than the interval of the laser pulses, i.e., 20 ms for the present 50 Hz laser, the clusters gain additional internal energy by absorbing another photon in the subsequent laser pulse, which eventually causes dissociation when the clusters acquire a sufficiently high internal energy by repeating this process. Such a process is regarded as an inter-pulse multi-photon process. On the other hand, if the photoexcited clusters are cooled down by buffer-gas collision before the subsequent pulse arrives, the dissociation events should be completed by a single laser pulse. This process is regarded as an intra-pulse process.

To address if the multi-photon process is driven in an intra-pulse manner, one should record the dissociation yield as a function of laser pulse energy within a single pulse. However, the present experiment has difficulty in obtaining dissociation yields with a single pulse due to the relatively low sensitivity of the depletion measurement of parent ions; we irradiate at least several laser shots in our measurements. Alternatively, the inter- vs. intra-pulse contribution can be examined as follows. If the cluster dissociates in an intra-pulse manner, a photodissociation yield should increase linearly as a function of the number of laser pulses because each pulse induces dissociation independently. In contrast, in an inter-pulse manner, preceding pulses contribute to an increase in the internal energy of clusters. Therefore, the dissociation rate of the cluster becomes higher as the number of pulses increases, which should lead to a nonlinear increase in the photodissociation yield.

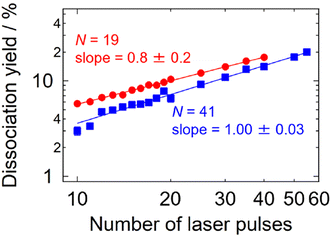
An additional experiment was carried out in this respect: dissociation yields were measured in the multi-photon size regime as a function of the number of irradiating laser pulses. The results shown in Fig. 4 indicate intra-pulse behaviors both for Ag₁₉⁺ (two-photon dissociation) and for Ag₄₁⁺ (three-photon dissociation), where the dissociation yields exhibit linear dependence on the number of laser pulses. This interpretation is also supported by the time-dependent internal energy simulated for Ag₁₉⁺ as shown in Fig. S5;† photoexcited Ag₁₉⁺ is well thermalized within 20 ms, i.e., before the arrival of the subsequent laser pulse. These results indicate that inter-pulse contributions are negligible under the present experimental conditions of the repetition rate of the laser pulses and the collisional cooling rate of the buffer gas. Note that the cooling rate of ions in a trap has been reported by Bouakil et al., who performed a pump–probe experiment on chromophore-tagged peptides to trace the temporal evolution of the dissociation yield caused by two photons of pump and probe pulses.²⁸ The result shows that cooling of the trapped ions proceeds with a time constant in the range of 0.6–2.6 ms depending on the buffer-gas pressure. If similar experiments were performed on the present silver clusters in the future, it would provide supporting data for their cooling rates.

Fig. 4 The photodissociation yields of Ag₁₉⁺ and Ag₄₁⁺ as a function of the number of laser pulses. The solid lines are the best linear fits to the logarithmic plots; the values of the slopes are indicated. The photon energy, the pressure and the temperature of the buffer gas were 3.81 eV, ∼2 Pa and 300 K, respectively, for both sizes.

Here one should note the reports of Oomens et al. on infrared multi-photon dissociation for cationic polyaromatic hydrocarbons employing a free electron laser FELIX.^25,26 They prepare sample ions by photoionizing effusive neutral molecules in a Paul-type quadrupole ion trap, which are irradiated with infrared pulses from FELIX. It produces 10 Hz macropulses with a duration of 5 μs; each macropulse consists of a train of micropulses with a picosecond duration separated by a 1 ns interval. They report that the multi-photon dissociation proceeds as follows. The sample ions accumulate internal energy by repetitive cycles of photoabsorption and relaxation into vibrational modes via IVR. The ions eventually dissociate when the internal energy reaches as high as about 6 eV, i.e., a typical energy required for these molecular ions to dissociate. This means that more than 50 photons are absorbed, where multiple micropulses in a 5 μs macropulse contribute to the multi-photon process. This is thus regarded as an inter-pulse process.

3.4. Direct measurements of photoabsorption spectra

As shown in Fig. 1, the spectral profiles are sharpened as the cluster size increases from N = 30 to 66, probably due to the nonlinearity inherent in multi-photon processes; the profile should be different from that of intrinsic photoabsorption. In addition, the nonlinear spectra do not provide absorption cross sections. To tackle these issues, we carried out further experiments to perform direct measurements of photoabsorption spectra, i.e., CRD spectroscopy,^18,40 without relying on photodissociation (see the ESI† for details). Fig. 5 displays photoabsorption spectra thus obtained for Ag₈⁺ and Ag₄₁⁺, where the corresponding photodissociation spectra are superimposed. The photoabsorption spectrum of Ag₄₁⁺ was obtained by two sets of high-reflectivity cavity mirrors that cover neighboring spectral ranges as displayed using green and red symbols. Note that the spectral range of measurement for each set of mirrors is limited because the signal-to-noise ratio is degraded at wavelengths where the reflectivity of the mirrors is not sufficiently high (see Fig. S9 in the ESI†).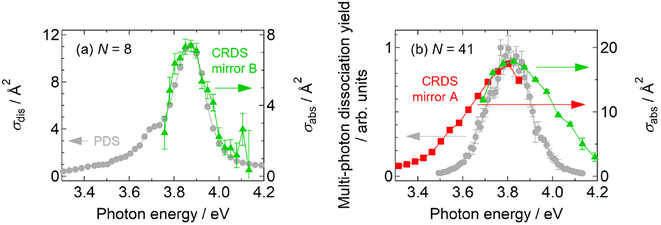

Fig. 5 Comparison between photodissociation action spectra (gray circles) and linear photoabsorption spectra obtained by CRD spectroscopy (colored symbols): (a) Ag₈⁺ and (b) Ag₄₁⁺.

Fig. 5a shows the result of Ag₈⁺ that dissociates by one-photon absorption; the two spectra are in reasonable agreement with each other especially in the profiles, indicating that the photodissociation action spectrum can be regarded as equivalent to a photoabsorption spectrum; the slight discrepancy in the absolute values of the cross sections, which is about 30%, is ascribed to the systematic error in the measurement due to the possible imperfect overlap of the cavity mode with the spatial distribution of the ions in the trap. The equivalence of both spectra has also been reported in our previous measurements on Ag₉⁺ and Ag₂⁺.^31,32 On the other hand, Fig. 5b for Ag₄₁⁺ shows that the photodissociation spectrum is indeed sharpened with respect to the photoabsorption spectrum; note that the absorption cross section is also evaluated. The present result implies that, although a photodissociation spectrum is equivalent to a linear photoabsorption spectrum in the one-photon regime, it gives a nonlinear spectrum in the multi-photon regime; the spectral peak energy is reliable, but the spectral profile is narrow.

We should note that it is necessary not to rely on multi-photon processes if one wishes to obtain intrinsic profiles as well as absolute cross sections of photoabsorption spectra to evaluate the oscillator strengths of optical transitions, for example. However, it should be noted also that it is not an easy task to conduct CRD spectroscopy. It requires several sets of high-reflectivity mirrors to cover a broad spectral range; high reflectivity is especially demanding for mirrors in the UV region. In addition, it is more time-consuming than photodissociation spectroscopy to acquire one data point. It is, therefore, not practical for obtaining a spectrum in the whole UV–Vis range. One should thus employ these techniques complementarily.

4. Conclusions

We investigated the photoabsorption of size-selected silver cluster cations in an ion trap both by photodissociation action spectroscopy and by linear absorption spectroscopy employing the CRD technique. As for photodissociation processes, the present experiments showed that small clusters dissociate upon one-photon absorption, whereas larger clusters tend to require multiple photons for dissociation. This size dependence was explained by the balance of the two competing processes that photoexcited clusters experience in the trap, i.e., dissociative relaxation and collisional cooling by the buffer gas. Based on the statistical RRK theory, the dissociation rate decreases at larger sizes due to a large number of vibrational degrees of freedom that accommodate the internal excess energy, which is in line with the previous study that pointed out possible underestimation of dissociation cross sections for large clusters due to their long lifetime for dissociation.⁴¹ Multi-photon processes emerge when the dissociation rate becomes lower than the cooling rate, which took place by a single ns laser pulse under the present experimental conditions. As for spectral measurements, although a photodissociation action spectrum was equivalent to a linear absorption spectrum for small sizes in the one-photon regime, it exhibited a sharpened spectral profile for large clusters in the multi-photon regime due to the nonlinearity in the photodissociation yields. In this regard, a linear absorption spectrum directly measured by CRD spectroscopy is important in providing both spectral profiles and absorption cross sections quantitatively even in a limited spectral range, which is materialized by combining an optical cavity for high-sensitivity measurement with an ion trap to prepare a high-density cluster sample. Nevertheless, spectral peak energies reliably obtained in a broad spectral range by multi-photon dissociation are also valuable for characterizing the size-dependent properties of silver and other metal clusters, which will be discussed in our forthcoming paper.

Author contributions

SK contributed to the investigation, formal analysis, data curation and writing – original draft; SF and TI contributed to the investigation and formal analysis; MA and TH contributed to the investigation and writing – review & editing; and AT contributed to the conceptualization, writing – review & editing, supervision, project administration and funding acquisition.

Data availability

The data supporting the findings of this study are available within the article and its ESI.†

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was supported by JSPS KAKENHI Grant Numbers JP25620017, JP18H03901, JP21J12060 and JP22H00317.

References

1. U. Kreibig and M. Vollmer, Optical Properties of Metal Clusters, Springer, Berlin, New York, 1995.
2. S. Nie and S. R. Emory, Science, 1997, 275, 1102.
3. H. A. Atwater and A. Polman, Nat. Mater., 2010, 9, 205.
4. A. Campos, N. Troc, E. Cottancin, M. Pellarin, H.-C. Weissker, J. Lermé, M. Kociak and M. Hillenkamp, Nat. Phys., 2019, 15, 275.
5. J. Tiggesbäumker, L. Köller, H. O. Lutz and K. H. Meiwes-Broer, Chem. Phys. Lett., 1992, 190, 42.
6. J. Tiggesbäumker, L. Köller, K.-H. Meiwes-Broer and A. Liebsch, Phys. Rev. A, 1993, 48, R1749.
7. J. Tiggesbäumker, L. Köller and K. H. Meiwes-Broer, Chem. Phys. Lett., 1996, 260, 428.
8. B. A. Collings, K. Athanassenas, D. M. Rayner and P. A. Hackett, Chem. Phys. Lett., 1994, 227, 490.
9. W. Begemann, K. H. Meiwes-Broer and H. O. Lutz, Phys. Rev. Lett., 1986, 56, 2248.
10. C. Ellert, M. Schmidt, C. Schmitt, T. Reiners and H. Haberland, Phys. Rev. Lett., 1995, 75, 1731.
11. M. Schmidt, C. Ellert, W. Kronmüller and H. Haberland, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 10970.
12. W. Harbich, S. Fedrigo and J. Buttet, Chem. Phys. Lett., 1992, 195, 613.
13. S. Fedrigo, W. Harbich and J. Buttet, Phys. Rev. B:Condens. Matter Mater. Phys., 1993, 47, 10706.
14. W. Harbich, S. Fedrigo and J. Buttet, Z. Phys. D: At., Mol. Clusters, 1993, 26, 138.
15. S. Fedrigo, W. Harbich, J. Belyaev and J. Buttet, Chem. Phys. Lett., 1993, 211, 166.
16. M. Harb, F. Rabilloud, D. Simon, A. Rydlo, S. Lecoultre, F. Conus, V. Rodrigues and C. Félix, J. Chem. Phys., 2008, 129, 194108.
17. C. Yu, R. Schira, H. Brune, B. von Issendorff, F. Rabilloud and W. Harbich, Nanoscale, 2018, 10, 20821.
18. M. Thämer, A. Kartouzian, P. Heister, T. Lünskens, S. Gerlach and U. Heiz, Small, 2014, 10, 2340.
19. T. Lünskens, P. Heister, M. Thämer, C. A. Walenta, A. Kartouzian and U. Heiz, Phys. Chem. Chem. Phys., 2015, 17, 17541.
20. M. Shibuta, K. Yamamoto, T. Ohta, T. Inoue, K. Mizoguchi, M. Nakaya, T. Eguchi and A. Nakajima, ACS Nano, 2021, 15, 1199.
21. T. Inoue, K. Mizoguchi, M. Tokita, M. Shibuta, M. Nakaya, T. Eguchi and A. Nakajima, Phys. Chem. Chem. Phys., 2024, 26, 16597.
22. D. Gerlich, Adv. Chem. Phys., 1992, 92, 1.
23. T. Majima, G. Santambrogio, C. Bartels, A. Terasaki, T. Kondow, J. Meinen and T. Leisner, Phys. Rev. A, 2012, 85, 053414.
24. C. Walther, St. Becker, G. Dietrich, H.-J. Kluge, M. Lindinger, K. Lützenkirchen, L. Schweikhard and J. Ziegler, Z. Phys. D: At., Mol. Clusters, 1996, 38, 51.
25. J. Oomens, A. J. A. van Roji, G. Meijer and G. von Helden, Astrophys. J., 2000, 542, 404.
26. J. Oomens, G. Meijer and G. von Helden, J. Phys. Chem. A, 2001, 105, 8302.
27. J. Oomens, A. G. G. M. Tielens, B. G. Sartakov, G. von Helden and G. Meijer, Astrophys. J., 2003, 591, 968.
28. M. Bouakil, A. Kulesza, S. Daly, L. MacAleese, R. Antoine and P. Dugourd, J. Am. Soc. Mass Spectrom., 2017, 28, 2181.
29. T. Doussineau, R. Antoine, M. Santacreu and P. Dugourd, J. Phys. Chem. Lett., 2012, 3, 2141.
30. A. Terasaki, T. Majima and T. Kondow, J. Chem. Phys., 2007, 127, 231101.
31. A. Terasaki, T. Majima, C. Kasai and T. Kondow, Eur. Phys. J. D, 2009, 52, 43.
32. K. Egashira, C. Bartels, T. Kondow and A. Terasaki, Eur. Phys. J. D, 2011, 63, 183.
33. S. Kawamura, M. Yamaguchi, S. Kono, M. Arakawa, T. Yasuike, T. Horio and A. Terasaki, J. Phys. Chem. A, 2023, 127, 6063.
34. H. Haberland, M. Karrais and M. Mall, Z. Phys. D: At., Mol. Clusters, 1991, 20, 413.
35. H. Haberland, History, Some Basics, and an Outlook, in Gas-Phase Synthesis of Nanoparticles, ed. Y. Huttel, John Wiley & Sons, Ltd, 2017, p. 23.
36. A. O'Keefe and D. A. G. Deacon, Rev. Sci. Instrum., 1988, 59, 2544.
37. O. K. Rice and H. C. Ramsperger, J. Am. Chem. Soc., 1927, 49, 7.
38. L. S. Kassel, J. Phys. Chem., 1928, 32, 225.
39. J. I. Steinfeld, J. S. Francisco and W. L. Hase, Chemical Kinetics And Dynamics, Prentice Hall, Upper Side River, 1989, p. 358.
40. T. Lünskens, A. von Weber, M. Jakob, T. Lelaidier, A. Kartouzian and U. Heiz, J. Phys. Chem. C, 2017, 121, 9331.
41. A. Terasaki, J. Phys. Chem. A, 2007, 111, 7671.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr03563a

‡ Present address: Department of Earth and Planetary Sciences, Faculty of Science, Kyushu University, 744 Motooka, Nishi-ku, Fukuoka 819-0395, Japan.

---