Open Access Article
Open Access ArticleEffect of the number ratio and size ratio on the formation of binary superlattices assembled from polymer-tethered spherical nanoparticles of two sizes†
Jinlan
Li
ab,
Xin
Yu
ab,
Jianing
Zhang
ac,
Jing
Jin
*ac,
Yanxiong
Pan
 *ab,
Xiangling
Ji
*ab,
Xiangling
Ji
 ab and
Wei
Jiang
ab and
Wei
Jiang
 *abc
*abc
aState Key Laboratory of Polymer Physics and Chemistry, Changchun Institute of Applied Chemistry, Chinese Academy of Sciences, Changchun 130022, China. E-mail: jjin@wtu.edu.cn; yxpan@ciac.ac.cn; weijiang@wtu.edu.cn
bSchool of Applied Chemistry and Engineering, University of Science and Technology of China, Hefei 230026, China
cSchool of Materials Science and Engineering, Wuhan Textile University, Wuhan 430200, China
First published on 12th November 2024
Abstract
Binary superlattices (BNSLs) with unique configurations are of great interest, attributed to the interaction between two kinds of nanoparticles, providing potential applications in sensing, electronic and optical fields. Here, polystyrene (PS) tethered spherical gold nanoparticles (AuNPs) with two core diameters spontaneously assembled into BNSLs via emulsion-confined self-assembly. BNSLs with specific stoichiometry and interparticle gaps of the NPs are prepared by tuning the number and size ratios of the two types of NPs. Moreover, after introducing long ligands, binary NPs are separated into macrophase separation or mixed together, depending on the interaction between polymer chains tethered to the AuNPs. Finally, PS-tethered AuNPs provide more possibilities for fabricating multifunctional BNSLs.
Introduction
Recently, the assembly of two kinds of metal nanoparticles (NPs) into well-defined binary superlattices (BNSLs) has resulted in diverse stoichiometries and lattice symmetries, leading to new properties owing to the interactions of the two kinds of nanoparticles.1–13 Long-ordered arrays or superlattices assembled from two kinds of NPs have attracted widespread attention owing to their potential applications in sensing, photonics, and plasmonics, among others.14–24 However, the macroscopic properties of BNSLs depend on their internal structures, which can be tuned by the structural parameters of the NPs, such as the size ratios, intrinsic shape, number ratios and the constituents of the two types of NPs.25–34When designing BNSLs with unique internal structures, the physical and chemical properties of ligands decorating the surfaces of the NPs play a dominant role.35–41 Up to now, various molecules (e.g., short-chain molecules and polymers) have been used as ligands to prepare BNSLs with unique internal structures. For instance, Murray et al. proved that the strength of near-field couplings between oleic acid-coated NPs could be adjusted by varying the spherical nanoparticle size, composition, and internal structures of BNSLs, leading to broadband spectral tunability of the collective plasmonic response of BNSLs across the entire visible spectrum.42 Interestingly, various soft materials are prepared when polymers are tethered with NPs through covalent or coordinative interactions. Conformational entropic and enthalpic interactions are generated after grafting the polymer onto the NPs.43–46 The energetic contributions can be adjusted by controlling the average molecular weight (Mn), architecture, chemical properties, and the surrounding solvent of the polymer. Thus, the adjacent spacing of the NPs is significantly expanded by modifying the polymer. In the last few decades, a great deal of effort has been dedicated to studying the self-organization of polymer-tethered NPs into well-defined superlattices. For example, Zhu and co-workers prepared three different types of BNSLs by controlling the Mn of polymer ligands and explained the features of two kinds of polymer-tethered spherical NPs during assembly and the corresponding co-assembly mechanism.47
In the past, we reported exquisite BNSLs assembled from polymer-tethered anisotropic and isotropic NPs and systematic research on the co-assembly of the different NPs and the corresponding physical mechanism.35,37 Herein, we study the assembly of two kinds of polystyrene (PS) tethered isotropic spherical gold nanoparticles (AuNPs@PS) through the emulsion-confined assembly strategy and explore the effect of the number ratio and size ratio of the two NPs on the final internal structure of the BNSLs, which are different from our previous report.35,37 The large AuNPs@PS building blocks are arrayed in a hexagonally close-packed or square structure, while smaller AuNP building blocks occupy the center of the periodically arranged large AuNP structure. Through the control of the effective size ratios and the number ratios of the two types of AuNPs, BNSLs with different internal periodic arrangements can be fabricated. Moreover, the BNSLs with diverse packing densities can be realized by tuning the Mn of the PS ligands modified on the surface of the AuNPs. After introducing long PS ligands, binary NPs are separated into macrophase separation or mixed together, depending on the interaction between polymer chains tethered to AuNPs, and the interparticle space between large AuNPs is tunable. Studying BNSLs assembled from polymer-tethered NPs may create new collective properties and provide more potential applications in data storage and optoelectronic devices.
Results and discussion
Effect of number ratios on the BNSLs
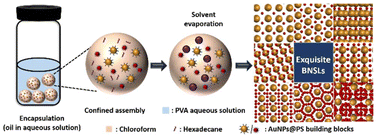
First, monodisperse AuNPs with two sizes (the average sizes are 15.4 ± 0.9 nm and 5.1 ± 0.4 nm, respectively) are synthesized according to previous literature (Fig. 1a and Fig. S1 in the ESI†),48 and thiol-terminated PS2k (PS2k-SH, Mn = 2.0 kg mol−1, and PDI = 1.35) are modified on the surface of the AuNPs to fabricate PS2k coated Au15.4NP (Au15.4NPs@PS2k) and PS2k coated Au5.1NP (Au5.1NPs@PS2k) building blocks (the subscripts refer to the diameter of the synthesized AuNPs) by the ligand exchange strategy.48 Well-defined BNSLs can be prepared, as shown in Scheme 1. Typically, Au15.4NPs@PS2k building blocks, Au5.1NPs@PS2k building blocks, and hexadecane in chloroform (CF) solution (1.0 wt%) were completely mixed in appropriate proportions. Subsequently, the NP and HD chloroform mixture was emulsified using a poly(vinyl alcohol) (PVA, 0.3 wt%, 1.0 mL) aqueous solution. As the CF slowly evaporated, the AuNPs@PS building blocks spontaneously transferred to the PVA/HD interface.35,37 The spontaneous co-assembly of two kinds of AuNPs@PS building blocks occurred upon further CF evaporation. After the CF solvent had evaporated entirely, well-defined superlattices were obtained. As shown in Fig. 1a, two high monodisperse Au15.4NPs@PS2k and Au5.1NPs@PS2k are used as building blocks to prepare AuNP superlattices, where AuNPs are arranged in a hexagonally close-packed configuration, to minimize the whole system energy. When small AuNPs@PS2k and large AuNPs@PS2k building blocks are mixed with a number ratio of ∼1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, an AB-type superlattice structure is prepared,26 which differs from the single-component system. Low and magnified transmission electron microscopy (TEM) images (Fig. 1b and c and Fig. S2†) also show that the formed BNSLs with larger AuNP building blocks were arranged in a square sublattice and the smaller ones were positioned in the interstices. In addition, the exquisite BNSLs with a special internal structure can be proved by scanning transmission electron microscopy (STEM) and the corresponding energy-dispersive X-ray spectra (EDX) elemental mapping of Au (Fig. 1d and e), and the dark background is filled almost entirely with PS ligands. Those features demonstrate the prepared BNSLs of two kinds of AuNPs@PS2k with an AB-type arrangement from the top view (Fig. 1f).
1, an AB-type superlattice structure is prepared,26 which differs from the single-component system. Low and magnified transmission electron microscopy (TEM) images (Fig. 1b and c and Fig. S2†) also show that the formed BNSLs with larger AuNP building blocks were arranged in a square sublattice and the smaller ones were positioned in the interstices. In addition, the exquisite BNSLs with a special internal structure can be proved by scanning transmission electron microscopy (STEM) and the corresponding energy-dispersive X-ray spectra (EDX) elemental mapping of Au (Fig. 1d and e), and the dark background is filled almost entirely with PS ligands. Those features demonstrate the prepared BNSLs of two kinds of AuNPs@PS2k with an AB-type arrangement from the top view (Fig. 1f).
To explore the fabrication of other assemblies using identical types of NPs, we systematically changed the number ratios of the Au5.1NPs@PS2k and Au15.4NPs@PS2k building blocks, as shown in Fig. 2. When the Au5.1NPs@PS2k and Au15.4NPs@PS2k building blocks are mixed with a number ratio ∼2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, free-standing AB2-type BNSLs are obtained (Fig. S3†).45 As shown in Fig. 2a and b, the larger Au15.4NPs@PS building blocks show a hexagonally packed arrangement, and the small Au5.1NPs@PS are located in the interstices of three neighboring larger AuNP building blocks. The inset in Fig. 2b shows the corresponding schematic diagram of the BNSLs, illustrating regular internal permutation of AuNPs, in which individual larger AuNPs have six small AuNP neighbors. The unique BNSL structure is further confirmed by STEM characterization and the corresponding EDX elemental mapping of Au (Fig. 2c and d).
1, free-standing AB2-type BNSLs are obtained (Fig. S3†).45 As shown in Fig. 2a and b, the larger Au15.4NPs@PS building blocks show a hexagonally packed arrangement, and the small Au5.1NPs@PS are located in the interstices of three neighboring larger AuNP building blocks. The inset in Fig. 2b shows the corresponding schematic diagram of the BNSLs, illustrating regular internal permutation of AuNPs, in which individual larger AuNPs have six small AuNP neighbors. The unique BNSL structure is further confirmed by STEM characterization and the corresponding EDX elemental mapping of Au (Fig. 2c and d).
Further increasing the number ratio of Au5.1NPs@PS2k to Au15.4NPs@PS2k ∼3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, AB2 (Fig. 3a and Fig. S4a†)27 and AB3-type BNSLs (Fig. 3b and Fig. S4b†)26 can be prepared. Notably, when the number ratio of the mixture increases to ∼7
1, AB2 (Fig. 3a and Fig. S4a†)27 and AB3-type BNSLs (Fig. 3b and Fig. S4b†)26 can be prepared. Notably, when the number ratio of the mixture increases to ∼7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, Cu3Au-type (Fig. 3c),42 CaB6-type (Fig. 3d),36 and the structure of small AuNPs around the larger AuNPs (Fig. 3e and Fig. S4c†) can be obtained. Further increasing the number ratio of the small AuNPs and large AuNPs to ∼13
1, Cu3Au-type (Fig. 3c),42 CaB6-type (Fig. 3d),36 and the structure of small AuNPs around the larger AuNPs (Fig. 3e and Fig. S4c†) can be obtained. Further increasing the number ratio of the small AuNPs and large AuNPs to ∼13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 results in phase-pure BNSLs of higher stoichiometries, i.e., NaZn13,42 which exhibits the cubic symmetry and the long-range arrangement of the two types of AuNPs (Fig. 3f and Fig. S4d†). It is worth noting that although these BNSLs have been prepared by previous methods,26,42 achieving eight kinds of BNSLs with different internal structures using NPs with a single effective size ratio is still a challenge.
1 results in phase-pure BNSLs of higher stoichiometries, i.e., NaZn13,42 which exhibits the cubic symmetry and the long-range arrangement of the two types of AuNPs (Fig. 3f and Fig. S4d†). It is worth noting that although these BNSLs have been prepared by previous methods,26,42 achieving eight kinds of BNSLs with different internal structures using NPs with a single effective size ratio is still a challenge.
As previously reported,35,37 the formation of well-defined BNSLs is determined by minimizing the Gibbs free energy. The overall change in the Gibbs free energy of the AuNPs@PS system can be expressed as:
| ΔG = ΔH − TΔS | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, an AB-type superlattice structure is prepared, as shown in Fig. 1. AB-type BNSLs have the most uniform distribution to minimize the Gibbs free energy. Similarly, the lattices in the small NPs are uniformly distributed around the big NPs, i.e., AB2-type, AB3-type, Cu3Au-type, and CaB6-type can be obtained by increasing the number ratio up to 7
1, an AB-type superlattice structure is prepared, as shown in Fig. 1. AB-type BNSLs have the most uniform distribution to minimize the Gibbs free energy. Similarly, the lattices in the small NPs are uniformly distributed around the big NPs, i.e., AB2-type, AB3-type, Cu3Au-type, and CaB6-type can be obtained by increasing the number ratio up to 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. However, if the ratio is increased to 13
1. However, if the ratio is increased to 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the small NPs are too many to be uniformly distributed around the big NPs, and the excess small NPs have to aggregate into the vertices formed by four big NPs uniformly. Therefore, an NaZn13-type superlattice can be obtained, as shown in Fig. 3f.
1, the small NPs are too many to be uniformly distributed around the big NPs, and the excess small NPs have to aggregate into the vertices formed by four big NPs uniformly. Therefore, an NaZn13-type superlattice can be obtained, as shown in Fig. 3f.
Effect of size ratios on the BNSLs
In addition to the number ratio of the two kinds of AuNPs@PS building blocks, the effective size ratio of AuNPs@PS (λeff), the ratio of the effective diameter of the PS tethered small AuNPs (deff) to that of the PS tethered large AuNPs (Deff), also plays a dominant role in the configuration of the BNSLs. λeff can be applied to access the loss of entropy after the introduction of the small AuNPs. The effective diameter of the AuNPs@PS building blocks including the NP core and PS shell can be measured as the center-point to center-point distance between the adjacent AuNPs@PS building blocks from single-component AuNP@PS hexagonal packing in TEM images (Fig. S5d†). Herein, AuNPs with various diameters (i.e., 1.7 nm, 8 nm, and 10 nm) were prepared (Fig. S5a–c†) and tethered with PS2k, and further co-assembly with Au15.4NPs@PS2k with a fixed number ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to explore the effect of λeff on the structure of the BNSLs.48,49 For the Au1.7NPs@PS2k (deff = 4.1 ± 0.6 nm) and Au15.4NPs@PS2k (Deff = 20.1 ± 1.3 nm) building blocks, λeff is thus calculated to be 0.2, and Au1.7NPs@PS2k building blocks are distributed in the gap between the Au15.4NPs@PS2k building blocks (Fig. 4a). In this case, as the diameter of Au1.7NPs@PS2k is so small, the conformational entropy of the introduced Au1.7NPs@PS2k can be ignored. Thus, the Au15.4NPs@PS2k building blocks maintain the hexagonal packing to minimize the whole Gibbs free energy of the BNSLs. After the increase of the core AuNP size to 5.1 nm (i.e., Au5.1NPs@PS2k, deff = 8.7 ± 0.8 nm), the calculated λeff is 0.4, and the BNSLs exhibit the aforementioned AB2-type arrangement (Fig. 2 and 4b). After deff further increases to 11.2 ± 0.8 nm (i.e., Au8NPs@PS2k), λeff is 0.5 and exquisite BNSLs can be prepared, as shown in Fig. 4c. In this case, Au15.4NPs@PS2k still shows a hexagonally packed arrangement, and Au8NPs@PS2k is positioned in the space surrounded by three neighboring Au15.4NPs@PS2k building blocks, whereas the packing density increases compared with λeff which is 0.4. However, if oversized AuNPs@PS2k (i.e., Au10NPs@PS2k, deff = 13.5 ± 0.5 nm, and λeff is 0.7) is used, the introduced Au10NPs@PS2k causes the loss of conformational entropy, so Au10NPs@PS2k is macroscopically separated from the hexagonal Au15.4NPs@PS2k matrix to reduce the global free energy (Fig. 4d). In particular, when the number ratio of Au10NPs@PS2k to Au15NPs@PS2k increases to ∼10
1 to explore the effect of λeff on the structure of the BNSLs.48,49 For the Au1.7NPs@PS2k (deff = 4.1 ± 0.6 nm) and Au15.4NPs@PS2k (Deff = 20.1 ± 1.3 nm) building blocks, λeff is thus calculated to be 0.2, and Au1.7NPs@PS2k building blocks are distributed in the gap between the Au15.4NPs@PS2k building blocks (Fig. 4a). In this case, as the diameter of Au1.7NPs@PS2k is so small, the conformational entropy of the introduced Au1.7NPs@PS2k can be ignored. Thus, the Au15.4NPs@PS2k building blocks maintain the hexagonal packing to minimize the whole Gibbs free energy of the BNSLs. After the increase of the core AuNP size to 5.1 nm (i.e., Au5.1NPs@PS2k, deff = 8.7 ± 0.8 nm), the calculated λeff is 0.4, and the BNSLs exhibit the aforementioned AB2-type arrangement (Fig. 2 and 4b). After deff further increases to 11.2 ± 0.8 nm (i.e., Au8NPs@PS2k), λeff is 0.5 and exquisite BNSLs can be prepared, as shown in Fig. 4c. In this case, Au15.4NPs@PS2k still shows a hexagonally packed arrangement, and Au8NPs@PS2k is positioned in the space surrounded by three neighboring Au15.4NPs@PS2k building blocks, whereas the packing density increases compared with λeff which is 0.4. However, if oversized AuNPs@PS2k (i.e., Au10NPs@PS2k, deff = 13.5 ± 0.5 nm, and λeff is 0.7) is used, the introduced Au10NPs@PS2k causes the loss of conformational entropy, so Au10NPs@PS2k is macroscopically separated from the hexagonal Au15.4NPs@PS2k matrix to reduce the global free energy (Fig. 4d). In particular, when the number ratio of Au10NPs@PS2k to Au15NPs@PS2k increases to ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, CaCu5-type BNSLs can be obtained,26 as shown in Fig. S6.† The results show that both the number ratio and effective size ratio of the NPs have a decisive effect on the final internal structure of BNSLs.
1, CaCu5-type BNSLs can be obtained,26 as shown in Fig. S6.† The results show that both the number ratio and effective size ratio of the NPs have a decisive effect on the final internal structure of BNSLs.
In addition to the diameter of the initial synthesized NPs, the thickness of PS ligands also contributes to the deff of AuNPs@PS as well as λeff, affecting the arrangement of NPs within the assemblies. Therefore, Au5.1NPs tethered with different PS ligands are synthesized (i.e., PS2k, PS5k, and PS12k) to investigate the impact of the thickness of the PS ligands modified on the surface of Au5.1NPs building blocks on the final distribution of the BNSLs (Fig. S7†). Based on the previous discussion, Au15.4NPs@PS2k and Au5.1NPs@PS2k are assembled into an AB2-type structure (Fig. 5a). With a further increase of Mn of the PS ligands to 5k (i.e., Au5.1NPs@PS5k), the deff value increases to 13.3 ± 0.9 nm, and the calculated λeff is 0.7. Au15.4NPs@PS2k still shows a hexagonal configuration and Au5.1NPs@PS5k is mainly irregularly distributed in the vertices formed by three adjacent Au15.4NPs@PS2k building blocks (Fig. 5b), which is different from the result in Fig. 4d, attributed to the partially or fully screened rigid nature of small NPs. With a further increase in the Mn of PS ligands to 12k, the deff is 17.2 ± 1.7 nm, and the λeff is 0.9. In this case, the Au15.4NPs@PS2k and Au5.1NPs@PS12k building blocks form a disordered state, as shown in Fig. 5c. At this time, the narrow space between Au15.4NPs@PS2k cannot be penetrated by Au5.1NPs@PS12k. On the other hand, the short polymer-tethered large AuNPs quickly settle via the evaporation of the CF, while the long polymer-tethered small AuNPs are still well dispersed.
Similarly, large Au15.4NPs tethered with PS ligands of different Mn (i.e., PS0.8k, PS5k, and PS12k) and Au5.1NPs@PS2k are synthesized (Fig. S8†) and co-assembled with a number ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 to further explore their final spatial distribution of the BNSLs. When Au15.4NPs@PS0.8k (Deff = 19.6 ± 1.2 nm and λeff = 0.4) are used to co-assemble with Au5.1NPs@PS2k, macroscopic phase separation is caused and almost no regular BNSLs can be noted, which is probably because Au5.1NPs@PS2k cannot penetrate the short PS0.8k brushes on the surface of large AuNPs (Fig. 6a). As PS ligands increase to 5k (Au15.4NPs@PS5k, Deff = 21.5 ± 1.4 nm, and λeff = 0.4), at this time, AB2-type BNSLs can be prepared (Fig. 6c). With a further increase in the Mn of PS ligands to 12k (Au15.4NPs@PS12k, Deff = 26.2 ± 0.9 nm, and λeff = 0.3), the formed BNSLs adopt an AB2-type structure (Fig. 6d). However, the small AuNPs within the BNSLs are not evenly distributed in the space surrounded by three adjacent large AuNPs because the increase of Mn of PS ligands provides more space to accommodate small AuNPs and the AB2-type structure is not close-packed. Through tuning of the Mn of the large AuNPs, AB2-type BNSLs with different stacking densities of AuNPs of two sizes can be prepared. For further exploring the size ratio and number ratio of the two kinds of AuNPs@PS building blocks, Au15.4NPs@PS0.8k and Au15.4NPs@PS12k are co-assembled with more Au5.1NPs@PS2k, and the results in Fig. S9† show that exquisite BNSLs can be fabricated through tuning the size ratio and number ratio of the two kinds of AuNPs. As shown in Fig. S9a,† when Au15.4NPs@PS0.8k building blocks are co-assembled with Au5.1NPs@PS2k with a number ratio of ∼1
2 to further explore their final spatial distribution of the BNSLs. When Au15.4NPs@PS0.8k (Deff = 19.6 ± 1.2 nm and λeff = 0.4) are used to co-assemble with Au5.1NPs@PS2k, macroscopic phase separation is caused and almost no regular BNSLs can be noted, which is probably because Au5.1NPs@PS2k cannot penetrate the short PS0.8k brushes on the surface of large AuNPs (Fig. 6a). As PS ligands increase to 5k (Au15.4NPs@PS5k, Deff = 21.5 ± 1.4 nm, and λeff = 0.4), at this time, AB2-type BNSLs can be prepared (Fig. 6c). With a further increase in the Mn of PS ligands to 12k (Au15.4NPs@PS12k, Deff = 26.2 ± 0.9 nm, and λeff = 0.3), the formed BNSLs adopt an AB2-type structure (Fig. 6d). However, the small AuNPs within the BNSLs are not evenly distributed in the space surrounded by three adjacent large AuNPs because the increase of Mn of PS ligands provides more space to accommodate small AuNPs and the AB2-type structure is not close-packed. Through tuning of the Mn of the large AuNPs, AB2-type BNSLs with different stacking densities of AuNPs of two sizes can be prepared. For further exploring the size ratio and number ratio of the two kinds of AuNPs@PS building blocks, Au15.4NPs@PS0.8k and Au15.4NPs@PS12k are co-assembled with more Au5.1NPs@PS2k, and the results in Fig. S9† show that exquisite BNSLs can be fabricated through tuning the size ratio and number ratio of the two kinds of AuNPs. As shown in Fig. S9a,† when Au15.4NPs@PS0.8k building blocks are co-assembled with Au5.1NPs@PS2k with a number ratio of ∼1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13, AB13-type BNSLs can be prepared. Similarly, when the number ratio of Au5.1NPs@PS2k building blocks and Au15.4NPs@PS12k increases, the structure of small NPs around Au15.4NPs@PS12k is prepared (Fig. S9b†). The study shows that the internal structure should be predicted using size and number ratios, which cannot be simply determined by one parameter.
13, AB13-type BNSLs can be prepared. Similarly, when the number ratio of Au5.1NPs@PS2k building blocks and Au15.4NPs@PS12k increases, the structure of small NPs around Au15.4NPs@PS12k is prepared (Fig. S9b†). The study shows that the internal structure should be predicted using size and number ratios, which cannot be simply determined by one parameter.
The above results show that λeff can be applied to assess the entropy loss after introducing the small AuNPs and predict the structure of the formed BNSLs. Moreover, λeff can be adjusted through the core diameter of the AuNPs and the Mn of the PS ligands modified on the surface of the AuNPs, and the corresponding stacking density of the BNSLs can also be tuned. However, when exploring the effect of λeff on the BNSLs, the ratio of AuNPs of two sizes should be fixed. The final structure of the BNSLs is determined by the number and size ratios of the AuNPs of two sizes (Table S1†).
Conclusions
In brief, we developed a strategy to fabricate exquisite BNSLs assembled from PS-tethered spherical AuNPs in two sizes. The large AuNPs display a square or hexagonal stacking arrangement in BNSLs, while the introduced small AuNPs@PS are located in the PS domain surrounded by adjacent large ones to minimize the total free energy. In this strategy, the final distributions of the two diameters of AuNPs within the BNSLs mainly depend on the number ratios and the effective size ratio of the AuNPs. By adjusting the number ratio of the two diameters of AuNPs, eight kinds of BNSLs with different internal structures can be prepared. However, when the number ratio remains at 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, by tuning the effective size ratio, the obtained AlB2-type BNSLs remain unchanged until the effective size ratio reaches 0.5. In particular, when the number ratio of the two AuNPs changes (Au15.4NPs@PS2k
1, by tuning the effective size ratio, the obtained AlB2-type BNSLs remain unchanged until the effective size ratio reaches 0.5. In particular, when the number ratio of the two AuNPs changes (Au15.4NPs@PS2k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Au5.1NPs@PS2k ∼1
Au5.1NPs@PS2k ∼1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13), the phase separation structure becomes an ordered structure. Our results show that both the number ratio and effective size ratio of the AuNPs dominate the ultimate structures of the BNSLs, providing helpful guidance for the design of BNSLs.
13), the phase separation structure becomes an ordered structure. Our results show that both the number ratio and effective size ratio of the AuNPs dominate the ultimate structures of the BNSLs, providing helpful guidance for the design of BNSLs.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (52433001).References
- S. Mourdikoudis, M. Menelaou, N. Fiuza-Maneiro, G. C. Zheng, S. Y. Wei, J. Pérez-Juste, L. Polavarapu and Z. Sofer, Nanoscale Horiz., 2022, 7, 941–1015 Search PubMed.
- Y. Wang, J. Chen, C. Zhu, B. Zhu, S. Jeong, Y. Yi, Y. Liu, J. Fiadorwu, P. He and X. Ye, Nano Lett., 2021, 21, 5053–5059 CrossRef CAS PubMed.
- K. Wang, H. Ling, Y. Bao, M. Yang, Y. Yang, M. Hussain, H. Wang, L. Zhang, L. Xie, M. Yi, W. Huang, X. Xie and J. Zhu, Adv. Mater., 2018, 30, e1800595 Search PubMed.
- Q. Shi, D. Sikdar, R. Fu, K. J. Si, D. Dong, Y. Liu, M. Premaratne and W. Cheng, Adv. Mater., 2018, 30, e1801118 Search PubMed.
- F. Schulz, O. Pavelka, F. Lehmkuhler, F. Westermeier, Y. Okamura, N. S. Mueller, S. Reich and H. Lange, Nat. Commun., 2020, 11, 3821 Search PubMed.
- Z. Nie, A. Petukhova and E. Kumacheva, Nat. Nanotechnol., 2010, 5, 15–25 Search PubMed.
- M. Marchioni, G. Veronesi, I. Worms, W. L. Ling, T. Gallon, D. Leonard, C. Gateau, M. Chevallet, P. H. Jouneau, L. Carlini, C. Battocchio, P. Delangle, I. Michaud-Soret and A. Deniaud, Nanoscale Horiz., 2020, 5, 507–513 Search PubMed.
- K. H. Ku, J. M. Shin, M. P. Kim, C. H. Lee, M. K. Seo, G. R. Yi, S. G. Jang and B. J. Kim, J. Am. Chem. Soc., 2014, 136, 9982–9989 Search PubMed.
- Y. Kang, X. Ye, J. Chen, Y. Cai, R. E. Diaz, R. R. Adzic, E. A. Stach and C. B. Murray, J. Am. Chem. Soc., 2013, 135, 42–45 Search PubMed.
- S. Gupta, Q. Zhang, T. Emrick, A. C. Balazs and T. P. Russell, Nat. Mater., 2006, 5, 229–233 Search PubMed.
- A. Dong, J. Chen, P. M. Vora, J. M. Kikkawa and C. B. Murray, Nature, 2010, 466, 474–477 Search PubMed.
- I. Cherniukh, G. Raino, T. V. Sekh, C. Zhu, Y. Shynkarenko, R. A. John, E. Kobiyama, R. F. Mahrt, T. Stoferle, R. Erni, M. V. Kovalenko and M. I. Bodnarchuk, ACS Nano, 2021, 15, 16488–16500 Search PubMed.
- S. Brittman, N. A. Mahadik, S. B. Qadri, P. Y. Yee, J. G. Tischler and J. E. Boercker, ACS Appl. Mater. Interfaces, 2020, 12, 24271–24280 Search PubMed.
- H. Yun, J. W. Yu, Y. J. Lee, J.-S. Kim, C. H. Park, C. Nam, J. Han, T.-Y. Heo, S.-H. Choi, D. C. Lee, W. B. Lee, G. E. Stein and B. J. Kim, Chem. Mater., 2019, 31, 5264–5273 Search PubMed.
- M. Xu, K. H. Ku, Y. J. Lee, T. Kim, J. J. Shin, E. J. Kim, S.-H. Choi, H. Yun and B. J. Kim, Macromolecules, 2021, 54, 3084–3092 Search PubMed.
- H. Wang, H. Qian, W. Li, K. Wang, H. Li, X. Zheng, P. Gu, S. Chen, M. Yi, J. Xu and J. Zhu, Small, 2023, 19, e2208288 CrossRef PubMed.
- K. Thorkelsson, J. H. Nelson, A. P. Alivisatos and T. Xu, Nano Lett., 2013, 13, 4908–4913 Search PubMed.
- C. Wang, Nanoscale Horiz., 2024, 9, 1853–1854 RSC.
- Z. Nie, D. Fava, E. Kumacheva, S. Zou, G. C. Walker and M. Rubinstein, Nat. Mater., 2007, 6, 609–614 CrossRef CAS PubMed.
- R. Liang, J. Xu, R. Deng, K. Wang, S. Liu, J. Li and J. Zhu, ACS Macro Lett., 2014, 3, 486–490 CrossRef CAS.
- F. Li, K. Wang, N. Deng, J. Xu, M. Yi, B. Xiong and J. Zhu, ACS Appl. Mater. Interfaces, 2021, 13, 6566–6574 CrossRef CAS.
- J. Kao and T. Xu, J. Am. Chem. Soc., 2015, 137, 6356–6365 CrossRef CAS PubMed.
- J. Gong, R. S. Newman, M. Engel, M. Zhao, F. Bian, S. C. Glotzer and Z. Tang, Nat. Commun., 2017, 8, 14038 Search PubMed.
- Y. Gao, Y. Zhou, X. Xu, C. Chen, B. Xiong and J. Zhu, Small, 2022, e2106880, DOI:10.1002/smll.202106880.
- C. Yi, Y. Yang, B. Liu, J. He and Z. Nie, Chem. Soc. Rev., 2020, 49, 465–508 Search PubMed.
- X. Ye, C. Zhu, P. Ercius, S. N. Raja, B. He, M. R. Jones, M. R. Hauwiller, Y. Liu, T. Xu and A. P. Alivisatos, Nat. Commun., 2015, 6, 10052 CrossRef.
- E. V. Shevchenko, D. V. Talapin, N. A. Kotov, S. O'Brien and C. B. Murray, Nature, 2006, 439, 55–59 CrossRef CAS PubMed.
- Y. Chen, T. W. Liang, L. Chen, Y. F. Chen, B. R. Yang, Y. H. Luo and G. S. Liu, Nanoscale Horiz., 2022, 7, 1299–1339 RSC.
- X. Lin, S. Ye, C. Kong, K. Webb, C. Yi, S. Zhang, Q. Zhang, J. T. Fourkas and Z. Nie, J. Am. Chem. Soc., 2020, 142, 17282–17286 CrossRef CAS PubMed.
- W. Li, K. Wang, P. Zhang, J. He, S. Xu, Y. Liao, J. Zhu, X. Xie and Z. Nie, Small, 2016, 12, 499–505 CrossRef CAS.
- J. Kao, P. Bai, J. M. Lucas, A. P. Alivisatos and T. Xu, J. Am. Chem. Soc., 2013, 135, 1680–1683 CrossRef CAS PubMed.
- C. Jenewein, J. Avaro, C. Appel, M. Liebi and H. Colfen, Angew. Chem., Int. Ed., 2022, 61, e202112461 CrossRef CAS.
- W. Dong, Y. Zhang, C. Yi, J. J. Chang, S. Ye and Z. Nie, ACS Nano, 2023, 17, 3047–3054 CrossRef CAS PubMed.
- P. Bai, S. Yang, W. Bao, J. Kao, K. Thorkelsson, M. Salmeron, X. Zhang and T. Xu, Nano Lett., 2017, 17, 6847–6854 CrossRef CAS.
- X. Yue, J. Li, N. Yan and W. Jiang, Small, 2023, 19, 2207984 CrossRef CAS PubMed.
- F. Rechberger and M. Niederberger, Nanoscale Horiz., 2017, 2, 6–30 Search PubMed.
- J. Li, X. Yu, J. Zhang, N. Yan, J. Jin and W. Jiang, ChemComm, 2023, 59, 12338–12341 RSC.
- J. Li, X. Liu, J. Jin, N. Yan and W. Jiang, Nanotechnology, 2022, 33, 385601 CrossRef CAS.
- X. Dai, H.-X. Wan, X. Zhang, W. Wei, W. Chen, L. Zhang, J. Li and L.-T. Yan, Chem. Res. Chin. Univ., 2023, 709–718 Search PubMed.
- M. I. Bodnarchuk, E. V. Shevchenko and D. V. Talapin, J. Am. Chem. Soc., 2011, 133, 20837–20849 CrossRef CAS PubMed.
- C. Yi, H. Liu, S. Zhang, Y. Yang, Y. Zhang, Z. Lu, E. Kumacheva and Z. Nie, Science, 2020, 369, 1369–1374 CAS.
- X. Ye, J. Chen, B. T. Diroll and C. B. Murray, Nano Lett., 2013, 13, 1291–1297 CrossRef CAS.
- X. Zhang, X. Dai, L. Gao, D. Xu, H. Wan, Y. Wang and L.-T. Yan, Chem. Soc. Rev., 2023, 52, 6806–6837 CAS.
- C. Yi, Y. Yang and Z. Nie, J. Am. Chem. Soc., 2019, 141, 7917–7925 CAS.
- A. Dong, X. Ye, J. Chen and C. B. Murray, Nano Lett., 2011, 11, 1804–1809 CrossRef CAS PubMed.
- M. I. Bodnarchuk, M. V. Kovalenko, W. Heiss and D. V. Talapin, J. Am. Chem. Soc., 2010, 132, 11967–11977 CrossRef CAS.
- K. Wang, F. Li, S.-M. Jin, K. Wang, D. Tian, M. Hussain, J. Xu, L. Zhang, Y. Liao, E. Lee, G.-R. Yi, X. Xie and J. Zhu, Mater. Chem. Front., 2020, 4, 2089–2095 RSC.
- Y. Zheng, X. Zhong, Z. Li and Y. Xia, Part. Part. Syst. Charact., 2014, 31, 266–273 CrossRef CAS.
- M. Brust, M. Walker, D. Bethell, D. J. Schiffrin and R. Whyman, J. Chem. Soc., Chem. Commun., 1994, 801–802 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr04032e |
| This journal is © The Royal Society of Chemistry 2025 |