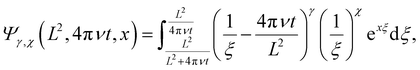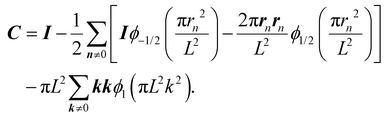DOI:
10.1039/D4NR04045G
(Paper)
Nanoscale, 2025,
17, 12727-12737
Start-up flow of nanoscale particles and their periodic arrays: insights from fundamental solutions of the unsteady Stokes equations
Received
1st October 2024
, Accepted 22nd March 2025
First published on 26th March 2025
Abstract
Start-up flows induced by nanoscale particles and their periodic arrays are studied theoretically. At nanoscopic lengths and time scales, the interplay between inertial and viscous forces in a fluid results in time-dependent (unsteady) flows, which are important in the study of nanoporous materials and microswimmer locomotion. Here, these flows are studied by developing fundamental solutions, i.e. Green's functions considering point particles, of the unsteady Stokes equations. It is found that the approach to the steady state is characterized by a viscous penetration depth l = (4νt)1/2, where ν is the kinematic viscosity and t is time. For an isolated particle, fluid inertia leads to vortex flows with a rotation axis located roughly a distance l from the particle. As time increases, the vortex distance to the particle increases diffusively as l2 ∼ 4νt, with the limit l → ∞ corresponding to the steady-state limit. In a periodic array, inertia also leads to vortex flows. Furthermore, the presence of other array particles results in an unsteady back flow that develops simultaneously to the local flow around a test particle. The back flow develops with a characteristic time scale proportional to L2/ν, where L is the size of the unit cell.
 Christian Aponte-Rivera | Christian Aponte-Rivera is an assistant professor in the Department of Chemistry at Stony Brook University. He received his B.S. in chemical engineering from the University of Puerto Rico, Mayagüez and Ph.D. in chemical and biomolecular engineering from Cornell University. He was a postdoctoral researcher in the Department of Mechanical Engineering and Materials Science at Duke University, after which he joined Stony Brook University as an IDEA Fellow. His research focuses on using scattering experiments, simulations and theory of soft materials to answer fundamental questions with applications in neurodegenerative disease pathology, nanomaterial design, and energy. His work has been recognized through awards such as the ACS PRF Doctoral New Investigator award. |
1 Introduction
Understanding the flow induced by nanoscale particles is essential for modeling particle dynamics,1–5 advanced materials such as nanoporous packed beds,6 and biological systems such as microswimming organisms.7–12 At these length scales, the ratio of inertial to viscous forces, also known as the Reynolds number, is much smaller than unity. Newtonian solvents are thus typically modeled with the Stokes equations,13–15 which assume that the flow reaches a steady state instantaneously. However, the approach to the steady state is determined by diffusion of momentum, which occurs on a finite time scale. If momentum has not diffused through the system, the interplay between inertial and viscous forces leads to time-dependent flows, which require the use of the unsteady Stokes equations.13–15 Experiments have been used to measure oscillatory unsteady Stokes flows using colloidal particles,16,17 and such flows are thought to play an important role in biological phenomena such as the beating of flagella/cilia.10,11,18
Early theoretical work studying unsteady Stokes flow considered the flow due to an oscillating sphere,19 while more recent developments include the effect of shape20–22 and oscillatory pressure fields,23 as well as the derivation of general solutions24–27 of the unsteady Stokes equations. Fundamental solutions, i.e., Green's functions, provide important insight by revealing general flow features that are independent of particle shape or boundary conditions. Solutions of this form have been derived for isolated impulse forces,3,15,19,28,29 and impulse forces near a wall.30 Generalized solutions in terms of Green's functions have also been reported.31 Applications of these solutions in analytical32,33 and numerical34 singularity methods have also been proposed. Previous work has thus focused primarily on oscillatory flows and impulse flows. However, start-up flows, characterized by the application of a force at an initial time and subsequent development of the flow to a steady state, have received significantly less attention in the literature.
Microscopic start-up flows are of interest in understanding the diffusive motion of nanoparticles, which can be connected to flow properties via the fluctuation–dissipation theorem.1,35 Since diffusive displacements are the sum of all previous independent random displacements, start-up flows are connected to diffusion at short lag times.† Despite its relevance, few studies have explored the start-up flow behavior of microscopic particles. Hill and co-workers6 studied start-up flows of porous materials using both periodic and random arrays of particles. For periodic arrays of widely separated spheres with simple cubic symmetry, they combined the steady-state Stokes flow solution36 and energy conservation arguments to develop a self-consistent theory for the start-up flow. The model suggests that the flow approaches the steady state exponentially, and the drag force computed from this flow agrees asymptotically with Lattice Boltzmann simulations close to the steady-state regime. While the self-consistent model provides insight into the time-dependent drag force in the periodic array, open questions remain due to the lack of a start-up flow solution for this system.
In this work, nanoscale start-up flows are studied by developing fundamental solutions of the unsteady Stokes equations. Fundamental solutions yield general features of the flow by modeling point particles in the fluid. They are most accurate at distances that are large compared to the particle size, where finite size contributions to the flow solution are not dominant. However, fundamental solutions capture features that are independent of particle shape and boundary conditions, making them useful in the study of numerous systems. The start-up flow of an isolated particle of size a is considered first, finding that fluid inertia leads to vortex flow patterns that move away from the particle as the steady state is approached. The solution also demonstrates that the distance of the vortex to the particle is well approximated by the viscous penetration length, i.e., the length over which momentum has diffused. To move beyond the single particle limit, periodic arrays with simple cubic symmetry are also considered. In a periodic array, fluid inertia also leads to vortex flows whose distance to a test particle is on the order of the viscous penetration length. In addition, it is found that the periodic array leads to a transient back flow that develops simultaneously to the local flow around a test sphere, but with a different characteristic time scale.
The article is organized as follows. Section 2 outlines the governing equations for the start-up flow of isolated particles and periodic arrays. In section 3, fundamental solutions for the start-up flow in each case are developed. In section 4, the start-up flow solutions are used to reveal general flow features and their impact on experimental measurements. The article is concluded in section 5 with a discussion of the findings and their implications for nanoscale objects.
2 Governing equations
The flow in a Newtonian fluid of dynamic viscosity η, density ρ and kinematic viscosity ν = η/ρ is considered. Fluid motion in this scenario is governed by the Navier–Stokes equations, which represent a mass and momentum balance in the fluid. At nanoscopic scales, it is useful to consider two dimensionless numbers that determine the flow regime. The first is the Reynolds number Re = Ua/ν, where U is a characteristic velocity and a the size of the particle(s) of interest. The Reynolds number represents the ratio of inertial to viscous forces in the fluid, and typically for nanometer to micrometer lengths Re ≪ 1. The second dimensionless number is the Strouhal number St = l/Uτ, where l is the length scale over which momentum has propagated and τ is a characteristic time. Propagation of momentum occurs over a diffusive time scale14τl ≈ l2/ν, with the diffusion coefficient equal to the kinematic viscosity ν. The Strouhal number St thus represents the ratio of l to a length scale Uτ of interest. On lengths larger than l, the flow is unsteady (i.e. time-dependent), while on lengths smaller than l, the flow is close to the steady state. The time-dependent, low Reynolds number flow is modeled by considering the limit Re ≪ 1 and  . This corresponds to a fluid where motion is governed by the unsteady Stokes equations:
. This corresponds to a fluid where motion is governed by the unsteady Stokes equations:| |  | (1a) |
Here, v is the velocity field, p is the pressure field, ∇ is the gradient with respect to position r, ∇2 = ∇·∇ is the Laplacian operator, and Fe is the force density acting on the fluid.
The nanoparticles are modeled as having a force density Fe acting on the fluid at a single point. An isolated particle is considered first, and corresponds to a force density applied at a time t0 = 0 and kept constant at all later times t ≥ 0. This is modeled as:
where
F is a constant force vector,
H(
t) is the step function with respect to time,
| |  | (3) |
and
δ(
r −
r0) is the delta function localizing the force density to a single point
r0.
The second case corresponds to an array of nanoparticles periodically arranged with simple cubic symmetry. This is modeled by using a periodic array of point forces:
| |  | (4) |
The simple cubic symmetry corresponds to point forces located at positions
| | | rn = n1x1 + n2x2 + n3x3, (n1, n2, n3=0, ±1, ±2...), | (5) |
with unit cell basis vectors
xi of magnitude |
xi| =
L. To find a solution, the velocity field around a test particle located at the origin
r0 = 0 is considered.
For both an isolated particle and particles in a periodic array, the step function implies the initial condition
for the velocity field
v(
t,
r).
3 Results
3.1 Start-up flow due to an isolated particle
To derive the start-up flow fundamental solution for an isolated particle, we must find a solution to eqn (1a)–(1c) with the forcing equal to eqn (2). A solution to this problem can be obtained by representing the step-function forcing of eqn (2) as an integral of the time-dependent delta function,  . That is, the forcing of the start-up flow problem can be modeled as a sum of impulse forces separated by an infinitesimal time step dt. Due to the linearity of the unsteady Stokes equations, the start-up flow velocity field can also be expressed as a superposition of the velocity fields due to impulse forces separated by a time step dt, which yields
. That is, the forcing of the start-up flow problem can be modeled as a sum of impulse forces separated by an infinitesimal time step dt. Due to the linearity of the unsteady Stokes equations, the start-up flow velocity field can also be expressed as a superposition of the velocity fields due to impulse forces separated by a time step dt, which yields| |  | (7) |
The tensor Jimp(t, r) is the fundamental solution to the unsteady Stokes equations if the force is equal to an impulse Fe = δ(t)δ(r)F, and is equal to3,19,28
| |  | (8) |
Here, Erf is the error function, I is the identity tensor and ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) is the radial unit vector. Substituting eqn (8) into eqn (7) and carrying out the integration (see Appendix A for a brief summary) yields the start-up velocity field
is the radial unit vector. Substituting eqn (8) into eqn (7) and carrying out the integration (see Appendix A for a brief summary) yields the start-up velocity field
| |  | (9) |
This solution satisfies the initial condition viso(t = 0, r) = 0 and recovers the steady-state Oseen tensor J = (I + ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif)
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) )/r as t → ∞. Inspection of the solution reveals the characteristic length l = (4νt)1/2, which is the time-dependent viscous penetration depth. For distances r ≪ l, the flow is close to the steady state, and for distances r ≫ l, the flow is unsteady. Furthermore, inspection of eqn (9) identifies the Green's function for the start-up flow as
)/r as t → ∞. Inspection of the solution reveals the characteristic length l = (4νt)1/2, which is the time-dependent viscous penetration depth. For distances r ≪ l, the flow is close to the steady state, and for distances r ≫ l, the flow is unsteady. Furthermore, inspection of eqn (9) identifies the Green's function for the start-up flow as
| |  | (10) |
Although eqn (9) and (10) have not been reported in the literature, they are equivalent to the result obtained by applying the generalized fundamental solution of Shu and Chwang31 to start-up flow.
3.2 Start-up flow due to a periodic array of particles
3.2.1 Fourier representation and real-space inversion.
For a nanoscale particle in a periodic array, we must find a solution to eqn (1a)–(1c) when the forcing is due to eqn (4). To do this, a strategy similar to that used by Hasimoto36 for the steady-state problem will be employed. The particle at the origin is treated as a test particle propagating a velocity field v(t, r). The velocity field v(t, r) and pressure gradient ∇p(t, r) are expanded into a Fourier series with respect to the spatial dimensions:| |  | (11a) |
| |  | (11b) |
Here, we used the Fourier space wave vector k defined as
| | | k = n1b1 + n2b2 + n3b3, | (12) |
with magnitude
k = |
k| and units of inverse length. The reciprocal lattice vectors
bi satisfy
k·xi =
ni and the identities
| |  | (13) |
Here, the symbol “×” represents the cross-product and the unit cell volume in physical space is given by
| |  | (14) |
Due to the simple cubic cell symmetry, the cell volume is  . Substituting eqn (11a) and (11b) into eqn (1a)–(1c), multiplying by
. Substituting eqn (11a) and (11b) into eqn (1a)–(1c), multiplying by  and integrating over the unit cell volume in real space yields the Fourier series representation:
and integrating over the unit cell volume in real space yields the Fourier series representation:
| |  | (15a) |
In Fourier space, the initial condition of eqn (6) is:
Taking the dot product of eqn (15a) with k demonstrates that the pressure is quasi-steady. This reflects that the fluid is incompressible, which implies that the velocity of sound is infinite and the pressure field propagates instantaneously. The quasi-steady pressure is thus obtained from Hasimoto's solution36
| |  | (17a) |
| |  | (17b) |
Substituting eqn (17b) into (15a) yields
| |  | (18) |
where
![[k with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006b_0302.gif)
=
k/
k.
Using standard methods for ordinary differential equations, eqn (18) is solved and the solution is substituted into eqn (11a) to obtain the Fourier representation of the velocity field
| | 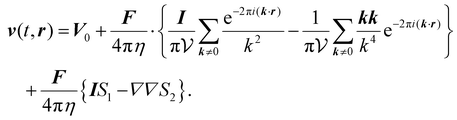 | (19) |
Inspection of eqn (19) reveals that the bracketed term in the first line of this equation is exactly the result obtained by Hasimoto36 and corresponds to the steady-state solution of the velocity field. Furthermore, we separated the zeroth Fourier mode V0 and the k ≠ 0 modes since, as demonstrated in the following sections, obtaining the real-space velocity field contribution for these two cases requires different methods. Note that the contribution of the k ≠ 0 modes is given by the following functions:
| |  | (20a) |
| |  | (20b) |
These scalar functions provide a representation more amenable to the integral and Ewald transformations utilized to find a real-space solution.
The last step to find a solution is to invert the Fourier space solution to real space. It is instructive to first consider the inversion method used for the steady-state limit. Hasimoto36 inverted the steady-state solution by using an integral transform in combination with Ewald's theta transformation and a Taylor expansion in the limit r/L → 0. The first line of eqn (19) exactly matches Hasimoto's Fourier space solution and has a known real-space representation. Our main concern is thus inverting the functions defined in eqn (20) and finding the zeroth mode V0. To invert S1 and S2, we follow a similar method to that of Hasimoto. An integral transform is used to replace the k−2 and k−4 terms in eqn (20). Afterwards, Ewald's theta transformation is used by treating time as a constant and carrying out the transformation with respect to the spatial variables. The result is Taylor expanded in the limit r/L → 0, and only terms of order  are retained. The necessary mathematical manipulations are outlined in Appendix B for the interested reader.
are retained. The necessary mathematical manipulations are outlined in Appendix B for the interested reader.
Using these results, we arrive at the solution:
| |  | (21) |
The scalar c and tensor C = CI were originally defined by Hasimoto36 (see also Appendix C of this work), and the scalar A(t) and tensor B(t) = B(t)I are defined in Appendix B. These quantities depend on quickly converging sums over the other particles in the periodic array. In Appendix C, it is shown that
| | | c = 2.8373, and C = CI = 0.9148I. | (22) |
In the same Appendix, A(t) and B(t) are evaluated numerically. The tensor B(t) simplifies to the form
and values of
A(
t) and
B(
t) for different times are given in
Tables 1 and
2, respectively.
Table 1 Numerical values of A(t) rounded to four decimal places
|
νt/a2 |
A(t) |
| 1 |
2.8373 |
| 10 |
2.8355 |
| 20 |
2.8303 |
| 100 |
2.7055 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
2.7605 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
3.0000 |
Table 2 Numerical values of B(t). All values are rounded to four decimal places
|
νt/a2 |
B(t) |
| 1 |
0.9225 |
| 10 |
0.9862 |
| 20 |
1.0468 |
| 100 |
1.2593 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
0.9988 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.0000 |
Note that while the Fourier expansion of eqn (11a) is valid for all position vectors r, the inverted solution in eqn (21) is only valid for regions near an arbitrary point particle (i.e., at distances r < L within an arbitrary unit cell). This is because, although the inversion accounts for the contribution from all the Fourier modes, it is developed using a Taylor expansion in the limit r < L and in a coordinate system with a test point particle at the origin. It is also useful to inspect eqn (21). The bracketed term in eqn (21) satisfies the initial condition of eqn (16) as t → 0. Note also that, similar to the problem considered in section 3.1, the viscous penetration depth l = (4νt)1/2 is an important characteristic length. Further inspection of eqn (21) reveals that in the limit![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L → ∞, i.e., in the limit of an isolated point particle, the bracketed term recovers eqn (9) to leading order. However, as t→∞, Hasimoto's steady-state solution is not recovered. As shown in the next section, the approach to the steady state is a singular limit which requires careful treatment of the V0 term.
L → ∞, i.e., in the limit of an isolated point particle, the bracketed term recovers eqn (9) to leading order. However, as t→∞, Hasimoto's steady-state solution is not recovered. As shown in the next section, the approach to the steady state is a singular limit which requires careful treatment of the V0 term.
3.2.2 Matched asymptotic expansion and the approach to the steady state.
As the start-up flow approaches the steady state, the divergence of two lengths must be considered. The first is the viscous penetration length l, which diverges as the steady state is approached and momentum diffuses through the entire system. The second is the length scale of the kth Fourier mode, k−1. The zeroth mode, k = 0, corresponds to k−1 → ∞ and can be interpreted as the velocity field contribution arising from particles that are infinitely far from the test particle. The presence of two diverging length scales is one of the hallmarks of singular limits.37 To obtain a solution, we thus use matched asymptotic expansions and treate eqn (21) as the solution to the “inner” problem in time (i.e., the solution at early times). In this section, we find a solution to the “outer” problem, i.e., the approach to the steady state at long times.
First, it is useful to make eqn (15a) dimensionless by defining the normalized variables of
| |  | (24) |
where time has been normalized by the time of the viscous penetration length
τl =
l2/
ν and pressure with a viscous scaling where the length scale of interest is
l. Furthermore, we define two additional time scales of interest,
| | 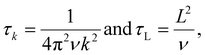 | (25) |
which correspond to the time it takes momentum to diffuse over length
k−1 and
L, respectively. Note that the time scales
τl,
τk and
τL have different interpretations. At time
τl, momentum has diffused a distance
l and regions a distance <
l to a test particle have reached the steady state. In contrast,
τk is the time required for Fourier space contributions associated with mode
k−1 to reach the steady state. This time is thus most meaningful when compared to
τl. If
τk <
τl, Fourier space contributions with modes
k−1 <
l have reached the steady state. The time
τL has a similar interpretation to
τk, and if
τL <
τl, regions a distance
L to a test particle have reached the steady state. Substituting these quantities into the governing equation and rearranging we obtain
| |  | (26) |
Eqn (26) demonstrates why the problem is singular. The flow reaches the steady state when momentum has propagated throughout the system, i.e., in the limit τl → ∞, which would eliminate the differential term in eqn (26). To model the approach to the steady state, we consider the limit τk/τl ≪ 1, which defines the small parameter ε = τk/τl. Furthermore, the stretched time variable T = ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) /ε is defined. Substituting these quantities and taking the limit as k → 0 gives
/ε is defined. Substituting these quantities and taking the limit as k → 0 gives
| |  | (27) |
where
τk→0 ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) τ0
τ0 is a characteristic time determining the approach to the steady state. Neglecting the

term in
eqn (27) yields an initial value problem solved by
| |  | (28) |
The characteristic time τ0 is determined by substituting V0 into eqn (21) and matching the inner and outer solutions. This procedure yields the characteristic time scale
| | 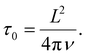 | (29) |
The V0 contribution is interpreted as a back flow arising from particles in the periodic array that are infinitely far from the origin. This back flow develops towards the steady state simultaneously with the local “inner” flow around the test sphere.
The uniform solution that incorporates both inner and outer problems is
| |  | (30) |
Eqn (30) recovers Hasimoto's steady-state solution in the limit![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t → ∞, as expected. It also yields the Green's function for the unsteady start-up flow in a periodic array as
t → ∞, as expected. It also yields the Green's function for the unsteady start-up flow in a periodic array as
| |  | (31) |
This result is comprised of an Oseen tensor contribution (first line of eqn (31)) and L-dependent terms that represent the flow induced by the periodic array. Note also that the velocity field solution represents the flow profile in a single unit cell and, since periodic array particles are indistinguishable, this is sufficient to fully specify the flow profile. Furthermore, it is instructive to compare the isolated point force solution of eqn (10) to the periodic array solution of eqn (31). Most notably, taking the limit L → ∞ of eqn (31) reveals that the solutions are in agreement to  . However, the periodic array solution does not recover the
. However, the periodic array solution does not recover the 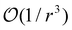 term in eqn (10), a consequence of retaining only
term in eqn (10), a consequence of retaining only  terms in the Taylor expansion. Although higher order corrections can be systematically incorporated into eqn (31), they are not expected to change the conclusions of this work and are thus left as a topic of future study.
terms in the Taylor expansion. Although higher order corrections can be systematically incorporated into eqn (31), they are not expected to change the conclusions of this work and are thus left as a topic of future study.
4 Discussion
To obtain qualitative insight into how the flow develops toward a steady state for isolated nanoparticles, we used eqn (9) to plot the streamlines of the fluid. For clarity, we plotted the streamlines in the xy-plane for a particle acted upon by a force vector F pointing along the positive x-direction. Fig. 1a–d show the streamlines at times tν/a2 = 1, 10, 20, and 100, respectively, for a particle located at the origin. All distances have been normalized by the particle radius a, and time has been normalized by the time it takes momentum to diffuse a distance equal to the particle radius a2/ν. The viscous penetration depth l = (4νt)1/2 provides an estimate of the distance between the particle and the axis of rotation of the vortex, e.g., for tν/a2 = 1, the vortex is estimated to be a distance l/a = 2 in agreement with Fig. 1a. Similar vortex flow patterns occur in oscillatory unsteady Stokes flows,16,17,19 but the vortex distance is determined by the frequency-dependent penetration depth lω ≈ (ν/ω)1/2 and is constant at a given frequency. In contrast to oscillatory flows, start-up flows result in vortices whose distance to the particle increases diffusively, i.e. proportional to t1/2. The steady state is reached as l → ∞ and the vortex moves infinitely far from the particle.
 |
| | Fig. 1 Streamlines for the velocity field of an isolated particle at the origin. The external force is applied at t = 0 and points in the positive x-direction. The plots (a), (b), (c), and (d) correspond to times ta2/ν = 1, 10, 20, and 100, respectively, after the force is applied. | |
In Fig. 2, eqn (30) is used to plot the streamlines of a test particle located at the origin and part of a periodic array of identical particles. The periodic array has simple cubic symmetry and a cell size L/a = 50. For clarity, the streamlines are plotted in the xy-plane for an object acted upon by a force vector F pointing along the positive x-direction and applied at t = 0. The streamlines at times tν/a2 = 1, 10, 20, and 100 are plotted in Fig. 2a–d, respectively. Similar to Fig. 1, the streamlines demonstrate that inertia results in vortex flows located at a distance approximately equal to the viscous penetration depth l. Note that we have used the same normalization as in Fig. 1. The long characteristic time of the back flow delays the approach to the steady state in periodic arrays as compared to isolated particles. This is reflected qualitatively in Fig. 2, where for each snapshot in time, the vortex flows are observed to be closer to the origin than the corresponding snapshot in Fig. 1.
 |
| | Fig. 2 Streamlines for the velocity field of a test particle located at the origin and part of a periodic array with simple cubic symmetry and a unit cell size L/a = 50. The external force is applied at t = 0 and points in the positive x-direction. The plots (a), (b), (c), and (d) correspond to times ta2/ν = 1, 10, 20, and 100, respectively, after the force is applied. | |
The flow induced by microscopic particles can be measured in experiments using an approach similar to two-point microrheology,38 where displacement correlations between a widely separated pair of particles are connected to the unknown fluid viscoelasticity and the velocity field Green's function via a fluctuation–dissipation relation. In contrast to two-point microrheology, measuring the flow is achieved by using a fluid of known viscoelastic properties and treating the velocity field Green's function as an unknown function. Using this strategy, the projection of the velocity field Green's function in directions along17,39 and perpendicular17 to the line connecting the center of two probe particles has been measured in unsteady oscillatory flow. The start-up flow of nanoparticles could be measured using a similar strategy, by tracking displacements of passively diffusing nanoparticles and computing their displacement correlations in the time domain. The normalized displacement correlations are predicted by the Green's functions in eqn (10) and (31) for the case of an isolated particle and a particle in a periodic array, respectively.
To predict the start-up flow pair correlations along and perpendicular to the line of centers between two widely separated particles, we consider a spherical coordinate system with a test particle at the origin and project the Green's function Jiso(t, r) from eqn (10) onto directions along and perpendicular to a radial unit vector ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) . Note that the fundamental solution is spherically symmetric, and these two projections are sufficient to fully specify the tensor. The projections along and perpendicular to
. Note that the fundamental solution is spherically symmetric, and these two projections are sufficient to fully specify the tensor. The projections along and perpendicular to ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) are plotted in Fig. 3a and b, respectively, as a function of distance normalized by the particle radius r/a. Fig. 3a and b show the projections in a linear–log plot, and the insets in each figure show the absolute value of the same curve in a log–log plot. Solid curves of different colors correspond to different times and, as shown in the legend, the black dash-dotted curve corresponds to the steady-state solution and the dashed red line marks the value zero across the horizontal axis.
are plotted in Fig. 3a and b, respectively, as a function of distance normalized by the particle radius r/a. Fig. 3a and b show the projections in a linear–log plot, and the insets in each figure show the absolute value of the same curve in a log–log plot. Solid curves of different colors correspond to different times and, as shown in the legend, the black dash-dotted curve corresponds to the steady-state solution and the dashed red line marks the value zero across the horizontal axis.
 |
| | Fig. 3 Projections of the start-up flow Green's function (a) along and (b) perpendicular to the radial direction. Due to the spherical symmetry of the solution, these projections are sufficient to specify the tensor. | |
As demonstrated in Fig. 3, a force applied along a radial direction ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) will induce a flow that is similar to the steady-state flow at distances r < l, making it proportional to 1/r at these shorter distances. At distances r > l, the flow has a decay proportional to 1/r3 (see the inset figure), reflecting the vortex flow pattern that arises at these larger distances. As l increases with time, the region where the flow decays as 1/r3 moves farther from the object, with the steady state corresponding to the limit where the distance of this region to the particle is infinite. For the perpendicular component, the effect of the vortex flow is more pronounced. At distances r < l, the flow is similar to the steady-state flow and is proportional to 1/r. However, at distances r > l, the projection not only decays proportional to 1/r3 but is also negative, meaning that the flow is in the direction opposite to the forcing. The region where the flow opposes the force moves farther as the time increases, and its distance to the particle is infinite at steady state.
will induce a flow that is similar to the steady-state flow at distances r < l, making it proportional to 1/r at these shorter distances. At distances r > l, the flow has a decay proportional to 1/r3 (see the inset figure), reflecting the vortex flow pattern that arises at these larger distances. As l increases with time, the region where the flow decays as 1/r3 moves farther from the object, with the steady state corresponding to the limit where the distance of this region to the particle is infinite. For the perpendicular component, the effect of the vortex flow is more pronounced. At distances r < l, the flow is similar to the steady-state flow and is proportional to 1/r. However, at distances r > l, the projection not only decays proportional to 1/r3 but is also negative, meaning that the flow is in the direction opposite to the forcing. The region where the flow opposes the force moves farther as the time increases, and its distance to the particle is infinite at steady state.
Experimentally, particles can be arranged into ordered array patterns by utilizing optical traps.12 This strategy could be used to create a periodic array of spheres with simple cubic cell symmetry. To measure the start-up flow induced by a periodic array of simple cubic symmetry, a passive tracer particle can be allowed to diffuse through the periodic array and pair correlations between the tracer and a test particle in the array measured. Pair correlations along (perpendicular to) the line of centers between the tracer and the test particle are predicted by the projection of eqn (31) in a direction along (perpendicular to) a radial vector ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) . Note that, in principle, the shape of the unit cell can result in deviations from the spherical symmetry that are quantified by the tensors C and B(t). Here, the simple cubic symmetry results in these tensors being isotropic (see Appendix C). The projection of eqn (31) in directions longitudinal and perpendicular to a radial vector
. Note that, in principle, the shape of the unit cell can result in deviations from the spherical symmetry that are quantified by the tensors C and B(t). Here, the simple cubic symmetry results in these tensors being isotropic (see Appendix C). The projection of eqn (31) in directions longitudinal and perpendicular to a radial vector ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) are shown in Fig. 4a and b, respectively. Fig. 4a shows that for distances r < l, the r-dependence of the longitudinal projection is similar to the steady-state dependence. In contrast to the case of an isolated object, the projection becomes negative at distances r > l, reflecting the back flow from the periodic array. Similar qualitative behaviors are observed for the perpendicular component in Fig. 4b, with the lower magnitude of the projection reflecting the flow is weaker in this direction.
are shown in Fig. 4a and b, respectively. Fig. 4a shows that for distances r < l, the r-dependence of the longitudinal projection is similar to the steady-state dependence. In contrast to the case of an isolated object, the projection becomes negative at distances r > l, reflecting the back flow from the periodic array. Similar qualitative behaviors are observed for the perpendicular component in Fig. 4b, with the lower magnitude of the projection reflecting the flow is weaker in this direction.
 |
| | Fig. 4 Projections of the start-up flow Green's function (a) along and (b) perpendicular to a test particle in a periodic array. The array has simple cubic cell symmetry and a unit cell size L/a = 50. Due to the spherical symmetry of eqn (31), these two components are sufficient to specify the tensor. | |
4.1 Start-up flow in experimental measurements
To use the above theoretical results in the interpretation of experiments, it is useful to first determine the time scales of interest. Fluid motion has been determined using a quasi-steady approximation for the pressure field, which propagates at the speed of sound. The results are thus valid for times longer than the time it takes sound to propagate through the system. The speed of sound can be estimated as (Ks/ρ)1/2, where Ks is the bulk modulus. Taking water at 25 °C as an example, with Ks = 2.2 × 109 Pa and ρ = 1000 kg m−3, the speed of sound travels a distance of 10 μm in ∼6 ns. The quasi-steady pressure assumption is thus not very restrictive when determining the start-up flow of nanoscale or micron-scale particles.
The predicted unsteady start-up flows can be measured experimentally with an approach similar to two-point microrheology.38 In this method, the Brownian motion of a pair of nanoparticles is tracked. The correlation between the particle displacements is quantified by a “pair-diffusion” tensor D(t, r)pair, which is connected to the induced flow using the fluctuation–dissipation theorem.35 This results in the relationship
| | | D(t, r)pair ≈ kTJ(t, r), | (32) |
which describes the correlation between two widely separated particles. By measuring the pair diffusion tensor as a function of time and particle separation distance, the Green's function for the unsteady flow can be extracted. Such fluctuation–dissipation relations are valid for times longer than the inertial relaxation time of the particle, which is estimated as
τinertia ≈
Vnpρnp/
aη with particle volume
Vnp and density
ρnp. For a spherical silica nanoparticle with a radius
a = 0.580 μm (
Vnp ≈ 0.8 μm
3 and
ρ ≈ 2634 kg m
−3) in water at 25 °C (
η = 0.89 × 10
–3 Pa), the inertial time is
τinertia ≈ 4 μs. The viscous penetration depth at these times is 2 μm,
i.e., it is comparable to the particle size. Using widely separated particles, with the center-to-center distance significantly larger than their size, would provide a suitable system to measure the unsteady flow. Indeed, Atakhorrami
et al.17 conducted similar experiments using silica particles of this size and measured the frequency-dependent unsteady Stokes flow using a custom-built inverted microscope. A more elaborate set up could trap particles in an array while leaving a freely diffusing tracer particle. Correlations between the tracer particle and the array fixed particles would provide a means to measure the unsteady flow.
5 Conclusions
In this work, fundamental solutions modeling point particles are used to provide insight into the start-up flow of isolated nanoscale particles and their periodic arrays. Similar to oscillatory unsteady Stokes flows, fluid inertia leads to vortex flow patterns whose distance to the particle can be estimated from the viscous penetration length. However, in start-up flows, the vortex distance to the particle increases as momentum diffuses, and the steady state is reached in the limit where the distance is infinite, i.e., in the limit l = (4νt)1/2 → ∞. For isolated spheres, the flow is proportional to 1/r at distance r < l, while at distances r > l, it is proportional to 1/r3. The faster decay at larger distances reflects the inertial vortex flows. In periodic arrays, the flow induced by a nanoparticle at the origin develops simultaneously to a back flow arising from the other particles in the infinite array. The characteristic time scale of the unsteady back flow, τ0 = L2/(4πνt), corresponds to the time it takes momentum to diffuse over a distance on the order of the unit cell size L. The back flow relaxes on a longer time scale than the local flow around a test particle, leading to a longer time-dependent flow regime as compared to that of an isolated particle.
Experimentally, oscillatory flows have been measured as a function of frequency17,39 by using widely separated pairs of particles. A similar strategy could be used to measure start-up flows, by tracking a pair of widely separated particles with enough temporal resolution to compute pair correlations in the unsteady flow regime. The temporal resolution required is dependent of the particle size and viscosity of the solvent. For example, as discussed in section 4.1, for a particle with radius a = 0.580 μm in aqueous solution, this requires temporal resolution on the order of hundreds of nanoseconds to microseconds. For particles in periodic arrays, a similar strategy can be used to measure start-up flows experimentally. A group of widely separated particles can be held in a periodic arrangement with simple cubic symmetry using optical tweezers. Computing displacement correlations between a freely diffusing tracer and a nearby particle belonging to the array could measure the start-up flow.
Fundamental solutions provide insight into general features that are independent of particle shape or boundary conditions. The solutions derived in this work can thus be used to estimate the effect of start-up flows in a range of nanoparticle systems, such as nanoparticles acted on by external fields, swimming microorganisms, and porous materials. Future work can use singularity methods to compute the effect of particle size and the time-dependent start-up flow drag-force acting on isolated particles and particles in a periodic array.
Data availability
Numerical computations reported in the article were carried out using Mathematica software version 13.3.0.0. Mathematica notebooks with the numerical computations are available upon request.
Conflicts of interest
The are no conflicts of interest to declare.
A. Time integration of the Green's function for an impulse force
To obtain the Green's function for the start-up flow of an isolated particle, we carry out the integration in eqn (7). Substitution of eqn (8) into (7) and integrating over the variable t′ yields the result| |  | (33) |
where Γ is the upper incomplete gamma function| |  | (34) |
Using integration by parts and eqn (34), we can derive the identity
| |  | (35) |
Substituting this identity in eqn (33) and rearranging yields eqn (9) as the solution.
B. Integral transforms and Ewald's theta transformation
To invert the spatial Fourier transform representations in eqn (20), we seek a representation of the velocity that is a function of the distance to the test particle at the origin, and for which the k-space contribution is at most a constant. The first step is to define the auxiliary function| |  | (36) |
Note that this auxiliary function with m = 1, 2 is related to eqn (20a) and (20b), respectively. We use the integral representation of k−2m to rearrange eqn (36) into
| |  | (37) |
This integral is now split into two integrations. The first integration is taken from 0 to a moderate constant, set to L2, and the second is taken from L2 to ∞. Ewald's theta transformation
| |  | (38) |
is applied to the first integration to eliminate the
k dependence in the exponential term. The key to this approach is treating time as a constant in
eqn (38), justified from the fact that the transformation is with respect to the spatial coordinates and their Fourier representation. The resulting expression for
σm is
| |  | (39) |
At this stage, it is useful to introduce the substitutions β = L2/ξ − 4πνt and β = L2ξ to the first and second integrals of eqn (39), respectively. This converts σm into
| |  | (40) |
where the functions
Ψγ,χ and
φγ have been defined as
| | 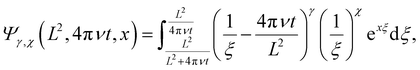 | (41a) |
| |  | (41b) |
We now use eqn (40–41b) to evaluate the functions S1 and∇∇S2. To obtain the fundamental solution, we expand the result in a Taylor series around r/L → 0 and truncate it to leading order. The resulting equations are
| |  | (42a) |
| |  | (42b) |
where the time-dependent scalar A(t) is defined as
| |  | (43) |
and the time-dependent tensor
B(
t) is
| |  | (44) |
C. Numerical evaluation of c, C, A(t), and B(t)
In this section, the values of the numerical computation of c, C, A(t) and B(t) are discussed. The quantities are reported rounded to four decimal places and all summations are truncated to index values that satisfy 0 < |ni| ≤ 2. Furthermore, due to the cubic symmetry of the problem, off-diagonal elements of the tensors C and B(t) are zero and they can be expressed as C = CI and B(t) = B(t)I, respectively. Therefore, for these quantities, the problem is reduced to finding the scalars C and B(t).
Ref. 36 reports the definition of c and C. Here, by setting α = L2 in the definition of ref. 36, we arrive at
| |  | (45) |
| | 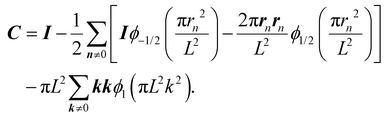 | (46) |
Furthermore, ref. 36 reports the value of c as
This result is reproduced by evaluating the summation truncated to index values of 0 <|ni| ≤ 2. Although the definition of C is reported in ref. 36, the numerical value of the scalar C is not reported. By evaluating the sums, it is found that
For the scalar A(t) defined by eqn (43), the summations are evaluated for times νt/a2 = 1, 10, 20, 102, 104, and 106. The results are reported in Table 1.
Evaluating the sums in eqn (44) yields the values reported in Table 2 for the scalar B(t).
Acknowledgements
C. Aponte-Rivera gratefully acknowledges support from the donors of the ACS Petroleum Research Fund under Doctoral New Investigator Grant ACS-PRF 66622-DNI7.
References
- E. J. Hinch, J. Fluid Mech., 1975, 72, 499 CrossRef.
- C. F. M. Coimbra and R. H. Rangel, J. Fluid Mech., 1998, 370, 53–72 CrossRef CAS.
- B. Cichocki and B. U. Felderhof, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 5383–5388 CrossRef CAS PubMed.
- A. M. Ardekani and R. H. Rangel, Phys. Fluids, 2006, 18, 103306 CrossRef.
- J. D. Schieber, A. Córdoba and T. Indei, J. Non-Newtonian Fluid Mech., 2013, 200, 3–8 CrossRef CAS.
- R. J. Hill, D. L. Koch and A. J. C. Ladd, J. Fluid Mech., 2001, 448, 213–241 CrossRef CAS.
- J. R. Blake, Math. Proc. Cambridge Philos. Soc., 1971, 70, 303 CrossRef.
- S. Wang and A. M. Ardekani, J. Fluid Mech., 2012, 702, 286–297 CrossRef.
- K. Ishimoto, J. Fluid Mech., 2013, 723, 163–189 CrossRef.
- D. R. Brumley, N. Bruot, J. Kotar, R. E. Goldstein, P. Cicuta and M. Polin, Phys. Rev. Fluids, 2016, 1, 081201 CrossRef PubMed.
- D. Wei, P. G. Dehnavi, M.-E. Aubin-Tam and D. Tam, J. Fluid Mech., 2021, 915, A70 CrossRef CAS.
- N. Bruot, P. Cicuta, H. Bloomfield-Gadêlha, R. E. Goldstein, J. Kotar, E. Lauga and F. Nadal, Phys. Rev. Fluids, 2021, 6, 053102 CrossRef.
-
J. Happel and H. Brenner, Low Reynolds Number Hydrodynamics with Special Applications to Particulate Media, Martinus Nijhoff Publishers, Hingham, MA, 1983 Search PubMed.
-
R. B. Bird, R. C. Armstrong and O. Hassager, Dynamics of Polymer Liquids Volume 1 Fluids Mechanics, John Wiley & Sons, 2nd edn, 1987 Search PubMed.
-
S. Kim and S. J. Karrila, Microhydrodynamics: Principles and Selected Applications, Dover Publications, Inc., Mineola, NY, 2005 Search PubMed.
- T. B. Liverpool and F. C. MacKintosh, Phys. Rev. Lett., 2005, 95, 208303 CrossRef CAS PubMed.
- M. Atakhorrami, G. H. Koenderink, C. F. Schmidt and F. C. MacKintosh, Phys. Rev. Lett., 2005, 95, 208302 CrossRef CAS PubMed.
- D. Wei, P. G. Dehnavi, M.-E. Aubin-Tam and D. Tam, Phys. Rev. Lett., 2019, 122, 124502 CrossRef CAS PubMed.
-
C. Oseen, Neuere Methoden Und Ergebnisse in Der Hydrodynamik, Akademische verlagsgesellschaft M.B.H., Leipzig, 1927 Search PubMed.
- C. J. Lawrence and S. Weinbaum, J. Fluid Mech., 1986, 171, 209 CrossRef CAS.
- C. J. Lawrence and S. Weinbaum, J. Fluid Mech., 1988, 189, 463–489 CrossRef CAS.
- S.-M. Yang and L. G. Leal, Phys. Fluids A, 1991, 3, 1822–1824 CrossRef CAS.
- A. M. Chapman and J. J. L. Higdon, Phys. Fluids A, 1992, 4, 2099–2116 CrossRef CAS.
- S.-M. Yang, Korean J. Chem. Eng., 1987, 4, 15–22 CrossRef CAS.
- P. Rao, Math. Comput. Modell., 1988, 10, 839–851 CrossRef.
- A. Venkatalaxmi, B. S. Padmavathi and T. Amaranath, Fluid Dyn. Res., 2004, 35, 229–236 CrossRef.
- I. Fouxon, A. Leshansky, B. Rubinstein and Y. Or, Phys. Rev. Fluids, 2022, 7, 094103 CrossRef.
- P. Mazur and D. Bedeaux, Physica, 1974, 76, 235–246 CrossRef.
- C. H. Hsiao and D. L. Young, J. Fluid Mech., 2019, 863, 1–31 CrossRef.
- I. Fouxon and A. Leshansky, Phys. Rev. E, 2018, 98, 063108 CrossRef CAS.
- J.-J. Shu and A. T. Chwang, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 051201 CrossRef CAS PubMed.
- C. Pozrikidis, Phys. Fluids A, 1989, 1, 1508–1520 CrossRef.
- M. Giona, G. Procopio and R. Mauri, Meccanica, 2022, 57, 1055–1069 CrossRef.
- C. H. Hsiao and D. L. Young, J. Mech., 2014, 30, 129–136 CrossRef.
- R. Kubo, Rep. Prog. Phys., 1966, 29, 255 CrossRef CAS.
- H. Hasimoto, J. Fluid Mech., 1959, 5, 317 CrossRef.
-
M. Van Dyke, Perturbation Methods in Fluid Mechanics, Academic Press, New York, 1964 Search PubMed.
- J. C. Crocker, M. T. Valentine, E. R. Weeks, T. Gisler, P. D. Kaplan, A. G. Yodh and D. A. Weitz, Phys. Rev. Lett., 2000, 85, 888–891 CrossRef CAS PubMed.
- S. Henderson, S. Mitchell and P. Bartlett, Phys. Rev. Lett., 2002, 88, 088302 CrossRef PubMed.
Footnote |
| † This is in contrast to the velocity autocorrelation function, which measures over what times particle motion remains coherent and is thus connected to impulse flows.1 |
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here. 
 . This corresponds to a fluid where motion is governed by the unsteady Stokes equations:
. This corresponds to a fluid where motion is governed by the unsteady Stokes equations:


 . That is, the forcing of the start-up flow problem can be modeled as a sum of impulse forces separated by an infinitesimal time step dt. Due to the linearity of the unsteady Stokes equations, the start-up flow velocity field can also be expressed as a superposition of the velocity fields due to impulse forces separated by a time step dt, which yields
. That is, the forcing of the start-up flow problem can be modeled as a sum of impulse forces separated by an infinitesimal time step dt. Due to the linearity of the unsteady Stokes equations, the start-up flow velocity field can also be expressed as a superposition of the velocity fields due to impulse forces separated by a time step dt, which yields

![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) is the radial unit vector. Substituting eqn (8) into eqn (7) and carrying out the integration (see Appendix A for a brief summary) yields the start-up velocity field
is the radial unit vector. Substituting eqn (8) into eqn (7) and carrying out the integration (see Appendix A for a brief summary) yields the start-up velocity field
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif)
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) )/r as t → ∞. Inspection of the solution reveals the characteristic length l = (4νt)1/2, which is the time-dependent viscous penetration depth. For distances r ≪ l, the flow is close to the steady state, and for distances r ≫ l, the flow is unsteady. Furthermore, inspection of eqn (9) identifies the Green's function for the start-up flow as
)/r as t → ∞. Inspection of the solution reveals the characteristic length l = (4νt)1/2, which is the time-dependent viscous penetration depth. For distances r ≪ l, the flow is close to the steady state, and for distances r ≫ l, the flow is unsteady. Furthermore, inspection of eqn (9) identifies the Green's function for the start-up flow as




 . Substituting eqn (11a) and (11b) into eqn (1a)–(1c), multiplying by
. Substituting eqn (11a) and (11b) into eqn (1a)–(1c), multiplying by  and integrating over the unit cell volume in real space yields the Fourier series representation:
and integrating over the unit cell volume in real space yields the Fourier series representation:



![[k with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006b_0302.gif) = k/k.
= k/k.
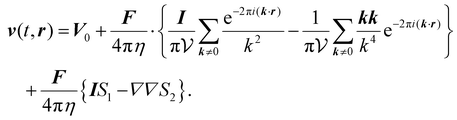


 are retained. The necessary mathematical manipulations are outlined in Appendix B for the interested reader.
are retained. The necessary mathematical manipulations are outlined in Appendix B for the interested reader.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L → ∞, i.e., in the limit of an isolated point particle, the bracketed term recovers eqn (9) to leading order. However, as t→∞, Hasimoto's steady-state solution is not recovered. As shown in the next section, the approach to the steady state is a singular limit which requires careful treatment of the V0 term.
L → ∞, i.e., in the limit of an isolated point particle, the bracketed term recovers eqn (9) to leading order. However, as t→∞, Hasimoto's steady-state solution is not recovered. As shown in the next section, the approach to the steady state is a singular limit which requires careful treatment of the V0 term.
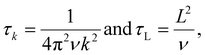

![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) /ε is defined. Substituting these quantities and taking the limit as k → 0 gives
/ε is defined. Substituting these quantities and taking the limit as k → 0 gives
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) τ0 is a characteristic time determining the approach to the steady state. Neglecting the
τ0 is a characteristic time determining the approach to the steady state. Neglecting the  term in eqn (27) yields an initial value problem solved by
term in eqn (27) yields an initial value problem solved by
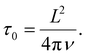

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t → ∞, as expected. It also yields the Green's function for the unsteady start-up flow in a periodic array as
t → ∞, as expected. It also yields the Green's function for the unsteady start-up flow in a periodic array as
 . However, the periodic array solution does not recover the
. However, the periodic array solution does not recover the  term in eqn (10), a consequence of retaining only
term in eqn (10), a consequence of retaining only  terms in the Taylor expansion. Although higher order corrections can be systematically incorporated into eqn (31), they are not expected to change the conclusions of this work and are thus left as a topic of future study.
terms in the Taylor expansion. Although higher order corrections can be systematically incorporated into eqn (31), they are not expected to change the conclusions of this work and are thus left as a topic of future study.![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) . Note that the fundamental solution is spherically symmetric, and these two projections are sufficient to fully specify the tensor. The projections along and perpendicular to
. Note that the fundamental solution is spherically symmetric, and these two projections are sufficient to fully specify the tensor. The projections along and perpendicular to ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) are plotted in Fig. 3a and b, respectively, as a function of distance normalized by the particle radius r/a. Fig. 3a and b show the projections in a linear–log plot, and the insets in each figure show the absolute value of the same curve in a log–log plot. Solid curves of different colors correspond to different times and, as shown in the legend, the black dash-dotted curve corresponds to the steady-state solution and the dashed red line marks the value zero across the horizontal axis.
are plotted in Fig. 3a and b, respectively, as a function of distance normalized by the particle radius r/a. Fig. 3a and b show the projections in a linear–log plot, and the insets in each figure show the absolute value of the same curve in a log–log plot. Solid curves of different colors correspond to different times and, as shown in the legend, the black dash-dotted curve corresponds to the steady-state solution and the dashed red line marks the value zero across the horizontal axis.![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) will induce a flow that is similar to the steady-state flow at distances r < l, making it proportional to 1/r at these shorter distances. At distances r > l, the flow has a decay proportional to 1/r3 (see the inset figure), reflecting the vortex flow pattern that arises at these larger distances. As l increases with time, the region where the flow decays as 1/r3 moves farther from the object, with the steady state corresponding to the limit where the distance of this region to the particle is infinite. For the perpendicular component, the effect of the vortex flow is more pronounced. At distances r < l, the flow is similar to the steady-state flow and is proportional to 1/r. However, at distances r > l, the projection not only decays proportional to 1/r3 but is also negative, meaning that the flow is in the direction opposite to the forcing. The region where the flow opposes the force moves farther as the time increases, and its distance to the particle is infinite at steady state.
will induce a flow that is similar to the steady-state flow at distances r < l, making it proportional to 1/r at these shorter distances. At distances r > l, the flow has a decay proportional to 1/r3 (see the inset figure), reflecting the vortex flow pattern that arises at these larger distances. As l increases with time, the region where the flow decays as 1/r3 moves farther from the object, with the steady state corresponding to the limit where the distance of this region to the particle is infinite. For the perpendicular component, the effect of the vortex flow is more pronounced. At distances r < l, the flow is similar to the steady-state flow and is proportional to 1/r. However, at distances r > l, the projection not only decays proportional to 1/r3 but is also negative, meaning that the flow is in the direction opposite to the forcing. The region where the flow opposes the force moves farther as the time increases, and its distance to the particle is infinite at steady state.![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) . Note that, in principle, the shape of the unit cell can result in deviations from the spherical symmetry that are quantified by the tensors C and B(t). Here, the simple cubic symmetry results in these tensors being isotropic (see Appendix C). The projection of eqn (31) in directions longitudinal and perpendicular to a radial vector
. Note that, in principle, the shape of the unit cell can result in deviations from the spherical symmetry that are quantified by the tensors C and B(t). Here, the simple cubic symmetry results in these tensors being isotropic (see Appendix C). The projection of eqn (31) in directions longitudinal and perpendicular to a radial vector ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) are shown in Fig. 4a and b, respectively. Fig. 4a shows that for distances r < l, the r-dependence of the longitudinal projection is similar to the steady-state dependence. In contrast to the case of an isolated object, the projection becomes negative at distances r > l, reflecting the back flow from the periodic array. Similar qualitative behaviors are observed for the perpendicular component in Fig. 4b, with the lower magnitude of the projection reflecting the flow is weaker in this direction.
are shown in Fig. 4a and b, respectively. Fig. 4a shows that for distances r < l, the r-dependence of the longitudinal projection is similar to the steady-state dependence. In contrast to the case of an isolated object, the projection becomes negative at distances r > l, reflecting the back flow from the periodic array. Similar qualitative behaviors are observed for the perpendicular component in Fig. 4b, with the lower magnitude of the projection reflecting the flow is weaker in this direction.