Thermodynamics and kinetics of early stages of carbon dot formation: a case of citric acid and ethylenediamine reaction

Abstract

Owing to their extraordinary photophysical properties, carbon dots (CDs) have found applications across various fields, including bioimaging, sensing, and environmental research. Despite huge application potential, the fabrication of CDs still lacks the desired control at the molecular level, and precise structural regulation towards property-tailored CDs remains elusive. The mechanistic details of nucleation, growth, and carbonization processes leading to CDs are still unknown, with key thermodynamic and kinetic parameters yet to be revealed. Herein, we performed quantum chemical calculations of explicitly micro-hydrated reaction systems to thoroughly explore the mechanism of a prototypical reaction of citric acid and ethylenediamine. The theoretical results showed activation barriers and thermodynamics along the reaction pathway, thus helping identify key heterocyclic intermediates and cyclization products. The cyclization and condensation reactions were further simulated via a reactive molecular dynamics protocol, suggesting potential growth scenarios and generating plausible structures for further exploration of the polymerization and carbonization processes. The theoretical calculations were cross-validated with NMR and MALDI-TOF measurements. The data obtained provide a comprehensive deterministic insight into the initial stages of CD formation, revealing new reaction intermediates and pathways, and rationally predicting the formation of specific structural arrangements of premature CDs. The presented deterministic approach represents an important step towards rational bottom-up design of these unique fluorescence systems.

---

Introduction

Carbon dots (CDs) represent an outstanding class of photoluminescent (PL) nanomaterials with diverse applications such as bioimaging, sensing, photocatalysis, and anti-counterfeiting.^1–8 CDs can be conveniently fabricated in large quantities via either top-down procedures from larger carbon sources (e.g., graphite, amorphous carbon, and carbon nanotubes) or bottom-up synthetic techniques from cost-effective molecular precursors or even biomass and waste through simple chemical processes.⁹ Their accessibility, biocompatibility, and non-toxic nature make them highly attractive and sustainable nanomaterials. The rational design of CDs is however largely hampered by the lack of detailed information concerning their structural features at the atomistic level.¹⁰

The exact classification of CDs is debatable due to blurred boundaries among individual sub-classes; however, four categories, i.e., graphene quantum dots (GQDs), carbon quantum dots (CQDs), carbon nanodots (CNDs), and polymer carbon dots (PCDs) are usually listed.^1,11,12 The chemical complexity of CDs further hinders their accurate classification and precise characterization. Usually, two parts of CDs, i.e., a core and a surface shell, can be distinguished. Depending on fabrication procedures, the core can exhibit a variable degree of disorder. On the one hand, there are highly disordered PCDs and CNDs with an amorphous core; on the other hand, there are ordered GQDs, CQDs, and some CNDs with a crystalline core, resembling (doped) graphene/graphite with abundant sp²-hybridized carbon atoms.¹³ The less structured surface shell usually comprises sp³-hybridized carbon atoms and various functional groups depending on the precursors, reaction conditions and post-processing modifications. Besides structurally variable CD domains, small heterocyclic molecular fluorophores (MFs) can be produced using bottom-up synthetic approaches.^14–18 They can be attached, embedded or covalently linked to CDs, largely affecting their structure and optical properties. MFs often exhibit intense fluorescence, contributing to the excitation-independent emission of CDs.

The large variability and heterogeneous nature of CDs bring significant challenges to the experimental characterization of their structure. Despite the application of advanced separation techniques, achieving uniform size distribution and structural uniformity remains a critical issue.¹⁹ Spectroscopic techniques such as X-ray photo-electron spectroscopy, Fourier-transform infrared spectroscopy (FTIR), Raman spectroscopy, nuclear magnetic resonance (NMR), and light-induced electron paramagnetic resonance spectroscopy provide valuable insights into the presence and abundance of specific structural features of CDs.^20–23 However, this information is averaged across the ensemble, preventing direct attribution to specific structural features. Microscopic techniques such as high-resolution transmission electron microscopy and atomic force microscopy provide direct evidence of carbon nanoparticles. However, their current capabilities do not allow for atomically resolved imaging of CDs.^24–26 On the other hand, computational chemistry tools are indispensable for understanding structure—property relationships applicable to CDs.^27,28 Yet, even the most sophisticated theoretical approaches require accurate CD models to generate reliable data. To address the problem of limited information on the CD structure, various strategies for model development have been applied. These include the construction and re-optimization of ad hoc molecular models by quantum mechanics (QM) methods.^27–32 Classical molecular dynamics (MD) simulations were also applied to analyze the dynamics and aggregation of CD fragments into multilayered self-assemblies,^23,33–35 oligomeric networks,³⁶ and highly disordered amorphous CD structures.³⁷ Although these models reflect relevant information gained from experiments, they still remain tentative without direct experimental validation.

Deterministic analysis of the reaction mechanisms leading to the formation of CDs represents an alternative strategy for identifying plausible chemical structures and deciphering the structural features of CDs. It can provide an overview of the entire process and help us understand how reaction conditions affect the structure and composition of the products, which is crucial for the rational design of CDs with specific characteristics. The formation of CDs is undoubtedly a complex process involving competitive reactions of precursors and intermediates, aggregation, polymerization, and carbonization.^11,38,39 Each of these reaction steps is challenging to model and requires appropriate computational tools for accurate representation. While the initial sequence of reactions can be addressed by standard QM methods, description of latter steps involving nucleation, aggregation and the growth of polymeric chains requires utilization of advanced techniques of molecular modelling including, e.g., the reactive MD approach. Modelling the carbonization phase, which includes further interlinking, reductive decarboxylation/deamination, and the formation of the sp² core, is expected to be even more complex and would require more sophisticated protocols and techniques of computational chemistry.

The reaction between citric acid (CA) and ethylenediamine (EDA) represents a prototypical synthetic route leading to an important class of nitrogen doped CDs with bright PL, which are relevant for various applications, including sensing,²² photocatalysis,⁴⁰ heavy metal detection,⁴¹ optoelectronics,⁴² anti-counterfeiting,⁴³ and bioimaging.⁴⁴ The reaction of CA with EDA under hydrothermal conditions was experimentally explored by Song et al.,³⁸ who revealed that the intense excitation-independent PL component of CA + EDA-based CDs can be attributed to the presence of a specific MF, i.e., 5-oxo-1,2,3,5-tetrahydroimidazo[1,2-a]pyridine-7-carboxylic acid (IPCA), whose presence was unambiguously confirmed by 2D-NMR. The authors tentatively proposed a sequence of reactions possibly leading to IPCA, although they did not describe the kinetics and thermodynamics of individual reaction steps, which are critical for a deep understanding of the reaction mechanisms.

Herein we use a sequential QM/reactive-MD computational protocol to analyse early steps of the reaction of CA and EDA and processes leading to oligomeric aggregates representing nucleation centres for the further development of CDs. The thermodynamic and kinetic parameters (i.e., activation barriers) of individual steps of the CA + EDA reaction were calculated using a composite DLPNO-CCSD(T)/def2-TZVPP//M06-2X-D3/6-31+G(d,p) approach applied to a combined explicit/implicit water model. This approach allowed us to compare the relative stability of all reaction intermediates and products and identify the rate-limiting steps of the proposed competitive pathways. Our study also explicitly highlights the importance of considering dissociated forms of reaction species and explicit water molecules that facilitate key reaction steps by proton transfers. Using the kinetic data from QM calculations, heuristic-aided reactive MD simulations were carried out to mimic the formation of low molecular mass intermediates and the growth process, identifying potential CD evolution scenarios. Theoretical calculations were cross-validated against NMR spectroscopy and matrix assisted laser desorption ionization-time of flight mass spectrometry (MALDI-TOF MS) experimental data for reaction mixtures attained in a short reaction time (1 hour), which also disclosed a new 5-membered ring cyclization pathway. This systematic study employing a combination of theoretical calculations with experiments on the transformation of molecular precursors to MFs and oligomeric structures offers comprehensive insights into the initial steps of CA-based CD formation. In addition, it provides reliable structural models of oligomeric aggregates mixed with MFs, which can be used for the exploration of structure–property relationships in polymeric CDs as well as in follow-up studies of the polymerization and carbonization processes occurring in the later stages of CD synthesis.

Results and discussion

Computational insights into the reaction of CA with EDA: cyclization versus polymerization

The standard reaction Gibbs energies (Δ_rG°(T = 180 °C)) and the activation barriers (ΔG^‡(T = 180 °C)) of individual reaction steps between CA and EDA in water have been computed along various reaction pathways (Scheme 1) using a composite approach at the DLPNO-CCSD(T)/def2-TZVPP//M06-2X-D3/6-31+G(d,p) level (Fig. 1).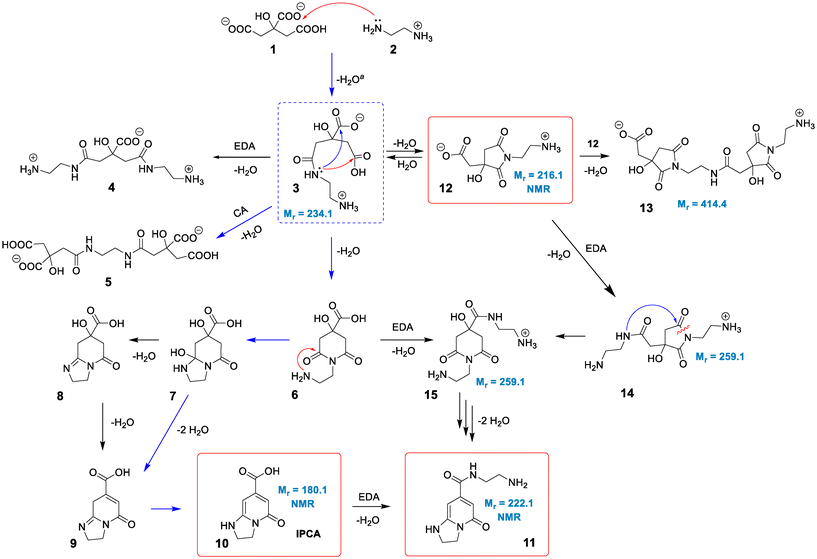

Scheme 1 Proposed mechanism for the reaction of CA and EDA under hydrothermal conditions. Species in red frames were confirmed by NMR and MS. The structures with given molecular masses were associated with observed MS signals. The pathway marked by blue arrows was tentatively proposed by Song et al.³⁸ Intermediate 3 in a blue dashed frame represents a crossroad point for various competitive reactions. ^aThe formation of 3 can proceed via a reaction of 2 with either 1 or CA anhydride (see text).

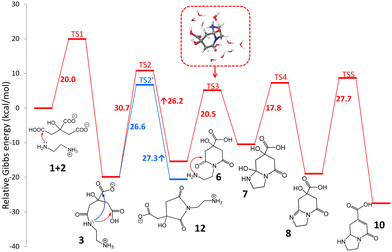Fig. 1 Standard Gibbs energy diagram (T = 180 °C) of the early stages of the reaction between CA and EDA in water (inset: micro-hydrated structure of TS3) obtained at the composite DLPNO-CCSD(T)/def2-TZVPP//M06-2X-D3/6-31+G(d,p) level. Details of individual steps including structural information are provided in the ESI† (Section 12).

As some of the reaction steps are facilitated by surrounding water molecules, key explicit water molecules (facilitating proton transfer reactions) were included in the model (as shown in the inset in Fig. 1), while the dielectric nature of the environment was taken into account by using an implicit solvent model (see Computational details). It should be noted that the previous literature did not consider the role of protonation states of the reaction species. The reaction species, i.e., CA, EDA and other reaction intermediates are predominantly present as charged species (or zwitterions) in water. The acid–base equilibria significantly affect the feasibility of competing cyclization and polymerization pathways, as also inferred from the influence of the pH value on the characteristics of products observed experimentally,³⁸ and therefore must be taken into account. The experimentally determined initial pH value (6.1) of a stoichiometric mixture of CA and EDA (2 : 3) implies that the dominant forms are anions CA(2−), CA(3−) and di-protonated cations EDA(2+), respectively (Table S1†).⁴⁵ As the activation barrier for a direct condensation of the ammonium group with carboxylate is rather high (∼31 kcal mol⁻¹), it can be expected that the first condensation reaction proceeds mainly via CA(2−) anions and a less abundant EDA(+) form with a much lower barrier (∼20 kcal mol⁻¹), systematically shifting the acid–base equilibria towards these forms due to their transformation to condensates. The formation of 3 presumably starts with a nucleophilic attack of the amine group onto protonated carboxylate with a small barrier (∼5 kcal mol⁻¹) leading to an intermediate 3a which transforms to 3 via a chain proton transfer reaction (ΔG^‡ = 18 kcal mol⁻¹) facilitated by surrounding water molecules ending with the detachment of a water molecule (Fig. S3 and S4†). Let us note that the barrier for this proton transfer without considering explicit water molecules is as high as ∼37 kcal mol⁻¹ (at the DFT level), highlighting the active role of the water environment in the reaction. Alternatively, the intermediate 3 can be formed via the reaction of EDA(+) with CA anhydrides (Fig. S5 and S6†), which may exist in minute quantities under the reaction conditions (computed K_eq = 3.4 × 10⁻⁴ at 180 °C).^46–48 The effective activation barrier for this reaction, calculated as the sum of Δ_rG°(T = 180 °C) for CA anhydride formation (7.2 kcal mol⁻¹) and the activation barrier for the subsequent nucleophilic attack by EDA(+) (12.4 kcal mol⁻¹) equals ∼20 kcal mol⁻¹. This suggests that the anhydride-based pathway is competitive with the direct reaction of CA(2−) and EDA(+). The condensate 3 appears to be a crossroad point of the whole process. At pH = 5–6, a protonated form of the terminal amine group of 3 is dominant, and therefore further condensations with CA towards intermediates 4 and 5 require overcoming the relatively high activation barrier (∼31 kcal mol⁻¹) for a direct reaction of an ammonium group with carboxylate. Although its reactivity can be elevated in the basic environment, the increase of pH would cause the depletion of the CA(2−) form impeding the condensation reactions. This is in keeping with the experimental evidence that the formation of MFs prevails over the polymerization and carbonization processes in the slightly basic environment.³⁸ The involvement of the terminal ammonium group in intramolecular cyclization reactions is also less probable compared to a neutral nitrogen atom of the amide group. Consequently, the cyclization can result in the formation of either 6-membered ring (6) or 5-membered ring (12) intermediates, depending on which of the carboxylic groups of 3 the nucleophilic attack takes place. Interestingly, the latter is both kinetically and thermodynamically favoured, which is in line with the undeniable experimental evidence of 12 in the lower temperature (150–180 °C) regimes (vide infra). Although the 5-membered ring structure can be involved in subsequent condensation reactions leading e.g. to the surmised structure 13 and thus can be present in the polymeric structures formed using longer reaction times, its transformation to IPCA (10) would require complex rearrangements involving concurrent ring opening and closure via a bicyclic intermediate (Scheme S1†) as well as hydrolysis of the amide group in the last step (transformation of 11 to 10). Therefore, we hypothesize that at higher temperatures the 5-membered ring of 12 reversibly opens back to 3, and the reaction further proceeds via a competitive 6-membered ring cyclization towards the thermodynamically most stable product 10, which is IPCA. This process advances via an intermediate 7 proposed by Song et al.,³⁸ which is however relatively unstable and transforms to 8. Then, the elimination of a water molecule results in 9 which readily changes to 10 by a hydrogen transfer facilitated by two water molecules (Fig. S13 and S14†). Notably, the elimination of a water molecule from the 5-membered ring (reaction 8 → 9) is more favorable (by ∼5 kcal mol⁻¹) compared to the alternative pathway starting with water elimination from the 6-membered ring of 7 (Fig. S16†). To sum up, the upper limit of the activation barrier of the rate-limiting step for the whole process leading to IPCA is estimated to be ∼31 kcal mol⁻¹ (3 → 6), which is relatively high but explains the preference for the 5-membered ring pathway at lower temperatures. The barrier is comparable to that calculated for the condensation of charged ammonium and carboxylate groups (∼31 kcal mol⁻¹) implying that polymerization and formation of IPCA become competitive pathways at elevated temperatures.

Experimental exploration of the reaction between CA and EDA

To decipher the early stages of IPCA/CD formation, we studied the composition of mixtures prepared by short-term (1 h) and long-term (10 h) hydrothermal reactions of CA (5 mmol) and EDA (5 mmol) in water (10 mL) at various temperatures by NMR spectroscopy and MALDI-TOF spectrometry. The samples attained by a 1-hour treatment at 150 °C, 180 °C, 210 °C, and 240 °C were denoted as CD-150-1, CD-180-1, CD-210-1, and CD-240-1, respectively, while those obtained using a longer reaction time were denoted analogously (e.g., CD-150-10 for T = 150 °C). Importantly, the shorter reaction time (unlike the standard 10 h treatment) should allow us to detect metastable intermediates preceding the formation of IPCA, e.g., compounds 6–9, and thus gain direct insights into the reaction mechanism. Indeed, the ¹H NMR analysis of CD-150-1 showed unreacted CA and EDA together with a partial conversion (∼20%) to a non-symmetric compound (bearing two pairs of diastereotopic –CH₂– hydrogen atoms together with a –CH₂–CH₂– moiety assigned to a fragment originating from EDA) which could correspond to hemiaminal 7 or imine 8. However, the structure 7 did not match the observed ¹³C NMR spectrum (no signal for carbon in the hemiaminal region – for more details, see the predicted and observed signals in Section 9 of the ESI†), and the presence of compound 8 in the sample was inconsistent with the observed m/z in MALDI-TOF (showing a peak in the positive mode at m/z 217.1 instead of expected m/z 199.1, as shown in Section 5 of the ESI†) nor with the ¹³C NMR spectrum (see Section 4 in the ESI†).

To elucidate the structure of the observed intermediate, we used ¹⁵N NMR technique which is known to be very sensitive to various nitrogen bonding modes. Surprisingly, besides the expected signal for sp³-nitrogen next to the electron-withdrawing carbonyl group at −207 ppm, the ¹H-¹⁵N HMBC spectrum of CD-150-1 also showed a relatively shielded signal at −351 ppm corresponding to a nitrogen with a similar character as in EDA (signals for hydrogen in amino groups of diprotonated EDA are observed at −353 ppm, compared to −365 ppm for the unprotonated species, as reported in ref. 49). This hints that the observed intermediate contains a free amino group, as in intermediate 6 resulting from a nucleophilic attack of the amide nitrogen to the edge carboxylate group in 3. However, 6 did not match the observed ¹H and ¹³C NMR data due to its C_S symmetry. Therefore, we concluded that the observed intermediate was formed via an alternative pathway involving a nitrogen attack on the central carboxylate and subsequent formation of a 5-membered heterocycle 12. The excellent agreement between the observed ¹³C and ¹⁵N chemical shifts and those predicted by the gauge-including atomic orbitals (GIAO) method supports this hypothesis (see Section 9 in the ESI†). To unambiguously prove the correct determination of structure 12, an alternative synthetic strategy leading to this intermediate was devised based on a previously reported procedure for the synthesis of similar 5-membered compounds (see Section 2 in the ESI†).^{50 1}H NMR spectrum of the product prepared in this manner exactly matched the signals observed in the spectra of samples prepared by a hydrothermal treatment of CA and EDA, thus confirming the presence of a 5-membered ring in 12.

The intermediate 12 was also formed at elevated temperatures. CD-180-1 contained approx. 35% of 12 along with unreacted CA and EDA. At 210 °C, CA and EDA were fully consumed, and although traces of 12 were still observed, the main component of the mixture was IPCA. Finally, at an even higher temperature (240 °C), the only species seen in the ¹H NMR spectrum was IPCA together with unspecified oligomers or polymers (as can be seen from an elevated baseline in the region 2.5–3.5 ppm, Fig. 2f).

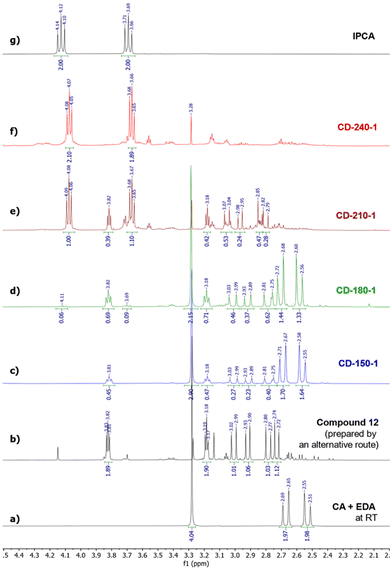Fig. 2 ¹H NMR spectra of (a) a CA/EDA mixture at room temperature; (b) intermediate 12; (c–f) a CA/EDA mixture after 1 h at 150–180 °C; and (g) pure IPCA.

The transformation of CA and EDA to IPCA via intermediate 12 is also reflected in the FTIR spectra of the above-mentioned samples (Fig. 3a) by changes of intense peaks at ca. 1700 cm⁻¹ (attributed to intermediate 12) and 1650 cm⁻¹ (attributed to IPCA). The FTIR spectra of CD-150-1 and CD-180-1 are similar to the FTIR spectrum of unreacted CA/EDA mixture, pointing to the presence of the precursors. The only significant difference is an increase of the peak at 1700 cm⁻¹, in line with the increasing amount of intermediate 12 (cf. the corresponding ¹H NMR spectra, Fig. 2c and d, showing approx. 20% and 35% conversion of CA/EDA to 12 in samples CD-150-1 and CD-180-1, respectively). The FTIR spectrum of CD-210-1 is significantly different: besides the peak for intermediate 12, an intense peak at 1650 cm⁻¹ appears, corroborating the presence of IPCA. At higher temperatures, the peak for intermediate 12 disappears, and the only observed peak in the 1600–1700 cm⁻¹ region corresponds to IPCA (1650 cm⁻¹). The FTIR spectra of samples attained after the 10 h reaction time reflect the progress of the ongoing reactions. The indicative peak for IPCA (1650 cm⁻¹) appears already at 150 °C, whereas the peak for 12 is no more present in the spectra above this temperature.

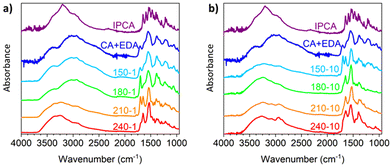Fig. 3 FTIR spectra of IPCA, CA/EDA mixture (1 : 1, no heating) and samples prepared by the hydrothermal treatment of CA/EDA mixture at 150–240 °C. Heating time: (a) 1 h; (b) 10 h.

The initial presence of 12 in large amounts and then its complete disappearance suggest that 12 can be converted to IPCA. Indeed, hydrothermal treatment of compound 12 alone (prepared by the above-mentioned alternative route) resulted in the formation of IPCA as the main product (for details, see Section 8 of the ESI†).

Although ¹H NMR and FTIR spectra detect the significant presence of IPCA only in the samples subjected to 1 hour hydrothermal treatment of CA/EDA mixtures at elevated temperatures (≥210 °C), IPCA was already present in trace amounts (<3%) in sample CD-150-1. These trace amounts were detected by MALDI-TOF spectrometry. This method also revealed other minor species present in trace quantities: simple CA/EDA amide 3 (m/z 235.1), present in low-temperature samples (150–180 °C), gradually converted into more complex systems (presumably via 5-membered derivative 12), such as species 14 or 15 (m/z 259.1) and even 13 (m/z 415.2). Experiments conducted at 150–210 °C using prolonged reaction time (10 h) showed the presence of IPCA, as evident from ¹H NMR (see Section 6 of the ESI†) as well as FTIR spectra (Fig. 3b). In samples prepared at 150 °C, the intermediate 12 is present even after 10 h of hydrothermal treatment (as evident from the NMR spectra shown in Section 6 of the ESI† and the FTIR peak at 1700 cm⁻¹ shown in Fig. 3b), but at higher temperatures, it gradually converts to IPCA (FTIR peak at 1650 cm⁻¹) and/or carbonization products (manifested by the increase of the spectral linewidth in the FTIR spectrum of the sample CD-240-10). The higher degree of decarboxylation and dehydration for longer lasting harsher conditions was also corroborated by the survey X-ray photoelectron spectroscopy (XPS) and high-resolution (HR) XPS C1s spectra showing systematically growing content of carbon (and C=C/C–C bonds) at the expense of oxygen (and C–O/C=O bonds) with the increasing reaction temperature and reaction time (see Section 10 in the ESI†).

Interestingly, if the reaction of an equimolar mixture of CA and EDA was conducted at 180 °C for 10 hours, after cooling to room temperature, formation of brownish crystals was observed, which were identified as pure IPCA. By evaporating the mother liquor, a dark brown powder was obtained, whose main component was also IPCA, as seen from ¹H NMR spectra. Partial crystallisation of products was also observed at 150 °C but in much less quantity. At temperatures above 180 °C, no crystals were formed. For the synthesis conducted at 240 °C, no IPCA was detected by ¹H NMR spectroscopy, suggesting that IPCA itself is thermally unstable and can undergo further decomposition/carbonisation reactions.

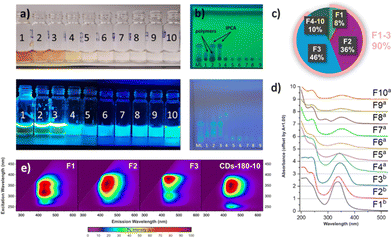
To further study the composition of the mother liquor from the sample CD-180-10, especially the presence of polymeric and/or carbonized species, which may be hard to observe by NMR, a part of the mother liquor (350 mg) was also separated using Sephadex chromatography. We obtained 10 fluorescent fractions (Fig. 4a), which were analysed by thin-layer chromatography (Fig. 4b), UV-VIS spectroscopy (Fig. 4d), and photoluminescence spectroscopy (Fig. 4e), and the most abundant fractions (1–3 and 10) also by ¹H NMR spectroscopy (after evaporation to dryness using a rotary evaporator – for details, see Section 7 of the ESI†).

Fig. 4 (a) Samples of fractions 1–10 obtained by Sephadex chromatography of the mother liquor (ML) from CD-180-10 under daylight (top) and 365 nm UV lamp (bottom); (b) TLC analysis of mother liquor and fractions 1–9 (TLC plate: SiO₂, eluent: ethyl-acetate/methanol (1 : 1, v/v)) viewed under 254 nm (top) and 365 nm UV lamp (bottom); (c) the content of individual fractions in the original mixture; (d) UV-VIS spectra of fractions 1–10. Samples marked a were measured as eluted from the column, samples marked b were diluted with deionized water (1 : 20); (e) PL excitation–emission color map of the most prominent extracted fractions (F1–F3) and the full (non-separated) sample CD-180-10 (“mother liquor”).

Size-exclusion chromatography allowed the separation of larger polymeric species (with ¹H NMR signals mainly in the aliphatic region, fraction 1, 30 mg), from smaller IPCA molecules (fraction 3, 160 mg) and their mixture (fraction 2, 125 mg). All other fractions contained less than 10 mg of the dissolved material and had only low absorption and fluorescence, as seen from UV-VIS spectroscopy and thin layer chromatography (TLC) analysis. Interestingly, after separation, the stationary phase remained slightly fluorescent, which suggested the presence of an analyte which was strongly noncovalently bonded to the Sephadex column. To isolate it, the column was purged with deionized water (approx. 2 L) and the eluate was concentrated in vacuo to afford a fraction 10 (8 mg). NMR analysis of this sample suggested a structure similar to IPCA, but containing two EDA fragments, therefore corresponding to compound 11 (also seen in MALDI-TOF at m/z 223.1). However, the influence of this newly discovered fluorophore on the properties of CDs is only insignificant, given its small abundance compared to IPCA.

Furthermore, all extracted samples were analyzed using photoluminescence (PL) spectroscopy. The PL excitation–emission maps of individual fractions revealed significant differences in optical properties (Fig. 4e). Given that fractions 1, 2, and 3 were the most prevalent in the mother liquor, the focus was on evaluating these fractions. Fraction 1 (Fig. 4e, F1) exhibited a PL emission maximum at 435 nm upon excitation at 320 nm and 350 nm. The comparable intensity of PL emission with different excitation wavelengths reflected the structural complexity of a mixture of hardly distinguishable species, which was consistent with ¹H NMR measurements. Fraction 2 (F2) exhibited a similar range of suitable excitation wavelengths to F1; however, individual excitation maxima could not be resolved. This, combined with a slight redshift from 435 nm to 443 nm in PL emission, indicated an increasing amount of IPCA in the mixture. Fraction 3 (F3) featured a narrow, excitation-independent PL emission at 443 nm, which implied the dominant abundance of IPCA, thus corroborating the findings from NMR measurements. Interestingly, a secondary emissive channel upon excitation at 300 nm was observed. Due to its significantly lower PL intensity and the same position of PL maxima, this could be attributed to either PL emission resulting from the excitation to higher excited states of IPCA or trace amounts of impurities, which were not detectable by NMR spectroscopy. Finally, the PL properties of the extracted fractions were compared to those of the crude solution (CD-180-10) to identify the main contributors to the overall PL. The PL excitation–emission map of CD-180-10 exhibited an excitation-independent character, with a PL maximum at 444 nm. Additionally, similar to F3, a second radiative channel was observed at higher energy excitation wavelengths (∼λ_ex = 250 nm), indicating that IPCA is the component contributing the most to the overall PL properties of the as synthesized assembly (Fig. 4e, CD-180-10). In the remaining fractions, the character of PL emission changed from excitation-dependent (F4 to F6, Section 7 in the ESI†) to excitation-independent (F7 to F10, Section 7 in the ESI†), the latter presumably associated with the presence of molecular fluorophores such as compound 11 identified by NMR. However, due to their low content (less than 10 mg) in the crude solution, they contributed only minimally to the overall PL.

Heuristic reactive molecular dynamics

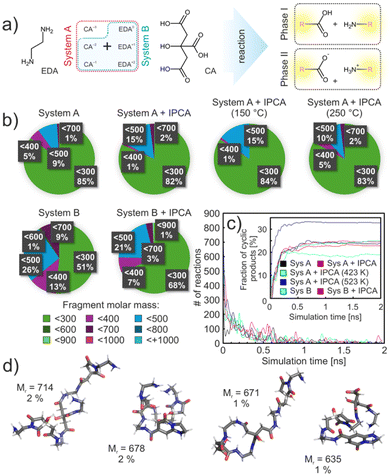
To explore dynamic aspects of the initial phases of the reaction between CA and EDA, we performed an extensive set of reactive MD simulations utilizing a heuristic protocol designed to model complex and predefined reactions, employing the classical fixed-valence method (for more details see Sections 10 and 13 in the ESI†).⁵¹ This approach allowed us to incorporate insights from the QM calculations, focusing on the competition of cyclization and polymerization pathways. Considering the kinetics and thermodynamics of this reaction, in particular a relatively high activation barrier for the condensation of charged ammonium and carboxylate groups, we divided the whole process into two main stages. The first simulation stage (phase I) involved a condensation reaction of neutral groups along with self-cyclization processes, while the more energetically demanding cross-linking of the charged ends was modelled in the second stage (phase II). It was expected that the first stage occurs much faster than the subsequent reactions between charged-end species. This division allowed for a more manageable modelling approach and ensured that each reaction phase was adequately represented within the given simulation time, adhering to the constraints of our heuristic protocol. We modelled the evolution of a mixture with two different compositions referred to as systems A and B, corresponding to slightly and strongly acidic environments, respectively, differing by the presence of fully deprotonated CA in the former (Fig. 5a; for the details on the compositions see ESI Table S3†). Moreover, we studied the effect of the presence of the thermodynamically most stable product (IPCA) in the reaction system from the beginning of the reaction. The IPCA anions as well as the fully deprotonated CA did not directly participate in the initial reaction stage but could influence the system mechanistically. The probabilities of condensation and cyclization reactions were set to qualitatively reflect the related activation barrier heights obtained from QM calculations.

Fig. 5 (a) A simplified diagram showing the composition of systems A and B and the division of simulation phases I and II; (b) Pie charts showing the distribution of products by molar mass of the product; (c) number of reactions per ns that occurred in the individual systems. The inset shows the number of cyclic reactions in the systems; (d) molecular structure of the 4 most common polymers according to molar mass, which were formed in the systems after both phases. Color code: oxygen, red; nitrogen, blue; carbon, gray; hydrogen, white.

At the beginning, each system was equilibrated for 10 ns in the NpT ensemble to the reaction temperature (200 °C), then switched into the reactive mode and simulated for additional 2 ns. After this time, the step-growth mechanism of the polymerization reached chemical equilibrium, regardless of the system composition, with no further reactions occurring in the system (Fig. 5a). In phase I, system A provided a large percentage of small products (∼85% of all product molecules) according to the mass distribution (Fig. 5b) comprising adducts of 1 CA molecule and 1 or 2 EDA molecules. Only an insignificant number of compounds above 700 g mol⁻¹ were identified. It was partly caused by the presence of a fully dissociated form of the CA that did not participate actively in the reaction phase I and thus limited the reaction space of the system. Moreover, it interacted strongly with other surrounding monomers or heterodimers/trimers and thus acted as a protection against further polymerization. Approximately 9% of the products had a molecular weight of 400–500 g mol⁻¹, which included chains with 2 CA molecules. A similar distribution of rather small products could also be seen in experimental measurements, where mostly small fragments were identified. As expected, in system B, corresponding to lower pH conditions, only singly and doubly deprotonated forms of CA were present (maintaining the same concentration of CA molecules in the system), and led to more reactions and, overall, to more diverse, yet still rather small, products. This was caused by the fact that system B contained more neutral groups than system A (by ca. 30%) that could participate in the reaction phase I.

The influence of IPCA molecules on the reaction of system A was only marginal. However, system B was surprisingly far more sensitive to the presence of IPCA molecules. Under the lower pH conditions, the total number of reactions and the number of products increased by 14% and 26%, respectively, compared to system B without IPCA (Table S4†). Furthermore, in the system without IPCA molecules, there was a higher proportion of formed small molecules (with molar mass up to 300 g mol⁻¹). Upon closer examination, it was found that the increased reactivity of system B containing IPCA was due to a greater proportion of minimal contacts between the –COOH and –NH₂ groups of CA(2−) and EDA(+), respectively (Fig. S17d†). This was not observed in system A, where the fully dissociated CA(3−) molecules competed presumably for the same binding sites, influencing their interactions with other molecules. Thus, the addition of IPCA anions into system A had a much smaller impact compared to system B.

In the next step, we compared the number of cyclic products created in different systems. Regardless of the system composition, on average 19% of all completed reactions formed cyclic products (see the inset of Fig. 5c). All the formed cycles were 5-membered compounds, corresponding to the experimentally isolated product 12, thus supporting the experimental observation. The 6-membered product was not observed in our systems at any point during the 2 ns simulation time, but its formation could not be excluded at longer timescales, which would be however computationally too demanding. Therefore, to address the ratio of formed 5- and 6-membered ring intermediates, in the next step we increased the probability of cyclization reactions by 2 orders of magnitude (still maintaining the same ratio between 5- and 6-membered reaction pathways). This bias only slightly increased the total percentage of cyclic products (∼24%) without affecting the total number of polymerization reactions. However, 5% of the cycles resulted in 6-membered intermediates. This number further increased to 15%, when the simulation temperature was increased to 250 °C. This corroborates the importance of the competitive branch of the reaction, which, due to the kinetics, may play an important role in the initial stages of CD formation.

Finally, we inspected the second stage of the reaction in which the charged-ends of species present in the systems at the end of phase I were allowed to react. Therefore, in phase II small oligomers including charged species and zwitterions could form bigger particles. Regardless of the system composition common products have been identified. 8% of all formed species were in the range of 600–800 g mol⁻¹, whereby a large number of the products had retained their small size from the first phase simulations (Fig. S17c†). In the presence of IPCA molecules, on average about 46% of the products had incorporated IPCA into their structure. This proportion increased with temperature, reaching up to 55% at 250 °C. The occurrence of 5/6-membered cycles in the structures was more pronounced in system B, where nearly twice as many products contained such cycles compared to system A (23%). A similar trend was observed in the system without IPCA, where the proportion of products containing 5/6-membered cycles increased to 51% in system B and 38% in system A. This increase is most likely due to the reduced number of possible reactions in system B/without the presence of IPCAs, allowing the system to follow an energetically more demanding pathway.

In general, the products exhibited a predominantly polymeric character, with occasional intra-chain cross-linking leading to the formation of cyclic aggregates. In system A, increasing the temperature led to a greater number of larger molecules (M_r ≥ 700), as expected. The largest observed clusters had molecular weights slightly exceeding 2000 g mol⁻¹, corresponding to approximately 14% of the theoretical maximum product weight. Reactive MD did not show much aggregation of the polymers due to a rather short simulation time scale. Long MD simulations of polymers with and without attached IPCA moieties showed clustering of polymers with IPCA more preferentially than without IPCA (Fig. S19†). In some cases, IPCAs from different polymers stacked on each other and therefore formed an aggregation center. Such agglomerates could act as possible nucleation centers during the growth of polymeric CDs and form a base for the carbonized phase. It is noteworthy that other products found in the reaction mixture, such as e.g. compound 11, which are structurally similar to IPCA, can also presumably act as nucleation centers; however, their abundance in the reaction mixtures is very low to contribute significantly to the nucleation process.

Conclusions

The high application potential of CDs urges gaining atomistic insights into their organization and understanding the links between precursors/reaction conditions and the structure of products. The formation of CDs involving initial reactions of low mass species, polymerization, nucleation, growth, and – at higher temperatures – carbonization is a multi-branch process resulting in high heterogeneity and complexity of CD structures. The modelling of these steps is highly challenging and requires a combination of various computational approaches. Here we focused on the analysis of the thermodynamic and kinetic aspects of processes occurring in early stages of CD evolution, i.e., before the carbonization phase. First, we performed a detailed QM investigation of the reaction between two very common precursors – CA and EDA – in an aqueous environment as a prototypical system leading to the formation of molecular fluorophores (predominantly IPCA) and oligomeric condensates which can further grow and aggregate, thus forming nucleation sites for later stages of CD formation. The QM analysis revealed that (i) condensation reactions preferentially proceed via contacts of neutral groups which are however much less abundant than charged ends under weakly acidic conditions, thus opening cyclization pathways; (ii) the formation of a 5-membered ring intermediate is kinetically more favourable than the 6-membered cyclization pathway; nevertheless, the latter path becomes dominant at elevated temperatures (>210 °C) due to high thermodynamic stability of IPCA; and (iii) the barriers for condensation of charged ends and the formation of IPCA are comparable; thus the polymerization and MF formation become competitive processes at higher temperatures. Importantly, water molecules surrounding the reaction sites play a crucial role in mediating proton transfers as well as dehydration steps. Reaction mixtures at early phases of the reaction between CA and EDA were analysed by NMR spectroscopy and MALDI-TOF spectrometry, unambiguously confirming the preferential formation of the 5-membered ring intermediate at lower temperatures, while higher amounts of IPCA and unspecified oligomers or polymers were observed at higher temperatures. To gain a deeper mechanistic insight into the cyclization and polymerization reactions, reactive MD simulations were performed. In line with the static QM picture and experimental data, low-mass molecular products formed in the first (fast) phase predominantly comprised 5-membered ring intermediates along with short (dimeric/trimeric) condensates of CA and EDA. The 6-membered ring species were formed to much smaller extent and only when the reaction probabilities of cyclization reactions were scaled up to mimic higher temperature conditions and longer reaction times. The reactive MD simulations of the second (slow) phase allowing for the reactions of charged ends revealed the formation of various oligomers with incorporated cyclic structures and IPCA moieties.

To sum up, the combination of QM calculations, experimental measurements, and reactive MD simulations enabled us to unravel the reaction mechanism in the early stages of CD formation from CA and EDA precursors, determine the rate limiting steps for the cyclization and polymerization pathways, and put forward plausible oligomeric structures forming a base for polymeric CDs. The latter can be used for further analysis of optical properties of this important class of CDs and also as a starting point for modelling later stages of CD formation such as aggregation and carbonization, which are the scope of our follow-up studies.

Author contributions

Conceptualization: MP, JN, CMC, RZ, ALR, MM, and MO; data curation: DR, MP, JN, ZB, and LZ; funding acquisition: RZ, ALR, MM, JN, and MO; investigation: MP, JN, DR, JF, MS, PZ, MPal, ChO, FM, AC, ZB, and LZ; methodology and supervision: CMC, FM, MM, and MO; visualization: MP, JN, DR, LZ, and MM; writing – original draft: MP, JN, DR, MPal, LZ, MM, and MO; writing – review and editing: MP, JN, FM, CMC, LZ, RZ, ALR, MM, and MO.

Data availability

The data that support the findings of this study are openly available on Zenodo at https://zenodo.org/records/14856824.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the project “Experimental and theoretical studies of near-infrared-emitting and chiral carbon dot luminophores” from the Moravian-Silesian Region, contract no. 00734/2023/RRC, and by the ERDF/ESF project TECHSCALE (No. CZ.02.01.01/00/22_008/0004587). M. M. and J. F. acknowledge the support of the Slovak Research and Development Agency (APVV-20-0098). J. N. acknowledges the funding by the EU NextGenerationEU through the Recovery and Resilience Plan for Slovakia under the project No. 09I03-03-V04-00428. The COST Action CA21101 is also acknowledged. This work was also supported by the Ministry of Education, Youth and Sports of the Czech Republic through the e-INFRA CZ (ID: 90254). This article has been also produced with the financial support of the European Union under the REFRESH – Research Excellence For Region Sustainability and High-tech Industries project number CZ.10.03.01/00/22_003/0000048 via the Operational Programme Just Transition. L. Z. also acknowledges Project APPROACH no. 101120397.

References

1. J. Liu, R. Li and B. Yang, ACS Cent. Sci., 2020, 6, 2179–2195.
2. D. Ozyurt, M. Al Kobaisi, R. K. Hocking and B. Fox, Carbon Trends, 2023, 12, 100276.
3. A. Döring, E. Ushakova and A. L. Rogach, Light: Sci. Appl., 2022, 11, 75.
4. M. Behi, L. Gholami, S. Naficy, S. Palomba and F. Dehghani, Nanoscale Adv., 2022, 4, 353–376.
5. W. Su, H. Wu, H. Xu, Y. Zhang, Y. Li, X. Li and L. Fan, Mater. Chem. Front., 2020, 4, 821–836.
6. G. Ragazzon, A. Cadranel, E. V. Ushakova, Y. Wang, D. M. Guldi, A. L. Rogach, N. A. Kotov and M. Prato, Chem, 2021, 7, 606–628.
7. B. Wang and S. Lu, Matter, 2022, 5, 110–149.
8. Y. Yu, Q. Zeng, S. Tao, C. Xia, C. Liu, P. Liu and B. Yang, Adv. Sci., 2023, 10, 2207621.
9. H. Liu, X. Zhong, Q. Pan, Y. Zhang, W. Deng, G. Zou, H. Hou and X. Ji, Coord. Chem. Rev., 2024, 498, 215468.
10. L. Đorđević, F. Arcudi, M. Cacioppo and M. Prato, Nat. Nanotechnol., 2022, 17, 112–130.
11. C. Xia, S. Zhu, T. Feng, M. Yang and B. Yang, Adv. Sci., 2019, 6, 1901316.
12. S. Zhu, Y. Song, X. Zhao, J. Shao, J. Zhang and B. Yang, Nano Res., 2015, 8, 355–381.
13. W. Liang, S. K. Sonkar, D. Saini, K. Sheriff, B. Singh, L. Yang, P. Wang and Y. Sun, Small, 2023, 19, 2206680.
14. F. Ehrat, S. Bhattacharyya, J. Schneider, A. Löf, R. Wyrwich, A. L. Rogach, J. K. Stolarczyk, A. S. Urban and J. Feldmann, Nano Lett., 2017, 17, 7710–7716.
15. J. Schneider, C. J. Reckmeier, Y. Xiong, M. von Seckendorff, A. S. Susha, P. Kasák and A. L. Rogach, J. Phys. Chem. C, 2017, 121, 2014–2022.
16. W. Kasprzyk, T. Świergosz, S. Bednarz, K. Walas, N. V. Bashmakova and D. Bogdał, Nanoscale, 2018, 10, 13889–13894.
17. D. Qu and Z. Sun, Mater. Chem. Front., 2020, 4, 400–420.
18. Y. Xiong, J. Schneider, E. V. Ushakova and A. L. Rogach, Nano Today, 2018, 23, 124–139.
19. J. B. Essner, J. A. Kist, L. Polo-Parada and G. A. Baker, Chem. Mater., 2018, 30, 1878–1887.
20. B. Bartolomei, A. Bogo, F. Amato, G. Ragazzon and M. Prato, Angew. Chem., Int. Ed., 2022, 61, e202200038.
21. Q. Zhang, R. Wang, B. Feng, X. Zhong and K. Ostrikov, Nat. Commun., 2021, 12, 6856.
22. S. Kalytchuk, L. Zdražil, Z. Bad'ura, M. Medved’, M. Langer, M. Paloncýová, G. Zoppellaro, S. V. Kershaw, A. L. Rogach, M. Otyepka and R. Zbořil, ACS Nano, 2021, 15, 6582–6593.
23. L. Zdražil, Z. Baďura, M. Langer, S. Kalytchuk, D. Panáček, M. Scheibe, Š. Kment, H. Kmentová, M. A. Thottappali, E. Mohammadi, M. Medveď, A. Bakandritsos, G. Zoppellaro, R. Zbořil and M. Otyepka, Small, 2023, 19, 2206587.
24. D. Hagmeyer, J. Ruesing, T. Fenske, H.-W. Klein, C. Schmuck, W. Schrader, M. E. M. da Piedade and M. Epple, RSC Adv., 2012, 2, 4690.
25. S. Khan, A. Sharma, S. Ghoshal, S. Jain, M. K. Hazra and C. K. Nandi, Chem. Sci., 2018, 9, 175–180.
26. M. Righetto, F. Carraro, A. Privitera, G. Marafon, A. Moretto and C. Ferrante, J. Phys. Chem. C, 2020, 124, 22314–22320.
27. M. Langer, M. Paloncýová, M. Medveď, M. Pykal, D. Nachtigallová, B. Shi, A. J. A. Aquino, H. Lischka and M. Otyepka, Appl. Mater. Today, 2021, 22, 100924.
28. F. Mocci, L. de Villiers Engelbrecht, C. Olla, A. Cappai, M. F. Casula, C. Melis, L. Stagi, A. Laaksonen and C. M. Carbonaro, Chem. Rev., 2022, 122, 13709–13799.
29. A. T. Sheardy, D. M. Arvapalli and J. Wei, J. Phys. Chem. C, 2020, 124, 4684–4692.
30. E. V. Kundelev, N. V. Tepliakov, M. Y. Leonov, V. G. Maslov, A. V. Baranov, A. V. Fedorov, I. D. Rukhlenko and A. L. Rogach, J. Phys. Chem. Lett., 2019, 10, 5111–5116.
31. S. Wang, I. S. Cole, D. Zhao and Q. Li, Nanoscale, 2016, 8, 7449–7458.
32. S. Lu, R. Cong, S. Zhu, X. Zhao, J. Liu, J. S. Tse, S. Meng and B. Yang, ACS Appl. Mater. Interfaces, 2016, 8, 4062–4068.
33. M. Langer, M. Paloncýová, M. Medved’ and M. Otyepka, J. Phys. Chem. Lett., 2020, 11, 8252–8258.
34. V. Strauss, J. T. Margraf, C. Dolle, B. Butz, T. J. Nacken, J. Walter, W. Bauer, W. Peukert, E. Spiecker, T. Clark and D. M. Guldi, J. Am. Chem. Soc., 2014, 136, 17308–17316.
35. P. Elvati, E. Baumeister and A. Violi, RSC Adv., 2017, 7, 17704–17710.
36. L. Vallan, E. P. Urriolabeitia, F. Ruipérez, J. M. Matxain, R. Canton-Vitoria, N. Tagmatarchis, A. M. Benito and W. K. Maser, J. Am. Chem. Soc., 2018, 140, 12862–12869.
37. J. T. Margraf, V. Strauss, D. M. Guldi and T. Clark, J. Phys. Chem. B, 2015, 119, 7258–7265.
38. Y. Song, S. Zhu, S. Zhang, Y. Fu, L. Wang, X. Zhao and B. Yang, J. Mater. Chem. C, 2015, 3, 5976–5984.
39. F. Rigodanza, M. Burian, F. Arcudi, L. Đorđević, H. Amenitsch and M. Prato, Nat. Commun., 2021, 12, 2640.
40. B. Jana, Y. Reva, T. Scharl, V. Strauss, A. Cadranel and D. M. Guldi, J. Am. Chem. Soc., 2021, 143, 20122–20132.
41. L. Zdražil, D. Panáček, V. Šedajová, Z. Baďura, M. Langer, M. Medveď, M. Paloncýová, M. Scheibe, S. Kalytchuk, G. Zoppellaro, Š. Kment, A. Cadranel, A. Bakandritsos, D. M. Guldi, M. Otyepka and R. Zbořil, Adv. Opt. Mater., 2023, 11, 2300750.
42. F. Yuan, Y.-K. Wang, G. Sharma, Y. Dong, X. Zheng, P. Li, A. Johnston, G. Bappi, J. Z. Fan, H. Kung, B. Chen, M. I. Saidaminov, K. Singh, O. Voznyy, O. M. Bakr, Z.-H. Lu and E. H. Sargent, Nat. Photonics, 2020, 14, 171–176.
43. S. Kalytchuk, Y. Wang, K. Poláková and R. Zbořil, ACS Appl. Mater. Interfaces, 2018, 10, 29902–29908.
44. D. Li, P. Jing, L. Sun, Y. An, X. Shan, X. Lu, D. Zhou, D. Han, D. Shen, Y. Zhai, S. Qu, R. Zbořil and A. L. Rogach, Adv. Mater., 2018, 30, 1705913.
45. CRC handbook of chemistry and physics, ed. W. M. Haynes, CRC Press, 96th edn, 2015.
46. C. Chumsae, L. L. Zhou, Y. Shen, J. Wohlgemuth, E. Fung, R. Burton, C. Radziejewski and Z. S. Zhou, Anal. Chem., 2014, 86, 8932–8936.
47. R. A. Poole, P. T. Kasper and W. Jiskoot, J. Pharm. Sci., 2011, 100, 3018–3022.
48. A. J. Repta and T. Higuchi, J. Pharm. Sci., 1969, 58, 1110–1114.
49. M. T. Albelda, M. I. Burguete, J. C. Frías, E. García-España, S. V. Luis, J. F. Miravet and M. Querol, J. Org. Chem., 2001, 66, 7505–7510.
50. R. Weaver and I. H. Gilbert, Tetrahedron, 1997, 53, 5537–5562.
51. J. R. Gissinger, B. D. Jensen and K. E. Wise, Macromolecules, 2020, 53, 9953–9961.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr04420g

‡ These authors contributed equally to this work.

---