Open Access Article
Open Access ArticleAtomistic modelling of electron beam induced structural transformations in deposited metal clusters†
Ioannis
Bounas
ab,
Alexey V.
Verkhovtsev
 c,
Theodoros
Pavloudis
c,
Theodoros
Pavloudis
 abd,
Gennady B.
Sushko
c,
Joseph
Kioseoglou
abd,
Gennady B.
Sushko
c,
Joseph
Kioseoglou
 bd,
Richard E.
Palmer
bd,
Richard E.
Palmer
 *a and
Andrey V.
Solov'yov
c
*a and
Andrey V.
Solov'yov
c
aNanomaterials Lab, Mechanical Engineering, Swansea University, Bay Campus, Fabian Way, Swansea SA1 8EN, UK. E-mail: R.E.Palmer@Swansea.ac.uk
bSchool of Physics, Faculty of Sciences, Aristotle University of Thessaloniki, GR-54124 Thessaloniki, Greece
cMBN Research Center, Altenhöferallee 3, 60438 Frankfurt am Main, Germany
dCenter for Interdisciplinary Research and Innovation, Aristotle University of Thessaloniki, GR-57001, Thessaloniki, Greece
First published on 4th February 2025
Abstract
Structural transformations in gold clusters deposited on a graphite substrate induced by the focused electron beam of a scanning transmission electron microscope are investigated using the classical molecular dynamics (MD) approach. The particular case study concerns Au309 clusters softly deposited on few-layer graphite and exposed to a 300 keV electron beam. Two mechanisms of energy transfer to the cluster during the irradiation are considered: (i) through the relaxation of collective electronic excitations and (ii) through the momentum transfer by the energetic primary electrons. A relativistic MD approach implemented in the MBN Explorer software package is used to simulate the collisions of energetic primary electrons with cluster atoms and to evaluate the amount of energy transferred to the cluster for different collision geometries. Characteristic times for the occurrence of these energy deposition events are estimated for realistic experimental irradiation conditions. The MD simulations of the cluster dynamics after irradiation show that the cluster temperature decreases rapidly during the first few tens of picoseconds, and the cluster cools down to a temperature close to its initial temperature within several hundred picoseconds. This time period is comparable to the characteristic time between two successive energy transfer events induced by plasmon excitations in the deposited cluster. A large number of successive energy transfer events (on the order of ∼103–104) during irradiation can cumulatively lead to substantial heating of the deposited cluster and induce its structural transformations.
1 Introduction
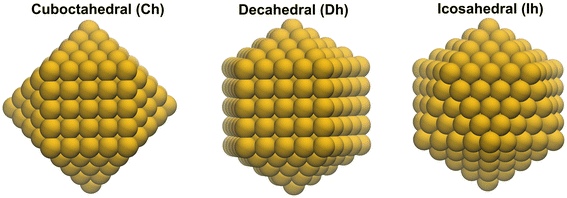
Structural transformations in free and deposited atomic clusters have been extensively studied over the last decades, see ref. 1–6 and references therein. Particular attention has been paid to the analysis of the structure and dynamics of clusters deposited or grown on surfaces using high-resolution electron microscopy.7–15 Scanning transmission electron microscopy (STEM) studies of size-selected gold clusters11,12 have revealed experimentally diverse structural transformations of the clusters after exposure to a high-energy electron beam.Previous STEM measurements of size-selected AuN clusters in the range N = 55–561 using a 200 keV electron beam have shown that, under ambient conditions, such cluster structures are often decahedral (Dh) or fcc in approximately equal proportions.16,17 However, recent STEM measurements of gold clusters of a similar size range at a beam current of 300 keV have led to different observations.18,19 For instance, for a Au309 cluster, the Dh fraction of atoms was found to be the most common ordered structure, with the remainder being fcc cuboctahedral (Ch) or icosahedral (Ih) structures18,19 (see the corresponding cluster structures in Fig. 1). It has been suggested that the thermal effects of higher beam currents may be significant, allowing the cluster to reach different temperatures. The recent study18 reported for the first time the observation of transitions between the competing structures for small metallic clusters, specifically for Au309. Analysis of the experimental results concluded that it is easier to transition between Dh and Ih structures than from one of these structures to an fcc structure.
A recent paper15 presented a theoretical and computational analysis of the physical mechanisms behind the electron beam-induced structural transformations of deposited metallic clusters, considering an Au923 cluster irradiated by a 200 keV electron beam as a case study. According to this study, the shape of the deposited cluster depends on the amount of energy transferred to the cluster by the energetic primary electrons and secondary electrons emitted from the substrate. Two mechanisms of energy transfer into the deposited clusters were considered in ref. 15, namely, elastic scattering of fast projectile electrons from cluster atoms (without excitation of the electronic subsystem of the cluster) and an inelastic scattering mechanism due to the relaxation of plasmon-type collective electronic excitations formed in the clusters.
This paper extends the analysis of the physical mechanisms contributing to electron beam-induced transformations in deposited metal clusters. In this paper, the structural transformations of a deposited Au309 cluster induced by irradiation with a 300 keV electron beam are explored in connection to the recent STEM experiments.18,19 The cluster softly deposited on a few-layer graphite substrate is considered as a case study. Following ref. 15, we analyse two mechanisms of structural transformations caused by the relaxation of collective electronic excitations in the cluster and the localised energy transfer due to hard collisions with energetic projectile electrons. The rates and characteristic appearance times of these events are evaluated for the real STEM experimental conditions.
Beyond the scope of previous work,15 the relativistic molecular dynamics (MD) method20 implemented in the MBN Explorer software package21 is used to simulate the collisions of 300 keV electrons with atoms of the Au309 cluster and, on this basis, to evaluate the amount of energy transferred to the cluster atoms under different kinematic conditions. The classical MD simulations show that the Au309-Ih cluster transforms into a Dh-like structure after deposition on the substrate and undergoes a further transformation into an Ih-like structure due to the relaxation of the energy transferred to the cluster by the above-mentioned mechanisms. Finally, the evolution of the cluster temperature during the relaxation is analysed using classical MD. The simulations of the cluster dynamics after irradiation show that the cluster temperature decreases rapidly during the first ∼20 ps, and the cluster cools down to a temperature close to its initial temperature within several hundred picoseconds.
2 Computational methodology
Classical (non-relativistic) and relativistic MD simulations were performed using the MBN Explorer software package21 for multiscale simulations of the structure and dynamics of various Meso-Bio-Nano (MBN) systems.22 The simulation results were mainly analysed using a multitasking toolkit MBN Studio.23 Some parts of the analysis presented in this study were performed using the OVITO software (OVITO Basic, version 3.10.6).242.1 Clusters and substrate: creation of the system
The Ih, Dh and Ch structural isomers of the Au309 cluster shown in Fig. 1 were constructed using the Atomic Simulation Environment (ASE) software package.25 The substrate, consisting of three stacked graphene layers, was created using the built-in modeller tool of MBN Studio.23 Each graphene layer has a size of 85.08 Å × 83.504 Å, and the distance between adjacent layers is set equal to 3.35 Å, corresponding to the interplanar distance in graphite.The many-body Gupta potential26,27 was used to describe the interactions between the Au atoms. The bonded interactions between C atoms within each layer were described by the Brenner potential,28 while the Lennard-Jones potential with the parameters from ref. 29 was used to describe the van der Waals interactions between the graphene layers. The interaction between the gold and carbon atoms was also described by the Lennard-Jones potential with the parameters derived in ref. 30. The free clusters and the substrate were structurally optimised using the velocity quenching optimisation method with a time step of 1 fs. After optimisation, each object was thermalised at 300 K for 1 ns using a Langevin thermostat and a damping time of 200 fs. Five independent NVT simulations have been performed to reflect the statistical nature of the initial state of the clusters.
2.2 MD simulations of cluster deposition
A simulation box of 85.08 × 83.504 × 80 Å3 was used for the MD simulations of cluster deposition. The cluster was placed above the geometric centre of the substrate, approximately 20 Å above the top graphite layer, to avoid the interaction of the cluster atoms with the substrate. The cluster was deposited onto the graphite surface at normal incidence, and the deposition energy was set equal to 0.06 eV per atom, which is the cluster deposition energy used in the corresponding experiments by the Swansea team (see the ESI, Table S1†).The simulations were performed in the NVE microcanonical ensemble with the initial velocity distributions taken from the preceding thermalisation simulations. The z-component of the velocity of each cluster atom was modified according to the chosen deposition energy. The simulation time was set to 1 ns, which is long enough to simulate the deposition of the Au309 cluster and its relaxation on the surface. After that, the system (i.e. the deposited cluster and the substrate) was thermalised at 300 K for 200 ps.
2.3 Relativistic MD simulations of electron scattering from the cluster atoms
The elastic scattering of a 300 keV electron from atoms of the deposited Au309 cluster was simulated using the relativistic MD method20 implemented in MBN Explorer.21 This method is based on the solution of the two coupled relativistic equations of motion for a fast projectile of charge q and mass m: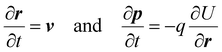 | (1) |
Here, r(t), ν(t) and p(t) = mγν(t) are the position vector, velocity, and momentum of the projectile electron at instant t, respectively, γ = (1 − ν2/c2)−1/2 = ε/mc2 is the relativistic Lorentz factor of a projectile, with ε and m being, respectively, its energy and mass, and c is the speed of light.
For the numerical solution of the nonlinear relativistic equations of motion (1), MBN Explorer uses a specially designed relativistic integrator,20 which employs the 4th-order Runge–Kutta scheme with an adaptive integration time step. The details of this implementation are given in ref. 20 and are briefly described below.
To maintain the accuracy of the calculations, energy conservation is checked at each step of the calculations. If the relative difference of the total system's energy is greater than a predefined threshold, the simulation step is repeated with a time step reduced by a factor of two. This procedure continues until either the desired accuracy is achieved, or the step size reaches its minimum allowable value. This computational approach has been successfully used to simulate the propagation of ultra-relativistic projectiles (electrons, positrons and pions) through linear, bent and periodically bent crystals, radiation emission and related phenomena, as described in detail in monographs31,32 and review papers.33,34 The relativistic MD approach has also been discussed in the recent roadmap paper35 in the context of the computational multiscale modelling approach to study the behaviour of condensed matter systems exposed to radiation.
In eqn (1), U = U(r) is the electrostatic potential acting on the projectile by the atoms of the medium (in this case, the gold cluster). This potential is expressed as the sum of the potentials Uat of individual atoms:
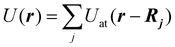 | (2) |
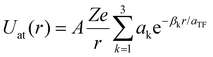 | (3) |
As described above, the relativistic MD approach in MBN Explorer has been widely used to model the channelling of ultra-relativistic projectiles and photon emission in oriented crystals (see ref. 20, 22 and 31–34 and references therein). In this study, this approach is used to simulate the collisions of an energetic 300 keV projectile from a focused electron beam of an electron microscope with the deposited gold cluster.
For the simulations of the electron–gold atom collision, an electron was introduced into the simulation box at a distance of 6 Å from the target gold atom. The initial x and y coordinates of the electron matched those of the target atom. The electron was then displaced along the x and y axes to simulate the collision for different values of the impact parameter b in the range from 0.003 to 0.03 Å. The velocity of the projectile electron at 300 keV was calculated to be ν ≈ 2327.95374 Å fs−1, corresponding to ν ≈ 0.78c.
The relativistic adaptive integration algorithm20,22 with a time step of 10−9 fs was used to ensure the conservation of the total energy of the system. Due to the short time of the electron-gold atom collision, this process was simulated for 0.01 fs. The ionic motion was taken into account by considering all gold atoms as moving objects. Thus, the momentum transfer during the elastic scattering of an energetic primary beam electron from the cluster atoms (i.e. without exciting the electronic subsystem of the cluster) was explicitly simulated.
The chosen simulation parameters were validated by simulating the collision of an electron with a single gold atom. The validated parameters were then used in the second set of simulations, in which the electron was targeted to different atoms on the surface of the gold cluster; see section 3.3 for further details.
2.4 MD simulations of post-irradiation relaxation of deposited clusters
As described in section 2.2, the thermalised geometries of the deposited cluster and the substrate were obtained at the end of the NVT simulations performed at 300 K. These geometries were used as input for the subsequent classical MD simulations of the structural relaxation of the cluster due to the two energy transfer mechanisms that take place when the cluster is irradiated by an energetic electron beam. The results of these simulations are presented in section 3.4, while the corresponding parameters for each of the considered energy transfer mechanisms are evaluated in sections 3.2 and 3.3.The classical MD approach allows the study of the dynamics of systems consisting of 103–105 atoms on a nanosecond time scale and has therefore been used in this study to simulate the post-irradiation relaxation dynamics of the deposited gold cluster. More elaborated computational methods, such as ab initio MD, are limited by their inherent complexity both in terms of system size (typically on the order of tens to several hundred atoms) and simulation time (typically, several tens of picoseconds). More details on the these and many other theoretical and computational methods for studying the behaviour of condensed matter systems exposed to radiation, as well as their areas of application and their limitations, can be found in the recent roadmap paper.35
In this study, the final velocity distribution for all the atoms in the system, corresponding to the temperature of 300 K, was used as input for the simulations described in section 3.4. Then, depending on the energy relaxation mechanism considered, either the velocity of a given gold atom or the velocities of all atoms of the Au309 cluster were increased with respect to the equilibrium velocities corresponding to 300 K. The initial velocities of the carbon atoms of the substrate were not changed and corresponded to the temperature of 300 K.
The simulations were performed for 1 ns with a time step of 1 fs. The velocities of the cluster atoms were recorded and used to calculate the instantaneous temperature of the cluster at different simulation steps.
2.5 Analysis of irradiation conditions
In this study, irradiation parameters corresponding to recent STEM experiments on deposited Au309 clusters18,19 have been used to evaluate the probabilities of the energy transfer events to the deposited cluster that can contribute to electron beam-induced structural transformations of the cluster. Two mechanisms of energy transfer to the cluster are considered: (i) the relaxation of collective electronic excitations by the vibrational excitation of cluster atoms and (ii) the elastic backscattering of fast projectile electrons from cluster atoms. In this section, we briefly analyse some of the irradiation parameters relevant to the analysis presented below in section 3. The complete set of irradiation parameters used in this analysis is given in the ESI, Table S1.†In STEM experiments, images are built up pixel by pixel by raster scanning the focused electron beam across a fixed field of view. In this analysis, the beam width is l = 50 pm and each pixel has an area of S = l2 = 2.5 × 10−3 nm2. Each individual pixel is exposed to the primary electron beam for a dwell time tdw = 20 μs.
The flux density of primary electrons hitting a pixel of the field of view is given by:
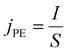 | (4) |
The interaction of the primary electrons with the substrate (in our case, made of carbon) leads to the emission of low-energy secondary electrons with a characteristic energy of ∼101–102 eV. The number of secondary electrons emitted from the substrate can be estimated using a semi-empirical model introduced in ref. 37 (see also ref. 15). For a 300 keV electron beam, the number of secondary electrons emitted from a carbon substrate is NSE ≈ 0.018NPE. This means that, on average, one secondary electron is produced by the substrate for every ∼56 primary beam electrons hitting a pixel area. Accordingly, the flux density of secondary electrons is 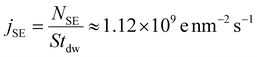 .
.
The acquisition time of one frame in the reference STEM experiments is equal to 2.65 s, during which a field of view with a total surface area of 326.89 nm2 is scanned (see Table S1†). Assuming that the deposited cluster has a semi-spheroidal shape, its contact radius (i.e. the radius of the lower part of the cluster in contact with the substrate) can be estimated38 by the formula R = rs (2N)1/3, where rs ≈ 1.592 Å is the Wigner–Seitz radius for gold39 and N = 309 is the number of atoms in the cluster. The contact area of the Au309 cluster is then equal to Scl = πR2 ≈ 5.78 nm2, which is ∼60 times smaller than the considered field of view area. By comparing these two values, one can evaluate the time period during which the cluster is irradiated per frame of STEM measurements, t ∼ 46.8 ms.
3 Results and discussion
3.1 Characterisation of the Au309 cluster deposited on graphite
Structural changes in the Au309 clusters during the deposition process were characterised by calculating the radial distribution function (RDF) for cluster atoms using the built-in analysis tool of MBN Studio23 and by performing structural analysis using the Common Neighbour Analysis (CNA) method implemented in the OVITO software.24,40 Five independent runs were carried out for the deposition of each Au309 isomer and the studied characteristics were averaged over the performed runs.The CNA is a widely used algorithm for characterising the local structural environment in crystalline systems. The local atomistic environment is characterised by determining and analysing all neighbouring atoms located within a given cutoff distance around a selected atom.41 The common neighbours of each atom pair are characterised by a set of indices (jkl), where j is the number of neighbours common to both atoms, k is the number of bonds between common neighbours, and l is the number of bonds in the longest chain among the common neighbours. Based on the known number of indices for ideal fcc, hcp, and bcc structures, the CNA method assigns atoms in the considered system to belong to one of the mentioned lattice structures or to none of them.40–42
In this study, we have used the so-called interval CNA (i-CNA) method,43 which considers an interval of cutoff distances instead of a fixed value of the cutoff distance as done in the conventional CNA method. The i-CNA method implemented in OVITO is known to provide a better structure recognition in local environments with larger atomic perturbations (e.g. at elevated temperatures) as compared to conventional CNA.43
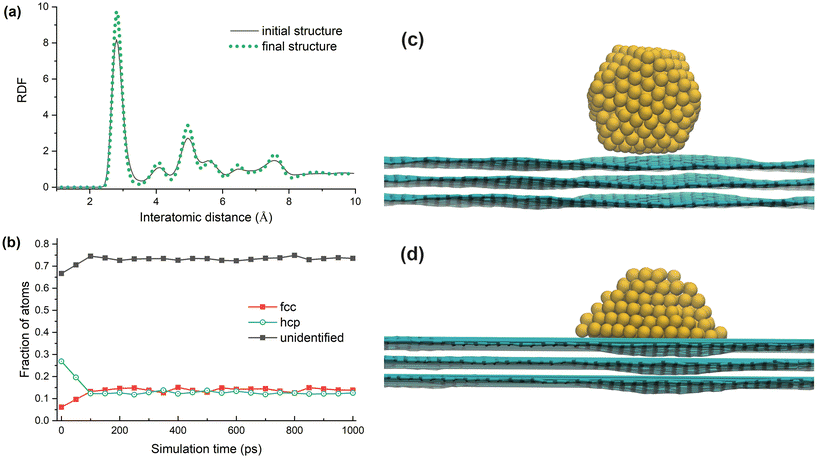
Fig. 2(a) shows the RDF for the Au309-Ih cluster before the deposition (thermalised at 300 K; solid black curve) and after the deposition and relaxation for 1 ns (dotted green curve). By definition, the RDF characterises the number of atoms at a given radial distance from a given atom, and the function is then calculated with respect to different atoms in the considered system (in this case, all cluster atoms). The RDF analysis indicates that the cluster structure has changed after the deposition, as shown by the variation of the peaks in the RDF in the range of interatomic distances from ∼4 to 8 Å.
Fig. 2(c) and (d) show simulation snapshots corresponding to the deposition of the Ih-Au309 isomer on the few-layer graphite substrate. The collision-induced deformation of the initial cluster structure occurs at the moment when the cluster hits the surface (see Fig. 2(c)). After the deposition, the cluster relaxes on the surface, and its structure transforms into that shown in Fig. 2(d). Similar collision-induced rearrangements have been studied by classical MD simulations for metal clusters and small nanoparticles softly landed on a few-layer graphite and MgO substrates.30,44
Results for the Au309-Ih isomer obtained using the i-CNA method are shown in Fig. 2(b). The CNA algorithm only identifies the atoms in the core of the cluster as crystalline. The 198 atoms of the outer layer lack the required number of neighbours and are therefore characterised as unidentified (non-crystalline). Thus, the CNA algorithm identifies only 111 atoms in the core of the free Au309-Ih cluster (see Fig. 1) as belonging to hcp and fcc lattices. In Fig. 2(b), the fraction of atoms assigned to the fcc and hcp lattices at the beginning of the simulation (∼0.06 and 0.27, respectively) corresponds to the optimised Ih cluster structure.
During the first 100 ps of the simulation, after the cluster has landed on the surface, the fractions of atoms belonging to fcc and hcp structures change visibly (see Fig. 2(b)). At the end of the 1 ns-long MD simulation of cluster relaxation, the cluster, which initially has the Ih structure, has ∼13% of atoms assigned to fcc and hcp lattice structures (i.e. about 40 atoms of each lattice type), while the remaining ∼74% of atoms are not assigned to any particular lattice structure. Approximately equal fractions of atoms locally arranged in the fcc and hcp lattices are characteristic of a Dh cluster structure, indicating that the Ih cluster has been transformed into a Dh-like structure as a result of the collision with the surface. Similar fractions of atoms assigned to fcc and hcp lattice structures (∼11–14%) were obtained in this study after the deposition of Dh and Ch Au309 isomers shown in Fig. 1.
The validity of the results obtained by the i-CNA method was checked by performing a similar analysis using the polyhedral template matching (PTM) method,45 also available in OVITO. The PTM method also allows the identification of lattice structures according to the topology of the local atomic environment. The comparison of the fractions of atoms of the Au309 cluster belonging to fcc and hcp lattices, as determined by the i-CNA and PTM methods, is presented in Table S2.†
It should be noted that more advanced CNA-based methods have been developed,46 which allow to go beyond the capabilities of the CNA method implemented in OVITO and to analyse other signatures e.g. related to the presence of 5-fold symmetry axes, fcc stacking faults or hcp stacking. Such features have been analysed for free metal clusters,46,47 but such an analysis for more distorted cluster geometries due to the presence of the substrate is beyond the scope of this study.
3.2 Energy transfer to the deposited cluster: plasmon excitations
In this section, we evaluate the energy transferred to the deposited cluster due to the relaxation of collective electron excitations formed in the cluster exposed to 300 keV primary electrons and low-energy secondary electrons emitted from the substrate. The analysis was performed following the methodology described in ref. 15.The contribution of the plasmon excitations to the singly differential inelastic scattering cross section, dσpl/dΔε, for an Au309 cluster as a function of the energy loss Δε of the incident electron is given by:48,49
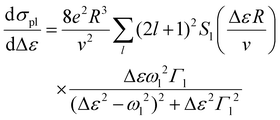 | (5) |
Here,
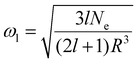 | (6) |
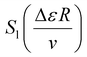 in eqn (5) reads as
in eqn (5) reads as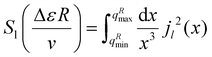 | (7) |
When calculating the plasmon resonance frequency using eqn (6), it is assumed that one valence (6s) electron from each cluster atom is delocalised over the whole cluster and involved in the formation of the plasmon excitation. This assumption follows from the previous studies of the dipole polarizability50 and the photoabsorption spectra51 of several three-dimensional gold clusters using static and time-dependent density functional theory. In both cited studies, it was concluded that about 1–1.5 electrons from each gold atom contribute to the linear response to an external field, indicating a low degree of delocalisation of the valence 5d electrons.
The singly differential inelastic scattering cross section dσpl/dΔε for an Au309 cluster was calculated as a function of the energy loss of the incident electron. Fig. 3 shows the cross sections calculated for three cases of low-energy electron impact (30, 50 and 100 eV), corresponding to secondary electrons emitted by the carbon substrate, as well as the primary 300 keV projectile electron. Fig. 3 shows that the maximum value of the cross section, attributed to the 30 eV secondary electrons, is larger by about three orders of magnitude than the corresponding value for the 300 keV primary electrons.
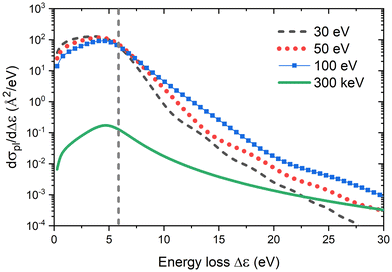 | ||
| Fig. 3 Contribution of the plasmon excitations to the singly differential cross section dσpl/dΔε for an Au309 cluster irradiated with electrons of specific energy as a function of their energy loss Δε. The vertical dashed line shows the ionisation potential of the Au309 cluster, Ip ≈ 5.87 eV, evaluated according to ref. 52 and 53. | ||
The maximum of the cross section dσpl/dΔε for an Au309 cluster is located at the energy loss values below the ionisation potential of the cluster, Ip ≈ 5.87 eV (see the vertical dashed line in Fig. 3). Therefore, plasmon excitations in the cluster with the excitation energies Δε < Ip will decay, with a significant probability, through the vibrational excitation of its ionic subsystem due to the electron–phonon coupling mechanism.54
The average excitation energy of the cluster is calculated as follows:
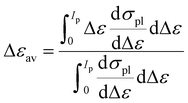 | (8) |
The characteristic average energy transferred to the Au309 cluster by electrons of different kinetic energies is plotted in Fig. 4. It shows a monotonic increase of the average energy transfer as the projectile electron's kinetic energy increases, and it tends to saturate at electron energies of ∼105 eV. As a result of the relaxation of a plasmon excitation induced by a secondary electron with a typical energy of 30 eV, the energy Δεav ∼ 3.20 eV is transferred to the vibrational motion of the cluster. For a 300 keV primary electron, the corresponding amount of energy is equal to Δεav ∼ 3.95 eV.
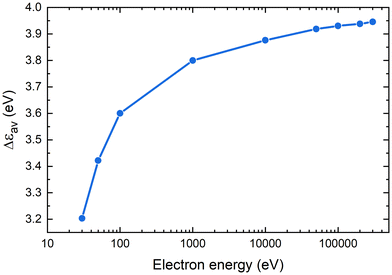 | ||
| Fig. 4 The average amount of energy Δεav transferred to the Au309 cluster below its ionisation potential by an electron of a specific incidence energy. | ||
Many successive plasmon excitations will be formed in the deposited Au309 cluster during the time the cluster is exposed to the electron beam of a STEM. The rate (probability per unit time) of inducing a plasmon excitation in the Au309 cluster by a projectile electron (either primary or secondary) that results in the transfer of an amount of energy below the ionisation potential (i.e. in heating of the cluster) is calculated as follows:
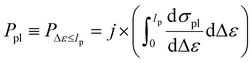 | (9) |
The calculated rates are equal to Ppl ≈ 0.35 ns−1 for a 300 keV primary electron (with the flux density j = jPE estimated in section 2.5) and Ppl ≈ 2.86 ns−1 for a 30 eV secondary electron (with the flux density j = jSE, see section 2.5). An inverse of these rates defines the characteristic time, τpl = 1/Ppl, for the occurrence of two such successive events induced by a 300 keV or 30 eV electrons, respectively. These times are equal to ∼0.35 ns for a 30 eV electron and ∼2.86 ns for a 300 keV electron.
The number of plasmon excitations formed during the dwell time of the electron beam on a single pixel (tdw = 20 μs) is 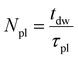 . During the irradiation of one pixel, ∼7.0 × 103 plasmon excitations by 300 keV primary beam electrons and ∼5.7 × 104 excitations by 30 eV secondary electrons will transfer the amount of energy Δεav ∼ 3.95 eV and 3.20 eV, respectively, to the Au309 cluster.
. During the irradiation of one pixel, ∼7.0 × 103 plasmon excitations by 300 keV primary beam electrons and ∼5.7 × 104 excitations by 30 eV secondary electrons will transfer the amount of energy Δεav ∼ 3.95 eV and 3.20 eV, respectively, to the Au309 cluster.
3.3. Energy transfer to the deposited cluster: elastic scattering of primary beam electrons
An energetic primary beam electron elastically scattering from atoms of a deposited gold cluster can transfer momentum to the cluster atoms without exciting the electronic subsystem of the cluster.55 In this work, the process of energy and momentum transfer to the Au309 cluster by primary 300 keV electrons was studied with taking into account relativistic kinematics. The elastic scattering of a 300 keV electron from the cluster was simulated using the relativistic MD approach,20 as described in section 2.3. In the simulations, the electron was targeted to different gold atoms located on the surface of the deposited Au309 cluster. Surface atoms close to the centre of the cluster, the cluster edge, and in between these two regions were selected as targets. As described in section 2.3, the initial position of the electron with respect to each target atom was varied to explore the range of impact parameter values b = 0.003–0.03 Å.The maximum energy transferred to the target atom as a result of a head-on collision (corresponding to the scattering angle θ = 180°) of a relativistic electron with a nucleus is given by:56
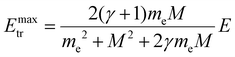 | (10) |
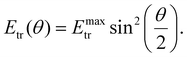 | (11) |
Fig. 5 shows the dependence of the energy Etr transferred to the gold atom on the impact parameter b and the scattering angle θ, obtained from the relativistic MD simulations. The transferred energy decreases rapidly as the impact parameter increases and the electron passes at a larger distance from the atomic nucleus. The increase of Etr with increasing the scattering angle indicates that electrons scattered in the backward direction induce a significant transfer of energy and momentum. The simulation results show that the maximum amount of energy transferred to the gold atom by a 300 keV electron in the head-on collision is Emaxtr ≈ 4.32 eV, in agreement with the analytical value given by eqn (10).
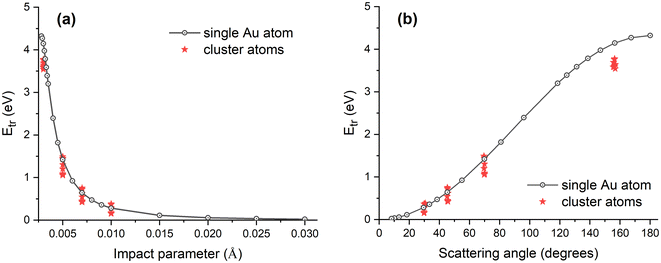 | ||
| Fig. 5 Energy transferred to a gold atom (either a free atom or an atom of the deposited Au309 cluster) as a function of the impact parameter (a) and scattering angle (b). For the cluster case, results are shown for several surface atoms close to the centre of the cluster, the cluster edge, and in between these two regions. The results have been obtained from the relativistic MD simulations using MBN Explorer.21 | ||
The average time between two consecutive primary electrons hitting a given pixel of the field of view can be estimated as:
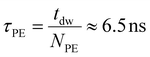 | (12) |
This value of τPE corresponds to the collision of primary electrons with gold atoms for all possible values of the impact parameter b. The probability of elastic electron scattering from the nucleus for impact parameters smaller than b is given by:
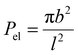 | (13) |
According to the simulation snapshot shown in Fig. 2(d), atoms in the deposited Au309 cluster can be considered to be aligned in columns at different orientations. It can be assumed that on average there are approximately three gold atoms in a column aligned with the electron beam. This increases the probability of energy transfer to the cluster due to the elastic scattering of a projectile electron at small values of the impact parameter. Thus, the number of events leading to a significant energy transfer during the dwell time is given by:
| Nel ≈ 3NPEPel | (14) |
This number is greater than 1 for the impact parameter values smaller than b = 0.003 Å, corresponding to an energy transfer Etr ∼ 4 eV (see Fig. 5(a)). For the impact parameter b = 0.003 Å, the number of events Nel ≈ 1.05 per dwell time for one pixel, suggesting that at least one close collision of a primary electron with a gold atom, leading to the large energy transfer of the order of several eV, takes place during the irradiation dwell time. The characteristic time between two such successive events is τel ≈ tdw/1.05 = 19.05 μs.
In the analysis presented above in this section and in section 3.2, the processes of energy transfer due to the vibrational excitation of the cluster by plasmon de-excitation and the localised energy transfer due to elastic scattering with the primary beam electrons have been considered independently. In reality, since ∼103–104 events of vibrational excitation of the whole cluster (see section 3.2) and at least one event of the localised energy transfer due to a head-on collision with one of the cluster atoms (see section 3.3 above) will occur during the dwell time, these events may occur simultaneously. In this case, the amount of energy transferred to the cluster will be the sum of the energy transferred by the plasmon excitation mechanism and the energy transferred by the head-on collision. Recalling that the ionisation potential of the Au309 cluster is Ip ≈ 5.87 eV, the maximum energy that can be deposited in the vibrational degrees of freedom of the cluster is about 6 eV.
3.4 Analysis of radiation-induced structural transformations and thermal effects
The relaxation of the cluster structure after the energy transfer by one of the above-described mechanisms was simulated by means of classical MD using MBN Explorer,21 following the procedure outlined in section 2.4.In the first set of simulations, the energy Δε = 3.20 eV was uniformly distributed throughout the cluster. This value corresponds to a characteristic energy deposited in the cluster due to a plasmon excitation, which will decay with a significant probability by the vibrational excitation of the ionic subsystem (see section 3.2).
Another set of five simulations was devoted to the relaxation of the cluster after localised energy transfer by a primary beam electron. In each simulation, one of the gold atoms located on the surface of the cluster was selected, and its velocity was rescaled to correspond to the energy transfer of 4 eV. As discussed in section 3.3, this amount of energy corresponds to the case of a close electron–atom collision at the small impact parameter b ∼ 0.003 Å.
Finally, the third set of simulations was devoted to the analysis of the correlated excitation events due to the simultaneous energy deposition in the cluster due to a plasmon excitation and localised energy transfer by the primary beam electron scattered at a small impact parameter. In this case, the velocities of all atoms in the cluster were rescaled to account for the uniform vibrational excitation due to the plasmon mechanism. An atom located at the cluster surface was then selected and its velocity rescaled so that the total energy transferred to the cluster was 6 eV.
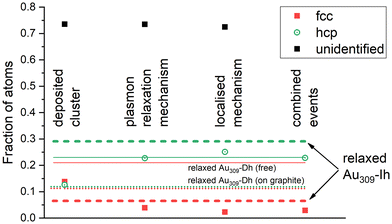
As described in section 2.4, in all cases, the dynamics of the system was simulated for 1 ns without a thermostat. The velocities of the cluster atoms were recorded and used to calculate the instantaneous temperature of the cluster at different simulation steps. Structural transformations of the cluster were analysed using the i-CNA algorithm, following a procedure similar to that discussed in section 3.1. The results of the performed simulations are summarised in Fig. 6. It shows the fraction of atoms corresponding to the two prevailing crystalline lattices (fcc and hcp) in the core of the deposited Au309 cluster after relaxation of the energy transferred to the cluster by the different mechanisms discussed in this study.
As discussed in section 3.1, after the soft deposition of the Au309-Ih cluster on the graphite substrate, the arrangement of atoms in the core of the cluster changes such that the fractions of atoms assigned to these two lattice structures are ∼12–14%, see Fig. 2(b) and Table S2.† A similarity in the fractions of atoms assigned to the fcc and hcp crystal lattices is indicative of a Dh-like structure (see thin solid and dotted lines in Fig. 6). After the vibrational excitation of the cluster by any of the mechanisms considered in the previous sections, a further structural transformation of the deposited cluster occurs. An indication of this transformation can be seen in Fig. 6 by an increase in the fraction of atoms assigned to the hcp lattice (up to 23–25%) with a simultaneous decrease in the corresponding fraction for atoms in the fcc lattice (to 2–4%). After the relaxation of the excess energy given to the cluster, the resulting local cluster structure (in terms of the fractions of atoms assigned to the fcc and hcp lattices) resembles that of the initial Au309-Ih structure, thermalised at 300 K (see the horizontal dashed lines). This indicates an irradiation-induced transformation from a Dh-like structure to an Ih-like structure. Snapshots of the Au309-Ih cluster after deposition and at the end of each post-irradiation energy relaxation simulation are presented in Fig. S1.†
The last part of this study is devoted to the analysis of the temporal evolution of the cluster temperature after the energy transfer events. As mentioned in section 1, the thermal effects of high beam currents in STEM experiments might be significant and responsible for the experimentally observed structural transformations of the clusters.18,19
Fig. 7 shows the temperature of the deposited Au309 cluster as a function of simulation time during a 1 ns-long MD simulation of cluster relaxation. The initial temperature of the cluster, equal to 296 K, is shown with a dashed red line. During the first 100 ps of the simulation, the instantaneous temperature was averaged over each 20 ps-long segment of the trajectory, while after 100 ps, the averaging was done for each 50 ps-long segment.
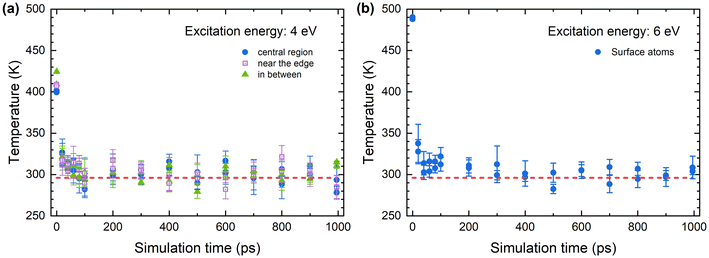 | ||
| Fig. 7 Instantaneous temperature of the deposited Au309 cluster as a function of simulation time for energy transferred to the cluster equal to 4 eV (a) and 6 eV (b). | ||
In the first set of simulations, six surface atoms located close to the cluster geometrical centre, at the edges and in between (two atoms of each type) were randomly selected. In each individual simulation, the selected atom was given an excess energy of 4 eV (see the discussion in section 3.3), and the calculated temperature values were averaged for each atom type. The results of these simulations are shown in Fig. 7(a). Due to the excess energy given to one of the cluster atoms, the temperature of the cluster rises to ∼400–420 K, which is high enough to induce a structural transformation, as shown in Fig. 6. Within the first 20 ps of the simulation, the cluster temperature decreases by ∼80–100 K, and the cluster cools down to the temperature close to its initial temperature within a period of ∼100 ps. An important conclusion from these simulations is the independence of the temperature variations from the location of the excited atom on the cluster surface. A similar analysis of the temperature variation of the graphite substrate indicates that the substrate temperature increases by 3–5 degrees due to heat transfer from the cluster.
Fig. 7(b) shows the results of a similar analysis for the case of a larger energy transfer of 6 eV to the cluster. As discussed at the end of section 3.3, this amount of energy represents the case of a correlated energy transfer event due to the two different mechanisms. For the sake of simplicity, it has been assumed that both events occur simultaneously, so that an excess energy of 6 eV is instantly given to the deposited cluster, causing a temperature increase of up to 490 K. Similar to the results shown in Fig. 7(a), there is a significant temperature drop during the first 20 ps. After the first 100 ps, the cluster temperature decreases to ∼315 K, which is higher than the initial temperature of the relaxed cluster of 296 K (see the dashed red line). During the rest of the simulation, the cluster temperature fluctuates by ±15 K around the initial temperature. Similar to the case described above, the substrate temperature is increased by ∼5 K.
As follows from the results presented in Fig. 7, the cluster cools down on the time scale of one hundred to several hundred picoseconds. This time scale is comparable to the characteristic time τpl between two successive plasmon excitations induced by low-energy secondary electrons, resulting in the energy transfer below the ionisation potential of the Au309 cluster (see section 3.2). Even if the cluster temperature is slightly increased (by a few degrees) during the time τpl, a large number of successive energy transfer events (on the order of ∼103–104) during the dwell time of the electron beam on an individual pixel can cumulatively lead to a strong heating of the deposited cluster, causing its structural transformation.
4 Conclusions
In this paper, the structural transformations of a gold cluster softly deposited on a graphite substrate and exposed to a high-energy STEM electron beam have been studied by means of classical and relativistic MD simulations using the MBN Explorer21 and MBN Studio23 software packages. The particular case study was a Au309 cluster irradiated by a 300 keV electron beam. The focus was made on the two mechanisms of energy transfer to the deposited cluster during irradiation, namely (i) the relaxation of collective electronic excitations in the cluster and (ii) the localised energy transfer due to hard collisions with energetic projectile electrons. The second energy transfer mechanism was studied by simulating the collision of an energetic primary electron with the cluster atoms using the relativistic MD method.20,33 The energy transferred to the cluster during the electron – gold atom collision was evaluated as a function of the impact parameter and the scattering angle. The rates and characteristic appearance times of the two energy transfer mechanisms were evaluated for the real STEM experimental conditions.The structural transformations induced by the considered energy transfer mechanisms have been studied using the classical MD approach and quantified using the CNA method. The simulations have shown that the icosahedral Au309 cluster, after deposition on the substrate, transforms into a decahedron-like structure and undergoes a further transformation into an icosahedron-like structure due to the relaxation of the energy transferred to the cluster by the above-mentioned mechanisms.
Finally, the thermal relaxation of the cluster after the energy deposition events has been studied by classical MD simulations. The analysis of the instantaneous cluster temperature in the course of the simulations has indicated a rapid temperature decrease during ∼20 ps and a time of several hundred picoseconds to reach the initial temperature of the cluster.
The theoretical and computational analysis applied here to the case of an Au309 cluster exposed to a 300 keV STEM electron beam can be extended to other cluster sizes, electron beam energies, and substrates. Of particular interest are also the effects of the cluster orientation on a surface and the cluster-surface bonding, e.g. in the presence of point defects.57 The use of more elaborated CNA-based methods for the analysis of atomistic structural environments46 can provide a more detailed characterisation of the structure of the deposited clusters.
Author contributions
I. B.: investigation, formal analysis, data curation, writing – original draft; A. V. V.: investigation, formal analysis, data curation, visualization, writing – original draft, writing – review & editing; T. P.: writing – original draft, writing – review & editing, G. B. S.: software, J. K.: supervision, writing – review & editing; R. E. P.: conceptualization, funding acquisition, supervision, writing – original draft, writing – review & editing; A. V. S.: conceptualization, funding acquisition, methodology, project administration, resources, supervision, writing – original draft, writing – review & editing.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the RADON project (GA 872494) within the H2020-MSCA-RISE-2019 call and the COST Action CA20129 MultIChem supported by COST (European Cooperation in Science and Technology). The possibility of performing computer simulations at the Goethe-HLR cluster of the Frankfurt Center for Scientific Computing is gratefully acknowledged. AVV kindly thanks A. V. Korol for fruitful discussions.References
- Clusters of Atoms and Molecules: Theory, Experiment, and Clusters of Atoms, Springer Series in Chemical Physics, ed. H. Haberland, Springer-Verlag, Berlin, 1994, vol. 52 Search PubMed.
- Metal Clusters, ed. W. Ekardt, Wiley, 1999 Search PubMed.
- Metal Clusters at Surfaces: Structure, Quantum Properties, Physical Chemistry, ed. K.-H. Meiwes-Broer, Springer-Verlag, Berlin, 1999 Search PubMed.
- Latest Advances in Atomic Clusters Collision: Structure and Dynamics from the Nuclear to the Biological Scale, ed. J.-P. Connerade and A. V. Solov'yov, Imperial College Press, London, 2008 Search PubMed.
- Computational Modelling of Nanoparticles, Frontiers of Nanoscience, ed. S. T. Bromley and S. M. Woodley, Elsevier, 2018, vol. 12 Search PubMed.
- Dynamics of Systems on the Nanoscale, ed. I. A. Solov'yov, A. V. Verkhovtsev, A. V. Korol and A. V. Solov'yov, Springer International Publishing, Cham, 2022 Search PubMed.
- D. J. Smith, A. K. Petford-Long, L. R. Wallenberg and J. O. Bovin, Dynamic atomic-level rearrangements in small gold particles, Science, 1986, 233, 872–875 CrossRef CAS PubMed.
- S. Iijima and T. Ichihashi, Structural instability of ultrafine particles of metals, Phys. Rev. Lett., 1986, 56, 616–619 CrossRef CAS PubMed.
- L. D. Marks, Experimental studies of small particle structures, Rep. Prog. Phys., 1994, 57, 603–649 CrossRef CAS.
- Z. Y. Li, N. P. Young, M. D. Vece, S. Palomba, R. E. Palmer, A. L. Bleloch, B. C. Curley, R. L. Johnston, J. Jiang and J. Yuan, Three-dimensional atomic-scale structure of size-selected gold nanoclusters, Nature, 2008, 451, 46–48 CrossRef CAS PubMed.
- Z. W. Wang and R. E. Palmer, Determination of the ground-state atomic structures of size-selected Au nanoclusters by electron-beam-induced transformation, Phys. Rev. Lett., 2012, 108, 245502 CrossRef CAS PubMed.
- S. R. Plant, L. Cao and R. E. Palmer, Atomic structure control of size-selected gold nanoclusters during formation, J. Am. Chem. Soc., 2014, 136, 7559–7562 CrossRef CAS PubMed.
- D. M. Foster, T. Pavloudis, J. Kioseoglou and R. E. Palmer, Atomic-resolution imaging of surface and core melting in individual size-selected Au nanoclusters on carbon, Nat. Commun., 2019, 10, 2583 CrossRef CAS PubMed.
- Z. Li, H.-Y. T. Chen, K. Schouteden, T. Picot, T.-W. Liao, A. Seliverstov, C. Van Haesendonck, G. Pacchioni, E. Janssens and P. Lievens, Unraveling the atomic structure, ripening behavior, and electronic structure of supported Au20 clusters, Sci. Adv., 2020, 6, eaay4289 CrossRef CAS PubMed.
- A. V. Verkhovtsev, Y. Erofeev and A. V. Solov'yov, Mechanisms of radiation-induced structural transformations in deposited gold clusters, Phys. Rev. B, 2023, 108, 115423 CrossRef CAS.
- D. M. Foster, R. Ferrando and R. E. Palmer, Experimental determination of the energy difference between competing isomers of deposited, size-selected gold nanoclusters, Nat. Commun., 2018, 9, 1323 CrossRef CAS PubMed.
- S. G. Lambie, G. R. Weal, C. E. Blackmore, R. E. Palmer and A. L. Garden, Contrasting motif preferences of platinum and gold nanoclusters between 55 and 309 atoms, Nanoscale Adv., 2019, 1, 2416–2425 RSC.
- M. Dearg, C. Roncaglia, D. Nelli, E. Y. El Koraychy, R. Ferrando, T. J. A. Slater and R. E. Palmer, Frame-by-frame observations of structure fluctuations in single mass-selected Au clusters using aberration-corrected electron microscopy, Nanoscale Horiz., 2024, 9, 143–147 RSC.
- M. Dearg, S. Lethbridge, J. M. Cormack, R. E. Palmer and T. J. A. Slater, Characterisation of the morphology of surface-assembled Au nanoclusters on amorphous carbon, Nanoscale, 2024, 16, 10827–10832 RSC.
- G. B. Sushko, V. G. Bezchastnov, I. A. Solov'yov, A. V. Korol, W. Greiner and A. V. Solov'yov, Simulation of ultra-relativistic electrons and positrons channeling in crystals with MBN Explorer, J. Comput. Phys., 2013, 252, 404–418 CrossRef CAS.
- I. A. Solov'yov, A. V. Yakubovich, P. V. Nikolaev, I. Volkovets and A. V. Solov'yov, MesoBioNano Explorer - A universal program for multiscale computer simulations of complex molecular structure and dynamics, J. Comput. Chem., 2012, 33, 2412–2439 CrossRef PubMed.
- I. A. Solov'yov, A. V. Korol and A. V. Solov'yov, Multiscale Modeling of Complex Molecular Structure and Dynamics with MBN Explorer, Springer International Publishing, Cham, Switzerland, 2017 Search PubMed.
- G. B. Sushko, I. A. Solov'yov and A. V. Solov'yov, Modeling MesoBioNano systems with MBN Studio made easy, J. Mol. Graphics Modell., 2019, 88, 247–260 CrossRef CAS PubMed.
- A. Stukowski, Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012 CrossRef.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, The atomic simulation environment – a Python library for working with atoms, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- R. P. Gupta, Lattice relaxation at a metal surface, Phys. Rev. B:Condens. Matter Mater. Phys., 1983, 23, 6265–6270 CrossRef.
- F. Cleri and V. Rosato, Tight-binding potentials for transition metals and alloys, Phys. Rev. B:Condens. Matter Mater. Phys., 1993, 48, 22–33 CrossRef CAS PubMed.
- D. W. Brenner, Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films, Phys. Rev. B:Condens. Matter Mater. Phys., 1992, 42, 9458–9471 CrossRef PubMed.
- J. Geng, I. A. Solov'yov, W. Zhou, A. V. Solov'yov and B. F. G. Johnson, Uncovering a solvent-controlled preferential growth of buckminsterfullerene (C60) nanowires, J. Phys. Chem. C, 2009, 113, 6390–6397 CrossRef CAS.
- A. V. Verkhovtsev, Y. Erofeev and A. V. Solov'yov, Soft landing of metal clusters on graphite: a molecular dynamics study, Eur. Phys. J. D, 2020, 74, 205 CrossRef CAS.
- A. V. Korol, A. V. Solov'yov and W. Greiner, Channeling and Radiation in Periodically Bent Crystals, Springer-Verlag, Berlin, Heidelberg, 2nd edn, 2014 Search PubMed.
- A. Korol and A. V. Solov'yov, Novel Lights Sources Beyond Free Electron Lasers, Springer Nature Switzerland AG, Cham, 2022 Search PubMed.
- A. V. Korol, G. B. Sushko and A. V. Solov'yov, All-atom relativistic molecular dynamics simulations of channeling and radiation processes in oriented crystals, Eur. Phys. J. D, 2021, 75, 107 CrossRef CAS.
- A. V. Korol and A. V. Solov'yov, Crystal-based intensive gamma-ray light sources, Eur. Phys. J. D, 2020, 74, 201 CrossRef CAS.
- A. V. Solov'yov, A. V. Verkhovtsev, N. J. Mason, R. A. Amos, I. Bald, G. Baldacchino, B. Dromey, M. Falk, J. Fedor, L. Gerhards, M. Hausmann, G. Hildenbrand, M. Hrabovský, S. Kadlec, J. Kočišek, F. Lépine, S. Ming, A. Nisbet, K. Ricketts, L. Sala, T. Schlathölter, A. E. H. Wheatley and I. A. Solov'yov, Condensed matter systems exposed to radiation: Multiscale theory, simulations, and experiment, Chem. Rev., 2024, 124, 8014–8129 CrossRef PubMed.
- G. Molière, Theorie der Streuung schneller geladener Teilchen I: Einzelstreuung am abgeschirmten Coulomb-Feld, Z. Naturforsch., A, 1947, 2, 133–145 Search PubMed.
- Y. Lin and D. C. Joy, A new examination of secondary electron yield data, Surf. Interface Anal., 2005, 37, 895–900 CrossRef CAS.
- D. N. Poenaru, R. A. Gherghescu, I. H. Plonski, A. V. Solov'yov and W. Greiner, Macroscopic-microscopic theory of semi-spheroidal atomic cluster, Eur. Phys. J. D, 2008, 47, 379–393 CrossRef CAS.
- P.-G. Reinhard and E. Suraud, Introduction to Cluster Dynamics, Wiley, 2004 Search PubMed.
- A. Stukowski, Structure identification methods for atomistic simulations of crystalline materials, Modell. Simul. Mater. Sci. Eng., 2012, 20, 045021 CrossRef.
- D. Faken and H. Jónsson, Systematic analysis of local atomic structure combined with 3D computer graphics, Comput. Mater. Sci., 1994, 2, 279–286 CrossRef CAS.
- W. Z. Polak, Efficiency in identification of internal structure in simulated monoatomic clusters: Comparison between common neighbor analysis and coordination polyhedron method, Comput. Mater. Sci., 2022, 201, 110882 CrossRef CAS.
- P. M. Larsen, Revisiting the common neighbour analysis and the centrosymmetry parameter, arXiv, 2020, arXiv:2003.08879 [physics.comp-ph], DOI:10.48550/arXiv.2003.08879.
- Y. Fortouna, P. de Vera, A. V. Verkhovtsev and A. V. Solov'yov, Molecular dynamics simulations of sodium nanoparticle deposition on magnesium oxide, Theor. Chem. Acc., 2021, 140, 84 Search PubMed.
- P. M. Larsen, S. Schmidt and J. Schiøtz, Robust structural identification via polyhedral template matching, Modell. Simul. Mater. Sci. Eng., 2016, 24, 055007 CrossRef.
- C. Roncaglia and R. Ferrando, Machine learning assisted clustering of nanoparticle structures, J. Chem. Inf. Model., 2023, 63, 459–473 CrossRef CAS PubMed.
- G. Rossi and R. Ferrando, Freezing of gold nanoclusters into poly-decahedral structures, Nanotechnology, 2007, 18, 225706 CrossRef.
- L. G. Gerchikov, A. V. Solov'yov, J.-P. Connerade and W. Greiner, Scattering of electrons on metal clusters and fullerenes, J. Phys. B: At., Mol. Opt. Phys., 1997, 30, 4133–4161 CrossRef CAS.
- A. V. Solov'yov, Plasmon excitations in metal clusters and fullerenes, Int. J. Mod. Phys. B, 2005, 19, 4143–4184 CrossRef.
- E. M. Fernández, J. M. Soler and L. C. Balbás, Planar and cagelike structures of gold clusters: Density-functional pseudopotential calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235433 CrossRef.
- A. V. Verkhovtsev, A. V. Korol and A. V. Solov'yov, Revealing the mechanism of the low-energy electron yield enhancement from sensitizing nanoparticles, Phys. Rev. Lett., 2015, 114, 063401 CrossRef CAS PubMed.
- M. Seidl, K.-H. Meiwes-Broer and M. Brack, Finite-size effects in ionization potentials and electron affinities of metal clusters, J. Chem. Phys., 1991, 95, 1295–1303 CrossRef CAS.
- M. Seidl, J. P. Perdew, M. Brajczewska and C. Fiolhais, Ionization energy and electron affinity of a metal cluster in the stabilized jellium model: Size effect and charging limit, J. Chem. Phys., 1998, 108, 8182–8189 CrossRef CAS.
- L. G. Gerchikov, A. N. Ipatov, A. V. Solov'yov and W. Greiner, Non-adiabatic electron-ion coupling in dynamical jellium model for metal clusters, J. Phys. B: At., Mol. Opt. Phys., 2000, 33, 4905–4926 CrossRef CAS.
- R. F. Egerton, Electron Energy-Loss Spectroscopy in the Electron Microscope, Springer Science+Business Media, New York, 3rd edn, 2011 Search PubMed.
- L. D. Landau and E. M. Lifshitz, Mechanics, Course of Theoretical Physics, Butterworth-Heinemann, Oxford, UK, 3rd edn, 1976, vol. 1 Search PubMed.
- T. Pavloudis, J. Kioseoglou and R. E. Palmer, Bonding of gold nanoclusters on graphene with and without point defects, Nanomaterials, 2020, 10, 2109 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Corresponding STEM experimental parameters and the complementary analysis of local atomistic environment in the deposited Au309 clusters. See DOI: https://doi.org/10.1039/d4nr04448g |
| This journal is © The Royal Society of Chemistry 2025 |