Open Access Article
Open Access ArticleStepwise kinetics of the early-stage nucleation in chiral perovskites via ab initio molecular dynamics and free-energy calculations†
Mariagrazia
Fortino
a,
Gioacchino
Schifino
a,
Matteo
Salvalaglio
 b and
Adriana
Pietropaolo
b and
Adriana
Pietropaolo
 *a
*a
aDipartimento di Scienze della Salute, Università“Magna Graecia” di Catanzaro, Catanzaro 88100, Italy. E-mail: apietropaolo@unicz.it
bThomas Young Centre and Department of Chemical Engineering, University College London, London WC1E 7JE, UK
First published on 6th February 2025
Abstract
This study provides a comprehensive molecular-level understanding of the early-stage nucleation process in chiral hybrid organic–inorganic perovskites (HOIPs). A combination of ab initio molecular dynamics (AIMD) based on density functional theory (DFT) and parallel bias metadynamics simulations was designed to explore a broad spectrum of the nucleation scenarios, disclosing how structural deviations affect the formation of chiral aggregates at the atomic scale. The workflow uses parallel replicas initialized from configurations characterised by different root-mean-square deviations (RMSD) relative to the crystallographic coordinates of the chiral ligands. The free-energy landscape and the kinetic pathways involved in chiral aggregate formation indicate a stepwise mechanism that governs the transition from disordered to chiral states. The computed free-energy barriers and corresponding transition timescales uncover several critical stages in this process, including rapid initial relaxations as well as slower, free-energy-intensive steps, with overall timescales on the order of microseconds as the system approaches its most chiral configuration.
Introduction
Hybrid organic–inorganic perovskites (HOIP) have emerged as a rapidly advancing class of materials, attracting significant attention due to their remarkable optoelectronic properties and potential applications in diverse technological areas.1–4 These include photovoltaics,5–7 light-emitting diodes,8–13 photodetectors14–19 as well as photonic lasers.20–22 One emerging field is the one of chiral hybrid perovskite, featuring the integration of chiral organic molecules into the perovskite framework. Chiral perovskites exhibit unique symmetry-breaking features that introduce peculiar properties with interesting applications in chiroptoelectronics, sensing, as well as quantum computing.23–29Chiral HOIPs typically adopt low-dimensional layered structures with inherent structural flexibility. Combined with their versatile elemental composition, this can induce chirality when appropriate chiral organic cations are incorporated. The synthesis of chiral perovskites using chiral ligands was first demonstrated for 1D and 2D single crystals in 2003 and 2006, respectively.30,31 Interest in chiral perovskites started in 2017 with the first chiroptical study.32 Since then, numerous contributions have highlighted their distinctive chiral signatures.33,34 Despite the growing experimental interest in these materials, their formation mechanisms at the molecular level are still poorly understood. Chiral perovskites can be synthesized through various methods, including solvent-based approaches, melt synthesis, and re-evaporation techniques, each offering unique advantages and challenges.35 Regardless of the synthesis method, the early stages of nucleation are crucial, as they dictate the structural and chiroptical properties of the final material. In this study, we focus specifically on the early-stage nucleation process to unravel the fundamental mechanisms governing the formation of chiral aggregates.36,37
A comprehensive understanding of the chiral nucleation and growth mechanisms, especially in terms of how chirality influences the formation of perovskite aggregates, is crucial for tailoring these materials for specific applications. However, unraveling the complex interplay between chirality, molecular interactions and aggregate formation processes necessitates advanced theoretical approaches.
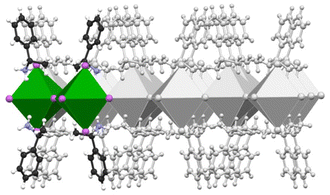
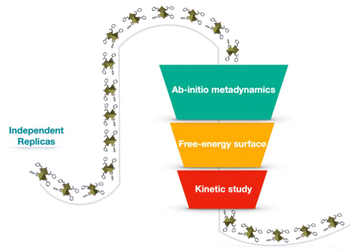
In this work, we employ a state-of-the-art computational approach combining ab initio quantum mechanical methods with parallel bias metadynamics38 simulations to study the early stages of nucleation and chiral aggregate formation in chiral hybrid perovskites. Ab initio molecular dynamics (AIMD) simulations based on density functional theory (DFT) were performed in conjunction with parallel bias metadynamics across 10 independent simulation replicas. A periodic model of the 2D S-MBA2PbI4 chiral perovskite comprising two lead iodide octahedra and four (S)-methyl benzyl ammonium (MBA) ligands (Scheme 1) was constructed from the experimental crystallographic coordinates39 and used as a starting point in each replica.
All the replicas were initialized from distorted configurations, with different root-mean-square deviation (RMSD) values, from 0 Å to 6 Å, relative to the crystallographic configuration of the chiral ligands. This setup enabled exploring a wide range of possible scenarios where chiral structures emerge from disordered molecular environments, thus elucidating how chiral crystalline arrangements nucleate at the atomic level (Scheme 2). Those simulations reveal crucial insights into the free energy landscape underpinning the nucleation of chiral environments, offering a detailed view of the transformation pathways and providing information on the associated ordering kinetics. The free-energy profile reconstructed from parallel bias simulations indicates that the transition from disordered to chiral configurations follows a stepwise mechanism, with overall timescales on the order of microseconds. This study provides a fundamental framework for understanding the early-stage formation mechanisms in chiral perovskites and highlights how theoretical methods can tailor experimental analysis.
Results and discussion
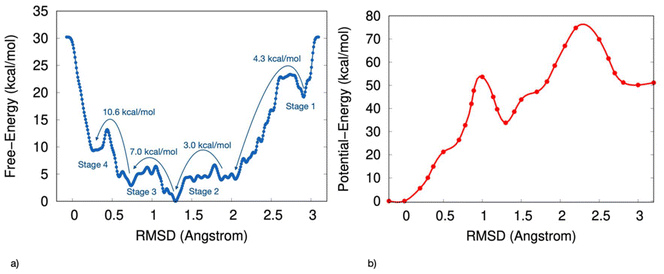
The computed free-energy profile indicates that the transition from disordered to chiral configurations for the S-MBA2PbI4 chiral HOIP follows a stepwise mechanism. The discrete stages along the transformation from disorder to chiral order observed in the AIMD simulations emerge as key features of the configurational landscape associated with the ordering process.Fig. 1a presents the one-dimensional free-energy profile derived from ab initio parallel bias metadynamics simulations as a function of RMSD values, capturing deviations in the positions of the four ligands within the unit cell from a perfectly ordered chiral configuration of S-MBA2PbI4 chiral perovskite (Fig. 1a).
The free-energy surface reveals several local minima, each corresponding to long-lived, metastable ensembles of configurations of MBA2PbI4 with progressively higher levels of local chirality. Fig. 1b shows the potential energy surface, calculated by averaging the potential energy across configurations at fixed RMSD values. This potential-energy profile also displays multiple local minima, although the absolute minimum differs between the two profiles.
Fig. 1a shows the transitions between these metastable states as stages 1 to 4, which mark the progression from the most disordered to the most chiral perovskite configurations.
It is worth highlighting that the term ‘most chiral perovskite’ is used to indicate the most ordered configuration, as it reflects the highest degree of structural order and alignment with the chiral reference configuration observed during the nucleation process.
Starting from a disordered arrangement, the first transition corresponding to stage 1 occurs as the RMSD decreases from 3.0 Å to 2.1 Å, overcoming a free-energy barrier of 4.3 kcal mol−1. At stage 2, a 3 kcal mol−1 barrier is encountered, leading to the global free-energy minimum at an RMSD approaching 1.2 Å. Comparison with the potential-energy profile (Fig. 1b) indicates that this absolute minimum represents an entropic minimum since, upon removing the kinetic effects, the minimum shifts towards an RMSD closer to 0 Å.
A 7 kcal mol−1 barrier is then required to further reduce the RMSD to 1.0 Å during stage 3. Finally, the most free-energy-intensive step occurs from 0.7 Å to 0.3 Å in RMSD, corresponding to stage 4 and requires overcoming a barrier of 10.6 kcal mol−1.
The rate constants were estimated from the calculated free-energy barriers using the procedure outlined in the Methods section and are reported in Table 1. These values provide insights into each stage's relative stability and timescale within the chiral nucleation pathway, identifying the kinetics associated with each transition.
| Stage | k (ps−1) | Time |
|---|---|---|
| 1 (RMSD 3.0–2.1 Å) | 4.4 × 10−3 | 227 ps |
| 2 (RMSD 2.1–1.3 Å) | 3.9 × 10−2 | 26 ps |
| 3 (RMSD 1.3–0.7 Å) | 4.6 × 10−5 | 21 ns |
| 4 (RMSD 0.7–0.2 Å) | 1.1 × 10−7 | 9 μs |
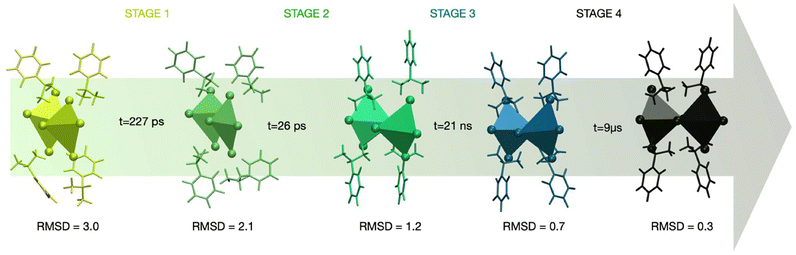
The first two stages (stage 1 and stage 2) occur on a timescale of picoseconds. A kinetic constant of 4.4 × 10−3 ps−1 was calculated for stage 1, corresponding to a time of 227 ps, while stage 2 has a kinetic constant of 3.9 × 10−2 ps−1 and a time of 26 ps. As illustrated in Fig. 2, these stages represent a transition from a highly disordered configuration where the ligands are arranged in a disposition with minimal interactions among them to a configuration with a chiral degree (with an RMSD value of 1.2 Å) characterized by a more packed arrangement of the ligands. This chiral ordering is stabilized by salt-bridge interactions between the NH3+ groups of the aromatic ring and the iodide atoms of the inorganic octahedra, with a distance approaching 2.4 Å. Stage 3 occurs on a nanosecond timescale, with a computed kinetic constant of 4.6 × 10−5 ps−1 and a time of 21 ns. During this stage, the transition toward the most chiral perovskite configuration involves displacements in the positions of the ligands in a staggered arrangement of the aromatic molecules along the C2-axis. This also leads to minor adjustments in the inorganic octahedra, particularly in the Pb–I coordination distances. Stage 4 is the slowest, with a kinetic constant of 1.1 × 10−7 ps−1 and a timescale of 9 μs.
The slow kinetics observed in stage 4 which is characterized by the highest free-energy barrier, can be attributed to the closest crystal packing achieved during this stage. This increased packing density results in greater rigidity of the system, which imposes structural constraints and limits the flexibility required for further configurational changes. The alignment of the hybrid perovskite toward the ideal crystallographic configuration thereby reaching the rotational symmetry of the C2 axis, contributes significantly to this enhanced rigidity, making this stage as the most energetically demanding in the nucleation process. The structural evolution during nucleation reveals how chirality is progressively transferred from the organic ligands to the inorganic framework and their interfaces.40 The alignment of the chiral ligands relative to the Pb–I octahedra has been analyzed to capture these transitions. The results show that initial chirality emerges from the asymmetric orientation of the organic ligands, which gradually induces distortions in the inorganic sublattice. These distortions propagate through the framework, ultimately resulting in a fully chiral configuration. This atomistic-level understanding provides deeper insights into the interplay between organic and inorganic components during chiral perovskite formation. While this study focuses on the chiral S-enantiomer of the perovskite, it is important to note potential differences in the free-energy behavior between chiral and racemic systems. Racemic compounds are expected to exhibit shallower free-energy minima and reduced free-energy barriers compared to chiral systems, due to their lack of overall chirality. This difference arises from the absence of chirality-induced structural constraints, indeed crucial in the ordering process of chiral materials. These insights highlight the distinct energetics associated with chiral systems and their potential implications for material design.
Methods
Ab initio steered molecular dynamics (SMD) simulations have been conducted to increase the disorder of the spatial organization of the ligands around the inorganic octahedra of the S-MBA2PbI4 chiral perovskite, thereby generating the initial configurations for the parallel-bias metadynamics replicas. The initial periodic model used for the ab initio SMD simulations derives from the crystallographic coordinates of the S-MBA2PbI4 chiral perovskite reported by Jana et al.39 and available in the Cambridge Crystallographic Data Center (CCDC) database with deposition number 2015617. The model includes two inorganic [PbI6]4− octahedral layers and four chiral MBA chains of the S-enantiomeric models to maintain a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometric ligand–perovskite ratio consistent with experimental reports.
1 stoichiometric ligand–perovskite ratio consistent with experimental reports.
The coordinates were first optimized using the PBE functional with Quantum Espresso software41,42 under periodic boundary conditions at fixed experimental cell parameters39 and with a vacuum of 14 Å orthogonal to the periodic layer. The simulations incorporated the D3 dispersion corrections developed by Grimme and coworkers.43 The acronym PBE-D3 in the text denotes the complete level of theory employed. The ultrasoft pseudopotentials used in the simulations include Pb.rel-pbe-dn-rrkjus_psl.1.0.0.UPF, I.pbe-n-rrkjus_psl.1.0.0.UPF, C.pbe-rrkjus.UPF, H.pbe-rrkjus.UPF and N.pbe-rrkjus.UPF is available within Quantum Espresso (https://www.quantum-espresso.org/).41,42 Then, SMD simulations were conducted starting from the optimized coordinates, maintaining the same level of theory, and using Quantum Espresso patched with the PLUMED 2.9 enhanced sampling plugin.44 An external pulling force with a spring constant of 500 kcal (mol Å2)−1 was applied. The RMSD with respect to the ligand's position of the energy-minimized structure was used as collective variable (CV). The RMSD relative to the reference crystallographic structure was chosen as collective variable due to its ability to capture global structural deviations during the nucleation process, despite its inherent degeneracy. This metric effectively tracks the progression of the system along the disordered-to-chiral transition pathway, enabling the identification of metastable states and associated free-energy barriers.
The SMD simulations have been carried out in the NVT ensemble using a velocity rescaling thermostat45 to maintain the temperature of 300 K.
From the computed SMD trajectory, 10 configurations were extracted with RMSD values ranging from 0 to 6 Å. The selected configurations have been used as starting points for the independent replicas. Ab initio parallel bias metadynamics were performed for each replica, once again using Quantum Espresso41,42 patched with PLUMED 2.9.44 The simulations have been run at PBE-D3 level of theory using Pb.rel-pbe-dn-rrkjus_psl.1.0.0.UPF, I.pbe-n-rrkjus_psl.1.0.0.UPF, C.pbe-rrkjus.UPF, H.pbe-rrkjus.UPF and N.pbe-rrkjus.UPF as pseudopotential41,42 and found to be consistent in predicting chiral perovskite structural features.46 All the simulations have been conducted under periodic boundary conditions at fixed experimental cell parameters, reported in ref. 39 and with a vacuum of 14 Å orthogonal to the periodic layer.
The RMSD relative to the ligand positions in the relaxed structure was used as a collective variable (CV). RMSD values were calculated for the pairs of ligands and represents the average deviation of all four ligand positions from the reference structure. Upper and lower walls have been defined, as implemented in the plumed plugin, to limit the region of the phase space accessible during the simulation, using the following collective variable (σd2):
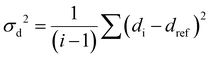 | (1) |
Gaussians with an initial height of 0.4 kcal mol−1 and a width of 0.05 Å were deposited with a stride of 1 fs. The simulations were conducted in the NVT ensemble using a velocity-rescaling thermostat to maintain the temperature. A time step of 1 fs and a temperature of 300 K were employed with a total simulation time of 300 ps.
The transition time from the disordered configuration to the chiral one has been evaluated as the inverse of the kinetics constant, computed as follows:
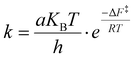 | (2) |
The potential energy profile was calculated by averaging the potential energy values obtained from the simulated ab initio trajectories across configurations extracted from the computed free-energy minima while maintaining fixed RMSD values. To evaluate the reliability of these averaged values, single-point PBE-D3 calculations were performed using Quantum Espresso software on a selection of configurations, each with RMSD values of 0.0, 0.5, 1.0, 1.5, 2.0, 2.5, and 3.0 Å. A comparison between the single-point PBE-D3 potential energy and the averaged potential energy values is presented in the ESI.†
Conclusions
Overall, this study presents a detailed molecular-level understanding of the early-stage emergence of chirality during the assembly of the S-MBA2PbI4 chiral hybrid perovskite through a combination of ab initio molecular dynamics and parallel bias metadynamics simulations. A stepwise mechanism governing the transition from disordered to chiral configurations was disclosed by reconstructing the free-energy landscape and estimating the kinetics along the pathway that emerged from configurational space exploration. The calculated free-energy barriers and corresponding timescales highlight key stages in this process, starting from rapid initial transitions to slower free-energy-intensive stages, as the low-dimensional hybrid perovskite approaches its most ordered chiral state. This latter reaching the C2 axis, with estimated timescales on the order of microseconds. The ability to map kinetic barriers and timescales offers valuable insights that complement experimental efforts, paving the way for future investigations to optimize the design and functionality of chiral perovskites. Overall, this work provides a fundamental framework for understanding the dynamics of local ordering of chiral perovskites to uncover the mechanisms that drive their chiral nucleation.Author contributions
MF and GS carried out the simulations, MG, GS, MS, AP planned the simulation workflows, MG, MS, AP wrote the manuscript.Data availability
The data supporting this article have been included as part of the ESI† and are available on the PLUMED-NEST repository – https://www.plumednest.org/.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The Italian Ministry for University and Research (MUR) and University “Magna Græcia” of Catanzaro are acknowledged for the financial support under PON “RICERCA E INNOVAZIONE” 2014–2020, ASSE IV “ISTRUZIONE E RICERCA PER IL RECUPERO” AZIONE IV.4 “DOTTORATI E CONTRATTI DI RICERCA SU TEMATICHE DELL0INNOVAZIONE” D. M. 1062/2021 program and under the research program PRIN20228PH3JX. We acknowledge the CINECA award under the ISCRA initiative, for the availability of high-performance computing resources and support. MS acknowledges funding from the ht-MATTER UKRI Frontier Research Guarantee Grant (EP/X033139/1).References
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050 CrossRef CAS PubMed.
- M. M. Lee, J. Teuscher, T. Miyasaka, T. N. Murakami and H. J. Snaith, Science, 2012, 338, 643 CrossRef CAS PubMed.
- Z. Li, T. R. Klein, D. H. Kim, M. Yang, J. J. Berry, M. F. A. M. van Hest and K. Zhu, Nat. Rev. Mater., 2018, 3, 18017 CrossRef CAS.
- Y. Fu, H. Zhu, J. Chen, M. P. Hautzinger, Y. X. Zhu and S. Jin, Nat. Rev. Mater., 2019, 4, 169 CrossRef CAS.
- D. H. Cao, C. C. Stoumpos, O. K. Farha, J. T. Hupp and M. G. Kanatzidis, J. Am. Chem. Soc., 2015, 137, 7843 CrossRef CAS PubMed.
- N. J. Jeon, H. Na, E. H. Jung, T. Y. Yang, Y. G. Lee, G. Kim, H. W. Shin, S. I. Seok, J. Lee and J. Seo, Nat. Energy, 2015, 3, 682 CrossRef.
- A. Filippetti, A. Kahmann, C. Caddeo, A. Mattoni, M. Saba, A. Bosin and M. A. Loi, J. Mater. Chem. A, 2021, 9, 11812 RSC.
- N. Wang, L. Cheng, R. Ge, S. Zhang, Y. Miao, W. Zou, C. Yi, Y. Sun, Y. Cao, R. Yang, Y. Wei, Q. Guo, Y. Ke, M. Yu, Y. Jin, Q. Ding, D. Di, L. Yang, G. Xing, H. Tian, C. Jin and F. Gao, Nat. Photonics, 2016, 10, 699 CrossRef CAS.
- X. Yang, X. Zhang, J. Deng, Z. Chu, Q. Jiang, J. Meng, P. Wang, L. Zhang, Z. Yin and J. You, Nat. Commun., 2018, 9, 570 CrossRef PubMed.
- Y. Zou, Q. Huang, Y. Yang, M. Ban, S. Li, Y. Han, T. Wu, Y. Tan, X. Gao, T. Song and B. Sun, Adv. Mater. Interfaces, 2018, 5, 1801030 CrossRef.
- J. Byun, H. Cho, C. Wolf, M. Jang, A. Sadhanala, R. H. Friend, H. Yang and T. W. Lee, Adv. Mater., 2016, 28, 7515 CrossRef CAS PubMed.
- J. Xing, Y. Zhao, M. Askerka, L. N. Quan, X. Gong, W. Zhao, J. Zhao, H. Tan, G. Long, L. Gao, Z. Yang, O. Voznyy, J. Tang, Z.-H. Lu, Q. Xiong and E. H. Sargent, Nat. Commun., 2018, 9, 3541 CrossRef PubMed.
- W. Su and Y. Fanglong, Trends Chem., 2022, 4, 965 CrossRef CAS.
- J. Li, J. Wang, Y. Zhang, H. Wang, G. Lin, X. Xiong, W. Zhou, H. Luo and D. Li, 2D Mater., 2018, 5, 021001 CrossRef.
- Y. Chen, Y. Sun, J. Peng, J. Tang, K. Zheng and Z. Liang, Adv. Mater., 2018, 30, 1703487 CrossRef PubMed.
- L. Ji, H. Y. Hsu, J. C. Lee, A. J. Bard and E. T. Yu, Nano Lett., 2018, 18, 994 CrossRef CAS PubMed.
- L. Dou, Y. M. Yang, J. You, Z. Hong, W. H. Chang, G. Li and Y. Yang, Nat. Commun., 2014, 5, 5404 CrossRef CAS PubMed.
- K. Leng, I. Abdelwahab, I. Verzhbitskiy, M. Telychko, L. Chu, W. Fu, X. Chi, N. Guo, Z. Chen, C. Zhang, Q. H. Xu, J. Lu, M. Chhowalla, G. Eda and K. P. Loh, Nat. Mater., 2018, 17, 908 CrossRef CAS PubMed.
- J. Li, J. Wang, J. Ma, H. Shen, L. Li, X. Duan and D. Li, Nat. Commun., 2019, 10, 806 CrossRef PubMed.
- B. R. Sutherland and E. H. Sargent, Nat. Photonics, 2016, 10, 295 CrossRef CAS.
- H. Zhu, Y. Fu, F. Meng, X. Wu, Z. Gong, Q. Ding, M. V. Gustafsson, M. T. Trinh, S. Jin and X. Y. Zhu, Nat. Mater., 2015, 14, 636 CrossRef CAS PubMed.
- C. M. Raghavan, T. P. Chen, S. S. Li, W. L. Chen, C. Y. Lo, Y. M. Liao, G. Haider, C. C. Lin, C. C. Chen, R. Sankar, Y. M. Chang, F. C. Chou and C. W. Chen, Nano Lett., 2018, 18, 3221 CrossRef CAS PubMed.
- Y. Shi, P. Duan, S. Huo, Y. Li and M. Liu, Adv. Mater., 2018, 30, 1705011 CrossRef PubMed.
- C. Yuan, X. Li, S. Semin, Y. Feng, T. Rasing and J. Xu, Nano Lett., 2018, 18, 5411 CrossRef CAS PubMed.
- G. Long, C. Jiang, R. Sabatini, Z. Yang, M. Wei, L. N. Quan, Q. Liang, A. Rasmita, M. Askerka, G. Walters, X. Gong, J. Xing, X. Wen, R. Quintero-Bermudez, H. Yuan, G. Xing, X. Wang, D. Song, O. Voznyy, M. Zhang, S. Hoogland, W. Gao, Q. Xiong and E. H. Sargent, Nat. Photonics, 2018, 12, 528 CrossRef CAS.
- Y. Yang, R. C. Da Costa, M. J. Fuchter and A. J. Campbell, Nat. Photonics, 2013, 7, 634 CrossRef CAS.
- S. Apergi, G. Brocks and S. Tao, J. Phys. Chem. Lett., 2023, 14, 11565 CrossRef CAS PubMed.
- Y. Zheng, X. Han, P. Cheng, X. Jia, J. Xu and H. Bu, J. Am. Chem. Soc., 2022, 144, 16471 CrossRef CAS PubMed.
- H. Zheng, A. Ghosh, M. J. Swamynadhan, Q. Zhang, W. P. D. Wong, Z. Wu, R. Zhang, J. Chen, F. Cimpoesu, S. Ghosh, B. J. Campbell, K. Wang, A. Stroppa, R. Mahendiran and K. P. Loh, Nat. Commun., 2024, 15, 5556 CrossRef CAS PubMed.
- D. G. Billing and A. Lemmerer, Acta Crystallogr., Sect. E:Struct. Rep. Online, 2003, 59, m381 CrossRef CAS.
- D. G. Billing and A. Lemmerer, CrystEngComm, 2006, 8, 686 RSC.
- J. Ahn, E. Lee, J. Tan, W. Yang, B. Kim and J. Moon, Mater. Horiz., 2017, 4, 851 RSC.
- H. Dui and M. A. Loi, Matter, 2021, 4, 3835 CrossRef.
- M. Fortino, A. Mattoni and A. Pietropaolo, J. Mater. Chem. C, 2023, 11, 9135 RSC.
- S. Driessen, S. Sarigul-Ozbek, C. M. Sutter-Fella and S. Tao, J. Phys.: Energy, 2024, 6, 042001 CAS.
- M. Moroni, C. Coccia and L. Malavasi, Chem. Commun., 2024, 60, 9310 RSC.
- A. Pietropaolo, A. Mattoni, G. Pica, M. Fortino, G. Schifino and G. Grancini, Chem, 2022, 8, 1231 CAS.
- J. Pfaendtner and M. Bonomi, J. Chem. Theory Comput., 2015, 11, 5062 CrossRef CAS PubMed.
- M. K. Jana, R. Song, H. Liu, D. R. Khanal, S. M. Janke, R. Zhao, C. Liu, Z. V. Vardeny, V. Blum and D. B. Mitzi, Nat. Commun., 2020, 11, 4699 CrossRef CAS PubMed.
- M. Pols, G. Brocks and S. Tao, J. Phys. Chem. Lett., 2024, 15(31), 8057 CrossRef CAS PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, et al., J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli and M. Cococcioni, et al., J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116(9), 5105 CrossRef CAS PubMed.
- The PLUMED consortium, Nat. Methods, 2019, 16, 670 CrossRef PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- M. Fortino, A. Mattoni and A. Pietropaolo, J. Phys.: Mater., 2024, 7, 045009 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr04735d |
| This journal is © The Royal Society of Chemistry 2025 |