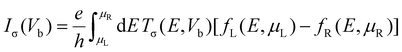Spin-state switching at the single-molecule level by distortion of the coordination sphere: validation based on quantum-chemistry calculations

Abstract

Different strategies have been proposed to trigger spin switching in single-molecule junctions based on spin-crossover complexes. Here, we report on a computational study aimed to validate one of the hypothesized mechanisms consisting of the distortion of the coordination sphere of the molecule. We focus on a series of heteroleptic [Fe^II(tpy)₂]⁺² complexes in a mechanically controlled break junction setup, displaying voltage-dependent bistabilities, related to the switching of the Fe^II centre between the LS and HS states. Our model for the molecular junction can explain the hysteretic behaviour found in some of the junctions, with a mechanism close to the hypothesized mechanism, but without the requirement of long-range interactions between the electrodes and different parts of the molecule. Our results predict the existence of a switching field able to foster the required distortion driving the switching between the LS and HS states.

---

1. Introduction

The possibility of using single molecules to perform basic functions of digital electronic devices has been successfully explored over the past decades.^1–4 A particularly interesting function at the molecular level is the switching between bistable states,^2,5–11 a function that can be activated by different external stimuli. Among the candidates for single-molecule switches, spin-crossover (SCO) iron(II) complexes have vast potential for applications.^12–19 In these systems, bistability occurs between the low-spin state (LS, S = 0 for iron(II)) and the high-spin state (HS, S = 2 for iron(II)), activated by temperature, light, pressure, and electric and magnetic fields.^{12,13,17,20–22}

To be used as switches at the molecular level, SCO molecules have to be deposited on metal surfaces or in between break junctions. At the single-molecule level, and unlike in the bulk, the switching is not triggered by temperature in most cases but by a stimulus applied under isothermal conditions. Usually, the stimulus is related to a voltage or current applied between the metal surface where the molecule is deposited and the tip of a scanning tunneling microscope (STM) or between the two electrodes of the nanogap break junction where the molecule is included. The two spin states may lead to different conductances, usually larger for junctions containing HS molecules compared to those with LS molecules,^15,19,23 and the resulting I-vs.-V plots can show a hysteretic switching behaviour. The first device based on SCO Fe(II) complexes with both spin-dependent conductance and hysteresis features, referred to as the memristive effect, was proposed by Miyamachi et al. consisting of [Fe^II(phen)₂(NCS)₂] deposited on a CuN/Cu(100) surface.^24,25 A similar effect was found for an Fe(III) complex [Fe^III(pap)₂]⁺ deposited on Cu₂N/Cu(100)²⁶ and an [Fe^II(bpz)₂(phen)] complex deposited on Au(111).⁹ Another interesting aspect of the junctions based on SCO complexes is the ability of the HS state to promote spin-polarized transport upon charge injection from the nonmagnetic metallic electrodes, hence acting as a spin valve/filter, a function of interest in spintronics.^27–29

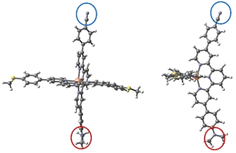
Regarding single-molecule junctions, Harzmann et al.³⁰ reported a series of four heteroleptic [Fe^II(tpy)₂]⁺² complexes in a mechanically controlled break junction (MCBJ) setup, showing voltage-dependent bistability features (Fig. 1). In these complexes, the terpyridine (typ) ligands are perpendicular to each other, one typ ligand is functionalized with terminal anchor groups to fix the molecule inside the junction and the other typ ligand contains two groups (R1 and R2) of different electronegativities (Fig. 1). A fraction of the resulting junctions based on these heteroleptic Fe^II complexes displayed voltage-dependent bistabilities related to the switching of the Fe^II centre between the LS and HS states, which present different conducting features. Three types of bistabilities were reported: a large hysteresis window around the switching point, negative differential conductance features and sudden jumps to different current states. The hypothesized switching mechanism consisted of the distortion of the Fe^II coordination sphere promoted by an external electric field. The intrinsic dipole moment of the complex, related to the R1 and R2 groups, acts as a push–pull system that senses the applied electric field and drives the distortion of the metal coordination sphere and finally triggers the spin transition. This hypothesis was supported by two main results: (i) the ratio of bistable junctions was correlated with the strength of the dipole moment of the immobilized molecule and (ii) a constant threshold value of the electric field was required to promote the switching.³⁰ Recently, it has been found that the yield of functional junctions can be improved by introducing bulky alkyne groups into the typ ligand bridging the electrodes that prevent (or reduce) the undesired potential interactions of the polar R1 and R2 groups or the phenyl-π system of the immobilized tpy ligand with the electrodes and increase the control of the Fe^II complex arrangement on the junction.³¹

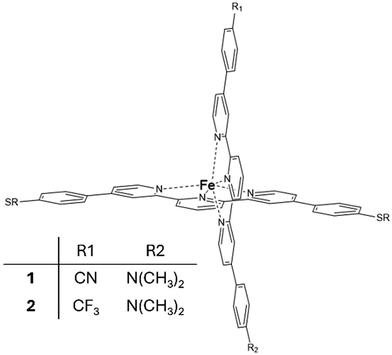Fig. 1 Heteroleptic [Fe^II(tpy)₂]⁺² complexes 1 and 2 with electron-withdrawing R1 and electron-donating R2 groups.

A similar idea was used by Frisenda et al.³² to build a molecular junction based on a related homoleptic [Fe^II(tpy)₂]⁺² complex, where the LS to HS switching is triggered mechanically by increasing the separation between the two gold electrodes. This produces the distortion of the perpendicular arrangement of the two tpy ligands, reducing the Fe(II) ligand field and finally favouring the HS state for a large enough separation of the electrodes.

The phenomena described in these previous studies prompt us to carry out a computational study with the aim of providing support for the hypothesized switching mechanism and give some clues on how the I–V bistability can be observed. We have combined different approaches to model the molecular junction, evaluate the transport properties of both spin states and determine the effect of an external applied field and the distortion of the metal coordination sphere on the HS–LS transition energy. Our model for the molecular junction can explain the hysteretic behaviour found in some of the junctions, with a mechanism close to the hypothesized mechanism by Harzmann et al.³⁰ for this type of junction, but without the requirement of long-range interactions between the electrodes and different parts of the molecule suggested by these authors. This study puts in evidence once again the strong sensitivity of the spin states of Fe(II) SCO complexes on the spatial arrangement of the ligands and the fine tuning among the different factors controlling the SCO behaviour in SCO-based single-molecule junctions.

2. Computational details

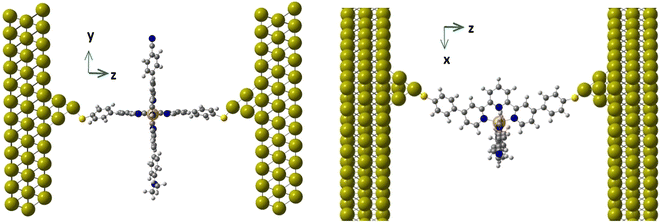
In the same way that the realization of working molecular junctions with voltage-dependent bistabilities is not a routine work (usually the fraction of junctions showing bistability is quite low, less than 9% in ref. 30 and 32), the simulation of these junctions is also a challenge from a computational point of view. Since many different factors can modulate the behaviour of the junction,^33–36 we used a model where the horizontal tpy ligand is connected to gold electrodes through sulphur anchoring atoms. In this configuration, the vertical ligand is far from the electrodes, and thus no long-range interactions are expected between them. This configuration allows controlling the position and orientation of the molecule with respect to the electrodes and focusing on the validation of the hypothesis formulated by Harzmann and coworkers about the voltage-triggered distortion of the ligands.

We focus on two of the reported heteroleptic [Fe(tpy)₂]⁺² complexes that showed the highest ratio of bistable junctions, differing in the electron-withdrawing R1 group, and hence in the molecule dipole moment. For molecules 1 and 2, the R1 group corresponds to CN and CF₃, respectively, while in both molecules, the electron-donating group is R2 = N(CH₃)₂ (Fig. 1). We first considered the isolated molecule, optimizing the geometries of the LS and HS states. These geometries were employed as the starting point to model the molecule inside the junction. Furthermore, we studied how an external electric field of increasing strength impacts the HS–LS transition energy of the immobilized molecule and how the energies of the LS and HS states evolve when the Fe(II) coordination sphere is distorted. To build our models, we used the available X-ray data of the homoleptic [Fe(II)(tpy)₂]⁺² complex (compound 8c in ref. 37) with two 4,4′′-[p-(methylthio)phenyl]terpyridine ligands (tpy). In our model, the two thiomethyl groups of the vertical tpy ligand are replaced by the R1 and R2 groups. For the interaction with the electrodes we considered, sulfur substituents at the para position of the horizontal tpy ligand act as anchor groups as in previous studies.^3,30–32,38 It is well known that the high binding affinity of sulfur with gold results in significant mechanical stability of sulfur–gold bonds.^31,32,38

The isolated molecules were optimized by means of density functional theory (DFT)-based calculations with the TPSSh functional and def2svp basis set³⁹ for all atoms, with pseudopotentials for the inner shell electrons of gold atoms. The same approach has been employed to evaluate the impact of the distortion of the coordination Fe(II) sphere and the external electric field on the transition energy. In such cases, the electrodes were simulated with a pyramidal cluster of ten gold atoms, whose geometry as well as that of the molecule was previously optimized in the junction with periodic conditions. All calculations of the gas-phase molecule were performed using the ORCA 5.0.3 package,⁴⁰ except the optimizations in the presence of an external electric field, where the Gaussian 09 package was used,⁴¹ with a basis set of def2-tzvp quality^42,43 for all atoms, except Au represented by means of the Los Alamos pseudopotential and the corresponding LANL2DZ basis set.⁴⁴

The QuantumATK software package⁴⁵ was used to obtain the complex's transport properties and perform all the necessary geometry optimizations for building the junctions. In these calculations, all atoms were represented using a double-ζ-polarized (DZP) basis set, along with PseudoDojo norm-conserving pseudopotentials.⁴⁶ We employed the rPBE exchange–correlation functional,⁴⁷ as it has been demonstrated to provide more accurate values for the gap between the high-spin (HS) and low-spin (LS) states in iron(II) spin-crossover complexes compared to other GGA functionals, at a lower computational cost than that of a hybrid functional, with comparable performance to TPSSh for SCO compounds.^48–52

For all calculations, the mesh cut-off energy was set to 210 Rydberg for both real and reciprocal space grids, with a self-consistency tolerance of 10⁻⁴ eV for the convergence of the Hamiltonian and density matrices.

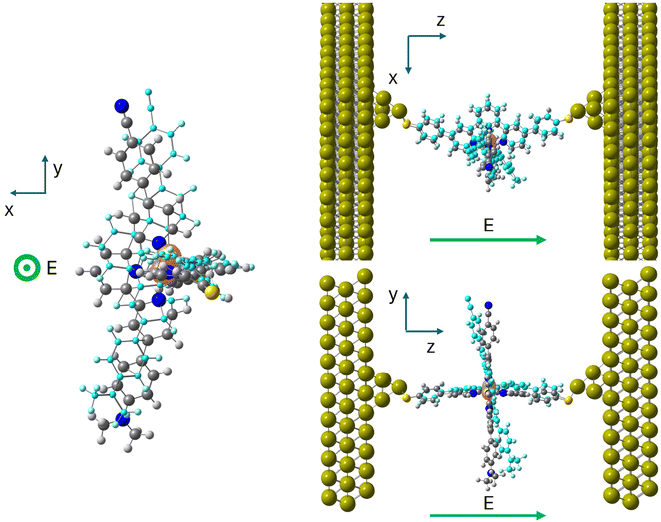
The molecular junctions (see Fig. 2 for a representative example) were created by first fully relaxing the geometry of the complex in both the HS and LS configurations. The complex was anchored to two Au(111) electrodes using terminal sulfur groups bonded to the top atom of a four-gold-atom pyramid attached to each surface. The unit cell was periodically repeated in three directions and consisted of the complex between two 12 × 9 Au(111) slabs, each three layers deep. This arrangement has six Au layers (approximately 12 Å) between the periodic repetitions of the complex in the transport direction and about 11 Å in the transverse directions. Throughout all geometry optimizations, the unit cell size was allowed to relax in the transport direction and kept fixed in the transverse directions.

Fig. 2 Side (left) and top (right) views of the molecule inside the junction.

To calculate the transport properties, both Au(111) surfaces were reduced to slabs of 5 × 4 atoms, with additional vacuum space added in the transverse directions to maintain a distance greater than 10 Å between the periodic images. The spin-resolved transport properties were computed using a combination of DFT and the Keldysh nonequilibrium Green's function (NEGF) formalism, known as the DFT-NEGF methodology.^53–55 Under a finite bias voltage V_b, the spin-resolved current I_σ through the junction is given by the Landauer–Büttiker formula:⁵⁶

where σ = α, β is the spin index, and f_L/R and μ_L/R are the Fermi distribution function and chemical potential, respectively, of the left (L) and right (R) electrodes. The spin-resolved transmission coefficient is defined by:

T_σ(E,V_b) = T_r[Γ_LG^rΓ_RG^a]

where G^r and G^a are the retarded and advanced Green's functions and Γ_L/R are the self-energy matrices, which describe the coupling between the electrodes and the central scattering region.

3. Results and discussion

3.1. Isolated molecule

We first optimized the geometries of both molecules 1 and 2 in the LS and HS states and evaluated the energy separation between these two spin states. The ΔE(HS–LS) transition energy evaluated from DFT calculations is 69.1 and 69.5 kJ mol⁻¹ for molecules 1 and 2, respectively (Table 1). The same HS–LS separation is found for molecule 1 with terminal thioacetyl groups in the horizontal tpy ligand (ΔE(HS–LS) = 68.5 kJ mol⁻¹). Then neither the terminal anchor groups nor the R1 and R2 groups (electron-withdrawing and electron-donating groups) affect the relative stability of the two spin states. The transition enthalpies, once the zero-point and thermal corrections are included, are 65.1 and 65.4 kJ mol⁻¹ at 298 K, respectively. These values are higher than those reported for thermally activated spin-crossover systems, usually in the range of 10–20 kJ mol⁻¹ for systems with transition temperatures around 150–250 K.^{13–17,20,57,58} In fact, the parent homoleptic [Fe(tpy)₂]⁺² compound is in the LS state at room temperature and even at temperatures as high as 450 K, which implies a large value of the transition enthalpy, and it can only be converted to the HS state by excitation with light.⁵⁹ Additionally, previous evaluation of the HS–LS gap in the homoleptic [Fe(tpy)₂]⁺² compound gave a value of 70.4 kJ mol⁻¹ at the CASSCF/CASPT2 level,⁶⁰ a large HS–LS gap value in line with our estimates for the heteroleptic [Fe(tpy)₂]⁺² complexes. Since the terminal R1 and R2 groups have a minor impact on the transition energy, we focus hereafter on molecule 1.

Table 1 Transition electronic energy (kJ mol⁻¹) and transition enthalpy (kJ mol⁻¹) and entropy (J K⁻¹ mol⁻¹) at 298 K for complexes 1 and 2 from TPSSh calculations with the def2svp basis set

	1	2
Two views of complex 1, the blue and red circles highlight the electron-withdrawing R1 and the electron-donating R2 groups, respectively.
R1	CN	CF3
R2	N(Me)2	N(Me)2
ΔE (HS–LS)	69.1	69.3
ΔH (HS–LS)	65.1	65.3
ΔS (HS–LS)	77.9	68.5

---

The main geometrical parameters of molecule 1 in the LS and HS states are presented in Table 2. They essentially differ by the Fe–N bond distances, larger for the HS state as expected. In both molecules, the tpy ligands are perpendicular to each other, but note that the N–Fe–N bond angles for the N atoms of the same tpy ligand are far from 180°, particularly for the HS molecule. Similar trends are obtained for molecule 2.

Table 2 Main geometrical parameters of molecule 1 isolated and inside the junction

	LS		HS
	Isolated	Junction	Isolated	Junction
Fe, N, C, and H atoms are represented by orange, blue, grey and white balls. Neq1, Neq2 and Neq3 belong to the horizontal tpy ligand, while Neq4, Nax5 and Nax6 belong to the vertical tpy ligand. Neq1–Fe–Neq2 and Neq3–Fe–Neq4 correspond to the bond angle between the Fe atom and two equatorial N atoms of the same tpy ligand or different tpy ligands, respectively. Bond distances are given in Å and angles are given in degrees (°).
Fe–Neq1	1.982	1.965	2.199	2.162
Fe–Neq2	1.982	1.973	2.200	2.154
Fe–Neq3	1.891	1.873	2.139	2.075
Fe–Neq4	1.890	1.874	2.126	2.069
Fe–Nax5	1.980	1.953	2.203	2.136
Fe–Nax6	1.982	1.961	2.158	2.187
Neq4–Fe–Nax5	81.1	81.3	74.1	75.4
Neq1–Fe–Neq2	162.2	162.1	149.1	150.0
Neq3–Fe–Neq4	179.8	178.7	176.4	177.9
Nax5–Fe–Nax6	162.2	162.3	148.9	150.3
C–C–C–S	179.8	169.4	179.6	163.8

---

3.2. Geometry and electronic structure of the molecule inside the junction

In a second step, molecule 1 is reoptimized inside the junction (Fig. 2), the horizontal tpy ligand contacts the gold electrodes through the sulfur anchoring atoms as in the hypothesized scenarios reported by Harzmann et al.³⁰ and in previous calculations on the homoleptic [Fe(tpy)₂]⁺² complex by Frisenda et al.³²

The main geometrical differences between the isolated and the in-junction molecule concern the position of the anchoring sulfur atom with respect to the terminal phenyl group (in/out of the phenyl plane, C–C–C–S torsion angle in Table 2) and the mean Fe–N distances, which are slightly shorter in the junction, as shown in Table 2. The Cartesian coordinates of the optimized junctions are reported in the ESI.† The ΔE(HS–LS) transition energy of the molecule in the junction decreases to 42.1 kJ mol⁻¹, calculated with the TPSSh functional as the isolated molecule. We used models containing the molecule in the LS or HS optimized geometry inside the junction and two 10 Au pyramids simulating the gold electrodes. This energy separation between the two spin states includes both the transition energy itself and the interaction with the electrodes that favours the HS solution. Then, just the immobilization inside the junction reduces the HS–LS gap, favouring the occurrence of spin transition.

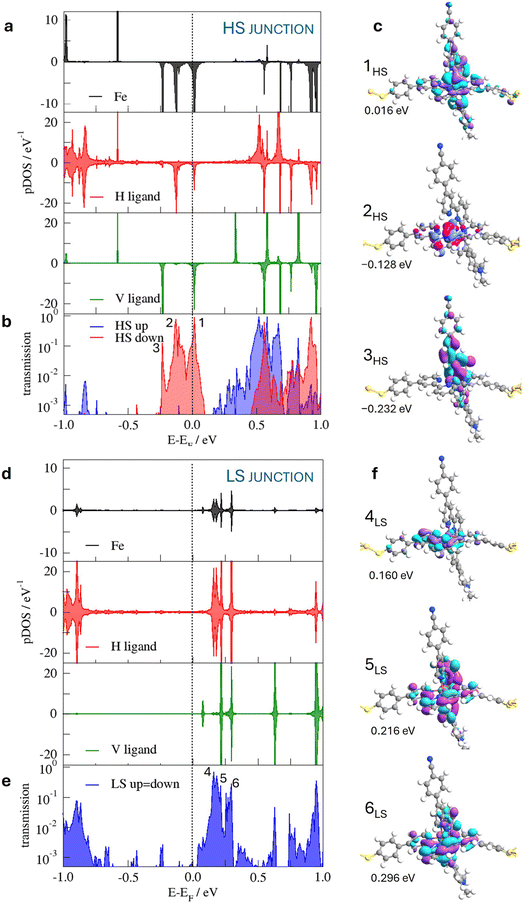
The densities of states of the LS and HS configurations of the molecule in the junction, projected on the Fe centre and the vertical and horizontal tpy ligands, are presented in Fig. 3. The pDOS is restrained in the region between −1 eV and 1 eV, corresponding to the states that can be probed with the bias voltages employed by Harzmann et al.³⁰ It is noted that the different states are found close to the Fermi level depending on the spin state of the molecule. The HS molecule presents occupied states close to the Fermi level with contributions from Fe 3d t2g-like orbitals and vertical tpy and horizontal tpy π ligands, absent in the case of the junction based on the LS molecule. The Fe 3d_xz and Fe 3d_yz orbitals mixed with the vertical tpy ligand π orbitals, while the Fe 3d_xy orbital just combined with the horizontal tpy ligand π orbitals. The projected spin-down population on each of these 3d tg-like orbitals is ∼0.3e (note that a smearing function is employed to facilitate the convergence and the 3d tg-like orbitals are quite close in energy) and the total magnetic moment of the Fe center is 3.68μ_B, in line with a local S = 2 spin state. In the case of the LS-based junction, the occupied Fe 3d t2g-like orbitals are far from the Fermi level; only the states resulting from the combination of the empty tpy ligand π orbitals with a minor contribution of the Fe 3d orbitals would participate in the conduction for low bias voltages.

Fig. 3 (a and d) Projected density of states on the Fe centre (black) and the horizontal (red) and vertical tpy (green) ligands for the HS (top) and LS (bottom) molecules in the junction. (b and e) Spin-resolved transmission spectra at zero-bias for the HS (top) and LS (bottom) molecules. (c and f) Transmission eigenfunctions at the transmission peaks close to the Fermi level for the HS (top) and LS (bottom) molecules in the junction.

This spin-dependent distribution of the accessible states of the SCO-based junction has an impact on the electronic coupling with the electrodes. In fact, at zero-bias, the conductance is higher for the HS state (6.74 × 10⁻² G₀) than for the LS state (1.91 × 10⁻³ G₀). The spin-resolved transmission spectra at zero-bias (Fig. 3) show the differences observed in the pDOSs for the HS and LS molecules. For the junction with the HS molecules, there are three transmission peaks close to the Fermi level, corresponding to the electronic coupling of the electrodes with occupied states of the molecule. In the resonance peak 1_HS, both the vertical and horizontal tpy ligand orbitals are involved; the transmission peak 2_HS is mainly dominated by the horizontal tpy ligand, while the principal contribution to the 3_HS peak comes from the vertical tpy ligand, as confirmed by the plots of the transmission eigenfunctions (Fig. 3). In the case of the LS-containing junctions the transmission peaks correlate with the coupling with empty states of the molecule, the peak at lower energy mainly localized on the horizontal tpy ligand (4_LS peak), while peaks at higher energy (5_LS and 6_LS) manifest the participation of both tpy ligands. Note that the Fe centre contributes to all the transmission peaks around the Fermi level, mainly in the HS-based junction. The π orbitals of the horizontal tpy ligand play a crucial role in the conduction for both spin states. The pDOS suggests that at low bias voltages, the transport is mainly by holes in the case of the HS-based junction and by electrons in the case of the LS junction.

3.3. External perturbation of the molecule inside the junction

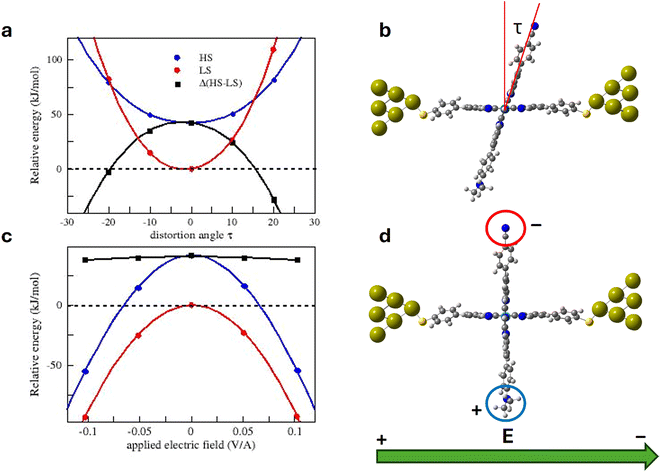
It has been hypothesized that in this family of systems, the applied electric field interacts with the molecule dipole and produces the distortion of the coordination sphere of the molecule. This distortion at the end is responsible for the switching. We have analysed the impact on the relative stability of the HS and LS molecules of both factors, respectively, and finally determined the electric field-triggered distortion from the optimization of the molecules in the presence of the applied field.

3.3.1 Distortion of the coordination sphere. We have explored the impact of the distortion of the dihedral angle between the two tpy ligands on the spin transition first in the absence of the electric field. Using the geometry adopted in the junction for each electronic state, the vertical tpy ligand was rotated in a clockwise (τ > 0) or anticlockwise direction (τ < 0). To reduce the computational costs of these calculations, the model of the electrodes was reduced to two 10-gold atom pyramids, with the geometry adopted in the junction. The distortion destabilizes both states, but the effect is markedly stronger for the LS state (red line in Fig. 4), reducing the separation between the HS and LS states. For a distortion of |τ| ∼ 15° with respect to the vertical tpy ligand, the HS and LS states are degenerated. A slight asymmetry with respect to the turning direction is observed, and the clockwise rotation reaches the degenerated states with a smaller distortion angle compared to the counterclockwise one. This asymmetry aligns with the slightly different reported values for the negative and positive switching voltages (−0.5 V vs. 0.7 V) in junctions with hysteresis.³⁰

Fig. 4 (a) Impact of the distortion of the coordination sphere of the Fe centre on the relative energy of the LS (red) and HS (blue) states in molecular junctions. All values referred to the non-distorted LS state as a function of the dihedral angle. The black color shows the energy difference between the LS and HS solutions. (b) Scheme of the distortion of the Fe coordination sphere. The positive and negative τ values correspond to the clockwise and anticlockwise turning directions, respectively. (c) Impact of the applied electric field along the horizontal tpy ligand on the relative LS and HS energies and the HS–LS gap. (d) Scheme of the molecule oriented with respect to the external electric field.

3.3.2 Impact of the external electric field on the relative energy of HS and LS states. Additionally, the external electric field associated with the applied bias voltage can modify the relative energy of the LS and HS states. We evaluated the energy of the molecule in the junction exposed to an external electric field along the S⋯Fe⋯S axis (z axis), emulating the electric field due to the applied bias voltage between the electrodes (Fig. 4). The geometry of the molecule is kept fixed, without further optimization. Hence, in this set of single-point calculations, we just analyse how the electrostatic interaction between the molecule and the applied electric field impacts the electronic energies of the HS and LS states. We take the convention such that the positive electric fields point from the left to the right electrode and correspond to negative bias voltages. The dipole moment of the molecule is larger for the HS state than for the LS state, but the dominant contribution of the dipole moment runs along the R1⋯Fe⋯R2 axis (y axis, see Fig. 2), orthogonal to the applied field. The interaction with the external field was then controlled by the z-component of the dipole moment, which although small, is larger for the HS state than for the LS state. As a result, the HS state is slightly favoured over the LS state, smoothly reducing the HS–LS separation (Fig. 4). This indicates that the electric field could promote the spin transition of the molecule immobilized in the junction, although high electric fields would be required if the molecule rigidly maintains the perpendicular arrangement of the two tpy ligands in the presence of the electric field.

3.3.3. Voltage-induced distortion. Distortion is a destabilizing perturbation that penalizes the LS state, while the electric field along the electrodes (slightly) favours the HS state due to the stabilizing interaction with the z-component of the electric dipole moment. Finally, we optimized the geometry of the molecule in the presence of a homogeneous positive electric field along the z axis (E = 0.1 V Å⁻¹), fixing the positions of the S atoms and the gold clusters. Fig. 5 shows the superposition of the geometry of the LS molecule optimized in the junction with and without the applied field (see Fig. S1† for a similar plot for the HS molecule-based junction).

Fig. 5 Three views of the LS molecule in the junction optimized in the presence of an external electric field of 0.1 V Å⁻¹ along the z axis. The orange, grey, blue, yellow and white balls correspond to the Fe, C, N, S and H atoms in the original position and the cyan atoms correspond to the molecule in the presence of the field.

The interaction of the electric field with the dipole moment of the molecule produces the counterclockwise rotation of the vertical tpy ligand for a positive electric field, as shown in Fig. 5. The dihedral angle between the tpy ligands in the presence of the applied field is about 10° for both spin states. The molecule not only rotates in the yz plane, but also in the xy plane, particularly the HS molecule (rotation around the z axis of about 16° for the LS molecule and about 36° for the HS molecule). The additional distortion on the xy plane is similar to the tpy rocking motion found in the parent homoleptic [Fe(tpy)₂]⁺², considered as a key motion to facilitate the intersystem crossing and favour the spin transition.⁶¹ The distorted geometry is not benefited in the absence of the electric field, as clearly shown in Fig. 4a, but the interaction between the dipole and the electric field compensates for the stability loss due to the distortion. Compared with the situation where only a 10° counterclockwise rotation is allowed, the rocking motion introduces an additional stabilization of both spin states, favoring the HS state over the LS state. Hence, in the presence of the electric field and once the geometry is relaxed, the energy separation between the two spin states is reduced by 25%. Then, there exists a certain value of the bias voltage that promotes such a distortion that both spin states are degenerated. The distortion is due to the interaction with the applied electric field, and this distortion at the end triggers the switching, as experimentally observed. It should be noted that our model just captures one of the possible arrangements of the molecule in the junction. The threshold voltage triggering the switching might vary from junction to junction, depending on the arrangement of the electrodes and the bridging molecule, as illustrated by the histogram of the switching bias voltages reported by Harzmann et al.³⁰ These authors also showed that for a given junction, the threshold voltage required to trigger the spin transition increases linearly with the separation between the electrodes. In other words, if the electrode spacing increases, a higher bias voltage would be necessary to reach the threshold value of the electric field.

It is also noted that the applied electric field of 0.1 V Å⁻¹ in our calculations corresponds to a bias voltage of ≈2 V (separation between the electrodes is about 20 Å). This value is higher than those employed in the experimental junctions displaying voltage-dependent bistabilities.³⁰ This discrepancy can be related to limitations of our computational model and/or methodology, but it is also important to keep in mind that the electric field due to the bias voltage is not homogeneous in the junction, and local electric fields two or three times larger than the homogeneous one can operate inside the junction.⁶² Then lower bias voltages could produce a similar effect on the molecule geometry.

3.4. Transport through the bridging molecule

The transport properties of the junction depend on the spin state of the bridging molecule. Fig. 6 shows the I–V curve for the junction with molecules in the HS state (blue dots) or the LS state (red dots). As expected, the current increases with increasing bias voltage, the changes being more significant for one of the spin states. The current through the HS molecule is higher than through the LS molecule in all the explored voltages (Fig. 6), in line with previous studies on single-molecule junctions containing SCO complexes,^{9,10,24,28,32,33,50,63} although a large diversity of behaviours has also been reported, as devices with indistinguishable HS–LS conductance⁶⁴ or the LS state being more conductive than the HS state.^65–68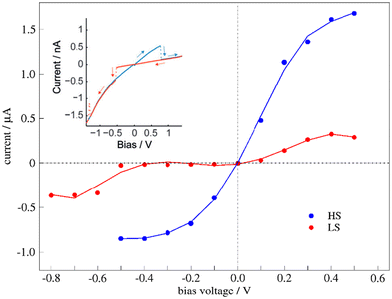

Fig. 6 Simulated I–V plots of the junction with a bridging molecule in the HS (blue line) or LS state (red line). The inset corresponds to the experimental I–V plots with a hysteresis window around the switching point, reproduced with permission from Angew. Chem., Int. Ed.³⁰ Copyright 2015 John Wiley and Sons.

If we compare it with the experimental I–V curves showing bistability (Fig. 6 inset), our model for the molecular junction nicely represents the situation with a hysteresis window. Then, for the reported hysteretic I–V characteristics, the high current regime in the hysteresis window corresponds to the HS molecule, while the low current regime represents the LS state of the immobilized molecule. Neither our I–V curves nor the experimental I–V plots are symmetrically distributed around the zero-bias voltage. Note that in our simulations of the transport properties at a certain V bias voltage, both electrodes are symmetrically shifted upward (+V/2) or downward (−V/2). The slight asymmetry observed in our simulated I–V plots, and for extension also in the experimental one, should be related to singularities of the molecule that distinguish between the clockwise and counterclockwise distortions (Fig. 4), and then between the positive and negative electric fields (bias voltage).

3.5. Mechanism for hysteretic switching

Once we have verified that the electric field can provide the energy required to distort the molecule and that there exists a certain electric field, the switching field, for which the LS and HS states are degenerated, we then analyze a possible scenario to explain the molecular junction bistability and the hysteretic I–V characteristics (Fig. 6).

The molecules in the junction are preferably in the LS state (1 in Fig. 7). Under a positive electric field (a negative bias voltage), the vertical tpy ligand rotates counterclockwise (2). For electric fields smaller than the switching field with a small torque, the LS state is more stable than the HS state, and it manifests as a low-current state. For a large enough positive electric field, the LS and HS states are degenerated (3). The LS to HS switching takes place and the current intensity increases with a jump to the high current state. For a stronger electric field, the molecule remains in the HS state (4). If now the voltage sweeping is reversed, the molecule rotates clockwise, retaining the high current state (HS) (5 and 6) until the applied field is large enough. Once the switching field is reached again (7), the molecule switches from the HS state to the LS state, and the current jumps to a low-current state. Increasing the voltage now does not change the current state (8). Fig. 7 shows diagrams of the possible configurations of the molecule in the junction during the forward and backward bias sweeps, as well as the corresponding current state in the I-vs.-V plot.

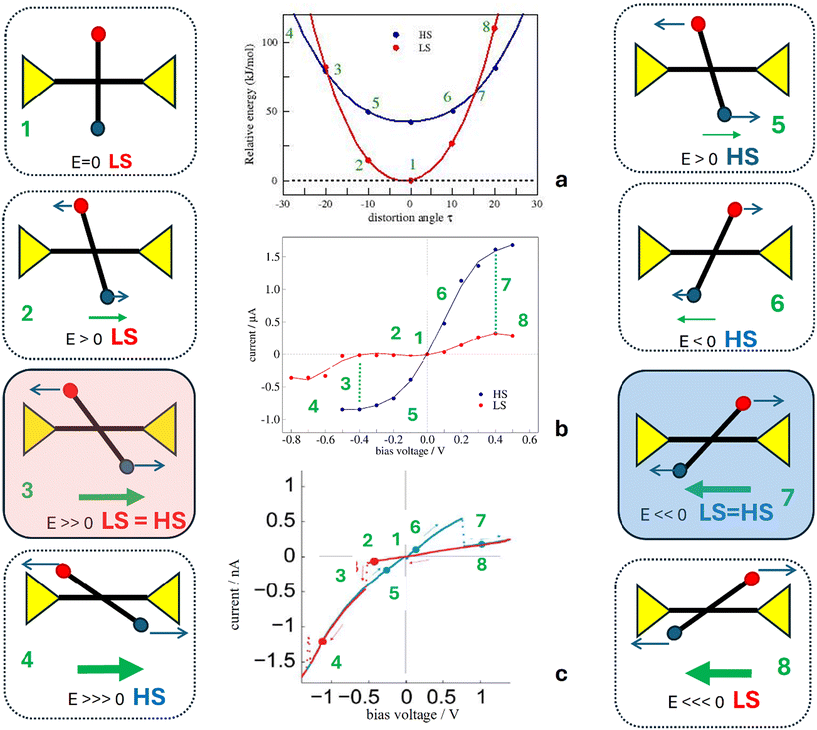Fig. 7 Sketch of a possible scenario for the molecular junction to explain the I–V hysteresis. The red and blue dots represent the electron-withdrawing R1 and electron-donating R2 groups, respectively. The distortion induced for the applied field modifies the HS and LS energies in different ways, as shown in panel (a) and also modifies the I–V characteristics resulting from the NEGF-DFT calculations, as shown in panel (b), compared with the observed bistability in the I–V characteristics in panel (c), adapted with permission from Angew. Chem., Int. Ed.³⁰ Copyright 2015 John Wiley and Sons.

4. Conclusions

The possibility of triggering the spin transition in SCO complexes by means of a bias voltage has been experimentally demonstrated many times, although in most of the cases, the mechanisms governing this process remain to be clarified. In this work, we have investigated by means of density functional theory-based calculations the mechanism controlling the voltage-dependent bistabilities found in a family of [Fe^II(tpy)₂]⁺² SCO complexes, in which one tpy ligand is functionalized with the R1 and R2 groups of different electronegativities, acting as a push–pull system.

We have explored a single conformation for the molecule inside the junction and tried to explain the most appealing of the different voltage-dependent bistability features found by Harzmann et al. with a hysteresis window.

A model of the molecular junction was built where the molecule is connected to gold through terminal sulfur groups in the horizontal tpy ligand. The simulated I-vs.-V curve presents features compatible with the hysteretic switching behaviour found in some of the experimental junctions, where the high current state can be associated with the HS molecule. The higher conductance of the junctions based on HS molecules can be rationalized by means of the projection of the density of states on the molecular orbitals and the corresponding transmission peaks close to the Fermi level. We demonstrated that a distortion of |τ| ∼ 15° on the dihedral angle formed by the tpy ligands is enough to equal the energy of the LS and HS states of the molecule and this distortion can be induced by an homogeneous electric field along the z-axis, besides additional motions on the xy plane, associated with the rocking of the tpy ligand.

Our results confirm the hypothesized mechanism for Harzmann et al.³⁰ to explain the hysteresis in this type of junction, but without the need for long-range interactions between the pending groups of the vertical tpy ligand and the electrodes. Additional configurations of the molecule inside the junction should be explored to explain the other types of bistabilities reported for this family of SCO-based molecular junctions.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the financial support through grant PID2021-127674NB-I00 funded by MICIU/AEI/10.13039/501100011033/FEDER/UE. The technical support of the Supercomputing Team of the Centro Informático Científico de Andalucía (CICA) and the access to the computational facilities of the “Centro de Servicios de Informática y Redes de Comunicaciones” (CSIRC, Universidad de Granada, Spain) are also acknowledged.

References

1. S. V. Aradhya and L. Venkataraman, Single-molecule junctions beyond electronic transport, Nat. Nanotechnol., 2013, 8, 399–410.
2. J. L. Zhang, J. Q. Zhong, J. D. Lin, W. P. Hu, K. Wu, G. Q. Xu, A. T. S. Wee and W. Chen, Towards single molecule switches, Chem. Soc. Rev., 2015, 44, 2998–3022.
3. L. Sun, Y. A. Diaz-Fernandez, T. A. Gschneidtner, F. Westerlund, S. Lara-Avila and K. Moth-Poulsen, Single-molecule electronics: from chemical design to functional devices, Chem. Soc. Rev., 2014, 43, 7378–7411.
4. M. L. Perrin, E. Burzurí and H. S. J. van der Zant, Single-molecule transistors, Chem. Soc. Rev., 2015, 44, 902–919.
5. P. Liljeroth, J. Repp and G. Meyer, Current-induced hydrogen tautomerization and conductance switching of naphthalocyanine molecules, Science, 2007, 317, 1203–1206.
6. J. Henzl, M. Mehlhorn, H. Gawronski and K. H. Rieder, Morgenstern, K. Reversible cis-trans isomerization of a single azobenzene molecule, Angew. Chem., Int. Ed., 2006, 45, 603–606.
7. X. H. Qiu, G. V. Nazin and W. Ho, Mechanisms of Reversible Conformational Transitions in a Single Molecule, Phys. Rev. Lett., 2004, 93, 196806.
8. N. Pavliček, B. Fleury, M. Neu, J. Niedenführ, C. Herranz-Lancho, M. Ruben and J. Repp, Atomic Force Microscopy Reveals Bistable Configurations of Dibenzo[a,h]thianthrene and their Interconversion Pathway, Phys. Rev. Lett., 2012, 108, 086101.
9. T. G. Gopakumar, F. Matino, H. Naggert, A. Bannwarth, F. Tuczek and R. Berndt, Electron-Induced Spin Crossover of Single Molecules in a Bilayer on Gold, Angew. Chem., Int. Ed., 2012, 51, 6262–6266.
10. F. Prins, M. Monrabal-Capilla, E. A. Osorio, E. Coronado and H. S. J. van der Zant, Room-Temperature Electrical Addressing of a Bistable Spin-Crossover Molecular System, Adv. Mater., 2011, 23, 1545–1549.
11. V. Prudkovskiy, I. Arbouch, A. Léaustic, P. Yu, C. Van Dyck, D. Guérin, S. Lenfant, T. Mallah, J. Cornil and D. Vuillaume, Terphenylthiazole-based self-assembled monolayers on cobalt with high conductance photo-switching ratio for spintronics, Nanoscale, 2022, 14, 5725–5742.
12. S. Kamilya, B. Dey, K. Kaushik, S. Shukla, S. Mehta and A. Mondal, Realm of Spin State Switching Materials: Toward Realization of Molecular and Nanoscale Devices, Chem. Mater., 2024, 36, 4889–4915.
13. P. Gütlich, A. Hauser and H. Spiering, Thermal and Optical Switching of Iron(II) Complexes, Angew. Chem., Int. Ed. Engl., 1994, 33, 2024–2054.
14. M. Gruber, V. Davesne, M. Bowen, S. Boukari, E. Beaurepaire, W. Wulfhekel and T. Miyamachi, Spin state of spin-crossover complexes: From single molecules to ultrathin films, Phys. Rev. B:Condens. Matter Mater. Phys., 2014, 89, 195415.
15. K. S. Kumar and M. Ruben, Sublimable Spin Crossover Complexes: From Spin-State Switching to Molecular Devices, Angew. Chem., Int. Ed., 2021, 60, 7502–7521.
16. J. A. Real, A. B. Gaspar and M. C. Muñoz, Thermal, pressure and light switchable spin-crossover materials, Dalton Trans., 2005, 2062–2079.
17. K. S. Kumar and M. Ruben, Emerging trends in spin crossover (SCO) based functional materials and devices, Coord. Chem. Rev., 2017, 346, 176–205.
18. N. Xin, J. X. Guan, C. G. Zhou, X. J. N. Chen, C. H. Gu, Y. Li, M. A. Ratner, A. Nitzan, J. F. Stoddart and X. F. Guo, Concepts in the design and engineering of single-molecule electronic devices, Nat. Rev. Phys., 2019, 1, 211–230.
19. E. Burzuri, A. Garcia-Fuente, V. Garcia-Suarez, K. S. Kumar, M. Ruben, J. Ferrer and H. S. J. van der Zant, Spin-state dependent conductance switching in single molecule-graphene junctions, Nanoscale, 2018, 10, 7905–7911.
20. A. Bousseksou, G. Molnár, L. Salmon and W. Nicolazzi, Molecular spin crossover phenomenon: recent achievements and prospects, Chem. Soc. Rev., 2011, 40, 3313–3335.
21. K. Kaushik, S. Mehta, M. Das, S. Ghosh, S. Kamilya and A. Mondal, Stimuli-responsive magnetic materials: impact of spin and electronic modulation, Chem. Commun., 2023, 59, 13107–13124.
22. G. Molnar, S. Rat, L. Salmon, W. Nicolazzi and A. Bousseksou, Spin Crossover Nanomaterials: From Fundamental Concepts to Devices, Adv. Mater., 2018, 30, 17003862.
23. D. Li, Y. Tong, K. Bairagi, M. Kelai, Y. J. Dappe, J. Lagoute, Y. Girard, S. Rousset, V. Repain and C. Barreteau, et al., Negative Differential Resistance in Spin-Crossover Molecular Devices, J. Phys. Chem. Lett., 2022, 13, 7514–7520.
24. T. Miyamachi, M. Gruber, V. Davesne, M. Bowen, S. Boukari, L. Joly, F. Scheurer, G. Rogez, T. K. Yamada and P. Ohresser, et al., Robust spin crossover and memristance across a single molecule, Nat. Commun., 2012, 3, 938.
25. M. Gruber, T. Miyamachi, V. Davesne, M. Bowen, S. Boukari, W. Wulfhekel, M. Alouani and E. Beaurepaire, Spin crossover in Fe(phen)₂(NCS)₂ complexes on metallic surfaces, J. Chem. Phys., 2017, 146, 092312.
26. T. Jasper-Toennies, M. Gruber, S. Karan, H. Jacob, F. Tuczek and R. Berndt, Robust and Selective Switching of an FeIII Spin-Crossover Compound on Cu2N/Cu(100) with Memristance Behavior, Nano Lett., 2017, 17, 6613–6619.
27. S. A. Tawfik, L. Weston, X. Y. Cui, S. P. Ringer and C. Stampfl, Near-Perfect Spin Filtering and Negative Differential Resistance in an Fe(II)S Complex, J. Phys. Chem. Lett., 2017, 8, 2189–2194.
28. N. Montenegro-Pohlhammer, S. K. Kuppusamy, G. Cárdenas-Jirón, C. J. Calzado and M. Ruben, Computational demonstration of isomer- and spin-state-dependent charge transport in molecular junctions composed of charge-neutral iron(II) spin-crossover complexes, Dalton Trans., 2023, 52, 1229–1240.
29. Y. Gu, Y. Hu, J. Huang, Q. Li and J. Yang, Spin-Crossover and Coherent Transport Behaviors of a Six-Coordinate Iron(II) Complex with a N₄O₂ Donor Set, J. Phys. Chem. C, 2019, 123, 16366–16372.
30. G. D. Harzmann, R. Frisenda, H. S. J. van der Zant and M. Mayor, Single-Molecule Spin Switch Based on Voltage-Triggered Distortion of the Coordination Sphere, Angew. Chem., Int. Ed., 2015, 54, 13425–13430.
31. T. Brandl, M. El Abbassi, D. Stefani, R. Frisenda, G. D. Harzmann, H. S. J. van der Zant and M. Mayor, Enhanced Separation Concept (ESC): Removing the Functional Subunit from the Electrode by Molecular Design, Eur. J. Org. Chem., 2019, 5334–5343.
32. R. Frisenda, G. D. Harzmann, J. A. Celis-Gil, J. M. Thijssen, M. Mayor and H. S. J. van der Zant, Stretching-Induced Conductance Increase in a Spin-Crossover Molecule, Nano Lett., 2016, 16, 4733–4737.
33. S. K. Kuppusamy, A. Mizuno, A. García-Fuente, S. van der Poel, B. Heinrich, J. Ferrer, H. S. J. van der Zant and M. Ruben, Spin-Crossover in Supramolecular Iron(II)–2,6-bis(1H-Pyrazol-1-yl)pyridine Complexes: Toward Spin-State Switchable Single-Molecule Junctions, ACS Omega, 2022, 7, 13654–13666.
34. S. M. Lindsay and M. A. Ratner, Molecular Transport Junctions: Clearing Mists, Adv. Mater., 2007, 19, 23–31.
35. S. Giménez-Santamarina, S. Cardona-Serra and A. Gaita-Ariño, Theoretical insights on the importance of anchoring vs molecular geometry in magnetic molecules acting as junctions, J. Magn. Magn. Mater., 2019, 485, 212–216.
36. L. A. Zotti, T. Kirchner, J.-C. Cuevas, F. Pauly, T. Huhn, E. Scheer and A. Erbe, Revealing the Role of Anchoring Groups in the Electrical Conduction Through Single-Molecule Junctions, Small, 2010, 6, 1529–1535.
37. G. D. Harzmann, M. Neuburger and M. Mayor, 4,4′′-Disubstituted Terpyridines and Their Homoleptic FeII Complexes, Eur. J. Inorg. Chem., 2013, 3334–3347.
38. R. Frisenda, S. Tarkuç, E. Galán, M. L. Perrin, R. Eelkema, F. C. Grozema and H. S. J. van der Zant, Electrical properties and mechanical stability of anchoring groups for single-molecule electronics, Beilstein J. Nanotechnol., 2015, 6, 1558–1567.
39. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
40. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, The ORCA quantum chemistry program package, J. Chem. Phys., 2020, 152, 224108.
41. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2016.
42. A. Schäfer, H. Horn and R. Ahlrichs, Fully optimized contracted Gaussian basis sets for atoms Li to Kr, J. Chem. Phys., 1992, 97, 2571–2577.
43. A. Schäfer, C. Huber and R. Ahlrichs, Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr, J. Chem. Phys., 1994, 100, 5829–5835.
44. P. J. Hay and W. R. Wadt, Ab initio effective core potentials for molecular calculations. Potentials for K to Au including the outermost core orbitals, J. Chem. Phys., 1985, 82, 299–310.
45. S. Smidstrup, T. Markussen, P. Vancraeyveld, J. Wellendorff, J. Schneider, T. Gunst, B. Verstichel, D. Stradi, P. A. Khomyakov and U. G. Vej-Hansen, et al., QuantumATK: an integrated platform of electronic and atomic-scale modelling tools, J. Phys.:Condens. Matter, 2020, 32, 015901.
46. M. J. van Setten, M. Giantomassi, E. Bousquet, M. J. Verstraete, D. R. Hamann, X. Gonze and G. M. Rignanese, The PseudoDojo: Training and grading a 85 element optimized norm-conserving pseudopotential table, Comput. Phys. Commun., 2018, 226, 39–54.
47. B. Hammer, L. B. Hansen and J. K. Nørskov, Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 7413–7421.
48. K. P. Kepp, Theoretical Study of Spin Crossover in 30 Iron Complexes, Inorg. Chem., 2016, 55, 2717–2727.
49. O. S. Siig and K. P. Kepp, Iron(II) and Iron(III) Spin Crossover: Toward an Optimal Density Functional, J. Phys. Chem. A, 2018, 122, 4208–4217.
50. N. Montenegro-Pohlhammer, R. Sánchez-de-Armas and C. J. Calzado, Deposition of the Spin Crossover FeII–Pyrazolylborate Complex on Au(111) Surface at the Molecular Level, Chem. – Eur. J., 2021, 27, 712–723.
51. D. Arias-Olivares, R. Sánchez-de-Armas and C. J. Calzado, Theoretical approach to the one-step versus two-step spin transitions in Hofmann-like FeII SCO metal-organic frameworks, Mater. Today Chem., 2023, 30, 101489.
52. D. Arias-Olivares, R. S. de Armas and C. J. Calzado, Guest-dependent spin transitions in Hofmann-like FeII SCO metal–organic frameworks: hints from quantum chemistry calculations, J. Mater. Chem. C, 2024, 12, 14924–14935.
53. J. Taylor, H. Guo and J. Wang, Ab initio modeling of quantum transport properties of molecular electronic devices, Phys. Rev. B:Condens. Matter Mater. Phys., 2001, 63, 245407.
54. J. Taylor, H. Guo and J. Wang, Ab initio modeling of open systems: Charge transfer, electron conduction, and molecular switching of a C₆₀ device, Phys. Rev. B:Condens. Matter Mater. Phys., 2001, 63, 121104.
55. M. Brandbyge, J.-L. Mozos, P. Ordejón, J. Taylor and K. Stokbro, Density-functional method for nonequilibrium electron transport, Phys. Rev. B:Condens. Matter Mater. Phys., 2002, 65(16), 165401.
56. M. Büttiker, Y. Imry, R. Landauer and S. Pinhas, Generalized many-channel conductance formula with application to small rings, Phys. Rev. B:Condens. Matter Mater. Phys., 1985, 31(10), 6207–6215.
57. L. Kipgen, M. Bernien, F. Tuczek and W. Kuch, Spin-Crossover Molecules on Surfaces: From Isolated Molecules to Ultrathin Films, Adv. Mater., 2021, 33, 2008141.
58. M. Paez-Espejo, M. Sy and K. Boukheddaden, Elastic Frustration Causing Two-Step and Multistep Transitions in Spin-Crossover Solids: Emergence of Complex Antiferroelastic Structures, J. Am. Chem. Soc., 2016, 138, 3202–3210.
59. A. Hauser, C. Enachescu, M. L. Daku, A. Vargas and N. Amstutz, Low-temperature lifetimes of metastable high-spin states in spin-crossover and in low-spin iron(II) compounds: The rule and exceptions to the rule, Coord. Chem. Rev., 2006, 250, 1642–1652.
60. M. Pápai, G. Vankó, C. de Graaf and T. Rozgonyi, Theoretical Investigation of the Electronic Structure of Fe(II) Complexes at Spin-State Transitions, J. Chem. Theory Comput., 2013, 9, 509–519.
61. J. Nance, D. N. Bowman, S. Mukherjee, C. T. Kelley and E. Jakubikova, Insights into the Spin-State Transitions in [Fe(tpy)2]2+: Importance of the Terpyridine Rocking Motion, Inorg. Chem., 2015, 54, 11259–11268.
62. N. Montenegro-Pohlhammer, R. Sánchez-de-Armas, M. Gruber and C. J. Calzado, Mechanisms for the Spin-State Switching of Strapped Ni-Porphyrin Complexes Deposited on Metal Surfaces: Insights from Quantum Chemical Calculations, Small, 2024, 2406313.
63. D. Aravena and E. Ruiz, Coherent Transport through Spin-Crossover Single Molecules, J. Am. Chem. Soc., 2012, 134, 777–779.
64. C. Lefter, S. Rat, J. S. Costa, M. D. Manrique-Juarez, C. M. Quintero, L. Salmon, I. Seguy, T. Leichle, L. Nicu and P. Demont, et al., Current Switching Coupled to Molecular Spin-States in Large-Area Junctions, Adv. Mater., 2016, 28, 7508–7514.
65. R. Sanchez-de-Armas, N. Montenegro-Pohlhammer, A. Develioglu, E. Burzuri and C. J. Calzado, Spin-crossover complexes in nanoscale devices: main ingredients of the molecule-substrate interactions, Nanoscale, 2021, 13, 18702–18713.
66. J. Villalva, A. Develioglu, N. Montenegro-Pohlhammer, R. Sánchez-de-Armas, A. Gamonal, E. Rial, M. García-Hernández, L. Ruiz-Gonzalez, J. S. Costa and C. J. Calzado, et al., Spin-state-dependent electrical conductivity in single-walled carbon nanotubes encapsulating spin-crossover molecules, Nat. Commun., 2021, 12, 1578.
67. A. Rotaru, J. Dugay, R. P. Tan, I. A. Gural'skiy, L. Salmon, P. Demont, J. Carrey, G. Molnar, M. Respaud and A. Bousseksou, Nano-electromanipulation of Spin Crossover Nanorods: Towards Switchable Nanoelectronic Devices, Adv. Mater., 2013, 25, 1745–1749.
68. J. Dugay, M. Giménez-Marqués, T. Kozlova, H. W. Zandbergen, E. Coronado and H. S. J. van der Zant, Spin Switching in Electronic Devices Based on 2D Assemblies of Spin-Crossover Nanoparticles, Adv. Mater., 2015, 27, 1288–1293.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr04935g

---