Open Access Article
Open Access ArticleMechanisms and effects of gas intercalation into ionic liquids confined within charged nanoscale volumes†
Fikret Aydin a,
Alex Abelson
a,
Alex Abelson b,
Stephen E. Weitzner
b,
Stephen E. Weitzner a,
Francesco Fornasiero
a,
Francesco Fornasiero a,
Tuan Anh Pham
a,
Tuan Anh Pham a,
Eric R. Meshot
a,
Eric R. Meshot b and
Steven F. Buchsbaum
b and
Steven F. Buchsbaum *b
*b
aPhysical and Life Sciences, Lawrence Livermore National Laboratory, Livermore, CA 94550, USA
bEngineering, Lawrence Livermore National Laboratory, Livermore, CA 94550, USA. E-mail: buchsbaum1@llnl.gov
First published on 25th February 2025
Abstract
Understanding the behavior of gas within confined ionic liquids (ILs) is important for a wide range of emerging energy, separation, and sensing technologies. However, the mechanisms governing gas solubility and molecular structure within these systems remain largely unknown. Here, we investigate the factors that dictate the intercalation and arrangement of CO2, N2 and O2, in a commonly used IL (1-butyl-3-methylimidazolium hexafluorophosphate, [BMIM+][PF6−]) confined within neutral and charged 2.1 nm diameter carbon nanotubes (CNTs) via molecular dynamics simulations and enhanced free energy sampling methods. Our simulations show that the gas selectivity in these systems can be explained by a competitive complex interplay between confinement, charge state of CNTs, and IL properties. We then experimentally validate a subset of these predictions using a novel device consisting of electrically addressable, IL-infilled CNTs which we expose to CO2 and O2 in a N2 background. Our findings help to disentangle the relative importance of tuning gas solubility and preferential proximity to the CNT wall for maximizing measurable changes of electrochemical signals. These insights provide a foundation for engineering future electrochemical systems utilized in gas sensing or separation applications.
1. Introduction
Ionic liquids (ILs) have gained significant attention in recent years due to their unique properties, such as low volatility, high electrochemical and thermal stability, and their ability to dissolve both polar and nonpolar substances.1 These liquid salts are further distinguished by the high degree of tunability of their physicochemical properties, which can be readily modulated by varying the chemical structure of each ion.2 Variations of the cation and anion, for example, have been shown to significantly affect the gas absorption capacity of ILs.3,4 The tunability of IL physicochemical properties can be further extended when ILs are placed under varying degrees of nanoconfinement, wherein the structural and transport behavior of ILs can deviate significantly from their bulk liquid state.5 Experimentally reported examples include shifting melting point,6 ion mobility,7,8 and accelerated charge-driven filling.9 In addition, confinement in 3–12 nm silica pores was demonstrated to enhance the solubility of CO2 in the IL.10 Such phenomena have motivated the incorporation of ILs into a wide variety of nano- and micro-structured fluidic and electronic devices designed to advance technologies, including energy storage, nanoreactors, gas/liquid separations, and sensing.11,12The unique combination of enhanced and tunable gas selectivity, fast transport properties, and broad material compatibility has elevated the interest in using confined ILs for gas separation and sensing applications. Despite significant progress towards this end, recent reports show mixed results when it comes to designing and testing laboratory scale devices. For example, studies aimed at assessing the performance of nanoconfined ILs for gas separation have yielded varying results, with some studies finding higher gas selectivity in ILs confined in nano or micro pores,13 while others report no improvement in selectivity.14 In addition, some studies demonstrate that the chemistry of the confining material can affect gas permeability, indicating that optimizing the properties of the IL alone may not be sufficient to effectively engineering gas separation technologies.15 Likewise, in the context of gas sensing applications, a variety of sensors based on confined-ILs have been tested including IL-filled nanopores on a quartz crystal microbalance16 and carbon nanotube (CNT)/IL paste resistive sensing;17 however, the exact role of confinement on sensing performance in these studies remains unclear.
The behavior of confined ILs is governed by a complex combination of different factors, such as short-range ion–ion interactions, molecular sizes and shapes, and charge distributions.18 This motivates the use of all-atom classical molecular dynamics (MD) simulations to clarify the set of chemical and structural features of confined ILs that promote favorable gas selectivity and transport behavior. Several computational studies employing MD have already been performed to examine the structural and transport behavior of confined ILs. For example, Pinilla et al.19 and Maolin et al.20 studied pure ILs under nanoconfinement and in contact with surfaces. The densities of both cations and anions in these studies were predicted to increase relative to the bulk state when the ILs were placed in contact with both hydrophilic and hydrophobic nanoporous materials such as silica pores or graphite surfaces.19,20 Several studies have also examined the interactions between CNTs and ILs. For example, Shim et al. have shown that ILs tend to self-organize into cylindrical shells around the outside of CNTs, whereas the structure of ILs confined within CNTs were observed to vary significantly depending on the diameter of the CNT.21 Additionally, self-diffusion coefficients of the ILs under nanoconfinement have been predicted to be much higher than those in bulk ILs.22,23
Compared to studies focusing on pure ILs under nanoconfinement, relatively few have considered the solubility and diffusion of gas molecules. For example, Tian et al. performed molecular dynamics and free energy simulations to investigate the diffusivity and solubility of CO2 and CH4 in an ionic porous-polymer aromatic framework.24 The authors showed that the polymeric structure creates nanoscale voids in the confined ILs, thus increasing gas solubility. Furthermore, it was found that gas solubility is higher in confined regions than in the bulk liquid, with CO2 having a greater solubility than CH4. In another study by Shi et al., Monte Carlo simulations were carried out to investigate gas absorption properties of an IL ([HMIM][Tf2N]) when confined in silica slit pores.25 Their findings revealed that the molar volume of the confined liquid is larger than its bulk counterpart, leading to a 1.1–3 times increase in the absorption of CO2, N2 and H2. Atomistic simulations were also used by Shi et al. to understand the effects of confinement on gas absorption in [HMIM][Tf2N] when confined within a model CNT.26 The ordered distribution of cations and anions in the CNTs was found to result in higher selectivity for CO2/H2 than both the bulk IL and the CNT.
In this study, we broaden the scope of previous investigations and further explore the impact of nanoconfinement and CNT surface charge on gas intercalation, resulting molecular rearrangements, and changes to charge distribution within the pore. In particular, 1-butyl-3-methylimidazolium hexafluorophosphate ([BMIM+][PF6−]) and CO2, O2 and N2 were selected for the IL and gasses, respectively. Single walled CNTs (SWCNTs) with an inner diameter of 2–3 nm were used as a model system to impose a high degree of confinement (i.e., pore and IL ion sizes of a similar order) and enable consistent computational and experimental analysis. We used atomistic MD simulations combined with enhanced free-energy sampling to study gas absorption within IL-filled CNTs with different types of surface charge. Selected computational predictions were then compared against measurements through the use of a new experimental platform that enables IL filling into horizontally aligned few-nm CNTs, electrochemical probing of their internal volume, and controlled delivery of gas to the surrounding environment. Our results enhance the understanding of the mechanisms governing gas behavior in nanoconfined ILs and provide insights into the key system factors that influence electrochemical signals. This provides a foundation for extrapolation to materials with varied pore sizes and degrees of disorder as well as developing improved design principles for gas separation and detection technologies.
2. Methods
2.1. Computational methods
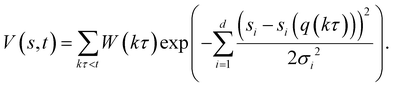 | (1) |
Here, σ is the width of the Gaussian for the ith CV, τ is Gaussian addition rate, W is the height of the Gaussian and si(q(kτ)) corresponds to the value of CV obtained from the configuration of the system at time kτ. By using this approach, the system is pushed to explore regions with different energy levels instead of residing in a local energy minimum for a long period of time. Unlike classical metadynamics, which risks overbiasing trajectories through the use of a constant Gaussian potential height,36 the WT-MetaD approach can achieve asymptotical convergence by tempering the Gaussian height over time via:
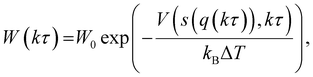 | (2) |
In this study, four independent WT-MetaD simulations were performed to determine the two-dimensional potential of mean force (2D PMF) for gas transport through a CNT filled with IL. Then, the minimum free energy path extracted from the 2D PMF was used to calculate one-dimensional (1D) PMF. The convergence of PMF curves was facilitated by using two CVs.37 The bias energy is deposited every 500 steps with a height of 0.018 kcal mol−1. In addition, the Gaussian potential height is tempered by a bias factor of 20, which corresponds to the ratio between the temperature of the CV and the system temperature.
 . The charge of each atom type was obtained from the site charge defined within the force field. The radial grid was configured to span from the center of the interior of the CNT (r = 0) to the CNT wall (r = R), with a bin spacing of Δr = R/(N − 1), grid sites at ri=(i − 1)Δr, and bin centers at
. The charge of each atom type was obtained from the site charge defined within the force field. The radial grid was configured to span from the center of the interior of the CNT (r = 0) to the CNT wall (r = R), with a bin spacing of Δr = R/(N − 1), grid sites at ri=(i − 1)Δr, and bin centers at 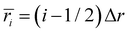 for i = 1,2, … N − 1, where N denotes the number of points along the radial grid. The charge in each bin was incremented each time an atom was found within the bin range (i.e., if ri≤ ratom < ri+1, then
for i = 1,2, … N − 1, where N denotes the number of points along the radial grid. The charge in each bin was incremented each time an atom was found within the bin range (i.e., if ri≤ ratom < ri+1, then 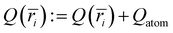 ). The charge density profile
). The charge density profile 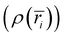 was subsequently generated by normalizing the charge histogram
was subsequently generated by normalizing the charge histogram 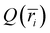 by the trajectory length and dividing by the corresponding bin volume Vi = Lπ(ri+12 − i2), where L is the length of the model CNT.
by the trajectory length and dividing by the corresponding bin volume Vi = Lπ(ri+12 − i2), where L is the length of the model CNT.2.2. Experimental methods
3. Results & discussion
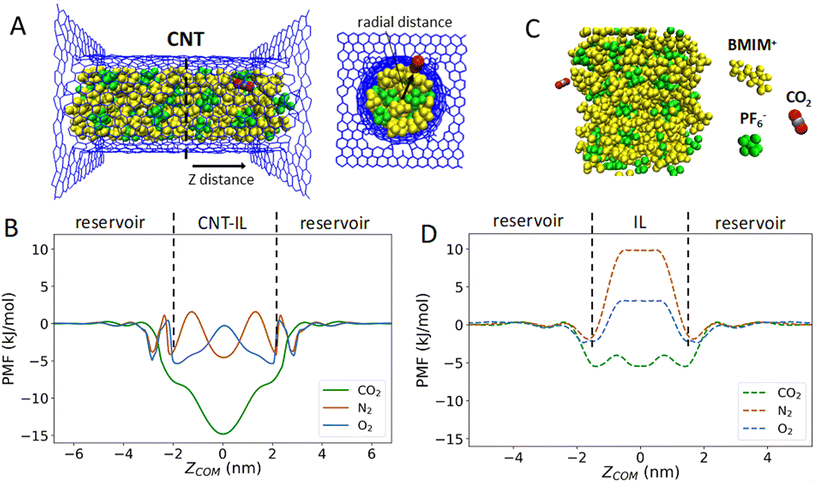
Our WT-MetaD simulations were performed using two collective variables (CVs), which have been shown to result in faster convergence of the free energy surface.40 The first CV is the center-of-mass (COM) distance between the gas molecule and CNT along the direction of the tube axis, whereas the second CV represents the radial position of the gas molecule with respect to the CNT center (see Fig. 1A).To probe the role of confinement in IL gas uptake mechanisms and energetics, we compared the uptake of a single gas molecule (CO2, O2 or N2) into [BMIM+][PF6−] confined within a CNT (Fig. 1A) or as a bulk liquid (Fig. 1C). The 1D PMFs for the uptake of the gas molecules in the presence and absence of a neutral CNT are shown in Fig. 1B and D, respectively. It is shown that the uptake of CO2, O2 and N2 into the IL-filled CNT is energetically more favorable than in the bulk, with a free energy gain ranging from a few kJ mol−1 to tens of kJ mol−1, indicating the gas solubility increases with the confinement of IL inside the CNT. Additionally, the degree of gas solubilities for CO2, O2 and N2 in bulk IL are consistent with experimentally measured Henry's law constants for these gas molecules.41 The energy barrier results from competition between the loss of entropy associated with confinement of the gas molecule (in both bulk and confined IL), the loss of enthalpy due to unfavorable interactions, and the gain of enthalpy due to favorable interactions between the gas molecule and IL/CNT. While confinement results in more favorable absorption into the CNT across the board, CO2 absorbs into the IL filled CNT better than the other gas molecules. In contrast, free energy profiles for N2 and O2 show only small fluctuations and a heterogeneous free energy surface inside the CNT.
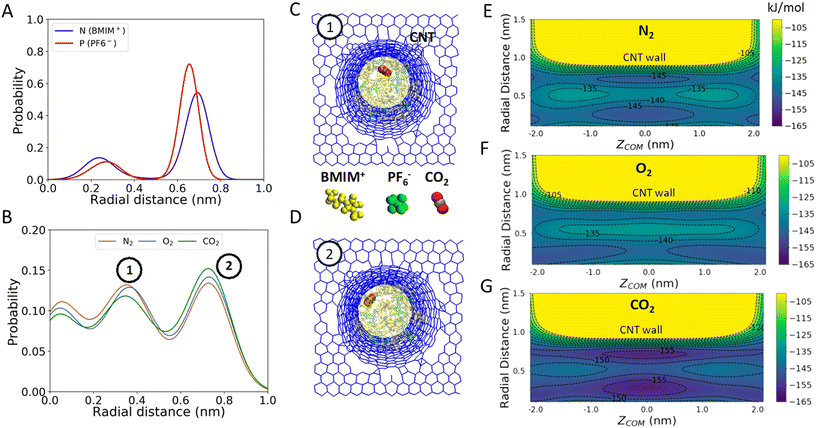
To understand how CNT confinement increases the favorability of gas uptake, we first analyzed the positions of BMIM+, PF6− and gas molecules (CO2, O2 and N2) inside the neutral CNT. The probability distributions of BMIM+ and PF6− in the CNT were obtained by calculating radial distances between N atoms of BMIM+ or P atoms of PF6− and COM of the CNT using the data obtained with WT-MetaD simulations. Similarly, the distributions of gas molecules were obtained by calculating radial distances between COMs of gas molecules and COM of the CNT. Fig. 2A shows that the density of IL molecules is higher near the CNT wall (versus the CNT center) and that cations and anions adopt a unique arrangement inside the CNT, as evident from the radial distance probability distributions. These findings are depicted in simulation snapshots showing a hollow circular arrangement of BMIM+ and PF6− (Fig. 2A and B). Moreover, gas molecules were found to locate in specific regions in the CNT that are offset from the IL molecules (Fig. 2C and D). Notably, the peak positions in Fig. 2C appear to be nearly independent of gas type, which would be expected if IL-ion steric factors were primarily at play in determining gas molecule position. This is in alignment with the idea that specific arrangements of IL molecules inside the CNT may create additional free volume which leads to a more favorable intercalation process under confinement. Calculation of the PF6− molecule number density in our simulations indeed shows a lower value in the CNT interior when compared to the bulk region (2.1 vs. 2.6 per nm3, respectively). A recently published experimental work also supports this hypothesis, suggesting that confinement of ILs induced by nanoscale porous material promotes a significant increase in nitrogen uptake via the formation of free volume induced by molecular rearrangement.42
To further elucidate the relationship between IL molecular rearrangement and gas uptake, WT-MetaD simulations were carried out and the 2D PMFs for the infiltration of gas molecules into CNT-[BMIM+][PF6−] were obtained as a function of two CVs described before. Fig. 2E–G demonstrate the 2D PMFs of gas intercalation inside the CNT (ZCOM = −2 nm to ZCOM = 2 nm), which excludes the free energy surface outside the CNT. The 2D free energy surfaces show that there are specific regions inside the CNT where gas molecules preferentially reside after entering. The relationship between high/low free energy regions and radial distance shows a common pattern for all gas molecules. In particular, the gas molecules favor locating near r = ∼0.3 nm and r = ∼0.7 nm. For N2 and CO2, there is a clear preference to position near ZCOM = 0, which correspond to the location visually shown in Fig. 2C and D, respectively. Notably, CO2 shows a tendency to locate near the CNT wall in a higher proportion when compared to the other gas molecules.
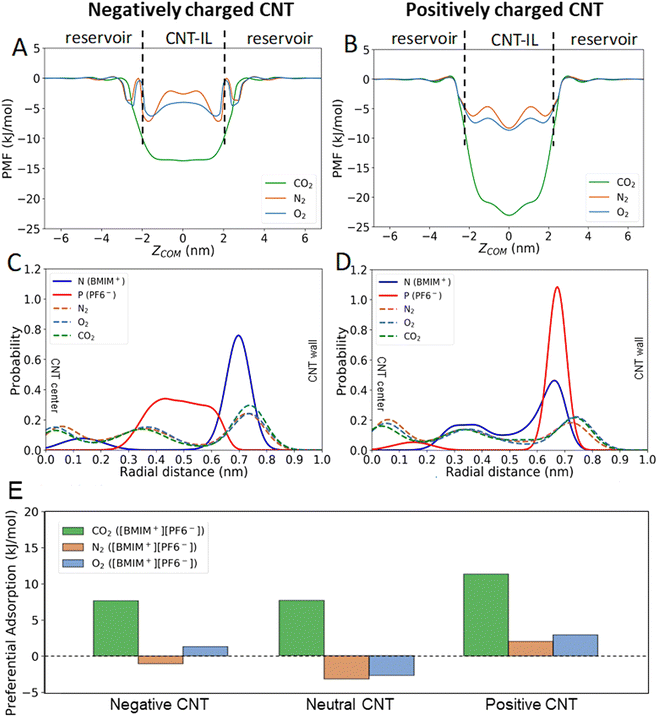
Next, we investigated how CNT electrostatic charging affects the absorption of gas molecules into the CNT-IL. WT-MetaD simulations were performed to obtain PMFs for absorption of CO2, N2 and O2 into negatively and positively charged CNTs (±10e) filled with [BMIM+][PF6−] (Fig. S1† and Fig. 3). The CNT charge state was found to affect the radial distributions of BMIM+ and PF6− in the CNT by pushing IL ions either towards the center of CNT (co-ions) or the CNT wall (counterions). For example, in the case of a positively charged CNT, the distribution of PF6− molecules shifts towards the CNT wall whereas the distribution of BMIM+ shifts away (Fig. 3B), as we would expect based on simple electrostatic considerations.
Comparison of 1D and 2D PMFs (Fig. 3, and S1†) indicates that energetically favorable regions change depending on the charge of the CNT wall, suggesting that the charge state of the CNT affects the infiltration for all the gas molecules. Additionally, CO2 molecules intercalate significantly better than O2 and N2 in all CNT charge states, following the trend seen in previous reports and earlier discussion in this text focused on the neutral case. Moreover, positive charging of the CNT most significantly impacts the energetics of gas infiltration (e.g., all gas molecules become energetically more favorable to infiltrate into the CNT-IL). We hypothesize that this is due in part to the asymmetry between the BMIM+ and PF6− ions. When a positive potential is applied to the CNT wall, the more symmetrical and less bulky anion is able to pack closer and more efficiently near the pore wall.43 As a result, there is both an increase in void space in the center of the pore due to an abundance of BMIM−, and an increase in the favorability of ion-gas interreacts near the wall due to an increased IL ion concentration (although with steric limitations potentially at play). Radial position distributions of BMIM+, PF6− and gas molecules (CO2, O2 and N2) in charged CNTs (Fig. 3C and D) show that gas molecules in the system with a positively charged CNT have a larger likelihood to be present near the center of the pore, relative to the pore wall, when compared to the negative case. This suggests that steric effects may be dominating. 2D PMF maps in Fig. S1† support an increase in the tendency for gas to infiltrate all regions of the pore in the case of a positive CNT wall, in agreement with Fig. 3A and B. These results indicate a complex interplay between steric hindrance and ion-gas interactions that govern where gas molecules prefer to sit within a charged and confined space.
To better understand charge-dependent gas infiltration into CNTs, the difference between average PMF in vacuum and in the CNT was calculated at different CNT states (e.g., charge state of CNT). Higher values of infiltration energy (PMFVACUUM − PMFCNT) correspond to more favorable infiltration of gas molecules into CNT-IL systems. Our results again demonstrate that the addition of positive charges to the CNT significantly enhances the CO2 uptake (Fig. 3E). Further, it is observed that the impact of charge on the CNT does not affect gasses in the same fashion. A negative charge, for example, has little impact on the CO2 adsorption, but significantly increases uptake of O2. In this way, tuning of the charged state of IL filled CNTs holds potential to allow for the dialing in of desired selectivity/uptake across different gas molecules.
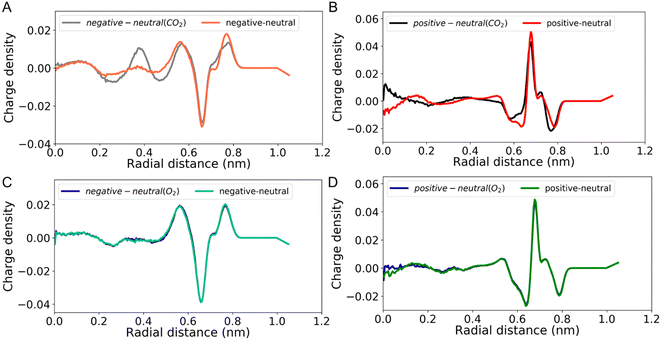
Motivated by these results, and to better study the interplay between gas uptake and the charge density distribution in the CNT, we designed a new system which simulates a scenario closer to what may be expected in real world applications. Here, 100 gas molecules were randomly added into two reservoirs located on both sides of the CNT (corresponding to 1 gas molecule per nm3). For this investigation, two gas types (CO2 and O2) were selected and the CNT was filled with [BMIM+][PF6−]. Simulations were performed at various conditions (neutral, negatively, or positively charged CNTs). Charge density distributions (see Methods section for the calculation details) were obtained using the simulations spanning 160 ns by skipping the first 16 ns. The effect of the CNT charge state on the charge density distribution was investigated by subtracting the charge density distribution of a neutral CNT from that of a charged CNT, as shown in Fig. 4. This approach was taken in an attempt to qualitatively inform on the magnitude of the electronic/electrochemical signal produced in a device which leverages changes induced by the presence of gas molecules (e.g., capacitance-based gas sensing).44
Our results show that CO2 uptake has a clear effect on the charge density distribution regardless of the charge state of CNTs. Comparison of the positive and negative charge state suggests that while both show a shift compared to the non-gas scenario, the negatively charged CNT offers the largest change across the conditions tested. Building on the conclusion of our previous simulations, we hypothesize that this is again driven by interplay between the favorability of a CO2 molecule to sit near an IL ion and the structural impact on the ion arrangement due to steric limitations. A positive CNT wall generates a nearby dense/packed PF6− ion arrangement, which is then only slightly perturbed compared to the non-gas case due to a sterically limited quantity of CO2 in this region. Charge density distributions near the center of the pore are moderately impacted, with significant gas uptake, due to ample void space being present. In the case of a negatively charged CNT, similar effects are at play, however the ion packing near the wall is less extreme due to a bulkier BMIM+ ion. Increased opportunity for CO2 to co-locate near this surface generates a larger alteration to the molecular structuring, and thus the charge density, compared to the neutral and positive cases. Notably, a signal arising from monitoring the double layer capacitance is expected to be most sensitive to changes near the surface. This highlights the importance of balancing overall gas quantity in a confined volume with its tendency to impart changes near the surface of interest. These results indicate that while the largest CO2 solubility may occur for a positive voltage, the largest electrochemical signal change may instead occur for a negative voltage in some systems. O2 uptake, on the other hand, shows very little change in the charge density distribution for either charge state. This may be due to the decreased tendency of O2 to coordinate with IL ions because of a lack of polar bonds.
To probe the impact of the selected IL, similar simulations were carried out using [BMIM+][Ace−]. It was found that, similar to [BMIM+][PF6−], CO2 showed the most favorable intercalation into the CNT and had the largest impact to charge distribution in response to a negative surface charge. Interestingly, there was larger variation in intercalation energies compared to the other gasses, suggesting potential for increased selectivity. Additional data and discussion is included in the ESI (Fig. S3†).
To qualitatively evaluate these computational predictions, we next carried out experiments to investigate the electrochemical double layer capacitive response of IL-filled carbon nanotubes exposed to different gas environments. [BMIM+][PF6−] was used to minimize the potential for unwanted reactions between the gas and IL.45 These measurements enable us to probe changes to the charge distribution within the CNTs, which we anticipate based on MD simulations to be driven by gas intercalation.
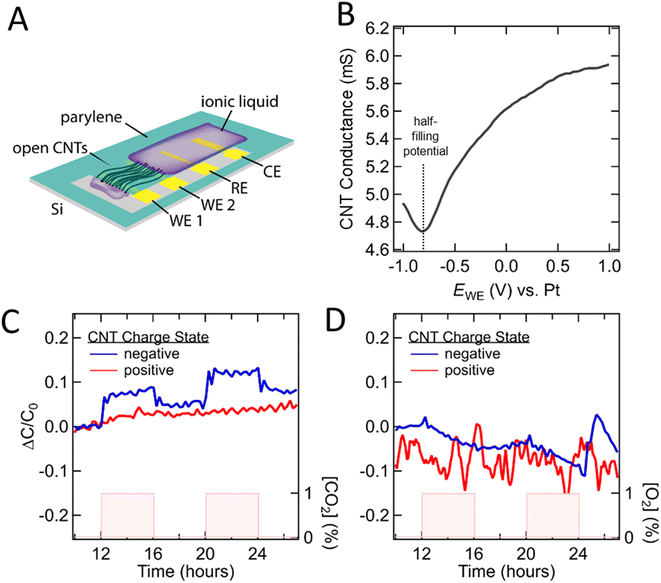
Fig. 5A shows a schematic of the device fabricated to enable these measurements. Vertically-aligned CNTs were grown on pre-patterned Si substrates, then rolled flat to obtain horizontally-aligned CNT films that bridge two Pt bottom contacts. Adjacent to these CNT films sit Pt counter and reference electrodes. Parylene was deposited in photolithographically-defined regions of the substrates to encapsulate all but the top and bottom tips of the aligned CNT films. Finally, the tips of the CNTs (on both ends) were selectively etched open in an oxygen plasma while the remaining CNT composite was shielded by a photoresist mask, yielding CNT electrochemical devices in which both ends of the CNTs are open. IL was then deposited at one end of the CNTs and allowed to wet into their internal volume through the open tips. A detailed description is provided in the Methods section and ESI.†
Chips loaded with IL were mounted in an air-tight probe station and purged with N2. A series of cyclic voltammetry scans were collected to evaluate device function and ensure filling of the CNT pores with IL. The measured capacitance of a typical [BMIM+][PF6−] loaded device at the slowest scan rate tested was observed to be ∼0.85 μF (Fig. S5†) which translates to an approximate areal capacitance of 2.57 μF cm−2 when normalized by the inner wall CNT surface area. This is comparable to previous reports describing [BMIM+][PF6−] at a graphene interface (∼5–7 μF cm2) and suggests that a large fraction of our CNTs are filled with IL.46 As further evidence, the resistance across the CNT blade was recorded during an EWE sweep and we observed a distinct change in the CNT electronic conductance (i.e., through the CNT walls connected by WE1 and WE2) indicating intimate IL-CNT contact across a substantial length of the CNTs (Fig. 5B). Finally, it was found that decreasing the sweep rate resulted in significantly increased capacitance, with no plateau down to 0.5 mV s−1. We attribute this to long diffusion times resulting from the extreme aspect ratio of our pores (∼2–3 nm in diameter, ∼350 μm in length). Taken together these results provide evidence that we are indeed probing the IL volume confined within few nm CNT pores.
To allow for direct comparison against the simulation results, we first determined the half filling potential of the CNTs as shown in Fig. 5B. Positive and negative charge states were specified as being to the left or right relative to the half-filling potential, which for [BMIM+][PF6−] was found to be −0.9 V. Direct assessment of the 0 V point was required to address the ill-defined chemical potential of the Pt pseudo-reference electrode. To study the impact of CO2 and O2 on the ionic liquid charge distributions within the CNTs, we collected cyclic voltammograms in the positive and negative charging regimes upon exposure to gas over the course of at least 5 on/off cycles. Total capacitance as a function of time was calculated as described in Fig. S6.† The charge vs. time data show drift and thus require baseline subtraction. It is well established that electrochemical studies involving ILs may be impacted by irreversible faradaic reactions within the electrochemical stability window.47 Our results, however, suggest that the impact to measured differential capacitance is minimal. The capacitance over time while the system is in steady state for >8 hours is relatively stable (see Fig. S6†). Further, the gas specific responses discussed below occur rapidly compared to the observed drift, return to near base line values once the gas is removed from the system, and show repeatable response magnitude over multiple cycles (Fig. S7†). The origin of non-reversible faradaic reactions in ionic liquids has been attributed to trace impurities and environmental contaminants (e.g., H2O).47 Additionally, oxygen-containing functional groups at the CNT tips resulting from our fabrication process are expected to be significantly more reactive than the CNT sidewalls, which we expect to localize redox byproducts outside of the CNTs.48
Gas-dependent capacitance traces for [BMIM+][PF6−] (see Fig. 5C) show that a step-like measurable change in capacitance occurs only when the CNTs are negatively charged and only for CO2 (not O2). This change appears to be relatively consistent across at least 6 cycles and returns to near baseline within minutes after the removal of CO2 (Fig. 5C and S7†). These experimental results qualitatively agree with the numerical results in Fig. 3 and 4, which show that the most significant IL ion and charge density rearrangement occurs for the negatively-charged CNT configuration in the presence of CO2. Further, these results highlight that predictions based on solubility alone are not sufficient when predicting the response of a sensor which leverages charge and confinement. We note the observation of a subtle, approximately linear change in capacitance that tracks with O2 presence. We hypothesize that while the O2 has minimal impact to the charge distribution in the confined volume, it may chemisorb onto the surface or CNT tips, leading to p-type doping that shifts the point of zero charge, and thus the measured differential capacitance.49 This data represents the first example of model informed gas sensing via modulations in the double layer capacitance of nanoscale confined IL and motivates future studies into the optimization and quantitative evaluation of device designs for ideal sensor responses (e.g., shorter CNTs, varied CNT diameters, tunable ILs). Additionally, the hypotheses and results reported here are likely to be sensitive to the dimensions and degree of order of the confining materials and thus it will be essential to expand the tested dataset moving forward to enable extrapolation to systems with larger and more disordered pore structures. These experimental results, coupled with our MD studies, demonstrate a potential approach to gas sensing by ionic liquids confined in CNTs and lay the groundwork for a new class of devices, designed by computation predictions, to maximize selectivity and performance.
4. Conclusions
In this work, we explored the effects of confinement and CNT charge state on the gas uptake and resulting molecular rearrangement in ILs confined in CNTs. We focused on a commonly used imidazolium-based IL, BMIM+ cation with PF6− anion, and investigated the uptake mechanism of CO2, N2 and O2 in this IL confined in neutral and charged CNTs using MD simulations combined with an enhanced free-energy sampling method called WT-MetaD. Our models generated key insights in predicting the likelihood of a gas molecule to intercalate into a confined volume and where it prefers to locate within. We then experimentally validated a subset of our results using a novel electrochemical device which represents a proof of concept for capacitive gas sensing in nanoconfined volumes. Our combined results offer insight into the conditions that optimize sensitivity and signal output in these types of systems. Specifically, we highlight that individual characteristics such as gas solubility, may be unable to accurately predict measured signals alone. Further studies will be required to build on these results and better predict the behavior of real-world devices. It will be particularly important to understand the impact of pore size, geometry, and degree of disorder as well as gas type and concentration. Our experimental platform and modeling framework are well suited to study these topics. CNT synthesis can be tuned to control the average and distribution of pore inner diameters, the degree of tube alignment can be adjusted, and alternate nanoporous materials could be substituted in their place. Variable gas environments can easily be delivered to our devices and experiments should be well informed by our WT-MetaD approach, which is general and transferable to other gases, so long as potential error from larger and more complex gas molecules is accounted for (e.g., care is taken to capture slower processes). Controlling the confinement, charges and type of IL are all knobs which can be turned to tune the design and performance of future gas sensing and separation devices leveraging nanoconfined volumes. This information also facilitates the design and fabrication of future novel electrochemical systems.Data availability
Data supporting the conclusions of this article has been included as part of the ESI.† Any additional data not included in the ESI† which is associated with this study is available from the authors upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory (LLNL) under Contract DE-AC52-07NA27344. Funding was provided by LLNL Laboratory Directed Research and Development (LDRD) Program Tracking No. 21-ERD-024 and 18-LW-064. This study was part of a user project at the Molecular Foundry, supported by the Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231.References
- D. S. Silvester and R. G. Compton, Electrochemistry in Room Temperature Ionic Liquids: A Review and Some Possible Applications, Z. Phys. Chem., 2006, 220(10), 1247–1274 CrossRef CAS.
- T. Welton, Ionic liquids: a brief history, Biophys. Rev., 2018, 10(3), 691–706 CrossRef CAS PubMed.
- J. Jacquemin, P. Husson, V. Majer and M. F. Costa Gomes, Influence of the Cation on the Solubility of CO2 and H2 in Ionic Liquids Based on the Bis(trifluoromethylsulfonyl)imide Anion, J. Solution Chem., 2007, 36(8), 967–979 CrossRef CAS.
- J. L. Anthony, J. L. Anderson, E. J. Maginn and J. F. Brennecke, Anion effects on gas solubility in ionic liquids, J. Phys. Chem. B, 2005, 109(13), 6366–6374 CrossRef CAS PubMed.
- S. Zhang, J. Zhang, Y. Zhang and Y. Deng, Nanoconfined Ionic Liquids, Chem. Rev., 2017, 117(10), 6755–6833 CrossRef CAS PubMed.
- S. Chen, G. Wu, M. Sha and S. Huang, Transition of ionic liquid [bmim][PF6] from liquid to high-melting-point crystal when confined in multiwalled carbon nanotubes, J. Am. Chem. Soc., 2007, 129(9), 2416–2417 CrossRef CAS PubMed.
- Q. Berrod, F. Ferdeghini, P. Judeinstein, N. Genevaz, R. Ramos, A. Fournier, J. Dijon, J. Ollivier, S. Rols, D. Yu, R. A. Mole and J. Zanotti, Enhanced ionic liquid mobility induced by confinement in 1D CNT membranes, Nanoscale, 2016, 8, 7845–7848 RSC.
- S. M. Chathoth, E. Mamontov, S. Dai, X. Wang, P. F. Fulvio and D. J. Wesolowski, Fast diffusion in a room temperature ionic liquid confined in mesoporous carbon, Epl-Europhys. Lett., 2012, 97(6), 66004 CrossRef.
- S. Kondrat, P. Wu, R. Qiao and A. A. Kornyshev, Accelerating charging dynamics in subnanometre pores, Nat. Mater., 2014, 13(4), 387–393 CrossRef CAS PubMed.
- J. Zhang, Q. Zhang, X. Li, S. Liu, Y. Ma, F. Shi and Y. Deng, Nanocomposites of ionic liquids confined in mesoporous silica gels: preparation, characterization and performance, Phys. Chem. Chem. Phys., 2010, 12(8), 1971–1981 RSC.
- Y. Pei, Y. Zhang, J. Ma, M. Fan, S. Zhang and J. Wang, Ionic liquids for advanced materials, Mater. Today Nano, 2022, 17, 100159 CrossRef CAS.
- G. Kaur, H. Kumar and M. Singla, Diverse applications of ionic liquids: A comprehensive review, J. Mol. Liq., 2022, 351, 118556 CrossRef CAS.
- W. Ying, J. Cai, K. Zhou, D. Chen, Y. Ying, Y. Guo, X. Kong, Z. Xu and X. Peng, Ionic Liquid Selectively Facilitates CO2 Transport through Graphene Oxide Membrane, ACS Nano, 2018, 12(6), 5385–5393 CrossRef CAS PubMed.
- J. J. Close, K. Farmer, S. S. Moganty and R. E. Baltus, CO2/N2 separations using nanoporous alumina-supported ionic liquid membranes: Effect of the support on separation performance, J. Membr. Sci., 2012, 390–391, 201–210 CrossRef CAS.
- F. Rahmani, P. Scovazzo, M. A. Pasquinelli and S. Nouranian, Effects of Ionic Liquid Nanoconfinement on the CO2/CH4 Separation in Poly(vinylidene fluoride)/1-Ethyl-3-methylimidazolium Thiocyanate Membranes, ACS Appl. Mater. Interfaces, 2021, 13(37), 44460–44469 CrossRef CAS PubMed.
- I. Goubaidoulline, G. Vidrich and D. Johannsmann, Organic Vapor Sensing with Ionic Liquids Entrapped in Alumina Nanopores on Quartz Crystal Resonators, Anal. Chem., 2005, 77(2), 615–619 CrossRef CAS PubMed.
- C. H. Park, V. Schroeder, B. J. Kim and T. M. Swager, Ionic Liquid-Carbon Nanotube Sensor Arrays for Human Breath Related Volatile Organic Compounds, ACS Sens., 2018, 3(11), 2432–2437 CrossRef CAS PubMed.
- M. V. Fedorov and A. A. Kornyshev, Ionic liquids at electrified interfaces, Chem. Rev., 2014, 114(5), 2978–3036 CrossRef CAS PubMed.
- C. Pinilla, M. G. Del Popolo, R. M. Lynden-Bell and J. Kohanoff, Structure and dynamics of a confined ionic liquid. Topics of relevance to dye-sensitized solar cells, J. Phys. Chem. B, 2005, 109(38), 17922–17927 CrossRef CAS PubMed.
- S. Maolin, Z. Fuchun, W. Guozhong, F. Haiping, W. Chunlei, C. Shimou, Z. Yi and H. Jun, Ordering layers of [bmim][PF6] ionic liquid on graphite surfaces: molecular dynamics simulation, J. Chem. Phys., 2008, 128(13), 134504 Search PubMed.
- Y. Shim and H. J. Kim, Solvation of carbon nanotubes in a room-temperature ionic liquid, ACS Nano, 2009, 3(7), 1693–1702 CrossRef CAS PubMed.
- A. Ghoufi, A. Szymczyk and P. Malfreyt, Ultrafast diffusion of Ionic Liquids Confined in Carbon Nanotubes, Sci. Rep., 2016, 6, 28518 CrossRef PubMed.
- V. V. Chaban and O. V. Prezhdo, Nanoscale carbon greatly enhances mobility of a highly viscous ionic liquid, ACS Nano, 2014, 8(8), 8190–8197 Search PubMed.
- Z. Tian, S. Dai and D.-e. Jiang, Confined Ionic Liquid in an Ionic Porous Aromatic Framework for Gas Separation, ACS Appl. Polym. Mater., 2018, 1(1), 95–102 CrossRef.
- W. Shi and D. R. Luebke, Enhanced gas absorption in the ionic liquid 1-n-hexyl-3-methylimidazolium bis(trifluoromethylsulfonyl)amide ([hmim][Tf2N]) confined in silica slit pores: a molecular simulation study, Langmuir, 2013, 29(18), 5563–5572 CrossRef CAS PubMed.
- W. Shi and D. C. Sorescu, Molecular simulations of CO2 and H2 sorption into ionic liquid 1-n-hexyl-3-methylimidazolium bis(trifluoromethylsulfonyl)amide ([hmim][Tf2N]) confined in carbon nanotubes, J. Phys. Chem. B, 2010, 114(46), 15029–15041 CrossRef CAS PubMed.
- S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comput. Phys., 1995, 117(1), 1–19 CrossRef CAS.
- G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, PLUMED 2: New feathers for an old bird, Comput. Phys. Commun., 2014, 185(2), 604–613 CrossRef CAS.
- S. E. Weitzner, T. A. Pham and E. R. Meshot, Theory-augmented informatics of ionic liquid electrolytes for co-design with nanoporous electrode materials, Nanoscale, 2022, 14(13), 4922–4928 RSC.
- J. G. Harris and K. H. Yung, Carbon Dioxide's Liquid-Vapor Coexistence Curve And Critical Properties as Predicted by a Simple Molecular Model, J. Phys. Chem., 1995, 99(31), 12021–12024 CrossRef CAS.
- C. S. Murthy, K. Singer, M. L. Klein and I. R. McDonald, Pairwise additive effective potentials for nitrogen, Mol. Phys., 1980, 41(6), 1387–1399 CrossRef CAS.
- K. Watanabe, N. Austin and M. R. Stapleton, Investigation of the Air Separation Properties of Zeolites Types A, X and Y by Monte Carlo Simulations, Mol. Simul., 1995, 15(4), 197–221 CrossRef CAS.
- A. Mondal and S. Balasubramanian, Quantitative Prediction of Physical Properties of Imidazolium Based Room Temperature Ionic Liquids through Determination of Condensed Phase Site Charges: A Refined Force Field, J. Phys. Chem. B, 2014, 118(12), 3409–3422 CrossRef CAS PubMed.
- J. Walther, R. Jaffe, T. Halicioglu and P. Koumoutsakos, Molecular Dynamics Simulations of Carbon Nanotubes in Water, 2000.
- A. Barducci, G. Bussi and M. Parrinello, Well-tempered metadynamics: a smoothly converging and tunable free-energy method, Phys. Rev. Lett., 2008, 100(2), 020603 CrossRef PubMed.
- A. Laio and M. Parrinello, Escaping free-energy minima, Proc. Natl. Acad. Sci. U. S. A., 2002, 99(20), 12562–12566 CrossRef CAS PubMed.
- F. Aydin, R. Sun and J. M. J. Swanson, Mycolactone Toxin Membrane Permeation: Atomistic versus Coarse-Grained MARTINI Simulations, Biophys. J., 2019, 117(1), 87–98 CrossRef CAS PubMed.
- E. R. Meshot, S. J. Park, S. F. Buchsbaum, M. L. Jue, T. R. Kuykendall, E. Schaible, L. B. Bayu Aji, S. O. Kucheyev, K. J. J. Wu and F. Fornasiero, High-yield growth kinetics and spatial mapping of single-walled carbon nanotube forests at wafer scale, Carbon, 2020, 159, 236–246 CrossRef CAS.
- S. J. Park, K. Moyer-Vanderburgh, S. F. Buchsbaum, E. R. Meshot, M. L. Jue, K. J. Wu and F. Fornasiero, Synthesis of wafer-scale SWCNT forests with remarkably invariant structural properties in a bulk-diffusion-controlled kinetic regime, Carbon, 2023, 201, 745–755 CrossRef CAS.
- R. Sun, Y. Han, J. M. J. Swanson, J. S. Tan, J. P. Rose and G. A. Voth, Molecular transport through membranes: Accurate permeability coefficients from multidimensional potentials of mean force and local diffusion constants, J. Chem. Phys., 2018, 149(7), 072310 CrossRef PubMed.
- J. Jacquemin, P. Husson, V. Majer and M. F. C. Gomes, Low-pressure solubilities and thermodynamics of solvation of eight gases in 1-butyl-3-methylimidazolium hexafluorophosphate, Fluid Phase Equilib., 2006, 240(1), 87–95 CrossRef CAS.
- I. Harmanli, N. V. Tarakina, M. Antonietti and M. Oschatz, “Giant” Nitrogen Uptake in Ionic Liquids Confined in Carbon Pores, J. Am. Chem. Soc., 2021, 143(25), 9377–9384 CrossRef CAS PubMed.
- E. Paek, A. Pak and G. Hwang, A Computational Study of the Interfacial Structure and Capacitance of Graphene in [BMIM][PF6] Ionic Liquid, J. Electrochem. Soc., 2012, 160, A1 CrossRef.
- Z. Wang, M. Guo, X. Mu, S. Sen, T. Insley, A. J. Mason, P. Král and X. Zeng, Highly Sensitive Capacitive Gas Sensing at Ionic Liquid–Electrode Interfaces, Anal. Chem., 2016, 88(3), 1959–1964 CrossRef CAS PubMed.
- M. I. Cabaço, M. Besnard, Y. Danten and J. A. P. Coutinho, Carbon Dioxide in 1-Butyl-3-methylimidazolium Acetate. I. Unusual Solubility Investigated by Raman Spectroscopy and DFT Calculations, J. Phys. Chem. A, 2012, 116(6), 1605–1620 CrossRef PubMed.
- J. Xia, F. Chen, J. Li and N. Tao, Measurement of the quantum capacitance of graphene, Nat. Nanotechnol., 2009, 4(8), 505–509 CrossRef CAS PubMed.
- S. Doblinger, T. J. Donati and D. S. Silvester, Effect of Humidity and Impurities on the Electrochemical Window of Ionic Liquids and Its Implications for Electroanalysis, J. Phys. Chem. C, 2020, 124(37), 20309–20319 CrossRef CAS.
- K. Gong, S. Chakrabarti and L. Dai, Electrochemistry at Carbon Nanotube Electrodes: Is the Nanotube Tip More Active Than the Sidewall?, Angew. Chem., Int. Ed., 2008, 47(29), 5446–5450 CrossRef CAS PubMed.
- D. Kang, N. Park, J.-h. Ko, E. Bae and W. Park, Oxygen-induced p-type doping of a long individual single-walled carbon nanotube, Nanotechnology, 2005, 16(8), 1048 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr05409a |
| This journal is © The Royal Society of Chemistry 2025 |