Progress in understanding triple ionic–electronic conduction in perovskite oxides for protonic ceramic fuel cell applications

Abstract

Protonic ceramic fuel cells offer a promising route to effectively generate electricity from various fuels at reduced temperatures. However, the viability of this technology is impeded by the sluggish kinetics of the oxygen reduction reaction at the cathode. Recently, triple ionic–electronic conductors have shown their promise as cathode materials with improved catalytic activity because of their enhanced mixed electron and ionic conductivities that can maximise the active sites for the reaction. This review examines the transport mechanism of holes, oxygen ions, and protons within triple ionic–electronic conductors. This review highlights the equilibrium among these charge carriers and their requirement for specific cationic environments to facilitate rapid transport. As a result, triple ionic–electronic conductors need to balance the transport of these charges to realise optimum oxygen reduction reaction activity. The review further identifies the transport of oxygen ions or protons as the current limiting factor in triple ionic–electronic conductors. This review concludes by emphasizing the importance of understanding the role of ionic transport in the oxygen reduction reaction to enhance the performance of triple ionic–electronic conductors.

---

Desheng Feng

Dr Desheng Feng is a postdoctoral research fellow in the Department of Chemical Engineering at the University of Melbourne, Australia. He completed his Bachelor of Engineering in the School of Chemical Engineering (2019) and Ph.D. (2024) from the University of Queensland. His current research focuses on the development of electrode materials and electrochemical processes for energy conversion.

Mengran Li

Dr Mengran Li is a lecturer and ARC DECRA fellow at the Department of Chemical Engineering, University of Melbourne (UoM). After obtaining his PhD from the University of Queensland (UQ) in 2016, he spent over five years as a postdoctoral research fellow at UQ and Delft University of Technology, working on developing CO2 electrolysis. In 2023, he joined UoM as a lecturer and led the Li Energy Lab, which focuses on advancing electrochemical technologies crucial for the global energy transition towards a greener future. His research includes CO2/water electrolysis, reactive carbon capture, fuel cells, and hydrogen separation and compression.

---

1. Introduction

Protonic ceramic fuel cells (PCFCs) are electrochemical systems that generate electricity from fuels at reduced temperatures (e.g., <600 °C) with high efficiency.^1–9 A PCFC contains a proton-conducting electrolyte, an anode for fuel oxidation, and a cathode for oxygen reduction reaction (ORR). Proton-conducting electrolytes, such as BaZr_0.1Ce_0.7Y_0.2O_3−δ and BaZr_0.1Ce_0.7Y_0.1Yb_0.1O_3−δ show conductivity higher than 0.003 S cm⁻¹ at temperatures as low as 400 °C, outperforming state-of-the-art oxygen ion-conducting electrolytes such as yttrium-stabilized zirconia and gadolinium-doped ceria.¹⁰ This advance in electrolyte material enables the potential operation of PCFCs at temperatures lower than 450 °C.¹¹

Oxygen reduction reaction at the cathode, as described in eqn (1), typically shows slow kinetics and is often the rate-limiting step for PCFC power density, particularly at reduced temperatures. Many studies report that most cell resistance in PCFCs originates from the ORR at reduced temperatures.^2,4,5,7,9

½O_2(g) + 2e⁻ + 2H⁺ → H₂O_(g) (1)

As shown in eqn (1), ORR in PCFC is a multiple-step reaction.^9,12,13 It begins with the adsorption of molecular oxygen onto the cathode surface.^9,12,13 The adsorbed oxygen then dissociates and gains electrons to form oxygen ions.^9,12,13 Simultaneously, protons react with these oxygen ions to produce water.^9,12,13 Each step of the ORR can only take place in regions where the necessary charges and reactants are available. In cathode materials designed for solid oxide fuel cells (e.g., pure electronic or mixed electronic and oxygen-ion conductors, MIECs),^14–17 the entire cathode surface is active for oxygen ion adsorption and reduction. However, the lack of proton conduction limits water formation to the contact line between the cathode, gas, and protonic-conducting electrolyte. As a result, most of the MIECs show limited ORR activities when serving as PCFC cathodes (as reflected by their high area-specific resistances, ASR), as shown in Fig. 1.^{2,4,5,9,13,18–35}

Fig. 1 The ASR and peak power density of reported MIECs and TIECs on PCFCs at 600 °C. Data are collected from ref. 2, 4, 5, 9, 13, 18–35, 43–46.

To address this critical issue, a new type of mixed conductors (or so-called triple ionic–electronic conductors, TIECs), such as BaCo_0.4Fe_0.4Zr_0.1Y_0.1O_3−δ (BCFZY) and Ba_0.875Fe_0.875Zr_0.125O_3−δ, enabling simultaneous transport of electron, oxygen ions and protons, have emerged as alternative material candidates for the PCFC cathodes.^{2,9,13,36–38} Compared to traditional MIECs, TIECs can absorb water and form hydroxide groups within their structure under humid conditions, a process often evaluated using methods such as thermogravimetric analysis³⁹ or H₂O temperature-programmed desorption.⁴⁰ Further, proton transport in TIECs can be further investigated using gas permeation methods⁴¹ or time-of-flight secondary ion mass spectrometry.⁴²

The additional proton conductivity in TIEC materials allows protons to reach the cathode surface and participate in ORR. As such, using TIEC-based cathodes can extend the ORR active sites beyond the gas-electrolyte-cathode boundaries to the entire cathode surface. Such an increase in the density of ORR-active sites leads to a significant improvement of cathode activity as compared to the MIEC-based cathode for PCFCs: as presented in Fig. 1, most of the TIEC-based cathodes show an ASR value of <0.2 Ω cm² at 600 °C, which is 5 to 10 times lower than those of MIECs. This advancement significantly increases the power output of PCFCs, from <500 mW cm⁻² to higher than 1000 mW cm⁻² at 600 °C.

However, even with TIECs-based cathodes, the cathode still accounts for more than 50% of the total cell resistance in current PCFCs. Especially at reduced temperatures, thermally activated charge transport in TIECs slows down,²⁹ further increasing the overall cell resistance.^5,7,9 For example, Bian et al. reported that the cathode contributes ∼50% of the resistance at 600 °C and this contribution increases to ∼90% at 400 °C.⁷ In another study, Liu et al. reveal that >90% of the PCFC cell resistance at 400 °C originates from electrodes, and a ∼60% resistance reduction can be achieved by just replacing the original cathode with an improved one, as shown in Fig. 2.⁵ These findings highlight the critical need for developing TIECs with improved ORR activity for PCFCs.^1–9

Fig. 2 Electrochemical impedance spectroscopy of PCFCs with a PrBa_0.5Sr_0.5Co_1.5Fe_0.5O_6−δ (PBSCF) and a Ba_0.62Sr_0.38CoO_3−δ–Pr_1.44Ba_0.11Sr_0.45Co_1.32Fe_0.68O_6−δ (BSC + PBSCF) cathode at 400 °C. The polarization resistance in EIS is mainly attributable to the cathode. This figure has been adapted from ref. 5 with permission from Springer Nature, copyright 2025.

Designing an active and stable TIEC-based cathode for PCFC is complicated due to the intricate interplay between structure, chemistry, and charge transport phenomena. This complexity is further exacerbated by reaction environments such as humidity, temperature, and gas atmosphere. Despite these challenges, the recent discovery of high-performance TIEC materials suggests that important physicochemical phenomena are only beginning to be uncovered. For readers seeking detailed insights into specific TIEC material design strategies, several recent review papers^{36,37,47–50} provide comprehensive summaries of advancements in TIEC materials tailored for PCFC cathodes. Instead, this review will focus on the current understanding of charge transport phenomena and their relationship to material design, complementing existing literature. Finally, we will discuss future directions for the rational design of TIEC materials in high-temperature electrochemical applications.

2. Structures of the TIECs

The most common TIEC cathodes for PCFC are metal oxides in a perovskite-type oxide structure.^{36,37,47–50} Perovskite oxides have a formula of ABO₃, where A-site cations are typically large alkaline-earth cations (e.g., Sr²⁺ and Ba²⁺) or lanthanoid cations (e.g., La³⁺ and Pr³⁺).⁵¹ The B-site is occupied by smaller transition metal cations, such as cobalt and iron.⁵¹ While TIECs with alternative structures, such as spinel^52,53 or Ruddlesden–Popper-type structures,⁵⁴ have been explored, this review will primarily focus on perovskite oxide-based TIECs due to the extensive data available in the literature.

Perovskite oxides are favoured as TIECs due to their exceptional versatility, offering extensive opportunities for A- and B-site substitution.^51,55 This unique characteristic enables precise control over their electrical and ionic transport properties, allowing us to fine-tune their hole, oxygen ion, and proton conductivities.^29,30,56,57 As a result, perovskite oxides are well-suited for tailoring materials to optimise ORR activity.

Additionally, perovskite-type oxides are notable for their high-symmetry crystal structures, such as cubic or layered forms.⁵⁸ These symmetrical structures significantly enhance hole, oxygen ion, and proton conductivities by providing more isotropic sites for charge transport.^55,59,60 Achieving such structures is often related to the Goldschmidt tolerance factor (τ) of perovskite oxides, which serves as an effective tool for guiding their design.⁶¹ Goldschmidt tolerance factor of perovskite oxides can be expressed as follows:

where R_A is the ionic radius of A-site cations, R_B is the ionic radius of B-site cations and R_O is the ionic radius of oxygen ion. In general, perovskite oxides with a Goldschmidt tolerance factor (τ) close to unity are more likely to adopt a high-symmetry cubic structure, which is preferred in TIEC design for rapid charge transfer.⁶² The following sections will mainly focus on the charge transport phenomena within these perovskite oxides.

3. Electronic and ionic transport

Charge transport is primarily governed by two key factors: the concentration of charge carriers and their mobility. This section will focus on the mechanisms responsible for charge carrier formation and transport within TIECs. A thorough understanding of these mechanisms is crucial for optimizing TIEC design and achieving well-balanced charge transport properties, which are essential for improving performance in practical applications.

3.1 Electron transport

Electron transport can occur in materials containing free electrons or electron holes.^63,64 Although some perovskite oxides could form free electrons under reducing atmospheres,⁶⁵ these free electrons are quickly consumed by oxygen under atmospheric oxygen partial pressure. As a result, TIECs for ORR mainly rely on holes for electron transport.³⁶

Hole formation in oxides is primarily associated with the presence of redox-active cations.^66,67 These cations show different oxidation states in perovskite oxides, such as Co²⁺/Co³⁺ for Co (ref. 68) and Ce³⁺/Ce⁴⁺ for Ce.⁶⁹ The oxidation of these cations facilitates hole formation in perovskite oxides. Thus, redox-active cations in high oxidation states are crucial for hole formation, and their absence makes hole formation more difficult. The lack of holes could explain why perovskite oxides containing no redox-active cations, such as LaAlO₃, show dielectric behaviour.⁷⁰

Holes are transferred through the B–O bond network in perovskite oxides.^71,72 This hole transport can be improved by increasing the overlap between B-site cations and oxygen ions.⁷³ The larger overlap leads to stronger hybridisation between the d orbit of B-site cations and the p orbit of oxygen ions, which enhances the mobility of holes across the B–O lattice.⁷³ Therefore, perovskite oxides with stronger B–O bond overlap, or have a more covalent B–O bond, typically show faster hole transport.

Further, hole transport also requires that redox-active cations form percolation pathways in perovskite oxides. The formation of percolation pathways requires the concentration of redox-active cations in the B-site to exceed a threshold, typically between 15–29%.^74,75 Below this threshold, the redox-active cations are scattered and holes formed by these cations become less mobile. This could explain why the electrical conductivity of Ba(Zr, Fe)O_3−δ drops by three orders of magnitude when Fe content reduces below 20% at 500 °C, as shown in Fig. 3a.⁷⁵ Similarly, as presented in Fig. 3b, Raffaelle et al. report that the conductivity of La(Cr, Mn)O₃ also increases by three orders of magnitude when Mn content increases from 10% to 40% at 700 K.⁷⁶ It should be noted that although these materials are mixed conductors, the electronic conductivity of these materials is much higher than ionic conductivities.^36,77 Therefore, the increase in conductivity of these materials should be primarily attributable to faster hole transport.

Fig. 3 (a) Electrical conductivity of Ba(Zr, Fe)O_3−δ system under 1 atm oxygen partial pressure at 500 °C. This figure has been adapted from ref. 36 with permission from Springer Nature, copyright 2025. (b) Electrical conductivity of La(Cr, Mn)O_3−δ system in air at 300–1300 K. This figure has been adapted from ref. 76 with permission from American Physical Society, copyright 2025.

In addition to composition, external factors such as temperature, humidity, and oxygen partial pressure significantly influence hole transport in oxides. Elevated temperatures provide additional energy for hole transport but also reduce the oxidation state of cations, which decreases the number of holes. This dual effect explains why the electrical conductivity of (La, Sr)(Co, Fe)O_3−δ initially increases and then decreases as the temperature rises from 200 to 1000 °C.⁷⁸ Conversely, high oxygen partial pressures increase the cation oxidation state, thereby enhancing the number of holes. As a result, elevated oxygen partial pressures consistently promote faster hole transport.⁷⁹ Furthermore, humidity also affects hole conductivity.⁸⁰ Perovskite oxides can form hydroxyl groups at the expense of holes in the presence of humidity, which will be discussed later in Section 3.3.

In summary, hole transport dominates electron conductivity in perovskite oxides used for ORR. Holes form via redox-active cations transitioning between oxidation states. These redox-active cations must reach a threshold concentration to form percolation pathways for efficient transport. Below this threshold, conductivity drops sharply. External conditions, including temperature and oxygen partial pressure, are critical for optimising hole transport.

3.2 Oxygen ion transport

Oxygen transport in perovskite oxides is governed by two key steps: surface exchange and bulk diffusion.^81,81 Surface exchange coefficient (k) describes the rate of oxygen surface exchange while oxygen ion diffusivity (D) determines the rate of oxygen ions transport through the bulk of perovskite oxides. Techniques such as isotope exchange⁸² or electrical conductivity relaxation^83,84 are used to distinguish between these two steps. Notably, studies demonstrate that bulk transport and surface exchange are highly correlated: materials with fast oxygen ion bulk transport also show fast surface exchange.⁵⁵ Therefore, this section mainly focuses on oxygen ion bulk transport.

Oxygen ion transport typically involves two distinct types of charge carriers: oxygen vacancies and interstitial oxygen ions. Most state-of-the-art oxygen conductors rely on oxygen vacancy mechanisms.^61,62 Even the state-of-the-art interstitial oxygen conductors that require less energy for migration (∼0.5 eV for interstitial oxygen cf. 1 eV for oxygen vacancies), such as La₄Mn₅Si₄O_22+δ as reported by Meng et al., they still appear to fall short of oxygen vacancy conductors, such as Ce_0.9Gd_0.1O_1.95 or La_0.8Sr_0.2Ga_0.83Mg_0.17O_3−δ.^85–87

Oxygen vacancies are formed to compensate for charge imbalance in oxides.⁵⁵ The concentration of oxygen vacancies can be quantified by oxygen non-stoichiometry, where a high oxygen non-stoichiometry indicates a high concentration of oxygen vacancies. When the positive charge in oxide is reduced, the lattice oxygen ions can react with holes to form oxygen gas while leaving an oxygen vacancy in the structure.^88–90 Notably, the formation of oxygen vacancies reduces hole concentration, thereby impairing electronic conductivity. The formation of oxygen vacancies can be described by the following equation:

Both lattice cationic environment and external conditions can affect the formation of oxygen vacancies. Compositions, including radius, charge, stoichiometry and electronegativity of A- and B-site cations, are crucial for oxygen vacancy formation.¹⁵ In general, cations with large radius, low electronegativity and low valence can promote the formation of oxygen vacancies.

Aside from compositions, external factors play a crucial role in oxygen vacancy formation.^15,55 Reducing atmospheres, such as those with elevated temperatures and lower oxygen partial pressures, tend to lower the oxidation states of cations and promote the formation of oxygen vacancies.^{14–16,91,92} Among these factors, temperature is the most widely studied in relation to oxygen vacancy concentrations. As temperature increases from ambient to elevated levels (e.g., 600 °C), oxygen non-stoichiometry can rise by more than 50%.¹⁵ Notably, humidity also reduces the concentration of oxygen vacancies, a topic that will be discussed in Section 3.3.

Experimental methods, including titration,⁹³ electron paramagnetic resonance,⁹⁴ X-ray photoelectron spectroscopy,⁹⁵ and neutron powder diffraction,⁹⁶ are often used to quantify the concentration of oxygen vacancies in perovskite oxides. Many of these methods need to first determine the oxidation state of ORR-active metal cations, such as Co and Fe, and then calculate the oxygen non-stoichiometry.

Recent efforts attempt to accelerate the discovery of perovskite materials with fast oxygen-ion transport through theory-derived descriptors or machine learning.^15,97–101 Building on the study of numerous reported materials, our group recently developed a comprehensive approach to predict oxygen vacancies in perovskite oxides, as shown in Fig. 4.¹⁵ This method considers the key role of the cationic lattice environment in determining the states of the active metal centres such as Co and Fe at different temperatures.¹⁵ The states of the cationic lattice environment can be further mathematically described using fundamental properties such as electronegativity, polarization power, charge, and cation size.¹⁵

Fig. 4 (a) Workflow of the prediction of the oxygen vacancies in ABO_3−δ perovskites. Comparison of the measured (δ_M) and predicted oxygen vacancy (δ_P) for (b) Co-based and (c) Fe-based perovskite oxides. This figure has been adapted from ref. 15 with permission from Springer Nature, copyright 2025.

This work shows that these properties tend to inversely affect the properties of the active metal centres through the cation–cation inductive effects. For example, doping inert elements with high oxidation states tends to lower the oxidation state of Co and Fe, which originate from the delocalized electron distribution that is commonly present in perovskite-structured cathode materials.¹⁵ With the assistance of machine learning, this insight allows for accurate prediction of oxygen vacancy concentrations in perovskite oxides across different temperatures, even without detailed knowledge of the specific states of ORR-active metal centres.¹⁵ This finding, together with other recent reports,^97–101 further highlights the important role of perovskite cations, structures, and temperatures in determining the concentrations of oxygen vacancies.

Notably, a high oxygen vacancy concentration also destabilizes the perovskite oxide structure and triggers phase transformation.^102,103 These phase transformations profoundly impact oxygen ion transport as well. A typical example is that the loss of lattice oxygen in a reducing atmosphere converts the structure of Pr_0.5Ba_0.5MnO_3−δ from cubic perovskite oxide to layered perovskite oxide.¹⁰³ Consequently, it is not always possible to create oxygen vacancies in perovskite oxides to promote oxygen ion transport.

In addition to the concentration of oxygen vacancies, the mobility of oxygen ions through these vacancies also determines oxygen transport. However, our recent studies based on DFT calculations over multiple perovskite models reveal that a high concentration of oxygen vacancies tends to reduce the mobility of oxygen ions, as presented in Fig. 5.¹⁵ Such a phenomenon should be related to covalency of the bond between active metal cations and oxygen. Specifically, an increase in B–O covalency of the active cations, such as cobalt, promotes oxygen vacancy formation but may make the oxygen ion less ionic. Conversely, enhancing the ionic character of the B–O bond improves oxygen ion mobility but suppresses the formation of oxygen vacancies.

Fig. 5 (a) formation and (b) mobility of oxygen vacancies as a function of oxygen vacancy concentration. This figure has been adapted from ref. 15 with permission from Springer Nature, copyright 2025.

Furthermore, the mobility of oxygen ions is also related to lattice-free volume, where a large lattice-free volume facilitates oxygen ion transport.¹⁰⁴ In perovskite-type oxides, oxygen ions need additional energy to pass through the gap formed by the A-site and two B-site cations, which is referred to as a “saddle point”.¹⁰⁵ Mogensen et al. report that the typical size of this saddle point is only ∼1.1 Å,¹⁰⁴ far smaller than the size of oxygen ions (1.4 Å), emphasizing the importance of lattice relaxation in enabling oxygen ion migration.¹⁰⁶ Oxygen ions therefore require additional energy to pass through this saddle point. A larger lattice can help lower the energy barrier for oxygen ions crossing this saddle point. Following this, Cook et al. report that the activation energy for oxygen ion transport reduces by 50% when the free volume in perovskite-type oxides increases from 20 to 30 ų,¹⁰⁷ as shown in Fig. 6a. Similar findings are reported in Ba(Fe, In)O_3−δ system, as shown in Fig. 6b.¹⁰⁸

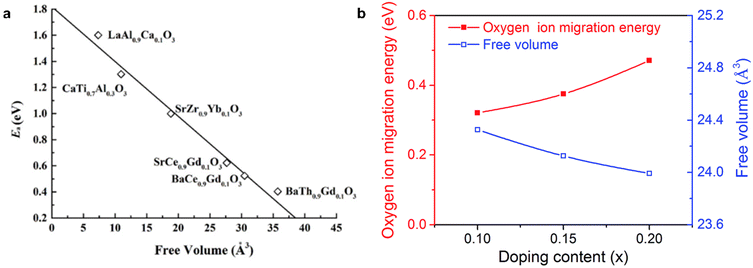Fig. 6 (a) high free volume significantly lowers the energy barrier for oxygen ion transport in various perovskite oxides. (b) Relationship between free volume and oxygen ion migration energy in Ba(Fe, In)O_3−δ system. This figure has been adapted from ref. 55 with permission from Springer Nature, copyright 2025.

To conclude this section, oxygen-ion transport normally requires oxygen vacancies as the charge carriers in most of the perovskite-based mixed conductors. The chemical composition, crystal structure, and operating conditions, all play crucial roles in determining the formation and mobility of these oxygen vacancies. The availability of the oxygen vacancies and the mobility of oxygen ions jointly determine the overall oxygen-ion transport in the lattice. However, trade-offs between the content of oxygen vacancies and oxygen mobility usually exist in these perovskite metal oxides, requiring careful fine-tuning of material compositions to maximise overall oxygen-ion transport.

3.3 Proton transport

Depending on the temperature, protons can be transported through TIECs in the bulk¹⁰⁹ and on the surface.^110,111 Proton surface transport primarily occurs in surface-adsorbed water at near-room temperatures (e.g., <50 °C).^112–114 This surface transport mechanism is not limited to perovskite oxides¹¹⁵ but can also occur on the surface of other metal oxides, such as ZrO₂¹¹⁶ or TiO₂.¹¹⁷ However, this surface transport mechanism tends to diminish at elevated temperatures due to the desorption of surface water.

Instead, proton transport is governed by proton bulk diffusion at elevated temperatures (e.g., >400 °C).^109,118 This proton bulk transport is mainly reported in perovskite oxides.¹¹⁵ At the same time, some studies also reported that other oxides, such as Ba₇Nb_3.9Mo_1.1O_20.05¹¹⁹ and La₁₀Si₆O₂₇,¹²⁰ also show high proton conductivity within this temperature regime. However, tuning these proton conductors into TIECs might be challenging.

Formation of hydroxyl groups. Most studies consider hydroxyl groups as the primary charge carriers for proton bulk transport in perovskite oxides.^121–125 Under humid conditions, proton-conducting perovskite oxides can form hydroxyl groups in their structures.¹²² The formation of hydroxyl groups has been confirmed by several studies using techniques such as infrared spectroscopy¹²⁶ or nuclear magnetic resonance.¹²⁷ However, these methods can only qualitatively confirm the presence of hydroxyl groups.

A common approach to quantifying the concentration of hydroxyl groups in perovskite oxides is to measure their specific weight gain under humid conditions.^128–130 This weight gain typically refers to water uptake by perovskite oxides and is related to the incorporation of both protons and oxygen ions in humid conditions.¹²⁴ A higher weight gain generally indicates a greater concentration of hydroxyl groups in perovskite oxides. However, distinguishing the contributions of protons and oxygen ions to the water uptake remains challenging. This is due to the complexity of the reaction between water and perovskite oxides: perovskite oxides can incorporate the entire water molecule (hydration) or just protons from the water molecule (hydrogenation).⁸⁰ Some studies also use in situ neutron powder diffraction (NPD) to directly probe the concentration of protons in the structure^131,132 but NPD is less available than other techniques.

Incorporating protons into the lattice increases the positive charges in perovskite oxides. As a result, perovskite oxides must either incorporate negatively charged oxygen ions with protons or reduce the oxidation state of metal cations to compensate for the charge imbalance.^80,122,133 When perovskite oxides form hydroxyl groups at the expense of oxygen vacancies, the hydration reaction occurs. Hydration reaction is an acid–base reaction, where perovskite oxides serve as a Brønsted–Lowry base. In the hydration reaction, the formation of two hydroxyl groups consumes one oxygen vacancy,¹²² which can be expressed by eqn (4) below:

If oxygen vacancies are depleted, or holes are more available than oxygen vacancies, perovskite oxides tend to consume holes to maintain charge neutrality within their structure.¹³⁴ This process is referred to as the hydrogenation reaction, which can be expressed by eqn (5).

The hydrogenation reaction can be considered a combination of the oxygen vacancy formation reaction in eqn (3) and the hydration reaction in eqn (4). These two reactions both show that the formation of hydroxyl groups under humid conditions needs to consume electron holes for electron transport or oxygen vacancies for oxygen ion transport. Therefore, hydrated perovskite oxides tend to show compromised hole or oxygen vacancy concentrations.

These trade-offs between different charge carriers were further explored by Poetzsch et al.¹²² After considering other factors, such as charge neutrality and stoichiometry of perovskite oxides, they revealed the relationship between holes, oxygen vacancies and hydroxyl groups in perovskite oxides, as shown in Fig. 7.¹²² In their study, the authors found that the concentration of these charge carriers depends on the product of water partial pressure and the equilibrium constant of hydration reaction in eqn (4) (K_w·P_H2O in Fig. 7) and the product of oxygen partial pressure and the equilibrium concentration of the reverse oxygen vacancy formation reaction in eqn (3) (K_O·P_O2^1/2 in Fig. 7).¹²² Their thermodynamic calculations show that materials tend to undergo the hydrogenation reaction when the concentration of holes exceeds that of oxygen vacancies and the hydration reaction when oxygen vacancies are more available.¹²² Further, since the total number of charge carriers is limited in perovskite oxides, achieving a high concentration of holes, oxygen vacancies and hydroxyl groups in TIECs is theoretically impossible. In other words, TIECs would need to achieve balanced transport properties to achieve optimum ORR activity.

Fig. 7 The concentration of holes, oxygen ions and hydroxyl groups in perovskite oxides as a function of water partial pressure (P_H2O) oxygen partial pressure (P_O) and equilibrium constants of hydration reaction (K_W) and oxygenation reaction (K_O). This figure has been adapted from ref. 122 with permission from John Wiley & Sons, copyright 2025.

Impact of composition on hydroxyl group formation. Although Poetzsch et al. established a general relationship for three charge carriers, their model does not account for the influence of material composition. The composition of perovskite oxides significantly affects the equilibrium constants K_W and K_O. For instance, materials with a higher equilibrium constant for the hydration reaction (K_W) require lower water partial pressures to achieve the same concentration of hydroxyl groups as those with lower equilibrium constants. This highlights the important role of composition in the formation of hydroxyl groups.

The hydration reaction is an acid–base reaction, with perovskite oxides acting as the base and water as the acid. As a result, increasing the alkalinity of the perovskite oxides tends to shift the hydration reaction towards the formation of hydroxyl groups.^109,124,135 Consequently, materials with higher alkalinity tend to show increased water uptake. For example, SrFeO₃ show negligible water uptake at 250 °C, whereas replacing Sr with Ba increases the water uptake to 3%.¹²⁴ The increased alkalinity promotes hydroxyl group formation in Ba-based perovskite oxides, which may contribute to their higher proton conductivity compared to Sr- and La-based counterparts.¹³⁶

Aside from the materials’ basicity, a high concentration of oxygen vacancies also favours the hydroxyl group formation. The most widely studied proton conducting systems are based on BaZrO₃ and BaCeO₃.¹³⁷ These systems typically contain limited oxygen vacancies in their structure.^132,138 A common approach to creating more oxygen vacancies in these proton conductors is doping low valence state rare earth metal cations (acceptors), such as Y³⁺ and Gd³⁺, into the perovskite oxide structure.^139–142 One possible reason for choosing rare earth metal cations could be related to their relatively high alkalinity compared to other transition metals, such as cobalt. Therefore, doping rare earth metal cations can promote oxygen vacancy formation while retaining the alkalinity of materials. It should be noted that the high concentration of oxygen vacancies refers to the concentration of oxygen vacancies in dry conditions. Under humid conditions, water can consume the additional oxygen vacancies. As a result, materials with high oxygen vacancies under dry conditions do not necessarily show high oxygen vacancies under humid conditions.

To further elucidate the role of oxygen vacancies and alkalinity in hydroxyl group formation, Zohourian et al. compared the water uptake of 18 perovskite oxides at 250 °C, where high water uptake indicates a high concentration of hydroxyl groups. As shown in Fig. 8, they changed the materials’ alkalinity by substituting Sr²⁺ with Ba²⁺ in the A-site and increasing the concentration of oxygen vacancies by tuning B-site cations. They reported that replacing Sr²⁺ with more alkaline Ba²⁺ increases the water uptake of perovskite oxides by more than 15 folds while increasing oxygen non-stoichiometry from 0.4 to 0.6 also increases the water uptake by 5 to 10 folds at 250 °C and 16 mbar H₂O. Similarly, Murphy et al. also reported that substituting Zr⁴⁺ with Hf⁴⁺ can increase the water uptake by the Ba(Ce, Zr, Hf, Y, Yb)O_3−δ system.¹⁴³ These findings emphasize the critical role of increasing material alkalinity and oxygen vacancies in boosting water uptake, which in turn benefits the formation of hydroxyl groups for proton transport.

Fig. 8 Proton concentration in perovskite oxides systems of (Ba, Sr, La)(Fe, Co, Zn)O_3−δ system at 250 °C and 16 mbar H₂O. (a) Effect of A-site cations (Ba, Sr and La) and (b) effect of B-site cations (Fe, Co and Zn). This figure has been adapted from ref. with permission from John Wiley & Sons, copyright 2025.

Transport of hydroxyl groups. Hydroxyl groups in perovskite oxide tend to transport through the bulk via the Grotthuss-like mechanism. This mechanism is supported by Quasi-elastic neutron scattering (QENS) measurements and modelling results.^144–148 While alternative mechanisms, such as surface proton transport and vehicle mechanisms, have also been reported,^149,150 they are less common compared to the Grotthuss mechanism. In the Grotthuss mechanism, the bond between proton and oxygen ions is not fixed: protons can rotate around the host oxygen ion without breaking the bond. In this bond reorientation process, protons might interact and form weaker hydrogen bonds with adjacent oxygen ions. If the protons acquire sufficient energy, they can cleave the existing bond with the host oxygen ion and transfer to neighbouring oxygen ions, a process known as proton hopping.^144,147,148

It is generally accepted that hopping is the rate-limiting step in proton transfer,^34,125,151 but it is challenging to determine the energy barrier for proton rotation and hopping experimentally. Therefore, modelling is the most common way to study hydroxyl transport in perovskite oxides. Modelling results typically show that the energy barrier is ∼0.2 eV for proton rotation and doubles to ∼0.4 eV for proton hopping.^34,125,151 This energy barrier is substantially higher than the energy barrier for proton short-range transport determined by QENS, which is typically <0.1 eV.¹⁵² However, it should be pointed out that most QENS measurements are conducted at relatively low temperatures (e.g., <300 °C).¹⁵² In this temperature regime, it is unclear if the Grotthuss-like mechanism is still the dominant proton transport mechanism in perovskite oxide. Pulsed-field gradient nuclear magnetic resonance (PFG-NMR) can also probe proton diffusion in proton conductors such as BaCeO₃ at elevated temperatures (e.g., >500 °C).¹⁵³ However, most TIECs contain ferromagnetic elements, such as Co and Fe, which causes significant challenges in PFG-NMR measurements.

Similar to its influence on oxygen-ion transport, the local cationic environment also affects the proton hopping energy barrier. Since short-range proton transport mechanisms are challenging to measure experimentally, most studies rely on modelling to assess the impact of doping. For example, Draber et al. found that doping Y into BaZrO₃ can reduce the proton hopping energy barrier from 0.41 eV to 0.22–0.35 eV.¹²⁵ Similarly, substituting Sr with K also reduces the proton hopping energy barrier by ∼50% in Sr₂Fe_1.5Mo_0.5O_6−δ.¹³⁸ These findings help explain the enhanced proton conductivity observed in doped materials.

While a lower energy barrier facilitates short-range proton transport between neighboring oxygen ions, it does not necessarily enhance long-range, macroscopic proton transport. This is because dopants that reduce the proton hopping energy also create local energy minima within the structure.^121,125 As a result, protons transport rapidly within these dopant-rich regions but require additional energy to escape, leading to a phenomenon known as the trapping effect, commonly observed in doped proton-conducting systems.^154–157 For example, Yamazaki et al. reported that proton hopping between different oxygen ions in the YO₆ octahedra shows an activation energy of 0.13 to 0.17 eV, as shown in Fig. 9a.¹²¹ However, these protons require 0.44–0.47 eV to leave the YO₆ octahedra.¹²¹ If protons lack sufficient energy to overcome this barrier, they remain trapped.¹²¹ This effect becomes more pronounced at lower temperatures (e.g., 400 °C), where protons have reduced thermal energy.^{121,158–160}

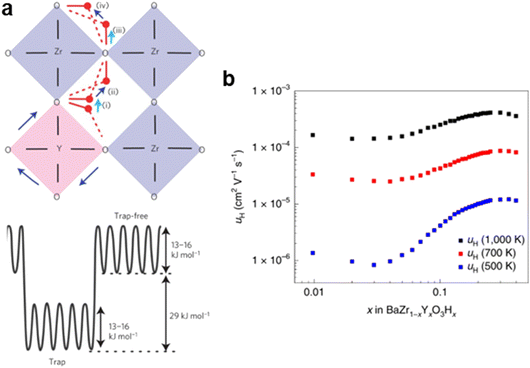Fig. 9 (a) Proton transport steps and the corresponding energies. This figure has been adapted from ref. 121 with permission from Springer Nature, copyright 2025. (b) Proton mobility in Ba(Zr, Y)O_3−δ at 500, 700 and 1000 K. A low Y doping level reduces the proton mobility. This figure has been adapted from ref. 125 with permission from Springer Nature, copyright 2025.

The traps are formed when dopants such as Y³⁺ are sparsely distributed within the host phase, particularly at low doping levels (e.g., <3%).¹²⁵ At these low concentrations, increasing the doping concentration leads to more trap sites, which can hinder long-range proton mobility.¹²⁵ For example, Draber et al. reported that when Y content in Ba(Zr, Y)O_3−δ increases from 1% to 3%, proton mobility decreases from 1.2 × 10⁻⁶ cm² V⁻¹ s⁻¹ to 0.9 × 10⁻⁶ cm² V⁻¹ s⁻¹ at 500 K, as shown in Fig. 9b.^125,161 This decrease in mobility is likely due to the greater number of traps associated with higher Y³⁺ concentrations. However, acceptor doping also promotes the formation of hydroxyl groups, increasing the overall charge carrier concentration. This effect can mitigate proton trapping, allowing the material to sustain or even slightly enhance proton conductivity despite the presence of traps.¹²⁵

At higher doping levels, the trapping zones formed by dopants begin to connect, creating percolation pathways that facilitate fast proton transport.¹²⁵ In Draber's study, proton mobility increases once the Y concentration exceeds 3%, as the interconnected trapping zones in the Ba(Zr,Y)O₃ system form continuous percolation pathways.¹²⁵ This effect becomes more pronounced when the Y concentration reaches ∼20%, as shown in Fig. 10.¹²⁵ The formation of these fast percolation pathways is a key factor contributing to the highest proton conductivity observed in BaZr_0.8Y_0.2O_3−δ, as shown in Fig. 11a.

Fig. 10 Number of percolation pathways (connected dots) in (a) BaZr_0.97Y_0.03O_3−δ (b)BaZr_0.95Y_0.05O_3−δ (c) BaZr_0.91Y_0.09O_3−δ and (d) BaZr_0.75Y_0.25O_3−δ in a 16 × 16 × 16 supercell. This figure has been adapted from ref. 125 with permission from Springer Nature, copyright 2025.

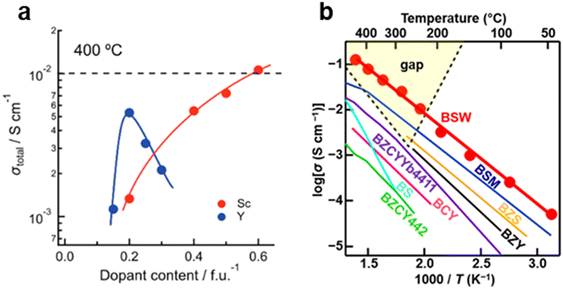Fig. 11 (a) Electrical conductivities of two proton conductors: Ba(Zr, Y)O_3−δ and Ba(Zr, Sc)O_3−δ at 400 °C. This figure has been adapted from ref. 165 with permission from Taylor & Francis Group, copyright 2024.¹⁵⁸ (b) Electrical conductivity of Sc-based proton conductors, Ba(Sc, Mo)O_3−δ (BSM) and Ba(Sc, W)O_3−δ (BSW) outperform BaZr_0.8Y_0.2O_3−δ. This figure has been adapted from ref. 168 with permission from Royal Society of Chemistry, copyright 2025.

However, an excessively high dopant concentration could also cause proton trapping,^162,163 possibly because, at this stage, the host cations themselves begin to act as trapping sites. As the doping level further increases, proton mobility decreases, ultimately hindering bulk proton transport.^164,165 This type of trapping is reported in systems such as Y- or Gd-doped BaZrO₃ and BaCeO₃.^121,155,166 This trapping effect could be the reason for the reduced proton conductivity of the materials with a high content of dopants, even though a high donor doping level benefits hydroxyl group formation.¹⁶⁷ For example, the proton conductivity of BaZr_0.7Y_0.3O_3−δ is only 60% of that of BaZr_0.8Y_0.2O_3−δ at 400 °C, as shown in Fig. 11a.

However, an exception to this trend is the Sc dopant, which does not exhibit a trapping effect in BaZrO₃.¹⁶³ Unlike other dopants, increasing the Sc concentration consistently enhances the proton conductivity of the Ba(Zr, Sc)O_3−δ system, as shown in Fig. 11a. Recent studies have even reported that BaScO₃, when stabilized by Mo or W, can achieve proton conductivities exceeding 0.01 S cm⁻¹ at temperatures as low as 250 °C, outperforming BaZrO₃ or BaCeO₃-based proton conductors, as presented in Fig. 11b.^168,169 While these results are promising, the precise role of Sc in proton transport remains insufficiently understood and requires further investigation.

Finally, grain boundaries can play a role in assisting proton transport at near room temperatures, but they tend to impede proton transport at elevated temperatures.¹⁷⁰ Some studies even report that grain boundaries contribute more than 90% of resistance for proton transport.^171–173 Reducing the number of grain boundaries by increasing grain size can decrease the grain boundary resistance, which can be achieved by sintering materials at increased temperatures for prolonged periods,¹⁷⁴ adding sinter aids,^175,176 or using methods such as pulsed laser deposition.⁴ Recently, Liu et al. demonstrated that increasing grain size significantly reduces the ohmic resistance of the electrolyte layer.⁵ They further reported that compositing nanoscale BCFZY with a microscale proton conductor enhances cathode ORR activity fourfold, attributed to the microscale proton conductor reducing grain boundary resistance for proton transport in the cathode.¹⁷⁷ Further, Bian et al. employed acid etching to increase electrolyte surface roughness, thereby enhancing the number of cathode–electrolyte–gas triple-phase boundaries, which doubled the cathode activity.⁷ Their findings suggest that these triple-phase boundaries show higher activity than the cathode–gas interface, possibly due to the high resistance of proton transport through grain boundaries limiting proton transport to the cathode surface.⁷ Collectively, these results indicate that grain boundary resistance may be a critical challenge for TIECs.

In summary, hydroxyl groups are the major charge carriers for proton transport in perovskite oxides at elevated temperatures. The formation of hydroxyl groups needs to consume electron holes or oxygen vacancies, which might negatively affect the transport of holes and oxygen ions. The mobility of the proton depends on several factors. The short-range proton transport can be described using the Grotthuss mechanism, which is significantly impacted by local cation environments. The formation of fast percolation pathways determines the long-range proton transport, especially in the doped proton conductors. The formation of percolation pathways is related to the distribution of cations in the lattice structure. Finally, grain boundaries generate high resistance to proton transport. The high resistance of grain boundaries might impair proton transport in porous TIECs for ORR. These results together highlight the importance of the cationic arrangement and material microstructures in enabling fast proton transport.

4. The importance of balancing charge transport in TIECs

It is generally accepted that transition metal cations, such as Co and Fe, are the active centres for catalysing ORR. Therefore, a high concentration of these cations in TIECs is critical for high ORR activity.^9,178 Meanwhile, as discussed in the sections above, it seems to be challenging to design a TIEC with improved content of holes, oxygen vacancies and hydroxyl groups due to their competitive charge-carrier formation.¹²²

Different from many MIECs operated in the region and proton conductors operated in the region as indicated in Fig. 7, the TIEC materials need to operate at a narrow regime with moderate concentrations for all charge carriers.¹²² This stringent requirement of the TIECs leads to compromised transport properties compared to proton conductors or MIECs. For example, Wang et al. compared the hydration enthalpy and entropy of proton conductors (electrolyte) and TIECs (cathode) and find that the hydration enthalpy of cathodes is typically less negative than proton conductors, as shown in Fig. 12a and b.³⁷ Therefore, the hydration reaction of cathode materials would have a less negative Gibbs free energy and a lower K_W compared to electrolyte materials. In another example, the typical TIEC, BCFZY, shows electrical conductivity (∼1 S cm⁻¹ at 500 °C) much lower than MIECs such as Ba_0.5Sr_0.5Co_0.8Fe_0.2O_3−δ (∼10 S cm⁻¹ at 500 °C) and (La, Sr)(Co, Fe)O_3−δ (∼300 S cm⁻¹ at 500 °C), as shown in Fig. 12c.¹⁷⁹ This might be partially attributable to the reduced hole concentration in BaCo_0.4Fe_0.4Zr_0.1Y_0.1O_3−δ, given that Zr and Y are not redox active.

Fig. 12 Comparison of hydration (a) enthalpy and (b) entropy of PCFC electrolytes and cathodes. Typical PCFC electrolytes are proton conductors while cathodes are TIECs. Typical cathodes show less negative hydration enthalpy than electrolytes. This figure has been adapted from ref. 37 with permission from John Wiley & Sons, copyright 2025. (c) The electrical conductivity of typical TIECs, MIECs, and BCFZY shows the lowest electrical conductivity among these materials. This figure has been adapted from ref. 125 with permission from Springer Nature, copyright 2025.

Furthermore, the transport of these charge carriers also requires different cationic environments. In general, hole transport requires relatively high valence states, such as La³⁺ and Pr³⁺ at the A-site and redox-active cations, such as Mn or Ti at the B-site.¹⁸⁰ These high valence state cations are essential for hole formation and suppress the oxygen vacancy formation reaction in eqn (3). The redox-active cations at the B-site also benefit hole percolation. However, oxygen ion transport might prefer cations with relatively low oxidation states, such as Sr²⁺ at the A-site and Co^2+/3+ at the B-site.^14,181 These cations can tune the cationic environment in perovskite oxides to realise the balance between high concentrations of oxygen vacancies and high mobility of oxygen ions.¹⁸¹ Further, most cations used in proton conductors are highly alkaline and redox-active inert, including Ba²⁺ at the A-site and Zr⁴⁺ and Y³⁺ at the B-site.^125,182 These cations are critical for a cationic environment with high alkalinity for hydroxyl group formation and the formation of percolation pathways.¹²⁵ Therefore, it is also challenging to design a composition that favours the transport of all three charge carriers.

4.1 Identifying dominant charge transport in accelerating the ORR kinetics

Since it is challenging to enhance all transport properties simultaneously, identifying the rate-limiting transport mechanisms in ORR becomes critical. Holes are the predominant charge carriers in most current TIECs. As a result, the electrical conductivity of these TIECs is very close to their electronic conductivities. Further, hole transport should be excessive in current TIECs. Liu et al. compared the electrical conductivity of several MIECs and TIECs. Their results reveal that BCFZY with the lowest electrical conductivity (∼1 S cm⁻¹cf. ∼10 S cm⁻¹ for Ba_0.5Sr_0.5Co_0.8Fe_0.2O_3−δ and ∼300 S cm⁻¹ for (La, Sr)(Co, Fe)O_3−δ) shows the highest ORR activities, as shown in Fig. 12b.^2,179 In another example, Liang et al. modified BCFZY via B-site nickel doping, which further reduces the electrical conductivity of BCFZY but enhances its ORR activity.^29,183 Also, applying current collectors can enhance the electrical conductivity of cathodes, making slow hole transport of these materials less of a problem. In summary, even with electrical conductivity less than 1 S cm⁻¹, the hole transport seems not to be the rate-limiting step in ORR.

Unfortunately, the transport of oxygen and proton is often much slower than the holes in TIECs and should play a role in determining the ORR activity of the TIECs.¹⁸⁴ However, it remains unclear by far which ionic transport (oxygen ion or proton) predominately limits the TIEC's ORR activity.¹⁸⁴ Part of the reason is related to the challenges in directly quantifying the transport of these two charges in TIECs. Many studies rely on multimodal characterisation techniques to access the transport properties of oxygen ions and protons in TIECs.^{29,31,45,133,185–187} The reliance on multiple characterization techniques complicates the accurate assessment of their contributions to overall conductivity and transport behaviour. Thus, more precise and unified approaches are needed to better understand and quantify these transport mechanisms.

Nevertheless, as aforementioned in sections 3.2 and 3.3, increasing the concentration of oxygen vacancies in the perovskite oxide structure could benefit proton transport by promoting the hydration reaction, and oxygen ion transport, even though the hydration reaction would consume oxygen vacancies.²⁹ Therefore, implying strategies that can promote oxygen vacancy formation can enhance the ORR activity of TIECs.^{29,178,188,189} However, increasing the oxygen vacancy concentration can reduce the oxygen ion mobility,¹⁸¹ and might also destabilise the perovskite oxide structure, converting perovskite oxides into brownmillerite structure¹⁰² or leading to the formation of a secondary phase.¹⁸⁵ Therefore, the design of single-phase TIECs requires dedicated control over the protonic and oxygen-ion transport to achieve an optimal ORR activity for PCFCs.

4.2 Composite TIECs for mixed ionic–electronic conduction

The development of composite TIECs can be an alternative strategy to the single-phase TIEC material design.^{5,133,185,190,191} Composite TIECs contain more than one phase to facilitate the charge transfer. In early PCFC cathode studies, Fabbri et al. composited (La, Sr)(Co, Fe)O_3−δ, an MIEC with proton conductors such as BaCe_0.9Y_0.1O_3−δ ¹⁹² and BaZr_0.5Pr_0.3Y_0.2O_3−δ.¹⁹³ When different conductors are mixed, protons can transport in the cathode within these proton conductors while holes and oxygen ions transport through (La, Sr)(Co, Fe)O_3−δ.¹⁹² The contact between these two phases becomes active for ORR.¹⁹² These increased ORR active sites improve the ORR activity of the cathode 2.5-fold.¹⁹² Similarly, Duan et al. also demonstrated that BCFZY, a TIEC cathode, also shows enhanced ORR activity after compositing with BaZr_0.3Ce_0.6Y_0.1O_3−δ.² Since the contact between phases is active for ORR, composites with more phase boundaries often show increased ORR activity. Fig. 13 compares the performance of some reported single-phase and composite TIECs on PCFCs. In general, composite TIECs show similar ORR activity compared to single-phase TIECs.

Fig. 13 The ASR and peak power density of reported single phase and composite TIECs on PCFCs at 600 °C. Data are collected from ref. 2, 4, 5, 9, 13, 18, 22, 29–34, 133, 185, 190, 194–197.

Traditional compositing methods, such as mechanical mixing,^2,191,198 tend to generate composites with phases loosely in contact with each other. Recently, many studies have focused on self-assembly composites to improve the contact between phases.^{5,133,179,185,190,199,200} These self-assembled composites can form nanoscale particles (e.g., ∼100 nm) during synthesis.^{133,143,185,190} For example, Song et al. report a self-assembly composite, BaCo_0.7(Ce_0.8Y_0.2)_0.3O_3−δ.¹⁹⁰ During synthesis, this composite forms a Co-rich mixed oxygen ion-electronic conducting phase, a Ce-rich mixed proton-electronic conducting phase, and a BaCoO_3−δ hole conducting phase.¹⁹⁰ Protons can transport from the electrolyte to the Ce-rich phase, while oxygen ions can transport through the Co-rich phase.¹⁹⁰ Protons and oxygen ions can combine to form water at the abundant boundaries of these two phases.¹⁹⁰ As a result, their composite cathodes show ORR activity higher than single-phase TIECs such as BCFZY. Other studies also show that forming nanoparticles such as metallic silver¹³³ or nickel oxide¹⁸⁵ at BCFZY surface can facilitate oxygen ion surface transport. These surface nanoparticles also increase the ORR activity of BCFZY more than twofold.^133,185,194 These studies together indicate that the superior ORR activity of self-assembled cathodes is closely related to the enhanced contact between these conducting phases.

5. Summary and outlook

In this review, we examined hole, oxygen ion, and proton transport in TIECs designed to catalyse the ORR in PCFC cathodes. Even the most advanced TIECs currently fall short of providing adequate ORR activity for practical PCFC applications, which could be related to imbalanced charge transport in TIECs. Charge transport depends on the concentration and mobility of charge carriers in TIECs, which are significantly impacted by the cationic environment in perovskite oxides. However, holes, oxygen ions and protons require distinct cationic environments for their fast transport, which creates trade-offs in the design of TIECs. Holes show the fastest transport among these charges, rendering it less likely to be the limiting transport for ORR, but whether oxygen ion or proton transport is the dominant contributor to the ORR activity in TIECs remains unclear. The transport of oxygen ions and protons is much slower than hole transport, and it is complicated to deconvolute their transports in TIECs under PCFC operating conditions. As a result, probing these ionic transports is challenging, but is necessary for understanding their role in ORR.

Further research efforts are demanded to address challenges in the development of TIECs with enhanced ORR activity. First, it remains difficult to quantitively measure the formation and transport of hydroxyl groups in TIECs, especially under PCFC operating conditions. Protons are light in weight and do not contain any electrons. Consequently, probing the behaviour of protons with high accuracy is challenging but necessary to understand proton transport in TIECs. It is possible to take advantage of technology that relies on nuclei instead of electrons, such as pulsed-gradient spin-echo nuclear magnetic resonance, mass spectroscopy, time-of-flight secondary ion mass spectrometry, quasi-elastic neutron scattering, to study the formation and transport of hydroxyl groups in TIECs further. The new knowledge gained from these investigations can help us design the next generation of TIECs with balanced proton and oxygen ion transports for enhanced ORR activity.

Furthermore, oxygen ion transport in TIECs under humid conditions should be investigated. The transport of oxygen ions is often measured under dry conditions using techniques such as ECR. However, the presence of humidity can deplete oxygen vacancies and might impair oxygen ion transport in TIECs. As a result, fast oxygen ion transport under dry conditions does not necessarily lead to their fast transport in humid conditions. Therefore, it should take the impact of humidity into account when measuring the transport of oxygen ions and measuring oxygen ion transport under PCFC operating conditions is highly encouraged.

Machine learning should also play a role in the next generation of TIEC designs. Machine learning shows the possibility of predicting the structure and properties of materials, including phase evolution, oxygen vacancy formation, ionic conductivities and more. Therefore, ML can accelerate the development of single-phase and self-assembled TIECs with balanced ionic conductivity. By leveraging vast datasets of material properties and performance metrics, ML algorithms might identify patterns, predict material behaviour, and guide the design of compositions with optimal ionic conductivity and ORR activity.

Finally, the design of TIECs also needs to consider the stability issue. Current TIECs are mainly Ba- or Sr-based perovskite oxides. These alkaline-earth elements are critical for fast proton transport but also are susceptible to gases such as CO₂ at reduced temperatures. The reaction between these alkaline-earth elements and trace amounts of CO₂ in air can lead to the formation of the carbonate phase and the depletion of the TIEC phase. As a result, the practical application of TIECs on PCFCs requires stabilising these alkaline-earth elements, such as bulk doping or surface modification, or even replacing them with lanthanoid elements such as La and Pr.

Data availability

No primary research results, software or code have been included and no new data were generated or analysed as part of this review.

Conflicts of interest

The authors declare that they have no financial interests or personal conflict of interest.

Acknowledgements

M. L. acknowledges the financial support from the Australian Research Council (DE230100637) and Australia Sunlight Group Pty Ltd (AUKRH000031). Z. Z. acknowledges the support from Australian Research Council Discovery Projects DP200101397 and DP250102334. D. F. and D. L. acknowledges the financial support from the Australian Research Council (FL180100029).

References

1. Y. Zhou, X. Guan, H. Zhou, K. Ramadoss, S. Adam, H. Liu, S. Lee, J. Shi, M. Tsuchiya, D. D. Fong and S. Ramanathan, Nature, 2016, 534, 231–234.
2. C. Duan, J. Tong, M. Shang, S. Nikodemski, M. Sanders, S. Ricote, A. Almansoori and R. O'Hayre, Science, 2015, 349, 1321–1326.
3. C. Duan, R. J. Kee, H. Zhu, C. Karakaya, Y. Chen, S. Ricote, A. Jarry, E. J. Crumlin, D. Hook, R. Braun, N. P. Sullivan and R. O'Hayre, Nature, 2018, 557, 217–222.
4. S. Choi, C. J. Kucharczyk, Y. Liang, X. Zhang, I. Takeuchi, H.-I. Ji and S. M. Haile, Nat. Energy, 2018, 3, 202–210.
5. F. Liu, H. Deng, D. Diercks, P. Kumar, M. H. A. Jabbar, C. Gumeci, Y. Furuya, N. Dale, T. Oku, M. Usuda, P. Kazempoor, L. Fang, D. Chen, B. Liu and C. Duan, Nat. Energy, 2023, 8, 1145–1157.
6. H. An, H.-W. Lee, B.-K. Kim, J.-W. Son, K. J. Yoon, H. Kim, D. Shin, H.-I. Ji and J.-H. Lee, Nat. Energy, 2018, 3, 870–875.
7. W. Bian, W. Wu, B. Wang, W. Tang, M. Zhou, C. Jin, H. Ding, W. Fan, Y. Dong, J. Li and D. Ding, Nature, 2022, 604, 479–485.
8. C. Duan, R. Kee, H. Zhu, N. Sullivan, L. Zhu, L. Bian, D. Jennings and R. O'Hayre, Nat. Energy, 2019, 4, 230–240.
9. Z. Wang, Y. Wang, J. Wang, Y. Song, M. J. Robson, A. Seong, M. Yang, Z. Zhang, A. Belotti, J. Liu, G. Kim, J. Lim, Z. Shao and F. Ciucci, Nat. Catal., 2022, 5, 777–787.
10. L. Yang, S. Wang, K. Blinn, M. Liu, Z. Liu, Z. Cheng and M. Liu, Science, 2009, 326, 126–129.
11. R. J. Gorte, Science, 2015, 349, 1290–1290.
12. Z. Wang, W. Yang, Z. Zhu, R. Peng, X. Wu, C. Xia and Y. Lu, J. Mater. Chem. A, 2014, 2, 16707–16714.
13. J. Kim, S. Sengodan, G. Kwon, D. Ding, J. Shin, M. Liu and G. Kim, ChemSusChem, 2014, 7, 2811–2815.
14. M. Li, M. Zhao, F. Li, W. Zhou, V. K. Peterson, X. Xu, Z. Shao, I. Gentle and Z. Zhu, Nat. Commun., 2017, 8, 13990.
15. Z. Li, X. Mao, D. Feng, M. Li, X. Xu, Y. Luo, L. Zhuang, R. Lin, T. Zhu, F. Liang, Z. Huang, D. Liu, Z. Yan, A. Du, Z. Shao and Z. Zhu, Nat. Commun., 2024, 15, 9318.
16. Z. Shao and S. M. Haile, Nature, 2004, 431, 170–173.
17. W. Zhou, J. Sunarso, M. Zhao, F. Liang, T. Klande and A. Feldhoff, Angew. Chem., Int. Ed., 2013, 52, 14036–14040.
18. M. Saqib, I.-G. Choi, H. Bae, K. Park, J.-S. Shin, Y.-D. Kim, J.-I. Lee, M. Jo, Y.-C. Kim, K.-S. Lee, S.-J. Song, E. D. Wachsman and J.-Y. Park, Energy Environ. Sci., 2021, 14, 2472–2484.
19. G. Taillades, J. Dailly, M. Taillades-Jacquin, F. Mauvy, A. Essouhmi, M. Marrony, C. Lalanne, S. Fourcade, D. J. Jones, J.-C. Grenier and J. Rozière, Fuel Cells, 2010, 10, 166–173.
20. Y. Lin, R. Ran, Y. Zheng, Z. Shao, W. Jin, N. Xu and J. Ahn, J. Power Sources, 2008, 180, 15–22.
21. L. Bi, E. Fabbri, Z. Sun and E. Traversa, Energy Environ. Sci., 2011, 4, 1352–1357.
22. H. Shi, C. Su, X. Xu, Y. Pan, G. Yang, R. Ran and Z. Shao, Small, 2021, 17, 2101872.
23. L. Bi, E. Fabbri, Z. Sun and E. Traversa, Energy Environ. Sci., 2011, 4, 409–412.
24. J. Dailly, G. Taillades, M. Ancelin, P. Pers and M. Marrony, J. Power Sources, 2017, 361, 221–226.
25. Q. Shao, W. Ge, X. Lu, Y. Chen, Y. Ding, B. Lin and Y. Ling, Ceram. Int., 2015, 41, 6687–6692.
26. K. Xie, R. Yan, X. Chen, D. Dong, S. Wang, X. Liu and G. Meng, J. Alloys Compd., 2009, 472, 551–555.
27. B. Lin, S. Zhang, L. Zhang, L. Bi, H. Ding, X. Liu, J. Gao and G. Meng, J. Power Sources, 2008, 177, 330–333.
28. L. Bi, S. Zhang, S. Fang, Z. Tao, R. Peng and W. Liu, Electrochem. Commun., 2008, 10, 1598–1601.
29. M. Liang, F. He, C. Zhou, Y. Chen, R. Ran, G. Yang, W. Zhou and Z. Shao, Chem. Eng. J., 2021, 420, 127717.
30. M. Liang, Y. Song, D. Liu, L. Xu, M. Xu, G. Yang, W. Wang, W. Zhou, R. Ran and Z. Shao, Appl. Catal., B, 2022, 318, 121868.
31. K. Pei, Y. Zhou, K. Xu, H. Zhang, Y. Ding, B. Zhao, W. Yuan, K. Sasaki, Y. Choi, Y. Chen and M. Liu, Nat. Commun., 2022, 13, 2207.
32. W. Zhang, Y. Zhou, X. Hu, Y. Ding, J. Gao, Z. Luo, T. Li, N. Kane, X.-Y. Yu, T. Terlier and M. Liu, ACS Energy Lett., 2023, 8, 3999–4007.
33. C. Zhou, J. Sunarso, Y. Song, J. Dai, J. Zhang, B. Gu, W. Zhou and Z. Shao, J. Mater. Chem. A, 2019, 7, 13265–13274.
34. X. Xu, H. Wang, M. Fronzi, X. Wang, L. Bi and E. Traversa, J. Mater. Chem. A, 2019, 7, 20624–20632.
35. M. Shang, J. Tong and R. O'Hayre, RSC Adv., 2013, 3, 15769–15775.
36. M. Papac, V. Stevanović, A. Zakutayev and R. O'Hayre, Nat. Mater., 2021, 20, 301–313.
37. N. Wang, C. Tang, L. Du, R. Zhu, L. Xing, Z. Song, B. Yuan, L. Zhao, Y. Aoki and S. Ye, Adv. Energy Mater., 2022, 12, 2201882.
38. T. P. Pandey, A. M. Maes, H. N. Sarode, B. D. Peters, S. Lavina, K. Vezzù, Y. Yang, S. D. Poynton, J. R. Varcoe, S. Seifert, M. W. Liberatore, V. D. Noto and A. M. Herring, Phys. Chem. Chem. Phys., 2015, 17, 4367–4378.
39. D. Poetzsch, R. Merkle and J. Maier, Phys. Chem. Chem. Phys., 2014, 16, 16446–16453.
40. Z. Luo, J. Tang, Z. Wang, G. Yang, T. Zhu, Z. Lin, S. Ping Jiang and Z. Shao, Energy Environ. Sci., 2024, 17, 4115–4125.
41. Y. Huang, R. Qiu, W. Lian, L. Lei, T. Liu, J. Zhang, Y. Wang, J. Liu, J. Huang and F. Chen, J. Power Sources, 2022, 528, 231201.
42. A. Seong, J. Kim, D. Jeong, S. Sengodan, M. Liu, S. Choi and G. Kim, Adv. Sci., 2021, 8, 2004099.
43. B. Liu, Y. Zheng, X. Yang, Y. Liu, D. Yan, J. Li and L. Jia, Chem. Eng. J., 2025, 505, 159163.
44. Y. Feng, P. Su, H. Liu, X. Sun, B. Zhang, Q. Duan, J. Li, Y. Shen and F. Wang, Chem. Eng. J., 2024, 500, 156758.
45. P. Yao, J. Zhang, Q. Qiu, Y. Zhao, F. Yu and Y. Li, Adv. Energy Mater., 2024, 2403335.
46. P. Yao, J. Zhang, Q. Qiu, Y. Zhao, F. Yu and Y. Li, J. Power Sources, 2024, 606, 234591.
47. E. Fabbri, D. Pergolesi and E. Traversa, Chem. Soc. Rev., 2010, 39, 4355–4369.
48. W. Zhang, X. Zhang, Y. Song and G. Wang, Sustainability, 2024, 3, 100028.
49. M. Wang, C. Su, Z. Zhu, H. Wang and L. Ge, Composites, Part B, 2022, 238, 109881.
50. J. Cao, Y. Ji and Z. Shao, Energy Environ. Sci., 2022, 15, 2200–2232.
51. M. A. Peña and J. L. G. Fierro, Chem. Rev., 2001, 101, 1981–2018.
52. J. Wang, Y. Lu, N. Mushtaq, M. A. K. Y. Shah, S. Rauf, P. D. Lund and M. I. Asghar, J. Rare Earths, 2023, 41, 413–421.
53. L. Huang and Y. Wu, Ceram. Int., 2024, 50, 5150–5159.
54. D. Huan, L. Zhang, X. Li, Y. Xie, N. Shi, S. Xue, C. Xia, R. Peng and Y. Lu, ChemSusChem, 2020, 13, 4994–5003.
55. Z. Li, M. Li and Z. Zhu, Electrochem. Energy Rev., 2022, 5, 263–311.
56. F. He, M. Liang, W. Wang, R. Ran, G. Yang, W. Zhou and Z. Shao, Energy Fuels, 2020, 34, 11464–11471.
57. Y. Shin, Y. Kim, M. Sanders, S. P. Harvey, M. Walker and R. O'Hayre, J. Mater. Chem. A, 2022, 10, 24839–24853.
58. B. Wang and K. Ohgushi, Sci. Rep., 2016, 6, 37896.
59. E. Robens, R. Rauschen, J. Kaub, J. P. Parras, D. Kemp, C. L. Freeman and R. A. De Souza, J. Mater. Chem. A, 2022, 10, 2388–2397.
60. K. D. Kreuer, Solid State Ionics, 1999, 125, 285–302.
61. V. M. Goldschmidt, Naturwissenschaften, 1926, 14, 477–485.
62. C. J. Bartel, C. Sutton, B. R. Goldsmith, R. Ouyang, C. B. Musgrave, L. M. Ghiringhelli and M. Scheffler, Sci. Adv., 2019, 5, eaav0693.
63. K. Yim, Y. Youn, M. Lee, D. Yoo, J. Lee, S. H. Cho and S. Han, Npj Comput. Mater., 2018, 4, 1–7.
64. H. He, Z. Yang, Y. Xu, A. T. Smith, G. Yang and L. Sun, Nano Converg., 2020, 7, 32.
65. R. Oja, M. Tyunina, L. Yao, T. Pinomaa, T. Kocourek, A. Dejneka, O. Stupakov, M. Jelinek, V. Trepakov, S. van Dijken and R. M. Nieminen, Phys. Rev. Lett., 2012, 109, 127207.
66. A. Gómez-Pérez, M. Yuste, J. C. Pérez-Flores, C. Ritter, M. T. Azcondo, J. Canales-Vázquez, M. Gálvez-Sánchez, K. Boulahya, F. García-Alvarado and U. Amador, J. Power Sources, 2013, 227, 309–317.
67. A. Gómez-Pérez, M. T. Azcondo, M. Yuste, J. C. Pérez-Flores, N. Bonanos, F. Porcher, A. Muñoz-Noval, M. Hoelzel, F. García-Alvarado and U. Amador, J. Mater. Chem. A, 2016, 4, 3386–3397.
68. A. Gómez-Pérez, M. Yuste, J. C. Pérez-Flores, C. Ritter, M. T. Azcondo, J. Canales-Vázquez, M. Gálvez-Sánchez, K. Boulahya, F. García-Alvarado and U. Amador, J. Power Sources, 2013, 227, 309–317.
69. R. Ganguly, A. K. Singh, R. Kumar, A. Gupta, A. K. Pandey and A. K. Pandey, in Nanotechnology in Modern Animal Biotechnology, ed. P. K. Maurya and S. Singh, Elsevier, 2019, pp. 29–35.
70. M. Fabián, B. I. Arias-Serrano, A. A. Yaremchenko, H. Kolev, M. Kaňuchová and J. Briančin, J. Eur. Ceram. Soc., 2019, 39, 5298–5308.
71. J. Richter, P. Holtappels, T. Graule, T. Nakamura and L. J. Gauckler, Monatsh. Chem., 2009, 140, 985–999.
72. D. Neagu and J. T. S. Irvine, Chem. Mater., 2011, 23, 1607–1617.
73. P. M. Raccah and J. B. Goodenough, Phys. Rev., 1967, 155, 932–943.
74. S. Kirkpatrick, Rev. Mod. Phys., 1973, 45, 574–588.
75. D. Kim, S. Miyoshi, T. Tsuchiya and S. Yamaguchi, Solid State Ionics, 2014, 262, 875–878.
76. R. Raffaelle, H. U. Anderson, D. M. Sparlin and P. E. Parris, Phys. Rev. B:Condens. Matter Mater. Phys., 1991, 43, 7991–7999.
77. Z. Sherafat, M. H. Paydar, I. Antunes, N. Nasani, A. D. Brandão and D. P. Fagg, Electrochim. Acta, 2015, 165, 443–449.
78. L.-W. Tai, M. M. Nasrallah, H. U. Anderson, D. M. Sparlin and S. R. Sehlin, Solid State Ionics, 1995, 76, 259–271.
79. C. S. Kim, S. R. Bishop and H. L. Tuller, J. Electroceramics, 2018, 40, 57–64.
80. T. Hong, W. Lu, K. Ren and T. Liu, Ionics, 2020, 26, 5293–5297.
81. S. B. Adler, Chem. Rev., 2004, 104, 4791–4844.
82. E. N. Armstrong, K. L. Duncan and E. D. Wachsman, Phys. Chem. Chem. Phys., 2013, 15, 2298–2308.
83. Z. Zhang, X. Xu, J. Zhang, D. Chen, D. Zeng, S. Liu, W. Zhou and Z. Shao, J. Membr. Sci., 2018, 563, 617–624.
84. A. Zomorrodian, H. Salamati, Z. Lu, X. Chen, N. Wu and A. Ignatiev, Int. J. Hydrogen Energy, 2010, 35, 12443–12448.
85. B. C. H. Steele, Solid State Ionics, 2000, 129, 95–110.
86. K. Huang, R. S. Tichy and J. B. Goodenough, J. Am. Ceram. Soc., 1998, 81, 2565–2575.
87. J. Meng, M. S. Sheikh, R. Jacobs, J. Liu, W. O. Nachlas, X. Li and D. Morgan, Nat. Mater., 2024, 23, 1252–1258.
88. Q. Li, Y.-X. Deng, Y.-A. Zhu, Y. Li, Z.-J. Sui, D. Chen and W.-K. Yuan, Catal. Today, 2020, 347, 142–149.
89. T. Roohandeh and E. Saievar-Iranizad, Appl. Phys. A, 2019, 125, 552.
90. E. Olsson, J. Cottom, X. Aparicio-Anglès and N. H. de Leeuw, Phys. Chem. Chem. Phys., 2019, 21, 9407–9418.
91. H. Ding, W. Wu, C. Jiang, Y. Ding, W. Bian, B. Hu, P. Singh, C. J. Orme, L. Wang, Y. Zhang and D. Ding, Nat. Commun., 2020, 11, 1907.
92. C. Duan, D. Hook, Y. Chen, J. Tong and R. O'Hayre, Energy Environ. Sci., 2017, 10, 176–182.
93. M. Li, W. Zhou and Z. Zhu, ChemElectroChem, 2015, 2, 1331–1338.
94. C. Sun, Y. Kong, L. Shao, K. Sun and N. Zhang, J. Power Sources, 2020, 459, 228017.
95. T. J. Frankcombe and Y. Liu, Chem. Mater., 2023, 35, 5468–5474.
96. K. S. Knight, Solid State Ionics, 2001, 145, 275–294.
97. S. Zhai, H. Xie, P. Cui, D. Guan, J. Wang, S. Zhao, B. Chen, Y. Song, Z. Shao and M. Ni, Nat. Energy, 2022, 7, 866–875.
98. L. Giordano, K. Akkiraju, R. Jacobs, D. Vivona, D. Morgan and Y. Shao-Horn, Acc. Chem. Res., 2022, 55, 298–308.
99. R. Jacobs, J. Liu, H. Abernathy and D. Morgan, Adv. Energy Mater., 2024, 14, 2303684.
100. Q. Tao, P. Xu, M. Li and W. Lu, Npj Comput. Mater., 2021, 7, 1–18.
101. Q. Tao, T. Lu, Y. Sheng, L. Li, W. Lu and M. Li, J. Energy Chem., 2021, 60, 351–359.
102. S. K. Jaiswal, V. K. Kashyap and J. Kumar, J. Asian Ceram. Soc., 2020, 8, 1018–1026.
103. S. Sengodan, S. Choi, A. Jun, T. H. Shin, Y.-W. Ju, H. Y. Jeong, J. Shin, J. T. S. Irvine and G. Kim, Nat. Mater., 2015, 14, 205–209.
104. M. Mogensen, D. Lybye, N. Bonanos, P. V. Hendriksen and F. W. Poulsen, Solid State Ionics, 2004, 174, 279–286.
105. R. A. De Souza, Adv. Funct. Mater., 2015, 25, 6326–6342.
106. R. D. Shannon, Acta Crystallogr., Sect. A, 1976, 32, 751–767.
107. R. L. Cook, J. J. Osborne, J. H. White, R. C. MacDuff and A. F. Sammells, J. Electrochem. Soc., 1992, 139, L19.
108. Y. Lu, H. Zhao, X. Cheng, Y. Jia, X. Du, M. Fang, Z. Du, K. Zheng and K. Świerczek, J. Mater. Chem. A, 2015, 3, 6202–6214.
109. K. D. Kreuer, Annu. Rev. Mater. Res., 2003, 33, 333–359.
110. G. Gregori, M. Shirpour and J. Maier, Adv. Funct. Mater., 2013, 23, 5861–5867.
111. F. Maglia, I. G. Tredici, G. Spinolo and U. Anselmi-Tamburini, J. Mater. Res., 2012, 27, 1975–1981.
112. S. Miyoshi, Y. Akao, N. Kuwata, J. Kawamura, Y. Oyama, T. Yagi and S. Yamaguchi, Chem. Mater., 2014, 26, 5194–5200.
113. S. Kim, H. J. Avila-Paredes, S. Wang, C.-T. Chen, R. A. D. Souza, M. Martin and Z. A. Munir, Phys. Chem. Chem. Phys., 2009, 11, 3035–3038.
114. Y. Meng, J. Gao, Z. Zhao, J. Amoroso, J. Tong and K. S. Brinkman, J. Mater. Sci., 2019, 54, 9291–9312.
115. T. Norby, Prog. Energy, 2024, 6, 043002.
116. R. Sato, S. Ohkuma, Y. Shibuta, F. Shimojo and S. Yamaguchi, J. Phys. Chem. C, 2015, 119, 28925–28933.
117. Y. Zhao, T. Shi, J. Shang, L. Ding, X. Cao, C. Chen and J. Zhao, Appl. Catal., B, 2020, 277, 119234.
118. T. Norby, Solid State Ionics, 1999, 125, 1–11.
119. R. Morikawa, T. Murakami, K. Fujii, M. Avdeev, Y. Ikeda, Y. Nambu and M. Yashima, Commun. Mater., 2023, 4, 1–9.
120. T. Nakao, A. Mineshige, M. Kobune, T. Yazawa and H. Yoshioka, Solid State Ionics, 2008, 179, 1567–1569.
121. Y. Yamazaki, F. Blanc, Y. Okuyama, L. Buannic, J. C. Lucio-Vega, C. P. Grey and S. M. Haile, Nat. Mater., 2013, 12, 647–651.
122. D. Poetzsch, R. Merkle and J. Maier, Adv. Funct. Mater., 2015, 25, 1542–1557.
123. T. Norby, in Perovskite Oxide for Solid Oxide Fuel Cells, ed. T. Ishihara, Springer US, Boston, MA, 2009, pp. 217–241.
124. F. M. Draber, C. Ader, J. P. Arnold, S. Eisele, S. Grieshammer, S. Yamaguchi and M. Martin, Nat. Mater., 2020, 19, 338–346.
125. R. Zohourian, R. Merkle, G. Raimondi and J. Maier, Adv. Funct. Mater., 2018, 28, 1801241.
126. K. Arai, Y. Asai, Y. Kokubo, M. Saito, M. Inada, K. Hayashi and T. Motohashi, J. Solid State Chem., 2023, 323, 124026.
127. H. Maekawa, N. Kashii, J.-I. Kawamura, Y. Hinatsu and T. Yamamura, Solid State Ionics, 1999, 122, 231–236.
128. D. Poetzsch, R. Merkle and J. Maier, Phys. Chem. Chem. Phys., 2014, 16, 16446–16453.
129. A. Løken, T. S. Bjørheim and R. Haugsrud, J. Mater. Chem. A, 2015, 3, 23289–23298.
130. S. Fop, K. S. McCombie, E. J. Wildman, J. M. S. Skakle, J. T. S. Irvine, P. A. Connor, C. Savaniu, C. Ritter and A. C. Mclaughlin, Nat. Mater., 2020, 19, 752–757.
131. T. Nagasaki, S. Shiotani, N. Igawa, M. Yoshino, K. Iwasaki, H. Fukazawa and W. Utsumi, J. Solid State Chem., 2009, 182, 2632–2639.
132. G. C. Mather, G. Heras-Juaristi, C. Ritter, R. O. Fuentes, A. L. Chinelatto, D. Pérez-Coll and U. Amador, Chem. Mater., 2016, 28, 4292–4299.
133. J. H. Kim, J. Hong, D.-K. Lim, S. Ahn, J. Kim, J. K. Kim, D. Oh, S. Jeon, S.-J. Song and W. Jung, Energy Environ. Sci., 2022, 15, 1097–1105.
134. H. Sakaguchi, K. Hatakeyama, S. Kobayashi and T. Esaka, Mater. Res. Bull., 2002, 37, 1547–1556.
135. K. D. Kreuer, Solid State Ionics, 1997, 97, 1–15.
136. N. Bonanos, in Encyclopedia of Applied Electrochemistry, ed. G. Kreysa, K. Ota and R. F. Savinell, Springer, New York, NY, 2014, pp. 1514–1520.
137. K. D. Kreuer, Annu. Rev. Mater. Res., 2003, 33, 333–359.
138. A. Perrichon, E. Jedvik Granhed, G. Romanelli, A. Piovano, A. Lindman, P. Hyldgaard, G. Wahnström and M. Karlsson, Chem. Mater., 2020, 32, 2824–2835.
139. D. Han, K. Shinoda, S. Sato, M. Majima and T. Uda, J. Mater. Chem. A, 2014, 3, 1243–1250.
140. H. Iwahara, Solid State Ionics, 1996, 86–88, 9–15.
141. H. Iwahara, T. Yajima, T. Hibino, K. Ozaki and H. Suzuki, Solid State Ionics, 1993, 61, 65–69.
142. P. A. Stuart, T. Unno, J. A. Kilner and S. J. Skinner, Solid State Ionics, 2008, 179, 1120–1124.
143. R. Murphy, Y. Zhou, L. Zhang, L. Soule, W. Zhang, Y. Chen and M. Liu, Adv. Funct. Mater., 2020, 30, 2002265.
144. R. Hempehnann, Ch. Karmonik, Th. Matzke, M. Cappadonia, U. Stimming, T. Springer and M. A. Adams, Solid State Ionics, 1995, 77, 152–156.
145. M. E. Björketun, P. G. Sundell, G. Wahnström and D. Engberg, Solid State Ionics, 2005, 176, 3035–3040.
146. M. Karlsson, Phys. Chem. Chem. Phys., 2015, 17, 26–38.
147. A. Perrichon, M. M. Koza, Z. Evenson, B. Frick, F. Demmel, P. Fouquet and M. Karlsson, Chem. Mater., 2023, 35, 6713–6725.
148. E. Naumovska, J. Orstadius, A. Perrichon, R. Lavén, M. M. Koza, Z. Evenson and M. Karlsson, J. Phys. Chem. C, 2023, 127, 24532–24541.
149. C. Xia, Y. Mi, B. Wang, B. Lin, G. Chen and B. Zhu, Nat. Commun., 2019, 10, 1707.
150. Q. Li, Q. Yin, Y.-S. Zheng, Z.-J. Sui, X.-G. Zhou, D. Chen and Y.-A. Zhu, Langmuir, 2019, 35, 9962–9969.
151. W. Münch, G. Seifert, K. D. Kreuer and J. Maier, Solid State Ionics, 1996, 86–88, 647–652.
152. D. Noferini, M. M. Koza and M. Karlsson, J. Phys. Chem. C, 2017, 121, 7088–7093.
153. K. D. Kreuer, Th. Dippel, Yu. M. Baikov and J. Maier, Solid State Ionics, 1996, 86–88, 613–620.
154. M. S. Islam, R. A. Davies and J. D. Gale, Chem. Commun., 2001, 661–662.
155. D. Vignesh, B. K. Sonu and E. Rout, Energy Fuels, 2022, 36, 7219–7244.
156. C. Karmonik, R. Hempelmann, T. Matzke and T. Springer, Z. Naturforsch., A:Phys. Sci., 1995, 50, 539–548.
157. M. S. Islam, P. R. Slater, J. R. Tolchard and T. Dinges, Dalton Trans., 2004, 3061–3066.
158. C. Y. Regalado Vera, H. Ding, J. Urban-Klaehn, M. Li, Z. Zhao, F. Stewart, H. Tian, X. Liu, Y. Dong, J. Li, M. Zhou, H. Luo and D. Ding, Chem. Mater., 2023, 35, 5341–5352.
159. K. Toyoura, W. Meng, D. Han and T. Uda, J. Mater. Chem. A, 2018, 6, 22721–22730.
160. L. P. Putilov and V. I. Tsidilkovski, Phys. Chem. Chem. Phys., 2019, 21, 6391–6406.
161. F. M. Draber, J. R. Denninger, P. C. Müller, I. K. Sommerfeld and M. Martin, Adv. Energy Sustainable Res., 2022, 3, 2200007.
162. C. Y. R. Vera, H. Ding, D. Peterson, W. T. Gibbons, M. Zhou and D. Ding, J. Phys. Energy, 2021, 3, 032019.
163. C. Y. Regalado Vera, H. Ding, J. Urban-Klaehn, M. Li, Z. Zhao, F. Stewart, H. Tian, X. Liu, Y. Dong, J. Li, M. Zhou, H. Luo and D. Ding, Chem. Mater., 2023, 35, 5341–5352.
164. S. Fujii, J. Hyodo, K. Shitara, A. Kuwabara, S. Kasamatsu and Y. Yamazaki, Sci. Technol. Adv. Mater., 2024, 25, 2416383.
165. D. Han, N. Hatada and T. Uda, J. Am. Ceram. Soc., 2016, 99, 3745–3753.
166. E. Makagon, O. Kraynis, R. Merkle, J. Maier and I. Lubomirsky, Adv. Funct. Mater., 2021, 31, 2104188.
167. A. Fluri, A. Marcolongo, V. Roddatis, A. Wokaun, D. Pergolesi, N. Marzari and T. Lippert, Adv. Sci., 2017, 4, 1700467.
168. K. Saito, K. Umeda, K. Fujii, K. Mori and M. Yashima, J. Mater. Chem. A, 2024, 12, 13310–13319.
169. K. Saito and M. Yashima, Nat. Commun., 2023, 14, 7466.
170. Y. Meng, J. Gao, Z. Zhao, J. Amoroso, J. Tong and K. S. Brinkman, J. Mater. Sci., 2019, 54, 9291–9312.
171. R. Pornprasertsuk, O. Kosasang, K. Somroop, M. Horprathum, P. Limnonthakul, P. Chindaudom and S. Jinawath, Solid State Sci., 2011, 13, 1429–1437.
172. S. M. Haile, G. Staneff and K. H. Ryu, J. Mater. Sci., 2001, 36, 1149–1160.
173. S. M. Haile, D. L. West and J. Campbell, J. Mater. Res., 1998, 13, 1576–1595.
174. Y. Yamazaki, R. Hernandez-Sanchez and S. M. Haile, Chem. Mater., 2009, 21, 2755–2762.
175. J. Li, C. Wang, X. Wang and L. Bi, Electrochem. Commun., 2020, 112, 106672.
176. I. A. Starostina, G. N. Starostin, M. T. Akopian, G. K. Vdovin, D. A. Osinkin, B. Py, A. Maradesa, F. Ciucci and D. A. Medvedev, Adv. Funct. Mater., 2024, 34, 2307316.
177. F. Liu, D. Diercks, P. Kumar, A. Seong, M. H. A. Jabbar, C. Gumeci, Y. Furuya, N. Dale, T. Oku, M. Usuda, P. Kazempoor, I. Ghamarian, L. Liu, L. Fang, D. Chen, Z. Wang, S. Skinner and C. Duan, Sci. Adv., 2025, 11, eadq2507.
178. Y. Shin, Y. Kim, M. Sanders, S. P. Harvey, M. Walker and R. O'Hayre, J. Mater. Chem. A, 2022, 10, 24839–24853.
179. Z. Liu, Z. Tang, Y. Song, G. Yang, W. Qian, M. Yang, Y. Zhu, R. Ran, W. Wang, W. Zhou and Z. Shao, Nano-Micro Lett., 2022, 14, 217.
180. S. Tao and J. T. S. Irvine, Nat. Mater., 2003, 2, 320–323.
181. Z. Li, X. Mao, D. Feng, M. Li, X. Xu, Y. Luo, L. Zhuang, R. Lin, T. Zhu, F. Liang, Z. Huang, D. Liu, Z. Yan, A. Du, Z. Shao and Z. Zhu, Nat. Commun., 2024, 15, 9318.
182. K. D. Kreuer, Annu. Rev. Mater. Res., 2003, 33, 333–359.
183. D. Hu, J. Kim, H. Niu, L. M. Daniels, T. D. Manning, R. Chen, B. Liu, R. Feetham, J. B. Claridge and M. J. Rosseinsky, J. Mater. Chem. A, 2022, 10, 2559–2566.
184. M. Papac, V. Stevanović, A. Zakutayev and R. O'Hayre, Nat. Mater., 2021, 20, 301–313.
185. M. Liang, Y. Zhu, Y. Song, D. Guan, Z. Luo, G. Yang, S. P. Jiang, W. Zhou, R. Ran and Z. Shao, Adv. Mater., 2022, 34, 2106379.
186. X. Zhang, C. Tang, Y. Yang, F. Zheng, Q. Su, H. Xiang, L. Meng, L. Du, Y. Aoki, D. Luo, N. Wang and S. Ye, Adv. Funct. Mater., 2025, 2421083.
187. C. Tang, B. Yuan, X. Zhang, F. Zheng, Q. Su, L. Meng, L. Du, D. Luo, Y. Aoki, N. Wang and S. Ye, Adv. Energy Mater., 2025, 2402654.
188. M. Liang, Y. Song, D. Liu, L. Xu, M. Xu, G. Yang, W. Wang, W. Zhou, R. Ran and Z. Shao, Appl. Catal., B, 2022, 318, 121868.
189. R. Ren, Z. Wang, C. Xu, W. Sun, J. Qiao, D. W. Rooney and K. Sun, J. Mater. Chem. A, 2019, 7, 18365–18372.
190. Y. Song, Y. Chen, W. Wang, C. Zhou, Y. Zhong, G. Yang, W. Zhou, M. Liu and Z. Shao, Joule, 2019, 3, 2842–2853.
191. L. Yang, C. Zuo, S. Wang, Z. Cheng and M. Liu, Adv. Mater., 2008, 20, 3280–3283.
192. E. Fabbri, S. Licoccia, E. Traversa and E. D. Wachsman, Fuel Cells, 2009, 9, 128–138.
193. E. Fabbri, L. Bi, D. Pergolesi and E. Traversa, Energy Environ. Sci., 2011, 4, 4984–4993.
194. K. Park, M. Saqib, H. Lee, D. Shin, M. Jo, K. M. Park, M. Hamayun, S. H. Kim, S. Kim, K.-S. Lee, R. O'Hayre, M. Choi, S.-J. Song and J.-Y. Park, Energy Environ. Sci., 2024, 17, 1175–1188.
195. S. Lei, J. Ma, W. Li, M. B. Hanif, C.-X. Li, D. Wang and S. Wang, J. Power Sources, 2025, 631, 236257.
196. D. Zou, Y. Yi, Y. Song, D. Guan, M. Xu, R. Ran, W. Wang, W. Zhou and Z. Shao, J. Mater. Chem. A, 2022, 10, 5381–5390.
197. S. H. Hwang, S. K. Kim, J.-T. Nam and J.-S. Park, Int. J. Hydrogen Energy, 2021, 46, 33551–33560.
198. L. Yang, Z. Liu, S. Wang, Y. Choi, C. Zuo and M. Liu, J. Power Sources, 2010, 195, 471–474.
199. W. Zhang, H. Muroyama, Y. Mikami, Q. Liu, X. Liu, T. Matsui and K. Eguchi, Chem. Eng. J., 2023, 461, 142056.
200. D. Feng, M. Li, V. K. Peterson, R. Lin, A. D’Angelo, O. Marenych, A. Yago, D. Appadoo, T. Zhu, M. Y. B. Zulkifli, S. Gao, Y. Wu, X. Tian, X. Du and Z. Zhu, Adv. Funct. Mater., 2025, 2417425.

---