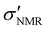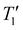Open Access Article
Open Access ArticleNMR studies of PEG chain dynamics on mesoporous silica nanoparticles for minimizing non-specific binding†
Xiaochong Li‡
,
Yang Liu‡,
Edmond C. N. Wong and
Mitchell A. Winnik *
*
Department of Chemistry, University of Toronto, 80 St. George Street, Toronto, Ontario M5S 3H6, Canada. E-mail: m.winnik@utoronto.ca
First published on 29th May 2025
Abstract
Mesoporous silica nanoparticles (MSNs) have garnered significant attention for diverse bioscience applications due to their tunable surface properties and high biocompatibility. Functionalization with hydrophilic polymers like poly(ethylene glycol) (PEG) via silane chemistry is commonly employed to reduce non-specific protein adsorption and enhance stability in physiological environments. However, characterizing surface ligands, particularly in aqueous environments, remains a key challenge. In this study, we utilized a comprehensive suite of nuclear magnetic resonance (NMR) techniques, including 1H quantitative NMR (qNMR), diffusion-ordered spectroscopy (DOSY), and relaxation time measurements (T1 and T2), to investigate PEG chain dynamics and conformation on MSN surfaces. Our analysis revealed the relationship between PEG grafting density and chain mobility, demonstrating a transition to a dense brush conformation at higher densities. DOSY and T2 experiments enabled the differentiation of covalently bound PEG from loosely adsorbed molecules. This approach provided a robust method for evaluating the efficacy of surface functionalization, ensuring the quality and consistency of PEGylated nanoparticles. Furthermore, we examined the relationship between NMR-derived parameters and protein adsorption resistance, demonstrating that densely packed PEG chains with a “dense brush” conformation can effectively reduce non-specific adsorption of human serum albumin. These findings provided valuable insights into the design of PEGylated MSNs, supporting improved quality, consistency, and functionality for biomedical applications.
Introduction
Mesoporous silica nanoparticles (MSNs) are porous inorganic particles with a high surface area, large pore volume and uniform pore size, typically ranging from 2 to 50 nm. Since the first discovery of mesoporous silica MS41 by the Mobil group in the early 1990s,1,2 their development using the organic–inorganic self-assembly strategy has been widely studied.3,4 They possess common properties such as excellent biocompatibility, physiochemical stability and biodegradability.5–8 Additionally, the abundance of silanol groups on the surface of MSNs makes them easy to functionalize with diverse ligands using organosilanes ((RO)3SiR′), allowing for tailored functionalities and properties for specific goals.4,9 Therefore, MSNs have attracted extensive attention for various applications in the fields of separation, catalysis, adsorption, and bioscience, among others.10–12Mass cytometry (MC) is a state-of-the-art technique for high-dimensional single-cell analysis, enabling detailed functional and immunophenotypic profiling of cells in heterogeneous populations.13 In this technique, antibodies labeled with heavy metal isotopes (“mass tags”) bind to target antigens and are detected by inductively coupled plasma time-of-flight mass spectrometry. Current reagents use metal chelating polymers (MCPs) to enable each antibody to carry 100 to 300 copies of an isotope. Recently, nanoparticles (NPs) have been proposed as reagents that can improve the detection signal intensity by increasing the number of metal atoms per antibody.14–16 For example, polymer-functionalized MSNs have been designed as a versatile platform for carrying various types of heavy metal ions. Their potential as high-sensitivity mass tag reagents has attracted considerable interest.17,18
To use MSN-based mass tags as effective high-sensitivity reagents for MC applications, one of the primary challenges lies in their high non-specific binding (NSB) to cells. When MSNs come into contact with live cells, such as human peripheral blood mononuclear cells (PBMCs), MSNs rapidly adsorb proteins, forming what is known as the protein “corona”.19 Consequently, this protein corona alters their “biological identity”, distinct from their “synthetic identity” and impacts their performance, particularly in therapeutic and diagnostic applications.20 For instance, in practical MC applications, any signal stemming from the NSB of MSNs can result in false positives, complicating and limiting the cell detection capabilities of the instrument. Therefore, surface modification of MSNs with hydrophilic polymers is necessary to reduce non-specific adsorption of serum proteins.
Among various approaches, NPs can be PEGylated, i.e., conjugated with linear poly(ethylene glycols) (PEGs). PEGylation is known not only for reducing non-specific protein adsorption but also for enhancing the biocompatibility and colloidal stability of NPs in water, phosphate-containing buffers and other physiological fluids.21–23 The general methods for PEGylation involve simple physical adsorption as well as either one- or two-step covalent functionalization procedures.24 In the case of MSNs, PEG-silanes are commonly used because they do not require pre-functionalization of the particles and the resulting covalent attachment is considered stable.
The efficacy of PEGylation for reducing NSB is critically dependent on the conformation and dynamics of the surface-grafted polymer chains.25 Theoretical models, including the ones proposed by Alexander–de Gennes and Milner–Witten–Cates, describe polymer brush behavior based on grafting density and chain length, predicting distinct conformational regimes such as mushroom, brush, and dense brush.26–29 However, experimental validation of these models on NP surfaces has been challenging due to the difficulty in directly observing polymer conformations at the molecular level.
A variety of traditional characterization techniques, such as small-angle neutron scattering (SANS), dynamic light scattering (DLS), and atomic force microscopy (AFM), provide valuable insights but often offer limited information on chain dynamics and the local environment.30–32 In recent years, nuclear magnetic resonance (NMR) spectroscopy has stood out for investigating the behavior of surface-grafted polymers due to its ability to provide exceptional detail about the chemical environments of constituent atomic nuclei. NMR techniques facilitate a deeper understanding of the structural and dynamic characteristics of functionalized nanomaterials, enabling non-destructive and quantitative analysis of grafting density, chain conformation, and molecular dynamics.33–35
Furthermore, solution NMR spectroscopy provides unique advantages for studying molecular dynamics at atomic resolution under solution conditions that closely mimic physiological environments.36 In the characterization of polymer-grafted NPs, quantitative NMR (qNMR) has been used to determine grafting density by comparing integrated signal intensities of grafted polymers on the NP surface with internal or external standards.34,37,38 Diffusion-ordered spectroscopy (DOSY) provides insights into polymer mobility by measuring translational diffusion, distinguishing between bound and free polymer populations.39,40 Additionally, relaxation time measurements (T1 and T2) probe polymer chain dynamics, offering information on segmental flexibility, molecular motion, as well as the local environment, thereby aiding in the study of their interactions with proteins and other biomolecules.34,36,41–44
However, despite these advancements, several challenges remain in the NMR analysis of PEGylated MSNs, including signal broadening due to reduced molecular tumbling, overlapping signals from different polymer populations, and potential interference from residual water or silanol groups. Addressing these challenges requires careful experimental design and data analysis. A comprehensive study correlating NMR-derived parameters with these functional properties is still lacking.
In this work, we built on the PEGylated MSNs from previous research and employed a suite of NMR techniques to investigate the conformation and dynamics of PEG chains grafted onto the surface. We first integrated three NMR techniques—qNMR, DOSY, and relaxation time measurements (T1 and T2)-to address several key issues and to provide a detailed, molecular-level understanding of the PEG behavior on MSN surfaces. A primary focus of our investigation was to understand how grafting density influences PEG chain conformation and mobility on MSN surfaces. We observed that the T1 relaxation times of PEG chains exhibit subtle variations with grafting density, exhibiting shorter T1 values at higher PEG coverage. This behavior is consistent with the formation of denser PEG brushes and more constrained chain dynamics, as predicted by the Alexander–de Gennes model.28 We also explored the capability of NMR techniques to differentiate between covalently bound and physically adsorbed PEG chains, as well as how purification processes influence the characteristics of the PEG layer. This information is vital for ensuring the quality and consistency of PEGylated nanoparticle preparation. Furthermore, we examined the relationship between NMR-derived parameters and the resistance of MSNs to non-specific protein adsorption, a critical factor in their biomedical applications. Our findings contribute to the rational design of PEGylated MSNs with optimized performance for various biomedical applications, bridging the gap between theoretical models and practical nanoparticle design.
Experimental
Materials
Tetraethyl orthosilicate (TEOS), triethanolamine (TEA), hexadecyl trimethyl ammonium chloride (CTAC, 25 wt%), (N,N-dimethylaminopropyl)trimethoxysilane (DMASi), concentrated hydrochloric acid (HCl, 37%), 1,3-propane sultone, albumin from human serum (HSA, protease free, ≥96%), dichloromethane (DCM) and all deuterated solvents were purchased from Sigma-Aldrich (CA). Silane-PEG5k-methoxy (M = 5000 g mol−1, mPEG5k) was purchased from JenKem Technology (USA). Silane-PEG2k-methoxy (M = 2000 g mol−1, mPEG2k) and silane-PEG10k-methoxy (M = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, mPEG10k) were purchased from Biopharma PEG (Watertown, MA, USA). 3-Methoxy(polyethyleneoxy)6–9-propyltrimethoxysilane (mPEG6–9 silane, 459–591 g mol−1) was purchased from Gelest (Morrisville, PA, USA). Phosphate-buffered saline (1× PBS solution, Fisher BioReagents), Pierce™ BCA Protein Assay Kit was purchased from Fisher Scientific. Ultrapure water (18.2 MΩ cm) used in all experiments was obtained using a Thermo Barnstead GenPure xCAD Ultrapure Water system.
000 g mol−1, mPEG10k) were purchased from Biopharma PEG (Watertown, MA, USA). 3-Methoxy(polyethyleneoxy)6–9-propyltrimethoxysilane (mPEG6–9 silane, 459–591 g mol−1) was purchased from Gelest (Morrisville, PA, USA). Phosphate-buffered saline (1× PBS solution, Fisher BioReagents), Pierce™ BCA Protein Assay Kit was purchased from Fisher Scientific. Ultrapure water (18.2 MΩ cm) used in all experiments was obtained using a Thermo Barnstead GenPure xCAD Ultrapure Water system.
Synthesis of PEGylated PMSNs-Zwi NPs with different PEG chain lengths
We began these experiments with a single sample of MSNs whose surface was modified with both a PEG6–9-silane and a zwitterionic (ZW) sulfobetaine silane. The synthesis of this sample, denoted PMSN-Zwi, is described in the ESI.† This sample was then further functionalized with longer PEG chains of different lengths (M = 2000, 5000 or 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, denoted as mPEG2k, mPEG5k or mPEG10k, respectively). The resulting NPs are denoted as PMSNs-Zwi-mPEGxk, where x = 2, 5, or 10, corresponding to the molecular weight (Mw) of the PEG chains. The synthesis of PMSNs-Zwi-mPEG5k is detailed here as an example. Typically, 10 mg of PMSNs-Zwi was added into a two-neck round-bottom flask (25 mL) and suspended in 4 mL anhydrous toluene. The suspension was purged with N2 for 15 minutes, and a solution of mPEG5k-silane in 1 mL anhydrous toluene (10 to 80 mg mL−1) was added dropwise. The reaction was stirred at 110 °C for 24 hours. After cooling down, the NPs were collected through centrifugation (20
000 g mol−1, denoted as mPEG2k, mPEG5k or mPEG10k, respectively). The resulting NPs are denoted as PMSNs-Zwi-mPEGxk, where x = 2, 5, or 10, corresponding to the molecular weight (Mw) of the PEG chains. The synthesis of PMSNs-Zwi-mPEG5k is detailed here as an example. Typically, 10 mg of PMSNs-Zwi was added into a two-neck round-bottom flask (25 mL) and suspended in 4 mL anhydrous toluene. The suspension was purged with N2 for 15 minutes, and a solution of mPEG5k-silane in 1 mL anhydrous toluene (10 to 80 mg mL−1) was added dropwise. The reaction was stirred at 110 °C for 24 hours. After cooling down, the NPs were collected through centrifugation (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000g, 15 min), washed twice with ethanol, and 1–3 times with water to remove the unreacted PEG silane. The final NPs were lyophilized to yield a free-flowing powder. By adjusting the amount of mPEG5k-silane while maintaining the same conditions, different grafting densities of mPEG5k could be obtained.
000g, 15 min), washed twice with ethanol, and 1–3 times with water to remove the unreacted PEG silane. The final NPs were lyophilized to yield a free-flowing powder. By adjusting the amount of mPEG5k-silane while maintaining the same conditions, different grafting densities of mPEG5k could be obtained.
Quantification of PEG chains (chains per nm2) using 1H qNMR
To ensure the accuracy and reliability of quantitative 1H NMR (qNMR) measurements, it is critical to allow sufficient time between scans for complete spin–lattice relaxation. For this purpose, we measured T1 relaxation values for the various PMSNs-Zwi-mPEGxk NP samples (x = 2, 5 or 10) by the standard T1 inversion recovery sequence. The DCM peak exhibited the longest T1 relaxation constant of 4.96 s. To ensure full relaxation of all nuclei, a relaxation delay of 35 s was selected for all experiments (>5 × T1).For each quantitative 1H NMR measurement, a 90° pulse scan program with 64 transients and a 35 s relaxation delay was used. Freeze-dried PMSNs-Zwi-mPEGxk NPs (2 mg) were redispersed in 400 μL of D2O via sonication and were pipetted into a 5 mm NMR tube. A sealed glass capillary tube containing 5 v/v% DCM in deuterated DCM (DCM-d2) was used as an external reference. The integration of the resonance corresponding to PEG units (δ = 3.50–3.65 ppm) was compared with the signal of external standard DCM at δ = 5.16 ppm to quantify the number of ethylene glycol units in the dispersion. The number of NPs in the dispersion was calculated based on the solids content of the dispersion, the average diameter obtained from the TEM image, and the density of silica assuming the NPs were mesoporous spheres. The surface area per nanoparticle was estimated based on the pore volume per nanoparticle, combined with the void surface due to the mesopores, assuming that mesopores are straight cylinders without defects and tortuosity. The chain number per nm2 surface was determined using the following equation:
 | (1) |
Diffusion-ordered spectroscopy (DOSY) NMR
DOSY experiments were performed with a sample concentration of 2.5 mg mL−1 in D2O at 298 K, using a 3 mm NMR tube to minimize convection effects. Measurements were carried out on a 600 MHz NMR spectrometer equipped with a z-gradient probe, using a Bipolar Pulse Pair Stimulated Echo (Dbppste) pulse sequence. The diffusion delay (Δ) varied from 300 to 350 ms, and the gradient pulse duration (δ) from 4 to 5 ms, and both were optimized in order to obtain 5–10% residual signal at 90–95% of the maximum gradient strength. Temperature was maintained at 298 K throughout the experiment.The self-diffusion coefficient (Ds) was calculated by integrating the peaks of interest (–CH2–CH2–O–, PEG repeating units) and fitting them to the Stejskal–Tanner equation using a single-component (mono-exponential) model:
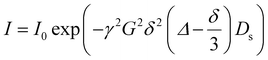 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500.
500.
NMR relaxation time analyses
yτ = B + F![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−τ/T1) exp(−τ/T1)
| (3) |
Iτ = I2fast![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−τ/T2fast) + I2slow exp(−τ/T2fast) + I2slow![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−τ/T2slow) exp(−τ/T2slow)
| (4) |
Results and discussion
Our experiments began with the synthesis of a mesoporous silica nanoparticle sample with a mean diameter dTEM = 45 nm and functionalized with a short methoxy-PEG (mPEG6–9). Details are provided in the ESI,† and we refer to this sample as PMSN. In brief, CTAC (2 g) and TEA (0.8 g) were dissolved in 20 mL of water. The solution was heated to 95 °C and stirred for an hour. TEOS (1.5 mL) was then added dropwise into the reaction while stirring. After 10 min, mPEG6–9-silane (650 μL) was introduced slowly and the mixture was stirred at 95 °C for another 30 min. After cooling the sample to room temperature, the CTAC-containing NPs were purified by three cycles of sedimentation–redispersion with ethanol. Following CTAC removal, PMSNs (50 mg) were treated with a sulfobetaine silane (SBS, 50 mg) at pH 9 and stirred at 80 °C for 24 h. The resulting PMSN-Zwi NPs were lyophilized and used for the PEGylation experiments described below. Both the short mPEGs and SBS were incorporated to promote colloidal stability and were presumed to coat both the pore walls and the outer surface of the NPs. The physicochemical characterization of PMSNs and PMSN-Zwi is presented in Fig. S1,† while nitrogen adsorption/desorption isotherms and the corresponding surface area, pore volume, and pore diameter are shown in Fig. S2 and Table S1.†PEGylation and PEG grafting density quantification
To further refine the nanoparticle surface, longer PEG chains (e.g., mPEG5k) were grafted onto the PMSN-Zwi outer surface, forming a hierarchical structure with both a short SBS/mPEG6–9 layer and a long PEG layer. The combination of long and short PEGs on an NP surface has been reported to improve suppression of non-specific binding compared to NPs carrying only the longer PEGs.45 A series of PEGylated mesoporous silica nanoparticles (PMSNs-Zwi-mPEG5k) with varying grafting densities were prepared by adjusting the nanoparticle-to-PEG mass ratio (NP/PEG w/w) during synthesis. The PEGylated NPs were washed twice with ethanol and only once with H2O to remove the unreacted mPEG5k silane. Their physicochemical characterization is shown in Fig. S1.† The grafting density was quantified using both TGA and qNMR. Fig. 1A shows the TGA curves for PMSNs-Zwi and PMSNs-Zwi-mPEG5k with different PEG loadings. The weight percentage of mPEG5k was determined by subtracting the weight loss of PMSNs-Zwi from that of PMSNs-Zwi-mPEG5k and summarized in Table S2.† Using these data and assuming spherical NPs with straight cylindrical mesopores that penetrate the volume, we calculated the grafting density (σTGA, chains per nm2) by using eqn (S1),† adapted from our previous work,18 as summarized in Table S2.†Complementary to TGA, we employed qNMR with an external standard to analyze the MSN surface coverage (Fig. 1B). The average number of PEG chains (σNMR, chains per nm2) was quantified by integrating the resonance signals corresponding to ethylene glycol units (−CH2–CH2O−, δ 3.5–3.65 ppm) and comparing them with the signal of DCM standard (δ 5.4–5.5 ppm). Since PEG6–9-silane is present on MSNs prior to the post-grafting of mPEG5k, a control qNMR measurement was conducted on PMSNs at the same concentration using the same external standard. The PEG signal contributed by PEG6–9-silane was subtracted from PMSNs-Zwi-mPEG5k NPs to obtain the net mPEG5k contribution for quantification. Based on the quantification of PEG and the total surface area of MSNs, the σNMR was determined using eqn (1), and these values are presented in Table 1. The detailed derivation of PEG grafting density based on NMR data is provided in the ESI.†
| NP/PEG w/w | Grafting densityb (σNMR, chains per nm2) | RF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c (nm) c (nm) |
Dd (nm) | Le (nm) | PEG conformationa |
|---|---|---|---|---|---|
| a The prediction of PEG conformation was based on the model of Alexander–de Gennes.28b Calculated with eqn (1), where ρ is 1.85 g cm−3.c Flory radius calculated using RF = αN3/5, where α is the monomer length (0.35 nm for PEG),46 N is the number of PEG repeating unit (108 for mPEG5k).d Calculated mean spacing between PEG anchor points, D = 2(1/σπ)1/2, where σ is the average from three tests.e Calculated brush height, L = N(α5/3)/D2/3. | |||||
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
0.39 ± 0.02 | 5.8 | 1.8 | 12.5 | Dense brush |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 20 |
0.45 ± 0.03 | 5.8 | 1.7 | 13.1 | Dense brush |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 40 |
0.57 ± 0.02 | 5.8 | 1.5 | 14.3 | Dense brush |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 60 |
0.55 ± 0.01 | 5.8 | 1.5 | 14.1 | Dense brush |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 80 |
0.51 ± 0.04 | 5.8 | 1.6 | 13.7 | Dense brush |
The grafting density calculated through NMR analysis closely matched the values obtained from TGA analysis (Fig. 1C, Table 1, and Table S2†). Both methods indicated that the grafting density of mPEG5k initially increased with the amount added, peaking at an NP/PEG w/w ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40, before slightly decreasing with further PEG addition. Note that all values reported here correspond to PEGylated NPs washed twice with ethanol and once with H2O. An additional H2O washing cycle led to somewhat lower grafting density values, an important result that will be discussed in a later section below. This trend differs from other reports, where the weight loss percentage of PEG continuously increased with the feeding amount until reaching a plateau.47,48 To verify the validity and reproducibility of this trend for this NP system, we have repeated the PEGylation experiment under identical conditions many times and measured the resulting grafting density independently by TGA for each sample in duplicate. The results were consistent and reproducible across repeated synthesis and measurements. To further validate this observation, we conducted similar PEGylations using mPEG2k silanes and mPEG750 silanes, respectively. The TGA data for each set of NPs had the same trend as obtained from mPEG5k, showing a peak grafting density at 10
40, before slightly decreasing with further PEG addition. Note that all values reported here correspond to PEGylated NPs washed twice with ethanol and once with H2O. An additional H2O washing cycle led to somewhat lower grafting density values, an important result that will be discussed in a later section below. This trend differs from other reports, where the weight loss percentage of PEG continuously increased with the feeding amount until reaching a plateau.47,48 To verify the validity and reproducibility of this trend for this NP system, we have repeated the PEGylation experiment under identical conditions many times and measured the resulting grafting density independently by TGA for each sample in duplicate. The results were consistent and reproducible across repeated synthesis and measurements. To further validate this observation, we conducted similar PEGylations using mPEG2k silanes and mPEG750 silanes, respectively. The TGA data for each set of NPs had the same trend as obtained from mPEG5k, showing a peak grafting density at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40, followed by a slight decrease at 10
40, followed by a slight decrease at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60, as shown in Fig. S3 in the ESI.†
60, as shown in Fig. S3 in the ESI.†
The conformational regimes of PEG polymers grafted on the MSN surface were calculated according to grafting densities obtained by TGA and NMR. According to the Alexander–de Gennes model,28 the structural conformation depends on the average spacing distance D (D = 2(1/σπ)1/2) between anchor points of adjacent PEG chains, the Flory radius of the polymer chains in solution (RF = αN3/5), and the length of grafted PEG (L) At a low grafting density where D > RF, adjacent PEG chains remain separated and do not overlap, therefore forming a mushroom regime with a relatively thin PEG layer. As grafting density increases (i.e., when D ≈ RF), individual PEG chains start to overlap. This overlap criterion defines the so-called mushroom-to-brush transition and is commonly used to signify the onset of brush-like behavior in the grafted polymer layer. When D < RF, PEG chains extend away from the nanoparticle surface and arrange in a brush conformation, resulting in a thicker layer. Under extreme conditions where L > 2RF, the grafted PEG chains on the NP surface form a dense brush conformation, as defined by Damodaran et al.25 In the present study, all the PEG layers exhibit either a brush or dense-brush conformational regime. This predominance of brush and dense brush conformations is attributed to the relatively high grafting densities achieved through our synthesis method. Such conformations are expected to enhance colloidal stability and reduce non-specific protein adsorption, properties that are crucial for the application of these NPs to MC.
Diffusion-ordered NMR spectroscopy (DOSY)
DOSY is a pseudo-two-dimensional NMR experiment, which is an application of the pulsed field gradient experiment. DOSY can separate NMR signals of different species according to their different self-diffusion coefficients (Ds) and has previously been used for characterizing ligands bound to functionalized NPs.49–53 In this study, DOSY NMR experiments were conducted to evaluate the diffusion behavior of PEG species associated with the PEGylated MSNs, particularly useful for identifying residual free PEG that may remain after standard purification, which cannot be resolved by qNMR alone.Typical sets of PFGSE 1H NMR spectra indicating the intensity profiles in a pulsed gradient are shown in Fig. S4A and S4B.† The measured Ds values for each PEGylated NP sample, along with the control mPEG5k silane, are listed in Table 2. PMSN NPs in D2O at 2.5 mg mL−1 and even higher concentrations (10 mg mL−1) were also measured, but the PEG6–9 signal intensities remained insufficient for Ds determination (Fig. S4C and S4D†).
| NP/PEG w/w | 1010 × Ds (m2 s−1) | dh (nm) |
|---|---|---|
| a NPs were measured at 2.5 mg mL−1.b Free mPEG5k-silane and mPEG5k-OH were measured at 0.05 mg mL−1. Very slightly smaller values of Ds were obtained at 0.5 mg mL−1 and 2 mg mL−1 (see Table S3†). | ||
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10a 10a |
1.04 | 3.85 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20a 20a |
1.05 | 3.82 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40a 40a |
1.07 | 3.74 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60a 60a |
1.00 | 4.02 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80a 80a |
1.00 | 4.00 |
| mPEG5k silaneb | 0.89 | 4.50 |
| mPEG5k OHb | 0.90 | 4.50 |
The measured Ds values of the –CH2–CH2–O– proton signals were comparable to that of free mPEG5k silanes in solution, prompting us to question the origin of the observed PEG signal. For spherical particles, their Ds can be linked to a hydrodynamic diameter (dh) using the Stokes–Einstein equation:
 | (5) |
Once these polymers are covalently bound to the nanoparticle surface, they would be forced to diffuse along with the particle. By DLS, we measured a diffusion coefficient of 4.5 × 10−12 m2 s−1 for these NPs, corresponding to a hydrodynamic diameter of 89 nm (Fig. S1F†).39 The measured Ds values in Table 2 are nearly 2 orders of magnitude faster than the values expected for fully grafted-PEG silanes, further confirming that the DOSY signals primarily arise from the highly mobile PEG populations—likely unbound PEG or loosely associated PEG chains—possibly due to incomplete purification or partial detachment of PEG-silane during dispersion in water.39 The unexpectedly high diffusion coefficients compared to free PEG5k further underscore the complexity of accurately characterizing polymer dynamics in nanoparticle systems. More rigorous purification and control experiments will be necessary to fully elucidate the behavior of surface-bound PEG chains in future studies.
NMR relaxation analysis and PEG structural mobility
Measuring NMR relaxation times provides insight into the segmental mobility of macromolecular chains near a solid surface. At low grafting densities, polymer chains tend to spread out on the surface in a flat conformation, significantly restricting their local segmental motions. This is reflected by an increase in T1. Conversely, as the grafting density increases, the polymer chains begin to repel each other and adopt a more extended “brush” configuration, often resulting in a decreased T1 value.42,54 To gain a deeper understanding of the ligand mobility of PEG chains on the MSN surface, we measured the T1 relaxation time for the protons of PEG repeating units of PMSNs-Zwi-mPEG5k NPs with different grafting densities.As shown in Fig. 2A, the phase of all the peaks gradually changed from negative to positive with the increasing relaxation delay. By fitting the integral data with eqn (3) (Fig. 2B), we determined the T1 values for the PEG repeating unit (–CH2–CH2–O–) of all NP samples listed in Table 3. It is worth noting the measured T1 values represent an average across the entire mPEG5k chain. The mobility of the –CH2–CH2– units at the very end should differ significantly from that of the units close to the surface.
 | ||
| Fig. 2 (A) The original NMR spectra of the spin–lattice relaxation time (T1) delay experiment. The recovery time (τ) varied from 10 ms to 30 s, with intensities measured at 13 incremental recovery times. (B) T1 analysis and fitted curves with one-phase exponential decay function with time constant parameter (y = B + F × exp(−τ/T1), eqn (3)). | ||
| NP/PEG w/w | Curve fitting parameters for T1 | T1 (s) |
|---|---|---|
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
B = 216.7, F = −411.7 (R2 = 1.0000) | 0.742 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 20 |
B = 215.8, F = −411.4 (R2 = 0.9998) | 0.739 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 40 |
B = 241.2, F = −451.8 (R2 = 0.9996) | 0.735 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 60 |
B = 297.8, F = −566.9 (R2 = 0.9995) | 0.744 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 80 |
B = 332.2, F = −628.4 (R2 = 0.9997) | 0.757 |
As shown in Table 3, the measured T1 values exhibit a subtle but consistent variation with nominal grafting density. Specifically, T1 values ranged from approximately 0.742 s (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10) to 0.735 s (10
10) to 0.735 s (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40) to 0.757 s (10
40) to 0.757 s (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80), with differences on the order of 2–3%. While there is a slight decrease in T1 with increasing grafting density up to 10
80), with differences on the order of 2–3%. While there is a slight decrease in T1 with increasing grafting density up to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40, followed by a modest increase at 10
40, followed by a modest increase at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 and 10
60 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80, these variations are small and do not establish a strict correlation. This subtle behavior mirrors trends observed in other studies of PEG-grafted nanoparticles, such as the work by Hristov et al.,42 where only a weak dependence of T1 on PEG coverage was reported for PEG5k on silica nanoparticles. Several factors could explain this phenomenon:
80, these variations are small and do not establish a strict correlation. This subtle behavior mirrors trends observed in other studies of PEG-grafted nanoparticles, such as the work by Hristov et al.,42 where only a weak dependence of T1 on PEG coverage was reported for PEG5k on silica nanoparticles. Several factors could explain this phenomenon:
1. Free chains: higher PEG feed ratios may increase the concentration of free PEG in solution, leading to slightly slower segmental motions.
2. Loosely associated chains: higher local PEG concentrations could promote more extended conformations with modestly faster segmental motions.
3. Population shifts: the changes in the relative population of free versus loosely associated PEG chains could subtly impact the average T1.
Overall, the subtle variation in T1 values (<3%) suggests that the dominant PEG populations experience relatively uniform local environments across different grafting densities. These PEG chains contributing to the measured T1 values are highly mobile, rather than tightly grafted chains near the particle surface, which is consistent with the DOSY results.
In addition to the T1 time, the spin–spin (or transverse, T2) relaxation time provides additional insights into molecular motions in our PEGylated nanoparticle system. Surface-bound polymers typically lose most of their rotational freedom due to the much bigger NP they are attached to, resulting in slower molecular tumbling and longer correlation times in solution. Therefore, particle-bound polymer features a faster T2 and a broadened spectral line width (Δv, Δv = 1/πT2) compared to the free, unbounded polymers in the solution (Fig. 3A).
 | ||
Fig. 3 (A) 1H NMR spectra overlap of free PEG5k silane (blue curve) and grafted PEG5k (black curve). (B) The original NMR spectra of the spin–spin relaxation time (T2) analysis. The time (τ) was varied from 10 ms to 3 s, with intensities measured at 25 incremental recovery times. (C) T2 analysis and fitted curves with a one-phase exponential decay function (I = I2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−τ/T2) + y0). (D) T2 analysis and fitted curves with a two-phase exponential decay function (I = I2fast exp(−τ/T2) + y0). (D) T2 analysis and fitted curves with a two-phase exponential decay function (I = I2fast![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−τ/T2fast) + I2slow exp(−τ/T2fast) + I2slow![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−τ/T2slow), eqn (4)). exp(−τ/T2slow), eqn (4)). | ||
For all PMSNs-Zwi-mPEG5k NPs, T2 NMR measurements were recorded using the standard CPMG pulse sequence. Spectra were collected in pseudo-2D mode, as shown in Fig. 3B. To calculate the T2 values, the integration of the –CH2–CH2–O– peak at each recovery time was initially fitted to a single exponential model (I = I2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−τ/T2) + y0), but this produced large residuals and a poor fit (Fig. 3C).
exp(−τ/T2) + y0), but this produced large residuals and a poor fit (Fig. 3C).
To improve the quality of the fit, we applied a bi-exponential decay model (I = I2fast![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−τ/T2fast) + I2slow
exp(−τ/T2fast) + I2slow![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−τ/T2slow)) to fit the T2 relaxation curves and performed a global chi-square minimization across the entire decay profile (Fig. 3D). Particular attention was paid to separately capturing the fast decay region and the slower tail, enabling effective time-domain deconvolution of the two overlapping relaxation contributions without relying on spectral transformations. This approach allowed us to resolve two distinct proton populations: a faster-relaxing component with short T2 (T2fast) and a slow-relaxing component with longer T2 (T2slow), with their relative populations reflected by the respective signal intensities, I2fast and I2slow. The faster-relaxing component (T2fast) likely represents PEG chains that are more constrained in their motion, potentially including surface-bound, entangled or aggregated PEG chains, leading to limited mobility and rapid dephasing. In contrast, the slower-relaxing component (T2slow) corresponds to more mobile PEG chains, either free in solution or loosely adsorbed, which maintain higher mobility and thus give longer T2. It is noteworthy that even the more mobile PEG chains associated with T2slow are not as dynamic as fully free PEG in solution, as evidenced by the fact that all T2slow values were smaller than that of free mPEG5k silane (T2 = 0.60 s, see Fig. S6†). This suggests that even the most mobile PEG population in the NP system experiences some degree of constraint or interaction, either with other PEG chains or the nanoparticle surface.
exp(−τ/T2slow)) to fit the T2 relaxation curves and performed a global chi-square minimization across the entire decay profile (Fig. 3D). Particular attention was paid to separately capturing the fast decay region and the slower tail, enabling effective time-domain deconvolution of the two overlapping relaxation contributions without relying on spectral transformations. This approach allowed us to resolve two distinct proton populations: a faster-relaxing component with short T2 (T2fast) and a slow-relaxing component with longer T2 (T2slow), with their relative populations reflected by the respective signal intensities, I2fast and I2slow. The faster-relaxing component (T2fast) likely represents PEG chains that are more constrained in their motion, potentially including surface-bound, entangled or aggregated PEG chains, leading to limited mobility and rapid dephasing. In contrast, the slower-relaxing component (T2slow) corresponds to more mobile PEG chains, either free in solution or loosely adsorbed, which maintain higher mobility and thus give longer T2. It is noteworthy that even the more mobile PEG chains associated with T2slow are not as dynamic as fully free PEG in solution, as evidenced by the fact that all T2slow values were smaller than that of free mPEG5k silane (T2 = 0.60 s, see Fig. S6†). This suggests that even the most mobile PEG population in the NP system experiences some degree of constraint or interaction, either with other PEG chains or the nanoparticle surface.
While the biexponential decay indicates two distinct PEG populations with different mobilities, the specific molecular origins of T2slow and T2fast components require further investigation. Theoretically, the faster-relaxing component should be less sensitive to the local environment, so we assume there is a common more restricted component among all NP samples resulting in consistent T2fast values. Therefore, we fixed the T2fast value using an average value from all NP samples and studied the T2slow values of each NP sample.
All parameters and T2 values are listed in Table 4. It is worth noting that the T2 value, whether T2fast or T2slow, determined through fitting for each sample represents the average T2 time for all protons from –CH2–CH2–O– of mPEG5k chains. By comparing the ratio of I2fast to I2slow, we found that the proportion of these two components across all NP samples was very similar. This suggests a consistent distribution of PEG in different mobility environments, regardless of the nominal grafting density. Subsequently, we compared the T2slow values among NP samples with different grafting densities, it is clear that T2slow values show a negative correlation with nominal grafting density. The T2slow value decreased from 0.57 to 0.48 s as the PEG density increased from NP/PEG w/w 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 to 10
10 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40, followed by a slight increase at higher PEG concentrations. The sample PMSNs-Zwi-mPEG5k-1040, which has the highest grafting density among the samples, exhibited the shortest T2slow value. This trend could be explained by:
40, followed by a slight increase at higher PEG concentrations. The sample PMSNs-Zwi-mPEG5k-1040, which has the highest grafting density among the samples, exhibited the shortest T2slow value. This trend could be explained by:
1. Increased chain–chain interactions at higher PEG concentrations, leading to reduced mobility.
2. A shift in the population balance between more and less mobile PEG chains.
3. Changes in the local environment (e.g., viscosity) are due to increased PEG concentration.
| NP/PEG w/w | Curve fitting parameters for T2 analysis | I2slow/I2fast | T2fast (s, fixed value) | T2slow (s) |
|---|---|---|---|---|
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
I2fast = 0.32, I2slow = 0.77 (R2 = 0.9996) | 2.4 | 0.036 | 0.57 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 20 |
I2fast = 0.33, I2slow = 0.78 (R2 = 0.9978) | 2.3 | 0.56 | |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 40 |
I2fast = 0.30, I2slow = 0.79 (R2 = 0.9998) | 2.6 | 0.48 | |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 60 |
I2fast = 0.30, I2slow = 0.79 (R2 = 0.9996) | 2.6 | 0.49 | |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 80 |
I2fast = 0.33, I2slow = 0.77 (R2 = 0.9999) | 2.3 | 0.56 |
Therefore, the T2 time for protons from –CH2–CH2–O– is lower for the denser brush conformation with higher grafting density.
These T2 results, while complex, are consistent with our DOSY observations of highly mobile PEG chains. They suggest a system where PEG exists in multiple states of mobility, possibly including loosely associated chains and perhaps a small population of more tightly bound surface chains. The apparent discrepancy between the DOSY results (suggesting highly mobile chains) and the T2 results (showing constrained mobility compared to free PEG) might be resolved by considering that DOSY measures translational diffusion over longer distances and timescales, while T2 is sensitive to local motions on shorter timescales.
The combined analysis of T1, T2, and DOSY data thus provides complementary insights into the PEG dynamics on MSN surfaces. While the DOSY experiments suggest the presence of highly mobile PEG chains, the T2 relaxation analysis confirms that these mPEG5k silanes are not entirely free, implying some degree of interaction or association with the nanoparticle surface. Furthermore, the observed changes in T1 and T2 relaxation times with varying grafting densities support our earlier conclusions about the transition to a denser brush conformation at higher grafting densities. However, the relatively weak dependence of T1 on grafting density highlights the complex interplay between chain confinement and mobility that warrants further investigation.
Changes in relaxation times and DOSY after further purification with H2O
The DOSY experiments described above indicated that un-grafted PEG chains that remained associated with the MSN samples became free chains in solution upon redispersion in water. This result suggested to us that additional sedimentation–redispersion steps in water might remove the un-grafted PEG. Initially, the PEGylated NPs were purified using three sedimentation–redispersion cycles (twice with ethanol and once with H2O) to remove unreacted mPEG5k silanes. This is a standard purification procedure adapted from literature.24,47,55 However, after this washing process, an additional H2O sedimentation–redispersion was performed, during which free PEG signals were detected in the supernatant (Fig. S7†). This observation indicated that the original purification protocol was insufficient for the complete removal of all un-grafted PEG silanes.We selected the PMSNs-Zwi-mPEG5k NP sample with an NP/PEG ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 w/w and monitored the changes in T2 time across multiple sedimentation–redispersion cycles with H2O. The NPs were washed with ethanol twice, followed by three additional washes with H2O. After each H2O purification step, the NPs were lyophilized and dispersed in D2O (2.5 mg mL−1) for T2 analysis. As shown in Fig. 4A and Table 5, the decay curves became progressively steeper with each H2O wash. By fitting these three curves with a two-component exponential decay function and comparing the ratio of weight factors I2slow and I2fast, the population of T2slow components in the NP gradually decreased and disappeared after three washes with H2O (Table 5). Given that surface-bound PEG5k polymers typically exhibit faster T2 values and silane chemistry is known for forming stable covalent bonds, the T2slow component is likely attributed to mPEG5k silane that was physically adsorbed onto the NP surface. This population exists in a state between fully mobile and very confined, explaining why its T2slow is smaller than that of free PEG but larger than the grafted PEG.
40 w/w and monitored the changes in T2 time across multiple sedimentation–redispersion cycles with H2O. The NPs were washed with ethanol twice, followed by three additional washes with H2O. After each H2O purification step, the NPs were lyophilized and dispersed in D2O (2.5 mg mL−1) for T2 analysis. As shown in Fig. 4A and Table 5, the decay curves became progressively steeper with each H2O wash. By fitting these three curves with a two-component exponential decay function and comparing the ratio of weight factors I2slow and I2fast, the population of T2slow components in the NP gradually decreased and disappeared after three washes with H2O (Table 5). Given that surface-bound PEG5k polymers typically exhibit faster T2 values and silane chemistry is known for forming stable covalent bonds, the T2slow component is likely attributed to mPEG5k silane that was physically adsorbed onto the NP surface. This population exists in a state between fully mobile and very confined, explaining why its T2slow is smaller than that of free PEG but larger than the grafted PEG.
 | ||
Fig. 4 (A) T2 analysis of PMSNs-Zwi-mPEG5k-1040 NPs with addition sedimentation–redispersion cycle in H2O. Each curve is fitted with a two-phase exponential decay function: I = I2fast![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−τ/T2fast) + I2slow exp(−τ/T2fast) + I2slow![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−τ/T2slow) (eqn (4)). (B) The –CH2–CH2–O– signal (δ = 3.65–3.5 ppm, orange frame) of the PMSNs-Zwi-mPEG5k-1040 NP sample after three washes with water disappeared in the DOSY experiment. exp(−τ/T2slow) (eqn (4)). (B) The –CH2–CH2–O– signal (δ = 3.65–3.5 ppm, orange frame) of the PMSNs-Zwi-mPEG5k-1040 NP sample after three washes with water disappeared in the DOSY experiment. | ||
| Number of washes with H2O | I2slow/I2fast | T2fast (s) | T2slow (s) |
|---|---|---|---|
| H2O × 1 | 78/22 | 0.036 | 0.568 |
| H2O × 2 | 45/55 | 0.589 | |
| H2O × 3 | 0 | N.A. |
As shown in Fig. 4B, after three washes with water, the –CH2–CH2–O– signal of the PMSNs-Zwi-mPEG5k-1040 NP sample disappeared in the DOSY experiment, in contrast to the typical DOSY spectra observed in Fig. S4A.† This indicates that, once the physically adsorbed PEG chains were fully removed, DOSY could no longer detect the signal from fully grafted PEG chains. This loss of signal in the DOSY experiment is likely related to the large size of the NPs and their slow diffusion. Additionally, the inability to detect diffusion signals from tightly grafted PEG chains in the DOSY experiment may stem from experimental limitations such as insufficient gradient strength, short diffusion times, or low signal-to-noise ratios for very slow-diffusing species. This observation explains the large difference between the observed Ds values in Table 2 and the expected Ds value for NP (10−10 vs. 10−12 m2 s−1). Furthermore, it supports our hypothesis that the observed Ds values in Table 2 correspond to the physically adsorbed PEG chains that desorbed in water under the conditions of the DOSY experiment.
Following the further purification, we re-measured the grafting density of PMSNs-Zwi-mPEG5k NP samples with NP/PEG w/w ratios of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, 10
10, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40, and 10
40, and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80. The TGA weight loss curves are shown in Fig. S8A.† The corresponding grafting density values obtained from TGA and qNMR are listed in Table 6. For these three samples, there is remarkable agreement between the values obtained by the two different techniques. Associated with each new grafting density value, we show in parentheses the values obtained from samples purified with only three sedimentation–redispersion cycles (twice with ethanol and once with H2O). In each case, there was a ca. 23% reduction in the number of PEG chains per nm2 (Table S4†). We also remeasured their T1 values, which are listed in Table 6. We now believe that these values represent the content of PEG chains that were truly end-grafted to the NP surface via covalent bonds. Moreover, the previously noted trend of grafting density initially increasing and then decreasing remains evident. The T1 values showed a slight increase compared to those in Table 3, supporting our previous hypothesis that T1 values might be predominantly influenced by free or loosely associated PEG rather than tightly grafted chains. After removing all loosely associated PEG, the trend of T1 values also persisted, showing a negative correlation with grafting density.
80. The TGA weight loss curves are shown in Fig. S8A.† The corresponding grafting density values obtained from TGA and qNMR are listed in Table 6. For these three samples, there is remarkable agreement between the values obtained by the two different techniques. Associated with each new grafting density value, we show in parentheses the values obtained from samples purified with only three sedimentation–redispersion cycles (twice with ethanol and once with H2O). In each case, there was a ca. 23% reduction in the number of PEG chains per nm2 (Table S4†). We also remeasured their T1 values, which are listed in Table 6. We now believe that these values represent the content of PEG chains that were truly end-grafted to the NP surface via covalent bonds. Moreover, the previously noted trend of grafting density initially increasing and then decreasing remains evident. The T1 values showed a slight increase compared to those in Table 3, supporting our previous hypothesis that T1 values might be predominantly influenced by free or loosely associated PEG rather than tightly grafted chains. After removing all loosely associated PEG, the trend of T1 values also persisted, showing a negative correlation with grafting density.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, 10
10, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 and 10
40 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 after two additional water washes following the original purification procedure
80 after two additional water washes following the original purification procedure
| NP/PEG w/w | (chains per nm2)a | (chains per nm2)b | PEG conformationc | d |
|---|---|---|---|---|
| a Calculated from the TGA using eqn (S1)† after further purification with H2O. Values in parentheses are the average of the two values determined by TGA before further purification (see Table S2†).b Calculated from the qNMR using eqn (1) after further purification with H2O. Values in parentheses are the values determined by qNMR before further purification (see Table 1).c The prediction of PEG conformation based on the model of Alexander–de Gennes.28d Obtained by fitting to eqn (3) for PMSNs-Zwi-mPEG5k NP samples subjected to two additional H2O washing cycles. | ||||
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
0.22 (0.28) | 0.29 (0.39) | Brush | 0.764 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 40 |
0.42 (0.53) | 0.44 (0.57) | Dense brush | 0.753 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 80 |
0.34 (0.45) | 0.39 (0.51) | Brush-dense brush | 0.770 |
This study highlights an often-overlooked detail in studies that employ PEGylated NPs: whether free PEG chains are fully removed in nanoparticle systems. Determining the optimal number of water washes for complete PEG removal is complex and varies depending on specific research applications and objectives. Inadequate purification can lead to data misinterpretation and incorrect conclusions about surface functionalization. One of the main conclusions that we can draw from this work is that DOSY NMR experiments provide a useful and convenient test for the presence of unbound or loosely bound PEG chains.
Effect of PEG grafting density on protein adsorption
After defining the PEG conformations, we investigated the correlation between PEG conformation and the stealth effect of the NPs. We conducted three studies using well-defined systems that involved: (i) varying PEG density while keeping the Mw constant at 5000 g mol−1, (ii) increasing PEG Mw from 2k to 10k while maintaining a constant grafting density of 0.3 chains per nm2, (iii) washing with and without excess water to fully remove the free PEG silanes.To study protein adsorption, we incubated NPs (5 mg mL−1 in 1× PBS) with a human serum albumin solution (HSA, 1 mg mL−1 in 1× PBS) at 37 °C for 2 h (Thermomixer, 500 rpm). All NPs remained stable in the albumin–PBS solution. Loosely bound proteins were removed from the NPs using spin filtration (Amicon, Ultra-0.5, 100 kDa), and the weight percentage of adsorbed HSA was determined using the Pierce™ BCA assay (Fig. 5A).
 | ||
| Fig. 5 (A) Calibration curve for the Pierce™ BCA assay used to quantify HSA. The absorbance of BSA standards at each concentration was measured in triplicate. (B–D) Absolute amount of adsorbed HSA measured by the Pierce™ BCA assay (n = 3). (B) Various PEG densities at a fixed Mw of 5000 g mol−1; reproduced from ref. 18. (C) Increasing Mw at a fixed grafting density of 0.3 chains per nm2. (D) Comparison of adsorbed HSA amounts on mPEG5k-functionalized MSNs with and without additional purification using H2O. | ||
As a comparison, we also examined the effect of PEG density on non-specific protein adsorption on PMSNs-Zwi-mPEG5k NPs as initially prepared and purified. One should note that these NPs were washed twice with ethanol and only once with H2O, and still contained some free PEG silanes as confirmed by T2 analysis. As shown in Fig. 5B, all PEGylated NPs significantly reduced HSA adsorption compared to bare MSNs and the PMSNs-Zwi sample. For mPEG5k-functionalized NPs, the amount of adsorbed serum albumin decreased with increasing PEG density, with the NP/PEG 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 sample exhibiting the lowest serum albumin adsorption among all PEGylated samples. Additionally, we examined the NSB levels of Tb-loaded PMSN-Zwi-mPEG5k NPs to peripheral blood mononuclear cells (PBMCs) at the titer of 10
40 sample exhibiting the lowest serum albumin adsorption among all PEGylated samples. Additionally, we examined the NSB levels of Tb-loaded PMSN-Zwi-mPEG5k NPs to peripheral blood mononuclear cells (PBMCs) at the titer of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 NPs per cell by MC in our previous work.18 NPs with NP/PEG weight ratios of 10
000 NPs per cell by MC in our previous work.18 NPs with NP/PEG weight ratios of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 and 10
10 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 showed significantly lower NSB levels (82 and 81 NPs per cell, respectively) compared to those with an NP/PEG ratio of 10
40 showed significantly lower NSB levels (82 and 81 NPs per cell, respectively) compared to those with an NP/PEG ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 (1287 NPs per cell). This trend aligns with the results in Fig. 5B, confirming the reliability of the HSA adsorption study and demonstrating the concept that denser brush-like PEG conformations more effectively inhibit non-specific protein adsorption.
80 (1287 NPs per cell). This trend aligns with the results in Fig. 5B, confirming the reliability of the HSA adsorption study and demonstrating the concept that denser brush-like PEG conformations more effectively inhibit non-specific protein adsorption.
We also investigated the effect of PEG Mw (i.e., 2k, 5k, and 10k) on serum albumin adsorption while maintaining a constant grafting density of ∼0.3 chains per nm2. These NPs were purified using the same protocol (ethanol × 2, H2O × 1), and their TGA curves and calculated grafting densities are presented in Fig. S8B and Table S5.† As shown in Fig. 5C, the amount of serum albumin decreased from 2.5 wt% to 0.6 wt% with increasing Mw, and this result is well correlated with PEG conformation at the NPs’ surface. The increase of PEG Mw from 2k to 10k resulted in a conformational transition from an intermediate (mushroom-brush) regime to a brush conformation regime. Densely packed PEG brushes have been reported to induce a reduction of protein adsorption on surfaces, with this suppression effect being intrinsic and independent of the addition or presence of proteins.23,43,46
Our T2 and DOSY experiments confirmed that using the original purification protocol (ethanol × 2, H2O × 1) left some ‘free’ mPEG5k silanes loosely associated with the NP surface. To further understand how fully removing this loosely bound PEG affects serum albumin adsorption, we compared HSA adsorption on PMSNs-Zwi-mPEG5k NPs before and after an additional H2O wash. Here, surprisingly, we observed a notable increase in adsorbed HSA on NPs that were purified to remove free PEG silanes (Fig. 5D). This increase can be attributed to the removal of loosely attached PEG molecules, which creates gaps or discontinuities in the PEG layer on the NP surface, reducing its effectiveness as a barrier against protein adsorption. Consequently, more silica surfaces become exposed, promoting interactions with proteins and increasing non-specific adsorption. Loosely bound PEG, even if not covalently attached, can still contribute to this effect by covering some surface areas and increasing the density of the protective PEG layer.
These results lead to the surprising conclusion that fully removing loosely bound or physically adsorbed PEG silanes on the NPs’ surface may not always be necessary or beneficial, especially for minimizing non-specific binding in our current study. Although inadequate purification can lead to data misinterpretation and incorrect conclusions about surface functionalization, residual PEG may be advantageous for certain applications.
Conclusions
This study highlights the power of solution NMR spectroscopy as a versatile tool to investigate the conformation, dynamics, and functional properties of PEGylated MSNs. By employing qNMR, DOSY, and relaxation time measurements (T1 and T2), we provided a detailed molecular-level understanding of PEG behaviour and the impact of grafting density on chain conformation and mobility on MSN surfaces.Specifically, qNMR provided precise quantification of PEG grafting density, showing strong consistency with TGA results, while DOSY enabled differentiation between covalently bound PEG chains and loosely adsorbed polymers. This distinction is critical for confirming the stability of functionalized nanoparticle surfaces. Relaxation time measurements provided critical insights into chain mobility and flexibility, revealing that PEG chains exhibit increased flexibility at higher grafting densities, though this dependence is relatively weak. Notably, these findings demonstrated that NPs with “dense brush” conformations can effectively minimize non-specific protein adsorption.
Overall, our findings establish a clear relationship between PEG surface conformation, segmental mobility, and functional performance, offering a valuable framework for the rational design of protein-resistant nanomaterials for biomedical applications. Interestingly, MSNs retaining residual loosely associated PEG chains exhibited greater reduction in non-specific protein adsorption than fully purified samples, highlighting the potential functional benefits of dynamic PEG populations at the nanoparticle interface.
Author contributions
Xiaochong Li: conceptualization, methodology, writing – original draft, formal analysis, investigation. Yang Liu: conceptualization, methodology, review & editing, formal analysis, investigation. Edmond C. N. Wong: formal analysis. Mitchell A. Winnik: conceptualization, review & editing, supervision, project administration, funding acquisition.Data availability
The data supporting the findings of this study are available within the article and its ESI.† Raw data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors thank NSERC Canada and Standard BioTools Canada Inc. (formerly Fluidigm Canada Inc.) for their support of this research. X.L. also acknowledges financial support from the China Scholarship Council (CSC, No. 201906240128). We also thank Daniel Majonis from Standard BioTools Canada Inc. (formerly Fluidigm Canada Inc.) for his assistance with the mass cytometry analyses.References
- C. T. Kresge, M. E. Leonowicz, W. J. Roth, J. C. Vartuli and J. S. Beck, Nature, 1992, 359, 710–712 CrossRef CAS.
- J. S. Beck, J. C. Vartuli, W. J. Roth, M. E. Leonowicz, C. T. Kresge, K. D. Schmitt, C. T. W. Chu, D. H. Olson, E. W. Sheppard, S. B. McCullen, J. B. Higgins and J. L. Schlenker, J. Am. Chem. Soc., 1992, 114, 10834–10843 CrossRef CAS.
- Y. Wan and D. Zhao, Chem. Rev., 2007, 107, 2821–2860 Search PubMed.
- F. Hoffmann, M. Cornelius, J. Morell and M. Froba, Angew. Chem., Int. Ed., 2006, 45, 3216–3251 CrossRef CAS PubMed.
- K. Zhang, L.-L. Xu, J.-G. Jiang, N. Calin, K.-F. Lam, S.-J. Zhang, H.-H. Wu, G.-D. Wu, B. Albela, L. Bonneviot and P. Wu, J. Am. Chem. Soc., 2013, 135, 2427–2430 Search PubMed.
- Y. Hu, S. Bai, X. Wu, S. Tan and Y. He, Ceram. Int., 2021, 47, 31031–31041 CrossRef CAS.
- F. Rizzi, R. Castaldo, T. Latronico, P. Lasala, G. Gentile, M. Lavorgna, M. Striccoli, A. Agostiano, R. Comparelli, N. Depalo, M. L. Curri and E. Fanizza, Molecules, 2021, 26(14), 4247 Search PubMed.
- F. Tang, L. Li and D. Chen, Adv. Mater., 2012, 24, 1504–1534 CrossRef CAS PubMed.
- S. Huh, J. W. Wiench, J. C. Yoo, M. Pruski and V. S. Y. Lin, Chem. Mater., 2003, 15, 4247–4256 Search PubMed.
- Z. Li, J. C. Barnes, A. Bosoy, J. F. Stoddart and J. I. Zink, Chem. Soc. Rev., 2012, 41, 2590–2605 RSC.
- J. Liang, Z. Liang, R. Zou and Y. Zhao, Adv. Mater., 2017, 29, 1701139 Search PubMed.
- H. Li, X. Chen, D. Shen, F. Wu, R. Pleixats and J. Pan, Nanoscale, 2021, 13, 15998–16016 Search PubMed.
- M. H. Spitzer and G. P. Nolan, Cell, 2016, 165, 780–791 CrossRef CAS PubMed.
- L. P. Arnett, R. Rana, W. W. Chung, X. Li, M. Abtahi, D. Majonis, J. Bassan, M. Nitz and M. A. Winnik, Chem. Rev., 2023, 123, 1166–1205 CrossRef CAS PubMed.
- J. Pichaandi, L. Tong, A. Bouzekri, Q. Yu, O. Ornatsky, V. Baranov and M. A. Winnik, Chem. Mater., 2017, 29, 4980–4990 CrossRef CAS.
- Y. Zhang, N. Zabinyakov, D. Majonis, A. Bouzekri, O. Ornatsky, V. Baranov and M. A. Winnik, Anal. Chem., 2020, 92, 5741–5749 CrossRef CAS PubMed.
- W. Ngamcherdtrakul, T. Sangvanich, S. Goodyear, M. Reda, S. Gu, D. J. Castro, P. Punnakitikashem and W. Yantasee, Bioengineering, 2019, 6(1), 23 CrossRef CAS PubMed.
- X. Li, Y. Liu, Y. Zhang, D. Majonis, M. Wang, M. Fashandi and M. A. Winnik, Chem. Mater., 2024, 36, 8174–8187 Search PubMed.
- T. Cedervall, I. Lynch, S. Lindman, T. Berggård, E. Thulin, H. Nilsson, K. A. Dawson and S. Linse, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 2050–2055 CrossRef CAS PubMed.
- C. D. Walkey and W. C. W. Chan, Chem. Soc. Rev., 2012, 41, 2780–2799 RSC.
- R. Gref, M. Lück, P. Quellec, M. Marchand, E. Dellacherie, S. Harnisch, T. Blunk and R. H. Müller, Colloids Surf., B, 2000, 18, 301–313 CrossRef CAS PubMed.
- V. Cauda, C. Argyo and T. Bein, J. Mater. Chem., 2010, 20, 8693–8699 Search PubMed.
- Q. He, J. Zhang, J. Shi, Z. Zhu, L. Zhang, W. Bu, L. Guo and Y. Chen, Biomaterials, 2010, 31, 1085–1092 Search PubMed.
- C. von Baeckmann, H. Kählig, M. Lindén and F. Kleitz, J. Colloid Interface Sci., 2021, 589, 453–461 CrossRef CAS PubMed.
- V. B. Damodaran, C. J. Fee, T. Ruckh and K. C. Popat, Langmuir, 2010, 26, 7299–7306 CrossRef CAS PubMed.
- S. T. Milner, T. A. Witten and M. E. Cates, Macromolecules, 1988, 21, 2610–2619 Search PubMed.
- B. Zhao and W. J. Brittain, Prog. Polym. Sci., 2000, 25, 677–710 CrossRef CAS.
- P. G. de Gennes, Macromolecules, 1980, 13, 1069–1075 CrossRef CAS.
- C. von Baeckmann, H. Kahlig, M. Linden and F. Kleitz, J. Colloid Interface Sci., 2021, 589, 453–461 CrossRef CAS PubMed.
- M. A. Rixman, D. Dean and C. Ortiz, Langmuir, 2003, 19, 9357–9372 CrossRef CAS.
- K. Ohno, T. Morinaga, S. Takeno, Y. Tsujii and T. Fukuda, Macromolecules, 2007, 40, 9143–9150 CrossRef CAS.
- S. Mourdikoudis, R. M. Pallares and N. T. K. Thanh, Nanoscale, 2018, 10, 12871–12934 RSC.
- A. G. Thomé, F. Schroeter, P. Bottke, J. Wittayakun and F. Roessner, Microporous Mesoporous Mater., 2019, 274, 342–346 CrossRef.
- C. I. C. Crucho, C. Baleizão and J. P. S. Farinha, Anal. Chem., 2017, 89, 681–687 CrossRef CAS PubMed.
- L. Polito, M. Colombo, D. Monti, S. Melato, E. Caneva and D. Prosperi, J. Am. Chem. Soc., 2008, 130, 12712–12724 CrossRef CAS PubMed.
- J. H. Prestegard, C. M. Bougault and A. I. Kishore, Chem. Rev., 2004, 104, 3519–3540 CrossRef CAS PubMed.
- S. Azizi, T. Tajouri and H. Bouchriha, Polymer, 2000, 41, 5921–5928 CrossRef CAS.
- R. Cheng, S. Wang, K. Moslova, E. Mäkilä, J. Salonen, J. Li, J. Hirvonen, B. Xia and H. A. Santos, ACS Biomater. Sci. Eng., 2022, 8, 4132–4139 CrossRef CAS PubMed.
- S. E. Lehman, Y. Tataurova, P. S. Mueller, S. V. S. Mariappan and S. C. Larsen, J. Phys. Chem. C, 2014, 118, 29943–29951 CrossRef CAS.
- J. Lu, Y. Xue, R. Shi, J. Kang, C.-Y. Zhao, N.-N. Zhang, C.-Y. Wang, Z.-Y. Lu and K. Liu, Chem. Sci., 2019, 10, 2067–2074 RSC.
- Y. Hitomi, K. Aoki, R. Miyachi, J. Ohyama, M. Kodera, T. Tanaka and F. Sugihara, Chem. Lett., 2014, 43, 1901–1903 CrossRef.
- D. R. Hristov, H. Lopez, Y. Ortin, K. O'Sullivan, K. A. Dawson and D. F. Brougham, Nanoscale, 2021, 13, 5344–5355 RSC.
- M. Li, S. Jiang, J. Simon, D. Paßlick, M.-L. Frey, M. Wagner, V. Mailänder, D. Crespy and K. Landfester, Nano Lett., 2021, 21, 1591–1598 CrossRef CAS PubMed.
- V. Brahmkhatri and H. S. Atreya, in NMR Spectroscopy for Probing Functional Dynamics at Biological Interfaces, ed. A. Bhunia, H. S. Atreya and N. Sinha, The Royal Society of Chemistry, 2022, ch. 9, pp. 236–253 Search PubMed.
- Q. Dai, C. Walkey and W. C. W. Chan, Angew. Chem., Int. Ed., 2014, 53, 5093–5096 CrossRef CAS PubMed.
- J. L. Perry, K. G. Reuter, M. P. Kai, K. P. Herlihy, S. W. Jones, J. C. Luft, M. Napier, J. E. Bear and J. M. DeSimone, Nano Lett., 2012, 12, 5304–5310 CrossRef CAS PubMed.
- A. Wani, G. H. L. Savithra, A. Abyad, S. Kanvinde, J. Li, S. Brock and D. Oupický, Sci. Rep., 2017, 7, 2274 Search PubMed.
- C. D. Walkey, J. B. Olsen, H. Guo, A. Emili and W. C. W. Chan, J. Am. Chem. Soc., 2012, 134, 2139–2147 CrossRef CAS PubMed.
- Z. Hens and J. C. Martins, Chem. Mater., 2013, 25, 1211–1221 CrossRef CAS.
- X. Li and D. F. Shantz, J. Phys. Chem. C, 2010, 114, 8449–8458 Search PubMed.
- X. Li and D. F. Shantz, Langmuir, 2011, 27, 3849–3858 CrossRef CAS PubMed.
- Y. Rao, B. Antalek, J. Minter, T. Mourey, T. Blanton, G. Slater, L. Slater and J. Fornalik, Langmuir, 2009, 25, 12713–12720 Search PubMed.
- A. Rivas-Cardona and D. F. Shantz, J. Phys. Chem. C, 2010, 114, 20178–20188 CrossRef CAS.
- M. Li, S. Jiang, J. Simon, D. Paßlick, M.-L. Frey, M. Wagner, V. Mailänder, D. Crespy and K. Landfester, Nano Lett., 2021, 21, 1591–1598 CrossRef CAS PubMed.
- M. Zhou, X. Du, W. Li, X. Li, H. Huang, Q. Liao, B. Shi, X. Zhang and M. Zhang, J. Mater. Chem. B, 2017, 5, 4455–4469 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5nr00936g |
| ‡ These authors contribute equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |