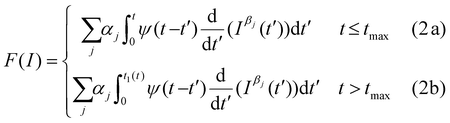Evidence of the bottom stiffness effect on atomic force microscopy-based cell mechanobiology

Abstract

AFM is the dominant method to characterize the nanomechanical properties of cells. These properties are obtained by model fitting. Semi-infinite contact mechanics models predict that the force depends on the cell's mechanical properties, indentation and the tip's geometry. Finite-thickness rheological models predict that the force should depend also on the rigidity of the substrate. The latter property has never been observed experimentally. It would make cells appear stiffer than they are. Here, we designed a force–distance curve experiment to reveal the influence of the rigidity of the substrate on the forces and the apparent moduli measured by AFM. Model fitting by using a semi-infinite power-law rheological model showed an increase of the apparent modulus with increasing force. This behavior was an artifact which disappeared when the force was fit with a bottom-effect correction model. Our findings demonstrated that the force applied on a cell depended intrinsically on the stiffness of the substrate while the mechanical properties (true values) did not.

---

Introduction

The mechanical properties of cells are of paramount relevance in mechanobiology. Atomic force microscopy (AFM) has become the most common technique to measure the elastic and viscoelastic properties of cells at the nanometer scale.^1–4 AFM measurements have significantly contributed to our current understanding of the relationship between mechanical forces, physiology and disease.^5–12

Several methods have been developed to determine the mechanical properties of cells with AFM, which include force–distance curves or nanoindentation,^3,5 oscillatory indentation,^13,14 load relaxation and creep measurements.¹⁵ These methods require culture of cells on a solid substrate such as glass or plastic. These substrates are significantly stiffer than mammalian cells. For example, the Young's modulus of a glass Petri dish is about 100 GPa while the Young's modulus of live mammalian cells is in the 0.5–10 kPa range. Furthermore, the height of a mammalian cell is relatively small. In many cell types, it varies from 2 μm (cytoplasm edge) to 7– 15 μm on the region located above the nucleus. The combination of the cell's softness and finite-thickness causes the compressive stress applied by the tip to propagate through the cell until it reaches the substrate. Then, the stress bounces back towards the tip. The net effect would be an increase of the force applied by the tip to the cell. This effect is known as the bottom stiffness effect.³ As a consequence, cells might appear stiffer than they are.

Dimitriadis and co-workers were the first to point out that the above effect might influence AFM measurements on soft materials.¹⁶ For a spherical tip, they proposed a model to estimate the force measured in AFM as a function of the Young's modulus and the material thickness (height). The theoretical model was generalized for any axisymmetric tip by Garcia and Garcia¹⁷ and extended to include viscoelastic interactions.^18,19 These models were generically called bottom-effect correction models.³ Finite element simulations and additional theoretical contributions have validated bottom-effect correction models.^17,20–25 The bottom stiffness effect, if it is not corrected, would introduce significant errors in the determination of the Young's modulus of a cell.^17,26

To date, theoretical predictions of the bottom stiffness effect on AFM measurements performed on cells have not been demonstrated. As a consequence, bottom-effect corrections have been sparsely applied to correct AFM measurements.^27,28 Therefore, the accuracy of the modulus values provided by some AFM experiments is questionable, in particular, for the measurements performed with tips of a large effective radius (R ≥ 1 μm). In contrast, experimental evidence of the bottom stiffness effect has been reported for AFM measurements performed on self-assembled and lipid bilayers deposited on mica substrates.^29,30 In those experiments, the thickness of the system was easily changed by increasing the number of monolayers. This approach enabled a straightforward comparison between experiment and theory. The theory predicted that the force should decrease when increasing the thickness of the system. AFM experiments verified the above prediction by reporting that for the same indentation, the force applied by the tip decreased with the number of layers.^29,30

Similar experiments cannot be done on live cells. Single cells cannot be piled up. In addition, mammalian cells have complex rheological behaviour which prevents a straightforward study. For example, a cross-section of a cell might show height variations from the cytoplasm edge (2 μm) to the region on top of the nucleus (7–15 μm). Therefore, a single cell could provide a platform to test the bottom stiffness effect by measuring the forces on different regions of the cell. However, the results of this experiment might be flawed. It has been shown that for some cells, the elastic and viscoelastic properties of the nucleus were markedly different from the mechanical properties of the cytoplasm.^31,32 Such experiments might give forces over the nucleus which are different from those measured on the cytoplasm. However, those differences might be attributed to the intrinsic mechanical property differences of the nucleus and the cytoplasm.

Gavara and Chadwick measured the spatial variation of the Young's modulus across an NIH 3T3 cell.³³ The results were interpreted in terms of the bottom stiffness effect. However, that interpretation was flawed. The values of the modulus changed considerably (10-fold) from nearby points. The analysis neglected the viscoelastic response of the different regions of the cell. Furthermore, the bottom-effect correction model derived in ref. 33 was found to be incorrect.^19,21

Here, we demonstrate that the stiffness of the substrate modifies the force applied and/or measured by AFM on a single cell. A series of force–distance curves were acquired on the cytoplasm and nuclear regions of HeLa cells cultured on a Petri dish as a function of the maximum value of the force. These curves were fit with semi-infinite and finite-thickness single power-law rheology models. A semi-infinite model, that is, a model that does not consider the height of a cell, gave a modulus that increased with the value of the force. On the other hand, the modulus remained nearly constant, that is, independent of the force, when the force was fit with a model that considered the finite height of the tip as an input. These trends were independently reproduced on cytoplasmic and nuclear regions. The above results were hallmarks of the influence of the rigidity of the substrate on the forces applied and/or measured in AFM. In addition, we found that the fluidity coefficient did not depend on the force value. The latter results were reproduced by both finite and semi-infinite single power-law rheology models.

Results and discussion

Bottom-stiffness effect

The bottom stiffness effect postulates that for a given indentation, the force applied to a cell is higher than the one measured on an ideal cell of semi-infinite height. The increase of the force reflects the rigidity of the substrate. This effect is parameterized by the ratio between the radius of the tip–cell contact area and the average height of the cell in that region. Therefore, the force would depend on the indentation, cell's mechanical properties, cell's height and substrate stiffness. However, the mechanical properties of a cell, being intrinsic to its structure, should not be modified by the rigidity of the substrate. In quasistatic measurements, mechanical properties might have spatial variations, but in any case, for non-invasive measurements, they should not depend on the force applied to probe the cell.

We remark that the bottom stiffness effect discussed here is different from the substrate stiffness effect described in mechanobiology.^34,35 The latter is related to the activation of mechanoresponsive proteins that respond to the rigidity and viscosity cues of the substrate. In AFM experiments both effects might happen simultaneously.

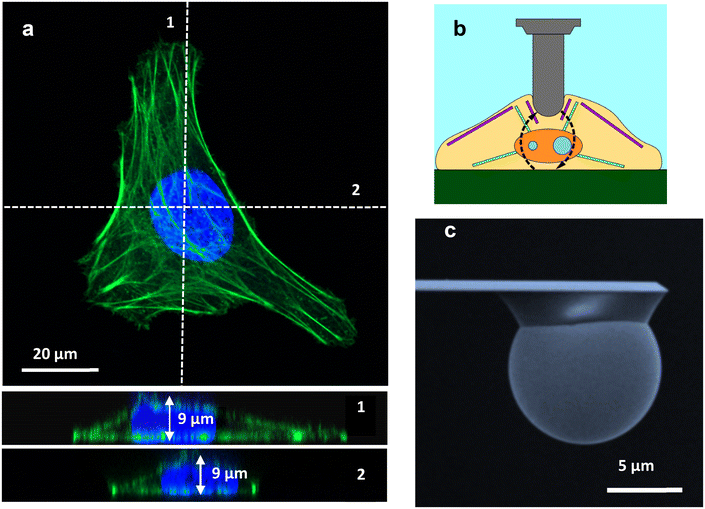
Fig. 1a shows a confocal microscopy image of a HeLa cell. The cross-section provides values of the cell's height as a function of the x coordinate. Height measurements from confocal microscopy in combination with AFM topography data were used to provide accurate estimations of the cell's height. Height values were needed as inputs to determine the force with a bottom-effect correction model. Fig. 1b shows a schematic of an AFM experiment designed to measure the mechanical properties of a cell. Fig. 1b illustrates how the stress caused by the AFM might be reflected back at the cell–solid support interface. Fig. 1c shows a SEM image of one of the spherical tips used in the measurements.

Fig. 1 (a) Top view and cross-section (dashed lines) of a HeLa cell. The cells were cultured under similar conditions to those used in the AFM experiments. The confocal microscopy image provides information on the cell's height at zero force. (b) Schematic of an AFM experiment designed to measure the mechanical properties of a cell. The arrows schematize the balance of the force associated with the bottom stiffness effect. (c) SEM image of a colloidal tip similar to the ones used in the experiments.

Power-law rheology model

The nanomechanical parameters of a cell were obtained by fitting the experimental data to the single power-law rheology model developed in ref. 19. The model included the geometry of the tip, the determination of the contact area as a function of the cell's deformation history and the finite-thickness of the cell. In this model, the relaxation function was expressed in terms of two parameters, the scaling modulus and the fluidity coefficient,where Γ is the Euler gamma function; E₀ is a scaling factor with units of force divided by area (scaling modulus). It has been identified as the elastic modulus of the material at time t₀ (commonly t₀ = 1 s). The value of the fluidity coefficient γ = 0 defines an elastic solid of Young's modulus E₀ while γ = 1 indicates a Newtonian viscous liquid with viscosity η_e = E₀t₀. The above model has been successfully applied to determine the viscoelasticity of cells at different speeds and indentation scales.^36,37

For a paraboloid tip of radius R, the force as a function of the indentation was calculated as follows:

where α_j and β_j are coefficients that depend on the geometry of the probe and the height (thickness) of the cell h (see table); t_max is the time at which indentation reached its maximum value (I_max); ψ(t − t′) is the viscoelastic relaxation function of the material and t₁(t) is the solution to determine the contact area during tip's retraction,¹⁸

The coefficients in Table 1 converged to the semi-infinite power-law rheology coefficients for h → ∞.¹⁹

Table 1 Bottom-effect correction coefficients for a parabolic tip of radius R

j	αj	βj
0	1.778R^1/2	3/2
1	2.014Rh^−1	2
2	2.661R^3/2h^−2	5/2
3	2.659R^2h^−3	3
4	1.342R^5/2h^−4	7/2

---

Experimental force–distance curves

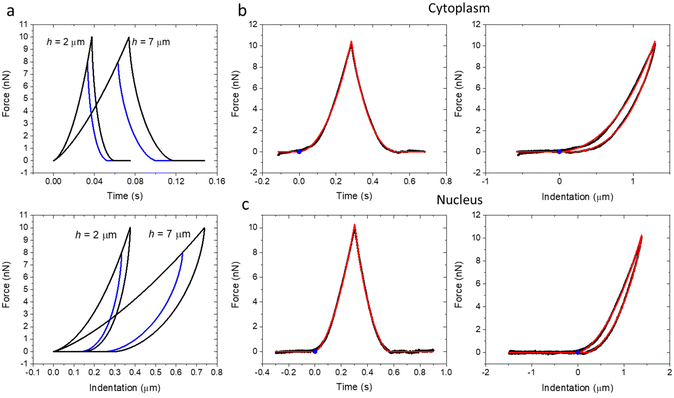
Fig. 2a shows a series of theoretical force–distance curves generated by using the above expressions for a tip of R = 5 μm (E₀ = 1 kPa and γ = 0.2). The thinner the cell, the smaller the indentation to reach the same force. The curves shared the same path during the approach. However, the retraction path depended on the maximum value of force applied. This is a history dependent behavior associated with the viscoelasticity of the system. Fig. 2b and c show some representative force–distance curves (black) taken over cytoplasmic and nuclear regions of a HeLa cell. The hysteresis of those curves revealed the existence of intrinsic energy dissipation processes within the cell. These effects were associated with the viscoelasticity of the cell. The FDC curves were plotted versus time and indentation. The fitting obtained by using the model described above is shown in red. The blue point shows the point of contact between the tip and the cell (approach curve).

Fig. 2 (a) Theoretical force–time and force–distance curves for two different cell heights (2 and 7 μm); E₀ = 1 kPa and γ = 0.3; R = 5 μm. (b) Force–time and force–distance curves measured on the cytoplasm region of a HeLa cell (v = 10 μm s⁻¹). (c) Force–time and force–distance curves measured on top of the nucleus ((v = 10 μm s⁻¹)). The red curves show the fitting obtained from the power-law rheology model with bottom-effect corrections. The blue dot represents the contact point. Microcantilever parameters: k = 0.08 N m⁻¹, Q = 2.00, f_o = 3.479 kHz.

Fig. 3 shows the nanomechanical parameters of two HeLa cells (scaling modulus and fluidity coefficient) as a function of the force. The experiments were performed on several HeLa cells (n = 7). We found the same trend in all the cells (ESI†). The panels are divided into two sections (left and right). The left panels show the results obtained by fitting the FDCs with the semi-infinite power-law rheology model. The right panels show the results obtained using the bottom-effect correction model (eqn (2) and Table 1). In agreement with the predictions of the bottom stiffness effect, the apparent modulus increased with the value of the maximum force (Fig. 3a–d, top panels). The above behavior did not depend on the cell region (nucleus versus cytoplasm). However, the apparent modulus values were higher on the cytoplasm than on the nucleus. This result was also consistent with the bottom stiffness effect because height was larger on top of the nuclear region than on the cytoplasm (Fig. 1). However, this finding by itself should not be taken as conclusive proof because the viscoelastic forces over the nucleus might be different from those over the cytoplasm. The influence of the substrate stiffness on the modulus was removed by fitting the FDCs with the bottom-effect correction model. The fitting led to modulus values which were independent of the applied force and, therefore, of the substrate stiffness. These values should be considered, for a given velocity, the true modulus values of the cell.

Fig. 3 Apparent and corrected nanomechanical parameters of HeLa cells cultured on a Petri dish. (a) Modulus and fluidity coefficients obtained over a cytoplasmic region (cell 1). (b) Modulus and fluidity coefficients obtained over a nuclear region (cell 1). (c and d) Modulus and fluidity coefficients obtained over cytoplasmic and nuclear regions (cell 2). Apparent values were obtained by fitting the force–distance curves with the semi-infinite single power-law rheology model. Corrected values were obtained by fitting the FDCs with the single power-law rheology model that includes bottom-effect corrections. The red points in top panels were generated by using the bottom-effect correction model. The agreement obtained with the experimental values is a self-validation of the model.

On the other hand, the fluidity coefficient did not show any dependence on the applied force (bottom panels). The values remained practically constant at about 0.15. We concluded that the fluidity coefficient of a cell was not affected by the substrate stiffness. Under quasistatic conditions and for relatively low velocities, the fluidity coefficient did not depend on the cell region.

The above findings were validated by estimating the cell's height from the fitting and re-calculating the dependence of the apparent modulus values on the force (red points and red discontinuous line). The agreement obtained between the experimental values and the simulations provided a self-consistent validation of the bottom stiffness effect.

To better understand why an increase of the modulus (apparent values) with the value of the force is direct evidence of the bottom stiffness effect, we need to recall its physical origin. This effect originated at the cell–substrate interface. There, the stress generated by the tip was reflected back towards it. The reflected stress was transformed into a force by integrating it over the contact area. Therefore, two parameters were involved besides the rigidity of the substrate, the height and the contact radius. Fig. 4a shows the dependence of the apparent modulus and the fluidity coefficient values on the force. The FDCs were calculated for several heights (2, 5, 10 and 15 μm). For a fixed height, the apparent modulus increases with the maximum value of the FDC. The above behavior is significantly enhanced when reducing the cell thickness from 15 μm to 2 μm. The fluidity coefficient (right panel) hardly changed with the applied force. This result was expected. Viscoelastic forces were mostly dominated by shear forces.

Fig. 4 (a) Dependence of the apparent modulus and fluidity coefficient on the force for different cell heights (simulation). (b) Simulation of the dependence of the ratio between the contact radius and the cell's height on the force for different heights. (c) Radius of the projected contact area as a function of the force for different cell heights (simulations). Data obtained by using eqn (2) with E₀ = 1 kPa and γ = 0.2; R = 5 μm. The discontinuous lines show the results for a semi-infinite system with the same E₀ and γ values.

The apparent increase of the modulus with the force (Fig. 4a) correlated with the dependence of the ratio between the contact radius and the cell height (Fig. 4b). For a given height, the ratio increased with the force. For a fixed force, the ratio increased when decreasing the cell's height. Notwithstanding the above, the simulations showed that for the same force, the contact radius increased with the cell's height (Fig. 4c).

Conclusions

We concluded that the rigidity of the substrate modified the forces measured in AFM. Therefore, in general the increase of the cell's modulus with the force must be considered an artefact. It was associated with the use of a semi-infinite contact mechanics model to fit the forces measured on a finite system. The proper values of the modulus were obtained by fitting the experimental data with a contact mechanics model that incorporated the finite height of a cell. In retrospect, the above findings provided an explanation to previous observations.³⁸

The bottom stiffness effect is a universal property of a finite thickness system subjected to compressive forces. It should be present in other types of single cell measurements such as those performed by micropipette aspiration. In some AFM measurements, its presence might be masked by the depth dependence of the mechanical properties associated with changes in the cell's structure (membrane, cortex, cytosol, nucleus).^39,40

We have experimentally demonstrated that the rigidity of the solid support modifies the force values measured in AFM. This effect is an intrinsic property of the cell–substrate interface. The rigidity of the substrate makes the modulus of a cell (apparent value) increase with the value of the force. The bottom stiffness effect is dependent on the ratio between the projected radius of the tip–cell contact area and the thickness. It became significant whenever the tip–cell contact radius was comparable to the cell thickness. Contrary to common wisdom, the use of large tips enhanced the error in the estimation of the modulus. This effect might lead to overestimation of the modulus by a factor of 5 or larger. The bottom stiffness effect might be easily corrected by processing the AFM data with bottom-effect correction models which provide the true nanomechanical parameters of the cell.

Methods

Force–distance curves

AFM experiments were performed with a JPK Nanowizard V atomic force microscope (Bruker Instruments) mounted on an inverted optical microscope (AXIO Observer D1; Carl Zeiss). All experiments were carried out with samples immersed in culture medium (see below). Colloidal probe cantilevers CP-PNPL-SiO (sQube) were used. These cantilevers have a nominal spring constant of 0.08 N m⁻¹ and a radius R = 5 μm (Fig. 1c). The actual spring constant of the cantilever was determined using the thermal noise method as implemented in the AFM. The FDCs were acquired by applying a triangular waveform with a speed of 10 μm s⁻¹.

FDCs were obtained on 5 different positions on the cytoplasm and five different positions over the nucleus; on each position, we acquired 10 FDCs.

The FDC curves used to generate the nanomechanical values represented in Fig. 3 are included in ref. 41.

Contact model fitting

The semi-infinite and bottom effect correction models were implemented in Python. The simulations and the processing and fitting of experimental measurements were performed using Numpy and Scipy libraries. The code used to process the FDCs is given in ref. 41.

Cells and culture

HeLa cells (Sigma-Aldrich) were cultured in Eagle's minimum essential medium (EMEM) with 10% calf serum-CS (Gibco Life Technologies), 1% penicillin/streptomycin (Gibco Life Technologies, UK) and 2 mM l-glutamine (Sigma-Aldrich, Missouri, USA). The cells were maintained at 37 °C under a controlled atmosphere with 90% humidity and 5% CO2. The cells were seeded in Petri dishes for 24–48 hours in the culture medium before the measurements. The AFM measurements were performed in the above Petri dishes and culture medium.

Author contributions

A. L. D. M., L. A. D. and J. S.: investigation, review and editing. J. R. T. and F. M. E.: methodology, investigation, writing, review and editing. R. G.: conceptualization, methodology, investigation, funding acquisition, supervision, writing, review and editing.

Data availability

All relevant data are provided within the manuscript and its additional files.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support from the Ministerio de Ciencia e Innovación grant PID2022-136851NB-I00/AEI/10.13039/501100011033 and EUR2022-134029 (RG), Comunidad de Madrid TEC-2024/TEC-158 (Tec4Nanobio-CM) and the European Commission (HORIZON-EIC-2022, project Piezo4Spine, no. 101098597) is acknowledged. ALDM acknowledges support from the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior – Brasil (CAPES).

References

1. P. H. Wu, D. R. B. Aroush, A. Asnacios, W. C. Chen, M. E. Dokukin, B. L. Doss, P. Durand-Smet, A. Ekpenyong, J. Guck, N. V. Guz, P. A. Janmey, J. S. H. Lee, N. M. Moore, A. Ott, Y. C. Poh, R. Ros, M. Sander, I. Sokolov, J. R. Staunton, N. Wang, G. Whyte and D. Wirtz, Nat. Methods, 2018, 15, 491–498.
2. Y. M. Efremov, T. Okajima and A. Raman, Soft Matter, 2020, 16, 64–81.
3. R. Garcia, Chem. Soc. Rev., 2020, 49, 5850–5884.
4. M. Li, N. Xi, Y. Wang and L. Liu, Nano Res., 2019, 12, 703–718.
5. M. Krieg, G. Fläschner, D. Alsteens, B. M. Gaub, W. H. Roos, G. J. L. Wuite, H. E. Gaub, C. Gerber, Y. F. Dufrêne and D. J. Müller, Nat. Rev. Phys., 2019, 1, 41–57.
6. A. Massey, J. Stewart, C. Smith, C. Parvini, M. McCormick, K. Do and A. X. Cartagena-Rivera, Nat. Rev. Phys., 2024, 6, 269–282.
7. A. Calzado-Martín, M. Encinar, J. Tamayo, M. Calleja and A. San Paulo, ACS Nano, 2016, 10, 3365–3374.
8. L. M. Rebelo, J. S. De Sousa, J. M. Filho and M. Radmacher, Nanotechnology, 2013, 24, 055102.
9. A. C. Dumitru, M. A. Poncin, L. Conrard, Y. F. Dufrêne, D. Tyteca and D. Alsteens, Nanoscale Horiz., 2018, 3, 293–304.
10. A. Dominguez-Bajo, A. González-Mayorga, C. R. Guerrero, F. J. Palomares, R. Garcia, E. Lopez-Dolado and M. C. Serrano, Biomaterials, 2019, 192, 461–474.
11. M. Hadzipasic, S. Zhang, Z. Huang, R. Passaro, M. S. Sten, G. M. Shankar and H. T. Nia, Biomaterials, 2024, 305, 122431.
12. C. Huerta-López, A. Clemente-Manteca, D. Velázquez-Carreras, F. M. Espinosa, J. G. Sanchez, Á. Martínez-del-Pozo, M. García-García, S. Martín-Colomo, A. Rodríguez-Blanco, R. Esteban-González, F. M. Martín-Zamora, L. I. Gutierrez-Rus, R. Garcia, P. Roca-Cusachs, A. Elosegui-Artola, M. A. del Pozo, E. Herrero-Galán, P. Sáez, G. R. Plaza and J. Alegre-Cebollada, Sci. Adv., 2024, 10, 9758.
13. A. Rigato, A. Miyagi, S. Scheuring and F. Rico, Nat. Phys., 2017, 13, 771–775.
14. P. V. Kolluru, M. D. Eaton, D. W. Collinson, X. Cheng, D. E. Delgado, K. R. Shull and L. C. Brinson, Macromolecules, 2018, 51, 8964–8978.
15. D. A. D. Flormann, C. Anton, M. O. Pohland, Y. Bautz, K. Kaub, E. Terriac, T. E. Schäffer, J. Rheinlaender, A. Janshoff, A. Ott and F. Lautenschläger, Front. Phys., 2021, 9, 711860.
16. E. K. Dimitriadis, F. Horkay, J. Maresca, B. Kachar and R. S. Chadwick, Biophys. J., 2002, 82, 2798–2810.
17. P. D. Garcia and R. Garcia, Biophys. J., 2018, 114, 2923–2932.
18. P. D. Garcia and R. Garcia, Nanoscale, 2018, 10, 19799–19809.
19. P. D. Garcia, C. R. Guerrero and R. Garcia, Nanoscale, 2020, 12, 9133.
20. A. C. Santos, L. M. Rebelo, A. C. Araujo, E. B. Barrosa and J. S. de Sousa, Soft Matter, 2012, 8, 4441.
21. B. L. Doss, E. K. Rahmani, K. Lin and R. Ros, Soft Matter, 2019, 15, 1776–1784.
22. D. F. S. Costa, J. L. B. de Araújo, C. L. N. Oliveira and J. S. de Sousa, J. Appl. Phys., 2022, 132, 214701.
23. P. Hermanowicz, Int. J. Mech. Sci., 2021, 193, 106138.
24. I. Argatov and X. Jin, Int. J. Solids Struct., 2024, 291, 112713.
25. I. Saito, R. J. Sheridan, S. Zauscher and L. C. Brinson, Macromolecules, 2024, 58, 980–988.
26. S. Pérez-Domínguez, S. G. Kulkarni, J. Pabijan, K. Gnanachandran, H. Holuigue, M. Eroles, E. Lorenc, M. Berardi, N. Antonovaite, M. L. Marini, J. L. Alonso, L. Redonto-Morata, V. Dupres, S. Janel, S. Acharya, J. Otero, D. Navajas, K. Bielawski, H. Schillers, F. Lafont, F. Rico, A. Podestà, M. Radmacher and M. Lekka, Nanoscale, 2023, 15, 16371–16380.
27. H. Schillers, C. Rianna, J. Schäpe, T. Luque, H. Doschke, M. Wälte, J. J. Uriarte, N. Campillo, G. P. A. Michanetzis, J. Bobrowska, A. Dumitru, E. T. Herruzo, S. Bovio, P. Parot, M. Galluzzi, A. Podestà, L. Puricelli, S. Scheuring, Y. Missirlis, R. Garcia, M. Odorico, J. M. Teulon, F. Lafont, M. Lekka, F. Rico, A. Rigato, J. L. Pellequer, H. Oberleithner, D. Navajas and M. Radmacher, Sci. Rep., 2017, 7, 5117.
28. S. G. Kulkarni, S. Pérez-Domínguez and M. Radmacher, J. Mol. Recognit., 2023, 36, e3018.
29. S. Chiodini, S. Ruiz-Rincón, P. D. Garcia, S. Martin, K. Kettelhoit, I. Armenia, D. B. Werz and P. Cea, Small, 2020, 16, 2000269.
30. V. G. Gisbert and R. Garcia, ACS Nano, 2021, 15, 20574–20581.
31. N. Caille, O. Thoumine, Y. Tardy and J. J. Meister, J. Biomech., 2002, 35, 177–187.
32. Y. M. Efremov, S. L. Kotova, A. A. Akovantseva and P. S. Timashev, J. Nanobiotechnol., 2020, 18, 1–11.
33. N. Gavara and R. S. Chadwick, Nat. Nanotechnol., 2021, 7, 733–736.
34. A. J. Engler, S. Sen, H. L. Sweeney and D. E. Discher, Cell, 2006, 126, 677–689.
35. O. Chaudhuri, J. Cooper-White, P. A. Janmey, D. J. Mooney and V. B. Shenoy, Nature, 2020, 584, 535–546.
36. J. G. Sanchez, F. M. Espinosa, R. Miguez and R. Garcia, Nanoscale, 2021, 13, 16339–16348.
37. V. G. Gisbert, F. M. Espinosa, J. G. Sanchez, M. C. Serrano and R. Garcia, Small, 2024, 20, 2304884.
38. N. Guz, M. Dokukin, V. Kalaparthi and I. Sokolov, Biophys. J., 2014, 107, 564–575.
39. C. Roduit, S. Sekatski, G. Dietler, S. Catsicas, F. Lafont and S. Kasas, Biophys. J., 2009, 97, 674–677.
40. C. R. Guerrero, P. D. Garcia and R. Garcia, ACS Nano, 2019, 13, 9629–9637.
41. A. L. D. Moura, J. R. Tejedor, F. M. Espinosa, L. A. Dominguez, J. S. de Sousa and R. Garcia, 2025,  DOI:10.5281/zenodo.15319534.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5nr01236h

‡ These authors contributed equally to this work.

---