DOI:
10.1039/D5PY00300H
(Paper)
Polym. Chem., 2025,
16, 2952-2961
Solvent and temperature effects in the photoiniferter RAFT polymerisation of PEG methacrylate†
Received
25th March 2025
, Accepted 27th May 2025
First published on 28th May 2025
Abstract
Photoiniferter (PI)-RAFT polymerization is a promising approach to synthesise a broad range of (meth)acrylic and styrenic polymers because of its highly ‘living’ nature. The lack of an imbalance between initiating and chain-transfer fragments minimises the inherent bimolecular termination of conventional RAFT. Poly(poly(ethylene glycol) methyl ether methacrylate) (P(PEGMA)) is a potential biocompatible material for biomedical applications, but the highly reactive free radical of PEGMA makes control of its polymerisation challenging. In this study, we investigated the synthesis of P(PEGMA) through PI-RAFT. Current studies on the PI-RAFT mechanisms are limited and the effect of solvents on kinetics has not been reported. We varied several reaction conditions: excitation wavelengths, monomer concentrations, temperatures, and solvents. The propagation constant (kp) values were affected by the RAFT main equilibrium. We calculated the Arrhenius parameters, enthalpy of activation (ΔH‡), and entropy of activation (ΔS‡) for polymerization in various solvents. Regression analysis was conducted to fit the results with extinction coefficients of CTA in seven common solvents, solvent physical properties, and solvatochromic scales. The effective collision factor A had a good fitting with an exponential regression model of the extinction coefficients, indicating a strong relationship between the reaction rate and excitation of the CTA. Solvent polarity scales, such as Kalmet–Abraham–Taft (KAT) and Catalan parameters, failed to predict kp, Arrhenius parameters, ΔH‡, and ΔS‡. A chain transfer constant Ctr > 1 for all syntheses indicated relatively good control over the polymerization through degenerative chain transfer with CTA radicals. In general, Ctr decreased with increasing temperatures, a result of the rate of excitation by photon absorption being constant, but the kp being increased by the temperature. Anisole was the best solvent, able to keep Đ = 1.30 even at 40 °C.
Introduction
Poly(PEGMA) (P(PEGMA)) is a bottle-brush homopolymer that has gained great interest, especially in the field of biomedical application. Unlike hydrophilic polyethylene glycol (PEG), it is always in the brush conformation instead of the random coil conformation, enhancing stealth effects,1–3 which makes P(PEGMA) a potential candidate for fabricating hydrogels, micelles, nanogels, and nanoparticles for in vivo applications.4–6 Further, since the individual PEG chains are small, it may avoid the immunogenic effects of PEG, since a minimal number of repeat units are necessary to be recognised by anti-PEG antibodies. This minimum value has been variously reported as 4–5,7 6-7,8 and 16 (when bound to a protein),9 but it appears the necessity is for an oxyethylene trimer to reach the binding site of the antibody.10 The only alternatives are to disrupt the PEG structure or to adopt an alternative polymer, such as poly(2-ethyl-2-oxazoline).11 In the case of PEGMA, PEGMA-300 (Mn of the PEG side chain ca. 200, or 4–5 EO units) is the shortest side-chain unit that is water soluble without lower critical solution temperature (LCST) effects, as the cloud point of Poly(PEGMA-300) is 55 °C.12 The bottlebrush side-chain is short enough and densely packed enough that reaching the antibody binding site is unlikely.
Much attention has been given to reversable deactivation radical polymerisations,13–15 such as (1) atom transfer radical polymerisation;16–18 (2) nitroxide mediated polymerisation;19–22 and (3) reversable addition-deactivation chain transfer polymerisation.19,23–27 Conventional thermal RAFT typically shows pseudo-1st order kinetics,28 but since it relies on an excess of R-groups over the CTA fragment to create propagating radicals, always shows some loss of livingness.29 To avoid this the radicals may be generated by a photocatalyst,30–35 or by the direct absorption of photons by the CTA to generate an excited state leading to photolysis and the formation of a propagating radical. This process is photoiniferter-RAFT (PI-RAFT, Scheme 1).
 |
| | Scheme 1 General mechanism of PI-RAFT polymerisation. The S–C bond is photolysed to generate a free radical (a, photoactivation). The propagating radical can either chain transfer the active centre (b, RAFT equilibrium) or combine with a photoiniferter radical to terminate reversibly (c, reversible termination). | |
In PI-RAFT, which was first report by Otsu,36,37 the CTA is directly activated by either (ultraviolet light excited) n → π* or (near UV or visible light excited) π → π* transitions, leading to S–C bond homolysis.38,39 As expected of a RAFT process, it retains ‘living’ characteristics40,41 due to persistent radical effect,38,42 but is oxygen-tolerant.43–45 Trithiocarbonate, dithiocarbamate, and xanthate CTAs can be used as the photoiniferter, but14,46 trithiocarbonates are of particular interest as they are excited by blue light and polymerise rapidly. In contrast, whilst dithiocarbonates are amenable to blue-light polymerisation, it is very slow.47 Xanthates can be combined with other CTA's to achieve visible light PI-RAFT.48
The reaction kinetics of PI-RAFT are affected by the activation mechanism, wavelength, and intensity, with n → π* excitation being more efficient.39 With TTC's, green light still provides some activation, although it is less efficient than blue light.49,50 Without temperature control, high light intensity accelerates the rate of polymerisation,41,50 but a loses livingness.51
The application of photoiniferters has been extended to various monomers.52 However, there is no universal photoiniferter, and its selection matters to achieve good control in livingness and dispersity (Đ). Trithiocarbonates are common CTAs/photoiniferters for acrylates, acrylamides, and methacrylates and gives pseudo-first order kinetics for these monomers,14,53–58 but methacrylates give broader dispersities as they form stable free radicals with lower deactivation rate constants.59–64
In order to have a very narrow dispersity value similar to living anionic polymerisation, the number of propagation events per activation needs to be ≪1, and hence Ctr ≫ 1. A better understanding of the kinetics of PI-RAFT seems necessary.
In this work, which is aimed to investigate a better synthetic method for potential biomedical material P(PEGMA), we investigated the effect of excitation wavelength, intensity, temperature, concentration, and solvents on the PI-RAFT of PEGMA, Mn = 300 g mol−1 (Fig. 1).
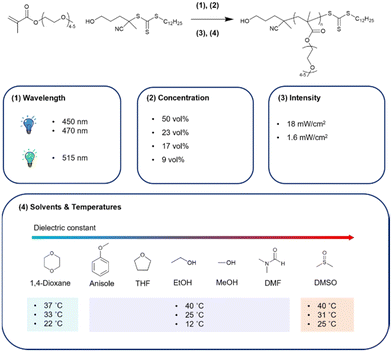 |
| | Fig. 1 P(PEGMA) synthesis scheme through the PI-RAFT approach and overview of this study. The synthesis in 1,4-dioxane and DMSO cannot be conducted at 12 °C because of the high melting point of solvents. | |
Experimental
Determination of extinction coefficient
The absorbance of CTA between 300–500 nm in various solvents (DMSO, 1,4-dioxane, anisole, THF, EtOH, MeOH, and DMF) was measured by UV-Vis in a standard quartz cuvette. The extinction coefficients (ε) were determined through Beer–Lambert's law (eqn (1)).
Synthesis of P(PEGMA) under blue and green light
P(PEGMA) was polymerised under blue (λmax = 470 nm, 1.6 mW cm−2) and/or green light (λmax = 515 nm, 1.6 mW cm−2) irradiation. PEGMA was dissolved in DMSO (concentration of 50 vol%, 1.75 M) with [M]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [I] = 100, where [M]0 is the initial monomer concentration, and [I] is the concentration of photoiniferter. The solution was sparged with N2 for 1 h. The reaction was carried out at 22 °C under blue light for 1.5 h, green light for 4 h, and switching from blue light (0.5 h) to green light (2.5 h). The target conversion was 50%. The reaction mixture was dialyzed with a 3.5 kDa Spectra/Por 3 dialysis membrane against 1 L demineralized water for 2 d, with subsequent lyophilization to isolate the polymers. Kinetic data was collected at various time points and analysed with 1H NMR in CDCl3. The conversion was calculated from the methylene protons on the ethylene glycol chain for the remaining monomer (4.23 ppm) and the corresponding signal of polymers (4.01 ppm, eqn (2), indicated in Fig. S1†).
[I] = 100, where [M]0 is the initial monomer concentration, and [I] is the concentration of photoiniferter. The solution was sparged with N2 for 1 h. The reaction was carried out at 22 °C under blue light for 1.5 h, green light for 4 h, and switching from blue light (0.5 h) to green light (2.5 h). The target conversion was 50%. The reaction mixture was dialyzed with a 3.5 kDa Spectra/Por 3 dialysis membrane against 1 L demineralized water for 2 d, with subsequent lyophilization to isolate the polymers. Kinetic data was collected at various time points and analysed with 1H NMR in CDCl3. The conversion was calculated from the methylene protons on the ethylene glycol chain for the remaining monomer (4.23 ppm) and the corresponding signal of polymers (4.01 ppm, eqn (2), indicated in Fig. S1†).| |  | (2) |
Synthesis of P(PEGMA) at different concentrations
Three PEGMA concentrations in DMSO were used to investigate the effect of concentration on Đ: 23 vol% (0.81 M), 16.7 vol% (0.58 M), and 9 vol% (0.32 M). Reaction mixtures were prepared as above, varying the concentration. Polymerisations were performed at 22 °C under blue light irradiation (λmax = 470 nm, 1.6 mW cm−2). The target conversion was 50%. The reaction mixture was dialyzed with a 3.5 kDa Spectra/Por 3 dialysis membrane against 1 L demineralized water for 2 d, with subsequent lyophilization to isolate the polymers. Kinetic data was collected at various time points and analyzed with 1H NMR in CDCl3.
Synthesis of P(PEGMA) in different solvents and at three different temperatures
Seven solvents (1,4-dioxane, anisole, THF, EtOH, MeOH, DMF, and DMSO) were used to investigate the effect of solvent properties on PEGMA polymerisation. We performed synthesis at three temperatures: (1) 40, 32, and 22 °C in 1,4-dioxane; (2) 40, 25, and 12 °C in anisole, THF, EtOH, MeOH, and DMF; and (3) 40, 31, and 25 °C in DMSO. Because of an unavoidable fluctuation in the environmental temperature due to the lack of temperature control, the ability to control the reaction temperature was limited. The system was warmed by insulation and cooled by compressed air or using a cold room of 4 °C, whilst the temperature of the air surrounding the reactor was measured. PI-RAFT polymerisation of PEGMA in DMSO and 1,4-dioxane was conducted at a higher temperature (ca. 30 °C) due to the relatively high melting point of the solvents. PEGMA monomer was dissolved in solvents (concentration of 50 vol%, 1.75 M) with [M]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [I] = 100. The solution was degassed under N2 for 1 h. The reactions were performed under a blue light source (λmax = 450 nm, 18 mW cm−2). For synthesis in anisole, THF, and 1,4 dioxane, the reaction mixture was precipitated in heptane (20× reaction volume) and further reprecipitated by dissolving in 1 mL DCM, followed by repeated precipitation in heptane (20× reaction volume). The isolated polymers were dried in a vacuum oven at room temperature. For synthesis in DMSO, DMF, EtOH, and MeOH, the reaction mixture (1–2 mL) was dialyzed with a 3.5 kDa Spectra/Por 3 dialysis membrane against 1 L demineralized water for 2 days, and subsequently lyophilised to isolate the polymers. Kinetic data was collected at various time points and analysed with 1H NMR in CDCl3.
[I] = 100. The solution was degassed under N2 for 1 h. The reactions were performed under a blue light source (λmax = 450 nm, 18 mW cm−2). For synthesis in anisole, THF, and 1,4 dioxane, the reaction mixture was precipitated in heptane (20× reaction volume) and further reprecipitated by dissolving in 1 mL DCM, followed by repeated precipitation in heptane (20× reaction volume). The isolated polymers were dried in a vacuum oven at room temperature. For synthesis in DMSO, DMF, EtOH, and MeOH, the reaction mixture (1–2 mL) was dialyzed with a 3.5 kDa Spectra/Por 3 dialysis membrane against 1 L demineralized water for 2 days, and subsequently lyophilised to isolate the polymers. Kinetic data was collected at various time points and analysed with 1H NMR in CDCl3.
Determination of the propagation rate constant (kp)
Photoiniferters can be efficiently initiated upon irradiance at the wavelengths of interest, and the propagating radical concentration is assumed to be the concentration of photoiniferter ([I]), and the equilibrium between the active and inactive states is subsumed in kp. The values of kp were determined by the reaction kinetics and eqn (3) (rearranged into eqn (4)),| |  | (3) |
| | 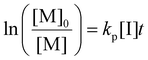 | (4) |
where 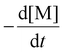 is the rate of change of monomer concentration, [M] is the monomer concentration at an instant during the course of polymerisation, and [M]0 is the initial monomer concentration.
is the rate of change of monomer concentration, [M] is the monomer concentration at an instant during the course of polymerisation, and [M]0 is the initial monomer concentration.
Determination of chain transfer coefficient (Ctr)
The Ctr value is defined as a ratio of the rate constant of deactivation by chain transfer toward a CTA (kdeact) to the propagation rate constant (kp) (eqn (5)). Under the steady state assumption, Ctr can be estimated from the Muller's model (eqn (6)),65–67| |  | (5) |
| |  | (6) |
where DPn is the number average degree of polymerization, and c is the monomer conversion.
Determination of Arrhenius parameters
The kp values were used to estimate the activation energy (Ea) and the effective collision frequency (A) in various solvents using the Arrhenius equation (eqn (7) and its rearranged form eqn (8)). The kp values at three temperatures were assumed to represent the expected linear correlation in eqn (8),| | 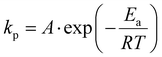 | (7) |
| |  | (8) |
where R is the gas constant, and T is the temperature (in K).
Determination of the enthalpy of activation (ΔH‡) and entropy of activation (ΔS‡)
The ΔH‡ and ΔS‡ values were calculated from the Eyring–Polanyi equation (eqn (9) and its rearranged form eqn (10)),| |  | (9) |
| |  | (10) |
where κ is the transmission coefficient, kB is the Boltzmann constant, and h is Planck's constant. κ was unity based on the assumption of irreversible propagation.68
Simple linear regression with solvent properties
The values of kp, Arrhenius parameters, ΔH‡, and ΔS‡ were correlated with the extinction coefficient (ε) of the photoiniferter in various solvents, solvent physical properties (Table S1†), Hildebrand solubility parameters (δH), and Dimroth ET(30) solvatochromic scale (Table S2†). Simple linear regression was carried out in Excel 2021.
Multivariate linear regression of kp, Arrhenius parameters, ΔH‡, and ΔS‡ with Kalmet–Abraham–Taft (KAT) and Catalan solvatochromic scales
The values of kp, Arrhenius parameters, ΔH‡, and ΔS‡ were correlated with KAT scales (eqn (11)) and Catalan scales (eqn (12)). The parameters used in this study are outlined in Table S2.† Multivariate linear regression was carried out in Matlab 2020a.| | | x = x0 + s·π* + a·α + b·β | (11) |
| | | x = x0 + p·SP + d·SdP + a·SA + b·SB | (12) |
Results and discussion
Verification of constant initiation
Before analysing rate constants etc., it must be verified that the proportion of CTA initiating chains is constant and ideally 100%. Plotting conversion against Mn measured by SEC (against PEG standards) shows extremely good correlation, and thus in all cases the initiation efficiency is the same (Fig. S2a†). It is extremely unlikely that such a correlation would result in any circumstances except ≈100% initiation efficiency. However, there was some induction, which was typically 5–10 min, but up to 20 min in one instance. This, we assume, was due to the last traces of oxygen being consumed by the radicals, but given the consistency of the molecular weight, we assume the loss of CTA in the induction phase is ≪1%. Plotting observed Mnvs. PEG standards against theoretical Mn (Fig. S2b†) gives a strong relationship with a gradient of 0.7156. Since P(PEGMA) is a brush copolymer which is expected to be less expanded in DMF than PEG, this is also consistent with full initiation. Hence it is assumed that initiation efficiency is ≈100%.
Effect of wavelength on PI-RAFT of PEGMA
Since, in general, slower polymerisations are more controllable, we aimed to decrease the rate of polymerisation by changing the wavelength of incident light from blue to green light (λmax = 515 nm, 1.6 mW cm−2), which has a lower absorbance for the CTA (Fig. 2). At an ambient temperature of 22 °C, the rate of polymerisation was half that as under blue irradiation (λmax = 470 nm, 1.6 mW cm−2) (Fig. 3). An increase in the induction period was observed, from negligible (ca. 5 min, which may be the temperature equilibrating) under blue light to ca. 21 min under green light.
 |
| | Fig. 2 Absorbance of CTA in DMSO, 5 mg mL−1. π → π* and n → π* transition as annotated in the spectrum. Shaded areas indicate the overlap of the excitation mechanism with wavelengths of light used in this study. | |
 |
| | Fig. 3 Polymerisation kinetics initiated under λmax = 470 and 515 nm, 1.6 mW cm−2 in DMSO at a monomer concentration of 50 vol%, [M]0/[I] = 100, 22 °C. | |
We further switched light sources during the course of polymerisation, with blue light irradiance for 0.5 h and green light irradiance for 2.5 h to reach a targeted conversion of 50%. Nevertheless, Đ turned out to be similar (Table 1 and Fig. S4†).
Table 1 Synthesis of P(PEGMA) excited by different wavelengths (1.6 mW cm−2, 22 °C, 50 vol%)
| No. |
λ
max [nm] |
Conv. [%] |
M
n, theo [kDa] |
M
w, SEC [kDa] |
M
n, SEC [kDa] |
Đ
|
C
tr
|
| 1 |
470 |
49.2 |
14.8 |
26.6 |
20.7 |
1.28 |
11.60 |
| 2 |
515 |
57.9 |
17.4 |
32.6 |
24.3 |
1.34 |
7.47 |
| 3 |
470 → 515 |
40.0 |
11.7 |
21.8 |
16.3 |
1.34 |
12.05 |
In this study, we estimated kp assuming fully initiated CTA through photolysis, and there were no observable signs of termination. A lower kp value under green light can be explained by the involved equilibria (Scheme 1). Since photons carrying a lower energy are less efficient in exciting n → π* transition of the intermediates, the activation is slowed down.
Effect of concentration on PI-RAFT of PEGMA
The most direct method to manipulate polymerisation kinetics is to vary the monomer concentration. We synthesised P(PEGMA) at three additional concentrations, ranging from 23 to 9 vol% (1.05–0.35 M) under blue light irradiance (λmax = 470 nm, 1.6 mW cm−2) (Table 2). The RAFT process consists of four major processes of interest: (1) activation, (2) propagation, (3) deactivation, and (4) termination. Since propagation is proportional to the monomer concentration, the propagation (2) rate will be significantly slowed upon dilution. Termination (4) would typically be observed by tails and shoulders in the distribution (SEC), and a curvature in the kinetic plots. We have not observed these in the SEC (Fig. S5†), and only one datapoint in the kinetics suggested termination (likely a slow thiol degradation)69 and required exclusion, whilst all other points are linear and show good control (Fig. 4a). Whilst the rate decreases with lowered concentration, the kp actually increases, and does so in a relationship close to e (Fig. 4b). This can be explained be the absorption of photons; as the concentration decreases, the decrease in light intensity through the beam path of the reactor is less, and so the average number of photons colliding with each CTA is higher.
 |
| | Fig. 4 (a) Polymerisation kinetics at different monomer concentrations (50, 23, 17, and 9 vol%) in DMSO. Reaction kinetics at 50% v/v is polymer 1 reported in Fig. 3 and Table 1. Initiated under λmax = 470 nm, 1.6 mW cm−2 in DMSO, [M]0/[I] = 100, 22 °C. The 18 h datapoint at 9% v/v is off trend and is excluded as an outlier, probably caused by the loss of active chain-ends. (b) Monomer concentration plotted against kp. | |
Table 2 Synthesis of P(PEGMA) at different concentrations (λmax = 470 nm, 1.6 mW cm−2, 22 °C)
| No. |
[M]0 [%v/v] |
k
p [L (mol s)−1] |
Conv. [%] |
M
n, theo [kDa] |
M
n/Mw, SEC [kDa] |
Đ
|
C
tr
|
| 4 |
23 |
9.20 × 10−3 |
89.6 |
26.9 |
37.6/47.7 |
1.27 |
4.66 |
| 5 |
17 |
1.26 × 10−2 |
89.5 |
26.8 |
37.4/47.2 |
1.26 |
4.96 |
| 6 |
9 |
1.48 × 10−2 |
90.1 |
27.3 |
38.1/48.6 |
1.28 |
4.40 |
Activation/deactivation relates to the concentration of propagating radicals, which has significant effect on the kinetics, and affects termination. It will have very little effect on the dispersity since, for a given [M]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [I], the probability of a collision between a propagating end and either a monomer or the CTA fragment will be relatively the same. In fact, the molecular weight distribution is largely dependent on the ratio of propagation to deactivation events. As a consequence of each activation, the active radical will propagate a number of times before being deactivated by the CTA fragment. This will be a Poisson distribution with Rp/Rdeact being the Poisson parameter λ of the individual distribution. However, during the polymerisation process the activation-propagation-deactivation cycle occurs many times. Ergo, the Poisson distribution becomes compounded, and thus becomes a Gamma distribution.
[I], the probability of a collision between a propagating end and either a monomer or the CTA fragment will be relatively the same. In fact, the molecular weight distribution is largely dependent on the ratio of propagation to deactivation events. As a consequence of each activation, the active radical will propagate a number of times before being deactivated by the CTA fragment. This will be a Poisson distribution with Rp/Rdeact being the Poisson parameter λ of the individual distribution. However, during the polymerisation process the activation-propagation-deactivation cycle occurs many times. Ergo, the Poisson distribution becomes compounded, and thus becomes a Gamma distribution.
Effect of solvent on PI-RAFT of PEGMA
To further understand how RAFT equilibria affect kp, we need to vary the Poisson parameter λ (Rp/Rdeact) by changing the activation energy Ea (eqn (7) and (8)). One way of doing this is to alter the solvent. The n → π* transition of CTA in various solvents (Fig. S6†) had a similar full width at half maximum and peaked at 447–448 nm, where the extinction coefficients were determined (Fig. S7†). We synthesised P(PEGMA) at three temperatures (Fig. 5), and by inspection, kp seems to be rather sensitive to the temperature. At 40 °C, the dispersity is wider for synthesis in most solvents because of the rapid propagation (Table 3, Fig. S8 and S9†). We used a blue light source higher in intensity (λmax = 450 nm, 18 mW cm−2), and polymer 27 in DMSO had a faster rate of propagation compared to polymer 1. This has been reported in many studies,38,50,70 and it is intuitive that more absorbed photons generate more of the active species. Nevertheless, the comparison in this study is indirect due to different reaction temperatures.
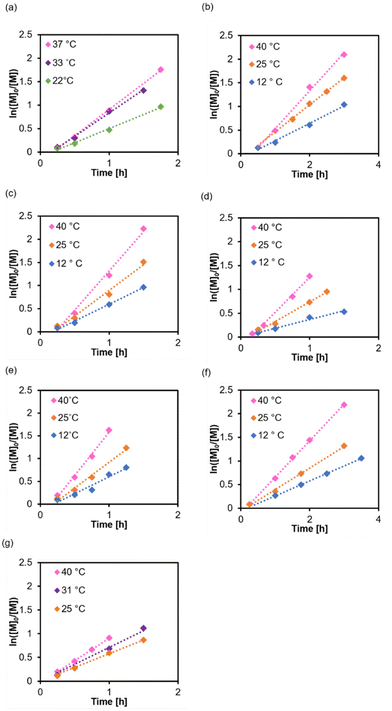 |
| | Fig. 5 Polymerisation kinetics at different temperatures and in various solvents: (a) 1,4-dioxane, (b) anisole, (c) THF, (d) EtOH, (e) MeOH, (f) DMF, and (g) DMSO. Initiated under λmax = 450 nm, 18 mW cm−2, [M]0/[I] = 100, [M]0 = 50 vol%. | |
Table 3 Synthesis of P(PEGMA) in various solvents and temperatures (λmax = 450 nm, 18 mW cm−2, 50 vol%). Only final materials are shown
| No. |
Temp. [°C] |
Reaction time [min] |
Conv. [%] |
k
p [L (mol s)−1] |
M
n, theo [kDa] |
M
w, SEC [kDa] |
M
n, SEC [kDa] |
Đ
|
C
tr
|
|
The kinetics and SEC for no. 25 are from two equivalent experiments carried out under identical conditions.
|
|
1,4-Dioxane
|
| 7 |
37 |
105 |
82.8 |
1.8 × 10−2 |
24.8 |
50.9 |
34.6 |
1.47 |
3.05 |
| 8 |
33 |
90 |
73.2 |
1.6 × 10−2 |
22 |
44.7 |
30.7 |
1.45 |
3.95 |
| 9 |
22 |
105 |
61.9 |
9.5 × 10−3 |
18.6 |
33.1 |
26 |
1.27 |
8.61 |
|
Anisole
|
| 10 |
40 |
180 |
87.8 |
1.3 × 10−2 |
26.3 |
49.2 |
36.8 |
1.34 |
3.84 |
| 11 |
25 |
180 |
73.1 |
9.1 × 10−3 |
23.9 |
43.2 |
33.3 |
1.3 |
5.15 |
| 12 |
12 |
180 |
64.5 |
5.9 × 10−3 |
19.4 |
35 |
27.1 |
1.29 |
7.45 |
|
THF
|
| 13 |
40 |
90 |
89.2 |
2.7 × 10−2 |
26.8 |
57.7 |
37.4 |
1.54 |
2.34 |
| 14 |
25 |
90 |
77.8 |
1.8 × 10−2 |
23.4 |
48.5 |
32.7 |
1.49 |
3.25 |
| 15 |
12 |
90 |
61.9 |
1.2 × 10−2 |
18.6 |
35.9 |
26 |
1.38 |
6.04 |
|
EtOH
|
| 16 |
40 |
60 |
72.1 |
2.3 × 10−2 |
21.6 |
43.0 |
30.2 |
1.42 |
4.34 |
| 17 |
25 |
75 |
61.4 |
1.3 × 10−2 |
18.4 |
35.0 |
25.7 |
1.36 |
6.54 |
| 18 |
12 |
90 |
47.2 |
5.8 × 10−3 |
14.2 |
26.8 |
19.8 |
1.35 |
9.72 |
|
MeOH
|
| 19 |
40 |
60 |
80.3 |
3.2 × 10−2 |
24.1 |
50.7 |
33.7 |
1.51 |
2.99 |
| 20 |
25 |
75 |
71 |
1.8 × 10−2 |
21.3 |
43.9 |
29.8 |
1.48 |
3.87 |
| 21 |
12 |
75 |
55.4 |
1.2 × 10−2 |
16.6 |
33.1 |
23.2 |
1.43 |
6.32 |
|
DMF
|
| 22 |
40 |
180 |
88.8 |
1.2 × 10−2 |
26.6 |
51.8 |
37.2 |
1.4 |
3.18 |
| 23 |
25 |
180 |
73.2 |
7.2 × 10−3 |
22 |
40.4 |
30.7 |
1.32 |
5.61 |
| 24 |
12 |
210 |
65.2 |
5.0 × 10−3 |
19.6 |
34.8 |
27.4 |
1.27 |
8.02 |
|
DMSO
|
| 25a |
40 |
60 |
63.6 |
1.51 × 10−2 |
19.1 |
37.7 |
26.7 |
1.41 |
5.37 |
| 26 |
31 |
90 |
67.3 |
1.27 × 10−2 |
20.4 |
36.3 |
27.6 |
1.31 |
6.48 |
| 27 |
25 |
90 |
58 |
9.8 × 10−3 |
17.4 |
31.3 |
24.3 |
1.29 |
8.82 |
From Arrhenius relationship eqn (7) and (8), Ea and A were calculated. The ΔH‡ and ΔS‡ values were calculated from Eyring–Polanyi equation (eqn (9) and (10)). The results are summarized in Fig. 6, 7, and Table 4. The values of Ea estimated from kp were similar in all solvents but still surprisingly low. Notably, the effective collision frequency A for EtOH and 1,4-dioxane was orders higher in magnitude compared to the other solvents. The highly negative values of ΔS‡ suggest an associative pathway involved in the formation of the activation complex.
 |
| | Fig. 6 Arrhenius plot for PI-RAFT synthesis of PPEGMA in various solvents. Initiated under λmax = 450 nm, 18 mW cm−2, [M]0/[I] = 100, 50 vol%. | |
 |
| | Fig. 7 Eyring–Polanyi plot for PI-RAFT synthesis of PPEGMA in various solvents. Initiated under λmax = 450 nm, 18 mW cm−2, [M]0/[I] = 100, 50 vol%. | |
Table 4 Arrhenius parameters, enthalpy of activation (ΔH‡), and entropy of activation (ΔS‡) for PI-RAFT synthesis of PPEGMA in various solvents (λmax = 450 nm, 18 mW cm−2, 50 vol%)
| Solvent |
E
a [kJ mol−1] |
A [L (mol s)−1] |
ΔH‡ [kJ mol−1] |
ΔS‡ [J (mol K)−1] |
| 1,4-Dioxane |
31.95 |
4.33 × 103 |
29.49 |
−183.54 |
| Anisole |
20.64 |
36.05 |
18.16 |
−223.44 |
| THF |
22.53 |
154.56 |
20.04 |
−211.36 |
| EtOH |
36.56 |
3.03 × 104 |
34.07 |
−167.46 |
| MeOH |
24.73 |
397.86 |
22.25 |
−203.47 |
| DMF |
23.64 |
104.99 |
21.16 |
−214.55 |
| DMSO |
21.98 |
71.72 |
19.44 |
−217.9 |
To deeper understand the reaction mechanism, we did simple linear regression to fit the data with physical properties, e.g., extinction coefficient ε, viscosity η, dipolarity, and dielectric constant (Table S3†). Very little correlation was observed. Dimroth ET(30) polarity scale in combination with the KAT equation is a useful approach to linear solvation energy relationship (LSER) analysis. Czerwinski was the first to apply LSER analysis to investigate the solvent effect on the free radical, where ln(kp) was a function of ET(30).71 LSER predictions were very successful for free radical polymerisation in highly polar solvents,72,73 but ET(30) scale is limited to describing dipolarity and hydrogen bond acidity of solvents. Hildebrand solubility parameter δH derived from cohesive energy of cavity formation also failed to fit to our results. The δH parameter was later introduced into the corrected KAT equations, but it overlaps with the dipolarity/polarizability term π* in eqn (12),74 which we will discuss later.
A weak correlation with extinction coefficient ε was found for kp and Ea, but a moderate correlation to ΔH‡ and ΔS‡. The pre-exponential factor A was fitted exponentially to the ε values with an adjusted R2 of 0.91 (Fig. 8). A small decrease in the photons absorbed led to an exponential increase in the effective collisions of forming an activation complex. Fewer photons are absorbed to efficiently excite the n → π* transition. Therefore, more photons are available to photolyse intermediates into propagating free radicals. The increased number of collision events result from an increased concentration of active radicals.
 |
| | Fig. 8 Pre-exponential factor A fitted to an exponential regression model correlated to the extinction coefficients ε (r2 = 0.93 to 2 d.p.). | |
The kp values had a moderate correlation with the refractive index nD. When incident light passes through the interfaces, the solvent with a larger refractive index will cause a stronger scattering event and, therefore, a lower kp.
We observed increased kp values with a decrease in boiling point (Fig. 9 and 10). The molecules in low-boiling point solvents are more kinetically energized, and radicals can easily escape from the solvent cage. The less successful prediction for kp and Ea is likely due to its complication with the equilibria, as we discussed earlier in the text. Hoogenboom et al. reported an unexpectedly high reactivity of PEGMA monomer (Mn = 1100 g mol−1) that also indicated a hybrid kp, with an apparent chain transfer constant Ctr < 1.75
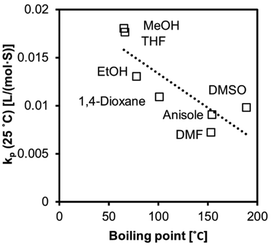 |
| | Fig. 9 The values of kp at 25 °C (r2 = 0.71) fitted to a linear regression model correlated to boiling points. | |
 |
| | Fig. 10 The values of kp at 40 °C (r2 = 0.77) fitted to a linear regression model correlated to boiling points. | |
The KAT (eqn (11)) and Catalan (eqn (12)) solvatochromic scales are useful tools to study the effect of solvent on reaction kinetics. The KAT equation was constructed with acidity (α), basicity (β), and a conflated term of dipolarity/polarizability (π*). The term x is observed properties, e.g., activation energy, and the natural logarithm of equilibrium constant. Multivariate linear regression using the KAT equation was statistically insignificant (Table S4 and Fig. S10†). Since the KAT scale is limited to specific interactions, namely acid–base interactions involving hydrogen bonding, Catalán proposed another solvatochromic scale that stresses nonspecific interactions. In the Catalan scale, except for acidity (SA) and basicity (SB), contributions from nonspecific interactions were isolated into dipolarity (SdP) and polarizability (SP) terms. Monnery et al. first applied the Catalan scale to predict the physiochemical properties of cationic ring opening polymerisation of 2-ethyl-2-oxazoline.76 Luo et al. extended the Catalan scale to the living anionic polymerisation of styrene.77 However, regression results turned out to be less significant (Table S5 and Fig. S11†).
The chain transfer constant Ctr (eqn (5)) was estimated from Đ using eqn (6). Ctr > 1 was observed for all the polymers 1–27, implying that deactivation is preferred compared to propagation, and thus PI-RAFT gains more control in P(PEGMA) synthesis compared to the conventional thermal RAFT, in which Ctr < 1.75 The Ctr values showed a negative correlation with Mn, SEC (Fig. 11). This can be attributed to diffusion-controlled deactivation.78 Benicewicz et al. determined decreasing diffusion coefficient of PMMA at higher molecular weights through diffusion-ordered spectroscopy (DOSY) 1H NMR.79 The Ctr values are generally lower at higher temperatures due to increasing kp but are not significantly affected by solvents that influence the intrinsic kp (Fig. S12†). The observed variation of kp in different solvents is thus a result of changing activation rates.
 |
| | Fig. 11
C
tr
vs. M
n, SEC for P(PEGMA) 1–27. | |
Mechanism
In summary, this study indicates that the mechanism of PI-RAFT is not only dependent on the quantum yield of the excitation, which can be expected, but also on the kinetics of the separation of the radical pair generated by homolytic cleavage (Fig. 12). The radical pair initially generated will, unless the radicals become individually solvated, simply collapse back into the dormant pair. However, if they become solvent separated, then they may collide with monomers until they finally collide with another CTA fragment. The ease of this remodelling is reflected in the boiling point of the solvent and, if the remodelling allows for the easy escape, then the propagation rate will increase, the deactivation rate decreases and control of the polymerisation would be lost.
 |
| | Fig. 12 Cartoon showing suggested mechanism of activation and reactivation. The remodelling of the solvent shell to generate solvent separated radicals is necessary for propagation. However, moving too far to the right in this model creates a loss of fidelity. | |
Conclusion
For the synthesis of P(PEGMA) by PI-RAFT, we conducted a detailed study on various factors affecting the kinetics: wavelength, concentration, temperature, and solvents. For all the attempts, chain transfer constant Ctr > 1, indicating that a good control through degenerative chain transfer was maintained. The kp values were affected by equilibria in each case, which explains the variation in the rate of polymerisation and molecular weight distribution. The CTA had a low absorbance in the green light, and the prolonged induction period and rate retardation indicated a lower quantum yield of excitation. We slowed down the rate of polymerisation by diluting the system. The molecular weight distribution that is closely linked to the kinetic chain length and was broadened by compounding of individual distributions. We further estimated the Arrhenius parameters, ΔH‡, and ΔS‡ in seven common solvents reported for P(PEGMA) synthesis. The Ea values were surprisingly low and accounted for the kp values being sensitive to ambient temperature. Most importantly, the decreasing extinction coefficient of the CTA, that is solvent-dependent, exponentially increases the effective collision factor A. This might be attributed to more frequent activation. We further attempted to fit these values into KAT and Catalan equations. However, no relationship was revealed by the regression analysis, meaning these factors were not dominant. However, there was a good relationship with the boiling point, indicating the dominant feature was the remodelling of the solvation shell. This has not been considered before, and warrants further investigation.
Author contributions
This paper was conceptualised by ISZ and BDM, with BDM developing the methodology. Investigation, formal analysis and primary writing were by RC, with BDM and ISZ supervising, reviewing and editing. Funding acquisition, data curation and administration were by ISZ.
Data availability
Data for this article, including raw 1H NMR and SEC data are available at Zenodo, https://doi.org/10.5281/zenodo.15079075.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work is supported by NWO VICI (18683) awarded to Inge S. Zuhorn. We thank J. Paulusse and B. van der Veen (UTwente) for SEC measurement, and Dr A.H. Hofman for critically reading the manuscript.
References
- M. Li, S. Jiang, J. Simon, D. Paßlick, M.-L. Frey, M. Wagner, V. Mailänder, D. Crespy and K. Landfester, Nano Lett., 2021, 21, 1591–1598 CrossRef CAS PubMed.
- D. Y. Joh, Z. Zimmers, M. Avlani, J. T. Heggestad, H. B. Aydin, N. Ganson, S. Kumar, C. M. Fontes, R. K. Achar, M. S. Hershfield, A. M. Hucknall and A. Chilkoti, Adv. Healthc. Mater., 2019, 8, 1801177 CrossRef PubMed.
- Y. Z. Qi, A. Simakova, N. J. Ganson, X. H. Li, K. M. Luginbuhl, I. Ozer, W. G. Liu, M. S. Hershfield, K. Matyjaszewski and A. Chilkoti, Nat. Biomed. Eng., 2017, 1, 0002 CrossRef CAS PubMed.
- H. Phan, V. Taresco, J. Penelle and B. Couturaud, Biomater. Sci., 2021, 9, 38–50 RSC.
- Y. F. Tian, S. S. Bian and W. L. Yang, Polym. Chem., 2016, 7, 1913–1921 RSC.
- P. Sarkar, S. Ghosh, R. Saha and K. Sarkar, RSC Adv., 2021, 11, 16913–16923 RSC.
-
J. K. Armstrong, in PEGylated Protein Drugs: Basic Science and Clinical Applications, ed. F. M. Veronese, Birkhäuser Basel, Basel, 2009, pp. 147–168, DOI:10.1007/978-3-7643-8679-5_9.
- A. W. Richter and E. Åkerblom, Int. Arch. Allergy Appl. Immunol., 1983, 70, 124–131 CrossRef CAS PubMed.
- T.-L. Cheng, C.-M. Cheng, B.-M. Chen, D.-A. Tsao, K.-H. Chuang, S.-W. Hsiao, Y.-H. Lin and S. R. Roffler, Bioconjugate Chem., 2005, 16, 1225–1231 CrossRef CAS PubMed.
- M. G. P. Saifer, L. D. Williams, M. A. Sobczyk, S. J. Michaels and M. R. Sherman, Mol. Immunol., 2014, 57, 236–246 CrossRef CAS PubMed.
- B. D. Monnery, V. V. Jerca, R. Hoogenboom and T. Swift, Polym. Chem., 2024, 15, 3077–3085 RSC.
- E. Martwong and Y. Tran, Langmuir, 2021, 37, 8585–8593 CrossRef CAS PubMed.
- N. Corrigan, K. Jung, G. Moad, C. J. Hawker, K. Matyjaszewski and C. Boyer, Prog. Polym. Sci., 2020, 111, 101311 CrossRef CAS.
- R. N. Carmean, T. E. Becker, M. B. Sims and B. S. Sumerlin, Chem, 2017, 2, 93–101 CAS.
- M. A. Beres, C. Boyer, M. Hartlieb, D. Konkolewicz, G. G. Qiao, B. S. Sumerlin and S. Perrier, ACS Polym. Au, 2025 DOI:10.1021/acspolymersau.4c00101.
- C. H. Peng, J. Kong, F. Seeliger and K. Matyjaszewski, Macromolecules, 2011, 44, 7546–7557 CrossRef CAS.
- N. V. Tsarevsky, T. Pintauer and K. Matyjaszewski, Macromolecules, 2004, 37, 9768–9778 CrossRef CAS.
- Y. Wang, Y. Z. Zhang, B. Parker and K. Matyjaszewski, Macromolecules, 2011, 44, 4022–4025 CrossRef CAS.
- P. Gurnani and S. Perrier, Prog. Polym. Sci., 2020, 102, 101209 CrossRef CAS.
- H. R. Lamontagne and B. H. Lessard, ACS Appl. Polym. Mater., 2020, 2, 5327–5344 CrossRef CAS.
- V. Sciannamea, R. Jérôme and C. Detrembleur, Chem.
Rev., 2008, 108, 1104–1126 CrossRef CAS PubMed.
- A. C. Schmidt, H. Turgut, D. Le, A. Beloqui and G. Delaittre, Polym. Chem., 2020, 11, 593–604 RSC.
- B. D. Fairbanks, P. A. Gunatillake and L. Meagher, Adv. Drug Delivery Rev., 2015, 91, 141–152 CrossRef CAS PubMed.
- X. M. Huang, J. M. Hu, Y. H. Li, F. Y. Xin, R. R. Qiao and T. P. Davis, Biomacromolecules, 2019, 20, 4243–4257 CrossRef CAS PubMed.
- W. T. Peng, Y. Y. Cai, L. Fanslau and P. Vana, Polym. Chem., 2021, 12, 6198–6229 RSC.
- A. Favier and M. T. Charreyre, Macromol. Rapid Commun., 2006, 27, 653–692 CrossRef CAS.
- D. J. Keddie, G. Moad, E. Rizzardo and S. H. Thang, Macromolecules, 2012, 45, 5321–5342 CrossRef CAS.
- A. Goto and T. Fukuda, Prog. Polym. Sci., 2004, 29, 329–385 CrossRef CAS.
- S. Perrier, Macromolecules, 2017, 50, 7433–7447 CrossRef CAS.
- M. L. Allegrezza and D. Konkolewicz, ACS Macro Lett., 2021, 10, 433–446 CrossRef CAS PubMed.
- B. Parnitzke, T. Nwoko, K. G. E. Bradford, N. D. Watuthanthrige, K. Yehl, C. Boyer and D. Konkolewicz, Chem. Eng. J., 2023, 456, 141007 CrossRef CAS.
- B. Hunter, K. Bell and C. W. Pester, ACS Appl. Polym. Mater., 2024, 6(23), 14057–14063 CrossRef CAS.
- A. Bagheri, C. W. A. Bainbridge, K. E. Engel, G. G. Qiao, J. T. Xu, C. Boyer and J. Y. Jin, ACS Appl. Polym. Mater., 2020, 2, 782–790 CrossRef CAS.
- E. P. F. Parra, B. Chouchene, J. L. Six, R. Schneider and K. Ferji, ACS Appl. Polym. Mater., 2021, 3, 3649–3658 CrossRef.
- T. Nwoko, B. Zhang, T. Vargo, T. Junkers and D. Konkolewicz, Macromolecules, 2024, 58(1), 488–494 CrossRef PubMed.
- T. Otsu and M. Yoshida, Polym. Bull., 1982, 7, 197–203 CAS.
- T. Otsu, M. Yoshida and A. Kuriyama, Polym. Bull., 1982, 7, 45–50 CAS.
- M. Hartlieb, Macromol. Rapid Commun., 2022, 43, e2100514 CrossRef PubMed.
- R. W. Hughes, M. E. Lott, J. I. Bowman and B. S. Sumerlin, ACS Macro Lett., 2022, 14–19, DOI:10.1021/acsmacrolett.2c00683.
- A.-C. Lehnen, J. A. M. Kurki and M. Hartlieb, Polym. Chem., 2022, 13, 1537–1546 RSC.
- A. C. Lehnen, J. Gurke, A. M. Bapolisi, M. Reifarth, M. Bekir and M. Hartlieb, Chem. Sci., 2023, 14, 593–603 RSC.
- H. Fischer, Chem. Rev., 2001, 101, 3581–3610 CrossRef CAS PubMed.
- Y. Huang, Y. Sun, Y. Y. Weng and W. D. Zhang, ChemistrySelect, 2022, 7(28), e202201583 CrossRef CAS.
- M. Rubens, P. Latsrisaeng and T. Junkers, Polym. Chem., 2017, 8, 6496–6505 RSC.
- C. Y. Li and S. S. Yu, Macromolecules, 2021, 54, 9825–9836 CrossRef CAS.
- G. Ramakers, M. Rubens, A. Krivcov, H. Möbius, V. Trouillet, A. Welle and T. Junkers, J. Polym. Sci., Part A: Polym. Chem., 2019, 57, 2002–2007 CrossRef CAS.
- M. L. Allegrezza, N. De Alwis Watuthanthrige, Y. Wang, G. A. Garcia, H. Ren and D. Konkolewicz, Polym. Chem., 2020, 11, 6129–6133 RSC.
- A.-C. Lehnen, J. Gurke, A. M. Bapolisi, M. Reifarth, M. Bekir and M. Hartlieb, Chem. Sci., 2023, 14, 593–603 RSC.
- J. Yeow, O. R. Sugita and C. Boyer, ACS Macro Lett., 2016, 5, 558–564 CrossRef CAS PubMed.
- M. A. Beres, J. Y. Rho, A. Kerr, T. Smith and S. Perrier, Polym. Chem., 2024, 15, 522–533 RSC.
- R. W. Lewis, R. A. Evans, N. Malic, K. Saito and N. R. Cameron, Polym. Chem., 2018, 9, 60–68 RSC.
- S. Perrier, Macromolecules, 2017, 50, 7433–7447 CrossRef CAS.
- K. J. Arrington and J. B. Matson, Polym. Chem., 2017, 8, 7452–7456 RSC.
- A. C. Lehnen, J. A. M. Kurki and M. Hartlieb, Polym. Chem., 2022, 13, 1537–1546 RSC.
- R. A. Olson, M. E. Lott, J. B. Garrison, C. L. G. Davidson, L. Trachsel, D. I. Pedro, W. G. Sawyer and B. S. Sumerlin, Macromolecules, 2022, 55, 8451–8460 CrossRef CAS.
- L. Hub, J. Koll, M. Held, M. Radjabian and V. Abetz, Macromolecules, 2024, 57(5), 2273–2286 CrossRef CAS.
- C. Hwang, S. Shin, D. Ahn, H. J. Paik, W. Lee and Y. Yu, Acs ACS Appl. Mater. Interfaces, 2023, 15, 58905–58916 CrossRef CAS PubMed.
- A. R. S. Santha Kumar, S. Allison-Logan, J. R. Finnegan, N. K. Singha, M. Ashokkumar and G. Qiao, ACS Macro Lett., 2023, 12, 1012–1018 CrossRef CAS PubMed.
- S. Shanmugam, J. Cuthbert, T. Kowalewski, C. Boyer and K. Matyjaszewski, Macromolecules, 2018, 51, 7776–7784 CrossRef CAS.
- S. Yang, L. Zhang, Y. Chen and J. Tan, Macromolecules, 2022, 55, 8472–8484 CrossRef CAS.
- A. Sivokhin, D. Orekhov, O. Kazantsev, O. Sivokhina, S. Orekhov, D. Kamorin, K. Otopkova, M. Smirnov and R. Karpov, Polymers, 2022, 14, 14010137 Search PubMed.
- Y. Du, S. Jia, Y. Chen, L. Zhang and J. B. Tan, ACS Macro Lett., 2021, 10, 297–306 CrossRef CAS PubMed.
- Q. Fu, T. G. McKenzie, S. Tan, E. Nam and G. G. Qiao, Polym. Chem., 2015, 6, 5362–5368 RSC.
- C. P. Easterling, Y. N. Xia, J. P. Zhao, G. E. Fanucci and B. S. Sumerlin, ACS Macro Lett., 2019, 8, 1461–1466 CrossRef CAS PubMed.
- A. H. E. Muller, D. Y. Yan, G. Litvinenko, R. G. Zhuang and H. Dong, Macromolecules, 1995, 28, 7335–7338 CrossRef.
- A. H. E. Muller, G. Litvinenko and D. Y. Yan, Macromolecules, 1996, 29, 2339–2345 CrossRef.
- S. Harrisson, Polym. Chem., 2018, 9, 1366–1370 RSC.
- H. Eyring, Rev. Mod. Phys., 1962, 34, 616–619 CrossRef.
- T. G. McKenzie, L. P. D. M. Costa, Q. Fu, D. E. Dunstan and G. G. Qiao, Polym. Chem., 2016, 7, 4246–4253 RSC.
- B. Cabannes-Boué, Q. Yang, J. Lalevée, F. Morlet-Savary and J. Poly, Polym. Chem., 2017, 8, 1760–1770 RSC.
- W. K. Czerwinski, Macromolecules, 1995, 28, 5405–5410 CrossRef CAS.
- C. Adam, L. García-Río, A. Godoy and J. R. Leis, Green Chem., 2006, 8, 596–598 RSC.
- A. Jelicic, N. García, H. G. Löhmannsröben and S. Beuermann, Macromolecules, 2009, 42, 8801–8808 CrossRef CAS.
- M. J. Kamlet, J. L. M. Abboud, M. H. Abraham and R. W. Taft, J. Org. Chem., 1983, 48, 2877–2887 CrossRef CAS.
- C. Pietsch, M. W. M. Fijten, H. M. L. Lambermont-Thijs, R. Hoogenboom and U. S. Schubert, J. Polym. Sci., Part A: Polym. Chem., 2009, 47, 2811–2820 CrossRef CAS.
- M. Vergaelen, B. D. Monnery, V. V. Jerca and R. Hoogenboom, Macromolecules, 2023, 56, 1534–1546 CrossRef CAS.
- S. Li, Z. X. Liu, Y. N. Zhou and Z. H. Luo, Macromol. React. Eng., 2024, 18(6), 2400021 CrossRef CAS.
- B. S. Casey, M. F. Mills, D. F. Sangster, R. G. Gilbert and D. H. Napper, Macromolecules, 1992, 25, 7063–7065 CrossRef CAS.
- E. Ruzicka, P. Pellechia and B. C. Benicewicz, Anal. Chem., 2023, 95, 7849–7854 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: 12 Figures and 5 tables. Fig. S1 (1H NMR spectra of PEGMA monomer and P(PEGMA) in DMSO solution, measured in CDCl3); S2 ((a) conversion plotted against Mn, SEC (b) Mn, SEC results vs. Mn, theoretical plot); S3 (1H NMR of P(PEGMA) in CDCl3); S4 ((a) molecular weight distribution of P(PEGMA) synthesised under different wavelengths. (b) Đ vs. Mn, SEC plot); S5 ((a) molecular weight distribution of P(PEGMA) synthesised at different monomer concentrations. (b) Đ vs. Mn, SEC plot); S6 (absorbance of CTA corresponding to n → π* transition in different solvents); S7 (Beer–Lambert plots for n → π* transition of CTA); S8 (molecular weight distribution of P(PEGMA) synthesised at different temperatures and in various solvents); S9 (Đ vs. Mn, SEC plot. of P(PEGMA) synthesised at different temperatures and in various solvents); S10 (predicted values of kp, Arrhenius parameters, enthalpy and entropy of activation from multivariate linear regression using the Kamlet–Abraham–Taft equation); S11 (predicted values of Arrhenius parameters, enthalpy and entropy of activation from multivariate linear regression using the Catalan equation), and S12 (Ctrvs. Mn, SEC for P(PEGMA) 7–27 synthesised at various temperatures and in 7 solvents). Tables S1 (solvent physical properties); S2 (solvatochromic scales and Hildebrand solubility parameters); S3 (adjusted R2 values of simple linear regression); S4 (result of multivariate linear regression using the Kamlet–Abraham–Taft equation) and S13 (Ctrvs. Mn, SEC for P(PEGMA) 7–27 synthesised at various temperatures and in 7 solvents). See DOI: https://doi.org/10.1039/d5py00300h |
| ‡ These authors contributed equally. |
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
Bryn D.
Monnery‡
,
Bryn D.
Monnery‡
 * and
Inge S.
Zuhorn‡
* and
Inge S.
Zuhorn‡
 *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [I] = 100, where [M]0 is the initial monomer concentration, and [I] is the concentration of photoiniferter. The solution was sparged with N2 for 1 h. The reaction was carried out at 22 °C under blue light for 1.5 h, green light for 4 h, and switching from blue light (0.5 h) to green light (2.5 h). The target conversion was 50%. The reaction mixture was dialyzed with a 3.5 kDa Spectra/Por 3 dialysis membrane against 1 L demineralized water for 2 d, with subsequent lyophilization to isolate the polymers. Kinetic data was collected at various time points and analysed with 1H NMR in CDCl3. The conversion was calculated from the methylene protons on the ethylene glycol chain for the remaining monomer (4.23 ppm) and the corresponding signal of polymers (4.01 ppm, eqn (2), indicated in Fig. S1†).
[I] = 100, where [M]0 is the initial monomer concentration, and [I] is the concentration of photoiniferter. The solution was sparged with N2 for 1 h. The reaction was carried out at 22 °C under blue light for 1.5 h, green light for 4 h, and switching from blue light (0.5 h) to green light (2.5 h). The target conversion was 50%. The reaction mixture was dialyzed with a 3.5 kDa Spectra/Por 3 dialysis membrane against 1 L demineralized water for 2 d, with subsequent lyophilization to isolate the polymers. Kinetic data was collected at various time points and analysed with 1H NMR in CDCl3. The conversion was calculated from the methylene protons on the ethylene glycol chain for the remaining monomer (4.23 ppm) and the corresponding signal of polymers (4.01 ppm, eqn (2), indicated in Fig. S1†).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [I] = 100. The solution was degassed under N2 for 1 h. The reactions were performed under a blue light source (λmax = 450 nm, 18 mW cm−2). For synthesis in anisole, THF, and 1,4 dioxane, the reaction mixture was precipitated in heptane (20× reaction volume) and further reprecipitated by dissolving in 1 mL DCM, followed by repeated precipitation in heptane (20× reaction volume). The isolated polymers were dried in a vacuum oven at room temperature. For synthesis in DMSO, DMF, EtOH, and MeOH, the reaction mixture (1–2 mL) was dialyzed with a 3.5 kDa Spectra/Por 3 dialysis membrane against 1 L demineralized water for 2 days, and subsequently lyophilised to isolate the polymers. Kinetic data was collected at various time points and analysed with 1H NMR in CDCl3.
[I] = 100. The solution was degassed under N2 for 1 h. The reactions were performed under a blue light source (λmax = 450 nm, 18 mW cm−2). For synthesis in anisole, THF, and 1,4 dioxane, the reaction mixture was precipitated in heptane (20× reaction volume) and further reprecipitated by dissolving in 1 mL DCM, followed by repeated precipitation in heptane (20× reaction volume). The isolated polymers were dried in a vacuum oven at room temperature. For synthesis in DMSO, DMF, EtOH, and MeOH, the reaction mixture (1–2 mL) was dialyzed with a 3.5 kDa Spectra/Por 3 dialysis membrane against 1 L demineralized water for 2 days, and subsequently lyophilised to isolate the polymers. Kinetic data was collected at various time points and analysed with 1H NMR in CDCl3.

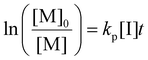
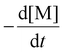 is the rate of change of monomer concentration, [M] is the monomer concentration at an instant during the course of polymerisation, and [M]0 is the initial monomer concentration.
is the rate of change of monomer concentration, [M] is the monomer concentration at an instant during the course of polymerisation, and [M]0 is the initial monomer concentration.


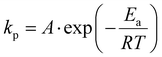





![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [I], the probability of a collision between a propagating end and either a monomer or the CTA fragment will be relatively the same. In fact, the molecular weight distribution is largely dependent on the ratio of propagation to deactivation events. As a consequence of each activation, the active radical will propagate a number of times before being deactivated by the CTA fragment. This will be a Poisson distribution with Rp/Rdeact being the Poisson parameter λ of the individual distribution. However, during the polymerisation process the activation-propagation-deactivation cycle occurs many times. Ergo, the Poisson distribution becomes compounded, and thus becomes a Gamma distribution.
[I], the probability of a collision between a propagating end and either a monomer or the CTA fragment will be relatively the same. In fact, the molecular weight distribution is largely dependent on the ratio of propagation to deactivation events. As a consequence of each activation, the active radical will propagate a number of times before being deactivated by the CTA fragment. This will be a Poisson distribution with Rp/Rdeact being the Poisson parameter λ of the individual distribution. However, during the polymerisation process the activation-propagation-deactivation cycle occurs many times. Ergo, the Poisson distribution becomes compounded, and thus becomes a Gamma distribution.










