Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Recent advances in computational modelling of mononuclear actinide single molecule magnets†
Sourav
Dey
 and
José J.
Baldoví
and
José J.
Baldoví
 *
*
Instituto de Ciencia Molecular, Universitat de València, 46980 Paterna, Spain. E-mail: j.jaime.baldovi@uv.es
First published on 10th January 2025
Abstract
Significant progress has been made in lanthanide-based single mononuclear SMMs in the past two decades, raising their magnetic memories to liquid nitrogen temperature. On the other hand, a handful of actinide-based mononuclear SMMs, primarily based on uranium, have been reported. Among the advantages of actinides over lanthanides are their more significant spin–orbit coupling and stronger metal–ligand covalency, which make them better candidates for providing mononuclear SMMs with high energy barriers. However, the lack of design criteria based on theoretical studies and their more challenging experimental preparation has led to limited results that are still distant from their promising potential. Recently, there has been an increasing interest in their ab initio modelling to understand their electronic structure and magnetic properties. This has led to setting up the first steps regarding their chemical design, thus opening new possibilities for improvement in the near future. In this review, we focus on these recent works and rationalise how far the field has come forward, exploring the potential of designing an advanced generation of actinide mononuclear SMMs.
Introduction
Magnetic molecules exhibiting slow magnetisation relaxation below a specific temperature, the so-called blocking temperature (TB), are known as single-molecule magnets (SMMs).1–4 This class of molecules has gained tremendous interest in the past three decades due to their potential application in high-density information storage devices, molecular spintronics and quantum computing.5–9 Indeed, discovering the second generation of mononuclear SMMs in 2003 amplified this interest, placing lanthanide-based compounds as leading players in molecular magnetism. This is due to their unquenched orbital angular momentum resulting from the buried 4f orbitals, which is critical to attaining higher magnetic anisotropies and thus increasing the two leading figures of merit of molecular nanomagnets,10,11i.e. TB and the effective energy barrier for magnetisation reversal (Ueff).10–13 Besides, the properties of mononuclear SMMs can be fine-tuned by carefully tailoring the ligand environment, which can result in unprecedented TB values that have recently been enhanced from 60 K to 80 K in dysprosocenium-based mononuclear SMMs.10–13Although much less explored, actinides have been proposed as a promising alternative to design even better mononuclear SMMs.14 This is because the more diffuse valence of the 5f orbital cloud compared to 4f leads to larger metal–ligand covalency, resulting in significant energy separation between crystal field states and thus limiting quantum tunnelling of the magnetisation (QTM).15,16–20 Furthermore, actinide-based coordination compounds possess (i) stronger spin–orbit coupling, (ii) an order of magnitude larger ligand field splitting and (iii) stronger magnetic exchange interactions with neighbouring metal centres.15,21–29 Hence, they can combine the best features of 3d and 4f nanomagnets since 5f electrons can present strong ligand-field potential and magnetic superexchange coupling. Despite these advantageous features, the number of actinide-based mononuclear SMMs still needs to be increased, and this promise of extraordinary properties is hindered by the challenging theoretical modelling of their properties.18,30,31 A major limitation of actinide single-molecule magnets (SMMs) is their generally lower J values compared to ions like Dy3+ or Er3+ (J = 15/2). This difference is key to understanding why actinides’ magnetic properties have so far been less competitive than those of lanthanides. On the other hand, the availability of depleted uranium compared to other actinides also puts them at the forefront of studying their magnetic properties.
In this work, we review the state-of-the-art electronic structure of all actinide-based mononuclear SMMs reported so far. This allows us to analyse the proposed design criteria to create novel derivatives with more advanced capabilities. We introduce all the reported mononuclear SMMs based on uranium(III), uranium(IV), uranium(V), neptunium(IV) and plutonium(III), discussing the critical role of the ligand field, coordination environment and symmetry on the magnetic properties of these complexes.
Theoretical background
Since the twentieth century, most of the actinide compounds are man-made. Thorium and uranium are found in noticeable amounts on Earth and are long-lived.32 In early actinides (Ac–Pu), the near degeneracy of 5f, 6d and 7s orbitals leads to more electrons forming bonds, resulting in a wide range of oxidation states from +3 to +7.33 On the other hand, in the late actinides, the most common oxidation state is +3, which is similar to that of the lanthanides. The relativistic effect is more pronounced in actinides than lanthanides due to their larger atomic number than the latter. Actinide-free ions are well described within the Russell–Saunders coupling scheme, where spin-free levels are used to build many-electron states, and these states are mixed by spin–orbit coupling. The states of the free ion are described as 2S+1LJ, where S, L, and J are spin, orbital and total angular momentum, respectively. Compared to lanthanides, in actinide complexes, (i) the interaction of 5f orbital with ligands becomes larger due to the less effective screening by 6s6p shell and larger radial expansion, (ii) the electron–electron repulsion is smaller due to the radial node, and (iii) the J-mixing is larger due to the larger spin–orbit coupling and the resulting states should be explained within intermediate coupling scheme. However, the lowest 2J + 1 states are well separated from excited states and, therefore, can be assigned to ground J-multiplet.Magnetic properties of mononuclear actinide-based SMMs governed by the low-lying states up to thermal energy. Although the ground state properties such as molecular geometries or vibrational frequencies of actinide SMMs can be accurately modelled with the scaler relativistic methods such as DFT (density functional theory), it cannot used to describe the excited states.34,35 As electron–electron repulsion, spin–orbit coupling, and ligand field are similar in magnitude, 5f orbitals should be adequately described to achieve qualitative and quantitative accuracy. The scaler relativistic effect can be easily described using he non-relativistic machinery.36 SA-CASSCF (state-averaged complete active space self-consistent field) is one of the central methods for studying actinide-based metal complexes, effectively incorporating static correlation through a zeroth-order wavefunction.37 This approach not only provides a reliable estimate of single-ion anisotropy but also reveals the origin of such anisotropy, offering principles for designing high-performance mononuclear actinide SMMs.38,39 In SA-CASSCF, orbitals are divided into three categories: closed, active, and virtual spaces (see Fig. 1). Because dynamic correlation is not fully captured in this method, techniques such as complete active space perturbation theory (CASPT2),40 N-electron valence shell perturbation theory (NEVPT2),41 or multireference configuration interaction (MRCI)42,43 are often employed to accurately estimate single-ion anisotropy parameters. The spin–orbit coupling is estimated in the last step as a state interaction between many-electron correlated wavefunctions.44 The first-principles calculations on actinide systems are challenging due to many aspects of quantum chemistry: (i) as they are open-shell multiconfiguration methods are necessary to describe them, (ii) consideration of both scaler and spin–orbit relativistic effects and (iii) incorporation of correlation effects.
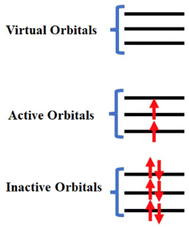 | ||
| Fig. 1 A schematic diagram to represent the inactive, active and virtual orbitals in CASSCF calculations. | ||
The success of SA-CASSCF depends on the choice of active space, specifically the electrons and orbitals under investigation. For example, in studies on U3+ systems, an active space of three electrons in seven 5f orbitals, denoted as CAS (3,7), is commonly used. However, the active space must be carefully selected based on the case, as this affects accuracy. For example, the smallest active space containing the outermost orbitals and their corresponding electrons suffices to reproduce the experimental magnetic data of 3d transition metal and lanthanide complexes, but this approach is not always suitable for actinides. Rajaraman and co-workers highlighted the role of empty 6d orbitals in the active space of mononuclear U3+ SMMs for reproducing magnetic properties, while Bolvin and co-workers emphasized the importance of CASPT2 for accurately describing the electronic structure of U3+ SMMs.39,45–47
These theoretical methods have been successfully applied over the years to explain the magnetic properties of actinide-based complexes and are now advanced enough to predict high-performance mononuclear actinide SMMs, including those yet to be synthesized or magnetically characterized. This review explores recent progress in this field, where theory and experiment complement each other to elucidate the origin of magnetic anisotropy in mononuclear actinide-based SMMs.
Crystal field parameters in mononuclear actinide-based SMMs
Within crystal field theory, the model-Hamiltonian describing the f electrons can be written as: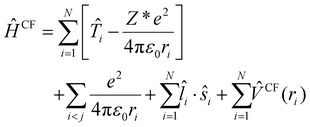 | (1) |
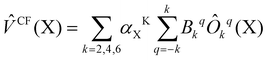 | (2) |
As CFPs depend on molecules's orientation in the cartesian frame, it is convenient to use the crystal field strength parameter (S) for the sake of comparison between different complexes:58
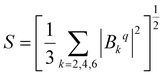 | (3) |
Note that S is rotationally invariant. The parameter S allows us to analyze the strength of the ligand field, resulting in the splitting of the ground J multiplet with only one parameter.
Magnetization relaxation in mononuclear SMMs
The mechanism of magnetization relaxation can be qualitatively described through various spin–lattice vibration pathways after estimating the spin-Hamiltonian and crystal field parameters, as discussed in previous sections.59,60 In the presence of an applied magnetic field, one of the MJ components of the spin–orbit eigenstates becomes more populated than the opposite component. During the demagnetization process, the spin relaxes back to the ground state via two relaxation pathways: (i) spin–lattice relaxation (T1) and (ii) spin–spin relaxation (T2).8,9 Spin–spin relaxation occurs in the presence of surrounding electron or nuclear spins, with the magnetic moment oriented perpendicular to the applied magnetic field. This relaxation process is crucial for applications in quantum information processing.61 In most mononuclear SMMs, relaxation proceeds through spin-phonon interactions via the Orbach mechanism (see Fig. 2).62 Recent advances in dysprocenium complexes have provided deeper insights into spin dynamics, aiding in the design of potential SMMs. Magnetization relaxation can be described as a combination of three processes: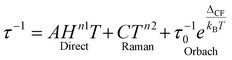 | (4) |
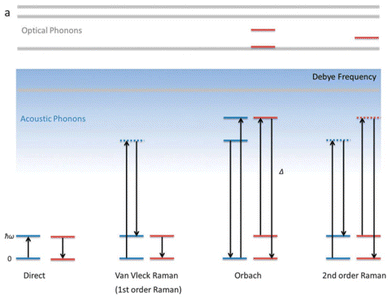 | ||
| Fig. 2 A schematic view of several spin-phonon relaxation pathways in mononuclear SMM. The blue lines describe the phonon energy of the lattice, while the red lines indicate the crystal field energy levels of the molecule. The Debye frequency represents the cutoff of acoustic phonons. Reprinted from Liddle et al.8 with permission from the Royal Society of Chemistry. | ||
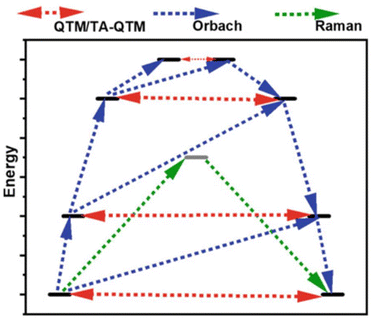 | ||
| Fig. 3 The mechanism of magnetization relaxation of a mononuclear SMM through low-energy KDs, including various relaxation pathways. | ||
Another pathway for magnetization relaxation is known as QTM, where spins tunnel between opposite magnetization (mJ) states in the ground state (Fig. 2 and red dotted arrow in Fig. 3).63 This phenomenon occurs due to a strong mixing coefficient of the opposite magnetization. For a free Kramers ion (with half-integer S or J values), this mixing is zero, as dictated by the Kramers theorem of degeneracy. However, in real molecules, non-axial crystal fields or non-zero nuclear spins can lead to significant QTM between mJ states. A small, applied dc magnetic field can suppress this QTM, but maintaining a high axial crystal field symmetry is essential for quenching QTM in the absence of a magnetic field. In non-Kramers systems (with integer S or J values), strong mixing results in the splitting of mJ states, which is referred to as tunnel splitting. This mixing can also occur through excited mJ states, which is termed thermally assisted QTM (TA-QTM).
In the first-order Raman process, the energy released during magnetization relaxation is absorbed through the superposition of two lattice phonons, one of which exists in a virtual intermediate state (Fig. 2).8 In contrast, the second-order Raman process involves both phonons and KDs, transitioning through a virtual intermediate state in a two-step manner (olive green dotted arrow in Fig. 3).64 Practically, a system may follow multiple relaxation pathways influenced by temperature. While molecular vibrations play a significant role in magnetization relaxation, a more detailed understanding necessitates considering unit cell vibrations and the corresponding density of states. Consequently, spin dynamics are crucial in determining the relaxation rate and effective energy barrier for magnetization relaxation in single-molecule magnets.
It is often observed that the calculated energy barrier for magnetization reversal (Ucal) tends to be overestimated compared to Ueff. Although expanding the active space and including dynamic correlation can improve this estimate to some extent, the discrepancy appears to be intrinsic. This can be attributed to several factors: (i) ab initio calculations do not provide the probabilities of quantum tunnelling mechanisms (QTM, TA-QTM) and Orbach processes; they only yield the corresponding matrix elements; (ii) intermolecular and hyperfine interactions present in the crystal structure are often neglected in ab initio calculations, which can promote under-barrier relaxation processes; and (iii) the presence of under-barrier Raman relaxation processes.
Mononuclear Uranium(III) SMMs
Until now, most of the reported actinide SMMs are based on uranium(III). This is due to the Kramers nature of U3+, which guarantees the doubly degenerate mJ ground state in the absence of a magnetic field. Furthermore, it possesses large orbital angular momentum (5f3, J = 9/2), which creates a significant energy separation between ligand field states, resulting in a higher energy barrier for magnetic relaxation. Mononuclear SMMs are ideal for a fundamental understanding of the slow relaxation of magnetisation. On the other hand, these systems can be modelled quite easily due to the absence of magnetic exchange.In this section, we will start by comparing U3+ mononuclear SMMs with their isoelectronic lanthanide analogue, Nd(III). Thereafter, we will review the theoretical modelling of the magnetic properties of reported U3+ coordination complexes exhibiting slow magnetisation relaxation, which are the most predominant actinide-based mononuclear SMMs. We have divided this section into two parts based on the ligand field and symmetry.
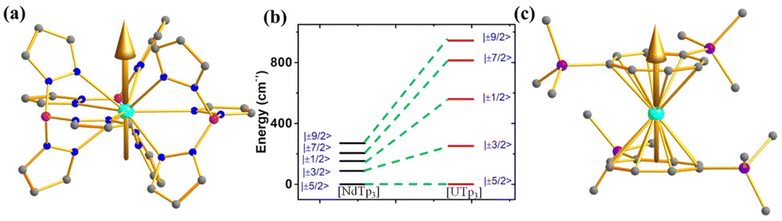
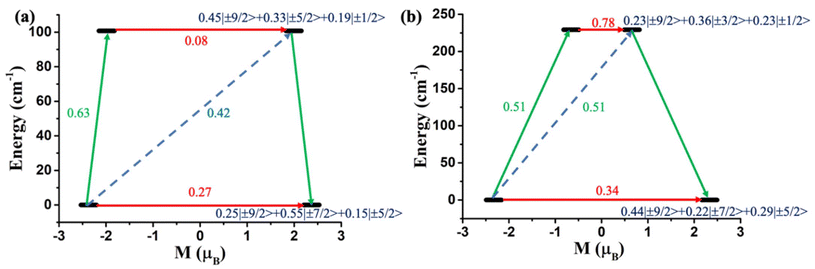
However, to make a direct comparison of slow magnetic relaxation between lanthanide and actinide complex, Long and co-workers studied two isostructural and valence isoelectronic actinide and lanthanide complex; [UTp3] (1, Fig. 4a) and [NdTp3] (2, Tp3 = trispyrazolylborate).67 The studies on low-temperature absorption spectra reveal about twice the energy splitting of the five kramers doublets (KDs, derived from 4I9/2 ground state) as well as KD1–KD2 energy gap in the uranium congener compared to the lanthanide analogue (Fig. 4b, (267 (1) vs. 115 cm−1 (2))). This is due to the larger spin–orbit coupling and crystal field in the former compared to the latter, as stated in the introduction. Furthermore, the magnetisation relaxation in 1 is found to be one order of magnitude slower than in 2 with an applied dc field of 100 Oe (Ueff = 4 cm−1 in 2 compared to lanthanide congener (Ueff = 3 cm−1)). To determine the splitting of KDs and associated wavefunctions, ab initio calculations were carried out by Rajaraman and co-workers, which unveiled large transverse anisotropy in ground KD in both complexes, resulting in significant QTM.68 The large transverse anisotropy originated from the strong mixing mJ = |±5/2〉 and |±7/2〉 in the ground KDs in both complexes. Calculations with an expanded active space that includes 6dz2 orbitals show a significant improvement in the computed χT values compared to experimental data, suggesting that agostic interactions between the hydrogen of the –BH group and uranium occur through this orbital. This interaction plays a vital role in the magnetic properties of uranium complexes with pyrazolyl borate ligands. However, using a different computational approach with the crystal field model, Coronado and co-workers also performed calculations on 1 and 2 to determine the nature of the ground state. Their model unveiled ground state KD is a combination of mJ = ±5/2〉 and |±7/2〉, suggesting significant QTM in the ground state, explaining the small Ueff observed in 2.69
One year later, in line with the previous studies, Murugesu and co-workers performed a comparison between isostructural and valence isoelectronic actinide and lanthanide mononuclear SMMs [Li(DME)3][U(COT′′)2] (3, Fig. 4c) and [Li(DME)3][Nd(COT′′)2] (4) (COT′′ = bis(trimethylsilyl)cyclooctatetraenyl dianion).70 As expected, complex 3 is found to possess a larger barrier height compared to 4 (Ueff = 19 (3) and 15 (4) cm−1). The ab initio calculations on both complexes reveal stabilisation of mJ = |±5/2〉 as ground KD. The ground and first excited KD energy gap is estimated to be 382 and 207 cm−1 for 3 and 4, respectively, which is one order of magnitude larger than the Ueff values.68 This is quite common in the early lanthanide and actinides as they do not follow the thermally activated process for magnetisation relaxation. However, the studies on complexes 1–4 suggest that screening of isoelectronic lanthanide analogues should provide the first step of deciphering potentially interesting actinide systems, especially the transuranic elements, due to the difficulty in modelling these complexes.
To enable an accurate and quantitative comparison of ligand fields in lanthanides (Ln) and actinides (An), Bolvin and co-workers estimated the crystal field strength parameter (S, see eqn (3)) for the [Ln(DPA)3]3− and [An(DPA)3]3− series (where DPA = dipicolinate) using calculated crystal field parameters (CFPs).71,72 The S values calculated for [An(DPA)3]3− from both AILFT and SO-CASPT2 were found to be twice as large as those for [Ln(DPA)3]3−, consistent with the twofold greater crystal field splitting of the ground J-multiplet in actinides compared to lanthanides. Additionally, S was observed to decrease with increasing atomic number in both series, a trend more pronounced in actinides due to their greater covalency relative to lanthanides. This same trend was also reproduced by Atanasov and co-workers for the [AnCl6]3− series.73
 | ||
| Fig. 5 Molecular structure of the complex (a) [U(Ph2BPz2)3] (5) and (b) [U(H2BPz2)3] (6). Colour code: U (cyan), B (pink), N (blue), C (grey). Hydrogens are omitted for clarity. (c) A comparison of experimental vs. computed temperature-dependent magnetic susceptibility of 6. Experiment (circles), SO-CASSCF (red), and SO-MS-CASPT2 (set 1 blue, set 2 green). They are reprinted with permission from ref. 77. Copyright 2017 American Chemical Society. | ||
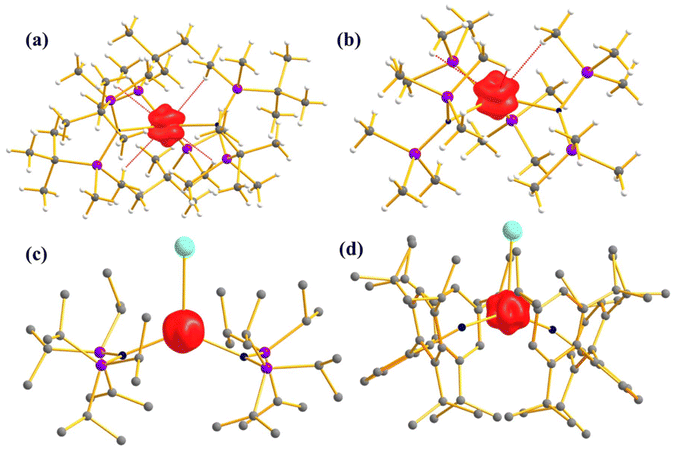
Furthermore, to determine the structural features governing the mononuclear SMM behaviour in actinide-based complexes, Almeida, Bart and co-workers studied four additional closely related mononuclear SMMs, namely, [U(TpMe2)I2(THF)2] (7, TpMe2 = hydrotris(3,5-dimethylpyrazolyl)borate, Fig. 6), [U(TpMe2)2I] (8, Fig. 6), [U(TpMe2)2CH2Ph] (9, Fig. 6) and [U(TpMe2)2(bipy)]I (10, Fig. 6).78–81 The calculations (see ESI† for computational details for 7 and 9) reveal a vigorous mixing between several mJ levels (dominated by mJ = |±7/2〉 and |±9/2〉, see Table 1 and Tables S1, S2†) leading to the significant QTM. The computed QTM is found to be in the order of 7 < 9 < 8 < 10 (Fig. 6 and 7). This is in the order of mixing between mJ levels; the larger the mixing, the larger the QTM. However, the calculations suggest that THF produces the weakest equatorial ligand field due to the ionic nature of the U–O bond. The computed crystal field splitting from 4I9/2 states is 7 < 8 < 10 < 9. Moving from 7 to 8, a significant increase in the crystal field splitting is observed due to an increase in the axial ligand field from the TpMe2 group. Complexes 8 and 10 are magnetically characterised, and both show slow relaxation of the magnetisation under an applied dc field, with Ueff of 21.0 and 18.2 cm−1 in complexes 8 and 10, respectively.77,79,82 However, the 2,2′-bipyridine radical complex [U(TpMe2)2(bipy.)] (11)83 interestingly exhibits slow magnetisation relaxation with Ueff of 20 cm−1 in zero field. This study indicates that the magnetic coupling of the U3+ ion with the radical ligand can suppress the QTM even in mononuclear actinide complexes.
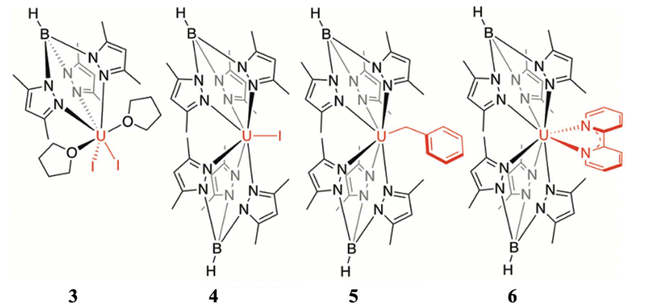 | ||
| Fig. 6 The molecular structure of [U(TpMe2)I2(THF)2] (7), [U(TpMe2)2I] (8), [U(TpMe2)2CH2Ph] (9) and [U(TpMe2)2(bipy)]I (10). The counter anion of complex 10 has been removed and reprinted with permission from ref. 80. Published by The Royal Society of Chemistry. | ||
| Complex | Local geometry around metal centre | Point group | U eff (cm−1) | KD1–KD2 (cm−1) | Ground state mJ | Field induced/zero field SMM | Ref. |
|---|---|---|---|---|---|---|---|
| [UTp3] (1) | Tricapped trigonal prismatic | D 3h | 3.8 | 251.5 | |±5/2〉+|±7/2〉 | Field induced | 67 and 68 |
| [Li(DME)3][U(COT′′)2] (3) | Sandwitched | D 8d | 18.7 | 382.0 | |±5/2〉 | Field induced | 70 and 68 |
| [U(Ph2BPz2)3] (5) | Trigonal prismatic | D 3h | 20 | 141.7 | |±3/2〉+|±5/2〉|±7/2〉 | Zero field | 74 and 76 |
| [U(H2BPz2)3] (6) | Tricapped trigonal prismatic | D 3h | 8 | 131.3 | |±1/2〉+|±3/2〉|±5/2〉 | Field induced | 75 and 76 |
| [U(TpMe2)2I] (8) | Pentagonal bipyramidal | D 5h | 21.0 | 213.6 | |±5/2〉+|±7/2〉+|±9/2〉 | Field induced | 76, 79 and 108 |
| [U(TpMe2)2(bipy)]I (10) | Distorted dodecahedral | C 2 | 18.2 | 138.0 | |±1/2〉+|±7/2〉+|±9/2〉 | Field induced | 78 and 76 |
| [U(TpMe2)2(bipy.)] (11) | Triangular dodecahedron | D 2d | 19.8 | Zero field | 83 | ||
| [(U{SiMe2NPh}3-tacn)(OPPh3)] (12) | Tricapped trigonal prismatic | D 3h | 15.2 | 147.0 | |±5/2〉+|±7/2〉 | Field induced | 6 |
| [U(BcMe)3] (13) | Tricapped trigonal prismatic | D 3h | 33.0 | 102.7 | |±5/2〉+|±7/2〉 | Field induced | 85 and 86 |
| [U(BpMe)3] (14) | Tricapped trigonal prismatic | D 3h | 0.0 | 169.2 | |±5/2〉+|±7/2〉 | Field induced | 85 and 86 |
| [U((OArAd,Me)3mes)] (15) | Octahedron | O h | 9.7 | 260.7 | |±9/2〉+|±5/2〉+|±3/2〉 | Zero field | 87 |
| [K(18c6)] [U(OSi(OtBu)3)4] (16) | Tetrahedral | T d | 18.1 | 97.6 | |±7/2〉+|±5/2〉 | Zero field | 26 and 76 |
| [K(18c6)] [U(N(SiMe3)2)4] (17) | Tetrahedral | T d | 16.0 | 229.8 | |±7/2〉 | Zero field | 26 and 76 |
| [U{N(SiMe2tBu)2}3] (18) | Trigonal planner | D 3h | 14.9 | 323.7 | |±1/2〉 | Field induced | 89 and 45 |
| [U{N(SiMe3)2}3] (19) | Trigonal pyramidal | C 3v | 21.5 | 211.7 | |±1/2〉 | Field induced | 88 and 45 |
| [UI3(THF)4] (22) | Pentagonal bipyramidal | C 2v | 12.9 | 304.8 | |±9/2〉+|±3/2〉 | Field induced | 88 and 76 |
| [U(BIPMTMS)(I)2(THF)] (23) | Spherical square pyramid | C 4v | 16.2 | 120.1 | |±9/2〉+|±5/2〉 | Field induced | 88 and 76 |
| [(η5-C5iPr5)2U] [B(C6F5)4] (24) | Sandwitched | D 8h | 0.0 | 296 | Field induced | 109 | |
| [{(SiMe2NPh)3-tacn}U(η2-N2Ph2C)] (27) | Triangular dodecahedron | D 2d | 9.8 | |±4〉+|±0〉 | Field induced | 93 | |
| [U(O)(TrenTIPS)] (28) | Trigonal bipyramidal | C 3v | 14.9 | 683 | |±3/2〉 | Field induced | 95 and 96 |
| [U(TrenTIPS)(N)][M(crown)2] (29) | Trigonal bipyramidal | C 3v | 14–28 | 677–824 | |±5/2〉 | Field induced | 96 |
| [U(TrenTIPS)(μ-N){M(crown)}] (30) | Trigonal bipyramidal | C 3v | 14–28 | 613–715 | |±5/2〉 | Field induced | 96 |
| [Np(COT)2] (31) | Sandwitched | D 8h | 28.5 | 1832 | |±5/2〉 | Field induced | 98 and 99 |
| [PuTp3] (32) | Tricapped trigonal prismatic | D 3h | 18.3 | 332.0 | |±5/2〉 | Field induced | 100 and 101 |
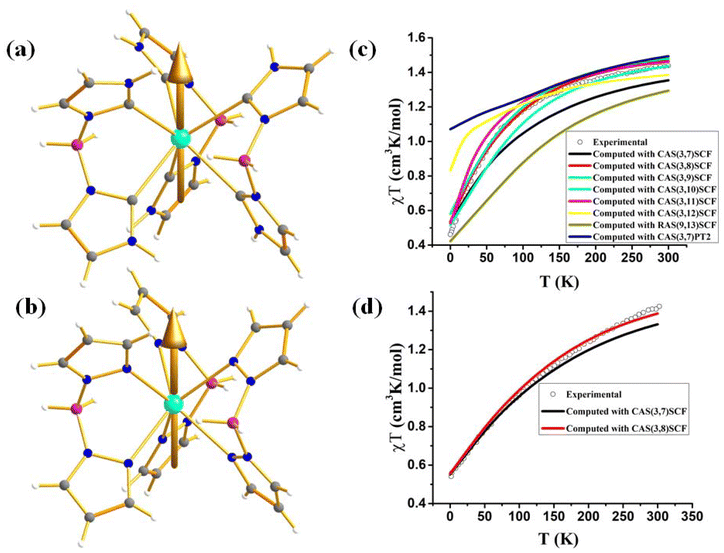
To investigate the effect of the axial ligand field on the magnetization relaxation, Slageren and co-workers studied [U({SiMe2NPh}3-tacn)(OPPh3)] (12, Fig. 8a) where OPPh3 ligand was introduced in the axial position.6 The complex shows slow relaxation of magnetisation in zero field with Ueff = 15.2 cm−1, which is 1/10 of the ab initio calculated ground and first excited state energy gap (147 cm−1) due to the spin-phonon relaxation with a non-Orbach process (Fig. 8c). The ab initio computed temperature-dependent magnetization of 12 was found to be overestimated compared to the experiment (Fig. 8b). To circumvent this issue, the temperature and field-dependent magnetisation was fitted with the following Hamiltonian Ĥ = ĤFI + ĤCF in CONDON, where FI corresponds to the free ion and CF corresponds to the crystal field. The ground state from the above fitting consists of a mixture of mJ = |±5/2〉 and |±7/2〉 contrary to |±1/2〉 from ab initio calculations. The computed energy levels showed good agreement with MCD spectra. This study indicates that an axial ligand field stabilises a large ground mJ, which promotes slow relaxation of magnetisation compared to the analogue complex [U({SiMe2NPh}3-tacn)] that does not have an axial ligand field.
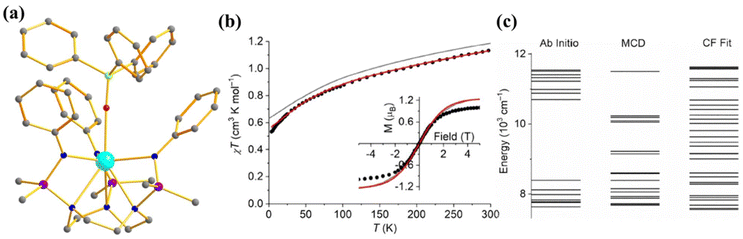 | ||
| Fig. 8 (a) The molecular structure of the complex [U({SiMe2NPh}3-tacn)(OPPh3)] (12). Colour code: U (cyan), N (blue), Si (violet), p (green) and C (grey). Hydrogens of complexes are omitted for clarity. (b) Experimental vs. computed temperature-dependent magnetic susceptibility of 12 (experiment: circles, ab initio: grey, fitted: red). The inset shows the M vs. H comparison of complex 12. (c) The experimental vs. computed crystal field splitting energy level of complex 12. Reprinted with permission from ref. 6 and reproduced with permission from John Wiley and Sons. | ||
As most U3+ based mononuclear SMMs are based on N-donor scorpionate ligands,84 it is interesting to compare the magnetisation relaxation with the ligand donor strength, keeping the molecular symmetry intact. In line with this idea, Long and co-workers studied two isostructural and isomeric mononuclear SMM, [U(BcMe)3] (13), ([BcMe]− = dihydrobis-(methylimidazolyl) borate, Fig. 9a) and [U(BpMe)3] (14), ([BpMe]− = dihydrobis(methylpyrazolyl)borate, Fig. 9b).85 The metal centre in both complexes resides in a tricapped trigonal prismatic coordination geometry (D3h symmetry) due to the significant U⋯H-BH agostic interaction. The magnetic studies reveal that strongly donating N-heterocyclic carbene ligand in 13 promotes slow relaxation of magnetisation with Ueff of 23 cm−1, the highest reported till now for a U3+ mononuclear SMM, while complex 14 relaxes via direct and Raman process with no blocking barrier. To rationalise this striking experimental observation, Rajaraman and co-workers performed ab initio calculations on both complexes.86 The bonding analysis through NBO (natural bond orbital) and AIM (atoms in molecules) showed stronger metal–ligand covalency and U⋯H-BH agnostic interaction in 13 compared to 14. To capture this significant metal–ligand covalency and agostic interaction, the 6d orbitals were added in the active space (Fig. 9c and d). The computed temperature-dependent susceptibility with the addition of 6dz2 orbital in the active space agrees well with the experiment, which implies that the agostic interaction occurs through the vacant 6dz2 orbitals of uranium. The striking difference in magnetic properties between 13 and 14 can be rationalised through significant superhyperfine coupling between uranium and nitrogen (I = 1) in 14, which is absent in 13. The studies on complexes 13 and 14 suggested that significant metal–ligand covalency is vital to increasing the Ueff of uranium mononuclear SMMs. Therefore, to improve the metal–ligand covalency further, an in-silico model was designed by replacing the carbons in the first coordination sphere of complex 13 with sulphur. The model calculations revealed an increase of the crystal field splitting of 200% compared to complexes 13 and 14. This suggests the importance of metal–ligand covalency in designing potential U3+ mononuclear SMM. Inspired by our study, Meyer and co-workers synthesized [U((OArAd,Me)3mes)] (15, Fig. 10) with a weaker sulphur-based ligand in the equatorial position.87 The ab initio calculations on 15 reveal minimal QTM and a large KD1–KD2 energy gap of 260.7 cm−1 (see ESI† for computational details). However, this complex is reported to have a blocking barrier of 10 cm−1, a fraction of the computed value, which can be ascribed to non-Orbach relaxation of magnetisation such as direct and Raman process. However, designing a sulphur-based ligand for the equatorial position and a nitrogen-based ligand for the axial position should be ideal to obtain U3+ mononuclear SMM with a high blocking barrier and a small QTM. To gain deeper insight into the role of the ligand bite angle in magnetic anisotropy, a magnetostructural correlation analysis was performed by varying the ligand bite angle in complex 13. This analysis revealed that an increased ligand bite angle enhances the magnetic axiality of complex 13. Since the ligand bite angle in 13 is larger than in 14, the greater magnetic axiality observed in 13 compared to 14 aligns with this magnetostructural correlation.
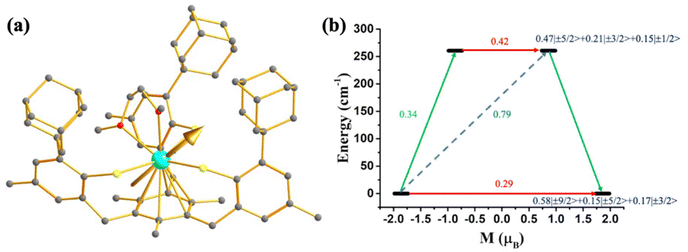 | ||
| Fig. 10 (a) The gzz axis of KD1 of complex [U((OArAd, Me)3mes)] (15). Colour code: U (cyan), S (yellow), O (red), C (grey). Hydrogens are omitted for clarity. (b) The mechanism of magnetisation relaxation of 8. See Fig. 7 for more details in the figure caption. | ||
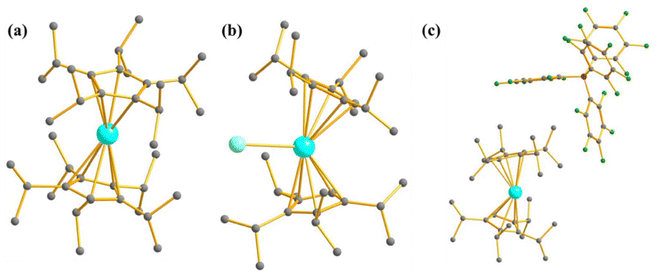
To elucidate the role of the coordinating atom in actinide-based mononuclear SMMs in lower coordination numbers, Mazzanti and co-workers studied two low coordinate U3+ mononuclear SMMs, [U(OSi(OtBu)3)4]− (16, Fig. 11a) and [U(N(SiMe3)2)4]− (17, Fig. 11b), where U3+ resides in tetrahedral geometry.26 Complexes 16 and 17 exhibit slow relaxation of magnetisation in zero field with Ueff of 18 and 16 cm−1, respectively. The larger Ueff of 16 is related to the smaller average U–O distance compared to the average U–N distance in 17. Very recently, ab initio calculations on these complexes unveiled a ground state of mJ = |±7/2〉 with |±5/2〉 in 16, while almost pure mJ = |±7/2〉 was found in 17.76 But the computed QTM is insignificant (<0.1μB), suggesting zero field mononuclear SMM behaviour of complex 17, which aligns with the experiment.
To investigate the effect of symmetry on the magnetic properties further, a T-shape model was constructed from complex 19, which yields mJ = |±9/2〉 in the ground state, resulting in the oblate type of ground state electron density. The KD1-KD2 energy gap on this model was estimated to be 1116 cm−1. As this is a model complex, a retro search in CCDC yielded two U3+ complexes with T-shape geometry, namely [U(NSiiPr2)2(I)] (20, Fig. 12c) and [U(NHAriPr6)2I] (21, AriPr6 = 2,6-(2,4,6-iPr3C6H2)2C6H3, Fig. 12d) which are magnetically characterised, but the Ueff is unknown. The ab initio calculations on both complexes also yielded mJ = |±9/2〉 as a ground state, with computed blocking barriers of magnetisation reversal of 908 and 932 cm−1 for complexes 20 and 21, respectively. In a nutshell, this study indicated that T-shape geometry should be targeted to achieve a sizeable blocking barrier of magnetisation reversal in U3+ mononuclear SMMs.
The effect of symmetry in the magnetic properties was further investigated in two additional complexes [UI3(THF)4] (22, Fig. 13a) and [U-(BIPMTMS)(I)2(THF)] (23, BIPMTMS = CH(PPh2NMononuclear SMMe3)2, Fig. 13b) by Mills and co-workers.88 The metal centre in complexes 22 and 23 resides in C3v and C1 point group symmetry, respectively. The effective energy barrier for slow relaxation was estimated to be 13 and 16 cm−1 for 22 and 23, respectively, a fraction of the ab initio calculated KD1–KD2 energy gap (305 (22) and 120 (23) cm−1). Furthermore, calculations revealed the ground state with a large mixing of mJ = |±9/2〉 and |±3/2〉 in 22, whereas mJ = |±9/2〉 and |±5/2〉 in 23. This results in a large QTM that explains the absence of zero-field mononuclear SMM behaviour in both.76 Although this study suggests symmetry has a minimal role in magnetic properties, it should be noted that complexes 22 and 23 possess different ligand fields.
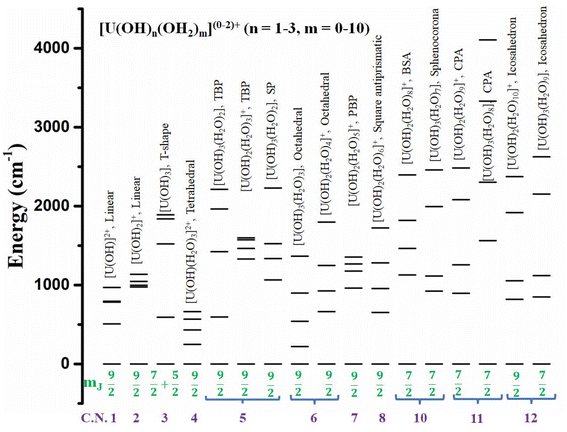
To obtain a more clear picture of the effect of geometry and coordination number in U3+ based mononuclear SMMs, Rajaraman and co-workers performed ab initio calculations on 42 fictitious in silico models [U(OH)n(H2O)m]0–2+ (n = 1–3, m = 0–10) from coordination number 1 to 12.76 Among them, 17 models were found to be the best-performing models with mJ = |±9/2〉 or |±7/2〉 as the ground state that makes the QTM minimal (Fig. 14). Furthermore, calculations have been performed on fifteen reported U3+ complexes that closely resemble those best-performing fictitious models to offer design principles of U3+ based on mononuclear SMMs. The calculations reveal mJ = |±9/2〉 (>90%) ground state for 1, 2, 4 (tetrahedral), 5 (trigonal bipyramidal and square pyramidal), 6 (octahedral), 7 (pentagonal bipyramidal), and 8 (square antiprismatic) coordinated models and dominant mJ = |±9/2〉 in one of the twelve coordinate icosahedron models. On the other hand, mJ = |±7/2〉 was stabilised for ten (bicapped square antiprismatic) coordinated models and a dominant mJ = |±7/2〉 in 11 coordinated (pentagonal antiprismatic) and 12 (icosahedron) models. Finally, a combination of mJ = |±5/2〉 and |±7/2〉 was stabilised in 3 (T-shape) coordinated models. Considering the Orbach process, the Ucal values of the models were estimated to be very large in the range of ca. 1000 cm−1 for most of the models and ca. 1500 cm−1 for some models (T-shaped, pentagonal antiprism). The extensive theoretical search for high Ucal values of U3+ mononuclear SMMs from coordination numbers 1 to 12 yielded several synthetic targets with Ucal values more than 1000 cm−1.
Mononuclear SMMs based on U(IV), U(V), Np(IV), Pu(III) and Cf(III)
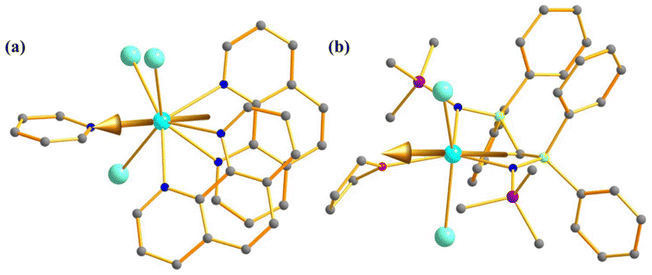
The magnetic behaviour of uranium compounds in the +4 oxidation state has barely been explored. U(IV) with 5f2 electron configuration possess a 3H4 ground term, which often leads to an orbital singlet ground state at low temperatures.66 Therefore, U(IV) is not guaranteed a suitable candidate for slow magnetisation relaxation. However, one mononuclear SMM containing U(IV) ion, [{(SiMe2NPh)3-tacn}U(η2-N2Ph2C)] (27, Fig. 16a) was studied by Almeida and co-workers, in which a radical azobenzene ligand is coupled with U(IV).93 Complex 27 exhibits slow magnetisation relaxation with Ueff of 10 cm−1, contrary to the analogous trivalent uranium compound, which does not show slow magnetisation relaxation. This is due to the coupling of radical with the metal centre, which provides a magnetization of 2.33 μB at 3 K. Furthermore, the χT values at 300 K were estimated to be 1.60 emu Kmol−1, substantially larger than the value found in U(IV) complexes (0.78–1.19 emu Kmol−1).31,94 The simulated magnetic susceptibility using the crystal field model reveals a good fit at high temperatures, but a significant discrepancy is observed in the low-temperature range (Fig. 16b). The computed energy splitting of the ground multiplet of 27 is larger than the corresponding U3+ analogue due to a more potent ligand field generated from the extra bipy radical in the former (Fig. 16c). The ground state 27 is estimated to be a combination of mJ = |±4〉and |±0〉.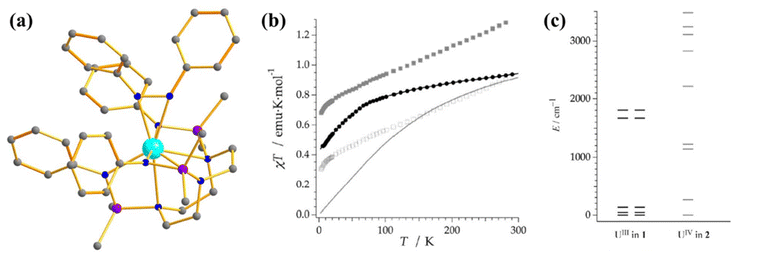 | ||
| Fig. 16 (a) The molecular structure of the complex [{(SiMe2NPh)3-tacn}U(η2-N2Ph2C)] (27). (b) Colour code: U (cyan), N (blue), Si (violet), C (grey). Hydrogens are omitted for clarity. (b) A comparison of experimental and computed temperature-dependent magnetic susceptibility of 27 (experiment: grey squares for 27 and black circles for its precursor, computed: solid line). (c) The ground state energy splitting of 27 (right) and its precursor (left). Reprinted with permission from ref. 93 and reproduced with permission from John Wiley and Sons. | ||
U(V) mononuclear SMMs are even more exotic, almost unexplored due to their smaller total angular momentum (2F5/2 ground state) and instability at room temperature. However, they have more substantial anisotropy and a more extensive ligand field splitting, making them suitable candidates to exhibit and overcome the mononuclear SMM characteristics concerning U3+. The first example reported was [U(O)(TrenTIPS)], (28, TrenTIPS = {N(CH2CH2NSiiPr3)3}3−, Fig. 17), in which the metal centre adopts trigonal bipyramidal geometry in C3v symmetry.95 The complex shows slow relaxation with Ueff of 15 cm−1 in an applied DC field of 1 kOe, in a similar order with the U3+ mononuclear SMMs. The strong axial ligand field generated by U–O in C3v symmetry generates a crystal field splitting that allows slow magnetisation relaxation. The EPR computed g tensor suggests almost pure mJ = |±3/2〉 ground state and offers its significant potential to behave as mononuclear SMM. Subsequently Liddle and co-workers studied other closely related U(V) mononuclear SMMs, [U(TrenTIPS)(N)][M(crown)2] (29, Fig. 17) and [U(TrenTIPS)(μ-N){M(crown)}] (30, Fig. 17), (M = Li, Na, K, Rb, and Cs) in which the O2− in 28 was substituted by N3− to obtain stronger ligand field.96 All these complexes display slow magnetisation relaxation with improved barrier heights of 14–28 cm−1 due to the larger ligand field splitting generated by N3− compared to O2−. The ab initio calculations reveal a ground state dominated by mJ = |±5/2〉 in 29 and 30, in contrast to mJ = |±3/2〉 in 28. This is due to the stronger ligand field of N3− in the former complexes. The computed g tensors align with EPR, evidencing the importance of the computational approach.
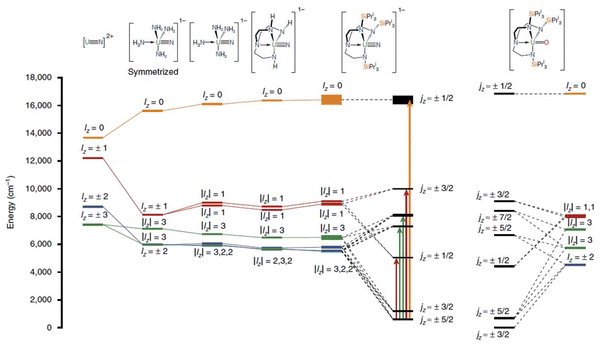 | ||
| Fig. 17 The energy level splitting of five ground KDs of [U(O)(TrenTIPS)] (28), [U(TrenTIPS)(N)][M(crown)2] (29), [U(TrenTIPS)(μ-N){M(crown)}] (30) and their precursors. Reprinted from the ref. 97 with permission from Springer Nature Publishing Group. | ||
Since the ground state electron configuration of Np(IV) and U3+ is similar, Np(IV) complexes are expected to possess mononuclear SMM behaviour. In line with this idea, Caciuffo and co-workers investigated a neptunocene complex, [Np(COT)2] (31, COT = C8H82−, Fig. 18a), in which Np(IV) is sandwiched between two COT rings in D8h symmetry.98 Complex 31 exhibits slow relaxation of magnetisation with an Ueff of 29 cm−1, which is 1/100th fraction of the ab initio computed KD1-KD2 energy gap (1832 cm−1). The calculated temperature and field-dependent molar magnetisation are in line with the experiment, which evidences that the metal–ligand covalency has been captured perfectly in the calculation (Fig. 18b). The ab initio calculations on 31 also revealed that the ground state is dominated by mJ = |±5/2〉, which is split by the Zeeman and hyperfine interaction (I = 5/2 for Np), leading to several crossing points between states with opposite mJ at low field. This opens up QTM-like multiple channels for magnetic relaxation. On the other hand, the computed energy of the five KDs span an energy range of 4228 cm−1, which is quite large compared to the uranium congener (2317 cm−1 in 25).99 It can be ascribed to the shorter Np–C bond resulting in stronger spin–orbit coupling of Np(IV) compared to U3+.
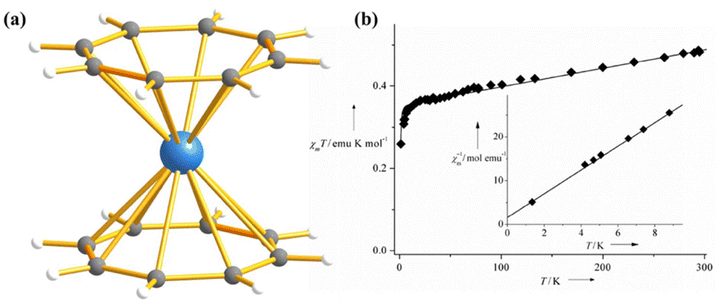 | ||
| Fig. 18 (a) Molecular structure of the complex [Np(COT)2] (31). Colour code: Np (sky blue), C (grey) and H (white). (b) A comparison of experimental and computed temperature-dependent magnetic susceptibility of 31 ((experiment: squares, added: line). Reprinted with permission from ref. 98. Published by The Royal Society of Chemistry. | ||
Inspired by the study of slow magnetic relaxation in [UTp3], Caciuffo and co-workers studied analogues Pu(III) mononuclear SMM, [PuTp3] (32, Tp = tri-1-pyrazolylborate) in the family of actinide-based mononuclear SMMs.100 The simulation of temperature-dependent molar magnetisation of 32 yields pure mJ = |±5/2〉 ground state with the first excited state at 373 cm−1 (mJ = |±3/2〉), which is again a fraction of the experimental Ueff value of 18 cm−1. This energy is well above that computed in uranium congener (251 cm−1) in 1 due to stronger spin–orbit coupling and shorter metal–ligand bond distance in the former.101 As the carbon donor ligand improves the magnetic properties in 13 compared to the nitrogen donor ligand in 14, Gagliardi and co-workers modelled a hypothetical complex 33 from 32, in which carbon is directly bonded to Pu instead of nitrogen. The computed Mulliken charge of Pu in 33 becomes significantly lower compared to 32, indicating stronger σ-donation from carbene ligand. Very recently, Rajaraman and co-workers performed DFT and ab initio calculations on an experimentally reported Pu(III) analogue of 19 ([Pu{N(SiMe3)2}3] (34)) to compare its electronic structure concerning pyramidal [U{N(SiMe3)2}3].45 The ab initio calculations on 34 revealed prolate-type electron density, which stabilises the highest mJ = |±5/2〉 as the ground state. The magnetisation relaxation is expected via the second excited KDs, resulting in the massive Ucal value of 1933 cm−1 in 34. The results suggest that a suitable metal ion is necessary to design a potential mononuclear SMM in three-coordinate pyramidal geometry.
So far, we have examined the magnetic properties of early actinides (with less than half-filled f-shells), where low ground-state J values inhibit the thermally activated relaxation process, resulting in a significantly overestimated ground-state-to-excited-state energy gap compared to Ueff. This behaviour is also observed in early lanthanides for similar reasons. In contrast, late lanthanides with more than half-filled f-shells, such as Dy(III) and Er(III) in single-molecule magnets (SMMs), possess larger J values, which promote thermally activated relaxation and bring the ground-state–excited-state energy gap closer to Ueff.
To explore the potential of late actinides in SMM properties relative to analogous lanthanides, Gagliardi and co-workers performed ab initio CASSCF/RASSI-SO/SINGLE_ANISO calculations on a hypothetical Cf(III) complex, [Cf(dbm)3(bpy)] (35, dbm = dibenzoylmethanoate; bpy = 2,2′-bipyridine), isostructural to [Dy(dbm)3(bpy)] (36).25,102,103 Their calculations revealed a twofold increase in crystal field splitting in 35 compared to 36, with magnetization relaxation occurring through the first excited KDs, resulting in a Ucal value of 329 cm−1—approximately 200 cm−1 higher than in 36. Calculations were extended to include the virtual 6d orbitals in the active space (CAS (9,12)) to account for covalency, which showed an increase in spin–orbit energy levels due to the large energy gap between the 5f and 6d orbitals. This separation is a common occurrence when expanding the active space. To address this, CASPT2 calculations were conducted with a reduced active space, CAS (3,7), yielding Ucal values of 162 cm−1 and 419 cm−1 for 35 and 36, respectively. It is noteworthy, however, that Cf undergoes α-decay to Cm, and calculations indicate that the Cm(III) analogue does not exhibit favourable magnetic properties for SMMs. Despite this, the study stimulated further synthesis of SMMs based on late actinides.
Inspired by the above study, Abergel and co-workers prepared Na[Cf(H2O)(DOTA)] (37, where DOTA = 1,4,7,10-tetraazacyclododecane-1,4,7,10-tetraacetate) and compared its magnetic properties to the lanthanide analogue Na[Dy(H2O)(DOTA)] (38).104–107 Notably, compound 37 exhibits slow magnetization relaxation, marking it as the first example of a Cf-based single-molecule magnet (SMM). The ligand field splitting of the eight Kramers doublets (KDs) in 37 was estimated to be twice as large as in the lanthanide analogue 38, implying a greater covalency in 37 compared to 38. The magnetization relaxation in complex 38 occurs via the first excited KD, yielding a calculated barrier (Ucal) of 32 cm−1, consistent with an effective barrier (Ueff) of 32 cm−1. Although the actinide analogue 37 has a larger first excited KD separation of 89 cm−1, it displays slow relaxation with a Ueff of 11 cm−1, about one-eighth of the first excited KD energy. This suggests an under-barrier relaxation process, such as QTM or Raman relaxation, common in U3+ SMMs, as previously discussed. The QTM can be attributed to mixing between the 6H15/2 and low-lying 4I9/2 spin–orbit states, along with hyperfine interactions due to the nuclear spin (I = 9/2) of 249Cf. However, this study opens new avenues for exploring the influence of ligand field and coordination symmetry in designing potential Cf(III)-based SMMs.
Discussion
The number of actinide-based mononuclear SMMs reported to date is limited. This is mainly due to (i) their complicated chemistry, which makes coordination complexes of most of them inaccessible from the experimental point of view, and (ii) their challenging modelling, which needs to include excited states in the calculation due to their larger crystal field splitting compared to lanthanides. In this perspective, we have discussed the effect of ligand field and symmetry on the magnetic properties of actinide mononuclear SMMs from the reported examples. The primary outcomes from this study are summarised as follows:(i) Comparison of mononuclear lanthanide and actinide analogous SMM: To showcase the better SMM behaviour of actinide compared to mononuclear lanthanide analogues we have considered two examples: [UTp3] (1) and [NdTp3] (2), [Li(DME)3][U(COT′′)2] (3) and [Li(DME)3][Nd(COT′′)2] (4). The calculation on these complexes reveals a smaller QTM and more significant KD1–KD2 energy gap in the actinide analogues compared to the lanthanide one.
(ii) Effect of ligand field: The mJ = |±9/2〉 KD of U3+ possesses oblate electron density, and it should be stabilized with a stronger axial and weaker equatorial ligand field.110 A close look at the ab initio computed results of complexes [U(Ph2BPz2)3] (5) and [U(H2BPz2)3] (6) reveals that U⋯H-BH agostic interaction weakens the axial ligand field in 6 compared to 5. This leads to a larger blocking barrier of 5 compared to 6. A similar scenario has been observed in [U(BcMe)3] (13) and [U(BpMe)3] (14). On the other hand, between complexes 7–10 in the [UTp2] family, complex 7, with the weaker equatorial ligand field from THF, produces a smaller QTM among all the complexes. Similarly, the sulphur-based ligand in the equatorial position in complex [U((OArAd,Me)3mes)] (12) makes mJ = |±9/2〉 with the dominant contribution in the ground KD, which makes the QTM minimal and therefore sulphur-based equatorial ligand should be designed to prepare high-performance U3+ mononuclear SMM.
To verify the role of the axial ligand field in quenching the QTM, we have performed ab initio CAS(3,7)/RASSI-SO/SINGLE-ANISO calculations on experimentally reported [UPc2][BF4] (39, Fig. 19) where two –Pc groups lies in the axial position.111 The calculations on this complex reveal mJ = |±9/2〉 ground state with minimal mixing with other states, resulting in quenching of QTM. The magnetisation relaxation should occur through the second excited state, reaching the Ucal value of 180 cm−1 (Fig. 19). Hence, experimental magnetic characterisation of 39 is necessary to design potential U3+ mononuclear SMMs.
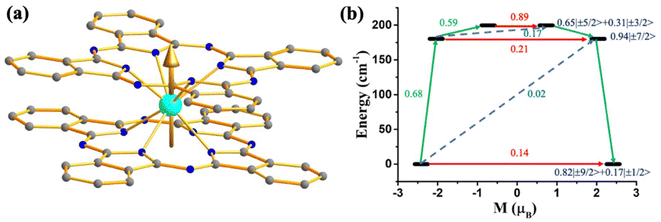 | ||
| Fig. 19 (a) The gzz axis of KD1 of [UPc2][BF4] (39). Colour code: U (cyan), N (blue), C (grey). Hydrogens are omitted for clarity. (b) The mechanism of magnetisation relaxation of 39. See Fig. 7 for more details. | ||
(iii) Choice of active space in capturing the covalency: In ab initio calculations of actinide SMMs, the choice of active space is crucial for accurately reproducing experimental magnetic data, as the more diffuse 5f orbitals in actinides form stronger metal–ligand bonds than those in lanthanides. Metal–ligand covalency can be accounted for in three ways: (i) incorporating ligand orbitals into the active space, (ii) adding virtual 6d orbitals to the active space, and (iii) including dynamic correlation via CASPT2. Expanding the active space by including the σ-orbitals of ligands does not significantly improve results, such as g-tensors and energy splitting of the ground J manifold, as demonstrated in studies on complexes [U(H2BPz2)3] (6) and [U(BcMe)3] (13). However, adding the 6d orbitals into the active space, which accounts for agostic interactions, leads to better alignment between computed and experimental results, as evidenced in [U(BcMe)3] (13) and [U{N(SiMe3)2}3] (19). Additionally, since the 5f and 6d orbitals are close in energy in actinides, incorporating the 6d orbitals allows for 5f to 6d charge transfer, providing more experimentally accurate outcomes. While SO-CASPT2 calculations are computationally demanding, they do not offer substantial improvements over SO-CASSCF. Thus, including 6d orbitals in the active space is advantageous, providing reliable results with a lower computational cost compared to SO-CASPT2.
(iv) Effect of symmetry: The study on complexes [U{N(SiMe3)2}3] (19), [UI3(THF)4] (22) and [U(BIPMTMS)(I)2(THF)] (23) implies that a field-induced mononuclear SMM behaviour can be obtained even if the complex possesses Cs symmetry due to the strong axial and weak equatorial ligand field. The computational study reveals that in the case of three-coordinate geometry, the use of a T-shape ligand gives rise to a very large blocking barrier. Hence, experimental magnetic characterisation of complexes [U(NSiiPr2)2(I)] (20) and [U(NHAriPr6)2I] (21) is necessary to verify the computational results.
(v) Uranium mononuclear SMMs with higher oxidation numbers: Apart from +3, there are few mononuclear SMMs reported on uranium in the +4 and +5 oxidation states. The choice of a +4-oxidation state to design uranium mononuclear SMMs is not a good idea due to its non-Kramer nature, which can lead to large tunnel splitting. On the other hand, U(V) mononuclear SMMs possess smaller angular momentum, which leads to the large QTM, and therefore, high-performance mononuclear SMMs seem to be difficult with uranium in a +5 oxidation state.
(vi) Role of magnetic exchange in quenching the QTM: As this review focuses on mononuclear actinide-based SMMs, we did not highlight the role of stronger magnetic exchange in enhancing the SMM behaviour of actinides. However, among the complexes discussed in this review, a closer look at structurally similar U3+ complexes, such as [U(TpMe2)I2(THF)2] (7), [U(TpMe2)2I] (8), [U(TpMe2)2CH2Ph] (9), and [U(TpMe2)2(bipy˙)]I (10), reveals that only the radical complex 10 exhibits zero-field slow relaxation of magnetization, whereas the others display field-induced slow relaxation. On the other hand, a U(IV) complex, [{(SiMe2NPh)3-tacn}U(η2-N2Ph2C˙)] (27), shows slow magnetization relaxation, while its U3+ analogue without the azobenzene radical lacks SMM behaviour at low temperatures. This difference is attributed to the quenching of QTM due to the coupling between U3+/U(IV) and the radical ligand. Thus, increased magnetic exchange in polynuclear actinide complexes could inspire the design of promising actinide-based SMMs.
(vii) Mononuclear SMMs based on transuranium elements: Beyond uranium, very few mononuclear SMMs based on neptunium, plutonium and californium were studied. Although the ab initio calculations on these complexes reveal extensive energy splitting, the experimental blocking barrier is minimal, which can be ascribed to the relaxation of magnetisation via the non-Orbach process.
Outlook
From the collected data in Table 1, we can observe a typical pattern among all reported actinide-based mononuclear SMMs, which present a vigorous mixing between the mJ levels in the ground KD. This can offer some early insights that lead to the significant QTM that hampers them to become a potential mononuclear SMM. This typical pattern occurs in all the geometries, suggesting that this is a general feature of J = 9/2 of U3+ complexes. Although dysprosocenium-based mononuclear SMMs are the best-performing mononuclear SMMs among lanthanide-based mononuclear SMMs, uranocenium derivatives are found to relax via direct and Raman processes. Indeed, in all cases, the blocking temperature is below 7 K, a region where Raman processes dominate over Orbach relaxation. Also, the theoretically estimated blocking barrier is one order of magnitude larger than the experimental Ueff values. This explains that actinide mononuclear SMMs do not follow a thermally activated relaxation mechanism for the magnetisation reversal. This contrasts with the case of reported lanthanides from the second half of the series, such as Dy(III) compounds; the L + S ground state leads to more prominent magnetic moments in the ground state and makes this kind of mononuclear SMMs follow an Orbach relaxation process. Similar to U(III), the performance of Nd(III) mononuclear SMMs is much more limited than that of Dy(III) mononuclear SMMs.112Therefore, to design promising actinide-based mononuclear SMMs, one needs to focus on elements from the second half-row among the actinides, for example, the dysprosium analogue of the series, i.e. californium, due to the stabilisation of a high L + S ground state (J = 15/2) that can lead to higher energy barriers and blocking temperatures. However, this element spontaneously converts to Cm, and magnetisation relaxation occurs through a non-Orbach process that shortcuts the blocking barrier. Furthermore, working with these elements requires specially equipped and approved laboratories. Hence, alternative ways need to be explored to design potential actinide-based mononuclear SMM.
In this regard, spin-phonon calculations may play a pivotal role in optimising the magnetic behaviour of mononuclear actinide-based SMMs, as they can unveil the low-energy vibrational modes associated with magnetisation relaxation.113–121 The higher covalency in actinides can lead to stronger coupling between spin energy levels and molecular vibrations compared to lanthanides, resulting in low energy vibrations promoting the Raman relaxation which is commonly observed in mononuclear actinide SMMs. Another problem of U3+ is its strongly mixed wave functions even in rather linear environments, as observed in uranocenium complexes where some extra diagonal terms strongly coupled to molecular vibrations in contrary to lanthanide complexes.92 Consequently, uranium-based mononuclear SMMs require unique design strategies and a deeper understanding of molecular vibrations governing the Raman relaxation. Simply substituting U3+ for Dy(III) in high-performance lanthanide SMMs does not yield equivalent results due to the dominant Raman relaxation in actinide SMMs. Chemical strategies to quench low-energy vibrational modes governing the Raman relaxation might be an exciting research direction that is currently almost unexplored. Although the challenges are colossal, this, combined with new chemical design strategies and exploring other actinide elements to create mononuclear coordination complexes, illustrates the main promising routes to improve actinide-based molecular nanomagnets’ performance and reach their maximum potential.
Data availability
Data will be available upon request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the EU (Grant No. 2D-SMARTiES ERC-StG-101042680 and Marie Curie Fellowship SpinPhononHyb2D 101107713), the Plan Gent of Excellence of the Generalitat Valenciana (Grant No. CIDEXG/2023/1).References
- A. Caneschi, D. Gatteschi, R. Sessoli, A. L. Barra, L. C. Brunel and M. Guillot, Alternating current susceptibility, high field magnetization, and millimeter band EPR evidence for a ground S = 10 state in [Mn12O12(Ch3COO)16 (H2O)4]·2CH3COOH·4H2O, J. Am. Chem. Soc., 1991, 113, 5873–5874 CrossRef CAS.
- R. Sessoli, D. Gatteschi, A. Caneschi and M. Novak, Magnetic bistability in a metal-ion cluster, Nature, 1993, 365, 141–143 CrossRef CAS.
- R. Sessoli, H. L. Tsai, A. R. Schake, S. Wang, J. B. Vincent, K. Folting, D. Gatteschi, G. Christou and D. N. Hendrickson, High-spin molecules:[Mn12O12(O2CR)16(H2O)4], J. Am. Chem. Soc., 1993, 115, 1804–1816 CrossRef CAS.
- D. Gatteschi, R. Sessoli and J. Villain, Molecular nanomagnets, Oxford University Press on Demand, 2006 Search PubMed.
- L. Escalera-Moreno, J. J. Baldoví, A. Gaita-Ariño and E. Coronado, Spin states, vibrations and spin relaxation in molecular nanomagnets and spin qubits: a critical perspective, Chem. Sci., 2018, 9, 3265–3275 RSC.
- J. T. Coutinho, M. Perfetti, J. J. Baldoví, M. A. Antunes, P. P. Hallmen, H. Bamberger, I. Crassee, M. Orlita, M. Almeida and J. van Slageren, Spectroscopic Determination of the Electronic Structure of a Uranium Single–Ion Magnet, Chem. – Eur. J., 2019, 25, 1758–1766 CrossRef CAS PubMed.
- L. Escalera-Moreno, J. J. Baldoví, A. Gaita-Arino and E. Coronado, Design of high-temperature f-block molecular nanomagnets through the control of vibration-induced spin relaxation, Chem. Sci., 2020, 11, 1593–1598 RSC.
- S. T. Liddle and J. van Slageren, Improving f-element single molecule magnets, Chem. Soc. Rev., 2015, 44, 6655–6669 RSC.
- S. G. McAdams, A.-M. Ariciu, A. K. Kostopoulos, J. P. Walsh and F. Tuna, Molecular single-ion magnets based on lanthanides and actinides: Design considerations and new advances in the context of quantum technologies, Coord. Chem. Rev., 2017, 346, 216–239 CrossRef CAS.
- K. R. McClain, C. A. Gould, K. Chakarawet, S. J. Teat, T. J. Groshens, J. R. Long and B. G. Harvey, High-temperature magnetic blocking and magneto-structural correlations in a series of dysprosium(III) metallocenium single-molecule magnets, Chem. Sci., 2018, 9, 8492–8503 RSC.
- C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Molecular magnetic hysteresis at 60 kelvin in dysprosocenium, Nature, 2017, 548, 439–442 CrossRef CAS PubMed.
- F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamaki and R. A. Layfield, A Dysprosium Metallocene Single-Molecule Magnet Functioning at the Axial Limit, Angew. Chem., Int. Ed., 2017, 56, 11445–11449 CrossRef CAS PubMed.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single-molecule magnet, Science, 2018, 362, 1400–1403 CrossRef CAS PubMed.
- M. Liu, X.-H. Peng, F.-S. Guo and M.-L. Tong, Actinide-based single-molecule magnets: alone or in a group?, Inorg. Chem. Front., 2023, 10, 3742–3755 RSC.
- S. Dey, G. Rajaraman and H. Bolvin, Analysis of the magnetic coupling in a Mn(II)–U(V)–Mn(II) Single Molecule Magnet, Chem. – Eur. J., 2022, 28, e202201883 CrossRef CAS PubMed.
- N. M. Edelstein, Comparison of the electronic structure of the lanthanides and actinides, J. Alloys Compd., 1995, 223, 197–203 CrossRef CAS.
- H. Crosswhite, H. Crosswhite, W. Carnall and A. Paszek, Spectrum analysis of U3+: LaCl3, J. Chem. Phys., 1980, 72, 5103–5117 CrossRef CAS.
- S. R. Chowdhury, C. A. Goodwin and B. Vlaisavljevich, What is the nature of the uranium(III)–arene bond?, Chem. Sci., 2024, 15, 1810–1819 RSC.
- C. Apostolidis, A. Morgenstern, J. Rebizant, B. Kanellakopulos, O. Walter, B. Powietzka, M. Karbowiak, H. Reddmann and H. D. Amberger, Electronic Structures of Highly Symmetrical Compounds of f Elements 44 [1]. First Parametric Analysis of the Absorption Spectrum of a Molecular Compound of Tervalent Uranium: Tris [hydrotris (1−pyrazolyl) borato] uranium(III), Z. Anorg. Allg. Chem., 2010, 636, 201–208 CrossRef CAS.
- H. Reddmann, C. Apostolidis, O. Walter and H. D. Amberger, Zur Elektronenstruktur hochsymmetrischer Verbindungen der f–Elemente. 40. Parametrische Analyse des Kristallfeld–Aufspaltungsmusters von Tris (hydrotris (1−pyrazolyl) borato) neodym (III), Z. fur Anorg. Allg. Chem., 2006, 632, 1405–1408 CrossRef CAS.
- L. Chatelain, J. P. Walsh, J. Pécaut, F. Tuna and M. Mazzanti, Self–Assembly of a 3d–5f Trinuclear Single–Molecule Magnet from a Pentavalent Uranyl Complex, Angew. Chem., 2014, 126, 13652–13656 CrossRef.
- V. Mougel, L. Chatelain, J. Hermle, R. Caciuffo, E. Colineau, F. Tuna, N. Magnani, A. de Geyer, J. Pécaut and M. Mazzanti, A Uranium–Based UO2+–Mn2+ Single–Chain Magnet Assembled trough Cation–Cation Interactions, Angew. Chem., 2014, 126, 838–842 CrossRef.
- L. Chatelain, J. Pécaut, F. Tuna and M. Mazzanti, Heterometallic Fe2II–UV and Ni2II–UV Exchange–Coupled Single–Molecule Magnets: Effect of the 3 d Ion on the Magnetic Properties, Chem. – Eur. J., 2015, 21, 18038–18042 CrossRef CAS PubMed.
- L. Chatelain, F. Tuna, J. Pécaut and M. Mazzanti, Synthesis and SMM behaviour of trinuclear versus dinuclear 3d–5f uranyl (v)–cobalt(II) cation–cation complexes, Dalton Trans., 2017, 46, 5498–5502 RSC.
- D. Ray, M. S. Oakley, A. Sarkar, X. Bai and L. Gagliardi, Theoretical Investigation of Single-Molecule-Magnet Behavior in Mononuclear Dysprosium and Californium Complexes, Inorg. Chem., 2023, 62, 1649–1658 CrossRef CAS PubMed.
- L. C. Pereira, C. M. Camp, J. T. Coutinho, L. Chatelain, P. Maldivi, M. Almeida and M. Mazzanti, Single-molecule-magnet behavior in mononuclear homoleptic tetrahedral Uranium(III) complexes, Inorg. Chem., 2014, 53, 11809–11811 CrossRef CAS PubMed.
- L. Chatelain, F. Tuna, J. Pécaut and M. Mazzanti, A zig-zag uranyl (v)–Mn (ii) single chain magnet with a high relaxation barrier, ChemComm, 2015, 51, 11309–11312 RSC.
- B. Teyar, S. Boucenina, L. Belkhiri, B. Le Guennic, A. Boucekkine and M. Mazzanti, Theoretical investigation of the electronic structure and magnetic properties of oxo-bridged uranyl (V) dinuclear and trinuclear complexes, Inorg. Chem., 2019, 58, 10097–10110 CrossRef CAS PubMed.
- N. Magnani, E. Colineau, R. Eloirdi, J.-C. Griveau, R. Caciuffo, S. Cornet, I. May, C. Sharrad, D. Collison and R. Winpenny, Superexchange coupling and slow magnetic relaxation in a transuranium polymetallic complex, Phys. Rev. Lett., 2010, 104, 197202 CrossRef CAS PubMed.
- K. R. Meihaus and J. R. Long, Actinide-based single-molecule magnets, Dalton Trans., 2015, 44, 2517–2528 RSC.
- D. R. Kindra and W. J. Evans, Magnetic susceptibility of uranium complexes, Chem. Rev., 2014, 114, 8865–8882 CrossRef CAS PubMed.
- A. Bencini and D. Gatteschi, Electron paramagnetic resonance of exchange coupled systems, Springer Science & Business Media, 2012 Search PubMed.
- L. J. Berliner, S. S. Eaton and G. R. Eaton, Distance measurements in biological systems by EPR, Springer Science & Business Media, 2006 Search PubMed.
- N. Kaltsoyannis, Transuranic computational chemistry, Chem. – Eur. J., 2018, 24, 2815–2825 CrossRef CAS PubMed.
- L. R. Morss, N. M. Edelstein and J. Fuger, The Chemistry of the Actinide and Transactinide Elements (Set Vol. 1–6), Springer, vol. 1–6, 2011 Search PubMed.
- T. Saue and L. Visscher, Relativistic All–Electron Approaches to the Study of f Element Chemistry, in Computational methods in lanthanide and actinide chemistry, 2015, pp. 55–87 Search PubMed.
- Q.-C. Luo and Y.-Z. Zheng, Methods and models of theoretical calculation for single-molecule magnets, Magnetochemistry, 2021, 7, 107 CrossRef CAS.
- A. Sarkar, S. Dey and G. Rajaraman, Role of coordination number and geometry in controlling the magnetic anisotropy in FeII, CoII, and NiII single-ion magnets, Chem. – Eur. J., 2020, 26, 14036–14058 CrossRef CAS PubMed.
- H. Bolvin, Computational Modelling of Molecular Nanomagnets, Springer, 2023, pp. 179–218 Search PubMed.
- K. Andersson, P. A. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, Second-order perturbation theory with a CASSCF reference function, J. Phys. Chem., 1990, 94, 5483–5488 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, n-electron valence state perturbation theory: A spinless formulation and an efficient implementation of the strongly contracted and of the partially contracted variants, J. Chem. Phys., 2002, 117, 9138–9153 CrossRef CAS.
- P. E. Siegbahn, Direct configuration interaction with a reference state composed of many reference configurations, Int. J. Quantum Chem., 1980, 18, 1229–1242 CrossRef CAS.
- M. Srnec, J. Chalupsky, M. Fojta, L. Zendlová, L. Havran, M. Hocek, M. Kyvala and L. Rulisek, Effect of Spin− Orbit Coupling on Reduction Potentials of Octahedral Ruthenium (II/III) and Osmium (II/III) Complexes, J. Am. Chem. Soc., 2008, 130, 10947–10954 CrossRef CAS PubMed.
- P.Å Malmqvist, B. O. Roos and B. Schimmelpfennig, The restricted active space (RAS) state interaction approach with spin–orbit coupling, Chem. Phys. Lett., 2002, 357, 230–240 CrossRef CAS.
- S. Dey and G. Rajaraman, Deciphering the Role of Symmetry and Ligand Field in Designing Three-Coordinate Uranium and Plutonium Single-Molecule Magnets, Inorg. Chem., 2022, 61, 1831–1842 CrossRef CAS PubMed.
- S. Dey, G. Velmurugan and G. Rajaraman, How important is the coordinating atom in controlling magnetic anisotropy in uranium(III) single-ion magnets? A theoretical perspective, Dalton Trans., 2019, 48, 8976–8988 RSC.
- F. Gendron, H. Bolvin and J. Autschbach, Organometallic Magnets, Springer, 2018, pp. 355–390 Search PubMed.
- K. Stevens, Matrix elements and operator equivalents connected with the magnetic properties of rare earth ions, Proc. Phys. Soc., Sect. A, 1952, 65, 209 CrossRef.
- M. Atanasov, D. Ganyushin, K. Sivalingam and F. Neese, A modern first-principles view on ligand field theory through the eyes of correlated multireference wavefunctions, in Molecular electronic structures of transition metal complexes II, 2012, pp. 149–220 Search PubMed.
- (a) F. Neese, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2012, 2, 73–78 CAS; (b) F. Neese, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. Fdez. Galván, N. Ferré, L. M. Frutos and L. Gagliardi, Molcas 8: New capabilities for multiconfigurational quantum chemical calculations across the periodic table, J. Comput. Chem., 2016, 37, 506–541 CrossRef CAS PubMed.
- L. Ungur and L. F. Chibotaru, Ab initio crystal field for lanthanides, Chem. – Eur. J, 2017, 23, 3708–3718 CrossRef CAS PubMed.
- J. S. Griffith, The theory of transition-metal ions, Cambridge University Press, 1964 Search PubMed.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, PHI: a powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS PubMed.
- S. Cardona-Serra, L. Escalera-Moreno, J. J. Baldoví, A. Gaita-Ariño, J. M. Clemente-Juan and E. Coronado, SIMPRE1. 2: Considering the hyperfine and quadrupolar couplings and the nuclear spin bath decoherence, J. Comput. Chem., 2016, 37, 1238–1244 CrossRef CAS PubMed.
- J. van Leusen, M. Speldrich, H. Schilder and P. Kögerler, Comprehensive insight into molecular magnetism via CONDON: Full vs. effective models, Coord. Chem. Rev., 2015, 289, 137–148 CrossRef.
- J. Jung, M. A. Islam, V. L. Pecoraro, T. Mallah, C. Berthon and H. Bolvin, Derivation of lanthanide series crystal field parameters from first principles, Chem. – Eur. J., 2019, 25, 15112–15122 CrossRef CAS PubMed.
- N. Chang, J. B. Gruber, R. P. Leavitt and C. A. Morrison, Optical spectra, energy levels, and crystal–field analysis of tripositive rare earth ions in Y2O3. I. Kramers ions in C2 sites, J. Chem. Phys., 1982, 76, 3877–3889 CrossRef CAS.
- C. Benelli and D. Gatteschi, Introduction to molecular magnetism: from transition metals to lanthanides, John Wiley & Sons, 2015 Search PubMed.
- S. Dey, T. Sharma, A. Sarkar and G. Rajaraman, Computational Modelling of Molecular Nanomagnets, Springer, 2023, pp. 291–394 Search PubMed.
- C. E. Jackson, I. P. Moseley, R. Martinez, S. Sung and J. M. Zadrozny, A reaction-coordinate perspective of magnetic relaxation, Chem. Soc. Rev., 2021, 50, 6684–6699 RSC.
- R. Orbach, Spin-lattice relaxation in rare-earth salts, Proc. R. Soc. London, Ser. A, 1961, 264, 458–484 CAS.
- L. Ungur, M. Thewissen, J.-P. Costes, W. Wernsdorfer and L. F. Chibotaru, Interplay of strongly anisotropic metal ions in magnetic blocking of complexes, Inorg. Chem., 2013, 52, 6328–6337 CrossRef CAS PubMed.
- P. Scott and C. Jeffries, Spin-lattice relaxation in some rare-earth salts at helium temperatures; observation of the phonon bottleneck, Phys. Rev., 1962, 127, 32 CrossRef CAS.
- K. S. Pedersen, K. R. Meihaus, A. Rogalev, F. Wilhelm, D. Aravena, M. Amoza, E. Ruiz, J. R. Long, J. Bendix and R. Clérac, [UF6]2−: A Molecular Hexafluorido Actinide (IV) Complex with Compensating Spin and Orbital Magnetic Moments, Angew. Chem., Int. Ed., 2019, 58, 15650–15654 CrossRef CAS PubMed.
- J. A. Seed, L. Birnoschi, E. Lu, F. Tuna, A. J. Wooles, N. F. Chilton and S. T. Liddle, Anomalous magnetism of uranium(IV)-oxo and-imido complexes reveals unusual doubly degenerate electronic ground states, Chem, 2021, 7, 1666–1680 CAS.
- J. D. Rinehart and J. R. Long, Slow magnetic relaxation in homoleptic trispyrazolylborate complexes of neodymium(III) and uranium(III), Dalton Trans., 2012, 41, 13572–13574 RSC.
- S. Dey and G. Rajaraman, In silico design of pseudo D 5 h actinide based molecular magnets: role of covalency in magnetic anisotropy, J. Chem. Sci., 2019, 131, 124 CrossRef CAS.
- J. J. Baldoví, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado and A. Gaita-Ariño, Modeling the properties of uranium-based single ion magnets, Chem. Sci., 2013, 4, 938–946 RSC.
- J. J. Le Roy, S. I. Gorelsky, I. Korobkov and M. Murugesu, Slow magnetic relaxation in uranium(III) and neodymium(III) cyclooctatetraenyl complexes, Organometallics, 2015, 34, 1415–1418 CrossRef CAS.
- M. A. Islam, C. Berthon, J. Jung and H. Bolvin, Bonding and Magnetic Trends in the [AnIII(DPA)3]3− Series Compared to the Ln(III) and An(IV) Analogues, Inorg. Chem., 2023, 62, 17254–17264 CrossRef CAS PubMed.
- M. Autillo, M. A. Islam, J. Jung, J. Pilmé, N. Galland, L. Guerin, P. Moisy, C. Berthon, C. Tamain and H. Bolvin, Crystallographic structure and crystal field parameters in the [AnIV(DPA)3]2− series, An = Th, U, Np, Pu, Phys. Chem. Chem. Phys., 2020, 22, 14293–14308 RSC.
- J. Jung, M. Atanasov and F. Neese, Ab initio ligand-field theory analysis and covalency trends in actinide and lanthanide free ions and octahedral complexes, Inorg. Chem., 2017, 56, 8802–8816 CrossRef CAS PubMed.
- J. D. Rinehart and J. R. Long, Slow magnetic relaxation in a trigonal prismatic uranium(III) complex, J. Am. Chem. Soc., 2009, 131, 12558–12559 CrossRef CAS PubMed.
- J. D. Rinehart, K. R. Meihaus and J. R. Long, Observation of a secondary slow relaxation process for the field-induced single-molecule magnet U (H2BPz2)3, J. Am. Chem. Soc., 2010, 132, 7572–7573 CrossRef CAS PubMed.
- S. Dey and G. Rajaraman, In silico design criteria for high blocking barrier uranium(III) SIMs, ChemComm, 2022, 58, 6817–6820 RSC.
- M. Spivak, K. D. Vogiatzis, C. J. Cramer, C. D. Graaf and L. Gagliardi, Quantum Chemical Characterization of Single Molecule Magnets Based on Uranium, J. Phys. Chem. A, 2017, 121, 1726–1733 CrossRef CAS PubMed.
- M. A. Antunes, L. C. Pereira, I. C. Santos, M. Mazzanti, J. Marcalo and M. Almeida, [U (TpMe2) 2(bipy)]+: A Cationic Uranium(III) Complex with Single-Molecule-Magnet Behavior, Inorg. Chem., 2011, 50, 9915–9917 CrossRef CAS PubMed.
- J. T. Coutinho, M. A. Antunes, L. C. Pereira, H. Bolvin, J. Marcalo, M. Mazzanti and M. Almeida, Single-ion magnet behaviour in [U(TpMe2)2I], Dalton Trans., 2012, 41, 13568–13571 RSC.
- N. J. Wolford, X. Yu, S. C. Bart, J. Autschbach and M. L. Neidig, Ligand effects on electronic structure and bonding in U (III) coordination complexes: a combined MCD, EPR and computational study, Dalton Trans., 2020, 49, 14401–14410 RSC.
- R. F. Higgins, C. J. Tatebe, S. C. Bart and M. P. Shores, Excited-state effects on magnetic properties of U (III) and U (IV) pyrazolylborate complexes, ChemComm, 2019, 55, 10611–10614 RSC.
- M. A. Antunes, I. C. Santos, H. Bolvin, L. C. Pereira, M. Mazzanti, J. Marçalo and M. Almeida, Crystal structure diversity in the bis [hydrotris (3, 5-dimethylpyrazolyl) borate] iodouranium(III) complex: from neutral to cationic forms, Dalton Trans., 2013, 42, 8861–8867 RSC.
- J. T. Coutinho, M. A. Antunes, L. C. Pereira, J. Marçalo and M. Almeida, Zero-field slow magnetic relaxation in a uranium(III) complex with a radical ligand, ChemComm, 2014, 50, 10262–10264 RSC.
- C. Apostolidis, A. Kovács, O. Walter, E. Colineau, J. C. Griveau, A. Morgenstern, J. Rebizant, R. Caciuffo, P. J. Panak and T. Rabung, Tris–{hydridotris (1−pyrazolyl) borato} actinide Complexes: Synthesis, Spectroscopy, Crystal Structure, Bonding Properties and Magnetic Behaviour, Chem. – Eur. J., 2020, 26, 11293–11306 CrossRef CAS PubMed.
- K. R. Meihaus, S. G. Minasian, W. W. Lukens Jr, S. A. Kozimor, D. K. Shuh, T. Tyliszczak and J. R. Long, Influence of pyrazolate vs N-heterocyclic carbene ligands on the slow magnetic relaxation of homoleptic trischelate lanthanide (III) and uranium(III) complexes, J. Am. Chem. Soc., 2014, 136, 6056–6068 CrossRef CAS PubMed.
- S. Dey, G. Velmurugan and G. Rajaraman, How important is the coordinating atom in controlling magnetic anisotropy in uranium(III) single-ion magnets? A theoretical perspective, Dalton Trans., 2019, 48, 8976–8988 RSC.
- D. Pividori, M. E. Miehlich, B. Kestel, F. W. Heinemann, A. Scheurer, M. Patzschke and K. Meyer, Uranium going the soft way: low-valent uranium(III) coordinated to an arene-anchored tris-thiophenolate ligand, Inorg. Chem., 2021, 60, 16455–16465 CrossRef CAS PubMed.
- F. Moro, D. P. Mills, S. T. Liddle and J. van Slageren, The inherent single–molecule magnet character of trivalent uranium, Angew. Chem., 2013, 125, 3514–3517 CrossRef.
- C. A. Goodwin, F. Tuna, E. J. McInnes, S. T. Liddle, J. McMaster, I. J. Vitorica-Yrezabal and D. P. Mills, [UIII {N (SiMe2tBu) 2} 3]: A Structurally Authenticated Trigonal Planar Actinide Complex, Chem. – Eur. J., 2014, 20, 14579–14583 CrossRef CAS PubMed.
- F. S. Guo, Y. C. Chen, M. L. Tong, A. Mansikkamäki and R. A. Layfield, Uranocenium: synthesis, structure, and chemical bonding, Angew. Chem., 2019, 131, 10269–10273 CrossRef.
- M. A. Boreen, D. J. Lussier, B. A. Skeel, T. D. Lohrey, F. A. Watt, D. K. Shuh, J. R. Long, S. Hohloch and J. Arnold, Inorg. Chem., 2019, 58, 16629–16641 CrossRef CAS PubMed.
- L. Escalera-Moreno, J. J. Baldoví, A. Gaita-Arino and E. Coronado, Exploring the high-temperature frontier in molecular nanomagnets: from lanthanides to actinides, Inorg. Chem., 2019, 58, 11883–11892 CrossRef CAS PubMed.
- M. A. Antunes, J. T. Coutinho, I. C. Santos, J. Marçalo, M. Almeida, J. J. Baldoví, L. C. Pereira, A. Gaita-Ariño and E. Coronado, A mononuclear uranium(IV) single–molecule magnet with an azobenzene radical ligand, Chem. – Eur. J., 2015, 21, 17817–17826 CrossRef CAS PubMed.
- S. J. Kraft, U. J. Williams, S. R. Daly, E. J. Schelter, S. A. Kozimor, K. S. Boland, J. M. Kikkawa, W. P. Forrest, C. N. Christensen and D. E. Schwarz, Synthesis, characterization, and multielectron reduction chemistry of uranium supported by redox-active α-diimine ligands, Inorg. Chem., 2011, 50, 9838–9848 CrossRef CAS PubMed.
- D. M. King, F. Tuna, J. McMaster, W. Lewis, A. J. Blake, E. J. McInnes and S. T. Liddle, Single–molecule magnetism in a single–ion triamidoamine uranium(V) terminal mono–oxo complex, Angew. Chem., 2013, 125, 5021–5024 CrossRef.
- D. M. King, P. A. Cleaves, A. J. Wooles, B. M. Gardner, N. F. Chilton, F. Tuna, W. Lewis, E. J. McInnes and S. T. Liddle, Molecular and electronic structure of terminal and alkali metal-capped uranium(V) nitride complexes, Nat. Commun., 2016, 7, 13773 CrossRef CAS PubMed.
- D. M. King, P. A. Cleaves, A. J. Wooles, B. M. Gardner, N. F. Chilton, F. Tuna, W. Lewis, E. J. McInnes and S. T. Liddle, Molecular and electronic structure of terminal and alkali metal-capped uranium(V) nitride complexes, Nat. Commun., 2016, 7, 1–14 Search PubMed.
- N. Magnani, C. Apostolidis, A. Morgenstern, E. Colineau, J. C. Griveau, H. Bolvin, O. Walter and R. Caciuffo, Magnetic memory effect in a transuranic mononuclear complex, Angew. Chem., Int. Ed., 2011, 50, 1696–1698 CrossRef CAS PubMed.
- S. K. Singh, C. J. Cramer and L. Gagliardi, Correlating Electronic Structure and Magnetic Anisotropy in Actinide Complexes [An(COT)2], AnIII/IV = U, Np, and Pu, Inorg. Chem., 2020, 59, 6815–6825 CrossRef CAS PubMed.
- N. Magnani, E. Colineau, J. C. Griveau, C. Apostolidis, O. Walter and R. Caciuffo, A plutonium-based single-molecule magnet, ChemComm, 2014, 50, 8171–8173 RSC.
- C. A. Gaggioli and L. Gagliardi, Theoretical Investigation of Plutonium-Based Single-Molecule Magnets, Inorg. Chem., 2018, 57, 8095–8105 CrossRef PubMed.
- Y. Dong, P. Yan, X. Zou and G. Li, Azacyclo-auxiliary ligand-tuned SMMs of dibenzoylmethane Dy(III) complexes, Inorg. Chem. Front., 2015, 2, 827–836 RSC.
- C. Gao, A. Genoni, S. Gao, S. Jiang, A. Soncini and J. Overgaard, Observation of the asphericity of 4 f-electron density and its relation to the magnetic anisotropy axis in single-molecule magnets, Nat. Chem., 2020, 12, 213–219 CrossRef CAS PubMed.
- L. M. A. Quintana, D. J. Lussier, J. N. Wacker, A. Bajaj, D. R. Russo, A. G. Cosby, A. N. Gaiser, J. J. Woods, A. A. Peterson, W. W. Lukens, C. H. Booth, S. G. Minasian, D. K. Shuh, J. Autschbach, J. R. Long and R. J. Abergel, Slow Magnetic Relaxation in a Californium Complex, J. Am. Chem. Soc., 2024, 146, 31671–31680 CrossRef PubMed.
- G. Cucinotta, M. Perfetti, J. Luzon, M. Etienne, P. E. Car, A. Caneschi, G. Calvez, K. Bernot and R. Sessoli, Magnetic anisotropy in a dysprosium/DOTA single–molecule magnet: beyond simple magneto–structural correlations, Angew. Chem., Int. Ed., 2012, 51, 1606–1610 CrossRef CAS PubMed.
- J. F. Desreux, Nuclear magnetic resonance spectroscopy of lanthanide complexes with a tetraacetic tetraaza macrocycle. Unusual conformation properties, Inorg. Chem., 1980, 19, 1319–1324 CrossRef CAS.
- P.-E. Car, M. Perfetti, M. Mannini, A. Favre, A. Caneschi and R. Sessoli, Giant field dependence of the low temperature relaxation of the magnetization in a dysprosium(III)–DOTA complex, ChemComm, 2011, 47, 3751–3753 RSC.
- M. A. Antunes, I. C. Santos, H. Bolvin, L. C. Pereira, M. Mazzanti, J. Marcalo and M. Almeida, Crystal structure diversity in the bis[hydrotris(3,5-dimethylpyrazolyl)borate]iodouranium(III) complex: from neutral to cationic forms, Dalton Trans., 2013, 42, 8861–8867 RSC.
- F. S. Guo, N. Tsoureas, G. Z. Huang, M. L. Tong, A. Mansikkamäki and R. A. Layfield, Isolation of a Perfectly Linear Uranium(II) Metallocene, Angew. Chem., Int. Ed., 2020, 59, 2299–2303 CrossRef CAS PubMed.
- J. D. Rinehart and J. R. Long, Exploiting single-ion anisotropy in the design of f-element single-molecule magnets, Chem. Sci., 2011, 2, 2078–2085 RSC.
- C. Tabata, H. Watanabe, K. Shirasaki, A. Sunaga, T. Fukuda, D. Li and T. Yamamura, Crystallographic and/or magnetic properties of neutral and cationic uranium(IV) sandwiched phthalocyanine complexes, J. Mol. Struct., 2023, 1277, 134870 CrossRef CAS.
- Y. Duan, L. E. Rosaleny, J. T. Coutinho, S. Giménez-Santamarina, A. Scheie, J. J. Baldoví, S. Cardona-Serra and A. Gaita-Ariño, Data-driven design of molecular nanomagnets, Nat. Commun., 2022, 13, 7626 CrossRef CAS PubMed.
- S. Dey, T. Sharma and G. Rajaraman, Unravelling the role of spin–vibrational coupling in designing high-performance pentagonal bipyramidal Dy (III) single ion magnets, Chem. Sci., 2024, 15, 6465–6477 RSC.
- A. Lunghi, F. Totti, S. Sanvito and R. Sessoli, Intra-molecular origin of the spin-phonon coupling in slow-relaxing molecular magnets, Chem. Sci., 2017, 8, 6051–6059 RSC.
- A. Lunghi and S. Sanvito, How do phonons relax molecular spins?, Sci. Adv., 2019, 5, eaax7163 CrossRef CAS PubMed.
- A. Lunghi and S. Sanvito, Multiple spin–phonon relaxation pathways in a Kramer single-ion magnet, J. Chem. Phys., 2020, 153, 174113 CrossRef CAS PubMed.
- A. Lunghi, F. Totti, R. Sessoli and S. Sanvito, The role of anharmonic phonons in under-barrier spin relaxation of single molecule magnets, Nat. Commun., 2017, 8, 1–7 CrossRef PubMed.
- L. Tesi, A. Lunghi, M. Atzori, E. Lucaccini, L. Sorace, F. Totti and R. Sessoli, Giant spin–phonon bottleneck effects in evaporable vanadyl-based molecules with long spin coherence, Dalton Trans., 2016, 45, 16635–16643 RSC.
- M. Atzori, L. Tesi, S. Benci, A. Lunghi, R. Righini, A. Taschin, R. Torre, L. Sorace and R. Sessoli, Spin dynamics and low energy vibrations: insights from vanadyl-based potential molecular qubits, J. Am. Chem. Soc., 2017, 139, 4338–4341 CrossRef CAS PubMed.
- M. Briganti, F. Santanni, L. Tesi, F. Totti, R. Sessoli and A. Lunghi, A Complete Ab Initio View of Orbach and Raman Spin–Lattice Relaxation in a Dysprosium Coordination Compound, J. Am. Chem. Soc., 2021, 143, 13633–13645 CrossRef CAS PubMed.
- A. Lunghi, Toward exact predictions of spin-phonon relaxation times: An ab initio implementation of open quantum systems theory, Sci. Adv., 2022, 8, eabn7880 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4qi02326a |
| This journal is © the Partner Organisations 2025 |