Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Determining the zero-field cooling/field cooling blocking temperature from AC susceptibility data for single-molecule magnets†‡
Yolimar Gil a,
María Mar Quesada-Moreno
a,
María Mar Quesada-Moreno *b,
María A. Palacios
*b,
María A. Palacios c,
Silvia Gómez-Coca*d,
Enrique Colacio
c,
Silvia Gómez-Coca*d,
Enrique Colacio *c,
Eliseo Ruiz
*c,
Eliseo Ruiz *d and
Daniel Aravena
*d and
Daniel Aravena *e
*e
aFacultad de Ciencias Químicas y Farmacéuticas, Universidad de Chile, Casilla 233, Santiago, Chile
bDepartamento de Química Física y Analítica, Universidad de Jaén, Campus Las Lagunillas, 23071, Jaén, Spain. E-mail: mqmoreno@ujaen.es
cDepartamento de Química Inorgánica, Facultad de Ciencias, Universidad de Granada, 18071Granada, Spain. E-mail: ecolacio@ugr.es
dDepartament de Química Inorgànica i Orgànica and Institut de Recerca de Química Teòrica i Computacional, Universitat de Barcelona, Diagonal 645, 08028 Barcelona, Spain. E-mail: silvia.gomez.coca@ub.edu; eliseo.ruiz@qi.ub.edu
eDepartamento de Química de los Materiales, Facultad de Química y Biología, Universidad de Santiago de Chile, Casilla 40, Correo 33, Santiago, Chile. E-mail: daniel.aravena.p@usach.cl
First published on 11th February 2025
Abstract
We present a general relationship between the magnetisation blocking temperature (TB) measured using the zero-field cooling/field cooling technique (ZFC/FC) and the temperature-dependent spin relaxation time obtained from AC susceptibility and magnetisation decay measurements. The presented mathematical approach supplies ZFC/FC blocking temperatures at any heating rate (RH), providing comparable values to those obtained experimentally, as demonstrated by testing 107 examples for reported single-molecule magnets (SMMs) where the ZFC/FC curve has been measured. This procedure is examined in further detail for a new single-molecule magnet, [Dy(OPAd2Bz)2(H2O)4Br]Br2·4THF (1) (OPAd2Bz: di(1-adamantyl)benzylphosphine oxide). For this compound, ZFC/FC measurements were made over a broad range of heating rates (0.01–5 K min−1), which agreed with the general behaviour predicted from AC susceptibility data. We discuss how the demagnetisation mechanism determines the sensitivity of TB with respect to the heating rate: TB is mostly insensitive to RH for Orbach relaxation, while there is a larger sensitivity for Raman-limited systems. Our conclusions provide a clear physical interpretation of ZFC/FC blocking temperatures, aiding in the proper contextualization of this figure of merit.
Introduction
In the early 1990s, the discovery of single molecule magnets (SMMs) sparked a revolution in the field of molecular magnetism. These molecular transition metal coordination compounds exhibit a magnetic memory effect, which arises from blocking magnetisation via an anisotropic barrier (Ueff) for prolonged periods in the absence of an external magnetic field and below a critical temperature known as the blocking temperature (TB).1–5 SMMs have been extensively investigated due to their immense technological potential in molecular spintronics, ultra-high-density data storage, and quantum information technologies using spin qubits.6–12However, a significant challenge in the field remains, necessitating the achievement of a magnetic memory effect at practical/high temperatures while maintaining high thermal stability in the presence of air and humidity.13,14 Mononuclear SMM complexes exhibit modulable magnetic anisotropy through chemical tuning of their coordination environment, representing the smallest nanomagnets which can be modulated by the rational selection of metal ions and ligands.15–26 Notably, the DyIII ion, with its unquenched orbital momentum and large magnetic anisotropy, has emerged as a leading candidate to revolutionize technology based on electron spin.15–20,27–29
Experimental and computational studies have revealed that strong axial crystal fields, achieved through axial distribution of ligands, are crucial for DyIII complexes to exhibit remarkable SMM behaviour.15–20,30–32 More recent approaches seek to attenuate vibrational displacements to hamper Raman relaxation.33,34 For future systems, some theoretical works suggest exploring the surface deposition of SMMs and uncommon oxidation states.35,36 In the quest to develop practical SMM applications, reaching a blocking temperature (TB) above liquid nitrogen temperature (77 K) is crucial. There are only two molecules that have surpassed this crucial barrier; both of them are Dy compounds. Mononuclear DyIII [Dy(C5Me5(CpiPr5))][B(C6F5)4]37 and mixed-valence DyIIIDyII dinuclear [Dy2I3(CpiPr5)2] metallocene38 compounds have achieved landmark performances with Ueff = 2217 K and 2347 K, respectively, and TB = 80 K in both cases. The uniaxial local symmetry stabilizes the largest mJ = ±15/2 ground state39,40 in the former, and the collinearity of the local anisotropic axes and the strong 4f-radical coupling in the latter, results in a significant separation from the first and higher excited states.38,41,42 However, compounds with such low coordination are unstable and the need for more stable systems with similar magnetic properties arises. Different high-order symmetry axes, such as those found in trigonal bipyramidal (D3h),43,44 square antiprismatic (D4d),45–49 sandwich,37,50–54 and pentagonal bipyramidal (D5h),55–73 have been recommended to favour slower relaxation of magnetisation by reducing transverse anisotropy and suppressing quantum tunnelling of the magnetisation (QTM). The presence of a high-order symmetry axis also promotes the collinearity of anisotropic axes of the excited and ground states, leading to larger Ueff values.74,75 Nonetheless, it is essential to engineer molecular vibrations to control the spin lifetime of SMM complexes,76 as flexible lattices are responsible for fast relaxation. Addressing the requirements of high-temperature performance and thermal air and humidity stability, mononuclear DyIII SMMs with D5h geometry hold a fair position, displaying, in many cases, stability against these factors with Ueff and TB values as high as 1162 K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 63 and 36 K,70 respectively. Although some recent mononuclear DyIII SMMs with D5h geometry have been shown to be air-sensitive, the majority are stable.60,61,73,77 Recently, the role of spin-vibrational coupling in designing high-performance pentagonal bipyramidal DyIII SMMs was revealed using a combination of density functional theory (DFT) and complete active space self-consistent field (CASSCF) calculations.33 There are about thirty examples of mononuclear DyIII SMMs with D5h geometry, but those employing axial bulky phosphine oxide type ligands (high electron density) and weak donor equatorial ones (e.g., water)56–59,62,64 are relatively scarce. These D5h based SMMs represent a highly efficient approach for constructing new high-performance SMMs.
63 and 36 K,70 respectively. Although some recent mononuclear DyIII SMMs with D5h geometry have been shown to be air-sensitive, the majority are stable.60,61,73,77 Recently, the role of spin-vibrational coupling in designing high-performance pentagonal bipyramidal DyIII SMMs was revealed using a combination of density functional theory (DFT) and complete active space self-consistent field (CASSCF) calculations.33 There are about thirty examples of mononuclear DyIII SMMs with D5h geometry, but those employing axial bulky phosphine oxide type ligands (high electron density) and weak donor equatorial ones (e.g., water)56–59,62,64 are relatively scarce. These D5h based SMMs represent a highly efficient approach for constructing new high-performance SMMs.
As mentioned previously, the DyIII metallocene compounds [Dy(C5Me5(CpiPr5))][B(C6F5)4] and [Dy2I3(CpiPr5)2] show the highest blocking temperature reported to date. This value was measured as the maximum temperature at which magnetic hysteresis is observed (herein TB–H). However, there are two other ways to quantify the blocking temperature: the temperature at which the magnetic relaxation time is equal to 100 s (TB-100) and the maximum of the zero-field cooled (ZFC) magnetic susceptibility (TB-ZFC/FC). For the dysprosium metallocene cation, these values are 67 and 52 K, respectively. This example indicates how different the blocking temperature can be depending on the measurement technique. Furthermore, key experimental parameters can also influence TB significantly. In the case of magnetic hysteresis measurements, TB–H varies with the field sweep rate, where faster sweep rate programs lead to higher blocking temperatures. Focusing on ZFC/FC experiments, TB-ZFC/FC is sensitive to the heating rate, with faster heating rates leading to higher blocking temperatures. Unfortunately, the experimentally employed heating rate is often missing from reports in the literature, hindering a rigorous comparison between systems from different publications. Another issue is related to a misunderstanding of the definition of TB-ZFC/FC, since some authors refer to this value as the temperature where the ZFC and FC curves diverge, which corresponds to the irreversibility temperature (Tirrev) and is higher than that of TB-ZFC/FC.78 Although TB-100 usually does not depend strongly on the measurement conditions, the 100 s definition is arbitrary and it is not clear why the blocking temperature at this specific relaxation time is more informative of SMM behaviour than other thresholds. Blocking temperatures are convenient as “single-molecule magnet” performance metrics since they condense a complex magnetic relaxation dependence into a single figure. Moreover, the existence of a magnetic blocking temperature provides a clear definition of a “molecular magnet” that goes beyond the presence of slow relaxation of magnetisation. However, other demagnetisation parameters, such as magnetic coercivities or demagnetisation barriers (Ueff) are also relevant for the assessment of SMM performance.
In this paper, we propose a new approach for estimating TB-ZFC/FC at any heating rate from the temperature-dependent spin relaxation time obtained from AC susceptibility and magnetisation decay measurements, to advance towards a more harmonized definition of TB. In this way, TB-ZFC/FC data from different studies can be better compared, as many examples of ZFC/FC experiments in the literature do not state the heating rate. Furthermore, the model allows for the estimation of TB-ZFC/FC in cases where the ZFC/FC experiment was not done. Experimentally, performing the ZFC/FC experiment together with AC magnetometry measurements is not a practical problem, so the main use of our proposed method is not to avoid the ZFC/FC experiment but to provide a new tool to contextualize and estimate ZFC/FC blocking temperatures.
To validate this new model, we compared TB-ZFC/FC values for 107 examples of SMMs from the literature for which ZFC/FC data were reported, including both lanthanide and transition metal systems. Furthermore, we conducted a detailed AC susceptibility and ZFC/FC study for a new DyIII SMM with D5h geometry. Concretely, we measured ZFC/FC curves for a wide range of heating rates, demonstrating that the presented model accurately predicted TB-ZFC values and captured the heating rate dependence of the blocking temperature.
Results and discussion
Mathematical model for ZFC/FC blocking temperature determined from AC susceptibility
Our first goal is relating the blocking temperature measured by zero field cooling experiments with an expression in terms of the temperature dependent relaxation time. Experimentally, susceptibility is calculated as the ratio between the magnetic moment and the applied magnetic field. The isothermal (static) susceptibility is:
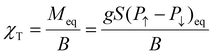 | (1) |
Combining the equilibrium and out of equilibrium expressions for magnetic susceptibility, χZFC is defined as:
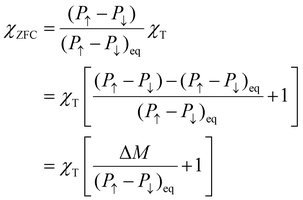 | (2) |
The numerator on the r.h.s. of eqn (2) is the difference between the equilibrium and out of equilibrium magnetic moments (ΔM).
The kinetic equation for a system after a perturbation is:
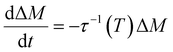 | (3) |
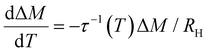 | (4) |
The general solution of eqn (4) is:
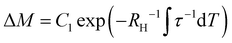 | (5) |
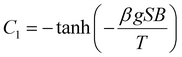 and the combination of eqn (2) and (5) yields the simple form:
and the combination of eqn (2) and (5) yields the simple form:
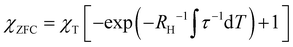 | (6) |
In practice, the magnetic moment is not zero at the beginning of the heating step. This is the typical situation in ZFC/FC experiments and depends on the orientational distribution of magnetic moments, their alignment with respect to the external field and operational parameters, as the time needed to stabilize the initial temperature in each experiment. Since this parameter is sample and experiment dependent, we assume it is an effective constant, 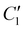 , with a value between 0 and 1. In this way, eqn (7) becomes:
, with a value between 0 and 1. In this way, eqn (7) becomes:
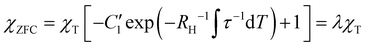 | (7) |
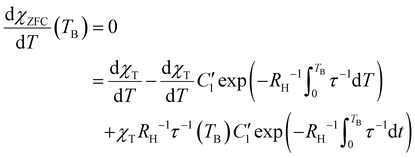 | (8) |
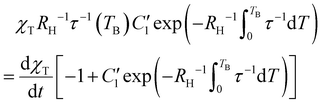 | (9) |
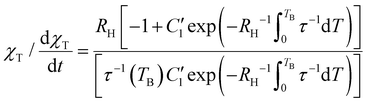 | (10) |
For simplicity, we consider that the isothermal susceptibility reasonably follows the Curie law:
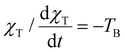 | (11) |
The assumption of the Curie law greatly simplifies the following equations but can be reversed if needed.
Hence, the blocking temperature is:
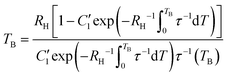 | (12) |
Eqn (12) can be expressed in a way that the l.h.s. coincides with the term in square brackets from eqn (7):
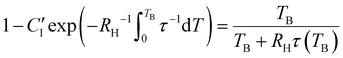 | (13) |
Thus, the blocking temperature can be estimated by knowing the heating rate, the temperature dependence of τ and 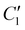 . In summary, TB can be obtained from either eqn (7) or (12), where the latter expression gives an explicit term for TB by assuming the Curie law. We analysed how these two approaches performed for a selected group of experimental examples from the literature (see section 4 and Table S8 in the ESI‡) and concluded that both equations provided satisfactory results for TB, especially for larger values of
. In summary, TB can be obtained from either eqn (7) or (12), where the latter expression gives an explicit term for TB by assuming the Curie law. We analysed how these two approaches performed for a selected group of experimental examples from the literature (see section 4 and Table S8 in the ESI‡) and concluded that both equations provided satisfactory results for TB, especially for larger values of 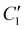 . In general, the Curie law assumption from eqn (13) gives slightly lower calculated TB values than eqn (7), which employs the experimental dependence of χ. In conclusion, we recommend employing either of the equations with
. In general, the Curie law assumption from eqn (13) gives slightly lower calculated TB values than eqn (7), which employs the experimental dependence of χ. In conclusion, we recommend employing either of the equations with 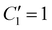 to obtain reliable estimations for TB-ZFC/FC.
to obtain reliable estimations for TB-ZFC/FC.
Synthesis and characterization of the DyIII SMM with D5h geometry
In view of previous considerations, we focused our efforts on the preparation of a mononuclear DyIII coordination complex, [Dy(OPAd2Bz)2(H2O)4Br]Br2·4THF (1) (OPAd2Bz: di(1-adamantyl)benzylphosphine oxide), close to ideal pentagonal bipyramidal geometry, which fulfilled all the desired characteristics to obtain SMMs with high Ueff and TB values, that is, a strong axial crystal field, humidity and air stability, and a rigid network to avoid rapid relaxation. A strong axial crystal field is created by the two bulky di(1-adamantyl)benzylphosphine oxide ligands located in the axial positions, which lead to a magnetic hysteresis that remains open up to 14 K, one of highest values for air/humidity stable SMMs synthesized to date. Four water molecules and one bromide anion are located in the equatorial positions; this is structurally different from previous compounds with axial phosphine oxide ligands, where five water molecules are located instead.56–59,62 Furthermore, we provide detailed insights into the mechanism that governs the magnetic relaxation of complex 1 by using ab initio CASSCF based computational methods.Complex 1 was prepared by the solvothermal reaction of the di(1-adamantyl)benzylphosphine oxide ligand with anhydrous DyBr3 in anhydrous tetrahydrofuran and in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
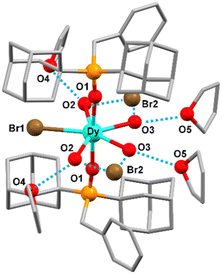
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio using a 23 mL Teflon-lined stainless steel container and keeping it at 100 °C for three days (see ESI‡ for further details). The resulting solution from the solvothermal reaction was allowed to evaporate at room temperature for several days, whereupon large colourless prismatic single-crystals of [Dy(OPAd2Bz)2(H2O)4Br]Br2·4THF (1) were obtained, which were air-stable (Fig. 1).
1 molar ratio using a 23 mL Teflon-lined stainless steel container and keeping it at 100 °C for three days (see ESI‡ for further details). The resulting solution from the solvothermal reaction was allowed to evaporate at room temperature for several days, whereupon large colourless prismatic single-crystals of [Dy(OPAd2Bz)2(H2O)4Br]Br2·4THF (1) were obtained, which were air-stable (Fig. 1).
The molecular structure of 1 consists of [Dy(OPAd2Bz)2(H2O)4Br]2+ cationic units, with are charge balanced by two free bromide anions, and four crystallization THF molecules (Figs. 1 and S3‡). The bromide anions and THF molecules interact with the cationic unit via hydrogen bonds. Within the cationic unit, the seven-coordinate DyIII centre exhibits a pentagonal bipyramidal geometry (PBPY-7), very close to an ideal D5h polyhedron, as supported by the continuous shape measurement analysis,79 which provides an S(PBPY-7) value of 0.948 (where 0 corresponds to the ideal D5h geometry) (Table S1, ESI‡). Two bulky OPAd2Bz ligands occupy the axial positions, whereas four water molecules and one bromide ion are in the equatorial plane (Fig. 1). The axial Dy–O1 distances (2.210(3) Å) are shorter than the equatorial Dy–O2/O3 (average value of 2.365 Å) and Dy–Br1 (2.8860(6) Å) ones; this indicates that the cationic unit shows a compressed PBPY-7 geometry with an almost linear axial O1–Dy–O1 angle (176.73(16)°) and equatorial Br1–Dy–O2, O2–Dy–O3 and O3–Dy–O3 angles of 74.24(9)°, 71.88(13)° and 68.12(17)°, respectively, close to the ideal angle of 72° (Table S3, ESI‡). The coordinated bromide atom seems to generate certain steric repulsion with the water molecules close to it, which is reflected in a Br1–Dy–O2 angle greater than 72°. In turn, this brings about the closeness between these two water molecules and the other two, thus showing O2–Dy–O3 and O3–Dy–O3 angles less than 72°. The P–O1–Dy angle is also very close to linearity (173.67(19)°) and the angles between the equatorial and axial atoms are around 90° (Table S3, ESI‡). Specifically, the local symmetry of the DyO6Br coordination sphere is C2v, with the C2 axis lying along the line connecting the coordinated bromide anion and the DyIII ion (Fig. 1). Each coordinated water molecule interacts with one free bromide anion and one THF molecule via hydrogen bonds. The O2⋯Br2 and O3⋯Br2 donor–acceptor distances show respective values of 3.161(4) Å and 3.154(3) Å, whereas those for the O2⋯O4(THF) and O3⋯O5(THF) donor–acceptor distances are 2.802(6) Å and 2.774(19) Å, respectively. Moreover, the shortest Dy⋯Dy intermolecular distance for 1 is 12.1090(3) Å, which indicates that the [Dy(OPAd2Bz)2(H2O)4Br]2+ units are well separated in the structure. There are no π⋯π stacking interactions between the aromatic benzene rings of different units. The free bromide atoms establish van der Waals interactions with the benzene hydrogens inside the same unit (3.0386(5) Å), and with the hydrogens of the CH2 (2.6475(5) Å) and adamantyl groups (2.7673(5) Å) of adjacent units (Fig. S3‡).
Magnetic measurements
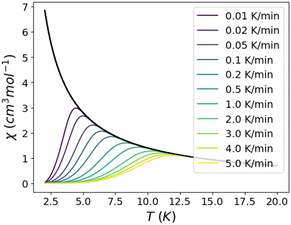
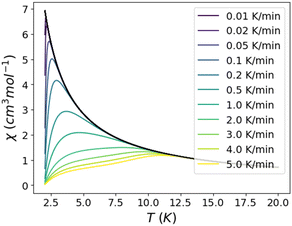
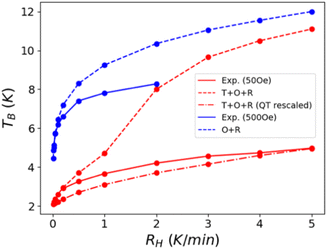
The DC magnetic properties of 1 were studied over the 2–300 K temperature range under an applied magnetic field of 0.5 T and magnetisation was studied over the field range of 0–7 T at temperatures between 2 and 7 K, see Fig. S4.‡ It is worth noting that the obtained curves clearly show the typical features of magnetisation blocking in an efficient mononuclear DyIII-SMM (sharp decrease of χMT at low temperature, sinusoidal behaviour of magnetisation at low field, divergence between FC and ZFC magnetic susceptibilities at low temperature, and magnetic hysteresis; see below and the magnetic studies section in the ESI‡).The ZFC/FC magnetic susceptibilities were collected at two magnetic fields and over a wide range of heating rates to evaluate TB and compare it with the proposed model (see Fig. 2). For the small field, 50 Oe, at very low heating rates, the ZFC/FC curves separate slightly at very low temperatures (Fig. S5‡). When increasing the heating rate, the ZFC and FC curves differ more and the temperatures at which the curves diverge rise to larger values. The maximum of the ZFC curve signalling TB goes from 2.5 K at 0.01 K min−1 to 5 K at 5 K min−1 (Table S4‡). When increasing the field to 500 Oe, the blocking temperatures rise significantly; this is probably due to the suppression of relaxation through QTM. At very low heating rates (0.01 K min−1), the blocking temperature is around 5 K and reaches 8 K at 2 K min−1. Faster heating rates did not provide values for the blocking temperature since the ZFC curve had no clear maximum (see Figs. 2 and S6‡).
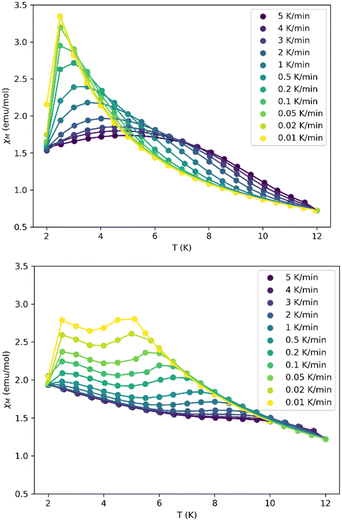 | ||
| Fig. 2 Temperature dependence of χM under ZFC conditions at different heating rates and with an applied field of 50 Oe (above) and 500 Oe (below). FC data are omitted for a better appreciation of the ZFC curves and their dependence on the heating rate. ZFC/FC curves for all data are available as ESI (Fig. S5 and S6‡). | ||
Alternating current (AC) magnetic susceptibility measurements were performed to study the slow relaxation of magnetisation. To obtain the maximum number of relaxation times and be able to study a larger temperature range, two pieces of equipment were employed to study the 1–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz frequency range: SQUID MPMS XL and PPMS-9 instruments (see details in the ESI‡). At zero external DC field, the in-phase
000 Hz frequency range: SQUID MPMS XL and PPMS-9 instruments (see details in the ESI‡). At zero external DC field, the in-phase 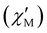 and out-of-phase
and out-of-phase 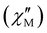 components of the AC susceptibility show frequency-dependent peaks (Figs. S7 and S8‡) with well-defined maxima in the
components of the AC susceptibility show frequency-dependent peaks (Figs. S7 and S8‡) with well-defined maxima in the 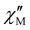 vs. T plot over the 20–40 K range for higher frequencies (Fig. S8‡), indicating a high magnetisation reversal barrier. The
vs. T plot over the 20–40 K range for higher frequencies (Fig. S8‡), indicating a high magnetisation reversal barrier. The 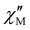 vs. frequency plot displays temperature-dependent maxima over the 19–27 K range (Fig. S9‡). The relaxation times were extracted from fitting of the frequency dependence of
vs. frequency plot displays temperature-dependent maxima over the 19–27 K range (Fig. S9‡). The relaxation times were extracted from fitting of the frequency dependence of 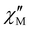 at different temperatures using the generalized Debye model. The extracted relaxation times (τ) are collected in Table S5.‡
at different temperatures using the generalized Debye model. The extracted relaxation times (τ) are collected in Table S5.‡
Magnetisation decay experiments were performed to evaluate relaxation times at lower temperatures. Exponential decay of the magnetisation was clearly observed until 8 K. The obtained data were fitted using a stretched exponential function (Fig. S11‡); this is commonly employed to obtain relaxation times from magnetisation decay measurements.80,81 The obtained τ values are collected in Table S6‡ and represented in Fig. 3 as the ln(τ−1) vs. temperature plot together with the obtained values from the AC susceptibility measurements. At very low temperature, there is a constant region indicative of quantum tunnelling relaxation. The onset of the Raman regime is discernible from magnetisation decay data, the trend in which matches with the lowest points measured by AC susceptibility. The transition between Raman and Orbach demagnetisation is clearly visible at around 18 K. As the three magnetic relaxation mechanisms are identified in the τ−1(T) curve, the following equation is employed:
| τ−1 = τQTM−1 + CTn + τ0−1eUeff/kT | (14) |
 | ||
| Fig. 3 Logarithmic plot of τ−1 vs. temperature for 1 (in the inset, τ−1 vs. temperature, as in eqn (14)). The values at lower temperatures correspond to those obtained from magnetisation decay and the values at higher temperatures are the ones derived from fitting of the AC susceptibility data to a generalized Debye function. The blue line corresponds to fitting of the data with eqn (14). | ||
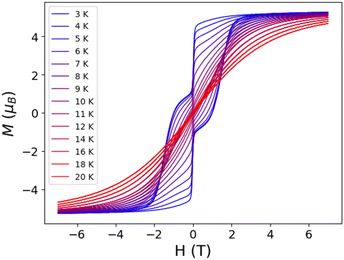
For completeness, the field dependent magnetisation measurements at different temperatures were acquired (Fig. 4), with a sweep rate of 20 mT s−1. Compound 1 shows a clear magnetic hysteresis, which remains open up to 14 K; this is one of highest values for air/humidity stable SMMs synthesized to date. The butterfly shape of the hysteresis loop arises from a faster relaxation around zero field and a slower relaxation at intermediate fields. This compound retains a large magnetisation that falls only when H < 20 mT, which can be attributed to unsuppressed quantum tunnelling of the magnetisation due to symmetry deviation and hyperfine and dipole interactions. When the temperature increases, the hysteresis loop narrows as the relaxation speeds up and results in smaller coercive fields and remanent magnetisation. The hysteresis loop shows a coercive field of 1 T and a remanent magnetisation of 2μB at 3 K at a sweep rate of 20 mT s−1,
Ab initio calculations
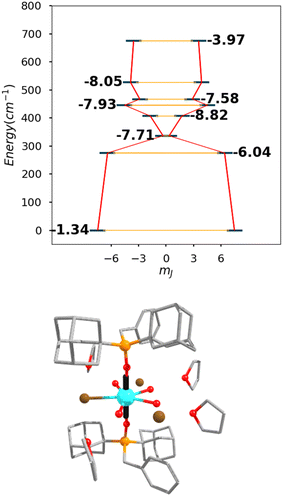
Ab initio calculations based on the experimental X-ray structural data were performed to provide insights into the mechanism that governed the magnetic relaxation of complex 1. In particular, multiconfigurational CASSCF calculations implemented in the ORCA 5.0.3 program package82–84 and the CASSCF/RASSI-SO/SINGLE_ANISO approach using OpenMOLCAS85–87 were carried out. Both programs agree in the general description of the double well potential associated with the ground 6H15/2 multiplet. To avoid redundancy in the discussion, we present the ORCA results in the manuscript while OpenMOLCAS data are presented in the ESI‡ for comparison.The eight computed Kramers’ doublets (KDs) for 1, corresponding to the 6H15/2 ground state of the DyIII ion, span an energy range of about 674 cm−1 (Table S7‡). The computed temperature dependence of χMT reproduces the experimental temperature dependence of χMT rather well (Fig. S4‡). The ground KD (KD1) is a pure mJ = |±15/2〉 state that is highly anisotropic (gzz = 19.86) with negligible transverse components (gxx ∼ gyy < 1 × 10−3), thus establishing a strong magnetic anisotropic axis. These g-values suggest strongly suppressed QTM within the ground KD (Fig. 5), which is consistent with the relatively large experimental value for τQTM (142.7 s). The anisotropic gzz axis is almost collinear with the pseudo-C5 axis lying along the axial O–Dy–O bonds (the deviation between the gzz axis and O–Dy–O direction is 1.5°, see Fig. S12‡ and Fig. 5 bottom). This strong uniaxial magnetic anisotropy is consistent with the weak ligand field from aqua and bromine ligands in the equatorial plane and the strong donor ligands in the axial positions.
The first excited state (KD2) lies 275.2 cm−1 above the ground state. This KD2 is also axial in nature, with gzz = 16.92, gxx = 0.13, and gyy = 0.27. In this case, the gz tensor passes through the O–Dy–O direction again and presents a deviation of 6.4° with respect to the gzz anisotropic axis of the ground state. The transverse components of KD2 can be large enough to promote magnetic relaxation via the first excited state, giving a calculated magnetisation barrier, Ucal, of 275.2 cm−1 (396 K), which is close to the experimental energy barrier, Ueff, of 427.7 K. The next excited state (KD3) is close in energy (336.6 cm−1, 484 K) and shows large transverse components of g (gxx = 0.42 and gyy = 1.63). Tunnelling relaxation times were calculated according to an ab initio model based on the spin–dipolar interaction.88 For the ground state (KD1), the calculated tunnelling time is 4.6 × 10−2 s while for the first excited state (KD2) it is much faster (9.1 × 10−7 s), which is consistent with the large transverse g-tensors obtained for the latter, confirming that magnetic relaxation for 1 occurs via the first excited state (KD2).
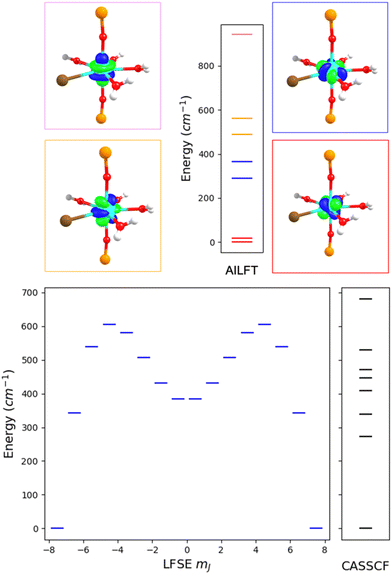
The effect of the f-orbital splitting on the observed magnetic anisotropy can be investigated in further detail by considering the individual contributions of each f±n orbital block to the demagnetisation barrier, as shown previously by some of us.89 In the case of 1, the high axiality of the coordination environment dictates orbital splitting where the most destabilized orbital corresponds to the f0 (fz3) orbital, lying along the z-axis with an energy of 854 cm−1 (violet level in Fig. 6, top). Interestingly, the most stable orbital block is not the one lying on the xy plane (fy(3x2−y2) and fx(x2−3y2) orbitals, collectively named f±3) but the next block, the functions of which have a first-order dependency with respect to z (fxyz and fz(x2−y2) orbitals, collectively named f±2) (red levels in Fig. 6, top). Fig. 6 (bottom) compares the CASSCF energies of the mJ sublevels of the ground 6H15/2 multiplet with the ones derived from the orbital energies weighted by their contributions to each sublevel in a ligand field stabilization energy (LFSE) approach.89 The agreement between both data sets is satisfactory as both present an isolated ground doublet, separated by ca. 300 cm−1 from a dense pack of seven doublets spanning around 300–400 cm−1. The pattern of the double well resembles the letter “M”, like the pattern derived from CASSCF (Fig. 5, top). Considering that magnetic relaxation probably proceeds via the first excited doublet, the contribution of each orbital block to anisotropy can be estimated from the LFSE energy difference between the mj = ±13/2 and mj = ±15/2 states, which is 2/3*(Ef±1 − Ef±2). In this case, the average energy of the f±1 and f±2 orbital blocks is 9.5 cm−1 and 523.7 cm−1, resulting in a gap of 342.8 cm−1.
Model assessment
The accuracy of the presented model can be evaluated for 1 since the temperature dependence of the relaxation time successfully fits to the combination of tunnelling, Raman and Orbach contributions. Employing eqn (7), the ZFC curve can be simulated, and the maximum is obtained numerically. The effect of different demagnetisation mechanisms can be analysed by modifying the τ(T) curve to include diverse combinations of Orbach, tunnel, and Raman mechanisms. Our analysis starts with the ZFC/FC determined using a field of 500 Oe. At this field, the tunnelling mechanism should be mostly suppressed so only the Orbach and Raman mechanisms are considered in the integration of τ−1(T). It is important to stress that the heating step in ZFC/FC measurements is done with an external magnetic field, which can affect demagnetisation parameters, especially tunnelling. Thus, care must be taken to account for this effect. Fig. 7 presents the simulated ZFC curves for all the experimentally determined heating rates (0.01–5 K min−1). Pleasingly, the positions of the ZFC maxima are similar to the temperature range of the experiment (vide supra). In the same way as the analysis of the experimental ZFC/FC curves, data associated with the slower heating rates show ZFC curves where TB-ZFC/FC is clearly discernible, while the faster heating rates show a less clear maximum.The former simulations are now repeated by incorporating tunnelling relaxation into the integration of τ−1(T). The reference experimental data are now in the ZFC/FC curve measured at 50 Oe, which should present a smaller quenching of tunnelling than the 500 Oe results. Fig. 8 shows the simulated curves under these conditions. The comparison between Fig. 7 and 8 clearly indicates that tunnelling is efficient at lowering TB-ZFC/FC for 1, in the same way that ZFC/FC data at 500 Oe show higher blocking temperatures than the 50 Oe results. This highlights an important and probably overlooked experimental parameter that affects the blocking temperatures measured by ZFC/FC experiments: the external field necessary to record the magnetic moment along the temperature program, which adds to the importance of reporting the heating rate for these experiments.
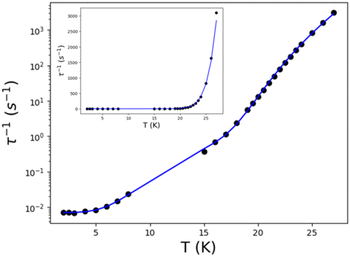
A more quantitative comparison between the experimental and calculated blocking temperatures is presented in Fig. 9. As mentioned earlier, the model can capture the effect of tunnelling in 1, which diminishes the blocking temperature by around 5 K. The agreement is quantitative at low heating rates but departs for faster heating rates (see the red dashed line in Fig. 9). Small modifications to the tunnelling value reveal a high sensitivity of the blocking temperature, where correcting the tunnelling time by a factor of 0.25 provides a simulated curve that agrees with the 50 Oe experiment over the complete range of heating rates (dotted–dashed red line in Fig. 9). This factor might seem a drastic correction, but it is significantly lower than the error bars of the magnetisation decay measurements calculated from the β parameter, according to Chilton and coworkers.90 In this case, the range of relaxation times is even larger since the magnetisation decay and AC susceptibility are combined. The 500 Oe data also agree with simulations, where the low heating rate results agree perfectly and depart by a couple of K at faster rates. Overall, the performance of the model is satisfactory since it allows us to predict TB-ZFC/FC accurately and capture the heating rate dependency.
The demagnetisation mechanism limiting the blocking temperature can be estimated by repeating the same simulations and including each demagnetisation mechanism separately. The tunnelling mechanism limits TB to 2–3 K for slow heating rates while it keeps most of the magnetic moment frozen at faster temperature programs, without reaching a maximum over the simulated temperature range (2–20 K) (see Fig. S14,‡ left). The Raman-only simulation is similar to the one for the Orbach + Raman results from Fig. 8, indicating that Raman relaxation is responsible for the simulated blocking between 4 and 12 K. The Orbach-only plot shows blocking temperatures over a higher temperature range (14–17 K). Hence, it does not determine the value of TB in this case (see Fig. S14,‡ right).
To assess the broader accuracy of the presented approach, a literature search for experimental examples of TB-ZFC/FC was performed. Such values can also be obtained for any single-molecule magnet system by introducing the spin relaxation parameters at the web page https://tbsim.ee.ub.edu. By reconstructing the τ(T) curve using fitting parameters, we can calculate TB using eqn (7). Unfortunately, the heating rate is not always reported, so we have assumed lower and higher limit values for this parameter when RH information is missing (0.2 K min−1 and 5 K min−1 to account for slow and fast sweeping rates).
Table S9‡ compares experimental and predicted values for ZFC/FC blocking temperatures for 97 lanthanide SMMs13,14,37,38,41,50,51,60,61,63,65,91–136 and ten transition metal complexes137–146 reported in the literature. The lanthanide benchmark set contains mononuclear and polynuclear complexes based on DyIII, TbIII, ErIII and HoIII ions, heteronuclear complexes containing DyIII or TbIII ions and transition metals, including diluted systems. The ten transition compounds are Mn12 complexes, a trinuclear Mn2Mo complex, and tetranuclear and mononuclear iron and cobalt complexes. The fitting parameters for AC susceptibility data range from systems involving combinations of Orbach, Raman, and tunnelling, Orbach and Raman, Orbach and tunnelling, and Raman and tunnelling to Orbach-only terms. Besides, the list includes complexes exhibiting two or three relaxation processes, where one of them (the main process) is considered to calculate TB. As observed in this list, some authors report Tirrev (indicated with an asterisk) instead TB-ZFC/FC, and others report both values. As expected, Tirrev is always higher than the TB-ZFC/FC value. In some cases, the difference between Tirrev and TB-ZFC/FC values exceeds 10 K (e.g. 78 K and ∼55 K, respectively, for complex 3 in Table S9‡). Another issue to highlight is the lack of information about the heating rate (RH). From the 107 complexes in Table S9,‡ RH values were only included in the original papers for 37 systems, and only for 3 transition metal complexes (see Fig. 10). Reported RH values range from 0.189 to 5 K min−1, demonstrating that there is no consensus on this important parameter that defines the TB value. In most cases, the reported TB-ZFC/FC value lies in the range of TB obtained with RH values of 0.2 K min−1 and 5 K min−1, or close to these values (see Fig. 11). Similarly, when RH is reported, the obtained TB value at this heating rate is close to the reported TB-ZFC/FC value (see Fig. 10), demonstrating the accuracy and broad applicability of the presented approach.
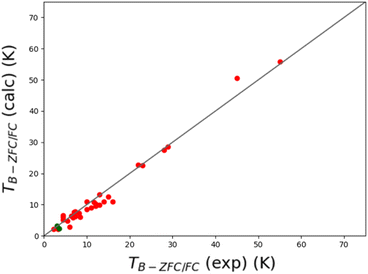 | ||
| Fig. 10 Comparison of the experimental zero-field cooling/field cooling blocking temperatures and the ones calculated using eqn (12). Only 38 cases (35 lanthanide and 3 transition metal compounds depicted in red and green, respectively) with a reported heating rate are considered (see Fig. 11 for the other systems). The black line represents perfect agreement between both values. | ||
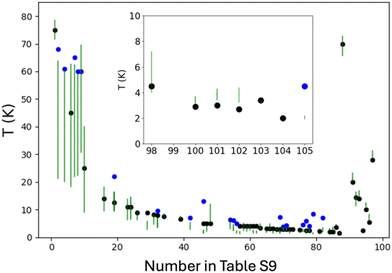 | ||
| Fig. 11 Comparison of the experimental TB-ZFC/FC blocking (black dots) or Tirrev irreversible (blue dots, values in Table S9‡ indicated with an asterisk) temperatures for the 62 lanthanide systems (for clarity, the 7 transition metal systems are in the inset) without a reported heating rate. The x-axis indicates the complex number in Table S9.‡ The green bar corresponds to the limit values calculated using eqn (12) using with RH = 0.2 K min−1 and 5 K min−1. | ||
The large amount of data collected in Table S9‡ allow us to investigate if a temperature at a fixed relaxation time like TB-100 can be useful as a descriptor for ZFC/FC blocking temperatures. Fig. S15‡ presents the relaxation time at the experimental TB-ZFC/FC value for the data presented in Table S9‡ as a function of the heating rate. Clusters of data are observed around the most common RH values (0.2–0.4 K min−1, 2 K min−1 and 5 K min−1). In all cases, a high dispersion of relaxation times at the experimental TB-ZFC/FC value is observed, especially for slow heating rates. In the case of the cluster located at 0.2–0.4 K min−1, the maximum and minimum relaxation times are 282 s and 1 s. Thus, the experimental TB-ZFC/FC value cannot be related with a unique treshold value of the relaxation time, even at a fixed heating rate.
For systems without a reported heating rate, the limiting values of the blocking temperature were calculated considering RH values of 0.2 K min−1 and 5 K min−1, as shown in Fig. 11. In practically all cases, the TB-ZFC/FC value falls within the calculated range. Furthermore, the Tirrev values tend to appear in the highest part or above the bars associated with the limiting RH values, in agreement with the fact that the irreversibility temperature (Tirrev) must be higher than TB-ZFC/FC.78
Conclusions
This work discusses the various metrics for quantifying blocking temperatures and the challenges associated with each method. The newly proposed approach for estimating TB-ZFC/FC from AC susceptibility parameters offers a practical way to compare the performance of SMMs in the literature and estimate TB-ZFC/FC without the need for additional measurements. Thus, the TB-ZFC/FC blocking temperature for a given heating rate can be estimated from the relaxation time data, which are the most common magnetic characterization data available for SMMs. In this context, the synthesis and characterization of the DyIII SMM with D5h geometry, [Dy(OPAd2Bz)2(H2O)4Br]Br2·4THF (1), enabled the predictions of the blocking temperature to be tested over a broad range of heating rates and two different static magnetic fields. Furthermore, complex 1 is an interesting example of an air- and humidity-stable SMM with high Ueff and TB values, adding to the restricted list of examples of SMMs with D5h geometry.Magnetic measurements confirm the SMM behaviour of complex 1, with a ZFC/FC blocking temperature in the range of 2.5–8 K, depending on the heating rate and the magnitude of the probe magnetic field. The presence of the magnetic hysteresis at zero-field with a large coercive field and remanent magnetisation values further supports the SMM properties of the complex. Additionally, AC magnetic susceptibility measurements reveal a high magnetisation reversal barrier, indicating slow relaxation of magnetisation. Ab initio calculations provide insights into the electronic structure and relaxation mechanism of complex 1. The calculations confirm the strong uniaxial magnetic anisotropy and reveal that magnetic relaxation occurs primarily via the first excited state (KD2).
In summary, the study of complex 1 exemplifies the potential of stable SMMs with D5h geometry and axial ligands for achieving high-performance SMMs. The proposed approach for estimating TB-ZFC/FC provided accurate values of the ZFC/FC blocking temperature of 1, properly captured the heating rate and probe field dependence of TB-ZFC/FC and highlighted their importance. The study also identified the Raman and tunnelling mechanisms as the ones determining the blocking temperature. The possibility of relating the spin relaxation mechanisms directly to the blocking temperature opens the way for a better understanding of TB tuning, which is a fundamental parameter of SMMs. Furthermore, the proposal successfully predicted blocking temperatures for many examples of SMMs in the literature, offering a valuable tool for characterising and comparing SMMs in future research.
Author contributions
Y. G. and M. A. P.: investigation, data analysis; D. A.: software; M. M. Q. M., E. C., S. G. C., E. R. and D. A.: conceptualisation, investigation, data analysis, validation, supervision, resources, funding acquisition; all authors contributed to the writing and editing of the article.Data availability
The data supporting this article have been included as part of the ESI.‡ Estimation of the blocking temperature for any single-molecule magnet system can be obtained by introducing the spin relaxation parameters at the web page https://tbsim.ee.ub.edu.Conflicts of interest
There are no conflicts to declare.Acknowledgements
D. A. thanks FONDECYT Regular 1210325 for financial support. Powered@NLHPC: this research was partially supported by the supercomputing infrastructure of the NLHPC (ECM-02). Financial support from the Ministerio de Ciencia e Innovación (projects PID2022-138090NB-C21, PID2021-122464NB-I00, TED2021-129593B-I00, CNS2023-144561 and Maria de Maeztu CEX2021-001202-M), the Junta de Andalucía (FQM-195 and FQM-337), FEDER/Junta de Andalucía (projects I + D + i P20_00692, C-EXP-140-UGR23 and M.1.B.B TA_000722, Programas Operativos FEDER 2014-2020 y 2021-2027, Consejería de Economía, Conocimiento, Empresas y Universidad), and the University of Granada (project I + D + i PPJIA2020.10) is greatly appreciated. The authors also acknowledge the Centro de Servicios de Informática y Redes de Comunicaciones (CSIRC) for computational time and facilities. M.M.Q.M. thanks the Ministerio de Ciencia e Innovación for a Ramón y Cajal contract (the publication is part of the project PID2022-138090NB-C21 and grant RYC2021-034288-I funded by MCIN/AEI/10.13039/501100011033 and by the European Union “NextGenerationEU”/PRTR”). E. R. also acknowledges the Generalitat de Catalunya for ICREA Academia and 2021-SGR-00286 grants, and for computational resources at CSUC.References
- S. M. J. Aubin, M. W. Wemple, D. M. Adams, H.-L. Tsai, G. Christou and D. N. Hendrickson, Distorted MnIVMnIII3 Cubane Complexes as Single-Molecule Magnets, J. Am. Chem. Soc., 1996, 118, 7746–7754 CrossRef CAS.
- R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Magnetic bistability in a metal-ion cluster, Nature, 1993, 365, 141–143 CrossRef CAS.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Lanthanide Single-Molecule Magnets, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS PubMed.
- A. Zabala-Lekuona, J. M. Seco and E. Colacio, Single-Molecule Magnets: From Mn12-ac to dysprosium metallocenes, a travel in time, Coord. Chem. Rev., 2021, 441, 213984 CrossRef CAS.
- N. F. Chilton, Molecular Magnetism, Annu. Rev. Mater. Res., 2022, 52, 79–101 CrossRef CAS.
- E. Coronado, Molecular magnetism: from chemical design to spin control in molecules, materials and devices, Nat. Rev. Mater., 2019, 5, 87–104 CrossRef.
- A. Gaita-Ariño, F. Luis, S. Hill and E. Coronado, Molecular spins for quantum computation, Nat. Chem., 2019, 11, 301–309 CrossRef PubMed.
- J. Long, Y. Guari, R. A. S. Ferreira, L. D. Carlos and J. Larionova, Recent advances in luminescent lanthanide based Single-Molecule Magnets, Coord. Chem. Rev., 2018, 363, 57–70 CrossRef CAS.
- R. Marin, G. Brunet and M. Murugesu, Shining New Light on Multifunctional Lanthanide Single–Molecule Magnets, Angew. Chem., Int. Ed., 2020, 60, 1728–1746 CrossRef PubMed.
- E. Moreno-Pineda and W. Wernsdorfer, Measuring molecular magnets for quantum technologies, Nat. Rev. Phys., 2021, 3, 645–659 CrossRef CAS.
- M. Shiddiq, D. Komijani, Y. Duan, A. Gaita-Ariño, E. Coronado and S. Hill, Enhancing coherence in molecular spin qubits via atomic clock transitions, Nature, 2016, 531, 348–351 CrossRef CAS PubMed.
- R. Vincent, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Electronic read-out of a single nuclear spin using a molecular spin transistor, Nature, 2012, 488, 357–360 CrossRef CAS PubMed.
- F. Liu, D. S. Krylov, L. Spree, S. M. Avdoshenko, N. A. Samoylova, M. Rosenkranz, A. Kostanyan, T. Greber, A. U. B. Wolter, B. Büchner and A. A. Popov, Single molecule magnet with an unpaired electron trapped between two lanthanide ions inside a fullerene, Nat. Commun., 2017, 8, 16098 CrossRef CAS PubMed.
- F. Liu, G. Velkos, D. S. Krylov, L. Spree, M. Zalibera, R. Ray, N. A. Samoylova, C.-H. Chen, M. Rosenkranz, S. Schiemenz, F. Ziegs, K. Nenkov, A. Kostanyan, T. Greber, A. U. B. Wolter, M. Richter, B. Büchner, S. M. Avdoshenko and A. A. Popov, Air-stable redox-active nanomagnets with lanthanide spins radical-bridged by a metal–metal bond, Nat. Commun., 2019, 10, 571 CrossRef CAS PubMed.
- B. M. Day, F.-S. Guo and R. A. Layfield, Cyclopentadienyl Ligands in Lanthanide Single-Molecule Magnets: One Ring To Rule Them All?, Acc. Chem. Res., 2018, 51, 1880–1889 CrossRef CAS PubMed.
- A. Dey, P. Kalita and V. Chandrasekhar, Lanthanide(III)-Based Single-Ion Magnets, ACS Omega, 2018, 3, 9462–9475 CrossRef CAS PubMed.
- K. L. M. Harriman and M. Murugesu, An Organolanthanide Building Block Approach to Single-Molecule Magnets, Acc. Chem. Res., 2016, 49, 1158–1167 CrossRef CAS PubMed.
- J.-L. Liu, Y.-C. Chen and M.-L. Tong, Symmetry strategies for high performance lanthanide-based single-molecule magnets, Chem. Soc. Rev., 2018, 47, 2431–2453 RSC.
- J. Tang and P. Zhang, Dinuclear Lanthanide Single-Molecule Magnets, in Lanthanide Single Molecule Magnets, Springer Berlin Heidelberg, 2015, pp. 91–126 Search PubMed.
- J. Wang, C. Y. Sun, Q. Zheng, D. Q. Wang, Y. T. Chen, J. F. Ju, T. M. Sun, Y. Cui, Y. Ding and Y. F. Tang, Lanthanide Single–molecule Magnets: Synthetic Strategy, Structures, Properties and Recent Advances, Chem. – Asian J., 2023, 18, e202201297 CrossRef CAS PubMed.
- A. J. Brown, D. Pinkowicz, M. R. Saber and K. R. Dunbar, A Trigonal-Pyramidal Erbium(III) Single-Molecule Magnet, Angew. Chem., Int. Ed., 2015, 54, 5864–5868 CrossRef CAS PubMed.
- Y. Chen, F. Ma, X. Chen, B. Dong, K. Wang, S. Jiang, C. Wang, X. Chen, D. Qi, H. Sun, B. Wang, S. Gao and J. Jiang, A New Bis(phthalocyaninato) Terbium Single-Ion Magnet with an Overall Excellent Magnetic Performance, Inorg. Chem., 2017, 56, 13889–13896 CrossRef CAS PubMed.
- C. R. Ganivet, B. Ballesteros, G. de la Torre, J. M. Clemente-Juan, E. Coronado and T. Torres, Influence of Peripheral Substitution on the Magnetic Behavior of Single-Ion Magnets Based on Homo- and Heteroleptic TbIII Bis(phthalocyaninate), Chem. – Eur. J., 2013, 19, 1457–1465 CrossRef CAS PubMed.
- N. Ishikawa, M. Sugita, N. Tanaka, T. Ishikawa, S.-y. Koshihara and Y. Kaizu, Upward Temperature Shift of the Intrinsic Phase Lag of the Magnetization of Bis(phthalocyaninato)terbium by Ligand Oxidation Creating an S = 1/2 Spin, Inorg. Chem., 2004, 43, 5498–5500 CrossRef CAS PubMed.
- W.-J. Xu, Q.-C. Luo, Z.-H. Li, Y.-Q. Zhai and Y.-Z. Zheng, Bis-Alkoxide Dysprosium(III) Crown Ether Complexes Exhibit Tunable Air Stability and Record Energy Barrier, Adv. Sci., 2024, 11, 2308548 CrossRef CAS PubMed.
- Z.-H. Li, Y.-Q. Zhai, W.-P. Chen, Y.-S. Ding and Y.-Z. Zheng, Air-Stable Hexagonal Bipyramidal Dysprosium(III) Single-Ion Magnets with Nearly Perfect D6h Local Symmetry, Chem. – Eur. J., 2019, 25, 16219–16224 CrossRef CAS PubMed.
- F. Benner, L. La Droitte, O. Cador, B. Le Guennic and S. Demir, Magnetic hysteresis and large coercivity in bisbenzimidazole radical-bridged dilanthanide complexes, Chem. Sci., 2023, 14, 5577–5592 RSC.
- J. Tang, I. Hewitt, N. T. Madhu, G. Chastanet, W. Wernsdorfer, C. E. Anson, C. Benelli, R. Sessoli and A. K. Powell, Dysprosium Triangles Showing Single-Molecule Magnet Behavior of Thermally Excited Spin States, Angew. Chem., Int. Ed., 2006, 45, 1729–1733 CrossRef CAS PubMed.
- P. Zhang, F. Benner, N. F. Chilton and S. Demir, Organometallic lanthanide bismuth cluster single-molecule magnets, Chem, 2022, 8, 717–730 CAS.
- N. F. Chilton, C. A. P. Goodwin, D. P. Mills and R. E. P. Winpenny, The first near-linear bis(amide) f-block complex: a blueprint for a high temperature single molecule magnet, Chem. Commun., 2015, 51, 101–103 RSC.
- J. D. Rinehart and J. R. Long, Exploiting single-ion anisotropy in the design of f-element single-molecule magnets, Chem. Sci., 2011, 2, 2078 RSC.
- L. Ungur and L. F. Chibotaru, Strategies toward High-Temperature Lanthanide-Based Single-Molecule Magnets, Inorg. Chem., 2016, 55, 10043–10056 CrossRef CAS PubMed.
- S. Dey, T. Sharma and G. Rajaraman, Unravelling the role of spin–vibrational coupling in designing high-performance pentagonal bipyramidal Dy(iii) single ion magnets, Chem. Sci., 2024, 15, 6465–6477 RSC.
- S. Mondal and A. Lunghi, Unraveling the Contributions to Spin–Lattice Relaxation in Kramers Single-Molecule Magnets, J. Am. Chem. Soc., 2022, 144, 22965–22975 CrossRef CAS PubMed.
- V. Vieru, S. Gómez-Coca, E. Ruiz and L. F. Chibotaru, Increasing the Magnetic Blocking Temperature of Single-Molecule Magnets, Angew. Chem., Int. Ed., 2024, 63, e202303146 CrossRef CAS PubMed.
- T. Sharma, A. Swain and G. Rajaraman, Pushing Boundaries in Single Molecule Magnets: An Ab Initio Perspective on Harnessing Unusual Oxidation States for Unprecedented Lanthanide SMM Performance, ChemRxiv, 2023. DOI:10.26434/chemrxiv-2023-wpc4r.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single-molecule magnet, Science, 2018, 362, 1400–1403 CrossRef CAS PubMed.
- C. A. Gould, K. R. McClain, D. Reta, J. G. C. Kragskow, D. A. Marchiori, E. Lachman, E.-S. Choi, J. G. Analytis, R. D. Britt, N. F. Chilton, B. G. Harvey and J. R. Long, Ultrahard magnetism from mixed-valence dilanthanide complexes with metal-metal bonding, Science, 2022, 375, 198–202 CrossRef CAS PubMed.
- D. Aravena and E. Ruiz, Shedding Light on the Single-Molecule Magnet Behavior of Mononuclear DyIII Complexes, Inorg. Chem., 2013, 52, 13770–13778 CrossRef CAS PubMed.
- N. F. Chilton, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and A. Soncini, An electrostatic model for the determination of magnetic anisotropy in dysprosium complexes, Nat. Commun., 2013, 4, 3551 Search PubMed.
- M. Gregson, N. F. Chilton, A.-M. Ariciu, F. Tuna, I. F. Crowe, W. Lewis, A. J. Blake, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and S. T. Liddle, A monometallic lanthanide bis(methanediide) single molecule magnet with a large energy barrier and complex spin relaxation behaviour, Chem. Sci., 2016, 7, 155–165 RSC.
- S. T. Liddle and J. van Slageren, Improving f-element single molecule magnets, Chem. Soc. Rev., 2015, 44, 6655–6669 RSC.
- K. L. M. Harriman, J. L. Brosmer, L. Ungur, P. L. Diaconescu and M. Murugesu, Pursuit of Record Breaking Energy Barriers: A Study of Magnetic Axiality in Diamide Ligated DyIII Single-Molecule Magnets, J. Am. Chem. Soc., 2017, 139, 1420–1423 CrossRef CAS PubMed.
- P. Zhang, L. Zhang, C. Wang, S. Xue, S.-Y. Lin and J. Tang, Equatorially Coordinated Lanthanide Single Ion Magnets, J. Am. Chem. Soc., 2014, 136, 4484–4487 CrossRef CAS PubMed.
- M. A. AlDamen, J. M. Clemente-Juan, E. Coronado, C. Martí-Gastaldo and A. Gaita-Ariño, Mononuclear Lanthanide Single-Molecule Magnets Based on Polyoxometalates, J. Am. Chem. Soc., 2008, 130, 8874–8875 CrossRef CAS PubMed.
- P.-E. Car, M. Perfetti, M. Mannini, A. Favre, A. Caneschi and R. Sessoli, Giant field dependence of the low temperature relaxation of the magnetization in a dysprosium(III)–DOTA complex, Chem. Commun., 2011, 47, 3751 RSC.
- K. Katoh, S. Yamashita, N. Yasuda, Y. Kitagawa, B. K. Breedlove, Y. Nakazawa and M. Yamashita, Frontispiece: Control of the Spin Dynamics of Single-Molecule Magnets by using a Quasi One-Dimensional Arrangement, Angew. Chem., Int. Ed., 2018, 57, 9262–9267 CrossRef CAS PubMed.
- L. Sorace, C. Benelli and D. Gatteschi, Lanthanides in molecular magnetism: old tools in a new field, Chem. Soc. Rev., 2011, 40, 3092–3104 RSC.
- A. M. Atkin, M. J. Giansiracusa, S. Calvello, E. Rousset, R. W. Gable, W. Phonsri, K. S. Murray, J. K. Howard, A. Soncini, R. A. Mole and C. Boskovic, bis(2,2′-bipyridine)-(methanol)-[3,4,5,6-tetrabromobenzene-1,2-diolato]-(3,4,5,6 tetrabromobenzene-1,2-diolato)-dysprosium(III), Inorg. Chem., 2023, 62, 1141 CrossRef CAS PubMed.
- C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Molecular magnetic hysteresis at 60 kelvin in dysprosocenium, Nature, 2017, 548, 439–442 CrossRef CAS PubMed.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, A Dysprosium Metallocene Single-Molecule Magnet Functioning at the Axial Limit, Angew. Chem., Int. Ed., 2017, 56, 11445–11449 CrossRef CAS PubMed.
- S.-D. Jiang, B.-W. Wang, H.-L. Sun, Z.-M. Wang and S. Gao, An Organometallic Single-Ion Magnet, J. Am. Chem. Soc., 2011, 133, 4730–4733 CrossRef CAS PubMed.
- L. Münzfeld, C. Schoo, S. Bestgen, E. Moreno-Pineda, R. Köppe, M. Ruben and P. W. Roesky, Synthesis, structures and magnetic properties of [(η9-C9H9)Ln(η8-C8H8)] super sandwich complexes, Nat. Commun., 2019, 10, 3135 CrossRef PubMed.
- A. H. Vincent, Y. L. Whyatt, N. F. Chilton and J. R. Long, Strong Axiality in a Dysprosium(III) Bis(borolide) Complex Leads to Magnetic Blocking at 65 K, J. Am. Chem. Soc., 2023, 145, 1572–1579 CrossRef CAS PubMed.
- A. B. Canaj, S. Dey, C. Wilson, O. Céspedes, G. Rajaraman and M. Murrie, Engineering macrocyclic high performance pentagonal bipyramidal Dy(iii) single-ion magnets, Chem. Commun., 2020, 56, 12037–12040 RSC.
- A. B. Canaj, M. K. Singh, C. Wilson, G. Rajaraman and M. Murrie, Chemical and in silico tuning of the magnetisation reversal barrier in pentagonal bipyramidal Dy(iii) single-ion magnets, Chem. Commun., 2018, 54, 8273–8276 RSC.
- Y.-C. Chen, J.-L. Liu, Y. Lan, Z.-Q. Zhong, A. Mansikkamäki, L. Ungur, Q.-W. Li, J.-H. Jia, L. F. Chibotaru, J.-B. Han, W. Wernsdorfer, X.-M. Chen and M.-L. Tong, Dynamic Magnetic and Optical Insight into a High-Performance Pentagonal Bipyramidal DyIII Single-Ion Magnet, Chem. – Eur. J., 2017, 23, 5630–5630 CrossRef CAS.
- Y.-C. Chen, J.-L. Liu, L. Ungur, J. Liu, Q.-W. Li, L.-F. Wang, Z.-P. Ni, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, Symmetry-Supported Magnetic Blocking at 20 K in Pentagonal Bipyramidal Dy(III) Single-Ion Magnets, J. Am. Chem. Soc., 2016, 138, 2829–2837 CrossRef CAS PubMed.
- I. F. Díaz-Ortega, J. M. Herrera, S. Dey, H. Nojiri, G. Rajaraman and E. Colacio, The effect of the electronic structure and flexibility of the counteranions on magnetization relaxation in [Dy(L)2(H2O)5]3+ (L = phosphine oxide derivative) pentagonal bipyramidal SIMs, Inorg. Chem. Front., 2020, 7, 689–699 RSC.
- Y.-S. Ding, N. F. Chilton, R. E. P. Winpenny and Y.-Z. Zheng, On Approaching the Limit of Molecular Magnetic Anisotropy: A Near-Perfect Pentagonal Bipyramidal Dysprosium(III) Single-Molecule Magnet, Angew. Chem., Int. Ed., 2016, 55, 16071–16074 CrossRef CAS PubMed.
- Y. S. Ding, T. Han, Y. Q. Zhai, D. Reta, N. F. Chilton, R. E. P. Winpenny and Y. Z. Zheng, A Study of Magnetic Relaxation in Dysprosium(III) Single–Molecule Magnets, Chem. – Eur. J., 2020, 26, 5893–5902 CrossRef CAS PubMed.
- S. K. Gupta, T. Rajeshkumar, G. Rajaraman and R. Murugavel, An air-stable Dy(iii) single-ion magnet with high anisotropy barrier and blocking temperature, Chem. Sci., 2016, 7, 5181–5191 RSC.
- Z. Jiang, L. Sun, Q. Yang, B. Yin, H. Ke, J. Han, Q. Wei, G. Xie and S. Chen, Excess axial electrostatic repulsion as a criterion for pentagonal bipyramidal DyIII single-ion magnets with high Ueff and TB, J. Mater. Chem. C, 2018, 6, 4273–4280 RSC.
- L.-L. Li, H.-D. Su, S. Liu, Y.-C. Xu and W.-Z. Wang, A new air- and moisture-stable pentagonal-bipyramidal DyIII single-ion magnet based on the HMPA ligand, Dalton Trans., 2019, 48, 2213–2219 RSC.
- J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer, S. Gao, X.-M. Chen and M.-L. Tong, A Stable Pentagonal Bipyramidal Dy(III) Single-Ion Magnet with a Record Magnetization Reversal Barrier over 1000 K, J. Am. Chem. Soc., 2016, 138, 5441–5450 CrossRef CAS PubMed.
- J.-L. Liu, Y.-C. Chen, Y.-Z. Zheng, W.-Q. Lin, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M.-L. Tong, Switching the anisotropy barrier of a single-ion magnet by symmetry change from quasi-D5h to quasi-Oh, Chem. Sci., 2013, 4, 3310 RSC.
- J. Long, A. N. Selikhov, E. Mamontova, K. A. Lyssenko, Y. Guari, J. Larionova and A. A. Trifonov, Single-molecule magnet behaviour in a Dy(iii) pentagonal bipyramidal complex with a quasi-linear Cl–Dy–Cl sequence, Dalton Trans., 2019, 48, 35–39 RSC.
- H. Wu, M. Li, B. Yin, Z. Xia, H. Ke, Q. Wei, G. Xie, S. Chen and S. Gao, Fine-tuning the type of equatorial donor atom in pentagonal bipyramidal Dy(iii) complexes to enhance single-molecule magnet properties, Dalton Trans., 2019, 48, 16384–16394 RSC.
- B. Zhang, X. Guo, P. Tan, W. Lv, X. Bai, Y. Zhou, A. Yuan, L. Chen, D. Liu, H.-H. Cui, R. Wang and X.-T. Chen, Axial Ligand as a Critical Factor for High-Performance Pentagonal Bipyramidal Dy(III) Single-Ion Magnets, Inorg. Chem., 2022, 61, 19726–19734 CrossRef CAS PubMed.
- L. Zhu, Y. Dong, B. Yin, P. Ma and D. Li, Improving the single-molecule magnet properties of two pentagonal bipyramidal Dy3+ compounds by the introduction of both electron-withdrawing and -donating groups, Dalton Trans., 2021, 50, 12607–12618 RSC.
- Y. Ma, Y.-Q. Zhai, Q.-C. Luo, Y.-S. Ding and Y.-Z. Zheng, Ligand Fluorination to Mitigate the Raman Relaxation of DyIII Single-Molecule Magnets: A Combined Terahertz, Far-IR and Vibronic Barrier Model Study, Angew. Chem., Int. Ed., 2022, 61, e202206022 CrossRef CAS PubMed.
- X. Ding, Q. Luo, Y. Zhai, X. Zhang, Y. Lv, X. Zhang, C. Ke, C. Wu and Y. Zheng, Rigid Dysprosium(III) Single-Molecule Magnets Exhibit Preserved Superparamagnetism in Solution, Chin. J. Chem., 2022, 40, 563–570 CrossRef CAS.
- K.-X. Yu, Y.-S. Ding, Y.-Q. Zhai, T. Han and Y.-Z. Zheng, Equatorial coordination optimization for enhanced axiality of mononuclear Dy(iii) single-molecule magnets, Dalton Trans., 2020, 49, 3222–3227 RSC.
- I. Oyarzabal, J. Ruiz, E. Ruiz, D. Aravena, J. M. Seco and E. Colacio, Increasing the effective energy barrier promoted by the change of a counteranion in a Zn–Dy–Zn SMM: slow relaxation via the second excited state, Chem. Commun., 2015, 51, 12353–12356 RSC.
- S. K. Singh, T. Gupta, M. Shanmugam and G. Rajaraman, Unprecedented magnetic relaxation via the fourth excited state in low-coordinate lanthanide single-ion magnets: a theoretical perspective, Chem. Commun., 2014, 50, 15513–15516 RSC.
- M. Briganti, F. Santanni, L. Tesi, F. Totti, R. Sessoli and A. Lunghi, A Complete Ab Initio View of Orbach and Raman Spin–Lattice Relaxation in a Dysprosium Coordination Compound, J. Am. Chem. Soc., 2021, 143, 13633–13645 CrossRef CAS PubMed.
- Y.-S. Ding, K.-X. Yu, D. Reta, F. Ortu, R. E. P. Winpenny, Y.-Z. Zheng and N. F. Chilton, Field- and temperature-dependent quantum tunnelling of the magnetisation in a large barrier single-molecule magnet, Nat. Commun., 2018, 9, 3134 CrossRef PubMed.
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford Academic, Oxford, 2006, pp. 58–61 Search PubMed.
- S. Alvarez, D. Avnir, M. Llunell and M. Pinsky, Continuous symmetry maps and shape classification. The case of six-coordinated metal compoundsESI (ESI) available: tables of CSD refcodes, structural parameters and symmetry measures for the studied compounds, New J. Chem., 2002, 26, 996–1009 RSC.
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford Academic, Oxford, 2006, pp. 108–159 Search PubMed.
- R. Orbach, On the Theory of Spin-Lattice Relaxation in Paramagnetic Salts, Proc. Phys. Soc., 1961, 77, 821–826 CrossRef CAS.
- F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- F. Neese, Software update: The ORCA program system—Version 5.0, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2022, 12, 1606 Search PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, The ORCA quantum chemistry program package, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. F. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P. Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, Molcas 8: New capabilities for multiconfigurational quantum chemical calculations across the periodic table, J. Comput. Chem., 2015, 37, 506–541 CrossRef PubMed.
- L. F. Chibotaru and L. Ungur, Ab initio calculation of anisotropic magnetic properties of complexes. I. Unique definition of pseudospin Hamiltonians and their derivation, J. Chem. Phys., 2012, 137, 064112 CrossRef CAS PubMed.
- A. A. Granovsky, Extended multi-configuration quasi-degenerate perturbation theory: The new approach to multi-state multi-reference perturbation theory, J. Chem. Phys., 2011, 134, 214113 CrossRef PubMed.
- D. Aravena, Ab Initio Prediction of Tunneling Relaxation Times and Effective Demagnetization Barriers in Kramers Lanthanide Single-Molecule Magnets, J. Phys. Chem. Lett., 2018, 9, 5327–5333 CrossRef CAS PubMed.
- Y. Gil and D. Aravena, Understanding Single-Molecule Magnet properties of lanthanide complexes from 4f orbital splitting, Dalton Trans., 2024, 53, 2207–2217 RSC.
- W. J. A. Blackmore, G. K. Gransbury, P. Evans, J. G. C. Kragskow, D. P. Mills and N. F. Chilton, Characterisation of magnetic relaxation on extremely long timescales, Phys. Chem. Chem. Phys., 2023, 25, 16735–16744 RSC.
- J. C. Vanjak, B. O. Wilkins, V. Vieru, N. S. Bhuvanesh, J. H. Reibenspies, C. D. Martin, L. F. Chibotaru and M. Nippe, A High-Performance Single-Molecule Magnet Utilizing Dianionic Aminoborolide Ligands, J. Am. Chem. Soc., 2022, 144, 17743–17747 CrossRef CAS PubMed.
- K. Randall McClain, C. A. Gould, K. Chakarawet, S. J. Teat, T. J. Groshens, J. R. Long and B. G. Harvey, High-temperature magnetic blocking and magneto-structural correlations in a series of dysprosium(III) metallocenium single-molecule magnets, Chem. Sci., 2018, 9, 8492–8503 RSC.
- P. Evans, D. Reta, G. F. S. Whitehead, N. F. Chilton and D. P. Mills, Bis-Monophospholyl Dysprosium Cation Showing Magnetic Hysteresis at 48 K, J. Am. Chem. Soc., 2019, 141, 19935–19940 CrossRef CAS PubMed.
- K.-X. Yu, J. G. C. Kragskow, Y.-S. Ding, Y.-Q. Zhai, D. Reta, N. Chilton and Y.-Z. Zheng, Enhancing Magnetic Hysteresis in Single-Molecule Magnets by Ligand Functionalisation, Chem, 2020, 6, 1777–1793 CAS.
- L. R. Thomas-Hargreaves, M. J. Giansiracusa, M. Gregson, E. Zanda, F. O'Donnell, A. J. Wooles, N. F. Chilton and S. T. Liddle, Correlating axial and equatorial ligand field effects to the single-molecule magnet performances of a family of dysprosium bis-methanediide complexes, Chem. Sci., 2021, 12, 3911–3920 RSC.
- P. Evans, D. Reta, C. A. P. Goodwin, F. Ortu, N. F. Chilton and D. P. Mills, A double-dysprosocenium single-molecule magnet bound together with neutral ligands, Chem. Commun., 2020, 56, 5677–5680 RSC.
- S. Gupta, S. Dey, T. Rajeshkumar, G. Rajaraman and R. Murugavel, Deciphering the role of anions and secondary coordination sphere in tuning anisotropy in Dy(III) air-stable D5h SIMs, Chem. – Eur. J., 2022, 28, e202103585 CrossRef CAS PubMed.
- S. Corner, G. Gransbury, I. Vitorica-Yrezabal, G. Whitehead, N. Chilton and D. Mills, Halobenzene adducts of a dysprosocenium single-molecule magnet, Inorg. Chem., 2024, 63, 9552–9561 CrossRef CAS PubMed.
- Y. Liu, Y.-C. Chen, J. Liu, W.-B. Chen, G.-Z. Huang, S.-G. Wu, J. Wang, J.-L. Liu and M.-L. Tong, Cyanometallate-Bridged Didysprosium Single-Molecule Magnets Constructed with Single-Ion Magnet Building Block, Inorg. Chem., 2020, 59, 687–694 CrossRef CAS PubMed.
- S. Demir, M. I. Gonzalez, L. E. Darago, W. J. Evans and J. R. Long, Giant coercivity and high magnetic blocking temperatures for N23− radical-bridged dilanthanide complexes upon ligand dissociation, Nat. Commun., 2017, 8, 2144–2144 CrossRef PubMed.
- W. Cai, J. D. Bocarsly, A. Gomez, R. J. Letona Lee, A. Metta-Magaña, R. Seshadri and L. Echegoyen, High blocking temperatures for DyScS endohedral fullerene single-molecule magnets, Chem. Sci., 2020, 11, 13129–13136 Search PubMed.
- S. Demir, J. M. Zadrozny, M. Nippe and J. R. Long, Exchange Coupling and Magnetic Blocking in Bipyrimidyl Radical-Bridged Dilanthanide Complexes, J. Am. Chem. Soc., 2012, 134, 18546–18549 Search PubMed.
- N. Mavragani, D. Errulat, D. A. Gálico, A. A. Kitos, A. Mansikkamäki and M. Murugesu, Radical–Bridged Ln4 Metallocene Complexes with Strong Magnetic Coupling and a Large Coercive Field, Angew. Chem., Int. Ed., 2021, 60, 24206–24213 CrossRef CAS PubMed.
- M. J. Giansiracusa, S. Al-Badran, A. K. Kostopoulos, G. F. S. Whitehead, D. Collison, F. Tuna, R. E. P. Winpenny and N. F. Chilton, A large barrier single-molecule magnet without magnetic memory, Dalton Trans., 2019, 48, 10795–10798 RSC.
- S. Bala, G.-Z. Huang, Z.-Y. Ruan, S.-G. Wu, Y. Liu, L.-F. Wang, J.-L. Liu and M.-L. Tong, A square antiprism dysprosium single-ion magnet with an energy barrier over 900 K, Chem. Commun., 2019, 55, 9939–9942 RSC.
- M. Fondo, J. Corredoira-Vázquez, A. M. García-Deibe, J. Sanmartín-Matalobos, S. Gómez-Coca, E. Ruiz and E. Colacio, Slow magnetic relaxation in dinuclear dysprosium and holmium phenoxide bridged complexes: a Dy2 single molecule magnet with a high energy barrier, Inorg. Chem. Front., 2021, 8, 2532–2541 RSC.
- X.-Q. Ji, J. Xiong, R. Sun, F. Ma, H.-L. Sun, Y.-Q. Zhang and S. Gao, Enhancing the magnetic performance of pyrazine-N-oxide bridged dysprosium chains through controlled variation of ligand coordination modes, Dalton Trans., 2021, 50, 7048–7055 RSC.
- H. Wu, M. Li, Z. Xia, V. Montigaud, O. Cador, B. Le Guennic, H. Ke, W. Wang, G. Xie, S. Chen and S. Gao, High temperature quantum tunnelling of magnetization and thousand kelvin anisotropy barrier in a Dy2 single-molecule magnet, Chem. Commun., 2021, 57, 371–374 RSC.
- Z. Zhu, C. Zhao, Q. Zhou, S. Liu, X.-L. Li, A. Mansikkamäki and J. Tang, Air-Stable Dy(III)-Macrocycle Enantiomers: From Chiral to Polar Space Group, CCS Chem., 2022, 4, 3762–3771 CrossRef CAS.
- X. L. Ding, Y. Q. Zhai, T. Han, W. P. Chen, Y. S. Ding and Y. Z. Zheng, A Local D4h Symmetric Dysprosium(III) Single–Molecule Magnet with an Energy Barrier Exceeding 2000 K, Chem. – Eur. J., 2021, 27, 2623–2627 CrossRef CAS PubMed.
- J. Xiong, H.-Y. Ding, Y.-S. Meng, C. Gao, X.-J. Zhang, Z.-S. Meng, Y.-Q. Zhang, W. Shi, B.-W. Wang and S. Gao, Hydroxide-bridged five-coordinate Dy(III) single-molecule magnet exhibiting the record thermal relaxation barrier of magnetization among lanthanide-only dimers, Chem. Sci., 2017, 8, 1288–1294 RSC.
- P. B. Jin, Y. Q. Zhai, K. X. Yu, R. E. P. Winpenny and Y. Z. Zheng, Dysprosiacarboranes as Organometallic Single–Molecule Magnets, Angew. Chem., Int. Ed., 2020, 59, 9350–9354 CrossRef CAS PubMed.
- A. B. Canaj, S. Dey, O. Céspedes, C. Wilson, G. Rajaraman and M. Murrie, There is nothing wrong with being soft: using sulfur ligands to increase axiality in a Dy(iii) single-ion magnet, Chem. Commun., 2020, 56, 1533–1536 RSC.
- K. L. M. Harriman, J. Murillo, E. A. Suturina, S. Fortier and M. Murugesu, Relaxation dynamics in see-saw shaped Dy(iii) single-molecule magnets, Inorg. Chem. Front., 2020, 7, 4805–4812 RSC.
- S. Demir, M. D. Boshart, J. F. Corbey, D. H. Woen, M. I. Gonzalez, J. W. Ziller, K. R. Meihaus, J. R. Long and W. J. Evans, Slow Magnetic Relaxation in a Dysprosium Ammonia Metallocene Complex, Inorg. Chem., 2017, 56, 15049–15056 CrossRef CAS PubMed.
- Z.-H. Li, Y.-Q. Zhai, W.-P. Chen, Q.-C. Luo, T. Han and Y.-Z. Zheng, Breaking the axiality of pentagonal–bipyramidal dysprosium(III) single-molecule magnets with pyrazolate ligands, Inorg. Chem. Front., 2020, 7, 4367–4376 RSC.
- M. Li, H. Wu, Z. Xia, L. Ungur, D. Liu, L. F. Chibotaru, H. Ke, S. Chen and S. Gao, An Inconspicuous Six-Coordinate Neutral DyIII Single-Ion Magnet with Remarkable Magnetic Anisotropy and Stability, Inorg. Chem., 2020, 59, 7158–7166 CrossRef CAS PubMed.
- J. Long, I. V. Basalov, N. V. Forosenko, K. A. Lyssenko, E. Mamontova, A. V. Cherkasov, M. Damjanović, L. F. Chibotaru, Y. Guari, J. Larionova and A. A. Trifonov, Dysprosium Single-Molecule Magnets with Bulky Schiff Base Ligands: Modification of the Slow Relaxation of the Magnetization by Substituent Change, Chem. – Eur. J., 2018, 25, 474–478 CrossRef PubMed.
- H.-M. Dong, H.-Y. Li, Y.-Q. Zhang, E.-C. Yang and X.-J. Zhao, Magnetic Relaxation Dynamics of a Centrosymmetric Dy2 Single-Molecule Magnet Triggered by Magnetic-Site Dilution and External Magnetic Field, Inorg. Chem., 2017, 56, 5611–5622 CrossRef CAS PubMed.
- T. Han, W. Shi, Z. Niu, B. Na and P. Cheng, Magnetic Blocking from Exchange Interactions: Slow Relaxation of the Magnetization and Hysteresis Loop Observed in a Dysprosium-Nitronyl Nitroxide Chain Compound with an Antiferromagnetic Ground State, Chem. – Eur. J., 2012, 19, 994–1001 CrossRef PubMed.
- G. Lu, Y. Liu, W. Deng, G.-Z. Huang, Y.-C. Chen, J.-L. Liu, Z.-P. Ni, M. Giansiracusa, N. F. Chilton and M.-L. Tong, A perfect triangular dysprosium single-molecule magnet with virtually antiparallel Ising-like anisotropy, Inorg. Chem. Front., 2020, 7, 2941–2948 RSC.
- S. Demir, M. Nippe, M. I. Gonzalez and J. R. Long, Exchange coupling and magnetic blocking in dilanthanide complexes bridged by the multi-electron redox-active ligand 2,3,5,6-tetra(2-pyridyl)pyrazine, Chem. Sci., 2014, 5, 4701–4711 RSC.
- Z. H. Li, Y. Q. Zhai, W. P. Chen, Y. S. Ding and Y. Z. Zheng, Air–Stable Hexagonal Bipyramidal Dysprosium(III) Single–Ion Magnets with Nearly Perfect D6h Local Symmetry, Chem. – Eur. J., 2019, 25, 16219–16224 CrossRef CAS PubMed.
- S. Jia, X. Zhu, B. Yin, Y. Dong, A. Sun and D.-f. Li, Macrocyclic Hexagonal Bipyramidal Dy(III)-Based Single-Molecule Magnets with a D6 h Symmetry, Cryst. Growth Des., 2023, 23, 6967–6973 CrossRef CAS.
- S.-S. Liu, Y.-S. Meng, Y.-Q. Zhang, Z.-S. Meng, K. Lang, Z.-L. Zhu, C.-F. Shang, B.-W. Wang and S. Gao, A Six-Coordinate Dysprosium Single-Ion Magnet with Trigonal-Prismatic Geometry, Inorg. Chem., 2017, 56, 7320–7323 CrossRef CAS PubMed.
- A. G. Bispo-Jr, L. Yeh, D. Errulat, D. A. Gálico, F. A. Sigoli and M. Murugesu, Improving the performance of β-diketonate-based DyIII single-molecule magnets displaying luminescence thermometry, Chem. Commun., 2023, 59, 8723–8726 RSC.
- J.-W. Yang, Y.-M. Tian, J. Tao, P. Chen, H.-F. Li, Y.-Q. Zhang, P.-F. Yan and W.-B. Sun, Modulation of the Coordination Environment around the Magnetic Easy Axis Leads to Significant Magnetic Relaxations in a Series of 3d-4f Schiff Complexes, Inorg. Chem., 2018, 57, 8065–8077 CrossRef CAS PubMed.
- G. Velkos, D. S. Krylov, K. Kirkpatrick, L. Spree, V. Dubrovin, B. Büchner, S. M. Avdoshenko, V. Bezmelnitsyn, S. Davis, P. Faust, J. Duchamp, H. C. Dorn and A. A. Popov, High Blocking Temperature of Magnetization and Giant Coercivity in the Azafullerene Tb2@C79N with a Single-Electron Terbium-Terbium Bond, Angew. Chem., Int. Ed., 2019, 58, 5891–5896 CrossRef CAS PubMed.
- J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, A N23− Radical-Bridged Terbium Complex Exhibiting Magnetic Hysteresis at 14 K, J. Am. Chem. Soc., 2011, 133, 14236–14239 CrossRef CAS PubMed.
- Z. Hu, H. Hu, Z. Chen, D. Liu, Y. Zhang, J. Sun, Y. Liang, D. Yao and F. Liang, Guest-Induced Switching of a Molecule-Based Magnet in a 3d–4f Heterometallic Cluster-Based Chain Structure, Inorg. Chem., 2020, 60, 633–641 CrossRef PubMed.
- K. R. Meihaus and J. R. Long, Magnetic Blocking at 10 K and a Dipolar-Mediated Avalanche in Salts of the Bis(η8-cyclooctatetraenide) Complex [Er(COT)2]−, J. Am. Chem. Soc., 2013, 135, 17952–17957 CrossRef CAS PubMed.
- A. P. Orlova, J. D. Hilgar, M. G. Bernbeck, M. Gembicky and J. D. Rinehart, Intuitive Control of Low-Energy Magnetic Excitations via Directed Dipolar Interactions in a Series of Er(III)-Based Complexes, J. Am. Chem. Soc., 2022, 144, 11316–11325 CrossRef CAS PubMed.
- H. Kong, J.-Y. Wang, J.-C. Liu, L. Zhang, P.-Y. Liao, Y.-Q. Qi, Z. Liu, S.-G. Wu and M.-L. Tong, Photochromic Dysprosium Single-Molecule Magnet Featuring Reversible Redox Transformation of Polyoxomolybdate Moiety, Angew. Chem., Int. Ed., 2024, e202422557 Search PubMed.
- S. K. Langley, D. P. Wielechowski, V. Vieru, N. F. Chilton, B. Moubaraki, B. F. Abrahams, L. F. Chibotaru and K. S. Murray, A {CrIII2DyIII2} Single-Molecule Magnet: Enhancing the Blocking Temperature through 3d Magnetic Exchange, Angew. Chem., Int. Ed., 2013, 52, 12014–12019 CrossRef CAS PubMed.
- B.-K. Ling, Y.-Q. Zhai, P.-B. Jin, H.-F. Ding, X.-F. Zhang, Y. Lv, Z. Fu, J. Deng, M. Schulze, W. Wernsdorfer and Y.-Z. Zheng, Suppression of zero-field quantum tunneling of magnetization by a fluorido bridge for a “very hard” 3d-4f single-molecule magnet, Matter, 2022, 5, 3485–3498 CrossRef CAS.
- H. Kwon, K. R. McClain, J. G. C. Kragskow, J. K. Staab, M. Ozerov, K. R. Meihaus, B. G. Harvey, E. S. Choi, N. F. Chilton and J. R. Long, Coercive Fields Exceeding 30 T in the Mixed-Valence Single-Molecule Magnet (CpiPr5)2Ho2I3, J. Am. Chem. Soc., 2024, 146, 18714–18721 CrossRef CAS PubMed.
- J. M. Zadrozny, D. J. Xiao, M. Atanasov, G. J. Long, F. Grandjean, F. Neese and J. R. Long, Magnetic blocking in a linear iron(I) complex, Nat. Chem., 2013, 5, 577–581 CrossRef CAS PubMed.
- A. W. Cook, J. D. Bocarsly, R. A. Lewis, A. J. Touchton, S. Morochnik and T. W. Hayton, An iron ketimide single-molecule magnet [Fe4(N=CPh2)6] with suppressed through-barrier relaxation, Chem. Sci., 2020, 11, 4753–4757 RSC.
- M. Heu, S. Yoon, B. J. Suh, D.-Y. Jung, J. W. Suk and Y. J. Kim, Magnetic Relaxation in a Single-Molecule Magnet Mn12-chlorobutylate, J. Korean Phys. Soc., 2003, 43, 544–547 CAS.
- S. Verma, A. Verma, A. K. Srivastava, A. Gupta, S. P. Singh and P. Singh, Structural and magnetic properties of Mn12-Stearate nanomagnets, Mater. Chem. Phys., 2016, 177, 140–146 CrossRef CAS.
- M. Laskowska, O. Pastukh, P. Konieczny, M. Dulski, M. Zalsiński and L. Laskowski, Magnetic Behaviour of Mn12-Stearate Single-Molecule Magnets Immobilized on the Surface of 300 nm Spherical Silica Nanoparticles, Materials, 2020, 13, 2624 CrossRef CAS PubMed.
- A. Verma, S. Verma, P. Singh and A. Gupta, Ageing effects on the magnetic properties of Mn12-based Acetate and Stearate SMMs, J. Magn. Magn. Mater., 2017, 439, 76–81 CrossRef CAS.
- L. A. Kushch, V. D. Sasnovskaya, A. I. Dmitriev, E. B. Yagubskii, O. V. Koplak, L. V. Zorina and D. W. Boukhvalov, New single-molecule magnet based on Mn12 oxocarboxylate clusters with mixed carboxylate ligands, [Mn12O12(CN-o-C6H4CO2)12 (CH3CO2)4(H2O)4]·8CH2Cl2: Synthesis, crystal and electronic structure, magnetic properties, Dalton Trans., 2012, 41, 13747–13754 RSC.
- D. Wu, D. Guo, Y. Song, W. Huang, C. Duan, Q. Meng and O. Sato, CoII Molecular Square with Single-Molecule Magnet Properties, Inorg. Chem., 2009, 48, 854–860 CrossRef CAS PubMed.
- S. K. Gupta, H. H. Nielsen, A. M. Thiel, E. A. Klahn, E. Feng, H. B. Cao, T. C. Hansen, E. Lelièvre-Berna, A. Gukasov, I. Kibalin, S. Dechert, S. Demeshko, J. Overgaard and F. Meyer, Multi-Technique Experimental Benchmarking of the Local Magnetic Anisotropy of a Cobalt(II) Single-Ion Magnet, JACS Au, 2023, 3, 429–440 CrossRef CAS PubMed.
- K. Qian, X.-C. Huang, C. Zhou, X.-Z. You, X.-Y. Wang and K. R. Dunbar, A Single-Molecule Magnet Based on Heptacyanomolybdate with the Highest Energy Barrier for a Cyanide Compound, J. Am. Chem. Soc., 2013, 135, 13302–13305 CrossRef CAS PubMed.
Footnotes |
| † We want to dedicate this paper to Prof. Miquel Julve from the Universitat de Valencia, who recently passed away. |
| ‡ Electronic supplementary information (ESI) is available. CCDC 2372498. For ESI and crystallographic data in CIF or other electronic formats, see DOI: https://doi.org/10.1039/d4qi03259d. |
| This journal is © the Partner Organisations 2025 |