 Open Access Article
Open Access ArticleThermal decomposition of neptunyl ammonium nitrate: mechanistic insights and structural characterization of the Np2O5 intermediate phase†‡
Kathryn M. Lawson *,
Tyler L. Spano
*,
Tyler L. Spano ,
Jordan M. Roach
,
Jordan M. Roach ,
Connor J. Parker
,
Connor J. Parker ,
Sara B. Isbill
,
Sara B. Isbill and
Andrew Miskowiec
and
Andrew Miskowiec
Oak Ridge National Laboratory, 1 Bethel Valley Road, Oak Ridge, TN 37830, USA. E-mail: lawsonkm@ornl.gov
First published on 22nd May 2025
Abstract
Neptunium (Np) possesses a rich and unique chemistry that often diverges from other actinide elements yet remains relatively underexplored compared with the other light actinides. A resurgence of interest in Np has been spurred by the application of 237Np for plutonium-238 (238Pu) production for use in radioisotope thermoelectric generators (RTGs), necessitating evaluation of Np chemical reactions and materials. The work presented here studied the thermal decomposition of neptunyl ammonium nitrate (NH4NpVIO2(NO3)3) for synthesis of neptunium dioxide (NpO2), which is the target material used for production of 238Pu. Additionally, structural characterization of the intermediate solid Np pentoxide (Np2O5) was performed. Advanced solid-state characterization techniques, including simultaneous thermal analysis (STA), powder X-ray diffraction (pXRD), Raman spectroscopy, and density functional theory (DFT) modeling have been combined to study the reaction pathways. Analysis revealed that NH4NpVIO2(NO3)3 thermally decomposes to a proposed neptunyl nitrate intermediate, followed by Np2O5 and finally NpO2, all within the temperature range of 150 °C–600 °C. Further characterization of the pentoxide intermediate provided the first Raman spectra of pure-phase Np2O5 and associated DFT modeling confirmed Raman peak assignments for this phase. These findings provide mechanistic information to advance production of the critical radioisotope 238Pu and advance the state of knowledge on Np materials chemistry using modern characterization techniques.
Introduction
Within the actinide series of elements, significant chemical research has been performed for uranium (U) and plutonium (Pu) due to their applications throughout commercial nuclear fuel cycles,1–4 known environmental contamination from global fallout and legacy waste disposal,5–7 and in the case of U, occurrence in nature.8–10 In contrast, the chemical understanding of neptunium (Np) and its 22 isotopes11 is underdeveloped in relation to its light actinide neighbors, leaving significant room for continued discovery. First isolated more than 80 years ago,11 the most prominent isotope of Np is neptunium-237 (237Np), which is produced in conventional nuclear reactors and is present at low levels in used nuclear fuel.12 In present day, the most significant application of Np is the use of 237Np as a target material to produce 238Pu.In the United States, 238Pu is used in radioisotope thermoelectric generators (RTGs), which harness the decay heat of 238Pu to provide sustained power and heat for NASA deep space missions and exploration. To obtain the necessary supply, 238Pu is produced in research reactors through a neutron capture reaction involving 237Np target material (eqn (1)).13 The flowsheet for 238Pu production involves four main steps:14 (1) production of 237Np targets, (2) irradiation of targets in research reactors, (3) separation and purification of 238Pu from 237Np and fission products, and (4) recycle of 237Np to restart step (1) again. The current flowsheet uses a target that is a blend of neptunium dioxide (237NpO2) and aluminum metal (Al) powders in a ceramic–metallic (cermet) pellet form.15
 | (1) |
Reliable production of NpO2 powder for targets necessitates a robust and scalable synthesis method. NpO2 can be effectively synthesized at scale using several methods, most commonly oxalate precipitation and calcination,16–20 but a modified direct denitration (MDD) process was selected for the 238Pu Supply Program. This process was selected based on historical research on uranium (U) chemical conversion. Early studies on the chemical mechanisms of uranyl nitrate denitration found unfavorable powder properties and ceramic properties of fuel pellets prepared from the uranyl nitrate system.21 However, efforts identified that an addition of ammonium nitrate to the feed solution, creating a modified denitration, produced free-flowing oxide with more favorable ceramic properties.22 This modified denitration process was then adapted for mixed oxide (MOX) fuel production21,23,24 and NpO2 pellet production.15,25–27
The chemical mechanisms associated with U-based MDD processes have been thoroughly described in the literature,21,28 providing insights into the nature of the process. The decomposition reaction of the dihydrate phase is outlined by Notz and Haas.21,28 The dehydration step (eqn (2)) was reported to occur at 40 °C, followed by the loss of the first mole of NH4NO3 (eqn (3)) at 170 °C and then the second mole of NH4NO3 (eqn (4)) at 270 °C.21 The generalized reaction mechanism was more recently confirmed by Kim et al.29 The dehydrated version of this solid ((NH4)2UO2(NO3)4) follows the same reaction path, with the exclusion of eqn (2), while NH4UO2(NO3)3 undergoes only eqn (4).21,28
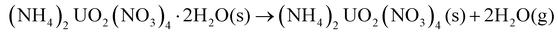 | (2) |
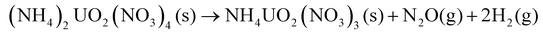 | (3) |
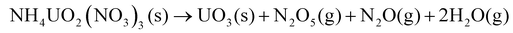 | (4) |
Although the chemistry behind MDD reactions is well documented for U, the MDD mechanism remains unclear for Np and the community lacks fundamental information on Np denitration reactions and the Np oxide materials synthesized through these reactions. While parallels can be drawn across the actinide series, each of these elements has unique chemical properties that must be accounted for. Np can be stabilized in the 4+, 5+, and 6+ oxidation states in both aqueous and solid phases, whereas U is most commonly stabilized in the 4+ and 6+ oxidation states, creating the possibility that the reaction mechanism that is reported for U will not be the same for Np. Some clues into the Np MDD mechanism exist from production-scale data, in which sampling of oxide materials from the MDD unit operation revealed the presence of both Np2O5 and NpO2 in the rotary kiln.30,31 This suggests that Np2O5 is a key intermediate oxide phase towards the production of NpO2 in the MDD reaction, which is distinct compared with the U system that has only one oxide product (UO3). This finding supports a need for further study of the decomposition pathway of Np in a controlled laboratory setting, rather than at production scale, to determine other distinct aspects of the decomposition reaction and elucidate this unique mechanism of neptunium oxide formation.
The presence of Np2O5 in this reaction pathway poses a unique opportunity to characterize an underreported neptunium solid. Np2O5 is one of only two Np binary oxides11—NpO2 and Np2O5—and although Np2O5 was first reported in the 1960s,32 the single crystal structure was not reported until 2006.33 Np2O5 has been synthesized hydrothermally33 or via thermal decomposition of Np(V) hydroxy nitrate,34 Np(V) hydroxide,35,36 and Np(VI) hydroxide.35,36 In this work, the initial neptunyl ammonium nitrate phase presents a novel route to synthesize Np2O5 compared with available literature on nitrate and hydroxide phases. Additionally, the availability of modern solid-phase characterization techniques, as compared with when much of the original work on neptunium oxides was performed in the 1960s and 1970s,18,32,34–38 presents a key opportunity to probe neptunium binary oxides, including Np2O5. Early literature on neptunium oxides reported the possibility of an Np3O8 phase,37 which was suggested as an analog to the U compound U3O8. Decades of research advances were required to definitely disprove the existence of Np3O8 and confirm that Np2O5 was the only other binary Np oxide along with NpO2.34 Recent work has collected Raman spectra of mixed binary Np oxide phases,39 but Raman analysis of pure-phase Np2O5 is still lacking in the literature, along with Raman assignments of Np2O5. The discrepancies in the early Np oxide literature and the occasionally incorrect parallels that are drawn between U and Np oxides necessitate continued investigation of Np oxide material properties to strengthen the understanding of these phases and the understanding of the unique aspects of the element Np.
This work aimed to clarify aspects of Np materials chemistry, specifically for nitrate and oxide phases, and highlight its unique properties within the actinide series by determining the decomposition mechanism of Np–ammonium nitrate double salts. This was achieved through a combination of solid-state techniques, including simultaneous thermal analysis (STA), powder X-ray diffraction (pXRD), and Raman spectroscopy, as well as density functional theory (DFT) modeling. Any one of these techniques for transuranic isotopes such as 237Np are scarce in the literature due to challenges and limitations associated with handling and analyzing highly radioactive materials, thus the multimodal analysis presented in this work is extremely rare for 237Np and adds significant chemical insights for an often-understudied element of the periodic table. This work seeks to not only synthesize and characterize Np materials but also to probe the potential chemical reactions of Np compounds and compare Np materials chemistry to the much deeper body of literature on other actinides, particularly U, which can help expand understanding of trends in the actinide series of the periodic table.
Methods
Caution: Neptunium-237 is an alpha-emitting radionuclide that decays to protactinium-233, a strong gamma-emitting radionuclide. Safe handling of these radioisotopes requires appropriate facilities and qualified personnel. Experiments were performed at Oak Ridge National Laboratory in HEPA-filtered fume hoods by radiologically trained personnel under purpose-designed work controls and monitoring protocols.Synthesis
A 143 mg 237Np mL−1 solution in approximately 1 M HNO3 and a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mole ratio of ammonium to 237Np was prepared for synthesis of neptunyl ammonium nitrate. 84 μL of the solution was transferred into a 1 mL conical bottom polypropylene vial and allowed to evaporate, open, inside a radiological fume hood. After the solution had completely evaporated and only solid remained, the solid was divided into aliquots for subsequent analysis. The same parent material was used in all experiments.
1 mole ratio of ammonium to 237Np was prepared for synthesis of neptunyl ammonium nitrate. 84 μL of the solution was transferred into a 1 mL conical bottom polypropylene vial and allowed to evaporate, open, inside a radiological fume hood. After the solution had completely evaporated and only solid remained, the solid was divided into aliquots for subsequent analysis. The same parent material was used in all experiments.
Simultaneous thermal analysis
Two thermal analysis experiments were performed—one that treated the 237Np salt to 1000 °C and one that treated the 237Np material to 350 °C. The second experiment was performed to collect the intermediate product formed between 300 °C and 500 °C for pXRD analysis. Thermal analyses were performed using a Netzsch STA 449 F1 Jupiter simultaneous thermal analysis (STA) instrument equipped with an Aeolos quadrupole mass spectrometer (QMS) for evolved gas analysis. STA includes thermogravimetric analysis (TGA) and dynamic scanning calorimetry (DSC). Analysis was performed with a TG-DSC sample carrier and Type-S thermocouple. Thirteen (13) mg of the initial 237Np solid was placed in an 85 μL alumina crucible with a lid containing a pinhole opening for off-gas release. Samples were measured under air (Airgas, ultra zero grade) purge gas (50 mL min−1) and argon (Airgas, ultra-high purity) gas protective flow (20 mL min−1). The buoyancy effect was corrected by measuring the empty crucible under the same measurement conditions used for the samples. Heat flow and temperature were calibrated using a six-point standard calibration using indium, tin, bismuth, zinc, aluminum, and gold. Temperature was increased at a rate of 10 °C min−1 to a final temperature of 350 °C or 1000 °C, and evolved gases were transferred to the Aeolos QMS via a heated (200 °C) transfer line. Mass spectra were scanned in the range of 1–80 amu. TG, DSC, and QMS data were analyzed and visualized using Netzsch Proteus Thermal Analysis 8.0. For QMS data, masses of background gases (air, argon) were subtracted from the spectra, and only masses with signal-to-noise ratios greater than 1 were considered for analysis.Powder X-ray diffraction (pXRD)
Because of sample size limitations and associated radiological hazards, the X-ray diffraction (XRD) patterns of the 237Np samples were collected on single crystal XRD loops instead of a traditional powder diffractometer. The samples were analyzed using a single crystal diffractometer and were prepared analogously to a single crystal data collection, but the diffraction pattern was collected using Debye rings from the powder during rotation. The 237Np powder samples (∼5 mg) were suspended into 1 droplet (∼20 μL) of epoxy (Minute Epoxy, J.B. Weld) after the hardening agent was added (Minute Epoxy Hardener, J.B. Weld). Powders were kept as condensed as possible to maximize reflection intensity and data quality for the small sample size. This droplet of epoxy was bound on the tip of a MiTeGen cryoloop. When the sample was hardened and dried, another layer of 1 min epoxy and hardener was added as a secondary form of radioactive contamination prevention. Samples were mounted and exposed to the X-rays for 600 s per 2θ frame, from 4° to 64° 2θ on the Bruker D8 Venture diffractometer, equipped with an Iμs 3.0 molybdenum X-ray source (λ = 0.71073 Å). Debye rings were integrated from the raw diffraction data to create a powder X-ray diffraction (pXRD) pattern. To account for any phase shifting along 2θ, LaB6 (CAS# 12008-21-8) solids were prepared using the same method as that used for the 237Np powders. Small quantities of LaB6 powder diffract strongly using the single crystal XRD method collecting Debye rings. Thus, the LaB6 pXRD pattern was compared with the LaB6 standard reference pattern to determine whether the sample preparation method (binding a small mass of powder in epoxy) would cause any phase shifting along 2θ. The peak locations of the LaB6 standard indicated minimal phase shifting.Raman spectroscopy
In situ Raman spectroscopic data were collected continuously during thermal denitration of neptunyl ammonium nitrate using a Renishaw InVia microRaman spectrometer and a Linkam THMS600 variable temperature stage. The sample of neptunyl ammonium nitrate was placed in an aluminum crucible and heated from room temperature (∼25 °C) to 350 °C at a heating rate of 1 °C min−1. A 785 nm excitation wavelength with low incident laser power (30 mW) was employed to reduce the likelihood of additional surface reactions of sample particles induced by laser heating. For each dataset, one accumulation of data in the range of 24–1246 cm−1 was collected, with a 10 s exposure time.Density functional theory (DFT) modeling
The experimental Np2O5 structure of Forbes et al.33 was relaxed using the Vienna ab initio Simulation Package (VASP 6.1)40–42 DFT software until forces on the atoms were less than 0.01 eV Å−1. Both ionic positions and lattice parameters were allowed to relax, so an expansion of the plane wave basis set of 800 eV was used to limit Pulay stress. The exchange–correlation functional of Perdew, Burke, and Ernzhoff modified for solids (PBEsol)43 was used to describe the interatomic interactions. A k-point spacing of 0.35 Å−1 was used to sample the irreducible Brillouin zone with spin-polarized electron occupations described using Gaussian smearing with a smearing width of 0.20 eV and an electronic convergence of 1 × 10−6 eV. An effective Hubbard + U value of 3.0 eV was applied to the neptunium atoms using the approach of Dudarev et al.44 to break the f-orbital degeneracy in accordance with previous work.45 Phonons were calculated using the finite displacement method as implemented in Phonopy, where forces for each displacement were calculated using VASP,46,47 and a 14 × 14 × 14 mesh was used to calculate the phonon density of states.Results and discussion
Thermal analysis
The pXRD data of the initial 237Np solid indicate the presence of NH4NpO2(NO3)3 (Fig. 1), which contains Np in the 6+ oxidation state. Although minor phase shift (∼0.15° 2θ) appears at higher angles, the pattern is most like the published structure of NH4NpO2(NO3)3 from Autillo et al.48 when compared with all other possible published Np solids relevant to the MDD reaction, particularly other Np nitrate phases. While pXRD is more appropriate for bulk analysis of the starting material prior to thermal decomposition, further confirmation of the chemical formula of the initial solid was performed using single crystal X-ray diffraction, specifically to address the observed minor phase shift at high angle. A single crystal from the same aqueous feed stock was isolated and the structure was solved (see ESI‡), supporting pXRD data that the material is NH4NpO2(NO3)3. While pXRD and single crystal diffraction data both provide evidence that the initial solid phase is primarily NH4NpO2(NO3)3, low intensity reflections observed in PXRD at ∼6.5, 8.5, and 12° 2θ suggest that a small quantity of NpO2(NO3)2·nH2O may be present, although the resolution of the powder by single crystal diffraction method limits definitive identification of these reflections. | ||
| Fig. 1 Powder X-ray diffraction patterns of initial Np solid used in thermal experiments (red trace) and the ICSD standard pattern48 for NH4NpO2(NO3)3 (black trace). Data were collected using an Iμs 3.0 molybdenum X-ray source (λ = 0.71073 Å). | ||
Thermal treatment of the NH4NpO2(NO3)3 solid up to 1000 °C using thermogravimetric analysis shows evidence of four decomposition steps between 150 °C–600 °C (Fig. 2). Simultaneously collected dynamic scanning calorimetry (DSC) shows a prominent exothermic step at 150 °C, while all other steps are endothermic (Fig. 2). The largest mass losses occur between 200 °C–300 °C, which has two nearly indistinguishable decomposition steps. The small mass loss between 550 °C–600 °C is notable given that the available mechanistic information on uranium denitration does not show any change in mass above 350 °C, suggesting that this is a unique aspect of the Np ammonium nitrate denitration mechanism. During thermal decomposition of the Np ammonium nitrate between 100 °C–300 °C, off-gas was measured using a coupled quadrupole mass spectrometer (QMS) and detected the presence of water, NH3, NO, and NO2 (Table 1). No measurable off-gas was recorded during the decomposition step at 550 °C–600 °C, likely because of the very low mass loss and correspondingly small release of off-gases.
 | ||
| Fig. 2 Thermogravimetric (green) and DSC (blue) data recorded during thermal treatment of neptunyl ammonium nitrate at 10 °C min−1 up to 1000 °C. | ||
| Temperature (°C) | Heat of reaction | Off-gases |
|---|---|---|
| 150 | Exothermic | H2O, NH3, NO |
| 250 | Endothermic | H2O, NH3, NO, N2O |
| 300 | Endothermic | H2O, N2O, NO |
| 575 | Endothermic | Not detectable |
Characterization of Np2O5
Given the unique decomposition step between 550 °C–600 °C, further characterization of the intermediate Np phase present between 300 °C–550 °C was pursued. A crystalline sample was collected after thermal treatment of neptunyl ammonium nitrate solid to 350 °C to determine whether the intermediate Np phase might be a nitrate or oxide phase. For this collection, a thermogravimetric analysis (TGA) experiment was terminated at 350 °C, and the sample was analyzed via pXRD. Data indicate the presence of Np2O5 at this temperature (Fig. 3), which agrees well with the published powder pattern from Forbes.33 The pentoxide has also been found in the production scale kiln of the MDD process,30,31 corroborating the finding. | ||
| Fig. 3 Powder X-ray diffraction patterns of Np sample taken at 350 °C (red trace) and the ICSD standard pattern33 for Np2O5 (black trace). Data were collected using an Iμs 3.0 molybdenum X-ray source (λ = 0.71073 Å). | ||
To further elucidate the structure of Np2O5 synthesized in denitration of neptunyl ammonium nitrate, the sample was also analyzed via Raman spectroscopy. At temperatures above 250 °C, conversion to Np2O5 is observed and density functional theory was used for vibrational mode assignments. Fig. 4 plots the Raman spectrum of Np2O5 as collected during a temperature-dependent Raman spectroscopy experiment together with analysis from DFT. Data in Fig. 4 are averaged from spectra collected between 250 °C and 350 °C. A post experiment Raman measurement of the material after cooling to room temperature showed no significant changes in the character of the Raman spectra. Data in Fig. 4 are plotted less an asymmetric least-squares background term (λ = 3000 and p = 0.0002) and smoothed with a Savitzky–Golay filter (window size 25 cm−1, 7th order polynomial).49
 | ||
| Fig. 4 Raman spectra of Np2O5 (black data) with the DFT-predicted Γ-point phonon frequencies (top, black lines), with the yl-like eigenvector amplitude as calculated in eqn (4) for Np(1), Np(2), and Np(3). Major contributions of yl-like eigenvector amplitude are observed at frequencies close to the major Raman peaks, suggesting that these features could be plausibly assigned to [O–Np–O] symmetric stretching vibrations. | ||
Major peaks are observed at 42, 89, 107, 109, 251, 266, 283, 393, 565, and 781 cm−1 in Np2O5. The 251, 266, and 283 cm−1 peaks form a continuous band of scattering. Several smaller peaks (near 180, 630, and a shoulder near 440 cm−1) also appear in the spectra but are considered too small to index.
Assignment of the Raman spectra is performed with the assistance of DFT calculations. Np2O5 in the P2/c space-group (Z = 4) contains 81 optical modes as 19Ag + 18Au + 23Bg + 21Bu. Only the Ag and Bg modes are Raman active; hence, there are 42 Raman active modes in Np2O5.
The partial phonon densities of states (pDOS) for individual neptunium atoms and oxygen atoms, in aggregate, are plotted in Fig. 5 to provide a qualitative picture of which atoms are moving at which frequencies, which is useful for mode assignment. The pDOS is distinct from the optical cross sections measured in Raman spectroscopy; however, it is related. There are two important differences to highlight here between the Raman spectra and the partial pDOS. First, the pDOS is averaged over the entire Brillouin zone, whereas long-wavelength optical spectroscopy (Raman and infrared spectroscopy) probes the phonon frequencies only very near to the Γ point. In most cases, though, the optical phonon dispersion is not so large that the pDOS cannot be used to aid the qualitative interpretation of optical spectra. Second, the pDOS does not contain any information related to the light–matter interaction. The Raman cross section for a given optical mode is proportional to the spatial derivative of the dielectric polarizability, which is not calculated here.
Panel (a) in Fig. 5 shows that above 200 cm−1 phonon motion is dominated by oxygen atoms. This result is unsurprising as the Np mass is substantially higher than O. A small phonon gap is opened between 700–725 cm−1, and the overall phonon DOS is terminated at 825 cm−1. In panel (b), which plots only the Np contributions to the total DOS, there is a clear phonon cutoff opens near 210 cm−1 for Np atoms. Interestingly, Np(3) has significant contributions to the pDOS near 400 and 500–600 cm−1, whereas minimal contributions from Np(1) and Np(2) are observed in these regions.
Np2O5 is theorized to contain so-called “actinyl–actinyl interactions” (AAI). AAIs are structural coordination geometries involving the adjacency of two actinyl ([AnO2]2+) groups. Forbes et al. described the neptunyl coordination in Np2O5 between sheets as “Np(1) and Np(2) neptunyl ion O atoms are equatorial vertices of the Np(3) square bipyramid of an adjacent sheet”.33 The assignment of the coordination geometry by Forbes et al. is based on the bond distances, with Np(1)–Oyl and Np(2)–Oyl bond distances equal to 1.866 and 1.885 Å. The structural motif in Np2O5, wherein the “Oyl” of Np(1) and Np(2) is also an equatorial ligand to Np(3), appears to be a common bonding arrangement in Np5+ crystal structures.50 From this, there is an outstanding question as to whether Np2O5 shows evidence of these AAIs in the vibrational Raman spectrum.
Previously, a qualitative method of analyzing phonon eigenvectors as predicted from DFT has been used to assist with spectral assignment in multimetal center systems.51 Conceptually, this considers that each phonon eigenvector, e(ω)i,j, contains information about the direction and amplitude of each atom (j) during excitation of each phonon with mode index i. Actinyl systems exhibit strong Raman scattering of the symmetric stretching mode of the [O–An–O]2+ unit. We calculate the following “yl-like eigenvector amplitude” quantity for each mode:
 | (5) |
Results of this analysis are shown in Fig. 4, where the colored lines below the data are placed at the calculated vibrational frequencies (for Raman-active modes only). Transparency of the lines indicates the magnitude of the yl-like eigenvector amplitude, with low transparency (higher opacity) representing larger magnitude. The magnitudes are normalized to unity, with the strongest modes for each Np center fully opaque. The solid black lines above the data are the DFT-calculated, Raman active Γ-point mode frequencies unweighted by the yl-like eigenvector amplitude.
The relatively strong intensity of the 565 and 781 cm−1 mode are reminiscent of excitations present in actinyl-like systems; hence, the logical assignment is to assign these modes to [NpO2]2+ νs symmetric stretching vibrations. Based on the yl-like eigenvector amplitude analysis, the 781 cm−1 mode (DFT-calculated frequency of 753 cm−1) originates from the collective symmetric Oyl stretching motion of all three Np centers. However, there is no significant “yl-like” character of phonon modes near 565 cm−1 based on DFT results. The nearest calculated phonon frequencies via DFT are 541 and 589 cm−1. Both of these modes are primarily in-plane (a/b plane) translational shearing modes between layers, involving little neptunyl oxygen motion. However, DFT determines a phonon frequency of 476 cm−1 for a mode containing motion highly reminiscent of yl-like motion. This mode, reproduced in Fig. 6 along with the mode at 781 cm−1, involves the symmetric motion of all “yl-like” oxygens. Note that Oyl atoms associated with all three Np centers are involved in this motion. Such a mode might be a vibrational indicator of hypothesized AAIs.
However, considering the Np2O5 crystal structure and the space group symmetry, a pure [NpO2]2+ symmetric stretching mode does not exist. The [NpO2]2+ units for Np(1) and Np(2) are inclined with respect to the c axis by 40 degrees. The strongest “yl-like” phonon eigenvectors (at 476 and 781 cm−1 in Fig. 6) are polarized along the c axis. These modes not being polarized directly along the [O–Np–O] bond does not preclude them from originating strong scattering in the Raman, as their scalar product along the [O–Np–O] bond is still large. Whether these modes can be truly referred to in the same concept as the traditional Raman-active actinyl stretching vibrations is a matter of further discussion.
Neptunyl ammonium nitrate decomposition mechanism
Combining the multimodal analysis of neptunyl ammonium nitrate and its decomposition pathway, including pXRD, STA, and Raman analysis, the multiple decomposition steps towards production of Np oxides can be deconvoluted. Phase identification via pXRD confirms that the initial Np solid is primarily NH4NpO2(NO3)3 (Fig. 1), which then undergoes four thermal decomposition steps between 150 °C–600 °C (Fig. 2). The intermediate phase at 350 °C is confirmed to be Np2O5 (Fig. 3) and is characterized above using Raman and DFT. However, there are additional transition steps observed in TGA and DSC data between NH4NpO2(NO3)3 and Np2O5 before the oxide is fully reduced to NpO2 (Fig. 7), necessitating further insights into the decomposition mechanism below 300 °C. | ||
| Fig. 7 Structures of identified crystalline decomposition products during thermal treatment of NH4NpO2(NO3)3. | ||
To understand the mechanism by which neptunyl ammonium nitrate undergoes degradation to Np2O5, in situ Raman spectroscopic maps were collected continuously from room temperature to 350 °C, with the resulting Raman spectroscopic heatmap shown in Fig. 8a. Below temperatures of ∼50 °C (Fig. 8b), Raman spectra collected for the sample are broadly in good agreement with that reported for a single crystal of (NH4)NpO2(NO3)3. As was seen in PXRD, however, small contributions from an additional minor Np phase may be present. Two low intensity peaks located at ∼725 and 825 cm−1 are present in our sample that do not appear in the reported spectrum of (NH4)NpO2(NO3)3. These peaks may be attributable to spectroscopic contributions from NpO2(NO3)2(H2O)2. Alternatively, the appearance of these low intensity features could be due to differences in Raman spectra collected for a single crystal of (NH4)NpO2(NO3)3 versus a polycrystalline powder in this work. Since only one spectrum for a single crystal of (NH4)NpO2(NO3)3 is reported in the literature, it is possible that polarization effects could be operative and additional vibrational modes are activated due to the random orientation of crystallites in our polycrystalline sample. Additional evidence for polarization dependence is observed in spectra collected in this work, with significant differences in observed intensity of Raman features relative to the spectrum reported by Autillo et al.48 Nevertheless, data are insufficient to definitively assign the additional features in the low temperature (≤50 °C) Raman spectra to either an impurity phase or differences resulting from sample type (single vs. polycrystal).
As was observed from pXRD, it is clear that (NH4)NpO2(NO3)3 is the majority phase fraction. The most prominent spectroscopic features include a doublet of ν1 symmetric stretching vibrational modes associated with NO3− and a ν1 peak attributed to [O–Np–O] (NpOyl) vibrations. The intense band centered at 665 cm−1, based on literature assignments, originates from symmetric stretching of axial O atoms that coordinate Np centers, and is in good agreement with the position of a band reported by Autillo et al.48 A lower intensity peak at 858 cm−1, also reported by Autillo et al.48 although unassigned by those authors, might be attributable to additional stretching modes of the NpOyl.52 Pyrch et al. assign bands at ∼850 cm−1 to ν3 antisymmetric stretching of NpOyl in materials with neptunyl–neptunyl interactions,52 although this assignment is inappropriate here based on selection rules for linear NpO2 units, which dictate that ν3 modes are Raman silent. Nevertheless, changes in the position and intensity of this 858 cm−1 peak are described. Although no significant changes in the position of the 665 cm−1 neptunyl mode are observed until a temperature of 175 °C is reached, attenuation of this band occurs at ∼75 °C. Conversely, low-energy lattice vibrations, often assigned to equatorial actinide–oxygen coordination environments, are seen between 35–250 cm−1 and become more diffuse during in situ heating, with a significant loss of resolution observed at ∼50 °C. The ν1 nitrate-related modes, centered at ∼1025 and 1043 cm−1, likely correspond to vibrations of two crystallographically distinct O atoms that coordinate N centers.48 Other nitrate-related vibrational modes, including ν2 symmetric bending modes, and ν3 wagging contributions are seen between 780–835 and 710–740 cm−1, respectively. Changes in the relative intensity and resolution of nitrate modes are observed with increasing temperature. Notably, at ∼50 °C, a peak centered at ∼795 cm−1, related to ν2 NO3− symmetric bending, increases in intensity relative to a second ν2 NO3− bending mode, suggesting modifications to nitrate connectivity with neptunyl centers as temperature increases.
Changes in the equatorial coordination of Np and the rearrangement of nitrate groups first observed around ∼50 °C persist until ∼150 °C. Notably, the two distinct ν1 peaks originating from NO3− gradually converge, with the lower energy mode decreasing in intensity with increasing temperature (Fig. 8c). The coordination around N is such that two of the three O atoms are crystallographically equivalent equatorial ligands of Np centers, and the remaining crystallographically distinct O atom is unshared. The decrease in intensity and convergence of ν1 NO3− peaks suggests that all O atoms coordinating N become increasingly crystallographically identical with increasing temperature. This structural rearrangement is further indicated by the diffusivity of equatorial vibrational modes seen in the low-energy (up to ∼250 cm−1) region of the spectra above 50 °C. The unidentified peak located at 858 cm−1 significantly decreases in intensity in this temperature range. Although unlikely, if this peak were attributable to ν3 antisymmetric stretching about the neptunyl center, then the loss of intensity here could be attributable to an increase in NpOyl bond rigidity imparted by equatorial O structural rearrangement.
At ∼170 °C and above (Fig. 8d), a significant blueshift is observed in the prominent NpOyl vibrational mode from 665 to ∼675 cm−1. This blueshift supports the observation that [O–An–O] bond rigidity increases with increasing temperature. Further, this 10 cm−1 shift in peak position indicates that a decrease in NpOyl bond lengths is likely in this temperature range. The increase in NpOyl bond strength imparted by shorter bond lengths is commensurate with both the decrease in intensity and the eventual disappearance of the 858 cm−1 peak and the behavior of vibrational modes associated with NO3−. Although the singular symmetric stretching vibration of N–O remains at ∼1047 cm−1 between 170 °C–230 °C, significant differences in the ν2 and ν3 modes are seen. Between 60 °C–150 °C (Fig. 8c) ν2 nitrate modes appear at 793 and 831 cm−1, but at higher temperature the lower energy mode shifts to 820 cm−1, again indicating a more rigid structure, this time about the N in addition to the Np center. Likewise, the ν3 nitrate modes, seen at ∼725 and 756 cm−1 between 60 °C–150 °C shift to 736 and 750 cm−1 at higher temperature.
Although no NH4+ vibrational modes are visible in the region examined during the in situ heating experiment, it can be inferred the behavior of this moiety from spectroscopic changes is the character of the neptunyl modes. N atoms of NH4+ moieties are situated directly between axial O atoms of NpOyl centers,48 with a distance of 2.97 Å between O and N. Given the approximate bond length of N–H in NH4+ (∼1.02 Å), and typical O–H bond distances (∼2.5–3.2 Å), it suggests that significant H bonding exists between axial O atoms that coordinate Np centers and the hydrogen atoms associated with ammonium groups. Thus, the blueshift observed in the neptunyl vibrational mode is very likely attributable to loss of ammonium at this temperature. This would also support the hypothesis of equatorial structural rearrangement, as reconfiguration of bond strength about the neptunium center would be required to account for the bond strength deficiencies associated with the loss of hydrogen bonding to the neptunyl oxygen. Interestingly, this temperature range also is characterized by a significant exothermic event in the DSC (Fig. 2), further supporting this assessment. As described previously, nitrate vibrational modes are still present even after the blueshift, which we ascribe to loss of ammonium indicating that these degradation steps occur separately. This is not unexpected as NH4+ occupies interstitial space between neptunyl centers, whereas NO3− is coordinated directly to Np polyhedra. It stands to reason that the interstitial species is more easily removed than the directly bonded moieties.
Further insight into the chemical changes below 300 °C is provided by the DSC and QMS data collected in combination with TGA data, corroborating the loss of ammonium nitrate at lower temperatures suggested by Raman data. The recorded off-gases show release of ammonia below 250 °C but not at the largest reaction step at 300 °C, suggesting the removal of the NH4 group from the structure occurs at lower temperature regimes. Additionally, the reaction that occurs around 150 °C is an exothermic step (Fig. 2). Decomposition reactions of ammonium nitrate (NH4NO3) can be strongly exothermic53 and loss of NH4NO3 during U denitration at 170 °C is also reported as an exothermic reaction,13 suggesting the observed step at 150 °C is associated with loss of NH4NO3 from the initial Np phase. These observations suggest that one mole of NH4NO3 is lost as a discrete step in the decomposition reaction, which would support the following reaction series:
 | (6) |
This set of equations proposes that the loss of NH4NO3 produces a neptunyl nitrate intermediate phase before Np2O5 formation. Although this intermediate is not expected based on U denitration, an intermediate neptunyl nitrate phase has been reported during decomposition of Np(V) hydroxy nitrate,34 which also subsequently converted to Np2O5 before producing NpO2. To further assess the possibility of these reactions, theoretical mass loss calculations were performed and compared with TGA data from Fig. 2. The theoretical and actual mass loss for the reaction steps of NpO2(NO3)2 to Np2O5, as well as Np2O5 to NpO2, align well (Table 2). However, this assumes that the recorded steps from 200 °C–300 °C are part of the same chemical reaction, despite appearing as two distinct steps in the TGA curve in Fig. 2. The initial reaction step below 175 °C has a lower recorded mass loss than expected for the theoretical mass loss, which is likely because of mass losses that occurred between room temperature (20 °C) and the first recorded temperature in the STA (60 °C). Another possible reason for slight variation in initial mass loss is the presence of a trace-level secondary phase, which has a lower theoretical mass loss than NH4NpO2(NO3)3. As discussed with the initial diffraction data, the possibility of trace-level impurities, while not identifiable through any characterization means employed here, cannot be fully excluded.
| Reaction step | Temperature range (°C) | Theoretical mass loss | Recorded mass loss |
|---|---|---|---|
| NH4NpO2(NO3)3 → NpO2(NO3)2 | 100–175 | 16.91 | 12.78 |
| NpO2(NO3)2 → Np2O5 | 200–300 | 24.52 | 24.09 |
| Np2O5 → NpO2 | 550–600 | 1.69 | 1.63 |
A limitation of this proposed set of reactions is the lack of phase identification during the 100 °C–300 °C period. Confirmation of the initial crystalline phase (NH4NpO2(NO3)3) and crystalline phase at 350 °C (Np2O5) was possible because of the ease of isolation and the relative stability of Np2O5 over a large temperature range for ex situ pXRD analysis. Isolation of any intermediate nitrates between 100 °C–300 °C during STA experiments would be unpredictable and potentially incorrect if samples were not isolated at the precise temperatures associated with the very rapid transitions that occur in this temperature regime. Alternatively, high-temperature pXRD could have been employed to study phase transitions during the reaction. However, X-ray studies of the analogous U system struggled to identify some intermediate phases, which were found to be amorphous,29 which is also likely for the intermediate Np nitrate phases. Despite this limitation, the multiple lines of evidence—theoretical mass losses, calorimetry, mass spectrometry of off-gas, and Raman spectroscopy—all provide pieces of the complex puzzle associated with Np phase transitions and support the assessment of the decomposition mechanism provided in eqn (6), along with corroboration from literature evidence available on Np and U denitration mechanisms.
Conclusions
Multimodal analysis of Np phases throughout thermal denitration NH4NpO2(NO3)3 was performed to uncover the reaction mechanisms of this unique element. Using a combination of thermal analysis, pXRD, and Raman spectroscopy, the intermediate phases during thermal decomposition are proposed to be NpO2(NO3)2 and Np2O5 in the 100 °C–300 °C range before final reduction of the oxide at ∼550 °C. As part of characterization of the Np2O5 intermediate, the first Raman spectra of pure phase Np2O5 are reported here, along with associated peak assignments, which are conclusively identified using DFT modeling. This combination of solid-state analytical techniques is rare for transuranic elements and represents important advances for solid-state Np chemistry. Continued pursuit of chemical studies for each actinide element on an individual basis is of vital importance, given the observed differences between known U denitration mechanisms and Np denitration mechanisms reported here. Future efforts for Np denitration should attempt to more conclusively identify intermediate nitrate phases in low-temperature regions, as well as evaluate potential mechanistic differences between Np(V) and Np(VI) nitrate phases.Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Data availability
The data supporting this article have been included as part of the ESI.‡ Crystallographic data has been deposited at CCDC under Deposition Number 2417020.‡Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the 238Pu Supply Program at the US Department of Energy's Oak Ridge National Laboratory with funding provided by the Science Mission Directorate of the National Aeronautics and Space Administration and administered by the US Department of Energy, Office of Nuclear Energy, under contract DEAC05-00OR22725. The authors wish to thank Cory Dryman, John Dyer, Kaara Patton, Curt Porter, and Joseph Renfro for their assistance in preparation and sampling of the 237Np stock used in these experiments.References
- R. C. Ewing, Long-term storage of spent nuclear fuel, Nat. Mater., 2015, 14, 252 CrossRef CAS PubMed.
- K. J. Pastoor, R. S. Kemp, M. P. Jensen and J. C. Shafer, Progress in uranium chemistry: driving advances in front-end nuclear fuel cycle forensics, Inorg. Chem., 2021, 60, 8347–8367 CrossRef CAS PubMed.
- R. Taylor, Reprocessing and recycling of spent nuclear fuel, Elsevier, 2015 Search PubMed.
- D. Olander, Nuclear fuels – Present and future, J. Nucl. Mater., 2009, 389, 1–22 CrossRef CAS.
- A. Kersting, D. Efurd, D. Finnegan, D. Rokop, D. Smith and J. Thompson, Migration of plutonium in ground water at the Nevada Test Site, Nature, 1999, 397, 56–59 CrossRef CAS PubMed.
- A. P. Novikov, S. N. Kalmykov, S. Utsunomiya, R. C. Ewing, F. Horreard, A. Merkulov, S. B. Clark, V. V. Tkachev and B. F. Myasoedov, Colloid transport of plutonium in the far-field of the Mayak Production Association, Russia, Science, 2006, 314, 638–641 CrossRef CAS PubMed.
- O. N. Batuk, S. D. Conradson, O. N. Aleksandrova, H. Boukhalfa, B. E. Burakov, D. L. Clark, K. R. Czerwinski, A. R. Felmy, J. S. Lezama-Pacheco and S. N. Kalmykov, Multiscale Speciation of U and Pu at Chernobyl, Hanford, Los Alamos, McGuire AFB, Mayak, and Rocky Flats, Environ. Sci. Technol., 2015, 49, 6474–6484 CrossRef CAS PubMed.
- R. Finch and T. Murakami, Systematics and paragenesis of uranium minerals, Rev. Mineral., 1999, 38, 91–180 CAS.
- I. Grenthe, J. Drożdżyński, T. Fujino, E. Buck, T. Albrecht-Schmitt and S. Wolf, in The Chemistry of the Actinide and Transactinide Elements, ed. L. R. Morrs, N. M. Edelstein, J. Fuger and J. J. Katz, Springer, Dordrecht, The Netherlands, 2006, vol. 1, pp. 253–698 Search PubMed.
- J. R. Lancelot, A. Vitrac and C. J. Allegre, The Oklo natural reactor: Age and evolution studies by UPb and RbSr systematics, Earth Planet. Sci. Lett., 1975, 25, 189–196 CrossRef CAS.
- Z. Yoshida, S. G. Johnson, T. Kimura and J. R. Krsul, in The Chemistry of the Actinide and Transactinide Elements, ed. L. R. Morss, N. M. Edelstein and J. Fuger, Springer, The Netherlands, 4th edn, 2010, ch. 6, vol. 2, pp. 699–812 Search PubMed.
- J. Bruno and R. C. Ewing, Spent nuclear fuel, Elements, 2006, 2, 343–349 CrossRef CAS.
- G. Burney and R. Harbour, Radiochemistry of neptunium, National Academies, 1974 Search PubMed.
- NRC, Radioisotope Power Systems, 2009 Search PubMed.
- E. D. Collins, R. N. Morris, J. L. McDuffee, P. L. Mulligan, J. S. Delashmitt, S. R. Sherman, R. J. Vedder and R. M. Wham, Plutonium-238 Production Program Results, Implications, and Projections from Irradiation and Examination of Initial NpO2 Test Targets for Improved Production, Nucl. Technol., 2022, 1–8, DOI:10.1080/00295450.2021.2021769.
- J. Duffey, Lab Scale Production of NpO2, SRS (US). Funding organisation: US Department of Energy, United States, 2003 Search PubMed.
- J. Duffey, Characterization of Neptunium Oxide Generated Using the HB-Line Phase II Flowsheet, SRS, 2003 Search PubMed.
- J. Porter, Production of Neptunium Dioxide, Ind. Eng. Chem. Process Des. Dev., 1964, 3, 289–292 CrossRef CAS.
- T. Severynse, Nuclear Material Processing at the Savannah River Site, Westinghouse Savannah River Company, Aiken, SC (United States); Westinghouse Savannah River Co., Aiken, SC (United States), 1998 Search PubMed.
- R. Myrick and R. Folger, Fabrication of Targets for Neutron Irradiation of Neptunium Dioxide, Ind. Eng. Chem. Process Des. Dev., 1964, 3, 309–313 CrossRef CAS.
- K. J. Notz and P. A. Haas, Properties and thermal decomposition of the double salts of uranyl nitrate-ammonium nitrate, Thermochim. Acta, 1989, 155, 283–295 CrossRef CAS.
- E. D. Collins, in Reprocessing and Recycling of Spent Nuclear Fuel, 2015, pp. 313–323. DOI:10.1016/b978-1-78242-212-9.00012-5.
- J. Mailen, D. Pruett and D. McTaggart, Direct thermal denitration to prepare mixed oxides for nuclear fuel fabrication, Oak Ridge National Lab. (ORNL), Oak Ridge, TN (United States), 1982 Search PubMed.
- P. A. Haas, R. D. Arthur and W. Stines, Development of Thermal Denitration to Prepare Uranium Oxide and Mixed Oxides for Nuclear Fuel Fabrication, 1981 Search PubMed.
- R. J. Vedder, Oak Ridge National Laboratory Preparation of Sintered 237NpO2 Pellets for Irradiation to Produce 238Pu Oxide, Report ORNL/TM-2017/728, Oak Ridge National Laboratory, 2018.
- D. W. Depaoli, D. Benker, L. H. Delmau, S. R. Sherman, F. Riley Jr, P. D. Bailey, E. D. Collins and R. M. Wham, Process Development for Plutonium-238 Production at Oak Ridge National Laboratory, Oak Ridge National Lab. (ORNL), Oak Ridge, TN (United States), 2019 Search PubMed.
- R. M. Wham, R. S. Owens, R. J. Vedder, J. H. Miller and S. Pierce, Automation of neptunium oxide–aluminum target fabrication, Richland, WA, 2019 Search PubMed.
- K. J. Notz and P. A. Haas, Properties and Thermal Decomposition of the Double Salts of Uranyl Nitrate—Ammonium Nitrate, Report ORNL/TM-7820, Oak Ridge National Laboratory, 1981.
- B. H. Kim, Y. B. Lee, M. A. Prelas and T. K. Ghosh, Thermal and X-ray diffraction analysis studies during the decomposition of ammonium uranyl nitrate, J. Radioanal. Nucl. Chem., 2012, 292, 1075–1083 CrossRef CAS PubMed.
- K. M. Peruski, C. J. Parker and S. K. Cary, Characterization of Neptunium Oxide Product from Modified Direct Denitration Process, Idaho Falls, ID, 2023 Search PubMed.
- K. M. Peruski, C. J. Parker and S. K. Cary, Analysis of Neptunium Oxides Produced Through Modified Direct Denitration, J. Nucl. Mater., 2023, 587, 154704 CrossRef CAS.
- D. Cohen and A. Walter, Neptunium pentoxide, J. Chem. Soc., 1964, 2696–2699 RSC.
- T. Z. Forbes, P. C. Burns, S. Skanthakumar and L. Soderholm, Synthesis, Structure, and Magnetism of Np2O5, J. Am. Chem. Soc., 2007, 129, 2760–2761 CrossRef CAS PubMed.
- J. Fahey, R. Turcotte and T. Chikalla, Decomposition, stoichiometry and structure of neptunium oxides, J. Inorg. Nucl. Chem., 1976, 38, 495–500 CrossRef CAS.
- V. Solntsev, I. Kapshukov, L. Sudakov and V. Chistyakov, On the Existence of neptunium protoxide–oxide, Proc. Moscow Symp. Chem. Transuranium Elem., 1976, 235–237 Search PubMed.
- L. Sudakov, V. Solntsev, I. Kapshukov, Y. I. Belyaev and V. Chistyakov, Concerning the occurrence of mixed neptunium oxides, Argonne National Lab., 1972 Search PubMed.
- J. Katz and D. Gruen, Higher oxides of the actinide elements. The preparation of Np3O8, J. Am. Chem. Soc., 1949, 71, 2106–2112 CrossRef CAS.
- W. Zachariasen, Crystal chemical studies of the 5f-series of elements. XII. New compounds representing known structure types, Acta Crystallogr., 1949, 2, 388–390 CrossRef CAS.
- S. E. Gilson, L. R. Sadergaski and A. J. Parkison, Improving understanding of NpO2 and Np2O5 through vibrational spectroscopy, J. Solid State Chem., 2024, 339, 124954 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed.
- G. I. Csonka, J. P. Perdew, A. Ruzsinszky, P. H. Philipsen, S. Lebègue, J. Paier, O. A. Vydrov and J. G. Ángyán, Assessing the performance of recent density functionals for bulk solids, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 155107 CrossRef.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+ U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 Search PubMed.
- Y. Yun, J. Rusz, M.-T. Suzuki and P. Oppeneer, First-principles investigation of higher oxides of uranium and neptunium: U 3 O 8 and Np 2 O 5, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 075109 CrossRef.
- L. Chaput, A. Togo, I. Tanaka and G. Hug, Phonon-phonon interactions in transition metals, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 094302 CrossRef.
- A. Togo, L. Chaput and I. Tanaka, Distributions of phonon lifetimes in Brillouin zones, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 094306 Search PubMed.
- M. Autillo, R. E. Wilson, M. Vasiliu, G. F. de Melo and D. A. Dixon, Periodic Trends within Actinyl (VI) Nitrates and Their Structures, Vibrational Spectra, and Electronic Properties, Inorg. Chem., 2022, 61, 15607–15618 CrossRef CAS PubMed.
- P. H. Eilers and H. F. Boelens, Baseline correction with asymmetric least squares smoothing, Leiden Univ. Med. Cent. Rep., 2005, 1, 5 Search PubMed.
- S. E. Gilson and P. C. Burns, The crystal and coordination chemistry of neptunium in all its oxidation states: An expanded structural hierarchy of neptunium compounds, Coord. Chem. Rev., 2021, 445, 213994 Search PubMed.
- T. L. Spano, A. E. Shields, B. Barth, J. D. Gruidl, J. L. Niedziela, R. J. Kapsimalis and A. Miskowiec, Computationally guided investigation of the optical spectra of pure β-UO3, Inorg. Chem., 2020, 59, 11481–11492 CrossRef CAS PubMed.
- M. M. Pyrch, L. J. Augustine, J. M. Williams, S. E. Mason and T. Z. Forbes, Use of vibrational spectroscopy to identify the formation of neptunyl–neptunyl interactions: a paired density functional theory and Raman spectroscopy study, Dalton Trans., 2022, 51, 4772–4785 RSC.
- V. Babrauskas and D. Leggett, Thermal decomposition of ammonium nitrate, Fire Mater., 2020, 44, 250–268 Search PubMed.
Footnotes |
| † This manuscript has been authored by UT-Battelle LLC under contract DE-AC05-00OR22725 with the US Department of Energy (DOE). The US government retains and the publisher, by accepting the article for publication, acknowledges that the US government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript, or allow others to do so, for US government purposes. DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (https://energy.gov/downloads/doepublic-access-plan). |
| ‡ Electronic supplementary information (ESI) available: Methods and data supporting single crystal X-ray diffraction. CCDC 2417020. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d5qi01015b |
| This journal is © the Partner Organisations 2025 |



