Rational design of superalkali-based novel calix[4]pyridine alkalides as high performance nonlinear optical materials

Abstract

In the present work, novel superalkali-based calix[4]pyridine alkalides have been designed as excess electron compounds using DFT simulations. The computed interaction energies (−32.3 to −64.5 kcal mol⁻¹) and vertical ionization energies (2.51 to 2.79 eV) indicate the stability of the designed alkalides. The highest charge at Li⁻ alkalide in the K₃O⁺CXP[4]Li⁻ is −0.486 |e| as analyzed by natural population analysis. The investigated complexes exhibit reduced HOMO–LUMO energy gaps (0.30–0.50 eV) in comparison to pure calix[4]pyridine (5.69 eV). The IRI and QTAIM analyses indicate that the CXP[4] interacts with superalkali clusters and Li metal via non-covalent interactions. These superalkali-based alkalides possess absorption maxima (727–1096 nm) in the visible to NIR region. The Na₃O⁺CXP[4]Li⁻ alkalide displays a significantly higher static first hyperpolarizability of 2.5 × 10⁶ au as compared to the β_o (3.4 × 10⁴ au) for superalkali-based calix[4]pyrrole alkalides. The β_vec and β_TL values show a similar trend to the static β_o values. Furthermore, the highest dynamic NLO responses for second harmonic generation, hyper-Rayleigh scattering and electro-optical Pockel's effect are 1.8 × 10⁸ au, 1.1 × 10⁸ au and 7.7 × 10⁷ au, respectively. These findings imply that designed alkalides offer a novel perspective on the rational designing of stable high-tech NLO materials.

---

1. Introduction

The design and synthesis of novel nanomaterials have gained substantial attention in the realm of modern science and optical communication. Nanomaterials, on interactions with high intensity ultrafast laser pulses, exhibit intriguing nonlinear optical (NLO) phenomena, including second harmonic generation (SHG),¹ ultrafast charge dynamics,² coherent anti-Stokes Raman scattering (CARS)³ and multiphoton absorption.⁴ Nonlinear optics has gained prominence in various fields including optical fiber communication, optical switches,⁵ high resolution imaging,⁶ ultrafast pulse measurement⁷ etc. Several commercially available organic and inorganic nonlinear optical (NLO) crystals such as L-prolinium tartrate,⁸ imidazolium L-tartrate (IMLT),⁹ and lithium iodate (LiIO₃) have been successfully synthesized and are employed in optoelectronic applications. However, the ongoing shift towards digitalization has spurred a significant expansion in the range of NLO materials for their on-chip integration in optoelectronics.

Organic NLO materials have surpassed inorganic ones in establishing a lead in NLO research due to their superior nonlinear optical susceptibilities, large transparency range, high laser damage thresholds, ultrafast response time, low dielectric constants, and improved processability.¹⁰ Additionally, organic NLO materials are capable of significant chemical alterations, particularly those that enhance a desirable physical property.¹¹ In this regard, significant endeavors have been dedicated to enhancing the NLO properties of different nanomaterials. In this regard, many approaches have been put forth and these strategies encompass the designing of octupolar molecules, bond length alternation (BLA) theory, designing metal organic frameworks (MOFs), extended π electron systems, incorporation of diradical character, reinforcement of push–pull effects and the introduction of diffuse excess electrons.¹² This introduction of excess electrons has emerged as a distinctive approach for enhancing the NLO behavior of materials. The introduction of loosely bounded electrons into various nanostructures can be achieved through the doping of complexants with different metal atoms.¹³ These excess electrons are located in diffuse molecular orbitals, often referred to as Rydberg orbitals, which are present outside the parent molecules.¹⁴

Electrides, alkalides, superalkalides, alkaline earthides, and transition metalides are typical representative of excess electron systems and exhibit remarkable optoelectronic properties.¹² Electrides are systems in which an electron is not attached to an atom, but localizes its density in an empty space and actively participates in the structure of the material.¹⁵ Alkalides are obtained via placing a second metal atom far away from electrides, and the excess electrons then enwrap the second alkali metal atom to form anionic sites. These loosely bound electrons of anionic metal atoms have a dispersive character due to their low electron affinity. First of all, Dye and coworkers carried out successful synthesis of an alkalide in 1974.¹⁶ They also synthesized K⁺(Me₆Aza222)Na⁻ and K⁺(Me₆Aza222)K⁻ alkalides, which are stable at room temperature. Similarly, Redko et al., achieved the synthesis of the Ba²⁺(H₅Azacryptand[2.2.2]⁻)Na⁻, a barium-based sodide, thereby expanding the scope of research within the realm of alkalides.¹⁷ The theoretical explorations of stable alkalides indicate that the highest NLO response (2.4 × 10⁴ au) has been exhibited by Li⁺(calix [4] pyrrole)M⁻.¹⁸ Later on, Jing et al., computed the optoelectronic properties of Li(NH₃)_nNa (n = 1–4) alkalides and hyperpolarizability values (7.7 × 10⁴ au) increase as the number of NH₃ ligand increases.¹⁹

However, the area of alkalides garnered significant attention after the effective development of superalkali-based alkalides. Superalkalis display better tendency to provide excess electrons to any system due to their lower ionization potential (IP) than alkali metal atoms (5.4–3.9 eV).²⁰ They retain their structural integrity like an atom and possess the ability to develop nanomaterials, hydrogen storage materials, noble gas tripping agents, as well as superbases. The intriguing implications of superalkalis have been expanded significantly, resulting in the development and assessment of pioneering superalkali-based nanosystems. In this regard, superalkali-based alkalides such as Li₃⁺/Li₃O⁺(calix[4]pyrrole)M⁻ have been designed by Sun et al.²¹ These superalkali-based alkalides exhibit a significant optical response of up to 3.4 × 10⁴ au. Similarly, a novel series of alkalides such as Li₃⁺(aza222)K⁻, OLi₃⁺(aza222)K⁻, FLi₂⁺(aza222)K⁻, and NLi₄⁺(aza222)K⁻ have been designed where superalkalis are encapsulated into an aza222 cage-complexant.²² These alkalides show better stability and improved NLO responses. Recently, superalkali-based crown ether Li₃O[12-cown-4]M alkalides have been designed and show significant NLO responses (9.30 × 10⁴–5.26 × 10⁶ au).²³ Besides superalkali clusters, these alkalides require a proper complexant to stabilize both the cationic and anionic states.²⁴ As a result, many ongoing efforts have been directed to designing and integrating stable electrides, alkalides, alkaline earthides and superalkalides by using specific molecules as complexants.

The calix-like, cup-shaped macromolecules, such as calix[n]arene, calix[n]pyrrole, and calix[n]pyridine (n = 1, 2, 3 …), have distinctive three-dimensional structures. These materials are suitable for various biological, industrial, and medicinal applications because their internal hollow region is an ideal place to locate the guest entity.²⁵ For example, these complexants were used in nanotechnology as high-resolution electron beam lithography, nonlinear optics, ion-sensitive electrodes, sensors, and selective membranes. The calix[4]pyrrole complexant has been employed widely as electride, alkalide and alkaline earthide in various NLO applications.²¹ Recently, the nonlinear optical response of excess electron based calix[4]arenes has been computed theoretically.²⁶ The calix[4]pyridine (CXP[4]), a member of the hetero-aromatic calixarene family, is similar to calix[4]arene and contains pyridine subunits in its macrocycle, which may resemble the core ring of a porphyrin molecule. In 1998, Sessler et al., have carried out the synthesis of calix[4]pyridine by the reaction of meso-octamethylcalix[4]pyrrole with dichlorocarbene (an insertion of the: CCl₂ unit) for the first time.²⁷ For instance, scientists have theoretically employed calix[4]pyridine as an anode material for lithium and sodium atom/ion batteries.²⁸ The results depict that the adsorption and electronic properties of CXP[4] substrate were altered in the presence of Li and Na atom/ion and their cell voltage value of 2.56 V illustrated their potential as anodes of metal-ion batteries.

In spite of the numerous breakthroughs in the field of nanomaterials based on superalkalis, there remains a notable scarcity of research focused on NLO investigations, particularly in the case of calix[4]pyridine. To the best of our knowledge, superalkali-based calix[4]pyridine alkalides have not been explored yet for their geometrical, electronic and nonlinear optical responses. This gap has sparked our curiosity to investigate the alkalide properties and NLO behavior of superalkali-based calix[4]pyridine alkalides. Additionally, static and dynamic second order NLO responses have been calculated for real-world applications. It is anticipated that the ongoing research will provide valuable insights for the fabrication of superalkali-based alkalides for their high-tech applications in optoelectronics.

2. Computational details

The geometries of pure calix[4]pyridine and doped complexes are optimized using hybrid B3LYP functional along with 6-31G(d,p) basis set. The B3LYP functional is reliable for optimization because it provides a strong correlation between experimental and theoretical results for the geometric and electronic properties of various nanosystems.²⁹ Frequency calculations of the optimized geometries are carried out at the same level of theory to verify the true minima at potential energy surface (PES). To check their thermodynamic stability, the binding energies of the designed alkalides are determined using the (eqn 1):

E_int = E_{superalkali(CXP[4])Li} − (E_CXP[4] + E_superalkali + E_Li) (1)

here, E_{superalkali(CXP[4])Li} is the energy of superalkali-based calix[4]pyridine complexes, E_CXP[4] is calix[4]pyridine energy, E_superalkali is energy of superalkalis (Li₃O, Na₃O & K₃O), and E_Li is the energy of Li metal, respectively. In addition, the counterpoise method is used to remove the basis set superposition error (BSSE) from the interaction energies, which is brought on by the overlapping of finite basis sets. Using the following eqn (2), the counterpoise corrected interaction energies (E_CP) are calculated.

E_CP = E_int + E_BSSE (2)

Moreover, the vertical ionization energy (VIE) calculations are also done at the same level of theory. Natural population analysis (NPA), frontier molecular orbitals (FMOs), interaction region indicator (IRI), quantum theory of atoms in molecules (QTAIM) and electron localization function (ELF) analyses have been carried out at B3LYP/6-31G(d,p) level of theory. Moreover, electron densities and other parameters of designed complexes were obtained by Multiwfn³⁰ and visual molecular dynamics³¹ softwares. The total density of states (TDOS) and partial density of states (PDOS) spectra are also generated via Multiwfn software.³⁰ The time dependent DFT calculations are performed at the TD-CAM-B3LYP/6-311++G(d) level of theory. The absorption spectra of the optimized structures, variations of dipole moments (Δμ), oscillator strength (f_o), and excitation energies (ΔE) are obtained by these TD-DFT simulations.

The optical properties are computed using the CAM-B3LYP, ωB97XD and M06-2X functionals along with the 6-311++G(d,p) basis set. The CAM-B3LYP is categorized as a long-range corrected functional,³² which is particularly vital for precise assessments of hyperpolarizabilities. Notably, it also incorporates 0.65 fractional non-local exchange at extended distances, a parameter of significant importance in the accurate determination of hyperpolarizabilities.³³ This functional yields accurate results in predicting molecular structures, hyperpolarizabilities and excitation energies. Furthermore, the nonlinear optical properties computed by this functional, in contrast to results from the other functionals (such as B3LYP or M06-2X) align well with experimental data, as previously reported.³⁴ The optical parameters such as dipole moment, polarizability and hyperpolarizability are computed using the eqn (3)–(5):

μ_o = (μ_x² + μ_y² + μ_z²)^1/2 (3)

β_o = [β_x² + β_y² + β_z²]^1/2 (5)

The beta vector (β_vec) can be computed by using eqn 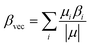(6):

To assess the practical applicability of the designed complexes, dynamic first hyperpolarizabilities (β(ω)) have been analyzed at CAM-B3LYP/6-311++G (d,p) level of theory at 532 nm, 1064 nm and 1907 nm, respectively. The β(ω) can be determined as using eqn (7):

β_(ω) = (β_x(ω)² + β_y(ω)² + β_z(ω)²)^1/2 (7)

In order to predict second order NLO responses like hyper Rayleigh scattering (HRS), second harmonic generation (SHG) and electro-optical Pockel's effect (EOPE), hyperpolarizability is a crucial factor. The eqn (8a) is used to get the β_HRS values:

Or the orientational average <β_HRS> can be expressed as eqn (8b):

Here, the molecular β_HRS tensor is the sum of an octupolar (J = 3) and a dipolar (J = 1) tensorial form. The final theoretical values and the relationship between the dipolar-octupolar components of β_HRS as well as the cartesian components are obtained by using the eqn (9) and (10):

The depolarization ratio is computed by eqn (11):

The results of hyper Rayleigh scattering measurement (β_HRS) and DR are obtained via Multiwfn software.³⁰ All the above DFT simulations are executed using the Gaussian 16 software³⁵ and GaussView 6.1.1. software³⁶ is used for the visualization of geometries.

3. Results and discussion

3.1. Geometric parameters and stabilities of designed complexes

Calix[4]pyridine (CXP[4]) is a three-dimensional macrocycle composed of four pyridyl nitrogen atoms and has been identified as a neutral ligand capable of binding to metal ions. Pure calix[4]pyridine exhibits a C_2v symmetry and the 1,3-alternate structure is substantially preferable in the CXP[4] host.³⁷ The reduced repulsions between lone pairs of nitrogen atoms might be responsible for the conformational stability of the pyridine moieties in CXP[4]. All of the isolated pyridine rings render a box-shape cavity due to the existence of methylene linkages in CXP[4]. The 1.33 Å, 1.39 Å and 1.51 Å bond lengths of N₁–C_c, C_c–C_b, and C_c–C_d (methylene linked) bonds in CXP[4] are in close agreement with its previously reported bond lengths.³⁷ Additionally, the optimized Li₃O superalkali exhibits a Li–O bond length of 1.69 Å, which closely matches the experimental Li–O bond length of Li–O–Li molecule.³⁸ Based on the findings, it can be concluded that the B3LYP/6-31G(d,p) level of theory is reliable for the present study. The optimized structures of the CXP[4] as well as the isolated superalkalis subunits are shown in Fig. 1.

Fig. 1 Optimized structures of pure calix[4]pyridine and superalkalis (Li₃O, Na₃O & K₃O).

In the current work, Li₃O, Na₃O & K₃O and Li metal are doped at calix[4]pyridine to examine the various interaction sites. Four orientations were considered in total, including two horizontal modes (top and bottom) and two vertical modes (top and bottom), for the each superalkali and Li metal doping on calix[4]pyridine (represented in the ESI (Fig. S1†)), as previously considered for calix[4]pyrrole complexes.²¹ Among the various considered sites, only the horizontal top orientation was taken into account for subsequent analyses. The majority of the structures were distorted in the case of the bottom modes, and the vertical top orientations converged to the horizontal ones. Similarly, the Li metal is doped at the other side of the calix[4]pyridine. The most stable superalkali based hetero-aromatic macrocycle complexes of M₃O⁺CXP[4]Li⁻ (horizontal top) are depicted in Fig. 2. All other optimized complexes of superalkali based M₃O⁺CXP[4]Li⁻ alkalides along with their energies are shown in the ESI (Fig. S2†).

Fig. 2 Optimized complexes of superalkali based M₃O⁺CXP[4]Li⁻ alkalides.

The structural integrity of CXP[4] remains intact after being doped with superalkalis and metal atom as there is a small variation in the dihedral angle of N₁–N₂–N₃–N₄ cavity of CXP[4]. Similarly, the Li–O, Na–O, K–O bond lengths of superalkalis in the designed M₃O⁺CXP[4]Li⁻ are 1.65 Å, 2.02 Å and 2.38 Å respectively, which are very close to those of the isolated superalkalis (Fig. 1). As a result, after being inserted into the calix[4]pyridine, the M₃O subunits maintain their structural integrity, with minimal alteration in the geometric parameters of superalkalis subunits, even in the presence of an additional Li metal atom on the opposite side. The M₃O⁺CXP[4]Li⁻ complexes exhibit positive values for their first frequencies (Table 1), indicating the presence of true local minima on potential energy surface.

Table 1 Optimized complexes with the first frequencies ν₁ (cm⁻¹), symmetries, dihedral angles (N₁–N₂–N₃–N₄ in degree), bond distance from CXP[4] to superalkali X_CXP[4]–M3O (Å), bond distance from CXP[4] to Li metal X_CXP[4]–Li (Å), bond distance from superalkalis to Li metal X_M3O–Li (Å), E_int (kcal mol⁻¹) and E_CP (kcal mol⁻¹)

Complex	ν1	Symmetry	N1–N2–N3–N4	XCXP[4]–M3O	XCXP[4]–Li	XM3O–Li	Eint	ECP
CXP[4]	16.29	C2v	−2.85	—	—	—	—	—
Li3O^+CXP[4]Li^−	17.19	C1	−3.69	2.08	5.75	6.68	−64.5	−62.9
Na3O^+CXP[4]Li^−	17.54	C1	−2.67	2.40	3.41	7.72	−39.7	−36.7
K3O^+CXP[4]Li^−	11.38	C1	−2.67	2.89	6.20	7.53	−32.3	−32.9

---

Superalkali subunits and Li metal doping have caused an alteration in the symmetry of CXP[4]. The free CXP[4] and M₃O entities exhibit C_2v and C_s point groups, whereas M₃O⁺CXP[4]Li⁻ complexes have the C₁ point group, providing further evidence that doping of superalkali can alter the symmetry of complexants.³⁹ The internuclear distances between M₃O and the center of the N₁–N₂–N₃–N₄ cavity of CXP[4] increases in the order: 2.08 Å (Li₃O⁺CXP[4]Li⁻) < 2.40 Å (Na₃O⁺CXP[4]Li⁻) < 2.89 Å (K₃O⁺CXP[4]Li⁻). The interaction distance between superalkalis and the center of the N₁–N₂–N₃–N₄ cavity in CXP[4] elongates as the atomic number of alkali metal atoms in M₃O cluster increases from Li to K (Table 1).

A similar monotonic trend of increasing interaction distance has been observed in previous studies involving superalkalis doping on C₆Li₆ and C₆S₆Li₆ organometallic complexes.^40,41 Another factor that supports the fact is the volume of pure superalkali subunits. The increasing trend of volume of superalkali subunits is as follow; K₃O (84.14 cm³ mol⁻¹) > Na₃O (60.82 cm³ mol⁻¹) > Li₃O (43.85 cm³ mol⁻¹), respectively and is consistent with the monotonic trend of increasing interaction distances. On the other hand, the X_CXP[4]–Li and X_M3O–Li internuclear distances follow an abnormal trend for Na₃O⁺CXP[4]Li⁻, but the internuclear distances increase from Li to K in the Li₃O⁺CXP[4]Li⁻ and K₃O⁺CXP[4]Li⁻ complexes.

The stability of complexes holds significant importance in the realm of practical uses for nonlinear optical materials. The E_int and VIE energies are the essential factors that determine the thermodynamic and chemical stability of any system. A higher interaction energy signifies a more stable system, indicating a closer interaction between the dopant and complexant.⁴² The interaction energies of the M₃O⁺CXP[4]Li⁻ alkalides reflect that these complexes have greater thermodynamic stability that can be inferred from their high exothermic nature (Table 1). The E_int values of Li₃O⁺CXP[4]Li⁻, Na₃O⁺CXP[4]Li⁻, and K₃O⁺CXP[4]Li⁻ are −64.5 kcal mol⁻¹, −39.7 kcal mol⁻¹, and −32.3 kcal mol⁻¹, respectively. The Li₃O⁺CXP[4]Li⁻ alkalide is recognized as the most stable one among the three superalkali based hetero-aromatic macrocycles. This stability arises from the least interaction distance between Li atom of Li₃O/Li⁻ (alkalide on opposite side as in X_CXP[4]–Li) and the complexant, leading to a stronger interaction. Moreover, the exceptional thermal stability of Li₃O⁺CXP[4]Li⁻ alkalide can be attributed to the low IP and small atomic size of Li metal. Consequently, Li₃O is regarded as the most favorable adsorbing species on the calix[4]pyridine macrocycle. Furthermore, the E_int values of M₃O⁺CXP[4]Li⁻ alkalides are also comparable to the Li₃O⁺(calix[4]pyrrole)M⁻ alkalides,²¹ and are greater than the E_int (−47.61 to −38.83 kcal mol⁻¹) of Li⁺(calix[4]pyrrole)M⁻ alkalides¹⁸ reported previously. The findings suggest that the superalkali-based alkalides exhibit stronger binding compared to alkali metal-based alkalides.

In order to account for the basis set superposition error (BSSE), counterpoise correction was applied to the superalkali-based CXP[4] alkalides. The counterpoise corrected energies (E_CP) of M₃O⁺CXP[4]Li⁻ alkalides are observed to range from −32.96 kcal mol⁻¹ to −62.9 kcal mol⁻¹ (Table 1). These E_CP values exhibit minimal deviation from the interaction energy (E_int), indicating that BSSE has a negligible impact on the doping of superalkalis and Li metal on the calix[4]pyridine. Therefore, the B3LYP/6-31G(d,p) level of theory proves to be a reliable choice for the current study. To verify the chemical stability of M₃O⁺CXP[4]Li⁻ alkalides, the vertical ionization energy (VIE) serves as an additional parameter. The VIE values for the designed superalkali-based calix[4]pyridine alkalides falls in the range of 2.51–2.79 eV (Table 2).

Table 2 NPA charges of Q_Li (|e|), Q_M1 (|e|), Q_M2 (|e|), Q_M3 (|e|), Q_O (|e|) and Q_M3O (|e|) and VIE (eV) of all complexes

Complexes	QLi	QM1	QM2	QM3	QO	QM3O	VIE
Li3O^+CXP[4]Li^−	−0.397	0.811	0.812	0.828	−1.623	0.828	2.79
Na3O^+CXP[4]Li^−	−0.452	0.803	0.81	0.641	−1.49	0.764	2.71
K3O^+CXP[4]Li^−	−0.486	0.622	0.825	0.747	−1.439	0.755	2.51

---

The Li₃O⁺CXP[4]Li⁻ alkalide, with Li₃O superalkali doping on the macrocycle, achieves the highest VIE value of 2.79 eV. On the other hand, K₃O⁺CXP[4]Li⁻ alkalide, which involves K₃O doping, has the lowest VIE of 2.51 eV. Comparing all the vertical ionization energies, it can be concluded that the M₃O⁺CXP[4]Li⁻ alkalides demonstrate chemical stability. These findings are in consistent with the previous literature,⁴³ indicating that the chemical stability of materials decreases as the size of superalkalis increases.

3.2. Charge transfer analysis and alkalide nature

The charge transfer between superalkalis, Li metal atom, and calix[4]pyridine has been confirmed by the natural population analysis (NPA). Total charge on superalkali (Q_M3O) subunits is positive ranging from 0.755 |e| to 0.828 |e| indicating that the superalkali clusters behave as excess electron donors (Table 2). In contrast, the Q_Li values of Li metal doped at the other side of the CXP[4] vary in the following order: −0.486 |e| (K₃O⁺CXP[4]Li⁻) > −0.452 |e| (Na₃O⁺CXP[4]Li⁻) > −0.397 |e| (Li₃O⁺CXP[4]Li⁻), implying that the charge on anionic Li is affected by the superalkali subunits. The K₃O⁺CXP[4]Li⁻ has the maximum negative charge Q_Li value of −0.486 |e|. This can be attributed to the observed trend in VIE values among superalkali subunits, where 2.673 eV (K₃O) < 3.201 eV (Na₃O) < 3.485 eV (Li₃O). This suggests that superalkali K₃O, with its smaller VIE value, exhibits a greater tendency to readily lose its excess electrons, leading to the maximum negative charge Q_Li value as observed in K₃O⁺CXP[4]Li⁻. In all M₃O⁺CXP[4]Li⁻ complexes, the charge on the Li metal is negative, indicating the alkalide nature of these macrocycles and these can be represented as M₃O⁺CXP[4]Li⁻. The alkalide charge values (−0.397 |e| to −0.486 |e|) of M₃O⁺CXP[4]Li⁻, computed at the present level of theory, also follows the same trend as the net alkalide charge values of previously reported M₃O⁺(calix[4]pyrrole)M⁻ complexes (CAM-B3LYP/6-311++G(d, p)).²¹ Moreover, alkalide complexes such as Li₃(NH₃)_nNa⁻ alkalides with alkalide charge values ranging from −0.291|e| to −0.509 |e| (at CAM-B3LYP/6-311++G(3df,3pd) have also been observed previously.⁴⁴ The findings suggest that calix[4]pyridine can serve as better complexant as compared to calix[4]pyrrole, making it a more suitable choice for designing NLO candidates.

3.3. Electronic properties

The optoelectronic properties of M₃O⁺CXP[4]Li⁻ alkalides are examined using the frontier molecular orbital (FMO) approach. This investigation involved analyzing the energy levels of the highest occupied molecular orbitals (HOMOs), the lowest unoccupied molecular orbitals (LUMOs), corresponding energy gaps (E_g), and their percentage reduction (% E_g). Materials with reduced energy gaps are quite suitable for remarkable optoelectronic properties.¹³ A wide energy gap (5.69 eV) in pure CXP[4] makes it difficult to be applied in optoelectronic devices. Its electronic properties have been improved significantly be doping superalkali subunits (Li₃O, Na₃O & K₃O) and Li metal on the calix[4]pyridine (Table 3).

Table 3 Energies of frontier molecular orbitals (eV), their energy gaps E_g (eV), and % E_g of M₃O⁺CXP[4]Li⁻ alkalides

Complexes	EHOMO	ELUMO	Eg	% Eg
CXP[4]	−6.26	−0.58	5.69	—
Li3O^+CXP[4]Li^−	−1.86	−1.36	0.50	91.1
Na3O^+CXP[4]Li^−	−1.94	−1.59	0.35	93.8
K3O^+CXP[4]Li^−	−1.75	−1.45	0.30	94.6

---

These findings show that the E_g values (0.30–0.50 eV) of superalkali-based M₃O⁺CXP[4]Li⁻ alkalides have been reduced significantly. The formation of new HOMO orbitals is the main reason for the reduction in the energy gaps. These new HOMOs are generated when diffuse excess electron densities from superalkali subunits are transferred to the Li alkalide present on the opposite side of CXP[4]. Furthermore, these results are in agreement with the prior ones, demonstrating that the transfer of electronic density results in the production of new HOMOs.³⁹ The designed alkalides exhibit a significant percentage reduction in the energy gap, ranging from 91.1% to 94.6%. Moreover, an outstanding electronic and conducting behavior of the designed M₃O⁺CXP[4]Li⁻ alkalides has been observed due to this enormous reduction in the energy gaps.¹⁰ The pictorial representation of electron densities in pristine calix[4]pyridine and M₃O⁺CXP[4]Li⁻ alkalides is shown in Fig. 3.

Fig. 3 Frontier molecular orbitals electron densities of M₃O⁺CXP[4]Li⁻ alkalides.

In pure calix[4]pyridine, the electron densities of HOMOs and LUMOs reside on the alternative pyridine rings with a small amount on the rest of the skeleton. The HOMOs electron densities of all the M₃O⁺CXP[4]Li⁻ complexes are residing at the Li metal present on the opposite side of superalkalis, confirming their alkalide nature. In the investigated alkalides, the diffuse excess electronic cloud has enwrapped the Li atom and created an anion (Li⁻) in all the three complexes. The intramolecular electron push–pull might be the major reason for the development of alkalide characteristics. A similar type of alkalide behavior has been observed previously by Sun et al., in superalkali based alkalides of calix[4]pyrrole.²¹

3.4. Density of states analysis

The number of different states that electrons are allowed to occupy at a given energy level are commonly termed the density of states (DOS). This study examines the TDOS (total density of states) and PDOS (partial density of states) spectra to confirm the electronic properties especially the formation of new HOMOs and contribution of individual fragments in the newly designed superalkali-based alkalides. The DOS spectra of CXP[4] and superalkali-based M₃O⁺CXP[4]Li⁻ alkalides are manifested in Fig. 4.

Fig. 4 Density of states spectra of CXP[4] and M₃O⁺CXP[4]Li⁻ alkalides.

The TDOS spectrum of bare calix[4]pyridine show that energy states are produced at lower energies in the occupied and virtual region. A substantial variation in the peak intensity of PDOS is observed after doping of CXP[4] with superalkalis and Li metal. As a result, the interaction between CXP[4], the M₃O clusters, and the Li metal leads to the creation of new high-energy HOMO orbitals. The DOS spectra of these superalkali-based alkalides show energy levels shifting, which confirms the formation of new HOMOs and a vertical dashed line indicates the presence of new HOMOs. These molecular orbitals range from −1.96 eV to −2 eV (in the high energy zone), as compared to the −6.00 eV of calix[4]pyridine which ultimately reduces the HOMO–LUMO energy gaps. The major contribution for the new HOMOs formation is from both superalkalis (blue line contribution) and Li alkalide (pink line contribution) in all M₃O⁺CXP[4]Li⁻ alkalides as superalkali subunits have donated the excess electrons and Li metal on the opposite side of calix ring has accepted these electrons. Additionally, the rise in intensities of superalkalis and Li metal also indicates their significant contribution in the investigated complexes. The DOS spectra of M₃O⁺CXP[4]Li⁻ alkalides reveal a substantial enhancement in both electronic and conductive properties.

3.5. Interaction region indicator (IRI) analysis

The IRI approach⁴⁵ is used to identify and to better analyze the nature of intra and intermolecular interactions. The recently introduced real-space function, IRI, can simultaneously identify several interactions within chemical systems. The IRI and RDG (reduced density gradient) differ by a constant pre-factor, which is essential for ensuring a balance between non-covalent and covalent forces. The IRI expression can be written as:where α is a variable parameter, α = 1.1 is an accepted value under the standard definition of IRI. It is essentially a scaled version of the gradient norm of electron density whereas the RDG is a dimensionless form of electron density gradient. The RDG can be determined as:where r is coordinate vector and ρ is the electron density. The repulsive, non-covalent, and attractive interactions are represented by the red, green, and blue patches on the 3D-IRI isosurfaces. The repulsive, non-covalent, and attractive interactions are shown by the red, green, & blue patches on the 3D-IRI isosurfaces. The nature of the interaction regions revealed by IRI can be depicted clearly by mapping sign (λ₂) ρ function onto the 2D-IRI plots. A region with a relatively a large magnitude of sign (λ₂)ρ and high electron density indicates a relatively strong interactions (hydrogen & halogen bonding etc.), whereas a region with a small sign (λ₂)ρ ≈ 0 and low ρ implies no apparent interaction or, at most, the van der Waals (vdW) interaction. Therefore, the interpretation of 3D-IRI isosurfaces and 2D-IRI plots of M₃O⁺CXP[4]Li⁻ alkalides has been carried out to gain an insight into the covalent and non-covalent interactions as depicted in Fig. 5.

Fig. 5 2D-isosurfaces and 3D-IRI scatter plots of M₃O⁺CXP[4]Li⁻ alkalides along with the standard color bar of the IRI.⁴⁵

The findings show that M₃O⁺CXP[4]Li⁻ alkalides have extensive green patches of weak dispersive vdW interactions and very small blue patches of hydrogen bonding. The K₃O⁺CXP[4]Li⁻ alkalide has more noticeable green patches followed by Na₃O⁺CXP[4]Li⁻ and Li₃O⁺CXP[4]Li⁻ complexes. Furthermore, the presence of distinct green spikes ranging from −0.01 to 0.01 au in the 2D-IRI plots of the investigated complexes also supports the presence of weak dispersive interactions. The spikes of Na₃O⁺CXP[4]Li⁻ and Li₃O⁺CXP[4]Li⁻ are less dense whereas the K₃O⁺CXP[4]Li⁻ complex has low gradient, low density, and sharp spikes and these findings also coincide with the above described interaction energies data.

3.6. Quantum theory of atoms in molecules (QTAIM) analysis

It is a topological tool to investigate the strength and nature of various interactions based on electron density and its various parameters at the bond critical points.⁴⁶ The QTAIM offers an elegant approach for determining the nature of a bond, which is dependent on its critical points, including the total electron density (ρ(r)), Laplacian ∇²ρ(r), total energy density (H), kinetic V(r) and potential G(r) electron energy densities. The value of electron density (ρ(r) has a significant impact on the strength of interactions. The strong bondings (i.e. electrostatic interactions and H-bonding) are demonstrated by a −ive Laplacian ∇²ρ(r), ρ(r) > 0.1 au, H(r) < 0, and −G(r)/V(r) < 1. On the other hand, weak interactions such as van der Waals are demonstrated by the presence of a +ive Laplacian ∇²ρ(r), ρ(r) < 0.1 au, H(r) > 0, and −G(r)/V(r) > 1 whereas partial covalent and partial electrostatic forces have only H(r) < 0 with +ive Laplacian ∇²ρ(r). For the investigated complexes, the topological diagrams with the corresponding BCPs are shown in Fig. 6 and the interaction parameters are given in Table S1†.

Fig. 6 Pictorial representation of QTAIM images (along BCPs) of M₃O⁺CXP[4]Li⁻ alkalides. Orange dots represent bond critical points (BCPs), green dots indicate ring critical points (RCPs) and yellow dots denote cage or cluster critical points (CCPs).

The results demonstrate that the examined alkalides have three different types of bond paths. The Li₃O⁺CXP[4]Li⁻ has BCPs at Li₃O–carbon (Li–C), Li₃O–nitrogen (Li–N), and Li₃O–hydrogen (O–H) bonds respectively. The Na₃O⁺CXP[4]Li⁻ has bond paths at Na₃O–nitrogen (Na–N), Na₃O–hydrogen (O–H) and one lithium to hydrogen (Li–H) present on the lower side of complexant and a similar pattern of BCPs was observed for the K₃O⁺CXP[4]Li⁻ complex. The results of computed topological values such as ρ(r) < 0.1 au, positive Laplacian ∇²ρ, H(r) = 0 or >0, and −G(r)/V(r) value ≥1 indicate that the bondings are weak van der Waals. Thus, one may examine the noncovalent interaction behavior of Na₃O⁺CXP[4]Li⁻ complexes from the bond critical points.

3.7. Electron localization function (ELF) analysis

An ELF map is a visualization tool that shows regions anticipated to contain electrons. It sheds light on the electronic structure and bonding of molecular systems. When an ELF map is projected onto the interval (0, 1), it can describe various types of interactions. High ELF values (around 1.0) are produced by purely ionic interactions, lone pairs of electrons or by non-bonding valence electrons, while very low values (around 0) are produced in the interstitial areas. The ELF values for the covalent bonding range from 0.6 to 0.8, depending on the bond's strength. To effectively characterize bonding, particularly in the M₃O⁺CXP[4]Li⁻ complexes, the ELF map analysis is employed and the maps are shown in Fig. 7.

Fig. 7 Colored filled shaded electron localization function maps of M₃O⁺CXP[4]Li⁻ alkalides.

The results of the color-filled shaded maps clearly depict that the regions of high electron localization are around the Li⁻ alkalide in all the designed M₃O⁺CXP[4]Li⁻ complexes. In contrast, the regions around C, N and H have lower values due to delocalization of electrons in the calix[4]pyridine substrate.

3.8. Absorption analysis

The time-dependent DFT absorption analysis has been carried out to study the absorption behavior of superalkali-based M₃O⁺CXP[4]Li⁻ alkalides. For their practical usability in optoelectronic applications, the examined alkalides should be transparent under the applied absorption region. The plotted absorption spectra of pure calix[4]pyridine and M₃O⁺CXP[4]Li⁻ complexes are displayed in Fig. 8 and their absorption maxima (λ_max), oscillator strength (f_o) and transition energies (ΔE) are given in Table 4.

Fig. 8 UV-Visible spectra of pure and M₃O⁺@CXP[4]Li⁻ alkalides.

Table 4 Transition energies (ΔE), oscillator strength (f_o), difference in dipole moments Δμ (Debye), absorption maxima (λ_max), and major transitions

Complexes	ΔE (eV)	fo	Δμ (Debye)	λmax (nm)	Major contribution
CXP[4]	5.29	0.0366	0.14	235	HOMO → LUMO+3
Li3O^+CXP[4]Li^−	1.26	0.1267	3.38	982	HOMO → LUMO+15
Na3O^+CXP[4]Li^−	1.71	0.1389	5.99	727	HOMO → LUMO+17
K3O^+CXP[4]Li^−	1.13	0.1111	1.61	1096	HOMO → LUMO+10

---

According to the absorption results for pristine CXP[4], the crucial excitation (HOMO → LUMO+3) requires 5.29 eV of energy, and the maximum absorption wavelength (λ_max) is observed at 235 nm. The shift of the λ_max to a longer wavelength after complexation demonstrates the strong impact of superalkalis and Li metal doping on upper and lower sides of CXP[4]. Moreover, the major electronic transitions along with their electron densities that hold electronic excitations in the maximum absorbance are also computed and are displayed in Fig. S3.† These findings demonstrate that M₃O⁺CXP[4]Li⁻ alkalides are entirely ultraviolet transparent and have maximum absorbance values of 727–1096 nm in the visible to near infrared (NIR) region. The lowering of HOMO–LUMO energy gaps of these complexes can be a reason for this bathochromic shift as observed in the previous studies.³⁹ The K₃O⁺CXP[4]Li⁻ alkalide exhibits a dominant red shift in its λ_max at 1096 nm, primarily attributed to the possession of its lowest excitation energy (1.13 eV), whereas Na₃O⁺CXP[4]Li⁻ alkalide has the lowest λ_max at 727 nm with the highest excitation energy (1.71 eV). Moreover, the oscillator strength (f_o) values are increased for the designed complexes and falls in the range of 0.1089 to 0.1389 which indicates the strong probability of quantum chemical transitions. These near-infrared M₃O⁺CXP[4]Li⁻ alkalides should be the most suitable candidates for fabricating optical detectors and for improving the SHG effect of various optical materials.

3.9. Dipole moment and variation in dipole moments

The dipole moment is an index that describes the net polarity of molecules as the larger the dipole moment, the greater the charge separation. The mean dipole moments (15.6–26.9 au) for the investigated M₃O⁺CXP[4]Li⁻ alkalides are significantly higher than those for the pure calix[4]pyridine complexant (Table 5).

Table 5 The dipole moment μ_o (Debye), and linear and nonlinear optical variables: α_o (au), β_o (au), β_vec (au), and β_HRS (au)

Complexes	μo	αo	βo	βTL	βvec	βHRS
CXP[4]	4.02	289	74.8	—	—	—
Li3O^+@CXP[4]Li^−	15.6	513	9.2 × 10^4	1.3 × 10^1	9.2 × 10^4	4.1 × 10^4
Na3O^+@CXP[4]Li^−	25.8	551	2.5 × 10^6	7.2 × 10^3	2.2 × 10^6	1.1 × 10^6
K3O^+@CXP[4]Li^−	26.9	966	1.1 × 10^6	3.3 × 10^3	1.1 × 10^6	4.9 × 10^5

---

The computed dipole moments (μ_o) of Li₃O⁺CXP[4]Li⁻, Na₃O⁺CXP[4]Li⁻, and K₃O⁺CXP[4]Li⁻ are 15.6, 25.8, and 26.9 au, respectively. The dipole moments (μ_o) (15.6–26.9 au) of M₃O⁺CXP[4]Li⁻ are greater than the μ_o values (5.96 to 15.07 au) of M⁺(hexaammine)M⁻ complexes⁴⁷ and the μ_o values (0.253 to 3.698 au) of Li₃(NH₃)_nNa⁻ alkalides.⁴⁴ Furthermore, an enhancement in charge separation implied by this monotonic increase in μ_o value from Li₃O to K₃O in the designed complexes is reflective of their distinctive optical properties, similar to the Cherepanov and his colleagues work.⁴⁸

Furthermore, an increasing trend of variation in dipole moments (Δμ) from 1.61 to 5.99 au has been observed for the designed alkalides as compared to pristine calix[4]pyridine (Table 4). The Na₃O⁺CXP[4]Li⁻ has the highest computed Δμ of 5.99 au and K₃O⁺CXP[4]Li⁻ has the lowest Δμ of 1.61 au. As a result, the alteration in dipole moments (associated with the critical transition) might be responsible for improved optoelectronic features of the alkalides under consideration.

3.10. Optical properties of M₃O⁺CXP[4]Li⁻ alkalides

3.10.1. Static linear and nonlinear optical properties. Introduction of diffuse excess electrons via metal atoms (i.e. alkali, superalkalis, transition, and alkaline earth) alters the optical features of nanosystems as evidenced by the prior studies.¹² The loosely bound excess electrons around the Li metal in the designed complexes, which are easily polarizable and exhibit typical alkalides nature, can be considered as essential candidates to trigger their nonlinear optical response. All of the variables that contribute to the potential linear and nonlinear optical response have been analyzed using DFT calculations (Table 5).

The linear optical response of newly designed M₃O⁺CXP[4]Li⁻ complexes is investigated through their polarizabilities (α_o). In comparison to pure calix[4]pyridine, the polarizability values of superalkali-based CXP[4] alkalides are increased up to 966 au, which is much higher than 289 au of CXP[4]. All M₃O⁺CXP[4]Li⁻ alkalides have α_o values that expand monotonically in the order K₃O⁺@CXP[4]Li⁻ (966 au) > Na₃O⁺@CXP[4]Li⁻ (551 au) > Li₃O⁺@CXP[4]Li⁻ (513 au). The polarization trend is mainly affected by the charge transfer and higher charge transfer is observed from superalkalis to Li⁻ alkalide in K₃O⁺@CXP[4]Li⁻ (−0.486 |e|), followed by Na₃O⁺@CXP[4]Li⁻ (−0.452 |e|) and Li₃O⁺@CXP[4]Li⁻ (−0.397 |e|). Therefore, the charge separation greatly affects the static polarizability values of M₃O⁺CXP[4]Li⁻ alkalides.

The static first hyperpolarizabilities (β_o) of M₃O⁺CXP[4]Li⁻ alkalides are also computed for the examination of NLO characteristics. The nonlinear optical responses of superalkali-based alkalides are greatly enhanced due to the presence of excess electrons (Table 4). It can be observed that β_o values (9.2 × 10⁴–2.6 × 10⁶ au) of M₃O⁺CXP[4]Li⁻ alkalides are remarkably enhanced as compared to β_o value (289 au) of pure calix[4]pyridine. Furthermore, the designed superalkali-based alkalides show higher NLO response at CAM-B3LYP functional than at the M06-2X and ωB97XD functionals (Table S2†) and it can be inferred that the CAM-B3LYP is a reliable functional for further investigations. The highest NLO response (2.6 × 10⁶ au) is observed for the Na₃O⁺CXP[4]Li⁻ and the lowest static first hyperpolarizability (9.2 × 10⁴ au) is obtained for Li₃O⁺CXP[4]Li⁻ alkalide. Additionally, the computed β_o value of the Na₃O⁺CXP[4]Li⁻ alkalide (2.5 × 10⁶ au) is substantially higher than the β_o value (3.4 × 10⁴ au) of earlier reported K₃O⁺(calix[4]pyrrole)K⁻ alkalide at the same level of theory.²¹ Besides this, the NLO response of designed alkalides is also compared with the some other earlier stated superalkali-based systems. The hyperpolarizabilities of investigated alkalides are also greater than β_o values 3.8 × 10⁴ au and 9.1 × 10⁴ au of Li₃(NH₃)_nNa (n = 1–4) alkalides⁴⁴ and ethylenediamine based superalkalides (M⁺(en)₃M₃′O⁻).⁴⁹ Thus it can be concluded that the doping of superalkali and Li metal to the calix[4]pyridine complexant can be propitious for improving the NLO response of conventional alkalides.

The beta vector (β_vec) is a useful tool for predicting the NLO properties of different nanomaterials. For the designed complexes, the β_vec outcomes are corresponding to the β_o values (Table 5). The Na₃O⁺CXP[4]Li⁻ alkalide, which has the highest β_o of 2.5 × 10⁶ au, also has the greatest β_vec value of 2.2 × 10⁶ au. Furthermore, to provide an in depth understanding of the first order hyperpolarizability and its influencing aspects, the β_TL values are calculated using the two-level model.⁵⁰ Mathematically, it can be represented as;

where, β_TL is obtained from the two-level expression using the sum-over-state (SOS) approach. Dipole moment variations (between ground and excited states), oscillator strength, and excitation energy are referred as Δμ, f_o, and ΔE, respectively. There is a direct correlation between the β_TL, f_o, and Δμ, whereas the β_TL is inversely related to the 3rd power of ΔE. The β_TL values of the M₃O⁺CXP[4]Li⁻ alkalides are significantly influenced by the crucial excitation energy and the hyperpolarizabilities of designed alkalides will increase as the critical excitation energy decreases as reported earlier.⁵¹ It can be observed that ΔE values (1.13 to 1.71 eV) of M₃O⁺CXP[4]Li⁻ alkalides are reduced as compared to ΔE value (5.29 eV) of pure calix[4]pyridine (Table 4). This reduction in energy difference has led to a significant enhancement in hyperpolarizabilities. The β_TL values obtained by SOS method are increasing in the following order: Na₃O⁺@CXP[4]Li⁻ (7.2 × 10³ au) > K₃O⁺@CXP[4]Li⁻ (3.3 × 10³ au) > Li₃O⁺@CXP[4]Li⁻ (1.3 × 10¹ au) (Table 5). Therefore, upon examining the comparison, it becomes evident that there is a strong correlation between β_o and β_TL. This correlation underscores the exceptional nonlinear optical (NLO) characteristics exhibited by these alkalide complexes. Strikingly, the other two factors, the highest variation in dipole moments (5.99 D) and the highest oscillator strength (0.1389) are also supporting the highest β_TL value for Na₃O⁺CXP[4]Li⁻ by employing two level expression.

3.10.2. Dynamic hyperpolarizabilities of M₃O⁺CXP[4]Li⁻ alkalides. The assessment of the feasibility of utilizing superalkali-based M₃O⁺CXP[4]Li⁻ alkalides for NLO applications involves the computation of dynamic hyperpolarizabilities. To mitigate the influence of damping effect and to avoid any potential overestimation of hyperpolarizabilities, three specific wavelengths (532 nm, 1064 nm & 1907 nm) are selected. The dynamic hyperpolarizability involves the computation of hyper-Rayleigh scattering (HRS), SHG and EOPE co-efficients and their results are listed in Table 6.

Table 6 Frequency dependent hyperpolarizabilities of M₃O⁺CXP[4]Li⁻ alkalides at working laser conditions

Complexes	EOPE (−ω, ω, 0)			SHG (−2ω, ω, ω)			HRS (−2ω, ω, ω)
	λ = 532 nm	λ = 1064 nm	λ = 1907 nm	λ = 532 nm	λ = 1064 nm	λ = 1907 nm	λ = 532 nm	λ = 1064 nm	λ = 1907 nm
Li3O^+@CXP[4]Li^−	1.6 × 10^5	3.7 × 10^4	3.1 × 10^4	2.6 × 10^5	5.6 × 10^4	2.3 × 10^5	2.1 × 10^5	2.3 × 10^5	5.5 × 10^5
Na3O^+@CXP[4]Li^−	7.7 × 10^7	1.3 × 10^7	3.1 × 10^4	6.4 × 10^6	2.3 × 10^6	2.5 × 10^6	1.5 × 10^7	3.2 × 10^6	4.5 × 10^6
K3O^+@CXP[4]Li^−	2.2 × 10^7	5.1 × 10^7	6.7 × 10^5	3.9 × 10^6	1.1 × 10^8	5.8 × 10^5	6.2 × 10^7	1.8 × 10^8	6.4 × 10^6

---

An encouraging method for experimentally assessing optical properties is through hyper Rayleigh scattering.⁵² Therefore, the β_HRS values of superalkali-based M₃O⁺CXP[4]Li⁻ alkalides are computed to offer insights that could prove valuable for the experimentalists. The results reveal distinct hyper-Rayleigh scattering based NLO responses (β_HRS) superalkali-based alkalides at varying wavelengths. Notably, the Li₃O⁺CXP[4]Li⁻ alkalide displays the lowest β_HRS value (2.3 × 10⁵ au) at a 532 nm laser wavelength, while K₃O⁺CXP[4]Li⁻ alkalide exhibits the highest β_HRS value (1.8 × 10⁸ au) at 1064 nm. Moreover, an increasing trend of β_HRS values of the designed alkalides is observed from Li₃O⁺CXP[4]Li⁻ to K₃O⁺CXP[4]Li⁻ at selected wavelengths. Additionally, the dipolar to octupolar β_HRS contributions of M₃O⁺CXP[4]Li⁻ alkalides along with their DR are also computed (Table S3†). The findings reveal that Li₃O⁺CXP[4]Li⁻ alkalide exhibits a notable β_J=3 value of 7.5 × 10⁴ au, accounting for 51.1% and displaying an octupolar nature with depolarization ratio of 4.06. On the other hand, the complexes Na₃O⁺@CXP[4]Li⁻ and K₃O⁺@CXP[4]Li⁻ are dipolar in nature, as indicated by their higher dipolar contributions with β_J=1 values of 1.9 × 10⁶ au (59.2%) and 9.1 × 10⁵ au (53.9%). The corresponding depolarization ratios are 5.62 and 4.83, for these complexes, respectively. These findings strongly suggest that the investigated superalkali-based M₃O⁺CXP[4]Li⁻ alkalides hold significant potential for nonlinear optical switches.⁵

Moreover, dynamic EOPE and SHG co-efficients of M₃O⁺CXP[4]Li⁻ alkalides are also computed for optical imaging and for various other optical applications at the aforementioned laser wavelengths. Notably, the results depict that the EOPE is particularly pronounced at 532 & 1064 nm whereas the EOPE is reduced at 1907 nm in the studied alkalides. The highest EOPE (7.7 × 10⁷ au) is computed for the Na₃O⁺@CXP[4]Li⁻at 532 nm, while the lowest EOPE (3.7 × 10⁴ au) at 1064 nm is observed for Li₃O⁺@CXP[4]Li⁻ alkalide.

In the similar way, the M₃O⁺CXP[4]Li⁻ alkalides exhibit more significant second harmonic generation at 532 & 1064 nm, in comparison to 1907 nm. Specifically, the highest SHG response (1.1 × 10⁸ au) is observed for K₃O⁺CXP[4]Li⁻ alkalide at 1064 nm, whereas the Li₃O⁺CXP[4]Li⁻ alkalide displays the least pronounced SHG effect of 5.6 × 10⁴ au at the same laser wavelength. These findings serve as compelling evidence supporting the utility of these superalkali-based calix[4]pyridines within the realm of nonlinear optics. Furthermore, these superalkali-based alkalides can be applied in Q-switching, cavity dumping, laser imaging and in various other fields due to the substantial impact of incident frequencies on SHG and EOPE co-efficients.

4. Conclusion

The concluding summary includes examination of geometric, electronic, and NLO responses of superalkali-based M₃O⁺CXP[4]Li⁻ alkalides via DFT simulations. The designed alkalides demonstrate both thermodynamic and chemical stability, which is evidenced by their enhanced interaction energy values (−32.3 to −64.5 kcal mol⁻¹) and vertical ionization energies (2.51 to 2.79 eV). These alkalides, being excess electron compounds, exhibit potential electronic properties and have significantly reduced HOMO–LUMO energy gaps (0.30–0.50 eV). The highest charge transfer of −0.486 |e| is obtained for the K₃O⁺CXP[4]Li⁻ alkalide using natural population analysis and their the alkalide nature is confirmed by electron density distribution. The complexant interacts non-covalently with superalkali clusters and Li metal as computed by IRI and QTAIM studies. The absorption analysis reflects that the superalkali-based alkalides have absorption maximum in the visible to near infrared region 727–1096 nm and might be suitable for enhancing SHG of designed alkalides. The highest static 2nd order NLO response of 2.5 × 10⁶ au is computed for Na₃O⁺CXP[4]Li⁻ alkalide which is greater than the highest β_o (3.4 × 10⁴ au) of superalkali-based calix[4]pyrrole alkalides. The highest dynamic β_SHG and β_HRS of 1.1 × 10⁸ au and 1.8 × 10⁸ au are observed at 1064 nm whereas the highest EOPE value of 7.7 × 10⁷ au is computed at 532 nm. These results demonstrate that these superalkali-based calix[4]pyridine alkalides can be substantial NLO materials to be utilized in Q-switching, cavity dumping, laser imaging and as wavelength converters.

Data availability

The data supporting this article have been included as part of the ESI.† Additional data will be available upon request from corresponding author.

Conflicts of interest

The authors declare no competing interest.

Acknowledgements

This article is derived from a research grant funded by the Research, Development, and Innovation Authority (RDIA) – Kingdom of Saudi Arabia – with grant number (12615-iu-2023-IU-R-2-1-EI-).

References

1. S. Shi, C. Lin, G. Yang, L. Cao, B. Li, T. Yan, M. Luo and N. Ye, A2Bi2 (SeO3) 3F2 (A= K and Rb): Excellent Mid-Infrared Nonlinear Optical Materials with Both Strong SHG Responses and Large Band Gaps, Chem. Mater., 2020, 32(18), 7958–7964,  DOI:10.1021/acs.chemmater.0c02837.
2. D. Lagarde, L. Bouet, X. Marie, C. R. Zhu, B. L. Liu, T. Amand, P. H. Tan and B. Urbaszek, Carrier and Polarization Dynamics in Monolayer MoS 2, Phys. Rev. Lett., 2014, 112(4), 47401,  DOI:10.1103/PhysRevLett.112.047401.
3. C. H. Camp Jr and M. T. Cicerone, Chemically Sensitive Bioimaging with Coherent Raman Scattering, Nat. Photonics, 2015, 9(5), 295–305,  DOI:10.1038/nphoton.2015.60.
4. H. S. Quah, W. Chen, M. K. Schreyer, H. Yang, M. W. Wong, W. Ji and J. J. Vittal, Multiphoton Harvesting Metal–Organic Frameworks, Nat. Commun., 2015, 6(1), 1–7,  DOI:10.1038/ncomms8954.
5. J. Quertinmont, P. Beaujean, J. Stiennon, Y. Aidibi, P. Leriche, V. Rodriguez, L. Sanguinet and B. Champagne, Combining Benzazolo-Oxazolidine Twins toward Multi-State Nonlinear Optical Switches, J. Phys. Chem. B, 2021, 125(15), 3918–3931,  DOI:10.1021/acs.jpcb.1c01962.
6. M. J. Miller, S. H. Wei, I. Parker and M. D. Cahalan, Two-Photon Imaging of Lymphocyte Motility and Antigen Response in Intact Lymph Node, Science, 2002, 296(5574), 1869–1873,  DOI:10.1126/science.1070051.
7. X. Liu, Q. Guo and J. Qiu, Emerging Low-dimensional Materials for Nonlinear Optics and Ultrafast Photonics, Adv. Mater., 2017, 29(14), 1605886,  DOI:10.1002/adma.201605886.
8. S. A. M. Britto Dhas and S. Natarajan, Growth and Characterization of L-prolinium Tartrate–A New Organic NLO Material, Cryst. Res. Technol. J. Exp. Ind. Crystallogr., 2007, 42(5), 471–476,  DOI:10.1002/crat.200610850.
9. C. Ji, T. Chen, Z. Sun, Y. Ge, W. Lin, J. Luo, Q. Shi and M. Hong, Bulk Crystal Growth and Characterization of Imidazolium L-Tartrate (IMLT): A Novel Organic Nonlinear Optical Material with a High Laser-Induced Damage Threshold, CrystEngComm, 2013, 15(11), 2157–2162,  10.1039/C3CE26942F.
10. J. Naeem, R. Bano, K. Ayub, T. Mahmood, S. Tabassum, A. Arooj and M. A. Gilani, Assessment of Alkali and Alkaline Earth Metals Doped Cubanes as High-Performance Nonlinear Optical Materials by First-Principles Study, J. Sci.:Adv. Mater. Devices, 2022, 7(3), 100457,  DOI:10.1016/j.jsamd.2022.100457.
11. E. Nestoros and M. C. Stuparu, Corannulene: A Molecular Bowl of Carbon with Multifaceted Properties and Diverse Applications, Chem. Commun., 2018, 54(50), 6503–6519,  10.1039/C8CC02179A.
12. R. Bano, M. Asghar, K. Ayub, T. Mahmood, J. Iqbal, S. Tabassum, R. Zakaria and M. A. Gilani, A Theoretical Perspective on Strategies for the Fabrication of High Performance Nonlinear Optical Materials, Front. Mater., 2021, 8, 532,  DOI:10.3389/fmats.2021.783239.
13. M. A. Gilani, S. Tabassum, U. Gul, T. Mahmood, A. I. Alharthi, M. A. Alotaibi, M. Geesi, R. Sheikh and K. Ayub, Copper-Doped Al12N12 Nano-Cages: Potential Candidates for Nonlinear Optical Materials, Appl. Phys. A, 2018, 124(1), 1–9,  DOI:10.1007/s00339-017-1425-0.
14. K. S. Kim, I. Park, S. Lee, K. Cho, J. Y. Lee, J. Kim and J. D. Joannopoulos, The Nature of a Wet Electron, Phys. Rev. Lett., 1996, 76(6), 956,  DOI:10.1103/PhysRevLett.76.956.
15. W.-M. Sun, X.-H. Li, D. Wu, Y. Li, H.-M. He, Z.-R. Li, J.-H. Chen and C.-Y. Li, A Theoretical Study on Superalkali-Doped Nanocages: Unique Inorganic Electrides with High Stability, Deep-Ultraviolet Transparency, and a Considerable Nonlinear Optical Response, Dalton Trans., 2016, 45(17), 7500–7509,  10.1039/C6DT00342G.
16. J. L. Dye, J. M. Ceraso, M. Lok, B. L. Barnett and F. J. Tehan, Crystalline Salt of the Sodium Anion (Na-), J. Am. Chem. Soc., 1974, 96(2), 608–609.
17. M. Y. Redko, M. Vlassa, J. E. Jackson, A. W. Misiolek, R. H. Huang and J. L. Dye, “Inverse Sodium Hydride”: A Crystalline Salt That Contains H+ and Na, J. Am. Chem. Soc., 2002, 124(21), 5928–5929,  DOI:10.1021/ja025655+.
18. W. Chen, Z. R. Li, D. Wu, Y. Li, C. C. Sun, F. L. Gu and Y. Aoki, Nonlinear Optical Properties of Alkalides Li+(Calix[4]Pyrrole) M- (M = Li, Na, and K): Alkali Anion Atomic Number Dependence, J. Am. Chem. Soc., 2006, 128(4), 1072–1073,  DOI:10.1021/ja056314+.
19. Y.-Q. Jing, Z.-R. Li, D. Wu, Y. Li, B.-Q. Wang and F. L. Gu, What Is the Role of the Complexant in the Large First Hyperpolarizability of Sodide Systems Li (NH3) n Na (N= 1− 4)?, J. Phys. Chem. B, 2006, 110(24), 11725–11729,  DOI:10.1021/jp060584c.
20. R. Bano, K. Ayub, T. Mahmood, M. Arshad, A. Sharif, S. Tabassum and M. A. Gilani, Mixed Superalkalis Are a Better Choice than Pure, Dalton Trans., 2022, 51, 8437–8453,  10.1039/d2dt00321j.
21. W. M. Sun, L. T. Fan, Y. Li, J. Y. Liu, D. Wu and Z. R. Li, On the Potential Application of Superalkali Clusters in Designing Novel Alkalides with Large Nonlinear Optical Properties, Inorg. Chem., 2014, 53(12), 6170–6178,  DOI:10.1021/ic500655s.
22. W.-M. Sun, Y. Li, X.-H. Li, D. Wu, H.-M. He, C.-Y. Li, J.-H. Chen and Z.-R. Li, Stability and Nonlinear Optical Response of Alkalides That Contain a Completely Encapsulated Superalkali Cluster, ChemPhysChem, 2016, 17(17), 2672–2678,  DOI:10.1002/cphc.201600389.
23. A. Ahsin and K. Ayub, Superalkali-Based Alkalides Li3O@[12-Crown-4] M (Where M= Li, Na, and K) with Remarkable Static and Dynamic NLO Properties; A DFT Study, Mater. Sci. Semicond. Process., 2022, 138, 106254,  DOI:10.1016/j.mssp.2021.106254.
24. A. Ahsan and K. Ayub, Adamanzane Based Alkaline Earthides with Excellent Nonlinear Optical Response and Ultraviolet Transparency, Opt. Laser Technol., 2020, 129(April), 106298,  DOI:10.1016/j.optlastec.2020.106298.
25. S. B. Nimse and T. Kim, Biological Applications of Functionalized Calixarenes, Chem. Soc. Rev., 2013, 42(1), 366–386,  10.1039/C2CS35233H.
26. H. R. Shamlouei and F. Parvinzadeh, Influence of Alkali Metal Atoms on Structure, Electronic and Non-Linear Optical Properties of Calix [4] Arene, Phys. E, 2021, 127, 114539,  DOI:10.1016/j.physe.2020.114539.
27. V. Král, P. A. Gale, P. Anzenbacher Jr, K. Jursíková, V. Lynch and J. L. Sessler, Calix [4] Pyridine: A New Arrival in the Heterocalixarene Family, Chem. Commun., 1998, 1, 9–10,  10.1039/A706018A.
28. A. Azadi and H. R. Shamlouei, Feasibility of Using the Anode Functionalized with Calix [4] Pyridine in Lithium and Sodium Atom/Ion Batteries: DFT Study, Comput. Theor. Chem, 2021, 1202, 113332,  DOI:10.1016/j.comptc.2021.113332.
29. T. De Meyer, K. Hemelsoet, V. Van Speybroeck and K. De Clerck, Substituent Effects on Absorption Spectra of PH Indicators: An Experimental and Computational Study of Sulfonphthaleine Dyes, Dyes Pigm., 2014, 102, 241–250,  DOI:10.1016/j.dyepig.2013.10.048.
30. T. Lu and F. Chen, Multiwfn: A Multifunctional Wavefunction Analyzer, J. Comput. Chem., 2012, 33(5), 580–592,  DOI:10.1002/jcc.22885.
31. W. Humphrey, A. Dalke and K. Schulten, VMD: Visual Molecular Dynamics, J. Mol. Graphics, 1996, 14(1), 33–38,  DOI:10.1016/0263-7855(96)00018-5.
32. T. Yanai, D. P. Tew and N. C. Handy, A New Hybrid Exchange–Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393(1–3), 51–57,  DOI:10.1016/j.cplett.2004.06.011.
33. D. Jacquemin, E. A. Perpète, M. Medved’, G. Scalmani, M. J. Frisch, R. Kobayashi and C. Adamo, First Hyperpolarizability of Polymethineimine with Long-Range Corrected Functionals, J. Chem. Phys., 2007, 126(19), 191108,  DOI:10.1063/1.2741246.
34. L. M. G. Abegao, R. D. Fonseca, F. A. Santos, J. J. Rodrigues, K. Kamada, C. R. Mendonça, S. Piguel and L. De Boni, First Molecular Electronic Hyperpolarizability of Series of π-Conjugated Oxazole Dyes in Solution: An Experimental and Theoretical Study, RSC Adv., 2019, 9(45), 26476–26482,  10.1039/C9RA05246A.
35. M. J. Frisch; G. W. Trucks; H. B. Schlegel; G. E. Scuseria; M. A. Robb; J. R. Cheeseman; G. Scalmani; V. Barone; G. A. Petersson; H. Nakatsuji; X. Li; M. Caricato; A. V. Marenich; J. Bloino; B. G. Janesko; R. Gomperts; B. Mennucci; H. P. Hratchian; J. V. Ortiz; A. F. Izmaylov; J. L. Sonnenberg; D. Williams-Young; F. Ding; F. Lipparini; F. Egidi; J. Goings; B. Peng; A. Petrone; T. Henderson; D. Ranasinghe; V. G. Zakrzewski; J. Gao; N. Rega; G. Zheng; W. Liang; M. Hada; M. Ehara; K. Toyota; R. Fukuda; J. Hasegawa; M. Ishida; T. Nakajima; Y. Honda; O. Kitao; H. Nakai; T. Vreven; K. Throssell; J. A. Montgomery; J. E. Peralta; F. Ogliaro; M. J. Bearpark; J. J. Heyd; E. N. Brothers; K. N. Kudin; V. N. Staroverov; T. A. Keith; R. Kobayashi; J. Normand; K. Raghavachari; A. P. Rendell; J. C. Burant; S. S. Iyengar; J. Tomasi; M. Cossi; J. M. Millam; M. Klene; C. Adamo; R. Cammi; J. W. Ochterski; R. L. Martin; K. Morokuma; O. Farkas; J. B. Foresman; and D. J. Fox. Gaussian 16, Revision B. 01., Gaussian, Inc., Wallingford CT, 2016.
36. R. Dennington; T. Keith and J. Millam. GaussView, Version 6.1.1. Semichem Inc., Shawnee Mission, KS. 2019.
37. D.-F. WANG and Y.-D. WU, A Theoretical Comparison of Conformational Features of Calix [4] Aromatics, J. Theor. Comput. Chem., 2004, 3(01), 51–68,  DOI:10.1142/S0219633604000908.
38. D. Bellert and W. H. Breckenridge, A Spectroscopic Determination of the Bond Length of the LiOLi Molecule: Strong Ionic Bonding, J. Chem. Phys., 2001, 114(7), 2871–2874,  DOI:10.1063/1.1349424.
39. M. F. Asif, R. Bano, R. Farooq, S. Muhammad, T. Mahmood, K. Ayub, S. Tabassum and M. A. Gilani, Shedding Light on the Second Order Nonlinear Optical Responses of Commercially Available Acidic Azo Dyes for Laser Applications, Dyes Pigm., 2022, 202, 110284,  DOI:10.1016/j.dyepig.2022.110284.
40. F. Ullah, K. Ayub and T. Mahmood, Remarkable Second and Third Order Nonlinear Optical Properties of Organometallic C6Li6–M3O Electrides, New J. Chem., 2020, 44(23), 9822–9829,  10.1039/D0NJ01670E.
41. N. Kosar, L. Zari, K. Ayub, M. A. Gilani and T. Mahmood, Static, Dynamic Nonlinear Optical (NLO) Response and Electride Characteristics of Superalkalis Doped Star like C6S6Li6, Surf. Interfaces, 2022, 31, 102044,  DOI:10.1016/j.surfin.2022.102044.
42. R. Bano, M. Arshad, T. Mahmood, K. Ayub, A. Sharif, S. Tabassum and M. A. Gilani, Superalkali (Li2F, Li3F) Doped Al12N12 Electrides with Enhanced Static, Dynamic Nonlinear Optical Responses and Refractive Indices, Mater. Sci. Semicond. Process., 2022, 143, 106518,  DOI:10.1016/j.mssp.2022.106518.
43. R. Bano, K. Ayub, T. Mahmood, M. Arshad, A. Sharif, S. Tabassum and M. A. Gilani, Diamondoid as Potential Nonlinear Optical Material by Superalkali Doping: A First Principles Study, Diamond Relat. Mater., 2023, 135(March), 109826,  DOI:10.1016/j.diamond.2023.109826.
44. W. Sun, D. Wu, Y. Li and Z. Li, Novel Alkalides with Considerably Large First Theoretical Study on Superalkali (Li3) in Ammonia: Hyperpolarizabilities, Dalt. Trans., 2014, 43, 486–494,  10.1039/c3dt51559a.
45. T. Lu and Q. Chen, Interaction Region Indicator: A Simple Real Space Function Clearly Revealing Both Chemical Bonds and Weak Interactions, Chem.:Methods, 2021, 1(5), 231–239,  DOI:10.1002/cmtd.202100007.
46. B. RFW, Atoms in Molecules: A Quantum Theory. Clarendon Press. Oxford A. E Reed, LA Curtiss F Weinhold, Chem. Rev., 1990, 88, 899.
47. A. Ahsan and K. Ayub, Extremely Large Nonlinear Optical Response and Excellent Electronic Stability of True Alkaline Earthides Based on Hexaammine Complexant, J. Mol. Liq., 2020, 297, 111899.
48. M. A. Buldakov, E. V. Koryukina, V. N. Cherepanov and Y. N. Kalugina, A Dipole-Moment Function of MeH Molecules (Me= Li, Na, K), Russ. Phys. J., 2007, 50, 532–537,  DOI:10.1007/s11182-007-0080-x.
49. J. Mai, S. Gong, N. Li, Q. Luo and Z. Li, A Novel Class of Compounds—Superalkalides: M+(En) 3 M 3′ O−(M, M′= Li, Na, and K; En= Ethylenediamine)—with Excellent Nonlinear Optical Properties and High Stabilities, Phys. Chem. Chem. Phys., 2015, 17(43), 28754–28764,  10.1039/C5CP03635F.
50. J. L. Oudar and D. S. Chemla, Hyperpolarizabilities of the Nitroanilines and Their Relations to the Excited State Dipole Moment, J. Chem. Phys., 1977, 66(6), 2664–2668,  DOI:10.1063/1.434213.
51. X. Li, Y. Zhang and J. Lu, Remarkably Enhanced First Hyperpolarizability and Nonlinear Refractive Index of Novel Graphdiyne-Based Materials for Promising Optoelectronic Applications: A First-Principles Study, Appl. Surf. Sci., 2019, 2020(512), 145544,  DOI:10.1016/j.apsusc.2020.145544.
52. W. Chen, Z.-R. Li, D. Wu, Y. Li, C.-C. Sun, F. Long Gu and Y. Aoki, Nonlinear Optical Properties of Alkalides Li + ((Calix[4]Pyrrole)M-(M)Li, Na, and K): Alkali Anion Atomic Number Dependence = 3Δμ‚f 0 2ΔE 3(1), J. Am. Chem. Soc., 2006, 128, 53,  DOI:10.1021/ja056314.

---

Footnote

† Electronic supplementary information (ESI) available: Additional theoretical details, including figures of optimized complexes of horizontal and vertical superalkali based M₃O⁺CXP[4]Li⁻alkalides, crucial transition states of the most stable M₃O⁺CXP[4]Li⁻alkalides and tables of AIM (atom in molecule) topological parameters, static first hyperpolarizabilities (au) at various functionals and dipolar (|β_J=1| (au)), octupolar (|β_J=3| (au)), depolarization ratio (DR), dipolar to octupolar contributions in the designed complexes are also provided (DOC). See DOI: https://doi.org/10.1039/d4ra08399g

---