Study of carbon matrix and hybrid nanocomposite for greenhouse gas storage

Abstract

Using the sol–gel preparation method, a Carbon Matrix (CM) based on pyrogallol–formaldehyde and a hybrid NanoComposite (NC) formed by incorporating nickel oxide nanoparticles into the carbon matrix were developed. The obtained samples were heat treated by a tubular furnace under an inert atmosphere and they were characterized by different techniques such as X-ray Diffraction, X-ray Photoelectron Spectroscopy (XPS) measurements, Scanning Electron Microscopy, Brunner–Emmett–Teller method, Thermogravimetric analysis, Transmission Electron Microscopy and Admittance Spectroscopy. Using a high-throughput experimental approach, measurements of the adsorption capacity of greenhouse gases were performed, including carbon dioxide (CO₂), methane (CH₄) and ethane (C₂H₆). The significant porous texture, the uniform dispersion of metallic nanoparticles within the amorphous matrix and the emergence of Multi-Walled Carbon Nanotubes (MWCN) in the hybrid nanocomposite play a key role in the variation of electrical conductivity and the adsorption capacities of real gases. These materials show great promise for greenhouse gas storage applications.

---

1. Introduction

Greenhouse gas emissions, including carbon dioxide, methane, and ethane, contribute significantly to global warming and health problems. Carbon dioxide (CO₂), in particular, accounts for around 70% of greenhouse gas emissions and is often employed as a refrigerant or cooling fluid in energy transfer applications.^1–3 Methane (CH₄), primarily produced from the decomposition of organic matter in agriculture and landfills, can serve as an energy source for generating electricity and heat.^4–6 Ethane (C₂H₆), abundant in natural gas and petroleum gases, is also used to create energy and as a source of ethylene-a key raw material in plastic manufacturing.^7–9 Currently, several methods exist to capture these gases, including adsorption on porous materials at low pressure and room temperature. In fact, porous materials have a significant capacity to interact with atoms, ions and molecules of gases either on the surface or throughout the volume of the material. The distribution of pore size, shape and volume have an direct effect on the adsorption capacity of these materials.

For many years, carbon materials have been widely used in the field of gas storage due to their high specific surface area, which can reach 3000 m² g⁻¹ under the influence of pyrolysis temperature.^10–12 Especially, carbon nanotubes have shown great promise for gas adsorption due to their tubular structure, which provides a suitable specific surface area, as well as their chemical and thermal stability.^13,14 For both allotropic forms of carbon nanotubes, Single-Walled (SWCN) and Multi-Walled (MWCN), it was observed that the presence of structural defects in SWCN enhanced the gas adsorption capacity compared to defect-free SWCN. This enhancement is attributed to the higher binding energy of gas molecules on the surface of the defective nanotube.¹⁵ In MWCN, the gas adsorption capacity at low pressure is generally low. However, it was shown that treatment of these nanotubes with acids such as HCl, HNO₃ and H₂SO₄ enhanced the gas adsorption.¹⁶ For both SWCN and MWCN, increasing the pressure leads to a higher amount of gas adsorbed, while increasing the temperature reduces the adsorption.^17,18 However, the formation of carbon nanotubes in carbon-based materials has been described through several models, such as the carbon filament growth model proposed by Baker¹⁹ and the silicon filament model introduced by Wagner and Ellis.²⁰ Specifically, the dissolution of carbon in a nanometer-sized metal particle during pyrolysis induces an explosive reaction that leads to the formation of carbon nanotubes. According to these models, the nucleation and growth of nanotubes at high temperatures occur through a series of steps: the adsorption of carbon gas on the nanoparticle surface, the diffusion of carbon across the nanoparticle, graphitization on the nanoparticle surface to form a tube nucleus, and tube growth via the incorporation of carbon at the carbon/nanoparticle interface. Dai et al.²¹ argue that the key to the growth mechanism lies in preventing the graphene sheet from adopting a free configuration, as such a state would result in energetically significant bonds. They propose that the initiation of nanotube formation stems from the disparity between the high surface tension of the nanometric molybdenum nanoparticle and the low surface energy of graphite.

From an electrical perspective, metal nanoparticles and carbon nanotubes significantly influence the electrical conductivity of nanocomposites. The electrical conductivity of a hybrid nanocomposite is largely determined by the formation of a three-dimensional network of conductive particles and/or carbon nanotubes within the organic matrix. Within this network, two primary mechanisms govern the electrical performance of the nanocomposite.²² The first and simplest mechanism occurs when direct contact exists between the particles and/or nanotubes, facilitating the transfer of electrons from one site to another. The second mechanism involves quantum tunneling, which arises when a thin insulating layer separates the conductive sites.²³ For both mechanisms, the establishment of an electrical network within the composite is critical. Several factors influence the formation of this network. First, the concentration of conductive particles and/or carbon nanotubes must be sufficient to enable the network to span the entire sample. Additionally, the geometry of the conductive particles, the type of carbon nanotubes whether SWCN or MWCN and their emergence in the studied materials play a crucial role in ensuring effective electrical conduction. Lastly, the manufacturing process, particularly the efficient dispersion of nanoreinforcements within the organic matrix, significantly enhances the electrical conductivity of the nanocomposite.

The main aim of this work is to study the different properties of Carbon Matrix (CM) and NanoComposite (NC) as well as their the performance in the field of storage of greenhouse gases, including carbon dioxide (CO₂), methane (CH₄) and ethane (C₂H₆). CM is amorphous and microporous, with its electrical conductivity increasing as the specific surface area and pore volume increase. In contrast, NC crystallizes, exhibiting one phase corresponding to MWCN and others associated with metallic nickel and nickel oxide. It is classified as mesoporous, and its electrical conductivity improves as the specific surface area and pore volume decrease. For both types of materials, CO₂ is the most adsorbed gas, while CH₄ is the least adsorbed. For all gases, MC treated at 1000 °C exhibited the highest adsorption capacity, whereas NC treated at the same temperature displayed minimal capacity. This behavior is attributed to the significant reduction in the specific surface area and pore volume of NC compared to CM. Notably, at a pyrolysis temperature of 650 °C, the adsorption of C₂H₆ by NC surpasses that of CM, despite CM having a larger specific surface area and pore volume than NC. This is likely caused by the strong interactions between C₂H₆ molecules and nickel nanoparticles on the active surface of the nanocomposite.

2. Experimental

2.1. Synthesis of samples

The preparation of Carbon Matrix (CM) was completed in three steps as shown in Fig. 1. First, pyrogallol (P) was dissolved in formaldehyde (F) and water (W) in the presence of picric acid as a catalyst, with the mixture stirred magnetically for 30 minutes. Next, the resulting solution was dried in a humid atmosphere at room temperature for two weeks. Finally, the compounds were subjected to heat treatment under an inert atmosphere at 650 and 1000 °C to get the CM-650 °C and CM-1000 °C.

Fig. 1 Synthesis of the carbon matrix (CM).

The synthesis of NanoComposite (NC) was carried out as follows (Fig. 2): first, nickel oxide (NiO) nanoparticles were prepared using the sol–gel process with supercritical drying, following the protocol described by Ben Mansour et al.^24–27 In this protocol, the nickel precursor (NiCl₂·6H₂O) was dissolved in methanol and the solution was magnetically stirred for 15 minutes. The solution was then dried in an autoclave under the supercritical conditions of ethyl alcohol to form an aerogel. This aerogel was subsequently treated in a muffle furnace at 500 °C for two hours. Next, the NiO nanoparticles were incorporated into the pyrogallol–formaldehyde matrix at a mass ratio of 5%. Finally, through conventional drying and heat treatment under an inert atmosphere at 650 and 1000 °C, the nanocomposites NC-650 °C and NC-1000 °C were obtained. Heat treatment of prepared samples was conducted using a tubular furnace while circulating a stream of dry nitrogen to initially expel the air from inside the furnace. After five minutes of this nitrogen purge, heating was carried out under a nitrogen atmosphere to the desired temperatures of 650 °C and 1000 °C for two hours. The temperature ramp rate was controlled using a programmer set to 5 °C min⁻¹, followed by conventional cooling to room temperature.

Fig. 2 Synthesis of the nanocomposite (NC).

2.2. Characterization

The X-ray diffraction (XRD) patterns of the compounds were recorded using a Bruker D5005 diffractometer equipped with Co Kα radiation, operating at 40 kV. The SEM and TEM images were captured using a JEOL JSM-5310 Scanning Electron Microscope and a JEOL-100C Transmission Electron Microscope, respectively. X-ray Photoelectron Spectroscopy (XPS) measurements were performed using a Kratos Analytical instrument (UK, SHIMADZU group) with Al-Kα radiation. Thermogravimetric analysis (TGA) was performed with a Setaram Labsys™ system was employed to study the effect of annealing on the weight loss of the samples during pyrolysis in a nitrogen atmosphere. The analysis was conducted at an annealing rate of 5 °C min⁻¹ up to a maximum temperature of 1000 °C. The conductivity was measured with an Agilent 4294A impedance analyzer. The nitrogen adsorption–desorption isotherms were obtained using a Micromeritics ASAP 2000 instrument. Gas adsorption measurements were performed at room temperature and pressures up to 10 bar using a custom-built high-throughput system.²⁸

3. Results and discussions

The X-ray diffractograms of CM and NC are presented in Fig. 3. At both 650 °C and 1000 °C, CM exhibits an amorphous structure, characterized by a broad band within 2θ = 40–50°, with a maximum at 2θ = 44°, corresponding to (101) plane of graphite (JCPDS 75-1621).²⁹ In contrast, NC displays a crystalline structure, with two distinct peaks at 2θ = 52° and 61°, assigned to the (200) diffraction planes of nickel (JCPDS 04-0850) and (220) of nickel oxide phase (JCPDS 04-0835),^30,31 respectively. Furthermore, for NC treated at 1000 °C, a prominent peak at 2θ = 30° is observed. This peak is attributed to the reflection of the intertubes, indicating that the interlays of graphitic structure were compressed through high heat treatment at a pyrolysis temperature of 1000 °C, resulting in the formation of MWCNT.³² The small peak around 50° is attributed to stacking faults (SF) that spontaneously appeared during the growth of MWCNT. The occurrence of these defects in NC-1000 °C can explain the agglomeration of nanoparticles due to the diffusion phenomenon, leading to an increase in their size.

Fig. 3 X-ray diffraction of different samples.

The average crystallites size was estimated using the Scherrer equation eqn (1):³³

where D is the average crystallite size, λ is the X-ray diffraction wavelength for cobalt (1.78901 Å), θ is the angle corresponding to the maximum of the diffraction peak and β is the peak width at half maximum. Using eqn (1), the crystallite size of our samples increased with the pyrolysis temperature. This is because higher temperatures enhance atomic mobility and reduce surface energy, promoting nanoparticle agglomeration and consequently increasing their size. Specifically, the crystallite size of graphite is approximately 1 nm in the carbon matrix treated at 650 °C and around 2 nm in that treated at 1000 °C. Similarly, the crystallite size of Ni increased from 24 nm to 26 nm and of NiO from 22 nm to 27 nm in the nanocomposites treated at 650 °C and 1000 °C, respectively. For the MWCNT observed in NC-1000 °C, the average crystal size is around 10 nm. The broad peaks observed in the CM at around 44° indicate a highly disordered structure for both the CM-650 °C and CM-1000 °C samples. A slight increase in the intensity of the peaks corresponding to Ni and NiO is observed between NC-650 °C and NC-1000 °C, suggesting a negligible increase in the size of Ni and NiO crystallites. In NC-1000 °C, the asymmetry of the peak at 30° is attributed to the presence of aliphatic side chains near the graphite crystallites. Moreover, the high intensity of this peak indicates the development of a more ordered structure with the formation of MWCNT. Thus, the XRD diffractograms of NC revealed structural transformations towards a more ordered material as the pyrolysis temperature increased from 650 to 1000 °C. On the other hand, no structural changes were observed in the CM with increasing temperature.

The increase in crystallite size with pyrolysis temperature in CM and NC had a significant impact on the variation in electrical conductivity and thus on the behavior of the final material. Indeed, the rise in pyrolysis temperature led to an increase in the size of conductive particles, thereby shifting the behavior of these materials from semiconductor at 650 °C to metallic at 1000 °C. Additionally, this change in crystallite size with increasing pyrolysis temperature played a crucial role in the texture of NC and consequently in its gas adsorption capacity. Specifically, a larger crystallite size resulted in a decrease in the specific surface area and therefore in the adsorption capacity of NC for the different greenhouse gases studied in this work.

Fig. 4 displays the SEM images of the various samples, revealing agglomerated microparticles with inhomogeneous distributions and visible gaps between them. These gaps are especially pronounced in NC-650 °C and CM-1000 °C compared to the other samples, suggesting a highly porous texture in these two composites.

Fig. 4 SEM images of different samples.

To better understand the significant porous texture of the matrix and nanocomposite, the nitrogen adsorption–desorption isotherms of the materials are shown in Fig. 5. Using the BET method (Brunauer, Emmett and Teller), the isotherms reveal that the carbon matrix (CM) is microporous, while the nanocomposite (NC) is mesoporous.

Fig. 5 Adsorption–desorption isotherm of nitrogen.

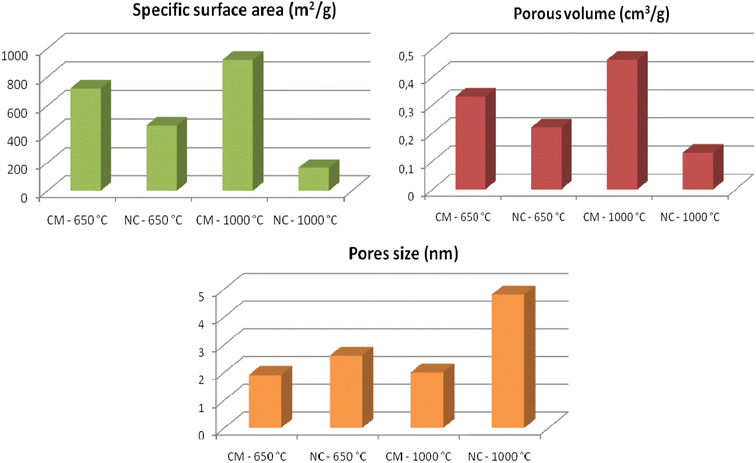
The histograms in Fig. 6 compile all textural parameter values. The pore size in CM is approximately 2 nm, whereas in NC, it ranges between 2 nm and 50 nm. These values confirm the classification of CM as microporous and NC as mesoporous.³⁴ The CM treated at 1000 °C exhibits the highest porosity, with a specific surface area of 920 m² g⁻¹ and a pore volume of 0.33 cm³ g⁻¹. In contrast, the NC treated at 1000 °C has the lowest specific surface area (163 m² g⁻¹) and the smallest pore volume (0.13 cm³ g⁻¹). This reduction in porosity for NC-1000 °C can be attributed to the formation of Multi-Walled Carbon Nanotubes (MWNT), which is known to have less significant textural properties compared to Single-Walled Carbon Nanotubes (SWNT).³⁵

Fig. 6 Histograms of porous volume, specific surface area and pore sizes for the different samples.

The TEM images in Fig. 7 confirm the findings from the XRD and textural studies. Specifically, the CM is amorphous, with nanopores present. For the NC treated at 650 °C, nanoparticles are dispersed within the amorphous carbon matrix. At 1000 °C, MWNT form around these nanoparticles. Indeed, under the influence of high pyrolysis temperatures and the presence of inorganic nanoparticles within the carbon matrix, an explosive reaction occurs, promoting the formation of MWCN.

Fig. 7 TEM images of different samples.

The high-resolution TEM images of the MWCN in the NC-1000 °C are shown in Fig. 8. These MWNT are formed by the concentric stacking of multiple SWNT, with a well-defined inter-wall spacing of approximately 3.4 Å, which corresponds to the interlayer distance in graphite. In fact, MWNT are commonly arranged parallel to each other in a two-dimensional triangular lattice structure, maintained by van der Waals interactions.³⁶

Fig. 8 High-resolution TEM images of the MWCN in the NC-1000 °C.

The surface elemental composition of different samples was determined using the XPS technique, as displayed in Fig. 9. Several peaks were observed at 285.2, 533.3, and 854.8 eV, which are ascribed to C1s, O1s, and Ni2p, respectively. Generally, the C1s peak can be attributed to various forms and structures of carbon, such as amorphous carbon, graphite, graphene and carbon nanotubes.^37–40 In our case, as observed in the TEM images (Fig. 5 and 6), this peak corresponds to amorphous carbon in the CM and in the NC-650 °C, whereas in NC-1000 °C, it corresponds to MWCN. Thus, the C1s peak can be assigned to a C–C bond.

Fig. 9 XPS spectra of different samples.

Table 1 presents the atomic concentrations of different elements. It is clearly noted that the carbon concentration in NC-1000 °C was increased compared to the other samples, while the nickel concentration was decreased in NC-1000 °C compared to NC-650 °C. This can be explained by the formation of MWCN after heat treatment at 1000 °C. These nanotubes cover the surface of the nanoparticles, leading to a decrease in nickel concentration.

Table 1 Surface elemental concentrations of prepared samples

Sample	C 1s (at%)	O 1s (at%)	Ni 2p (at%)
CM-650 °C	87.05	12.94	—
NC-650 °C	88.12	10.14	1.73
CM-1000 °C	86.60	13.39	—
NC-1000 °C	94.71	4.25	1.03

---

Fig. 10 depicts the thermogravimetric analysis of CM and NC, revealing a total weight loss of approximately 67% for CM and 45% for NC. Three distinct weight loss stages were observed: the first, occurring between 40 and 130 °C, is attributed to water desorption; the second, between 130 and 300 °C, corresponds to precursor desorption; and the third, above 300 °C, is associated with decomposition reactions during the carbonization process, leading to the formation of C–C bonds. The reduced weight loss in NC highlights its superior thermal stability compared to CM, likely due to the formation of MWCN at elevated temperatures.

Fig. 10 TGA curves of carbon matrix (CM) and nanocomposite (NC).

Fig. 11 shows the variation of conductance as a function of frequency at room temperature. The increase in conductance at high frequencies indicates the semiconducting behavior of CM and NC treated at 650 °C. The conductance of CM is higher than that of NC across the entire frequency range. In fact, the presence of conductive nanoparticles in the carbon matrix enhances electrical conductivity by reducing the distance between conduction sites. At the pyrolysis temperature of 1000 °C, the decrease in conductance at high frequencies indicates the dominance of metallic behavior in both samples. At low frequencies, the conductance of NC is higher than that of CM. However, at higher frequencies (around 10⁵ Hz), the conductance of NC becomes lower than that of CM. This is because the MWCN align under the influence of the AC applied electric field. This orientation also causes the separation of metallic and semiconducting MWCN due to their distinct electrical properties. Metallic MWCN aggregate at the electrodes, while semiconducting MWCN tend to remain within the nanocomposite.⁴¹

Fig. 11 Variation of conductance with frequency at room temperature.

It should also be noted that the electrical conductivity exhibits distinct trends depending on the pore structure of the materials. In the case of CM (microporous), conductivity increases with a rise in specific surface area and pore volume. Conversely, in NC (mesoporous), conductivity decreases as specific surface area and pore volume increase. This phenomenon arises because mesoporosity, characterized by pore sizes between 2 and 50 nm, introduces resistance to charge transfer within the NC, thereby reducing conductivity with increasing specific surface area and pore volume.

Fig. 12 illustrates the adsorption capacities of CO₂, CH₄, and C₂H₆ for the various samples at room temperature. Adsorption increases with increasing pressure. The CM sample treated at 1000 °C exhibits the highest gas adsorption capacity, attributed to its larger specific surface area and pore volume compared to the other samples. For materials treated at 650 °C, the CM demonstrates a higher adsorption capacity for CO₂ and CH₄ compared to the NC, whereas the NC shows a superior adsorption capacity for C₂H₆ relative to the CM. This is likely due to the strong interactions between C₂H₆ molecules and metallic nanoparticles on the active surface of the NC, facilitated by van der Waals forces.⁴² The adsorption capacity of NC-1000 °C decreased significantly for various gases due to the presence of MWCN in the sample, which inhibited the penetration of gases into the pores.

Fig. 12 Amount of adsorption of CO₂, CH₄ and C₂H₆ for the different samples.

The histogram of gas adsorption at 8 bar pressure is shown in Fig. 13. CO₂ demonstrates the highest adsorption capacity, whereas CH₄ shows the lowest across the various samples. The maximum adsorption capacity of CO₂ was observed in CM-1000 °C, with a value of approximately 5 mmol g⁻¹. Conversely, the minimum adsorption capacity of CH₄ was recorded in NC-1000 °C, with a value below 1 mmol g⁻¹. The higher adsorption capacity of various samples for CO₂ highlights the quadrupolar nature of the CO₂ molecule, attributed to the presence of the C=O double bond, in contrast to the nonpolar, tetrahedral structures of CH₄ and C₂H₆. The lower adsorption capacity of the samples for CH₄ and C₂H₆, compared to CO₂, can be explained by the larger kinetic diameters of C₂H₆ (0.39 nm) and CH₄ (0.38 nm) in contrast to the smaller kinetic diameter of CO₂ (0.33 nm). Another key parameter influencing adsorption is molecular mass. In this context, CO₂, which has the largest molecular mass (44.01 g mol⁻¹), demonstrates higher adsorption, whereas CH₄, with the smallest molecular mass (16.04 g mol⁻¹), exhibits the lowest adsorption capacity.

Fig. 13 Histogram of gases storage at room temperature and at 8 bars for the different samples.

The various gas adsorption results obtained with CM-1000 °C and NC-650 °C at room temperature (298 K) and at a pressure of about 8 bars surpass some of the results reported in the literature. Table 2 presents a comparison between our samples and those selected from other studies. João Pires et al. observed adsorption capacities of 1.7, 1.4 and 0.8 mmol g⁻¹ for CO₂, C₂H₆ and CH₄, respectively in porous clay heterostructures at room temperature (298 K) and at low pressure (1 bar).⁴³ Similarly, Xinran Yu et al. reported adsorption amounts of 2.6, 1.9 and 1.3 mmol g⁻¹ for CO₂, C₂H₆ and CH₄, respectively in shale kerogens at high temperature (323 K) and at high pressure (20 bar).⁴⁴

Table 2 Comparison of gas adsorption capacities between our samples and those selected from other studies

Sample	CO2 uptake (mmol g^−1)	C2H6 uptake (mmol g^−1)	CH4 uptake (mmol g^−1)
Clay heterostructures^43	1.7	1.4	0.8
Shale kerogens^44	2.6	1.9	1.3
CM-1000 °C this work	5	3.6	3.1
NC-650 °C this work	4.1	3.5	2.5

---

4. Conclusion

A pyrogallol–formaldehyde based carbon matrix and a hybrid nanocomposite formed by incorporating nickel oxide nanoparticles into the carbon matrix, were synthesized using the sol–gel method. Heat treatment of the materials was performed under an inert atmosphere at two different pyrolysis temperatures. The first, 650 °C, corresponds to a semiconducting behavior, while the second, 1000 °C, results in a metallic behavior of both the carbon matrix and the hybrid nanocomposite. The incorporation of NiO nanoparticles into the carbon matrix transformed the structure from an amorphous carbon material to a crystalline hybrid nanocomposite, featuring a phase corresponding to Multi-Walled Carbon Nanotubes (MWCN) and others corresponding to metallic nickel and nickel oxide. The texture of the samples also shifted, evolving from a microporous structure in the CM to a mesoporous texture in the hybrid NC. The gas adsorption capacity is strongly influenced by the specific surface area, pore volume and the interaction between gas molecules and the material surface. It reaches its maximum in the CM treated at 1000 °C, exhibiting a CO₂ adsorption capacity of 5 mmol g⁻¹, a C₂H₆ adsorption capacity of 3.6 mmol g⁻¹ and a CH₄ adsorption capacity of 3.1 mmol g⁻¹. These results highlight the superior performance of our materials compared to some values reported in the literature.

Data availability

All data are available on request.

Conflicts of interest

The authors declare that there is no conflict of interest.

Acknowledgements

This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-DDRSP2502).

References

1. L. Fu, Z. Ren, W. Si, Q. Ma, W. Huang, K. Liao, Z. Huang, Y. Wang, J. Li and P. Xu, J. CO2 Util., 2022, 66, 102260.
2. J. M. Belman-Flores, V. Pérez-García, J. F. Ituna-Yudonago, J. L. Rodríguez-Muñoz and J. J. Ramírez-Minguela, J. Energy South. Africa, 2014, 25(2), 2413.
3. B. T. Austin and K. Sumathy, Renewable Sustainable Energy Rev., 2011, 15(8), 4013.
4. T. K. Wood, I. Gurgan, E. T. Howley and I. H. Riedel-Kruse, Renewable Sustainable Energy Rev., 2023, 188, 113749.
5. I. Karakurt, G. Aydin and K. Aydiner, Renewable Energy, 2012, 39(1), 40.
6. N. J. Themelis and P. A. Ulloa, Renewable Energy, 2007, 32(7), 1243.
7. Z. A. Tzompa-Sosa, E. Mahieu, B. Franco, C. A. Keller, A. J. Turner and D. Helmig, J. Geophys. Res.:Atmos., 2017, 122(4), 2493.
8. M. Huff and L. D. Schmidt, J. Phys. Chem., 1993, 97, 11815.
9. R. Chauhan, R. Sartape, N. Minocha, I. Goyal and M. R. Singh, Energy Fuels, 2023, 37(17), 12589.
10. Y. M. Shulga, E. N. Kabachkov, V. I. Korepanov, I. I. Khodos, D. Y. Kovalev, A. V. Melezhik, A. G. Tkachev and G. L. Gutsev, Nanomaterials, 2021, 11, 1324.
11. Z. Geng, C. Zhang, D. Wang, X. Zhou and M. Cai, J. Energy Chem., 2015, 24(1), 1.
12. T. Ramesh, N. Rajalakshmi and K. S. Dhathathreyan, J. Energy Storage, 2015, 4, 89.
13. C. Liu, Y. Chen, C. Z. Wu, S. T. Xu and H. M. Cheng, Carbon, 2010, 48, 452.
14. P. Chen, X. Wu, J. Lin and K. L. Tan, Science, 1999, 285, 91.
15. N. A. Ogolo, O. C. Anih and M. O. Onyekonwu, Technium, 2020, 2(6), 14.
16. M. Razoolzadeh, S. Fatemi, M. Gholamhosseini and M. A. Moosaviyan, Iran. J. Chem. Chem. Eng., 2008, 3(27), 127.
17. S. Shokri, R. Mohammed, H. Abolghasemi, A. Mohebbi, H. Hashemipour, M. Marvast and S. J. Nejad, Int. J. Chem. Eng. Appl., 2010, 1(1), 63.
18. M. Delavar, A. A. Ghoreyshi, M. Jahanshi, S. Khalil and N. Nabian, Chem. Ind. Chem. Eng. Q., 2012, 18(2), 193.
19. R. T. K. Baker, Carbon, 1989, 27, 315.
20. R. S. Wagner and W. C. Ellis, Appl. Phys. Lett., 1964, 4, 89.
21. H. Dai, A. G. Rinzler, P. Nikolae, A. Thess, D. T. Colbert and R. E. Smalley, Chem. Phys. Lett., 1996, 260, 471.
22. F. H. Gojny, M. H. G. Wichmann, B. Fiedler, I. A. Kinloch, W. Bauhofer, A. H. Windle and K. Schulte, Polymer, 2006, 47, 2036.
23. C. Li, E. T. Thostenson and T. W. Chou, Appl. Phys. Lett., 2007, 91, 223114.
24. N. Ben Mansour and L. El Mir, Appl. Surf. Sci., 2014, 308, 10.
25. N. Ben Mansour and L. El Mir, J. Mater. Sci.: Mater. Electron., 2016, 27(11), 11682.
26. N. Ben Mansour and L. El Mir, Solid State Sci., 2018, 85, 38.
27. N. Ben Mansour and L. El Mir, J. Phys. Chem. Solids, 2019, 127, 1.
28. W. Djeridi, A. Ouederni, N. Ben Mansour, P. L. Llewellyn, A. Alyamani and L. El Mir, Mater. Res. Bull., 2015, 73, 130.
29. D. W. Jung, J. H. Jeong, B. C. Cha, J. B. Kim, B. S. Kong, J. K. Lee and E. S. Oh, Met. Mater. Int., 2011, 17(6), 1021.
30. L. Liu, J. Guan, W. Shi, Z. Sun and J. Zhao, J. Phys. Chem. C, 2010, 114, 13565.
31. S. Ravichandran, P. Sengodan and J. Radhakrishnan, Ceram. Int., 2023, 49(8), 12408.
32. A. Kumar, K. Kumar, P. K. Ghosh and K. L. Yadav, Ultrason. Sonochem., 2018, 41, 37.
33. H. Saeki, H. Tabata and T. Kawai, Solid State Commun., 2001, 120, 439.
34. S. Brunaner, P. H. Emmett and E. Teller, J. Am. Chem. Soc., 1938, 60, 309.
35. M. Monthioux, P. Serp, E. Flahaut, M. Razafinimanana, C. Laurent, A. Peigney, W. Bacsa and J. M. Broto, Springer Handbook of Nanotechnology, New York ( 2010) p. 47.
36. Y. Saito, T. Yoshikawa, S. Bandow, M. Tomita and T. Hayashi, Phys. Rev. B, 1993, 48(3), 1907.
37. S. T. Jackson and R. G. Nuzzo, Appl. Surf. Sci., 1995, 90(2), 195.
38. D. Yang, A. Velamakanni, L. Gu Bozoklu, S. Park, M. Stoller, R. D. Piner, S. Stankovich, I. Jung, D. A. Field, C. A. Ventrice Jr and R. S. Ruoff, Carbon, 2009, 47, 145.
39. H. J. Shin, K. K. Kim, A. Benayad, S. M. Yoon, K. P. Hyeon, I. S. Jung, M. H. Jin, H. K. Jeong, J. M. Kim, J. Y. Choi and H. Y. Lee, Adv. Funct. Mater., 2009, 19, 1987.
40. S. H. Lim, H. I. Elim, X. Y. Gao, A. T. S. Wee, W. Ji, J. Y. Lee and J. Lin, Phys. Rev. B, 2006, 73, 045402.
41. C. A. Martin, J. K. W. Sandler, A. H. Windle, M. K. Schwarz, W. Bauhofer, K. Schulte and M. S. P. Shaffer, Polymer, 2005, 46, 877.
42. J. N. Israelachvili, Intermolecular and Surface Forces, 3rd edn, Elsevier Inc., ( 2011).
43. J. Pires, M. Bestilleiro, M. Pinto and A. Gil, Sep. Purif. Technol., 2008, 61, 161.
44. X. Yu, J. Li, Z. Chen, K. Wuc, L. Zhang, S. Yang, G. Hui and M. Yang, Chem. Eng. J., 2021, 410, 127690.

---