Cluster model study of the mechanism and origins of enantio- and chemoselectivity in non-heme iron enzyme-catalyzed C–H azidation

Abstract

The mechanisms and enantio- and chemoselectivities of non-heme iron enzyme-catalyzed C–H azidation were investigated using density functional theory (DFT) calculations. A detailed active site cluster model comprising 337 atoms was constructed, incorporating essential features of the first- and second-coordination spheres and substrate-binding pockets. The catalytic cycle involves N–F bond activation, hydrogen atom transfer (HAT), and radical rebound steps. DFT calculations suggest that the observed enantioselectivity arises from steric effects between the substrate and key active-site residues. Additionally, in the non-heme Fe(N₃)F complex, the Fe–N₃ bond, which has a lower diabatic bond dissociation energy, preferentially rebounds to form the azidation product.

---

1. Introduction

Organic azides have become widely used as valuable intermediates in organic synthesis due to their versatile reactivity.^1–3 Since the preparation of phenyl azide, the first organic azide, in 1864,^4,5 numerous azidation reactions have been developed, enabling the synthesis of organic azides from various functional groups.⁶ One effective method for achieving C–H azidation is through hydrogen atom transfer (HAT) followed by azide transfer.^7–10

In 2014, Bollinger and colleagues discovered that SyrB2, a non-heme Fe^II/α-ketoglutarate (αKG)-dependent halogenase, is capable of catalyzing direct C–H azidation.¹¹ Typically, SyrB2 catalyzes the C–H chlorination of its native substrate, L-threonine, during the biosynthesis of syringomycin E.¹² Researchers discovered that replacing chloride with azide in SyrB2 enabled the formation of azidation products. When L-d₂-aminobutyrate was used as the substrate, wild-type SyrB2 produced azidation products at a low yield of approximately 1%. The A118G mutation further improved the azidation reactivity, enhancing it by around 13-fold. The reaction proceeds via a HAT/azide transfer mechanism, in which the oxoiron(IV) complex abstracts a hydrogen atom from L-d₂-aminobutyrate, generating an iron(III) intermediate. This intermediate subsequently captures the substrate radical through azide transfer, ultimately leading to the formation of the azidation product (Scheme 1a). Inspired by enzymatic catalysis, several biomimetic models have been developed to emulate the active sites of αKG-dependent halogenases and hydroxylases.^13–16 However, a mixture of R–OH and R–N₃ products was obtained when using the organocatalysts. Goldberg and co-workers synthesized the Fe^III(BNPA^Ph2O)(OH)(N₃) complex, which reacts with carbon radicals, resulting in a mixture of alcohol (30%) and azide (40%) products (Scheme 1b).¹⁷

Scheme 1 (a) Azidation by non-heme enzymes. (b) Azidation by synthetic non-heme iron complex. (c) Unnatural azidation by non-heme enzymes.

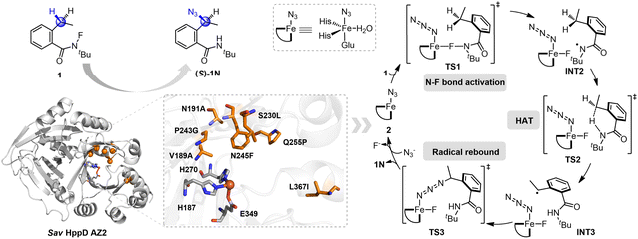
Aside from synthesizing organic catalysts, artificial enzymes constitute another class of catalysts that mimic the functions of natural enzymes.^18–21 By integrating proteins with organocatalysts, artificial enzymes have emerged as a powerful strategy for developing enzymes capable of driving new-to-nature reactions.^20–22 In 2022, Huang, Garcia-Borràs, Guo and colleagues reported an unnatural C(sp³)–H azidation reaction catalyzed by non-heme iron-dependent enzymes, utilizing sodium azide as the external azide source.²³ The wild-type Sav HppD (4-hydroxyphenyl)pyruvate dioxygenase from (Streptomyces avermitilis) achieved the azidation product with 250 total turnovers (TTN), an enantiomeric ratio (e.r.) of 63 : 37, and a chemoselectivity of 9 : 1 favoring azidation over fluorination (Scheme 1c). Through a screening process, two outstanding enzyme variants, AZ1 (Sav HppD V189A/F216A/P243A/N245Q/Q255A/L367I) and AZ2 (Sav HppD V189A/N191A/S230L/P243G/N245F/Q255P/L367I), were identified. Variant AZ1 displayed higher TTN, while AZ2 demonstrated enhanced enantioselectivity (the mutation sites involved in AZ2 are shown in Scheme 2).²³ Additionally, a simplified model—substituting two histidines with imidazole and one glutamate with acetate—was employed to study the reaction mechanism, encompassing N–F bond activation, HAT, and radical rebound steps (Scheme 2). The rate-determining step is N–F bond activation, while the enantioselectivity-determining step is the radical rebound.²³ However, the origins of enantioselectivity and chemoselectivity in this C–H azidation reaction remain unclear.

Scheme 2 Proposed mechanism for azidation reaction catalyzed by non-heme iron enzymes.

In this study, we present a computational investigation into the mechanism and, in particular, the origin of selectivity in the azidation reaction, using a large cluster model of over 300 atoms that incorporates both the first- and second-coordination spheres around the iron and substrate. The AZ2 enzyme variant was selected due to its higher enantioselectivity. In recent years, cluster models have been widely utilized in biocatalysis research.^24–28

2. Computational methods

2.1 Active site model

The cluster model of the active site used to investigate the reaction mechanism and selectivity was based on the structure of the variant AZ2 complex, which was derived from molecular dynamics (MD) simulations (see ESI† for MD simulation details). The model includes the iron, N₃⁻, N-fluoroamide substrate 1, water, and amino acid residues within 4 Å of the substrate, including the side chains of H187, A189, A191, L228, L230, G243, F245, P255, I256, Q269, H270, L293, L323, Q334, F336, F347, E349, F359, G360, K361, N363, F364, I367 (Fig. 1). The C^α atoms of amino acid residues (H187, A189, A191, L228, L230, F245, L293, L323, Q334, F336, F347, E349, I367) were replaced with hydrogen atoms and fixed to maintain side chain orientations similar to those in the protein structure. The C^β atoms of these residues included in the cluster model were also fixed during geometry optimization to preserve their positions as in the protein structure. Additionally, the main chain carbonyl or nitrogen atoms of residues (G243, I256, Q269, H270, F359, K361, N363, F364) were replaced with hydrogen atoms and fixed, while the C^α atoms of these residues were also fixed. In addition, a methyl group was added to the main chain nitrogen atom of P255.²⁹ The cluster model consists of 337 atoms in total, with an overall charge of 0.

Fig. 1 Cluster model used for DFT calculations. Atoms marked with asterisks are fixed during geometry optimization. For clarity, only the polar hydrogen atoms are depicted.

2.2 Technical details

All the calculations were carried out with Gaussian 16.³⁰ Geometry optimizations were performed with (U)B3LYP method.^31,32 We conducted an overlay analysis of the structure optimized by B3LYP method and the MD structure (see ESI Fig. S2† for details). The SDD basis set³³ with ECP was used for Fe, and the 6-31G(d) basis set^34–36 was used for other atoms. To ensure that the correct unrestricted wavefunctions were obtained, a stability test was carried out with Gaussian keyword stable = opt. Frequency analysis was conducted at the same level of theory to verify that the stationary points are minima or saddle points. Single-point energies were computed at the M06 ³⁷/def2-TZVP level³⁸ of the theory on gas phase optimized geometries in diethylether (ε = 4.3) with the application of the CPCM solvation model.^23,39 Due to the constraints applied during geometry optimization, the reported values are the computed enthalpies (ΔH).²⁷ The independent gradient model (IGM) analysis^40,41 was conducted with the aid of Multiwfn program,^42,43 and the results were visualized with VMD program.⁴⁴ The 3D diagrams of computed species were generated using PyMOL⁴⁵ and CYLview.⁴⁶

3. Results and discussion

3.1 Reaction mechanism

The energy profile for the non-heme iron-catalyzed C–H azidation of the N-fluoroamide substrate 1 is shown in Fig. 2 and 3. The open-shell singlet state ¹2 and the triplet state ³2 are 43.9 and 31.6 kcal mol⁻¹ higher in energy than the quintet state ⁵2, respectively. This suggests that the quintet state ⁵2 is the most stable state for 2 in this reaction, which is consistent with the simplified model.²³ Starting with the non-heme iron compound 2, the initial N–F activation (⁵TS1) occurs with a barrier of 8.5 kcal mol⁻¹ with respect to ⁵INT1, leading to the formation of intermediate ⁵INT2. Subsequently, the benzyl hydrogen atom is transferred to the N-centered radical. The transfer of the benzyl pro-S hydrogen atom via ⁵TS2_S requires an energy barrier of 6.1 kcal mol⁻¹ relative to ⁵INT2, leading to the formation of intermediate ⁵INT3. In contrast, the transfer of the benzyl pro-R H atom to the N-centered radical via ⁵TS2_R requires a barrier of 9.6 kcal mol⁻¹ relative to ⁵INT2, resulting in intermediate ⁵INT4.

Fig. 2 Reaction energy profiles for the N–F activation and hydrogen atom transfer (HAT) steps.

Fig. 3 The energy associated with the radical rebound steps. For clarity, only the reactive center and polar hydrogen atoms are shown. The distances are shown in Å, and the energies are shown in kcal mol⁻¹.

Through the analysis of the C2–C3–C4–C5 dihedral angle in the MD simulations, the results demonstrate that INT3 and INT4 can undergo interconversion (see ESI Fig. S3† for details). From INT3, the azide group can approach either the re- or si-face of the benzyl radical of the substrate to produce either the (R)-product or (S)-product (Fig. 3), the same applies to INT4. In both INT3 and INT4, the energy barrier for the azide group to rebound to the same side as the departing hydrogen atom is higher than for the rebound to the opposite side. Specifically, ⁵TS4_S is 2.7 kcal mol⁻¹ higher than ⁵TS3_R, and ⁵TS6_R is 3.7 kcal mol⁻¹ higher than ⁵TS5_S. Furthermore, the calculated energy barrier for the formation of the (S)-product via ⁵TS5_S is 1.9 kcal mol⁻¹ lower than for the (R)-product via ⁵TS3_R, suggesting that (S)-product formation is more favorable than (R)-product formation. This calculated enantioselectivity aligns with Huang's experimental observations.²³

3.2 Origin of enantioselectivity

The optimized structures of the azide rebound transition states (⁵TS3_R and ⁵TS5_S) are shown in Fig. 4. These two transition states differ in activation energy by 1.9 kcal mol⁻¹, favoring the (S)-product, which is consistent with experimental observations.²³ To investigate the origin of the stereoselectivity, we performed IGM,^40,41 analysis of the rebound transition state, which selectively visualizes attractive and repulsive intermolecular noncovalent interactions (blue for attractive and stabilizing, red for repulsive and destabilizing, and green for van der Waals interactions). As shown in Fig. 4, a clear steric repulsion is observed between the substrate's methyl group and L230 in the transition state ⁵TS3_R, which leads to the formation of the (R)-product. In ⁵TS3_R, the distance between a hydrogen atom on the substrate and a hydrogen atom of L230 is 2.20 Å, smaller than the sum of the van der Waals radii of hydrogen (1.2 Å). In contrast, the H⋯H distance in ⁵TS5_S is 2.56 Å. Therefore, enantioselectivity is primarily governed by steric effects in the rebound transition states, where the mutated amino acid plays S230L a critical role in determining enantioselectivity.

Fig. 4 Optimized structures and IGM analysis of the radical rebound transition state. For IGM analysis, blue, attraction; green, weak interaction; red, steric effect. Isosurface value 0.005. The distances are shown in Å, and the energies are shown in kcal mol⁻¹. For clarity, only the polar hydrogen atoms and the hydrogen atoms on the substrates are depicted.

3.3 Origin of chemoselectivity

The radical rebound step also serves as the chemoselectivity-determining step, there are three types of radical rebound pathways in INT4: two pathways involve TS5 (terminal N3 rebound) or TS7 (nitrogen N1 rebound) to generate the azidation product, while the third pathway involves TS8 (fluorine rebound) to produce the fluorine product (Fig. 5a). Both azide rebound pathways—terminal N3 rebound via ⁵TS5_S and nitrogen N1 rebound via ⁵TS7_S—are highly favorable, with energy barriers of 7.9 kcal mol⁻¹ and 14.6 kcal mol⁻¹, respectively, relative to ⁵INT4. In contrast, the fluorine rebound transition state (⁵TS8_S) requires a higher energy barrier of 15.6 kcal mol⁻¹ from ⁵INT4. Thus, azidation is more favorable than fluorination. The calculated enantioselectivity and chemoselectivity align with experimental observations, confirming that the (S)-azidation product is the major product.²³

Fig. 5 (a) Optimized transition-state structures of chemoselectivity-determining TSs. (b) The diabatic BDE values for the Fe–N₃ and Fe–F bonds of Fe(N₃)F complex. The distances are shown in Å, and the energies are shown in kcal mol⁻¹.

The diabatic bond dissociation energies (BDEs) of Fe–N₃ and Fe–F in the Fe(N₃)F complex were also calculated and are displayed in Fig. 5b. Diabatic BDEs are useful for explaining the selectivity observed in hydroxylation and halogenation reactions involving synthetic non-heme iron complexes.^9,47,48 The results show that the diabatic BDE of the Fe–F bond exceeds that of the Fe–N₃ bond by 38.9 kcal mol⁻¹, indicating that azide groups are more likely to rebound, consistent with experimental findings.²³ Additionally, the energy of ⁵TS5_S is 6.7 kcal mol⁻¹ lower than that of ⁵TS7_S. A simplified model study of the azide rebound transition state reveals that the dihedral angle of N–C1–C2–C3 in the substrate is approximately 116° (Fig. S4†). In ⁵TS7_S, where N1 rebounds to the carbon radical, the dihedral angle of N–C1–C2–C3 (the four atoms marked with green circles in Fig. 5a) is 97°. This configuration results in significant steric repulsion due to the close proximity between the substrate and the F245 residue in the enzyme environment. The distance between a hydrogen atom on the substrate's benzene ring and a hydrogen atom of F245 is 2.14 Å, which is smaller than the sum of the van der Waals radii of hydrogen (1.2 Å). In contrast, ⁵TS5_S avoids this steric clash, with a dihedral angle of N–C1–C2–C3 of 120°, and the corresponding H⋯H distance increases to 2.42 Å.

4. Conclusions

In this study, a detailed computational investigation of the C–H azidation catalyzed by a non-heme iron enzyme is presented. A comprehensive active-site model containing over 300 atoms was constructed based on MD simulations. The reaction mechanism involves initial N–F bond activation, followed by hydrogen atom transfer to N-centered radical, resulting in the formation of Fe(N₃)F complex and carbon-centered radical intermediates. The process concludes with the rebound of the azide group to form the final product. In the Fe(N₃)F complex associated with carbon-centered radical, the azide group can approach either the re- or si-face of the benzyl radical on the substrate, leading to the formation of either the (R)- or (S)-product. DFT calculations indicate that azide rebound to the opposite face of the hydrogen atom transfer is more favorable. The computed energy difference between the enantioselective azide rebound transition states, ⁵TS3_R and ⁵TS5_S, is 1.9 kcal mol⁻¹, aligning with experimental observations. IGM analysis of the azide rebound transition state reveals that enantioselectivity is primarily governed by steric interactions between the substrate and L230. Moreover, the radical rebound step is identified as the chemoselectivity-determining step in the C–H azidation reaction. Thermochemical analysis of the diabatic BDE of the Fe(N₃)F complex demonstrates that the N₃ group, having a lower diabatic BDE, preferentially rebounds to form the azidation product. These findings offer valuable insights into the mechanisms and selectivities of radical-based biocatalytic reactions, providing guidance for the development of novel biocatalytic processes.

Data availability

The data supporting this article have been included as part of the ESI.† And data for this article, including [XYZ coordinates, topology files, simulation parameters] are available at [Zenodo] at https://doi.org/10.5281/zenodo.14871340.

Author contributions

Hang Liu: calculation, data curation, and writing – original draft. Xiahe Chen: calculation, data curation, and writing – original draft – review & editing. Hongli Wu: calculation. Yuanbin She: conceptualisation, project administration. Yun-Fang Yang: conceptualisation, supervision, writing – review & editing, and funding acquisition. All authors contributed to the analysis and interpretation of the data. All authors have approved the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support by National Natural Science Foundation of China (22371256, 22138011), the Zhejiang Provincial Natural Science Foundation of China (LR25B020002), the Fundamental Research Funds for the Provincial Universities of Zhejiang (RF-C2022006) is gratefully acknowledged.

Notes and references

1. S. Bräse, C. Gil, K. Knepper and V. Zimmermann, Organic azides: an exploding diversity of a unique class of compounds, Angew. Chem., Int. Ed., 2005, 44, 5188–5240.
2. Z. Liu, Q. Zhao, Y. Gao, Y. Hou and X. Hu, Organic azides: versatile synthons in transition metal-catalyzed C(sp²)–H amination/annulation for N-heterocycle synthesis, Adv. Synth. Catal., 2021, 363, 411–424.
3. F. Gholami, F. Yousefnejad, B. Larijani and M. Mahdavi, Vinyl azides in organic synthesis: an overview, RSC Adv., 2023, 13, 990–1018.
4. P. Griess, Ueber eine neue klasse organischer verbindungen, in denen wasserstoff durch stickstoff vertreten ist, Adv. Cycloaddit., 1866, 137, 39–91.
5. D. J. R. Duarte, M. S. Miranda and J. C. G. E. da Silva, Computational study on the vinyl azide decomposition, J. Phys. Chem. A, 2014, 118, 5038–5045.
6. P. Sivaguru, Y. Ning and X. Bi, New strategies for the synthesis of aliphatic azides, Chem. Rev., 2021, 121, 4253–4307.
7. X. Huang, T. M. Bergsten and J. T. Groves, Manganese-catalyzed late-stage aliphatic C–H azidation, J. Am. Chem. Soc., 2015, 137, 5300–5303.
8. X. Huang and J. T. Groves, Taming Azide radicals for catalytic C–H azidation, ACS Catal., 2015, 6, 751–759.
9. A. Timmins, M. G. Quesne, T. Borowski and S. P. de Visser, Group transfer to an aliphatic bond: a biomimetic study inspired by nonheme iron halogenases, ACS Catal., 2018, 8, 8685–8698.
10. R. O. Torres-Ochoa, A. Leclair, Q. Wang and J. Zhu, Iron-catalysed remote C(sp³)–H azidation of O-acyl oximes and N-acyloxy imidates enabled by 1,5-hydrogen atom transfer of iminyl and imidate radicals: synthesis of γ-azido ketones and β-azido alcohols, Chem.–Eur. J., 2019, 25, 9477–9484.
11. M. L. Matthews, W.-C. Chang, A. P. Layne, L. A. Miles, C. Krebs and J. M. Bollinger, Direct nitration and azidation of aliphatic carbons by an iron-dependent halogenase, Nat. Chem. Biol., 2014, 10, 209–215.
12. F. H. Vaillancourt, J. Yin and C. T. Walsh, SyrB2 in syringomycin E biosynthesis is a nonheme Fe^II α-ketoglutarate- and O₂-dependent halogenase, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10111–10116.
13. P. C. A. Bruijnincx, G. van Koten and R. Gebbink, Mononuclear non-heme iron enzymes with the 2-His-1-carboxylate facial triad: recent developments in enzymology and modeling studies, Chem. Soc. Rev., 2008, 37, 2716–2744.
14. G. Mukherjee, J. K. Satpathy, U. K. Bagha, M. Q. E. Mubarak, C. V. Sastri and S. P. de Visser, Inspiration from nature: influence of engineered ligand scaffolds and auxiliary factors on the reactivity of biomimetic oxidants, ACS Catal., 2021, 11, 9761–9797.
15. X. Xiao, K. Xu, Z. Gao, Z. Zhu, C. Ye, B. Zhao, S. Luo, S. Ye, Y. Zhou, S. Xu, S. Zhu, H. Bao, W. Sun, X. Wang and K. Ding, Biomimetic asymmetric catalysis, Sci. China Chem., 2023, 66, 1553–1633.
16. G. Zhao, H. Dong, K. Xue, S. Lou, R. Qi, X. Zhang, Z. Cao, Q. Qin, B. Yi, H. Lei and R. Tong, Nonheme iron catalyst mimics heme-dependent haloperoxidase for efficient bromination and oxidation, Sci. Adv., 2024, 10, eadq0028.
17. V. Yadav, L. Wen, R. J. Rodriguez, M. A. Siegler and D. P. Goldberg, Nonheme iron(III) azide and iron(III) isothiocyanate complexes: radical rebound reactivity, selectivity, and catalysis, J. Am. Chem. Soc., 2022, 144, 20641–20652.
18. C. Van Stappen, Y. Deng, Y. Liu, H. Heidari, J. Wang, Y. Zhou, A. P. Ledray and Y. Lu, Designing artificial metalloenzymes by tuning of the environment beyond the primary coordination sphere, Chem. Rev., 2022, 122, 11974–12045.
19. Z. Zhou and G. Roelfes, Synergistic catalysis in an artificial enzyme by simultaneous action of two abiological catalytic sites, Nat. Catal., 2020, 3, 289–294.
20. M. Garcia-Borràs, S. B. J. Kan, R. D. Lewis, A. Tang, G. Jimenez-Osés, F. H. Arnold and K. N. Houk, Origin and control of chemoselectivity in cytochrome c catalyzed carbene transfer into Si–H and N–H bonds, J. Am. Chem. Soc., 2021, 143, 7114–7123.
21. B. Brouwer, F. Della-Felice, J. H. Illies, E. Iglesias-Moncayo, G. Roelfes and I. Drienovská, Noncanonical amino acids: bringing new-to-nature functionalities to biocatalysis, Chem. Rev., 2024, 124, 10877–10923.
22. Z. Liu and F. H. Arnold, New-to-nature chemistry from old protein machinery: carbene and nitrene transferases, Curr. Opin. Biotechnol., 2021, 69, 43–51.
23. J. Rui, Q. Zhao, A. J. Huls, J. Soler, J. C. Paris, Z. Chen, V. Reshetnikov, Y. Yang, Y. Guo, M. Garcia-Borràs and X. Huang, Directed evolution of nonheme iron enzymes to access abiological radical-relay C(sp³)–H azidation, Science, 2022, 376, 869–874.
24. F. Himo, Recent trends in quantum chemical modeling of enzymatic reactions, J. Am. Chem. Soc., 2017, 139, 6780–6786.
25. X. Sheng and F. Himo, Enzymatic pictet–spengler reaction: computational study of the mechanism and enantioselectivity of norcoclaurine synthase, J. Am. Chem. Soc., 2019, 141, 11230–11238.
26. Q. Cheng and N. J. DeYonker, QM-cluster model study of the guaiacol hydrogen atom transfer and oxygen rebound with cytochrome P450 enzyme GcoA, J. Phys. Chem. B, 2021, 125, 3296–3306.
27. T. Wang, B. Mai, Z. Zhang, Z. Bo, J. Li, P. Liu and Y. Yang, Stereoselective amino acid synthesis by photobiocatalytic oxidative coupling, Nature, 2024, 629, 98–104.
28. Y. Cao, S. Hay and S. P. de Visser, An active site Tyr residue guides the regioselectivity of lysine hydroxylation by nonheme iron lysine-4-hydroxylase enzymes through proton-coupled electron transfer, J. Am. Chem. Soc., 2024, 146, 11726–11739.
29. M. E. S. Lind and F. Himo, Theoretical study of reaction mechanism and stereoselectivity of arylmalonate decarboxylase, ACS Catal., 2014, 4, 4153–4160.
30. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford, CT, 2019.
31. C. Lee, W. Yang and R. G. Parr, Development of the colle-salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
32. A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652.
33. M. Dolg, U. Wedig, H. Stoll and H. Preuss, Energy-adjusted ab initio pseudopotentials for the first row transition elements, J. Chem. Phys., 1987, 86, 866–872.
34. R. Ditchfield, W. J. Hehre and J. A. Pople, Self-consistent molecular-orbital methods. IX. An extended gaussian-type basis for molecular-orbital studies of organic molecules, J. Chem. Phys., 1971, 54, 724–728.
35. W. J. Hehre, R. Ditchfield and J. A. Pople, Self-consistent molecular orbital methods. XII. Further extensions of gaussian-type basis sets for use in molecular orbital studies of organic molecules, J. Chem. Phys., 1972, 56, 2257–2261.
36. P. C. Hariharan and J. A. Pople, The influence of polarization functions on molecular orbital hydrogenation energies, Theor. Chim. Acta, 1973, 28, 213–222.
37. Y. Zhao and D. G. Truhlar, The m06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four m06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120, 215–241.
38. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297.
39. M. Cossi, N. Rega, G. Scalmani and V. Barone, Energies, structures, and electronic properties of molecules in solution with the C-PCM solvation model, J. Comput. Chem., 2003, 24, 669–681.
40. C. Lefebvre, G. Rubez, H. Khartabil, J.-C. Boisson, J. Contreras-García and E. Hénon, Accurately extracting the signature of intermolecular interactions present in the NCI plot of the reduced density gradient versus electron density, Phys. Chem. Chem. Phys., 2017, 19, 17928–17936.
41. T. Lu and Q. Chen, Independent gradient model based on hirshfeld partition: a new method for visual study of interactions in chemical systems, J. Comput. Chem., 2022, 43, 539–555.
42. T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592.
43. T. Lu, A comprehensive electron wavefunction analysis toolbox for chemists, multiwfn, J. Chem. Phys., 2024, 161, 082503.
44. W. Humphrey, A. Dalke and K. Schulten, VMD: visual molecular dynamics, J. Mol. Graph., 1996, 14, 33–38.
45. L. L. C. Schrödinger, Version 1.8., 2015, https://pymol.org/2/.
46. C. Y. Legault, CYLView, 1.0b, Université de Sherbrooke, 2009, https://www.cylview.org.
47. M. G. Quesne and S. P. de Visser, Regioselectivity of substrate hydroxylation versus halogenation by a nonheme iron(IV)–oxo complex: possibility of rearrangement pathways, J. Biol. Inorg. Chem., 2012, 17, 841–852.
48. M. Yang, X. Chen, X. Su, Y. She and Y. Yang, Mechanistic study of chemoselectivity for carbon radical hydroxylation versus chlorination with Fe^III(OH)(Cl) complexes, Chem.–Asian J., 2023, 18, e202201311.

---

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinates and computed energies of the calculated structures. See DOI: https://doi.org/10.1039/d5ra00632e

---