Platinum clusters Pt_n^+/0/– (n = 3–21): from triangles to remarkable tubular architectures

Abstract

This paper reports on a theoretical investigation of Pt_n^+/0/– clusters with n = 3–21 in three-charge states using density functional theory with the B3PW91 functional in conjunction with the aug-cc-pVTZ-PP and Def2-TZVP basis sets. Geometric structures of Pt_n^+/0/– in the small-to-medium size range are primarily derived from Pt₆^+/0/–; whereas Pt₁₀^+/0/–, Pt₁₄^+/0/– and Pt₁₈^+/0/– also emerge as building blocks. The sizes Pt₄, Pt₆, Pt₁₀ and Pt₁₈ emerge as magic clusters, in part in agreement with experimental mass spectrometry. Tubular Pt structures are identified at the sizes of Pt₁₂, Pt₁₈ and Pt₂₄ clusters that can be constructed by either stacking planar Pt₆ or assembling prismatic Pt₆ units. These tubular configurations are energetically favorable and present an effective pathway for the design of more complex Pt-based nanostructures. The Pt₆ triangle features six σ bonds, six conjugated π-bonds of (2c–1e) delocalization and six (6c–1e) bonds reflecting a fully SP² hybridization. The Pt₆ prism contains three (6c–1e) bonds and nine σ-bonds from (2c–1e) delocalization, spanning its edges and faces. These delocalized bonds facilitate the structural integrity and connectivity of tubular Pt₁₂, Pt₁₈ and Pt₂₄ isomers. In these tubular clusters, increased bond coordination and redistribution of electron contributions among s, p and d orbitals enhance bonding interactions and promote stabilized structural assemblies.

---

1. Introduction

Pure and doped platinum clusters as well as their integration into nanomaterials have attracted considerable attention, in part due to their extensive applicability as efficient catalysts for diverse chemical reactions.^1–4 These nanomaterials possess remarkable catalytic power, rendering them valuable across diverse fields of science and technology.⁵ They are variously utilized in, among others, fuel cells,^6,7 gas reforming,^8,9 automotive conversion,¹⁰ as well as various oxidation,^11–13 and redox^14,15 reactions. Furthermore, they hold application promise in medicine, particularly in anticarcinogenic treatments.^16–18

Nevertheless, particularly for heavy elements like the Pt atom, inherent relativistic effects can wield importance, influencing both the structure of their compounds and their chemical behavior. The notable relativistic impact of the Pt atom and its distinct metal bonding characteristics often present a significant obstacle to achieve a comprehensive understanding solely through the knowledge derived from individual Pt atoms and complexes. In this context, the understanding of platinum clusters' structures remains a big challenge due to, beside relativistic effects, the intricate interplay between spin exchange stabilization and electron correlation effects.¹⁹ The presence of a largely open d shell within these clusters gives rise to multiple electronic states that encompass a large range of spin multiplicities, thus introducing intricacy to their structural and spectroscopic attributes. Several studies were carried out to investigate the structure and magnetism of Pt clusters, but a number of contentions persist even at their small sizes.^20–28

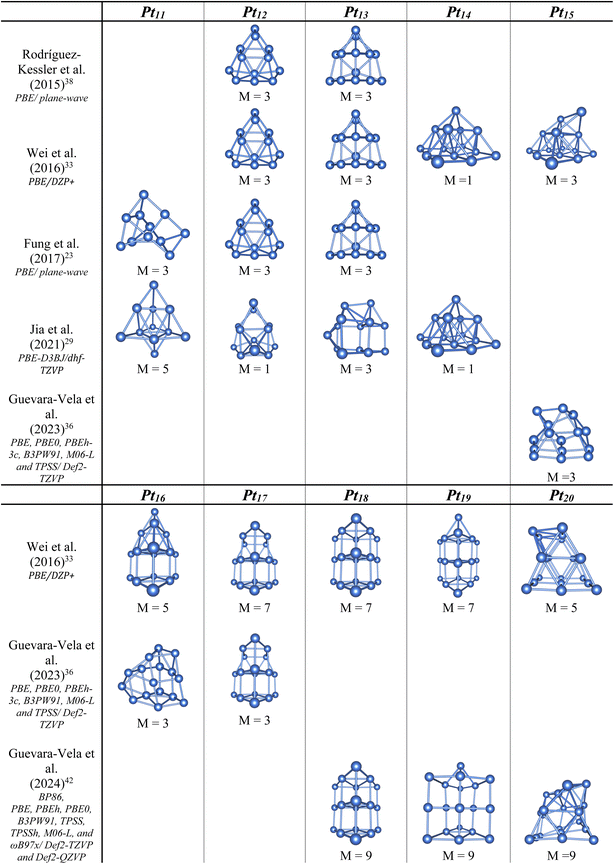
In previous studies, stable structures of Pt_n clusters were found with intriguing shapes at high spin states. It has been observed that small size Pt_n^+/0/– clusters in the negative, neutral and positive charge states typically prefer planar shapes.^27,29 In the negatively charged clusters, the Pt_n⁻ anions continue to favor planar structure up to size n = 7.²⁸ However, it becomes more complicated in the cationic and neutral counterparts. It is particularly intriguing that in a 2014 investigation by Chaves et al.,²⁴ the Pt₆⁺ cations were reported to adopt a D_3h planar triangular structure, despite the fact that three-dimensional (3D) configurations already emerge at smaller sizes n = 4 and 5.²⁷ This raises a legitimate question as to whether the planar structure is truly favored for cations at size n = 6. A similar question arises for neutral Pt_n clusters where planar structures reappear at sizes n = 8 and 9 after a shift to 3D configurations at size n = 7.²⁷ The situation becomes even more complex when considering a subsequent report from Singh et al.,²³ which found that the most stable structures for both neutral Pt₈ and Pt₉ clusters are, in fact, 3D structures.²⁶ Both studies, remarkedly, used rather low-level computational methods that lack sufficient precision. While the Chaves et al. study²⁴ employed the PBE functional with a light-tier 2 NAO basis set, the Singh et al. study²³ used both B3LYP and B3PW91 functionals in conjunction with the small LAN2DZ and LAN2MB basis sets. More recently, Rodríguez-Kessler et al. used the PBE with a plane-wave basis set³⁰ and found that the Pt₇ structure aligns with Chaves et al.’s findings, whereas the Pt₉ structure matches that of Singh et al. (cf. Scheme 1).

Scheme 1 Previously reported structures of neutral Pt_n clusters with n = 7–9.

When it comes to larger sizes, the problems become even more elusive when the number of itinerant d electrons are significantly pronounced. Apart from the stable tetrahedral structure observed across different charge states at size n = 10, the anionic Pt₁₀⁻, neutral Pt₁₀, cationic Pt₁₀⁺ and di-cationic Pt₁₀²⁺, each of these displays high magnetic moment of approximately 7,^28,29 8,^{23,25,26,29,31} 9 (ref. 29) and 10 (ref. 32) μ_B, respectively. A considerable inconsistency still appears regarding the structures and spin states of other Pt_n clusters. Previous findings reported by different groups produced varying results and no clear consensus emerges on either their preferred configurations or spin states.^{13,23,25,28,29,31}

For neutral clusters, although numerous studies have focused on the n = 10–20 size range,^{13,23,30,33–42} the spin states corresponding to their ground state configurations remain largely uncertain (cf. Scheme 2), with significant discrepancies among these studies.^33,42

Scheme 2 Previously reported structures and magnetism of neutral Pt_n with n = 11–20.

Concerning anionic Pt_n⁻ clusters, the stable Pt₆⁻ anion was identified as having a planar triangular structure in a doublet state.²⁸ However, only the triangular Pt₆⁻ structure aligns well (profile factor R_w = 1.7%) with experimental data measured from trapped ion electron diffraction (TIED), while larger anions require the inclusion of higher-energy isomers to achieve reasonable agreement with experiment.²⁸ Furthermore, beyond the Chaves et al.'s study mentioned above, there has been no other investigation into the positively charged counterparts, underscoring the need for more definitive studies in this area. A main issue is that the ground electronic states identified for the stable structures in these charge states also remain largely elusive.

In this context, to gain a better understanding of the structural growth mechanisms of Pt_n^+/0/– clusters, especially in the small to medium size range, we set out to conduct a thorough re-evaluation and expanded investigation. With such an objective, the present study aims to re-evaluate and extend by employing higher accuracy quantum chemical methods to determine low-energy structures, exploring a more comprehensive range of structural configurations and examining a larger set of sizes of Pt_n with n = 3–21, crossing the anionic, neutral and cationic charge states. This approach facilitates a detailed analysis of the preferred configurations and structural evolution of Pt_n^+/0/− clusters, offering deeper insights into the factors driving their formation across different sizes and charges.

2. Computational methods

All standard electronic structure calculations in this study are performed using the Gaussian 16 set of programs.⁴³ We employ two basis sets where the effective core potentials include relativistic effects for heavy atoms, namely the Dunning correlation consistent aug-cc-pVTZ-PP^44,45 and the Ahlrichs Def2-TZVP⁴⁶ basis sets. The B3PW91 (ref.47 and 48) is used on the basis of its previously shown effectiveness in modeling Pt_n cluster structures, offering a favorable balance between computational efficiency and accuracy compared with experimental data.^4,32,36,42 This choice of functional ensures consistency with earlier theoretical studies allowing meaningful comparisons across studies.

To identify low-energy geometric isomers, an extensive exploration of the potential energy surface of each size is conducted, involving a combination of both manual and automated structure generation methods. Initially, trial structures are constructed manually by considering previously reported structures (as discussed in Introduction) and by systematically expanding smaller clusters through the addition of atoms to vertices, edges, or faces to create larger ones. These guess structures are then optimized using the B3PW91 functional in conjunction with the small LANL2DZ basis set.⁴⁹ To further enhance structural diversity for clusters from Pt₁₀^+/0/– onward, a stochastic generation approach⁵⁰ is employed, utilizing an algorithm improved from the random kick method.⁵¹ In this process, the lowest-energy isomers within 2 eV obtained from the initial optimizations are used as seeds in both genetic algorithm and modified random kick routines. The two methods are used iteratively, feeding new structures from one into the other, until no additional unique structures are identified, thus allowing for a thorough sampling of the structural configuration.

All guess structures generated in such a way are optimized across multiple spin states using the B3PW91/LANL2DZ method. If a novel structure emerged in one spin state, it is then re-optimized under other multiplicities. For closely related structures with nearly identical energies, symmetry-constrained re-optimization is performed to confirm their point group. This systematic workflow allows a comprehensive set of stable configurations to be explored across different charge states and multiplicities.

For each size and charge state, local minima with relative energies lying within 5 eV to the lowest-energy minimum are re-optimized using the same B3PW91 but with the larger aug-cc-pVTZ-PP basis set for the sizes from n = 3–18 and the Def2-TZVP basis set for the sizes of n = 3–21. Harmonic vibrational frequency calculations at these levels are carried out to confirm equilibrium geometries and provide zero-point energy (ZPE) corrections.

Electronic properties, including natural electron configurations (NEC) and spin densities, are analyzed using the NBO 5.0 program⁵² to detail chemical bonding and charge transfer patterns. Additionally, the adaptive natural density partitioning (AdNDP)⁵³ is performed using the Multiwfn program⁵⁴ to further emphasize bonding characteristics. These methodologies allow us to obtain insights into the electronic and bonding properties of the lowest-energy isomers.

3. Results and discussion

3.1. Geometric structures

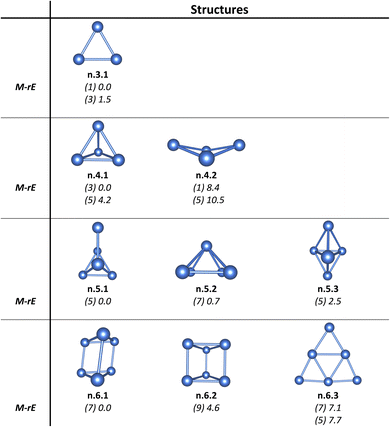
As for a convention, the notation x.y.z is used to specify the Pt_n^+/0/– isomers considered. Accordingly, x represents the charge state with c for cationic, a for anionic and n for neutral isomers. While y indicates the number of Pt atoms, z denotes the relative energy ranking, with z = 1, 2, 3, etc., corresponding to isomers of increasing relative energy. For instance, c.3.1 refers to the most stable isomer of the Pt₃⁺ cation. Relative energies given in the following sections are determined from B3PW91/Def2-TZVP + ZPE computations. Isomers having an energy difference within 2.3 kcal mol⁻¹ or 0.1 eV are considered as nearly degenerate. This threshold is smaller than the expected error margin of ±7 kcal mol⁻¹ (∼0.3 eV) commonly associated with energetic parameters obtained from DFT computations.^55,56

For the Pt_n^+/0/– clusters with sizes ranging from n = 3 to 21, the potential energy surface for each size exhibits a large number of local minima and a variety of nearly degenerate isomers across different geometric configurations and spin states. Therefore, we focus exclusively only on the low-lying isomers, highlighting those with relative energies lying within ∼12 kcal mol⁻¹ (∼0.5 eV) from the most stable configuration. The structures, spin states, and relative energies of the neutral Pt_n clusters, obtained from B3PW91/Def2-TZVP computations, are presented in Fig. 1–8. Additional details, including data across all three charge states and results from both B3PW91/Def2-TZVP and B3PW91/aug-cc-pVTZ-PP calculations, are provided in Fig. S1–S8 of the (ESI)† file.

In general, results obtained from both sets of B3PW91/Def2-TZVP and B3PW91/aug-cc-pVTZ-PP calculations show no significant differences. However, the B3PW91/aug-cc-pVTZ-PP calculations require considerably more computational time and are more challenging to converge for both SCF and geometry optimization as the system size increases. Consequently, for a heavy transition metal cluster system like Pt_n, the Def2-TZVP basis set offers a more practical and effective balance between computational cost and accuracy as compared to the augmented correlation consistent aug-cc-pVTZ-PP basis set.

n = 3 and 4. In agreement with previous findings of Chaves et al.,²⁷ while the anionic Pt₃⁻ cluster adopts a linear structure, both cationic Pt₃⁺ and neutral Pt₃ exhibit a triangular geometry. However, for Pt₄⁻ anion, the lowest-lying structure does not have a squared planar shape as reported by Chaves et al.²⁷ but rather a skewed rhombus at its ⁴A₁ ground electronic state, which is ∼3 kcal mol⁻¹ (∼0.1 eV) more stable than the planar one (cf. Fig. S1, ESI† file). In contrast to the anion, both cationic Pt₄⁺ and neutral Pt₄ adopt a tetrahedral form, stabilized at the ³A and ⁴A₁ ground electronic states, respectively (cf. Fig. 1).

Fig. 1 Structures, multiplicities (M, in bracket) and relative energies (rE, kcal mol⁻¹) of the low-lying neutral Pt_n with n = 3–6 calculated using the B3PW91/D-ef2TZVP + ZPE method.

n = 5. Low-lying structures in both anionic and neutral charges display energy degeneracy. For Pt₅⁻, this degeneracy is observed between two distinct 3D configurations, namely, an edge-added square and an edge-added skewed rhombus. The energy difference between these configurations is only ∼2 kcal mol⁻¹ which is reduced to ∼1 kcal mol⁻¹ when calculated using the aug-cc-pVTZ-PP basis set.

For neutral Pt₅, unlike the structures previously reported by both Chaves et al. and Singh et al.,^26,27 Pt₅ exhibits an energy degeneracy between an edge-added tetrahedron and a pyramid (cf. Fig. 1), with an energy difference of only 0.7 kcal mol⁻¹. Similarly to its neutral counterpart, the lowest-lying structure of cationic Pt₅⁺ is not the shape of two congruent regular tetrahedra glued together at their bases as reported previously,²⁷ but instead it adopts a pyramidal skeleton.

n = 6. The anion Pt₆⁻ exhibits a competition for the most stable structure between a 2D triangular planar configuration, as reported in previous studies,^27,28 and a 3D triangular prism configuration. For the neutral and cationic counterparts, however, a 2D triangular planar structure, contrary to earlier reports,^{25–27,29,30} is not the most stable configuration. Instead, we find a distorted 3D triangular prism structure which is more energetically favorable, being ∼7 kcal mol⁻¹ lower for the neutral and ∼23 kcal mol⁻¹ lower for the cation. Notably, both the triangular planar and triangular prism structures can serve as basic building blocks in the construction of larger clusters, thus highlighting their structural significance.

n = 7. From this size onward, the clusters no longer prefer 2D structures. The anionic Pt₇⁻, consistent with previous studies,^27,28 adopts a face-added triangular configuration. In contrast, the cationic and neutral clusters shift away from this arrangement as previously reported;^27,29,30 instead favoring the face-added triangular prism configuration (Fig. 2).

Fig. 2 Structures, multiplicities (M, in bracket) and relative energies (rE, kcal mol⁻¹) of the low-lying neutral Pt_n with n = 7–10 calculated at the B3PW91/Def2-TZVP + ZPE method.

n = 8. An energy degeneracy is observed between two structures across all three charge states considered of Pt₈ (cf. Fig. 2). The first configuration consists of two triangular prisms joined together by sharing a face,²⁸ while the second configuration is formed by adding two Pt atoms onto two different faces of a single triangular prism.²⁶

n = 9 and 10. Addition of a Pt atom to the second configuration of Pt₈^+/0/– produces Pt₉^+/0/– clusters,^26,28 which adopt a pre-tetrahedral shape. Further addition of another Pt atom to the Pt₉^+/0/− completes the formation of the well-known tetrahedral structure of Pt₁₀^+/0/– clusters,^25–28 that are stabilized at the high spin ⁸A, ⁹A₁ and ¹⁰A electronic states for anionic, neutral, and cationic charges, respectively (cf. Fig. 2 and S2†).

n = 11–13. Following this trend, the structures of Pt₁₁^+/0/–, Pt₁₂^+/0/–, and Pt₁₃^+/0/– are derived from the tetrahedral Pt₁₀^+/0/–, with Pt atoms added to various positions, leading to asymmetric configurations at these sizes. The structures and spin states of neutral Pt₁₂ and Pt₁₃ are in agreement with previous findings of Rodríguez-Kessler et al.²⁹ and Wei et al.^33,38 (cf. Fig. 3).

Fig. 3 Structures, multiplicities (M, in bracket) and relative energies (rE, kcal mol⁻¹) of the low-lying neutral Pt_n with n = 11–14 calculated at the B3PW91/Def2-TZVP + ZPE method.

n = 14. In addition to the pyramidal structure reported in previous studies,^27,30 a newly discovered structure formed by two congruent regular tetrahedrons joined at their bases competes for the global minimum. This results in an energy degeneracy between the two structures with an energy difference of <1 kcal mol⁻¹. The latter structure is essentially an elongated version of the former, achieved by replacement of the square base by a rhombus (cf. Fig. 3).

n = 15. The structures of Pt₁₅^+/0/– and Pt₁₆^+/0/– are constructed based on the pyramidal building block of Pt₁₄^+/0/–. For Pt₁₅, a newly identified structure with a triangular prism-like arrangement at a quintet state is ∼3 kcal mol⁻¹ lower in energy than the face-added pyramidal structure previously reported by Rodríguez-Kessler et al.,^35,36 thus competing for the globally stable configuration (cf. Fig. 4).

Fig. 4 Structures, multiplicities (M, in bracket) and relative energies (rE, kcal mol⁻¹) of the low-lying neutral Pt_n with n = 15–16 calculated at the B3PW91/Def2-TZVP + ZPE method. (*) denotes structures reported in ref. 36.

n = 16. A newly discovered configuration in the present work (cf. Fig. 4) is associated with a septet state, featuring two Pt atoms symmetrically added to the faces of the Pt₁₄ pyramid; this is over 20 kcal mol⁻¹ more stable than the three structures reported earlier by Guevara-Vela et al.³⁶

n = 17. The lowest-lying structures of Pt₁₇^+/0/– feature a distorted triangular prism frame with one missing vertex (Fig. S5†). In neutral form, this structure is most stable at the septet state and is ∼8 kcal mol⁻¹ more stable than the most stable structure reported by Guevara-Vela et al.³⁶ (cf. Fig. 5). Accordingly, the high spin structures appear to be favored in these sizes.

Fig. 5 Structures, multiplicities (M, in bracket), and relative energies (rE, kcal mol⁻¹) of the low-lying neutral Pt_n with n = 17–18 calculated at the B3PW91/Def2-TZVP + ZPE method. (*) denotes structures reported from ref. 36.

n = 18. The Pt₁₈^+/0/– structure is well-known for its perfect triangular prism, formed by stacking three layers of planar triangles Pt₆^+/0/– (cf. Fig. 5 and S5†). Alternatively, the Pt₁₈^+/0/– can also be conceptualized as being formed by an arrangement of six prismatic Pt₆^+/0/– units, accumulated by sharing their bases.

n = 19–21. The structures of Pt₁₉^+/0/–, Pt₂₀^+/0/– and Pt₂₁^+/0/– are derived from the stable Pt₁₈^+/0/– triangular prism. The lowest-lying structure of Pt₁₉^+/0/– is obtained by adding an Pt atom to a rectangular face of a Pt₆^+/0/– prism from Pt₁₈^+/0/– (cf. Fig. S6†). In the neutral state, this configuration is ∼5 kcal mol⁻¹ lower in energy than the triangular face-added structure reported by Guevara-Vela⁴² (cf. Fig. 6). Similarly, the lowest-lying structure of Pt₂₀^+/0/– is formed by diagonally adding a Pt atom to the rectangular face of another Pt₆^+/0/– prism of Pt₁₉^+/0/–, resulting in a configuration also ∼5 kcal mol⁻¹ lower in energy than the three structures previously reported by Guevara-Vela⁴² (cf. Fig. 7 and S7†). Finally, the Pt₂₁^+/0/– is constructed by adding another Pt atom to a rectangular face of a different Pt₆^+/0/– prism belonging to the Pt₁₉^+/0/– (cf. Fig. 8 and S8†).

Fig. 6 Structures, multiplicities (M, in bracket), and relative energies (rE, kcal mol⁻¹) of the low-lying neutral Pt₁₉ calculated at the B3PW91/Def2-TZVP + ZPE method. (*) denotes structures reported from ref. 42.

Fig. 7 Structures, multiplicities (M, in bracket), and relative energies (rE, kcal mol⁻¹) of the low-lying neutral Pt₂₀ calculated at the B3PW91/Def2-TZVP + ZPE method. (*) denotes structures reported from ref. 42.

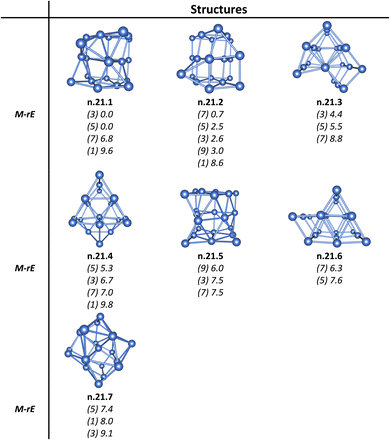Fig. 8 Structures, multiplicities (M, in bracket), and relative energies (rE, kcal mol⁻¹) of the low-lying neutral Pt₂₁ calculated at the B3PW91/Def2-TZVP + ZPE method.

Accordingly, Pt₆^+/0/–, Pt₁₀^+/0/–, Pt₁₄^+/0/– and Pt₁₈^+/0/– serve as key structural building blocks in the assembly of various Pt_n^+/0/– clusters in the medium-to-large size range. These units appear repeatedly as core frameworks that guide the growth and structural evolution of larger clusters (see Fig. 9 for neutral clusters and Fig. S9† for anionic and cationic counterparts).

Fig. 9 Structural evolution of the Pt_n clusters with n = 3–21.

3.2. Thermodynamic stability

To evaluate the thermodynamic stability of the clusters considered as well as the influence of sizes and charge states on their stability, the average binding energies (E_b), adiabatic ionization energies (IE_a), adiabatic electron affinities (EA_a) and second-order energy differences (Δ²E) are employed. In this study, the E_b, IE_a, EA_a and Δ²E values of the lowest-lying Pt_n^+/0/– (n = 3–21) structures in all three charge states are calculated using the following formulas (eqn (1)–(8)):

❖ Average binding energy (eV)

For neutral Pt_n clusters: E_b(Pt_n) = [nE(Pt) – E(Pt_n)]/n (1)

For cationic Pt_n⁺ clusters: E_b(Pt_n⁺) = [(n – 1)E(Pt) + E(Pt⁺) – E(Pt_n⁺)]/n (2)

For anionic Pt_n⁻ clusters: E_b(Pt_n⁻) = [(n – 1)E(Pt) + E(Pt⁻) – E(Pt_n⁻)]/n (3)

❖ Adiabatic ionization energy:

IE_a(Pt_n) = E(Pt_n⁺) – E(Pt_n) (4)

❖ Adiabatic electron affinity:

EA_a(Pt_n) = E(Pt_n) – E(Pt_n⁻) (5)

❖ Second-order energy differences:

For neutral Pt_n clusters: Δ²E (Pt_n) = E(Pt_n+1) + E(Pt_n−1) −2E(Pt_n) (6)

For cationic Pt_n⁺ clusters: Δ²E (Pt_n⁺) = E(Pt_n+1⁺) + E(Pt_n−1⁺) − 2E(Pt_n⁺) (7)

For anionic Pt_n⁻ clusters: Δ²E (Pt_n⁻) = E(Pt_n+1⁻) + E(Pt_n−1⁻) − 2E(Pt_n⁻) (8)

In these equations, E(Pt), E(Pt⁺) and E(Pt⁻) represent the total energies of a single platinum atom, platinum cation, and platinum anion, respectively. E(Pt_n), E(Pt_n⁺), and E(Pt_n⁻) stand for the total energies of the lowest-lying neutral, cationic and anionic Pt_n^+/0/– clusters, respectively. E(Pt_n±1), E(Pt_n±1⁺), and E(Pt_n±1⁻) stand for the total energies of the lowest-lying neutral, cationic, and anionic Pt_n±1^+/0/– clusters, respectively.

The results shown in Fig. 10 highlight the critical role of charge in determining overall stability (see Table S1 in the ESI† file for detailed data). Fig. 10A clearly reveals a stability trend across clusters studied, following this order: Pt_n⁺ > Pt_n⁻ > Pt_n. Specifically, charged species demonstrate greater stability as compared to their neutral counterparts, with cationic states being the most stable.

Fig. 10 (A): Average binding energies of Pt_n^+/0/– clusters considered. (B): Adiabatic ionization energies of Pt_n clusters, (C): Adiabatic electron affinities of Pt_n clusters and (D): Second-order energy difference of Pt_n^+/0/– clusters with n = 3–21. Values are obtained from B3PW91/Def2-TZVP + ZPE computations.

The adiabatic ionization energies IE_a and the adiabatic electron affinities EA_a illustrated in Fig. 10B and C further highlight the size- and charge-dependent trends. While the IE_a decreases with increasing cluster size, indicating that larger clusters facilitate easier electron detachment, the EA_a shows an increasing trend with respect to cluster size, signifying that electron acceptance becomes progressively more favorable as the clusters grow. The electron affinities of the sizes n = 20 and 21 amount to ∼3.4 eV making them quasi-super halogen species.

This stability's preference of charged clusters over the neutral counterpart is also shown via the dissociation energies D_e(x) in Table 1, where x represents the fragmentation channels D_e(1) to D_e(5). The formulae for these channels are outlined below:

D_e(1) = E(Pt_n−1) + E(Pt) − E(Pt_n);

D_e(2) = E(Pt_n−1) + E(Pt⁻) − E(Pt_n⁻); D_e(3) = E(Pt_n−1⁻) + E(Pt) − E(Pt_n⁻);

D_e(4) = E(Pt_n−1) + E(Pt⁺) − E(Pt_n⁺); D_e(5) = E(Pt_n−1⁺) + E(Pt) − E(Pt_n⁺)

Table 1 Dissociation energies (D_e, eV) obtained from the B3PW91/Def2-TZVP + ZPE computational method for various fragmentation channels in three charge states of Pt_n^+/0/– (n = 3–21)

n	De(1)	De(2)	De(3)	De(4)	De(5)
2	2.76	2.87	2.87	2.88	2.88
3	3.01	3.24	3.13	4.43	4.31
4	3.02	3.52	3.28	5.62	4.19
5	2.97	3.79	3.30	5.19	2.60
6	3.30	4.51	3.69	5.62	3.41
7	3.35	4.54	3.33	5.58	3.26
8	3.52	4.81	3.63	5.51	3.28
9	3.69	5.04	3.75	5.87	3.89
10	4.13	5.23	3.89	6.17	4.00
11	3.20	4.49	3.38	5.47	3.43
12	3.67	4.84	3.55	6.21	3.93
13	3.65	4.94	3.77	6.25	3.72
14	3.55	4.94	3.66	6.15	3.55
15	3.60	5.00	3.61	6.26	3.66
16	3.90	5.35	3.94	6.56	3.89
17	4.01	5.49	4.05	6.69	4.03
18	3.91	5.29	3.82	6.74	4.06
19	3.24	4.67	3.29	6.12	3.29
20	3.72	5.23	3.81	6.55	3.67
21	3.85	5.41	3.90	6.77	3.94

---

Pt_n^+/0/– clusters tend to favor a detachment of a neutral Pt atom over a charged one, indicating a preference for charge retention during dissociation. This behavior aligns with the above discussion on the greater stability of charged clusters compared to their neutral counterparts.

In addition, relative stabilities of clusters are investigated using second-order energy differences (cf. Fig. 10D). As shown in both Fig. 10A and D, the cationic Pt₄⁺ cluster exhibits unusually high stability, which is consistent with previous studies that combined experimental mass spectrometry with calculated second-order energy differences.⁵⁷ Likewise, Pt₁₀^+/– clusters were also reported as particularly stable and even chemically inert.²⁹ In the present study, in addition to the confirmed stability of Pt clusters at the sizes n = 4 and 10, clusters with enhanced stability are also identified at the sizes n = 6 and 18 across all three charge states.

Results presented in Fig. 10D indicate that clusters at sizes n = 4, 6, 10 and 18 exhibit significantly higher thermodynamic stability. Addition or removal of a Pt atom from these magic clusters tend to lead to a marked decrease in stability of the resulting derivatives. Consequently, clusters at sizes n = 5, 7, 9, 11, 15 and 19, with odd numbers of atoms, become considerably less stable (cf. Fig. 10D). Overall, cationic, neutral and anionic Pt_n^+/0/– clusters are consistently more stable at even-numbered sizes, in part in agreement with previous experiment.^29,57

3.3. Formation of multi-layer structures from the planar Pt₆ triangle

Although the platinum clusters studied here exhibit relatively uniform charge distributions and low overall polarity (cf. Tables S2–S7†), and thus lack distinct Lewis acidic sites, their metallic bonding and delocalized electronic structures remain effective in facilitating strong interactions and maintaining high electron density on the cluster surfaces.

The planar triangular structure of neutral Pt₆ at the ⁷A₁ electronic state possesses 60 valence electrons distributed in a set of 42 localized d-electrons and a set of 18 delocalized electrons. The localized electrons reside on individual atoms, with 24 paired and 18 unpaired (cf. Fig. S10†). The 18 delocalized electrons form twelve (2c–1e) bonds and six (6c–1e) bonds, collectively strengthening the interactions among the six Pt atoms and stabilizing the triangular configuration (cf. Fig. 11 and S10†).

Fig. 11 The metallic aromaticity arising from (2c–1e) and (6c–1e) bonds of the triangular Pt₆ cluster via AdNDP analysis (B3PW91/Def2-TZVP).

Specifically, the twelve (2c–1e) bonds include six σ bonds and six conjugated π bonds arising from d-orbital overlaps, which tend to strengthen the outer triangular framework. In addition to these two-center bonds, the six (6c–1e) bonds are delocalized across one S-type molecular orbital (S-MO) and two P-type molecular orbitals (P-MOs) in both alpha and beta sides. This distribution reflects a SP² hybridization which accounts for the planar triangular geometry of Pt₆, with three central Pt atoms acting as a unified center of hybridization.

Evidence of a SP² hybridization is further supported by electron populations that show a decrease of ∼0.2 e on 6S orbitals and an increase of ∼0.4 e on 6P orbitals of the three central Pt atoms (cf. Table S2 for neutral isomers and Tables S3 and S4† for charged isomers). Together, these delocalized bonds lead to an aromatic character in the Pt₆ triangle.

A structural motif can be constructed by stacking multiple layers of the planar Pt₆ triangle (cf. Scheme 3). Following such an assembling, the triangular Pt₆ units can evolve into tubular structures forming larger clusters including Pt₁₂, Pt₁₈ and Pt₂₄. These structures are energetically favorable, representing local minima on the potential energy surface. The repeated stacking along a longitudinal axis suggests a viable pathway for constructing one-dimensional, tube-like architectures. This approach offers an effective strategy for designing larger, more complex Pt-based nanostructures, facilitating the creation of Pt tubes with promising electronic and catalytic properties.

Scheme 3 Growth into tubular structures through the stacking of multiple planar Pt₆ triangles or connecting prismatic Pt₆ by sharing their base and side faces.

The larger clusters of Pt₁₂, Pt₁₈, and Pt₂₄ can also be regarded as being assembled from prismatic Pt₆ units, interconnected by sharing their base and side faces (Scheme 3). Each prismatic Pt₆ unit features twelve delocalized bonds, comprising nine (2c–1e) bonds and three (6c–1e) bonds that span across the edges and faces of the prism (cf. Fig. 12 and S11†). These bonds not only secure the six atoms within each Pt₆ unit but also facilitate robust connections between adjacent Pt₆ units, further contributing to the structural integrity and thermodynamic stability of the larger Pt₁₂, Pt₁₈, and Pt₂₄ tubular clusters.

Fig. 12 The metal aromaticity arising from (2c–1e) and (6c–1e) bonds of the prismatic Pt₆ cluster via AdNDP analysis (B3PW91/Def2-TZVP).

The coordination numbers of Pt atoms in the larger Pt₁₂, Pt₁₈, and Pt₂₄ clusters are higher than the ones in a single triangular Pt₆. Correspondingly, the Wiberg bond indices for the vertex Pt atoms in the Pt₆ layers of the larger clusters amount to ∼2.5, while those for the central Pt atoms are ∼3 (cf. Table S5–S7†). In comparison, Wiberg bond indices for the vertex and central Pt atoms in the single Pt₆ triangular cluster amount to ∼2 and ∼2.5, respectively (cf. Table S2†).

Furthermore, the density of states (DOS) maps shown in Fig. 13–15 reveal notable differences in the DOS profiles and the contributions from s, p, and d orbitals between the single Pt₆ triangular cluster and the Pt₆ layers within the Pt₁₂, Pt₁₈ and Pt₂₄ clusters, irrespective of whether the layers are positioned at the outer or middle region. Specifically, in the single Pt₆ triangle, the d-orbital contributions are more sharply defined and localized within specific regions. Conversely, in the Pt₆ layers of the larger Pt₁₂, Pt₁₈ and Pt₂₄, the d-orbital contributions exhibit a more balanced distribution. Additionally, the s and p orbital contributions are enhanced in the Pt₆ layers of the larger clusters as compared to the single Pt₆ cluster.

Fig. 13 Calculated density of states (DOS) for (A) n.6.3 isomer at ⁷A state and (B) the Pt₆ layer (highlighted in pink) within n.12.3 isomer at ³A state. Positive and negative DOS represent spin-up (alpha) and spin-down (beta) electrons, respectively.

Fig. 14 Calculated density of states (DOS) for (A) the outer Pt₆ layer (highlighted in pink) and (B) the middle Pt₆ layer (highlighted in pink) within the n.18.1 isomer at ⁷A state. Positive and negative DOS represent spin-up (alpha) and spin-down (beta) electrons, respectively.

Fig. 15 Calculated density of states (DOS) for (A) the outer Pt₆ layer (highlighted in pink) and (B) the middle Pt₆ layer (highlighted in pink) within the n.24.1 isomer at ¹³A state. Positive and negative DOS represent spin-up (alpha) and spin-down (beta) electrons, respectively.

The latter change in electron contribution is further evidenced in the natural electron configurations, which reveal a significant increase in the 6S and 6P electrons and a decrease in the 5d electrons for the Pt atoms in the larger clusters compared to those in the single Pt₆ triangular cluster (cf. Tables S2 and S5–S7†). Such an electron redistribution indicates an increased hybridization between the s, p, and d orbitals, contributing to stronger bonding interactions and greater electron delocalization.

As a result, the combined effect of increased bond coordination and altered electron contribution leads to stronger bonding and effective structural construction in larger Pt₁₂, Pt₁₈, and Pt₂₄ clusters.

4. Concluding remarks

In this theoretical study, the pure platinum clusters Pt_n^+/0/– with n = 3–21 are reinvestigated using DFT calculations with the B3PW91 functional in conjunction with both aug-cc-pVTZ-PP and Def2-TZVP basis sets. Computed findings yield several key conclusions:

❖ A comprehensive and updated depiction of the structures of cationic, neutral and anionic Pt_n^+/0/– clusters is presented, along with the identification of newly discovered lowest-lying isomers across a broad range of sizes from n = 3 to n = 21. In general, the structures of Pt_n^+/0/– clusters in the small-to-medium size range are primarily derived from key building blocks, including Pt₆^+/0/–, Pt₁₀^+/0/–, Pt₁₄^+/0/–, and Pt₁₈^+/0/– clusters.

❖ Clusters with even number of atoms tend to be thermodynamically more stable than their odd number counterparts. The sizes Pt₄, Pt₆, Pt₁₀ and Pt₁₈ emerge as magic clusters, in part in agreement with experimental mass spectrometry.

❖ Charged clusters exhibit greater stability than their neutral counterparts with respect to atom detachment, with the cationic state being the most stable.

❖ Tubular structures of Pt₁₂, Pt₁₈, and Pt₂₄ clusters are constructed by either stacking planar Pt₆ triangles or assembling prismatic Pt₆ units interconnected through shared base and side faces. These tubular configurations are energetically favorable and offer an appropriate strategy for designing complex Pt-based structures such as nanowires.

❖ Both triangular and prismatic Pt₆ clusters exhibit a metallic aromaticity characterized by effective electron delocalization, facilitating bonding interactions:

• Pt₆ triangle: this form features six σ and six conjugated π bonds arising from (2c–1e) delocalization and six (6c–1e) bonds reflecting a fully SP² hybridization and accounting for its geometry.

• Pt₆ prism: this form possesses three (6c–1e) bonds and nine σ bonds from (2c–1e) delocalization, spanning across edges and faces of the prism.

❖ In larger Pt₁₂, Pt₁₈ and Pt₂₄ tubes, the combined effect of increased bond coordination on Pt atoms and redistributed electron contribution among s, p and d orbitals tend to strengthen bonding interactions and contribute to effective structural assembly.

❖ Last but not least, concerning the methods, the Def2-TZVP basis set offers a more practical and efficient balance between computational cost and accuracy as compared to the correlation consistent aug-cc-pVTZ-PP basis set.

Data availability

The quantum chemical program Gaussian 16 has been used. Reference of this program is given in the list of references. The additional datasets supporting this article are given as part of the ESI† file which includes the Cartesian coordinates of the optimized geometries, information on the electronic structures, density of states maps of the clusters considered.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

BNNH and MTN are grateful to Van Lang University. PHMP acknowledges Ho Chi Minh City University of Technology (HCMUT), VNU-HCM for supporting this study.

References

1. T. Imaoka, Y. Akanuma, N. Haruta, S. Tsuchiya, K. Ishihara, T. Okayasu, W.-J. Chun, M. Takahashi and K. Yamamoto, Platinum clusters with precise numbers of atoms for preparative-scale catalysis, Nat. Commun., 2017, 8(1), 688.
2. P. L. Rodríguez-Kessler, A. Muñoz-Castro, P. A. Alonso-Dávila, F. Aguilera-Granja and A. R. Rodríguez-Domínguez, Structural, electronic and catalytic properties of bimetallic Pt_nAg_n (n = 1–7) clusters, J. Alloys Compd., 2020, 845, 155897.
3. P. L. Rodríguez-Kessler, A. R. Rodríguez-Domínguez, P. Alonso-Dávila, P. Navarro-Santos and A. Muñoz-Castro, Structural and electronic properties for Be-doped Pt_n (n = 1–12) clusters obtained by DFT calculations, Phys. Chem. Chem. Phys., 2022, 24(13), 7856–7861.
4. P. Ferrari, J. Vanbuel, N. M. Tam, M. T. Nguyen, S. Gewinner, W. Schöllkopf, A. Fielicke and E. Janssens, Effects of Charge Transfer on the Adsorption of CO on Small Molybdenum-Doped Platinum Clusters, Chem. A Eur. J., 2017, 23(17), 4120–4127.
5. C. Schmitt, N. Da Roit, M. Neumaier, C. B. Maliakkal, D. Wang, T. Henrich, C. Kübel, M. Kappes and S. Behrens, Continuous flow synthesis of atom-precise platinum clusters, Nanoscale Adv., 2024, 6(9), 2459–2468.
6. S. Zhu, X. Wang, E. Luo, L. Yang, Y. Chu, L. Gao, Z. Jin, C. Liu, J. Ge and W. Xing, Stabilized Pt Cluster-Based Catalysts Used as Low-Loading Cathode in Proton-Exchange Membrane Fuel Cells, ACS Energy Lett., 2020, 5(9), 3021–3028.
7. R. Wang, D. Li, S. Maurya, Y. S. Kim, Y. Wu, Y. Liu, D. Strmcnik, N. M. Markovic and V. R. Stamenkovic, Ultrafine Pt cluster and RuO₂ heterojunction anode catalysts designed for ultra-low Pt-loading anion exchange membrane fuel cells, Nanoscale Horiz., 2020, 5(2), 316–324.
8. J. Niu, Y. Wang, E. S. Liland, K. S. Regli, J. Yang, K. R. Rout, J. Luo, M. Rønning, J. Ran and D. Chen, Unraveling Enhanced Activity, Selectivity, and Coke Resistance of Pt–Ni Bimetallic Clusters in Dry Reforming, ACS Catal., 2021, 11(4), 2398–2411.
9. A. Gamal, K. Eid and A. M. Abdullah, Engineering of Pt-based nanostructures for efficient dry (CO₂) reforming: Strategy and mechanism for rich-hydrogen production, Int. J. Hydrogen Energy, 2022, 47(9), 5901–5928.
10. Y. Li, K.-B. Low, A. Sundermann, H. Zhu, L. E. Betancourt, C. Kang, S. Johnson, S. Xie and F. Liu, Understanding the nature of Pt-Rh synergy for three-way conversion catalysis, Appl. Catal., B, 2023, 334, 122821.
11. J. Kim, H. Kim, S. Kim, J.-H. Jang, H. Sohn, S. J. Hong, J. Kim, G. H. Han, S. Choe, Y.-E. Sung, S. Y. Kim, H. W. Jang, T. H. Jo, H.-K. Lim, S. J. Yoo and S. H. Ahn, Atomic Pt clusters on Au dendrite for formic acid oxidation, Chem. Eng. J., 2023, 451, 138664.
12. M. Taleblou, M. F. Camellone, S. Fabris and S. Piccinin, Oxidation of Gas-Phase and Supported Pt Nanoclusters: An Ab Initio Investigation, J. Phys. Chem. C, 2022, 126(26), 10880–10888.
13. T. Imaoka, H. Kitazawa, W.-J. Chun, S. Omura, K. Albrecht and K. Yamamoto, Magic Number Pt₁₃ and Misshapen Pt₁₂ Clusters: Which One is the Better Catalyst?, J. Am. Chem. Soc., 2013, 135(35), 13089–13095.
14. G. Shu, Y. Lin, S. Wang, S. Zhang, L. Fan, C. Wang, C. Zhou, L. Song, L. Zheng, J. Zhang, K. Ma and H. Yue, Dynamic Metal–Support Interaction-Activated Sub-Nanometer Pt Clusters on FeO_x Supports for Aqueous Phase Reforming and Hydrogenolysis of Glycerol, ACS Catal., 2023, 13(13), 8423–8436.
15. C. Especel, G. Lafaye and F. Epron, Bimetallic Catalysts for Sustainable Chemistry: Surface Redox Reactions For Tuning The Catalytic Surface Composition, ChemCatChem, 2023, 15(3), e202201478.
16. J. Depciuch, M. Stec, B. Klebowski, A. Maximenko, E. Drzymała, J. Baran and M. Parlinska-Wojtan, Size effect of platinum nanoparticles in simulated anticancer photothermal therapy, Photodiagn. Photodyn. Ther., 2020, 29, 101594.
17. A. Abed, M. Derakhshan, M. Karimi, M. Shirazinia, M. Mahjoubin-Tehran, M. Homayonfal, M. R. Hamblin, S. A. Mirzaei, H. Soleimanpour, S. Dehghani, F. F. Dehkordi and H. Mirzaei, Platinum Nanoparticles in Biomedicine: Preparation, Anti-Cancer Activity, and Drug Delivery Vehicles, Front. pharmacol., 2022, 13, 797804.
18. C. Zhang, C. Xu, X. Gao and Q. Yao, Platinum-based drugs for cancer therapy and anti-tumor strategies, Theranostics, 2022, 12(5), 2115–2132.
19. D. Dai and K. Balasubramanian, Potential energy surfaces for platinum (Pt₃)⁺ hydrogen atom and palladium (Pd₃)⁺ hydrogen atom interactions, J. Phys. Chem., 1992, 96, 3279–3282.
20. V. Kumar and Y. Kawazoe, Evolution of atomic and electronic structure of Pt clusters: Planar, layered, pyramidal, cage, cubic, and octahedral growth, Phys. Rev. B, 2008, 77(20), 205418.
21. A. Nie, J. Wu, C. Zhou, S. Yao, C. Luo, R. C. Forrey and H. Cheng, Structural evolution of subnano platinum clusters, Int. J. Quantum Chem., 2007, 107(1), 219–224.
22. L. Xiao and L. Wang, Structures of Platinum Clusters: Planar or Spherical?, J. Phys. Chem. A, 2004, 108(41), 8605–8614.
23. V. Fung and D.-e. Jiang, Exploring Structural Diversity and Fluxionality of Pt_n (n = 10–13) Clusters from First-Principles, J. Phys. Chem. C, 2017, 121(20), 10796–10802.
24. R. Li, M. Odunlami and P. Carbonnière, Low-lying Pt_n cluster structures (n = 6–10) from global optimizations based on DFT potential energy surfaces: sensitivity of the chemical ordering with the functional, Comput. Theor. Chem., 2017, 1107, 136–141.
25. A. S. Chaves, M. J. Piotrowski and J. L. F. Da Silva, Evolution of the structural, energetic, and electronic properties of the 3d, 4d, and 5d transition-metal clusters (30 TM_n systems for n = 2–15): a density functional theory investigation, Phys. Chem. Chem. Phys., 2017, 19(23), 15484–15502.
26. N. B. Singh and U. Sarkar, Structure, vibrational, and optical properties of platinum cluster: a density functional theory approach, J. Mol. Model., 2014, 20(12), 2537.
27. A. S. Chaves, G. G. Rondina, M. J. Piotrowski, P. Tereshchuk and J. L. F. Da Silva, The Role of Charge States in the Atomic Structure of Cu_n and Pt_n (n = 2–14 atoms) Clusters: A DFT Investigation, J. Phys. Chem. A, 2014, 118(45), 10813–10821.
28. D. Bumüller, A. G. Yohannes, S. Kohaut, I. Kondov, M. M. Kappes, K. Fink and D. Schooss, Structures of Small Platinum Cluster Anions Pt_n^–: Experiment and Theory, J. Phys. Chem. A, 2022, 126(22), 3502–3510.
29. Y. Jia, X. Yu, H. Zhang, L. Cheng and Z. Luo, Tetrahedral Pt₁₀^– Cluster with Unique Beta Aromaticity and Superatomic Feature in Mimicking Methane, J. Phys. Chem. Lett., 2021, 12(21), 5115–5122.
30. P. L. Rodríguez-Kessler, A. R. Rodríguez-Domínguez and A. Muñoz-Castro, Systematic cluster growth: a structure search method for transition metal clusters, Phys. Chem. Chem. Phys., 2021, 23(8), 4935–4943.
31. K. Bhattacharyya and C. Majumder, Growth pattern and bonding trends in Pt_n (n = 2–13) clusters: Theoretical investigation based on first principle calculations, Chem. Phys. Lett., 2007, 446(4), 374–379.
32. B.-N. Nguyen-Ha, C.-T. Phan Dang, L. Van Duong, M. P. Pham-Ho, M. T. Nguyen and N. M. Tam, Formation of pyramidal structures through mixing gold and platinum atoms: the Au_xPt_y²⁺ clusters with x + y = 10, RSC Adv., 2023, 13(47), 32893–32903.
33. G.-F. Wei and Z.-P. Liu, Subnano Pt Particles from a First-Principles Stochastic Surface Walking Global Search, J. Chem. Theory Comput., 2016, 12(9), 4698–4706.
34. X. Wang and D. Tian, Structures and structural evolution of Pt_n (n = 15–24) clusters with combined density functional and genetic algorithm methods, Comput. Mater. Sci., 2009, 46(1), 239–244.
35. P. L. Rodríguez-Kessler, A. Muñoz-Castro, A. R. Rodríguez-Domínguez and J. L. Cabellos, Structure effects of Pt₁₅ clusters for the oxygen reduction reaction: first-principles calculations, Phys. Chem. Chem. Phys., 2023, 25(6), 4764–4772.
36. J. M. Guevara-Vela, T. Rocha-Rinza, P. L. Rodríguez-Kessler and A. Muñoz-Castro, On the structure and electronic properties of Pt_n clusters: new most stable structures for n = 16–17, Phys. Chem. Chem. Phys., 2023, 25(42), 28835–28840.
37. S. K. Ignatov, A. G. Razuvaev, A. S. Loginova and A. E. Masunov, Global Structure Optimization of Pt Clusters Based on the Modified Empirical Potentials, Calibrated using Density Functional Theory, J. Phys. Chem. C, 2019, 123(47), 29024–29036.
38. P. L. Rodríguez-Kessler and A. R. Rodríguez-Domínguez, Size and structure effects of Pt_N (N = 12−13) clusters for the oxygen reduction reaction: first-principles calculations, J. Chem. Phys., 2015, 143(18), 184312.
39. N. Watari and S. Ohnishi, Atomic and electronic structures of Pd₁₃ and Pt₁₃ clusters, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58(3), 1665–1677.
40. E. Aprà and A. Fortunelli, Density-Functional Calculations on Platinum Nanoclusters: Pt₁₃, Pt₃₈, and Pt₅₅, J. Phys. Chem. A, 2003, 107(16), 2934–2942.
41. C. M. Chang and M. Y. Chou, Alternative Low-Symmetry Structure for 13-Atom Metal Clusters, Phys. Rev. Lett., 2004, 93(13), 133401.
42. J. M. Guevara-Vela, M. Gallegos, T. Rocha-Rinza, Á. Muñoz-Castro, P. L. R. Kessler and Á. Martín Pendás, New global minimum conformers for the Pt₁₉ and Pt₂₀ clusters: low symmetric species featuring different active sites, J. Mol. Model., 2024, 30(9), 310.
43. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda; J. Hasegawa; M. Ishida; T. Nakajima; Y. Honda; O. Kitao; H. Nakai; T. Vreven; K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers; K. N. Kudin, V. N. Staroverov, T. A. Keith; R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell; J. C. Burant, S. S. Iyengar, J. Tomasi; M. Cossi, J. M. Millam, M. Klene, C. Adamo; R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
44. D. Figgen, K. A. Peterson, M. Dolg and H. Stoll, Energy-consistent pseudopotentials and correlation consistent basis sets for the 5d elements Hf–Pt, J. Chem. Phys., 2009, 130(16), 164108.
45. T. H. Dunning and P. J. Hay, Gaussian Basis Sets for Molecular Calculations, in Methods of Electronic Structure Theory, ed. Schaefer, H. F., Springer US, Boston, MA, 1977; pp pp 1–27.
46. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305.
47. A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98(7), 5648–5652.
48. J. P. Perdew, P. Ziesche and H. Eschrig, Electronic Structure of Solids' 91, Akademie Verlag, Berlin, 1991.
49. P. J. Hay and W. R. Wadt, Ab initio effective core potentials for molecular calculations. Potentials for K to Au including the outermost core orbitals, J. Chem. Phys., 1985, 82(1), 299–310.
50. H. T. Pham, L. V. Duong, B. Q. Pham and M. T. Nguyen, The 2D-to-3D geometry hopping in small boron clusters: The charge effect, Chem. Phys. Lett., 2013, 577, 32–37.
51. M. Saunders, Stochastic search for isomers on a quantum mechanical surface, J. Comput. Chem., 2004, 25(5), 621–626.
52. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales and F. Weinhold, NBO, version 5.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2001.
53. D. Y. Zubarev and A. I. Boldyrev, Developing paradigms of chemical bonding: adaptive natural density partitioning, Phys. Chem. Chem. Phys., 2008, 10(34), 5207–5217.
54. T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33(5), 580–592.
55. E. J. Baerends, V. Branchadell and M. Sodupe, Atomic reference energies for density functional calculations, Chem. Phys. Lett., 1997, 265(3), 481–489.
56. S. Pittalis, S. Kurth and E. K. U. Gross, On the degeneracy of atomic states within exact-exchange (spin-) density functional theory, J. Chem. Phys., 2006, 125(8), 084105.
57. P. Ferrari, K. Hansen, P. Lievens and E. Janssens, Stability of small cationic platinum clusters, Phys. Chem. Chem. Phys., 2018, 20(46), 29085–29090.

---

Footnote

† Electronic supplementary information (ESI) available: (i) The structures, multiplicities and relative energies (rE, kcal mol⁻¹) of the of the low-lying Pt_n^+/0/− (n = 3–21) calculated at the B3PW91/ aug-cc-pVTZ-PP + ZPE and B3PW91/ Def2-TZVP + ZPE methods; (ii) structural evolution of anionic and cationic Pt_n^−/+ clusters (n = 3–21); (iii) AdNDP analysis showing muti-center bonds in the n.6.1 and n.6.3 isomers; (iv) detailed values of the average binding energy of Pt_n^+/0/− clusters (n = 1–21), as well as adiabatic ionization energy and adiabatic electron affinity of Pt_n clusters (n = 1–21); (v) natural electron configuration (NEC), natural charge and Wiberg bond index of low-lying isomers of Pt₆^+/0/−, Pt₁₂, Pt₁₈ and Pt₂₄, (vi) Coordinates of the lowest-lying Pt_n^+/0/− clusters (n = 3–21). See DOI: https://doi.org/10.1039/d5ra02668g

---