 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Predictive stochastic modeling of mechanically alloyed particle size and shape
Anand Prakash Dwivedi *ah,
Emad Iranmaneshb,
Katerina Sofokleousc,
Vassilis Drakonakisc,
Amin Hamed Mashhadzadehi,
Maryam Zarghami Dehaghanid,
Boris Golman
*ah,
Emad Iranmaneshb,
Katerina Sofokleousc,
Vassilis Drakonakisc,
Amin Hamed Mashhadzadehi,
Maryam Zarghami Dehaghanid,
Boris Golman e,
Christos Spitasf and
Charalabos C. Doumanidis
e,
Christos Spitasf and
Charalabos C. Doumanidis g
g
aMechanical Engineering and Robotics, Guangdong Technion Israel Institute of Technology, Shantou, China. E-mail: anand.dwivedi@gtiit.edu.cn
bSchool of Electronic and Computer Engineering, Peking University Shenzhen Graduate School, Shenzhen, China. E-mail: iranmanesh.emad@yahoo.com
cAMDM Composites, Nicosia, Cyprus. E-mail: katerina@amdmcomposites.com; vassilis@amdmcomposites.com
dInstitute for Materials and Processes, School of Engineering, University of Edinburgh, Edinburgh, Scotland, UK. E-mail: maryam.zarghamid@gmail.com
eDepartment of Chemical and Materials Engineering, Nazarbayev University, Kazakhstan. E-mail: boris.golman@nu.edu.kz
fDepartment of Mechanical Materials and Manufacturing Engineering, University of Nottingham, Ningbo, China. E-mail: christos.spitas@nottingham.edu.cn
gSenior Technical Advisor, AMDM Composites, Nicosia, Cyprus. E-mail: hdoumani@gmail.com
hDepartment of Mechanical Engineering, Indian Institute of Technology Kanpur, Kanpur, India
iDepartment of Mechanical Engineering, Nazarbayev University, Kazakhstan. E-mail: amin.hamed.m@gmail.com
First published on 18th June 2025
Abstract
Mechanical alloying of bimetallic materials by ball milling produces particulate products where, aside from internal structure, the size and shape of particles is of importance for various applications. This article introduces real-time modeling tools for the particle species demographics of size and aspect ratio, their dynamic evolution and dependence on processing conditions. Its highlight is a simple, analytical stochastic model of external particle features based on statistical formulations of impact energetics, friction and plastic deformation effects, as well as bonding and fracture transformations of the particles during the process. The model is calibrated and validated experimentally by measurements on laboratory micrographs and literature data in low- and high-energy ball milling of Al–Ni powders at different molar ratios. Its size and shape predictions offer insights to population growth of particles through mechanical alloying phenomena for material design and optimization and process observation for real-time feedback control.
1. Introduction
Mechanical alloying of metallic and composite particulate materials by ball milling (BM) has been a popular synthesis and batch fabrication method over the past few decades, because of its simplicity, flexibility and affordability.1–3 A variety of magnetic intermetallic nanostructures,4–6 reactive bimetallic and thermite nanoheaters7–9 etc. have been successfully fabricated by BM and tested in hard and super-paramagnetic, self-heated micro-soldering and other applications.10 Emphasis has been given to the study of internal structure and composition of these mechanically alloyed particles, as they directly relate to their structural, magnetic and thermal properties and function.11,12 Such investigations have shown that structural evolution of globular particle agglomerates in the original metallic powders into micro/nanoscale lamellar networks in the final composites during BM plays a key role in their diffusion, heat, electric and magnetic field transport during operation, therefore allowing for new engineered and custom-designed functionalities.10Comparatively less attention has been paid in the literature to the size and shape distributions of such intermetallic particulates and their evolution during mechanical alloying, e.g. of high-energy BM Al–Ni powders.13 Spinel Fe3O4 nanoparticle size profiles produced by low-energy BM have been shown to follow log-normal distributions,4 and ternary Al–V–Cu, Ni, Mn mechanical alloyed nanoparticles imaged by TEM were synthesized.5 The time evolution of size and composition of Sm–Co particles prepared by BM was also assessed,6 and that of Ni–Ta binary particulates was investigated.14 Reduction of particle size during planetary BM was reported,15 while for ball grinding and stirred BM the diminishing mean size and increasing standard deviation of log-Gaussian particle distributions with processing time and power was also studied experimentally.16 The shape evolution of ellipsoid particles and their planarization or spheronization upon random or flow-directed ball impacts was investigated by simulation.17 Last, qualitative insights to deformation, micro-welding and fracturing mechanisms of BM particles leading to their Gaussian-like distributions and their dynamics were illustrated.2
However, the approach in the previous bibliography has been predominantly either descriptive, i.e. towards empirical models by fitting of laboratory data, or theoretical, i.e. towards computational deterministic simulations of particle deformation. This leaves an outstanding need for predictive models of particulate size and shape distributions from their BM processing conditions, calibrated and validated through experimental results, and based on stochastic numerical formulations. Such predictive modeling is enabled by recent development of a dynamic computational simulation of the internal particulate structure evolution during BM.18 This real-time computationally efficient model simulates the mechanics of powder and cluster particle impact, contact, friction, deformation, assembly, integration and fracturing upon random collisions with the vial walls and milling balls of known energetics.19
By contrast, the novelty of this present work is in establishing a parsimonious analytical, stochastic predictive, true real-time model to estimate the external particle size and shape of bimetallic BM particulates, which to the authors' knowledge is unavailable in the literature. This provides a valuable tool for design and optimization of compacted pellet products from BM particles, such as loose Al–Ni particulates (Fig. 1a), e.g. into compressed foils clad with external Al layers (Fig. 1b). Upon local ignition of such cold-bonded compacts, the self-propagating exothermic reaction of the BM particulates10,12 depends on conductive heat and diffusive mass transfer across their joint boundary surfaces. The local area and direction of these interfaces, as well as their thermal resistance, is determined by the original size and shape of the particle components. In addition, the model also establishes a novel in-process observer of the experimentally inaccessible BM process in real time, as the basis for much-needed adaptive process control schemes, to deliver the specified size and shape of the particulate product while still processed.
 | ||
Fig. 1 SEM micrographs of Al–Ni (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) composite particulates by BM (300 rpm): (a) loose particulate external and internal structure (after 13 hours of BM)10 (b) compacted into 800 μm-thick foils sandwiched with Al overlayers (9 hours of BM).12 1) composite particulates by BM (300 rpm): (a) loose particulate external and internal structure (after 13 hours of BM)10 (b) compacted into 800 μm-thick foils sandwiched with Al overlayers (9 hours of BM).12 | ||
Therefore, this article addresses the stochastic formulation, experimental calibration and laboratory testing of such predictive models of BM particle size and shape, based on the previous numerical simulation and empirical data of the literature. Section 2 describes the laboratory BM conditions for the Al–Ni mechanical alloying experiments, as well as the fundamental underpinnings of the real-time structural model, with emphasis on the probabilistic collision, directional assembly and demographic classification of random particle components. Section 3 establishes a stochastic formulation for population growth of particulate species with various size and size distributions through friction, plastic deformation, bonding and fracture during BM. Section 4 describes model calibration and validation through literature data and laboratory results, and obtains insights from simulation results. Finally, Section 5 summarizes conclusions and further steps towards utilization of the outcomes towards property design of particulate products and BM process control.
2. Experimental and computational methods
2.1 Experimental setup
The well-studied in the literature bimetallic Al–Ni system,11,13 known for formation of ignitable, exothermically reactive particulates with internal lamellar nanostructures10,12 (Fig. 1), was selected for the experiments. Al (99.97% purity) and Ni (99.8% purity) powders (Alfa Aesar)24–26 with initial narrow size distribution at −325 mesh (40 + 4 μm) were used at molar ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 1
1 or 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, and total loading mass of 32 g.27–30 The Brunauer Emmett Teller (BET) nitrogen adsorption/desorption isotherm-based specific surface area of these mixtures was determined to 112–138 m2 g−1.31–35 Their texture analysis by selected area electron diffraction (SAED) is also available in the literature.36–39 Dry planetary ball milling (Fritsch Pulverisette) was performed in continuous low-energy (300 rpm)11 and interrupted high-energy (400 rpm, 30 min BM alternated with 10 min rest steps)13 configurations. Powders were processed with 5–20 stainless steel balls (Ø5–20 mm) and cylindrical vials (80 ml) at various ball-to-powder mass ratios (10
3, and total loading mass of 32 g.27–30 The Brunauer Emmett Teller (BET) nitrogen adsorption/desorption isotherm-based specific surface area of these mixtures was determined to 112–138 m2 g−1.31–35 Their texture analysis by selected area electron diffraction (SAED) is also available in the literature.36–39 Dry planetary ball milling (Fritsch Pulverisette) was performed in continuous low-energy (300 rpm)11 and interrupted high-energy (400 rpm, 30 min BM alternated with 10 min rest steps)13 configurations. Powders were processed with 5–20 stainless steel balls (Ø5–20 mm) and cylindrical vials (80 ml) at various ball-to-powder mass ratios (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1–21.8
1–21.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), in nitrogen or argon inert atmosphere. Electrical power to BM motor was measured by a current ammeter to determine total energy consumption during the transient upon process startup,19 and the thermal energy stored in the BM container and contents was measured by a digital bomb calorimeter (Apex) at the end of ball milling, in order to calibrate the process friction and plasticity efficiencies for the model.18
1), in nitrogen or argon inert atmosphere. Electrical power to BM motor was measured by a current ammeter to determine total energy consumption during the transient upon process startup,19 and the thermal energy stored in the BM container and contents was measured by a digital bomb calorimeter (Apex) at the end of ball milling, in order to calibrate the process friction and plasticity efficiencies for the model.18
The size and shape of the particles was analyzed by removal of small samples (∼0.5 g) from the BM load upon brief process intervals in an inert gas (nitrogen) filled glove box to avoid potential contamination and pyrophoricity effects. These samples were imaged in 2D micrographs by scanning electron microscopy (SEM, Tescan VEGA) with secondary electrons (SE) and back-scattered electrons (BSE), as well as laser profilometry (Ambios, Fig. 2).11 Pairs of images of the respective samples were processed via grayscale edge detection for blob segmentation and particle identification methods, along with quadtree raster techniques for spatial occupancy measurement of the perimeter length L and section area A of each particle, via commercial scale-independent software.20,21 These blob features were used for particle classification into species according to their size and aspect ratio as in the next Section, and their population probability density function (pdf) characteristics were identified by standard statistical sampling and fitting algorithms.
 | ||
Fig. 2 Micrographs of Al–Ni (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) particles after (a) 2 h, (b) 4 h, (c) 6 h and (d) 8 h of BM at 300 rpm11 (Top row): SEM secondary electron (SE) images; (Bottom row): Laser profilometer scans. 3) particles after (a) 2 h, (b) 4 h, (c) 6 h and (d) 8 h of BM at 300 rpm11 (Top row): SEM secondary electron (SE) images; (Bottom row): Laser profilometer scans. | ||
2.2 Computational framework
The predictive real-time model18 enables dynamic computational simulation of a representative particulate internal microstructure on a 2D section, matching the fractal structure of the planar laboratory micrographs above as it evolves during BM. The model represents monometallic domains originating from the initial powders in the BM vial by warped ellipsoids (Fig. 3), i.e. flexible primitives matching the evolving domain shapes from spheroidal powders to planarized lamellae, through parametric variation of their major axis lengths, angles and curvatures. However, despite this domain representation by 2D ellipsoids (e.g. of half-axis lengths a and b, Fig. 3), all mechanics and energetics computations are carried out on 3D solid topologies, assuming a third normal half-axis of length equal to the geometric mean of the others (i.e. ). Random assemblies of such domains are impacted by the milling balls and vial walls during BM (Fig. 4), according to impactor kinematics following experimentally assessed Maxwell–Boltzmann velocity pdfs.19 Such collisions create initial elastic Hertzian conditions at contacting surfaces of domains upon their compression, along with Coulomb friction and boundary slip. In the domain bulk, stored elastic energy determined by Castigliano strain methods is recast upon yield into plastic deformation work of work-hardening materials, leaving a balance of residual stress fields and kinetic energy restored to the BM impactors.
). Random assemblies of such domains are impacted by the milling balls and vial walls during BM (Fig. 4), according to impactor kinematics following experimentally assessed Maxwell–Boltzmann velocity pdfs.19 Such collisions create initial elastic Hertzian conditions at contacting surfaces of domains upon their compression, along with Coulomb friction and boundary slip. In the domain bulk, stored elastic energy determined by Castigliano strain methods is recast upon yield into plastic deformation work of work-hardening materials, leaving a balance of residual stress fields and kinetic energy restored to the BM impactors.
Friction and plasticity of domains dissipate mechanical energy as heat, raising local temperatures and altering material properties. When critical thresholds of dissipated specific energy per surface area are exceeded for monometallic or bimetallic contacts, micro-welded joints develop at domain boundaries, resulting in their integration and growth of the particulate. Upon subsequent collisions, when elastic tensile or shear stress fields developed at the joints exceed the energy thresholds, the micro-welds fracture separating the particulate into partial clusters. Thus, starting with the initial powders, these processes generate a diversity of particle species i (powders, clusters, particulates), each numbering ni members for a varying total particle population in the vial  at each time. The population fraction of each species is therefore p(i) = ni/N with
at each time. The population fraction of each species is therefore p(i) = ni/N with 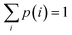 , reflecting the demographics of the BM contents. For quantitative further detail on this structural simulation, the interested reader is referred to its original account.18 The discussion below elaborates on certain of its stochastic aspects pertinent to the foundation of the size and shape model in the next Section.
, reflecting the demographics of the BM contents. For quantitative further detail on this structural simulation, the interested reader is referred to its original account.18 The discussion below elaborates on certain of its stochastic aspects pertinent to the foundation of the size and shape model in the next Section.
2.3 Probabilistic structural modeling
3. Stochastic modeling of particle size and shape
3.1 Particle size and aspect ratio
If only the particulate external size and shape are of interest rather than its internal structure, the previous full real-time model can be simplified in its inter-domain transformation aspects towards a more efficient stochastic model. The size si of any species i particle (powder, cluster or particulate) is hereafter defined from its planar area Ai (or solid volume Vi) as:
 | (1) |
For a planar ellipsoid particle with half-axes a, b (Fig. 3) and A = πab, its size is  ; this remains the same for a solid ellipsoid with third half-axis
; this remains the same for a solid ellipsoid with third half-axis 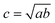 and
and  as surmised above. This definition of size s makes it invariant under transformations of the species conserving its planar mass (i.e. area A) or density (i.e. volume V), which is assumed below for surface friction shear and bulk plastic deformation. For a species i, joining from or fracturing into j components of areas Aj (or solid volumes Vj) yields, because of the assumed planar or solid mass conservation:
as surmised above. This definition of size s makes it invariant under transformations of the species conserving its planar mass (i.e. area A) or density (i.e. volume V), which is assumed below for surface friction shear and bulk plastic deformation. For a species i, joining from or fracturing into j components of areas Aj (or solid volumes Vj) yields, because of the assumed planar or solid mass conservation:
| Ai = A1 + A2… + Aj ⇒ si2 = s12 + s22… + sj2(Vi = V1 + V2… + Vj ⇒ si3 = s13 + s23… + sj3 | (2) |
i.e. component sizes add up in the power law (Pythagorean) sense23 (Fig. 6).
 | ||
| Fig. 6 (a) Particle bonding and fracture. (b) Fracture size relationship and probability distribution. | ||
The shape of species i is defined through its aspect ratio ri, from its planar perimeter Li (or solid surface Si) and size si as follows:
 | (3) |
It can be shown that always r ≥ 0, ranging between r = 0 for a circular or spherical species, and r = 1 for an ideal fractal species boundary (i.e. with Hausdorff dimension >1 for a planar curve, or >2 for a solid surface23) where L (or S) → ∞. For a planar ellipsoid with L = π(a + b), the aspect ratio is  . For a species i assembled from or separated into j components of sizes sj and perimeters Lj (or surfaces Sj) through k joints of length dk (or areas Dk), this yields (Fig. 6):
. For a species i assembled from or separated into j components of sizes sj and perimeters Lj (or surfaces Sj) through k joints of length dk (or areas Dk), this yields (Fig. 6):
 | (4) |
3.2 Ball milling energetics and assumptions
Thus, modeling of the BM process is implemented via successive stochastic transformation operations on an orthogonal raster of species i(si,ri) with population fraction p(i) = p(si,ri), initially defined by the particle statistics of the original powders in the BM vial. The dynamics of size and aspect ratio are simulated using their 2D definitions above, congruent with the planar laboratory micrographs (Fig. 1 and 2) and real-time structural model predictions. Thermomechanical steady state conditions are assumed during the BM period, and variation of composition, material properties and process conditions during transients are ignored. Energy for species transformations is provided by the milling ball and vial motion, while enthalpic effects from residual elastic fields, phase change, chemical reaction, thermoelectricity etc. are neglected. The impactor kinematics are modeled by an experimentally validated Brownian-like probability density function for kinetic energy U:19
 | (5) |
The stochastic model operates upon sequential discrete collision events, steadily timed at a period 1/f = l/Zυ as in the previous Section. For each collision, a pair of values for the impactor kinetic energy Uin and Uout before and after impact respectively are randomly chosen via the pdf of eqn (5), with Uin > Uout, along with an incidence angle ψ. The specific mechanical work of impact per planar area of processed particles is computed over their average area A from their RMS size s according to their current population pdf p(si):
 | (6) |
The energy difference ΔU = Uin − Uout is to be dissipated as heat during the collision event through friction slip and plastic deformation, occasionally causing particle bonding or fracture and generating new species as in the following paragraphs. For this purpose, a first species object i is randomly selected for each collision from the current population demographics raster p(si,ri), on which the size and shape transformations below are implemented.
3.3 Friction and plasticity effects
Surface friction at the impactor and/or anvil contacts with the particle object i, as well as at the interfaces among its internal domains, cause thermal loss of an energy amount ΔUf:18
 | (7) |
 | (8) |
Both factors ζ and ξ are dependent on the internal structure and composition, as well as material properties and loading conditions of the particle species, which are explicitly considered by the real-time simulation,18 but not by the present stochastic model. Therefore, their values are randomly selected from exponential logistic function pdfs (Fig. 7), statistically matched to the respective results of the real-time model above, while simulating the same BM process examined:
| p(ζ) = (α + 1)(α + 2)ζ(1 − ζ)α, p(ξ) = (β + 1)(β + 2)ξβ(1 − ξ) | (9) |
ΔU ← ΔU − ΔUdi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) where ΔUdi = ΔUfi + ΔUpi where ΔUdi = ΔUfi + ΔUpi
| (10) |
 | ||
| Fig. 7 Probability density functions of tribological factor ζ, plasticity factor ξ and fracture size s1/s resulting from real-time model and fitted by eqn (9), (15) and (20). | ||
Surface friction shear is assumed not to alter the particle area and perimeter length, and therefore preserves its size and aspect ratio. However bulk plastic deformation, while maintaining the density and thus the particle area Ai and size si, does alter its perimeter Li and shape ri. For an ellipsoid of fixed area Ai (Fig. 8), strain along its half-axis lengths a, b upon deformation yields:
 | (11) |
 | (12) |
 | (13) |
The sign of deformation ε (extension or compression) of the major axes in eqn (11)–(13) depends on the incidence angle ψ of the impact load (Fig. 8) exceeding a critical value:
 | (14) |
i.e., ε > 0 for ψ in (−ψc, ψc) and ε < 0 for ψ in (−π/2, −ψc) or in (ψc, π/2). It is noteworthy here that for uniformly random incidence ψ collisions and oblate objects (ri > 0, e.g. a > b in Fig. 8), ψc > π/4 and the first angle range is wider than the second. This condition yields a higher probability for further planarization of such particles (i.e., Δri > 0), with a lower probability for their spheronization (Δri < 0), thus inducing quicker planarization for more oblate objects (higher r). This theoretical result is in agreement with and explains statistical data from prior computer simulations.17
3.4 Bonding and fracture dynamics
Bonding transformations are applied to particle pairs i and j joined into a single particle, while multi-particle bonding is implemented by sequentially joining of the outcome to a third particle k etc. Thus, along with the already selected particle i, a second particle j is randomly chosen from the current population raster according to probability p(j) = p(sj,rj). To be bonded, the two particles need to be located with touching boundaries. The probability pb for such bonding of particles i and j is proportional to the perimeter length of each particle with a normalizing contact factor γ, and thus follows a logistic parabola function of their respective sizes (Fig. 7), i.e.:
 | (15) |
Once in touch and upon collision of the impactor, initial elastic impact loading of the particles creates compressive linear boundary contact along their interface of length dij (Fig. 4 and 6), given by Hertzian theory.18 When in addition the dissipated specific energy per contact length Δud exceeds a critical value for bonding, then a micro-welded joint forms along the contacting boundaries:
 | (16) |
| pu(Δud) = [1 + e−k(Δud−u)]−1(≈0 for Δud < u, 0.5 for Δud = u, 1 for Δud > u) | (17) |
The size s and aspect ratio r of the bonded new particle species are according to eqn (2) and (4) (Fig. 6):
 | (18) |
Therefore the probability for a new species (s,r) to be generated out of all possible combinations of bonded particles i and j with suitable sizes and shapes as above is:
 | (19) |
Fracture transformations of particles by abrasion, compression and impact fatigue1,2 also take place by their separation into two new species i and j at a time, while splitting into multiple particles is implemented via subsequent dichotomies of each species. The probability for cracking of a particle (s,r) along its previous surface boundary joints and/or its internal domain thickness is proportional to the perimeter length and size of the species, with a normalizing parting factor δ. Moreover, the probability pc for such a fracture to generate two species (si,ri) and (sj,rj) conforming to the previous size and aspect ratio constraints (eqn (18) and Fig. 6) follows a logistic function of the areas Ai, Aj of the two parts (Fig. 6b), such that:
 | (20) |
Therefore upon each collision, the stochastic model performs the species transformations above, updates the population demographics raster p(s,r), and reduces the available energy ΔU accordingly (eqn (10)). While ΔU > 0 the calculation repeats more species transformation steps as in paragraphs 3.3 and 3.4, until ΔU is depleted. At this time the model proceeds with the next collision by repeating the energetic computations from paragraph 3.2, until the conclusion of the BM processing period.
4. Results and discussion
4.1 Model calibration and ball milling tests
As described in Section 2, BM experimentation was employed to test the real-time structural model and the statistical size and shape formulation of the particles for a trial case of Al–Ni powder processing at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio and at 300 rpm. The laboratory measurements of transient power and thermal steady state were initially used to calibrate the real-time model effective friction and plastic yield parameters mentioned previously,18 and the structural simulation was run to emulate the BM process computationally. The resulting statistics for the pdfs p(ζ) of the tribological factor ζ and p(ξ) of the plasticity factor ξ (eqn (9)), as well as the bonding pb(i,j) (eqn (15)) and fracture pc(i,j) (eqn (20)) occurrence pdfs between species i and j, which are inaccessible experimentally in real time, were recorded during simulation. These were used next to calibrate the values of the friction α = 2.1 and plasticity β = 1.8 exponents, along with the contact γ = 1.82 10−4 μm2 and parting δ = 8.1 10−4 μm−2 factors, by fitting the respective logistic functions of the stochastic model to the statistical data of the simulation (Fig. 7). The physical parameters of the BM materials, i.e. mass m = 4.14 g, elastic modulus E = 120 GPa, yield stress σ = 78.7 MPa and bonding/fracture threshold u = 6.4 10−6 J μm−1 were calculated via the molar law of mixtures.18
1 molar ratio and at 300 rpm. The laboratory measurements of transient power and thermal steady state were initially used to calibrate the real-time model effective friction and plastic yield parameters mentioned previously,18 and the structural simulation was run to emulate the BM process computationally. The resulting statistics for the pdfs p(ζ) of the tribological factor ζ and p(ξ) of the plasticity factor ξ (eqn (9)), as well as the bonding pb(i,j) (eqn (15)) and fracture pc(i,j) (eqn (20)) occurrence pdfs between species i and j, which are inaccessible experimentally in real time, were recorded during simulation. These were used next to calibrate the values of the friction α = 2.1 and plasticity β = 1.8 exponents, along with the contact γ = 1.82 10−4 μm2 and parting δ = 8.1 10−4 μm−2 factors, by fitting the respective logistic functions of the stochastic model to the statistical data of the simulation (Fig. 7). The physical parameters of the BM materials, i.e. mass m = 4.14 g, elastic modulus E = 120 GPa, yield stress σ = 78.7 MPa and bonding/fracture threshold u = 6.4 10−6 J μm−1 were calculated via the molar law of mixtures.18
The stochastic model results for this trial case are comprehensively illustrated in Fig. 9, in terms of the species population fraction pdf p distribution for the range of BM times t and particle sizes s (Fig. 9a) or aspect ratios r (Fig. 9b). Fig. 9c and d compare the distribution p of particle size s and aspect ratio r respectively for the laboratory measurements, real-time model simulations and stochastic model results, at various BM time sections t (0, 4, 8, 10 and 12 h). Classification of particle species in the experimental micrographs is performed on an orthogonal size-shape raster of elements measuring Δs = 10 μm, Δr = 0.1, while for the real-time model the tessellation resolution is Δs = 2 μm, Δr = 0.02 and for the stochastic formulation is Δs = 1 μm, Δr = 0.01. Results are recorded every Δt = 1 h of BM time over a range of several hours. Execution of the structural simulation on standard desktop computer hardware keeps up with laboratory BM rates up to ∼10 h, after which it falls behind process speeds due to increasing complexity of the representative particulate structure. The stochastic model runs steadily faster than actual BM processing by a factor of ∼8–15 depending on the size range. Matching of the experimental measurements by the simulation predictions and the size and shape estimates confirms calibration of the real-time model and the stochastic formulation for the specific BM processing conditions.
4.2 Validation and results analysis
Validation of the size and shape predictions of both models was subsequently carried out using literature data for BM at different revolution speeds and powder molar ratios. In these comparisons the structural model parameters were adjusted through a simple testing procedure,18 while the logistic exponents and factors of the stochastic model were fitted to the computational results. For BM at 400 rpm and Al–Ni molar ratio maintained at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, for which particle SEM micrographs are reported (Fan et al.13), Fig. 10a and b illustrate the population fraction profiles p of size s and shape r of experimental data, real-time simulations and stochastic model predictions with parameter values α = 2.17, β = 1.72, γ = 3.1 10−4 μm2 and δ = 10.2 10−4 μm−2. Similarly, for BM speed maintained at 300 rpm and Al–Ni powder ratio changed to 1
1, for which particle SEM micrographs are reported (Fan et al.13), Fig. 10a and b illustrate the population fraction profiles p of size s and shape r of experimental data, real-time simulations and stochastic model predictions with parameter values α = 2.17, β = 1.72, γ = 3.1 10−4 μm2 and δ = 10.2 10−4 μm−2. Similarly, for BM speed maintained at 300 rpm and Al–Ni powder ratio changed to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (Hadjiafxenti et al.,11 Fig. 2), Fig. 11a and b show the demographics of size and shape of micrograph measurements, real-time and stochastic model estimates with α = 2.05, β = 1.86, γ = 1.2 10−4 μm2 and δ = 6.3 10−4 μm−2. In both cases, comparison of the experimental with computational results attests to the validity of the two models, with some parameter adjustment of statistical factors needed for the stochastic formulation.
3 (Hadjiafxenti et al.,11 Fig. 2), Fig. 11a and b show the demographics of size and shape of micrograph measurements, real-time and stochastic model estimates with α = 2.05, β = 1.86, γ = 1.2 10−4 μm2 and δ = 6.3 10−4 μm−2. In both cases, comparison of the experimental with computational results attests to the validity of the two models, with some parameter adjustment of statistical factors needed for the stochastic formulation.
 | ||
Fig. 10 Population fraction pdfs p for validation BM tests using Fan et al.13 (Al–Ni 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 400 rpm) (a) literature data, RTM simulations and stochastic results of size s for various times t (b) literature data, RTM simulations and stochastic results of aspect ratio r for various times t. 1, 400 rpm) (a) literature data, RTM simulations and stochastic results of size s for various times t (b) literature data, RTM simulations and stochastic results of aspect ratio r for various times t. | ||
 | ||
Fig. 11 Population fraction pdfs p for BM tests using Hadjiafxenti et al.11 (Al–Ni 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 300 rpm) (a) literature data, RTM simulations and stochastic results of size s for various times t (b) literature data, RTM simulations and stochastic results of aspect ratio r for various times t. 3, 300 rpm) (a) literature data, RTM simulations and stochastic results of size s for various times t (b) literature data, RTM simulations and stochastic results of aspect ratio r for various times t. | ||
Finally, for all three BM test conditions above i.e. Fan's13 (Fig. 10), Hadjiafxenti11 (Fig. 11) and laboratory (Fig. 9) results, Fig. 12a and b summarize the time variation of the statistical metrics for particle size and shape, i.e. the mean value, standard deviation and most probable size and aspect ratio, as derived by the validated stochastic model. As it appears in Fig. 9c, 10a and 11a, in these BM tests and at a certain time snapshot the particle size distribution exhibits a log-normal shaped profile, consistent with previous observations,4 and starting with a Gaussian-like initial pdf of the powders (Figs. 9c and 11a).16 Similarly in Figs. 9d, 10b and 11b, the respective aspect ratio demonstrates a hyperbolic-normal distribution, with highest likelihood for spheroidal shaped particles (most probable r* → 0).17
 | ||
| Fig. 12 Time variation of particle size and shape in Fan,13 Hadjiafxenti11 and lab BM tests (a) mean s, standard deviation sd and most probable value s* of size s (b) mean r and standard deviation rd of aspect ratio r. | ||
After the beginning of the process and in the first few hours, the size profiles p(s) initially broaden drastically, with their mean value, standard deviation and most probable s all increasing rapidly with time (Fig. 12a), confirming previous arguments.2 This is due to the growing friction and plastic deformation effects, raising the BM temperature and softening the particle materials, with bonding rates prevailing over fracture events, thus generating larger and more intricately shaped particles. This similarly leads the aspect ratio distributions p(r) to initially spread out quickly (Fig. 12b), with the exception of high-energy BM,13 where the original rougher powder particles tend to coagulate into spheronized bonded particulate agglomerates at the early process stages.17 As time progresses, successive impactor collisions lead to work-hardening of the BM materials, in agreement with prior accounts,2 along with formation of bimetallic solid solutions by progressing diffusion at interface contacts and joints, causing growing fracture rates to gradually balance bonding events. This results in progressive narrowing of the size pdfs p(s) in Fig. 9c, 10a, 11a over longer BM periods, with their statistical measures s, sd and s* generally decreasing with time (Fig. 12a) in accordance with previous results.15,16 The exception here is in standard deviation of size at the calibration tests, increasing apparently because of a persistent population of larger welded and hardened particles (Fig. 9c), similar to ref. 4. Oppositely to size effects, fracture of cracking particulates creates rough-shaped particles with their characteristics r and rd increasing slowly (Fig. 12b), reflecting gradual broadening of the shape p(r) profiles in Figs. 9d, 10b and 11b.
As for varying BM process conditions, an increase of the low-energy rotation speed from 300 to 400 rpm high-energy BM,13 appears to significantly enhance the friction and plastic deformation effects, along with respective parameters in calibration of the real-time model. In the stochastic formulation this is reflected in slightly varied exponents α and β, both shifting the weight of logistic distributions in Fig. 7 to lower tribological and plasticity factors ζ and ξ (eqn (9)), thus increasing heat dissipation (eqn (7) and (8)), as previously observed.15,16 At the same time drastically higher joining contact γ and larger parting δ factors indicate higher bonding and fracture rates with increased revolution speed. On the contrary, a modified Al–Ni ratio from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1
1 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3,11 i.e., less Al and more Ni content, reduces friction slip and plastic yield effects, changing logistic exponents α and β in the opposite direction, i.e., towards lower heat dissipation. Finally, the reduced bonding rates due to the lower Al content, and fracture proclivity because of higher Ni concentration, is also reflected in the diminishing respective γ and δ factors in the stochastic model.
3,11 i.e., less Al and more Ni content, reduces friction slip and plastic yield effects, changing logistic exponents α and β in the opposite direction, i.e., towards lower heat dissipation. Finally, the reduced bonding rates due to the lower Al content, and fracture proclivity because of higher Ni concentration, is also reflected in the diminishing respective γ and δ factors in the stochastic model.
4.3 Comparative evaluation
Therefore, the previous account has introduced two computational modeling tools for studying bimetallic particle species demographics, their population evolution and dependence on the BM process conditions: the first model is a full structural simulation of the internal domain microstructure in a representative particulate, with probabilistic representations of impactor collisions, particle assembly and amplification of species; the second model is a key improvement over the numerical18,19 and experimental literature40–42 as it provides a simpler stochastic formulation of particle external size and shape only, with impactor energetics, friction and plasticity effects. along with bonding and fracture transformations of species, rendered by proper probability distribution functions. The full simulation is multi-physics based, enables prediction of both internal and external particulate structure, and is experimentally calibrated via two physically meaningful parameters. However, it yields more noisy estimates of particle size and shape, and is more computationally demanding, maintaining real-time execution capability only up to ∼10 BM hours. The stochastic model, on the other hand, has higher computation efficiency and yields smoother profiles of particle populations, running 8–15 times faster compared to the BM numerical simulation or experiments, and therefore enabling a true real-time in-process model. However, it is based on statistical formulations of the BM phenomena, and relies on calibration of four logistical parameters on the basis of experimentally unmeasurable transformation rate data, provided by and thus requiring access to the full simulation model.5. Conclusion and applications
In summary, two complementary models were implemented, calibrated and validated in low- and high-energy BM of Al–Ni powders at different molar ratios, through a laboratory setting via SEM micrograph image processing, along with related bibliographic data. Their results offer insights to the role of friction, plastic deformation as well as joining and cracking mechanisms, in the particle size and shape distributions, their dynamics and reliance on material and process parameters. Since such attributes are of importance to operational performance of particle products, but are also difficult or impossible to observe non-invasively and non-destructively in-process during BM, the highlighted predictive stochastic model offers new off-line material design and optimization capabilities for a variety of applications.Future research should explore integrating machine learning algorithms with the stochastic framework to enhance predictive accuracy across diverse material systems and processing conditions. Additionally, experimental validation through closed-loop ball milling trials – using the model's real-time predictions for adaptive process control – could decisively bridge the gap between computational modeling and industrial-scale implementation.
At the same time and given its real-time implementation potential, the model provides in-process observer tools for surrogate feedback control of particle size and shape during BM fabrication.
Data availability
The data supporting this article have been included in the main manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported in part by a GTIIT startup fund.References
- C. C. Koch, Materials Synthesis by Mechanical Alloying, Annu. Rev. Mater. Sci., 1989, 19, 121–143 CrossRef CAS.
- C. Suryanarayana, Mechanical Alloying and Milling, Prog. Mater. Sci., 2001, 46, 1–184 CrossRef CAS.
- K. V. Nagesha, M. Rajanish and D. Shivappa, A Review on Mechanical Alloying, Int. J. Eng. Res. Appl., 2013, 3(3), 921–924 Search PubMed.
- G. F. Goya, Handling the Particle Size and Distribution of Fe3O4 Nanoparticles Through Ball Milling, Solid State Commun., 2004, 130, 783–787 CrossRef CAS.
- K. Y. Chang, K. B. Moon and K. S. Lee, A Study on the Microstructural Evolution of Al-25 At. pct V-12.5 At. pct M (M = Cu, Ni, Mn) Powders by Planetary Ball Milling, Metall. Mater. Trans., 2004, 35A, 1853–1860 CrossRef CAS.
- N. Poudyal, C. B. Rong and J. P. Liu, Effects of Particle Size and Composition on Coercivity of Sm-Co Nanoparticles Prepared by Surfactant-Assisted Ball Milling, J. Appl. Phys., 2010, 107, 09A703 CrossRef.
- K. Morsi, Review: Reaction Synthesis Processing of Al-Ni Intermetallic Materials, Natl. Sci & Eng. A, 2001, 299(1–2), 1–15 Search PubMed.
- A. S. Rogachev, D. O. Moskovskikh, A. A. Nepapushev, T. A. Sviridova, S. G. Vadchenko, S. A. Rogachev and A. S. Mukasyan, Experimental Investigation of Milling Regimes in Planetary Ball Mill and Their Influence on Structure and Reactivity of Gasless Powder Exothermic Mixtures, Powder Technol., 2015, 274, 44–52 CrossRef CAS.
- C. Rebholz, I. E. Gunduz, T. Ando and C. C. Doumanidis, Miniature Thermal Matches: From Nanoheaters to Reactive Fractals, Mater. Res. Express, 2015, 2, 045009 CrossRef.
- Z. Gu, Q. Cui, J. Chen, J. Buckley, T. Ando, D. Erdeniz, P. Wong, A. Hadjiafxenti, P. Epameinonda, I. E. Gunduz, C. Rebholz and C. C. Doumanidis, Fabrication, Characterization and Applications of Novel Nanoheater Structures, Surf. Coating. Technol., 2013, 215, 493–502 CrossRef CAS.
- A. Hadjiafxenti, I. E. Gunduz, T. Kyratsi, C. C. Doumanidis and C. Rebholz, Exothermic Reaction Characteristics of Continuously Ball-Milled Al/Ni Powder Compacts, Vacuum, 2013, 96, 73–78 CrossRef CAS.
- I. E. Gunduz, A. Kyriakou, N. Vlachos, T. Kyratsi, C. C. Douamnidis, S. Son and C. Rebholz, Spark Ignitable Ni–Al Ball-Milled Powders for Bonding Applications, Surf. Coat. Technol., 2014, 260, 396–400 CrossRef CAS.
- G. Fan, L. Geng, Y. Feng, X. Cui and X. Yan, Solid State Reaction Mechanism and Microstructure Evolution of Al-Ni Powders During High Energy Ball Milling Revisited by TEM, Microsc. Microanal., 2015, 21, 953–960 CrossRef CAS PubMed.
- P. Y. Lee, J. L. Yang and H. M. Lin, Amorphization behavior in Mechanically Alloyed Ni-Ta Powders, J. Mater. Sci., 1998, 33, 235–239 CrossRef CAS.
- H. Mio, J. Kano and F. Saito, Scale-Up Method of Planetary Ball Mill, Chem. Eng. Sci., 2004, 59, 5909–5916 CrossRef CAS.
- M. Gao and E. Forssberg, Prediction of Product Size Distributions for a Stirred Ball Mill, Powder Technol., 1995, 84, 101–106 CrossRef CAS.
- I. C. Sinka, A Model for the Deformation of an Ellipsoid Subject to a Large Number of Successive Impacts with Special Reference to Spheronization, Powder Tech., 2015, 270, 592–598 CrossRef CAS.
- M. Aureli, C. C. Doumanidis, I. E. Gunduz, A. G. Hussien, Y. Liao, C. Rebholz and C. C. Doumanidis, Mechanics and Energetics Modeling of Ball-Milled Metal Foil and Particle Structures, Acta Mater., 2016, 123, 305–316 CrossRef.
- C. C. Doumanidis, H. A. Al Kaabi, A. S. M. Alzaabi, I. E. Gunduz, C. Rebholz and C. C. Doumanidis, Brownian-like Kinematics of Ball Milling for Particulate Structural Modeling, Powder Technol., 2016, 301, 1077–1084 CrossRef CAS.
- L. Bretzner and T. Lindeberg, Feature Tracking with Automatic Selection of Spatial Scales, Comput. Vis. Image Understand., 1998, 71(3), 385392 Search PubMed.
- R. C. Gonzalez, R. E. Woods and L. Edins, “Digital Image Processing Using MATLAB®”, Gatesmark Publishing, 2nd edn, 2009 Search PubMed.
- M. de Berg, M. van Kreveld, M. Overmars and O. Schwrazkopf, “Computational Geometry”, Springer Verlag, 2nd edn, 2000 Search PubMed.
- M. Schroeder, “Fractals, Chaos, Power Laws”, Dover Publications, Mineola, NY, 1991 Search PubMed.
- A. K. Yedluri and H. J. Kim, Wearable super-high specific performance supercapacitors using a honeycomb with folded silk-like composite of NiCo2O4 nanoplates decorated with NiMoO4 honeycombs on nickel foam, Dalton Trans., 2018, 47, 15545 RSC.
- S. A. Hira, S. Nagappan, D. Annas, Y. A. Kumar and K. H. Park, NO2-functionalized metal–organic framework incorporating bimetallic alloy nanoparticles as a sensor for efficient electrochemical detection of dopamine, Electrochem. Commun., 2021, 125, 107012 CrossRef CAS.
- Y. A. Kumar and H. J. Kim, Preparation and electrochemical performance of NiCo2O4@NiCo2O4 composite nanoplates for high performance supercapacitor applications, New J. Chem., 2018, 42, 19971–19978 RSC.
- Y. A. Kumar and H. J. Kim, Effect of Time on a Hierarchical Corn Skeleton-Like Composite of CoO@ZnO as Capacitive Electrode Material for High Specific Performance Supercapacitors, Energies, 2018, 11(12), 3285 CrossRef CAS.
- Y. Duan, Y. Huo, Y. Qi, L. Li, Q. Wu, C. Wang and Z. Su, Uniform NiCo2O4/NiFe2O4 hollow nanospheres with excellent properties for Li-ion batteries and supercapacitors, J. Alloys Compd., 2021, 767, 223–231 CrossRef.
- Y. A. Kumar and H. J. Kim, Enhanced electrochemical performance of nanoplate nickel cobaltite (NiCo2O4) supercapacitor applications, RSC Adv., 2019, 9, 1115–1122 RSC.
- T. Anitha, A. E. Reddy, Y. A. Kumar, Y. R. Cho and H. J. Kim, Correction: One-step synthesis and electrochemical performance of a PbMoO4/CdMoO4 composite as an electrode material for high-performance supercapacitor applications, Dalton Trans., 2019, 48, 10652–10660 RSC.
- Y. A. Kumar, K. D. Kumar and H. J. Kim, Reagents assisted ZnCo2O4 nanomaterial for supercapacitor application, Electrochim. Acta, 2019, 330, 135261 CrossRef.
- Y. A. Kumar, S. Singh, D. K. Kulurumotlakatla and H. J. Kim, A MoNiO4 flower-like electrode material for enhanced electrochemical properties via a facile chemical bath deposition method for supercapacitor applications, New J. Chem., 2020, 44, 522–529 RSC.
- Y. A. Kumar, K. D. Kumar and H. J. Kim, A novel electrode for supercapacitors: efficient PVP-assisted synthesis of Ni3S2 nanostructures grown on Ni foam for energy storage, Dalton Trans., 2020, 49, 4050–4059 RSC.
- Y. A. Kumar, K. D. Kumar and H. J. Kim, Facile preparation of a highly efficient NiZn2O4–NiO nanoflower composite grown on Ni foam as an advanced battery-type electrode material for high-performance electrochemical supercapacitors, Dalton Trans., 2020, 49, 3622–3629 RSC.
- D. K. Kulurumotlakatla, Y. A. Kumar and H. J. Kim, Hierarchical NiCo2S4 nanostructure as highly efficient electrode material for high-performance supercapacitor applications, J. Energy Storage, 2020, 31, 101619 CrossRef.
- S. A. Hira, D. Annas, S. Nagappan, Y. A. Kumar, S. Song, H. J. Kim, S. Park and K. H. Park, Electrochemical sensor based on nitrogen-enriched metal–organic framework for selective and sensitive detection of hydrazine and hydrogen peroxide, J. Environ. Chem. Eng., 2021, 9, 105182 CrossRef CAS.
- M. R. Pallavolu, Y. A. Kumar, G. Mani, R. A. Alshgari, M. Ouladsmane and S. W. Joo, Facile fabrication of novel heterostructured tin disulfide (SnS2)/tin sulfide (SnS)/N-CNO composite with improved energy storage capacity for high-performance supercapacitors, J. Electroanal. Chem., 2021, 899, 115695 CrossRef CAS.
- Y. A. Kumar, D. K. Kulurumotlakatla and I. K. Park, Interface engineering for enhancing the performance of novel sodium-doped MoS2 nanocomposite: Synthesis and characterization functioning as a high-performance supercapacitor, Korean J. Chem. Eng., 2023, 40, 2847–2854 CrossRef CAS.
- A. Kumari, J. A. Abraham, C. Sreelekshmi, M. Manzoor, A. Kumar, A. K. Mishra, D. Fouad, Y. A. Kumar and R. Sharma, Ab-initio investigation of novel lead-free halide based Rb2CsXI6 (X = Ga, In) double perovskites: Mechanical, structural, thermoelectric, and optoelectronic potential for photovoltaics and green energy applications, Mater. Sci. Eng., B, 2024, 310, 117708 CrossRef CAS.
- K. D. Kumar, T. Ramachandran, Y. A. Kumar, A. A. A. Mohammed and M. C. Kang, Hierarchically fabricated nano flakes-rod-like CoMoO–S supported Ni-foam for high-performance supercapacitor electrode material, J. Phys. Chem. Solids, 2024, 185, 111735 CrossRef CAS.
- K. D. Kumar, Y. A. Kumar, T. Ramachandran, A. A. A. Kahtani and M. C. Kang, Cactus-Like Ni-Co/CoMn2O4 composites on Ni foam: Unveiling the potential for advanced electrochemical materials for pseudocapacitors, Mater. Sci. Eng., B, 2023, 296, 116715 CrossRef CAS.
- A. Dixit, J. A. Abraham, M. Manzoor, M. Altaf, Y. A. Kumar and R. Sharma, A comprehensive DFT analysis of the physical, optoelectronic and thermoelectric attributes of Ba2lnNbO6 double perovskites for eco-friendly technologies, Mater. Sci. Eng., B, 2024, 307, 117530 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2025 |





