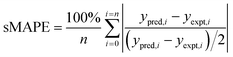Active learning enabled reactor characterization for mass transfer in aerobic oxidation reactions

Abstract

Determination of mass transfer coefficients (k_La) plays a critical role in multiple biopharmaceutical operations ranging from aerobic oxidation reactions for small molecule process development to cell-culture based processes for large molecule process development. Accurate determination of k_La across different scales and reactor configurations is required to develop such processes in a robust and scalable manner. We report the development of a machine learning (ML) based model that accurately predicts k_La across different scales ranging for 100 mL to 100 L. We demonstrate that the ML model can further be used for predictive modeling, such as interpreting sensitivity and estimating impact of new process conditions. Furthermore, integrating the ability to estimate uncertainty in the model prediction, we developed a general framework for a diversified uncertainty-based active learning (AL) algorithm which iteratively recommends experiments based on information criteria and design-space exploration. The novel application of this framework enables automated mass transfer characterization of a previously unexplored reactor configuration. Specifically, we show that using this AL-guided iterative design of experiment led to progressive improvement in the model's forecasting accuracy, improving from 39% at the beginning of AL iterations to 90% at the completion of five AL iterations. Our results confirm that this AL framework offers an efficient closed-loop experimentation strategy that minimizes experimental burden required to accurately characterize mass transfer coefficients for aerobic oxidation processes.

---

Introduction

In the field of pharmaceutical development, biocatalysis has emerged as a powerful toolbox for greener synthesis of complex molecules.^1,2 Biocatalytic processes offer several major benefits as an enabling technology, including their ability to mediate chemical transformations with high stereoselectivity, regioselectivity, and chemoselectivity.³ As a result, in recent years, the application of biocatalysis has led to several notable drug developments including islatravir,^4,5 molnupiravir,^6,7 and belzutifan.⁸ Among different classes of biocatalytic transformations, enzyme catalyzed oxidation reactions are of particular interest for selective formation of alcohols, aldehydes, ketones, and carboxylic acids. In many cases, such enzymatic chemical transformations require supply of molecular oxygen from compressed air as an oxidant for the reaction.^9,10 Typically, these reactions are performed in a stirred batch reactor with continuous sparging of compressed air to the reaction volume. Stirred tank reactors facilitate gas–liquid oxygen transfer through the use of mechanical mixing to increase surface-to-volume ratio. The stirring creates turbulent mixing, enhancing the contact between the gas and liquid phase, while continuous sparging ensures a steady supply of air and thus maximizes the oxygen availability to the reactants. As a result, the rate of oxygen transfer significantly impacts the performance of the reaction because oxidative enzymes tend to consume oxygen faster than it can feasibly be replenished with traditional reactor designs. Moreover, the oxygen transfer rate (OTR) depends on several parameters that vary across scale, like reactor geometry, position and design of agitator and gas distribution systems, etc.^11–14 Therefore, robust process development of aerobic oxidation reactions, and their successful transfer to commercial operation, requires accurate estimation of OTR in different reactor configurations across scales ranging from small scale laboratory reactors to large scale manufacturing reactors.

In addition to small molecule biocatalytic processes such as the aerobic oxidation reactions, the principles of accurately estimating the OTR are equally critical in the large molecule production and biologics manufacturing. For instance, in cell culture-based production of therapeutic proteins such as monoclonal antibodies, OTR plays a vital role in maintaining the optimal cell growth and productivity.¹⁵ Accurate estimation and control of OTR is thus essential to prevent oxygen limitation, and maintain the metabolic balance required for high-yield production across scales ranging from lab-scale bioreactors to large-scale manufacturing of large molecules.

The product of the volumetric mass transfer coefficient (k_La) and the thermodynamic driving force (C_sat − C) describes the overall OTR between gas and liquid phases.¹¹ The thermodynamic driving force is represented as the difference between the bulk liquid oxygen concentration (C) and the theoretical saturation of oxygen (C_sat) at the gas–liquid interface. The kinetic component of the OTR (k_La) thus becomes a vital scaling parameter, ensuring that the OTR is consistent across different reaction vessels and scales when held constant.¹² Ensuring consistent k_La for the process is thus essential for all process optimization and characterization activities that otherwise influence process design or measure important process effects. However, k_La is highly sensitive to small changes in the process parameters, making its accurate determination notably difficult.¹¹ Traditionally, extensive k_La characterization experiments are conducted across all scales to map experimental and operational variables to this key process parameter.^9,16 Often, these require varying several different inputs (such as temperature, fill volume, air sparge rates, sparger type, and agitation) simultaneously to identify the optimal operating conditions, thus making the overall characterization process tedious and expensive in both time and resources.

Several empirical models have been previously reported for predicting k_La and correlating various process parameters such as agitation rate and volumetric flow rate of sparged air.^17–19 While these models provide a foundation for qualitative understanding of k_La behavior in reactor vessels, they often fall short in accurately capturing the complex correlation between process parameters and the reactor configurations such as vessel geometry, number of baffles, size of spargers, etc. (more detailed discussion is provided later in the results section). Moreover, these empirical correlations are often not accurate in estimating k_La at small scale reactors (<200 mL that have drastically different reactor dimensions and geometry) where significant process development is conducted.¹¹ These limitations underscore the need for developing a more efficient predictive model that can accurately predict k_La in various reactor configurations across different scales. Moreover, these challenges of accurately estimating the OTR in a process are not specific to development enzymatic oxidation reactions, but also apply to aerobic fermentation and cell culture processes for biopharmaceutical manufacturing as well.^20,21

Advancements in machine learning (ML) techniques for building predictive models have been demonstrated as promising alternatives to empirical models in several different domains.²² ML models based on deep neural networks for instance can leverage vast amounts of process data to identify the intricate patterns and relationships that the empirical models lack.^23–25 However, training ML algorithms often require large number of training datasets; application to mass transfer characterization would require execution of a large number of k_La characterization experiments across different reactor configurations. Recently, we reported an automated end-to-end workflow that automates the extraction of k_La coefficients under any given process conditions and reactor configuration.¹¹ Leveraging this data-rich experimentation approach that combines process automation and a streamlined data workflow allowed us to execute a large number of k_La characterization experiments (>1000 across different scales) across a diverse set of reactor geometries and scales. These experimental k_La datasets in turn can enable the development of more accurate predictive ML-based models by serving as a diverse training dataset. The focus of our previously reported work¹¹ was thus on developing a robust experimental workflow that enables experimental extraction of k_La values by executing automated experiments. The same workflow for k_La extraction has been leveraged in this work as well. However, the aim of this work is to (i) develop an accurate ML-based model that can predict k_La values under different conditions and reactor configuration by leveraging the existing experimental datasets, thus eliminating the need to execute additional k_La characterization experiments, and (ii) use this developed ML model to design the most informative set of k_La characterization experiments (executed using the same workflow as previously reported¹¹) through an active learning framework.

Building ML-based predictive models on existing datasets, however, limits their application to only those reactor configurations that are included in the available training dataset, without risks of difficult extrapolation. To estimate k_La across the design space of a new reactor configuration thus necessitates inclusion of a significant number of additional training data on this previously unexplored reactor configuration, so that the model can accurately learn this expanded design space. This in turn requires extensive k_La characterization experiments, often using conventional design of experiments techniques to explore a large multi-dimensional design space.¹¹ A more resource efficient approach would be to leverage the model that is trained on some existing reactor configurations to design optimal experiments in an iterative fashion until the model has adequately learned the design space of the new reactor configuration, according to some defined statistical target. This approach of using a ML model to design iterative experiments that are most informative for the model is known as active learning (AL).²⁶

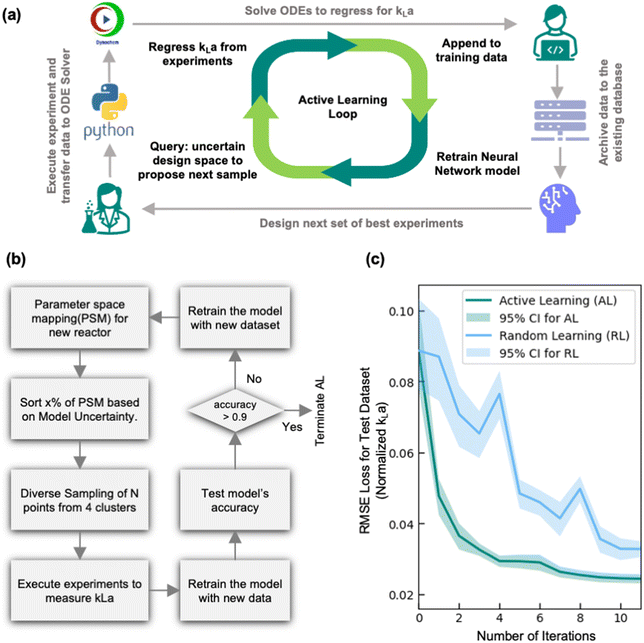
Integrating ML-based, predictive models with iterative experimental design using AL framework has been recently demonstrated as an efficient approach to reduce experimental burden in chemical space exploration, thus eliminating the need for exhaustive reaction screening.^27,28 Several AL techniques using algorithms such as Bayesian optimization, ensemble neural networks, and genetic algorithms, have also been applied for optimization tasks in different domains such as organic chemistry, nanomaterials, etc. to optimize complex multidimensional processes while minimizing the number of experiments needed to achieve optimal conditions.^29–31 Such approaches typically require two key components (1) a ML model that can accurately map the design space, and (2) a sampling strategy that can be used to design the next-best batch of experiments to achieve an optimal condition. Using AL to guide mass transfer characterization of a reactor can be considered analogous to these optimization problems, with the exception that the objective of the AL algorithm is to reduce prediction uncertainty in the multidimensional design space rather than identifying an optimal condition. Developing an AL framework thus offers a promising and yet unexplored approach for developing more autonomous and resource-efficient workflows for characterization, including reactor mass-transfer performance. Moreover, the workflow used to execute the experiments and then extract k_La values for model validation or active learning iterations is kept same as our previously reported work.

In this work, we developed and benchmarked various ML models to accurately learn the design space and predict k_La in different reactor configurations across scales. We demonstrate that interpretation of the developed ML model also enables critical insights into how the underlying parameters interact and impact the estimation of k_La values. Next, we developed a diversified uncertainty-based AL framework for efficient characterization of new, previously unexplored reactor configurations, while requiring a minimal number of experiments. By iteratively designing and selecting the most informative experiments, the AL framework enables an efficient closed-loop mass transfer characterization workflow, thus overcoming the need for an exhaustive design space exploration.

Results and discussion

Reactor database

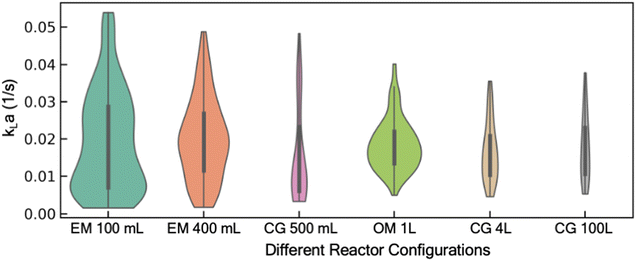
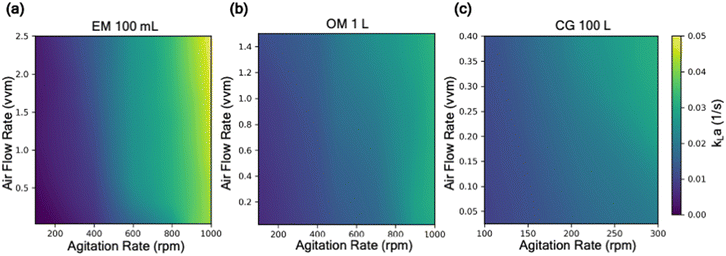
With the aim to develop a predictive model for k_La, we first focus on the k_La database, its curation, and feature selection. A comprehensive mass transfer characterization to evaluate k_La under different operating conditions of a reactor often requires execution of many experimental trials, typically designed using full-factorial or mixed-factorial design of experiments. Given the wide range of possible operating conditions (temperature, fluid volume, air flow rate, and agitation rate) and reactor configurations (spargers, agitators, and their relative location inside the reactor), manual execution of these DoE studies are expensive in both time and resources. In response, we recently reported an end-to-end automated workflow for automated reactor control and data processing to regress k_La value from dissolved oxygen profiles.¹¹ This methodology was used to collect k_La data from different combinations of operating conditions and reactor configurations. This database includes results from our historical k_La experiments in reactors ranging from 100 mL lab-scale reactors to 100 L kilo scale reactors (Fig. 1).¹¹ It should be noted that in this work, k_La is reported in s⁻¹ units rather than more commonly reported h⁻¹ units. The discrepancy in the preferred unit for reporting k_La stems from the difference in the domain. Generally, large molecule bioprocess-focused literature reports k_La in h⁻¹ units in contrast to the small molecule focused literature that tends to report k_La values in s⁻¹ units.^32,33 Moreover, the order of magnitude of the k_La range reported for large molecule processes (0.1–100 h⁻¹) is similar to the range shown in Fig. 1 (0.005–0.05 s⁻¹i.e., 18–180 h⁻¹) for the reactor configurations used in this work.¹⁵ We used this database to first train a predictive model that can learn the function to map the input features (different operating conditions and reactor configurations) to the output feature (experimentally estimated k_La). The input features are represented by 5 continuous input parameters (sparger size, fill volume of the reactor vessel, temperature, agitation rate, and VVM: volumetric flow rate of air per reactor volume), and 1 categorical input parameter (reactor configuration). Reactor configuration features such as the specific reactor geometry, shape of the agitator blade, the number of baffles (including in situ process probes such as temperature, pH, and dissolved oxygen probes) and their relative position in the reactor are all combined in this single categorical feature for the model. Although each of these features for the reactor configuration can be treated as a separate input to the model, that would require a significantly larger and more diverse dataset for the model to learn how each of these individual feature impacts k_La. Moreover, the accurate representation of complex geometric features such as shape of the agitator blade, or specific three-dimensional representation of the reactor design offers additional challenge. Hence, in this work, we combined all features related to the reactor configuration into a single categorical feature for simplicity. The one-hot encoding technique is used to represent this categorical feature as a numerical input to the model. The trained model can then be used to estimate k_La under new and previously unexplored process conditions.

Fig. 1 Violin plot showing the distribution of data in the existing database across scales ranging from 100 mL lab scale reactor to 100 L kilo scale reactors (EasyMax (EM)100 mL, EasyMax (EM) 400 mL, Chemglass (CG) 500 mL, OptiMax (OM) 1 L, Chemglass (CG) 4 L, Chemglass (CG) 100 L).

Model development and deployment

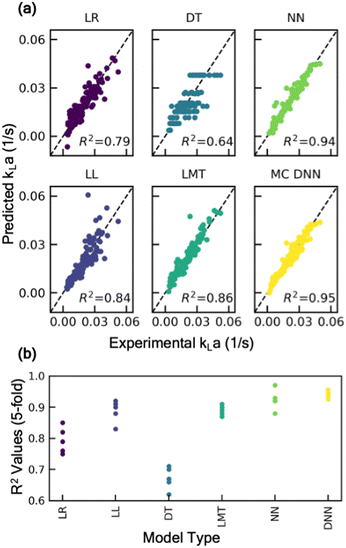
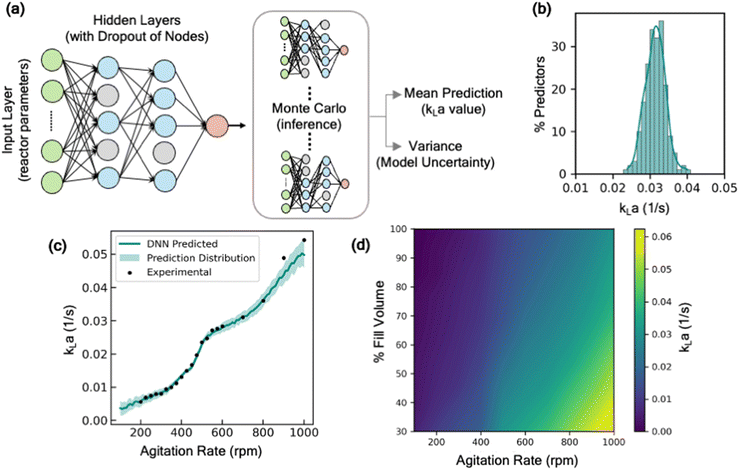
The rationale behind the selection of appropriate model architecture to build a predictive model often depends on several factors including the type of dataset, computational cost, and the desired outcome from the model. For instance, models with high interpretability such as linear models or decision-trees, offer the benefit of representing the input and output features through relatively simple mathematical relationship, thus making it easier to understand how each input feature influences the outcome. However, due to their inherent simplicity and structural limitations, such models may not capture complex parameter interactions. Alternatively, more complex, and less interpretable models like deep neural networks offer the advantage of potentially achieving higher accuracy, as well as the ability to estimate model prediction uncertainty by incorporating probabilistic models. To identify an appropriate model architecture, we explored multiple different class of ML models: linear regression models, tree-based models, and neural network-based models. Fig. 2 shows the performance of these models on the test dataset. For each of these models, 20% of the dataset was withheld for testing the predictive performance of the model and the remaining was used to train the model and optimize hyperparameters. More details on the model training methodology are discussed in the supplementary information (section S1†). Our comparative analysis elucidates the nuanced trade-off between model complexity and interpretability. Linear models, for instance, are expected to behave similar to empirical models for estimating k_La, and thus offer a simpler and more interpretable approach to understand the impact of different parameters on k_La values. Here, we explored two types of linear models: (i) standard linear regression with no data transformations, and (ii) log-transformed linear models, where log transformation is applied to the data for linearity and normality. The details of the data transformation and model training are discussed in the supplementary information (section S1†). Despite their simplicity, linear models yielded limited accuracy on the test dataset, with mean R² values in the range of 0.79 to 0.84, thus failing to capture the sensitivity of k_La to minor changes in the operating conditions (Fig. 2). Additionally, a linear model tree (LMT) design that combines linear regression with decision tree (DT)-based architecture, offers slight improvement in capturing the complex relation between the input variables. LMT can be seen as a hybrid approach where some interpretability can be maintained due to linear regression at the tree branches and splits while also letting the model learn the complex hierarchical relation between different configurations. However, this also comes at the cost of model interpretability due to the multitude of decision rules involved in making predictions. In contrast, Monte Carlo dropout neural networks (MC-DNN), a variation of deep neural networks (Fig. 3a), yielded high prediction accuracy with R² values up to 0.95 on the test data. Although complete interpretability is a longstanding challenge for deep neural networks, our benchmarking study suggests that it significantly outperforms other models for predicting k_La, likely due to their ability to learn complex hierarchical representations of the data through multiple layers of interconnected neurons. MC-DNN offers two additional major advantages over standard neural networks: (1) during the training of the model, it randomly ‘drops out’ a fraction of neurons in the hidden layer (Fig. 3a and b), thus offering an inexpensive regularization technique to prevent the model from overfitting output variance to a specific subset of nodes; and (2) during the inference or prediction from the model, randomized dropout masks are applied to the hidden layer to give a probabilistic distribution of the predicted value from multiple ensembles of the trained model, thus providing an estimate for uncertainty in model's prediction (Fig. 3b), rather than a single prediction value that is provided by standard neural network models.³⁴

Fig. 2 (a) Parity plot showing the performance of different machine learning models on validation dataset: linear regression (LR) with no transformations, log-transformed linear regression (LL), decision tree (DT), linear model tree (LMT), neural network (NN), Monte-Carlo dropout neural network (MC DNN). (b) R-Squared values evaluated for each model based on 5-fold cross validation.

Fig. 3 (a) Schematic representation of Monte-Carlo dropout neural network. During inference, dropout is applied to estimate a predictive distribution by using the ensemble of trained model. (b) Distribution plot showing the prediction from 200 samples from the MC-dropout masked neural network. (c) Prediction of k_La vs. agitation curve for EM 100 mL reactor, along with the 95% prediction interval shown by the shaded region, along with experimental data shown as the scatter points. (d) Predicted contour plot of k_La in EM 100 mL with varying fill volume of the vessel and agitation rate at fixed volumetric flow rate of sparged air per unit volume (vvm).

Model validation. To further validate the generalizability of the MC-DNN model in learning the relation between process conditions and k_La values, the model was used to predict the profile of k_La as a function of agitation rate for a Rushton turbine agitator in a 100 mL reactor (EM 100 mL) under conditions that were held out from the model training (air flow rate: 100 sccm, fill volume: 50 mL, temperature 25 °C, sparger outer diameter: 0.125 inch). The results suggest that the model's prediction band accurately captures the sigmoidal shape of the k_La vs. agitation curve and matches closely with the experimentally observed k_La values (Fig. 3c). The inflection in the k_La vs. agitation curve is observed both by (i) model's prediction of k_La as a function of agitation as well as (ii) confirmed through experimental data obtained at different agitation rates. It should be noted that empirical models like those proposed by Van't Reit³⁵ are unable to capture the inflection in the curve.¹¹ This is likely because the wide agitation range in the reactor covers a transition in mass transfer regime from sparging-limited effect at lower agitation rate to vortex- or drawdown-limited effect at high agitation rates. Additionally, Fig. 3d shows the model-predicted impact of fill volume on k_La under different agitation rates, while maintaining same air flow rate in terms of volume of air sparged per unit liquid volume per minute (vvm) units. As expected, k_La values decrease with the increase in fill volume. The k_La values are more sensitive to fill volume at higher agitation rates. These findings from the model prediction are qualitatively in alignment with what we expect from Van't Reit's empirical model³⁵ that suggests that k_La is proportional to power input (function of agitation rate) per unit volume.

Moreover, the predictions are also accompanied with an estimate of prediction certainty. For instance, the model has lower prediction certainty in the design space regions where the training data is scarce (low k_La region i.e., at lower agitation rate), and higher certainty in the design space region where historical data used for training was present in abundance (Fig. 3c). The estimation of the model uncertainty along with the prediction allows a more-informed decision for determining the appropriate operating ranges for the desired oxidation process.

Model interpretation. ML models such as MC-DNN used in this work can accurately map the correlation between the input features (scale and process conditions) and the output feature (k_La values) by identifying intricate patterns that might not be evident through traditional empirical techniques. However, interpreting these models to understand the impact of different input features can be challenging due to their black-box type design. This is where Shapley additive explanations (SHAP) analysis becomes invaluable. SHAP analysis offers a robust method to understand how different input parameters influence the output k_La values. By calculating the marginal contribution of individual features to the model's predictions over a randomly sampled and simulated design space, SHAP values reveal the individual impact of variables on the predicted k_La values. More details on the SHAP analysis are included in the supplementary information (section S3†). By visualizing the SHAP results for the entire dataset (Fig. 4a), we observed that the agitation rate, followed by reactor geometry are the two most impactful parameters for predicting k_La values, together contributing to more than 60% of the combined impact of all parameters. This finding further highlights the importance of considering reactor geometries as input feature for estimating k_La values and the importance of consistent geometry for process development activities.¹¹ SHAP analysis on different reactor scales shows an interesting trend in the impact of process parameters. At smaller scale (EM 100 mL reactor), the predicted k_La values are largely dictated by agitation rate and fill volume (Fig. 4b) while all additional features have minimal impact on k_La. However, at larger scales (CG 100 L reactor), all five parameters contribute significantly to the k_La predictions, thus suggesting that the k_La values at larger scales are much more sensitive to small changes in any of the five parameters considered in this model. Additionally, the relationship between parameter SHAP values and feature values are opposite for many parameters suggesting very different general mass transfer behaviours across different reactor scales even for similar geometries (both 100 mL and 100 L reactors are baffled cylindrical tanks). A more traditional empirical modelling technique based on power number correlations assumes that agitation is the main predictor of OTR and thus subsequently fail to capture the intricate contributions of the other parameters such as reactor geometry. As a result, multiple individual empirical models would be required for every unique reactor geometry in order to achieve high accuracy predictive models. This analysis highlights the complexity of k_La data and the difficulty in predicting performance across reactors. These insights from the interpretation of the ML model are crucial for process development as it informs hypothesis-driven process optimization and design using identifiable input–output relationships based on meaningful physical quantities.

Fig. 4 Interpretation of machine learning model in terms of impact of each parameter (a) absolute Shapley-additive explanations (SHAP) values for each parameter as a metric to measure the impact of each input feature on k_La prediction. (b) SHAP values for all parameters for EM 100 mL reactor configuration and (c) CG 100 L reactor configuration.

Prediction across scale. A major advantage of developing predictive models is that the model can be used to populate in silico experiments to visualize how k_La values change across scales and process conditions. For example, Fig. 5 shows model-predicted design space mapping of k_La across the entire operation range of three different reactor configurations from 100 mL small lab scale reactors to 100 L kilo lab scale reactors. One of the key considerations for developing an aerobic oxidation process is identifying process conditions at each scale that can ensure maintaining similar k_La across all scales. The design space mapping thus offers crucial insights for process developers. For instance, the lab scale process development should be conducted at a k_La value that is routinely achievable across all scales ranging from lab scale to commercial scale, and not necessarily the maximum value achievable in a particular reactor geometry. The design space mapping thus enables identification of optimal operating conditions that allow process development to be conducted at similar k_La values across different reactor configurations and scales. For example, to achieve a consistent k_La value of 0.025 s⁻¹ across all reactor configurations, agitation rates should be maintained between 200–300 rpm (by varying the air flow rate from 0.35 to 0.04 vvm) in kilo lab scale (CG 100 L) reactors and 650 to 700 rpm (by varying air flow rate from 1.15 to 0.15 vvm) at smaller lab scale (EM 100 mL) reactors (Fig. 5). Furthermore, several different combinations of process conditions can yield the same k_La values across all reactor scales. In practice, depending on reaction compositions, process developers often choose to run experiments that maintain the same k_La value but at varying process conditions to explore the effects of mixing or other parameters, independent from mass transfer and k_La.⁹ Leveraging the model prediction of design space thus enables scientists to develop scalable processes for aerobic oxidations by exploring mass transfer effects and selecting optimal process conditions.

Fig. 5 Predicted k_La with varying agitation rate and air flow rate (vvm) across reactor configuration at 3 different scales: (a) 100 mL, (b) 1 L, (c) 100 L. The range of air flow rate and agitation rate in each reactor configuration is constrained by the operational limit of the reactor.

Next we demonstrate that these predictive ML tools can also be easily democratized through broad deployment using an intuitive web application-based interface,³⁶ thus empowering scientists within the organization to access and utilize the trained ML model without requiring programming or data science expertise. All complex data manipulations are kept in the back end of the interface with the user only exposed to the necessary inputs to allow them to explore predicted k_La values with calculated model uncertainty. The details of the web app deployment for predicting k_La are shown and discussed in ESI† (section S2). This tool serves two primary use cases: (i) enabling scientists to estimate predicted k_La under specific operating conditions, and (ii) allowing them to explore the design space to find operating conditions that achieve the desired k_La for their processes. By providing a simple to use graphical user interface, this web app streamlines workflow and facilitates broader adoption of such technologies.

Active learning

The developed MC-DNN model is highly accurate when predicting k_La in reactors with extensive prior characterization but is not able to extrapolate beyond the design space to make predictions in new reactor geometries/configurations. To accurately predict k_La in this extrapolation region thus requires retraining the model with additional training data specific to this new reactor configuration. Hence, we next explored the ability of using an active learning (AL) framework in combination with the developed MC-DNN model to efficiently characterize a new, previously unexplored reactor configuration. The AL framework offers an efficient experimental design strategy that utilizes ML models to iteratively design the next set of best experiments to perform by leveraging and assessing the uncertainty in the model's prediction. In our case, by using the MC-DNN model, we can estimate the model's uncertainty across the entire parameter space then sample conditions that exhibit the highest uncertainty in terms of relative width of the prediction band from their mean value. These selected experiments are then conducted to evaluate k_La at these conditions, and the results are incorporated in the training dataset. The model is then retrained with the updated training dataset and the process is repeated. This iterative process (summarized in Fig. 6a) of querying the design space to design experiments, executing the experiments, appending the data, and retraining the model continues until the model accurately characterizes the new reactor configuration based on a pre-determined threshold or criteria. For instance, the stopping criteria in this work was based on model reaching 90% forecasting accuracy (i.e., how well can the model predict the outcome of the experiments proposed in the current iteration). Alternate stopping criteria such as those that are based on improvement in overall model certainty across the design space can also be used depending on the application and objective of the AL-guided experiments. This AL framework thus enables an automated, closed-loop k_La characterization workflow to fully characterize a new and previously uncharacterized reactor configuration while minimizing the number of required experimental trials.

Fig. 6 (a) Schematic representation of the active learning (AL) workflow and (b) flow chart of the underlying AL algorithm using diversified uncertainty sampling. (c) Comparison of diversified uncertainty-based AL used in this work with random sampling-based approach for a simulated reactor configuration (OM 1 L) in terms of the loss trajectory (evaluated in terms of RMSE: root mean square error) as a function of AL iterations. Each trajectory is an average of 25 runs of the corresponding algorithms, and the shaded region shows the 95% confidence interval.

One of the most critical aspects of this AL workflow is the choice of sampling strategy, i.e., how does the model decide which experiment to run next. In practice, rather than executing single experiment at a time, it is generally more resource-efficient to either execute multiple experiments in parallel or execute multiple experiments in a sequential fashion by leveraging laboratory automation tools. Hence, the AL sampling strategy explored in this work is designed to propose a batch of experimental conditions, rather than a single experimental condition. A variety of different batch sampling strategies have been used for different AL applications.^27,37,38 One of the most common is uncertainty-based sampling. In this approach, the AL algorithm simply queries the condition with the highest uncertainty. This strategy is widely used due to its simplicity of implementation. However, one of the major drawbacks of this strategy is that if a specific region in the design space has very high uncertainty (such as low air flow rate and agitation rate), either due to high noise in the experimental data in that region, or high noise in the data processing protocols (such as regression of dissolved oxygen profile), then the algorithm may sample iteratively and exclusively from a specific region of the design space. While this strategy may improve accuracy in this specific region, the sampled conditions in a batch of experiments are very similar to each other and thus add limited new knowledge to the overall model. This can lead to large number of experimental iterations before the algorithm starts to explore a new region of lower uncertainty. This challenge is analogous to what is observed in the field of algorithmic process optimization using Bayesian approach, where the algorithm must balance between exploitation of promising performance with the exploration of areas of uncertainty to avoid oversampling a globally inferior local optimal solution.³⁹ To mitigate this challenge, we leveraged a diversified uncertainty-based sampling strategy for the AL algorithm, which have been demonstrated to be more generalizable and efficient compared to sampling based on uncertainty only.³⁸ This novel application highlights a different focus from traditional applications in which the goal of the AL framework proposed in this work is not to find optimal conditions, but instead to accurately map the entirety of a specified design space. Fig. 6b shows the flowchart of the AL framework using diversified uncertainty sampling. Specifically, when the parameter space is mapped based on the model's predictions, the next set of experimental conditions are sampled by considering both the geometric diversity of the points in the experimental batch as well as the prediction uncertainty. First, the parameter space map (PSM) prediction is sorted based on uncertainty, and then a fraction of the most uncertain points is selected (where the fraction can be adjusted as a hyperparameter) and clustered into 4 clusters using the k-means clustering algorithm. Followed by this, samples with specified batch size (N) are drawn equally from each cluster. This approach of diversified uncertainty sampling thus allows us to design diverse batches of experimental conditions that balance broad design space exploration with investigation of areas with high prediction uncertainty.

Validation using simulated data. We first validated this diversified uncertainty-based AL framework on simulated experiments by starting with a surrogate model that was trained on our dataset including all reactor configurations except one (OM 1 L). OM 1 L reactor was used to validate the AL framework and hence was withheld from the initial training of the surrogate model. The AL framework was then used to iteratively sample additional training data for this withheld reactor configuration. Random sampling, in which training data points are randomly selected during each iteration to train the model, was used as a benchmark against which the diversified uncertainty-based AL framework was evaluated. Fig. 6c shows the direct comparison between the two techniques in terms of how loss error on the test dataset propagates with increasing AL iterations (each with an experimental batch size of 12). The diversified uncertainty-based AL approach shows rapid decrease in test error within the first 3 iterations and then steadily decreases as more data is added to the model in subsequent iterations. Random learning requires more than 10 iterations to minimize error, beyond which the average of random learning error is significantly higher than the diversified uncertainty-based AL approach. These results highlight the benefits of using diversified uncertainty-based AL approach for progressively learning the design space of a new reactor configuration while minimizing the experimental iterations.

Experimental validation. Next, we extend this AL approach through a human-in-the-loop automated k_La characterization, i.e., the experiments designed by the AL framework are executed through an automated experimentation workflow,¹¹ with human intervention needed for data transfer and analysis between experimental rounds. We demonstrated this by experimentally characterizing a new large-scale (100 L) reactor configuration that was not previously characterized and hence was not present in the existing database used to train the initial model. The AL workflow (as described in Fig. 6) was used to suggest experiments in a batch size of 12 for each iteration by varying three key process parameters: agitation rate, air flow rate, and volume. These experiments were then performed through our recently developed automated k_La characterization workflow¹¹ and included in the training dataset at the end of each iteration to retrain the model and propose the next batch of experiments. Fig. 7b shows the experimental conditions and corresponding k_La values from six iterations of AL guided experimentation. In addition, the fractional deviation of prior predicted k_La values from future experimentally measured k_La values are also shown as bar plots in Fig. 7b for each iteration. A deviation value closer to zero suggests that the model is performing more predictively on unseen data. The deviation bar plots offer a real-time evaluation of how the model is performing through each iteration loop. As evident in Fig. 7b, the deviation from experimental k_La for each condition in the first iteration is high, as expected, since no training data is available at the beginning of the AL iteration. However, as more AL-guided experiments are executed and included in the model training, the deviation bars start to approach zero within five iterations, suggesting that the model can accurately map the input and output features. Symmetric mean absolute percentage error (sMAPE) can be used as the metric to quantify the average deviation for each iteration.^40,41 sMAPE is expressed as:
where y_pred,i and y_expet,i are the predicted and experimental k_La values for each sample in the AL iteration, and n is the number of samples in the AL iteration.

Fig. 7 Results of active learning (AL) implementation to learn the design space of a new reactor configuration. (a) Parity plot showing progressive improvement in predicted vs experimental k_La value with increasing AL iterations (from left to right). (b) Experimental conditions (fill volume, agitation rate, air flow rate), experimentally measured k_La, and fractional deviation in predicted k_La from experimental k_La value are all shown as bar plots for each AL iteration.

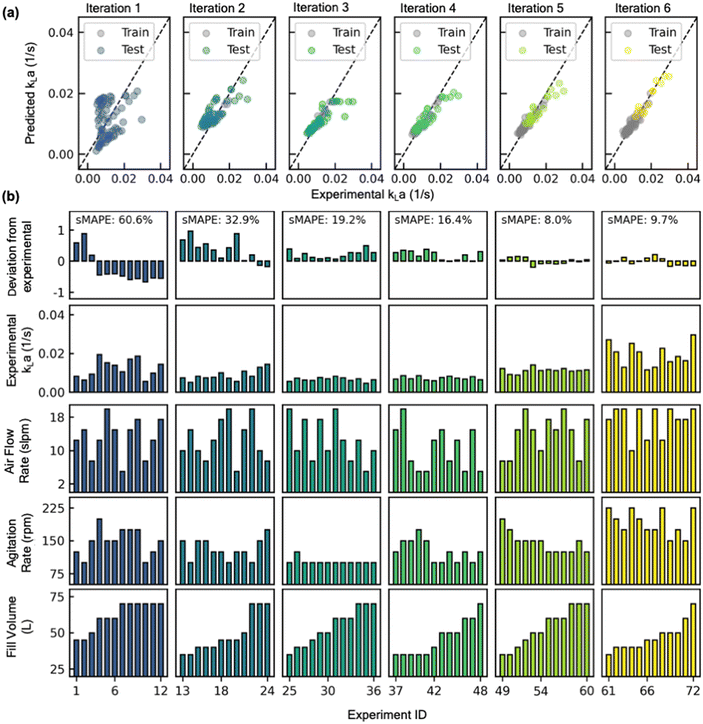
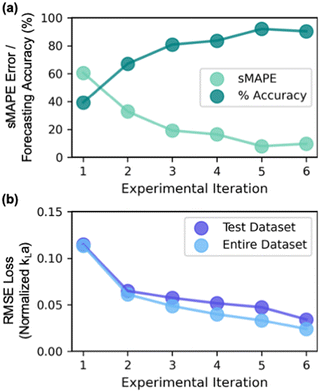
Starting with a sMAPE value of 60.6% (i.e., forecasting accuracy of 39.4%) at the beginning of the AL iteration, the model progressively improves after each AL iteration, yielding a sMAPE value of 9.7% (i.e., forecasting accuracy of 90.3%) at the completion of the AL iteration (Fig. 8a).

Fig. 8 Performance of the model with increasing active learning (AL)-guided experimental iteration. (a) Symmetric mean absolute error (sMAPE) and forecasting accuracy (100 – sMAPE) is calculated based on experimental and predicted k_La for all experiments performed in each AL iteration; sMAPE decreases and forecasting accuracy increases progressively with increase in AL iterations. (b) root mean square error is evaluated on the test dataset and the entire dataset as the model progresses through the AL iterations. Both show improvement with increase in AL iteration.

The improvement in model's performance can also be evaluated and confirmed through the retrospective analysis of the model. At the beginning of each iterative cycle, the model trained on all prior experiments was stored. At the conclusion of all six iterations, the performance of the model from each iteration was assessed in terms of prediction parity (Fig. 7a) on test dataset (i.e., all experimental data that is collected in the subsequent iterations) and the entire complete dataset collected throughout the six iterations. As evident, the root mean squared error (RMSE) value between experimental k_La and predicted k_La on test dataset progressively improves from 0.11 at the beginning of AL to 0.03 at the conclusion of AL iterations (Fig. 8b). Through strategic selection and incorporation of the new experimental conditions into the training process, the model continuously refines its estimate of the parameter interactions and the underlying relations between different process conditions across the entirety of the reactor design space. Moreover, the progressive improvement in the model's prediction underscores the effectiveness of active learning in designing optimal experiments that could be most informative for building a predictive model in a previously unexplored design space.

Conclusions

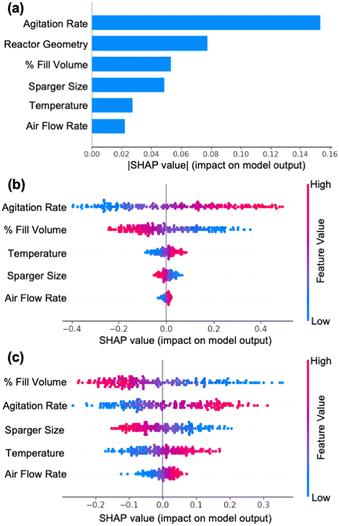
In this work, we demonstrate a generalizable active learning framework as a promising tool for efficiently characterizing mass transfer coefficients (k_La) in reactors by iteratively selecting and proposing experiments that are most informative for the model. This was accomplished through first developing and benchmarking different ML models in the context of accurately predicting k_La across scale and then integrating the developed model with an active learning framework. Our benchmarking study of different ML models suggests that Monte-Carlo dropout neural networks (MC-DNN) outperform the other models investigated. Moreover, using SHAP analysis for interpretation of the MC-DNN model, we showed that sensitivity and impact of different process conditions (such as agitation rate, fill volume, and air sparge) vary significantly across different reactor configuration and scales, thus highlighting the importance of replacing existing generalized empirical models with machine learning-based models for estimating k_La. The MC-DNN model also enabled estimation of uncertainty in model prediction, that allowed us to integrate it with a diversified-sampling based AL framework. Our results show that the diversified uncertainty-based AL approach enables design of diverse and informative experiments that yields a progressive improvement in the overall accuracy of the model while minimizing the number of experiments required. After completion of five iterative experiments, the AL algorithm allowed us to fully characterize a new and previously unexplored reactor configuration. This is evident from the observed improvement in the model's forecasting accuracy from 39% at the beginning to 90% at the conclusion of AL-guided experiments. These results demonstrate that the AL-guided experimentation strategy presented in this work offers a promising workflow to reduce the experimental burden of conducting exhaustive experimentation for characterizing k_La in reactors.

The active learning framework of iteratively exploring the design space (i.e., querying the design space to propose experiments, executing the experiments, appending the experimental data, and then retraining the model with the new information until the model accurately learns the design space) offers a promising path forward towards developing fully autonomous platforms for process characterization at large. Future research in this area should focus on integrating this active learning approach with process and laboratory automation alongside streamlined data pipelines to further reduce the manual burden of characterizing new reactor configurations. Although, the work reported here utilized water (with no added reagents) as the choice of media for k_La characterization, the generalizable framework presented here can be further extended to develop models that also account for the impact of added reagents, such as antifoam or reaction media, on the predicted k_La values and the resulting oxygen transfer rates. For example, the amount of antifoam added (a continuous parameter) and the type of reaction media used (a categorical parameter) can be incorporated as additional input features to the model. This would enable the model to learn the correlation between k_La values and the amount of antifoam and cell media. In addition, the overall workflow presented in this work can be extended and adopted for a wide range of applications, where the objective is to efficiently design the most informative experiments to build predictive machine learning models for a process. Further implementation and adoption of such technologies across different aspects of drug process development will facilitate acceleration of timelines with the most effective use of resources, while also maximizing valuable process insights.

Data availability

The data related to the hyperparameters of all the machine learning models developed in this article has been included as part of the ESI.† Additional data related to the mass transfer characterization are available upon request from the authors.

Author contributions

A. V. (conceptualization, methodology, investigation, formal analysis, and writing – original draft), K. A. M. (conceptualization, investigation, supervision, writing – review & editing), S. T. G. (conceptualization, supervision, project administration, and writing – review & editing).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank Kevin Stone for reviewing the manuscript.

References

1. N. N. Zhang, P. D. de Maria, S. Kara and A. Salomone, Catalysts, 2024, 14, 84.
2. A. Fryszkowska and P. N. Devine, Curr. Opin. Chem. Biol., 2020, 55, 151–160.
3. C. K. Winkler, J. H. Schrittwieser and W. Kroutil, ACS Cent. Sci., 2021, 7, 55–71.
4. H. C. Johnson, S. G. Zhang, A. Fryszkowska, S. Ruccolo, S. A. Robaire, A. Klapars, N. R. Patel, A. M. Whittaker, M. A. Huffman and N. A. Strotman, Org. Biomol. Chem., 2021, 19, 1620–1625.
5. M. A. Huffman, A. Fryszkowska, O. Alvizo, M. Borra-Garske, K. R. Campos, K. A. Canada, P. N. Devine, D. Duan, J. H. Forstater, S. T. Grosser, H. M. Halsey, G. J. Hughes, J. Jo, L. A. Joyce, J. N. Kolev, J. Liang, K. M. Maloney, B. F. Mann, N. M. Marshall, M. McLaughlin, J. C. Moore, G. S. Murphy, C. C. Nawrat, J. Nazor, S. Novick, N. R. Patel, A. Rodriguez-Granillo, S. A. Robaire, E. C. Sherer, M. D. Truppo, A. M. Whittaker, D. Verma, L. Xiao, Y. J. Xu and H. Yang, Science, 2019, 366, 1255–1259.
6. J. A. McIntosh, T. Benkovics, S. M. Silverman, M. A. Huffman, J. Kong, P. E. Maligres, T. Itoh, H. Yang, D. Verma, W. L. Pan, H. I. Ho, J. Vroom, A. M. Knight, J. A. Hurtak, A. Klapars, A. Fryszkowska, W. J. Morris, N. A. Strotman, G. S. Murphy, K. M. Maloney and P. S. Fier, ACS Cent. Sci., 2021, 7, 1980–1985.
7. W. Holman, W. Holman, S. McIntosh, W. Painter, G. Painter, J. Bush and O. Cohen, Trials, 2021, 22, 561.
8. D. A. DiRocco, Y. L. Zhong, D. N. Le, S. D. McCann, J. C. Hethcox, J. Kim, J. N. Kolev, B. Kosjek, S. M. Dalby, J. P. Mcmullen, R. Gangam and W. J. Morris, Org. Process Res. Dev., 2024, 28, 404–412.
9. J. Kim, V. C. R. Zhang, K. Abe, Y. Z. Qin, D. A. Dirocco, J. P. McMullen, A. L. X. D. Sun, R. Gangam, M. Chow, A. Pitts-McCoy and A. S. Malkani, Org. Process Res. Dev., 2024, 28, 422–431.
10. W. L. Cheung-Lee, J. N. Kolev, J. A. Mcintosh, A. A. Gil, W. L. Pan, L. Xiao, J. E. Velasquez, R. Gangam, M. S. Winston, S. S. Li, K. Abe, E. Alwedi, Z. E. X. Dance, H. Y. Fan, K. Hiraga, J. Kim, B. Kosjek, D. N. Le, N. S. Marzijarani, K. Mattern, J. P. Mcmullen, K. Narsimhan, A. Vikram, W. Wang, J. X. Yan, R. S. Yang, V. Zhang, W. Zhong, D. A. Dirocco, W. J. Morris, G. S. Murphy and K. M. Maloney, Angew. Chem., 2024, 63, e202316133.
11. K. Mattern and S. T. Grosser, Org. Process Res. Dev., 2023, 27, 1992–2009.
12. L. K. Zhu, B. Xu, X. Y. Wu, J. G. Lei, D. L. Hacker, X. Liang and F. M. Wurm, 3 Biotech, 2020, 10, 397.
13. M. Aroniada, S. Maina, A. Koutinas and I. K. Kookos, Biochem. Eng. J., 2020, 155, 107458.
14. W. Klöckner, R. Gacem, T. Anderlei, N. Raven, S. Schillberg, C. Lattermann and J. Büchs, J. Biol. Eng., 2013, 7, 28.
15. S. Xu, L. Hoshan, R. B. Jiang, B. Gupta, E. Brodean, K. O'Neill, T. C. Seamans, J. Bowers and H. Chen, Biotechnol. Prog., 2017, 33, 1146–1159.
16. Y. Z. Qin, K. A. Mattern, V. C. R. Zhang, K. Abe, J. Kim, M. Zheng, R. Gangam, A. Kalinin, J. N. Kolev, S. Axnanda, Z. E. X. Dance, U. Ayesa, Y. N. Ji, S. T. Grosser, E. Appiah-Amponsah and J. P. McMullen, Org. Process Res. Dev., 2024, 28, 432–440.
17. M. Nocentini, Chem. Eng. Res. Des., 1990, 68, 287–294.
18. R. Kayser, Prog. Water Technol., 1979, 11, 23–36.
19. I. T. M. Hassan and C. W. Robinson, Biotechnol. Bioeng., 1977, 19, 661–682.
20. S. Schaepe, A. Kuprijanov, C. Sieblist, M. Jenzsch, R. Simutis and A. Lübbert, J. Biotechnol., 2013, 168, 576–583.
21. S. Goldrick, K. Lee, C. Spencer, W. Holmes, M. Kuiper, R. Turner and S. S. Farid, Biotechnol. J., 2018, 13, e1700607.
22. T. Y. Zhao, S. C. Liu, J. Xu, H. L. He, D. Wang, R. Horton and G. Liu, Agric. For. Meteorol., 2022, 323, 109080.
23. T. T. Khuat, R. Bassett, E. Otte, A. Grevis-James and B. Gabrys, Comput. Chem. Eng., 2024, 182, 108585.
24. G. N. Huang, Y. N. Guo, Y. Chen and Z. W. Nie, Materials, 2023, 16, 5977.
25. Y. D. Liu, Q. Yang, Y. Li, L. Zhang and S. Z. Luo, Youji Huaxue, 2020, 40, 3812–3827.
26. D. Cohn, L. Atlas and R. Ladner, Mach. Learn., 1994, 15, 201–221.
27. N. S. Eyke, W. H. Green and K. F. Jensen, React. Chem. Eng., 2020, 5, 1963–1972.
28. A. Pomberger, A. A. P. McCarthy, A. Khan, S. Sung, C. J. Taylor, M. J. Gaunt, L. Colwell, D. Walz and A. A. Lapkin, React. Chem. Eng., 2022, 7, 1368–1379.
29. M. Christensen, L. P. E. Yunker, F. Adedeji, F. Hase, L. M. Roch, T. Gensch, G. Dos Passos Gomes, T. Zepel, M. S. Sigman, A. Aspuru-Guzik and J. E. Hein, Commun. Chem., 2021, 4, 112.
30. A. Vikram, K. Brudnak, A. Zahid, M. Shim and P. J. A. Kenis, Nanoscale, 2021, 13, 17028–17039.
31. R. J. Hickman, M. Aldeghi, F. Häse and A. Aspuru-Guzik, Digital Discovery, 2022, 1, 732–744.
32. Z. D. Chen and J. J. J. Chen, Mixing and Crystallization, Springer, 2000, pp. 43– 56.
33. W. Tran, T. C. Seamans and J. S. Bowers, Biotechnol. Prog., 2023, 39, e3382.
34. Y. Gal and Z. Ghahramani, Proc. Int. Conf. Mach. Learn., 2016, 48, 1050–1059.
35. K. Van't Riet, Ind. Eng. Chem. Process Des. Dev., 1979, 18, 357–364.
36. J. A. G. Torres, S. H. Lau, P. Anchuri, J. M. Stevens, A. G. Doyle, J. E. Tabora, J. Li, A. Borovika and R. P. Adams, J. Am. Chem. Soc., 2022, 144, 19999–20007.
37. K. Y. Zhang, B. Y. Qian, J. S. Wei, C. C. Yin, S. L. Cao, X. Y. Li, Y. J. Cao and Q. H. Zheng, Egypt. Inform. J., 2023, 24, 100412.
38. J. T. Ash, C. Zhang, A. Krishnamurthy, J. Langford and A. Agarwal, arXiv, 2019, preprint, arXiv:1906.03671,  DOI:10.48550/arXiv.1906.03671.
39. B. Shahriari, K. Swersky, Z. Y. Wang, R. P. Adams and N. de Freitas, Proc. IEEE, 2016, 104, 148–175.
40. Y. Sheng, Y. S. Wu, J. Yang, W. C. Lu, P. Villars and W. Q. Zhang, npj Comput. Mater., 2020, 6, 1–7.
41. N. Jiscoot, E. A. Uslamin and E. A. Pidko, Digital Discovery, 2023, 2, 994–1005.

---

Footnote

† Electronic supplementary information (ESI) available: Additional details on model training, data transformations, model deployment, and model interpretation. See DOI: https://doi.org/10.1039/d4re00410h

---