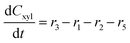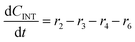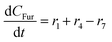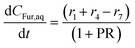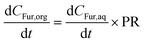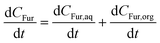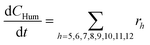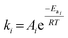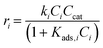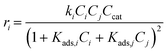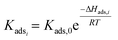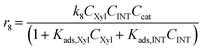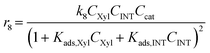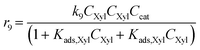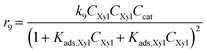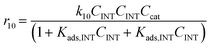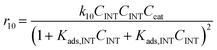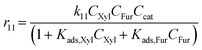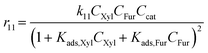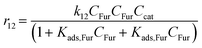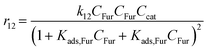Dehydration of xylose to furfural in a biphasic system: catalyst selection and kinetic modelling discrimination†
Received
22nd November 2024
, Accepted 3rd January 2025
First published on 4th January 2025
Abstract
Furfural (Fur) represents an interesting bio-based platform chemical to pave the way to enhanced biorefinery integration in the modern chemicals industry. The production of this xylose- derived compound by its dehydration is catalysed by Brønsted acidity and has effectively been performed in biphasic systems using methyl isobutyl ketone (MIBK), where furfural is effectively partitioned. A selection of commercially available solid acid catalysts were evaluated (different ion exchange resins, zeolites and sulfated zirconia), with top candidates being subjected to recycling experiments over six runs with carbon deposition removal and acid site regeneration. A sulfated zirconia (SO2/ZrO2-1) catalyst proved effective with maximum yield of Fur of 53.8% after 180 min at 160 °C, with xylose conversion of 98.4%. A phenomenological approach to model developments was employed to describe the formation of each component of the reaction scheme and distribution in a biphasic system, with 18 separate kinetic models including both homo- and heterogeneous reaction pathways reported. The most optimal model, identified through statistical model discrimination (RMSE = 0.088), was a pseudohomogenous model with first-order reaction kinetics for xylose conversion to Fur via a reactive intermediate and second-order with respect to humin formation. Apparent activation energies for xylose dehydration were reported at 44.70 ± 7.89 kJ mol−1, with results stating the formation of Fur proceeded preferentially through this reactive intermediate.
1. Introduction
Persistent and sustained over-depletion of fossil-based resources for the production of fuels and chemicals has necessitated a shift in the modern research paradigm towards sustainable alternatives, such as integration of biorefinery concepts and a bioeconomy. Lignocellulosic biomass valorisation provides an avenue for focus towards production of bio-based platform chemicals, such as furans. The two most promising furans are furfural (Fur) from dehydration of pentose (xylose) and 5-hydroxymethylfurfural (HMF) from dehydration of hexose (fructose/glucose) feedstocks.1,2 The relative underutilisation of xylose as feedstock makes the production of Fur an attractive prospect due to the large amounts of xylose present in woody biomass, which is generated in industrial processes such as the kraft pulping process.3,4 The attractiveness of Fur as a platform chemical stems from the relative ease of synthetic upgrading afforded and the vast array of potential products. These products include furfuryl alcohol or tetrahydrofurfuryl alcohol used as solvents, furfurylamine and furoic acid, used in pharmaceutical synthesis, and 2-methylfuran as an octane number enhancer.5–7
Frequently, the dehydration of xylose to Fur is conducted in water at temperatures between 110 and 200 °C with an acid catalyst.2,5 However, these monophasic systems commonly experience low yield and selectivity due to the occurrence of undesired side reactions such as aldol condensation reactions towards insoluble humin polymers.2,8,9 Efforts have been made to mitigate these effects through the use of biphasic systems, where reaction with in situ extraction leverages thermodynamic driving forces to selectively extract Fur from the aqueous phase into an organic phase in a single unit operation.10–13 Design of biphasic systems requires considerations on both the reaction component and the extraction component. Our previous work provides a framework for green solvent selection for HMF and Fur extraction, through combined experimental and computational methods.11 These indicate the use of three greener extraction solvents for Fur extraction, methyl isobutyl ketone (MIBK), cyclohexanone and isophorone. The relative difference in volatility between Fur and MIBK despite the slightly lower partitioning over cyclohexanone makes this a suitable choice as an extraction solvent when considering downstream separations through simple distillation procedures. Furthermore, MIBK is frequently used as a benchmark solvent with widespread use in research environments for in situ extraction of Fur and identified as a green solvent per the CHEM21 green solvent selection guide.14,15
Dehydration of pentose sugars, xylose primarily, towards Fur prefers the use of an acidic medium, specifically those with high-Brønsted acidity, with homogeneous catalysts such as H2SO4 seeing widespread use.16–18 In the theme of process development with considerations of downstream processing, a shift from homogenous to easily separated heterogeneous catalysts is emerging in the literature for sugar dehydration.19,20 Minimisation of environmental impacts is instrumental to longevity of chemical processes; as such the use of heterogeneous catalysts, with reduced corrosiveness over mineral acids such as H2SO4 and HCl, coupled with reduced risk of environmental contamination effects, motivates this shift in catalytic material. Various classes of solid acid catalysts have been explored such as ion exchange resins (IERs), zeolites and metal oxides, for example, supported and unsupported sulfated zirconia and titania.21–28 Kinetic modelling of dehydration using heterogeneous catalysts has been reported in the literature such as Rakić et al. detailing Hβ-catalysed xylose dehydration and Gómez Millán et al. for cordierite-supported sulfated zirconia. These authors developed pseudohomogenous first-order models for all reactions described in an aqueous system.29,30 Additionally, kinetics using a homogeneous acid, HCl, are detailed in the literature by Choudhary et al.31 However, studies modelling biphasic systems are more limited, with Weingarten et al. detailing a H2O/MIBK system that concludes the biphasic system does not alter the fundamental kinetics present in the aqueous phase and facilitates a higher yield.32 Finally, Guo et al. explored the use of HCl/AlCl3 Brønsted/Lewis acid catalysts in a continuous reaction of xylose to Fur in a biphasic microflow reactor. These authors implemented a pseudohomogeneous first-order model for the subsequent reaction kinetics, although considerations of the rates of extraction between water and MIBK were also explored.33 The relative scarcity of literature detailing models for reaction kinetics using heterogeneous catalysts identifies a significant gap in the knowledge vital for industrial scale-up and production of Fur.
Effective process design necessitates the implementation of accurate kinetic models; oversimplification of said models may lead to incorrect sizing of units and inappropriate operating conditions. Additionally, over-parametrisation may induce a forced fit; thus, statistical criteria can be employed to evaluate the model, ensuring a balance between complexity and fit.34 Commonly used metrics to penalise complexity include the Akaike information criteria (AIC) and the Bayesian information criteria (BIC), and Fischer F-values.35,36 Herein, this work details the development of a kinetic model with up to 18 variations to describe the solid acid catalysed dehydration of xylose towards Fur in biphasic media. The literature frequently describes the formation of humins as pseudohomogenous first-order reactions, however we employ phenomenological considerations to expand these simplified models to include bimolecular reactions on heterogeneous catalyst surfaces. Additionally, statistical analysis was performed to discriminate among the models and offer recommendations for biphasic kinetic modelling of Fur production and degradation products.
2. Experimental methodology
2.1. Chemicals and materials
MIBK (CAS: 108-10-1, purity ≥99%) was purchased from Alfa Aesar. Furfural (CAS: 98-01-1, purity ≥99%), isopropyl alcohol (IPA) (CAS 67-63-0, purity ≥99.5%,), and xylose (CAS:58-86-6, purity ≥99%) were purchased from Sigma-Aldrich. H2SO4 (CAS: 7664-93-9, purity 98%) was purchased from Fisher Chemicals. All chemicals were used as received without further treatment. Milli-Q water was supplied by Elga PureLab option Q DV25 at 18.2 mΩ. Ion exchange resins, DOWEX Monosphere 650C (CAS: 127361-69-7), AmberLyst 36 (39389-20-3), and AmberLyst 15 (39389-20-3) were purchased from Sigma-Aldrich. The zeolites HY30 (CAS: 1318-02-1, CVB760), HY15 (CAS: 1318-02-1, CVB720) and mordenite (MOR) (CAS: 1318-02-1, CVB2A) were purchased from Zeolyst. Finally, sulfated zirconia (SO4/ZrO2-1, SO4/ZrO2-2 and SO4/ZrO2-3) were kindly gifted by Luxfer MEL.
2.2. Catalyst characterization methods
Temperature-programmed desorption of ammonia (NH3-TPD) was performed using an Altamira AMI200 instrument with a thermal conductivity detector (TCD) detector. A gas mix of 5% NH3/He with 20 ml min−1 flow rate was run for 30 min at 100 °C; the gas was switched to pure He at 20 ml min−1. Once the TCD baseline was established, the analysis was initiated with a ramp from 100 °C to Tmax (545 °C) at 10 °C min−1 with a 90 min hold at Tmax. Finally, a pulse calibration occurs, wherein a known volume of 5%NH3/He from a loop is pulsed into the He flow, and the detector response is measured over five pulses for an average value. Surface area and total pore volumes were obtained through liquid nitrogen adsorption at −196 °C using a Micromeritics TriStar 3020 analyser, with samples degassed at 300 °C for 30 min under vacuum prior to analysis. Analysis of particle sizes was carried out with a Mastersizer 3000E instrument equipped with laser diffraction. Thermogravimetric analysis (TGA) was performed using a Shimadzu TGA-550 instrument, wherein the samples were heated from 20 °C to 900 °C at a rate of 10 °C min−1 with 40 ml min−1 of air. The preparation of sulfated zirconia catalysts is detailed in Table S1,† where varying dopant loadings of SO3 were used in conjunction with ZrO2 at 610–650 °C for 2 h.
2.3. Catalyst screening and kinetic experiments
Catalytic screening and kinetic runs for the dehydration of xylose was performed in an Anton Paar Monowave 400 microwave (MW) reactor as batch reactions in 30 ml thick-walled glass MW vials. The reaction system comprised a biphasic system H2O/MIBK at a volume ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. The solvents were pre-saturated in each other to avoid volume changes due to their mutual solubility, even if this is limited.37 A 2 wt% catalyst and 10 wt% xylose loading with respect to the aqueous phase was adhered to throughout. All materials were weighed with a Mettler Toledo NewClassic MS (±0.0001 g) balance.
2. The solvents were pre-saturated in each other to avoid volume changes due to their mutual solubility, even if this is limited.37 A 2 wt% catalyst and 10 wt% xylose loading with respect to the aqueous phase was adhered to throughout. All materials were weighed with a Mettler Toledo NewClassic MS (±0.0001 g) balance.
For catalyst screening, the reaction vessels were heated at 160 °C (ramp rate 160 °C min−1) and held for 2 h with magnetic stirring at 800 rpm. Similarly, the kinetic runs were heated to the desired temperature (140–170 °C) at the corresponding ramp rates for different lengths of time, with each data point being obtained from an individual experiment. This batch approach has already been used successfully for the acquisition of kinetic data in a similar reaction.38 Upon reaction completion, the glass vial was air-cooled to 70 °C and then quenched in ice-water before being centrifuged at 3000 rpm for 5 min with an Eppendorf Centrifuge 5702. Finally, both the aqueous and the organic phases were sampled and diluted in a volume ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 with deionised water and IPA, respectively, prior to analysis.
50 with deionised water and IPA, respectively, prior to analysis.
2.4. Catalyst recycling and regeneration
The recyclability of catalysts was determined through a series of recycle and regeneration experiments, with reaction system composition and conditions being identical to those in the catalyst screening. After an initial run, the solid catalyst was separated from the medium by centrifugation followed by vacuum filtration and washed with a solution of IPA and deionised water in equal volumetric parts. Post-wash, the samples were left to dry overnight in a vacuum oven (Thermoscientific VacuTherm VT 6025) at 70 °C at 100 mbar. This procedure was repeated until five recycle runs had been completed. The remaining catalyst after recycling was regenerated through calcination in air using a Nabertherm N7/H furnace at 550 °C for 4 h to remove carbon deposition. A further experimental run was completed with the calcined catalyst, whose acid site regeneration was conducted through the addition of 10 ml 1 M H2SO4 g−1 catalyst for 2 h, with the samples washed with deionised water to remove any acid residue before repeating the final catalytic run.
2.5. Analytical method
Quantitative analysis of reaction samples was conducted using an Agilent 1260A Infinity HPLC system equipped with a Bio-Rad Aminex 87H-HPX ion exclusion column, with 5 mM H2SO4 mobile phase at 50 °C for 60 min. Detection of furfural was achieved through a diode array detector (DAD) at 277 nm and refractive index detector (RID) at 50 °C for xylose. Conversion of xylose was then evaluated through eqn (1).| | 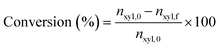 | (1) |
where nxyl,0 is the initial number of moles of xylose and nxyl,f the final. Subsequently, yields and selectivity of components were calculated through eqn (2) and (3), respectively, where ni,f is the moles of desired product i at the end of the reaction.| | 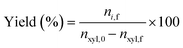 | (2) |
| | 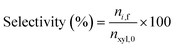 | (3) |
2.6. Kinetic modelling
The kinetic models were developed using the Python language in the JupyterLab 4.0.11 environment. Component mass balances were defined as ordinary differential equations (ODEs) and the Livermore solver for ordinary differential equations with automatic method switching (LSODA) was implemented as the integration method due to robustness when dealing with switches between stiff and non-stiff ODEs.39 An objective function was defined through summation of the root mean square error (RMSE) of each component, eqn (S1),† and the Nelder–Mead minimisation algorithm was employed with a convergence tolerance of 10−5.
For model discrimination, different information criteria and statistical metrics were considered, namely the AIC (eqn (S2)†),40 BIC (eqn (S3)†)41 and Fischer F values (eqn (S4)†). In general, a lower value of RMSE and higher value of F designate an improved model fit with experimental data. Over-parameterisation of models can lead to a forced fit; the AIC and BIC penalises this through determination of parameter adjusted log likelihood, with a more negative value presenting a model closer to true fit.
3. Results and discussion
3.1. Catalyst screening
An initial catalyst screening was performed, evaluating the xylose conversion and Fur yield in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 H2O/MIBK biphasic system. This ratio of aqueous to organic phase volume was chosen as the literature commonly utilises phase volume ratios between 1
2 H2O/MIBK biphasic system. This ratio of aqueous to organic phase volume was chosen as the literature commonly utilises phase volume ratios between 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 of aqueous to organic phase.2,12 Furthermore, the 1
4 of aqueous to organic phase.2,12 Furthermore, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 phase volume ratio would allow minimised downstream separation costs with less costly solvent recycling in the context of a full process concept. A total of nine solid acid heterogeneous catalysts were chosen for the screening from three classes, IERs, sulfated zirconia and zeolites (Table 1). These catalysts were selected for their strong acidity, specifically Brønsted, for the direct dehydration of xylose and commercial availability.
2 phase volume ratio would allow minimised downstream separation costs with less costly solvent recycling in the context of a full process concept. A total of nine solid acid heterogeneous catalysts were chosen for the screening from three classes, IERs, sulfated zirconia and zeolites (Table 1). These catalysts were selected for their strong acidity, specifically Brønsted, for the direct dehydration of xylose and commercial availability.
Table 1 List of the selected heterogeneous solid acid catalysts screened in this work with their acidity, pore volume and surface areas
| Catalyst |
Total acidity (mmol g−1) |
Pore volume (cm3 g−1) |
Specific surface area (m2 g−1) |
|
Acidity obtained by NH3-TPD.
Pore volume and specific surface area were determined using liquid nitrogen adsorption at −196 °C with a Micromeritics TriStar 3020 analyser.
|
| SO4/ZrO2-1 |
5.99a |
0.14b |
98b |
| SO4/ZrO2-2 |
7.13a |
0.29b |
113b |
| SO4/ZrO2-3 |
8.92a |
0.47b |
153b |
| MOR |
0.82 (ref. 42) |
0.36 (ref. 42) |
867 (ref. 42) |
| HY15 |
0.48 (ref. 42) |
0.55 (ref. 42) |
947 (ref. 42) |
| HY30 |
0.63 (ref. 42) |
0.58 (ref. 42) |
946 (ref. 42) |
| Amberlyst-15WET (A15) |
4.70 (ref. 43) |
0.40 (ref. 44) |
53 (ref. 44) |
| Amberlyst-36WET (A36) |
5.40 (ref. 43) |
0.20 (ref. 45) |
33 (ref. 45) |
| DOWEX Monosphere 650C (DOWEX) |
4.80 (ref. 46) |
0.61 (ref. 46) |
35 (ref. 46) |
Preparation details for the sulfated zirconia supplied by Luxfer MEL are detailed in Table S1,† with the calcination temperature set at either 650 °C (SO4/ZrO2-1 and SO4/ZrO2-2) or 610 °C (SO4/ZrO2-3) for 2 h, with SO3 dopant loadings of 6%, 8.1% and 6%, respectively, for SO4/ZrO2-1, SO4/ZrO2-2 and SO4/ZrO2-3. Additional information on catalyst characterisation is available in Table S2.†Fig. 1 presents Fur yield in both the aqueous and the organic phases alongside the xylose conversion at 160 °C after 2 h for the nine studied catalysts; a non-catalytic run was also presented. This non-catalytic dehydration of xylose demonstrated the autocatalytic nature of the reaction.9 At elevated temperatures, the concentration of OH− and H3O+ increases, thus providing the acidity required for the dehydration reaction of xylose to proceed, where at 190 °C the equivalent acidity of pure water is approximately 2.93 μmol g−1.47 The maximum yield achieved by Jakob et al. was reported as 45% after 165 min at 190 °C, compared to the 20.4% achieved in this work at 160 °C for 2 h.9 Brønsted acidity was the primary requirement for initial catalysts selection, alongside those exhibiting Lewis acidity to a lesser extent, where the IER only exhibited Brønsted acidity and the sulfated zirconia and zeolites presented both Brønsted and Lewis acidity. Dehydration of xylose with a solid acid catalyst with both Brønsted and Lewis acidity generates a reaction intermediate, as detected by HPLC, as shown in Fig. S1.† This intermediate, xylulose, according to previous studies, is plausible owing to Lewis acidity typically promoting the isomerisation of sugars, as is the case of glucose to fructose isomerisation,30,33 which is of relevance in the HMF production reaction.48 This was confirmed by the presence of the intermediate in six out of the nine catalysts, with only the IERs showing no formation of xylulose due to the lack of Lewis acidity present.29 The Lewis acidity for the sulfated zirconia and zeolites arises from the structures of the metal framework ions through coordinately unsaturated cations. Conversely, the IER contains purely the sulfonic groups for the Brønsted acidity with a polymeric framework structure instead.
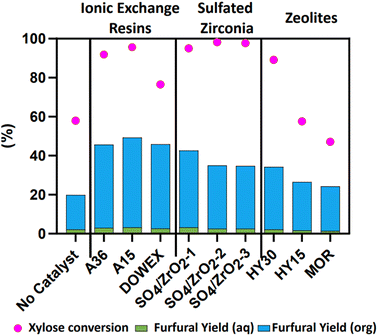 |
| | Fig. 1 Catalyst screening (2 wt% loading) for the dehydration of 10 wt% xylose in a H2O/MIBK system (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 by volume) at 160 °C for 2 h at 800 rpm. 2 by volume) at 160 °C for 2 h at 800 rpm. | |
The highest-performing catalyst in terms of total Fur yield was A15 at a value of 49.2% at 95.5% xylose conversion. Additionally, the DOWEX catalyst was observed to have the highest selectivity among the IER at a value of 59.95%. As a whole, IERs exhibited yields of Fur greater than 40%, although some literature reports yield with A36 as low as 0.75%.49 Sulfated zirconia reported lower yields than IERs but higher than the zeolites, with SO4/ZrO2-1 being the best candidate at 39.4% and SO4/ZrO2-2, SO4/ZrO2-3 both at 32% with a similar conversion of xylose. MOR and HY15 both have similar yields of Fur with the lowest conversion rates of 47% and 57%, respectively. Gürbüz et al. reported yields of 79% at 175 °C in a monophasic H2O–GVL system of 10 wt% water; the authors concluded that increased water concentrations greatly diminished Fur yields.50
3.2. Catalyst recycling
Reusability, stability and regeneration of catalysts through multiple reaction cycles is of paramount importance to developing robust, scalable, and economic chemical processes. For this reason, from the previous screening, the top performing catalysts, based on Fur yield, of each class were chosen for recyclability experiments, namely A15, SO4/ZrO2-1 and HY30. These were subsequently recycled for a total of five runs, with post-reaction washing with IPA and deionised water to remove any soluble material from surfaces and finally dried in a vacuum oven (Fig. 2). Initially considering the performance of A15, the total yield fell from a total yield of 46% to 26% with notable visible changes in colour of the individual structures (Fig. 2a). HY30 and SO4/ZrO2-1 were regenerated through calcination in air to remove any carbon deposition on the surface generated through humin production, although this approach was unsuitable for A15 due to its entire degradation in the furnace considering its limited maximum operating temperature of 120 °C,44 which would also make it unsuitable for long-term operation, even under the assumption that it would not be recycled. For SO4/ZrO2-1 and HY30, the TGA results shown in Fig. S2† indicate that the carbon deposition was completely removed at temperatures greater than 500 °C, which agrees with previous work in the literature for the production of furans.51,52 Visible changes of the catalysts post-wash with an equal mix of deionised water and IPA are presented in Fig. S3,† where a clear change in colour from white to dark brown is observed over the course of reactions and the white colour returned after calcination, hence showing the effectiveness of the regeneration approach. The SO4/ZrO2-1 suffered performance loss across the cycles, yet this was to a lesser degree than the A15 (Fig. 2b). Remarkably, the yields generated from HY30 (Fig. 2c) remained constant throughout the runs, affirming that it may be a strong choice for long-running continuous processes or numerous sequential batch reactions. Calcination returned both the SO4/ZrO2-1 and HY30 to near initial yields of 40.6% and 30.3%, respectively. Subsequent regeneration of the acid sites with 1 M H2SO4 g−1 catalyst returned both catalysts to original performance, signalling that the primary method of deactivation was due to the carbon deposition on the catalyst structures. Selectivities of both SO4/ZrO2-1 and HY30 are comparable after the initial run at values of 44.4% and 46.3%, respectively, with final selectivities of 49.9% and 53.9%. This selectivity, in conjunction with the greater yields observed, allows for the clear selection of SO4/ZrO2-1 as the best candidate for kinetic modelling. The dismissal of A15 as a candidate can be attributed to the inability to effectively remove humin deposition through calcination and continued operation above the manufacturer's temperature limit.
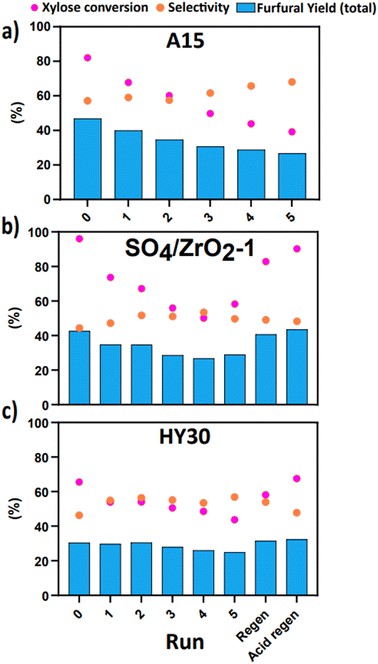 |
| | Fig. 2 Cyclic deactivation test for the dehydration of 10 wt% xylose in a H2O/MIBK system (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 by volume) at 160 °C for 2 h at 800 rpm over (a) A15, (b) SO4/ZrO2-1 and (c) HY30 (2 wt% loading). 2 by volume) at 160 °C for 2 h at 800 rpm over (a) A15, (b) SO4/ZrO2-1 and (c) HY30 (2 wt% loading). | |
3.3. Catalyst dehydration of xylose with sulfated zirconia
Effective evaluation of mass transfer limitations is vital to ensure that the experimental results show reaction performance and not a combination of this phenomenon with mass transfer phenomena. To prove this, the reaction performance was tested through variation of agitation rates in a range of 100–800 rpm (Fig. S4†).53 Results clearly show no significant effect in rate of change of Fur yield or conversion of xylose over the first 30 min of experimental runs. Thus, it can be concluded that there are no prevailing external mass transfer limitations. Internal mass transfer limitations are resultant from intraparticle diffusion, where the reactants diffuse from the bulk phase to the catalyst pores and vice versa for the products. This internal diffusion can be rate limiting at sufficient particle size; however, this can be deemed negligible and ignored due to the low particle size of the SO4/ZrO2-1 catalyst (d90 <8.3 μm and d50 <2.7 μm).54
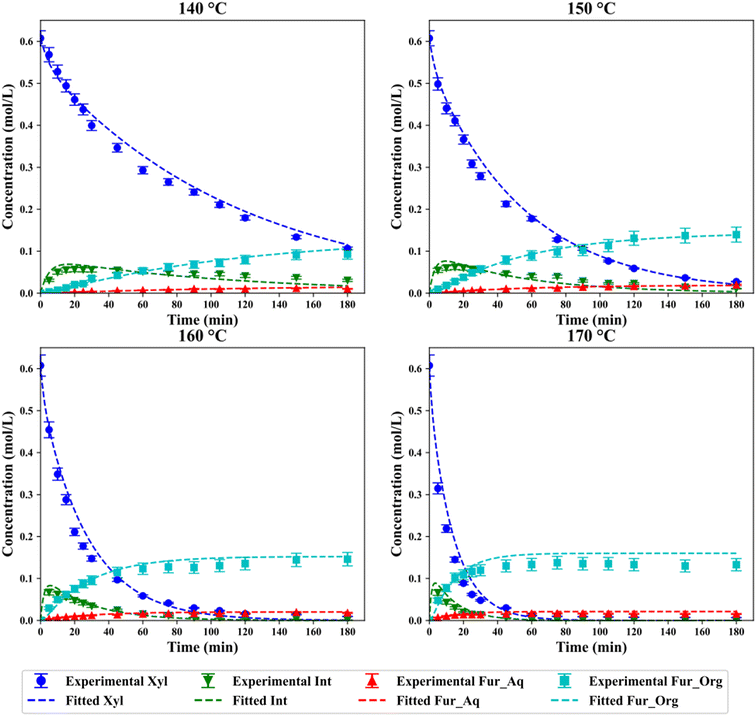
Catalytic experiments with SO4/ZrO2-1 were performed with a total of four temperatures chosen from 140–170 °C, with the evolution of the yield of Fur and xylose conversion shown in Fig. 3a and b, respectively.
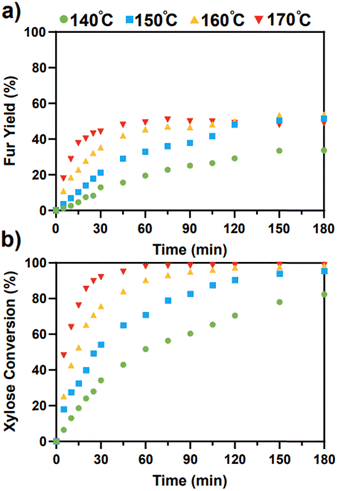 |
| | Fig. 3 (a) Fur yield and (b) xylose conversion with 2 wt% SO4/ZrO2-1 and 10 wt% xylose loading in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 H2O/MIBK system. 2 H2O/MIBK system. | |
The highest yield of Fur was observed after 150 min at 160 °C, with a value of 53.4%, although similar yields were attained in just 75 min at 170 °C. This decreased total yield of Fur at higher temperatures and plateaus observed indicates the degradation of Fur at higher temperatures.9 Gómez Millán et al. reported a yield of 38% of Fur after 60 min at 170 °C with sulfated zirconia on a cordierite support in a monophasic system, which is lower than the 49% observed under the same conditions in this work.29 This initial comparison indicates the improvements that the separation of Fur into a secondary phase have on the final yields, although Fur is still maintained at the higher temperatures which may lead to further degradation. As expected, the conversion of xylose increased with respect to temperatures, with maximal conversions at 140, 150, 160 and 170 °C of 82.4%, 95.4%, 98.4% and 98.9%, respectively.
3.4. Kinetic modelling considerations
3.4.1. Reaction pathway.
Kinetic modelling of the reaction network is essential for subsequent reactor design as well as process design and simulation. Considering the nature of the reaction studied and the observed reaction intermediate, identified in the literature as xylulose (see Fig. S1†), Fig. 4a presents the possible reaction pathway.9,55,56 Furthermore Choudhary et al. determined that the isomerisation of xylose to xylulose is more kinetically and thermodynamically favourable than the epimerisation towards lyxose. As expressed in Fig. 4a, here the initial substrate can directly dehydrate to Fur (r1). Alternatively, it could also isomerise to xylulose (denoted intermediate), which typically is a reaction in equilibrium (r2 and r3), with xylulose further reacting to Fur (r4). Operating in a biphasic medium, there would also be the transfer of Fur to the MIBK phase by extraction. In addition, humins can be produced as degradation products from the reactions from xylose (r5), the intermediate (r6) and Fur (r7). Pseudohomogeneous kinetics for formation of humins have been detailed in the literature before by authors such as Rakić et al. and Weingarten et al.30,32 However, issues could arise from considering the formation of humins as a single entity, for this reason, as reflected in Fig. 4b; here we also consider the possibility of bimolecular mechanisms, associated with heterogeneous catalysis, where humins may result from self- or cross-condensation reactions of all species present, i.e. xylose, intermediate and Fur.
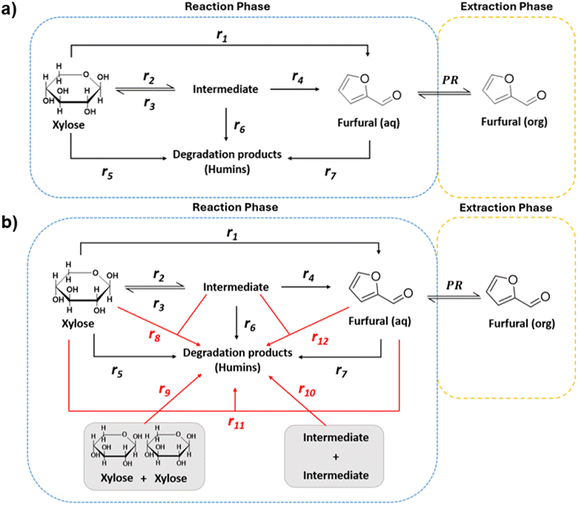 |
| | Fig. 4 Reaction pathways for the dehydration of xylose to Fur. (a) Pseudohomogeneous mechanisms for all species, (b) bimolecular heterogeneous mechanisms for degradation product formation. | |
3.4.2. Assumptions and simplifications of the model.
A number of key assumptions have been made in order to develop the model. As addressed in the previous section, at the selected stirring conditions (800 rpm) and considering the small particle size (d90 < 8.3 μm), it can be assumed that operation occurs under a regime with no bulk mass transfer limitations.54 Consequently, the extraction phenomenon of Fur from the aqueous to the organic phase can be assumed to occur instantaneously.32 Thus, it can be considered that the concentration of Fur in the MIBK phase is proportional to that in the aqueous phase, which is described through the partition ratio (PR), as described in eqn (4).| | 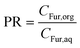 | (4) |
where PR is defined as the concentration (g L−1) of Fur in the organic phase, CFur,org, over the concentration (g L−1) in the aqueous phase, CFur,aq.
The initial volume ratio of the H2O/MIBK system was set at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, with pre-saturation of phases to mitigate volume changes resulting from mutual solubilities,11 which otherwise would have to be considered.38 In the microwave device employed, the set temperature is reached after approximately 1 min,57 which can be considered a negligible amount of time in comparison to the duration of the reaction until quantitative conversion is attained. For this reason, a temperature gradient is dismissed in this model and the consequent variation of system properties that it could entail.38 However, for the kinetic experiments, the volume and phase ratio changes owing to operation at temperatures greater than room temperature are considered. Guo et al. developed a correlation for H2O/MIBK at various ratios of organic to aqueous volumes (Org
2, with pre-saturation of phases to mitigate volume changes resulting from mutual solubilities,11 which otherwise would have to be considered.38 In the microwave device employed, the set temperature is reached after approximately 1 min,57 which can be considered a negligible amount of time in comparison to the duration of the reaction until quantitative conversion is attained. For this reason, a temperature gradient is dismissed in this model and the consequent variation of system properties that it could entail.38 However, for the kinetic experiments, the volume and phase ratio changes owing to operation at temperatures greater than room temperature are considered. Guo et al. developed a correlation for H2O/MIBK at various ratios of organic to aqueous volumes (Org![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Aq).38 The results indicate that volume and phase ratio changes are significant and these have been considered, using the information featured in Table S3,† with the resultant ratios (Org
Aq).38 The results indicate that volume and phase ratio changes are significant and these have been considered, using the information featured in Table S3,† with the resultant ratios (Org![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Aq) presented in Table S4.†
Aq) presented in Table S4.†
where
γ is the correction factor to the change of volume of each phase (aqueous or organic) after separation at temperature
T in °C, and
u,
v and
w, are fitting parameters determined by Guo
et al. at varying temperatures and Org
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
Aq ratios using Aspen Plus simulations.
38
3.4.3. Mass balances.
Component mass balances for an ideal isothermal batch reaction with no internal or external mass transfer limitations are derived from Fig. 4a with all concentrations of components (Ci) given in units of mol L−1, which can be expressed by the following ordinary differential equations:| | 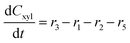 | (6) |
| | 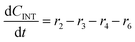 | (7) |
| | 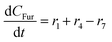 | (8) |
When considering a biphasic system, the CFur (mol L−1), the separation of terms into the concentration in the organic and aqueous phase must be implemented (eqn (9)–(11)). Here, PR is used as a proportionality constant between the concentration of Fur in each phase. Fig. S5† shows an analysis of PR value at different temperatures considering each experimental data point across the full experimental time of 180 min. Thus, for simplicity in modelling the value of PR was considered constant at 7.5 in accordance with the negligible variation if the standard deviations are considered.| | 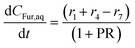 | (9) |
| | 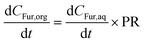 | (10) |
| | 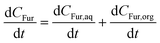 | (11) |
These component balances are developed as the base case model, wherein there are no additional terms considered for bimolecular heterogeneous reactions towards degradation products. Finally, due to inhomogeneity in the humin degradation products, which renders accurate direct quantification impossible by the chromatography analytic technique applied, these have therefore been considered as a lumped species denoted “humins”, and calculated from the mole balance (eqn (12)), where n refers to the number of moles of component at 0, the start, or f, the end of reaction.| | | nhum,f = nxyl,0 − (nxyl,f + nint,f + nfur,f) | (12) |
Considering the different reaction pathways in Fig. 5, the dynamic evolution of humins can be expressed by different combinations of reactions, with reactions r5, r6 and r7 and different combinations featuring either r8, r9, r10, r11 or r12, as will be described in the cases considered:| | 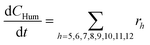 | (13) |
where h represents a reaction that produces humins as per the corresponding assumption.
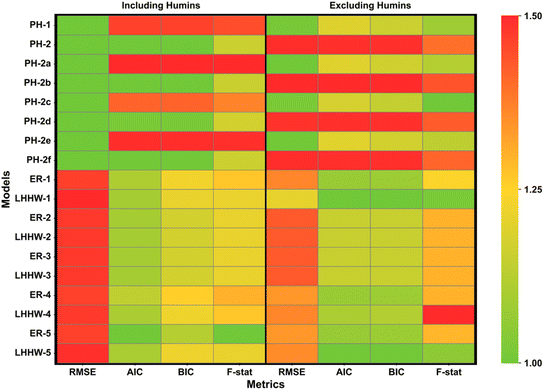 |
| | Fig. 5 Comparison of models considered; data are normalised with respect to the most favourable value, both including and excluding humins from fitting criteria. | |
3.4.4. Reaction rates and model cases considered.
Rate constants for pseudohomogeneous (PH) models can be calculated through eqn (14),where ri is the rate of reaction for reaction i, ki the rate constant for reaction i, and Cmi the concentration of component i in mol L−1 in the order of reaction m. Ccat is the concentration of active sites of SO4/ZrO2-1 (at 2.39 × 10−2 mmolcat L−1).
The dependency of the rate constants with respect to temperature is given by the Arrhenius equation, eqn (15):
| | 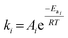 | (15) |
where
Ai is the pre-exponential factor of reaction
i,
Eai the activation energy (kJ mol
−1), with the ideal gas constant
R (J mol
−1 K
−1) at temperature
T (K).
The dehydration of xylose through an intermediate towards Fur and humins was initially modelled exclusively as a pseudohomogeneous model.9,30 However, the generation of humins could be regarded as heterogeneous bimolecular reactions; thus, the models considered can be expanded to include the Eley–Rideal (ER), and Langmuir–Hinshelwood–Hougen–Watson (LHHW) heterogeneous catalytic mechanisms, whose general equations are presented in eqn (16) and (17). These models include the adsorption of species (Kads,i) onto the catalyst surface, where this adsorption constant is calculated through the van't Hoff equation (eqn (18)), where Kads,0 is the pre-exponential factor and ΔHads,i is the enthalpy of adsorption (kJ mol−1), also dependent on temperature:
| | 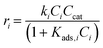 | (16) |
| | 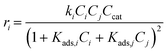 | (17) |
| | 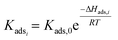 | (18) |
The literature frequently details the dehydration of xylose through pseudo first-order homogenous kinetics.
9,29,30 Thus, it was appropriate to use this model as a base case, with the general form for all reactions
r1 to
r7 and denote this PH-1 (
eqn (19)). However, the specific details of formation of humins as a degradation product are less understood; hence the proposal of second-order reactions for the direct formation of humins was developed, with the initial model PH-2 (
eqn (20)–(22)), where all reactions towards humins were considered as second order (
r5,
r6,
r7). To investigate the influences that individual components have on the generation of humins, various combinations of second-order reactions were evaluated. PH-2a, PH-2b and PH-2c consider the second-order reactions of xylose, intermediate and Fur to humins, respectively (
eqn (23)–(25)). Finally, combinations of two components with second-order kinetics were considered in PH-2d (xylose and intermediate,
eqn (26) and
(27)), PH-2e (xylose and Fur,
eqn (28) and
(29), and PH-2f (xylose and Fur,
eqn (30) and
(31)).
PH-1
PH-2
PH-2a
PH-2b
PH-2c
PH-2d
PH-2e
PH-2f
With the complexity of the aldol condensation reactions towards humins, heterogeneous models may be more appropriate to describe the bimolecular process. Hence, a selection of 10 heterogenous models are presented, five of which are derived from ER kinetics and the remainder from LHHW. These cases considered include the base case reactions in first-order pseudohomogeneous (
r1–
r7) in addition to the relevant additional reaction pathways for heterogenous cases considered (
r8–
r12). Similar models have been implemented for the dehydration of sorbitol and methyl salicylate, for mono-molecular heterogeneous kinetics for dehydration.
58,59 The first heterogeneous models considered were the combination of xylose and intermediate, denoted ER-1 and LHHW-1 (
eqn (32) and
(33)). Considering two molecules of either xylose or intermediate are detailed by ER-2/LHHW-2 (
eqn (34) and
(35)) and ER-3/LHHW-3, respectively (
eqn (36) and
(37)). Finally, those involving Fur and xylose or intermediate are specified by ER-4/LHHW-4 (
eqn (38) and
(39)) and ER-5/LHHW-5 (
eqn (40) and
(41)), correspondingly.
ER-1
| | 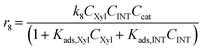 | (32) |
LHHW-1
| | 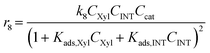 | (33) |
ER-2
| | 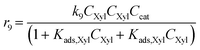 | (34) |
LHHW-2
| | 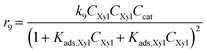 | (35) |
ER-3
| | 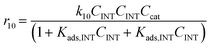 | (36) |
LHHW-3
| | 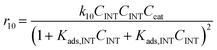 | (37) |
ER-4
| | 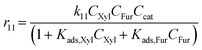 | (38) |
LHHW-4
| | 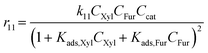 | (39) |
ER-5
| | 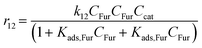 | (40) |
LHHW-5
| | 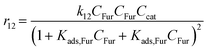 | (41) |
3.5. Model discrimination
Fitting of a total of 18 different variations of the kinetic model to the experimental data collected was conducted. To evaluate the performance of each model, the values of RMSE, AIC, BIC and F were assessed, where the lower the values of RMSE, AIC and BIC and the higher the F value, the better model performance. Fig. 5 presents a heatmap of normalised values of each discrimination criterion, where green and red represent more and less favourable model performance, respectively. The difficulty in describing humin formation with mathematical approaches justified the evaluation of model performance including and excluding the evolution of humin concentrations in the metrics. The true pre-normalised metrics are provided in Table S5,† with normalisation against the lowest (RMSE, AIC and BIC) or highest metric (F values) within the series applied to allow generation of a heatmap.60
PH-1, treated as the base case in this work, performs relatively well in all aspects with RMSE values <0.10, and AIC and BIC values of −1845 and −1771, respectively. PH-2, PH-2b, PH-2d, and PH-2f all performed to similar standards when accounting for humin formation, with PH-2 chosen as the best model due to the inclusion of second-order rate towards humins for all three degradation pathways. PH-2b surprisingly performed well, with one of the highest F values in the set (86.2), despite the relatively low concentrations of intermediate generated in the reaction as a fraction of total mass. The fast production of this reactive intermediate species and final route to either Fur or humins indicate heavily that this may be a second-order reaction. As a whole, homogeneous model RMSE values were lower than those of heterogeneous models, agreeing with the literature that the dehydration of xylose primarily follows a pseudohomogeneous model.61
The performance of heterogeneous models exceed that of the homogeneous model sets when excluding the humin formation. The core of this is as a result of enhanced fits for both xylose and Fur in the organic phase, both frequently overpredicted in all cases. The standout heterogenous models are LHHW-1 and LHHW-5, which consider the bimolecular reactions of xylose−intermediate (r8) and intermediate−Fur (r12), respectively. Additionally, LHHW-1 performs well even when including the humin production with RMSE of 0.12, AIC of −1916, BIC of −1816 and an F value of 82.4. These statistical metrics, penalising over-parameterisation in the case of AIC and BIC, indicate that despite the increased parameters over the homogeneous models (an additional six parameters) the fitting is sufficient. When considering the exclusion of humin formation from the homogenous model sets, the opposite results appear as to when the inclusion was considered; thus the second-order reaction rates heavily favour humin production, as intended, yet limit the performance of fitting other components. The model selection for the remainder of this work focused specifically on the best performing model when humins were included, PH-2, and when humins were excluded, LHHW-1. From a holistic point of view towards process development, the exclusion of humins from reaction engineering is unadvised, although this does provide an insight into the influence that these degradation products hold in any acid-catalysed sugar dehydration in aqueous medium.
3.6. Model performance
Model discrimination yields two potential models for the dehydration of xylose, PH-2 for the complete system and LHHW-1 excluding humin production. The fitted model for PH-2 is displayed in Fig. 6, with errors applied to the experimental work. Fittings in general for all components except for humins lie within a suitable range with an overall RMSE of 0.088. Consistent overprediction of humins and Fur in the organic phase after approximately 60 min is observed, with minor over-predictions for the remaining components at all temperatures. The overestimation of humins could be attributed to the consideration of humin as a final end product, which may not be accurately describing the intricacies of the aldol condensation reactions occurring.9,62 Quantitative evaluation of overestimation of the model through mole balances at each temperature results in a maximum of 8.45% overestimation at 150 °C and 150 min, with the average mole balance overestimation at temperatures of 140–170 °C at 1.09%, 2.52% 4.85% and 5.06%, respectively. Finally, the latter half of the modelled data for all temperatures at time >90 min exhibited the highest overestimation with a value of 6.02 ± 2.42%. The operation of the reaction within the kinetic regime <45 min observed only minor deviations from the experimental results and modelled data with an average of −1.23%.
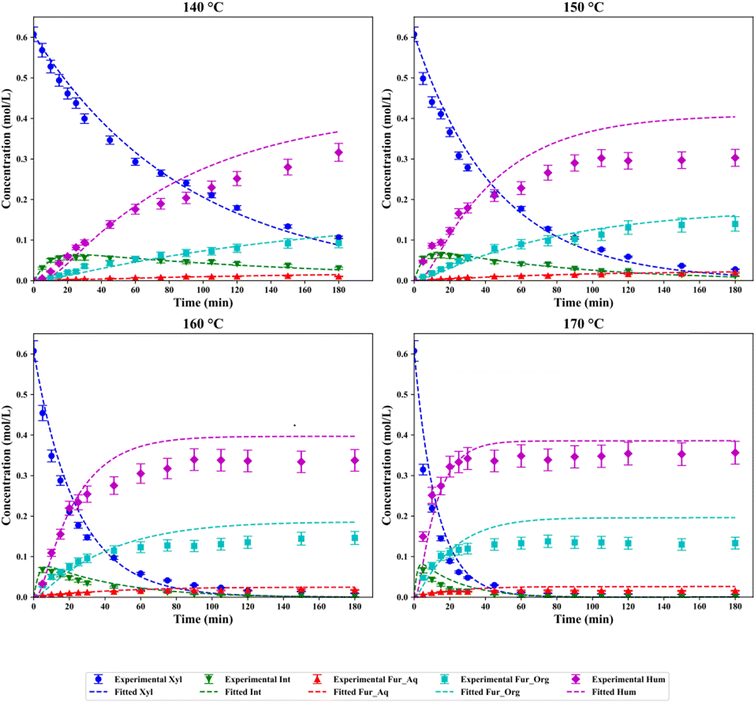 |
| | Fig. 6 Experimental and fitted data for the dehydration of xylose in a H2O/MIBK system at temperatures of 140–170 °C for the PH-2 model. | |
Optimised parameters achieved through minimisation of the objective function using the Nelder–Mead minimisation algorithm are shown in Table 2. The direct dehydration of xylose to Fur (r1) yields an apparent activation energy of 44.70 ± 7.89 kJ mol−1 for the SO4/ZrO2-1 catalyst in this work. Gómez Millán et al. used a cordierite-supported sulfated zirconia and reported an activation energy of 121 kJ mol−1.29 The direct dehydration is detailed in numerous other studies with a variety of heterogeneous catalysts in monophasic media such as Glu-TsOH-Zr (222.18 ± 12.2 kJ mol−1), Nafion NR50 (112 kJ mol−1) and H-SAPO-34 (120.4 kJ mol−1),63–65 although typical ranges for the dehydration are cited in the literature from approximately 112–123 kJ mol−1.66 Other authors have reported activation energies of as low as 30 ± 3 and 47.5 ± 9.9 kJ mol−1, which are more in line with those reported in this work.9,30 These studies also consider the formation of a reactive intermediate in the presence of Lewis acidity, proposed to be xylulose, which further degrades to Fur or isomerises back towards xylose, reducing the activation energy for the direct xylose to Fur pathway.67 This reactive intermediate, according to the rate constants, preferentially favours the forward reaction towards Fur rather than isomerisation back to xylose with a magnitude of 103. This is in accordance with Jakob et al., where the authors proposed that the Lewis acidity driven forward isomerisation rates were several orders of magnitude greater than the reverse counterpart at 8.4 × 10−1 min−1versus 6.97 × 10−6 min−1, with an Hβ catalyst at 160 °C.9 Magnitudes of rates of reactions, which can be calculated through eqn (14) and (15) and data provided in Table 2, confirm the favourability of the progression of reaction through the intermediate species. This rapid generation, degeneration and Fur production can be shown in Fig. 6 due to the relatively small minor fractions quantified in results analysis, at peak values <10% of xylose feed. The large involvement of the intermediate in formation of either Fur or humins is supported by the model discrimination employed, where for the model variations including second-order kinetics for intermediate species, the statistical criteria are more favourable, as seen in Fig. 5.
Table 2 Pre-exponential factors and activation energies for the dehydration of xylose using model PH-2 at a temperature range of 140–170 °C with SO4/ZrO2-1. Errors at 95% confidence interval
| Reaction |
A (L2 mol−1 mmolcat−1 min−1) |
E
a (kJ mol−1) |
| 1 |
0.37 ± 0.04 |
44.70 ± 7.89 |
| 2 |
2.10 × 1012 ± 7.53 × 1010 |
100.12 ± 5.83 |
| 3 |
5.23 ± 3.02 × 105 |
62.36 ± 6.14 |
| 4 |
9.28 × 1011 ± 4.30 × 1010 |
96.10 ± 11.97 |
| 5 |
1.74 ± 0.14 |
41.75 ± 9.34 |
| 6 |
3.22 × 1010 ± 2.74 × 109 |
70.46 ± 8.65 |
| 7 |
4.31 ± 0.42 |
86.18 ± 12.96 |
Whilst the direct effects of MW heating and subsequent MW responsivity of the SO4/ZrO2-1 catalyst were not specifically investigated here, it has been reported that MW absorption can positively influence reaction kinetics at the solid interface,32,68 where sulfated zirconia is microwave transparent at low temperatures (<200 °C), although rapid evolution of the dielectric loss factor was reported at temperatures greater than 600 °C.69,70
However, overestimations are observed for humin generation at all temperatures. Maximum overestimates were observed at 180 min of 33.8% at 150 °C and 8.3% at 170 °C, with respect to the average experimental value, although such overprediction becomes less apparent considering the experimental error. The parity plot depicted in Fig. 7 provides insight into the experimental versus predicted concentrations, where the consideration of a simple linear regression of the entire set of data retrieved an R2 value of 0.9519. The plot also depicts the ±10% confidence limits, with the results displaying minor underestimation of component concentrations at low values, except for the intermediate formation which is primarily overpredicted. This overprediction comes from the difficulty in capturing the rapid nature of intermediate formation and consumption, especially at higher temperatures where after 60 min at 170 °C no intermediate is observed. Overprediction was particularly prevalent in humin formation and, to a lesser extent, in Fur formation in the organic phase, especially in the latter stages of the reactions.
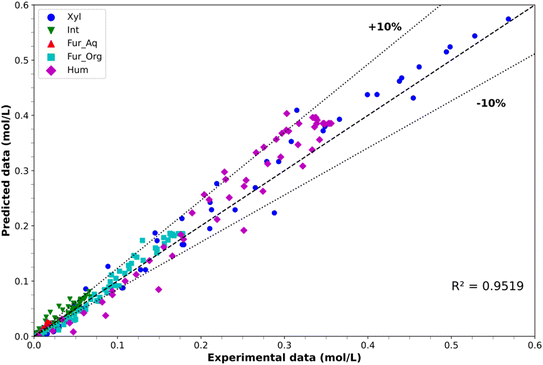 |
| | Fig. 7 Experimental concentration vs. predicted concentration parity plot for model PH-2. | |
Finally, the removal of humins from considerations of model fittings leads to the selection of LHHW-1 as an effective model. Here the deviation in the remaining components is less than that of the PH-1 model, as can be observed in Fig. 8, with an RMSE of 0.0455. Prediction of component concentrations with respect to time and the errors in experimental points are accurately captured for the most part. The prediction of Fur in the organic phase is also more akin to experimental data than that of the PH-2 model.
 |
| | Fig. 8 Experimental vs. fitted concentration profiles for the SO4/ZrO2-1 catalysed dehydration of xylose with the LHHW-1 model, and humin fitting excluded. | |
Effective evaluation of the application of LHHW-1 for the dehydration of xylose requires physical and phenomenological evaluation of generated activation energies and adsorption enthalpies. The modelled parameters are detailed in Table 3. Activation energy for the direct conversion of xylose to Fur is significantly higher than that proposed by the PH-2 model at a value of 146.10 ± 15.67 kJ mol−1, and subsequently an order of magnitude greater than those involving the reactive intermediate. The higher barrier to activation implies that the reactive intermediate to Fur formation is the dominant path from xylose, in conjunction with the extremely large pre-exponential factors, A2, A3, A4, and A6. An unusually high value of activation energy for the degradation of Fur to humins of 424.1 ± 90.89 kJ mol−1 is determined by the model, although this supports that the degradation of Fur to humins is not the primary mechanism. The remaining reactions towards humins all proceed with activation energies in the range 21.99–148.90 kJ mol−1, with the bimolecular reaction of xylose and intermediate being the highest at 148.9 ± 16.33 kJ mol−1. Further insights into the reaction mechanism phenomena can be garnered from the values of adsorption enthalpy of xylose (ΔHa,1 = −2265.14 ± 734.86 kJ mol−1) and the intermediate (ΔHa,2 = −205.36 ± 12.54 kJ mol−1). This difference in magnitude supports the claim of the intermediate being the more reactive species for humin formation as well.33
Table 3 Pre-exponential factors, activation energies and adsorption enthalpies for the dehydration of xylose using model LHHW-1 in the temperature range of 140–170 °C with SO4/ZrO2-1. Errors at 95% confidence intervala
| Reaction |
A (L mmolcat−1 min−1) |
E
a (kJ mol−1) |
| 1 |
0.38 ± 0.09 |
146.10 ± 15.67 |
| 2 |
1.08 × 1011 ± 0.17 × 1011 |
86.99 ± 21.54 |
| 3 |
1.68 × 107 ± 0.24 × 107 |
51.72 ± 8.95 |
| 4 |
1.19 × 1012 ± 0.07 × 1012 |
96.74 ± 12.31 |
| 5 |
3.93 ± 1.03 |
21.99 ± 4.66 |
| 6 |
1.52 × 1011 ± 0.19 × 1011 |
86.01 ± 8.75 |
| 7 |
8.55 ± 2.31 |
424.1 ± 90.89 |
| 8 |
24.8 ± 3.97a |
148.9 ± 16.33 |
| Component adsorption |
K
a,0 (L mol−1) |
ΔHa (kJ mol−1) |
|
L2 mol−1 mmolcat−1 min−1.
|
| Xylose |
6.59 × 10−2 ± 3.14 × 10−2 |
−2265.14 ± 734.86 |
| Intermediate |
5.65 × 102 ± × 0.78 × 102 |
−205.36 ± 12.54 |
4. Conclusion
This work provides a comprehensive evaluation of catalytic performance for the dehydration of xylose to Fur with its in situ extraction in a H2O/MIBK biphasic system, from catalyst screening, recycling and determination of kinetic parameters. The stability and recyclability of commercial sulfated zirconia, SO4/ZrO2-1, proved effective. 18 variations of kinetic models were generated to account for the phenomenology. These variations included the generation of a reactive intermediate compound as well as the non-uniformity and complexity of humin production through homogeneous and heterogeneous approaches considering mono- and bimolecular mechanisms.
Applying statistical model discrimination criteria, the results conclude that the model that best describes the evolution of the species in the reaction is PH-2, where the formation of humin degradation products are modelled as second-order pseudohomogeneous reactions, with the rest first-order. However, the general minor overestimation of pseudohomogeneous models coupled with the poor fitting of heterogenous models indicates that the humin production mechanism remains elusive. The presence of Lewis acidity drives the isomerisation to a reactive intermediate, although the direct reaction catalysed by Brønsted acidity observes a lower energy barrier of 44.70 ± 7.89 kJ mol−1 compared to 96.10 ± 11.97 kJ mol−1 for intermediate to Fur production. The potential for Fur to degrade into humins suggests that the reaction times could be conducted at higher temperatures (>170 °C) for shorter reaction times (>60 min), where the model provides excellent linearity of predictions with R2 at 0.9512.
The outlook of the results detailed in this work have implications in the design of efficient biphasic systems for the production of Fur from xylose, where humin production is a significant issue.
Data availability
The data supporting this article have been included either in the main manuscript or as part of the ESI.†
Author contributions
Dominik Soukup-Carne: conceptualization, methodology, formal analysis, investigation, data curation, software, validation, writing – original draft, writing – review & editing, visualization. Ben Hillman: methodology, investigation, visualization. Christopher M. A. Parlett: conceptualization, resources, writing – review & editing, supervision. Xiaolei Fan: conceptualization, writing – review & editing, supervision, project administration, funding acquisition. Jesús Esteban: conceptualization, methodology, investigation, resources, writing – original draft writing – review & editing, supervision, project administration, funding acquisition.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The University of Manchester is acknowledged for a PhD scholarship for DSC. JE gratefully acknowledges grant RYC2022-035654-I funded by MICIU/AEI/10.13039/501100011033 and by ESF+. The authors would also like to thank LuxferMEL for kindly supplying the sulfated zirconia catalysts and characterisation data.
References
- J. J. Bozell and G. R. Petersen, Technology development for the production of biobased products from biorefinery carbohydrates—the US Department of Energy's “Top 10” revisited, Green Chem., 2010, 12(4), 539–554 RSC.
- D. Soukup-Carne, X. Fan and J. Esteban, An overview and analysis of the thermodynamic and kinetic models used in the production of 5-hydroxymethylfurfural and furfural, Chem. Eng. J., 2022, 442, 136313 CrossRef CAS.
- T. Oksanen, J. Buchert and L. Viikari, The Role of Hemicelluloses in the Hornification of Bleached Kraft Pulps, Holzforschung, 1997, 51(4), 355–360 CrossRef CAS.
- G. Gómez Millán, R. P. Bangalore Ashok, P. Oinas, J. Llorca and H. Sixta, Furfural production from xylose and birch hydrolysate liquor in a biphasic system and techno-economic analysis, Biomass Convers. Biorefin., 2021, 11(5), 2095–2106 CrossRef.
- N. W. Dulie, B. Woldeyes, H. D. Demsash and A. S. Jabasingh, An Insight into the Valorization of Hemicellulose Fraction of Biomass into Furfural: Catalytic Conversion and Product Separation, Waste Biomass Valoriz., 2021, 12(2), 531–552 CrossRef CAS.
- B. M. Matsagar, C.-Y. Hsu, S. S. Chen, T. Ahamad, S. M. Alshehri, D. C. W. Tsang and K. C. W. Wu, Selective hydrogenation of furfural to tetrahydrofurfuryl alcohol over a Rh-loaded carbon catalyst in aqueous solution under mild conditions, Sustainable Energy Fuels, 2020, 4(1), 293–301 RSC.
-
H. E. Hoydonckx, W. M. Van Rhijn, W. Van Rhijn, D. E. De Vos and P. A. Jacobs, Furfural and Derivatives, in Ullmann's Encyclopedia of Industrial Chemistry, 2007 Search PubMed.
- G. A. D. Castro, R. C. Batista, R. D. C. S. de Sousa, A. D. C. O. Carneiro and S. A. Fernandes, Green synthesis of furfural from xylose and corn cob biomass, React. Chem. Eng., 2023, 8(8), 1969–1980 RSC.
- A. Jakob, B. Likozar and M. Grilc, Aqueous conversion of monosaccharides to furans: were we wrong all along to use catalysts?, Green Chem., 2022, 24(21), 8523–8537 RSC.
- A. I. Stankiewicz and J. A. Moulijn, Process intensification: transforming chemical engineering, Chem. Eng. Prog., 2000, 96(1), 22–34 CAS.
- D. Soukup-Carne, P. López-Porfiri, F. S. Bragagnolo, C. S. Funari, X. Fan, M. González-Miquel and J. Esteban, Extraction of 5-Hydroxymethylfurfural and Furfural in Aqueous Biphasic Systems: A COSMO-RS Guided Approach to Greener Solvent Selection, ACS Sustainable Chem. Eng., 2024, 12(9), 3766–3779 CrossRef CAS PubMed.
- J. Esteban, A. J. Vorholt and W. Leitner, An overview of the biphasic dehydration of sugars to 5-hydroxymethylfurfural and furfural: a rational selection of solvents using COSMO-RS and selection guides, Green Chem., 2020, 22(7), 2097–2128 RSC.
- C. Aellig, D. Scholz, P. Y. Dapsens, C. Mondelli and J. Pérez-Ramírez, When catalyst meets reactor: continuous biphasic processing of xylan to furfural over GaUSY/Amberlyst-36, Catal. Sci. Technol., 2015, 5(1), 142–149 RSC.
- D. Prat, A. Wells, J. Hayler, H. Sneddon, C. R. McElroy, S. Abou-Shehada and P. J. Dunn, CHEM21 selection guide of classical- and less classical-solvents, Green Chem., 2016, 18(1), 288–296 RSC.
- L. K. Rihko-Struckmann, O. Oluyinka, A. Sahni, K. McBride, M. Fachet, K. Ludwig and K. Sundmacher, Transformation of remnant algal biomass to 5-HMF and levulinic acid: influence of a biphasic solvent system, RSC Adv., 2020, 10(42), 24753–24763 RSC.
- O. Ershova, J. Kanervo, S. Hellsten and H. Sixta, The role of xylulose as an intermediate in xylose conversion to furfural: insights via experiments and kinetic modelling, RSC Adv., 2015, 5(82), 66727–66737 RSC.
- J. N. Chheda, Y. Román-Leshkov and J. A. Dumesic, Production of 5-hydroxymethylfurfural and furfural by dehydration of biomass-derived mono- and poly-saccharides, Green Chem., 2007, 9(4), 342–350 RSC.
- B.-I. Na and J.-W. Lee, Kinetic study on the dilute acid catalyzed hydrolysis of waste mushroom medium, J. Ind. Eng. Chem., 2015, 25, 176–179 CrossRef CAS.
- J. Slak, B. Pomeroy, A. Kostyniuk, M. Grilc and B. Likozar, A review of bio-refining process intensification in catalytic conversion reactions, separations and purifications of hydroxymethylfurfural (HMF) and furfural, Chem. Eng. J., 2022, 429, 132325 CrossRef CAS.
- P. L. Dhepe and R. Sahu, A solid-acid-based process for the conversion of hemicellulose, Green Chem., 2010, 12(12), 2153–2156 RSC.
- O. Ogundowo and H. Ibrahim, Promising sulfonated carbon-based zirconia catalyst for renewable furfural production, Biomass Convers. Biorefin., 2024, 14(6), 7743–7751 CrossRef CAS.
- R. O'Neill, M. N. Ahmad, L. Vanoye and F. Aiouache, Kinetics of Aqueous Phase Dehydration of Xylose into Furfural Catalyzed by ZSM-5 Zeolite, Ind. Eng. Chem. Res., 2009, 48(9), 4300–4306 CrossRef.
- W. Song, H. Liu, J. Zhang, Y. Sun and L. Peng, Understanding Hβ Zeolite in 1,4-Dioxane Efficiently Converts Hemicellulose-Related Sugars to Furfural, ACS Catal., 2022, 12(20), 12833–12844 CrossRef CAS.
- W. Jeon, C. Ban, J. E. Kim, H. C. Woo and D. H. Kim, Production of furfural from macroalgae-derived alginic acid over Amberlyst-15, J. Mol. Catal. A:Chem., 2016, 423, 264–269 CrossRef CAS.
- I. Agirrezabal-Telleria, A. Larreategui, J. Requies, M. B. Güemez and P. L. Arias, Furfural production from xylose using sulfonic ion-exchange resins (Amberlyst) and simultaneous stripping with nitrogen, Bioresour. Technol., 2011, 102(16), 7478–7485 CrossRef CAS PubMed.
- H. Kim, S. Yang and D. Kim, One-pot conversion of alginic acid into furfural using Amberlyst-15 as a solid acid catalyst in γ-butyrolactone/water co-solvent system, Environ. Res., 2020, 187 DOI:10.1016/j.envres.2020.109667.
- A. Chareonlimkun, V. Champreda, A. Shotipruk and N. Laosiripojana, Catalytic conversion of sugarcane bagasse, rice husk and corncob in the presence of TiO2, ZrO2 and mixed-oxide TiO2–ZrO2 under hot compressed water(HCW) condition, Bioresour. Technol., 2010, 101(11), 4179–4186 CrossRef CAS PubMed.
- X. Shi, Y. Wu, P. Li, H. Yi, M. Yang and G. Wang, Catalytic conversion of xylose to furfural over the solid acid SO42-/ZrO2–Al2O3/SBA-15 catalysts, Carbohydr. Res., 2011, 346(4), 480–487 CrossRef CAS PubMed.
- G. Gómez Millán, Z. El Assal, K. Nieminen, S. Hellsten, J. Llorca and H. Sixta, Fast furfural formation from xylose using solid acid catalysts assisted by a microwave reactor, Fuel Process. Technol., 2018, 182, 56–67 CrossRef.
- E. Rakić, A. Kostyniuk, N. Nikačević and B. Likozar, Reaction microkinetic model of xylose dehydration to furfural over beta zeolite catalyst, Biomass Convers. Biorefin., 2023 DOI:10.1007/s13399-023-04969-1.
- V. Choudhary, S. I. Sandler and D. G. Vlachos, Conversion of Xylose to Furfural Using Lewis and Brønsted Acid Catalysts in Aqueous Media, ACS Catal., 2012, 2(9), 2022–2028 CrossRef CAS.
- R. Weingarten, J. Cho, J. W. C. Conner and G. W. Huber, Kinetics of furfural production by dehydration of xylose in a biphasic reactor with microwave heating, Green Chem., 2010, 12(8), 1423–1429 RSC.
- W. Guo, H. C. Bruining, H. J. Heeres and J. Yue, Insights into the reaction network and kinetics of xylose conversion over combined Lewis/Brønsted acid catalysts in a flow microreactor, Green Chem., 2023, 25(15), 5878–5898 RSC.
- J. Esteban, M. Ladero and F. García-Ochoa, Kinetic modelling of the solventless synthesis of solketal with a sulphonic ion exchange resin, Chem. Eng. J., 2015, 269, 194–202 CrossRef CAS.
- B. D. Turner, B. J. Henley, S. B. Sleap and S. W. Sloan, Kinetic model selection and the Hill model in geochemistry, Int. J. Environ. Sci. Technol., 2015, 12(8), 2545–2558 CrossRef.
- H. Bozdogan, Model selection and Akaike's Information Criterion (AIC): The general theory and its analytical extensions, Psychometrika, 1987, 52(3), 345–370 CrossRef.
- P. López-Porfiri, P. Gorgojo and M. Gonzalez-Miquel, Green solvents selection guide for bio-based organic acids recovery, ACS Sustainable Chem. Eng., 2020, 8(24), 8958–8969 CrossRef.
- W. Guo, Z. Zhang, J. Hacking, H. J. Heeres and J. Yue, Selective fructose dehydration to 5-hydroxymethylfurfural from a fructose-glucose mixture over a sulfuric acid catalyst in a biphasic system: Experimental study and kinetic modelling, Chem. Eng. J., 2021, 409, 128182 CrossRef CAS.
- K. Postawa, J. Szczygieł and M. Kułażyński, A comprehensive comparison of ODE solvers for biochemical problems, Renewable Energy, 2020, 156, 624–633 CrossRef CAS.
- J. E. Cavanaugh and A. A. Neath, The Akaike information criterion: Background, derivation, properties, application, interpretation, and refinements, Wiley Interdiscip. Rev. Comput. Stat., 2019, 11(3), e1460 CrossRef.
- A. A. Neath and J. E. Cavanaugh, The Bayesian information criterion: background, derivation, and applications, Wiley Interdiscip. Rev. Comput. Stat., 2012, 4(2), 199–203 CrossRef.
- R. Zhang, S. Xu, D. Raja, N. B. Khusni, J. Liu, J. Zhang, S. Abdulridha, H. Xiang, S. Jiang and Y. Guan,
et al., On the effect of mesoporosity of FAU Y zeolites in the liquid-phase catalysis, Microporous Mesoporous Mater., 2019, 278, 297–306 CrossRef CAS.
-
DuPont, DuPont Amberlyst Polymeric Catalysts, 2021, p. 4 Search PubMed.
-
DuPont, DuPont™ AmberLyst™ 15DRY Polymeric Catalyst, 2023, p. 2 Search PubMed.
- M. Mekala and V. R. Goli, Kinetics of esterification of acetic acid and methanol using Amberlyst 36 cation-exchange resin solid catalyst, Prog. React. Kinet. Mech., 2015, 40(4), 367–382 CrossRef CAS.
- D. M. Reinoso and D. E. Boldrini, Kinetic study of fuel bio-additive synthesis from glycerol esterification with acetic acid over acid polymeric resin as catalyst, Fuel, 2020, 264, 116879 CrossRef CAS.
- A. V. Bandura and S. N. Lvov, The Ionization Constant of Water over Wide Ranges of Temperature and Density, J. Phys. Chem. Ref. Data, 2005, 35(1), 15–30 CrossRef.
- V. Choudhary, S. H. Mushrif, C. Ho, A. Anderko, V. Nikolakis, N. S. Marinkovic, A. I. Frenkel, S. I. Sandler and D. G. Vlachos, Insights into the Interplay of Lewis and Brønsted Acid Catalysts in Glucose and Fructose Conversion to 5-(Hydroxymethyl)furfural and Levulinic Acid in Aqueous Media, J. Am. Chem. Soc., 2013, 135(10), 3997–4006 CrossRef CAS PubMed.
- O. Yemis and G. Mazza, Catalytic Performances of Various Solid Catalysts and Metal Halides for Microwave-Assisted Hydrothermal Conversion of Xylose, Xylan, and Straw to Furfural, Waste Biomass Valoriz., 2019, 10(5), 1343–1353 CrossRef CAS.
- E. I. Gürbüz, J. M. R. Gallo, D. M. Alonso, S. G. Wettstein, W. Y. Lim and J. A. Dumesic, Conversion of Hemicellulose into Furfural Using Solid Acid Catalysts in γ-Valerolactone, Angew. Chem., Int. Ed., 2013, 52(4), 1270–1274 CrossRef PubMed.
- J. Gong, M. J. Katz and F. M. Kerton, Catalytic conversion of glucose to 5-hydroxymethylfurfural using zirconium-containing metal–organic frameworks using microwave heating, RSC Adv., 2018, 8(55), 31618–31627 RSC.
- S. Souzanchi, L. Nazari, K. T. V. Rao, Z. Yuan, Z. Tan and C. Xu, Catalytic isomerization of glucose to fructose using heterogeneous solid Base catalysts in a continuous-flow tubular reactor: Catalyst screening study, Catal. Today, 2019, 319, 76–83 CrossRef CAS.
- A. Sandid, T. Attarbachi, R. Navarro-Tovar, M. Pérez-Page, V. Spallina and J. Esteban, Production of triacetin from industrially derived
purified glycerol: Experimental proof of concept, kinetic model derivation and validation, Chem. Eng. J., 2024, 496, 153905 CrossRef CAS.
- C. Aellig and I. Hermans, Continuous D-Fructose Dehydration to 5- Hydroxymethylfurfural Under Mild Conditions, ChemSusChem, 2012, 5(9), 1737–1742 CrossRef CAS PubMed.
- V. Choudhary, S. Caratzoulas and D. G. Vlachos, Insights into the isomerization of xylose to xylulose and lyxose by a Lewis acid catalyst, Carbohydr. Res., 2013, 368, 89–95 CrossRef CAS PubMed.
- V. Choudhary, A. B. Pinar, S. I. Sandler, D. G. Vlachos and R. F. Lobo, Xylose Isomerization to Xylulose and its Dehydration to Furfural in Aqueous Media, ACS Catal., 2011, 1(12), 1724–1728 CrossRef CAS.
- H. Xiang, S. Zainal, H. Jones, X. Ou, C. D'Agostino, J. Esteban, C. M. A. Parlett and X. Fan, Hierarchical zeolite catalysed fructose dehydration to 5-hydroxymethylfurfural within a biphasic solvent system under microwave irradiation, RSC Sustainability, 2023, 1(6), 1530–1539 RSC.
- Y. Wang, Z.-L. Xie, Z.-L. Zeng, C.-C. Li, J.-H. An, Q.-Q. Hao, H.-B. Ge, H.-Y. Chen, X.-X. Ma and Q.-X. Luo, Kinetics and Mechanism of Integrated Catalytic Ammonolysis and Dehydration from Methyl Salicylate over ZnAl2O4 Spinel, ACS Catal., 2024, 14(14), 10475–10490 CrossRef CAS.
- M. R. Kamaruzaman, X. X. Jiang, X. D. Hu and S. Y. Chin, High yield of isosorbide production from sorbitol dehydration catalysed by Amberlyst 36 under mild condition, Chem. Eng. J., 2020, 388, 124186 CrossRef CAS.
-
G. James, D. Witten, T. Hastie, R. Tibshirani and J. Taylor, An introduction to statistical learning: With applications in python, Springer Nature, 2023 Search PubMed.
- L. F. Zilnik, M. Crnomarkovic, U. Novak, M. Grilc and B. Likozar, Modelling, optimal solvent screening and separation of 5-hydroxymethylfurfural or furfural from catalytic conversion reactor stream in downstream purification process, Chem. Eng. Res. Des., 2023, 194, 376–387 CrossRef.
- W. Guo, H. C. Bruining, H. J. Heeres and J. Yue, Efficient synthesis of furfural from xylose over HCl catalyst in slug flow microreactors promoted by NaCl addition, AIChE J., 2022, 68(5), e17606 CrossRef CAS.
- O. Ogundowo, G. Sadanandam and H. Ibrahim, Furfural from flax straw using sulfonated carbonaceous acid catalyst: parametric and kinetic studies, React. Kinet., Mech. Catal., 2023, 136(5), 2535–2554 CrossRef CAS.
- X. Li, J. Yang, R. Xu, L. Lu, F. Kong, M. Liang, L. Jiang, S. Nie and C. Si, Kinetic study of furfural production from Eucalyptus sawdust using H-SAPO-34 as solid Bronsted acid and Lewis acid catalysts in biomass-derived solvents, Ind. Crops Prod., 2019, 135, 196–205 CrossRef CAS.
- S. Le Guenic, D. Gergela, C. Ceballos, F. Delbecq and C. Len, Furfural Production from D-Xylose and Xylan by Using Stable Nafion NR50 and NaCl in a Microwave-Assisted Biphasic Reaction, Molecules, 2016, 21(8) DOI:10.3390/molecules21081102.
- P. J. Oefner, A. H. Lanziner, G. Bonn and O. Bobleter, Quantitative studies on furfural and organic acid formation during hydrothermal, acidic and alkaline degradation of D-xylose, Monatsh. Chem., 1992, 123(6), 547–556 CrossRef CAS.
- T. Suzuki, T. Yokoi, R. Otomo, J. N. Kondo and T. Tatsumi, Dehydration of xylose over sulfated tin oxide catalyst: Influences of the preparation conditions on the structural properties and catalytic performance, Appl. Catal., A, 2011, 408(1), 117–124 CrossRef CAS.
- W. C. Conner, G. Tompsett, K.-H. Lee and K. S. Yngvesson, Microwave Synthesis of Zeolites: 1. Reactor Engineering, J. Phys. Chem. B, 2004, 108(37), 13913–13920 CrossRef CAS.
- T. Garnault, D. Bouvard, J.-M. Chaix, C. Harnois and S. Marinel, Is direct microwave heating well suited for sintering ceramics?, Ceram. Int., 2021, 47(12), 16716–16729 CrossRef CAS.
- D. P. Thompson, A. M. Dickins and J. S. Thorp, The dielectric properties of zirconia, J. Mater. Sci., 1992, 27(8), 2267–2271 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article acde,
Xiaolei
Fan
acde,
Xiaolei
Fan
 af and
Jesús
Esteban
af and
Jesús
Esteban
 *ag
*ag
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. The solvents were pre-saturated in each other to avoid volume changes due to their mutual solubility, even if this is limited.37 A 2 wt% catalyst and 10 wt% xylose loading with respect to the aqueous phase was adhered to throughout. All materials were weighed with a Mettler Toledo NewClassic MS (±0.0001 g) balance.
2. The solvents were pre-saturated in each other to avoid volume changes due to their mutual solubility, even if this is limited.37 A 2 wt% catalyst and 10 wt% xylose loading with respect to the aqueous phase was adhered to throughout. All materials were weighed with a Mettler Toledo NewClassic MS (±0.0001 g) balance.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 with deionised water and IPA, respectively, prior to analysis.
50 with deionised water and IPA, respectively, prior to analysis.
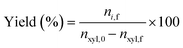
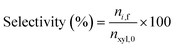
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 H2O/MIBK biphasic system. This ratio of aqueous to organic phase volume was chosen as the literature commonly utilises phase volume ratios between 1
2 H2O/MIBK biphasic system. This ratio of aqueous to organic phase volume was chosen as the literature commonly utilises phase volume ratios between 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 of aqueous to organic phase.2,12 Furthermore, the 1
4 of aqueous to organic phase.2,12 Furthermore, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 phase volume ratio would allow minimised downstream separation costs with less costly solvent recycling in the context of a full process concept. A total of nine solid acid heterogeneous catalysts were chosen for the screening from three classes, IERs, sulfated zirconia and zeolites (Table 1). These catalysts were selected for their strong acidity, specifically Brønsted, for the direct dehydration of xylose and commercial availability.
2 phase volume ratio would allow minimised downstream separation costs with less costly solvent recycling in the context of a full process concept. A total of nine solid acid heterogeneous catalysts were chosen for the screening from three classes, IERs, sulfated zirconia and zeolites (Table 1). These catalysts were selected for their strong acidity, specifically Brønsted, for the direct dehydration of xylose and commercial availability.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 by volume) at 160 °C for 2 h at 800 rpm.
2 by volume) at 160 °C for 2 h at 800 rpm.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 by volume) at 160 °C for 2 h at 800 rpm over (a) A15, (b) SO4/ZrO2-1 and (c) HY30 (2 wt% loading).
2 by volume) at 160 °C for 2 h at 800 rpm over (a) A15, (b) SO4/ZrO2-1 and (c) HY30 (2 wt% loading).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 H2O/MIBK system.
2 H2O/MIBK system.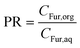
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, with pre-saturation of phases to mitigate volume changes resulting from mutual solubilities,11 which otherwise would have to be considered.38 In the microwave device employed, the set temperature is reached after approximately 1 min,57 which can be considered a negligible amount of time in comparison to the duration of the reaction until quantitative conversion is attained. For this reason, a temperature gradient is dismissed in this model and the consequent variation of system properties that it could entail.38 However, for the kinetic experiments, the volume and phase ratio changes owing to operation at temperatures greater than room temperature are considered. Guo et al. developed a correlation for H2O/MIBK at various ratios of organic to aqueous volumes (Org
2, with pre-saturation of phases to mitigate volume changes resulting from mutual solubilities,11 which otherwise would have to be considered.38 In the microwave device employed, the set temperature is reached after approximately 1 min,57 which can be considered a negligible amount of time in comparison to the duration of the reaction until quantitative conversion is attained. For this reason, a temperature gradient is dismissed in this model and the consequent variation of system properties that it could entail.38 However, for the kinetic experiments, the volume and phase ratio changes owing to operation at temperatures greater than room temperature are considered. Guo et al. developed a correlation for H2O/MIBK at various ratios of organic to aqueous volumes (Org![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Aq).38 The results indicate that volume and phase ratio changes are significant and these have been considered, using the information featured in Table S3,† with the resultant ratios (Org
Aq).38 The results indicate that volume and phase ratio changes are significant and these have been considered, using the information featured in Table S3,† with the resultant ratios (Org![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Aq) presented in Table S4.†
Aq) presented in Table S4.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Aq ratios using Aspen Plus simulations.38
Aq ratios using Aspen Plus simulations.38