Protonation pattern as a controlling factor of thermal reactions of aryl o-divinylbenzenes in acidic media: an integrated experimental–theoretical study

Abstract

The thermal transformations of various thienyl and phenyl derivatives of o-divinylbenzene in acidic media were investigated in an integrated experimental–theoretical study. Several derivatives (9–12) led to cyclization products when heated under acidic conditions, while some (13 and 14) were found to be non-reactive. The reactivity or non-reactivity of the investigated compounds is closely related to the position of the preferred protonation site in the investigated compounds, as shown by DFT calculations. If the preferred position of proton entry into the molecule coincides with the protonation position required for cyclization, the reaction proceeds, otherwise the derivatives are non-reactive. By blocking a preferred protonation position with a suitable substituent in the non-reactive precursors, protonation can be prevented at the undesired site and proton entry can be redirected to the site that allows the reaction to proceed. A detailed insight into the mechanism of the thermal reactions of 9–12 was presented.

---

Introduction

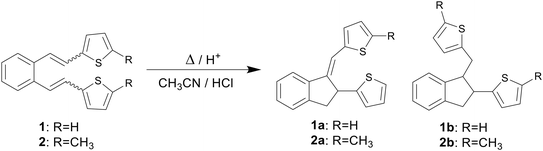
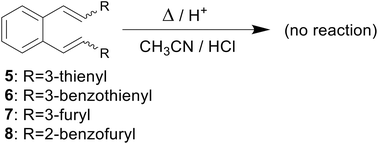
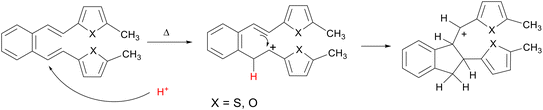
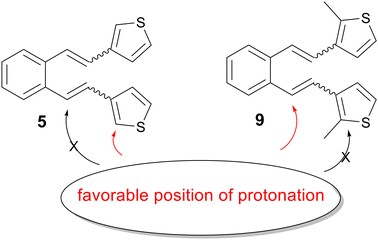
Computational methods^1,2 play a key role in modern chemistry, enabling detailed analysis and understanding of chemical reactions at the molecular level. Thanks to the rapid development of information technologies during the last few decades, computational chemistry³ is becoming an equal and necessary collaborator of experimental research.^4,5 The time required for the synthesis and testing of different compounds is several times shorter than using classical experimental methods.^6,7 Also, in the case of computational methods of experimentation, exposure to harmful chemicals is avoided.^8,9 Finally, in terms of their accuracy, the results of computer simulations are comparable to those of most modern experiments, and they are widely used today as a supplement, guidance and very often as a complete replacement of experimental research, especially those that are financially demanding and ecologically inappropriate.¹⁰

Computational chemistry enables the calculation and prediction of almost all chemical and physical properties of molecules and their interactions,^11,12 giving a deeper insight into the nature of the chemical process and the explanation of the obtained experimental data.^13,14 In one of our previous papers,¹⁵ an attempt was made to explain the thermal reactivity of furan and thiophene derivatives of o-divinylbenzene under acidic conditions¹⁶ using computational methods. Several derivatives (1–4)¹⁷ by heating under acidic conditions gave cyclization products (1a–b, 2a–b, 3a and 4a–d), while some (5–8) proved to be non-reactive, depending on the position of the heteroatom in the heterocyclic moiety (Schemes 1–3). Furthermore, quantum chemical calculations led to the assumption that one of the reasons for the reactivity, or non-reactivity, of compounds is the position of entry of protons into the molecule (Scheme 4). Namely, if the double bond is protonated, a carbocation is formed, followed by ring closure and formation of cyclization products. In the case of non-reactive derivatives, protonation is directed to the heterocyclic moiety,^18,19 which prevents the formation of carbocation intermediates.

Scheme 1 Reactivity of thiophene derivatives 1 and 2.

Scheme 2 Reactivity of furan derivatives 3 (a) and 4 (b).

Scheme 3 Non-reactive derivatives 5–8.

Scheme 4 Formation of carbocation intermediates.

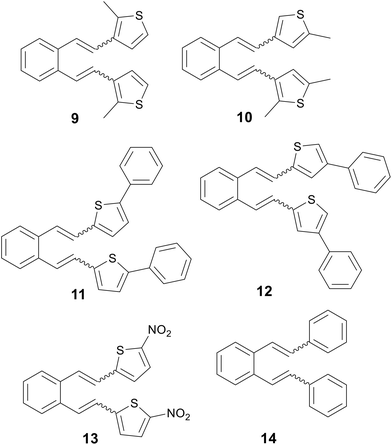
The main goal of this work is the experimental verification of the previously established computational assumptions about the protonation orientation. Therefore, several derivatives (Fig. 1), including some substituted on the heterocyclic core of previously unreactive precursors, are prepared and their thermal transformation under acidic conditions is studied, providing a detailed insight into the mechanism of the reactions through quantum chemical calculations. In addition, the idea of blocking a specific position in the case of unreactive precursors with a suitable substituent to prevent unwanted protonation at the heterocyclic moiety, which could control the position of protonation and direct it to the target double bond (Fig. 2), was confirmed.

Fig. 1 Investigated o-divinylbenzene derivatives 9–14.

Fig. 2 Favorable protonation position.

Results and discussion

Chemistry

Compounds 9–14 were synthesized by the Wittig reaction from o-xylylenebis(triphenylphosphonium bromide) and the corresponding aldehydes. 5-Nitrothiophene-2-carbaldehyde, 5-phenylthiophene-2-carbaldehyde, 4-phenylthiophene-2-carbaldehyde and benzaldehyde are commercially available chemicals, while 2-methylthiophene-3-carbaldehyde and 2,5-dimethylthiophene-3-carbaldehyde were prepared previously. Due to steric hindrances and the entry of the methyl group at the unhindered C-5 position, it was not possible to prepare 2-methylthiophene-3-carbaldehyde by direct methylation of thiophene-3-carbaldehyde. Therefore, the synthesis was carried out according to the previously published procedure by methylation of thiophene-3-carbaldehyde in the presence of N,N,N′-trimethylethylenediamine, which coordinates the entry of the methyl group into desired position C-2 (Scheme 5).²⁰ 2,5-Dimethylthiophene-3-carbaldehyde was prepared by Vilsmeier–Haack reaction from 2,5-dimethylthiophene.

Scheme 5 Synthesis of 2-methylthiophene-3-carbaldehyde.

Thermal reactions have been conducted on all prepared compounds (Scheme 6). In addition to compounds 9 and 10, whose main role is to direct the protonation to the double bond by substitution of the heterocyclic core, phenyl derivatives 11 and 12 were also investigated, as compounds with a steric hindrance group. The role of the nitro-substituted derivative 13 is to investigate the effect of an electron-withdrawing group, while that of compound 14 (ref. 21) is to explore the presence of a non-heterocyclic aromatic core. Experiments were carried out by heating the mixture of cis,cis-, cis,trans- and trans,trans-isomers of 9–14 to the reflux temperature of acetonitrile, with the addition of 3.5 eq. hydrochloric acid, respectively. In the case of derivatives 9–12, the reaction proved to be successful and indene derivatives were isolated as the main products, respectively.

Scheme 6 Reactivity of compounds 9–12.

Compounds 13 and 14 did not yield thermal reaction products and only a mixture of initial isomers was isolated. The reactivity of compounds 9 and 10 is consistent with previous predictions about the manipulation of the protonation position by introducing suitable substituents. Also, the influence of the sterically hindered group turned out to be insignificant, with a similar reactivity as in other previously investigated 2-substituted thiophene derivatives.

Computational study

A calculation study for the thermal transformations of compounds 9–14 was presented. Only the trans,trans-isomers of the investigated compounds were subjected to the calculations (all names of the compounds therefore refer to their trans,trans isomers), since the trans,trans-isomers occur with over 95% of the population in the initial mixtures of the reactants, as shown by the DFT calculations (Table S1†).

The previous study has shown that a favorable position for the entry of the proton into the molecule is closely related to reactivity or non-reactivity in thermal transformations under acidic conditions of the compounds studied. Namely, it is necessary that the favorable protonation position coincides with that leading to 1,5-ring closure, which is the vinyl double bond (Scheme 4), and formation of cyclization products. If the favorable protonation site does not match that required for 1,5-ring closure, an attempt is made to block this site to prevent protonation at this preferred (but undesirable) position and thereby redirect protonation to the position required for the reaction to proceed, which should ultimately lead to a reactive derivative. In a previous study on the protonation sites of 3-substituted thiophene derivative 5, it was found that the most thermodynamically favorable protonation site does not coincide with the site required for 1,5-ring closure, but is located on the heterocyclic moiety.¹⁵ In the current study, the entry of the proton at a specific position of the heterocyclic moiety was blocked by targeted substitution with a methyl group (9, Fig. 1), which redirected the favorable proton entry position (Fig. 2), as shown by quantum chemical calculations (Table S2†). This gave rise to a reactive derivative which was confirmed by experimental results. The additional substitution was performed to obtain the derivative 10 (Fig. 1), which showed similar properties regarding thermal reactivity under acidic conditions. The Gibbs free energies for all possible protonation forms obtained by protonation at the different sites of compounds 9 and 10 are given in the ESI† (Table S2).

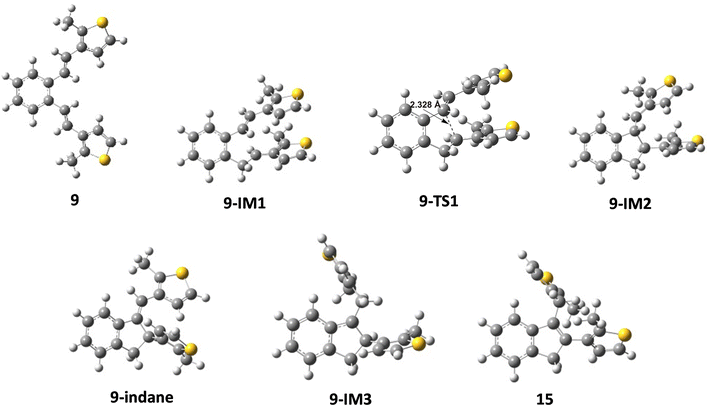
The proposed mechanism of thermal transformation of derivatives 9 and 10 in acidic media to indane and indene products via carbocation intermediates A and B is shown in Scheme 7.

Scheme 7 Possible mechanism of formation of indane and indene products.

The reaction begins with the protonation of the double bond of the starting compound, followed by a 1,5-ring closure to form the carbocation intermediate A. In the next step, carbocation A is deprotonated to obtain the indane product, from which the carbocation intermediate B is formed by further protonation. Finally, the deprotonation of carbocation B follows, which leads to the formation of an indene product. The free energy profiles for the possible mechanism of the formation of indane and indene products starting from 9 and 10 are shown in Fig. 3, while the structures along the given reaction pathways are depicted in Fig. 4 and 5.

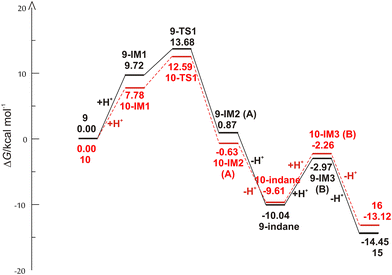Fig. 3 Free energy profiles for the possible reaction routes of the formation of indane and indene products of starting compounds 9 and 10.

Fig. 4 Optimized structures along the pathways from compound 9 to indane and indene products.

Fig. 5 Optimized structures along the pathways from compound 10 to indane and indene products.

As revealed by the free energy profiles, the first step of the thermal transformations of compounds 9 and 10 is accompanied by an endergonicity of 9.72 kcal mol⁻¹ and 7.78 kcal mol⁻¹, respectively, meaning that the initial reaction step, the protonation of the vinyl double bond, is slightly favorable for the starting compound 10. In the next step, the protonated forms 9-IM1 and 10-IM1 transform into 9-IM2 and 10-IM2 (carbocation A) via the transition states 9-TS1 and 10-TS1 with relative free energies of 13.68 kcal mol⁻¹ and 12.59 kcal mol⁻¹, thus overcoming the free energy barriers of 3.96 kcal mol⁻¹ and 4.81 kcal mol⁻¹ (Fig. 4 and 5). Inspection of the normal mode of the single imaginary vibration in 9-TS1 (pictorially presented in Fig. S1†) reveals the strong C–C interaction with the imaginary vibration exhibiting a negative frequency of 151.5i cm⁻¹ and the distance between these two atoms shortened to 2.328 Å (Fig. 4). In the case of 10-TS1, the strong C–C interaction is associated with the imaginary vibration (pictorially presented in Fig. S1†), exhibiting a negative frequency of 173.3i cm⁻¹, while the distance between these two atoms is shortened to 2.197 Å. After the ring is formed, the system is stabilized by the release of substantial free energies of 12.81 kcal mol⁻¹ and 13.22 kcal mol⁻¹ to form 9-IM2 and 10-IM2 (carbocation A). Further stabilization occurs by the release of protons, which is associated with an exergonicity of 10.91 kcal mol⁻¹ and 8.98 kcal mol⁻¹ to form the indane products 9-indane and 10-indane, respectively. It turns out that the formation of the indane product 9-indane is thermodynamically slightly favorable in comparison with the formation of the indane product 10-indane. Protonation of 9-indane with an energy uptake of 7.07 kcal mol⁻¹ to form 9-IM3 and that of 10-indane with an energy uptake of 7.35 kcal mol⁻¹ to form 10-IM3 (carbocation B) is followed by deprotonation to form products 15 and 16 with free energy release of 11.48 kcal mol⁻¹ and 10.86 kcal mol⁻¹ in the final steps. As the reaction profile shows, the final products are very stable. Comparison of the relative free energies of 15 and 16 showed a difference of 1.33 kcal mol⁻¹ in favor of product 15. This is in line with the experimental results which showed that the thermal transformations in acidic media of compounds 9 to 15 and 10 to 16 proceed with relative yields of 75% and 15%, respectively.

The experimentally determined reactivity of 5-phenyl derivative 11 and 4-phenyl derivative 12 (Fig. 1) appeared to be in full agreement with the computational predictions of the outcome of the thermal reactions under consideration. The quantum chemical calculations showed that the most thermodynamically favorable position coincides with the position where protonation must occur for 1,5-ring closure to take place and for the reaction to proceed (Table S1†), for both derivatives 11 and 12. Therefore, the proton was expected to choose the required position for the 1,5-ring closure, which allows the reaction to proceed. The Gibbs free energies for all possible protonation forms obtained by the protonation at the different sites within compounds 11 and 12 are given in the ESI† (Table S2). The proposed mechanism for the thermal conversion of derivatives 11 and 12 to indane and indene products in an acidic medium is fully consistent with the mechanism proposed for thermal conversion of derivatives 9 and 10, which is shown in Scheme 7.

Free energy profiles for the possible reaction routes of the formation of indane and indene products of starting compounds 11 and 12 are depicted in Fig. 6, while optimized structures along the given reaction pathways are shown in Fig. 7 and 8.

Fig. 6 Free energy profiles for the possible reaction routes of the formation of indane and indene products of starting compounds 11 and 12.

Fig. 7 Optimized structures along the pathways from 11 to indane and indene products.

Fig. 8 Optimized structures along the pathways from 12 to indane and indene products.

Inspection of the reported free energy profiles shows that the first step, the protonation of the double bond of the starting compound, is associated with a lower endergonicity for the 5-phenylthiophene derivative 11 compared to the 4-phenylthiophene derivative 12 (7.26 kcal mol⁻¹vs. 10.64 kcal mol⁻¹), indicating that this step is more favourable for derivative 11. The subsequent 1,5-ring closure proceeds via11-TS1 and 12-TS1 transition states (the imaginary normal modes for corresponding transition states are pictorially presented in Fig. S1†), with 12-TS1 having a slightly higher free energy than 11-TS1 (13.42 kcal mol⁻¹vs. 12.88 kcal mol⁻¹), leading to carbocation A (11-IM2 and 12-IM2, respectively), which also has a higher energy for the 12-IM2 derivative than for the 11-IM2 derivative (3.63 kcal mol⁻¹vs. −0.38 kcal mol⁻¹). Barrier-free deprotonation leads to the indane products (11-indane and 12-indane), with the 12-indane derivative exhibiting higher stability compared to the 11-indane derivative (−11.09 kcal mol⁻¹vs. −8.47 kcal mol⁻¹). For the final products 17 and 18, the relative stability appears to be very close to each other, indicating that the position of the steric hindrance group can be considered insignificant, with product 18 being just slightly favored. One can notice that the latter is not consistent with the experimental results in terms of the yield of 17 compared to the yield of 18 (Scheme 6), probably due to the different stability of the starting compounds, or the influence of environmental conditions.

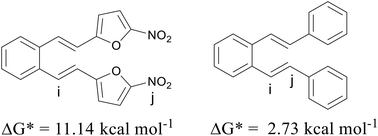
As mentioned above, compounds 13 and 14 (Fig. 9) proved to be non-reactive, and only a mixture of the original isomers was isolated as reaction products. In order to clarify the present experimental findings, the reactivity of the respective starting compounds was analyzed using computational methods. Quantum chemical calculations have shown that the reactivity or non-reactivity of compounds is closely related to the position of proton entry into the molecule (Fig. 1) and its coincidence with the position required for 1,5-cyclization. Therefore, the starting compounds 13 and 14 were examined for the coincidence of the most thermodynamically favorable position for the proton entry into the molecule with the position required for the reaction to proceed. The effect of an electron-withdrawing group (–NO₂) on the heterocyclic moiety on the reactivity/non-reactivity of the thiophene derivatives was investigated on the nitro-substituted derivative 13. The quantum chemical calculations have shown that the nitro group (–NO₂) represents the most thermodynamically favorable protonation position within the compound, which is consistent with the electronegativity of the corresponding group and its high proton affinity. The protonation reaction is therefore directed towards the nitro group (–NO₂), which prevents protonation at the exocyclic double bond (vinyl group) and the formation of a carbocation intermediate, which is a necessary prerequisite for the 1,5-ring closure and the further progress of the reaction. Since it turns out that the most favorable protonation site, namely the oxygen atom of the nitro group, in the given compound does not coincide with the site required for 1,5-ring closure, non-reactivity is to be expected, which is fully consistent with the experimental findings. The deviation in the Gibbs free energy of the most favorable protonated species (protonated the oxygen position at the nitro group) and that protonated at the position required for 1,5-ring closure is calculated to be 11.14 kcal mol⁻¹ (Fig. 10). The Gibbs free energies for all possible protonation forms obtained by protonation at the different positions in compound 13 are given in the ESI† (Table S2).

Fig. 9 Optimized structures of compounds 13 and 14.

Fig. 10 Positions of site “i” required for the reaction to proceed and the most favorable protonation site “j” for compounds 13 and 14, together with the differences in Gibbs free energy between protonated species “i” and “j”, ΔG*.

Finally, the effect of a non-heterocyclic aromatic core on the thermal transformation of o-divinylbenzene derivatives to indane/indene products under acidic conditions was investigated in compound 14. As indicated by the quantum chemical calculations, the most thermodynamically favourable protonation site is located at the exocyclic double bond, but not at the position required for 1,5-ring closure, as shown in Fig. 10. Therefore, the 1,5-ring closure and the formation of indane/indene products were not expected, which was fully consistent with the experimental findings. The deviation in the Gibbs free energy of the most favorable protonated species and that protonated at the position required for 1,5-ring closure is calculated to be 2.73 kcal mol⁻¹ (Fig. 10). The Gibbs free energies for all possible protonation forms obtained by protonation at the different sites in compound 14 are given in the ESI† (Table S2).

Materials and methods

General experimental information

The ¹H NMR spectra were recorded on a spectrometer at 300 and 600 MHz. The ¹³C NMR spectra were registered at 75 and 150 MHz. All NMR spectra were measured in CDCl₃ using tetramethylsilane as the reference. The assignment of the signals is based on 2D-CH correlation and 2D-HH-COSY and NOESY experiments. Melting points were obtained using a microscope equipped with apparatus and are uncorrected. HRMS analysis was carried out on an Agilent 6545 Q-TOF LC/MS (G6545B) connected to an Agilent 1290 Infinity II UPLC system (high pressure pump G7120A, autosampler G7129B, column compartment G7116B, DAD detector G7117B).

Silica gel (0.063–0.2 mm) was used for chromatographic purification. Thin-layer chromatography (TLC) was performed on silica gel 60 F254 plates. Solvents were purified by distillation. 5-Nitrothiophene-2-carbaldehyde, 5-phenylthiophene-2-carbaldehyde, 4-phenylthiophene-2-carbaldehyde and benzaldehyde are commercially available chemicals, while 2-methylthiophene-3-carbaldehyde and 2,5-dimethylthiophene-3-carbaldehyde were prepared according to the literature.^20,22

General procedure for the synthesis of compounds 9–14 (Wittig reaction)

To a stirred solution of the phosphonium salt and corresponding aldehyde (2.2 eq.) in absolute ethanol (100 mL), the solution of sodium ethoxide (2.2 eq, 14 mg in 5 mL of absolute ethanol) was added dropwise, respectively. The reaction was completed within 3–4 h (usually left to stand overnight). After the removal of the solvent, the residue was worked up with water and toluene. The toluene extracts were dried (anhydrous MgSO₄) and concentrated. The crude reaction mixture was purified and the isomers of products 9–14 were isolated, respectively, by column chromatography on silica gel using petroleum ether as the eluent. In the case of products 9, 12 and 13, trans,trans-isomers were isolated and characterized, while 10 and 11 were used in further thermal reaction without isolation isomers.

1,2-bis((E)-2-(2-Methylthiophene-3-yl)vinyl)benzene (tt-9). 24%; ¹H NMR (CDCl₃; 300 MHz) δ/ppm: 7.52–7.58 (m, 2H), 7.24–7.31 (m, 4H), 7.21 (d, 2H, J = 16.2 Hz), 7.07 (d, 2H, J = 5.4 Hz), 6.97 (d, 2H, J = 16.0 Hz), 2.51 (s, 6H); ¹³C NMR (CDCl₃; 75 MHz) δ/ppm: 136.3, 136.0, 135.5, 127.5, 126.5, 126.2, 125.2, 123.8, 122.0, 13.2; HRMS (LC-Q/TOF) m/z: [M + H⁺] calculated for C₂₀H₁₈S₂ 323.0923; found 323.0923.

1,2-bis((E)-2-(4-Phenylthiophene-2-yl)vinyl)benzene (tt-12). 54%; ¹H NMR (CDCl₃; 300 MHz) δ/ppm: 7.51–7.63 (m, 4H), 7.20–7.48 (m, 16H), 7.13 (d, 2H, J = 16.1 Hz); ¹³C NMR (CDCl₃; 75 MHz) δ/ppm: 143.6, 142.8, 135.6, 135.4, 128.8, 127.9, 127.3, 126.7, 126.4, 126.3, 125.3, 124.4, 119.5; HRMS (LC-Q/TOF) m/z: [M + H⁺] calculated for C₃₀H₂₂S₂ 447.1229; found 447.1236.

1,2-bis(2-(5-Nitrothiophene-2-yl)vinyl)benzene (tt-13). 97%; ¹H NMR (CDCl₃; 600 MHz) δ/ppm: 7.87 (d, 2H, J = 3.5 Hz), 7.56–7.60 (m, 2H), 7.44 (d, 2H, J = 16.2 Hz), 7.37–7.41 (d, 2H, J = 3.5 Hz), 7,04 (d, 2H, J = 16.2 Hz); ¹³C NMR (CDCl₃; 150 Hz) δ/ppm: 149.8, 149.6, 134.6, 130.6, 129.5, 129.3, 127.3, 125.3, 125.2, 123.6; HRMS (LC-Q/TOF) m/z: [M + H⁺] calculated for C₁₈H₁₂N₂O₄S₂ 385.0315; found 385.0311.

Thermal reaction of 9–14 in acetonitrile/hydrochloric acid solutions

A mixture of cis,cis-, cis,trans- and trans,trans-isomers of 9–14 (4 × 10⁻³ M) was dissolved in acetonitrile with addition of hydrochloric acid (36%, 1 ml, 35 eq.) and refluxed for 3 hours, respectively. After cooling to room temperature, the reaction mixture was neutralized with a solution of sodium hydroxide (10%) and extracted with ethyl acetate (4 × 5 ml). After drying over magnesium sulphate, the solvents were removed in vacuo and the oily residue was chromatographed on a silica gel column using petroleum ether as the eluent. In the case of 13 and 14, only a mixture of starting isomers was isolated, while compounds 9–12 gave indene products 15–18, with traces of indane derivatives, respectively.

2-Methyl-3-((2-(2-methylthiophene-3-yl)-lH-indene-3-yl)methyl)thiophene (15). 75%; ¹H NMR (CDCl₃; 300 MHz) δ/ppm: 7.46 (d, 1H, J = 6.9 Hz), 7.14–7.23 (m, 3H), 7.08–7.10 (m, 1H), 6.85–6.88 (m, 1H), 6.87 (d, 1H, J = 5.0 Hz), 6,86 (d, 1H, J = 5.0 Hz), 6,64 (d, 1H, J = 5.0 Hz), 3,71 (s, 2H), 3.66 (s, 2H), 2.37 (s, 3H), 2.32 (s, 3H); ¹³C NMR (CDCl₃; 75 MHz) δ/ppm: 145.7, 143.1, 138.6, 138.0, 135.1, 134.7, 134.5, 132.9, 129.1, 129.0, 126.3, 124.5, 123.4, 121.8, 120.7, 119.9, 42.2, 29.7, 14.3, 13.0; HRMS (LC-Q/TOF) m/z: [M + H⁺] calculated for C₂₀H₁₈S₂ 323.0923; found 323.0923.

(E)-3-((2-(2,5-Dimethylthiophene-3-yl)-2,3-dihidro-1H-indene-1-yldene)methyl)-2,5-dimethylthiophene (16). 14%; ¹H NMR (CDCl₃; 600 MHz) δ/ppm: 7.44 (d, 1H, J = 7.4 Hz), 7,23 (d, 1H, J = 7.4 Hz), 7,15–7,20 (m, 2H), 6.52 (d, 1H, J = 0.9 Hz), 6.27 (s, 1H), 2.42 (s, 3H), 2.29 (s, 3H), 2.27 (s, 3H), 2.26 (s, 3H); ¹³C NMR (CDCl₃; 75 MHz) δ/ppm: 145.9, 143.0, 138.3, 138.1, 135.7, 134.7, 134.4, 134.2, 128.4, 127.3, 127.1, 127.0, 126.3, 124.4, 123.3, 119.9, 42.2, 29.7, 15.3, 15.2, 15.1, 14.3; HRMS (LC-Q/TOF) m/z: [M + H⁺] calculated for C₂₂H₂₂S₂ 351.1223; found 351.1236.

(E)-2-Phenyl-5-((2-(5-phenylthiophene-2-yl)-2,3-dihidro-1H-indene-1-ylidene)methyl)thiophene (17). 89%; ¹H NMR (CDCl₃; 300 MHz) δ/ppm: 7.66 (d, 1H, J = 7.9 Hz), 7.54 (d, 2H, J = 7.9 Hz), 7.49 (d, 2H, J = 7.9 Hz), 7.32–7.36 (m, 2H), 7.22–7.32 (m, 7H), 7.17–7.22 (m, 2H), 7.05 (d, 1H, J = 3.6 Hz), 7.03 (d, 1H, J = 3.6 Hz), 6.85 (d, 1H, J = 3.6 Hz), 4.92 (d, 1H, J = 7.8 Hz), 3.67 (dd, 1H, J = 7,8 Hz, 16.3 Hz), 3.17 (d, 1H, J = 16.3 Hz); ¹³H NMR (CDCl₃; 75 MHz) δ/ppm: 146.1, 144.0, 142.6, 141.7, 141.1, 138.7, 135.7, 135.4, 134.5, 134.1, 128.9 (2C), 128.7 (2C), 127.6, 127.1, 126.7, 126.5, 126.0, 125.7 (2C), 125.6, 125.5 (2C), 125.3, 123.5, 123.4, 122.8, 41.2, 29.7; ¹³C NMR; HRMS (LC-Q/TOF) m/z: [M + H⁺] calculated for C₃₀H₂₂S₂ 447.123; found 447.1236.

4-Phenyl-2-((2-(4-phenylthiophene-2-yl)-lH-indene-3-yl)methyl)thiophene (18). 39%; ¹H NMR (CDCl₃; 300 MHz) δ/ppm: 7.59 (d, 2H, J = 7.5 Hz), 7.46–7.54 (m, 2H), 7.18–7.43 (m, 12H), 4.46 (s, 2H), 3.94 (s, 2H); ¹³H NMR (CDCl₃; 75 MHz) δ/ppm: 146.0, 142.6, 142.5, 142.1, 141.7, 139.9, 136.1, 136.0, 135.6, 135.4, 128.9 (2C), 128.7 (2C), 127.3, 127.0, 126.8, 126.4 (2C), 126.3 (2C), 125.4, 124.6, 124.3, 123.5, 120.2, 119.7, 118.6, 41.4, 27.5; HRMS (LC-Q/TOF) m/z: [M + H⁺] calculated for C₃₀H₂₂S₂ 447.1229; found 447.1236.

Quantum chemical DFT calculations

All calculations were performed by means of quantum chemical calculations at the density functional theory (DFT) level using the Gaussian 16 program (revision C.01).²³ The M06-2X hybrid meta-GGA exchange–correlation functional designed by Truhlar's group, which is recommended most highly for the thermodynamic and kinetic study of the main-group elements, was selected.²⁴ Pople's split-valence double-ξ polarized 6-31G(d,p) basis set was utilized.²⁵ The geometric structures of the molecules were optimized by minimizing energies with respect to all geometrical parameters without imposing any molecular symmetry constraints and using a tight convergence condition. The Berny algorithm using redundant internal coordinates was employed. Frequency calculations were performed under the harmonic approximation on all the optimized structures at the same level of theory with no scaling in order to confirm that the structures correspond to the true minima (reactants, products and intermediate states), meaning that no imaginary frequencies were present, or to the transition states being characterized by a single imaginary frequency, as well as to extract thermal Gibbs free energy corrections. IRC calculations were performed to confirm that the proposed transition states connect to the expected reactants and products along the reaction pathway. The final single point energies were obtained using a highly flexible 6-311+G(2df,2pd) basis set. Geometry optimizations, frequency calculations and single point energy evaluations were conducted by taking into account the solvent effects. To evaluate the bulk solvent effects (acetonitrile, ε = 35.69), the implicit SMD polarizable continuum solvation model²⁶ was employed. It represents a very practical approach to simulate the solvation environment and determine the effect of the medium on the structure and stability of solutes in a solution.

The discussion is based on the Gibbs free energies, , in the liquid computed using the expression:

where the term E^Tot_soln corresponds to the total electronic energy of a density functional theory calculation using the SMD model, while the term (thermal correction to Gibbs free energy) encompasses vibrational, rotational and translational contribution to the solution free energy, computed by applying the ideal gas partition functions to the frequencies calculated in the dielectric medium and the 1 M standard state. The experimental value of 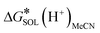= −254.3 kcal mol⁻¹ was utilized,²⁷ which together with the gas-phase Gibbs free energy value for the proton of G*(H⁺) = −6.28 kcal mol⁻¹ gives an employed value of 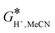= −260.58 kcal mol⁻¹. The conformational space for each species considered was manually sampled, the number of conformations was optimized, and then the most thermodynamically stable ones were selected for the report. A more negative value of the 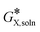implied the more stable species. Optimized structures are visualized using GaussView.²⁸

Conclusions

The mechanism of the thermal reaction of thienyl- and phenyl-o-divinylbenzenes (9–14) under acidic conditions and the formation of the products were explained in detail using quantum chemical calculations at the SMD/M06-2X/6-311+G(2df,2pd)//SMD/M06-2X/6-31G(d,p) level and confirmed experimentally. The calculations showed that the protonation of the double bond of o-divinylbenzenes 9–12 and the formation of a carbocation intermediate as a result of 1,5-ring closure allows the formation of the indane (9-indane–12-indane) and indene (15–18) products. It was found that the most favorable position of protonation in derivatives 9–12 coincides with the position at the vinyl double bond required for 1,5-ring closure, allowing the reaction to proceed. The reactivity of compounds 9 and 10 was found to be the result of manipulating the protonation position in their unsubstituted, non-reactive precursor (5) by introducing suitable substituents at specific positions on the heterocyclic moiety that redirected the favorable protonation and allowed 1,5-ring closure. Compounds 13 and 14 yielded no thermal reaction products, and only a mixture of the original isomers was isolated. When considering the most favorable proton entry position in these compounds, it was found that this position does not coincide with the position required for 1,5-ring closure, preventing the formation of cyclization products. In summary, the reactivity/non-reactivity of the studied compound is closely related to the correspondence between the thermodynamically preferred protonation site and the site required for 1,5-ring closure. If the preferred protonation site matches with the site required for cyclization, the reaction proceeds; otherwise, the derivatives appear to be non-reactive. By blocking a specific position with a suitable substituent in non-reactive precursors, it is possible to prevent protonation at the undesired position and redirect it to the position that allows the appropriate reaction. These results provide valuable information for predicting the outcome of thermal reactions using computational methods and open a new avenue for future research.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

Conceptualization, D. V. and I. D.; methodology, V. L. and M. Z.; software, I. D.; validation, D. V. and I. D.; formal analysis, J. L. C. and V. L.; investigation, V. L. and M. Z.; resources, D. V. and I. D.; data curation, V. L., J. L. C., D. V. and I. D.; writing – original draft preparation, D. V. and I. D.; writing – review and editing, D. V. and I. D.; visualization, V. L. and I. D.; supervision, D. V. and I. D.; project administration, D. V.; funding acquisition, D. V. and I. D. All authors have read and agreed to the published version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was funded by a short-term scientific grant from the University of Zagreb under the title “Synthesis and biological activity of new heteropolycyclic systems” (121195). The above support was gratefully acknowledged. The authors would like to thank the Zagreb University Computing Centre (SRCE) for generously granting computational resources on the supercomputer Supek.

References

1. B.-E. Oded, Y. Diskin-Posner, V. Marks, H. Kornweitz and F. Grynszpan, Eur. J. Org. Chem., 2023, 26, e202300697,  DOI:10.1002/ejoc.202300697.
2. H. Li, M. Mansoori Kermani, A. Ottochian, O. Crescenzi, B. G. Janesko, D. G. Truhlar, G. Scalmani, M. J. Frisch, I. Ciofini and C. Adamo, J. Am. Chem. Soc., 2024, 146(10), 6721–6732,  DOI:10.1021/jacs.3c12713.
3. M. A. Chiacchio and L. Legnani, Int. J. Mol. Sci., 2024, 25, 1298,  DOI:10.3390/ijms25021298.
4. D. C. Young, Computational Chemistry: A Practical Guide for Applying Techniques to Real-World Problems, A John Wiley & Sons, Inc., New Jersey, 1998, pp. 1–145,  DOI:10.1002/0471220655.
5. O. Amiria and A. Bazgir, Phys. Chem. Chem. Phys., 2024, 26, 24431–24437,  10.1039/D4CP02458C.
6. H. Al-Mahayni, X. Wang, J.-P. Harvey, G. S. Patience and A. Seifitokaldani, Can. J. Chem. Eng., 2021, 99, 1885–1911,  DOI:10.1002/cjce.24127.
7. M. Nakajima, Y. Adachi and T. Nemoto, Nat. Commun., 2022, 13, 152,  DOI:10.1038/s41467-021-27546-4.
8. D. Peláez, J. F. Arenas, J. C. Otero and J. Soto, J. Chem. Phys., 2006, 125, 164311,  DOI:10.1063/1.2360259.
9. J. Soto, D. Peláez and M. Algarra, J. Chem. Phys., 2023, 158, 204301,  DOI:10.1063/5.0147631.
10. E. G. Lewars, Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics, Springer Science+Business Media B.V., 2011, vol. 2, pp. 585–653,  DOI:10.1007/978-90-481-3862-3.
11. X. Ma, J. Phys.: Conf. Ser., 2022, 2386, 012005,  DOI:10.1088/1742-6596/2386/1/012005.
12. B. Kirste, Chem. Sci. J., 2016, 7, 127,  DOI:10.4172/2150-3494.1000127.
13. G.-J. Cheng, X. Zhang, L. W. Chung, L. Xu and Y.-D. Wu, J. Am. Chem. Soc., 2015, 137, 1706–1725,  DOI:10.1021/ja5112749.
14. D. J. Tantillo, Applied theoretical organic chemistry, World Scientific Publishing Europe Ltd., 2018, pp. 1–78,  DOI:10.1142/q0119.
15. V. Lovrinčević, D. Vuk, I. Škorić and I. Despotović, New J. Chem., 2023, 47, 17937–17950,  10.1039/d3nj02245e.
16. D. Vuk, Ž. Marinić, K. Molčanov, B. Kojić-Prodić and M. Šindler-Kulyk, Croat. Chem. Acta, 2012, 85(4), 425–434,  DOI:10.5562/cca2120.
17. D. Vuk, Ž. Marinić, K. Molčanov, B. Kojić-Prodić and M. Šindler-Kulyk, Tetrahedron, 2012, 68, 6873–6880,  DOI:10.1016/j.tet.2012.06.019.
18. Z. Zhao, H. Yan, Y. Zhou, W. Xue, L. Gu and S. Zhang, Org. Lett., 2025, 27, 1030–1035,  DOI:10.1021/acs.orglett.4c04632.
19. D. Zhao, X. Wang, J. Huang, T. Yu, E. Hao, S. Ni and K. Sun, Chin. J. Chem., 2024, 42, 2049–2055,  DOI:10.1002/cjoc.202400158.
20. D. L. Comins and M. O. Killpack, J. Org. Chem., 1987, 52, 104–109,  DOI:10.1021/jo00377a019.
21. W. H. Laarhoven, Th. J. H. M. Cuppen and R. J. F. Nivard, Tetrahedron, 1970, 26, 1069–1083,  DOI:10.1016/S0040-4020(01)98783-6.
22. P. Dallemagne, L. P. Khanh, A. Alsaïdi, O. Renault, I. Varlet, V. Collot, R. Bureau and S. Raul, Bioorg. Med. Chem., 2002, 10, 2185–2191,  DOI:10.1016/S0968-0896(02)00070-6.
23. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
24. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241,  DOI:10.1007/s00214-007-0310-x.
25. P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222,  DOI:10.1007/BF00533485.
26. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396,  DOI:10.1021/jp810292n.
27. W. R. Fawcett, Langmuir, 2008, 24, 9868–9875,  DOI:10.1021/la7038976.
28. R. Dennington, T. A. Keith and J. M. Millam, GaussView, Version 5.0.9, Semichem Inc., Shawnee Mission, KS, 2009.

---

Footnotes

† Electronic supplementary information (ESI) available: Supporting information file 1. Additional figures and tables and Cartesian coordinates with selected energy values file format: PDF. See DOI: https://doi.org/10.1039/d5re00052a

‡ Present name and address: Department of Reaction Engineering and Catalysis, University of Zagreb Faculty of Chemical Engineering and Technology, Marulićev trg 19, 10 000 Zagreb, Croatia.

---